Exploring the Phase-Locking Mechanisms Yielding Delayed and Anticipated Synchronization in Neuronal Circuits

1. Introduction

Brain rhythms have been extensively studied and related to plenty of neurocognitive tasks in the last decades (Buzsáki, 2006). According to the communication through coherence hypothesis (Fries, 2005), neuronal oscillation locked at the appropriate phase may facilitate information transmission between brain regions. Despite the fact that the phase relations are associated to synaptic delays between distant regions, non-linear ingredients as inhibition and external noise acting locally can also control the phase relation between coupled areas. When the oscillations of certain area A influence and lock those of another area B, it is expected that the phase between A and B (defined as ϕ_B − ϕ_A) be positive [a regime we refer to as delayed synchronization (DS)]. However, a counterintuitive phase relation was observed between cortical regions in primates (Brovelli et al., 2004; Salazar et al., 2012). Under certain circumstances, a directional influence between two cortical areas is accompanied by a negative time delay (i.e., by a negative phase difference). This phenomenon has been explained by the concept of anticipated synchronization (AS) (Voss, 2000; Matias et al., 2014).

As proposed by Voss, two identical autonomous dynamical systems unidirectionally coupled in a sender-receiver configuration can exhibit anticipated synchronization if the receiver is subject to a delayed negative self-feedback:

$\begin{array}{lll}\stackrel{\bullet }{\text{S}}& =& \text{f}(\text{S}(t)),\\ \stackrel{\bullet }{\text{R}}& =& \text{f}(\text{R}(t))+K\left[\text{S}(t)-\text{R}(t-t_d)\right],& (1)\end{array}$

where f(S) is a vector function that describes the autonomous dynamical system, K is the coupling matrix and the delayed term R(t − t_d) is the self-feedback (Voss, 2000). The solution R(t) = S(t + t_d) characterizes the regime of anticipated synchronization and has been verified in a variety of theoretical (Voss, 2000, 2001a,b, 2016, 2018; Masoller and Zanette, 2001; Hernández-García et al., 2002; Ciszak et al., 2003; Kostur et al., 2005; Sausedo-Solorio and Pisarchik, 2014) and experimental (Sivaprakasam et al., 2001; Tang and Liu, 2003; Ciszak et al., 2009; Stepp and Turvey, 2017) studies.

The AS regime has been reported in systems without the explicit delay term. For example, for a specific parameter mismatch between the sender and the receiver system that gives a first-order approximation to the delayed coupling (Corron et al., 2005). AS has also been reported in a chain consisting of a sender and two receivers with switching parameters (Pyragienè and Pyragas, 2015), between two Hodgkin-Huxley neurons with different depolarization parameters (Simonov et al., 2014) and in the presence of an inhibitory loop mediated by an interneuron with a free-running frequency greater than the others (Matias et al., 2017). It has also been shown that AS may appear between two neuron models directly coupled provided that the mean frequency of the free receiver is greater than the mean frequency of the sender with (Hayashi et al., 2016) and without the explicit time-delay (Pyragienè and Pyragas, 2013; Dima et al., 2018). AS has been verified in a system in which the delayed feedback has been replaced by a simple, low-order all-pass filter (Pyragiene and Pyragas, 2017). More recently, a novel theoretical viewpoint based on the mathematical object called canard, has been used to explain anticipation in excitable systems (Ersös et al., 2019)

In neuronal rhythms the relative phase between two coupled regions is an important characteristic of the dynamics since it can modulate the information flow of an unexpected stimuli (Barardi et al., 2014). Here we investigate the mechanisms underlying the transition from positive to negative phase locking (or equivalently the transition between the DS and AS regimes) on multiple scales. For synchronized systems, it is equivalent to define the phase relation or the time delay between peaks of activity. We simulate three different motifs of unidirectionally coupled systems in which the negative delayed feedback of Equation (1) is replaced by a synaptic inhibitory loop. We extend previous results for three coupled neurons (Matias et al., 2011) and cortical-like populations (Matias et al., 2014), showing that the AS-DS transition can be mediated not only by the inhibitory synaptic conductance but also by the external stimulus at the receiver. We also show that a neural mass model, known to exhibit zero-lag synchronization (Gollo et al., 2014), can operate in the anticipated synchronization regime and the AS-DS transition can be mediated by the stimuli acting on the receiver as well by an inhibitory loop. Moreover, we show that when the sender and receiver are uncoupled the inhibitory loop and an external current acting at the receiver system change its internal dynamics which is reflected in its free running frequency. More important, we found that the phase difference between the sender and the receiver decreases when the free running frequency of the receiver increases. Therefore, we propose that for an excitation/inhibition balance and biologically plausible parameters a faster internal dynamics of the receiver as compared to the emitter is the mechanism underlying AS. We also suggest that the DS-AS transition studied here could be mediated by any parameter that turns the internal dynamics of the free-receiver faster (or equivalently the free-running frequency of the sender slower) and could also account for delay compensation in cortical systems.

2. Materials and Methods

2.1. Microcircuit

The model for the 3-neurons motif is the one proposed by Matias et al. (2011). Neurons are described by the Hodgkin-Huxley model (Hodgkin and Huxley, 1952) composed by the currents I_Na, I_K and I_L:

$\begin{array}{llll}{C}_m\frac{dV}{dt}& =& I_{Na}+I_K+I_L+I_{ext}+I_{syn},& (2)\end{array}$

where C_m = 9πμF is the membrane capacitance of a 30 × 30 × π μm² equipotential patch of membrane, I_ext is the external constant current that sets the neuron excitability and I_syn is the pre-synaptic current.

The ion channels follows the Hodgkin-Huxley formalism: dx/dt = ϕ[α_x(V)(1 − x) − β_x(V)x], being ϕ = 1 the temperature factor. The sodium current $I_{Na}=g_{Na}{m}^{3}h(V_{Na}-V)$ has a maximal conductance g_Na = 1080π mS, and rate constants ${\alpha }_m(V)=0.1(25-V)/(e^{0.1(25-V)}-1)$, ${\beta }_m(V)=4e^{-V/18}$, ${\alpha }_h(V)=0.07e^{-V/20}$ and ${\beta }_h(V)=1/(e^{0.1(30-V)}+1)$. The delayed-rectifier potassium current $I_K=g_k{n}^4(V_K-V)$ has a maximal conductance g_K = 324π mS and rate constants ${\alpha }_n(V)=0.01(10-V)/(e^{0.1(10-V)}-1)$ and ${\beta }_n(V)=0.125e^{-V/80}$. The leakage current I_L = g_L(V_L − V) has a maximal conductance g_L = 2.7π mS. The reversal potentials are V_Na = 115 mV, V_K = −12 mV and V_L = 10.6 mV. In all the expressions above, V is measured in mV.

The synaptic current I_syn = g_synr(V_syn − V) comprises the gating variable r following dr/dt = α[T](1 − r) − βr, where α and β are rate constants and $\left[T\right](V_{pre})=T_{max}/(1+e^{(V_p-V_{pre})/K_p})$ is the neurotransmitter concentration in the synaptic cleft. In this model AMPA (A) and GABA_A (G) are the excitatory and inhibitory synapses, respectively. The parameters concerning the synapses are: α_A = 1.1 (mM⁻¹ms⁻¹), β_A = 0.19 (ms⁻¹), α_G = 5.0 (mM⁻¹ms⁻¹), β_G = 0.30 (ms⁻¹), T_max = 1 mM⁻¹, K_p = 5 mV, V_p = 62 mV, V_syn,AMPA = 60 mV and V_syn,GABA = −20 mV. The three neurons are: sender, receiver, and interneuron. The sender projects excitatory synapses onto the receiver. The receiver projects excitatory and receives inhibitory synapses from the interneuron (see Figure 1). We kept g_A = 10.0 nS, $I_{ext}^S=280.0$ pA and $I_{ext}^{Inter}=280.0$ pA fixed throughout all the simulations. The free parameters of this model are g_G and $I_{ext}^R$. When $g_G^R$ was varied, $I_{ext}^R=280$ pA was kept fixed, whereas when $I_{ext}^R$ was varied, $g_G^R=20.0$ nS was kept fixed.

FIGURE 1

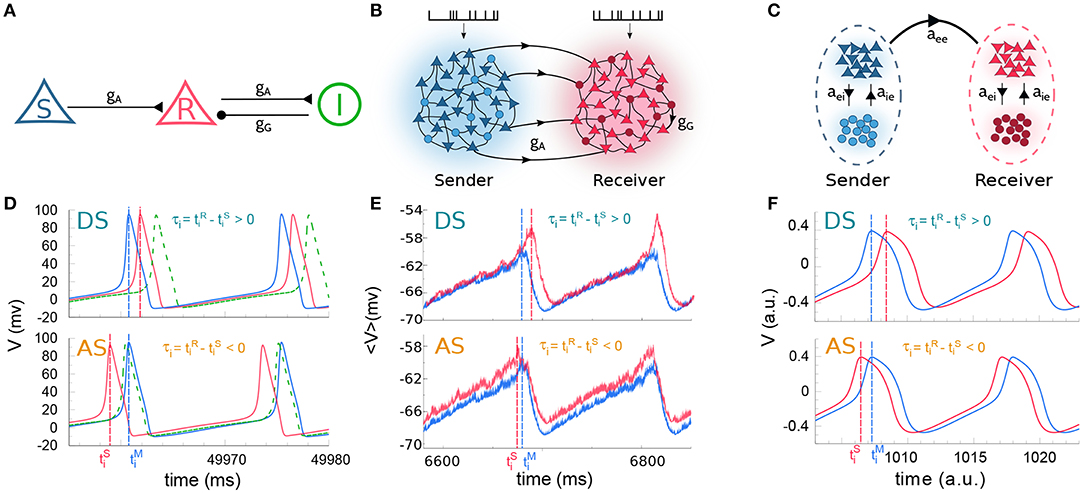
Figure 1. Cortical motif circuits. Schematic representation of the models: (A) 3-neuron motif, (B) two cortical populations, and (C) two neural masses. (D) Membrane potential of three neurons in a regime of delayed-synchronization (DS, top) and anticipated-synchronization (AS, bottom). (E,F) Average membrane potential in a regime of DS (top) and AS (bottom), for populations and neural masses, respectively. For the sake of clarity, the data in (D–F) correspond to simulations where the external parameter was varied. The parameters used were: (D) g_G = 20.0 nS with ${\text{I}}_{ext}^R=280$ pA (DS) and ${\text{I}}_{ext}^R=320$ pA (AS); (E) g_G = 8.0 nS with ${\lambda }_{Ext}^R=2.8$ kHz (DS) and ${\lambda }_{Ext}^R=3.0$ kHz (AS); (F) g_G = 1.4 with ${\text{I}}_{ext}^R=0.1$ (DS) and ${\text{I}}_{ext}^R=0.75$ (AS). For (A–C) excitatory and inhibitory neurons are represented by triangle and circle, respectively. Also, the colors used in (D–F), respectively, stand for the same colors as in (A–C).

2.2. Neuronal Populations

For two cortical populations we follow the ideas proposed by Matias et al. (2014). Each population, sender (S) and receiver (R), is composed of excitatory (80%) and inhibitory (20%) neurons, whose dynamics is described by the Izhikevich model (Izhikevich, 2003):

$\begin{array}{llll}\frac{dv}{dt}& =& 0.04v^2+5v+140-u+{\displaystyle \sum }{I}_{syn},& (3)\end{array}$

$\begin{array}{llll}\frac{du}{dt}& =& a(bv-u),& (4)\end{array}$

where v and u stands for the membrane potential of the neuron and the membrane recovery variable (activation of K⁺ and inactivation of Na⁺ ionic currents), respectively. a, b, c and d are dimensionless parameters that account for the firing patterns heterogeneity which are randomly distributed accordingly to the neuron's nature. For excitatory neurons a = 0.02, b = 0.20, c = −65 + 15σ² and d = 8 − 6σ², whereas for inhibitory neurons a = 0.02 + 0.08σ, b = 0.25 − 0.05σ, c = −65.0 and d = 2.0. σ ∈ (0, 1) is a random variable. If a spike occurs, i.e., v ⩾ −30mV, v is reset to c and u to u + d.

The synaptic transmissions are mediated by excitatory AMPA (A) and inhibitory GABA_A (G). The pre-synaptic current is described as I_syn = −g_synr(v − V_syn), where V_A = 0 mV and V_G = −65 mV. g_syn is the maximal conductance, g_A for excitatory and g_G for inhibitory synapses. r is the gating variable and follows a first-order kinetic dynamics: ${\tau }_{syn}dr/dt=-r+D\sum _j\delta (t-t_j)$, where τ_A = 5.26 ms, τ_G = 5.60 ms and the summation over j stands for the neighbor's pre-synaptic spikes at the previous time steps {t_j}. D is taken, without loss of generality, equal to 0.05.

The populations S and R are composed of 500 neurons each, among which 80% are pyramidal cells and 20% inhibitory interneurons. In the S population, each neuron receives 50 randomly chosen synapses from other neurons with excitatory conductances $g_A^S=0.5$ nS and inhibitory conductances $g_G^S=4$ nS, which remained fixed throughout the simulations. In the R population, each neuron receives 10 inhibitory synapses ($g_G^{R,I}=4$ nS for inhibitory neurons and $g_G^R$ for excitatory neurons) and 40 excitatory synapses ($g_A^R=0.5$ nS). For both populations, no autapses are allowed. The connectivity between S and R populations is such that all neurons within the R population receive 20 randomly chosen excitatory synapses from the S population ($g_A^{SR}=0.5$ nS, unless otherwise specified). Also, all neurons, within the S and R populations, are subject to an independent noisy spike train described by a Poisson distribution with rate λ. The input mimics excitatory synapses from neurons that are not included in the populations, with a maximal conductance g_A = 0.5 nS. Without loss of generality, we assume for the S population λ^S = 2.4 kHz. So, the free parameters for this model are $g_G^R$ and ${\lambda }_{ext}^R$. When $g_G^R$ was varied, ${\lambda }_{ext}^R=2.4$ kHz was kept fixed, whereas when ${\lambda }_{ext}^R$ was varied, $g_G^R=8.0$ nS was kept fixed.

2.3. Neural Mass Models

The large-scale circuit model is the one used in Gollo et al. (2014). Briefly, the neural mass model (NMM) is composed by three state variables: V is the mean membrane potential of pyramidal neurons; Z, the mean membrane potential for interneurons; and W is the average number of open potassium ion channels. Here we made use of two ensembles i = S, R, namely Sender and Receiver. The equations for the dynamics are given by:

$\begin{array}{l}\frac{d{V}^i(t)}{dt}=-\{g_{Ca}+(1.0-C_{ji})r_{NMDA}{a}_{ee}{Q}_V^i(t)\\ +C_{ji}{r}_{NMDA}{a}_{ee}<Q_V^j(t-\tau )>\}{m}_{Ca}(V^i(t)-V_{Ca})\\ -g_K{W}^i(t)(V^i(t)-V_K)-g_L(V^i(t)-V_L)\\ -\{g_{Na}{m}_{Na}+a_{ee}(1.-C_{ji})Q_V^i(t)\\ +C_{ji}{a}_{ee}<Q_V^j(t-\tau )>\}(V^i(t)-V_{Na})\\ -a_{ie}{Z}^i(t)Q_Z^i+a_{ne}{I}_{ext}^E,& (5)\end{array}$

$\begin{array}{llll}\frac{d{Z}^i(t)}{dt}& =& b(a_{ni}{I}_{ext}^I+a_{ei}{V}^i(t)Q_V^i(t)),& (6)\end{array}$

$\begin{array}{llll}\frac{d{W}^i(t)}{dt}& =& \frac{\varphi \left\{m_K-W^i(t)\right\}}{{\tau }_W},& (7)\end{array}$

$\begin{array}{ll}{m}_{ion}=0.5[1+\tanh \left(\frac{V^i(t)-T_{ion}}{{\delta }_{ion}}\right)],& (8)\end{array}$

$\begin{array}{ll}{Q}_V^i(t)=0.5Q_{Vmax}[1+\tanh \left(\frac{V^i(t)-V_T}{{\delta }_V}\right)],& (9)\end{array}$

$\begin{array}{ll}{Q}_Z^i(t)=0.5Q_{Zmax}[1+\tanh \left(\frac{Z^i(t)-Z_T}{{\delta }_Z}\right)],& (10)\end{array}$

where m_ion and $Q_{V,Z}^i$ are the fraction of open channels and neuronal firing rates, respectively.

The parameters are: g_Ca = 1.1, g_K = 2, g_L = 0.5, g_Na = 6.7, r_NMDA = 0.25, ϕ = 0.7, τ_W = 1.0, b = 0.1, T_K = 0, T_Ca = −0.01, T_Na = 0.3, δ_K = 0.3, δ_Na = 0.15, δ_Ca = 0.15, V_Ca = 1, V_K = −0.7, V_L = −0.5, V_Na = 0.53, V_T = Z_T = 0, Q_Vmax = Z_Vmax = 0, δ_V = δ_Z = 0.65, a_ei = 2, a_ee = 0.4, a_ne = 1, a_ni = 0.4 and $I_{ext}^I=0.02$ (here the upper index stands for the inhibitory sub-population in both sender and receiver groups). All quantities are dimensionless. In the sender, the maximal conductance from interneurons to pyramidal neurons as well as the external current in the excitatory neurons are kept constant, $a_{ie}^S=2.4$ and $I_{ext}^S=0.20$, respectively. Thus, $a_{ie}^R$ and $I_{ext}^R$ are the free parameters of this model. The coupling (C_ji) between the two neural masses are: C_RS = 0 and C_SR = 0.4, thus guaranteeing an unidirectional master-slave configuration between S and R. When $a_{ie}^R$ was varied $I_{ext}^R=0.3$ was kept fixed, whereas when $I_{ext}^R$ was varied $a_{ie}^R=1.4$ was kept fixed.

2.4. Numerical Methods and Data Analysis

The model for 3-neurons-motif was implemented in a C code and simulated using a forth-order Runge-Kutta method with a time step of 5 × 10⁻³ ms. The equations for the neuronal populations and neural masses were implemented in a C++ code and simulated using the Euler method, with a time step of 5 × 10⁻² ms for neuronal populations and of 10⁻³ (arbitrary units) for neural masses. To compute the mean response of the membrane potential in NMMs we averaged over 10 realizations of the initial conditions while for the populations we averaged over 10 realizations of the external noise, network connectivity and neuron parameters.

The population membrane potential was estimated from the average value of the individual cell's membrane potential (a variable comparable to the local field potential (LFP) recorded in experiments). In order to smooth the noisy signal of the membrane potential we used a Butterworth low-pass filter of fourth order and cutoff frequency of 5 rad/s. From the filtered signal we and extract the peak at times t_i. We then calculate the time delay in each cycle as ${\tau }_i=t_i^R-t_i^S$ (see Figure 1E). Also, the main frequency (ω) of the neuronal population was obtained detecting the peak of the power spectrum computed via the Fast-Fourier Transform (FFT). For the 3-neurons-motif and also for NMMs, we compute the period in each cycle as the difference between consecutive peaks at times t_i, i.e., $T_i^{*}=t_{i+1}^{*}-t_i^{*}$ (^* = R,S). The time delay is estimated as in the case of neuronal populations.

3. Results

We investigated the phase locking characteristics, or equivalently in this case the synchronization characteristics, of a unidirectionally coupled system A → B. Our main analysis assumes that the two dynamical nodes A and B are phase locked such that computing the phase difference is equivalent to compute the time difference between peaks. For this reason, from now on we talk about synchronization instead of phase locking. In a delayed synchronization condition, the time difference between the spikes in A and B is positive (A leads B), i.e., the pulse in B occurs after the pulse in A. In the less intuitive case of anticipated synchronization, the pulse in B precedes that in A, yielding a negative time difference.

3.1. The DS-AS Transition Can be Mediated by the External Input at the Receiver

In this section we analyze how an input in the receiver side can induce a transition from DS to AS (or vice versa) for the three systems under study.

3.1.1. 3-Neuron Motif

We start by studying the spiking dynamics of a circuit composed of 3 Hodgkin-Huxley cells coupled by chemical synaptic connections as in Matias et al. (2011) (for a schematic representation of the network architecture see Figure 1A and the Methods section for more details). The sender (S) neuron excites the receiver (R) neuron which also participates in an inhibitory loop mediated by an interneuron. For the simplest situation in which g_G = 20 nS and all cells receive the same external current $I_{ext}^S=I_{ext}^R=I_{ext}^{Inter}=280$ pA, the neurons synchronize in the expected DS regime which exhibits the expected pre-post spike order. The neuronal time series show that the R neuron fires right after the S neuron (top panels of Figure 1D).

For an external constant current, after a transient time and within a synchronized state, the spike time difference converges to a constant value τ = τ_i that is independent of the initial conditions. By definition, DS is characterized by a positive τ (or phase difference) and AS by a negative τ (or phase difference). As we increase the inhibitory conductance g_G, the spike time difference τ decreases, eventually changing sign and reaching negative values (see Matias et al., 2011). When this happens, the S and R neurons fire in a post-pre order (see bottom panel of Figure 1D for g_G = 20 nS and $I_{ext}^R=320$ pA) characteristic of the AS regime. A similar effect can be obtained by increasing the external current at the receiver $I_{ext}^R$, without changing the value of the conductance g_G, as discussed below.

The dependence of τ with g_G has been previously studied in Matias et al. (2011) for a large region of parameter space. The transition from DS to AS is continuous and smooth, and τ is a function of g_G (see Figure 2A). Here we extend these findings, showing that a similar transition from DS to AS can be mediated by a different mechanism, namely increasing the external current of the R neuron. Starting from a DS regime in which $I_{ext}^S=I_{ext}^R$ and g_G = 20 nS, the spiking time difference τ decreases as we increase $I_{ext}^R$ (see Figure 2D).

FIGURE 2

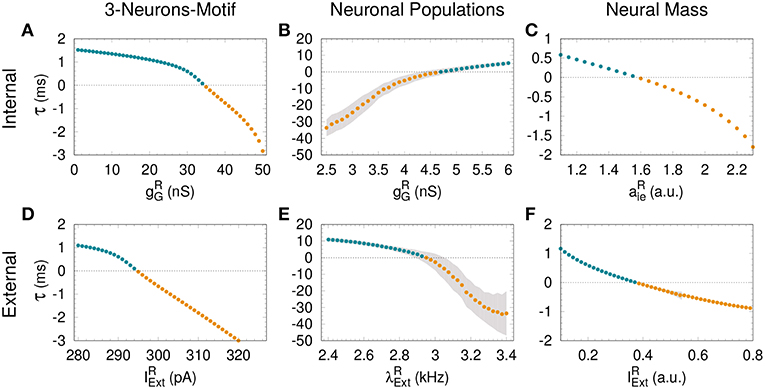
Figure 2. Assessing anticipated and delayed synchronization in cortical motifs. For all the models—3-neurons-motif (left), neuronal populations (middle) and neural masses (right)—a transition from delayed synchronization (DS, τ > 0, cyan dots) to anticipated synchronization (AS, τ < 0, yellow dots) is possible increasing the inhibition in the receiver (A–C); or increasing the external stimulus (D–F). Gray shadow represents the standard deviation over 10 runs (see Methods). For the parameters used here see Methods.

3.1.2. Neuronal Populations

Similar patterns of out-of-phase synchronization have been reported for two unidirectionally coupled cortical-like populations composed of hundreds of neurons connected by chemical synapses (see Matias et al., 2014, Figure 1B and Methods for more details). Each population is composed by excitatory and inhibitory neurons, each of them receiving an independent Poisson input with rate λ, which accounts for excitatory synapses from neurons that are not included in the population. By construction, both Sender (S) and receiver (R) populations have inhibitory loops within the populations. Depending on the synaptic conductances and the external Poisson current, the mean activity of all neurons in each population may exhibit an oscillatory component. Moreover, the activity of the S and R populations can synchronize with a specific phase difference or equivalently time difference. As an example, it can be seen in the top panel of Figure 1E that if the neurons from both populations receive a noisy spike train with distribution rate ${\lambda }_{ext}^S=2.4$ kHz and ${\lambda }_{ext}^R=2.8$ kHz and the inhibitory synaptic conductance are $g_G^S=4.0$ nS and $g_G^R=8.0$ nS, the system operates in a DS regime. The peak of the mean activity 〈V〉 of the S population occurs before the peak of the R population. For the populations the spike time difference in each cycle i defined as ${\tau }_i=t_i^R-t_i^S$, where $t_i^S$ is the peak of the mean activity of all neurons in S at the i−th cycle. Due to the noise, we can also define a spike time difference τ as the mean of τ_i averaged over many cycles. If we increase the external Poisson input at the R population, τ decreases and the system reaches an AS regime (see the bottom panel of Figure 1E for ${\lambda }_{ext}^R=3.0$ kHz). The transition from DS to AS is continuous and smooth (see Figure 2E). To our knowledge, this is the first time that the DS-AS transition mediated by the level of noise in the receiver system is reported. Conversely, the dependence of τ with the inhibitory conductance has been previously reported in Matias et al. (2014) (see Figure 2B).

3.1.3. Neural Mass Models

To further investigate the robustness of the relationship between the local parameters of the receiver system and the existence of anticipated synchronization we also studied the case of two unidirectionally coupled neural mass models, which represents a reduced model of spontaneous cortical dynamics. The neural mass model used here accounts for the neuronal population dynamics and uses three non-linear differential equations per node: one equation for the excitatory subpopulation, one for the inhibitory subpopulation and one for the number of open potassium channels. By its own definition the model has an inhibitory loop mediated by an effective conductance a_ei from excitatory to inhibitory neurons and a_ie from inhibitory to excitatory neurons (see Figure 1C). We find, as in previous cases, that two neural masses unidirectionally connected may synchronize and the inhibitory conductance a_ie as well as the external current $I_{ext}^R$ at the receiver node can control the phase-locking difference between them (see Figure 1F). The transition from DS to AS via zero-lag can be obtained by increasing a_ie or $I_{ext}^R$ (see Figures 2C,F).

3.2. The Frequency of the Free-Running Receiver Serves as a Mechanism Underlying the Synchronization Transition

Based on previous work on anticipated synchronization in the framework of Equation (1) (Pyragienè and Pyragas, 2013; Hayashi et al., 2016; Dima et al., 2018), we studied the effect that an inhibitory connection and the external current plays in determining the frequency of the receiver system when the sender and the receiver are uncoupled (the receiver free-running frequency ω_R). In fact, we find that both the inhibitory conductance and the external stimuli modify the receiver internal dynamics. More important, we find a correlation between the transition from DS to AS regime and the increase of the receiver free running frequency ω_R, and consequently in ω_R − ω_S since ω_S is fixed. We find that the DS-AS transition can be mediated by a change in the receiver free running frequency in multiple scales and by two different parameters (see Figure 4). Therefore, we propose that a faster free-running frequency of the receiver is the mechanism yielding anticipation. Similarly, it is also possible to obtain AS by keeping the Receiver intact and slowing-down the Sender free-running frequency.

An increasing external stimuli increases the frequency of the uncoupled receiver for the three systems (see Figures 3D–F). On the contrary, an increasing inhibitory conductance increases the receiver frequency for the 3-neuron motif and the neural mass model but decreases the free-running frequency in the case of neuronal populations (compare Figures 3A,C with Figure 3B). Despite the fact that more inhibition is typically associated to less activity, it is well-established that resonant neurons, as Hodgkin Huxley model, can exhibit inhibition-induced spiking (Izhikevich, 2003). For neuronal populations and the neural mass model, the transition from DS to AS occurs roughly when the receiver pulses faster than the sender, whether it is due to the internal (Figures 4B,C) or the external factor (Figures 4E,F). Nevertheless, this effect cannot be observed for the 3-neuron motif (Figures 4A,D), when the system is uncoupled; the Receiver always pulses at the same frequency or faster than the Sender (Figures 3A–D). This is due to the fact that, unlike other motifs, the Sender neuron is not subjected to any kind of inhibition. This means that in the uncoupled configuration, in the absence of inhibition at the receiver and same external current both neurons are identical and consequently ω_R = ω_S.

FIGURE 3

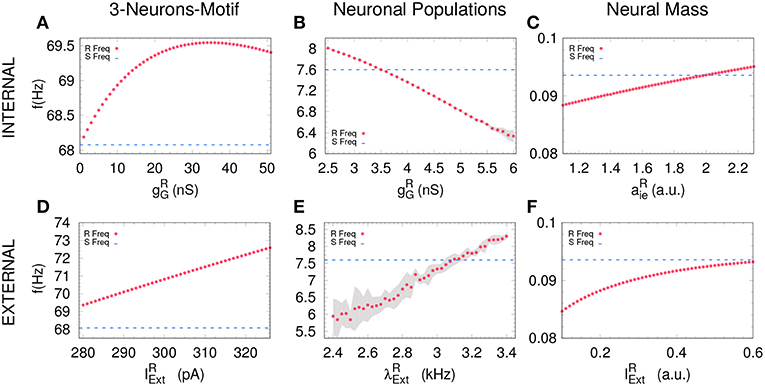
Figure 3. Receiver free-running frequency. Assessing the free-running frequency of the receiver when uncoupled from the sender for all the models. (A–C) show how the receiver's frequency changes when varying the internal parameter while (D–F) when changing an external parameter. Blue dashed line represents the sender's natural frequency and magenta dots represents the receiver's frequency. Gray shadow represents the standard deviation over 10 runs (see Methods). For the parameters used here see Methods.

FIGURE 4

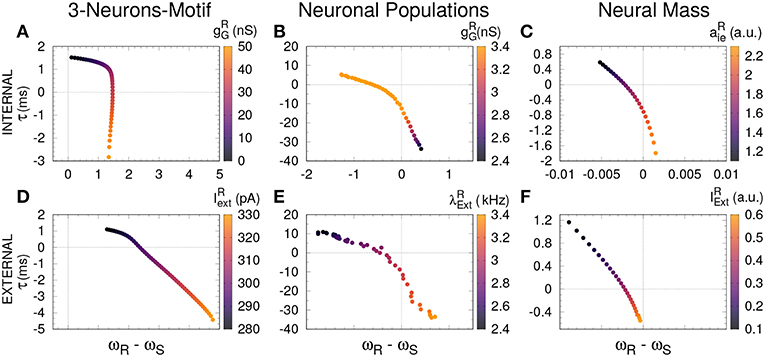
Figure 4. Delayed and anticipated synchronization as a function of the free-running frequency. For all the cases, τ (y-axis) was computed in a coupled system, while the frequency difference (x-axis) was computed for an uncoupled system; the parameters used in both cases are specified by the color code. (A–C) Internal parameter vs. frequency differences and (D–F) external parameter vs. frequency differences, for 3-neurons-motif, neuronal populations, and neural masses, respectively. Horizontal and vertical dashed lines represent zero−lag synchronization (coupled system) and a perfect match between sender and receiver free-running frequencies, respectively. For the parameters used here see Methods.

4. Discussion

In this paper we have studied the effects that a change in the inhibitory conductance or an increase in the external forcing play in the transition from delayed to anticipated synchronization in neuronal circuits. Our study covers three cases of unidirectionally coupled systems: two Hodgkin-Huxley (HH) neurons where the receiver neuron is coupled to an inhibitory interneuron, two populations and two neural mass (NM) models. The results obtained for the HH neurons and the neuron populations confirmed that, when changing the inhibitory conductance in the receiver side, the systems can undergo a delayed to anticipated synchronization transition (Matias et al., 2011, 2014). Similar results were obtained when analyzing two coupled neural mass (NM) models. Interestingly, we found a second mechanism that yields similar results. If we fix the inhibitory conductance in all cases but change the external input (external current for the HH and NM models or the Poisson rate in the populations) the system can also undergo a DS to AS transition.

To unveil if the two mechanisms are independent or not, we studied how the pulsating frequency of an isolated system (a pair of excitatory-inhibitory neurons, a single population containing excitatory and inhibitory neurons or a NM model) changes when changing the inhibitory conductance or the external forcing. We found for the excitatory-inhibitory pair and the NM model that an increase in the inhibitory conductance indeed increases the pulsating frequency (see Figures 3A–C), as happens when we increase the external current. However, for the parameters we have used for the populations, an opposite behavior is observed: an increase in the inhibitory conductance decreases the oscillating frequency of the population. These results suggest that the two mechanisms might be independent although a more exhaustive analysis is necessary. Nevertheless, we propose that the unifying mechanism that promotes the transition between DS and AS in the sender-receiver motif is indeed an increase of the internal dynamics of the receiver system. This was observed at the three scales that we examined. This result is in agreement with previous studies of AS in a theoretical framework with the explicit time-delay in Equation (1) (Hayashi et al., 2016) and in simplified neural models without the explicit time-delay (Pyragienè and Pyragas, 2013, 2015; Dima et al., 2018).

Previous studies have shown that a biologically plausible mechanism for anticipation of pre-synaptic inputs is a combination of short-term synaptic depression (STD) and intrinsic spike-frequency adaptation (SFA) (Puccini et al., 2006, 2007). In the presence of both STD and SFA the post-synaptic system approximately computes the derivative a pre-synaptic stimuli which allows it to anticipate temporally incoming synaptic inputs. Their findings quantitatively agree with experimental results on anticipatory responses to moving stimuli in the primary visual cortex (Jancke et al., 2004; Puccini et al., 2007). We propose that the DS-AS transition studied here could be mediated by any parameter that turns the internal dynamics of the free-receiver faster and could also account for delay compensation in cortical systems. Specially the DS-AS transition could explain commonly reported short latency in visual systems (Orban et al., 1985; Nowak et al., 1995; Kerzel and Gegenfurtner, 2003; Jancke et al., 2004; Puccini et al., 2007; Stepp and Turvey, 2010, 2017; Martinez et al., 2014). Therefore, our results open new possibilities to further experimental investigation of anticipatory dynamics in neuronal systems.

Data Availability

The raw data supporting the conclusions of this manuscript will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

LD, FM, PC, MC, and CM designed the research and wrote the article. LD, AdS, and AA performed the simulations. LD performed the data analysis.

Funding

We thank CAPES (grant PVE 88881.068077/2014-01) for financial support. MC received financial support from CNPq (grants 301744/2018-1 and 425329/2018-6) and FAPESP Center for Neuromathematics (grant 2013/07699-0, Sao Paulo Research Foundation). PC received financial support from FACEPE (APQ 0826-1.05/15). MC, PC, and AdS received support from CAPES PROEX program 534/2018 (grant 23038.003382/2018-39). FM was supported by CNPq (grant 432429/2016-6) and CAPES (grant 88881.120309/2016-01). CM acknowledge the Spanish State Research Agency, through the Severo Ochoa and María de Maeztu Program for Centers and Units of Excellence in R&D (MDM-2017-0711). MC and PC acknowledge support from FACEPE Grant No. APQ-0642-1.05/18.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Barardi, A., Sancristóbal, B., and Garcia-Ojalvo, J. (2014). Phase-coherence transitions and communication in the gamma range between delay-coupled neuronal populations. PLoS Comput. Biol. 10:e1003723. doi: 10.1371/journal.pcbi.1003723

PubMed Abstract | CrossRef Full Text | Google Scholar

Brovelli, A., Ding, M., Ledberg, A., Chen, Y., Nakamura, R., and Bressler, S. L. (2004). Beta oscillations in a large-scale sensorimotor cortical network: Directional influences revealed by granger causality. Proc. Natl. Acad. Sci. U.S.A. 101, 9849–9854. doi: 10.1073/pnas.0308538101

PubMed Abstract | CrossRef Full Text | Google Scholar

Buzsáki, G. (2006). Rhythms of the Brain (New York, NY: Oxford University Press).

Google Scholar

Ciszak, M., Calvo, O., Masoller, C., Mirasso, C. R., and Toral, R. (2003). Anticipating the response of excitable systems driven by random forcing. Phys. Rev. Lett. 90:204102. doi: 10.1103/PhysRevLett.90.204102

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciszak, M., Mirasso, C. R., Toral, R., and Calvo, O. (2009). Predict-prevent control method for perturbed excitable systems. Phys. Rev. E 79:046203. doi: 10.1103/PhysRevE.79.046203

PubMed Abstract | CrossRef Full Text | Google Scholar

Corron, N. J., Blakely, J. N., and Pethel, S. D. (2005). Lag and anticipating synchronization without time-delay coupling. Chaos 15:023110. doi: 10.1063/1.1898597

PubMed Abstract | CrossRef Full Text | Google Scholar

Dima, G. C., Copelli, M., and Mindlin, G. B. (2018). Anticipated synchronization and zero-lag phases in population neural models. Int. J. Bifur. Chaos 28:1830025. doi: 10.1142/S0218127418300252

CrossRef Full Text | Google Scholar

Fries, P. (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cognit. Sci. 9, 474–480. doi: 10.1016/j.tics.2005.08.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Gollo, L. L., Mirasso, C., Sporns, O., and Breakspear, M. (2014). Mechanisms of zero-lag synchronization in cortical motifs. PLoS Comput. Biol. 10, 1–17. doi: 10.1371/journal.pcbi.1003548

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayashi, Y., Nasuto, S. J., and Eberle, H. (2016). Renormalized time scale for anticipating and lagging synchronization. Phys. Rev. E 93:052229. doi: 10.1103/PhysRevE.93.052229

PubMed Abstract | CrossRef Full Text | Google Scholar

Hernández-García, E., Masoller, C., and Mirasso, C. (2002). Anticipating the dynamics of chaotic maps. Phys. Lett. A 295, 39–43. doi: 10.1016/S0375-9601(02)00147-0

CrossRef Full Text | Google Scholar

Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Neurophysiol. 117, 500–544. doi: 10.1113/jphysiol.1952.sp004764

PubMed Abstract | CrossRef Full Text | Google Scholar

Izhikevich, E. M. (2003). Simple model of spiking neurons. IEEE Trans. Neural Netw. 14, 1569–1572. doi: 10.1109/TNN.2003.820440

PubMed Abstract | CrossRef Full Text | Google Scholar

Jancke, D., Erlhagen, W., Schöner, G., and Dinse, H. R. (2004). Shorter latencies for motion trajectories than for flashes in population responses of cat primary visual cortex. J. Physiol. 556, 971–982. doi: 10.1113/jphysiol.2003.058941

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerzel, D., and Gegenfurtner, K. R. (2003). Neuronal processing delays are compensated in the sensorimotor branch of the visual system. Curr. Biol. 13, 1975–1978. doi: 10.1016/j.cub.2003.10.054

PubMed Abstract | CrossRef Full Text | Google Scholar

Köksal Ersös, E., Desroches, M., and Mirasso, C. R. S. (2019). Anticipation via canards in excitable systems. Chaos 29, 01311-1–01311-18. doi: 10.1063/1.5050018

CrossRef Full Text | Google Scholar

Kostur, M., Hänggi, P., Talkner, P., and Mateos, J. L. (2005). Anticipated synchronization in coupled inertial ratchets with time-delayed feedback: a numerical study. Phys. Rev. E 72:036210. doi: 10.1103/PhysRevE.72.036210

PubMed Abstract | CrossRef Full Text | Google Scholar

Martinez, L. M., Molano-Mazón, M., Wang, X., Sommer, F. T., and Hirsch, J. A. (2014). Statistical wiring of thalamic receptive fields optimizes spatial sampling of the retinal image. Neuron 81, 943–956. doi: 10.1016/j.neuron.2013.12.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Masoller, C., and Zanette, D. H. (2001). Anticipated synchronization in coupled chaotic maps with delays. Phys. A 300, 359–366. doi: 10.1016/S0378-4371(01)00362-4

CrossRef Full Text | Google Scholar

Matias, F. S., Carelli, P. V., Mirasso, C. R., and Copelli, M. (2011). Anticipated synchronization in a biologically plausible model of neuronal motifs. Phys. Rev. E 84:021922. doi: 10.1103/PhysRevE.84.021922

PubMed Abstract | CrossRef Full Text | Google Scholar

Matias, F. S., Carelli, P. V., Mirasso, C. R., and Copelli, M. (2017). Anticipated synchronization in neuronal circuits unveiled by a phase-response-curve analysis. Phys. Rev. E 95:052410. doi: 10.1103/PhysRevE.95.052410

PubMed Abstract | CrossRef Full Text | Google Scholar

Matias, F. S., Gollo, L. L., Carelli, P. V., Copelli, M., and Mirasso, C. R. (2014). Modeling positive Granger causality and negative phase lag between cortical areas. Neuroimage 99:411. doi: 10.1016/j.neuroimage.2014.05.063

PubMed Abstract | CrossRef Full Text | Google Scholar

Nowak, L. G., Munk, M. H., Girard, P., and Bullier, J. (1995). Visual latencies in areas v1 and v2 of the macaque monkey. Vis. Neurosci. 12, 371–384. doi: 10.1017/S095252380000804X

PubMed Abstract | CrossRef Full Text | Google Scholar

Orban, G. A., Hoffmann, K. P., and Duysens, J. (1985). Velocity selectivity in the cat visual system. I. Responses of lgn cells to moving bar stimuli: a comparison with cortical areas 17 and 18. J. Neurophysiol. 54, 1026–1049. doi: 10.1152/jn.1985.54.4.1026

PubMed Abstract | CrossRef Full Text | Google Scholar

Puccini, G. D., Sanchez-Vives, M. V., and Compte, A. (2006). Selective detection of abrupt input changes by integration of spike-frequency adaptation and synaptic depression in a computational network model. J. Physiol. 100, 1–15. doi: 10.1016/j.jphysparis.2006.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Puccini, G. D., Sanchez-Vives, M. V., and Compte, A. (2007). Integrated mechanisms of anticipation and rate-of-change computations in cortical circuits. PLoS Comput. Biol. 3:e82. doi: 10.1371/journal.pcbi.0030082

PubMed Abstract | CrossRef Full Text | Google Scholar

Pyragienè, T., and Pyragas, K. (2013). Anticipating spike synchronization in nonidentical chaotic neurons. Nonlinear Dyn. 74, 297–306. doi: 10.1007/s11071-013-0968-7

CrossRef Full Text | Google Scholar

Pyragienè, T., and Pyragas, K. (2015). Anticipating chaotic synchronization via act-and-wait coupling. Nonlinear Dyn. 79, 1901–1910. doi: 10.1007/s11071-014-1782-6

CrossRef Full Text | Google Scholar

Pyragiene, T., and Pyragas, K. (2017). Anticipatory synchronization via low-dimensional filters. Phys. Lett. A 381, 1893–1898. doi: 10.1016/j.physleta.2017.04.005

CrossRef Full Text | Google Scholar

Salazar, R. F., Dotson, N. M., Bressler, S. L., and Gray, C. M. (2012). Content-specific fronto-parietal synchronization during visual working memory. Science 338, 1097–1100. doi: 10.1126/science.1224000

PubMed Abstract | CrossRef Full Text | Google Scholar

Sausedo-Solorio, J., and Pisarchik, A. (2014). Synchronization of map-based neurons with memory and synaptic delay. Phys. Lett. A 378, 2108–2112. doi: 10.1016/j.physleta.2014.05.003

CrossRef Full Text | Google Scholar

Simonov, A. Y., Gordleeva, S. Y., Pisarchik, A., and Kazantsev, V. (2014). Synchronization with an arbitrary phase shift in a pair of synaptically coupled neural oscillators. JETP Lett. 98, 632–637. doi: 10.1134/S0021364013230136

CrossRef Full Text | Google Scholar

Sivaprakasam, S., Shahverdiev, E. M., Spencer, P. S., and Shore, K. A. (2001). Experimental demonstration of anticipating synchronization in chaotic semiconductor lasers with optical feedback. Phys. Rev. Lett. 87:154101. doi: 10.1103/PhysRevLett.87.154101

PubMed Abstract | CrossRef Full Text | Google Scholar

Stepp, N., and Turvey, M. T. (2010). On strong anticipation. Cognit. Syst. Res. 11, 148–164. doi: 10.1016/j.cogsys.2009.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Stepp, N., and Turvey, M. T. (2017). Anticipation in manual tracking with multiple delays. J. Exp. Psychol. Hum. Percept. Perform. 43:914. doi: 10.1037/xhp0000393

PubMed Abstract | CrossRef Full Text | Google Scholar

Tang, S., and Liu, J. M. (2003). Experimental verification of anticipated and retarded synchronization in chaotic semiconductor lasers. Phys. Rev. Lett. 90:194101. doi: 10.1103/PhysRevLett.90.194101

PubMed Abstract | CrossRef Full Text | Google Scholar

Voss, H. U. (2000). Anticipating chaotic synchronization. Phys. Rev. E 61:5115. doi: 10.1103/PhysRevE.61.5115

PubMed Abstract | CrossRef Full Text | Google Scholar

Voss, H. U. (2001a). Dynamic long-term anticipation of chaotic states. Phys. Rev. Lett. 87:014102. doi: 10.1103/PhysRevLett.87.014102

PubMed Abstract | CrossRef Full Text | Google Scholar

Voss, H. U. (2001b). Erratum: anticipating chaotic synchronization [phys. rev. e 61, 5115 (2000)]. Phys. Rev. E 64:039904. doi: 10.1103/PhysRevE.64.039904

CrossRef Full Text | Google Scholar

Voss, H. U. (2016). Signal prediction by anticipatory relaxation dynamics. Phys. Rev. E 93:030201. doi: 10.1103/PhysRevE.93.030201

PubMed Abstract | CrossRef Full Text | Google Scholar

Voss, H. U. (2018). A delayed-feedback filter with negative group delay. Chaos Interdiscip. J. Nonlinear Sci. 28:113113. doi: 10.1063/1.5052497

PubMed Abstract | CrossRef Full Text | Google Scholar