Department of Biological Sciences, Howard Hughes Medical Institute, Columbia University, New York, NY, USA
Laser microscopy has generally poor temporal resolution, caused by the serial scanning of each pixel. This is a significant problem for imaging or optically manipulating neural circuits, since neuronal activity is fast. To help surmount this limitation, we have developed a “scanless” microscope that does not contain mechanically moving parts. This microscope uses a diffractive spatial light modulator (SLM) to shape an incoming two-photon laser beam into any arbitrary light pattern. This allows the simultaneous imaging or photostimulation of different regions of a sample with three-dimensional precision. To demonstrate the usefulness of this microscope, we perform two-photon uncaging of glutamate to activate dendritic spines and cortical neurons in brain slices. We also use it to carry out fast (60 Hz) two-photon calcium imaging of action potentials in neuronal populations. Thus, SLM microscopy appears to be a powerful tool for imaging and optically manipulating neurons and neuronal circuits. Moreover, the use of SLMs expands the flexibility of laser microscopy, as it can substitute traditional simple fixed lenses with any calculated lens function.
Laser microscopy has had a major impact in neuroscience. In particular, confocal (Amos and White, 2003
) and two-photon microscopy (Denk et al., 1990
) have enabled systematic high-resolution optical experiments in live samples, including both imaging and photochemical manipulation of neurons or neuronal processes. However, because laser microscopy is typically performed by sequentially scanning a single laser beam across a sample, it is essentially speed-limited. The time required for a microscope to acquire a complete two-dimensional image of a field-of-view (FOV) – a frame – determines the frame-rate of the system, and hence the microscope’s temporal resolution. In laser-scanning microscopes, the frame rate is intrinsically limited by two major factors. The first is the physical response time of the scanners, typically galvanometer mirrors. The second, and more fundamental constraint on the overall speed of the system, is related to the physical processes of imaging. For each point on the sample (corresponding to a pixel, or pixels, on the detector), the integrated illumination must be sufficiently high to be able to “see” the sample (collect enough photons of the signal), while at the same time, the intensity of the illumination must be kept as low as possible to minimize the photodamage generated by the excitation.
The intersection of these two conditions yields an optimal light intensity, which then sets the dwell time – the illumination time required per pixel to yield an image with a high enough signal-to-noise ratio for subsequent analysis. With linear excitation, that is, single photon absorption, the high absorption cross-sections of the chromophores allow for excitation with relatively weak light sources. Essentially all excitation sources have ample power to perform wide-field excitation, and are capable of imaging the whole FOV simultaneously. However, with single photon excitation, photobleaching and photodamage is strong, and strong scattering in the sample reduces the effective penetration depth, lowering the overall resolution and contrast. Confocal detection greatly improves the quality of the image, but at the cost of reducing the overall acquisition frame rate. On the other hand, non-linear imaging methods, such as multi-photon fluorescence or second-harmonic generation (SHG) microscopy, greatly mitigate photo-induced problems, reducing scattering, increasing penetration depth, decreasing photodamage, and supplying inherent optical sectioning. Unfortunately, the temporal resolution is especially restricted in non-linear biological microscopy because efficient wide-field illumination is not practical, since current laser systems do not provide sufficient power to efficiently excite the whole FOV simultaneously. Therefore, most non-linear microscopes employ raster scanning with a single-beam, and thus have low effective frame rates and correspondingly poor temporal resolution (usually hundreds of milliseconds or longer for a full frame). This limits their use in the study of processes with faster kinetics, such as fast neural responses.
One possible solution for increasing the temporal resolution of a raster scanned microscope is to simply increase scanning speed. Some examples of this strategy are microscopes with resonant scanning mirrors (>30 frames per second (fps); Fan et al., 1999
), acousto-optical deflectors (AODs; 30 fps; Kremer et al., 2008
; Ng et al., 2002
; Reddy et al., 2008
; Ryzsa et al., 2007
) or polygon-mirror scanners (Amos and White, 2003
). In fact, even one of the first confocal microscopes, based on polygon mirrors, generated 4000 unidirectional lines per second (White et al., 1987
). There have also been two-photon and other non-linear microscopes that have used similar techniques (Evans et al., 2005
; Kim et al., 1999
; Rajadhyaksha et al., 1999
; Warger et al., 2007
). However, all these strategies still rely on raster scanning, or, in the case of certain AOD implementations, sequential scanning (Reddy et al., 2008
; Ryzsa et al., 2007
). But even with the fastest motions possible, with only a single excitation beam it may not be possible to provide sufficient integrated illumination to achieve reasonable signal-to-noise ratios for fast frame rate imaging. For example, though polygon-mirror scanners can perform extremely fast raster scanning (Kim et al., 1999
) at 40 μs per line, which corresponds to speeds well above video rate (30 fps for non-interlaced define “p” progressive video format), it is still necessary to collect enough photons from each pixel, within the given dwell time, to generate a usable image. The excitation intensity cannot be arbitrarly increased, because high levels cause photodamage and photobleaching. In fact, even if photodamage could be prevented, the excited states of most biologically relevant fluorophores have lifetimes between ∼1 and 10 ns. Therefore, regardless of the excitation power, these fluorophores cannot produce more than a certain number of excitation-emission cycles per unit time. The signal cannot be made stronger with increased power, since it is effectively saturated (Hopt and Neher, 2001
; Koester et al., 1999
). Saturation is a more significant problem for non-linear excitation, because pulsed lasers are needed, with higher peak powers, so the effective duty cycle must be adjusted to correspond with excited state lifetimes (Ji et al., 2008
).
An alternative solution to improve the temporal resolution of laser-scanning, while still collecting more total photons per unit time without saturation, would be to split the excitation beam into multiple beamlets and scan the sample in several different spatial locations simultaneously. Single-beam raster imaging is inefficient for most samples, because usually, only a subset of the FOV actually contains features of interest. As a result, during the scan, much of the time the excitation beam is illuminating areas between points of interest. This “wastes” time, and for non-linear microscopies, more importantly, excitation power that could otherwise be directed toward regions of interest. For multiplexed beam approaches, wide-field detectors (such as cameras, photodiodes arrays or photomultiplier tube arrays) are necessary because they can resolve the spatially multiplexed excited regions simultaneously, while maintaining the high frame rates required record functional optical signals. In microscopes using multiple excitation beamlets, the effective acquisition rate is approximately equal to the original single-beam rate multiplied by the number of beamlets. The multiple beamlet approach has been implemented for linear (single photon) excitation, with spinning-disk confocal microscopy (Petran et al., 1968
). More recently, an improved spinning-disk with micro-lens has been used with rates up to 1000 fps (Tanaami et al., 2002
). The use of a spinning-disk has also been extended to two-photon fluorescence (Bewersdorf et al., 1998
) and SHG (Kobayashi et al., 2002
). A similar concept, based on semitransparent mirror-based beam-splitters and traditional galvanometer scanners, has also been proposed (Nielsen et al., 2001
). Finally, in the limit of many beamlets, one returns back to wide-field excitation. In fact, wide-field phase-modulated non-linear excitation has been suggested as a solution to the scanning problem (Oron et al., 2005
). In this case, although high resolution is achieved in three dimensions, exposure times required to generate a reasonable image are long. In fact, using currently available lasers, these systems are incapable of delivering images with sufficient signal-to-noise ratios with the frame rates required for monitoring fast, transient signals, such as those present in neurons.
In spite of these problems, the use of beamlets for multiplexed imaging still seems to be a natural solution for increasing the speed of imaging. Here, we introduce a different, flexible method of generating multiple beamlets, following the pioneering work of Gabor (1948)
: splitting the beam with a spatial light modulator (SLM). A similar strategy was presented in a recent description of a single photon “holographic” uncaging microscope (Lutz et al., 2008
). Our prototype can be used for non-linear microscopies, such as two-photon excitation uncaging and imaging, and may eventually result in a completely scanless microscope.
Microscope Design
Our SLM microscope consists of a custom microscope system that employs a diffractive SLM to produce any desired spatial profile of excitation light on the image (sample) plane (Figure 1
, see figure legend). We use a model 1080P phase SLM from Holoeye (Berlin, Germany), which has a resolution of 1920 × 1080 pixels, 8-bit phase quantization, and, for visible and near infra red light, is capable of complete 2π phase modulation at each pixel, with a 60-Hz refresh rate. The SLM is able to generate arbitrary patterns because of a fundamental property in optics: that of the optical Fourier transform. For an transparent object placed exactly one focal length in front of a thin lens, the Fourier transform of that object will be formed one focal length behind the lens (Chartier, 2005
). Thus, if the incoming field at focalfront is represented by the complex amplitude Ek, the field at focalback is Fk, where Ek, and Fk are Fourier transform pairs. In our microscope, though the optical path is made more complex by a system of relay lenses, the SLM is essentially located at focalfront and sample plane at focalback. A phase-only SLM acts only on the phase of the field, not the amplitude. Once acted upon by the SLM, the electric field is Ek = A0 exp (i·Φk), where A0 is the original amplitude, and Φk the phase instilled by the SLM. The phase, Φk, is computed such that the desired intensity pattern is produced in the far field (sample plane).
Figure 1. Optical design of SLM microscope. (A) Optical diagram of our system. (B) Photograph of the SLM bix highlighted on panel (A). Red lines illustrates laser excitation pathway. We describe below with some detail the design and logic behind our instrument. The elements of the optical pathway are listed approximately in the functional order of signal propagation. Individual mirrors are not numbered, and unless otherwise noted we used EO3 dialectical mirrors from Thorlabs (Newton, NJ, USA), optimized for near-infrared region (700–1200 nm) and do not introduce noticeable pulse broadening.
- Source of illumination – ultrafast pulsed (modelocked) laser. Chameleon Ultra from Coherent Inc. (Santa Clara, CA, USA).
- Pockels cell (Conoptics model 350-160). It is controlled by a data acquisition board through a high-voltage driver (275 linear amplifier) from Conoptics, Inc. (Danbury, CT, USA).
- Beam sizing/reshaping telescope. It also works as a spatial filter if a pinhole (3b) is placed at the plane of focus of the first lens (3a), and the second lens (3c) re-collimates the beam. We used standard BK7 thin plano-convex lenses from Thorlabs (Newton, NJ, USA) with anti-reflection coating optimized for near-infrared. By choosing different 3b lenses and placing them at the corresponding focal distances from the pinhole it is possible to change the size of the output beam without need for additional realignment. It is convenient to use a lens kit from Thorlabs (such as LSB01-B) to have the freedom to adjust the size of the beam easily. We also found it convenient to mount lenses on FM90 Thorlabs’ flip mounts, to be able to easily re-configure the optical path, changing the type and position of the lens (3b) in this case. Alternatively, low-profile 9891 flip mounts from New Focus (San Jose, CA, USA) are also very convenient and we use them in other parts of the optical path.
- Polarizing half-wave plate (AHWP05M-950 achromatic λ/2 plate, 690–1200 nm from Thorlabs). It is mounted on PRM1 rotational mount (Thorlabs). The functional role of this element is to rotate the plane of polarization to “turn on/off” diffraction of the SLM (our liquid-crystal SLM is fully sensitive to polarization). The SLM works essentially as a passive mirror when the diffraction is “off” and allows regular scan-image using galvanometer scanners (for high-resolution calibration images).
- Periscope mirrors. We use an upright microscope, so it is convenient to bring the light from the plane of the optical table up to the “second floor” – a raised breadboard with other optical elements that have to be in vicinity of the input port of the upright microscope. A shutter (5c) is used to block laser light when we are not scanning of the sample. This “safety” shutter is not absolutely necessary since the Pockels cell or even SLM itself can also block the beam.
- Secondary beam-resizing telescope. It is similar to (3) and implemented using a pair of thin plano-convex lenses. The main function of this telescope is to make the laser beam large enough to fill the aperture of the SLM (0.7″ chip), and therefore use all available pixels as well as spread the power across larger area to avoid any damage to SLM by a high power laser. The telescope is not absolutely required because its function can be fulfilled by (3), so we have it only for convenience.
- Diffractive SLM. We use a reflective 1080P phase SLM from Holoeye (Berlin, Germany). It is important to try to minimize angle of reflection for the SLM to avoid distortions.
- Second SLM telescope. It is also realized as a pair of thin plano-convex lenses. This SLM imaging telescope images the surface of the SLM to the optical plane that is conjugated to the back-aperture of the microscope objective. The same plane is also occupied by galvanometer scanning mirrors (10) that are left from the original Olympus Fluoview system. The first lens 8a is LA1906-B F = 500 mm (1″ diameter) from Thorlabs. We use a larger (2″ diameter) second lens 8b (LA1417-B from Thorlabs, F = 150 mm) to accommodate the full range of scanning angles necessary for the full field-of-view. The mirror (also 2″ in diameter) is placed in between just in order to save space. The chosen ratio of the telescope (∼1:3) shrinks the beam and increases deflection angles to match the range of angles “expected” by the scan lens of the microscope imaging port.
- Zero-order beam block. It allows only the diffracted (first-order diffraction) beam to reach the sample. We use a small piece of metal foil glued to a thin glass cover slide. The element is mounted onto a FM90 Thorlabs flip mount for quick reconfiguration between SLM and traditional one-beam lightpaths in which the diffraction is “turned off” by a (4) half-wave plate (for high-resolution standard imaging).
- Galvanometer scanning mirrors (Olympus FV200 system). We use standard Olympus Fluoview software for slow, high-resolution imaging, which is used calibration purposes (locating objects of interest, such as spines or neuronal cell bodies).
- Scan (or pupil transfer) lens. It is a standard part of Olympus Fluoview system (FVX-PL-IBX50/T). In combination with the microscope tube lens (12b), it forms a telescope and images the plane of galvanometers (and therefore also the plane of the SLM chip) onto the back-aperture of microscope objective.
- Olympus BX50WI upright microscope, without significant modifications. We use (12a) a dichroic mirror (Chroma, Rockingham, VT, USA) to reflect excitation (NIR) light toward the sample and transmit emitted visible fluorescence back from the sample to the detector.
- Short-pass (IR-block) filter or a combination of an IR-block and band-pass filter (Chroma). They are used to reject scattered excitation light, and detect the signal in chosen spectral region. The trinocular tube (12b) (Olympus FV3-LVTWI) allows switching between two imaging ports: for multi-beam SLM imaging with the camera (13c) or single-beam whole-field of view scanning imaging using a PMT (13d). We use a Hamamatsu Orca C9100-12 cooled EM CCD camera (13c) as well as Hamamatsu H7422-40P cooled GaAs PMTs (13d).
- Signal amplifier PE 5113 preamplifier (Signal Recovery AMETEK Advanced Measurement Technology, Wokingham, UK). In combination with a current-to-voltage converter (a passive 5 KΩm load resistor in the simplest case), it converts signals into convenient range of voltages for digitizing.
- Data acquisition system. We use standard Olympus Fluoview scanning software where the signal from the PMT is digitized by the standard FV 200 data acquisition module. In special cases, we also use generic data-acquisition cards (such as PCI-6052E from National Instruments, Austin, TX, USA) and custom software.
- Alternatively, optical signal can be detected in a transmissive configuration. We have a separate PMT installed after the microscope condenser, and this detector is used to detect either second channel of two-photon fluorescence (different color) or second-harmonic generation (SHG) signals (depending on used chromophores and corresponding band-pass filters in front of this detector). It is possible to install a camera in this pathway for multi-beam imaging configuration of transmissive SHG signal.
- Computer. It receives images from the camera and/or digitizes PMT signals. The PC is also used to control excitation intensity via Pockels cell. We are actually use three PCs with their software is synchronized by TTL triggers.
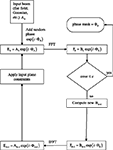
The phase mask can be computed using software from Holoeye, as well as from custom-developed software based on standard iterative–adaptive algorithms (Fienup and Wackerman, 1986
). A flowchart of the algorithm is shown in Figure 2
. The algorithm starts with the known intensity distribution of the laser, and then adds a random phase (speeds convergence), generating Ek = A0 exp (i·Φk). It then computes the FFT, Fk = Bk exp (i·Θk) and compares the computed image to the desired image. If the error exceeds a threshold, the amplitude, but not the phase, is modified to better match the desired image. An inverse transform is performed, and constraints applied, such as phase quantization, giving rise to a new input field, and the cycle begins again. We have deliberately been non-specific about the comparison process and modification, because we have yet to find one that we feel is optimal. More complete information on the variety of algorithms can be found in Kuznetsova (1988) and Bauschke et al. (2002)
.
Figure 2. SLM phase mask formation. Block diagram of the phase mask algorithm, described in more detail in section “Materials and Methods”.
In our microscope, collimated light from our laser passes through an optional Pockels cell, which regulates total power, and after beam reshaping and resizing, hits the reflective phase-only SLM. A system of lenses relays the image of the SLM surface to the back-aperture of the main microscope objective. The galvanometer scanners are optional, and can be used to shift the whole illumination pattern if desired. They are also useful for acquiring traditional single-beam raster scanned images, which we used for calibration purposes and for localization of regions that be targeted using the SLM.
Some small fraction (<25%) of the incoming light remains undiffracted – this is the “zero-order” beam. We currently use an “on-center” configuration wherein the non-diffracted beam is present in the FOV, and we employ a small beam-stop to remove it. There is no real practical consequence to blocking this central beam; it is blocked in a plane conjugate to the sample, and as such, it only impacts a very small area on the sample plane, and does not disturb the phase pattern used to generate the target image. However, as the illumination pattern, and overall position of the beamlets on the sample is under our control, it is easy to place this dark zone on an uninteresting area of the sample. Furthermore, if desired, we can use an “off-center” configuration, in which the desired target pattern is angularly displaced from the zero-order beam, which is then directed outside the FOV, so that no area of the sample plane is affected.
Imaging was done at depths of 50–150 μm, using a variety of water-immersion objectives from Olympus: a 60×, 0.9 NA objective was used to acquire images for spine uncaging experiments, and a 20×, 0.95 NA objective was used for multi-spot imaging and stimulation of neurons. We also used a 40×, 0.8 NA objective for calibration purposes. For standard, non-SLM imaging, fluorescence was detected with a top-mounted Hamamatsu H7422-P40 PMT connected to a PE 5113 preamplifier (Signal Recovery AMETEK Advanced Measurement Technology, Wokingham, UK), whose output was connected to the Fluoview system. CCD-based images were collected using a Hamamatsu C9100-12 camera.
Slice Preparation and Electrophysiology
Animal handling and experimentation was done according to NIH and local IACUUC guidelines. Mice were either quickly decapitated or anaesthetized with Ketamine–Xylazine (50 and 10 mg/kg–1) and 300 μm thick coronal slices of visual cortex were prepared from P14-16 C57BL/6 mice. Slices were made using a Leica VT1000-S vibratome with a cutting solution containing (in mM): 27 NaHCO3, 1.5 NaH2PO4, 222 Sucrose, 2.6 KCl, 3 MgSO4, 0.5 CaCl2. Slices were incubated at 32°C for 30 min in ACSF (pH 7.4), saturated with 95% O2 and 5% CO2, containing (in mM): 126 NaCl, 3 KCl, 2 MgSO4, 2 CaCl2, 1.1 NaH2PO4, 26 NaHCO3, and 10 dextrose. Slices were then kept at room temperature for at least 30 min before transferring them to the recording chamber. The recording chamber was also bathed in ACSF different temperatures, as explained in the last paragraph of this section.
For AM-loading, slices were deposited onto the bottom of a small Petri dish (35 mm × 10 mm) filled with 2 ml of ACSF, ventilated with 95%O2/5%CO2 and placed in a slide warmer at 37°C (Fisher Scientific, Waltham, MA, USA). An aliquot of Fura-2AM or mag-Indo-1AM (Molecular Probes, Eugene, OR, USA) was prepared in 10 μl DMSO and 2 μl of Pluronic F-127 (Molecular Probes). For combined loading we used 50 μg Fura-2AM and 5 μg mag-Indo-1AM. The dye aliquot was then placed on top of the slice in the Petri dish and slices were incubated in the dark at 35–37°C for up to 60 min. Slices were then kept at room temperature for at least 30 min before transferring them to the recording chamber.
For spine uncaging experiments layer 5 pyramidal neurons were filled with 200 μM Alexa 488 (Molecular Probes, Eugene, OR, USA) through the recording pipette. Pipette solution contained (in mM): 135 K-methylsulfate, 10 KCl, 5 NaCl, 10 HEPES, 2.5 Mg-ATP, 0.3 GTP, pH 7.3. Dendritic spines were selected for imaging and uncaging after cells were fully loaded with dye (15–30 min after break in).
For circuit uncaging experiments, whole-cell electrodes (5–7 MΩ) were filled with an intracellular solution (pH 7.25) containing (in mM): 135 K-methylsulfate, 10 HEPES, 8 NaCl, 7 phosphocreatine, 2 Mg-ATP, 0.3 Na-GTP, and, in some cases, with 0.1 Alexa 594. For calcium imaging experiments, we filled neurons with an intracellular solution mix of 50 μM Fura-2 pentapotassium salt and 10 μM Alexa 594. This “red” Alexa dye was added to help localize the cell targeted by the patch pipette using the corresponding emission filter set.
Fast SLM imaging experiments were conducted at room temperature (22–25°C), whereas simultaneous spine glutamate uncaging experiments were done at 37°C.
Glutamate Uncaging
4-Methoxy-7-nitroindolinyl-caged L-glutamate (2.5 mM; Tocris Cookson, UK) was bath-applied. Imaging and uncaging were performed at 725 nm. Laser power was controlled by the Pockels cell. Laser pulses were 5 ms with 2-s intervals between pulses. Light was directed toward the sample plane with about 20–30 mW per individual target. For the calibration images (taken in raster mode with galvonometer scanners), 5–8 mW of laser power was used. Voltage deflections due to the glutamate uncaging (uncaging potentials) were recorded from the soma in whole-cell current-clamp mode while maintaining a resting potential of −65 mV using a Multiclamp 700B amplifier (Molecular Devices, Union City, CA, USA). Data were analyzed off-line with Igor (WaveMetrics, Inc., Lake Oswego, OR, USA) and MATLAB (MathWorks, Natick, MA, USA).
Two-photon stimulation of neurons
The same concentration of MNI-glutamate (2.5 mM) and wavelength (725 nm excitation) used for spine stimulation was used to activate neurons. Neurons were filled with 100 μM Alexa594 and scanned at 800 nm for target selection/detection. Laser pulses were separated by 2 s, ranging in duration from 40 to 150 ms. For uncaging, 260 mW total power was used on sample. Data were analyzed with MATLAB and Axograph X (Axograph Scientific).
Laser Multiplexing with Spatial Light Modulators
Our system was developed from an earlier version of a two-photon microscope, where we employed a diffractive optical element (DOE) to multiplex the laser beam for imaging or uncaging (Nikolenko et al., 2007
). Multi-beam scanning with DOEs increased the speed and signal-to-noise ratio of the imaged samples, but was still limited by many of the problems that plague raster scanning, such as small dwell time for excitation per pixel. To surmount these limitations and make our imaging system more flexible, we performed beam multiplexing with SLMs (Figures 1 and 2
; see Section “Materials and Methods”). While typical DOEs split the beam in a fixed, static pattern, diffractive phase-only SLMs can dynamically adjust the number and location of active beamlets. Essentially, SLMs are computer-controlled, reprogrammable analogues of DOEs, based upon the modulation of the phase of the waveform (Gabor, 1948
; Weiner et al., 1992
). This beam-multiplexing property is similar to the more traditional methods of producing arbitrary two-dimensional illumination patterns, such as digital micromirror devices (DMDs), based on wide-field illumination and use of a physical mask (Wang et al., 2007
). But, as opposed to DMDs, phase-only SLMs generate an image (diffraction pattern) by modulating the phase, and not the amplitude, of the incoming light beam. While the phase-only SLM imprints the incoming beam with the phase pattern that produces the desired spatial profile of the excitation light in the far field, it does so not by removing light, like the DMDs, but by redistributing it. Because the full power of the laser is available, non-linear excitation is possible (e.g., multi-photon absorption or SHG).
Diffractive SLMs thus provide ultimate beam flexibility, by allowing the production of a pattern of any desired shape on the image plane. We explored their use in two-photon microscopy by generating a series of arbitrary laser beam patterns (Figures 3
A,B, left panels), created by computing the phase mask of the original images (Figures 3
A,B, second panels), and projecting them onto the sample plane. To demonstrate effective non-linear excitation we used samples consisting of a fluorescent dye dissolved in an agarose gel. This perhaps represents the worst possible contrast scenario: a thick three-dimensional scattering media, where any point can emit fluorescence, if excited. With linear excitation, such as one-photon fluorescence, the sample will fluoresce along the entire light path, leading to reduced contrast and blurred images. Confocal detection would be necessary to minimize the effect of the strong out-of-focus excitation, and resolve objects. Two-photon excitation, however, with its inherent sectioning, should preserve the spatial resolution of the excitation. In fact, the excitation depth of an SLM microscope should be equivalent to, or better than, a “normal” two-photon microscope, because it is possible to use the SLM to correct for aberrations in the transmitted beam caused by any index mismatches. The generated fluorescence, on the other hand, is subject to scatter, so with multipoint excitation, and an area detector, increased depth will cause increased scatter, and thus will blur the image, reducing contrast and resolution. However, this problem is very minor compared with that of single photon excitation, because in that case, excitation, and hence emission, occur along the entire light path, which then scatters, generating strong background. Empirically, as can be seen in our images, the scattering was relatively small, and the degradation minor, especially in the case of well separated objects. Indeed, using these SLM-projected patterns we were able to image complicated binary and grayscale patterns of excitation, adequately resolving small spatial details in the patterns (Figures 3
A,B, right panels). These two-photon fluorescence images were very well matched to the square (to mimic two-photon excitation) of the image calculated from the phase mask (Figures 3
A,B, third panels). Thus, we concluded that the SLM transform does not significantly degrade the original pattern.
Figure 3. SLM light patterning and depth focusing. Imaging of samples of an agarose gel saturated with Alexa 488 fluorescence indicator for testing the efficiency of two-photon excitation. Images were acquired using 60× 0.9NA objective. Scale 20 μm. (A) A simple Binary bitmap pattern (“COLUMBIA”) was uploaded into the SLM software, and the obtained phase mask is shown in the second panel. Grayscale corresponds to phase shift from 0 to 2π. The resulting two-photon fluorescence image of acquired with microscope CCD camera from the sample (recording chamber) is shown on the right panel. For comparison, the output of the phase mask was also used to calculate the projected pattern, and was squared to better resemble a two-photon process (third panel). Note the excellent correspondence between the calculated pattern and the obtained image. This data also demonstrate that liquid-crystal based diffractive SLM can withstand illumination by a powerful pulsed mode-locked ultrafast laser and be effectively used for structured non-linear illumination. (B) Complex grayscale patterns can be used to program SLM. We used a stylized picture of Santiago Ramón y Cajal, based on a historical photograph. Panels are similar to panel (A). (C) Focusing with an SLM. Our SLM software allows applying additional optical functions on top of the phase mask. In this example we used a lens function to shift the focus of excitation in axial dimension. The panel shows the original image and corresponding phase mask, as well as lens phase function alone and added to original phase mask. −10, −100, +10 and +100 are arbitrary units used by software to indicate correspondingly negative/positive lens and relative optical strength. (D) Two-photon fluorescence image of the test pattern acquired with the CCD camera. The virtual focus plane is moved away in both directions from the original plane using a lens function of corresponding strength. A 40× 0.8 NA objective was used. Scale 50 μm. These data illustrate that SLMs can be used as a “universal scanners” that do not require physically moving parts.
We also exploited the optical flexibility of SLMs to mimic different lens functions or move the excitation beam in three dimensions (Figure 3
C). Indeed, SLM-generated patterns were easily scaled and shifted in X–Y with appropriate phase patterns. Importantly, because the SLM allows one to alter the wavefronts of the incoming light beam, we could also alter the depth of focus of our image, in addition to the X–Y position, without moving any physical part of the microscope (Figure 3
D; Movie 1 in Supplementary material). In principle, SLMs can even allow for the independent focusing of multiple beamlets of light, each at a different depth in Z (Sinclair et al., 2004
). Hence a phase-only SLM could be potentially used to make a novel “scanless” microscope, allowing linear and non-linear excitation of different regions of the sample with three-dimensional resolution.
Two-Photon Activation of Multiple Spines with SLMs
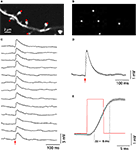
We then explored the use of SLM microscopy in biological samples. Our system was originally designed for spatially restricted two-photon photostimulation of neurons and dendritic compartments, by photoreleasing (uncaging) glutamate. To test this we performed simultaneous stimulation of several dendritic spines by uncaging glutamate near their heads (Figure 4
), an extension of our previous single-spine uncaging experiments (Araya et al., 2006b
, 2007
). Specifically, using whole-cell electrodes we recorded the somatic membrane potential of pyramidal neurons in slices, bathed with MNI-glutamate. We then imaged their basal dendrites and selected arrays of dendritic spines with conventional raster scanning and used those high-resolution images to compute phase masks positioned next to the tips of their heads (Figures 4
A,B). We then simultaneously activated up to five spines with the SLM phase masks, generating reliable uncaging potentials with fast 10–90% risetime (6.5 ± 0.4 ms, n = 15) and decay kinetics (39.3 ± 2.7 ms for 37% decay, n = 15; Figures 4
C–E). These kinetics were similar to those measured in physiological excitatory postsynaptic potentials measured in these same type of neuron (Araya et al., 2006b
). The simultaneous stimulation of multiple individual spines, or dendritic locations, could help explore fundamental problems in dendritic biophysics – such as measuring input summation (Araya et al., 2006a
; Cash and Yuste, 1998
; Losonczy and Magee, 2006
).
Figure 4. SLM glutamate uncaging of dendritic spines. (A) Basal dendrite from a layer 5 pyramidal neuron, loaded with Alexa-488, in a mouse neocortical slice bathed in MNI-glutamate. Red spots indicate sites of simultaneous uncaging. Image acquired with galvanometers raster scanning. (B) First, a bitmap file was generated with the uncaging locations selected in (A); then a Fourier transform of the image was set as the command to the spatial light modulator (SLM) to generate a phase mask and the desired diffraction pattern, in this case five uncaging spots next to spine heads (A). (C) Whole-cell patch-clamp recording from the same cell as (A). Fifteen individual uncaging potentials generated after simultaneously uncaging glutamate next to the spines shown in (A). (D) Average of the uncaging potentials shown in (C). (E) The red trace represents the uncaging laser pulse. The black trace is the average uncaging potential as shown in (D). Light gray in (D) and (E) is ±SEM.
Two-Photon Activation of Neurons with SLMs
Another application of glutamate uncaging of multiple targets is the optical manipulation neural circuits. Using DOEs, we recently developed an optical stimulation technique that provided “quasi-simultaneous” activation of multiple neurons in the FOV (Nikolenko et al., 2007
). We therefore explored the use of SLMs to perform simultaneous photostimulation of multiple neurons (Figure 5
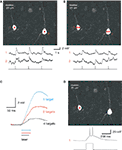
). With whole-cell electrodes, we recorded from pairs of pyramidal neurons in brain slices, bathed with MNI-glutamate. Then, using a diffractive SLM, we generated phase masks, positioning the selected areas of interest over the somata, in order to simultaneously stimulate them with uncaging laser pulses (Figure 5
, red spots). Uncaging in these areas of interest with one or two spots per neuron generated reliable membrane depolarizations (Figures 5
A,B). Presumably as a consequence of the smaller power per spot, increasing the number of targets decreased the amplitude and kinetics of the resulting depolarizations (Figure 5
C). Increasing the duration of the uncaging pulse also increased the magnitude of the depolarization, eventually resulting in action potential generation (Figure 5
D). These results demonstrated the feasibility of SLM microscopy for activating neurons in a circuit.
Figure 5. SLM glutamate uncaging of neurons. (A) Upper panel: Image of two layer 5 pyramidal neurons, recorded from with whole-cell electrodes and filled with 100 μM Alexa 594, during a photostimulation experiment. Each neuron was excited at a single location by 725 nm light to uncage MNI-glutamate. Lower panel: Current clamp recordings (top traces) during the laser uncaging pulses (bottom trace). Note how both neurons were simultaneously depolarized by the uncaging events. (B) Similar experiment to (A), but with two excitation beams focused on each neuron. Note the smaller depolarizations elicited as compared to (A). (C) Increasing beam multiplexing results in smaller and slower cell depolarization. Traces are averages of three to seven individual trials. (D) Suprathreshold two-photon activation of neurons is possible using a diffractive SLM. In this example, a single excitation point on a single neuron elicited multiple action potentials from the resting membrane potential. Bottom trace: laser pulse.
Fast Calcium Imaging of Neuronal Circuits with SLMs
Finally, we explored the potential of SLMs for increasing the imaging speed of two-photon microscopy. We were specifically interested in imaging calcium transients from a population of neurons, a method to optically monitor the action potentials generated by a circuit (Lillis et al., 2008
; Nikolenko et al., 2007
; Smetters et al., 1999
; Yuste, 1994
; Yuste and Katz, 1991
). To detect neuronal activity in a population of cells with SLM-based calcium imaging our strategy was the following: first, use conventional raster scanning to generate an image of the circuit (Figure 6
A) and detect the cell bodies of neurons (Figures 6
B,C). Then, use the centers of mass to generate a phase mask over all detected neurons (Figures 6
D,E), and finally, measure one-dimensional time-lapse functional signals from each cell (Figure 6
F).
Figure 6. SLM multi-beam imaging: theory. Proposed strategy for SLM multi-spot imaging, with arrows marking the experimental workflow. (A) An image of the objects (for example a two-photon fluorescence image of neurons bulk-loaded with a calcium indicator or transgenic neurons labeled with fluorescent proteins) is acquired. (B) Contours of objects of interest are detected (in example, using custom software, as in Cossart et al., 2003)
. (C) Pixel centers of mass of each contour are calculated, and their coordinates (D) are used as a command image uploaded to SLM software. (E) SLM works as a beamsplitter to illuminate all or as subset of objects of interest. A wide-field detector (a CCD camera, or photodiode arrays or multi-anode PMTs), with spatial resolution suitable to resolve individually illuminated objects, is used to record time-lapsed signals from all illuminated spots simultaneously. (F) Optical signals from the objects, acquired simultaneously. If more than one pixel of the detector is allocated to each illuminated spot, the integration step is necessary, in order to extract time-lapsed signals corresponding to different objects. Contours detected during steps (B–C) could be used for this integration.
We performed several successful experiments with this general strategy (Figure 7
). A neocortical slice was first bulk-loaded with a calcium indicator to identify neurons and image action potential activity (Figure 7
A). Fifty neurons were then selected for fast multi-spot imaging and we generated a phase mask targeting their somata (Figure 7
B). These regions of interest were then continuously illuminated by the two-photon laser and a CCD camera was then used to image the fluorescent signals. Simultaneously, one of the neurons was recorded in current clamp using a patch pipette, which was used for injection of current pulses and triggering different number of action potentials. Signals extracted from the CCD pixels that corresponded to patched neurons, and from control neurons, were individually integrated and analyzed, demonstrating reliable correspondence between action potentials and optical signals. Specifically, at camera exposures of 66 ms (15 fps), we measured large downward deflections of fluorescent signal that were synchronized to current-pulse injections and corresponded to different number of action potentials (Figures 7
C,D). The signal-to-noise ratio of these measurements was even adequate to detect single action potentials (Figure 7
D1, left transients). To increase imaging speed, we decreased the number of neurons illuminated simultaneously in order to provide more excitation power per target and still achieve a comparable signal-to-noise ratio to the longer, 66 ms exposures data. With camera exposures of 16 ms (60 fps), we illuminated a smaller subset of 20 neurons and were also able to detect individual action potentials with good signal-to-noise ratio (Figures 7
E,F). At these faster speeds, we did not notice any photobleaching, even after minutes of continuous exposure with >10 mW of excitation power per spot (20× 0.95 NA objective). These results demonstrated the feasibility of two-photon calcium imaging with SLMs.
Figure 7. SLM multi-beam imaging: practice. (A) A neocortical slice (L2/3, area S1, P15 mouse) was bulk-loaded with a Ca indicator (10/1 mix Fura-2AM/mag-Indo-1AM). Panel shows image taken using standard two-photon raster imaging mode (790 nm excitation). Fifty neurons were targeted for imaging using diffractive SLM (red spots). One of the neurons (labeled “1”) was targeted for patch-clamp recording in order to trigger action potentials using current injection. The intracellular solution contained 50 μM Fura-2 pentapotassium salt, a concentration roughly corresponds to intracellular concentration of Fura-2 achieved by bulk loading (Peterlin et al., 2000
). The pipette also contained 10 μM Alexa-594 for localization of patched neuron using a different emission filter. (B) Command image file for SLM software and corresponding phase mask. (C) Image of two-photon fluorescence from multiple locations obtained with the camera. Diffractive SLM splits laser beam in order to continuously illuminate spatially different locations with a static pattern (∼4.4 mW of average excitation power per spot on the sample plane). Red contours were detected using custom software in order to quantify time-lapsed signals from different cells. Notice correspondence between patterns on upper and lower panels. Scale 50 μm. (D) Calcium signals recorded from stimulated cell (D1) corresponding to different number of elicited action potentials (the panel shows nine current pulses that triggered triplets of 1, 2 and 4 action potentials respectively). Even individual spikes can be detected with good signal-to-noise ratio. Neurons 2 and 3 were not stimulated and do not exhibit change in fluorescent signals. Imaging was performed with ∼15 frames/s temporal resolution (66 ms/frame). (E,F) Similar results were obtained with ∼60 frames/s (16 ms/frame), but with higher excitation power per each excitation spot. Seven current pulses were injected, two of them triggered two action potentials, and five triggered individual spikes. No noticeable photobleaching or photodamage was observed over the course of the experiment (several minutes of continuous illumination).
A Scanless SLM Microscope
We introduce here a “scanless” microscope that does not require moving parts in order to deflect light into a dynamic, arbitrary complex, three-dimensional pattern (Figure 3
). This form of beam modulation solves some of the problems of laser-scanning microscopy and therefore it extends its application, particularly for non-linear excitation. In an SLM microscope, the frame rate is limited not by the physical motion of the scanning device, but only by the sampling rate of the detector and the power required to achieve the desired signal-to-noise ratio in the measurement. In addition, SLM microscopy also limits the total photodamage to the sample by exciting only points of interest, with the minimum necessary beam power, and not the space, or biological tissue, between them.
Our microscope, designed for this “structural illumination”, differs from other methods used to illuminate multiple location based on masking unwanted pixels (such as DMDs), because it generates an image by redistributing the excitation light to the regions of interest. The diffractive phase-only SLM can operate directly on the wavefront of the incoming electromagnetic waves and therefore can be considered “an ultimate optic”. The majority of standard optical elements, such as lenses, essentially perform simple wavefront modification, and thus can be mimicked by an SLM, even down to the attenuation, rastering or even focusing of the light (Figures 3
C,D; Movie 1 in Supplementary material). Therefore, one can imagine a microscope with a SLM as its sole optical element, at least in its excitation path, where the SLM could condition light and substitute the multiple lenses and objectives of a traditional microscope. In practice, this approach will be constrained by the spatial and phase resolution of the SLM, the maximal available NA of the virtual SLM lenses or the distance to the sample. Other constraints, such as the finite refresh rate of the SLM, and power limitations caused by power spilling over into higher diffractive orders, make a combination of an SLM and traditional lenses more practical. But even a “mixed” SLM microscope, such as our prototype, offers great advantages and flexibility for biological microscopy. Finally, we used a diffractive SLM as a computer-controlled beamsplitter, the concept of multi-spot imaging is independent of the particular hardware used to create multiple beams. This strategy could be implemented using any optical design that allows efficient splitting the beam into multiple beamlets to illuminate pre-selected regions of interest.
Using SLM Microscopy in Neuroscience
We developed our SLM microscope for the imaging and optical manipulation of neuronal circuits. More specifically, we took advantage of the optical flexibility of SLMs for spatially restricted photochemical control of our biological samples, by photostimulating multiple neuronal compartments or multiple neurons simultaneously (Figures 4 and 5
). These two types of experiments are optical methods of interrogating neuronal biophysics and circuit properties and they are both notably improved by the use of an SLM. Specifically, the activation of several dendritic spines in any arbitrary spatio-temporal pattern appears as an ideal experimental approach with which to explore dendritic integration. Moreover, the near synchronous activation of multiple cells could be an important requirement for the engagement of cortical circuits (Abeles, 1991
) and the ability to simultaneously activate arbitrary groups of neurons has the potential to significantly aid the burgeoning field of circuit neuroscience. Therefore we think it likely that SLM will be useful in circuit neuroscience.
SLM microscopy is not particular to multi-photon stimulation and can be used for one-photon photostimulation without any substantial change in our hardware configuration. But the spatial resolution of photostimulation, particularly in the axial dimension, is better with non-linear excitation. In addition, although we relied on two-photon uncaging of caged neurotransmitters to stimulate neurons up to this point, one could also achieve the direct stimulation of multiple neurons, using the genetically encoded photosensitive systems, such as channelrhodopsin-2 genetically modified neurons (Boyden et al., 2005
; Nagel et al., 2003
), providing that probes with sufficiently high effective two-photon cross-sections are developed.
In addition to multi-spot photostimulation, the diffractive SLM can be used to speed-up imaging (Figures 6 and 7
). The strategy is to simultaneously and continuously illuminate multiple regions of interest, defined by a previously computed SLM phase pattern. Then, a camera, or any other light-gathering device with spatial resolution, can be used to simultaneously measure the emission from these illuminated regions. By splitting the excitation beam efficiently and specifically with an SLM, one directs the individual beamlets precisely to the points of interest. This abolishes the need to scan, because regions of interest are continuously illuminated, and functional signals (fluorescence, or any other imaging modality) can be simultaneously detected using a wide-field detector.
Also, while we have not completely characterized the optical properties of the SLM, such as any added dispersion or potential distortion of the point-spread function (PSF) of the microscope, we can at this point comment empirically on our findings. Because of the exquisite sensitivity of the two-photon excitation signal to the quality of the incoming beam (PSF and temporal profile) we would expect to see large changes in both the sectioning ability and total strength of the signal if either was degraded significantly, and we see neither. In our experiments, the signal, and sectioning power, in images from SLM created patterns was similar to those taken without the SLM, for the same average power. For experiments using significantly shorter laser pulses, dispersion may become a problem.
Relation with Past Work
Phase-modulating holography was first developed as a novel form of microscopy (Gabor, 1948
). Nevertheless, the use of diffractive phase-only SLMs, more sophisticated than amplitude-based SLMs, is relatively novel for microscopy. In the past, diffractive phase-only SLMs had been used within the framework of holographic storage devices (Purvis, 2008
) or three-dimensional displays (Favalora et al., 2005
). Only recently has a holographic form of microscopy been described (Lutz et al., 2008
). This “holographic microscope” was implemented for one-photon excitation and used for uncaging, and is in excellent agreement in theoretical principles and goals with our design.
Microscopes based on phase-only SLMs appear superior to DMD-based devices because DMDs work essentially as amplitude masks. DMDs generate a far field image by removing light from the image, with dark areas formed by deflecting light out of the image. This diminishes the total power available on the sample, while the bright spots are created by simply allowing the incoming beam to be reflected. Although this strategy is adequate for one-photon excitation, DMDs are still impractical for non-linear excitation of a broad range of targets because this requires high local intensities of light, more than what current laser systems can provide. Phase-only SLMs, on the other hand, redistribute light from dark areas onto illuminated areas of the image, thus increasing the power available on the regions of interest for non-linear processes.
Limitations of SLM Microscopy
Our current prototype uses a diffractive SLM based on a liquid-crystal phase-only modulator. One of its drawbacks is the relatively low duty cycle at which the phase mask can be changed (60 Hz in the SLMs used in our microscope). This response is limited by the time required for complete reorientation of the nematic liquid-crystals, used to alter the phase. Other types of controllable beam splitting devices, including better phase-only SLMs could have faster responses. For example, commercially available types of phase-only SLMs have faster response times (hundreds of Hz), although it is usually achieved at the expense of other parameters such as phase modulation (i.e., <2π modulation in each pixel) or lower pixel resolution (i.e., 256 × 256 pixels).
Another drawback of our current liquid-crystal based SLM microscope is its relatively poor total efficiency. The combined throughput in the first diffraction order (the dominant one, used for our experiment) of the SLM and imaging telescope (Figure 1
) is roughly 25% of input power. Some of the losses are caused by mundane sources, such as overfilling the SLM, and reflective losses on the additional optical surfaces, others are more subtle. Though the theoretical efficiency of a spatially quantized and phase quantized SLM is reduced compared to an ideal device (Arrizón and Testorf, 1997
; Dallas, 1971
), these effects should be very small for our SLM. It is more likely that we need additional optimizations in the calculation of the phase mask. Until then, power limitations will continue to be an issue for multiple excitation targets. As a modification of the described imaging approach, in cases where there is insufficient power to excite all points of interest simultaneously, one could use a “quasi-continuous” excitation, whereby the entire set of points of interest is split into several subsets, each of which consists of points that are excited and imaged simultaneously. The number of points in each sub-group could be tailored to guarantee efficient excitation of the targets.
A related concern is the inefficient photorelease of caged glutamate with increased beam multiplexing, which sets a limit on the number of neurons (or spines) that can be activated simultaneously. We anticipate that improvements in photorelease chemistry (Ellis-Davies, 2005
; Zayat et al., 2005
), increases in effective laser power (Ji et al., 2008
) and improved phase patterns for the SLM will help alleviate this issue, allowing simultaneous two-photon activation of user-defined neuronal populations.
Finally, we should mention that although SLM microscopy has the potential for three-dimensional imaging, the focusing lens function that we demonstrate in Figure 3
only focuses the excitation light, and not the emitted light. Therefore, to completely substitute for physically focusing the sample, at this point one would need, not only to focus the excitation light by changing the SLM lens function, but also to move the detector accordingly. Nevertheless, it is possible to imagine strategies in which the same SLM could serve to focus the excitation and emission light path, thus truly creating a focusing microscope without any moving pieces.
Future Developments
Even with the limits of today’s technology, it is clear that scanless SLM imaging, with its ability to address many targets simultaneously, while still retaining all of the advantages of multi-photon excitation – deeper penetration into tissue, and high spatial selectivity – could open opportunities for in vivo and potentially clinical use of non-linear microscopy, especially in case of brain imaging of upper cortical layers, as well as other superficial tissues (skin, muscles, etc). A related possible future use of this technology, with its faster and more effective optical stimulation capabilities, is in the development of brain–machine interfaces (BMI) for prosthesis purposes (Hochberg et al., 2006
), based on stimulation of individual neurons. BMIs are still at very early stage, but they have been proposed as a core technology for the next generation of neuro-prosthesis devices, based on optically triggering neuronal activity in different regions of the brain. This premise is similar to the one currently underlying deep brain stimulation, i.e., that triggering or inhibiting neuronal activity in specific regions of the brain could modify neuronal signal transduction pathways, leading to behavioral changes. In fact, it has already been demonstrated that photostimulation could trigger therapeutically useful behavioral changes (Adamantidis et al., 2007
).
In summary, SLM microscopy can be used effectively for one (Lutz et al., 2008
) and two-photon (this manuscript) excitation, and provides unprecedented flexibility in the spatio-temporal light patterning (Figure 3
). Its demonstrated usefulness for imaging neuronal activity (Figure 7
) and for photochemical manipulation of spines (Figure 4
) and neurons (Figure 5
) presages a wide future applicability for the study of neuronal circuits.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We thank Adam Packer for help with software, members of the laboratory for comments and anonymous reviewers for their suggestions. Supported by the Kavli Institute for Brain Science and the National Eye Institute.
Supplementary movie file can be found online at: http://www.frontiersin.org/neuralcircuits/paper/10.3389/neuro.04/005.2008/.