1
Institute for Nonlinear Science, University of California, La Jolla, San Diego, CA, USA
2
Balaton Limnological Research Institute of the Hungarian Academy of Sciences, Tihany, Hungary
3
Lab Neurodinâmica/Neurobiofisica, Instituto de Fisica de São Carlos, São Carlos, São Paulo, Brasil
4
Department of Neurosciences/Neuroscience Research, Medical University of South Carolina, Charleston, SC, USA
The lobster gastric mill central pattern generator (CPG) is located in the stomatogastric ganglion and consists of 11 neurons whose circuitry is well known. Because all of the neurons are identifiable and accessible, it can serve as a prime experimental model for analyzing how microcircuits generate multiphase oscillatory spatiotemporal patterns. The neurons that comprise the gastric mill CPG consist of one interneuron, five burster neurons and six tonically firing neurons. The single interneuron (Int 1) is shared by the medial tooth subcircuit (containing the AM, DG and GMs) and the lateral teeth subcircuit (LG, MG and LPGs). By surveying cell-to-cell connections and the cooperative dynamics of the neurons we find that the medial subcircuit is essentially a feed forward system of oscillators. The Int 1 neuron entrains the DG and AM cells by delayed excitation and this pair then periodically inhibits the tonically firing GMs causing them to burst. The lateral subcircuit consists of two negative feedback loops of reciprocal inhibition from Int 1 to the LG/MG pair and from the LG/MG to the LPGs. Following a fast inhibition from Int 1, the LG/MG neurons receive a slowly developing excitatory input similar to that which Int 1 puts onto DG/AM. Thus Int 1 plays a key role in synchronizing both subcircuits. This coordinating role is assisted by additional, weaker connections between the two subsets but those are not sufficient to synchronize them in the absence of Int 1. In addition to the experiments, we developed a conductance-based model of a slightly simplified gastric circuit. The mathematical model can reproduce the fundamental rhythm and many of the experimentally induced perturbations. Our findings shed light on the functional role of every cell and synapse in this small circuit providing a detailed understanding of the rhythm generation and pattern formation in the gastric mill network.
Neural circuits display a remarkable capacity to produce complex, temporally structured firing patterns which are modulated both by transient sensory inputs as well as neurohormonal factors acting on longer time scales. Compact motor networks of invertebrates known as central pattern generators (CPG) are prime examples of such circuits, particularly because they provide a unique opportunity to understand the cellular and synaptic mechanisms for the generation of patterned, oscillatory neural activity and its modulation by extrinsic factors. Among the many well-known, mostly invertebrate, motor networks the crustacean stomatogastric ganglion (STG) has been a fascinating subject of research inspiring generations of neurophysiologists as well as computational neuroscientists. Indeed, the STG stands out as a prime example of a compact neural circuit capable of producing oscillatory neural dynamics at multiple time scales and with high flexibility of phasing among the component neural oscillators. Nevertheless, cellular and synaptic mechanisms for the generation of oscillatory activity and the formation of a multi-phasic burst pattern are still not sufficiently understood in this system.
The purpose of this work is to describe the mechanisms by which a small CPG produces a multiphase rhythmic motor pattern. Our experimental subject, the 11 neuron circuit, which drives the striated muscles of the lobster gastric mill, produces a six-phase “fictive” motor pattern in vitro when it receives modulatory input from higher centers (Russell, 1976
). The motor pattern consists of approximately 3 s bursts in six groups of motor neurons at a frequency of about 0.1 Hz (Figures 1
A,B). The basic gastric pattern can be altered by sensory inputs and “descending” commands from other neural centers (Katz and Harris-Warrick, 1989a
; Combes et al., 1999
). Despite the fact that all neurons and their synaptic connections in the CPG have been identified (Mulloney and Selverston, 1974a
,b
; Selverston and Mulloney, 1974
), the basic mechanisms responsible for the integration of oscillatory elements, with strong differences in their intrinsic frequencies, into a coherent signal are not understood. The gastric CPG merits reexamination for several reasons. There has been increased interest in how neural circuits generate rhythmic activity using oscillatory elements with drastic differences in their intrinsic frequencies and also because such activity is needed for controlling sensory processing and cognitive behavior (Buzsáki, 2006
; Gelperin, 2006
). There has, in addition, been a recent resurgence of interest in microcircuits as more easily understood modules of brain function (Grillner and Graybiel, 2004
). Progress in the use of computer modeling has helped to suggest ways in which neural circuits might operate (Grillner, 2003
; Markram, 2006
) and even suggestions of how they may be useful in understanding cortical activity which often has oscillatory behavior associated with it (Yuste et al., 2005
). The gastric circuit is unique in that despite its small size, it produces a rather complex firing pattern. Additionally, manipulations of all of the neurons and synapses involved are possible and the effects of these perturbations can be monitored in the entire network. To the best of our knowledge, there are no neurons that may be part of the gastric CPG lurking in the background so a complete description of how the circuit operates is feasible and can be reaffirmed with computational models.
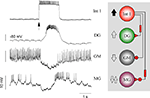
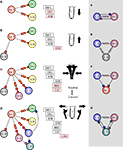
Figure 1. Firing patterns of the gastric mill neurons. (A) Extracellular recordings from peripheral motor nerves in a combined in vitro preparation(with intact neuromodulatory inputs). This “fictive” motor pattern illustrates the complete burst pattern responsible for movements of the three “teeth” in the gastric mill. (B) Simultaneous intracellular recordings of all of the motor neurons except the LPGs but showing the activity of Int 1 in relation to the motoneuron bursts. (C) The synaptic connectivity of the canonical gastric mill neural circuit. Large and small filled circles represent strong and weak inhibitory synapses respectively. Filled triangles represent excitatory synapses. Rectangles indicate delay mechanisms and resistors are electrical connections. Abbreviations of neurons are given in Table 1
.
For any CPG, the mechanisms generating the rhythm (rhythmogenesis), and those involved with the formation of the sequential pattern are the most important to understand. The genesis of the rhythm is generally framed as being due to two possible mechanisms: neurons with pacemaker properties drive the rest of the circuit; or, alternatively, the rhythm is a result of synaptic interactions sometimes termed a network rhythm generator (Getting, 1989
). As we will demonstrate, this bipartite classification tends to oversimplify the actual mechanisms involved which usually involve elements of both.
With regard to the formation of the pattern, the in vitro gastric pattern is generated by highly interconnected motor neurons with only one interneuron present. The rhythm can be altered both in frequency and sequence by sensory feedback from mechano- and chemoreceptors (Katz and Harris-Warrick, 1989b
; Elson et al., 1994
; Combes et al., 1999
; Beenhakker and Nusbaum, 2004
). It can also be significantly reconfigured by neuromodulatory substances released into the STG or by those reaching the STG via the circulatory system (Heinzel, 1988a
). The gastric rhythm is also affected by direct synaptic connections descending from higher centers (Nusbaum and Beenhakker, 2002
). An in vitro combined preparation consists of the STG, the small esophageal ganglion and paired commissural ganglia (CG). This preparation produces a canonical six-phase pattern consistently and for hours at a time allowing long sessions of intracellular recording and stimulation.
Short Summary of the Gastric Circuit
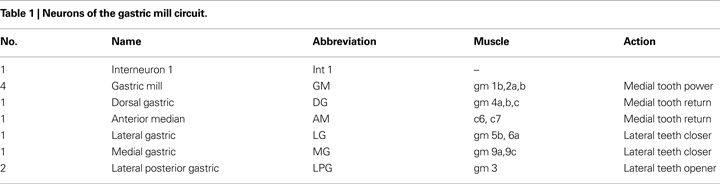
The gastric mill CPG consists of 10 motor neurons and one interneuron all located within the STG (Table 1
). The burst pattern recorded extracellularly is illustrated in Figure 1
A. This is the in vitro activity pattern which is reliably observed when the paired CG are attached to the STG. The pattern has a frequency of ca. 0.1 Hz, with bursts from each motor neuron lasting about 3 s. The connections the STG makes with the CGs are required for a robust gastric rhythm (Russell, 1976
). Simultaneous intracellular recordings of six neurons are shown in Figure 1
B. Intracellular voltage waveforms of many of the neurons are characteristic and often provide visual clues for their identification. The Int 1 emits spikes with greater amplitude than the rest of the cells. Additionally, the AM and DG neurons display a characteristic pyloric modulation (effectively splitting their gastric timed bursts into shorter, pyloric timed sub-bursts). The synaptic connectivity of the gastric network is shown in Figure 1
C. The AM, DG and four GMs, along with the single Int 1 comprise the medial tooth subcircuit and the LG, MG and the two LPGs along with the Int 1 make up the lateral teeth subcircuit. There is only one Int 1 and it makes connections with neurons from both subcircuits. In addition to the Int 1 connections, there are several other synaptic connections that exist between the two subcircuits and help insure the entire CPG circuit works in a coordinated fashion. The STG contains the gastric mill network and the much better known pyloric CPG as well. Direct chemical and electrical connections between the gastric and pyloric circuits exist (Mulloney, 1977
) resulting in a number of interesting types of interactions and modes of synchronization (e.g. the pyloric modulation of the DG and AM neurons). Each CPG sends bursts of activity from the interneurons to the paired CG where they inhibit two pair of “descending” interneurons the P and E neurons, in a way that causes pyloric timed bursts in the P cells and gastric timed bursts in the E cells (Nagy and Moulins, 1986
). The E and P neurons then return bursts of excitation back onto both gastric and pyloric CPGs respectively. Interestingly, the pyloric timed P cell input synapses onto some of the gastric neurons and is especially noticeable as excitatory bursts of PSPs in a ca. 2 Hz pyloric frequency. In combined preparations, i.e. those with the CG still attached to the STG, bursts of activity from a third CPG the cardiac sac CPG, can sometimes be seen to disrupt both the gastric and pyloric rhythms (Ayali and Harris-Warrick, 1998
). We mention these various inputs here only because their activity is recognizable in many of the recordings we will show. The CG also are the origin of additional descending fibers that may play an important role in the mechanisms underlying gastric CPG activity. For the most part these have been studied intensively in the crab CPG system (Nusbaum and Beenhakker, 2002
) and will be included in our discussion where appropriate. Indeed, in most preparations intact connections from the anterior centers are required for the production of a robust gastric rhythm. While there are specific synaptic inputs to some gastric neurons, it appears more likely that the presence of neuromodulators released into the STG from descending fibers are the principle enablers of the CPG. In fact, when the sole input pathway, the stomatogastric nerve (stn) is cut, rhythmic activity is arrested but can be reintroduced by superfusion of the STG with different neuromodulatory substances such as pilocarpine (Dickinson et al., 1988
; Elson and Selverston, 1992
), proctolin, cholecystokinin (Turrigiano and Selverston, 1990
) and others (Harris-Warrick et al., 1992
). This observation suggests that rhythm-generating mechanisms within the STG are sufficient to produce gastric oscillation in some form.
Previous work has suggested that the DG, AM, LG, MG neurons and the Int 1 all burst endogenously (Russell and Hartline, 1984
). It is possible that the bursts could also be the result of descending excitation since similar bursts of activity could be recorded from the stn when the system was active. However, bursting was occasionally seen when the stn was cut (n = 4; see also Mulloney and Selverston, 1974a
). We hypothesize that bursting in gastric cells is conditionally dependent upon neuromodulatory inputs from the CGs. Bursting activity in the stn is due to gastric-timed excitatory inputs from the commissurals and whose function is to raise the general excitability level of the whole system but direct synaptic drive from or interactions with extrinsic neurons is not required for the gastric mill network for its operation. Besides, we hypothesize that the single Interneuron 1 plays a central role not only in the generation of the gastric rhythm but also in the coordination of the medial and lateral subcircuits. As we will show, Int 1 performs this dual role by differentially regulating the activity of the postsynaptic targets in part by conventional synaptic transmission as well as by a slower, possibly modulatory, action.
We have organized our results in the following way. First, to get at the question of rhythmicity we reexamine which of the component neurons have pacemaker properties using several different experimental techniques. Second, we examine the mechanisms used by the circuit to produce the correct spatiotemporal pattern. Although the gastric CPG operates as a unit, we divide the cellular components into two subsets, the neurons that drive the medial tooth and the neurons that control the two lateral teeth and study their mechanisms separately. Third, we explain the mechanisms used to synchronize the two subsets into a coordinated rhythm capable of producing effective behavior.
Animals
Panulirus interruptus were obtained from Don Tomlinson Commercial Fishing (San Diego, CA, USA). The animals were kept in aerated and circulated seawater at 15–16°C. Prior to dissection the animals were anesthetized by packing them in ice for 40 min.
Solutions
The standard Panulirus physiological saline we used was composed of (in mM) 483 NaCl, 12.7 KCl, 13.7 CaCl2, 10 MgSO4, 4 NaSO4, 5 HEPES, and 5 TES; pH was set to 7.40. A reduced configuration of the gastric circuit was achieved by applying picrotoxin (PTX; 8 μM) in the bath. Here, fast glutamatergic inhibitory interconnections were blocked while the slow cholinergic synapses were left operational. In another set of experiments we applied atropine (2 mM) to block cholinergic inhibitory connections and to obtain another synaptic configuration of the circuit. Near complete pharmacological isolation of the neurons were achieved by combined application of PTX and atropine.
Preparation
The stomatogastric nervous system containing the STG and the anterior commissural and esophageal ganglia was separated from the stomach (Mulloney and Selverston, 1974a
) and pinned in a silicone elastomer-lined Petri dish. Nerves interconnecting the anterior centers as well as the output motor nerves of the STG were left intact. The connective sheath of the STG was removed using sharp forceps to facilitate access to the somata of the neurons. The STG was enclosed in a small well made of petroleum jelly that served as a separate perfusion chamber of ∼2 ml volume. PTX and atropine and other drugs were applied to the STG while the anterior ganglia were bathed in normal physiological saline. Functional disconnection of the gastric neurons from anterior ganglia was achieved by the sucrose gap technique (Russell and Hartline, 1978
). Here, a 1–2 cm section of the stn was enclosed in a small vaseline well and the physiological saline was replaced with isomolar sucrose solution. This treatment effectively and reversibly blocked signal conduction in the stn. Under these conditions, gastric neurons typically ceased their burst oscillations and either became hyperpolarized or kept firing tonically.
Electrophysiology
Intracellular voltage traces were measured using Neuroprobe 1600 amplifiers (A-M Systems Inc., Carlsborg, WA, USA) in bridge mode. Microelectrodes were filled with 3 M K-acetate plus 0.1 M KCl solution with a resistance of 12–15 Mohm. Cell identification was achieved by visual inspection of the voltage waveforms and by comparing intracellular membrane potential traces with simultaneous extracellular recordings from the output nerves. Extracellular signals were measured using an A-M 1700 differential AC amplifier (A-M Systems). We performed voltage clamp experiments in a smaller number of experiments to directly observe transmembrane currents during presynaptic stimulation. Here, the postsynaptic neuron was voltage clamped at various holding levels (from −50 to −100 mV) and the selected presynaptic neuron was stimulated intracellularly using a rectangular current pulse. Under such conditions the presynaptic neuron produced a short burst episode in response to the stimulation and the transmitter (or modulator)-evoked postsynaptic current was measured using the two-electrode voltage clamp method (Axoclamp-2B, Axon CNS/Molecular Devices, Sunnyvale, CA, USA). Deletion of selected gastric cells was achieved by the photoinactivation technique. Here, carboxyfluorescein-filled microelectrodes were inserted into the neuron previously identified with a normal electrode. Intracellular filling of the cell was facilitated by application of negative current (−2 nA). Full intracellular filling was achieved usually within 20 min and the cell was then illuminated with strong focused blue light.
Data Acquisition
Voltage traces were acquired and digitized at 20 kHz by a computer equipped with a PCI-MIO-16E4 data acquisition board (National Instruments, Austin, TX, USA) and running the DASYLab 6.0 program (Datalog GmbH, Germany). Acquisition protocols (worksheets) were written by the authors. Action potential (spike) occurrences were detected in real-time by calculating the first time-derivative of the intracellular membrane potential and observing the local maxima of the derivative time series. The arrival times of spikes of each recorded neuron were saved sequentially into separate ASCII files. Data from some experiments were acquired using the Axoscope software (Axon Instruments, Foster City, CA, USA).
Data Analysis
Detailed quantitative analysis was performed using the spike trains {ti} = {t1, t2, t3,…tN}, where t1 < t2 < t3 … are successive spike arrival times available for each recorded neuron. Spike density functions were calculated by convolving the spike trains with a Gaussian kernel (250 ms half-width, 10 ms sampling resolution). The regularity and periodicity of the burst oscillations was characterized by Fourier amplitude spectra. The Fourier amplitude spectra were calculated from 100 s sections of the spike density time series before and during the application of drugs. Fourier amplitudes were calculated at 5 mHz resolution. All spike time analysis was performed with our own software
1
.
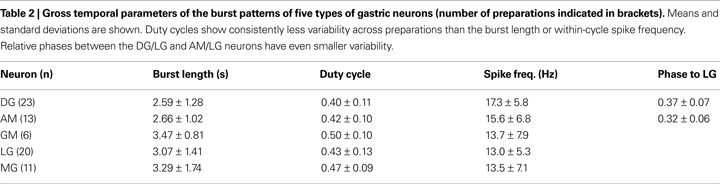
Intrinsically Bursting Neurons
The in vitro gastric mill CPG produces a characteristic oscillatory pattern of firing and bursting in the component neurons. In our experiments the mean burst frequency of the “healthy” gastric preparations varied in a relatively wide range between 0.23 and 0.08 Hz, averaging 0.16 ± 0.04 Hz (n = 31, mean ± SD). At the same time, burst temporal parameters of the component neurons from different preparations (Table 2
) displayed nearly twofold variations exceeding those in the pyloric circuit (Szücs and Selverston, 2006
). Nevertheless, the phase-relationships between bursts of different neurons were well preserved across preparations even with significantly different burst frequencies. Endoscopic analysis has shown earlier that the burst frequency of the in vitro gastric rhythm is also the approximate frequency for movements of the teeth in the gastric mill in situ, although there is considerable more variability in the intact animal (Heinzel, 1988a
,b
). The origin of CPG rhythmicity has usually been thought of as being due to the intrinsic conductance properties of one or more neurons or as synaptic interactions, particularly reciprocal inhibition, or a combination of bursting and network properties (Harris-Warrick et al., 1992
). To determine which mechanisms exist in the gastric CPG, we employed three methods commonly used for the identification of intrinsically bursting neurons:
• Cell isolation by pharmacologically blocking synapses. The gastric system, like the pyloric uses two neurotransmitters, glutamate and acetylcholine (Marder, 1986
). The distribution of these two transmitters among the gastric neurons except Int 1 is known. Both can be almost completely blocked pharmacologically. We used PTX for blocking glutamate (Bidaut, 1980
; Elson and Selverston, 1995
) and atropine for ACh (Marder and Eisen, 1984
).
• Cell isolation by deleting (photoinactivating) or hyperpolarizing presynaptic neurons. We cannot assume that these procedures result in similar effects. After hyperpolarization of presynaptic neurons there are both immediate effects and longer term (adaptive) responses sometimes not developing for several minutes.
• Injection of temporally varying current waveforms such as sinusoids into selected presynaptic neurons. Periodic current inputs are effective in revealing synchronization modes and regimes of the entire gastric network and show the relative importance of circuit elements.
To assess the endogenous voltage dynamics of gastric neurons, their complete synaptic isolation is required. Commonly used pharmacological techniques are not always sufficient to achieve their isolation, therefore, additional techniques such as hyperpolarization of presynaptic neurons or sucrose block (see below) might be useful. Figures 2
A–C show the effects of the application of 10 μM PTX and, subsequently, 2 mM atropine on four cell types. PTX alone does not prevent rhythm generation in a normal bursting preparation, rather, it boosts the activity of many gastric neurons inducing bursts with more intense firing than in control conditions. Commonly, within-cycle firing rate of most neurons, including the LG, MG as well as the GM and DG neurons (n = 4) doubles after blocking glutamatergic inhibition. A combination of PTX and atropine reliably blocks the gastric oscillation and decouples most of the gastric neurons. While the Int 1 neuron continues to burst intrinsically, its postsynaptic inhibitory action on the GM, LG and MG neurons is removed by atropine (n = 7). The GM neuron fires tonically in such conditions while the LG and MG keep bursting weakly or cease firing completely (Figure 2
C). It is noteworthy that a slow excitatory effect of Int 1 on the DG and AM neurons and in less degree, in the LG and MG neurons survive the combined application of PTX and atropine (e.g. MG in Figure 1
C).
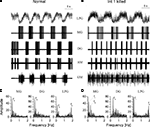
Figure 2. Pharmacological block of synapses by picrotoxin (PTX) and atropine reveals strong intrinsic bursting properties in the Int 1 neuron. (A) Control firing pattern of four neurons of the gastric network. (B) Shows the firing pattern after blocking the glutamatergic synapses by 10 μM picrotoxin and (C) shows the effects of adding 2 mM atropine to block both glutamatergic and cholinergic synapses. While PTX has a relatively weak effect on the overall pattern, the firing, especially in the MG becomes more intense (B). When both types of chemical synapses are blocked, the GM becomes tonic but Int 1 and MG continue bursting. At the same time, MG starts bursting in-phase with Int 1. The LG here is silent but in many cases it too continues bursting in-phase with the Int 1. Note that the fast inhibition from Int 1 to MG is lost and there is a phase advance of its burst. This is due to the remaining excitatory component from Int 1 which is atropine insensitive.
When Int 1 is hyperpolarized below threshold (Figure 6
B) or killed by photoinactivation (Figure 9
B) then the AM and DG cells receive no more excitatory input from the STG (extrinsic projection and P-cell inputs remain). Under such conditions these neurons continue to burst although somewhat more irregularly. The intrinsic bursting capability of the DG neuron is also clearly demonstrated in another set of experiments utilizing the sucrose knife technique (Russell, 1976
). Here, commissural neuromodulatory inputs are removed by applying isotonic sucrose solution to the stn, which effectively and reversibly blocks connections between the STG and the anterior ganglia. Under such conditions the gastric neurons typically cease bursting and also their synaptic interactions are greatly attenuated (not shown). Nevertheless, the DG and AM neurons display characteristic and robust intrinsic bursting when the sucrose block is initiated (not shown, n = 6). Neurons without intrinsic burst capability, such as the GM and LPG, become tonic when PTX and atropine are used. Under such conditions fast cholinergic inhibition from Int 1 to GM and that from the LG to LPG is blocked (n = 4).
Int 1, as well as other intrinsically bursting neurons in the network, demonstrate a strong dependence of burst frequency on the membrane voltage. In the experiments of Figure 3
, we applied variable levels of hyperpolarizing current to the Int 1 neuron. This manipulation exerted a characteristic effect on its burst cycle period and duty cycle. We find a U-shaped relationship between the injected current and the burst cycle period, while the duty cycle of the bursts appears as a linear function of the injected current (Figures 3
B,C). These features of the voltage output are characteristic of intrinsically bursting and pacemaker-type neurons (Selverston, 1974
; Benson and Adams, 1989
) such as the anterior burster in the pyloric network. In sum, our results suggest that based on their activity under pharmacological/intracellular manipulation we can consider Int 1 and DG to be strong bursters and AM, LG and MG to be weak bursters. Other cells (i.e. the GMs and the LPGs) behave as rate-modulated spiking neurons, that is, their instantaneous firing rate is directly proportional to the level of their depolarization. These latter neurons display no intrinsic bursting properties.
Figure 3. Voltage sensitive changes in the burst frequency and duty cycle of the Int 1 neuron. Various levels of intracellular current was injected into the Int 1 neuron and the resulting voltage output is shown for five different values (A). The burst cycle period (B) and the duty cycle (C) of the bursts are shown in the right panels.
The Medial Tooth Subcircuit
The medial tooth subcircuit consists of six motor neurons and one interneuron. Two of the motor neurons, the DG and the AM innervate muscles that reset the tooth after the four GM neurons have activated muscles that provide the powerstroke. The DG and AM fire almost together and are antagonistic to the GMs, a common arrangement for muscles controlling structures that show reciprocal oscillation. Interneuron 1 has two functions in the medial subcircuit – it excites the DG and AM but with a delay inversely proportional to the intensity of its burst (Figure 5
D) and it strongly inhibits the four GM neurons. There are several important points to take note of here. First, the motor neurons are acting within the pattern generating circuit by using mainly inhibitory synapses but also provide excitatory input to the muscles they innervate, i.e. they have dual actions. Intracellular recordings of the four medial neuron types is shown in Figure 1
B (top four traces). Note that the DG and AM begin firing after the Int 1 burst has started as a result of delayed excitation (also Figure 5
A). The onset of the DG burst is usually steeper than that in the AM neuron reflecting the strong intrinsic bursting properties of the DG. At the same time, the timing of the DG burst is mainly determined by the excitatory input from the Int 1. Also note that the pyloric modulation (∼2 Hz) is especially apparent in the DG and AM cells due to short volleys of EPSPs from the P cells in the CG (that are bursting in pyloric time).
The firing pattern of the medial subset neurons consists of approximately 3 s bursts in the antagonist motor neurons (See Table 2
for the general parameters of the burst patterns). Although electrically coupled, the DG neuron usually fires slightly ahead of the AM neuron. Here, the intensity and phasing of the pyloric modulatory input also affects the burst structure and relative timing of the DG/AM bursts. Together they fire out of phase with the GMs. Bursting in the GMs is largely due to periodic strong inhibition of their tonic firing by bursts in Int 1.
As described previously, the AM, DG and Int 1 neurons are all intrinsic bursters whose endogenous frequencies can be observed when they are synaptically isolated but still connected to the more anterior CG. This suggests that the DG/AM pair will oscillate approximately together even without input from Int 1 because of the electronic connection between them. Int 1’s role is to entrain the DG/AM pair in a way that makes them fire out of phase with the GMs. The burst envelope (spike density waveform) of the Int 1 neuron is typically asymmetric, the onset of the burst is slower than its termination. As the Int 1 firing frequency gradually increases, it leads to termination of the GM bursts and the start of the next DG/AM bursts. If Int 1 is hyperpolarized below firing threshold, the immediate response is for the GMs to become tonic and the DG and AM neurons to shut off (Figure 13
, before Int 1 release) until their intrinsic burst generating mechanisms resume (Figure 6
). Afterward, the DG and AM neurons can drive a slightly irregular rhythmic pattern in the medial subcircuit. When Int 1 is depolarized to the point where it is firing almost continuously the DG and AM continue to burst (Figures 4
A,B). If however, Int 1 is strongly depolarized by intracellular current injection and held in this condition, DG becomes overly excited and fires tonically (Figure 4
C). The Int 1 excitation of DG and AM therefore appears to not simply entrain their bursting but to provide a general excitatory drive.
Figure 4. The effects of Int 1 depolarization on the activity of the medial tooth subcircuit. The normal rhythm of the subcircuit is shown in the (A) panel. A small depolarization of Int 1 to a steady firing level permits DG and AM to continue oscillatory activity (B). Panel (C) shows that under intense depolarization with increased firing frequency in Int 1, the DG is driven to tonic activity while the activity of the GM neuron is terminated.
While the Int 1-to-DG connection is one of the key circuit elements in the gastric CPG, the precise physiological mechanism by which Int 1 causes the delayed excitation remains to be resolved. We performed a series of current clamp and voltage clamp experiments to investigate the voltage dependence and kinetics of the Int 1-to-DG connection, which turned out to be far from trivial. Figure 5
demonstrates the effects of a sudden depolarization of Int 1 (burst elicited by release from hyperpolarization) on the DG neuron held at various membrane potentials. One of the prominent features of the slow excitatory response is that its amplitude (i.e. the amount membrane depolarization) remains virtually unchanged as the membrane potential is lowered by the injection of hyperpolarizing current (Vm values indicated). One-to-one monosynaptic EPSPs are never observed in the voltage trace of the DG neuron during the stimulation of the Int 1 unlike in the GM neuron where clear monosynaptic IPSPs can be distinguished at the same time. In the example of Figure 5
A, the STG was functionally disconnected from the modulatory inputs that normally arrive from the anterior ganglia (CGs), using the sucrose block technique. As noted, under such conditions, extrinsic synaptic inputs such as the P-cell EPSPs are blocked and the gastric neurons typically cease their burst oscillations. The sucrose block method is therefore very useful to study the cell-to-cell connections within the circuit and to observe the postsynaptic responses in their purest form. The Int 1-induced depolarization of the DG is shown as an inward current under voltage clamp conditions (Figure 5
B). Here, the sucrose knife technique was not used and the P-cell input caused the apparent rhythmic P-cell volleys in the current trace of the DG neuron. Again, the amplitude of the inward current remains the same (∼1.5 nA) in a 40 mV wide range of DG membrane potentials (Figure 5
B). An I–V relationship built from data from several voltage clamp experiments reveals a flat voltage dependence of the inward current (i.e. no tendency for reversal is observed).
Figure 5. Current and voltage clamp study of the slow excitatory coupling from Int 1 to the DG neuron. (A) Delayed excitation of DG following depolarizing pulse to Int 1 recorded in current clamp. Note the almost constant size of the responses at various levels of DG membrane potential, i.e. lack of reversal in a 90 mV range. Here, anterior inputs were blocked using the sucrose knife technique. (B) Transmembrane current of the DG neuron in voltage clamp. Int 1 induced depolarization of the DG manifests as an inward current. 2 Hz oscillation of the membrane current appears as a result of the input from the P cell (pyloric modulation, anterior connections present). Panel (C) shows relative inward current amplitudes from 6 voltage clamp experiments (currents normalized to the absolute value of current measured at Vm = −70 mV). The I–V relationship is nearly flat suggesting no reversal in the physiological range of membrane potential. Panel (D) shows the dependence of the DG response delay on the firing frequency of the Int 1 neuron measured during the first 1 s of the rebound burst. Delay times were normalized to the values measured at fInt 1 = 40 Hz. The observed relationsip is very clear and well conserved across preparations (n = 5).
From a functional point of view it is remarkable that such a long delay of the Int 1-to-DG signal transfer and slow onset of the response has an important effect on the DG and AM firing patterns. Particularly, this slow excitatory connection entrains the bursting of the DG and AM neurons to occur after the powerstroke muscles for the medial tooth (controlled by the GMs) have been fully inhibited. This connection is not blocked by PTX and atropine (n = 4). Interestingly, the Int1-induced slow excitation of the DG shows some resemblance to that induced by the activation of the gastropyloric stretch receptor (Kiehn and Harris-Warrick, 1992
). It has been shown that the input from the serotonergic gastropyloric receptor excites the DG via a dual conductance mechanism. Nevertheless, CsCl known to interfere with the serotonergic response in the DG neuron via blocking the hyperpolarization-activated IH current, was ineffective in our experiments (n = 2). Apparently, the Int 1-induced depolarization of the DG neuron is not due to the activation or upregulation of its H-current by neuromodulatory action from the Int 1. Cinanserine, a specific blocker of serotonin receptors in the stomatogastric nervous system was also ineffective in blocking the Int 1-to-DG excitatory connection (n = 3).
Regarding the activity patterns and synaptic interactions of the GM neurons the picture is less complex. Although the primary inhibition of the GMs comes from the Int 1, they are also inhibited by their antagonists DG and AM (Figure 6
) but to a somewhat lesser degree. The effects of the DG/AM neurons on the GMs can be seen more clearly, when Int 1 is hyperpolarized below firing threshold. Figure 6
B shows that various combinations of DG and AM burst intensity have limited effectiveness in inhibiting the GMs. The results of the medial tooth experiments clearly show that Int 1 excites and entrains the DG and AM to fire in bursts that are slightly out of phase while simultaneously inhibiting the four GMs (n = 14). Rapid cholinergic inhibition of the GMs (atropine sensitive response) always precedes the excitation of the DG/AM pair. The cooperative action of this ensemble of cell and synaptic properties generate the four phases of the medial tooth rhythm.
Figure 6. Int 1, DG and AM supply the most inhibition to the four GMs but the DG and AM synapses are much weaker than that from the Int 1. Panel (A) shows control medial tooth activity. (B) When the Int 1 is hyperpolarized below threshold the DG and AM resume their intrinsic bursting after a few minutes. Under such conditions, the DG and AM neurons will deliver inhibitory input to the GMs without the action of the Int 1. Note that when both DG and AM burst strongly and concurrently (2 and 4 bursts) the GMs are almost completely inhibited. A single weak AM burst (third) barely inhibits the GMs.
The Lateral Teeth Subcircuit
The lateral teeth subset of stomatogastric neurons consists of the LG, MG and two LPG motor neurons and the Int 1 neuron that is shared by both subcircuits. The LPGs innervate the opener muscles of the lateral teeth and when the gastric mill is inactive, their tonic activity holds the two teeth in the open position (Turrigiano and Heinzel, 1992
). When the gastric mill is activated, the tonic firing is periodically interrupted by nearly simultaneous bursts in the LG and MG cells which draw the two teeth together. This pattern can be seen in the bottom three traces of Figure 1
A. Basically LG and MG fire towards the end of the Int 1 burst (Figure 1
B) and between LPG bursts, i.e. the LG/MG pair and the two LPGs are antagonists. We note that the LPG is the most intensely firing neuron in the gastric circuit and its activity is more like a rate-modulated firing than separate bursts. It is not uncommon that the LPG can sustain firing at a reduced frequency even during the peak phase of the LG/MG bursts. Regarding the phasing of the LG and MG bursts, that of the MG usually precedes the LG burst although there is some variability here. LG and MG are weak endogenous bursters and when isolated from Int 1, in the majority of preparations they are too weak too sustain a regular lateral subset rhythm (Figure 9
B). Like the DG/AM pair, LG and MG are excited by Int 1 after a delay. But unlike Int 1’s action on DG and AM, the excitation here is preceded by a fast inhibition (Figure 8
) hence the effect of the excitation is delayed by a much greater period of time. Consequently, the Int 1 neuron imposes a biphasic action on the LG and MG with distinct kinetics and synaptic mechanisms operating during each phase. Atropine removes the rapid inhibition from Int 1 to LG and MG. Comparing the traces of Figure 2
B (PTX) and C (PTX and atropine) we find marked differences in the relative timing of the Int 1 and MG bursts. Int 1 and MG fire in anti-phase when the cholinergic inhibition is not blocked. Clearly, this strong inhibitory input delays the onset of the MG burst relative to the Int 1 burst. However, when atropine removes the inhibitory component, the two neurons start bursting more in-phase. The effect of removing cholinergic inhibition is also very prominent in the GM neuron and it is therefore likely that Int 1 uses ACh as the primary inhibitory neurotransmitter in both the medial and lateral subcircuits. However, the slow excitatory component (Int1-to-LG/MG) remains in atropine. This is clearly shown in Figure 2
C where Int 1 produces robust bursts in the presence of atropine (and PTX) and the MG neuron displays weaker bursts in-phase with the Int 1 activity. Here, rapid inhibition from Int 1 is blocked by atropine but the slow excitatory component remains intact. As with the delayed excitation to DG and AM, the cause of the excitation is not known. Also similar to DG and AM, the LG/MG pair fire slightly out of phase. While varying amounts of IA and IH in each neuron may contribute to this initial time disparity (Harris-Warrick, 2002
), LG and MG are both electrically coupled (Mulloney and Selverston, 1974a
) and connected with rapidly depressing asymmetric reciprocal inhibitory synapses (Figure 7
). This arrangement allows the two neurons to fire phase locked with the MG bursting slightly before the LG in most preparations (n = 9). Due to the asymmetry of the inhibitory coupling between the two neurons, i.e. LG sending stronger inhibition to MG than vice versa, the bursts of the MG neuron tend to terminate earlier than those of its counterpart.
Figure 7. Interactions between the LG and MG neurons. In normal conditions, the two neurons burst in-phase with MG slightly ahead of the LG (A). When both neurons are hyperpolarized, the gastric rhythm even in the rest of the network is greatly diminished and the membrane potential traces of both LG and MG become flat (apart from the 2 Hz pyloric modulation) (B). Releasing LG from hyperpolarization triggers an immediate inhibition of the MG (see gray arrow), but this inhibition rapidly stops due to synaptic depression (C). Releasing MG from hyperpolarization has a weaker effect on LG. Here, only a weak inhibition is observed, but the LG burst gets stronger due to electrotonic coupling (D).
Also in a way that is very similar to the GMs in the medial tooth circuit, the LPG neurons fire tonically when the overall gastric rhythm is inactive. Besides, the LPGs show clear pyloric modulation arriving from the P cells (Figures 9
C,D, see fp in the Fourier spectra). At the same time, unlike the GMs in the medial tooth circuit that are being inhibited by both Int 1 and the DG/AM pair, the LPGs are inhibited principally by the LG and MG with some weak inhibition from the DG. While the medial tooth circuit is almost entirely feed forward, the lateral teeth circuit has two inhibitory feedback loops. The LPGs provide feedback inhibition to the LG and MG (see Figure 1
C) and the LG and MG feed back to Int 1.
One of the most interesting results of examining the Int 1 to LG and MG synaptic connections was the discovery that the fast inhibition, which has been described previously (Mulloney and Selverston, 1974a
), is followed by a delayed excitatory response similar to that seen for the DG and AM neurons but with a longer delay (Figure 8
). The two different forms of delayed excitation are therefore poised to play an important role in determining the overall firing pattern.
Figure 8. The role of Int 1 in synchronizing the medial and lateral subsets. A depolarizing pulse to Int1 reliably excites DG after a delay. At the same time, the GM is inhibited while the MG is inhibited then excited in a biphasic manner. (The LG behaves similarly but not shown here.) These recordings demonstrate the differential effects of Int 1 on its follower cells.
Lateral and Medial Subcircuit Synchronization
Principle connections
The lateral and medial subcircuits together form the gastric network which can be considered a unit CPG, i.e. a self-contained microcircuit capable of producing the six-phase rhythmic motor pattern that drives and coordinates the movements of the gastric mill. Obviously, the two subcircuits must be synchronized for effective maceration of the food. The power stroke “chewing” movement of the medial tooth must occur while the lateral teeth are gripping the food particle. To achieve this, the two subcircuits are linked together with a set of strong synapses we term the principle connections. The most important of these arrive from the Int 1 neuron. Both subsets share Int 1, in a way that produces synchronized activity, and determines the frequency of the overall oscillation. The basis of this coordination can be seen in Figure 8
. When Int 1 is depolarized, it produces opposite effects in the medial tooth antagonists by exciting DG and inhibiting GM. But at the same time, because of the biphasic action just described, it first inhibits and then excites the MG (and LG). When the MG and LG fire they inhibit the tonically firing LPGs. This can be seen clearly when Int 1 is removed from the circuit by hyperpolarization or photoinactivation (n = 6). Hyperpolarization of Int 1 causes dramatic changes, but this procedure does not really demonstrate Int 1’s role very accurately. This is mainly because the short term effect of Int 1 hyperpolarization is often different from that seen in longer time scales. Immediately after Int 1 hyperpolarization LG and DG activity is terminated because of the absence of excitation, while the GMs become tonic due to lack of inhibition. At the same time, the absence of LG and MG also removes the most potent inhibition to the LPGs so that they start to fire tonically as well.
A clearer picture of the synchronizing role of Int 1 can be seen after its complete photoinactivation. Under such conditions the intrinsic bursting properties of the remaining neurons start playing a more dominant role in the formation of medial and lateral tooth rhythms, these being now more independent than when the Int 1 is intact. Figure 9
shows that the lateral and medial subsets can still generate bursts, but somewhat more irregularly and at different frequencies. It is, however important to note that synaptic connections between the two subsets, other than those through Int 1 still exist, hence the medial and lateral neurons are not entirely independent. When the medial and lateral burst patterns are fairly regular, such as in the example of Figure 9
, one can observe a tendency toward integer-ratio coupling between the subsets. Indeed, the lateral neurons produce approximately 1 burst per 3 cycles of the medial neurons, as confirmed by the Fourier-analysis (Figure 9
D). At the same time, without the main coordinating element, the Int 1 neuron, the gastric neurons no longer behave as a unit CPG and they would be completely ineffective in producing a coordinated motor output.
Figure 9. Photoinactivation of the Int 1 neuron abolishes the synchronization between the medial and lateral tooth subcircuits. Control recordings in (A) show the normal rhythm in a combined preparation. One hour after the Int 1 neuron has been photoinactivated a fairly regular rhythm is observed in both the medial and lateral teeth neurons (B). However, the two subcircuits are running at different burst frequencies, the medial neurons being nearly three times faster than the lateral ones. At the same time, neurons within the subcircuits are synchronized. In control, the gastric rhythm runs at fg = 0.15 Hz (C) and the pyloric modulation is also clearly observed in the LPG (fp = 1.86 Hz). (D) When Int 1 is killed, the medial subset neurons oscillate at fm = 0.31 Hz and the lateral neurons at fl = 0.11 Hz). Note that the medial peak clearly appears in the Fourier spectrum of the MG neuron. This is due to the DG-MG inhibitory connection.
Continuous depolarization of Int 1 can prove so stimulatory it can cause DG to fire tonically (Figure 4
C). Under these conditions inhibition from Int 1 to MG appears to overcome any excitatory drive causing the MG to shut down. Tonic inhibition of the MG by Int 1 (i.e. the rapid inhibitory component overcomes the delayed excitatory component from the same neuron. MG’s lack of inhibition to LPG allows it to fire tonically and Int 1’s conventional inhibitory drive to GMs shuts them off completely. Conversely, a mild steady depolarization of Int 1 simply slows down the rhythm without disrupting the spatial pattern.
The LG neuron, usually working in concert with MG, form another set of principle connections for the synchronization of the overall rhythm. Hyperpolarization or depolarization of this cell affects the medial tooth subset principally via inhibitory synapses onto the Int 1 neuron. Hyperpolarization removes this inhibition and allows Int 1 to fire faster thus producing longer bursts in DG and AM and shorter bursts in the GMs. Depolarization of LG produces greater inhibition of Int 1 which removes excitation to DG and AM and inhibition to the GMs. Continuous depolarization of LG is usually interrupted by escape of the Int 1 neuron, which gives some idea of Int 1’s intrinsic burst strength, but LG’s effects on other neurons can be seen even when this occurs. The inhibitory feedback from LG and MG to Int 1 appears to play a stabilizing role in the network by helping to terminate Int 1 bursts (see also forcing data below). We know that when this feedback is blocked pharmacologically Int 1 can still burst intrinsically (n = 4, see also Figure 1
C).
The two LPG neurons fire tonically in a non-cycling preparation and their only synaptic output connections are inhibitory feedback to the LG and MG. But because LG and MG are important in synchronizing the rhythm, the LPGs can also have a role in network coordination. One can see in Figure 10
that a long depolarizing pulse to just one LPG is enough to shut down LG (and presumably MG) thus removing their inhibitory effect on Int 1, leading to an increase of Int 1’s firing rate. Int 1’s increased firing means the GM is kept off while the DG and probably AM, are strongly excited.
Figure 10. Feedback from the LPGs to the LG forms a reciprocal inhibitory loop that also has effects on the rest of the network. Here a long depolarizing pulse into the LPG neuron terminates LG bursting subsequently removing LG inhibition from the Int 1 (trace not shown). In turn, Int 1 strongly excites DG producing a prolonged burst in its activity. Meanwhile, the GM is shut down.
While constant level depolarization or hyperpolarization of selected presynaptic neurons reveals important effects in the dynamics of postsynaptic cells, gastric neurons are normally not in a steady state but oscillating or bursting periodically. Hence, a temporally variable stimulation such as the intracellular injection of sinusoidal current would serve as a more naturalistic input. Under such conditions, various modes of synchronization can be expected and one can evaluate the functional importance of different presynaptic neurons in driving the rest of the circuit. In the following set of experiments we injected sinusoidal current waveforms into different gastric neurons so their firing patterns consisted of separate bursts with a cycle period that was equal of the period of the input current. This manipulation acted as a periodic forcing for postsynaptic neurons through the synaptic inputs from the stimulated neuron. We used forcing periods ranging from 0.2 to 4 times the burst cycle period of the ongoing (spontaneous) gastric rhythm while keeping the amplitude of the sinusoidal waveform constant. Figure 11
demonstrates the results of one such experiment. In this example the cycle period of the spontaneous rhythm was 4.1 s but the injection of periodic current into the Int 1 synchronized the entire gastric circuit in a wide range (from 2.2 ± 0.5 to 9.2 ± 1.0 s; n = 2) of cycle periods (Figures 11
B,D). Clearly, Int 1 exerts a strong impact and a coordinating action in the network. The LG neuron was also potent in synchronizing the rest of the gastric neurons, and the effective range was close to that of Int 1 (from 3.6 ± 0.5 to 10.8 ± 1.2 s, n = 5) (Figures 11
C,E). At the same time sinusoidal forcing of the DG neuron had only minor impact on the other neurons (Figure 11
F). When comparing results of such experiments from different preparations, one has to take into account that burst cycle periods of the spontaneous rhythm can vary among them. Hence, it is useful to normalize the period of the external forcing to the burst cycle period of the spontaneous rhythm. The ranges of normalized forcing periods for different presynaptic neurons appeared to be fairly consistent, with Int 1 and LG having the widest range (from 0.53 to 2.23 for Int 1 and from 0.86 to 2.60 for LG) and with the GMs showing the least amount of capacity for synchronizing the rest of the circuit (n = 4).
Figure 11. Sinusoidal forcing of gastric neurons reveals a wide dynamical range of the network and shows the relative importance of circuit elements. The neurons were stimulated with a constant amplitude (3 nA) but variable frequency sinusoidal current and the synchronization of the follower cells was evaluated as a function of the input frequency. Top panels show the voltage waveforms of the neurons and extracellular traces ((A) is without stimulation). In the lower panels we displayed the burst cycle period of three neurons as a function of the input frequency of the intracellular current that was injected in the Int 1 (D), LG (E) or DG neuron (F). Int 1 was the most effective in entraining the entire network (B,D). Similarly, LG entrained the gastric circuit in a wide range of frequencies (C,E). At the same time, virtually no synchronization was observed when the DG neuron was stimulated (F). The gray line in the lower panels marks the burst frequency of the spontaneous rhythm.
Subsidiary synchronizing connections
In addition to Int 1 whose connections span both subcircuits, there are five additional connections, most of them quite weak, which assist in synchronizing the network (see Figure 1
C). They are not equivalent in strength or importance to those associated with Int 1, but they do play a role that can be observed when they are individually manipulated or removed from the circuit. The connections are:
LG inhibition to DG, AM and the GMs. LG very weakly inhibits all of the medial tooth neurons (Mulloney and Selverston, 1974b
). A very strong burst in LG will interfere with DG and AM activity but the weak synapses appear to depress quickly so their action is short lived. LG effects are more likely mediated through Int 1 than directly. The strong LG burst is insufficient to produce noticeable effects on GM bursting.
LG and MG electrical coupling to the four GMs. It is uncertain what role this coupling plays in synchronizing the rhythm aside from locking the GMs with the LG and MG during certain behaviors. Simultaneous firing of these groups would pull the medial tooth across the “clenched” lateral teeth.
DG inhibition to LG, MG and the LPGs. This inhibition is strong enough to provide additional synchronizing effect between the medial and lateral subset neurons. A slight depolarization of DG increases its burst frequency and this also seems to entrain lateral teeth neurons. However, this connection is not strong enough to overcome the normal driving force from Int 1.
A Model of the Canonical Gastric Circuit
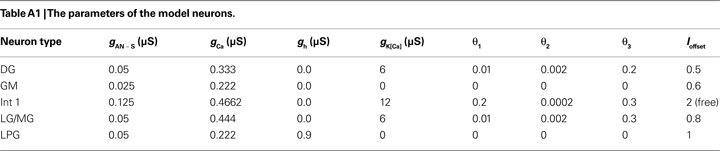
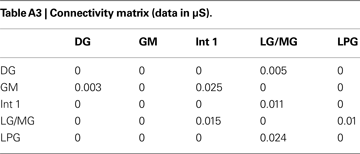
To verify the functional role and relative importance of the synaptic interconnections and to test the cooperative dynamics of the entire gastric system as an engine for the production of a six-phase coordinated rhythm, we developed a conductance based mathematical model of a simplified gastric mill CPG. The details of the model are given in the Appendix. As shown in Figure 12
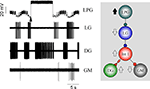
, a simulation of the network produces a five-phase rhythmic pattern consisting of bursts from four motor neurons and the fifth from the Int 1 neuron. Since the DG was lumped together with the AM and the LG was lumped with the MG, only four motor neuron burst patterns were simulated. In actuality, the AM and MG burst slightly out of phase with their cohort. The conductance parameters were able to show the correct phase relationships between the bursts of the component neurons. Especially important was the fact that overlap between Int 1 and the two key neurons which it drives, DG and LG, were appropriately timed. In order to test the validity of the model it was perturbed by hyperpolarizing and depolarizing Int 1 (as in experiments with intracellular current injection) without changing any of the intrinsic parameters of the neurons and synapses. When biological Int 1 is hyperpolarized, there are initial transient effects that dissipate over time. In order for the model to predict both the transient and the final oscillation the model requires adaptation of the parameters. The slow adaptation of the currents is not well understood yet. Thus modeling both the transient effects of Int 1 removal and the long-term stable states of the other neurons remains a computational challenge to be addressed in later simulations. With hyperpolarization of Int 1, the model correctly predicted the initial behavior of the network, specifically that DG would be moved below threshold and GM would fire tonically. At the same time, LG in the lateral subset would burst intrinsically and it would maintain bursting in the LPGs by inhibition. When Int 1 was strongly depolarized, the simulation predicted tonic firing in DG and LPG but no activity in GM and LG/MG. These results nicely agree with data from biological experiments where the Int 1 was strongly depolarized (see Figure 4
C). The structural stability test of this model consists of modifying slightly the parameters and determining whether the phase relationships remain in place. Many of the parameters given in the Appendix can reasonably be modified.
Figure 12. The computational model of the gastric circuit nicely reproduces the voltage output of the neurons. The normal regular burst oscillation appears on the left panels (A). Hyperpolarizing Int 1 below firing threshold removes the rhythm in the medial tooth neurons but the LG and LPG neurons keep bursting (B) – this is also observed in some of the biological circuits. When Int 1 is depolarized (C), the LG ceases firing and the LPG becomes tonic. Here, oscillatory activity stops in the entire network. See Figure 4
C for comparison. DG represents the lumped DG/AM neurons while LG corresponds to the lumped LG/MG pair.
It has generally been useful to consider two principal mechanisms underlying CPG function, one to produce a basic rhythm and a second to generate the sequential pattern of motor neuron activity. In the simplest case, rhythmicity can be achieved by one or more neurons having intrinsic oscillatory properties and therefore directly responsible for oscillatory behavior or for driving a more complex circuit of non-bursty neurons. In some cases single pacemaker neurons can be completely isolated from synaptic inputs and neuromodulatory agents and still continue to burst (Cooke, 2002
). More common however are “conditionally” bursting neurons, i.e. those that require neuromodulatory activation of burst generating conductances. The frequency of bursting in these neurons is determined by the kinetics of these conductances which in turn are strongly influenced by the specific neuromodulatory agent. Groups of intrinsically bursting neurons can be synchronized by electrotonic coupling or disreguard become synchronized in a sequential manner by the topology of their synaptic interactions. In this case the rhythmicity is due to the pacemaker cells and the pattern due to the synaptic interactions. Absent any intrinsically bursting neurons, some networks alone can produce reliable spatiotemporal rhythmic activity as an “emergent” property. There are many examples of such networks and there are experimental manipulations to distinguish them from burster or hybrid circuits (Katz et al., 2004
).
Several years ago Getting postulated CPGs that drove behaviors that are active continuously like heartbeat, respiration etc., use circuits that are driven by intrinsically bursting neurons (Getting, 1989
). Where reliability is paramount, CPGs controlled by bursting neurons are thought to be the mechanism of choice. However CPGs that burst as a result of both synaptic interactions and the biophysical properties of their neurons have been described for many organisms and have been supported by direct experimental evidence as well as computer simulations (Kristan et al., 2005
) (Turrigiano and Heinzel, 1992
). It has been suggested that the outputs of these circuits are more flexible that those driven by pacemaker neurons and therefore more likely to be found controlling behaviors that are intermittent and more influenced by sensory feedback (Getting, 1989
). Network CPGs can have a variety of topologies from simple reciprocal inhibition (Perkel and Mulloney, 1974
) to recurrent excitation (Cangiano and Grillner, 2003
) to recurrent cyclic inhibition (Székely, 1965
).
The gastric circuit that we have studied was initially described in rudimentary form by Maynard (Maynard, 1972
) as part of an initial study of the crustacean STG. The complete circuit was determined a few years later using pre- and postsynaptic intracellular recordings from isolated ganglia (Mulloney and Selverston, 1974a
,b
; Selverston and Mulloney, 1974
). The behavior of the teeth was described subsequently (Hartline and Maynard, 1975
). Although the circuitry has remained virtually unchanged since the initial description, the mechanisms responsible for the formation of the pattern have remained, at best, ambiguous. The gastric burst pattern was observed only rarely in isolated preparations but the basis for the rhythmicity and the spatial pattern, although never fully determined, was assumed to be due to the synaptic connections since no evidence for endogenously bursting cells was initially found. When excitatory inputs from the CG were discovered, it became possible to make “combined” preparations that produced reliable rhythmic gastric patterns for many hours (Russell, 1976
).
The idea that the gastric CPG rhythm was a result of network interactions was initially challenged by observations that attempted to show that the DG neuron was an endogenous burster (Hartline and Russell, 1984
). The principle evidence was that in combined preparations and occasionally in isolated ganglia, DG appeared to burst without having visible phasic inputs. Tonic firing in DG could be converted to bursting with hyperpolarizing currents and could be driven from an inactive to a actively bursting state by stimulation of the ION nerves which help connect the STG to the CG. Two other criteria for endogenous bursting were described – reset of the burst by depolarizing or hyperpolarizing pulses and voltage sensitivity of the burst frequency. They concluded that the DG had “plateau” properties, instabilities that could be triggered by pulse depolarizations and kept the cell in a depolarized, plateau state probably as a result of a persistent Na current.
The same authors also demonstrated that the AM, LG, MG and Int 1 contained the slow regenerative depolarizing potentials they had found in DG (Russell and Hartline, 1984
). However initial resetting experiments failed to clearly show that these cells were endogenous bursters during normal activity in combined preparations. With a more detailed study of the burst patterns, resetting could be achieved by these neurons and further that the power stroke neurons (LG, MG and the GMs) had variable durations at different frequencies while the return stroke neurons (DG, AM and LPG) are constant in duration for different frequencies (Russell, 1985a
). By applying depolarizing pulses to particular neurons they concluded DG and AM had little effect on the rhythm but GMs, Int 1 and LG could reset the timing for the whole pattern. Their conclusions from this work were that the network components within the STG were sufficient to generate the gastric pattern. Polarization of Int 1, LG, MG or GM could reset the rhythm and suggested they either generate the rhythm or affect cells that do. None of the neurons generated phase response curves consistent with those found for endogenously bursting neurons. Another interesting conclusion from this work was that there were only two phases to the pattern – a power stroke synergy and a return stroke synergy.
In an accompanying paper, Russell attempted to get at the mechanisms that were the basis for the coordination of the three teeth by a detailed series of individual cell polarizations during the ongoing rhythm (Russell, 1985b
). Some of his important observations were that the powerstroke neurons for the lateral teeth (LG and MG) actually start to fire before the powerstroke neurons for the medial tooth. The LG and MG firings help the GMs fire more intensely due to electrical connections and reduce firing in DG and AM due to inhibitory connections. He thought Int 1 was the link between the two subcircuits, exerting opposite effects on each. Int 1 excited DG but was not necessary for burst formation with the long delay after Int 1 firing due to a gating effect of some unknown neuron. Russell’s principle conclusions were that although GM, LG, MG and Int 1 could effect cycle period and have access to the generator, strong hyperpolarization of any of them did not permanently abolish the rhythm leading to some ambiguity between network and cellular rhythmogenesis.
There is often a clear distinction between CPGs thought to be driven by neurons with intrinsically bursting conductances and those which produce bursts as a result of their synaptic connections. What our results demonstrate is that such division can lead to artificial constraints on interpretation of CPG data because both the intrinsic properties of neurons and the sum of all network interactions are what determine the underlying mechanisms. Reductionism is necessary from an experimental point of view, but an integrative synthesis of all the data is required and in fact why modeling is especially important in achieving this synthesis.
Rhythmogenesis
As just mentioned, the initial idea that some of the gastric neurons were bursters was based on the observation that (1) they did not display synaptic inputs while bursting (2) that they demonstrated plateau potentials and (3) they did reliably reset the rhythm. We have reexamined this question by pharmacologically blocking all or most synaptic inputs to the cells thus effectively isolating them from the rest of the network but not from the neuromodulatory input they normally receive (except of course Ach which is released by neurons in the STG and might act as an intrinsic neuromodulator by spill over). The neurons in the gastric CPG are either cholinergic or glutaminergic. Atropine (Marder and Eisen, 1984
) and PTX (Bidaut, 1980
) are able to block most synaptic transmission and thus unmask neurons capable of bursting intrinsically. When isolated, Int 1, DG and AM appear to be strong bursters while LG and MG also burst but are much weaker. Bursting appears to rely strongly on persistent sodium currents (Elson and Selverston, 1997
). Studies on DG have shown that serotonin from sensory cells as well as from descending fibers may also play a role in the induction of plateau properties in crabs (Kiehn and Harris-Warrick, 1992
) The bursting cells also show a characteristic voltage sensitivity, bursting at higher frequencies as they become depolarized. We conclude that 5 of the 11 neurons in the gastric mill have voltage sensitive intrinsic conductances that produce bursting pacemaker potentials. It is the activity of the strongest burster, which appears to be Int 1, that determines the frequency of the entire system. The voltage sensitivity of Int 1, shown in Figure 3
, shows that its burst cycle period and duty cycle can vary over a wide range and appears to be able to be able to synchronize both subsets of the circuit over a wider range than any of the other burster cells when driven by varying frequencies of sinusoidal current waveforms.
Medial Tooth Subcircuit
The three phases of the medial tooth movements are formed by seven neurons. Bursts from DG and AM reset the tooth after bursts from the four GM neurons have pulled the tooth forward. The DG and AM neurons are strong intrinsic bursters that are entrained by delayed excitation from Int 1. There is a small separation in phase between DG and AM activity as a result of their individual responses to Int 1 but they are electrically coupled and act functionally as agonists. A burst in Int 1 slightly precedes the firing of DG and AM and the eventual barrage of inhibition from all three neurons are very effective in silencing the tonic firing in the GM neurons. Note that without this inhibition the extrinsic GM muscles fire continuously, keeping the medial tooth locked in the forward position when the mill is inactive. The medial circuit is basically feedforward, relying heavily on the pacemaker properties of Int 1 and the DG/AM pair. There is weak inhibitory feedback from LG to all of the medial tooth neurons that our modeling studies show to be quite important. This is somewhat surprising because physiological experiments initially indicated that this is not a very important synapse in terms of pattern formation. The model would not produce a reliable rhythm without this connection.
Lateral Teeth Subcircuit
There are only five neurons in the lateral teeth subcircuit: Int 1 (shared by the medial subcircuit), the electrically coupled LG and MG neurons and the two LPGs. The LPGs control the two lateral teeth opener muscles, which like the GMs, are extrinsic (the muscle origin is attached to the hard carapace) and fire continuously when the mill is inactive. This activity keeps the lateral teeth in the open position. The LG and MG are weak bursters that like the DG and AM are entrained by Int 1. However the entrainment is significantly different from that of the medial tooth. Int 1 first inhibits LG and MG via conventional fast ligand-gated conductances that can be blocked with atropine. As the inhibition depresses, a very delayed excitation triggers strong bursts in both neurons. The LG and MG bursts are staggered as a result of their differential responses to Int 1 and their reciprocal inhibitory connections but differences in their IA conductance have not been ruled out since the phase differences disappear when applying 4-AP, a potent blocker of IA in STG neurons (Graubard and Hartline, 1991
; Szücs and Selverston, 2006
). Unlike the medial tooth subcircuit, the LG and MG provide negative feedback to Int 1 and play a role in terminating its activity. The LG and MG pair also strongly inhibit the tonically firing LPGs that are connected to them with reciprocal inhibitory synapses. This reciprocal inhibitory pathway could play a “network” role in sustaining the antagonistic firing pattern observed between the lateral teeth openers and closers. Our results support the idea that the Int 1-LG/MG connections are the most important for producing robust bursting in the entire CPG circuit.
Some Comments on Delayed Excitation from Int 1
Delayed excitation plays a key role in determining the firing pattern of DG and AM and performs a similar function in driving LG and MG firing but with the added complexity of being preceded by fast inhibition. The timing effects of Int 1 input to the DG/AM pair on the one hand and LG/MG on the other is to establish the firing sequence for the entire gastric CPG. The role of Int 1 in establishing the firing sequence for the entire system is summarized in Figure 13
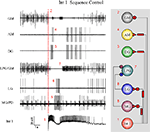
. The initial (short-term) effects of Int 1 hyperpolarization are to generally reduce overall gastric circuit activity. When Int 1 is released from hyperpolarization there is a strong burst due to PIR. In the preparation illustrated, the circuit was barely cycling so the firing order due to the intense burst of Int 1 spikes (1) can be clearly seen (see Figure 13
to find the appropriate numbers 1 to 7). The first observable result is an immediate inhibition of the tonically firing GM cells (2). Then the DG and AM start firing, slightly out of phase, after a short delay (3 and 4). Next there is fast inhibition of LG and MG followed immediately by their delayed excitation (5 and 6). As with the DG and AM, LG and MG begin to fire slightly out of phase. Finally at the termination of the LG and MG bursts, inhibition is removed from the LPGs and they start to burst (7).
Figure 13. Post-inhibitory rebound following steady hyperpolarization of the Int 1 neuron sets up a cascade of events that illustrate how the firing sequence for the entire gastric network is established. The start of the Int 1 burst (1) at the vertical red line immediately terminates GM activity (2) which can be seen both in the GM and LPG/GM traces. This is followed by a delayed burst in DG (3) and AM (4) and successive bursts in the MG (5) and LG (6) neurons. This later activity keeps the LPG off until both the LG and MG stop firing. The LPG activity (see the smaller unit in the combined trace) resumes after the LG/MG bursts terminate (7). Small units in the top GM trace are contamination.
What is the mechanism underlying the delay between the Int 1 burst and the depolarization of DG, AM, LG and MG? Delayed excitation has been described previously for other invertebrate circuits. The inking circuitry in Aplysia has a synapse between two neurons with an excitatory delay on the order of seconds (Byrne, 1980
) that appeared to be caused by a transient potassium current. Similar delayed excitation times (up to 4 s) have been reported for neurons in Tritonia (Getting, 1983
) and shown by voltage clamp experiments to also be due to an A-current. Neurons in the nucleus tractus solitarius of guinea pigs were found to have a delay of over 760 ms following the onset of a depolarizing stimulus, a delay also thought due to IA. However when we tried to block IA using 4-AP (Harris-Warrick, 2002
), there were strong effects on cycle frequency but no effect on the delayed excitatory response. Additionally, the slow excitation is also observed in voltage clamp conditions when the membrane potential of the DG neuron is being held constant, when A-currents are not being activated and cannot impose a delaying effect on the depolarizing response. Furthermore the excitatory depolarization of the cell did not have a reversal potential. This suggested the delayed excitation might be due to some non-ionotropic mechanism such as activation of metabotropic receptors by some substance other than Ach. One possibility was serotonin (5-HT) which had been shown to be contained in a sensory neuron (the gastro-pyloric muscle receptor, GPR) in crab that has inputs to the DG neuron (Kiehn and Harris-Warrick, 1992
) and known to depolarize DG via a dual conductance mechanism (Kiehn and Harris-Warrick, 1992
). We hypothesized if a co-released modulatory agent, perhaps 5-HT from Int 1 upregulates IH in the postsynaptic DG then a complete block of IH would remove the excitatory response. However, Cs application failed to block the excitatory response in DG. Although an immunohistochemical survey of stomatogastric neurons for 5-HT did not include Int 1 (Beltz et al., 1984
), it would be easy to miss because of its small size. If 5-HT were the cause of the delayed excitation it should be blocked with cinanserin which has been shown to be an effective antagonist in the STG system (Zhang and Harris-Warrick, 1994
). But, once more, this blocker proved to be ineffective. We have not yet explored the possibility of whether a second messenger system activated by some unknown neuromodulator could be the cause of the delayed excitatory response. Delayed excitatory synapses were shown in Tritonia neurons that received input from 5-HT containing cells. The responses had both a fast and slow component with the slow component being reduced in half by blocking G-protein activation with GDPβs while the opposite effects were obtained with G-protein analogues (Clemens and Katz, 2001
). Either way, the slow excitatory effect of Int 1 on multiple neurons of the medial and lateral tooth subcircuits appears to play a fundamental role not only in the generation of the overall gastric rhythm but also in setting the phases of the components. The remarkable robustness and interesting kinetic properties of this type of connection open the possibility that such excitatory connections exist in other rhythm generating systems and even in more complex brain circuits. It is noteworthy that an intense background synaptic activity with overlapping EPSPs and IPSPs can easily mask the slow excitatory wave in the intracellular recordings. Intense synaptic bombardment is common in complex brain circuits, hence, uncovering delayed excitatory responses in such systems, similar to those we found in the DG/AM and MG/LG neurons would be more challenging.
Synchronization of the Two Subsets
By strongly influencing the behavior of both the lateral and medial subsets, Int 1 provides the principle, but not the sole synchronizing force for the two rhythms. The actual mechanisms for how Int 1 plays this role are quite surprising since they involve more than inhibitory forcing of coupled oscillators as in the pyloric rhythm (Bal et al., 1988
). Instead Int 1 entrains key neurons from each subcircuit by using delayed excitation in one case and combined fast inhibition and delayed excitation in the other. There is a fast acting inhibition of LG and MG before the delayed excitation takes place and this appears very similar to the inhibitory response in the GMs where individual monosynaptic IPSPs from Int 1 are clearly visible Since the inhibition can be removed with atropine without affecting the delayed excitation, it is likely that two separate mechanisms are involved. By producing different time delays, Int 1 is able to control the temporal sequence of the motoneuron firing pattern. If the Int 1 soma membrane is driven with a sine wave shaped current all of the neurons in the gastric system follow the frequency of the sinusoidal input over a wide range.
In a small but complex neural circuit like the gastric CPG, the role of individual cells can be determined. There are not “extra” neurons to provide redundancy so the role of each neuron is well defined. But there still remains the question of whether some neurons play a more important role than others. There are two ways to address this question. Individual neurons can be killed and removed from the circuit. In a network of 11 neurons the removal of a single neuron is likely to have observable effects. Second, individual identified neurons can be perturbed with pulses of current or driven at different frequencies by sine wave currents and the effects of the perturbation in driving or resetting the overall rhythm observed. These procedures have shown that Int 1 is crucial to the operation of the network. Can we say the same for any of the other neurons? We can hypothesize that the MG/LG pair is crucial because they both excite the lateral teeth closer muscles and indirectly inhibit their antagonists the LPGs. Because the LG and MG are synergists, killing MG alone reduces some of the inhibition to the LPGs but LG and the medial tooth neurons are not affected at all. However, when both LG and MG are killed, a significant amount of inhibition from the LPGs is removed and their bursting is greatly diminished. Bursting in the GMs is also greatly reduced suggesting Int 1 is not operating properly. Only the DG and AM continue to have observable burst structures. The immediate removal of inhibition from Int 1 allows it to fire at a high frequency which immediately shuts off the GMs and induces strong bursting in DG and AM. Without MG and LG therefore the LPGs fire tonically. While LG and MG appear to play an integral role in the functioning of the gastric circuitry, the GMs and LPGs have generally been considered to be “followers” because they have a paucity of outputs to other neurons. This is true more for the GMs than the LPGs because they provide inhibitory feedback to LG and MG. Perturbations to the GMs have very little effect on the rest of the network. But perturbations to the LPGs show immediate effects on the whole system (Figure 10
). Hyperpolarizing even one LPG instantly increases the LG firing rate which then presumably decreases Int 1 firing thus allowing the single GM unit (shown in the figure) to fire weakly and the DG to shut off. The reverse is true when the LPG is depolarized – LG shuts off leading to a strong burst in DG and a shut down of GM.
Our computational model of the simplified circuit was able to reproduce the correct overlap of phase relationships between Int 1 and the DG/AM pair and the LG/MG pair. We did not test the overall stability of the circuit to every possible perturbation but the pattern changes that resulted from hyperpolarization or depolarization of Int 1 were accurate. We found that the inhibitory synapse from the LG to DG are very important in the model despite the fact that this feedback connection appeared to be quite weak when examined physiologically. LG also makes very weak inhibitory connections back to the GMs and their role may be more for insuring stability that establishing correct phase relationships. The slow excitatory connection is also very important to keep the proper phases in the model. Removal of that connection often leads to quasiperiodicity, which is a type of behavior not observed experimentally.
On the Generalization of Results
The mechanisms underlying bursting and pattern formation in the gastric mill CPG reported here are significant for two reasons. One is that they extend our knowledge of invertebrate CPGs to include a system with six separate phases in each cycle. As such it the most complicated behavior thus far described in terms of the interactions between individual identified cells. A second reason is that they provide clues as to what mechanisms might be operative in the complicated, multiphasic pattern generators found in vertebrates. CPGs have been studied effectively in a large number of invertebrate preparations where good explanations for CPG function at the cellular and circuit level now exist. While some of these are quite complicated, they rarely involve more than two or three phases per cycle. This paper adds significantly to this body of work since it describes in detail how a multiphasic rhythmic pattern is generated and some of the mechanisms we have described have not previously been observed. Nevertheless, it is legitimate to ask if understanding the lobster gastric mill CPG has any significance to those working outside the field of invertebrate neuroethology. Research on invertebrate CPG circuits over he last 40 years has clearly demonstrated that although basic oscillatory patterns contain many similarities, the actual wiring diagrams and the properties of the cells and synapses are unique to every species. A few general principles that are common to all have been suggested and principles that might be applicable to larger systems can help in modeling and analyzing them. Many examples of phenomena found at the cellular level have been shown to exist in both vertebrates and invertebrates including plateau potentials, non-spiking transmitter release, postinhibitory rebound and intrinsic bursting. The functional rewiring of CPG circuits by neuromodulators has also been demonstrated in small and large systems. Oscillatory activity, the usefulness of inhibition and mechanisms to advance or retard bursts of activity are features that can be found in vertebrates as well as invertebrates. But since the actual circuit layout and mechanisms of CPG circuits vary enormously between different invertebrate species, it will be a challenge to try and determine how the study of small circuits can help to get at the mechanisms used by large circuits, even if the problem of scaling is linear. We should be cautious in applying what we have learned to brain circuitry where observable phenomena are quite different. If invertebrate principles can be useful at all, they will likely be in helping to understand vertebrate circuits with similar functions such as those responsible for locomotion or respiration.
Summary
How do 11 neurons produce a reliable and remarkably stable six-phase motor pattern? Essentially, the main coordinating interneuron and 4 of the 10 motor neurons are intrinsic bursters. Like the pyloric system they form a system of coupled oscillators using mostly inhibitory synaptic connections but here there is an important excitatory connection as well. The basic rhythmicity and overall frequency of the CPG are due to the pacemaker properties of key neurons. The pattern itself is explained by the following thought experiment illustrated in Figure 14
.
Figure 14. Summary of synchronization of lateral and medial teeth circuits by Interneuron 1. Arbitrarily starting with an Int 1 burst exciting DG and AM, three phases of activity are set up (A). The DG and AM are motor neurons that reset the medial tooth are directly excited by Int 1. At the same time Int 1 also inhibits GM (B) so that it fires out-of-phase with the DG/AM pair and moves the tooth forward. Int 1 firing also activates the LG and MG neurons (C) but with a longer delay and this pulls the two lateral teeth together. Finally when LG and MG terminate their bursts, the LPGs can resume firing (D) and the lateral teeth are opened. See text for subsidiary connections shown in the box. Labels in the anatomical drawings: C, cusp; S, serrations; F, medial tooth; H, hinge.
• The intrinsically bursting and electrically coupled DG and AM are entrained by delayed excitation from the pacemaker neuron Int 1. Because DG is usually brought to threshold before AM, there is a small separation between these two agonists whose function is to reset the medial tooth (Figure 14
A).
• When the DG, AM and Int 1 bursts terminate, the four GMs are disinhibited and their bursts cause a forward (powerstroke) movement of the medial tooth (Figure 14
B).
• Int 1 firing first produces fast inhibition and then delayed excitation to LG and MG bringing them both to threshold about three quarters of the way through the Int 1 burst (Figure 14
C). LG provides strong inhibition to DG. Like DG and AM, there is a slight separation between the LG and MG phases. The LG and MG bursts act to close the lateral teeth (Figure 14
C).
• Finally, when the LG and MG bursts are terminated, the two LPGs are disinhibited and start firing which causes the two lateral teeth to be pulled open (Figure 14
D).
• There are therefore seven total synchronized phases produced by this simplified network operating at a frequency of about 0.1 Hz. This is somewhat faster than the in vivo gastric mill rhythms that have been reported in crabs (Powers, 1973
; Heinzel et al., 1993
) and lobsters (Turrigiano and Selverston, 1990
). In addition to the intrinsic burst frequency of Int 1, the presence of synapses with different strengths and time constants also contribute to the long bursts of motoneuron activity (Elson and Selverston, 1995
).
The connections not shown in the simplified diagram but having some role in the overall pattern, are illustrated in the box of Figure 14
.
• LG and MG are reciprocally connected with rapidly depressing inhibitory synapses and also with a strong electrical connection. The inhibitory synapses cause one neuron to fire before the other and the electrical synapses assures their synergistic action (Figure 14
A).
• The LG and MG are connected to the GMs with electrical connections to assure their synchrony as well (Figure 14
B). Behaviorally this causes the two lateral teeth to hold the food securely while the medial tooth is being pulled over them.
• MG and LG feed back inhibition to Int 1 which helps terminate the Int 1 burst (Figure 14
C). The reciprocal inhibitory connections may also contribute to the rhythmicity.
• The LPGs also are connected to the LG and MG with reciprocal inhibition and this may similarly contribute to the overall rhythmicity (Figure 14
D).
The total gastric circuit can be seen to consist of two subsets of neural oscillators. One of these, the medial tooth subcircuit is essentially a feedforward system of oscillators. Int 1 entrains the DG/AM pair by delayed excitation and this pair periodically inhibits the tonically firing GMs at a frequency controlled by Int 1. The other subset consists of two negative feedback loops, from Int 1 to LG/MG and from LG/MG to the LPGs. Of these, experimental evidence shows the first loop to be the most important in driving the circuit and imposing some stability onto the whole system. Finally, while Int 1 does much to synchronize the two subsystems, modeling studies show that the negative feedback from LG to DG/AM is vital in controlling the burst durations of the medial tooth neurons.
Canonical Model Neuron
The gastric CPG neurons were modeled using a two compartment conductance based model. We used this canonical model to capture the basic oscillatory pattern of these neurons so that their properties could be adjusted with a few free parameters. There is not sufficient information available to have a complete description of the ionic channels involved in the oscillatory patterns of these neurons. But we did have some idea of stomatogastric currents based on previous studies of the pyloric system (Golowasch and Marder, 1992
). Thus we used considerable intuition to determine the best currents that were capable of reproducing the gastric rhythm. The model was made of two compartments to simulate the small spikes on top of the bursts. The slow currents were situated in the equivalent of the soma, while the fast spikes were in the axon-neuropil compartment and assumed to be located far from the soma (Falcke et al., 2000
; Huerta et al., 2000
). The fast spike generator or axon-neuropil compartment is
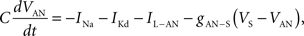
where INa is the fast sodium current, IKd is the delayed rectifier, IL is the leakage axon-neuropil, gAN − S represents the conductance between the soma and the axon-neuropil compartment, and C = 0.33 in units of nF that, for simplicity, will be the same for all the neurons in the circuit. The soma is given by the following ordinary differential equation:
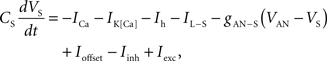
where ICa is the Calcium current, IK[Ca] is the calcium dependent potassium current, Ih is the low threshold depolarizing current, Ioffset is an offset current that is used to set the model neurons at different depolarized levels, Iinh is the inhibitory current delivered into the cell due to the other neurons interaction, Iexc is the excitatory current, and CS = 0.5 for all the model neurons in the gastric circuit. Each of the individual currents is modeled as the standard Hodgkin–Huxley formalism:
INa = gNa m∞ (VAN)3 n (t) (VAN − 50 mV),
IKd = gKd h (t)4 (VAN + 80 mV),
IL − AN = gL − AN (VAN + 65 mV), IL − S = gL − S (VS + 65 mV),
Ih = gh s (t) (VS + 15 mV),
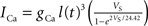 for room temperature, and
for room temperature, andIK[Ca] = gK[Ca] u (t) (VS + 70 mV).
The Sodium current assumes instantaneous current activation because it saves computational time without affecting too strongly the shape of the spike. The calcium dependent potassium current differs from the most common approach because we introduced an activating variable that depends on the intracellular calcium levels. This change allowed for a better control of the burst duration. The Calcium current follows the Goldman–Hodgkin–Katz formalism due to the large difference between the intracellular and extracellular calcium concentrations. It is worth noting that this current has an inherent singularity in the computer implementation for VS = 0. Therefore it is advisable to make the first order expansion of ICa in the proximity of VS = 0 as gCa l (t)3 (VS − 24.42)/2. Note that we left many other currents intentionally out of the model because we wanted a minimal model that could still produce a reasonable agreement with the experimental data. Two notable currents that were left out in this model are the IA which is generally a pretty strong current in the pyloric system and the persistent Sodium current which is responsible for prolonged periods of spiking activity. The persistent Sodium current is partially represented by using constant depolarizing current for each of the neurons. The rest of the equations that are dependent on membrane potential are described as
m∞ (VAN) = Γ (VAN, 8.5, 5.29),
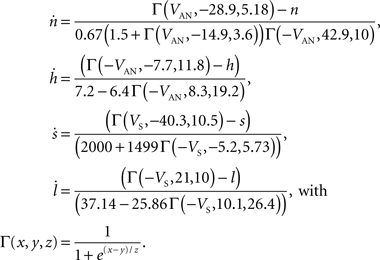
The differential equation that controls the activation of the IK[Ca] as a function of the Calcium concentration is
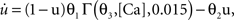
where the parameters will be given below and the Calcium concentration time evolution is governed by a simple a standard first order kinetic equation:
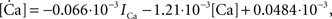
where [Ca] has units of μM and time has units of milliseconds.
The parameters that will be the same for all the model neurons are:
gNa = 80 μS, gKd = 20 μS, gL − AN = 0.024 μS, gL − S = 0.0024 μS,
and the free parameters individualized for each neuron are:
gAN − S, gh, gCa, gK[Ca], θ1, θ2, θ3, Ioffset.
We recommend introducing the parameter values as stated in this section for computer code implementation. The parameters of the Calcium dynamics can be optimized for numerical precision, but the slow variation and simple dynamics does not make it necessary.
The Model of the Gastric Circuit
For modeling purposes we assume there are six principle neuron types in the central pattern generator: DG, GM, Int 1, LG, MG, and LPG. The LG and MG are lumped together because they have a strong gap junction that synchronizes them very strongly.
The parameter gAN − S regulates the size of the spikes on top of the burst (Table A1
). gCa controls the strength of the depolarization of the burst. This parameter cannot be moved freely because it has a nonlinear impact on the other parameters. gh gives rebound depolarization. gK[Ca] determines the sharpness of the end of the burst, θ1 θ2 θ3 allows to better control the duration of the burst of each individual neuron, Ioffset is the most convenient manner to shift the neuron from bursting to spiking behavior and it also helps to replicate to some extent the impact of the persistent Sodium current. In particular, the LPG is highly depolarized. An example of the voltage traces of the model can be seen in Figure 12
.
Synaptic and Non-Synaptic Interactions: Neuron to Neuron Interaction
Most of the connections are graded fast inhibition. These can be easily modeled by using
Isyn = gsyn r (Vpre) (VS − Vpost)
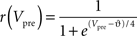
Each neuron has its separate threshold of activation ϑ. The Table A2
is given below. The connectivity matrix between the gastric neurons is given in Table A3
.
The Int 1 has synaptic depression in the inhibitory connection that can be modeled by using
Isyn = gsyn r (Vpre) (0.6 + 0.4 (1 − s (t)) (VS − Vpost)
with
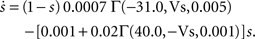
The shunting variable gets activated with a slow time scale such that when it reaches the maximum value it can reduce the strength of the connection by 40%.
The Int 1 has excitatory connections to the DG and to the LG/MG. This connection is slow and does not have reversal potential dependence on the post connection neuron as a standard synaptic connections do. The mathematical model for this synapse is
Isyn = gexc ρ (t)
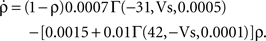
Note that ρ is bounded between 0 and 1. It also has a slow activation as observed experimentally with a reset mechanism that quickly drives the variable to 0 when the membrane potential drops below 42 mV. We also introduce a depression in this excitatory connection as
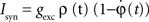
In this case the excitatory connection shuts down completely when the Int 1 has fired for a long time. Note that the equations for the activation and inactivation have a very similar form and that the main difference is just the time scale.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Support for this work came from the National Institute of Health under grant NINDS R01 NS050945.
Katz, P. S., and Harris-Warrick, R. M. (1989a). A new role for proprioceptive feedback to CPGS: neuromodulation by serotonergic/cholinergic mechanosensory afferents to the stomatogastric ganglion of crabs. In Neural Mechanisms of Behavior, J. Erber, R. Menzel and H. Pfluger, eds (Stuttgart, Georg Thieme Verlag), p. 229.