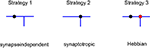Cold Spring Harbor Laboratory, Cold Spring Harbor, NY, USA
In developing brain, axons and dendrites are capable of connecting to each other with high precision. Imaging of axonal and dendritic dynamics in vivo shows that the majority of axonal and dendritic branches are formed ‘in error’, only to be retracted later. The functional significance of the overproduction of branches is not clear. Here we show that branching of both axons and dendrites can accelerate finding appropriate synaptic targets during the development of neuronal circuitry. We suggest that branching rules implemented by axons and dendrites minimize the number of erroneous branches. We find that optimal branching rules are different for axons and dendrites in agreement with experimentally observed branch dynamics. Thus, our studies suggest that the developing neural system employs a set of sophisticated computational strategies that facilitate the formation of required circuitry in the fastest and most frugal way.
Neural development is a dynamic process that leads to the establishment of precise connectivity (Ruthazer and Cline, 2004
). In vivo time lapse imaging has shown that the formation of axonal and dendritic arbors involves the simultaneous creation and elimination of neuronal branches and synapses (Alsina et al., 2001
; Niell et al., 2004
; Haas et al., 2006
; Meyer and Smith, 2006
; Ruthazer et al., 2006
; Sanchez et al., 2006
). The high rate of branch turnover results in the formation of a number of branches that substantially exceeds the number maintained in the mature brain (Rajan et al., 1999
; Meyer and Smith, 2006
). These observations suggest that a form of ‘trial-and-error’ search algorithm is implemented by axons and dendrites (Hua and Smith, 2004
).
The branching of axons and dendrites depends upon the synapses they form. First, branch survival depends on the presence and strength of the synapses it bears (Niell et al., 2004
; Meyer and Smith, 2006
; Ruthazer et al., 2006
). Second, a spatial bias of the locations of branch points towards synapses has been reported (Alsina et al., 2001
; Meyer and Smith, 2006
), suggesting that new branches are formed preferentially in the vicinity of synapses. Finally, it has been shown that the rates of branch additions and retractions are affected by neuronal electric activity. These rates increase for retinal axons and decrease for tectal dendrites after an NMDAR antagonist is applied to a developing Xenopus laevis retinotectal system (Rajan et al., 1999
; Sin et al., 2002
). The branching rules, therefore, are different for axons and dendrites. The functional significance of the asymmetry between axons and dendrites is not clear.
Here, we theoretically investigate the role of branching in the formation of neural connectivity. We ask three questions stemming from the experimental findings mentioned above. First, we ask: what is the functional significance of branching, from the standpoint of neural development? Second, we ask why axons and dendrites preferentially form branches in the vicinity of synapses. Third, we address the asymmetry in the branching rules between axons and dendrites that has been revealed in experiments on NMDA receptor blockade. To answer these questions, we have developed a computational model that allows us to compare different branching strategies, based upon the speed of development of target circuitry and the number of ‘erroneous’ branches formed. We show that three prominent features of axon and dendrite dynamics can be viewed as evolutionary adaptations that save time and minimize the number of errors. We propose experimental tests that can differentiate the various branching strategies used by axons and dendrites.
We propose a mathematical description of the dynamics of axonal and dendritic arbors, using the theoretical model of stochastic growth. In this model, new branches are created, eliminated, elongated and retracted randomly, with probabilities dependent upon how the energy of the system changes after a segment of a branch is added or removed. The neural connections are formed in the model by creating synapses between the branches of spatially overlapping axons and dendrites. Similarly to branches, the synapses can be created, maintained, or retracted, in a stochastic manner, depending on the energy change that results from these actions. We simulate the developmental process using the Metropolis Monte Carlo algorithm. On each Monte Carlo step, one of the six changes is attempted: formation, elimination, extension or retraction of branches, or creation or elimination of synapses. The attempts for every possible configuration changes are equally likely. Thus we attempt to form a synapse between every pair of overlapping axonal and dendritic branch segments with the same probability but the acceptance probabilities for these attempts are different. Similarly, the attempts to eliminate every existing synapse are equally likely but their survival probabilities differ. The acceptance probabilities for every configuration change depend upon the change in the energy function that occurs during these processes, ΔE, and are given by:
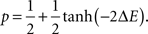
Acceptance probability is smaller/larger than 1/2 if the underlying change in the energy function is positive/negative. As a result, the system performs the stochastic minimization of its energy. The exact form of the energy function defines both the dynamics of the arbors and the final connectivity configuration (Tsigankov and Koulakov, 2006
).
The energy function incorporates the affinity that exists between connected cells and the configuration of the arbors. It contains additive contributions from axonal and dendritic branches and synaptic connections:
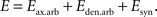
The contribution from arbors to the energy function is positive, meaning that there is a cost associated with the formation of branches. We also suggest that the synaptic contribution is negative, reflecting the tendency of neurons to form synapses. This contribution is different in magnitude for every synapse, and depends upon interactions between the connected cells. Combined together, these contributions reflect the synaptotropic hypothesis (Hua and Smith, 2004
; Meyer and Smith, 2006
), since the cost of a branch bearing a synapse is reduced, and such a branch is more stable than a branch without synapses.
The synaptic part of the energy function depends on the connectivity between axons and dendrites, given by the weight matrix Wij which is step-wise updated according to the evolution of axonal and dendritic arborizations during the simulation. We previously have studied the form of the synaptic energy function for the system of point-like dendrites and a single synapse per axon (Tsigankov and Koulakov, 2006
). Here, we reformulate it for the system of axons and dendrites with spatially distributed arbors that have multiple synaptic connections. The weight matrix Wij consists of the integer numbers representing the number of synapses made between ith tectal dendrite and the jth retinal axon anywhere on their arbors. There are three additive terms in the synaptic part of energy, representing different contributions:
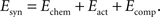
The chemoaffinity term depends upon the interactions between the chemical labels expressed on axons and dendrites. For the retinocollicular system, this is given by the expression levels of EphA and EphB receptors on axons, and of ephrinA and ephrinB ligands on dendrites:
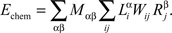
Here, indices α and β denote the chemical labels; the matrix Mαβ defines the affinities for receptor/ligand pairs; and 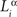 ,
, 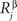 are the concentrations of ligand α and receptor β on the ith dendrite and the jth axon, respectively. Throughout the paper, we have adopted the simplest description, where we distinguish only two types of receptor and ligand expressed in the gradients in perpendicular directions in both the target and retina; for details see (Koulakov and Tsigankov, 2004
; Tsigankov and Koulakov, 2006
).
are the concentrations of ligand α and receptor β on the ith dendrite and the jth axon, respectively. Throughout the paper, we have adopted the simplest description, where we distinguish only two types of receptor and ligand expressed in the gradients in perpendicular directions in both the target and retina; for details see (Koulakov and Tsigankov, 2004
; Tsigankov and Koulakov, 2006
).
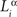 ,
, 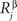 are the concentrations of ligand α and receptor β on the ith dendrite and the jth axon, respectively. Throughout the paper, we have adopted the simplest description, where we distinguish only two types of receptor and ligand expressed in the gradients in perpendicular directions in both the target and retina; for details see (Koulakov and Tsigankov, 2004
; Tsigankov and Koulakov, 2006
).
are the concentrations of ligand α and receptor β on the ith dendrite and the jth axon, respectively. Throughout the paper, we have adopted the simplest description, where we distinguish only two types of receptor and ligand expressed in the gradients in perpendicular directions in both the target and retina; for details see (Koulakov and Tsigankov, 2004
; Tsigankov and Koulakov, 2006
).The activity-dependent term is obtained from the Hebbian learning rule and has the form:
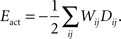
Here, Dij is the correlation of electrical activity between tectal dendrite i and retinal axon j. The correlations Dij change over the course of development and depend on the weight matrix Wij. They arise from the correlations of activity between retinal axons that are driving the activity of tectal dendrites, through the following expression:
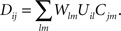
Cjm is the correlation of activity between retinal axons j and m that emerges from the spontaneous retinal waves of activity or early visual experience, and is assumed to be unvaried during the development. Uil is the strength of the lateral connections between tectal cells i and l and is also assumed to be constant. Both these functions are assumed to depend only upon the spatial separation that exists between the origins of axons j and m in retina and dendrites i and l in tectum, respectively and are given by (Tsigankov and Koulakov, 2006
):
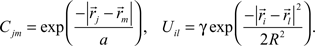
The last term Ecomp in the synaptic part of the energy function describes axonal and dendritic competition and ensures the tendency of neurons to form synapses. This term is negative and depends upon the number of synapses made by each neuron, similarly to what was proposed for the system of neuromuscular junctions (Barber and Lichtman, 1999
). If the energy gain decreases with an increase in the total number of synapses per cell, then cells with fewer synapses have a competitive advantage to form new synapses. As a result, every axon and every dendrite maintains approximately the same number of synapses. In our model, we used the following form of energy contribution with this property that has the least number of parameters:
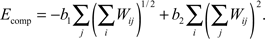
The sums in the brackets give the number of synapses made by axons and dendrites respectively; b1 > 0 and b2 > 0 are the constants defining the average number of synapses per cell and overall strength of competition.
The arbor parts of the energy function that describe the costs for axonal and dendritic branching are given by:
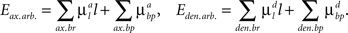
Here the first sum over axonal and dendritic branches yields the cost for the branch with length l, and the second sum represents the additional cost for the formation of the branch points. We assume that the costs of the branches per unit length 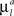 and
and 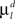 are constant and are taken to be the same for axons and dendrites, in order to ensure symmetry between axons and dendrites.
are constant and are taken to be the same for axons and dendrites, in order to ensure symmetry between axons and dendrites.
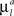 and
and 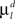 are constant and are taken to be the same for axons and dendrites, in order to ensure symmetry between axons and dendrites.
are constant and are taken to be the same for axons and dendrites, in order to ensure symmetry between axons and dendrites.In contrast, we vary the costs of branch points 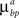 and
and 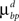 and use different forms for different branching strategies. If axons or dendrites use synapse-independent branching Strategy 1, we use the same branching cost everywhere on the arbor:
and use different forms for different branching strategies. If axons or dendrites use synapse-independent branching Strategy 1, we use the same branching cost everywhere on the arbor:
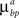 and
and 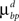 and use different forms for different branching strategies. If axons or dendrites use synapse-independent branching Strategy 1, we use the same branching cost everywhere on the arbor:
and use different forms for different branching strategies. If axons or dendrites use synapse-independent branching Strategy 1, we use the same branching cost everywhere on the arbor: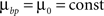 .
.For synaptotropic branching Strategy 2, we use
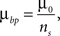
where ns is the number of synapses on the arbor in the same unit square with a branch point. Thus it is easier (less costly) to create branch points at locations that contain several synapses.
Finally, for Hebbian branching Strategy 3, the cost has the form
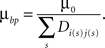
Here, the sum is taken over synapses made on branches in the same unit square with a branch point, and Dij is the correlation of the electrical activity between dendrite i and axon j connected with these synapses. This form makes it less costly to create branch points at synapses with correlated activity.
In this description, for every branching strategy used, we vary the overall amount of branching by changing the single parameter μ0. If it equals to zero then there is no additional cost for formation of new branches and the branching is the most elaborate. If it tends to infinity there is essentially no branching and each arbor has only one branch tip. We then change parameter μ0 to investigate the role of branching on the performance of developmental algorithm for every branching strategy.
To compare the performance of different branching strategies we vary every parameter in the branching part of the energy function and keep every parameter in the synaptic part of the energy function constant. For every set of parameters in the energy function we have averaged over 100 random initial conditions. More precisely we start with axons entering the target from the anterior edge, randomly arranged along dorsal ventral axis with a single branch tip representing the point like initial arbors on the edge of the target. The initial conditions for dendritic arbors are point like initial arbors arranged topographically across the target. Therefore only random initial conditions of axons vary from simulation to simulation. Initially the system contains no synapses. All synapses are therefore created during the simulation. To show that different initial conditions can be a sole reason for the asymmetry between axons and dendrites we present the simulation results for the symmetric case when axons and dendrites have the same cost per branch length.
For all 9 combinations of branching strategies we used 10 different values for both axonal and dendritic branching cost, thus 10 × 10 sets of 100 simulations with different initial conditions. Thus the comparison of different branching strategies is obtained from almost 100,000 simulation runs each taking about 4 h each on a high-performance computing cluster.
Formation of Retinotectal Connectivity is Influenced by Several Factors
The projections from the retina to optic tectum often are used as a model system to study the development of neural circuitry. While establishing this projection, the axons of retinal ganglion cells (RGC) arrive at the optic tectum and make topographically ordered connections with dendrites in the target. This implies that axons originated from neighboring points in retina terminate at proximal tectal dendrites, thus preserving a topographic representation of the visual world. This form of connectivity is often called a ‘topographic map’.
Several factors contribute to the formation of topographic maps. A set of chemical labels is thought to encode coordinates in the retina and tectum (McLaughlin and O’Leary, 2005
). Thus, the nasal–temporal (NT) axis in the retina is encoded by the graded expression of EphA receptor tyrosine kinases on RGC axons (Flanagan and Vanderhaeghen, 1998
). The recipient anterior–posterior coordinate in the tectum is established by graded expression of ephrin-A, which can bind to and activate EphA receptors, and transmit to RGC axons information about their position in the target. A similar chemical labeling system, involving an EphB/ephrin-B receptor/ligand pair, exists for the mapping of the dorso-ventral (DV) axis of the retina to the medial-lateral (ML) direction of the optic tectum. The two approximately perpendicular expression profiles appear to be in place to bias axonal branching in the direction of the correct termination site (Lemke and Reber, 2005
).
The precision of axonal projections is further enhanced through mechanisms based upon correlated neural activity (Ruthazer and Cline, 2004
). Due to correlations in the visual stimuli or the presence of retinal waves during development, electrical activity is similar in neighboring RGC axons in the retina (McLaughlin et al., 2003
). Correlated activity, therefore, provides additional information about relative positions of axonal origins in retina, and contributes to the precision of topographic projection (McLaughlin et al., 2003
; Pfeiffenberger et al., 2005
). Finally, competition between axons in the target is thought to be an important factor in the formation of the map (Hua et al., 2005
). The interplay of chemo-specificity, activity-dependent factors, and competition results in the formation of connectivity that sometimes can achieve single-cell precision (Hamos et al., 1987
).
Precise connectivity requires spatial overlap between an axonal arbor and the arbors of appropriate dendrites. This is because the synapses can be made only between segments of axonal and dendritic branches that are in close proximity; i.e., have the potential to form connectivity (Stepanyants and Chklovskii, 2005
). Thus, before appropriate axons and dendrites are connected, they must solve the search problem, which implies that axons have to arrive in the area of appropriate dendrites. This task is achieved by creating and eliminating new axon and dendrite branches (Alsina et al., 2001
; Ruthazer et al., 2003
; Meyer and Smith, 2006
). The exact rules by which axonal and dendritic branching occurs and their functional significance are not known. Here, we identify the axonal and dendritic branching rules that implement the optimal search strategy, based upon the conservation of material and time.
Branching Allows for Faster Formation of Target Connectivity
To compare various search strategies, we have developed a computational model for the stochastic growth of axonal and dendritic arbors. This model describes the behavior of RGC axons that form synapses with a matching set of tectal dendrites (Figure 1
). Both axons and dendrites can create, eliminate, extend, and retract their branches. In addition, an axon and a dendrite with overlapping arbors can form a new synapse or eliminate the existing one. All these events occur stochastically, with probabilities biased towards the formation of a topographic map. A conventional method to describe such a bias is to introduce an energy function (Fraser and Perkel, 1990
; Koulakov and Tsigankov, 2004
; Tsigankov and Koulakov, 2006
). With this approach, the stochastic events of creation and elimination of new branches and synapses are biased in the direction of an overall decrease in energy function. The energy function includes both contributions from the binding and activation of chemical labels, such as Eph receptors, and the contribution arising from the correlations in electric activity that exist between retinal axons (see Materials and Methods for details). The exact form of the energy function defines both the dynamics of the arbor formation and the structure of the ultimately established connectivity.
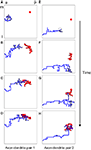
Figure 1. The structure of developing axons and dendrites in silico as a function of time. (A–D) The evolution of the axonal (blue) and dendritic (red) arbor in the model is achieved by creating and eliminating new branches and retracting and elongating existing ones. A particular pair of axons and dendrites is shown out of 900 simultaneously evolving axonal and dendritic arbors. The shown dendrite is the main recipient of the synaptic connections (black circles) for the shown axon, once topography is established. (E–H) The evolution of another pair of axon and dendrite is shown for the same simulation.
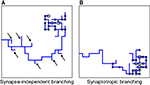
Using this approach, we investigated different branching strategies available to axons and dendrites. One possibility is that formation of new branches occurs everywhere on the arbor with the same probability, independent of the locations of synapses. We call this type of branching strategy synapse-independent or Strategy 1 (Figure 2
). Another option is to preferentially form new branches in the vicinity of existing synapses. This strategy is called synaptotropic or Strategy 2. Finally, we considered the possibility that branches are formed preferentially in the vicinity of synapses with correlated pre- and post-synaptic activity. This form of branching rules is called Hebbian or Strategy 3. To implement these branching rules, we introduced the cost of the formation of a branch point that differs for the different strategies. This cost was included in the cost function, as described in Materials and Methods. Thus for strategies 2 and 3 we set the probability of branching at non-synaptic sites to zero. We show below that every branching strategy is capable of producing the required connectivity, but their efficiencies differ.
Figure 2. Different branching strategies available to axons and dendrites. Strategy 1: a new branch point on the arbor (blue) can be formed anywhere, independent of the location of synapses (black circle). Strategy 2: new branch points are formed preferentially in the vicinity of existing synapses. Strategy 3: new branch points are formed preferentially in the vicinity of synapses with correlated pre- and postsynaptic activity only (red circle).
As measures of the efficiency of different branching strategies, we used the time and the total number of branches formed (dendritic and axonal) that are required to achieve target mapping precision. The mapping precision is determined by the average mapping error of every synapse as compared to the perfect topographic map. Thus for every synaptic connection we calculate the mismatch between the position of the axonal origin (RGC body) and the position of post-synaptic cell body in the target. We propose that a more efficient developmental mechanism should allow for the formation of required connectivity using less physical time and less material for creating and elongating neuronal branches. These two separate criteria are not independent and cannot be minimized simultaneously. In fact, we show that there is a trade-off between time and the number of branches: if connectivity is formed faster, it uses a greater number of branches, and vice versa.
To illustrate the trade-off between time and the number of branches formed, we consider the case in which both axons and dendrites implement synapse-independent branching (Strategy 1). One of the parameters that can be varied in the model is the probability of forming a new branch point on an axon. If this probability is small, axon arbors have a simple structure with few branch points (see inset on Figure 3
A). Nevertheless, the mapping error is decreased over time and can always reach the target value (Figure 3
A), even if virtually no branches are formed. If the branching probability is increased, the arbor structure becomes more complex with more branch tips. This results in a faster convergence of map precision, because multiple branches are searching for the correct partners in parallel. At the same time, higher branching frequency results in a greater number of transient branches formed by the time connectivity with the required precision is established (Figure 3
B). Thus, faster convergence of the map can be accomplished by forming a larger number of branches, implying a trade-off between the time of development and the amount of material used. These findings suggest a possible functional role for axonal branching, as an effective parallel search algorithm that allows for the conservation of time during development.
Figure 3. The influence of branching on time and material cost. (A) The time dependence of mapping precision is shown for simulations involving different probabilities of axonal branching when both axons and dendrites use branching Strategy 1. When the probability of branching is low, axons have very few branches; meanwhile, when the probability is high, the axonal arbors are complex (inset). Mapping with the same degree of precision is established faster when the probability of branching is higher. (B) The time-dependence of the number of branches formed is shown for the same set of simulations, as in (A). Each circle in (B) corresponds to a circle in (A) and shows the time and the number of branches formed when a 15% level of mapping precision is reached. A mapping precision level of 15% implies that the standard deviation of synapse location is 15% of the map size. (C) A set of curves similar to that shown in (B) is obtained when both axonal and dendritic branching probabilities are varied. Points corresponding to the same axon/dendrite branching probabilities are connected by solid/dashed lines. The lower boundary of the collection of these points [blue line in (C)] gives the performance boundary for this combination of branching strategies used by axons and dendrites.
Synaptotropic Branching Minimizes the Total Number of Branches Formed
We next optimized the total number of transient branches formed for varying frequencies of both axonal and dendritic branching if they use synapse-independent branching Strategy 1. To this end, we obtained a series of curves similar to those shown in Figure 3
B for different values of dendrite branching frequency. The lower boundary (blue in Figure 3
C) of the collection of these curves defines the optimal performance of this combination of branching strategies (Strategy 1 for axons and Strategy 1 for dendrites). This performance boundary depicts the minimal number of branches that are required to establish the connectivity with given level of precision after a given period of physical time.
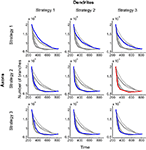
To compare the efficiency of different branching strategies, we obtained the performance boundaries for all 9 combinations of strategies used by axons and dendrites; i.e., strategies 1 through 3 for axons and 1 through 3 for dendrites (Figure 4
). The combination of branching strategies with the lowest boundary allows for the most effective formation of circuitry.
Figure 4. Performance boundaries for different combinations of branching strategies used by axons and dendrites. The performance boundary depicts the minimal number of branches that are required to establish connectivity with a given level of precision after a given length of time. Alternatively, it provides the minimal time required to achieve the configuration with a given level of precision using a predetermined number of branches. In each panel, the colored curve (blue or red) represents the boundary for a specified combination of branching strategies. The boundaries for other combinations are shown in grey, for comparison. The red curve depicts the optimal performance boundary that corresponds to the combination of Strategies 2 and 3, used by axons and dendrites, respectively.
One of the findings evident from Figure 4
is that both synaptotropic strategies (activity-dependent and -independent) generally outperform the synapse-independent strategy. Thus, if both axons and dendrites implement synapse-independent branching (Figure 4
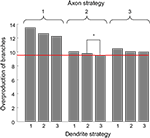
, top left panel), the performance boundary represents the worst solution. This is because the performance boundary for this case is higher than all eight other performance boundaries. The same conclusion follows from examining the number of branches averaged along the performance boundary (Figure 5
). The three bars on the left, representing the synapse-independent strategy implemented by axons, are higher than all others, reflecting the inefficiency of the synapse-independent branching rule. A similar conclusion is reached comparing the dendritic strategies (Figure 5
). Therefore, for both axons and dendrites, synaptotropic branching improves the performance of the search algorithm over synapse-independent rules. This finding suggests a functional role for the spatial correlations between the branch points and synapses observed among axons (Alsina et al., 2001
; Meyer and Smith, 2006
). According to our results, the increased probability to form a branch point at an existing synapse (synaptotropic branching) allows for the establishment of required connectivity using fewer transient branches.
Figure 5. The average overproduction of branches for nine combinations of branching strategies used by axons and dendrites. The overproduction of branches is the ratio of the number of branches formed to the minimal number of branches required to establish the topographic map. We then average this value over the performance boundaries from Figure 4
. The most effective is the combination of branching Strategy 2 for axons and Strategy 3 for dendrites (level shown by red line). The statistical difference between the optimal combination of branching strategies and the second best combination (shown by the star) corresponds to p-value less than 10−4.
The Optimal Branching Rules are Different for Axons and Dendrites
What is the optimal synaptotropic branching strategy? In our simulations (Figures 4 and 5
) the most efficient combination of branching rules is achieved when axons implement Strategy 2 (synaptotropic), while dendrites implement Strategy 3 (Hebbian). The performance boundary for this combination of branching rules (red in Figure 4
) is lower than all other eight curves. This implies that the optimal branching rules are different for axons and dendrites. To minimize the total amount of material spent on transient branches, axons branch in the vicinity of existing synapses. But the frequency of such branching does not depend upon the correlations in patterned pre- and post-synaptic activity. At the same time, optimal dendritic branching is achieved when new branches are formed more likely in the vicinity of synapses with higher levels of correlated activity.
If axons and dendrites implement different branching strategies, they can react differently to activity blockade. Consequently, our findings could explain the differences in the reaction to the blockade of NMDA receptors observed in developing retinotectal projections of Xenopus laevis (Rajan et al., 1999
). To mimic the blockade of NMDA receptors in the model, we set the activity correlations to zero during simulations. We used the optimal combination of synaptotropic branching strategies (Strategy 2 for axons and Strategy 3 for dendrites). We observed that, for axons, both the rate of addition and retraction of branches increase after activity blockade (Figure 6
). This is because, while the frequency of axonal branching does not change at any location on the arbor if axons implement activity-independent branching rules, the area occupied by the axonal arbor increases due to the loss of map precision induced by the activity block. Hence, larger arbors produce an increased rate of branch turnover.
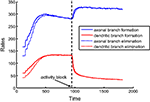
Figure 6. Rates of branch additions and retractions before and after activity block. The time dependence of axonal (blue) and dendritic (red) dynamics is shown for when axons implement the activity-independent synaptotropic branching strategy and dendrites use Hebbian branching strategy. This combination of branching strategies is optimal. The rates of branch additions (solid curves) and retractions (dotted curves) increase for axons and decrease for dendrites after the activity strength is set at zero (arrow) during simulation. In this simulation, the costs of dendritic and axonal branch lengths are unequal, so as to produce shorter dendrites.
At the same time, the rates of formation and elimination of dendritic branches are decreased after the levels of activity are reduced. This is a consequence of the activity-dependent branching rule (Strategy 3) implemented by dendrites, because the frequency of branching in the vicinity of the synapses is reduced. Therefore, in our model, the behavior of axons and dendrites is different, due to the differences in the optimal branching strategies. The experimentally-observed asymmetry in the reaction of axons and dendrites to NMDA receptor blockade could be a manifestation of different branching strategies being implemented by axons and dendrites in developing brain.
During neural development, axons solve the problem of locating the dendrites of appropriate cells and creating synapses with them. Finding appropriate synaptic partners occurs in the presence of other axons and dendrites, and is influenced by several factors, such as molecular labels and correlations in electric activity. How can precise connectivity be formed in the developing brain under the constraints of limited resources, like time and material? It is common to benchmark different algorithms based upon the number of steps that they require to solve particular problems. The algorithm that solves a given problem with the smallest number of iterations usually is implemented. In this study, we benchmarked various algorithms for axonal and dendritic branching, and derived the branching rule that solves the problem of forming connectivity with the smallest number of steps. We assumed that the elementary step in the development of brain circuitry is the formation or elimination of an axonal or dendritic branch. We, thus, compared different branching rules, in terms of the total number of branches needed to form target circuitry. We assumed that the search strategy that allows for the location of targets using the fewest number of transient branches is implemented in the developing brain. This point is similar to the wiring optimization argument (Chklovskii and Koulakov, 2004
).
We centered our studies on the role of synapses in the development of connectivity. In the developing retinotectal projection, synapses are formed and eliminated, as axons (Alsina et al., 2001
; Meyer and Smith, 2006
; Ruthazer et al., 2006
) and dendrites (Niell et al., 2004
; Haas et al., 2006
; Sanchez et al., 2006
) refine their connectivity. The role of synapses in this process may be diverse: they stabilize existing axon branches (Meyer and Smith, 2006
) in a way that is dependent upon synaptic maturation (Ruthazer et al., 2006
) and may contribute to the process of forming new branches (Meyer and Smith, 2006
). The latter possibility is highlighted by strong correlations between the locations of synaptic puncta and the branch points observed for both axons and dendrites (Alsina et al., 2001
). The effect of synapses on branch formation and elimination sets the basis for the synaptotropic hypothesis, according to which the formation of axonal and dendritic arbors is instructed by synapses. Here, we investigated the functional significance of the instructive role of synapses in the formation of new branches. To this end, we compared the branching rule that does not take into account the location of synapses (synapse-independent) with the synaptotropic branching rules. The latter make forming a new branch at the location of existing synapse more likely. We found that the synaptotropic branching rule allows for the formation of target connectivity using fewer erroneous branches (fewer steps). Consequently, our study implies that the functional significance of the observed correlations between branch points and synapses (Alsina et al., 2001
) are the result of a frugal developmental mechanism.
We illustrate the advantage of synaptotropic branching rules for axons in Figure 7
. The axonal arbor has segments proximal to its correct termination zone (TZ) and segments distal to its TZ. The formation of new branches along the proximal segments of the arbor contributes to arbor growth towards its TZ, while formation of new branches along distal segments is a waste of material. How can axons distinguish between the proximal and distal regions of the arbor? The transient synapses are located on the segments of the arbor closest to the correct TZ, because they are made with more appropriate dendritic partners and, thereby, are more stable. As a result, synaptotropic branching allows for avoidance of the formation of erroneous branches on distal parts of the arbor, and for establishing spatial overlap between appropriate pairs of axonal and dendritic arbors using fewer steps.
Figure 7. Comparing synapse-independent branching and synaptotropic branching for axons. (A) If the branching is synapse-independent, new branches are formed along all segments of the arbor, both proximal and distal to the correct TZ. (B) In the case of synaptotropic branching, new branches are formed only along the arboreal segment closest to the correct TZ, and there are no erroneous branches formed along segments that are far away from its future TZ [marked by arrows in (A)]. Thus, synaptotropic branching allows for axons to reach the correct TZ using fewer branches.
We have further investigated the possible role of correlated electric activity on the synaptotropic branching rules. We compared the activity-independent synaptotropic branching strategy when new branches are formed with the same probability in the vicinity of all existing synapses versus Hebbian activity-dependent synaptotropic branching when the branches are preferentially formed at the synapses with high correlations between the activity of pre- and post-synaptic cells. We found that there is a slight decrease in the total number of branches used, if dendrites but not axons implement Hebbian branching. These results suggest that axons and dendrites have different optimal branching strategies.
What is the origin of asymmetry in the optimal branching rules between axons and dendrites? Axons and dendrites solve similar search problems during the formation of connectivity but there is a difference in the initial conditions. When axons of retinal ganglion cells enter the optic tectum, they lack spatial order. In contrast, dendritic arbors originate from somas of tectal cells that are topographically arranged in the target. To reflect this difference in the model, the axons were initially arranged along one of the edges of the simulation volume corresponding to anterior tectum. The initial positions of axons within the edge were completely random. On the other hand, dendrites started to grow in the beginning of the simulation from topographically arranged positions. We argue that the difference in initial conditions led to the asymmetry of optimal strategies between axons and dendrites. Indeed, our model has no difference in the branching rules between axons and dendrites. Although synaptic part of the energy function includes a small asymmetry, synapses influence the branching rules identically. Therefore, axons and dendrites can implement identical branching rates when use the same branching strategies. The most substantial quantitative difference between axons and dendrites is in the initial conditions. We suggest that this difference is primarily responsible for the asymmetry in the optimal branching strategies between axons and dendrites.
The possibility that dendrites may use Hebbian branching strategy gets experimental support from observations of dendritic arbor geometries in developing tectal neurons in Xenopus (Ewald et al., 2008
). The ability to detect correlated synaptic input is decreased in tectal neurons following the knockdown of NMDAR (Ewald et al., 2008
). The dendritic arbors of the neurons with decreased detection of correlated inputs were found to have larger inter branch tip distances than those of the control arbors (Ewald et al., 2008
). Such a decrease of the local branch clustering is a characteristic feature of Hebbian branching strategy (Strategy 3). On the other hand, for axons to employ Hebbian branching strategy they have to access the information about correlations in activity on post-synaptic side. This information is available to dendrites in the form of e.g. the amount of calcium entering through the NMDA receptor. Therefore dendrites can readily implement Hebbian branching strategy. Axons could gain access to these correlations if a specialized retroactive marker diffused back to the presynaptic side. It is not clear if such marker does indeed exist. The point is however that a specialized system has to be implemented for axons to recognize these correlations and implements strategy 3. The advantage gained by the organism from this system is weak, if non-existent, as we have shown.
The hypothesis that axons and dendrites use different branching strategies is consistent with existing experiments on the blockade of NMDA receptors (Rajan et al., 1999
). Our modeling shows that axons accelerate the formation and elimination of new branches, while the branching of dendrites slows down under conditions of reduced correlated activity (Figure 6
). The latter finding is a direct result of the instructive role of activity in dendritic, but not axonal branching. In our model, acceleration of axonal branching is a result of removing the activity-dependent stabilization of synapses that exists in the condition of NMDA receptor blockade, which ultimately leads to more dynamic axons. Our results permit us to interpret the asymmetry that transpires in the changes occurring in the dynamics of branch formation, under the conditions of NMDA receptor blockade (Rajan et al., 1999
).
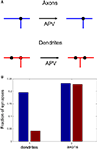
We now propose ways in which this asymmetry in branching strategy can be further tested experimentally. We suggest that, if an NMDAR antagonist is applied to developing optic tectum, the spatial correlations between axonal branch points and synapses should remain the same as in the control case. In contrast, the correlations between the locations of dendritic branch points and synapses should be reduced after NMDAR blockade. We illustrate this prediction in Figure 8
, where we measure the fraction of synapses that are located in the vicinity of axonal and dendritic branch points before and after activity block in the model. Such observations recently were made in Xenopus for both axons (Meyer and Smith, 2006
; Ruthazer et al., 2006
) and dendrites (Niell et al., 2004
; Sanchez et al., 2006
) without the application of NMDAR antagonists.
Figure 8. The role of activity block on the spatial correlations between branch points and synapses. (A) Schematic representation of the predictive capacity of the model. If axons implement an activity-independent synaptotropic branching strategy and dendrites implement Hebbian branching strategy, the consequences of activity blockade are different for axons and dendrites. The spatial correlations between synapses and branch points remain unchanged for axons, and are reduced for dendrites after an NMDAR antagonist is applied. (B) The fraction of synapses located at branch points before (blue) and after (red) activity block in the simulation, when axons and dendrites implement optimal branching strategies.
We propose the functional role of axonal and dendritic branching from a developmental point of view. With this approach, branching is required to speed up the developmental process. Acceleration in the location of correct targets due to branching is accomplished via the use of a parallel search algorithm. Another possibility is that branching is required to optimize the functionality of the mature circuit; for example, to improve the signal transmission properties of the network by minimizing the path length and attenuation of the signal between connected neurons (Wen and Chklovskii, 2005
), or to perform nonlinear computation of the inputs in the dendritic arbor (Poirazi et al., 2003
).
In conclusion, we studied computationally-different branching rules for axons and dendrites within a developing retinotectal projection. Our studies suggest that branching serves to accelerate the formation of neuronal circuitry through the use of the parallel search of targets. We argue that the observed abundance of synapses on branch points for both axons and dendrites serves to minimize the number of erroneous transient branches. We also explain the asymmetry that is observed experimentally in the reaction to NMDA receptor blockade between axons and dendrites. We suggest that this asymmetry stems from the branching of dendrites, but not axons, being directly instructed by correlations in electric activity. Finally, we propose experimental tests that could verify that optimal branching rules, indeed, are being implemented in developing brain.
This work was supported by National Institute of Health (R01EY018068), by the German Federal Ministry of Education and Research (BMBF) (01GQ0430) and a postdoctoral fellowship from Swartz foundation.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.