California Institute of Technology, Pasadena, CA, USA
Fundamental questions in neural coding are how neurons encode, transfer, and reconstruct information from the pattern of action potentials (APs) exchanged between different brain structures. We propose a general model of neural coding where neurons encode information by the phase of their APs relative to their subthreshold membrane oscillations. We demonstrate by means of simulations that AP phase retains the spatial and temporal content of the input under the assumption that the membrane potential oscillations are coherent across neurons and between structures and have a constant spatial phase gradient. The model explains many unresolved physiological observations and makes a number of concrete, testable predictions about the relationship between APs, local field potentials, and subthreshold membrane oscillations, and provides an estimate of the spatio-temporal precision of neuronal information processing.
Whatever code neurons use for encoding, transferring, and decoding sensory information in the central nervous system (CNS) must be robust to a number of compromising factors. The integrity of the information transferred in massively parallel pathways of the brain is highly sensitive to distortions from different conduction delays (Rockland et al., 1997
) and from intrinsic correlations due to the divergence and convergence of axonal projections (de la Rocha et al., 2007
). Nevertheless, neuronal responses are increasingly specific to objects and progressively invariant with respect to incidental physical features, the times of occurrences, and the spatial locations of stimuli as we follow the activation from the sensory neurons through the primary sensory and ultimately to associational cortical areas. The high specificity of neuronal representations in higher cortical and associational areas relies on an unknown mechanism that enables the generation of action potentials (APs) in the same neuron consistently and independent of its neighbors (“sparse coding”) (Quiroga et al., 2005
). This requires precise coincidences of membrane depolarization with the arrival of excitatory postsynaptic potentials (EPSPs) at the level of individual neurons (Abeles, 1982
). I investigated through numerical simulations whether the phase of APs relative to the intrinsic subthreshold membrane potential oscillations (SMOs) could encode and retain information with high spatial and temporal selectivity. Our model relied on two basic assumptions: first, that the timing of AP initiation is dependent on the phase of the SMO (Llinas et al., 1991
); and second, that SMO is nearly synchronized with a phase gradient across a local population of neurons (Benucci et al., 2007
; Bringuier et al., 1999
; Grinvald et al., 1994
; Prechtl et al., 2000
). To relate the second assumption to empirical data, we further assumed that the SMO correlates with local field potentials (LFP, Buzsáki et al., 2003
; Lagier et al., 2004
; Leung and Yim, 1986
). The results derived from the model are consistent with empirical data, and they provide a unified framework to answer a diverse set of daunting problems (see Table 1 in Supplementary Material).
The indirect evidence for the tight relationship between AP timing and SMO derives from observations of high correlation between extracellular APs and LFP. High coherency between APs and LFP oscillations is predominant at the gamma and theta frequency bands in the awake brain (Bragin et al., 1995
; Chrobak and Buzsaki, 1998
; Kamondi et al., 1998
; Womelsdorf et al., 2007
), and phase lock between APs and high frequency LFP occurs during slow wave sleep (Buzsaki et al., 1992
; Chrobak and Buzsaki, 1996
; Cisse et al., 2007
). Gamma and theta oscillations also phase lock in the hippocampus and in the entorhinal cortex during active exploration of the environment and processing of sensory input (Chrobak and Buzsaki, 1998
; Robbe et al., 2006
). At the same time, APs phase lock with gamma oscillations (Chrobak and Buzsaki, 1998
). Moreover, gamma band LFP and AP coherence has been found to be sensitive to motor task (Mehring et al., 2003
) and preparatory activity during working memory (Pesaran et al., 2002
) and related to selective visual attention (Fries et al., 2008
). The autocorrelogram of multiunit activity in visual cortical areas of the cat is strongly modulated at 40–60 Hz and correlates with the gamma LFP, suggesting a functional link between AP generation and gamma oscillations (Gray and Singer, 1989
). The multiunit–multiunit and the multiunit–LFP coherences are both increased during visual stimulation in the gamma (Womelsdorf et al., 2007
) and during decision making in the beta frequency bands (Pesaran et al., 2008
). Although AP-LFP phase coherency has been observed within the low-frequency LFP bands in the primary visual cortex of anesthetized primates (Montemurro et al., 2008
), the feature-dependence of AP-LFP coherency in primary sensory areas is yet to be investigated. Notably, APs phase lock to 20–40 Hz LFP in the primate somatosensory cortex (Murthy and Fetz, 1996
). The majority of pyramidal cells fire at the trough of the theta cycle and align to the gamma (Bragin et al., 1995
), and specific types of interneurons also phase lock to gamma (Tukker et al., 2007
). Moreover, pyramidal cell firing in the hippocampus and entorhinal cortex of rodents also express a progressive theta phase precession consistent with the animal’s position relative to the place field (O’Keefe and Recce, 1993
) leading to the proposal that the AP phase relative to theta may encode the precise location of the animal (O’Keefe and Burgess, 2005
; O’Keefe and Recce, 1993
; Skaggs et al., 1996
). All previous models of hippocampal phase coding assumed that phase precession is generated inside of the hippocampus as a result of interaction between two slightly different frequency theta oscillations (Blair et al., 2008
; Lengyel et al., 2003
; O’Keefe and Burgess, 2005
); phase precession originating from the phase-coded sensory input and imposed on the hippocampus by the entorhinal cortex has not yet been proposed. Likewise, oscillatory interference models, relying on multiple oscillators, were proposed to explain grid cell behavior in the entorhinal cortex (Burgess, 2008
; Burgess et al., 2007
). However, as we show, coincidences of phase-modulated sensory input with a single propagating oscillation field are able to generate grid topography without further assumptions.
The mechanism by which local SMOs synchronize and generate coherent LFP relies on inhibitory interneurons (Lagier et al., 2004
; Soltesz and Deschenes, 1993
; Traub et al., 1996
). To simplify terminology, we refer to LFP as the extracellular indicator of SMO; however, the performance of the model does not depend on the equivalence of LFP and SMO.
The aim of this study is twofold. First, we present a model that explains how feature-dependent phase coding may be employed in sensory information processing. Second, we investigate potential benefits of phase coding through examples, including generalization of 1-D phase coding to 2-D fields, information compression, selective reconstruction from combined representations, retaining stimulus invariants, and spatio-temporal transformations.
Computational Model
The core computational model consists of three layers, an input layer, a transformation layer, and an output layer. Each layer contains n neurons arranged in a 1-D array or a 2-D grid structure. The sensory input (1-D or 2-D) maps to the first layer. The first two layers are connected through n one-to-one unidirectional connections. In contrast, the second and third layers are connected through a single channel. Thus, the complete architecture is an n-to-n to one-to-n feed-forward network. For the sake of simplicity, we first consider a 1-D array of neurons to introduce the basic operations, and then we demonstrate that these operations are applicable to a 2-D grid as well.
I modeled neurons as deterministic state machines with binary AP or non-AP states and a real-valued baseline function φ(t) representing the voltage of the SMO. The state of each neuron is defined by the combination of these two parameters. Although time is a continuous variable in the model, for numerical simulations we applied a discrete timescale ∼0.2 ms (Tγ = 0.01).
We denote φi(t) as a wave function with frequency γ and period T = 1/γ corresponding to each neuron’s SMO. We assume that φi(t) is coherent among the neurons of a given layer with a constant phase offset diΔΦ proportional to the distance of the neurons from the origin of the oscillation (di), like a propagating wave

where ΔΦ has units of time/distance. For an n-dimensional grid of neurons (n = 1, 2, 3), this phase gradient causes the neurons to express a coherent but phase-shifted n-dimensional oscillation field, where the phase difference between grid points is proportional to the difference between their distances from the center of oscillation (Figure 2
E). At grid points where the phase difference reaches 2π, neurons have a zero phase-lag difference. The phase gradient starts to increase from homogeneously distributed centers and attenuates at the edges where spreading oscillations derived from adjacent centers meet (Benucci et al., 2007
; Rubino et al., 2006
).
The sequence of events from encoding to decoding are as follows:
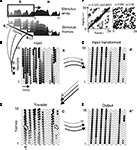
(1) Encoding phase (layer 1): First we generate a 1-D input pattern S, a stimulus vector of length n representing the intensity of the stimulus acting on each of the respective n neurons (Figure 1
stage 1). We now define A as the pattern of APs induced by S. A is an n × n binary matrix with elements ai,t, representing the time t at which each neuron i receives an input, that is computed by converting the intensity vector S to a latency vector such that a higher intensity input induces a shorter latency AP (Figure 1
stage 2) (Hopfield, 1995
).
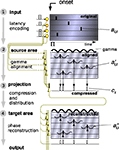
Figure 1. Flow chart of information encoding and reconstruction. Stages are numbered at the left from 1 to 4. (1) Input: An intensity-modulated signal is presented to the input of the neurons and encoded as an AP latency vector (ai,t) (Gollisch and Meister, 2008
). (2) Source Area: The latency encoding AP vector, when interacting with a propagating field of local oscillations, becomes aligned to the nearest SMO peaks (a′i,t). (3) Projection: The SMO-aligned AP vector is collapsed into a single AP stream via convergent connections. At the same stage, the AP vector is distributed via divergent connections (not shown), and identical AP trains are transferred to the next stage (ct) (Dan et al., 1998
). (4) Target Area: this area receives identical copies of the AP vector through parallel pathways. When APs interfere with the local waves of SMO, a single input AP evokes a single output AP only in neurons where the input AP coincides with the peak of the local SMO. Provided that the SMOs have the same voltage gradient at the input and target areas, it is guaranteed that the coincidence pattern will reconstruct the original spatio-temporal pattern of the input (a″i,t). Output: As a result, the output AP vector reliably reproduces the phase aligned input vector.

The function f assigns each input value si to a time ti, where

and γ is the frequency of SMO. The role of n is to scale the AP times to encompass multiple SMO periods. Importantly, the exact function in Eq. 2 does not matter as long as the latency is a monotonic function of the si input. Moreover, it does not matter whether the input is sensory or it was derived from another brain region; the model is only concerned with the pattern of APs that is induced by S.
(2) Transformation phase (layer 2): Now, we define A′ as the gamma-aligned pattern of APs in A. More precisely, A is transformed into A′ by delaying each AP until the neuron reaches the local maximum of its SMO. As a result, each i-th neuron generates an AP at a peak of φi(t). We implement this delay by aligning each binary AP event to the peak of the respective neuron’s intrinsic oscillation φi(t) (Eqs. 4 and 5).

where

and max is defined as the next local maximum of φi(t) after the time of the received input ai,t. Here 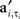 are the elements of A′, a matrix with binary elements, where columns correspond to 0.1 ms time bins and rows correspond to specific neurons. A “1” in position
are the elements of A′, a matrix with binary elements, where columns correspond to 0.1 ms time bins and rows correspond to specific neurons. A “1” in position 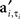 represents an AP for neuron i at time t while a “0” represents the lack of AP (Figure 1
stage 3).
represents an AP for neuron i at time t while a “0” represents the lack of AP (Figure 1
stage 3).
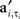 are the elements of A′, a matrix with binary elements, where columns correspond to 0.1 ms time bins and rows correspond to specific neurons. A “1” in position
are the elements of A′, a matrix with binary elements, where columns correspond to 0.1 ms time bins and rows correspond to specific neurons. A “1” in position 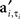 represents an AP for neuron i at time t while a “0” represents the lack of AP (Figure 1
stage 3).
represents an AP for neuron i at time t while a “0” represents the lack of AP (Figure 1
stage 3).(3) Transfer (layer 2–3): Then A′ is collapsed into an array C by summing across all neurons for each time bin.

Since the sum is a binary function, C contains the APs derived from all neurons with their original time stamps. Although the neuronal specificity is lost in the sum, the precise timestamps of APs unambiguously relate the individual APs to specific locations through their phases. Thus, the spatial information is retained by the relative phases of APs (Figure 1
stage 3).
At the same step, C was “cloned” to n copies and fed into the next layer of n neurons.

where j = {1,…,n}. The information in C is transferred from the input layer to the target layer. Since all the information from the input layer neurons is collapsed into a single channel (stage 3), this information is vulnerable to errors deriving from different conductivity delays. Therefore, a redistribution of C over multiple channels is necessary to increase redundancy for error correction.
(4) Reconstruction (layer 3): The final step is reconstruction. Here the task is to create a matrix A″ by assigning each individual AP in C to a neuron such that there is a topographic mapping between A and A″, consequently recovering the original spatio-temporal structure of APs from the compressed code. To do so, we simultaneously broadcast the cj copies to each k-th neuron (k = {1,…,n}) in the target layer. Neurons in the target layer will only generate APs if the input cjt coincides with a peak of their membrane oscillation φk(t) within a precision of Δτ (Figure 1
stage 4 and Movie 1 in Supplementary Material). Given that the gamma phase gradients are identical between the source and the target (but see Figure 1 in Supplementary Material), these coincidences must occur in neurons at the same grid position within the target layer as the grid position of neurons stimulated in the input layer. Consequently, the topography and timing of the coincidences between the C and the SMO, which generates the APs at the target layer, will reproduce the topography and timing of the input APs. To implement this, we define a matrix B with n × T/Δτ binary elements, where 1-s represent the positive peaks of SMO and 0-s represent all other voltage values, with a Δτ precision:
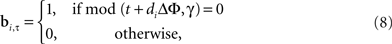
where bi,τ represents the binary state of the i-th the neuron at τ time. Since the input layer SMO is identical to the target layer SMO, it is necessary that the intersection A″ of B and C:

will reproduce the original matrix A′ (Figure 1
stage 4). The output pattern A″ can be transferred as input to other target areas. Equation 9 will be referred to as the “interference operator”, and Equations 8 and 9 as the “interference principle”.
Selective Reconstruction from Combined Phase Codes
Let us define input images SA and SB and encode them separately as Aα and Aβ. Next, align Aα and Aβ to field gradients ΔΦα and ΔΦβ, respectively, and compress the aligned A″α and A″β matrices into corresponding Cα and Cβ representations. Next, we combine the two compressed representations as Cγ by simply merging and sorting the AP times in ascending order:

Given that φα(t) has a phase gradient ΔΦα and φβ(t) has a phase gradient ΔΦβ, the two different SMO fields must be able to selectively reconstruct the two AP patterns, A″α and A″β, both retaining the main features of A′α and A′β, respectively:

and

With simulations (Figure 5
) we demonstrated that given ΔΦα ≠ ΔΦβ, A′α can be recovered from the interference of Bα and Cγ without confusion with A′β. Likewise, matrix A′β can be recovered from the interference of Bβ and Cγ without confusion with A′α.
This mechanism provides the capacity to combine information from different sources within the same target layer and selectively recall them by different SMOs.
Numerical Implementation of the Model
Numerical simulations were implemented using Matlab (Mathworks Inc., Natick, MA, USA). For the numerical implementation, instead of simulating spiking neurons with incremental time, we computed the state of all neurons in time at once using matrix operations. We remark that it was unnecessary to introduce a spiking neuron model since all the state transitions were deterministic and the interactions were linear. Thus, the state changes of neurons, i.e., the AP times, at a given layer as a function of the state changes at the subordinate layer were analytically solvable. Therefore, numerical simulations were performed by computing the complete AP time vectors as a function of the AP time vectors in the previous layer instead of deriving the membrane voltage Vt at every time step recursively from Vt−1.
Architecturally, the neuronal network consisted of three layers: input-layer, projection-layer and output-layer. The input layer contained n or n × n neurons, individually assigned to each pixel of the input image. We implemented the algorithm on feed-forward networks using three types of projections between layers: (i) A 1-D vector of n values (input vector) was projecting to a 1-D array of n input-layer neurons, which were connected through projection neurons to the same number of output-layer neurons. The connectivity between the values of the input vector and input-layer neurons was one-to-one; between the input-layer and projection-layer was n-to-one; between the projection-layer and output-layer was one-to-n. (ii) A 2-D input image, digitized as n × n pixels, projecting on a 1-D array of n2 input-layer neurons. The architecture from the input-layer to the output-layer was similar as in (i), however, the output was visualized in 2-D to compare the reconstructed pattern with the input image. (iii) A 2-D (n × n) input matrix was projecting on a 2-D grid of n × n input-layer neurons by emulating “receptive fields”. For this, the input matrix was partitioned into n subfields and the input-layer neurons were arranged into n non-overlapping groups that processed the n input subfields separately. Likewise, the output-layer neurons were arranged into n number of groups, emulating a topographical projection from the sensory organ to a primary sensory cortical area. The precise connectivity pattern between the input matrix and input-layer group was repeating across the groups but it was varied from simulation to simulation (see next paragraph). All neurons from a given group were converging on a single projection neuron, which in turn, terminated on all the neurons of a given output-layer group. Thus, each input-layer group was interfacing with the corresponding output-layer group through a single projection neuron.
Operatively, the input was either a 1-D (n) or a 2-D (n × n) matrix mapped to the input-layer neurons. The correspondence between the input matrix elements and the input-layer neurons was one-to-one. The 1-D simulations always used random vectors as input with the range of values from 0 to 2π and transferred to n neurons. As input to the 2-D simulations, we used a set of digitized images, including photos of people, animals, complex structures of rubber bands and grid patterns. They were selected to test the accuracy and geometric preservation of the reconstruction. Images were digitized with 256 × 256 pixel resolution and converted to grayscale. We down-sampled them to fit to the neuronal grid with a square geometry (16 × 16, 18 × 18, 32 × 32, 36 × 36, 60 × 60) and input them to the neurons. The input layer contained n or n × n neurons, individually assigned to each pixel of the input image. As described earlier, the projection-layer was different for the 1-D and 2-D network. For a 1-D solution, the projection-layer contained only one neuron (one channel). All the APs from the n input layer neurons were collapsed into a single channel, serving as a projection neuron. For the n × n solution, the projection layer contained n neurons (channels), thus the n × n grid of input layer was broken down into m subfields (receptive fields) and the APs from all the input neuron of a given subfield were collapsed into a single channel. The combined m channels served as a projection pathway. All the neurons at a given subfield of the output layer received a common input from a single projection neuron, containing the combined activity from the input subfield. Different mappings between the input and input-layer neurons were implemented by connection patterns, emulating different receptive field geometries (for details on modeling different receptive field architectures, see Supplementary Material).
The SMO was modeled by sinusoids. The phase gradient was either linear, emulating a propagating wave with a constant time lag of SMO between neighbor neurons, or non-linear, emulating oscillations deriving from randomly dispersed sources (for details on constructing non-linear SMO fields, see Supplementary Material below). APs were modeled as binary events. The duration of these events was the smallest time unit of the simulation (Δτ), defined as a constant fraction of π, the half period of the SMO. Alignment to the nearest SMO peak was implemented by reassigning each AP to the nearest subsequent peak of SMO. Combining before transferring APs via the projection neurons was done by concatenating the AP time series. Coincidences at the output layer were detected when the latency difference between the incoming AP pulse and the peak of local SMO is < Δτ. APs were assigned to neurons of the network where coincidences occurred. The output was the temporal pattern of APs on the grid of n × n neurons, converted to an image by an inverse of the image conversion applied to the image when it was converted to a temporal pattern. To quantify the efficiency reconstruction, we computed Pearson’s correlation coefficients on the AP times between the input patterns and output patterns, neuron-to-neuron, as well as between the SMO-aligned input patterns and the output patterns. The implementation of the algorithm for numerical simulations is described in the Supplemental Computational Methods. Demo codes written in Matlab are available at the following URL: http://www.vis.caltech.edu/∼zoltan/mcodes/phasecode.tgz
Algorithm and Biological Motivations
The model that we introduce explains how oscillations might be used in the brain to coordinate APs to encode and reconstruct information between distant cortical areas. First, we distinguish four information processing stages and corresponding neuronal layers representing the results of each stage (Figure 1
): (1) Input layer: latency encoding; (2) Source layer: gamma alignment; (3) Projection: compression and distribution, (4) Target area: reconstruction. The output of the target area may serve as an input to a connected area. The input layer may represent a group of sensory neurons or a group of cortical pyramidal cells. Postsynaptic to these neurons are neurons that encode the input and exhibit intrinsic SMO. Postsynaptic to encoding neurons are the projection neurons, such as sensory ganglia or long-range cortico-cortical connections. Postsynaptic to projection neurons are the target neurons, such as cortical layer-4 granule cells or layer 2–3 pyramidal neurons, which are the ultimate targets of sensory or cortico-cortical projections.
Each neuron was described by its grid location and layer, its connections, and its state. The state was defined by three variables: a continuous oscillating membrane potential implementing the SMO of the soma, a binary input, and a binary output, corresponding to AP or no AP. The probability of generating an AP was dependent on the input state and the actual SMO, which determined how close the membrane potential was to the threshold. In the absence of input, the membrane potential remained subthreshold, by definition. The SMO for each neuron was modeled by a sinusoid, and the grid of neuronal SMOs formed a 2-D field (SMO field) with a common frequency and a uniform phase gradient between adjacent neurons. Thus, the SMOs of neighboring neurons were near-synchronized, with a distance dependent phase delay, mimicking a spreading wave (Benucci et al., 2007
; Bringuier et al., 1999
; Grinvald et al., 1994
; Prechtl et al., 2000
). Each neuron generated an AP when the input, received from a presynaptic neuron (i.e., from an earlier stage), coincided with the neuron’s own local SMO maximum, where the neuron’s membrane potential is nearest threshold. We implemented a task in which these neurons encode and reconstruct an image using exclusively a feed-forward architecture in four steps corresponding to the four stages. For the sake of simplicity, we first illustrate these steps on a 1-D example, after which we extend it to 2-D examples using real images (see Section “Results”).
Encoding
First we generate a 1-D input pattern S that represents intensity values of an image (Figures 2 and 3
A). Each element of the S vector is assigned to the input of a neuron. Next, we compute the neuronal responses to S. We employ a latency encoding scheme (Gollisch and Meister, 2008
; Hopfield, 1995
), which converts the intensity values to AP latencies, inversely proportional to the intensity of stimulus component, generating a spatio-temporal activity vector A (Eqs. 2 and 3).
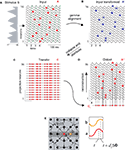
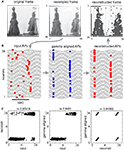
Figure 2. Stages of information encoding, transfer, and reconstruction illustrated on a 16-neuron simulation. (A) INPUT: Neurons at the input layer convert the stimulus, represented by an analog intensity vector (left), to a latency vector where the delay of AP (red markers) is inversely proportional to the intensity of input. Oscillations in adjacent neurons are phase shifted by a constant 0.1 π relative to each other (green ticks mark oscillation peaks). (B) GAMMA ALIGNMENT: AP generation is most likely when the input pattern coincides with the maxima of the ongoing SMO (blue markers). Time is shifted one period at each stage. (C) TRANSFER: All APs from all neurons are collapsed into a single sequence of APs, and this sequence is distributed over an array of projection neurons (red markers). (D) OUTPUT: When one of the AP sequences is transferred to the target layer, it provides the same input to each neuron (dashed lines). However, only those APs that coincide with at least one neuron’s membrane oscillation maximum are effective in generating AP (red markers). Given that the membrane oscillations at the output layer share the same spatial gradient as that of the input layer, the topography and timing of the output layer interferences will reproduce the topography and timing of input layer APs (B). (E) The scheme of the spatio-temporal distribution of SMOs in a grid of neurons (filled circles). Each neuron’s membrane potential is affected by a radial spread of SMO ϕi(t) that has a constant spatial voltage gradient, causing a ΔΦ phase lag between the SMO peaks of adjacent neurons (red and orange neurons and corresponding traces of SMO). Examples in (A–D) related to a linear array of neurons (within the dark gray rectangle) sorted according to phase, but the same algorithm can be generalized to a 2-D grid (light gray area).
Figure 3. Topographic preservation of reconstruction. (A) The original digital grayscale image (left panel) was downsampled to an 18 × 18 matrix and partitioned into 18 sub-regions mimicking receptive fields (RFs) (second panel, only four receptive fields are shown). The total of 18 RFs were projecting on 18 groups of neurons of the input layer, each consisting of 18 neurons. The inputs from the RFs (covering 3 × 6 pixels; color coded on the second panel) were vectorized and mapped on separate arrays of neurons (color coded rectangles on the third panel). The reconstruction using the “interference operator” (Eq. 9) retained most of the information from the input (forth panel). (B) Examples of encoding the input by four RFs [color bars relate the codes to corresponding RFs on (A)]. The gray levels within RFs were converted to AP latency vectors in the corresponding neurons (red markers). (C) APs were aligned to the nearest subsequent maxima of the local SMO oscillation (blue markers). (D) The spatiotemporal pattern of APs from each group was collapsed into a single sequence and combined in 18 AP sequences (red markers) to transfer through projection neurons. The sinusoid traces correspond to the first neuron’s SMO of a given receptive field in (C). The first four traces correspond to the RFs on (A). (E) Reconstruction of the information from the compressed code in (D). The interference between the input and the neuron’s intrinsic SMO peaks generated patterns (red markers) that reproduced the original gamma-aligned patterns. To compare the reconstruction with the original input, we converted the AP latencies from all the neurons to gray level pixels (A; fourth panel). Note that the reconstruction of the original phase relationship between the APs and local SMO is near perfect (C,E and A fourth panel).
Gamma alignment
The latency-encoded pattern A is transferred to the next layer of neurons exhibiting a coherent field of SMOs. The SMO field consists of local oscillations spreading through the grid of neurons as a linear or radial wave with a neuron-specific phase gradient (Eq. 1). A neuron of this layer generates APs only when the sustained input from a neuron at the previous layer coincides with its own next SMO maximum. As a result, the temporal pattern of A is transformed in an SMO aligned pattern A′ (Eqs. 4 and 5). Since we considered gamma oscillation as one of the main frequency components of local SMOs, we refer to this operation as “gamma alignment” (Figures 1 and 2
B), though phase coding does not depend on the frequency of SMO. Note, that with gamma alignment this model is critically different from synfire chain (Abeles, 1991
) and AP-latency encoding (Hopfield, 1995
). Gamma alignment is possible through rapid spike-time-dependent-plasticity (Bi and Poo, 1998
; Cassenaer and Laurent, 2007
; Markram et al., 1997
).
Compression
A′ is then collapsed across all neurons into one AP sequence C by eliminating the neuronal identity (Figures 1 and 2
C, and Eq. 6). This AP sequence represents all the APs pooled across all of the neurons. Pooling can be implemented by convergent feed-forward synaptic connections on a single neuron. Although neuronal identities are seemingly lost by collapsing APs over neurons, the spatial origin of the AP is still referenced by the timing, which associates the AP with the original location of the neuron through the gamma alignment. A phase difference of the local SMO, to which the AP is aligned, is preserved by the small latency differences between APs after collapsing them. The resulting new sequence is “compressed” because information from all neurons were collapsed into a single sequence of APs of the same duration, and “compact” because it contains all the information about A′, including time and location.
Distribution
At the same stage, the collapsed AP vector is copied over the same number of projection neurons as in A (Eq. 7). Compression and distribution are accomplished in a single step within a feed-forward network by convergent and divergent synaptic connections, respectively. As a result, all APs from the original A′ pattern are represented in all the projection neurons by pattern C, with a redundancy (Figures 1 and 2
C). These packets of C patterns can be broadcasted to many neurons simultaneously or exchanged between distant cortical areas. Since all projection neurons carry the same AP sequence, any of them is able to broadcast the complete information indiscriminately to any brain area. Notably, after compression the information content is no longer sensitive to different conduction delays. Errors deriving from differential conduction delays are self-corrected by synchronization of APs in crossed-over feed-forward pathways, typical in thalamo-cortical, callosal and long-range associational projection systems.
Reconstruction
This is the final stage where the original information A′ (the gamma-aligned representation of A) is reconstructed from the pattern C as input to this layer. The parallel pathway of projection neurons broadcasts the complete C input to each neuron at the target layer, such as layer 4 of the cerebral cortex. The target layer neurons also express an SMO field similar to the one at the input layer. Here, we apply a principle similar to the input layer, except a neuron only generates APs if the input coincides with the neuron’s SMO maxima within a Δτ time window (Figures 1 and 2
D). Such coincidences between the input and the local SMO occur only in selected neurons, which are located at the same grid positions as the active input-layer neurons (Movie 1 in Supplementary Material). Since the relative timing of AP is preserved, the coincidences reproduce the original A′ pattern due to the “interference principle” (Eqs. 8 and 9). Therefore, to achieve a near perfect reconstruction, it is assumed that the SMOs at the input layer and the target layer share similar spatial and spectral properties, including the frequency and phase gradient topography (but see isomorphic reconstruction and Figure 1 in Supplementary Material). Since the interference occurs at selected neurons, the input pattern C will activate a sparse set of neurons, with topographic positions similar to the original neurons. Therefore, it is necessary that the reconstructed pattern A″ resemble closely to the gamma-aligned original pattern A′ and consequently, the original pattern A as well. The reconstructed pattern can be combined with patterns deriving from other input structures and a new cycle of encoding, gamma-alignment, compression and reconstruction is initiated that propagates the now combined representation to a different brain area (Figure 5
).
For the sake of simplicity and algorithmic clarity, we first used a 1-D encoding and reconstruction example. A vector containing 16 random real numbers from 0 to 1 was used as the input to the network. Next, this input was converted to latencies within the range of eight SMO cycles (Figure 2
A). This pattern was aligned to the neurons’ own SMO which slightly altered the precise temporal pattern of APs relative to the original latency code (Figure 2
B). This spatio-temporal pattern was collapsed into a single AP train by removal of the spatial dimension. At the same time the resulting AP string was distributed over 16 neurons which transferred the code from one brain structure to another with redundancy (Figure 2
C). One of these AP strings was applied as input to a target network, consisting of 16 neurons. In addition to the input, we rendered each neuron with an SMO that shared the same phase gradient and frequency as the SMO field at the input layer. Although each individual neuron received the same AP sequence as input, due to the interference principle (Eqs. 8 and 9) only those APs that “precisely” coincided with the neuron’s own SMO were effective in generating output APs (Figure 2
D). We quantify the precision of coincidence later. As a result the ouput-layer neurons reproduced the spatio-temporal pattern of the original gamma-aligned input with high fidelity.
To demonstrate the algorithm in 2-D we used a set of grayscale images sampled at neuron resolution and projected them on the input-layer neurons so that each neuron processed one pixel, allowing no interactions between neurons of the same layer (Figure 3
). By varying the precise projection between the image pixels and neurons we were able to test different receptive field configurations (see Supplementary Material on modeling different receptive field architectures). Each set of input-layer neuron processed the receptive field independently throughout the four stages, and at the end, the reconstructed patterns were combined from each set. Finally, AP latencies were converted to grayscale values (Figures 3
A,E). The close resemblance of the output image to the original implies that most of the information encoded from the input were correctly recovered from the phase of APs alone, thus phase coding is efficient.
Biological Significance of Model Parameters
The efficiency of reconstruction was sensitive to a number of parameters, including the connectivity, the input size, the density of neurons, the SMO oscillation, and the time window of coincidence. The operative range of these parameters must be consistent with that measured in the living brain in order for the model to be biologically relevant. To understand how these parameters influence the reconstruction efficiency, we performed simulations. The independent variables were the number of neurons, the number of gamma cycles (i.e., the duration of reconstruction), the temporal resolution Δτ (equivalent to the time window of coincidence), the phase gradient ΔΦ of gamma oscillation, the connectivity pattern, and the complexity of receptive fields (the number of pixels covered). The dependent variable was the reconstruction efficiency, quantified as the pixel-to-pixel Pearson’s correlation coefficients either between the original image A and the reconstructed image A″ (r = rA, A″) or between the gamma-aligned image A′ A″ (r′ = rA′, A″).
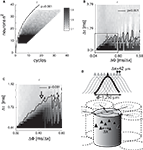
First, r and r′ were tested against combinations of number of neurons and number of gamma cycles. The reconstruction efficiency is expected to inversely scale with the number of neurons since the more neurons’ APs are combined in a single projection neuron, the more confusion occurs due to spurious interferences (aliasing errors). A few gamma cycles were expected to be sufficient to reconstruct the most of the information and certainly less gamma cycles than neurons are necessary. The steep exponential function [f(x) = 22.45 × x0.3 − 13.83; R2 = 0.99; root mean square = 0.78] of the significant correlations (six cycles over the increase of 800 neurons) suggests that as few as 64 neurons and three to four gamma cycles (75∼100 ms) were sufficient to retain the information with r > 0.9 (Figure 4
A); consistent with the reaction time across species.
Figure 4. The efficiency of reconstruction depends on the number of neurons, gamma cycles, temporal resolution and phase gradient. (A) Average correlation coefficients (r) between original and reconstructed images (grayscale) as a function of number of gamma cycles (abscissa) and number of neurons (ordinate). The right side of the exponential curve represents combinations of number of neurons and gamma cycles that enabled precise reconstructions (P < 0.001). (B-C) Average r as a function of temporal resolution (DT) and gamma phase gradient between adjacent neurons (ΔΦ). Unit is [ms/Δx] where Δx is the average nearest neighbor distance between pyramidal cells (D). (C) A higher resolution simulation within parameter ranges of ΔΦ = 0–0.8 and Δτ = 0.01–1.52 ms [the rectangular area in (B)] revealed the optimum phase gradient ΔΦ = 0.4. The contour line represents the P = 0.001 confidence limit. (D) Estimating the cortical area of precise reconstruction. Given Δx ≈ 42 μm average nearest-neuron distance and ΔΦ ≈ 0.4 ms at gamma frequency (from B–C), we extrapolate d ≈ 1,250 μm as the diameter of a cylindrical cortical volume comprising a neuron population necessary and sufficient to reconstruct the complete information transferred within a single gamma cycle. Filled triangles represent neurons, cosine functions represent phases of a spreading gamma wave and arrows represent radial propagation of gamma waves.
Second, we systematically varied the temporal resolution Δτ between 0.1 and 2.5 ms and the phase gradient ΔΦ between adjacent neurons from 0.012 to 5 ms. Since the reconstruction efficiency relies on the neuronal specificity recovered from the AP phases, the temporal resolution of phase, i.e., the precision of APs, is critical. This resolution determines whether neurons at the target area are able to discern the close succession of input APs and detect coincidences between APs and gamma peaks selectively. Likewise, the gamma phase gradient between adjacent neurons determines the specificity of AP-gamma coincidences with respect to the neuron’s position and with respect to the wavelength of the spreading oscillation. Since Δτ and ΔΦ are independent parameters of the model while both contributing to the precision of coincidences, we expected a tight relationship between them. Our simulations confirmed a monotonic relationship between temporal resolution and reconstruction efficiency from 0.1 to 1.5 ms and uncovered a surprising non-linear relationship between the gamma phase gradient and coding efficacy. At Δτ > 1.5 ms no precise reconstruction was possible, thus setting a boundary for precise information processing consistent with empirical data (Shmiel et al., 2005
). The lowest temporal resolution, or the largest time window of coincidence, which allowed a near perfect reconstruction (r > 0.9) was <0.72 ms, as precise as the duration of an AP. The first peak of the corresponding gamma phase gradient was ΔΦ = 0.4 ± 0.1 ms, followed by a series of subharmonics from 0.6 to 1.59 ms (Figures 4
B,C). Given that the average pyramidal cell density in layer 4 of the cerebral cortex is near 2.4 × 104 (Holmgren et al., 2003
) and 2.5 × 104 cells/mm3 (Peters and Yilmaz, 1993
), the average nearest cell-to-cell distance derived by Monte Carlo simulations was Δx = 42 μm (for details on computing neuron-to-neuron distance, see Supplementary Material), and that the optimal phase gradient was 0.4 ± 0.1 ms between adjacent neurons, we estimated the speed of SMO propagation (v) and the diameter (d) of the cortical cylinder that would be covered by a radial wave of a single SMO cycle of f frequency and v speed. Assuming that fgamma ≈ 40 Hz and Tπ ≈ 12.5 ms, and applying v = Δx/ΔΦ we calculated v = 0.1 mm/ms as the speed of propagation, which is consistent with the 0.09–0.4 mm/ms expansion speeds of SMO measured from various species, cortical and allocortical areas (Benucci et al., 2007
; Bringuier et al., 1999
; Grinvald et al., 1994
; Prechtl et al., 2000
). To estimate d, we extrapolated how far a single radial oscillation period (T) would propagate as λ = T × v. Given that T = f −1 ≈ 25 ms and v ≈ 0.1 mm/ms the estimated diameter range of integrative cortical units are d = λ/2 ≈ 1,250 μm (Figure 4
D), consistent with the 900–1,000 μm center-to-center distance of iso-orientation columns in the cat V1 (Lowel et al., 1988
; Peters and Payne, 1993
). Considering that the reconstruction efficiency is near perfect at as low as ΔΦ = 0.1 ms and does not improve beyond ΔΦ = 0.8 ms, a broader range of spatial domains (578 μm < d < 4.6 mm) could satisfy gamma frequency integration. This range is consistent with the 590 μm center-to-center distance of cytochrome oxidase blobs (Murphy et al., 1998
), the 430 ± 139 μm center-to-center distance of cortical biocytin patches in primate V1 and 600 μm in cat V1 (Lund et al., 1993
) and 1.5–2.7 mm, the space constant (d = 2 × space constant) of the radial spread of stimulus induced transmembrane voltage change (Grinvald et al., 1994
). The estimated d was also consistent with the reported range of cortical columns 600–900 μm (Jones, 2000
) and 350–400 μm (Favorov et al., 1987
), and the 400–500 μm projection field of layer 2/3 and layer 4 neurons in the rat barrel cortex (Lubke et al., 2003
). Notably, the relationship between oscillation λ and column diameter is further supported by the observation that the dominant LFP in the primate motor cortex (area 4) is 20–25 Hz (Rubino et al., 2006
), half of that of V1, while the center-to-center distance of cortical biocytin patches is twice of that of V1 (Lund et al., 1993
). In summary, the operative ranges of model parameters satisfy the dynamic and structural constraints of the brain.
Information Reconstruction from Combined Codes
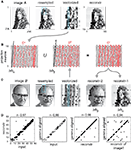
We thought it would substantially increase the performance of phase coding if neuronal architectures were able to combine codes of independent inputs into one compressed stream of APs and selectively reconstruct these representations at the target location by the same pool of neurons. Therefore, we asked whether the interference operator (Eq. 9) is able to recover multiple representations from a superimposed phase code of different input patterns. We used two different images, image Sα and image Sβ and two slightly different field gradients, ΔΦα and ΔΦβ (Figures 5
A–C). First, processing image Sα generated the Aα latency code, transformed into A′α by gamma alignment to a field with gradient ΔΦα. The pattern A′α was collapsed into Cα and reconstructed S′α at the target using ΔΦα (Figure 5
A). Likewise, we processed image Sβ with the field gradient ΔΦβ and computed A′β and Cβ (Figures 5
B,C). Next, before the reconstruction, we combined the two compressed codes Cα ∪ Cβ = Cγ, so that APs encoding image Sβ were interleaved with APs encoding image Sα (Eq. 10). The combined code included both sequences of APs, derived from two different input images, without labeling them according to the neuron of origin (Figure 5
B). Next, we transferred the combined code Cγ to the target, where the postsynaptic neurons successfully recovered image S′α and image S′β from the mixed code by applying field gradients ΔΦα and ΔΦβ, respectively (Eqs. 11 and 12, Figure 5
C). The reconstruction efficiency, quantified as the correlation between the gamma-aligned input and the recovered image, was near perfect (r′ > 0.9, P < 0.001) when compared with the original input (Figure 5
D). Since the variance of the correlation between the original and the gamma-aligned input was the same as the variance of the correlation between the original and reconstructed image, most of the differences between the original and reconstructed images were attributed to the gamma alignment rather than to the reconstruction.
Figure 5. Reconstruction of individual images from combined representations. (A,C) Two different images were digitally sampled at 18 × 18 pixel resolution and grayscales were encoded by AP phases relative to SMO field by using slightly different phase gradients ΔΦA for image A and ΔΦB for image B. The third panel represents the projection of input on a non-topographically organized array of neurons. The fourth panel is the reconstruction when only image A was applied. The receptive field was a 3 × 6 rectangle. Turquoise rectangles highlight the projection of a receptive field on the neurons. (B) APs collected from a single receptive field were collapsed into a single stream and processed by one of the 18 projection neurons. The left panel represents the phase code of APs derived from image A projected on the SMO field. The middle panel represents the same, derived from image B. The right panel represents the result after combining the two codes into one. This compressed AP sequence is transferred to the site of reconstruction. The last two images on (C) represent the reconstruction from the combined code with using ΔΦA vs. ΔΦB. (D) Correlations between: input image B and its reconstruction from the combined code; input image B and SMO aligned pattern B′; the SMO aligned pattern B′ and reconstruction of image B from the combined code; and the SMO aligned pattern A′ and reconstruction of image A from the combined code.
The reconstruction from the combined phase code has intrinsic limitations. If the difference between the oscillation field gradients is small, the delay by which the two oscillation peaks reach adjacent neurons may be smaller than Δτ, causing the neurons to confuse the input APs originating from different images. Spurious phase coincidences of the two fields may also occur if the two field gradients are very different. In order to avoid this, for a given phase gradients ΔΦα the second phase gradient ΔΦβ should be less than ΔΦα/(n × Δτ). Since n is relatively small (<9), especially when the architecture is partitioned into small receptive fields, this condition is easy to meet and does not compromise reconstruction.
Storing and retrieving multiple representations from the same pool of neurons by cueing them with slightly different SMO oscillations can be utilized as a very efficient mechanism for storing long-term memories. For the sake of algorithmic clarity, we postulated the independence of APs and SMO. However, in living tissue, large synchronized EPSPs and IPSPs may reset the field of SMOs, thus allowing selective cueing of information.
Real-Time Motion Processing With Phase
Under natural conditions, images on the retina change rapidly either due to objects and the observer moving relative to each other or due to the observer’s eye movements. A sequence of images, when presented with a frame rate ≥16 frame × s−1, is perceived as motion, (Wertheimer, 1912
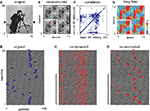
) and motion percept does not improve beyond 48 frame × s−1. This implies that under specific condition, single gamma cycles should be sufficient to process information from individual frames to generate a motion percept. It also implies that the human visual system does not benefit from a frame rate of higher than one frame per gamma cycle. We asked how phase coding would implement compression and reconstruction of a complete frame within a single gamma period with a rate of 40 frame × s−1, in order to remain consistent with human motion perception. According to our simulations, a single SMO cycle is capable of capturing and retaining significant quality of the original image (r = 0.87 P < 0.01) and nearly complete representation of the gamma-aligned image (r = 0.92, Figure 6
). In this simulation we used a 36 × 36 neuron architecture with 6 × 6 receptive fields converging to 36 projection neurons and reconstructed on a 36 × 36 neuron layer at the destination. For the SMO field we used a predefined set of 24 phase gradients. The SMO field gradients were generated by three randomly dispersed gamma sources slowly drifting frame-by-frame with Brownian motion. The input was a 24-frame segment extracted from an Eadweard Muybridge movie clip. Input frames were presented iteratively and each reconstruction was computed independently from the previous frame. The Δτ was 0.001, and a single gamma oscillation period was used for encoding. Because a faithful reconstruction of grayscale image requires n > 4 oscillation periods (Figure 4
A), phase coding within a single oscillation period allowed to retain only the binary values per pixel (black-and-white) with no grayscale qualities processed (Figure 6
A). Despite the black-and-white representation, the spatial reconstruction of the original frames was relatively good (r = 0.874, Figure 6
C), which confirmed that sampling continuous motion by single SMO cycles is necessary and sufficient to encode a motion sequence. Notably, most differences between the original and the reconstructed image frames derived from the AP alignment (Figure 6
C). The limited capacity to process textural details and motion at the same time is consistent with the anatomical and functional segregation of fast achromatic magno-cellular motion pathway and slow chromatic parvo-cellular pathway (Conley and Fitzpatrick, 1989
; Fitzpatrick et al., 1985
; Michael, 1988
; Perry et al., 1984
).
Figure 6. Motion processing by successive SMO cycles. (A) An example frame of a 24-frame original movie segment by Muybridge capturing the motion of two women (left), a 36 × 36 pixel down-sampled input (middle) and the reconstruction of the frame (right). (B) APs evoked by image at the input layer (left), after alignment to SMO (middle) and the reconstructed APs (right). Only one row of neurons is shown. Red markers represent the APs, and waves represent the ongoing SMO per neuron. Scale bar indicates one SMO period. (C) Correlations between the latency-encoded input and the reconstructed AP times (left); between the latency-encoded input and the aligned APs (middle); and between the aligned APs and reconstructed APs (right). Correlation values are shown on the top. Note that most of the variances derive from the alignment to SMO. Time units are relative to the length of an SMO cycle.
Phase Code Generates Grid Representations
Since the discrimination time window is limited to one SMO cycle, the largest discriminative power is comprised in an area corresponding to λ (the distance that SMO travels in one oscillation). Beyond that diameter, representations likely repeat because spurious interferences will activate neurons that share the same SMO phase as they are multiples of λ apart. If the same input pixel is reconstructed by multiple neurons, separated by λ distances, as our model predicts, then it is necessary that different inputs are reconstructed by the same neuron, assuming finite input and neuron spaces. Consequently, individual neurons must endow multiple receptive fields, just like grid cells do in the medial entorhinal cortex (MEC) of rodents (Hafting et al., 2005
). To provoke multiple cortical representations by spurious interferences, we performed pattern reconstructions on an image, tracking a prolonged interval of 144 gamma cycles with increased phase gradient (ΔΦ = 0.1) (Figure 7
). The reconstruction, as predicted, yielded multiple representations of the original image (Figure 7
E). This was due to systematic reconstruction errors caused by spurious interferences that occurred at neurons near λ distances apart within the neuronal matrix. The confusion of AP times across neurons of the output layer is clearly seen as clusters offset of the identity line of the input–output AP latency correlogram (Figure 7
F). The consequence of these errors is twofold: (i) they generate multiple cortical representations of the same spatial location, as seen in Figure 7
E; and (ii) these errors must make a given output layer neuron active not only when the input image is at the original position, but also a number of other positions that are multiple of a constant distance away from the original position. In order to test this hypothesis, we kept track of the activity of an arbitrarily selected output-layer neuron (red arrow in Figure 7
E) while circular shifting the original image matrix in 36 × 36 different positions. If the image on Figure 7
A represents a square-shaped spatial environment from the rat’s point of view, then shifting the image emulates an exhaustive exploration of this environment in a rat-centered coordinate system. For example, moving the image by 5 pixels north and 6 pixels east is equivalent to the rat moving 5 units south and 6 units west, where the unit is proportional to the rat’s size. Next we plotted the firing probability of this neuron according to the positions of the rat in the environment (Figure 7
G). Confirming the prediction (ii), the firing probability revealed a multifold periodic receptive-field architecture, where receptive fields were constant distance apart, reproducing false-colored copies of the original image, evenly tessellating the space. This architecture is consistent with the periodic architecture of the spatial firing fields of MEC neurons (Hafting et al., 2005
). Moreover, the model provides a physiological meaning to the constant spatial separation of the observed firing fields by relating it to the λ of SMO within the MEC. In addition to grid cells, according to (i), the model predicts that the actual spatial location of the rat activates not one but multiple grid cells with shared firing fields, and these neurons must be anatomically arranged in a grid-like periodic architecture over the entorhinal cortical sheet (Figure 7
E) that mirrors the periodic receptive field architecture of individual grid cells. Consistent with the proposed relationship between the grid cell geometry and phase coding, the frequency of SMO in MEC neurons, and thus λ, has been reported to scale with grid cell field spacing (Giocomo et al., 2007
). We remark that the periodic structure of reconstruction necessarily occurs in 1-D but that the exact geometry in 2-D depends on the location of neurons where spurious interferences occur. Most likely, the spurious interferences generate confusions of different degrees. Neurons that are integer cycles apart share nearly identical SMO phases. Consequently, when APs are reconstructed from phases, these neurons generate confusions, which manifest in reproduction of the original image in nearly perfect copies. These neurons represent the main-grid points of the output representation (seen as the multiple images of the photographer in Figures 7
E,G). Other neurons generate only partial confusion. These neurons are usually half the distance of the main-grid points and they partially reproduce the original input (seen as phantom images of the photographer in the upper right and lower right corners of the area within the white frame in Figure 7
E). Because the partial and complete confusion grids have the same period but with a half-period offset between them in both X and Y coordinates, the superposition of the two grid structures constitutes an elongated hexagonal grid topography (Figures 7
E,G). Since there are also other ways of achieving a hexagonal structure, this may or may not be the mechanism by which the stereotypical grid cells in the MEC acquire precisely such geometry.
Figure 7. Construction of multiple cortical representations by spurious interferences. (A) A 36 × 36 grayscale image was used as input and partitioned into 36 non-overlapping receptive fields, which were mapped on a 36 × 36 input neuron matrix. (B) The activity pattern of a row of neurons [between arrowheads in (A)] that receives input from a single receptive field. Blue-filled circles represent the APs by neurons (ordinate) after the gamma alignment, spreading through 108 cycles (abscissa). Applying a relatively steep SMO gradient (ΔΦ = 0.1π) ensured that multiple neurons shared identical (< Δτ SMO phases, thus facilitating interferences of individual APs of the compressed code with multiple target neurons. (C) The activity of 1,296 neurons total was compressed into 36 channels (one receptive field per neuron). APs are represented by red dots. (D) The spatio-temporal pattern of APs (red-filled circles) after the reconstruction. Note the spatially periodic structure of the APs (a complete period is shown within the vertical bracket). (E) As a result of multiple interferences, the reconstructed image retains multiple representations of the original input. The original 36 × 36 reconstruction (within the white square) was expanded to a 72 × 72 neuron architecture to make the multiple representations more apparent. (F) The interference that led to multiple reconstructions is evident from the correlation plot between the original input AP times and the reconstructed AP times. The dot clusters different from the diagonal are the results of spurious reconstructions, which led to the multiple representations on (E). The abscissa represents input AP times, the ordinate represents reconstructed AP times in SMO cycles. (G) Firing field of a neuron (marked by a red arrow on E) in spatial coordinates. Colors represent the probability of APs generated while the neuron is exposed to a given image displacement. Construction of the plot is explained in the text. Note the grid-cell like periodic receptive field architecture.
Phase Code Exhibits AP Phase Precession
Among the most prevalent evidence for the behavioral significance of systematic phase variation is the phase precession of hippocampal pyramidal cell firing relative to the local theta oscillation while a rat traverses through the place field of the neuron (O’Keefe and Recce, 1993
). These pyramidal neurons also exhibit theta frequency SMO (Leung and Yim, 1986
). Since our model requires nothing more than that AP timing be dependent on a coherent oscillatory drive (SMO) that propagates in space, we investigated whether phase precession can occur without further assumptions. We implemented the spatial navigation condition by defining a 16 × 16 matrix of topographically arranged place cells where neuron aij at the ith column and jth row was driven by the input corresponding to the rat being at the location defined by its Xi and Yj coordinates. Thus, the place field of the rat when moving through XiYj was modeled by neuron aij being exposed to a transient stimulus. Theoretically, this is equivalent to a transient stimulus, defined as a 2-D Gaussian, moving through the receptive field of a neuron (Figure 8
A). This is similar to the real-time motion processing example in Figure 6
, except that the SMO here represents theta instead of gamma. The complete path of the rat was modeled by a series of 20 frames consisting of 16 × 16-pixel-resolution snapshots, in which the 2-D Gaussian advanced one pixel per frame. Since the diameter of the Gaussian was larger than the place field of a neuron, the rat’s position evoked activity in adjacent place cells proportional to the amplitude of the Gaussian intersecting with their place fields. The square area outlined in Figure 8
A covers the place fields of nine neurons. Multiple neurons were activated when the rat was crossing this area. The phase-coded APs of these neurons were combined into a compressed code and shared among the nine neurons before reconstruction. When we tracked the activity of these neurons while the location of the rat changed across frames, the compressed AP sequences displayed a systematic phase precession as a function of the distance from the center of the Gaussian, consistent with the empirical phase precession of hippocampal end entorhinal cortical neurons (Hafting et al., 2008
; O’Keefe and Recce, 1993
). We controlled only one parameter in these simulations, the phase gradient of the SMO field. Figures 8
B–E shows that the direction of phase precession depended on the geometry of the SMO field applied to both input encoding and reconstruction. When unidirectional propagating waves (traveling waves) were applied, depending on the direction of propagation relative to the activation sequence of place cells, we observed different monotonic phase precession effects. Wave propagation in the direction opposite of the place cell activation sequence enabled progressive phase advancement, while wave propagation in the direction of place cell activation sequence enabled progressive phase delay (Figures 8
B,D, respectively). By reducing the SMO phase gradient ten times decreased the slope of phase precession 10 times from 280° to 28° (Figures 8
B,C). Furthermore, when a radial propagation of SMO field was applied (from a single or from multiple sources) the precession started with increasing phase advancement until the animal, i.e., the center of the Gaussian, reached the center of the neuron’s place field, followed by a progressive phase delay as the animal was leaving the center of place field (Figure 8
E). The dependency of phase precession angle on the SMO gradient relative to the activation sequence of the place cells suggests that hippocampal pyramidal neurons may be able to “read out” the rat’s heading direction from the phase precession, assuming that the local SMO field gradient does not change rapidly over time (Huxter et al., 2008
). In summary, phase precession derives naturally from phase coding, without making any additional assumptions, such as asymmetric synaptic potentiation (Mehta et al., 2000
) or dual-oscillator drive (Blair et al., 2008
; Burgess, 2008
; Lengyel et al., 2003
). Phase precession is controlled by a single parameter, the SMO field gradient. Furthermore, consistent with experimental data, phase precession in our model does not require multiple trials to develop but it does require SMO (Hafting et al., 2008
). Since object locations in the environment, according to this model, are originally encoded by phase, we propose that phase precession (phase advancement and phase delay) is expressed in all cortical and limbic structures, including the MEC (Hafting et al., 2008
) and primary sensory areas of the neocortex where the spatial representations are continuously updated due to behavior.
Figure 8. Phase code exhibits phase precession. (A) The input to hippocampal place cells was modeled by generating a 20-frame translation of a 2-D Gaussian representing the rat’s position (rendered with colors) relative to the environment (rectangle). The area was evenly tiled with place fields individually mapped on a 16 × 16 grid of input layer neurons. The size of the Gaussian was chosen such that 9–12 neurons were simultaneously exposed to the rat’s location, but the composition of neurons driven by a given input frame changed with the rat’s location. The four blue and red framed panels represent the four processing stages of the initial and terminal frames, respectively: (I) the rat’s location, represented by a 2-D Gaussian, (II) the discrete sampling of the input by the grid of neurons (input), (III) the input phases in grayscale after APs are aligned to the SMO, and (IV) the reconstructed activity pattern of neurons encoding the rat’s own location. The outlier pixels in both frames are reconstruction errors. (B–E) Effects of SMO field topography on phase precession. Left panels represent the SMO ((B–D) in time-neuron and (E) in neuron space). Second and third panels represent snapshots of the activity of three projection neurons at different magnifications. These neurons in the model represent hippocampal pyramidal cells with adjacent place fields within the outlined area [dashed rectangle on (A)]. The APs evoked by consecutive frames are projected between the SMO waves of adjacent neurons and color-coded according to the input frame in (A) corresponding to the rat’s location. The abscissa represents the time of the APs. The forth panels represent the phase of APs during a single run as a function of the rat’s location. (B) When a traveling wave SMO field gradient was applied the neurons expressed a monotonically advancing AP phase precession spanning 280° theta phase angle. (C) By reducing the phase gradient of SMO ten times the AP phase precession angle decreased proportionally to 28°. In both examples (B,C) the traveling direction of SMO was set to be the opposite to the place cell activation sequence. (D) We reversed the direction of phase precession relative to (B,C) from monotonically increasing advancements to monotonically increasing delays by changing the SMO phase gradient such that it traveled in the direction of the activation sequence of neurons. (E) A bidirectional AP phase precession was enabled by a radially propagating SMO field, where the AP phases advanced continuously until the animal reached the place field center [outlined area in (A)] and developed an increasing delay as the animal exited. Phase scale bars represent ¼ π. Arrows signify the directions of phase precessions.
Modeling Stimulus Invariants
In order to represent stable objects in a dynamic world, neurons must encode object features invariantly with respect to a few common transformations such as position, rotation and time. In order to address whether or not phase coding is able to retain some of these features in spite of spatial or temporal discontinuities, we modeled four different types of invariant stimulus conditions: (i) space-time invariant 1-D stimulus, (ii) 2-D stimulus embedded in random background noise, (iii) 2-D transposition-invariant stimulus and (iv) character recognition. We classified these invariants with respect to either temporal or spatial transformations. Among the invariants we tested, (i) and (ii) were time invariant, while (iii) and (iv) were invariant to spatial transformations. (Implementations of the ii, iii and iv types of invariant preservations are described in the Supplementary Material.)
For (i) we constructed a 1-D random vector R containing 32 values [r1,…,r32]. Next we defined “frames” as the possible subsets of this vector containing 16 adjacent values. We then began an iterative cycle, where first we inputted the first frame [r1,…,r16] to a network of 16 neurons [s1,…,s16] and performed all four phases of information processing from encoding to reconstruction. During each of the next 16 cycles, we incremented the frame position by one step [s1,…,s16] = [ri,…,ri+15], where i = {2,…,17}, and performed all four phases of information processing. Thus in each iteration, 15 out of 16 frame values remained identical to the values in the previous frame, but each of the 15 values was projected onto a different neuron at each exposure (Figure 9
A). Presenting the neurons with only part of the complete pattern in each cycle, such that each neuron’s input value changes every cycle, allowed us to address how a constant (time-invariant) spatial pattern is represented by the phase code in the array of neurons over time (Figures 9
B–E). When we superimposed the temporal patterns of APs of the compressed codes (transfer stage) from all of the 17 successive trials, we observed a marked conservation of AP latencies along with sudden transitions of gamma re-alignments (Figure 9
D). The conservation of time-invariant patterns is reflected by the temporal consistency of APs over time. This consistency was quantified by correlating the AP times (wrapped around 3π) from one frame with the AP times of the next frame and comparing it to the correlation obtained when the stimulus frames were uncorrelated random patterns (i.e., when there was no overlap between successive frames). The return plots in Figure 9
F summarize these correlations. As seen on the left return plot, invariant stimulus frames evoke AP patterns in the compressed code that are highly correlated across frames, despite phase transitions and despite the fact that each neuron receives a different input from each frame. In contrast, uncorrelated frames evoke APs that are uncorrelated across successive frames. This conservation of the AP pattern for an invariant stimulus has implications for visual information processing. For example, we predict that V1 projecting LGN neurons should generate self-similar and stimulus-dependent AP sequences for slowly moving images. These AP sequences are expected to be invariant of position shifts of the whole image on the retina within a certain range of eye movements.
Figure 9. Phase coding is sensitive to stimulus invariance. (A) A 16-sample-wide window (S) was applied to a stimulus vector (R) containing 32 intensity values and the result inputted to 16 neurons of the input layer. The window was slid across R, one sample at a time, to generate 17 successive frames. In this figure we illustrate only 5 of the 17 frames using different grayscales. The network processed each frame as an independent stimulus vector from the encoding to the reconstruction stage (B–E). (B) Superposition of the AP patterns induced by all 16 frames. The grayscale values of filled circles correspond to the frame in (A). (C) The temporal variability of APs is reduced after aligning them to gamma oscillations. (D) The compressed AP streams, superimposed across frames, show a preserved temporal pattern with sudden phase transitions (open arrows) at points where APs from a new frame are assigned to the next gamma cycle. (E) Superimposed traces of the reconstructed patterns. (F) Return plots represent the recurrence of AP-times from frame i to frame i + 1. The left return plot was calculated from the AP pattern in (D) when stimulus (A) was presented. The right return plot was calculated from an example where consecutive frames were uncorrelated. Although each neuron processed different input from every frame, the temporal patterns of APs across successive frames were highly correlated (left). In contrast, when input frames were random and independent from one another the AP patterns became uncorrelated (right). Both plots contain the same number of data points. AP latencies were wrapped around 3π. (The r and P values are shown above the plots.)
We presented theoretical support for phase coding in the CNS with the following two questions in focus: How can the precise spatio-temporal structure of a stimulus be encoded by the phase of APs, and how then can it be recovered from the phase of APs? The model outlined above interprets phase locking as a mechanism by which the phase of APs encodes the precise spatiotemporal structure of the visual input using gamma oscillations as a reference. Utilizing the phase the brain is able to keep different stimulus features separated within the same code (impossible with rate coding) until these features are separated by individual neurons upstream, consistent with sparse coding (Figure 5
). At the same time the phase code allows simultaneous information to be bound together by referencing them to the same gamma cycle, which allows a smooth tracking of sensory input, such as that illustrated on the example of motion processing at a physiological rate (Figure 6
). Aside from the capability of modeling thalamo-cortical and cortico-cortical information processing, phase coding demonstrates a remarkable flexibility in reproducing known functional features of the allocortex, such as the grid cells of the entorhinal cortex and the phase precession of hippocampal pyramidal cells (Figures 8 and 9
, respectively). Moreover, phase coding allows the extraction of stimulus features that are invariant with respect to spatial and temporal transformations (Figure 9 and Figure 2 in Supplementary Material).
Remarkably, phase coding does not contradict with rate coding. The two encoding schemes are compatible (Ahissar et al., 2000
), they may coexist (O’Keefe and Burgess, 2005
) and/or may complement each other (Gollisch and Meister, 2008
; Kayser et al., 2009
) simply because the likelihood of coincidences between the presynaptic AP and postsynaptic SMO scales with the frequency of APs. Moreover, modulation of firing rate is concomitant with changing the phase structure of APs (Margrie and Schaefer, 2003
). Immediate predictions made based on phase coding are summarized in Table 1
.
Nevertheless, the robustness of the model depends on a number of limiting factors, which remain to be investigated. One is the dependency of phase coding on the need for compression before transmission. A key assumption we made for the sake of theoretical clarity in the 1-D model was the n-to-1 dimensionality reduction from the n input layer neurons to a single channel and a 1-to-n dimensionality expansion by information reconstruction at the target layer. This extreme information compression was feasible within the parameter space specified in Figure 4
(Section “Biological Significance of Model Parameters”). However, considering parameters closer to the physiological condition, such as a large n with intrinsic noise in membrane potential affecting AP generation, combined with certain variance of oscillations, and heterogeneous axonal composition within the projection pathways, the n-to-1 reduction is neither necessary nor feasible. This has two consequences. First, a substantial saving in axonal volume can still be achieved with an n-to-m mapping, where n > m ≥ 1, which would not be possible without phase coding. Second, by clustering neurons into m groups, where instead of n a smaller n′ = n/m neurons converges on a single channel, the need for m projection neurons would still substantially improve the reconstruction efficacy, consistent with the known convergence of sensory input on single neurons that constitutes for receptive fields (Figure 3
).
Another limiting factor is the precision of neural code. The phase coding model requires neurons to resolve ∼1.5 ms coincidences between input and intrinsic SMO under the assumption that SMO is 40 Hz. Whether or not the CNS is able to maintain this high precision has been argued (Shadlen and Newsome, 1998
; Shmiel et al., 2005
). Since the ∼1.5 ms precision would guarantee that neighboring neurons do not confuse the origin of two input APs coinciding with their slightly different SMO, this precision is most likely to be verified in the cross-correlograms of nearby neurons. Another factor of precision is the frequency of SMO. In structures where the predominant SMO has a less than 40 Hz frequency, such as the 5–7 Hz in the entorhinal cortex (Giocomo et al., 2007
), the required precision is proportionally less, only Δt < 12 ms. Thus ∼1.5 ms precision is the most extreme requirement for precision.
The third limiting factor is the coherency of oscillations between the source and target area. Phase coding is extremely sensitive for the degree of coherence between source and target. A number of physiological mechanisms have been suggested to maintain high cross-structural coherence, such as the thalamo-cortical loop (Llinas and Ribary, 1993
; Steriade et al., 1996
), entrainment of cortical gamma rhythms by hippocampal theta (Sirota et al., 2008
), cortical theta reset (Rizzuto et al., 2003
), and gap-junctions (Traub et al., 1996
), but direct evidence for an overall synchronizing mechanism that would ensure precise coherence between sensory structures and corresponding cortical areas is lacking.
The fourth limiting factor is the noise tolerance of phase coding. We argued that the compression of the phase code before transference through the projection pathways improves the noise tolerance, and we suggested that compression combined with a feed-forward parallel distribution would improve reliability by implementing an error correction mechanism.
The last limiting factor is the lack of direct evidence for phase-shifted fields of SMO. This pre-assumption was made based on combining two sources of evidence. One is the direct observation of propagating membrane potential changes by intrinsic optical signal and voltage-dependent Ca2+ imaging (Benucci et al., 2007
; Bringuier et al., 1999
; Grinvald et al., 1994
; Prechtl et al., 2000
) and propagating LFP waves (Prechtl et al., 2000
; Rubino et al., 2006
). The other source of evidence derives from direct intracellular observations of single neuronal oscillations, such as subthreshold membrane oscillations (Giocomo et al., 2007
; Hutcheon and Yarom, 2000
; Llinas et al., 1991
). Based on the high correlation between LFP and SMO of individual neurons, the conjecture of phase-shifted field of SMO is plausible.
In conclusion, we demonstrated through various examples that the benefit of encoding information by the phase of APs relative to the intrinsic neuronal oscillations is multifold:
(i) Allows different types of sensory data to be converted to a common coding scheme in which information is referenced by the field of local oscillations and decoded independent of the neuronal distance from the original location and time in the brain, given that the reference oscillation field has the same spectral properties as at the source.
(ii) Protects the code against potential distortions due to the variance of conductivity during transmission in long projection pathways.
(iii) Enables deployment of the same compressed information over large areas of the cerebral cortex and selective “reading-out” of the local information (Figure 5
) without point-to-point mapping between the neurons of the input and target areas.
(iv) Effectively compresses the spatio-temporal pattern of APs before transmission (n-to-1 and 1-to-n).
(v) Enables invariant temporal relations to be encoded independent of the delay and duration of sensory information processing. Similarly, it enables invariant spatial relations to be encoded independent of the absolute spatial location of the agent (Figure 9 and Figure 2B in Supplementary Material).
(vi) It provides an intrinsic biological mechanism for stimulus segmentation.
(vii) It enables information reconstruction at single-neuronal precision (sparse coding) without confusion of information between neighboring neurons.
(viii) It implements spatial and temporal transformations between cortical representations (spatio-temporal receptive fields), which cannot otherwise be achieved by simply changing the topographic mapping between interconnected cortical areas (Figure 1 in Supplementary Material).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by the National Eye Institute. I thank R. A. Andersen for support, reviewing and providing feedback on the manuscript. I further thank S. Gibson, C. Ustun, G. Mulliken, M. Brozovic, H. Cui, C. Stetson and C. Montz for valuable comments; and V. Shcherbatyuk for technical assistance.
The Supplementary Material for this article can be found online at http://www.frontiersin.org/systemsneuroscience/paper/10.3389/ neuro.06/006.2009/