Naftali Tishby1,3,4
- 1 The Interdisciplinary Center for Neural Computation, The Hebrew University, Jerusalem, Israel
- 2 IBM Haifa Research Lab, Haifa, Israel
- 3 The School of Engineering and Computer Science, The Hebrew University, Jerusalem, Israel
- 4 The Edmond and Lily Safra Center for Brain Sciences, The Hebrew University, Jerusalem, Israel
- 5 Department of Medical Neurobiology (Physiology), Institute of Medical Research Israel-Canada, Hadassah Medical School, The Hebrew University, Jerusalem, Israel
Previous reinforcement-learning models of the basal ganglia network have highlighted the role of dopamine in encoding the mismatch between prediction and reality. Far less attention has been paid to the computational goals and algorithms of the main-axis (actor). Here, we construct a top-down model of the basal ganglia with emphasis on the role of dopamine as both a reinforcement learning signal and as a pseudo-temperature signal controlling the general level of basal ganglia excitability and motor vigilance of the acting agent. We argue that the basal ganglia endow the thalamic-cortical networks with the optimal dynamic tradeoff between two constraints: minimizing the policy complexity (cost) and maximizing the expected future reward (gain). We show that this multi-dimensional optimization processes results in an experience-modulated version of the softmax behavioral policy. Thus, as in classical softmax behavioral policies, probability of actions are selected according to their estimated values and the pseudo-temperature, but in addition also vary according to the frequency of previous choices of these actions. We conclude that the computational goal of the basal ganglia is not to maximize cumulative (positive and negative) reward. Rather, the basal ganglia aim at optimization of independent gain and cost functions. Unlike previously suggested single-variable maximization processes, this multi-dimensional optimization process leads naturally to a softmax-like behavioral policy. We suggest that beyond its role in the modulation of the efficacy of the cortico-striatal synapses, dopamine directly affects striatal excitability and thus provides a pseudo-temperature signal that modulates the tradeoff between gain and cost. The resulting experience and dopamine modulated softmax policy can then serve as a theoretical framework to account for the broad range of behaviors and clinical states governed by the basal ganglia and dopamine systems.
Introduction
Many studies have characterized basal ganglia (BG) activity in terms of reinforcement learning (RL) algorithms (Barto, 1995; Schultz et al., 1997; Bar-Gad et al., 2003b; Gurney et al., 2004; Balleine et al., 2007). Early physiological works revealed that phasic dopamine activity encodes the mismatch between prediction and reality or the RL temporal difference (TD) error signal (Schultz et al., 1997; Dayan and Balleine, 2002; Fiorillo et al., 2003; Satoh et al., 2003; Morris et al., 2004; Nakahara et al., 2004; Bayer and Glimcher, 2005). In accordance with these RL models of the BG network, dopamine has been shown to modulate the efficacy of cortico-striatal transmission (Reynolds et al., 2001; Surmeier et al., 2007; Kreitzer and Malenka, 2008; Pan et al., 2008; Pawlak and Kerr, 2008; Shen et al., 2008). However most RL models of the BG do not explicitly discuss the issue of BG-driven behavioral policy, or the interactions between the acting agent and the environment.
This work adopts the RL actor/critic framework to model the BG networks. We assume that cortical activity represents the state and modulates the activity of the BG input stages – the striatum. Cortico-striatal synaptic efficacy is adjusted by dopamine modulated Hebbian rules (Reynolds et al., 2001; Reynolds and Wickens, 2002; McClure et al., 2003; Shen et al., 2008). Striatal activity is further shaped in the downstream BG network (e.g., in the external segment of the globus pallidus, GPe). Finally, the activity of the BG output structures (the internal part of the globus pallidus and the substantia nigra pars reticulata; GPi and SNr respectively) modulate activity in the brainstem motor nuclei and thalamo-frontal cortex networks that control ongoing and future actions (Deniau and Chevalier, 1985; Mink, 1996; Hikosaka, 2007). It is assumed that the mapping of the BG activity and action does not change along the BG main axis (from the striatum to the BG output stages) or in the BG target structures. Therefore, the specific or the distributed activity of the striatal neurons and the neurons in the downstream BG structures represents the desired action. Moreover, the excitatory cortical input to the striatum as dictated by the cortical activity and the efficacy of the cortico-striatal synapses represents the specific state–action pair Q-value.
To simplify our BG model, we modeled the BG main axis as the connections from the D2 containing projection neurons of the striatum, through the GPe, to the BG output structures. We neglected (at this stage) many of the other critical features of the BG networks such as the BG direct pathway structures (direct connections between D1 dopamine receptors containing striatal cells and the GPi/SNr), the subthalamic nucleus (STN) and the reciprocal connections between the GPe and the striatum and the STN. We further assumed that the activity of the BG output structures inhibits their target structures – the thalamus and brainstem motor nuclei (Hikosaka and Wurtz, 1983; Deniau and Chevalier, 1985; Parush et al., 2008); thus the action probability is considered to be inversely proportional to the BG output distributed activity.
Most previous RL models of the BG network assume that the computational goal of the BG is to maximize the (discounted) cumulative sum of a single variable – the reward (pleasure) prediction error. Thus, the omission of reward and aversive events are considered events with negative reward values as compared to the positive values of food/water predicting cues and delivery. However, in many cases the cost of an action is different from a negative gain. We therefore suggest that the emotional dimensions of behavior in animals and humans must be represented by more than a single axis. In the following sections we present a behavioral policy that seeks the optimal tradeoff between maximization of cumulative expected reward and minimization of cost. Here we use policy complexity as the representative of a cost. We assume that agents pay a price for a more complicated behavioral policy, and therefore try to minimize the complexity of their behavioral policy. We simulate the behavior of an agent aiming at multi-dimensional optimization of its behavior while engaged in a decision task similar to the multi-armed bandit problem (Vulkan, 2000; Morris et al., 2006).
Although we used two axes (gain and cost), we obviously do not claim that there are no other, or better, axes that span the emotional space of the animal. For example, arousal, novelty, and minimization of pain could all be functions that the BG network attempts to optimize. Nevertheless, we believe that the demonstration of the much richer repertoire of behavioral policy enabled by the multi-dimensional optimization processes sheds light on the goals and algorithms of the BG network. Future research should enable us to determine the actual computational aim and algorithms of the BG networks.
“Minimal Complexity – Maximal Reward” Behavioral Policy
When an agent is faced with the task of selecting and executing an action, it needs to perform a transformation from a state representing the present and past (internal and external) environment to an action. However, at least two competitive principles guide the agent. On the one hand, it aims to maximize the valuable outcome (cumulative future-discounted reward) of the selected action. On the other hand, the agent is interested in minimizing the cost of its action, for example to act according to a policy with minimal complexity.
The transition from state to action requires knowledge of the state identity. A state identity representation can be thought of as a long vector of letters describing the size, shape, color, smell, and other variables of the objects in the current environment. The longer the vector representing the state, the better is our knowledge of that state. The complexity of the state representation required by a policy reflects the complexity of the policy. Therefore we define policy complexity as the length of the state representation required by that policy. We can estimate the length of the representation of the state identity required by a policy by observing the length of the state that can be extracted on average given the chosen actions. This definition therefore classifies policies that require detailed representations of the state as complex. On the other hand, a policy that does not commit to a specific pair of actions and states, and therefore does not require a lengthy state representation, has low complexity. Formally, we can therefore define the state–action mutual information – MI(S; A) (for a brief review of the concepts of entropy and mutual information – see Box 1) as a measure of policy complexity (see formal details in Appendix 1).
BOX 1. Entropy, mutual information, and uncertainty
The entropy function quantifies in bits the amount of “randomness” or “uncertainty” of a distribution. If |X| = n, x ∈ X is a variable with distribution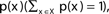 
, then the entropy is defined by: 
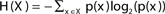(Cover and Thomas, 1991).
The entropy values range from 0 to log2(n).
The situation where H(X) = 0 is obtained when there is no randomness associated with the variable; i.e., the identity of x is known with full certainty. For example: p(x = c) = 1, p(x ≠ c) = 0.
The situation where H(X) = log2(n) is obtained when x is totally random: p(x) = 1/n for all values of x. Intermediate values correspond to intermediate levels of uncertainty.
Entropy quantifies the amount of “uncertainty” when dealing with two variables.
H(X|Y) denotes the entropy of variable x ∈ X given variable y ∈ Y; i.e.,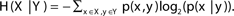 
. The entropy of a pair of variables is given by H(X, Y) = H(X) + H(Y|X).
The mutual information between two variables can be defined as the number of bits of “uncertainty” of one of the variables reduced by knowledge of the other variable (on average): MI(X; Y) = H(X) − H(X|Y).
The mutual information between two variables can also be defined by the Kullback–Leibler divergence (Dkl) between the actual probability of the pair X, Y [p(x, y)] and the expected probability if the variables were independent [p(x)*p (y)] (Cover and Thomas, 1991):
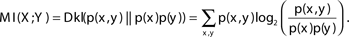
The following example can serve to better understand the notion of representation length and policy complexity. Assume an agent is facing one of four possible states S1,S2,S3,S4 with equal probability, and using policy A, B, or C chooses one of two possible actions A1,A2. Policy A determines that action A1 is chosen for all states, policy B chooses the action randomly for all states, and policy C determines that action A1 is chosen for states S1,S2, and action A2 is chosen for states S3,S4. In policies A and B determining the action does not require knowledge of the state (and the state can not be extracted given the chosen action), and therefore there is no required state representation, and the representation length and policy complexity is 0. By contrast in policy C determining the action does not require full knowledge of the state but only whether the state is S1,S2 or S3,S4. Therefore the required state representation only needs to differentiate between two possibilities. This could be done using a codeword of one bit (for example 0 representing S1,S2 and 1 representing S3,S4). Hence the representation length and policy complexity is 1 bit. As expected, it can be shown that for policies A and B MI(S; A) = 0, and for policy C MI(S; A) = 1.
The policy complexity is a measure of the policy commitment to the future action given the state (see formal details in Appendix 1). Higher MI values make it possible to classify the action (given a state) with higher resolution. In the extreme high case, the specific action is determined from the state, MI(S; A) = log2(number of possible actions), and all the entropy (uncertainty) of the action is eliminated. In the extreme low case MI(S; A) = 0, and the chosen action is completely unpredictable from the state.
Combining both expected reward and policy complexity factors produces an optimization problem that aims at minimal commitment to state–action mapping (maximal exploration) while maximizing the future reward. A similar optimization can be found in (Klyubin et al., 2007; Tishby and Polani, 2010). Below we show that the optimization problem introduces a tradeoff parameter β that balances the two optimization goals. Setting a high β value will bias the optimization problem toward maximizing the future reward, while setting a low β value will bias the optimization problem toward minimizing the cost, i.e., the policy complexity.
We solve the optimization problem of minimum complexity – maximum reward by a generalization of the Blahut-Arimoto algorithm for rate distortion problems (Blahut, 1972; Cover and Thomas, 1991, and see Appendix 2 for details). This results in the following equation:
where p(a|s) is the probability of action a given a state s, or the behavioral policy, p(a) is the overall probability of action a, averaged over all possible states. Q(s,a) is the value of the state–action pairs, and β is the inverse of the pseudo-temperature parameter, or the tradeoff parameter that balances the two optimization goals. Finally, Z(s) is a normalization factor (summed over all possible actions) that limits p(a|s) to the range of 0–1.
In the RL framework the state–action Q-value is updated as a function of the discrepancy between the predicted Q value and the actual outcome. Thus, when choosing the next step, the behavioral policy influences which of the state–action pairs is updated. In the more general case of an agent interacting with a stochastic environment, the behavioral policy changes the state–action Q-value (expected reward of a state–action pair), which in turn may change the policy. Thus, another equation concerning the expected reward (Q(s,a) values) should be associated with the previous equations (convergence of value and policy iterations, Sutton and Barto, 1998). However, in our simplified BG model, the policy and Q-value are not changed simultaneously since the Q-value is modified by the cortico-striatal synaptic plasticity, and the policy is modified by the level of dopamine. These two specific modifications may occur through different molecular mechanisms, e.g., D1 activation that affects synaptic plasticity and D2 activation that affects post synaptic excitability (Kerr and Wickens, 2001; Pawlak and Kerr, 2008; but see Shen et al., 2008) and at different timescales (Schultz, 1998; Goto et al., 2007). At this stage of our model, we therefore do not require simultaneous convergence of the expected reward values with the policy.
The behavioral policy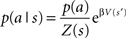 
that optimizes the reward/complexity tradeoff resembles the classical RL softmax distribution where the probability of choosing an action is exponentially dependent on the action’s expected reward and β – the inverse of the pseudo-temperature parameter (Sutton and Barto, 1998). Here, the probability of choosing an action given a specific state p(a|s) is exponentially dependent on the state–action Q-value multiplied by the prior probability of choosing the specific action independently of the state – p(a). This prior probability gives the advantage to actions that are chosen more often, and for this reason was dubbed the “experience-modulated softmax policy” here. This is in line with preservation behavior, where selected actions are influenced by the pattern of the agent’s past choices (Slovin et al., 1999; Lau and Glimcher, 2005; Rutledge et al., 2009). In cases where the a-priori probability of all actions is equal, the experience-modulated softmax policy is equivalent to the classical softmax policy. Finally, in single state scenarios (i.e., an agent is facing only one state, but still has more than one possible action) where p(a|s) = p(a), the policy maximizes the expected reward without minimizing the state–action MI. Therefore, p(a) = 1 for the action with the highest Q-value.
The Dual Role of Dopamine in the Model
Many studies have indicated that dopamine influences BG firing rate properties directly and not only by modulating cortico-striatal synaptic plasticity. Apomorphine (an ultrafast-acting D2 dopamine agonist) has an immediate (<1 min) effect on Parkinsonian patients and on the discharge rate of BG neurons (Stefani et al., 1997; Levy et al., 2001; Nevet et al., 2004). There is no consensus regarding the effect of dopamine on the excitability of striatal neurons (Nicola et al., 2000; Onn et al., 2000; Day et al., 2008), probably since the in vivo effect of dopamine on striatal excitability is confounded by the many closed loops inside the striatum (Tepper et al., 2008), and the reciprocal connections with the GPe and the STN. Nevertheless, most researchers concur that high tonic dopamine levels decrease the discharge rate of BG output structures, whereas low levels of tonic dopamine increase the activity of BG output (in rodents: Ruskin et al., 1998; in primates: Filion et al., 1991; Boraud et al., 1998, 2001; Papa et al., 1999; Heimer et al., 2002; Nevet et al., 2004; and in human patients: Merello et al., 1999; Levy et al., 2001). These findings strongly indicate that tonic dopamine plays a significant role in shaping behavioral policy beyond a modulation of the efficacy of the cortico-striatal synapses. We suggest that dopamine serves as the inverse of β; i.e., as the pseudo-temperature, or the tradeoff parameter between policy complexity and expected reward (Eq. 1).
In our model, dopamine thus plays a dual role in the striatum. First, dopamine has a role in updating the Q-values by modulating the efficacy of the cortico-striatal connections, and second, in setting β (the inverse of the pseudo temperature). However, since changing the excitability is faster than modulating synaptic plasticity, dopamine acts at different timescales and the effects of lack or excess of dopamine may appear more rapidly as changes in the softmax pseudo-temperature parameter of the behavioral policy than in the changes in the Q-values.
The following description can provide a possible characterization of the influence of dopamine on the computational physiology of the BG. The baseline activity of the striatal neurons, and by extension of the BG output neurons that represent all actions, is modulated by the tonic levels of striatal dopamine. In addition, striatal neural activity is modulated by the specific state–action value (Q-value), and in turn determines the activity of the BG output neurons which encode a specific probability for each action. High dopamine levels decrease the dynamic range of the Q-value’s influence (the baseline activity of the striatal neurons decreases, and consequently the dynamic range of the additional decrease in their discharge is reduced). Therefore different Q-values will result in similar BG output activity, and consequently the action probability will be more uniform. On the other hand, low dopamine levels result in a large dynamic range of striatal discharge, producing a probability distribution that is more closely related to the cortical Q-values preferring higher values. At moderate or normal dopamine levels the probability distribution of future action is dependent on the Q-values.
This behavior is also captured in the specifics of our model. A high amount of dopamine is equivalent to low β values (or a high pseudo temperature), yielding a low state–action MI. This policy resembles gambling, where the probability of choosing an action is not dependent on the state and therefore is not correlated with the outcome prospects. Lowering the amount of dopamine, increasing β, causes an increase in the MI. In this case, the action probability is specifically related to the state–action Q-value preferring higher reward prospects. In the extreme and most conservative case, the policy chooses deterministically the action with the highest reward prospect (greedy behavior).
Simulating a Probabilistic Two-Choice Task
We simulated the behavior of the experience modulated softmax model in a probabilistic two-choice task similar to one used previously in our group (Morris et al., 2006). We only simulated the portion of the task in which there are multiple states in which the subject is expected to choose one of two actions (either move left or right). Intermingled with the trials on the binary decision task are forced choice trials (not discussed here). The different states are characterized by their different (action dependent) reward prospects. Actions can lead to a reward with one of the following probabilities: 25, 50, 75, or 100%. The task states consist of all combinations of the different reward probabilities. The states are distributed uniformly (i.e., all 16 states have equal probability). Note that since both sides are symmetrically balanced between high and low probabilities, there should be no prior preference for either of the actions (the trials on the forced choice task are also symmetrically balanced). Therefore, there is equal probability of choosing either of the sides (p(left)=p(right)=0.5), and the experience-modulated softmax behaves like the regular softmax policy.
Figures 1–4 illustrate the simulation results. Figure 1 illustrates the expected reward as a function of the state–action MI for different dopamine levels. Since in our model dopamine acts as 1/β, decreasing the dopamine level causes both the state–action MI (complexity of the policy, cost) and the average expected reward (gain) to increase until they reach a plateau. On the other hand, increasing the dopamine level leads to conditions with close to 0 complexity and reward (“no pain, no gain” state).
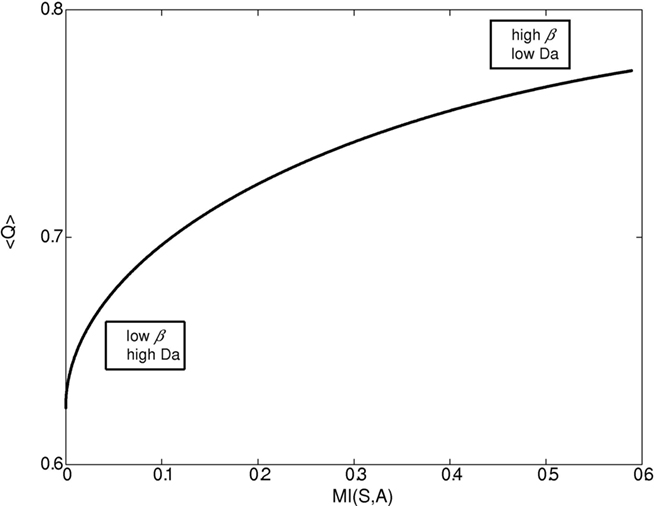
Figure 1. Expected reward as a function of the complexity of the behavioral policy for different β/dopamine levels. High dopamine (Da) or low β (inverse of the softmax pseudo-temperature variable) lead to a simple reward policy, e.g., a random policy with low state–action mutual information (MI(s,a)), and low expected reward <Q>. On the other hand, a low dopamine level leads to a complex (deterministic) policy with high MI and high expected reward. In general, both state–action MI and expected reward <Q> increase with beta (though when beta is close to 0, the increase in MI is very slow).
Figure 2 illustrates, for different dopamine levels, the probability of choosing an action as a function of the expected reward relative to the total sum of expected rewards. At low dopamine levels the expected reward is maximized, and therefore the action with a higher expected reward is always chosen (greedy behavioral policy). At moderate dopamine levels (i.e., simulating normal dopamine conditions) the probability of choosing an action is proportional to its relative expected reward. This is very similar to the results seen in (Morris et al., 2006), and in line with a probability matching action selection policy (Vulkan, 2000) where the probability of choosing an action is proportional to the action’s relative expected reward. High dopamine levels yield a random policy, where the probability of choosing an action is not dependent on its expected reward.
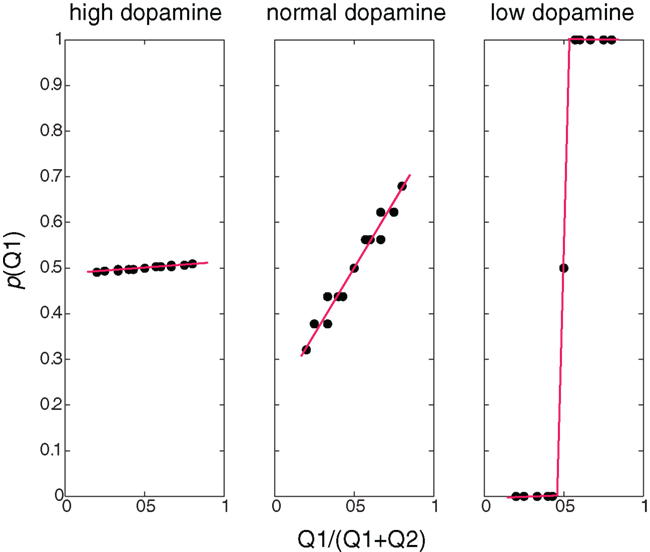
Figure 2. Behavioral policies at different β/dopamine levels. Probability of choosing Q1 as a function of the ratio between Q1 and (Q1+Q2): high dopamine (low β) – random policy, not dependent on the Q-value, normal (moderate dopamine and β) – policy dependent on the Q-value (preferring higher values), low dopamine (high β) – deterministic (greedy) policy – choosing the higher Q-values, and the dots represent values calculated in the simulation, and the lines are linear curve fittings of these points.
A unique feature of the multi-dimensional optimization policy (Eq. 1) is the effect of an a priori probability for action (modulation by experience). Figure 3 illustrates the behavioral policy of an agent with moderate dopamine levels in two scenarios. In the first scenario the agent is facing a uniform state distribution, whereas in the second scenario the agent is facing an asymmetrical distribution in which states with a higher reward probability on the left side appear twice as often as states with a higher reward probability on the right. In the latter distribution there is clear preference for the left side (e.g., the policy prefers the left over the right side in states with equal reward probability on both sides). Thus, the history or the prior probability to perform an action influences the action selection policy. Figure 4 illustrates the expected reward as a function of the state–action MI for both the experience-modulated softmax and the regular softmax policies. As expected, since the experience-modulated softmax policy is driven by minimizing the state–action MI while maximizing the reward, the experience-modulated softmax policy will result in higher expected reward values.
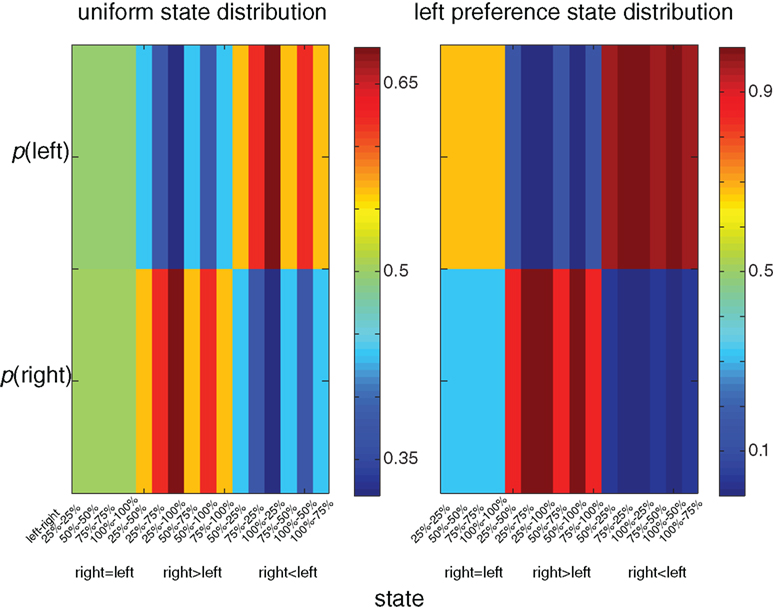
Figure 3. Color coded illustration of behavioral policies for different state distributions. In the left column the agent is facing a uniform state distribution, whereas in the right column the agent is facing an asymmetrical distribution in which states with the higher reward probability on the left side appear twice as often as states with a higher reward probability on the right. In the right column there is a clear preference for the left side (e.g., the policy prefers the left over the right side in states with equal reward probability on both sides).
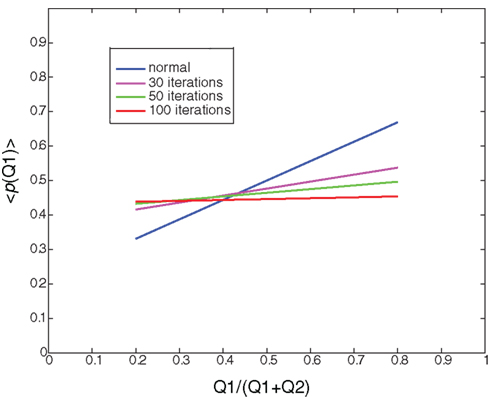
Figure 4. Random learning: Illustration of the average probability of choosing Q1 as a function of the ratio between Q1 and (Q1+Q2) after 0 (normal), 30, 50, and 100 iterations of random learning. Random learning will eventually lead to a random policy (policy after 100 iterations, red curve).
Modeling Dopamine Related Movement Disorders
Our simulations depict a maximization (greedy) action selection policy for low dopamine levels. However, in practice, an extreme lack of dopamine causes Parkinsonian patients to exhibit akinesia – a lack of movement. Severe akinesia cannot be explained mathematically by our model. The normalization of the softmax equation ensures that the sum of p(a|s) over all a is 1, and for this reason there cannot be a condition where all p(a|s), for all a and all s, are close to 0. We suggest that in these extreme cases the BG neural network does not unequivocally implement the experience-modulated softmax algorithm. Since the activity of the BG output structures inhibits their target structures, and a lack of dopamine increases the BG output activity, extremely low dopamine levels can result in complete inhibition and therefore total blockage of activity, i.e., akinesia. In these cases an extraordinary high Q-value may momentarily overcome the inhibition and cause paradoxical kinesia (Keefe et al., 1989; Schlesinger et al., 2007; Bonanni et al., 2010).
Another dopamine related movement disorder is levo-3,4-dihydroxyphenylalanine (l-DOPA) induced dyskinesia. Dopamine replacement therapy (DRT) by either l-DOPA or dopamine agonists is the most effective pharmacological treatment for Parkinson’s disease. However, almost all patients treated with long term DRT develop dyskinesia – severely disabling involuntary movements. Once these involuntary movements have been established, they will occur on every administration of DRT. Our model provides two possible computational explanations for l-DOPA induced dyskinesia. First, the high levels of dopamine force the system to act according to a random or gambling policy. The second possible cause of dyskinesia is related to the classical role of dopamine in modulating synaptic plasticity and reshaping the cortico-striatal connectivity (Surmeier et al., 2007; Kreitzer and Malenka, 2008; Russo et al., 2010). Thus high (but not appropriate) dopamine levels randomly reinforce state–action pairs. We define this type of random reinforcement as random learning. Figure 5 illustrates the average action policy caused by random learning over time. Thus, dyskinesia may be avoided by dopaminergic treatments that do not modulate the cortico-striatal synaptic efficacy (less D1 activation) while maintaining all other D2 therapeutic benefits.
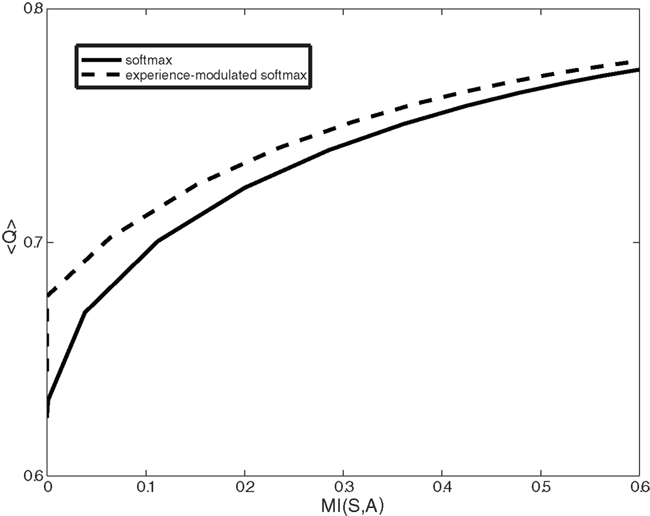
Figure 5. Expected reward (<Q>) as a function of the complexity of the behavioral policy (MI(S,A)) for both the experience-modulated softmax and the regular softmax policies in the case of asymmetrical distribution of states. The agent is facing an asymmetrical distribution in which states with the higher reward probability on the left side appear twice as often as states with a higher reward probability on the right. In this scenario, for given complexity values, the experience-modulated softmax policy yields a higher expected reward value.
Discussion
In contrast to previous BG models that have concentrated on either explaining pathological behavior (e.g., Albin et al., 1989) or on learning paradigms and action selection (e.g., Schultz et al., 1997; Cohen and Frank, 2009; Wiecki and Frank, 2010), here we attempt to integrate both the phasic and tonic effects of dopamine to account for both normal and pathological behaviors in the same model. We presented a BG related top-down model in which the tonic dopamine level balances maximizing the expected reward and reducing the policy complexity. Our agent aims to maximize the expected reward while minimizing the complexity of the state description, i.e., by preserving the minimal information for reward maximization. This approach is also related to the information bottleneck method (Tishby et al., 1999), where dimensionality reduction aims to reduce the MI between the input and output layers while maximizing the MI between the output layer and a third variable. Hence, the transition from input to output preserves only relevant information. In the current model, the dimensionality reduction from state to action, or at the network level from cortex to BG (Bar-Gad et al., 2003b), preserves relevant information on reward prospects. This dimensionality reduction can also account for the de-correlation issues associated with the BG pathway (Bar-Gad et al., 2003a,b). In addition, the complexity of the representation of the states can be considered as the “cost” of the internal representation of these states. Hence the model solves a minimum cost vs. maximum reward variation problem. This is the first BG model to show that a softmax like policy is not arbitrary selected, but rather is the outcome of the optimization problem solved by the BG.
Like the softmax policy (Sutton and Barto, 1998), our model experience-modulated softmax policy is exponentially dependent on the expected reward. However in this history-modulated distribution, the probability of an action a, given a state s, is also dependent on the prior action probability. In cases where the prior probability uniformly distributes over the different actions, the experience-modulated softmax policy behaves like the regular softmax. Therefore our model can account for softmax and probability matching action selection policies seen in previous studies (Vulkan, 2000; Morris et al., 2006). Furthermore, it would be interesting to confirm these predictions by replicating these or similar experiments while manipulating the prior action statistics (for example as seen in Figure 3).
Changing the dopamine level from low to high shifts the action policy from a conservative (greedy) policy that chooses the highest outcome to a policy that probabilistically chooses the action according to the outcome (probability matching). Eventually, with a very high level of dopamine, the policy will turn into a random (gambling) policy where the probability of choosing an action is independent of its outcome. This shift in behavioral policy can result from normal or pathological transitions. High dopamine levels can be associated with situations that involve excitement or where the outcome provides high motivation (Satoh et al., 2003; Niv et al., 2006). Pathological lacks or excesses of dopamine also change the policy as is seen in akinetic and dyskinetic states typical of Parkinson’s disease. We suggest that blocking the dopamine treatment effects leading to random learning while preserving the pseudo-temperature effects of the treatment may lead to amelioration of akinesia while avoiding l-DOPA induced dyskinesia.
To conclude, the experience-modulated soft-max model provides a new conceptual framework that casts dopamine in the role of setting the action policy on a scale of risky to conservative and normal to pathological behaviors. This model introduces additional dimensions to the problem of optimal behavioral policy. The organism not only aims to satisfy reward maximization but also other objectives. This pattern has been observed in many experiments where behavior is not in line with merely maximizing task return (Talmi et al., 2009). In the future, other objectives can be added to the model as well as other balancing substances. These additional dimensions will introduce richer behavior to the BG model that will more closely resemble real life decisions and perhaps account for other pathological cases as well.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was partly supported by the FP7 Select and Act grant (Hagai Bergman) and by the Gatsby Charitable Foundation (Naftali Tishby).
References
Albin, R. L., Young, A. B., and Penney, J. B. (1989). The functional anatomy of basal ganglia disorders. Trends Neurosci. 12, 366–375.
Balleine, B. W., Delgado, M. R., and Hikosaka, O. (2007). The role of the dorsal striatum in reward and decision-making. J. Neurosci. 27, 8161–8165.
Bar-Gad, I., Heimer, G., Ritov, Y., and Bergman, H. (2003a). Functional correlations between neighboring neurons in the primate globus pallidus are weak or nonexistent. J. Neurosci. 23, 4012–4016.
Bar-Gad, I., Morris, G., and Bergman, H. (2003b). Information processing, dimensionality reduction and reinforcement learning in the basal ganglia. Prog. Neurobiol. 71, 439–473.
Barto, A. G. (1995). “Adaptive critics and the basal ganglia,” in Models of Information Processing in the Basal Ganglia, eds J. C. Houk, J. L. Davis and D. G. Beiser (Cambridge: The MIT Press), 215–232.
Bayer, H. M., and Glimcher, P. W. (2005). Midbrain dopamine neurons encode a quantitative reward prediction error signal. Neuron 47, 129–141.
Blahut, R. E. (1972). Computation of channel capacity and rate distortion function. IEEE Trans. Inform. Theory IT 18, 460–473.
Bonanni, L., Thomas, A., Anzellotti, F., Monaco, D., Ciccocioppo, F., Varanese, S., Bifolchetti, S., D’Amico, M. C., Di Iorio, A., and Onofrj, M. (2010). Protracted benefit from paradoxical kinesia in typical and atypical parkinsonisms. Neurol. Sci. 31, 751–756.
Boraud, T., Bezard, E., Bioulac, B., and Gross, C. E. (2001). Dopamine agonist-induced dyskinesias are correlated to both firing pattern and frequency alterations of pallidal neurones in the MPTP-treated monkey. Brain 124, 546–557.
Boraud, T., Bezard, E., Guehl, D., Bioulac, B., and Gross, C. (1998). Effects of L-DOPA on neuronal activity of the globus pallidus externalis (GPe) and globus pallidus internalis (GPi) in the MPTP-treated monkey. Brain Res. 787, 157–160.
Cohen, M. X., and Frank, M. J. (2009). Neurocomputational models of basal ganglia function in learning, memory and choice. Behav. Brain Res. 199, 141–156.
Day, M., Wokosin, D., Plotkin, J. L., Tian, X., and Surmeier, D. J. (2008). Differential excitability and modulation of striatal medium spiny neuron dendrites. J. Neurosci. 28, 11603–11614.
Dayan, P., and Balleine, B. W. (2002). Reward, motivation, and reinforcement learning. Neuron 36, 285–298.
Deniau, J. M., and Chevalier, G. (1985). Disinhibition as a basic process in the expression of striatal functions. II. The striato-nigral influence on thalamocortical cells of the ventromedial thalamic nucleus. Brain Res. 334, 227–233.
Filion, M., Tremblay, L., and Bedard, P. J. (1991). Effects of dopamine agonists on the spontaneous activity of globus pallidus neurons in monkeys with MPTP-induced parkinsonism. Brain Res. 547, 152–161.
Fiorillo, C. D., Tobler, P. N., and Schultz, W. (2003). Discrete coding of reward probability and uncertainty by dopamine neurons. Science 299, 1898–1902.
Goto, Y., Otani, S., and Grace, A. A. (2007). The Yin and Yang of dopamine release: a new perspective. Neuropharmacology 53, 583–587.
Gurney, K., Prescott, T. J., Wickens, J. R., and Redgrave, P. (2004). Computational models of the basal ganglia: from robots to membranes. Trends Neurosci. 27, 453–459.
Heimer, G., Bar-Gad, I., Goldberg, J. A., and Bergman, H. (2002). Dopamine replacement therapy reverses abnormal synchronization of pallidal neurons in the 1-methyl-4-phenyl-1,2,3,6-tetrahydropyridine primate model of parkinsonism. J. Neurosci. 22, 7850–7855.
Hikosaka, O., and Wurtz, R. H. (1983). Visual and oculomotor functions of monkey substantia nigra pars reticulata. IV. Relation of substantia nigra to superior colliculus. J. Neurophysiol. 49, 1285–1301.
Keefe, K. A., Salamone, J. D., Zigmond, M. J., and Stricker, E. M. (1989). Paradoxical kinesia in parkinsonism is not caused by dopamine release. Studies animal model. Arch. Neurol. 46, 1070–1075.
Kerr, J. N., and Wickens, J. R. (2001). Dopamine D-1/D-5 receptor activation is required for long-term potentiation in the rat neostriatum in vitro. J. Neurophysiol. 85, 117–124.
Klyubin, A. S., Polani, D., and Nehaniv, C. L. (2007). Representations of space and time in the maximization of information flow in the perception-action loop. Neural Comput. 19, 2387–2432.
Kreitzer, A. C., and Malenka, R. C. (2008). Striatal plasticity and basal ganglia circuit function. Neuron 60, 543–554.
Lau, B., and Glimcher, P. W. (2005). Dynamic response-by-response models of matching behavior in rhesus monkeys. J. Exp. Anal. Behav. 84, 555–579.
Levy, R., Dostrovsky, J. O., Lang, A. E., Sime, E., Hutchison, W. D., and Lozano, A. M. (2001). Effects of apomorphine on subthalamic nucleus and globus pallidus internus neurons in patients with Parkinson’s disease. J. Neurophysiol. 86, 249–260.
McClure, S. M., Daw, N. D., and Montague, P. R. (2003). A computational substrate for incentive salience. Trends Neurosci. 26, 423–428.
Merello, M., Balej, J., Delfino, M., Cammarota, A., Betti, O., and Leiguarda, R. (1999). Apomorphine induces changes in GPi spontaneous outflow in patients with Parkinson’s disease. Mov. Disord. 14, 45–49.
Mink, J. W. (1996). The basal ganglia: focused selection and inhibition of competing motor programs. Prog. Neurobiol. 50, 381–425.
Morris, G., Arkadir, D., Nevet, A., Vaadia, E., and Bergman, H. (2004). Coincident but distinct messages of midbrain dopamine and striatal tonically active neurons. Neuron 43, 133–143.
Morris, G., Nevet, A., Arkadir, D., Vaadia, E., and Bergman, H. (2006). Midbrain dopamine neurons encode decisions for future action. Nat. Neurosci. 9, 1057–1063.
Nakahara, H., Itoh, H., Kawagoe, R., Takikawa, Y., and Hikosaka, O. (2004). Dopamine neurons can represent context-dependent prediction error. Neuron 41, 269–280.
Nevet, A., Morris, G., Saban, G., Fainstein, N., and Bergman, H. (2004). Rate of substantia nigra pars reticulata neurons is reduced in non-parkinsonian monkeys with apomorphine-induced orofacial dyskinesia. J Neurophysiol. 92, 1973–1981.
Nicola, S. M., Surmeier, J., and Malenka, R. C. (2000). Dopaminergic modulation of neuronal excitability in the striatum and nucleus accumbens. Annu. Rev. Neurosci. 23, 185–215.
Niv, Y., Joel, D., and Dayan, P. (2006). A normative perspective on motivation. Trends Cogn. Sci. 10, 375–381.
Onn, S. P., West, A. R., and Grace, A. A. (2000). Dopamine-mediated regulation of striatal neuronal and network interactions. Trends Neurosci. 23: S48–S56.
Pan, W. X., Schmidt, R., Wickens, J. R., and Hyland, B. I. (2008). Tripartite mechanism of extinction suggested by dopamine neuron activity and temporal difference model. J. Neurosci. 28, 9619–9631.
Papa, S. M., DeSimone, R., Fiorani, M., and Oldfield, E. H. (1999). Internal globus pallidus discharge is nearly suppressed during levodopa-induced dyskinesias. Ann. Neurol. 46, 732–738.
Parush, N., Arkadir, D., Nevet, A., Morris, G., Tishby, N., Nelken, I., and Bergman, H. (2008). Encoding by response duration in the basal ganglia. J. Neurophysiol. 100, 3244–3252.
Pawlak, V., and Kerr, J. N. (2008). Dopamine receptor activation is required for corticostriatal spike-timing-dependent plasticity. J. Neurosci. 28, 2435–2446.
Reynolds, J. N., Hyland, B. I., and Wickens, J. R. (2001). A cellular mechanism of reward-related learning. Nature 413, 67–70.
Reynolds, J. N., and Wickens, J. R. (2002). Dopamine-dependent plasticity of corticostriatal synapses. Neural Netw. 15, 507–521.
Ruskin, D. N., Rawji, S. S., and Walters, J. R. (1998). Effects of full D1 dopamine receptor agonists on firing rates in the globus pallidus and substantia nigra pars compacta in vivo: tests for D1 receptor selectivity and comparisons to the partial agonist SKF 38393. J. Pharmacol. Exp. Ther. 286, 272–281.
Russo, S. J., Dietz, D. M., Dumitriu, D., Morrison, J. H., Malenka, R. C., and Nestler, E. J. (2010). The addicted synapse: mechanisms of synaptic and structural plasticity in nucleus accumbens. Trends Neurosci. 33, 267–276.
Rutledge, R. B., Lazzaro, S. C., Lau, B., Myers, C. E., Gluck, M. A., and Glimcher, P. W. (2009). Dopaminergic drugs modulate learning rates and perseveration in Parkinson’s patients in a dynamic foraging task. J. Neurosci. 29, 15104–15114.
Satoh, T., Nakai, S., Sato, T., and Kimura, M. (2003). Correlated coding of motivation and outcome of decision by dopamine neurons. J. Neurosci. 23, 9913–9923.
Schlesinger, I., Erikh, I., and Yarnitsky, D. (2007). Paradoxical kinesia at war. Mov. Disord. 22, 2394–2397.
Schultz, W. (1998). The phasic reward signal of primate dopamine neurons. Adv. Pharmacol. 42, 686–690.
Schultz, W., Dayan, P., and Montague, P. R. (1997). A neural substrate of prediction and reward. Science 275, 1593–1599.
Shannon, C. E. (1959). Coding theorems for a discrete source with a fidelity criterion. IRE Nat. Conv. Rec. 4, 142–163.
Shen, W., Flajolet, M., Greengard, P., and Surmeier, D. J. (2008). Dichotomous dopaminergic control of striatal synaptic plasticity. Science 321, 848–851.
Slovin, H., Abeles, M., Vaadia, E., Haalman, I., Prut, Y., and Bergman, H. (1999). Frontal cognitive impairments and saccadic deficits in low-dose MPTP-treated monkeys. J. Neurophysiol. 81, 858–874.
Stefani, A., Stanzione, P., Bassi, A., Mazzone, P., Vangelista, T., and Bernardi, G. (1997). Effects of increasing doses of apomorphine during stereotaxic neurosurgery in Parkinson’s disease: clinical score and internal globus pallidus activity. Short communication. J. Neural. Transm. 104, 895–904.
Surmeier, D. J., Ding, J., Day, M., Wang, Z., and Shen, W. (2007). D1 and D2 dopamine-receptor modulation of striatal glutamatergic signaling in striatal medium spiny neurons. Trends Neurosci. 30, 228–235.
Sutton, R. S., and Barto, A. G. (1998). Reinforcement Learning – An Introduction. Cambridge, MA: The MIT Press.
Talmi, D., Dayan, P., Kiebel, S. J., Frith, C. D., and Dolan, R. J. (2009). How humans integrate the prospects of pain and reward during choice. J. Neurosci. 29, 14617–14626.
Tepper, J. M., Wilson, C. J., and Koos, T. (2008). Feedforward and feedback inhibition in neostriatal GABAergic spiny neurons. Brain Res. Rev. 58, 272–281.
Tishby, N., Pereira, F., and Bialek, W. (1999). “The information bottelneck method 9-9-1999,” in The 37th Annual Allerton Conference on Communication, Control, and Computing, Allerton.
Tishby, N., and Polani, D. (2010). “Information theory of decisions and actions,” in Perception-Reason-Action Cycle: Models, Algorithms and Systems eds C. Vassilis, D. Polani, A. Hussain, N. Tishby and J. G. Taylor (New York: Springer), 601–636.
Keywords: basal ganglia, dopamine, softmax, reinforcement-learning
Citation: Parush N, Tishby N and Bergman H (2011) Dopaminergic balance between reward maximization and policy complexity. Front. Syst. Neurosci. 5:22. doi: 10.3389/fnsys.2011.00022
Received: 31 December 2010; Paper pending published: 14 February 2011;
Accepted: 20 April 2011; Published online: 09 May 2011.
Edited by:
Charles J. Wilson, University of Texas at San Antonio, USAReviewed by:
Charles J. Wilson, University of Texas at San Antonio, USAThomas Boraud, Universite de Bordeaux, France
Copyright: © 2011 Parush, Tishby and Bergman. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence: Naama Parush, The Interdisciplinary Center for Neural Computation, The Hebrew University, Jerusalem, Israel. e-mail: naama.parush@gmail.com