- 1PERFORM Centre, Concordia University, Montreal, QC, Canada
- 2Department of Physics, Gina Cody School of Engineering and Computer Science, Concordia University, Montreal, QC, Canada
- 3Department of Electrical and Computer Engineering, Concordia University, Montreal, QC, Canada
Multilayer networks have permeated all areas of science as an abstraction for interdependent heterogeneous complex systems. However, describing such systems through a purely graph-theoretic formalism presupposes that the interactions that define the underlying infrastructures are only pairwise-based, a strong assumption likely leading to oversimplification. Most interdependent systems intrinsically involve higher-order intra- and inter-layer interactions. For instance, ecological systems involve interactions among groups within and in-between species, collaborations and citations link teams of coauthors to articles and vice versa, and interactions might exist among groups of friends from different social networks. Although higher-order interactions have been studied for monolayer systems through the language of simplicial complexes and hypergraphs, a systematic formalism incorporating them into the realm of multilayer systems is still lacking. Here, we introduce the concept of crossimplicial multicomplexes as a general formalism for modeling interdependent systems involving higher-order intra- and inter-layer connections. Subsequently, we introduce cross-homology and its spectral counterpart, the cross-Laplacian operators, to establish a rigorous mathematical framework for quantifying global and local intra- and inter-layer topological structures in such systems. Using synthetic and empirical datasets, we show that the spectra of the cross-Laplacians of a multilayer network detect different types of clusters in one layer that are controlled by hubs in another layer. We call such hubs spectral cross-hubs and define spectral persistence as a way to rank them, according to their emergence along the spectra. Our framework is broad and can especially be used to study structural and functional connectomes combining connectivities of different types and orders.
1 Introduction
Multilayer networks (De Domenico et al., 2013; Boccaletti et al., 2014; Kivelä et al., 2014) have emerged over the last decade as a natural instrument in modeling myriads of heterogeneous systems. They permeate all areas of science as they provide a powerful abstraction of real-world phenomena made of interdependent sets of units interacting with each other through various channels. The concepts and computational methods they purvey have been the driving force for recent progress in the understanding of many highly sophisticated structures such as heterogeneous ecological systems (Pilosof et al., 2017; Timóteo et al., 2018), spatiotemporal and multimodal human brain connectomes (Griffa et al., 2017; Mandke et al., 2018; Pedersen et al., 2018), gene–molecule–metabolite interactions (Liu et al., 2020), and interdisciplinary scientific collaborations (Vasilyeva et al., 2021). This success has led to a growing interdisciplinary research investigating fundamental properties and topological invariants in multilayer networks.
Some of the major challenges in the analysis of a multilayer network are to quantify the importance and interdependence among its different components and subsystems, and describe the topological structures of the underlying architecture to better grasp the dynamics and information flow between its different network layers. Various approaches extending concepts, properties, and centrality indices from network science (Newman, 2003; Fortunato and Hric, 2016) have been developed, leading to tremendous results in many areas of science (Solá et al., 2013; Boccaletti et al., 2014; Sánchez-García et al., 2014; Flores and Romance, 2018; Timóteo et al., 2018; Wu et al., 2019; Liu et al., 2020; Yuvaraj et al., 2021). However, these approaches assume that inter- and intra-communications and relationships between the networks involved in such systems rely solely on node-based interactions. The resulting methods are, therefore, less insightful when the infrastructure is made up of higher-order intra- and inter-connectivities among node aggregations from different layers—as is the case for many phenomena. For example, heterogeneous ecosystems are made up of interactions among groups of the same or different species, social networks often connect groups of people belonging to different circles, and collaborations and citations form a higher-order multilayer network made of teams of co-authors interconnected to articles. Many recent studies have explored higher-order interactions and structures in monolayer networks (Benson et al., 2016; Iacopini et al., 2019; Lucas et al., 2020; Schaub et al., 2020; Bianconi, 2021) using different languages, such as simplicial complexes and hypergraphs (Shi et al., 2021; Young et al., 2021; Lotito et al., 2022; Majhi et al., 2022). However, a general mathematical formalism for modeling and studying higher-order multilayer networks is still lacking.
Our goal in this study is twofold. First, we propose a mathematical formalism that is rich enough to model and analyze multilayer complex systems involving higher-order connectivities within and in-between their subsystems. Second, we establish a unified framework for studying topological structures in such systems. This is performed by introducing the concepts of crossimplicial multicomplex, cross-homology, cross-Betti vectors, and cross-Laplacians. Before we dive deeper into these notions, we shall give the intuition behind them by considering the simple case of an undirected two-layered network Γ; here, Γ consists of two graphs (V1, E1) and (V2, E2), where V1, V2 are the node sets of Γ, Es ⊆ Vs × Vs, s = 1, 2 are the sets of intra-layer edges, and a set E1,2 ⊆ V1 × V2 of inter-layer edges. Intuitively, Γ might be seen as a system of interactions between two networks. It means that the node set V1 interacts not only with V2 but also with the edge set E2 and vice versa. Similarly, intra-layer edges in one layer interact with edges and triads in the other layer, and so on. This view suggests a more combinatorial representation by some kind of two-dimensional generalization of the fundamental notion of simplicial complex from algebraic topology (Mac Lane, 1963; Hatcher, 2000). The idea of crossimplicial multicomplex defined in the present work allows such a representation. In particular, when applied to a pairwise-based multilayer network, this concept allows to incorporate, on one hand, the clique complexes (Lim, 2020; Schaub et al., 2020) corresponding to the network layers, and on the other, the clique complex representing the inter-layer relationships between the different layers into one single mathematical object. Moreover, Γ can be regarded through different lenses, and each view displays different kinds of topological structures. The most naive perspective flattens the whole structure into a monolayer network without segregating the nodes and links from one layer or the other. Another viewpoint is of two networks with independent or interdependent topologies communicating with each other through the inter-layer links. The rationale for defining cross-homology and the cross-Laplacians is to view Γ as different systems, each with its own intrinsic topology but in which nodes, links, etc., from one system have some restructuring power that allows them to impose and control additional topologies on the other. This means that in a multilayer system, a layer network might display different topological structures depending on whether we look at it from its own point of view, from the lens of the other layers, or as a part of a whole aggregated structure. We describe this phenomenon by focusing on the spectra and eigenvectors of the lower-degree cross-Laplacians. We shall, however, remark that our aim here is not to address a particular real-world problem but to provide broader mathematical settings that reveal and quantify the emergence of these structures in any type of multilayer network.
2 Crossimplicial multicomplexes
2.1 General definitions
Given two finite sets, V1 and V2, and a pair of integers k, l ≥−1, a (k, l)– crossimplex a in V1 × V2 is a subset
An abstract crossimplicial bicomplex X (or a CSB) on V1 and V2 is a collection of crossimplices in V1 × V2, which is closed under the inclusion of crossfaces, i.e., the crossface of a crossimplex is also a crossimplex. A crossimplex is maximal if it is not the crossface of any other crossimplex. V1 and V2 are called the vertex sets of X.
Given a CSB X, for fixed integers k, l ≥ 0, we denote, by Xk,l, the subset of all its (k, l)-crossimplices. We also use the notations X0,−1 = V1, X−1,0 = V2, and X−1,−1 =∅. Recursively, Xk,−1 will denote the subset of crossimplices of the form
The dimension of a (k, l)-crossimplex is k + l + 1, and the dimension of CSB X is the dimension of its crossimplices of the highest dimension. The n-skeleton of X is the restriction of X to (k, l)-crossimplices such that k + l + 1 ≤ n. In particular, the 1-skeleton of CSB is a two-layered network, with X0,0 being the set of inter-layer links. Conversely, given a two-layered network Γ formed by two graphs Γ1 = (V1, E1) and Γ2 = (E2, V2) with the inter-layer edge set E1,2 ⊂ V1 × V2, define a (k, l)-clique in Γ as a pair (σ1, σ2), where σ1 is a k-clique in Γ1 and σ2 is an l-clique in Γ2 with the property that (i, j) ∈ E1,2 for every i ∈ σ1 and j ∈ σ2. We define the cross-clique bicomplex X associated with Γ by letting Xk,l to be the set of all (k + 1, l + 1)-cliques in Γ.
Now, a crossimplicial multicomplex (CSM)
2.2 Orientation on crossimplices
The orientation of a (k, l)-crossimplex is an ordering choice over its vertices. When equipped with an orientation, the crossimplex is said to be oriented and will be represented as
Specifically, a (0, −1)-crossimplex is a vertex in the top layer; a (0,0)-crossimplex is a cross-edge between layers V1 and V2; a (1, −1)-crossimplex (resp (−1, 1)-crossimplex) is a horizontal edge on V1 (resp. V2); a (0,1)-crossimplex or a (1,0)-crossimplex is a cross-triangle; a (2, −1)-crossimplex or (−1, 2)-crossimplex is a horizontal triangle on layer V1 or V2; a (3, −1)-crossimplex or (−1, 3)-crossimplex is a horizontal tetrahedron on V1 or V2; and a (1,1)-crossimplex, a (2,0)-crossimplex, or a (0,2)-crossimplex is a cross-tetrahedron (see Figure 1 for illustrations). On the other hand, horizontal edges, triangles, tetrahedrons, are just usual simplices on the horizontal complexes. One can consider a cross-edge as a connection between a vertex from one layer to a vertex on the other layer. In the same vein, a cross-triangle can be considered a connection between a vertex from one layer and two vertices on the other, and a cross-tetrahedron as a connection between either two vertices from one layer and two vertices on the other, or one vertex from one layer to three vertices on the other.

FIGURE 1. Crossimplices. Schematic representation of (A) A (0, −1)-crossimplex (a top vertex), a (1, −1)-crossimplex (top horizontal edge), and a (−1, 2)-crossimplex (bottom horizontal triangle); (B) (0,0)-crossimplex (a cross-edge); (C) (1,0)-crossimplex (a top cross-triangle); (D) (1,1)-crossimplex (a cross-tetrahedron); and (E) (0,2)-crossimplex (also a cross-tetrahedron). Notice that cross-edges are always oriented from the vertex of the top layer to that in the bottom layer. Therefore, cross-edges belonging to a cross-triangle are always of opposite orientations with respect to any orientation of the cross-triangle. There are two types of cross-triangles: the (1,0)-crossimplices (top cross-triangles) and (0,1)-crossimplices (bottom cross-triangle). Moreover, there are three types of cross-tetrahedrons: the (0,2)-crossimplices, (2,0)-crossimplices, and (1,1)-crossimplices.
2.3 Weighted CSBs
A weight on CSB X is a positive function
3 Topological descriptors
3.1 Cross-boundaries
CSB X defines a bi-simplicial set (Moerdijk, 1989; Goerss and Jardine, 2009) by considering, respectively, the top and bottom crossface maps
where the hat over a vertex means dropping the vertex. Moreover, for a fixed l ≥−1,
Now, two (k, l)-crossimplices a, b ∈ Xk,l are said to be as follows:
• top-outer (TO) adjacent, which we write
• top-inner (TI) adjacent, which we write
• bottom-outer (BO) adjacent, which we write
• bottom-inner (BI) adjacent, which we write
3.2 Degrees of crossimplices
Given a weight function w on X, we define the following degrees of a (k, l)-crossimplex a relative to w.
• The TO degree of a is the number:
• Similarly, the TI degree of a is defined as follows:
• Analogously, the BO degree of a is given as follows:
• The BO degree of a is as follows:
Observe that in the particular case where the weight function is equal to one everywhere, the TO degree of a is precisely the number of (k + 1, l)-crossimplices in X, of which a is the top crossface, while degTI(a) is the number of top crossfaces of a, which equals to k + 1. Analogous observations can be made about the BO and BI degrees.
3.3 Cross-homology groups
The space Ck,l of (k, l)-cross-chains is defined as the real vector space generated by all oriented (k, l)-crossimplexes in
for s = 1, 2 and a generator a ∈ Xk,l, where
It is straightforward to see that in particular
and
are the usual boundary maps of simplicial complexes. For this reason, we focus more on the mixed case where both l and k are non-negative. We will often drop the indices and write ∂(1) and ∂(2) to avoid cumbersome notations. To see how these maps operate, let us compute, for instance, the images of the crossimplices (b), (c), (d), and (e) illustrated in Figure 1. We obtain the following:
Notice that
For k ≥ 0 and l ≤ 0,
3.4 Cross-Betti vectors
The cross-homology groups are completely determined by their dimensions, the top and bottom (k, l)-cross-Betti numbers
Now, given a CSM
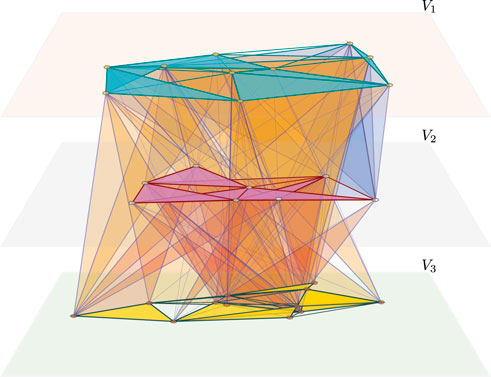
FIGURE 2. Schematic representation of a two-dimensional crossimplicial multicomplex
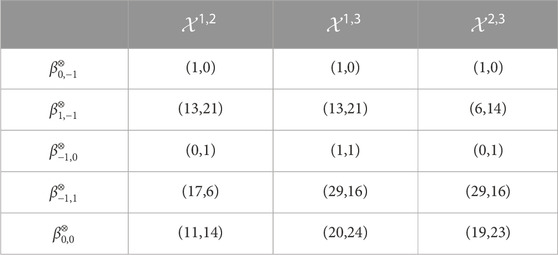
TABLE 1. Cross-Betti table. The cross-Betti table for CSM of Figure 2. The table quantifies the connectedness of the three horizontal complexes, the number of cycles in each of them, the number of nodes in each layer that are not connected to the other layers, the number of intra-layer edges not belonging to any cross-triangles, and the number of paths of length 2 connecting the nodes in one layer and passing through a node from another layer.
To illustrate what the cross-Betti vectors represent, we consider the simple two-dimensional CSB X of Figure 3. We get
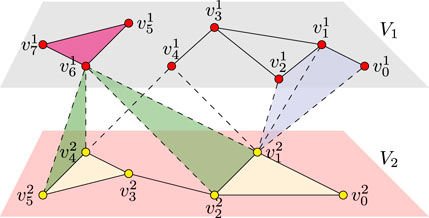
FIGURE 3. Cross-Betti vectors. Schematic representation of a two-dimensional CSB with 14 nodes in total, whose oriented maximal crossimplices are the intra-layer triangle
Using algebraic topological methods to calculate the cross-Betti vectors for larger multicomplexes can quickly become computationally heavy. We provide powerful linear-algebraic tools that not only allow to easily compute βk,ls but also tell exactly where the topological structures being counted are located within the multicomplex.
4 Spectral descriptors
4.1 Cross-forms
Notice that a natural basis of Ck,l is given by the following set of linear forms:
called elementary cross-forms, where
which naturally identify Ck,l with Ck,l. Now, the maps
for ϕ ∈ Ck,l, a ∈ Xk+1,l and c ∈ Xk,l+1. Next, given a weight w on X, we get an inner product on cross-forms by the following setting:
It can been seen that, with respect to this inner product, elementary cross-forms form an orthogonal basis, and by simple calculations, the dual maps are given by the following equation:
for ϕ ∈ Ck+1,l, a ∈ Xk,l. We also obtain a similar formula for the dual
4.2 The cross-Laplacian operators
Identifying Ck,l with Ck,l and equipping it with an inner product, as (21), we define the following self-adjoint linear operators on Ck,l for all k, l ≥−1:
- the top (k, l)-cross-Laplacian is as follows:
- and the bottom (k, l)-cross-Laplacian is as follows:
Being defined on finite dimensional spaces, these operators can be represented as square matrices indexed over crossimplices. Specifically, denoting Nk,l = |Xk,l|,
Moreover, the null spaces, the elements of which we call harmonic cross-forms, are easily seen to be in one-to-one correspondence with cross-cycles on X. In other words, we have the following isomorphisms (see Methods 7.2 for the proof):
It follows that in order to compute the cross-Betti vectors, it suffices to determine the dimensions of the eigenspaces of the zero-eigenvalues of the cross-Laplacians.
It should be noted that in addition to being much easier to implement, the spectral method to compute cross-homology has the advantage of providing a geometric representation of the cross-Betti numbers through eigenvectors. However, before we see how this works, let us make a few observations. Notice that
4.3 Harmonic cross-hubs
For the sake of simplicity, it is assumed that X is equipped with the trivial weight ≅1. Then, by (26), the (0,0) cross-Laplacians
and
Applied to the toy example of Figure 3,
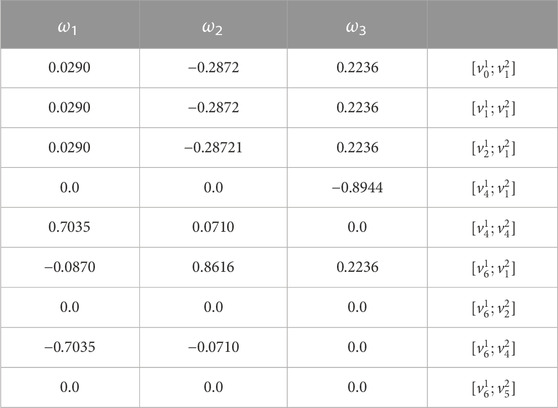
TABLE 2. Harmonic (0,0) cross-forms. The three eigenvectors of the eigenvalue 0 of
Each coordinate in the eigenvectors is seen as an “intensity” along the corresponding cross-edge. Cross-edges with non-zero intensities sharing the same bottom node define certain communities in the top complex that are “controlled” by the involved bottom node. These community structures depend on both the underlying topology of the top complex and its interdependence with the other complex layer. We then refer to them as harmonic cross-clusters, and the bottom nodes controlling them are considered harmonic cross-hubs (HCHs). The harmonic cross-hubness of a bottom node is the L1-norm of the intensities of all cross-edges having it in common. Here, in the eigenvectors of the eigenvalue 0, there are two subsets of cross-edges with non-zero coordinates: the cross-edges with
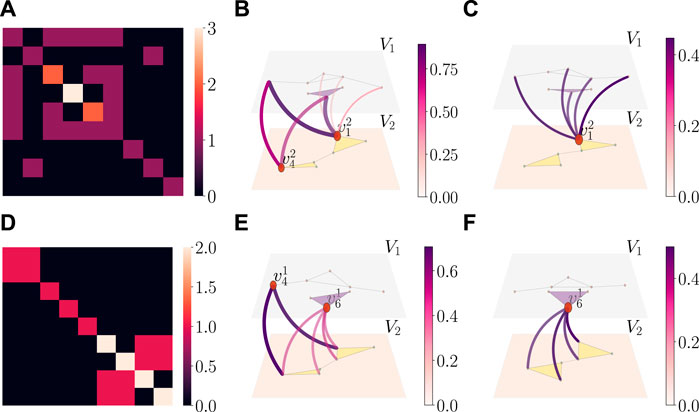
FIGURE 4. Cross-Laplacians, harmonic, and principal cross-hubs. (A) and (D) Heat-maps of the top and bottom (0,0) cross-Laplacian matrices for the example in Figure 3. Both matrices are indexed over the cross-edges of CSB, and the diagonal entries correspond to one added to the number of cross-triangles containing the corresponding cross-edge.
4.4 Spectral persistence of cross-hubs
To better grasp the idea of cross-hubness, let us have a closer look at the coordinates of the eigenvectors of the (0,0) cross-Laplacians ((10) and (11)) whose eigenvalues are all non-negative real numbers. Suppose
where χ is such that χ(ai, aj) = 1 if i = j or if ai and aj are adjacent but do not belong to a top cross-triangle, and χ(ai, aj) = 0 otherwise. It follows that the cross-edge intensity |xi| grows larger as degTO (ai) → λT. In particular, for λT = 0, the intensity is larger for cross-edges that belong to a large number of cones and to the smallest number of top cross-triangles. Now, consider the other extreme of the spectrum, namely,
Taking the case of a two-layered network, for λT = 0, |xi| is larger for a cross-edge pointing to a bottom node interconnecting the largest number of top nodes that are not directly connected with intra-layer edges; for λT = łmax, |xi| is larger for a cross-edge pointing to a bottom node interconnecting a large number of top intra-layer communities both with each other and with a large number of top nodes that are not directly connected to each other via intra-layer edges.
More generally, applying the same process to each distinct eigenvalue, we obtain clustering structures in the top layer that are controlled by the bottom nodes and that vary along the spectrum
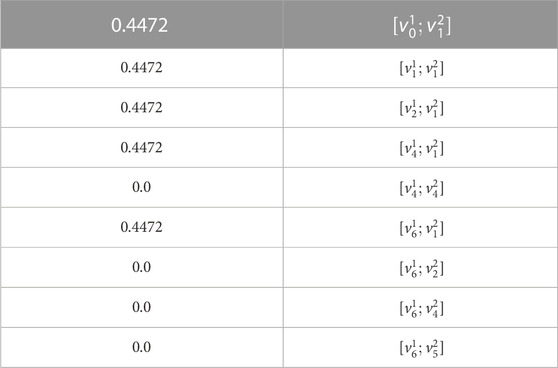
TABLE 3. Principal eigenvector of
There is only one PCH in the bottom layer with respect to the top layer, which is the bottom node
Interestingly, the number of SCHs that appear for a given eigenvalue tend to vary dramatically with respect to the smallest eigenvalues before it eventually decreases or stabilizes at a very low number (see Figure 5; Figure 6). Some cross-hubs may appear at one stage along the spectrum and then disappear at a future stage. This suggests the notion of spectral persistence of cross-hubs. Nodes that emerge the most often or live longer as cross-hubs along the spectrum might be seen as the most central in restructuring the topology of the other complex layers. The further we move away from the smallest non-zero eigenvalue, the more powerful are the nodes that emerge as hubs facilitating communications between aggregations of nodes in the other layer. The emergence of spectral cross-hubs is represented by a horizontal line—spectral persistence bar—running through the indices of the corresponding eigenvalues (Figure 5). The spectral persistence bars corresponding to all SCHs (the spectral bar codes) obtained from
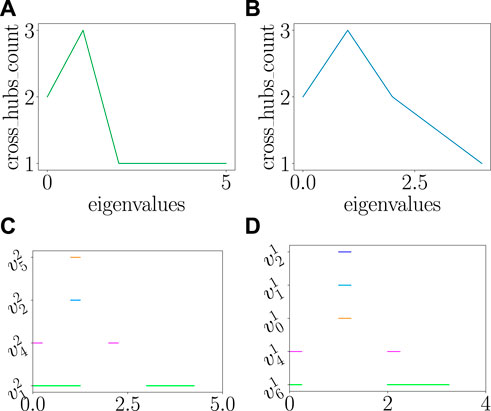
FIGURE 5. Spectral persistence of cross-hubs. Schematic illustrations of the variations in spectral cross-hubs along the eigenvalues and the spectral persistence bars codes for the toy CSB of Figure 3: (A) shows the number of bottom nodes that emerge as spectral cross-hubs with respect to the top layer as a function of the eigenvalues of
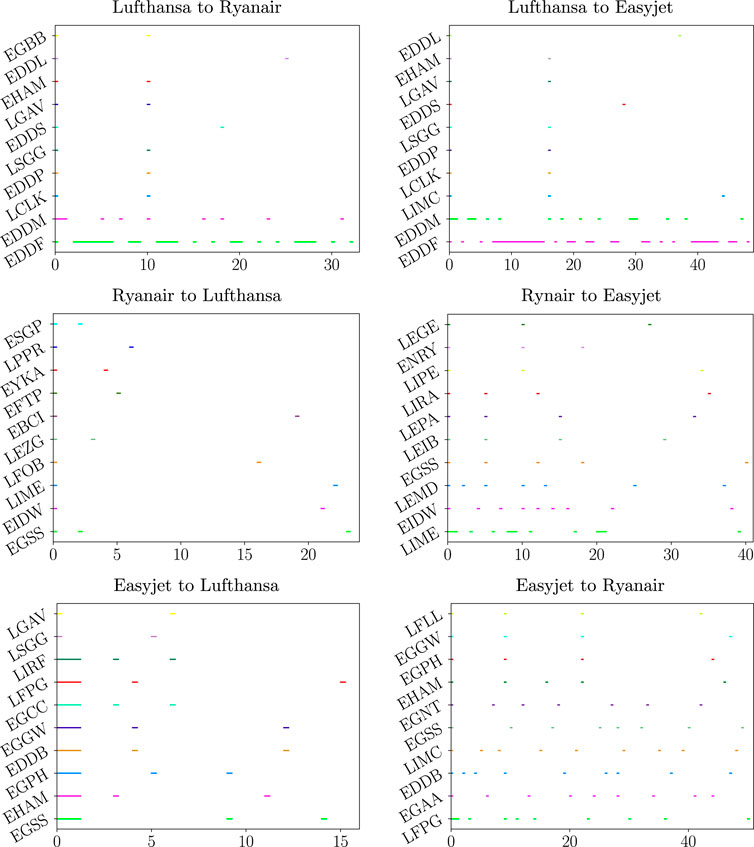
FIGURE 6. Spectral persistent cross-hubs. The spectral persistence bar codes of the six diffusion bicomplexes of the European ATN multiplex. The nodes represent European airports labeled with their ICAO codes (see https://en.wikipedia.org/wiki/ICAO_airport_code). The most persistent cross-hubs correspond to the airports that provide the most efficient correspondences from the first airline network to the second.
5 Experiments on multiplex networks
5.1 Diffusion CSBs
Let
For every pair of distinct indices s, t, we define the two-dimensional CSB Xs→t on V × V such that
5.2 Cross-hubs in air transportation networks
We used a subset of the European air transportation network (ATN) dataset (from Cardillo et al., 2013) to construct a three-layered multiplex
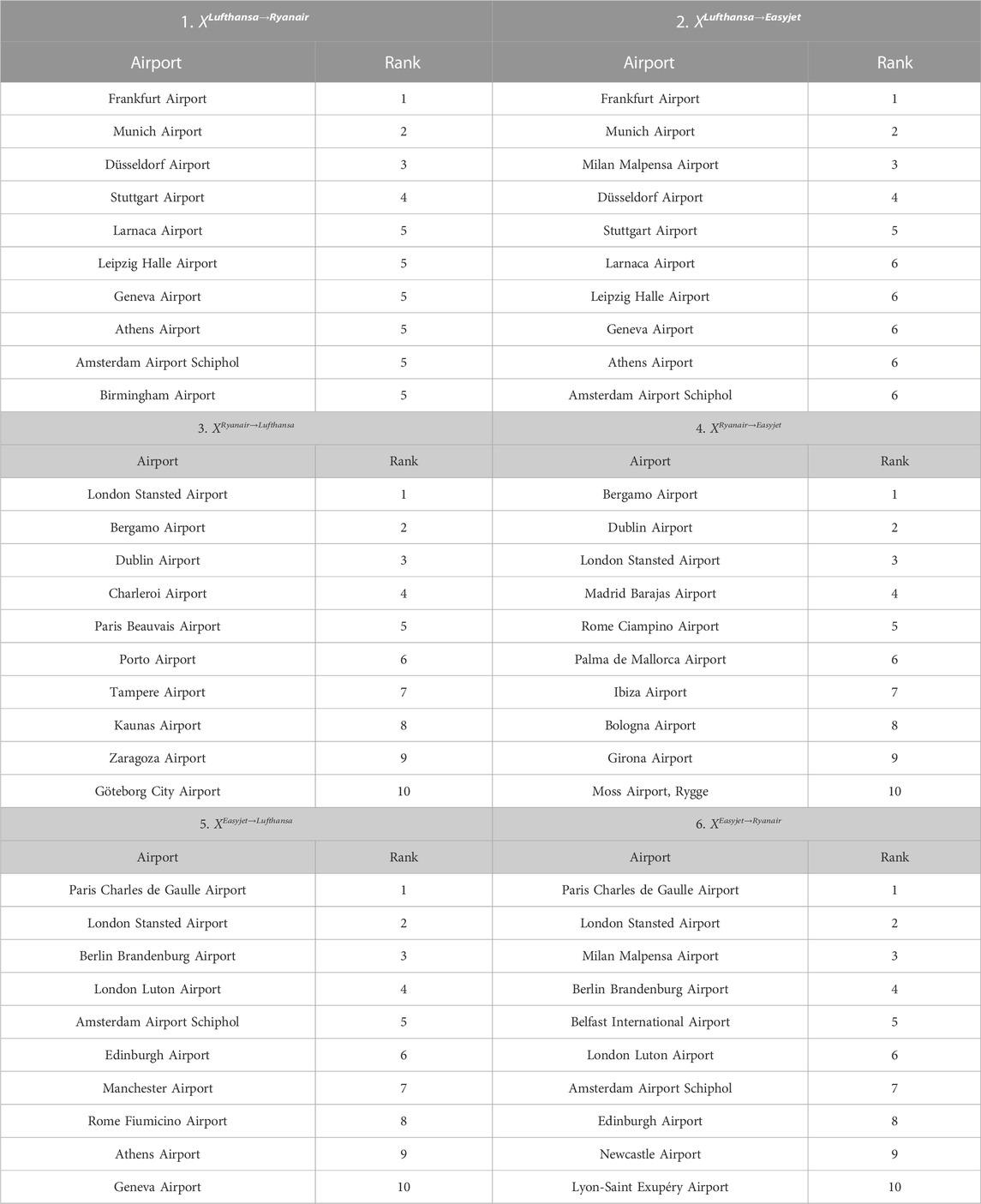
TABLE 4. Ranking of the 10 most persistent SCHs for the diffusion bicomplexes associated with the European air transportation multiplex network.
6 Discussion and conclusion
We have introduced CSM as a generalization of both the notions of simplicial complexes and multilayer networks. We further introduced cross-homology to study their topology and defined the cross-Laplacian operators to detect more structures that are not detected by homology. Our goal here was to set up a mathematical foundation for studying higher-order multilayer complex systems. Nevertheless, through synthetic examples of CSM and applications in multiplex networks, we have shown that our framework provides powerful tools to reveal important topological features in multilayer networks and address questions that would not arise from the standard pairwise-based formalism of multilayer networks. We specially focused on the (0,0) cross-Laplacians to show how their spectra quantify the extent to which nodes in one layer control topological structures in other layers in a multilayer network. Specifically, we saw that the spectra of these matrices allow detection of nodes from one layer that serve as inter-layer connecting hubs for clusters in the other layer; we referred to such nodes as SCHs. Such hubs vary in function of the eigenvalues, and they can be ranked according to their spectral persistence along the spectra of the cross-Laplacians. SCHs obtained from the largest eigenvalues (principal cross-hubs or PCHs) are those that interconnect the most important structures of the other layer. We should note that a PCH is not necessarily spectrally persistent, and two SCHs can be equally persistent but at different ranges of the spectrum. This means that, depending on the applications, some choices need to be made when ranking SCHs based on their spectral persistence. It might be the case that two SCHs persist equally long enough to be considered the most persistent ones, but that one persists through the first quarter of the spectrum, while the other persists through the second quarter of the spectrum so that none of them is PCH.
One can observe that the topological and geometric interpretations given for
Finally, many recent advances in structural and functional neuroimaging and genomics are based on the analysis of complex network representations of the human brain. The proposed framework will enable us to analyze the intimate relationships between the brain structure, genomics, and functional representations within unified multilayered structures.
7 Methods
7.1 Cones, kites, and the (0,0) cross-Betti numbers
Let
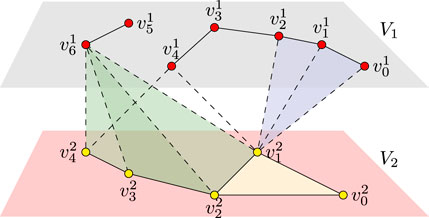
FIGURE 7. Two-dimensional crossimplicial bicomplex containing kites and cones.
It is worth noting that if
By a cross-chain on a kite, we mean one that is a linear combination of the triangles composing the kite; in other words, a cross-chain on the kite
where
Now, given a pair
•
• the triple
We also say that
An immediate consequence of a triple
in which case, the cone is said to be closed; it is called open otherwise.
Cones in a crossimplicial bicomplex are classified by the top and bottom (0,0)-cross-homology groups of the bicomplex. Specifically, we have the following topological interpretation of
Theorem 7.1. The (0,0) cross-homology group
Here, by the cross-homology class of the cone
Proof. We prove the theorem for
is clearly a (0,0) cross-cycle with a non-trivial cross-homology class, i.e.,
so that
and
It follows that
and
where the coefficients satisfy (15). Furthermore, it is straightforward to see that
is a kite. In that case, we get
and where, for r = 1, … , p, the coefficients
This shows that trivial cross-homology classes in
7.2 Inner product, cross-Laplacians, and harmonic cross-forms
We define the following maps on cross-forms:
by the following equations:
for ϕ ∈ Ck,l(X), a ∈ Xk+1,l and c ∈ Xk,l+1.
Now, for each pair of integers (k, l), we choose inner products ⟨⋅,⋅⟩k,l, ⟨⋅,⋅⟩k+1,l and ⟨⋅,⋅⟩k,l+1 on the real vector spaces Ck,l(X), Ck+1,l(X) and Ck,l+1(X), respectively. The adjoint operators
for ϕ ∈ Ck,l(X), ψ ∈ Ck+1,l(X), and ψ′ ∈ Ck,l+1(X).
Any weight w on X defines such inner products on cross-forms by the following setting:
It can be seen that, with respect to such an inner product, elementary cross-forms form an orthogonal basis. Moreover, given a weight function w and such an inner product, we get the following by simple calculations using (20):
for ϕ ∈ Ck+1,l(X), a ∈ Xk,l. In addition, we obtain a similar formula for
Definition 7.2. We define the following self-adjoint linear operators on Ck,l(X) for all k, l ≥−1:
• the top-outer (k, l)-cross-Laplacian (or TO-Laplacian of order (k, l)
• the top-inner (k, l)-cross-Laplacian (or TI-Laplacian of order (k, l)
• the top (k, l) cross-Laplacian
• and similarly, the bottom-outer (k, l) cross-Laplacian (BO-Laplacian of order (k, l))
• the bottom-inner (k, l)-cross-Laplacian (BI-Laplacian)
• and the bottom (k, l)-cross-Laplacian
The null spaces of these operators, defined as the following sub-groups
are called the spaces of harmonic top (resp. bottom) cross-forms on X.
There is a one-to-one correspondence between cross-cycle classes and harmonic cross-forms on CSB X. In other words, we have the following group isomorphisms generalizing (Eckmann, 1944; Horak and Jost, 2013).
Lemma 7.3. For s = 1, 2 and for all k, l ≥−1, we have
where we have used the notations
Proof. Let us prove this result for s = 1 (similar arguments apply to s = 2). First, notice that from the identification Ck,l(X) = Ck,l(X), we obtain the following:
and the analog holds for
Therefore,
and the isomorphism (23) follows from (24).
It follows that the eigenvectors corresponding to the zero eigenvalue of the (k, l) cross-Laplacian
7.3 Matrix representations
Since the sets Xk,l are finite, the vector spaces Ck,l(X) and Ck,l(X) are finite dimensional, and as we have seen, the latter has the elementary cross-forms ea, a ∈ Xk,l as orthogonal basis with respect to inner products defined from weight functions. So, the cross-Laplacian operators
and
In particular, when ϕ is an elementary cross-form eb, b ∈ Xk,l, we obtain the following:
and
It follows that the (ea, eb)-th entry of the matrix representation of the top (k, l) cross-Laplacian
It is clear that we get similar matrix representation for the bottom (k, l) cross-Laplacian
Data availability statement
Publicly available datasets were analyzed in this study. These data can be found at: http://complex.unizar.es/∼atnmultiplex/.
Author contributions
EM: conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing–original draft, and writing–review and editing. OA: writing–review and editing. HB: Funding acquisition, investigation, project administration, resources, supervision, validation, visualization, and writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by the Natural Sciences and Engineering Research Council of Canada through the CRC grant NC0981.
Acknowledgments
The code used for visualizations and computations will be made available upon request.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Benson, A. R., Gleich, D. F., and Leskovec, J. (2016). Higher-order organization of complex networks. Science 353 (6295), 163–166. doi:10.1126/science.aad9029
Boccaletti, S., Bianconi, G., Criado, R., Del Genio, C. I., Gómez-Gardenes, J., Romance, M., et al. (2014). The structure and dynamics of multilayer networks. Phys. Rep. 544 (1), 1–122. doi:10.1016/j.physrep.2014.07.001
Cardillo, A., Gómez-Gardenes, J., Zanin, M., Romance, M., Papo, D., Pozo, F. d., et al. (2013). Emergence of network features from multiplexity. Sci. Rep. 3 (1), 1344–1346. doi:10.1038/srep01344
De Domenico, M., Solé-Ribalta, A., Cozzo, E., Kivelä, M., Moreno, Y., Porter, M. A., et al. (2013). Mathematical formulation of multilayer networks. Phys. Rev. X 3 (4), 041022. doi:10.1103/physrevx.3.041022
Eckmann, B. (1944). Harmonische funktionen und randwertaufgaben in einem komplex. Comment. Math. Helvetici 17, 240–255. doi:10.1007/bf02566245
Flores, J., and Romance, M. (2018). On eigenvector-like centralities for temporal networks: discrete vs. continuous time scales. J. Comput. Appl. Math. 330, 1041–1051. doi:10.1016/j.cam.2017.05.019
Fortunato, S., and Hric, D. (2016). Community detection in networks: a user guide. Phys. Rep. 659, 1–44. doi:10.1016/j.physrep.2016.09.002
Goerss, P. G., and Jardine, J. F. (2009). Simplicial homotopy theory. Springer Science and Business Media.
Griffa, A., Ricaud, B., Benzi, K., Bresson, X., Daducci, A., Vandergheynst, P., et al. (2017). Transient networks of spatio-temporal connectivity map communication pathways in brain functional systems. NeuroImage 155, 490–502. doi:10.1016/j.neuroimage.2017.04.015
Horak, D., and Jost, J. (2013). Spectra of combinatorial laplace operators on simplicial complexes. Adv. Math. 244, 303–336. doi:10.1016/j.aim.2013.05.007
Iacopini, I., Petri, G., Barrat, A., and Latora, V. (2019). Simplicial models of social contagion. Nat. Commun. 10 (1), 2485. doi:10.1038/s41467-019-10431-6
Kivelä, M., Arenas, A., Barthelemy, M., Gleeson, J. P., Moreno, Y., and Porter, M. A. (2014). Multilayer networks. J. complex Netw. 2 (3), 203–271. doi:10.1093/comnet/cnu016
Liu, X., Maiorino, E., Halu, A., Glass, K., Prasad, R. B., Loscalzo, J., et al. (2020). Robustness and lethality in multilayer biological molecular networks. Nat. Commun. 11 (1), 6043. doi:10.1038/s41467-020-19841-3
Lotito, Q. F., Musciotto, F., Montresor, A., and Battiston, F. (2022). Higher-order motif analysis in hypergraphs. Commun. Phys. 5 (1), 79. doi:10.1038/s42005-022-00858-7
Lucas, M., Cencetti, G., and Battiston, F. (2020). Multiorder laplacian for synchronization in higher-order networks. Phys. Rev. Res. 2 (3), 033410. doi:10.1103/physrevresearch.2.033410
Mac Lane, S. (1963). Homology. Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete. Springer Berlin, Heidelberg: Academic Press. doi:10.1007/978-3-642-62029-4
Majhi, S., Perc, M., and Ghosh, D. (2022). Dynamics on higher-order networks: a review. J. R. Soc. Interface 19 (188), 20220043. doi:10.1098/rsif.2022.0043
Mandke, K., Meier, J., Brookes, M. J., O’Dea, R. D., Van Mieghem, P., Stam, C. J., et al. (2018). Comparing multilayer brain networks between groups: introducing graph metrics and recommendations. NeuroImage 166, 371–384. doi:10.1016/j.neuroimage.2017.11.016
Moerdijk, I. (1989). Bisimplicial sets and the group-completion theorem. Dordrecht: Springer Netherlands, 225–240.
Newman, M. E. (2003). The structure and function of complex networks. SIAM Rev. 45 (2), 167–256. doi:10.1137/s003614450342480
Pedersen, M., Zalesky, A., Omidvarnia, A., and Jackson, G. D. (2018). Multilayer network switching rate predicts brain performance. Proc. Natl. Acad. Sci. 115 (52), 13376–13381. doi:10.1073/pnas.1814785115
Pilosof, S., Porter, M. A., Pascual, M., and Kéfi, S. (2017). The multilayer nature of ecological networks. Nat. Ecol. Evol. 1 (4), 0101. doi:10.1038/s41559-017-0101
Sánchez-García, R. J., Cozzo, E., and Moreno, Y. (2014). Dimensionality reduction and spectral properties of multilayer networks. Phys. Rev. E 89 (5), 052815. doi:10.1103/physreve.89.052815
Schaub, M. T., Benson, A. R., Horn, P., Lippner, G., and Jadbabaie, A. (2020). Random walks on simplicial complexes and the normalized hodge 1-laplacian. SIAM Rev. 62 (2), 353–391. doi:10.1137/18m1201019
Shi, D., Chen, Z., Sun, X., Chen, Q., Ma, C., Lou, Y., et al. (2021). Computing cliques and cavities in networks. Commun. Phys. 4, 249. doi:10.1038/s42005-021-00748-4
Solá, L., Romance, M., Criado, R., Flores, J., García del Amo, A., and Boccaletti, S. (2013). Eigenvector centrality of nodes in multiplex networks. Chaos (Woodbury, N.Y.) 23, 033131. doi:10.1063/1.4818544
Timóteo, S., Correia, M., Rodríguez-Echeverría, S., Freitas, H., and Heleno, R. (2018). Multilayer networks reveal the spatial structure of seed-dispersal interactions across the great rift landscapes. Nat. Commun. 9 (1), 140. doi:10.1038/s41467-017-02658-y
Vasilyeva, E., Kozlov, A., Alfaro-Bittner, K., Musatov, D., Raigorodskii, A., Perc, M., et al. (2021). Multilayer representation of collaboration networks with higher-order interactions. Sci. Rep. 11, 5666. doi:10.1038/s41598-021-85133-5
Wu, M., He, S., Zhang, Y., Chen, J., Sun, Y., Liu, Y.-Y., et al. (2019). A tensor-based framework for studying eigenvector multicentrality in multilayer networks. Proc. Natl. Acad. Sci. 116, 15407–15413. doi:10.1073/pnas.1801378116
Young, J.-G., Petri, G., and Peixoto, T. P. (2021). Hypergraph reconstruction from network data. Commun. Phys. 4 (1), 135. doi:10.1038/s42005-021-00637-w
Keywords: multilayer networks, cross-homology, multicomplexes, Laplacian, cross-hubs, spectral persistence
Citation: Moutuou EM, Ali OBK and Benali H (2023) Topology and spectral interconnectivities of higher-order multilayer networks. Front. Complex Syst. 1:1281714. doi: 10.3389/fcpxs.2023.1281714
Received: 22 August 2023; Accepted: 19 October 2023;
Published: 20 November 2023.
Edited by:
Byungjoon Min, Chungbuk National University, Republic of KoreaReviewed by:
Flaviano Morone, New York University, United StatesWei Wang, Chongqing Medical University, China
Copyright © 2023 Moutuou, Ali and Benali. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elkaïoum M. Moutuou, elkaioum.moutuou@concordia.ca
 Elkaïoum M. Moutuou
Elkaïoum M. Moutuou Obaï B. K. Ali
Obaï B. K. Ali Habib Benali
Habib Benali