Heritability of pulmonary function estimated from pedigree and whole-genome markers

Asthma and chronic obstructive pulmonary disease (COPD) are major worldwide health problems. Pulmonary function testing is a useful diagnostic tool for these diseases, and is known to be influenced by genetic and environmental factors. Previous studies have demonstrated that a substantial proportion of the variation in pulmonary function phenotypes can be explained by familial relationships. The availability of whole-genome single nucleotide polymorphism (SNP) data enables us to further evaluate the extent to which genetic factors account for variation in pulmonary function and to compare pedigree- to SNP-based estimates of heritability. Here, we employ methods developed in the animal breeding field to estimate the heritability of forced expiratory volume in one second (FEV₁), forced vital capacity (FVC), and the ratio of these two measures (FEV₁/FVC) among subjects in the Framingham Heart Study dataset. We compare heritability estimates based on pedigree-based relationships to those based on genome-wide SNPs. We find that, in a family-based study, estimates of heritability using SNP data are nearly identical to estimates based on pedigree information, and range from 0.50 for FEV₁ to 0.66 for FEV₁/FVC. Therefore, we conclude that genetic factors account for a sizable proportion of inter-individual differences in pulmonary function, and that estimates of heritability based on SNP data are nearly identical to estimates based on pedigree data. Finally, our findings suggest a higher heritability for FEV₁/FVC compared to either FEV₁ or FVC.

Introduction

Airway diseases are a major health burden, and one of the leading causes of death in the United States and worldwide (Lopez et al., 2006). Although there have been many successful efforts at identifying environmental and lifestyle risk factors (Mannino and Buist, 2007), our understanding of genetic risk factors remains limited, as it does for many complex traits, owing to multiple factors, such as an incomplete assessment of all genetic variation, and inappropriate statistical approaches (Manolio et al., 2009).

Pulmonary function as measured by spirometry serves as a diagnostic tool for diseases such as COPD and asthma. The heritability of pulmonary function, defined as the proportion of phenotypic variation that can be accounted for by genetic variation, has been estimated using twin and family studies. Estimates range from approximately 40 to 55% (Redline et al., 1989; Givelber et al., 1998; Xu et al., 1999; Wilk et al., 2000). These studies therefore suggest that genetic factors explain a substantial portion of inter-individual variation in pulmonary function. Heritability estimates using SNP-based methods, as opposed to pedigree-based methods, may allow for the accounting of variation introduced by chromosomal segregation. However, pedigree-based methods may capture more common environmental factors than captured by genetic markers.

Recent genome-wide association studies (GWAS) have identified several loci that are associated with pulmonary function and are biologically plausible candidates, such as TNS1, GSTCD, HTR4, AGER, and THSD4 (Hancock et al., 2010; Repapi et al., 2010; Weiss, 2010; Artigas et al., 2011). Although genetic variation is expected to account for approximately 50% of phenotypic variation, the loci discovered thus far account for a very small proportion of the variation in pulmonary function (Artigas et al., 2011). There is therefore a need to develop and apply methods that are capable of making use of more genetic information. Statistical methods developed in the field of animal breeding use information on thousands of genetic variants across the genome to explain phenotypic variation (Meuwissen et al., 2001). These methods have proven to be successful for production traits in livestock and plants, and have recently been shown to be useful in the context of family data for the analysis and prediction of complex human traits such as height (Makowsky et al., 2011), and less heritable traits such as lifespan (de Los Campos et al., 2012). In the case of height, heritability estimates derived using genome-wide SNP information collected in family data are essentially identical to the heritability estimate using pedigree information, and to previous estimates of height heritability based on twin and family studies (Makowsky et al., 2011). In this study, our objective is to estimate the genetic variance of pulmonary function traits by using thousands of markers distributed across the genome. Our models will be compared with those in which pedigree information is used instead.

Methods

Sample

Residents of Framingham, MA, USA, have been recruited since 1948 to participate in a long-term study to understand the risk factors for heart disease (Dawber et al., 1951). Spirometry testing was performed on subjects from three generations of the Framingham Heart Study. Specifically, these phenotypes were obtained from exam 19 of the Original Cohort, exams 3, 5, 6, 7, and 8 from the Offspring Cohort, and exam 1 from the Third Generation Cohort. For each Offspring cohort participant, we used in our analyses the phenotypic value from the latest examination. We included only participants who self-identified as White. A total of 6967 participants (3181 males, 3786 females) between the ages of 19 and 92 with both genotype and phenotype data were used in this analysis. We used FEV₁ (forced expiratory volume in 1 s), FVC (forced vital capacity), and FEV₁/FVC as the primary phenotypes of interest.

Genotypes

Subjects were genotyped using the Affymetrix GeneChip Human Mapping 500K Array Set. For details on genotyping, see http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000007.v3.p2. SNPs and individuals with call rates less than 90%, as well as SNPs with a minor allele frequency (MAF) less than 0.5% were excluded. The remaining missing genotypes were imputed by sampling from a binomial distribution using the empirical MAF estimate under the assumption of Hardy-Weinberg Equilibrium. Given the low genotype missingness (approximately 1%), we do not expect that a more robust method of imputation will significantly affect the results. Genotypes from 444,938 SNPs were considered in the analysis. The first two principal components (PCs) of approximately 1000 markers that are informative for the within-Europe geographical/ancestral origin of European and European-American individuals (Drineas et al., 2010) were used as covariates in the analyses.

Statistical Models

The outcome (y_i) (i = 1, …, 6967) consisted of the residual of linear regressions with FEV₁, FVC, and FEV₁/FVC as outcomes, and sex, age, PC1 and PC2, and cohort (to account for changes in spirometry measurement techniques) as predictors. Phenotype residuals were modeled according to an additive model of the form y_i = β₀ + u_i + ε_i where β₀ is an intercept, u_i is an additive genetic effect, representing the collective additive actions of genes potentially affecting the trait of interest, and ε_i is a component of the phenotype that cannot be explained by additive genetic effects. Stacking all the above equations from i = 1 to i = n (n = number of individuals) into vectors, we have

$y=1{\beta }_0+u+\epsilon$

where y = (y₁,…, y_n)′, u = (u₁,…, u_n)′ and ε = (ε₁,…,ε_n)′ are vectors of phenotype, additive genetic effects, and model residuals, respectively.

Pedigree Model

Following the standards of the additive infinitesimal model (Fisher, 1918; Wright, 1921; Henderson, 1975), we assumed that additive genetic effects follow a multivariate normal distribution of the form u = a ~ N(0, A*σ²_a), where σ²_a is an additive genetic variance and A is an n-dimensional matrix whose entries are pedigree-derived additive relationships (twice kinship coefficients).

Genomic Model

In this model, we replace the matrix of pedigree-derived additive relationships A, with a marker-derived estimate G, whose entries were: $G_{ik}=\frac{1}{p}{\displaystyle {\sum }_{j=1}^p\frac{\left(x_{ij}-2{\theta }_j\right)\left(x_{kj}-2{\theta }_j\right)}{2{\theta }_j\left(1-{\theta }_j\right)}}$, where x_ij is the count of allele coded as 1 for the i^th individual at the j^th SNP, x_kj is the count of allele coded as 1 for the k^th individual at the j^th SNP, θ_j is the estimated frequency of the allele coded as 1 at the jth SNP, and p is the number of SNPs considered (p = 444,938). Therefore, in this model we have: u = g ~ N (0, G * σ²_g), where σ²_g is the genomic variance.

The entries of the matrix A give the expected patterns of genetic similarity between pairs of individuals. However, for any given pair of individuals, the expected and realized proportion of allele sharing will differ because of Mendelian sampling (Hill and Weir, 2011). The entries of the G matrix quantifies realized genetic similarity at markers (de los Campos et al., 2013).

In the models described above, narrow sense heritability is defined as the ratio of the genetic variance to the total variance, that is: $h_a^2=\frac{{\sigma }_a^2}{{\sigma }_a^2+{\sigma }_{\epsilon }^2}$ for the pedigree model, and $h_g^2=\frac{{\sigma }_g^2}{{\sigma }_g^2+{\sigma }_{\epsilon }^2}$ for the genomic model. The latter can be interpreted as the proportion of inter-individual differences in the trait of interest that can be explained by regression on common SNPs in the training sample. The parameters of the above-described model were estimated in a Bayesian framework using the BLR package (de los Campos and Pérez, 2010) in R (R Development Core Team, 2011). The variance parameters, both the residual variance and the variances of the genetic effects, were assigned an inverse chi-square distribution with scale and degree of freedom parameters equal to 2 and 5, respectively. This setting gives a relatively un-informative prior.

Results

Heritability of Pulmonary Function

The estimated coefficients for sex, age, and cohort and their statistical significance are shown in Table 1. We find a negative association between age and FEV₁ and FVC, suggesting a significant difference between males and females, with males having higher FEV₁ and FVC, and earlier cohorts having lower FEV₁ and FVC. For FEV₁/FVC, we find that females have a higher mean value than males (p < 5 × 10⁻¹⁴). The correlation between FEV₁ and FVC is 0.95. However, the correlation between each of these and FEV₁/FVC is much lower (0.46 for FEV₁, and 0.17 for FVC).

TABLE 1

Table 1. Estimated effects and p-values for sex, age, and cohort in relation to three pulmonary phenotypes.

A plot of the G-based (i.e., SNPs) relationship coefficients for different levels of A-based (i.e., pedigree) relationship coefficients is shown in Figure 1. For each level of the pedigree-based relationship coefficient, the genomic relationship coefficient varies considerably, and increasingly so at higher relationship coefficients.

FIGURE 1

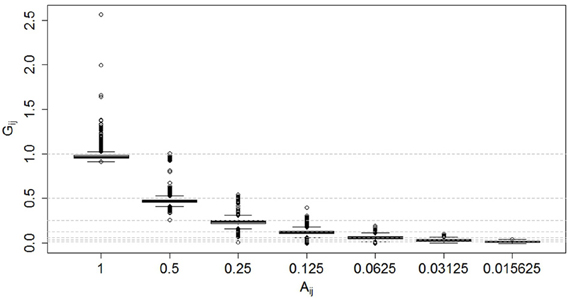
Figure 1. Genomic relationship coefficients (G_ij) for various levels of pedigree-based relationship coefficients (A_ij). Horizontal dashed lines indicate the different levels of expected coefficients on the y-scale.

Heritability estimates are shown in Table 2. Using the genomic relationship matrix, we find that approximately 50% of the variation in FEV₁ is accounted for by the variation captured by the SNP-based relationship matrix. We obtain a slightly higher estimate when using the pedigree-based matrix. For FVC, we find that 54% of the phenotypic variation is accounted for by the SNP-based relationship matrix, while 56% is captured by the pedigree-based matrix. For FEV₁/FVC, we find substantially higher estimates of heritability overall: 64% using the pedigree-based relationship matrix, and 66% using the SNP-based relationship matrix.

TABLE 2

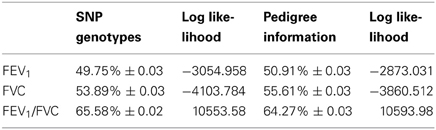
Table 2. Heritability estimates and log-likelihood of models for pulmonary phenotypes based on SNP genotypes and on pedigree information (±standard error).

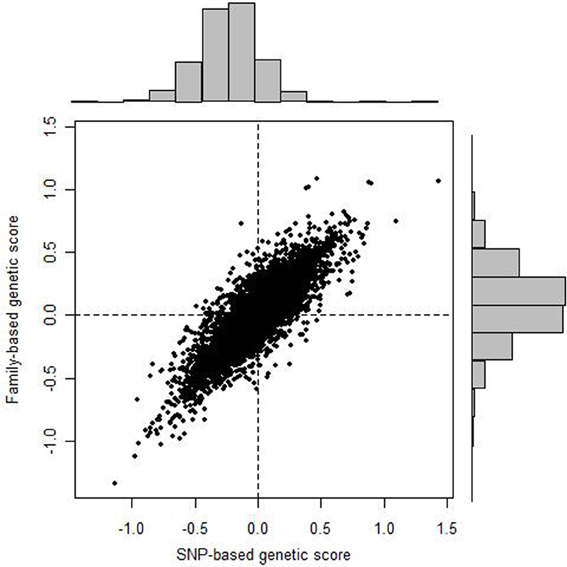
Finally, we assessed the correspondence, on an individual level, between predicted genetic values derived from pedigree and from markers. Figure 2 shows the scatter plot of predicted values for FEV₁. The predicted values are based on both fixed effects (sex, age, PC1, PC2, and cohort), and random effects (individual). The correlation between these estimates is approximately 0.86, 0.86, and 0.87, respectively, for FEV₁, FVC, and FEV₁/FVC.

FIGURE 2

Figure 2. Scatter plot of pedigree-based vs. SNP-based values of FEV₁.

Discussion

Pulmonary function has previously been found to have a heritable basis. We examine and compare the heritability of pulmonary function using pedigree information and whole-genome SNP data. Our estimates of heritability with the SNP-based and pedigree-based methods are similar to previous estimates (Coultas et al., 1991; Ingebrigtsen et al., 2011). Interestingly the estimates for FEV₁/FVC are considerably higher than for either FEV₁ or FVC. It may be that by taking the ratio of FEV₁ and FVC, much of the variation due to environmental factors is removed, compared to just FEV₁. Indeed, it does appear that the correlation of both FEV₁ and FVC with FEV₁/FVC is rather low. Additionally, it may suggest a higher heritability for obstructive lung diseases such as COPD in which FEV₁/FVC is typically reduced, as opposed to restrictive lung diseases such as fibrosis, in which FEV₁/FVC is not typically decreased since both FEV₁ and FVC are decreased together (Crapo, 1994; Swanney et al., 2008). A full multi-trait genetic analysis (e.g., Burgueño et al., 2012) of pulmonary phenotypes and lung diseases may provide more insight. Since we did not segregate analyses to cohorts with either restrictive or obstructive disease, another potential explanation for the higher heritability of FEV₁/FVC is a greater genetic basis for airway dynamics and airflow for which the ratio might be a more precise measure. Such differences in heritability between FEV₁/FVC and each of the measures on their own were not observed in previous studies (Wilk et al., 2000).

The relationship observed between the values of the A- and G-based relationship coefficients is not unexpected. We can think of realized genomic relationships as random variables whose realized values depend on the expected value (given by 1*kinship computed from the pedigree, A_ij) and a deviation (d) from the expected value given by the sampling of alleles at meiosis (i.e., G_ij = A_ij + d_ij). Therefore, the average value of G_ij is simply A_ij. On the other hand, Hill and Weir (2011) showed that the variance of G_ij (around its mean, that is, around A_ij) increases as A_ij does (simply because large chunks segregate together), and this is why we observe larger variability of G_ij around its mean when A_ij is larger.

One might expect that the SNP-based estimates of heritability would be higher than the pedigree-based estimates of heritability since the SNP information would theoretically capture information about segregation not captured by pedigree information On the other hand, pedigree-based estimates could be higher (albeit, artificially) than SNP-based estimates since pedigree information could capture more shared environmental factors than SNP information. However in this study, we find that both estimates of heritability are essentially identical, except for a slightly higher SNP-based estimate in the case of FEV₁/FVC.

We have shown that the heritability of pulmonary phenotypes is substantial, and that the use of genome-wide SNPs in a family-based study results in essentially identical estimates of heritability as those obtained using pedigree information. Both heritability estimates could be confounded with common environmental effects that may result in inflated heritability estimates, although this is likely more of a concern in the pedigree-based estimates.

In addition to estimating overall genetic variance, the use of genome-wide SNP information also has the potential to further our understanding of the genetic basis of pulmonary function and diseases such as asthma and COPD. Given that these traits are likely highly polygenic, it will be important to continue using high-dimensional methods (both at the level of sample size and of predictors) to identify causal loci, and to better understand the genetic architecture of these traits. These causal variants are likely to be numerous and located across the genome and may be at lower frequencies than SNPs in GWAS. Improved knowledge of the genetic basis of pulmonary function could then lead to improved individualized prediction of airway disease and to targeted therapeutic options.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank the Framingham Heart Study organizers and participants. This study was supported by National Heart, Lung, and Blood Institute (NHLBI) Award T32HL105346. The contents are solely the responsibility of the authors and do not necessarily represent the official views of the National Institutes of Health.

References

Artigas, M. S., Loth, D. W., Wain, L. V., Gharib, S. A., Obeidat, M., Tang, W., et al. (2011). Genome-wide association and large-scale follow up identifies 16 new loci influencing lung function. Nat. Genet. 43, 1082–1090. doi: 10.1038/ng.941

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Burgueño, J., De los Campos, G., Weigel, K., and Crossa, J. (2012). Genomic prediction of breeding values when modeling genotype × environment interaction using pedigree and dense molecular markers. Crop Sci. 52, 707. doi: 10.2135/cropsci2011.06.0299

CrossRef Full Text

Coultas, D. B., Hanis, C. L., Howard, C. A., Skipper, B. J., and Samet, J. M. (1991). Heritability of ventilatory function in smoking and nonsmoking New Mexico Hispanics. Am. Rev. Respir. Dis. 144, 770–775. doi: 10.1164/ajrccm/144.4.770

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Crapo, R. O. (1994). Pulmonary-function testing. N. Engl. J. Med. 331, 25–30. doi: 10.1056/NEJM199407073310107

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Dawber, T. R., Meadors, G. F., and Moore, F. E. Jr. (1951). Epidemiological approaches to heart disease: the Framingham study. Am. J. Public Health Nations Health 41, 279–281. doi: 10.2105/AJPH.41.3.279

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

de Los Campos, G., Klimentidis, Y. C., Vazquez, A. I., and Allison, D. B. (2012). Prediction of expected years of life using whole-genome markers. PLoS ONE 7:e40964. doi: 10.1371/journal.pone.0040964

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

de los Campos, G., and Pérez, P. (2010). BLR: bayesian linear regression. R package Version 1.2. Available online at: http://cran.r-project.org/web/packages/BLR/index.html

de los Campos, G., Vazquez, A. I., Fernando, R. L., Klimentidis, Y. C., and Sorensen, D. A. (2013). Prediction of complex human traits using the genomic best linear unbiased predictor. PLoS Genet. 9:e1003608. doi: 10.1371/journal.pgen.1003608

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Drineas, P., Lewis, J., and Paschou, P. (2010). Inferring geographic coordinates of origin for Europeans using small panels of ancestry informative markers. PLoS ONE 5:e11892. doi: 10.1371/journal.pone.0011892

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Fisher, R. A. (1918). The correlation between relatives on the supposition of Mendelian inheritance. Trans. R. Soc. Edinb. 52, 399–433. doi: 10.1017/S0080456800012163

CrossRef Full Text

Givelber, R. J., Couropmitree, N. N., Gottlieb, D. J., Evans, J. C., Levy, D., Myers, R. H., et al. (1998). Segregation analysis of pulmonary function among families in the Framingham Study. Am. J. Respir. Crit. Care Med. 157, 1445–1451. doi: 10.1164/ajrccm.157.5.9704021

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hancock, D. B., Eijgelsheim, M., Wilk, J. B., Gharib, S. A., Loehr, L. R., Marciante, K. D., et al. (2010). Meta-analyses of genome-wide association studies identify multiple loci associated with pulmonary function. Nat. Genet. 42, 45–52. doi: 10.1038/ng.500

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Henderson, C. R. (1975). Best linear unbiased estimation and prediction under a selection model. Biometrics 31, 423–447. doi: 10.2307/2529430

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Hill, W. G., and Weir, B. S. (2011). Variation in actual relationship as a consequence of Mendelian sampling and linkage. Genet. Res. 93, 47–64. doi: 10.1017/S0016672310000480

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Ingebrigtsen, T. S., Thomsen, S. F., van Der Sluis, S., Miller, M., Christensen, K., Sigsgaard, T., et al. (2011). Genetic influences on pulmonary function: a large sample twin study. Lung 189, 323–330. doi: 10.1007/s00408-011-9306-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lopez, A. D., Shibuya, K., Rao, C., Mathers, C. D., Hansell, A. L., Held, L. S., et al. (2006). Chronic obstructive pulmonary disease: current burden and future projections. Eur. Respir. J. 27, 397–412. doi: 10.1183/09031936.06.00025805

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Makowsky, R., Pajewski, N. M., Klimentidis, Y. C., Vazquez, A. I., Duarte, C. W., Allison, D. B., et al. (2011). Beyond missing heritability: prediction of complex traits. PLoS Genet. 7:e1002051. doi: 10.1371/journal.pgen.1002051

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Mannino, D. M., and Buist, A. S. (2007). Global burden of COPD: risk factors, prevalence, and future trends. Lancet 370, 765–773. doi: 10.1016/S0140-6736(07)61380-4

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Manolio, T. A., Collins, F. S., Cox, N. J., Goldstein, D. B., Hindorff, L. A., Hunter, D. J., et al. (2009). Finding the missing heritability of complex diseases. Nature 461, 747–753. doi: 10.1038/nature08494

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Meuwissen, T. H., Hayes, B. J., and Goddard, M. E. (2001). Prediction of total genetic value using genome-wide dense marker maps. Genetics 157, 1819–1829.

Pubmed Abstract | Pubmed Full Text

R Development Core Team. (2011). R: a language and environment for statistical computing. R Foundation for statistical computing. Available online at: http://www.r-project.org/

Pubmed Abstract | Pubmed Full Text

Redline, S., Tishler, P. V., Rosner, B., Lewitter, F. I., Vandenburgh, M., Weiss, S. T., et al. (1989). Genotypic and phenotypic similarities in pulmonary function among family members of adult monozygotic and dizygotic twins. Am. J. Epidemiol. 129, 827–836.

Pubmed Abstract | Pubmed Full Text

Repapi, E., Sayers, I., Wain, L. V., Burton, P. R., Johnson, T., Obeidat, M., et al. (2010). Genome-wide association study identifies five loci associated with lung function. Nat. Genet. 42, 36–44. doi: 10.1038/ng.501

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Swanney, M. P., Ruppel, G., Enright, P. L., Pedersen, O. F., Crapo, R. O., Miller, M. R., et al. (2008). Using the lower limit of normal for the FEV1/FVC ratio reduces the misclassification of airway obstruction. Thorax 63, 1046–1051. doi: 10.1136/thx.2008.098483

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Weiss, S. T. (2010). Lung function and airway diseases. Nat. Genet. 42, 14–16. doi: 10.1038/ng0110-14

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wilk, J. B., Djousse, L., Arnett, D. K., Rich, S. S., Province, M. A., Hunt, S. C., et al. (2000). Evidence for major genes influencing pulmonary function in the NHLBI family heart study. Genet. Epidemiol. 19, 81–94. doi: 10.1002/1098-2272(200007)19:1<81::AID-GEPI6>3.0.CO;2-8.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Wright, S. (1921). systems of mating. II. the effects of inbreeding on the genetic composition of a population. Genetics 6, 124–143.

Pubmed Abstract | Pubmed Full Text

Xu, X., Yang, J., Chen, C., Wang, B., Jin, Y., Fang, Z., et al. (1999). Familial aggregation of pulmonary function in a rural Chinese community. Am. J. Respir. Crit. Care Med. 160, 1928–1933. doi: 10.1164/ajrccm.160.6.9902013

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text