Challenges in Reproducibility, Replicability, and Comparability of Computational Models and Tools for Neuronal and Glial Networks, Cells, and Subcellular Structures

1. Introduction

All areas of science are facing problems with reproducibility and replicability (Baker, 2016; Eglen et al., 2017; Munafò et al., 2017; Rougier et al., 2017), and computational neuroscience is no exception. We aim to contribute to the ongoing discussion on reproducibility and replicability by presenting several efforts to systematize and compare, rerun and replicate, as well as reimplement, simulate, and reproduce models and knowledge within our fields of expertise. By comparability, we mean comparing either the simulation results of different simulation tools when the same model has been implemented in them or the simulation results of different models. By replicability, we mean rerunning the publicly available code developed by the authors of the study and replicating the original results from the study. By reproducibility, we mean reimplementing the model using the knowledge from the original study, often in a different simulation tool or programming language from the one reported in the study, and simulating it to verify the results from the study. These definitions are consistent with the terminology on replicability and reproducibility used in the literature (see also Crook et al., 2013; McDougal et al., 2016). However, there is an ongoing discussion on optimal use of terminology and several alternatives have been proposed (see e.g., Goodman et al., 2016; Rougier et al., 2017; Benureau and Rougier, 2018). The lack of universally accepted terminology, solutions proposed in other scientific disciplines, and possible solutions for computational neuroscience are also discussed by Plesser (2018). In order to focus on our findings and conclusions rather than terminology, we will adopt the definitions described above without further discussion about the alternatives.

There is an evident need to evaluate, compare, and systematize tools and models. With the increasing number of published models, it is becoming difficult to evaluate the unique contribution in each of them or assess the scientific rigor. The published articles might provide incomplete information, due to accidental mistakes or limited space and publication format. The original model implementations are not always available. The overhead of model reimplementation and reproduction of the results could be significant. More systematic model description (Nordlie et al., 2009), publishing the code in addition to the article (Eglen et al., 2017; Rougier et al., 2017), and efforts on independent reproduction and replication of the published models (Manninen et al., 2017; Rougier et al., 2017) improve quality and reliability of results in computational neuroscience. Better systematization and classification of the models provide more straightforward recommendations for the scientists initiating new projects or for the training of young researchers entering the field (see also Akil et al., 2016; Amunts et al., 2016; Nishi et al., 2016). All these can better support the reuse and extension of the published models which is often necessary when building models of complex phenomena. The development of new experimental techniques and the new experimental findings also pose new questions for the computational neuroscience. The models that address these questions are often built on top of the existing ones, and heavily depend on the reusability and reliability of the published work. These issues become even more important with the increasing interest and current intensive development of multiscale models. Multiscale models include fine details of all levels of physical organization (molecular reaction networks, individual cells, local neuronal networks, glial networks, large-scale networks, and even complete functional brain systems), and naturally such complex and demanding models must rely even more on the existing knowledge and models. Furthermore, as the complexity of the models increases it becomes more difficult to duplicate the original work even if only one parameter value is mistyped, or completely omitted.

The listed challenges have been extensively discussed within the computational neuroscience and neuroinformatics community. Several publications have proposed improvements in model development and description recommending a clear and compact tabular format for model description (see e.g., Nordlie et al., 2009; Topalidou et al., 2015; Manninen et al., 2017). The issue of reproducibility in computational neuroscience has been emphasized through development of model description and simulation tools: the standardization of tools significantly accelerates development of new models and reproduction of the published models. An overview of the existing simulation tools, their features and strengths, as well as a discussion on future developments are presented in recent publications (Brette et al., 2007; Crook et al., 2013; McDougal et al., 2016). In addition, journals rarely explicitly state that they accept replicability and reproducibility studies (Yeung, 2017). However, the ReScience initiative was started to encourage researchers to reimplement published models and reproduce the research results (Rougier et al., 2017). During the review process in the ReScience Journal, both the manuscript and the reimplementation of the model are tested and checked by the reviewers, and both are made publicly available for the scientific community. In our previous study (Manninen et al., 2017), we addressed the reproducibility of a small set of computational glial models. Based on this study, we emphasize the necessity for giving out all information about the models, such as the inputs, equations, parameters, and initial conditions, in a tabular format, in addition to making the model code publicly available. Similar holds for complex network-level models composed of many interacting neurons where every small error might lead to a large deviation in the simulation outcome.

Equally important concept that should be discussed in the context of reproducibility and replicability is the development of validation strategies for comparability of various computational models. Better mathematical and computational tools are needed to provide easy and user-friendly evaluation and comparison. As can be seen from the reviews of previous modeling work in the field (Manninen et al., 2010, 2018a,b), many new models are built on top of pre-existing models, with some further parameter estimation based on experimental data. Often the validation against existing similar models is too tedious to do and, consequently, is skipped. To facilitate the usability of models, future computational neuroscience research should pay more attention to the questions of reproducibility, replicability, and validation of simulation results. As indicated, this issue becomes even more important with the current trends toward developing multiscale models.

In this study, we evaluate a number of computational models describing a very diverse set of neural systems and phenomena, as well as simulation tools dedicated to these models. We evaluate and discuss a versatile choice of simulation tools, from simulation tools of biochemical reactions, to relatively new simulation tools of growth in cell cultures, to relatively mature and widely adopted tools for modeling spiking neuronal networks. The computational models are equally diverse, including the models of intracellular signal transduction for neurons and glial cells, in addition to single glial cells, neuron-glia interactions, and neuronal networks. Although we take into account a range of models, some classes of models are not considered in this study. We omit single neuron models which are already well developed, compared, and systematized in the literature (Izhikevich, 2004; Sterratt et al., 2011). Furthermore, we do not intend to provide any extensive evaluation of neuronal network models, which are numerous in the literature, but instead discuss an illustrative data-driven modeling example and specific reproducibility, replicability, and comparability issues that emerge in this type of studies. The models for glial networks and the larger models of neuron-glia networks are also excluded from this work and might be subject of future studies. Through the evaluation of examples under consideration, we present the state-of-the-art in reproducibility and replicability of computational models of neuronal and glial systems, summarize our recent findings about reproducibility in computational neuroscience, and propose some good practices based on our present and previous work.

2. Material and Methods

2.1. Simulation Tools

In this section, we describe a range of simulation tools utilized to simulate the spiking neuronal networks, biochemical reactions, and neuronal growth. Simulation tools that allow constructing, simulating, and analyzing whole-cell and neuronal circuit models attracted the most attention in the past and are among the most developed tools used in computational neuroscience. Typical models range from multicompartmental neurons integrating some level of morphological and physiological details of the certain neuron type to the highly abstract models containing large number of low-dimensional model neurons and statistical description of connectivity rules. In computational systems biology, the simulation tools developed for different kinds of biological systems, such as gene regulatory networks, metabolic networks, and signal transduction, have been the focus of development. These tools are relatively mature, standardized, and well-known in the research community. On the other hand, the simulation tools for neurodevelopment are not so well-known, and thus we give more details about these tools in the upcoming sections. All the simulation tools tested and compared in this work are listed in Table 1.

TABLE 1

Table 1. List of simulation tools and model repositories.

2.1.1. Simulation Tools for Biochemical Reactions

Mathematical modeling of biochemistry is important for understanding complex biochemical processes that underlie many neuronal, glial, and synaptic phenomena. Recent interest in modeling biochemical networks in systems biology and in neuroscience have provided several tools that can be used to simulate time-series behavior of the networks (see e.g., Lemerle et al., 2005; Pettinen et al., 2005; Alves et al., 2006; Gilbert et al., 2006; Strömbäck et al., 2006; Wierling et al., 2007; Bergmann and Sauro, 2008; Blackwell, 2013; Schöneberg et al., 2014; Bartocci and Lió, 2016; Olivier et al., 2016). In this study, we used the following simulation tools: GENESIS/Kinetikit (Wilson et al., 1989; Bower and Beeman, 1998; Bhalla and Iyengar, 1999; Bhalla, 2001, 2002), Gepasi (Mendes, 1993, 1997; Mendes and Kell, 1998), Jarnac/JDesigner (Sauro, 2000, 2001), XPPAUT (Ermentrout, 2002), SimTool (Aho, 2003), Dizzy (Ramsey et al., 2005), Copasi (Hoops et al., 2006), NEURON (Carnevale and Hines, 2006), Systems Biology Toolbox (Schmidt and Jirstrand, 2006), and Narrator (Mandel et al., 2007) (see Table 1). Here, we do not provide any detailed overview of the simulation tools, because the topic has been already extensively discussed previously. However, we want to point out the differences in these tools by providing information about the methods used for modeling and simulation.

In the listed simulation tools, the model is often implemented using chemical reactions presented by the law of mass action and Michaelis-Menten kinetics. These reactions form coupled ordinary differential equations (ODEs) presenting the biochemical network, and these equations are then solved numerically when simulating the model. However, for example, in XPPAUT, the model is directly implemented using the ODEs and not the chemical reactions. Several of the tools also provide stochastic approaches to model and simulate the reactions (see e.g., Manninen et al., 2006a; Gillespie, 2007), such as the discrete-state Gillespie stochastic simulation algorithm (Gillespie, 1976, 1977) and τ-leap method (Gillespie, 2001), as well as continuous-state chemical Langevin equation (Gillespie, 2000) and several other stochastic differential equations (SDEs, Manninen et al., 2006a,b). Few simulation tools providing hybrid approaches also exist. They combine either deterministic and stochastic methods or different stochastic methods (see e.g., Salis et al., 2006; Lecca et al., 2017). The increased computing power has recently made it possible also to take into account diffusion processes. The reaction-diffusion simulation tools often use combined Gillespie algorithm or τ-leap method for both reaction and diffusion processes, such as STEPS (Wils and De Schutter, 2009; Hepburn et al., 2012) and NeuroRD (Oliveira et al., 2010), or track each molecule individually in a certain volume with Brownian dynamics combined with a Monte Carlo procedure for reaction events, such as MCell (Stiles and Bartol, 2001; Kerr et al., 2008) and Smoldyn (Andrews et al., 2010). Few studies to compare different reaction-diffusion tools exist (Dobrzyński et al., 2007; Oliveira et al., 2010; Schöneberg et al., 2014). In this study, however, we were only interested in comparing simulation tools with simple reaction models, and thus reaction-diffusion tools and models were not tested. The more detailed testing of reaction-diffusion tools remains for future work and will most probably be accelerated once more models for reaction-diffusion systems become available. The simulation tools for biochemical reactions addressed in this work have been studied in detail in our previous work (Pettinen et al., 2005; Manninen et al., 2006c; Mäkiraatikka et al., 2007) and the here presented results are a summary of our previous work. We recommend to consult the earlier studies for more details.

2.1.2. Simulation Tools for Neurodevelopment

We examined relatively new and promising tools for modeling neurodevelopment. They facilitate exploring through computational means individual biophysical mechanisms involved in development and growth of neuronal circuits and analyzing the properties that arise from those mechanisms. We examined two simulation tools, NETMORPH (Koene et al., 2009) and Cortex3D (Zubler and Douglas, 2009), the full references and links to these tools are given in Table 1. Because these tools are newer, less known and used than the other simulation tools presented in this study, we describe them with additional details.

NETMORPH implements a phenomenological model of neurite growth (in 2D or 3D) based on extensive statistical characterization of dendritic morphology in developing circuits conducted by the authors of the simulation tool (van Pelt and Uylings, 2003; Koene et al., 2009). It can simulate formation of synaptic contacts based on morphology and the proximity between axonal and dendritic segments. The simulation tool was developed in C++ under Unix/Linux and can be installed straightforwardly under the same environment. In Windows, it can be installed using Cygwin. The inputs are text files containing a list of model components and the belonging parameters. The components include description of neuronal population, morphology for each neuron type, parameters determining synapse formation, and a set of flags describing the format of simulation outputs. Model equations are evaluated at fixed time steps, and the output can be generated either at specified time points or at the end of a simulation. Three types of outputs are possible: visualization of neuronal morphologies and networks, raw data containing the list of all generated model components, and the statistics computed from the raw data.

Cortex3D is a simulation platform that supports modeling biophysical and mechanistic details of neural development. As such it does not specify any particular model but rather a set of underlying mechanisms that can be used to implement and simulate user-defined models. The mechanisms embedded into the simulation tool include discretization of space occupied by a model, production, diffusion, degradation, and reactions between chemical species, the effect of mechanical and chemical forces between components of the model, and movement of objects inside the model. The model is solved at a fixed time grid. Parts of the model represented by dynamical equations are solved using Euler method, but numerical integration is replaced by analytical solution whenever possible to avoid overshoot for large time steps. The simulation tool is organized into layers of abstraction, with the discretization of space mapped into the lowest layer, the physical properties of the objects being specified one layer above, and the biological properties mapped into the top two layers. Most of the user-defined model properties can be specified in the top “cell” layer (Zubler and Douglas, 2009). The simulation tool was implemented in Java and is easy to install on any platform. A parallelized version of the simulation tool is also available (Zubler et al., 2011, 2013). Recently, a new simulation tool capable of modeling neuronal tissue development, inspired by Cortex3D and based on the same computational principles, was proposed (https://biodynamo.web.cern.ch/). To specify a model in Cortex3D, a user should write Java module containing the description of model components, interactions between the components, and model parameters. The output of the simulation tool is an Extensible Markup Language (XML) schema compatible with NeuroML containing the details of the obtained model. The simulation tool also integrates Java packages that allow visualization of the simulation evolution. We tested and compared NETMORPH and Cortex3D by implementing and running the same model compatible with both tools and evaluating the simulated data. In addition to tool evaluation, we were interested in promoting the usefulness of these new and underutilized simulation tools.

2.1.3. Simulation Tools for Neuronal Networks

Computational studies of individual neurons and neuronal circuits were the first attempts at computational modeling in neuroscience, have the longest history, and are still the most represented level of abstraction when addressing the function and organization of neuronal systems. They originate from the experimentally verified models of neurons, the ground truth of neuron electrophysiology based on Hodgkin-Huxley (HH, Hodgkin and Huxley, 1952) formalism and the mathematical description of ion channel dynamics. Individual neurons can be described either as single compartmental models representing the somatic membrane potential or as multicompartmental models including parts of dendritic and axonal arbors. In addition, the simulation tools provide a number of simpler and computationally less demanding neuron models based on an integrate-and-fire (IF) modeling formalism. They also provide mechanisms to construct networks of model neurons, from generic random networks to specific brain circuits. Some of these simulation tools also have a capacity to implement subcellular models (NEURON, XPPAUT, and GENESIS). Consequently, these simulation tools are widely accepted and well known within the scientific community and can be considered mature. All of these simulation tools implement deterministic methods to solve the systems of ODEs, and some of them also have possibility to implement SDE models (see e.g., Stimberg et al., 2014). Deterministic integration methods for solving ODEs use either a fixed or adaptable integration step size. For some neurons of IF type, it is possible to solve the ODE exactly between the spike times and update the model at each spike time, thus significantly increasing the accuracy of numerical integration. The extensive discussion about numerical methods can be found in the literature (Rotter and Diesmann, 1999; Lytton and Hines, 2005; Carnevale and Hines, 2006; Brette et al., 2007; Stimberg et al., 2014). Here, we do not aim at giving an overview of simulation tools or comparing their properties, these topics have been extensively discussed elsewhere (see e.g., Brette et al., 2007; McDougal et al., 2016). Instead, we will present our unpublished user experiences from describing and simulating spiking neuronal networks using NEST (Eppler et al., 2015), Brian (Goodman and Brette, 2008; Stimberg et al., 2014), and PyNN (Davison et al., 2009).

2.2. Models

In this section, we give an overview of computational models used in our reproducibility, replicability, and comparability studies. These include the models of intracellular signal transduction for neurons and glial cells, in addition to single glial cells, neuron-glia interactions, and neuronal networks. We tabulated the following properties for the models whenever suitable:

• Neuron model: Multicompartmental or point neuron models adopted from the literature.

• Synapse model: Types of synaptic models and receptors.

• Neuron-astrocyte synapse model: Types of synaptic models and receptors.

• Connectivity: Statistical description of connectivity schemes.

• Intracellular signaling; Intracellular calcium signaling (e.g., leaks, pumps, and receptors that are not named under other categories) in addition to different intracellular chemical species taken into account either in neurons or astrocytes.

• Data analysis: Description of the methods used to analyze in silico data from spiking neuronal network models.

Some of the models we used in this study were found available in model repositories. These repositories are listed in Table 1.

2.2.1. Neuronal Signal Transduction Models

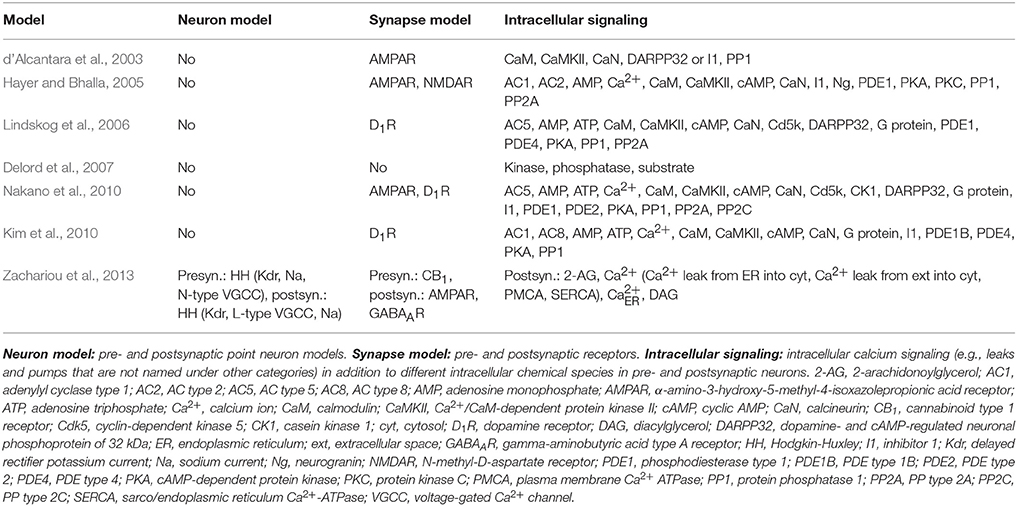
More than a hundred intracellular biochemical species are important in synaptic plasticity. Hundreds of neuronal signal transduction models have been developed to test the criticality of different chemical species. Several reviews of the models exist, some focus on just a few different models whereas others give an overview of more than hundred models (Brown et al., 1990; Neher, 1998; Hudmon and Schulman, 2002a,b; Bi and Rubin, 2005; Holmes, 2005; Wörgötter and Porr, 2005; Ajay and Bhalla, 2006; Klipp and Liebermeister, 2006; Zou and Destexhe, 2007; Morrison et al., 2008; Ogasawara et al., 2008; Bhalla, 2009; Ogasawara and Kawato, 2009; Tanaka and Augustine, 2009; Urakubo et al., 2009; Castellani and Zironi, 2010; Gerkin et al., 2010; Graupner and Brunel, 2010; Hellgren Kotaleski and Blackwell, 2010; Manninen et al., 2010; Shouval et al., 2010). The models range from a simple models with just a single reversible reaction to very detailed models with several hundred reactions. In Table 2, we list the neuronal signal transduction models for plasticity that we evaluated in this study. The models by d 'Alcantara et al. (2003) and Delord et al. (2007) were the simplest with just a few reactions, whereas the model by Zachariou et al. (2013) had both pre- and postsynaptic single-compartmental neurons and rest of the models had very detailed intracellular signaling pathways taken into account. The models by d 'Alcantara et al. (2003), Delord et al. (2007), and Zachariou et al. (2013) we used in the reproducibility studies. In the comparability studies (Manninen and Linne, 2008; Manninen et al., 2011), we tested the models by d 'Alcantara et al. (2003), Hayer and Bhalla (2005), Lindskog et al. (2006), Delord et al. (2007), Nakano et al. (2010), and Kim et al. (2010).

TABLE 2

Table 2. Summary of the neuronal signal transduction models.

2.2.2. Astrocyte Models

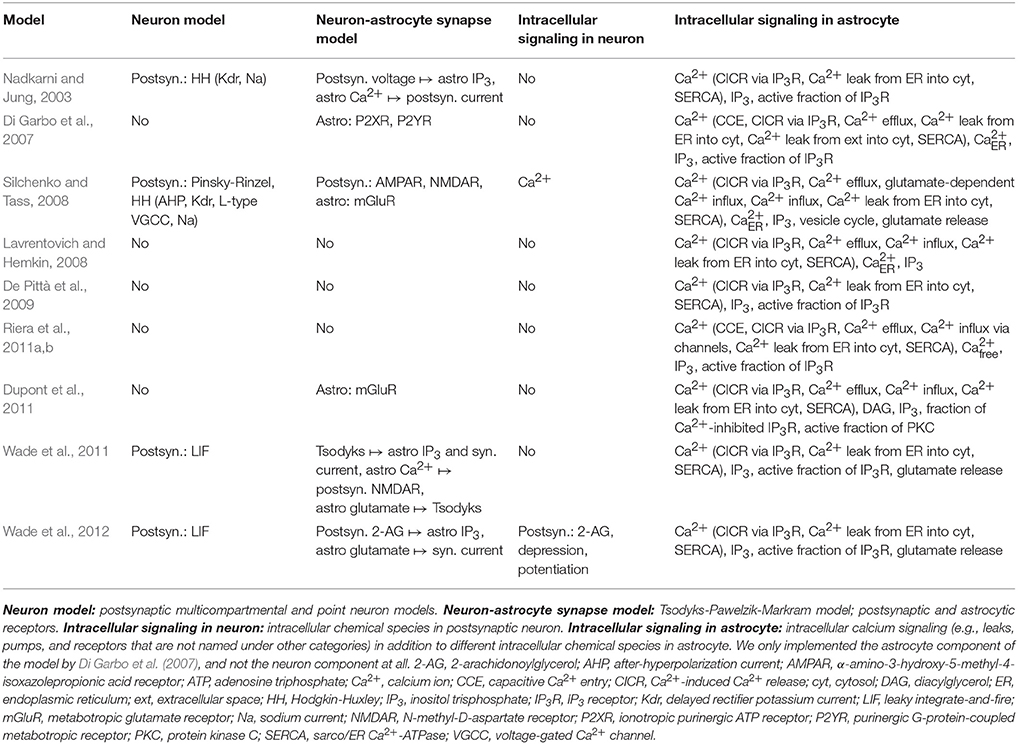
Similarly to neuronal signal transduction models, hundreds of single astrocyte, astrocytic network, and neuron-astrocyte interaction models have been developed to study different phenomena. Several reviews of computational astrocyte and neuron-astrocyte models have appeared during the last few years, some focusing only to a few models and some giving a general overview of the field (see e.g., Jolivet et al., 2010; Mangia et al., 2011; De Pittà et al., 2012, 2016; Fellin et al., 2012; Min et al., 2012; Volman et al., 2012; Wade et al., 2013; Linne and Jalonen, 2014; Tewari and Parpura, 2014; Manninen et al., 2018a,b). In Table 3, we list the models that we evaluated in this study. We chose five single astrocyte and signal transduction models (Di Garbo et al., 2007; Lavrentovich and Hemkin, 2008; De Pittà et al., 2009; Dupont et al., 2011; Riera et al., 2011a,b) and four neuron-astrocyte interaction models (Nadkarni and Jung, 2003; Silchenko and Tass, 2008; Wade et al., 2011, 2012). Silchenko and Tass (2008) used a two-compartmental neuron model, whereas the other three (Nadkarni and Jung, 2003; Wade et al., 2011, 2012) used single-compartmental models. The models by Nadkarni and Jung (2003), Di Garbo et al. (2007), Silchenko and Tass (2008), Lavrentovich and Hemkin (2008), De Pittà et al. (2009), Riera et al. (2011a,b), Dupont et al. (2011), and Wade et al. (2011, 2012) were tested in the reproducibility studies (see also Manninen et al., 2017, 2018b). In addition, the models by Lavrentovich and Hemkin (2008), De Pittà et al. (2009), Riera et al. (2011a,b), and our modified version of the model by Dupont et al. (2011) were used in the comparability study (see also Manninen et al., 2017).

TABLE 3

Table 3. Summary of the astrocyte and neuron-astrocyte models.

2.2.3. Spiking Neuronal Network Models

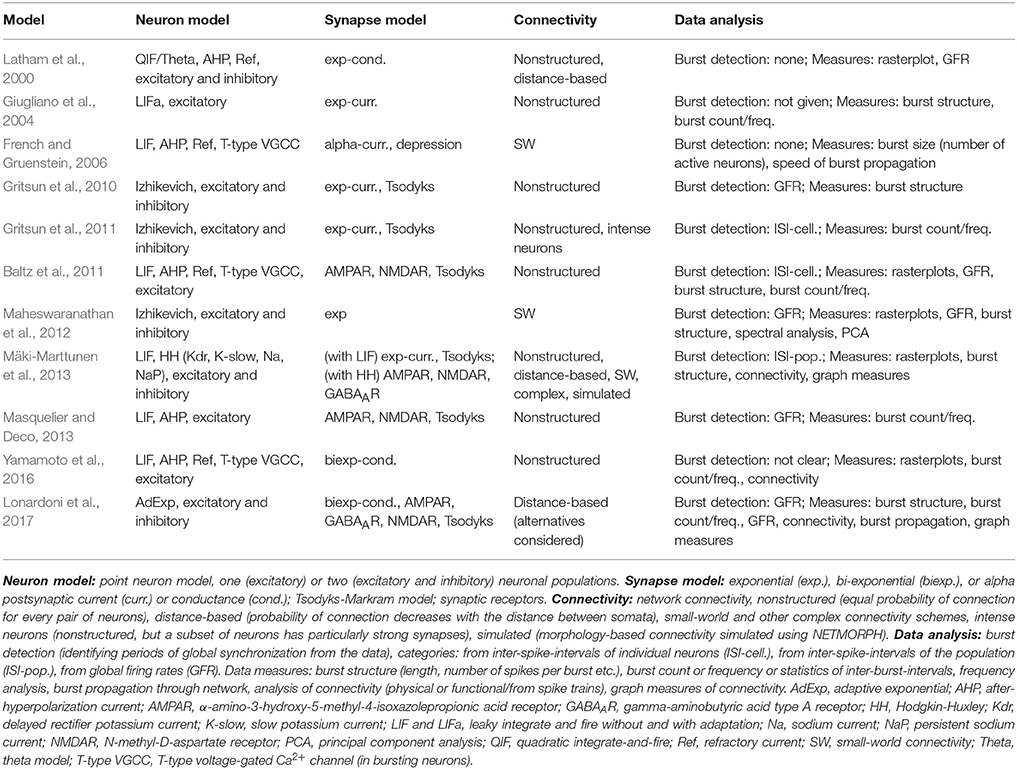
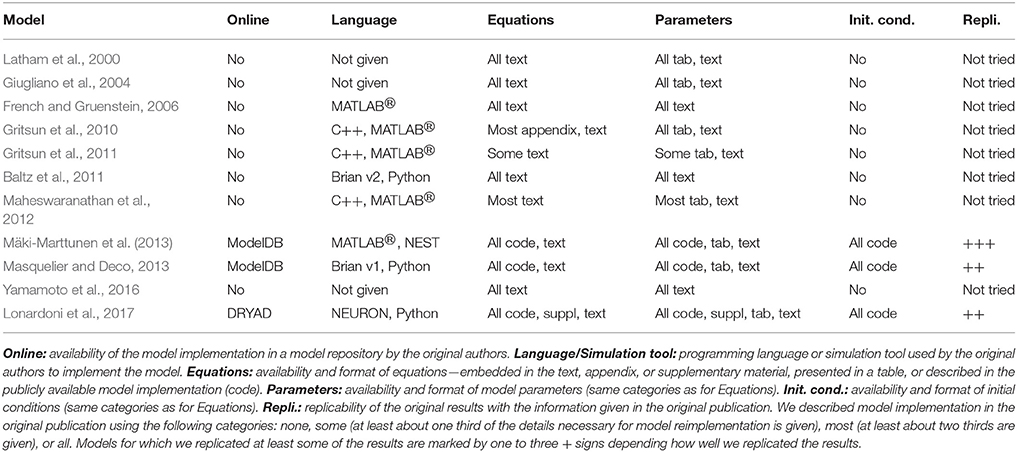
Spiking neuronal network models are numerous in the literature and used to model various phenomena and brain structures. In order to constrain this evaluation to a reasonable set of models, we selected only those models which are developed for the spontaneously synchronized population activity from dissociated neuronal cultures in vitro (for more details, see Robinson et al., 1993; Teppola et al., 2011). The focus on data-driven models gives us an opportunity to emphasize the need for reproduction of both model and data analysis tools. We compared several publications (Latham et al., 2000; Giugliano et al., 2004; French and Gruenstein, 2006; Gritsun et al., 2010, 2011; Baltz et al., 2011; Maheswaranathan et al., 2012; Mäki-Marttunen et al., 2013; Masquelier and Deco, 2013; Yamamoto et al., 2016; Lonardoni et al., 2017), that use similar models, address similar questions, and should converge toward similar conclusions. Some differences emerge from the experimental preparation, from the recording technology, or variations in model composition. The publications by Gritsun et al. (2010, 2011) present two parts of the same study. They are considered as one study, but are presented separately in Table 4 due to the small differences in model construction and data analysis. The publication by Mäki-Marttunen et al. (2013) is not, strictly speaking, modeling the experimental data but rather uses the theoretical concepts to explore models and synthetic data typical for this same type of experiments. All of the studies under consideration implement networks of point-neurons (a few hundred to few thousand neurons) with none or short-term plasticity in synapses and statistical description of connectivity. Similar models have been extensively analyzed in theoretical studies exploring feasible dynamical regimes, and some of them are available in public repositories dedicated to reproducible model development (see OpenSourceBrain; http://www.opensourcebrain.org/). In this study, we do not consider recent attempts to model the effects of non-neuronal cells, and we also leave out the mean field approaches to modeling the same type of experiments and data. The 10 selected studies are summarized in Table 4.

TABLE 4

Table 4. Summary of the spiking neuronal network models.

3. Results

We here evaluate first the simulation tools we used for biochemical reactions, growth in cell cultures, and spiking neuronal networks, and last the computational models for signal transduction in neurons, astrocytes, and spiking neuronal networks.

3.1. Evaluation of Simulation Tools

3.1.1. Simulation Tools for Biochemical Reactions

In our previous studies, we have extensively used and evaluated both deterministic and stochastic simulation tools for biochemical reactions (see Table 1), categorized their basic properties, benefits, and drawbacks, as well as tested the tools by implementing test cases and running simulations (Pettinen et al., 2005; Manninen et al., 2006c; Mäkiraatikka et al., 2007). At first, we tested four deterministic simulation tools, GENESIS/Kinetikit (versions 2.2 and 2.2.1 of the GENESIS and versions 8 and 9 of the Kinetikit), Jarnac/JDesigner (version 2.0 of Jarnac and version 1.8k of JDesigner), Gepasi (version 3.30), and SimTool, by implementing the same test case for every simulation tool and running simulations (Pettinen et al., 2005). Next, we tested three stochastic simulation tools, Dizzy (version 1.11.2), Copasi (release candidate 1, build 17), and Systems Biology Toolbox (version 1.5), the same way (Manninen et al., 2006c; Mäkiraatikka et al., 2007). Last, we tested the possibility to easily exchange models between stochastic simulation tools using Systems Biology Markup Language (SBML) (Mäkiraatikka et al., 2007). As a surprise, only a few of the tools that were supposed to support SBML import were capable of simulating the selected test case when imported as SBML file (Mäkiraatikka et al., 2007). Of the tools that we tested for that study, only Dizzy, Narrator, and XPPAUT succeeded in simulating the imported SBML file. We found out in all of our studies (Pettinen et al., 2005; Manninen et al., 2006c; Mäkiraatikka et al., 2007) that the simulation results between the tools were convergent. Using the same test case as by Pettinen et al. (2005), we also found out in a separate set of tests that NEURON produced similar results as the other tools mentioned above. Based on our studies, we concluded that the comparability of the simulation results needed several requirements to be fulfilled. First, the usability of the simulation tools and existence of proper manuals were crucial. For example, even beginners were able to use Dizzy, Gepasi, Copasi, and Jarnac/JDesigner, but former experience in MATLAB^Ⓡ was required for Systems Biology Toolbox and SimTool. Second, the lack of standards and interfaces between tools also made the comparability problematic. For example related to SBML import, graphical user interfaces designed to help the SBML import were not intuitive, the error messages were not informative enough, and not all the SBML levels were supported. Furthermore, for stochastic simulations with the Gillespie stochastic simulation algorithm, all the chemical reactions in the model had to be implemented as irreversible. Although the test case was implemented and exported with only irreversible reactions, we found simulation tools that mistook some of the irreversible reactions for reversible reactions during the SBML import and thus, we were not able to run stochastic simulations with these tools (Mäkiraatikka et al., 2007). In addition, problems arose when having various biochemical and physiological units because during manual conversion the chance of making errors was significant. Third, the utilization of realistic external stimuli was not possible in all simulation tools. Out of the tested simulation tools, GENESIS/Kinetikit was one of the good examples where external stimuli were enabled. Fourth, only a few of the tools had built-in automated parameter estimation methods to tune the models and their unknown parameter values. However, several methodology improvements have been made in the field in order to perform sophisticated parameter estimation. The use may, however, require some more detailed knowledge in computer science. Thus, all these difficulties and deficiencies present in simulation tools can make the comparison of simulation results difficult.

3.1.2. Simulation Tools for Neurodevelopment

We tested two simulation tools dedicated to modeling neurodevelopmental mechanisms, NETMORPH and Cortex3D (Aćimović et al., 2011). While other simulation tools (e.g., NEURON) can be used to implement models at particular developmental age, NETMORPH and Cortex3D implement the mechanisms behind developmental changes. NETMORPH and Cortex3D can be used to address the same questions, but they are fundamentally different in methodology, approach, and philosophy of modeling being therefore complementary rather than competing. NETMORPH and Cortex3D were implemented using different programming languages. Running simulations beyond making simple changes to the provided examples required a deeper understanding of the tools.

In short, we implemented a phenomenological model, compatible with both simulation tools, of neurite growth and formation of synaptic contacts based on morphology criteria (for more details see Aćimović et al., 2011). The choice is determined by model components and mechanisms available in NETMORPH. To analyze the simulation results, we wrote own MATLAB^Ⓡ code which converted both simulated data sets to the same format and computed the statistics from the data. We examined the simulated morphologies, analyzed the number of generated synapses at different simulation times, and compared the synapse counts to the experimental data extracted from the literature (see Figure 1). As a conclusion, the two simulation tools produced qualitatively similar growth dynamics. The simulated results were consistent with the experimental data in the early phase of growth but deviated in the latter phase. Cortex3D gave somewhat shorter neurites with less synaptic contacts and less precise control of the orientation of neurite segments than NETMORPH. While NETMORPH implements a set of equations derived to produce precise statistics for all relevant parameters of neurite morphology, Cortex3D focuses on the underlying mechanisms of growth, for example the tensions resulting from elongation and the production of resources needed for growth. These mechanisms affect neurite morphology in a complex and not fully predictable way. The computational model used for testing and comparing the simulation tools was a natural choice for NETMORPH and therefore easier to implement, faster to simulate, and less memory consuming. However, Cortex3D offers more flexibility to implement user-defined models for various phases of neurodevelopment, and can be used to study many other mechanisms in addition to neurite growth.

FIGURE 1

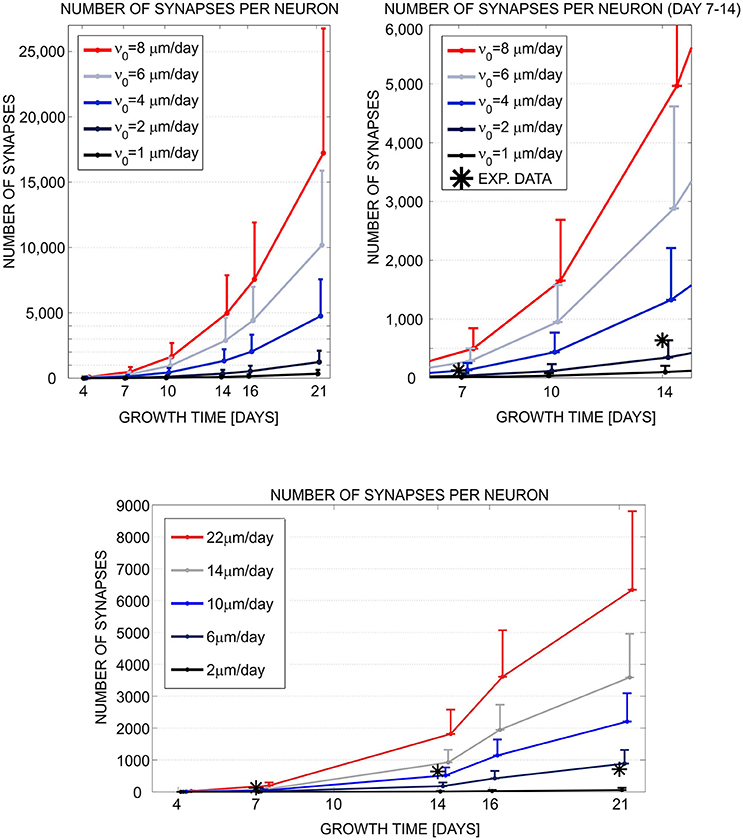
Figure 1. Evaluation and comparison of the neuronal growth simulation tools (NETMORPH and Cortex3D). Panels illustrate the increase in synapse counts during simulation time equivalent to 4–21 days in vitro. The number and position of somata were fixed. For each neuron, the neurites grew according to the implemented model and formed synaptic contacts based on proximity between axonal and dendritic branches. In this figure, we varied one of the parameters that controlled neurite growth, the elongation rate ν₀ (see legend), and different colors correspond to different parameter values. The results show mean (line) and standard deviation (bar) for the number of synapses per neuron, averaged over all neurons in the culture. Stars indicate experimental values extracted from the literature (Ichikawa et al., 1993). (Top left) Synapse counts obtained from NETMORPH, elongation rates equal to 1, 2, 4, 6, and 8 μm/day. (Top right) Zoomed interval 7–14 days from the panel (Top left). (Bottom) Synapse counts obtained from Cortex3D, elongation rates equal to 2, 6, 10, 14, and 22 μm/day. x axis—growth time in days, y axis—number of synapses per neuron. For days 4–14 and ν₀ = 2μm/day (NETMORPH) or ν₀ = 10μm/day (Cortex3D), the simulated values corresponded to the experimental ones. After 14 days the simulated values increased while the experimental values saturated as no synaptic pruning was implemented in this test. The neurite growth was slower for Cortex3D which was visible from the values for ν₀. Reproduced from Aćimović et al. (2011) with permission from Hindawi.

3.1.3. Simulation Tools for Spiking Neuronal Networks

We present our user experience with three common tools for simulation of large spiking networks of point neuron models. In addition to testing and comparing the simulation tools, we discuss the flexibility of simulation tools to implement user-defined model components. We tested the common tools, NEST (version 2.8.0) with PyNN (version 0.8.0) used as an interface and Brian (version 2.0). All of the tested packages are well documented and additional support is offered through user groups. The general tendency to develop Python based simulation tools or Python interface to simulation tools saves time when analyzing the obtained simulation results, since the same Python modules for analysis and visualization of data can be combined with each simulation tool. Parallelization is supported by NEST and PyNN, however it is still under development in Brian. An earlier version of Brian offers a model fitting method for tuning the statistics of the interspike intervals in spiking neuron models. In Brian version 2.0, this option is under development. NEST and PyNN do not provide direct tools for model fitting. However, both Brian and NEST can easily be combined with external Python modules for model fitting. For fast exploration of models, for example in the early phase of model development, or for incorporating nonstandard biophysical mechanisms in the model, Brian offered more flexibility. In NEST and PyNN, the components of the model have to be either selected from the list of existing models or implemented by extending the simulation tool to include new models. Brian provides more flexible framework for implementation of user-defined models. Model components are specified directly as strings of ODEs. Various models can easily be implemented, however they still rely on the existing functionalities of the simulation tool.

3.2. Evaluation and Comparison of Computational Models

3.2.1. Neuronal Signal Transduction Models

Based on our large review of postsynaptic signal transduction models for long-term potentiation and depression (Manninen et al., 2010), we found out that it would have been often time consuming or even impossible to try to reproduce the simulations results. First, not all the details of the models, such as equations, variables, inputs, outputs, compartments, parameters, and initial conditions, were given in the original publications. For example, even just missing to give the inputs in the publications makes the reimplementation and reproduction of the simulation results difficult or impossible with signal transduction models. Second, most of the models were not available in model databases or were not open access, and sometimes even the simulation tool or programming language used was not named in the publications. Third, comparison to previous models was non-existent. Even qualitative comparison was difficult because only a few publications provided graphical illustrations of the model components or the graphical illustrations were misleading by having also components that were not actually modeled. We concluded that the value of computational models for understanding molecular mechanisms of synaptic plasticity would be increasing only with detailed descriptions of the published models and sharing the codes online.

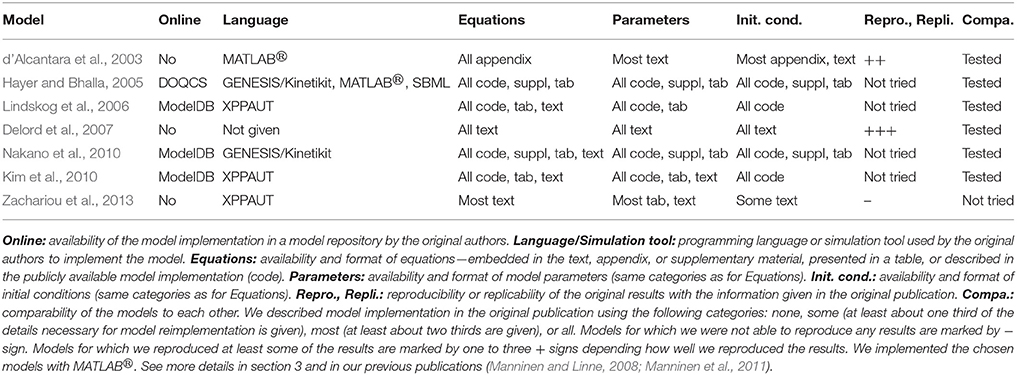
We listed the models we tried to reimplement, resimulate, and compare based on the information in the original publications in Tables 2, 5. In Table 5, we can see that four out of seven models were available in the model repositories but this is because four of the models were chosen to this study because of the availability of the code. Thus, the ratio of models available online is generally not this high. In addition, most of the publications gave all the details of the models as text, tabular format, supplementary material, or at least in the model code. We were able to reproduce Figure 1C of the publication by Delord et al. (2007). From the publication by d 'Alcantara et al. (2003), we decided to reproduce only Figures 3D–F. After fixing one mistake in the equations by d 'Alcantara et al. (2003), we were able to reproduce most of the simulation results. We were able to reproduce all the other curves, except our maximum value for α-amino-3-hydroxy-5-methylisoxazole-4-propionic acid receptor (AMPAR) activity was about 220 % whereas the original maximum value in Figure 3D was about 280 %. The reason behind the different value might be that not all parameter and initial values were given in the original publication. We were not able to completely implement the model by Zachariou et al. (2013) because not all the information of the model was given in the original publication. More information about the reproducibility issues of the models can be found in our previous publications (Manninen and Linne, 2008; Manninen et al., 2011).

TABLE 5

Table 5. Evaluation of the neuronal signal transduction models.

We were the first ones to provide a computational comparison of postsynaptic signal transduction models for synaptic plasticity (Manninen et al., 2011). We evaluated altogether five models, of which two were developed for hippocampal CA1 neurons (d'Alcantara et al., 2003; Kim et al., 2010), two were developed for striatal medium spiny neurons (Lindskog et al., 2006; Nakano et al., 2010), and one was a generic model (Hayer and Bhalla, 2005) (see Tables 2, 5). The model by d 'Alcantara et al. (2003), we implemented ourselves in MATLAB^Ⓡ, but the others we took from model databases. The models by Kim et al. (2010) and Lindskog et al. (2006) we took from ModelDB (Migliore et al., 2003; Hines et al., 2004) in XPPAUT format. The codes were properly commented and clearly written, which made it easy to find the values we wanted to modify. The model by Nakano et al. (2010) we took from ModelDB in GENESIS/Kinetikit format. The model codes were neither intuitive nor commented. However, the database and simulation tool provided helpful explanation files to ease the use of the model files (see more details in Manninen et al., 2011). The model by Hayer and Bhalla (2005) we took from the Database of Quantitative Cellular Signaling (DOQCS, Sivakumaran et al., 2003) in MATLAB^Ⓡ format. However, the MATLAB^Ⓡ implementation of the model was hard to modify due to issues with parameter handling. Precisely, it was challenging to identify model parameters as the authors opted to hard code numerical values to the MATLAB^Ⓡ script instead of using parameter names (see more details in Manninen et al., 2011). We compared the simulation results of the models by using the same input for the models. We ran a set of six simulations with different total concentrations of calcium/calmodulin-dependent protein kinase II and protein phosphatase 1 to see how the behavior of the models changed. Our study showed that when using the same input for all the models, models describing the plasticity phenomenon in the very same neuron type produced partly different responses. On the other hand, the models by d 'Alcantara et al. (2003) and Nakano et al. (2010) produced partly similar responses even though they had been built for neurons in different brain areas, and Nakano et al. (2010) did not report using the details of the model by d 'Alcantara et al. (2003) when building their model. The models by Lindskog et al. (2006) and Kim et al. (2010) produced also partly similar responses even though they had been built for neurons in different brain areas, but Kim et al. (2010) stated that they used the details of the model by Lindskog et al. (2006) when building their model. Based on these results, we concluded that there is a demand for a general setup to objectively compare the models (see more details in Manninen et al., 2011). In our other study (Manninen and Linne, 2008), we compared the models by d 'Alcantara et al. (2003) and Delord et al. (2007) with the same input and the total concentration of AMPARs. We verified that the model by d 'Alcantara et al. (2003) was only able to explain the induction of plastic modifications, whereas the model by Delord et al. (2007) was able to explain both induction and maintenance (see also d'Alcantara et al., 2003; Delord et al., 2007).

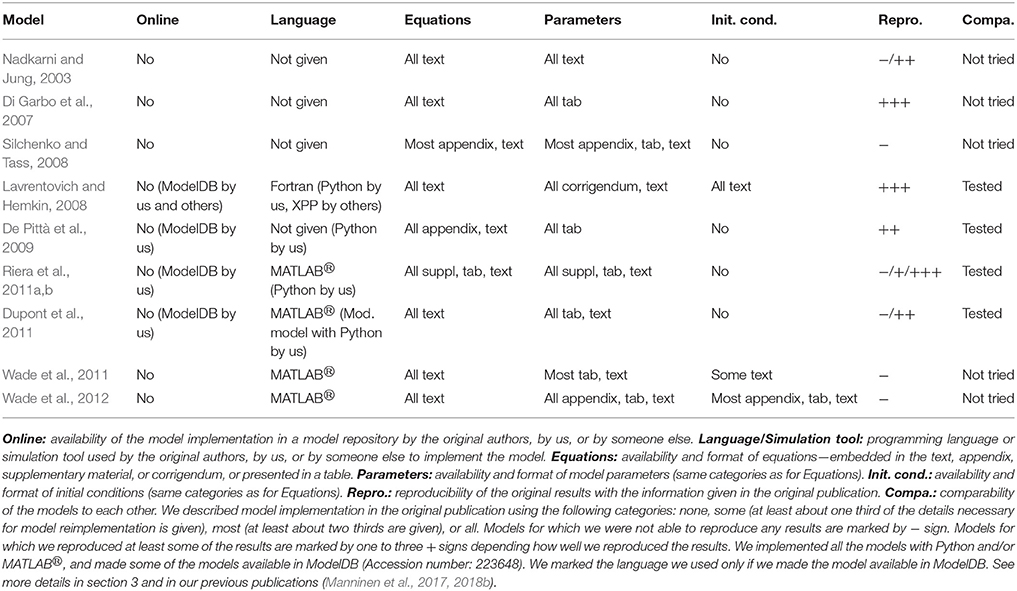
3.2.2. Astrocyte Models

After categorization of astrocyte and neuron-astrocyte models in our previous studies (Manninen et al., 2018a,b), we realized that these models have the same shortcomings as listed in the previous section for neuronal signal transduction models, such as several publications lacked important model details, model codes were rarely available online, graphical illustrations of these models were misleadingly plotting also model components that were not part of the actual model, mathematical equations were sometimes incorrect, and selected model components were not often justified.

In our previous studies (Manninen et al., 2017, 2018b), we tried to reimplement altogether seven astrocyte models. In the present study, we tried to reimplement two more models. None of the models were available in model repositories by the original authors. However, the model by Lavrentovich and Hemkin (2008) is in ModelDB submitted by someone else (Accession number: 112547). We have provided our implementation for four out of nine models in ModelDB [the models by Lavrentovich and Hemkin (2008), De Pittà et al. (2009), and Riera et al. (2011a,b), and modified version of the model by Dupont et al. (2011), Accession number: 223648]. Most of the publications provided all the details of the models, except the initial conditions, either in text, tabular format, appendix, supplementary material, or in corrigendum. We were able to reproduce all of the chosen original results by Di Garbo et al. (2007) and Lavrentovich and Hemkin (2008) (see Table 6). We reproduced Figures 2, 5, and 8 by Di Garbo et al. (2007) and Figures 3, 4, 5, 7, and 9 by Lavrentovich and Hemkin (2008). We were not able to reproduce any of the important features of the original results by Riera et al. (2011a,b) with the original equations, but after we fixed the found error in one of the equations we were able to reproduce some of the original results in Figure 4B by Riera et al. (2011a) when X_IP3 was 0.43 μM/s between 100 and 900 s and 0 otherwise and all of the original results when X_IP3 was 0.43 μM/s between 100 and 900 s and 0.2 μM/s otherwise. We were able to reproduce most of the original results in Figure 12 by De Pittà et al. (2009). We were able to reproduce well the amplitude modulation but not the frequency modulation part of the figure. Thus the problem might be that the original authors did not provide all the model details correctly for the frequency modulation. We were not able to reproduce any of the important features of the original results in Figures 2 and 3 by Dupont et al. (2011) with the original equations. After we tested our implementation, we realized that there had to be a mistake in the original calcium equation. We tested several different calcium equations based on the equations published by the same authors and were able to reproduce most of the original results with one of the tested equations. At first, we were not able to reproduce Figure 2 by Nadkarni and Jung (2003). After we fixed mistakes in one of the original equations and parameter values, we were able to reproduce most of the original results in Figure 2 by Nadkarni and Jung (2003). Due to several deficiencies in the original model descriptions, we were not able to reproduce the simulation results of the models by Wade et al. (2011, 2012) (see Table 6). In addition, we were not able to completely implement the model by Silchenko and Tass (2008) because not all the information of the model was given in the original publication. More details about the reproducibility issues of the astrocyte models can be found in our previous publications (Manninen et al., 2017, 2018b).

TABLE 6

Table 6. Evaluation of the astrocyte and neuron-astrocyte models.

In addition to testing reproducibility, we also addressed the comparability of the astrocyte models in our previous study (Manninen et al., 2017). We compared the model by Riera et al. (2011a,b) to the model by Lavrentovich and Hemkin (2008), and the model by De Pittà et al. (2009) to our modified version of the model by Dupont et al. (2011). We chose these models because they described similar biological processes. The models by Riera et al. (2011a,b) and Lavrentovich and Hemkin (2008) were spontaneously oscillating models, whereas the other two models used glutamate as stimulus. The overall dynamical behaviors of the models were relatively different. The model by Lavrentovich and Hemkin (2008) oscillated less frequently than the model by Riera et al. (2011a,b). We found out that both models were sensitive to parameter values. Especially, when using the parameter values from the model by Riera et al. (2011a,b) in the model by Lavrentovich and Hemkin (2008), the model by Lavrentovich and Hemkin (2008) behaved differently compared to the behavior with its own parameter values. With a constant glutamate stimulus, the models by De Pittà et al. (2009) and our modified version of the model by Dupont et al. (2011) showed partly similar kind of behavior but there were a few exceptions. First, a higher constant glutamate stimulus value produced higher calcium concentrations with the model by De Pittà et al. (2009) and lower calcium concentrations with our modified version of the model by Dupont et al. (2011). Second, the higher the constant glutamate stimulus value, the faster the model by De Pittà et al. (2009) ceased to oscillate. With pulse wave stimuli, the model by De Pittà et al. (2009) and our modified version of the model by Dupont et al. (2011) produced differing results. In our modified version of the model by Dupont et al. (2011), the calcium concentration oscillated even with the minimum concentration value of the glutamate stimulus pulse. This did not happen with the model by De Pittà et al. (2009). More details about the comparability issues of the astrocyte models can be found in our previous publication (Manninen et al., 2017).

3.2.3. Spiking Neuronal Network Models

We evaluated 10 models listed in Table 4. The majority of the examined publications presented a complete set of equations describing the neuron and synapse models, either in the methods section, appendices, or supplementary material. We found an incomplete set of equations in two of the publications. All model parameters were presented, however not in an easily tractable format. Only one publication presented all the parameters in a tabular format, 6/10 (7/10 if the supplementary material was included) publications partially summarized parameters in a tabular format. None of the publications used the recommendable model description format introduced by Nordlie et al. (2009). Non-systematic model description increases the chance of errors both in the publication and when reimplementing the model. We found several minor errors: wrong naming of parameters, same name used for different parameters in the same article, missing to define some relevant parameters before using them, ambiguities in defining probability distributions used to randomize some of the parameters (e.g., using the wrong name for probability distribution, ambiguity about implementation of probability distribution in the utilized simulation tool), and ambiguities in describing the connectivity scheme. In addition, most of the publications did not give the initial conditions.

Description of network connectivity scheme is equally important part in presentation of network models. The unstructured connectivity is used in 6/10 studies, thus each pair of neurons was connected with equal probability. The other studies included additional connectivity schemes, often distance-dependent connectivity, where the probability of connection decreased with the distance between the pair of neurons, or the small-world connectivity that allows the majority of local and a few long-distance connections. A careful description of the connectivity generating algorithm is advisable for all but the simplest (unstructured) connectivity in order to avoid implementation errors. For example, in one of the publications the authors described network connectivity as “scale-free random” but then assigned a number of outputs to each neuron using a uniform random instead of a power-law distribution. The two studies by Mäki-Marttunen et al. (2013) and Lonardoni et al. (2017) paid additional attention to the generation of connectivity matrix. Both included supplementary material to describe implementations and implications of different connectivity schemes.

The comparison between simulated and experimental data requires extensive data analysis. The lack of standardization of methodology and the ambiguity in presentation of the applied algorithms pose additional obstacles to reproducibility and replicability. All of the models under consideration generated the same type of data, the spontaneous activity exhibiting network-wide bursts, thus the intervals of intensive spiking activity reflecting global synchronization. The analysis of this data often consists of two steps: bursts detection, segmenting the population spike-data into intervals containing bursts, and computing the statistics of different quantitative measures based on the burst detection or on original non-segmented data. Burst detection itself might not be very reliable. A recent review article conducted evaluation of a broad range of burst detection methods and tested them against a carefully crafted benchmark data (Cotterill et al., 2016). The authors concluded that none of the algorithms performed ideally, and suggested a combination of several methods for improving the precision. The issue was not so dramatic in studies that we examined. All of them focused on relatively large bursting events that were easier to identify, compared to the study by Cotterill et al. (2016). Typically, burst detection algorithms depend on free parameters that are manually tuned to the data. However, the fact that methods used in various studies differ and that authors rarely provide the implementation of the algorithms creates an additional obstacle in reproducing the published results. Even bigger variability is presented in selection of methodology to quantify bursting dynamics. The last column in Table 4 illustrates this variability and lists the data measures used in different publications. In the table, burst detection methods are classified into three categories: methods based on spike-data of individual electrodes/neurons, based on population spike-data, and based on global/population firing rate. The measures used to quantify data include analysis of the spike-data statistics, analysis of burst profiles or frequency of their occurrences, frequency analysis, principal component analysis applied to global firing rates, spatial burst propagation, extraction of connectivity from the spike-data of individual neurons, as well as graph theoretic analysis of the extracted connectivity. This lack of standardization in data representation somewhat hinders the comparison between different studies. Reproducibility of the model requires reimplementation of the model equations, burst detection method, and measures used to quantify the data.

The simulation tools range from the custom-made software in MATLAB^Ⓡ or C++ to the public simulation tools of spiking neuronal networks (e.g., Brian, NEST, and NEURON). Three out of 10 listed studies provide the full model implementation, namely Masquelier and Deco (2013), Mäki-Marttunen et al. (2013), and Lonardoni et al. (2017). From these studies, we attempted to replicate the results that demonstrate time evolution of model variables and the global dynamical regime of the model, for example adaptation variables, cell membrane potential, and spike raster plots. The replicability of the three studies is summarized in Table 7. The model by Masquelier and Deco (2013) is available in Brian version 1.4.0 and Python version 2.6, and we ran it in Brian version 1.4.1 and Python version 2.7. The code contains model implementation, the list of parameters, and the plotting function sufficient to replicate Figures 4, 5 from the article. The replication of Figure 4, the illustration of neuron and network dynamics, was straightforward. In Figure 5, the neuronal adaptation mechanism was examined and the basic model was tested for two different values of the adaptation time constant τ_a. We replicated the result obtained for τ_a = 1.6 s but failed to replicate the results for τ_a = 1.2 s. This might be caused by different versions of Python and Brian used in the original study and in our replicability test. The model by Lonardoni et al. (2017) is available in NEURON/Python format (versions of the software not indicated). It required installation of an additional nonstandard Python package. The model is well documented and supported by many implementation details. The code downloaded from DRYAD repository included model implementation, the code for generating connectivity matrices, as well as three test examples and three examples of connectivity matrices. The first attempt to run the model using Neuron 7.1. produced errors. After contacting the authors, we obtained the correct version for the simulation tool (Neuron 7.3) and Python packages, as well as valuable instructions how to use the code. Under Neuron 7.3, all three test examples worked. We were able to use two out of three connectivity matrices, but not the biggest one (N = 4,096 neurons) used in the article. Attempt to run the biggest matrix failed most likely due to memory issues. However, we managed to replicate the rasterplots in Figure 2A by Lonardoni et al. (2017) using a smaller matrix (N = 1,024 neurons) and after modifying one parameter. In a smaller network, the burst propagation in Figure 2B by Lonardoni et al. (2017) was somewhat less evident. Thus, we were able to replicate most of the original results by Lonardoni et al. (2017). The study by Mäki-Marttunen et al. (2013) contains two models, a network of HH neurons and a network of leaky-IF (LIF) neurons. We replicated Figure 3 from the article. The first, HH model, is available in MATLAB^Ⓡ format (version R2010a/R2011b) using own code and it was possible to replicate it. The second, LIF model, is available in PyNEST format (Python version 2.4.3 and NEST version 2.0.0). The software versions are indicated in the code. We managed to replicate the result using Python version 2.7 and NEST version 2.2.1. Running the same code in a newer version of the simulation tool, NEST version 2.8.0, failed to produce any bursting dynamics. All of the studies provided well-documented models and full set of parameters. However, the replicability of the results was hindered by common problems related to versions of the utilized software. These examples illustrate the need to provide detailed information about simulation environment, in addition to model description and implementation.

TABLE 7

Table 7. Evaluation of the spiking network models.

3.2.4. Summary of Reproducibility and Replicability Studies

Figure 2 shows our subjective evaluation of the difficulty in timewise to reproduce and replicate the original simulation results and the percentage of reproduced and replicated original results. The list of issues affecting the evaluation of models included: (1) complexity of the reproduced/replicated model, (2) model description in the original publication (in a tabular format, as text, or as a supplementary material, and the amount of details given), (3) possible errors in the model description, (4) report of versions of the simulation tools and packages, (5) person who reimplemented the model, thus the experience of the researcher, and (6) user support from the authors of the model.

FIGURE 2

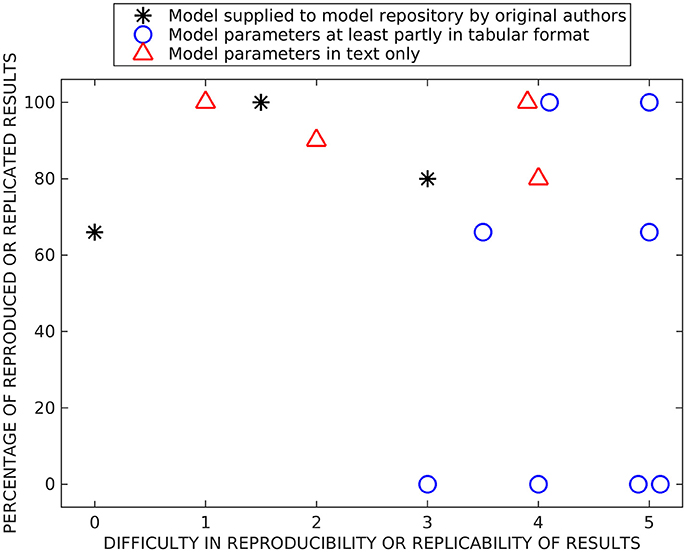
Figure 2. Summary of reproducibility and replicability studies. Both x- and y-values are based on subjective estimation. On the x-axis, we present the difficulty to reimplement, simulate, and reproduce or rerun and replicate previous results (numbers mean the following: 0—immediately, 1—after a few hours of working on the model, 2—after 1 day, 3—after a few days, 4–after 1 week, and 5—after 2 weeks or more). On the y-axis, we present the percentage of reproduced or replicated results. The models are separated into three categories based on were they supplied in model repositories by original authors, were at least part of the parameter values given in a tabular format, and were parameter values given only in text format.

We separated all tested reproducibility and replicability models (see Tables 5–7) into three classes according to presentation in related publications: models described fully in the text (all parameters embedded in the text), models with parameters at least partially (and in some cases entirely) given in a tabular format, and the studies which supplied model implementation to the public repositories. We carried out reproducibility studies for the first two categories and replicability studies for the last category. As expected, the replicability studies were less difficult than most of the reproducibility studies, the replication times ranged from working immediately to 2 days. The percentage of replicated results was high in all studies (more than 60 %), and the main obstacle was incompatibility of simulation tool versions. Reproduction time for models described entirely in text ranged from a few hours to a week. Surprisingly, we were able to reproduce on average better the results from these models than the rest of the models, including the three models that we tried to replicate by rerunning the available model implementations (see Figure 2). The reason might be a difference in complexity of models, as these models tended to be simpler than others. The majority of the reproduced models presented most or all the parameter values in a tabular format. The time needed for reproducing these models ranged from a few days to more than 2 weeks. Even though parameter values were given, at least partly, in a tabular format for eight models, we were able to reproduce the original results completely only with two of these models and none of the original results with four of these models. Thus, this category of models had a huge variation in percentage of reproduced results, indicating that some other issues, in addition to model presentation in the article, determined the success of reproduction. The difficulty to reproduce the results increased even when only one parameter value was missing or one mistake in equations. Our results showed that the four models for which we were able to reproduce all the original results gave all the equations and parameter values in the original publication, including corrigenda and supplementary material. However, one of the completely reproduced models had a mistake in one of the equations that we had to fix, for all the other completely reproduced models all the details were given correctly in the publications. Moreover, if all the details of the models were given in the original publication, it did not mean that we were able to reproduce all the results. The reason was that often the models had mistakes in parameter values or equations. We should emphasize that small number of model examples in some categories affected the conclusions (only three replication tests and four tests with models fully described in text are shown).

Figure 2 shows some level of correlation between difficulty and accuracy of reproduction/replication studies: all studies that were done relative fast (up to a few days) achieved relatively high reproduction/replication of the original results. The studies that required more time ranged from no reproduction to perfect reproduction. This also reflects the way how these studies were carried out, some models immediately gave good results while others required long time and numerous tests without guarantee of success. The distribution of values reflecting the success was somewhat bimodal, the reproduction results either failed or succeeded with over 60 % reproduced results. The percentage of replicated results were over 60 % for all models. Finally, the large distribution of precisions for some classes of models indicated that additional issues affect the success of reproduction, particularly the complexity and the accuracy of the model description. This should be emphasized in the light of increasing interest for very complex and biophysically accurate multiscale models. While simpler models provide solid reproducibility in relatively short time, complex models require detailed description of the model, preferably with model implementation made publicly available.

4. Discussion

We have continually evaluated computational neuroscience and systems biology software and computational models since 2004 while developing new methods and models for computational neuroscience. In this study, we partly summarized results from our previous studies and partly presented new results. We examined selected simulation tools that are intended for simulation of biochemical reactions and subcellular networks in neuronal and glial cells (see also Pettinen et al., 2005; Manninen et al., 2006c; Mäkiraatikka et al., 2007) and for studying the growth and development of neocortical cultures (see also Mäki-Marttunen et al., 2010; Aćimović et al., 2011) and the dynamics of spiking neuronal networks. We have previously provided an extensive overview of more than hundred computational models for postsynaptic signal transduction pathways in synaptic plasticity (Manninen et al., 2010) and more than hundred computational models for astrocytes and neuron-astrocyte interactions (Manninen et al., 2018a,b), where our purpose was to categorize the models in order to make their similarities and differences more readily apparent. In this study, we provided reproducibility and comparability results for some of these models (see also Manninen et al., 2011, 2017, 2018b) with an aim to present the state-of-the-art in the field and to provide solutions for better reproducibility. Additionally, we provided replicability results for spiking neuronal network models.

Our results show that the different simulation tools we tested were able to provide same simulation results when the same models were implemented in them. On the other hand, it was somewhat difficult to reproduce the original simulated results after reimplementing and simulating the models based on the information in the original publications. We were able to reproduce all the original simulation results of four models out of 12 models we tested. The more complete and correct description the model had in the original publication, the more likely we were able to reimplement the model and reproduce the original results. When the parameter values were in a tabular format, it was much easier to reimplement the model because there was no need to go through the whole article looking for the possible values. Mistyped or missing equations and parameter values in the original publications made the reproducibility of the simulation results most difficult. In our replicability studies, we were able to replicate one study and most of the results from the other two studies. The issues encountered while rerunning the models can be attributed to mismatch in versions of the software used for replication and for original model development. Our experiences emphasize the need to supply not only the model description and implementation but also the details of simulation environment, the versions of the software, and the list of necessary packages. The need for better tracking and documentation of the simulation environment and possible solutions are discussed by Crook et al. (2013).

When developing new simulation tools, a multitude of questions should be asked. Naturally, every simulation tool is limited with the adopted modeling framework but should aim at providing the maximal flexibility within that framework. In that context, the following challenges and questions are relevant:

• How big programming load is needed to implement new biological mechanisms?

• How easy is it to incorporate the model components into the existing models from the literature and public databases?

• Does the simulation tool allow flexible level of details when describing different model components?

• Do the version of the simulation tool and packages needed to run the simulations pose a problem for replicability?

Most of the existing simulation tools of spiking neuronal networks impose strict constraint on selection of model components. Those components are implemented as part of the model source code, and the new ones can be added only through extension of the source code which prevents fast modification of model components. Simulation tools that provide basic mechanisms for model implementation and allow flexible description of details, for example directly implementing the model as either ODEs or SDEs (Brian, XPPAUT), by providing interface for adding new components (NEURON), or by providing unit checks (Brian), offer easier manipulation and modification of the model. For the same reason, the simulation tools of this type allow easier extension and reuse of the published models. Several existing tools support development of multiscale models [MOOSE (Ray et al., 2008), GENESIS, NEURON] or implementation of models using more than one standard simulation tool (MUSIC, Djurfeldt et al., 2010). These tools support models where different mechanisms are represented at different level of details. The different versions of the simulation tools and the packages needed can make replicability problematic. It is very important for the tool developers to take this into account.

Our findings on a specific set of published models for different biological systems stress the importance of a variety of aspects of model development. The following challenges and questions are relevant:

• Has the model been checked carefully in the review process and can it produce the results in the publication?

• Is the quality of the code sufficient?

• Is the model properly validated against experimental wet-lab data and correctly representing the biological findings?

• What new biological, modeling, and computational aspects the model provides on top of the previously published models?

• Are all the details of the model equations and biological components given in the publication in a clear way, preferably in a tabular format?

• Which programming language or simulation tool was used to implement the model, which data analysis methods were used, and are the implementation of the model and data analysis methods available online?

It is important to emphasize that a good-quality model implementation supplied with the original publication improves not only replicability of the study but also understanding of the model itself. This is already important during the review process. Reviewers should have the possibility to rerun the model code, check the simulated results, and compare the simulated and experimental data during the review process (see also Eglen et al., 2017; Rougier et al., 2017). Equally important is to clearly explain what new components the model has in comparison to previously published models and what old and new results the model can show. Verbal description is a suboptimal way to present complex mathematical formalisms and algorithms. It often turns out to be incomplete and a number of ambiguities emerge when attempting to reimplement a model, usually not evident at first. More systematic and compact description of all model details, such as equations, parameter values, initial conditions, and stimuli, using, for example, a tabular format proposed by Nordlie et al. (2009) and Manninen et al. (2017) and a supplementary material presenting a metadata and meta-code are needed for successful reproduction of the published scientific results. Tools to manage, share, and, most importantly, analyze and understand large amounts of both experimental and simulated data are still needed (Bouchard et al., 2016). However, suggestions how to design workflows for electrophysiological data analysis (Denker and Grün, 2016) and how to structure, collect, and distribute metadata of neurophysiological data (Zehl et al., 2016) has already been proposed. Our example of replicability of spiking network models points at a bottleneck in reproducibility and replicability created by the lack of commonly adopted methodology and publicly available code for analysis of simulated data. Following the good practices in development of data-analysis methods, careful description of the methods in the article, and supplying the code with method implementation in addition to the model implementation are necessary steps to ensure model reproducibility and replicability.

Best practices for description of neuronal network models (Nordlie et al., 2009) and minimum information requirements for reproduction (Le Novère et al., 2005; Waltemath et al., 2011a) have been suggested. Moreover, many XML-based model and simulation representation formats, such as SBML (Hucka et al., 2003), CellML (Lloyd et al., 2004), NeuroML (Gleeson et al., 2010), SED-ML (Waltemath et al., 2011b), and LEMS (Cannon et al., 2014), have been developed. On the other hand, Jupyter Notebook (earlier known as IPython Notebook) could be a potential solution to enhance reproducibility and accessibility. In addition to giving all the details needed for model implementation, it is equally important to categorize the biological details of the models, such as neuron models, ion channels, pumps, receptors, signaling pathways, synapse models, in tabular format in publications (see e.g., Manninen et al., 2010, 2018a,b). If not possible to publish via journal due to page limitations, providing the implementation of the model and data-analysis method in a public and widely adopted simulation tool or programming language (e.g., Python) in some of the available model repositories, for example in ModelDB and BioModels database (Le Novère et al., 2006), is a must. Regardless of all the available formats and tools, many authors do not publish their models in a format that is easily exchangeable between different simulation platforms or provide their models at all in model repositories. All these issues should be carefully considered in the training of both experimental and computational neuroscientists (see also Akil et al., 2016).

Throughout this study, we evaluated, reimplemented and reproduced, and replicated a range of models incorporating different levels of biological details and modeling scales. The models and biological mechanisms included some relatively conventional examples but also some that only recently attracted larger attention within the computational community. As the experimental methodology and protocols advance and various neurobiological mechanisms become better understood, the new challenges for computational modeling emerge. Few examples are molecular diffusion in synaptic clefts, dendritic spines, and in other neural compartments (Chay et al., 2016; Hepburn et al., 2017), models of neurodevelopmental phenomena (Tetzlaff et al., 2010; van Ooyen, 2011), or wider range of plasticity mechanisms explored using conventional spiking networks (Miner and Triesch, 2016). Finally, one can aim beyond network modeling formalism and include extracellular space, for example similarly to the approach adopted in the Cortex3D simulation tool (Zubler and Douglas, 2009).

All the above suggestions would greatly improve the replicability and reproducibility of the published results, reduce the time needed to compare the model details and results, and support model reuse in complementary studies or in the studies extending the range of biophysical mechanisms and experimental data.

Author Contributions

TM: Designed the study, acquired and reimplemented the neuronal signal transduction and astrocyte models, simulated the models, evaluated and tabulated the results, and coordinated the production of the final version; JA: Designed the study, evaluated the simulation tools for growth and spiking neuronal networks, acquired and reran the spiking neuronal network models, and evaluated and tabulated the results; RH: Contributed to the design of the study, reimplemented, simulated, and evaluated an astrocyte model, contributed to the testing of the simulation tools for growth, and interpreted biological terminology and knowledge; HT: Contributed to the design of the study, contributed to the interpretation of network growth and activity studies, and interpreted biological terminology; M-LL: Conceived, funded, and designed the study, took part in the selection and evaluation of all models and tools, and interpreted the results in terms of replicability and reproducibility. All contributed to the drafting of the manuscript and approved the final version of the manuscript. All other work reported in the present publication, as motivation for the topic, is cited and is based on the work done previously in Computational Neuroscience Research Group in Tampere, Finland.

Funding

This project received funding from the European Union's Seventh Framework Programme (FP7) under grant agreement No. 604102 (HBP RUP), the European Union's Horizon 2020 research and innovation programme under grant agreement No. 720270 (HBP SGA1), and the Academy of Finland (decision No. 297893).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors wish to thank Tampere University of Technology Graduate School, Emil Aaltonen Foundation, The Finnish Concordia Fund, and Ulla Tuominen Foundation for support for RH and Tampere University of Technology Graduate School, Finnish Foundation for Technology Promotion, Finnish Cultural Foundation, Pirkanmaa Regional Fund of Finnish Cultural Foundation, and Finnish Brain Foundation sr. for HT.

References

Aćimović, J., Mäki-Marttunen, T., Havela, R., Teppola, H., and Linne, M.-L. (2011). Modeling of neuronal growth in vitro: comparison of simulation tools NETMORPH and CX3D. EURASIP J. Bioinf. Syst. Biol. 2011:616382. doi: 10.1155/2011/616382

PubMed Abstract | CrossRef Full Text | Google Scholar

Aho, T. (2003). Simulation Tool for Genetic Regulatory Networks. Master's thesis, Department of Information Technology, Tampere University of Technology, Tampere.

Ajay, S. M., and Bhalla, U. S. (2006). Synaptic plasticity in vitro and in silico: insights into an intracellular signaling maze. Physiology 21, 289–296. doi: 10.1152/physiol.00009.2006

PubMed Abstract | CrossRef Full Text | Google Scholar

Akil, H., Balice-Gordon, R., Cardozo, D. L., Koroshetz, W., Norris, S. M. P., Sherer, T., et al. (2016). Neuroscience training for the 21st century. Neuron 90, 917–926. doi: 10.1016/j.neuron.2016.05.030

PubMed Abstract | CrossRef Full Text | Google Scholar

Alves, R., Antunes, F., and Salvador, A. (2006). Tools for kinetic modeling of biochemical networks. Nat. Biotechnol. 24, 667–672. doi: 10.1038/nbt0606-667

PubMed Abstract | CrossRef Full Text | Google Scholar

Amunts, K., Ebell, C., Muller, J., Telefont, M., Knoll, A., and Lippert, T. (2016). The Human Brain Project: creating a European research infrastructure to decode the human brain. Neuron 92, 574–581. doi: 10.1016/j.neuron.2016.10.046

PubMed Abstract | CrossRef Full Text | Google Scholar

Andrews, S. S., Addy, N. J., Brent, R., and Arkin, A. P. (2010). Detailed simulations of cell biology with Smoldyn 2.1. PLoS Comput. Biol. 6:e1000705. doi: 10.1371/journal.pcbi.1000705

PubMed Abstract | CrossRef Full Text | Google Scholar

Baker, M. (2016). 1,500 scientists lift the lid on reproducibility. Nature 533, 452–454. doi: 10.1038/533452a

PubMed Abstract | CrossRef Full Text | Google Scholar

Baltz, T., Herzog, A., and Voigt, T. (2011). Slow oscillating population activity in developing cortical networks: models and experimental results. J. Neurophysiol. 106, 1500–1514. doi: 10.1152/jn.00889.2010

PubMed Abstract | CrossRef Full Text | Google Scholar

Bartocci, E., and Lió, P. (2016). Computational modeling, formal analysis, and tools for systems biology. PLoS Comput. Biol. 12:e1004591. doi: 10.1371/journal.pcbi.1004591

PubMed Abstract | CrossRef Full Text | Google Scholar

Benureau, F., and Rougier, N. (2018). Re-run, repeat, reproduce, reuse, replicate: transforming code into scientific contributions. Front. Neuroinform. 11:69. doi: 10.3389/fninf.2017.00069

PubMed Abstract | CrossRef Full Text | Google Scholar

Bergmann, F. T., and Sauro, H. M. (2008). Comparing simulation results of SBML capable simulators. Bioinformatics 24, 1963–1965. doi: 10.1093/bioinformatics/btn319

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhalla, U. S. (2001). “Modeling networks of signaling pathways,” in Computational Neuroscience: Realistic Modeling for Experimentalists, ed E. De Shutter (New York, NY: CRC Press LLC), 25–48.

Google Scholar

Bhalla, U. S. (2002). “Use of Kinetikit and GENESIS for modeling signaling pathways,” in Methods in Enzymology, Vol. 345, eds J. D. Hildebrandt and R. Iyengar (San Diego, CA: Academic Press), 3–23.

Google Scholar

Bhalla, U. S. (2009). “Molecules, networks, and memory,” in Systems Biology: The Challenge of Complexity, eds S. Nakanishi, R. Kageyama, and D. Watanabe (Tokyo: Springer), 151–158.

Google Scholar

Bhalla, U. S., and Iyengar, R. (1999). Emergent properties of networks of biological signaling pathways. Science 283, 381–387. doi: 10.1126/science.283.5400.381

PubMed Abstract | CrossRef Full Text | Google Scholar

Bi, G.-Q., and Rubin, J. (2005). Timing in synaptic plasticity: from detection to integration. Trends Neurosci. 28, 222–228. doi: 10.1016/j.tins.2005.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Blackwell, K. T. (2013). Approaches and tools for modeling signaling pathways and calcium dynamics in neurons. J. Neurosci. Methods 220, 131–140. doi: 10.1016/j.jneumeth.2013.05.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Bouchard, K. E., Aimone, J. B., Chun, M., Dean, T., Denker, M., Diesmann, M., et al. (2016). High-performance computing in neuroscience for data-driven discovery, integration, and dissemination. Neuron 92, 628–631. doi: 10.1016/j.neuron.2016.10.035

PubMed Abstract | CrossRef Full Text | Google Scholar

Bower, J. M., and Beeman, D. (1998). The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System, 2nd Edn. New York, NY: Telos; Springer-Verlag.

Brette, R., Rudolph, M., Carnevale, T., Hines, M., Beeman, D., Bower, J. M., et al. (2007). Simulation of networks of spiking neurons: a review of tools and strategies. J. Comput. Neurosci. 23, 349–398. doi: 10.1007/s10827-007-0038-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Brown, T. H., Kairiss, E. W., and Keenan, C. L. (1990). Hebbian synapses: biophysical mechanisms and algorithms. Annu. Rev. Neurosci. 13, 475–511. doi: 10.1146/annurev.ne.13.030190.002355

PubMed Abstract | CrossRef Full Text | Google Scholar

Cannon, R. C., Gleeson, P., Crook, S., Ganapathy, G., Marin, B., Piasini, E., et al. (2014). LEMS: a language for expressing complex biological models in concise and hierarchical form and its use in underpinning NeuroML 2. Front. Neuroinform. 8:79. doi: 10.3389/fninf.2014.00079

PubMed Abstract | CrossRef Full Text | Google Scholar

Carnevale, T., and Hines, M. (2006). The NEURON Book, 1st Edn. Cambridge, UK: Cambridge University Press.

Castellani, G. C., and Zironi, I. (2010). “Biophysics-based models of LTP/LTD,” in Hippocampal Microcircuits: A Computational Modelers Resource Book, eds V. Cutsuridis, B. Graham, S. Cobb, and I. Vida (New York, NY: Springer), 555–570.

Google Scholar

Chay, A., Zamparo, I., Koschinski, A., Zaccolo, M., and Blackwell, K. T. (2016). Control of βAR- and N-methyl-D-aspartate (NMDA) receptor-dependent cAMP dynamics in hippocampal neurons. PLoS Comput. Biol. 12:e1004735. doi: 10.1371/journal.pcbi.1004735

PubMed Abstract | CrossRef Full Text | Google Scholar

Cotterill, E., Charlesworth, P., Thomas, C. W., Paulsen, O., and Eglen, S. J. (2016). A comparison of computational methods for detecting bursts in neuronal spike trains and their application to human stem cell-derived neuronal networks. J. Neurophysiol. 116, 306–321. doi: 10.1152/jn.00093.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

Crook, S. M., Davison, A. P., and Plesser, H. E. (2013). “Learning from the past: approaches for reproducibility in computational neuroscience,” in 20 Years of Computational Neuroscience, ed J. M. Bower (New York, NY: Springer), 73–102.

Google Scholar

d'Alcantara, P., Schiffmann, S. N., and Swillens, S. (2003). Bidirectional synaptic plasticity as a consequence of interdependent Ca²⁺-controlled phosphorylation and dephosphorylation pathways. Eur. J. Neurosci. 17, 2521–2528. doi: 10.1046/j.1460-9568.2003.02693.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Davison, A., Brüderle, D., Eppler, J., Kremkow, J., Muller, E., Pecevski, D., et al. (2009). PyNN: a common interface for neuronal network simulators. Front. Neuroinform. 2:11. doi: 10.3389/neuro.11.011.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

De Pittà, M., Brunel, N., and Volterra, A. (2016). Astrocytes: orchestrating synaptic plasticity? Neuroscience 323, 43–61. doi: 10.1016/j.neuroscience.2015.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

De Pittà, M., Goldberg, M., Volman, V., Berry, H., and Ben-Jacob, E. (2009). Glutamate regulation of calcium and IP₃ oscillating and pulsating dynamics in astrocytes. J. Biol. Phys. 35, 383–411. doi: 10.1007/s10867-009-9155-y

PubMed Abstract | CrossRef Full Text | Google Scholar

De Pittà, M., Volman, V., Berry, H., Parpura, V., Volterra, A., and Ben-Jacob, E. (2012). Computational quest for understanding the role of astrocyte signaling in synaptic transmission and plasticity. Front. Comput. Neurosci. 6:98. doi: 10.3389/fncom.2012.00098

PubMed Abstract | CrossRef Full Text | Google Scholar

Delord, B., Berry, H., Guigon, E., and Genet, S. (2007). A new principle for information storage in an enzymatic pathway model. PLoS Comput. Biol. 3:e124. doi: 10.1371/journal.pcbi.0030124

PubMed Abstract | CrossRef Full Text | Google Scholar

Denker, M., and Grün, S. (2016). “Designing workflows for the reproducible analysis of electrophysiological data,” in Brain-Inspired Computing. BrainComp 2015. Lecture Notes in Computer Science, Vol. 10087, eds K. Amunts, L. Grandinetti, T. Lippert, and N. Petkov (Cham: Springer), 58–72.

Google Scholar

Di Garbo, A., Barbi, M., Chillemi, S., Alloisio, S., and Nobile, M. (2007). Calcium signalling in astrocytes and modulation of neural activity. Biosystems 89, 74–83. doi: 10.1016/j.biosystems.2006.05.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Djurfeldt, M., Hjorth, J., Eppler, J. M., Dudani, N., Helias, M., Potjans, T. C., et al. (2010). Run-time interoperability between neuronal network simulators based on the MUSIC framework. Neuroinformatics 8, 43–60. doi: 10.1007/s12021-010-9064-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Dobrzyński, M., Rodríguez, J. V., Kaandorp, J. A., and Blom, J. G. (2007). Computational methods for diffusion-influenced biochemical reactions. Bioinformatics 23, 1969–1977. doi: 10.1093/bioinformatics/btm278

PubMed Abstract | CrossRef Full Text | Google Scholar

Dupont, G., Lokenye, E. F. L., and Challiss, R. A. J. (2011). A model for Ca²⁺ oscillations stimulated by the type 5 metabotropic glutamate receptor: an unusual mechanism based on repetitive, reversible phosphorylation of the receptor. Biochimie 93, 2132–2138. doi: 10.1016/j.biochi.2011.09.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Eglen, S. J., Marwick, B., Halchenko, Y. O., Hanke, M., Sufi, S., Gleeson, P., et al. (2017). Toward standard practices for sharing computer code and programs in neuroscience. Nat. Neurosci. 20, 770–773. doi: 10.1038/nn.4550

PubMed Abstract | CrossRef Full Text | Google Scholar

Eppler, J. M., Pauli, R., Peyser, A., Ippen, T., Morrison, A., Senk, J., et al. (2015). NEST 2.8.0. Zenodo. doi: 10.5281/zenodo.32969

CrossRef Full Text | Google Scholar

Ermentrout, B. (2002). Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students, 1st Edn. Philadelphia, PA: Society for Industrial & Applied Mathematics (SIAM).

Google Scholar

Fellin, T., Ellenbogen, J. M., De Pittà, M., Ben-Jacob, E., and Halassa, M. M. (2012). Astrocyte regulation of sleep circuits: experimental and modeling perspectives. Front. Comput. Neurosci. 6:65. doi: 10.3389/fncom.2012.00065

PubMed Abstract | CrossRef Full Text | Google Scholar

French, D. A., and Gruenstein, E. I. (2006). An integrate-and-fire model for synchronized bursting in a network of cultured cortical neurons. J. Comput. Neurosci. 21, 227–241. doi: 10.1007/s10827-006-7815-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Gerkin, R. C., Bi, G.-Q., and Rubin, J. E. (2010). “A phenomenological calcium-based model of STDP,” in Hippocampal Microcircuits: A Computational Modelers Resource Book, eds V. Cutsuridis, B. Graham, S. Cobb, and I. Vida (New York, NY: Springer), 571–591.

Google Scholar

Gilbert, D., Fuß, H., Gu, X., Orton, R., Robinson, S., Vyshemirsky, V., et al. (2006). Computational methodologies for modelling, analysis and simulation of signalling networks. Brief. Bioinform. 7, 339–353. doi: 10.1093/bib/bbl043

PubMed Abstract | CrossRef Full Text | Google Scholar

Gillespie, D. T. (1976). A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 22, 403–434. doi: 10.1016/0021-9991(76)90041-3

CrossRef Full Text | Google Scholar

Gillespie, D. T. (1977). Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361. doi: 10.1021/j100540a008

CrossRef Full Text | Google Scholar

Gillespie, D. T. (2000). The chemical Langevin equation. J. Chem. Phys. 113, 297–306. doi: 10.1063/1.481811

CrossRef Full Text | Google Scholar

Gillespie, D. T. (2001). Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 115, 1716–1733. doi: 10.1063/1.1378322

CrossRef Full Text | Google Scholar

Gillespie, D. T. (2007). Stochastic simulation of chemical kinetics. Annu. Rev. Phys. Chem. 58, 35–55. doi: 10.1146/annurev.physchem.58.032806.104637

PubMed Abstract | CrossRef Full Text | Google Scholar

Giugliano, M., Darbon, P., Arsiero, M., Lüscher, H.-R., and Streit, J. (2004). Single-neuron discharge properties and network activity in dissociated cultures of neocortex. J. Neurophysiol. 92, 977–996. doi: 10.1152/jn.00067.2004

PubMed Abstract | CrossRef Full Text | Google Scholar

Gleeson, P., Crook, S., Cannon, R. C., Hines, M. L., Billings, G. O., Farinella, M., et al. (2010). NeuroML: a language for describing data driven models of neurons and networks with a high degree of biological detail. PLoS Comput. Biol. 6:e1000815. doi: 10.1371/journal.pcbi.1000815

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodman, D., and Brette, R. (2008). Brian: a simulator for spiking neural networks in Python. Front. Neuroinform. 2:5. doi: 10.3389/neuro.11.005.2008

PubMed Abstract | CrossRef Full Text | Google Scholar

Goodman, S. N., Fanelli, D., and Ioannidis, J. P. A. (2016). What does research reproducibility mean? Sci. Transl. Med. 8:341ps12. doi: 10.1126/scitranslmed.aaf5027

PubMed Abstract | CrossRef Full Text | Google Scholar

Graupner, M., and Brunel, N. (2010). Mechanisms of induction and maintenance of spike-timing dependent plasticity in biophysical synapse models. Front. Comput. Neurosci. 4:136. doi: 10.3389/fncom.2010.00136

PubMed Abstract | CrossRef Full Text | Google Scholar

Gritsun, T., le Feber, J., Stegenga, J., and Rutten, W. L. C. (2011). Experimental analysis and computational modeling of interburst intervals in spontaneous activity of cortical neuronal culture. Biol. Cybern. 105, 197–210. doi: 10.1007/s00422-011-0457-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Gritsun, T. A., Le Feber, J., Stegenga, J., and Rutten, W. L. C. (2010). Network bursts in cortical cultures are best simulated using pacemaker neurons and adaptive synapses. Biol. Cybern. 102, 293–310. doi: 10.1007/s00422-010-0366-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayer, A., and Bhalla, U. S. (2005). Molecular switches at the synapse emerge from receptor and kinase traffic. PLoS Comput. Biol. 1:e20. doi: 10.1371/journal.pcbi.0010020

PubMed Abstract | CrossRef Full Text | Google Scholar

Hellgren Kotaleski, J., and Blackwell, K. T. (2010). Modelling the molecular mechanisms of synaptic plasticity using systems biology approaches. Nat. Rev. Neurosci. 11, 239–251. doi: 10.1038/nrn2807

CrossRef Full Text | Google Scholar

Hepburn, I., Chen, W., Wils, S., and De Schutter, E. (2012). STEPS: efficient simulation of stochastic reaction-diffusion models in realistic morphologies. BMC Syst. Biol. 6:36. doi: 10.1186/1752-0509-6-36

PubMed Abstract | CrossRef Full Text | Google Scholar

Hepburn, I., Jain, A., Gangal, H., Yamamoto, Y., Tanaka-Yamamoto, K., and De Schutter, E. (2017). A model of induction of cerebellar long-term depression including RKIP inactivation of Raf and MEK. Front. Mol. Neurosci. 10:19. doi: 10.3389/fnmol.2017.00019

PubMed Abstract | CrossRef Full Text | Google Scholar

Hines, M. L., Morse, T., Migliore, M., Carnevale, N. T., and Shepherd, G. M. (2004). ModelDB: a database to support computational neuroscience. J. Comput. Neurosci 17, 7–11. doi: 10.1023/B:JCNS.0000023869.22017.2e

PubMed Abstract | CrossRef Full Text | Google Scholar

Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. doi: 10.1113/jphysiol.1952.sp004764

PubMed Abstract | CrossRef Full Text | Google Scholar

Holmes, W. R. (2005). “Calcium signaling in dendritic spines,” in Modeling in the Neurosciences: From Biological Systems to Neuromimetic Robotics, 2nd Edn, eds G. N. Reeke, R. R. Poznanski, K. A. Lindsay, J. R. Rosenberg, and O. Sporns (Boca Raton, FL: CRC Press), 25–60.

Google Scholar

Hoops, S., Sahle, S., Gauges, R., Lee, C., Pahle, J., Simus, N., et al. (2006). COPASI – a complex pathway simulator. Bioinformatics 22, 3067–3074. doi: 10.1093/bioinformatics/btl485

PubMed Abstract | CrossRef Full Text | Google Scholar

Hucka, M., Finney, A., Sauro, H. M., Bolouri, H., Doyle, J. C., Kitano, H., et al. (2003). The systems biology markup language (SBML): a medium for representation and exchange of biochemical network models. Bioinformatics 19, 524–531. doi: 10.1093/bioinformatics/btg015

PubMed Abstract | CrossRef Full Text | Google Scholar

Hudmon, A., and Schulman, H. (2002a). Neuronal Ca²⁺/calmodulin-dependent protein kinase II: the role of structure and autoregulation in cellular function. Annu. Rev. Biochem. 71, 473–510. doi: 10.1146/annurev.biochem.71.110601.135410

PubMed Abstract | CrossRef Full Text | Google Scholar

Hudmon, A., and Schulman, H. (2002b). Structure-function of the multifunctional Ca²⁺/calmodulin-dependent protein kinase II. Biochem. J. 364, 593–611. doi: 10.1042/BJ20020228

PubMed Abstract | CrossRef Full Text | Google Scholar

Ichikawa, M., Muramoto, K., Kobayashi, K., Kawahara, M., and Kuroda, Y. (1993). Formation and maturation of synapses in primary cultures of rat cerebral cortical cells: an electron microscopic study. Neurosci. Res. 16, 95–103. doi: 10.1016/0168-0102(93)90076-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Izhikevich, E. M. (2004). Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 15, 1063–1070. doi: 10.1109/TNN.2004.832719

PubMed Abstract | CrossRef Full Text | Google Scholar

Jolivet, R., Allaman, I., Pellerin, L., Magistretti, P. J., and Weber, B. (2010). Comment on recent modeling studies of astrocyte–neuron metabolic interactions. J. Cereb. Blood Flow Metab. 30, 1982–1986. doi: 10.1038/jcbfm.2010.132

PubMed Abstract | CrossRef Full Text | Google Scholar

Kerr, R. A., Bartol, T. M., Kaminsky, B., Dittrich, M., Chang, J.-C. J., Baden, S. B., et al. (2008). Fast Monte Carlo simulation methods for biological reaction-diffusion systems in solution and on surfaces. SIAM J. Sci. Comput. 30, 3126–3149. doi: 10.1137/070692017

PubMed Abstract | CrossRef Full Text | Google Scholar

Kim, M. S., Huang, T., Abel, T., and Blackwell, K. T. (2010). Temporal sensitivity of protein kinase A activation in late-phase long term potentiation. PLoS Comput. Biol. 6:e1000691. doi: 10.1371/journal.pcbi.1000691

PubMed Abstract | CrossRef Full Text | Google Scholar

Klipp, E., and Liebermeister, W. (2006). Mathematical modeling of intracellular signaling pathways. BMC Neurosci. 7(Suppl 1):S10. doi: 10.1186/1471-2202-7-S1-S10

PubMed Abstract | CrossRef Full Text | Google Scholar

Koene, R. A., Tijms, B., van Hees, P., Postma, F., de Ridder, A., Ramakers, G. J. A., et al. (2009). NETMORPH: a framework for the stochastic generation of large scale neuronal networks with realistic neuron morphologies. Neuroinformatics 7, 195–210. doi: 10.1007/s12021-009-9052-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Latham, P. E., Richmond, B. J., Nelson, P. G., and Nirenberg, S. (2000). Intrinsic dynamics in neuronal networks. I. Theory. J. Neurophysiol. 83, 808–827. doi: 10.1152/jn.2000.83.2.808

PubMed Abstract | CrossRef Full Text | Google Scholar

Lavrentovich, M., and Hemkin, S. (2008). A mathematical model of spontaneous calcium (II) oscillations in astrocytes. J. Theor. Biol. 251, 553–560. doi: 10.1016/j.jtbi.2007.12.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Le Novère, N., Bornstein, B., Broicher, A., Courtot, M., Donizelli, M., Dharuri, H., et al. (2006). BioModels Database: a free, centralized database of curated, published, quantitative kinetic models of biochemical and cellular systems. Nucleic Acids Res. 34, D689–D691. doi: 10.1093/nar/gkj092

PubMed Abstract | CrossRef Full Text | Google Scholar

Le Novère, N., Finney, A., Hucka, M., Bhalla, U. S., Campagne, F., Collado-Vides, J., et al. (2005). Minimum information requested in the annotation of biochemical models (MIRIAM). Nat. Biotechnol. 23, 1509–1515. doi: 10.1038/nbt1156

PubMed Abstract | CrossRef Full Text | Google Scholar

Lecca, P., Bagagiolo, F., and Scarpa, M. (2017). Hybrid deterministic/stochastic simulation of complex biochemical systems. Mol. BioSyst. 13, 2672–2686. doi: 10.1039/C7MB00426E

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemerle, C., Di Ventura, B., and Serrano, L. (2005). Space as the final frontier in stochastic simulations of biological systems. FEBS Lett. 579, 1789–1794. doi: 10.1016/j.febslet.2005.02.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Lindskog, M., Kim, M., Wikström, M. A., Blackwell, K. T., and Hellgren Kotaleski, J. (2006). Transient calcium and dopamine increase PKA activity and DARPP-32 phosphorylation. PLoS Comput. Biol. 2:e119. doi: 10.1371/journal.pcbi.0020119

PubMed Abstract | CrossRef Full Text | Google Scholar

Linne, M.-L., and Jalonen, T. O. (2014). Astrocyte–neuron interactions: from experimental research-based models to translational medicine. Prog. Mol. Biol. Transl. Sci. 123, 191–217. doi: 10.1016/B978-0-12-397897-4.00005-X

PubMed Abstract | CrossRef Full Text | Google Scholar

Lloyd, C. M., Halstead, M. D. B., and Nielsen, P. F. (2004). CellML: its future, present and past. Prog. Biophys. Mol. Biol. 85, 433–450. doi: 10.1016/j.pbiomolbio.2004.01.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Lonardoni, D., Amin, H., Di Marco, S., Maccione, A., Berdondini, L., and Nieus, T. (2017). Recurrently connected and localized neuronal communities initiate coordinated spontaneous activity in neuronal networks. PLoS Comput. Biol. 13:e1005672. doi: 10.1371/journal.pcbi.1005672

PubMed Abstract | CrossRef Full Text | Google Scholar

Lytton, W. W., and Hines, M. L. (2005). Independent variable time-step integration of individual neurons for network simulations. Neural Comput. 17, 903–921. doi: 10.1162/0899766053429453

PubMed Abstract | CrossRef Full Text | Google Scholar

Maheswaranathan, N., Ferrari, S., VanDongen, A., and Henriquez, C. (2012). Emergent bursting and synchrony in computer simulations of neuronal cultures. Front. Comput. Neurosci. 6:15. doi: 10.3389/fncom.2012.00015

PubMed Abstract | CrossRef Full Text | Google Scholar

Mäki-Marttunen, T., Aćimović, J., Ruohonen, K., and Linne, M.-L. (2013). Structure-dynamics relationships in bursting neuronal networks revealed using a prediction framework. PLoS ONE 8:e69373. doi: 10.1371/journal.pone.0069373

PubMed Abstract | CrossRef Full Text | Google Scholar

Mäki-Marttunen, T., Havela, R., Aćimović, J., Teppola, H., Ruohonen, K., and Linne, M.-L. (2010). “Modeling growth in neuronal cell cultures: network properties in different phases of growth studied using two growth simulators,” in Proceeding of the 7th International Workshop on Computational System Biology (WCSB 2010), eds M. Nykter, P. Ruusuvuori, C. Carlberg, and O. Yli-Harja (Luxemburg), 75–78.

Google Scholar

Mäkiraatikka, E., Manninen, T., Saarinen, A., Ylipää, A., Teppola, H., Hituri, K., et al. (2007). “Stochastic simulation tools for cellular signaling: survey, evaluation, and quantitative analysis,” in Proceedings of the 2nd Conference on Foundations of Systems Biology in Engineering (FOSBE 2007), eds F. Allgöwer and M. Reuss (Stuttgart), 171–176.

Google Scholar

Mandel, J. J., Fuß, H., Palfreyman, N. M., and Dubitzky, W. (2007). Modeling biochemical transformation processes and information processing with Narrator. BMC Bioinformatics 8:103. doi: 10.1186/1471-2105-8-103

PubMed Abstract | CrossRef Full Text | Google Scholar

Mangia, S., DiNuzzo, M., Giove, F., Carruthers, A., Simpson, I. A., and Vannucci, S. J. (2011). Response to ‘comment on recent modeling studies of astrocyte–neuron metabolic interactions’: much ado about nothing. J. Cereb. Blood Flow Metab. 31, 1346–1353. doi: 10.1038/jcbfm.2011.29

PubMed Abstract | CrossRef Full Text | Google Scholar

Manninen, T., Havela, R., and Linne, M.-L. (2017). Reproducibility and comparability of computational models for astrocyte calcium excitability. Front. Neuroinform. 11:11. doi: 10.3389/fninf.2017.00011

PubMed Abstract | CrossRef Full Text | Google Scholar

Manninen, T., Havela, R., and Linne, M.-L. (2018a). Computational models for calcium-mediated astrocyte functions. Front. Comput. Neurosci. 12:14. doi: 10.3389/fncom.2018.00014

PubMed Abstract | CrossRef Full Text | Google Scholar

Manninen, T., Havela, R., and Linne, M.-L. (2018b). “Computational models of astrocytes and astrocyte-neuron interactions: characterization, reproducibility, and future perspectives,” in Mathematical Methods in Modeling of Neuron-Glia Interactions, eds M. De Pittà and H. Berry (Springer), 2018.

Manninen, T., Hituri, K., Hellgren Kotaleski, J., Blackwell, K. T., and Linne, M.-L. (2010). Postsynaptic signal transduction models for long-term potentiation and depression. Front. Comput. Neurosci. 4:152. doi: 10.3389/fncom.2010.00152

PubMed Abstract | CrossRef Full Text | Google Scholar

Manninen, T., Hituri, K., Toivari, E., and Linne, M.-L. (2011). Modeling signal transduction leading to synaptic plasticity: evaluation and comparison of five models. EURASIP J. Bioinf. Syst. Biol. 2011:797250. doi: 10.1155/2011/797250

PubMed Abstract | CrossRef Full Text | Google Scholar

Manninen, T., and Linne, M.-L. (2008). “Stochastic kinetic simulations of activity-dependent plastic modifications in neurons,” in Proceedings of the 5th International Workshop on Computational Systems Biology (WCSB 2008), eds M. Ahdesmäki, K. Strimmer, N. Radde, J. Rahnenfuhrer, K. Klemm, H. Lähdesmäki, and O. Yli-Harja (Leipzig), 101–104.

Google Scholar

Manninen, T., Linne, M.-L., and Ruohonen, K. (2006a). Developing Itô stochastic differential equation models for neuronal signal transduction pathways. Comput. Biol. Chem. 30, 280–291. doi: 10.1016/j.compbiolchem.2006.04.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Manninen, T., Linne, M.-L., and Ruohonen, K. (2006b). A novel approach to model neuronal signal transduction using stochastic differential equations. Neurocomputing 69, 1066–1069. doi: 10.1016/j.neucom.2005.12.047

CrossRef Full Text | Google Scholar

Manninen, T., Mäkiraatikka, E., Ylipää, A., Pettinen, A., Leinonen, K., and Linne, M.-L. (2006c). “Discrete stochastic simulation of cell signaling: comparison of computational tools,” in Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC 2006) (New York, NY), 2013–2016.

Google Scholar

Masquelier, T., and Deco, G. (2013). Network bursting dynamics in excitatory cortical neuron cultures results from the combination of different adaptive mechanisms. PLoS ONE 8:e75824. doi: 10.1371/journal.pone.0075824

PubMed Abstract | CrossRef Full Text | Google Scholar

McDougal, R. A., Bulanova, A. S., and Lytton, W. W. (2016). Reproducibility in computational neuroscience models and simulations. IEEE Trans. Biomed. Eng. 63, 2021–2035. doi: 10.1109/TBME.2016.2539602

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendes, P. (1993). GEPASI: a software package for modelling the dynamics, steady states and control of biochemical and other systems. Comput. Appl. Biosci. 9, 563–571. doi: 10.1093/bioinformatics/9.5.563

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendes, P. (1997). Biochemistry by numbers: simulation of biochemical pathways with Gepasi 3. Trends Biochem. Sci. 22, 361–363. doi: 10.1016/S0968-0004(97)01103-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Mendes, P., and Kell, D. B. (1998). Non-linear optimization of biochemical pathways: applications to metabolic engineering and parameter estimation. Bioinformatics 14, 869–883. doi: 10.1093/bioinformatics/14.10.869

PubMed Abstract | CrossRef Full Text | Google Scholar

Migliore, M., Morse, T. M., Davison, A. P., Marenco, L., Shepherd, G. M., and Hines, M. L. (2003). ModelDB: making models publicly accessible to support computational neuroscience. Neuroinformatics 1, 135–139. doi: 10.1385/NI:1:1:135

PubMed Abstract | CrossRef Full Text | Google Scholar

Min, R., Santello, M., and Nevian, T. (2012). The computational power of astrocyte mediated synaptic plasticity. Front. Comput. Neurosci. 6:93. doi: 10.3389/fncom.2012.00093

PubMed Abstract | CrossRef Full Text | Google Scholar

Miner, D., and Triesch, J. (2016). Plasticity-driven self-organization under topological constraints accounts for non-random features of cortical synaptic wiring. PLoS Comput. Biol. 12:e1004759. doi: 10.1371/journal.pcbi.1004759

PubMed Abstract | CrossRef Full Text | Google Scholar

Morrison, A., Diesmann, M., and Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike timing. Biol. Cybern. 98, 459–478. doi: 10.1007/s00422-008-0233-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Munafò, M. R., Nosek, B. A., Bishop, D. V. M., Button, K. S., Chambers, C. D., du Sert, N. P., et al. (2017). A manifesto for reproducible science. Nat. Hum. Behav. 1:0021. doi: 10.1038/s41562-016-0021

CrossRef Full Text | Google Scholar

Nadkarni, S., and Jung, P. (2003). Spontaneous oscillations of dressed neurons: a new mechanism for epilepsy? Phys. Rev. Lett. 91:268101. doi: 10.1103/PhysRevLett.91.268101

PubMed Abstract | CrossRef Full Text | Google Scholar

Nakano, T., Doi, T., Yoshimoto, J., and Doya, K. (2010). A kinetic model of dopamine- and calcium-dependent striatal synaptic plasticity. PLoS Comput. Biol. 6:e1000670. doi: 10.1371/journal.pcbi.1000670

PubMed Abstract | CrossRef Full Text | Google Scholar

Neher, E. (1998). Usefulness and limitations of linear approximations to the understanding of Ca²⁺ signals. Cell Calcium 24, 345–357. doi: 10.1016/S0143-4160(98)90058-6

CrossRef Full Text | Google Scholar

Nishi, R., Castañeda, E., Davis, G. W., Fenton, A. A., Hofmann, H. A., King, J., et al. (2016). The global challenge in neuroscience education and training: the MBL perspective. Neuron 92, 632–636. doi: 10.1016/j.neuron.2016.10.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Nordlie, E., Gewaltig, M.-O., and Plesser, H. E. (2009). Towards reproducible descriptions of neuronal network models. PLoS Comput. Biol. 5:e1000456. doi: 10.1371/journal.pcbi.1000456

PubMed Abstract | CrossRef Full Text | Google Scholar

Ogasawara, H., Doi, T., and Kawato, M. (2008). Systems biology perspectives on cerebellar long-term depression. Neurosignals 16, 300–317. doi: 10.1159/000123040

PubMed Abstract | CrossRef Full Text | Google Scholar

Ogasawara, H., and Kawato, M. (2009). “Computational models of cerebellar long-term memory,” in Systems Biology: The Challenge of Complexity, 1st Edn, eds S. Nakanishi, R. Kageyama, and D. Watanabe (Tokyo: Springer), 169–182.

PubMed Abstract | Google Scholar

Oliveira, R. F., Terrin, A., Di Benedetto, G., Cannon, R. C., Koh, W., Kim, M., et al. (2010). The role of type 4 phosphodiesterases in generating microdomains of cAMP: large scale stochastic simulations. PLoS ONE 5:e11725. doi: 10.1371/journal.pone.0011725

PubMed Abstract | CrossRef Full Text | Google Scholar

Olivier, B. G., Swat, M. J., and Moné, M. J. (2016). “Modeling and simulation tools: from systems biology to systems medicine,” in Systems Medicine. Methods in Molecular Biology, Vol. 1386, eds U. Schmitz and O. Wolkenhauer (New York, NY: Humana Press), 441–463.

Google Scholar

Pettinen, A., Aho, T., Smolander, O.-P., Manninen, T., Saarinen, A., Taattola, K.-L., et al. (2005). Simulation tools for biochemical networks: evaluation of performance and usability. Bioinformatics 21, 357–363. doi: 10.1093/bioinformatics/bti018

PubMed Abstract | CrossRef Full Text | Google Scholar

Plesser, H. E. (2018). Reproducibility vs. replicability: a brief history of a confused terminology. Front. Neuroinform. 11:76. doi: 10.3389/fninf.2017.00076

PubMed Abstract | CrossRef Full Text | Google Scholar

Ramsey, S., Orrell, D., and Bolouri, H. (2005). Dizzy: stochastic simulation of large-scale genetic regulatory networks. J. Bioinform. Comput. Biol. 3, 415–436. doi: 10.1142/S0219720005001132

CrossRef Full Text | Google Scholar

Ray, S., Deshpande, R., Dudani, N., and Bhalla, U. S. (2008). A general biological simulator: the multiscale object oriented simulation environment, MOOSE. BMC Neurosci. 9:P93. doi: 10.1186/1471-2202-9-S1-P93

CrossRef Full Text | Google Scholar

Riera, J., Hatanaka, R., Ozaki, T., and Kawashima, R. (2011a). Modeling the spontaneous Ca²⁺ oscillations in astrocytes: inconsistencies and usefulness. J. Integr. Neurosci. 10, 439–473. doi: 10.1142/S0219635211002877

PubMed Abstract | CrossRef Full Text | Google Scholar

Riera, J., Hatanaka, R., Uchida, T., Ozaki, T., and Kawashima, R. (2011b). Quantifying the uncertainty of spontaneous Ca²⁺ oscillations in astrocytes: particulars of Alzheimer's disease. Biophys. J. 101, 554–564. doi: 10.1016/j.bpj.2011.06.041

PubMed Abstract | CrossRef Full Text | Google Scholar

Robinson, H. P., Kawahara, M., Jimbo, Y., Torimitsu, K., Kuroda, Y., and Kawana, A. (1993). Periodic synchronized bursting and intracellular calcium transients elicited by low magnesium in cultured cortical neurons. J. Neurophysiol. 70, 1606–1616. doi: 10.1152/jn.1993.70.4.1606

PubMed Abstract | CrossRef Full Text | Google Scholar

Rotter, S., and Diesmann, M. (1999). Exact digital simulation of time-invariant linear systems with applications to neuronal modeling. Biol. Cybern. 81, 381–402. doi: 10.1007/s004220050570

PubMed Abstract | CrossRef Full Text | Google Scholar

Rougier, N. P., Hinsen, K., Alexandre, F., Arildsen, T., Barba, L. A., Benureau, F. C. Y., et al. (2017). Sustainable computational science: the ReScience initiative. PeerJ Comput. Sci. 3:e142. doi: 10.7717/peerj-cs.142

CrossRef Full Text | Google Scholar

Salis, H., Sotiropoulos, V., and Kaznessis, Y. N. (2006). Multiscale Hy3S: hybrid stochastic simulation for supercomputers. BMC Bioinformatics 7:93. doi: 10.1186/1471-2105-7-93

PubMed Abstract | CrossRef Full Text | Google Scholar

Sauro, H. M. (2000). “JARNAC: a system for interactive metabolic analysis,” in Animating the Cellular Map: Proceegings of the 9th International Meeting on BioThermoKinetics (Stellenbosch: Stellenbosch University Press), 221–228.

Google Scholar

Sauro, H. M. (2001). JDesigner: A Simple Biochemical Network Designer. Technical report.

Schmidt, H., and Jirstrand, M. (2006). Systems Biology Toolbox for MATLAB: a computational platform for research in systems biology. Bioinformatics 22, 514–515. doi: 10.1093/bioinformatics/bti799

PubMed Abstract | CrossRef Full Text | Google Scholar

Schöneberg, J., Ullrich, A., and Noé, F. (2014). Simulation tools for particle-based reaction-diffusion dynamics in continuous space. BMC Biophys. 7:11. doi: 10.1186/s13628-014-0011-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Shouval, H. Z., Wang, S. S. H., and Wittenberg, G. M. (2010). Spike timing dependent plasticity: a consequence of more fundamental learning rules. Front. Comput. Neurosci. 4:19. doi: 10.3389/fncom.2010.00019

PubMed Abstract | CrossRef Full Text | Google Scholar

Silchenko, A. N., and Tass, P. A. (2008). Computational modeling of paroxysmal depolarization shifts in neurons induced by the glutamate release from astrocytes. Biol. Cybern. 98, 61–74. doi: 10.1007/s00422-007-0196-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Sivakumaran, S., Hariharaputran, S., Mishra, J., and Bhalla, U. S. (2003). The Database of Quantitative Cellular Signaling: management and analysis of chemical kinetic models of signaling networks. Bioinformatics 19, 408–415. doi: 10.1093/bioinformatics/btf860

PubMed Abstract | CrossRef Full Text | Google Scholar

Sterratt, D., Graham, B., Gillies, A., and Willshaw, D. (2011). Principles in Computational Modeling in Neuroscience. New York, NY: Cambridge University Press.

Google Scholar

Stiles, J. R., and Bartol, T. M. (2001). “Monte Carlo methods for simulating realistic synaptic microphysiology using MCell,” in Computational Neuroscience: Realistic Modeling for Experimentalists, ed E. De Schutter (Boca Raton, FL: CRC Press), 87–127.

Google Scholar

Stimberg, M., Goodman, D. F. M., Benichoux, V., and Brette, R. (2014). Equation-oriented specification of neural models for simulations. Front. Neuroinform. 8:6. doi: 10.3389/fninf.2014.00006

PubMed Abstract | CrossRef Full Text | Google Scholar

Strömbäck, L., Jakoniene, V., Tan, H., and Lambrix, P. (2006). Representing, storing and accessing molecular interaction data: a review of models and tools. Brief. Bioinform. 7, 331–338. doi: 10.1093/bib/bbl039

PubMed Abstract | CrossRef Full Text | Google Scholar

Tanaka, K., and Augustine, G. J. (2009). “Systems biology meets single-cell physiology: role of a positive-feedback signal transduction network in cerebellar long-term synaptic depression,” in Systems Biology: The Challenge of Complexity, 1st Edn, eds S. Nakanishi, R. Kageyama, and D. Watanabe (Tokyo: Springer), 159–168.

Google Scholar

Teppola, H., Okujeni, S., Linne, M.-L., and Egert, U. (2011). “AMPA, NMDA and GABA_A receptor mediated network burst dynamics in cortical cultures in vitro,” in Proceedings of the 8th International Workshop on Computational Systems Biology (WCSB 2011), eds H. Koeppl, J. Aćimović, J. Kesseli, T. Mäki-Marttunen, A. Larjo, and O. Yli-Harja (Zurich), 181–184.

Google Scholar

Tetzlaff, C., Okujeni, S., Egert, U., Wörgötter, F., and Butz, M. (2010). Self-organized criticality in developing neuronal networks. PLoS Comput. Biol. 6:e1001013. doi: 10.1371/journal.pcbi.1001013

PubMed Abstract | CrossRef Full Text | Google Scholar

Tewari, S., and Parpura, V. (2014). Data and model tango to aid the understanding of astrocyte-neuron signaling. Front. Comput. Neurosci. 8:3. doi: 10.3389/fncom.2014.00003

PubMed Abstract | CrossRef Full Text | Google Scholar

Topalidou, M., Leblois, A., Boraud, T., and Rougier, N. P. (2015). A long journey into reproducible computational neuroscience. Front. Comput. Neurosci. 9:30. doi: 10.3389/fncom.2015.00030

PubMed Abstract | CrossRef Full Text | Google Scholar

Urakubo, H., Honda, M., Tanaka, K., and Kuroda, S. (2009). Experimental and computational aspects of signaling mechanisms of spike-timing-dependent plasticity. HFSP J. 3, 240–254. doi: 10.2976/1.3137602

PubMed Abstract | CrossRef Full Text | Google Scholar

van Ooyen, A. (2011). Using theoretical models to analyse neural development. Nat. Rev. Neurosci. 12, 311–326. doi: 10.1038/nrn3031

PubMed Abstract | CrossRef Full Text | Google Scholar

van Pelt, J., and Uylings, H. B. M. (2003). Growth functions in dendritic outgrowth. Brain Mind 4, 51–65. doi: 10.1023/A:1024160131897

CrossRef Full Text | Google Scholar

Volman, V., Bazhenov, M., and Sejnowski, T. J. (2012). Computational models of neuron-astrocyte interaction in epilepsy. Front. Comput. Neurosci. 6:58. doi: 10.3389/fncom.2012.00058

PubMed Abstract | CrossRef Full Text | Google Scholar

Wade, J., McDaid, L., Harkin, J., Crunelli, V., and Kelso, S. (2012). Self-repair in a bidirectionally coupled astrocyte-neuron (AN) system based on retrograde signaling. Front. Comput. Neurosci. 6:76. doi: 10.3389/fncom.2012.00076

PubMed Abstract | CrossRef Full Text | Google Scholar

Wade, J., McDaid, L., Harkin, J., Crunelli, V., and Kelso, S. (2013). Biophysically based computational models of astrocyte ~ neuron coupling and their functional significance. Front. Comput. Neurosci. 7:44. doi: 10.3389/fncom.2013.00044

PubMed Abstract | CrossRef Full Text

Wade, J. J., McDaid, L. J., Harkin, J., Crunelli, V., and Kelso, J. A. S. (2011). Bidirectional coupling between astrocytes and neurons mediates learning and dynamic coordination in the brain: a multiple modeling approach. PLoS ONE 6:e29445. doi: 10.1371/journal.pone.0029445

PubMed Abstract | CrossRef Full Text | Google Scholar

Waltemath, D., Adams, R., Beard, D. A., Bergmann, F. T., Bhalla, U. S., Britten, R., et al. (2011a). Minimum information about a simulation experiment (MIASE). PLoS Comput. Biol. 7:e1001122. doi: 10.1371/journal.pcbi.1001122

PubMed Abstract | CrossRef Full Text | Google Scholar

Waltemath, D., Adams, R., Bergmann, F. T., Hucka, M., Kolpakov, F., Miller, A. K., et al. (2011b). Reproducible computational biology experiments with SED-ML - the simulation experiment description markup language. BMC Syst. Biol. 5:198. doi: 10.1186/1752-0509-5-198

PubMed Abstract | CrossRef Full Text | Google Scholar

Wierling, C., Herwig, R., and Lehrach, H. (2007). Resources, standards and tools for systems biology. Brief. Funct. Genomic. Proteomic. 6, 240–251. doi: 10.1093/bfgp/elm027

PubMed Abstract | CrossRef Full Text | Google Scholar

Wils, S., and De Schutter, E. (2009). STEPS: modeling and simulating complex reaction-diffusion systems with Python. Front. Neuroinform. 3:15. doi: 10.3389/neuro.11.015.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Wilson, M. A., Bhalla, U. S., Uhley, J. D., and Bower, J. M. (1989). “GENESIS: a system for simulating neural networks,” in Advances in Neural Information Processing Systems, ed D. S. Touretzky (San Francisco, CA: Morgan Kaufmann Publishers Inc.), 485–492.

Google Scholar

Wörgötter, F., and Porr, B. (2005). Temporal sequence learning, prediction, and control: a review of different models and their relation to biological mechanisms. Neural Comput. 17, 245–319. doi: 10.1162/0899766053011555

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamamoto, H., Kubota, S., Chida, Y., Morita, M., Moriya, S., Akima, H., et al. (2016). Size-dependent regulation of synchronized activity in living neuronal networks. Phys. Rev. E 94:012407. doi: 10.1103/PhysRevE.94.012407

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeung, A. W. K. (2017). Do neuroscience journals accept replications? A survey of literature. Front. Hum. Neurosci. 11:468. doi: 10.3389/fnhum.2017.00468

PubMed Abstract | CrossRef Full Text | Google Scholar

Zachariou, M., Alexander, S. P. H., Coombes, S., and Christodoulou, C. (2013). A biophysical model of endocannabinoid-mediated short term depression in hippocampal inhibition. PLoS ONE 8:e58926. doi: 10.1371/journal.pone.0058926

PubMed Abstract | CrossRef Full Text | Google Scholar

Zehl, L., Jaillet, F., Stoewer, A., Grewe, J., Sobolev, A., Wachtler, T., et al. (2016). Handling metadata in a neurophysiology laboratory. Front. Neuroinform. 10:26. doi: 10.3389/fninf.2016.00026

PubMed Abstract | CrossRef Full Text | Google Scholar

Zou, Q., and Destexhe, A. (2007). Kinetic models of spike-timing dependent plasticity and their functional consequences in detecting correlations. Biol. Cybern. 97, 81–97. doi: 10.1007/s00422-007-0155-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Zubler, F., and Douglas, R. (2009). A framework for modeling the growth and development of neurons and networks. Front. Comput. Neurosci. 3:25. doi: 10.3389/neuro.10.025.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

Zubler, F., Hauri, A., Pfister, S., Bauer, R., Anderson, J. C., Whatley, A. M., et al. (2013). Simulating cortical development as a self constructing process: a novel multi-scale approach combining molecular and physical aspects. PLoS Comput. Biol. 9:e1003173. doi: 10.1371/journal.pcbi.1003173

PubMed Abstract | CrossRef Full Text | Google Scholar

Zubler, F., Hauri, A., Pfister, S., Whatley, A., Cook, M., and Douglas, R. (2011). An instruction language for self-construction in the context of neural networks. Front. Comput. Neurosci. 5:57. doi: 10.3389/fncom.2011.00057

PubMed Abstract | CrossRef Full Text | Google Scholar