- 1Research and Development Service, Veterans Affairs Greater Los Angeles Healthcare System, Los Angeles, CA, USA
- 2Complex Biological Systems Alliance, North Andover, MA, USA
Grover's quantum (search) algorithm exploits principles of quantum information theory and computation to surpass the strong Church–Turing limit governing classical computers. The algorithm initializes a search field into superposed N (eigen)states to later execute nonclassical “subroutines” involving unitary phase shifts of measured states and to produce root-rate or quadratic gain in the algorithmic time (O(N1/2)) needed to find some “target” solution m. Akin to this fast technological search algorithm, single eukaryotic cells, such as differentiated neurons, perform natural quadratic speed-up in the search for appropriate store-operated Ca2+ response regulation of, among other processes, protein and lipid biosynthesis, cell energetics, stress responses, cell fate and death, synaptic plasticity, and immunoprotection. Such speed-up in cellular decision making results from spatiotemporal dynamics of networked intracellular Ca2+-induced Ca2+ release and the search (or signaling) velocity of Ca2+ wave propagation. As chemical processes, such as the duration of Ca2+ mobilization, become rate-limiting over interstore distances, Ca2+ waves quadratically decrease interstore-travel time from slow saltatory to fast continuous gradients proportional to the square-root of the classical Ca2+ diffusion coefficient, D1/2, matching the computing efficiency of Grover's quantum algorithm. In this Hypothesis and Theory article, I elaborate on these traits using a fire-diffuse-fire model of store-operated cytosolic Ca2+ signaling valid for glutamatergic neurons. Salient model features corresponding to Grover's quantum algorithm are parameterized to meet requirements for the Oracle Hadamard transform and Grover's iteration. A neuronal version of Grover's quantum algorithm figures to benefit signal coincidence detection and integration, bidirectional synaptic plasticity, and other vital cell functions by rapidly selecting, ordering, and/or counting optional response regulation choices.
Introduction
Modern analog, digital, and quantum descriptions of phylogenetically diverse cell functions (e.g., Monod and Jacob, 1961; McAdams and Shapiro, 1995; McAdams and Arkin, 2000) date to Twentieth-century revelations in computational and information sciences (e.g., Szilárd, 1929; Turing, 1936; Shannon, 1938, 1948a,b; Landauer, 1961; Feynman, 1982; Deutsch, 1985). Continued advances in systems biology, synthetic biology, and micro- and nanobiotechnology increasingly drive states-of-knowledge and -art in computational cell biology toward trends in logic gate, circuit, and algorithm designs (e.g., Ehrenfeucht et al., 2003; Amos, 2006; Baumgardner et al., 2009; Friedland et al., 2009; Adamatzky, 2010; Clark, 2010a,b,c,d, 2011, 2012b, 2013a; Norris et al., 2011; Karafyllidis, 2012; Mehta and Schwab, 2012; Daniel et al., 2013; Goñi-Moreno et al., 2013; Ji et al., 2013), especially for “programmable” group and solitary cellular decisions mediated by genetic, epigenetic, and somatic regulatory networks. Unsurprisingly, given their preeminent status as computational units (cf. Koch and Segev, 2000; Grillner, 2006), single neurons are still favored models for bioinspired smart technologies (e.g., Liu et al., 2013). Yet, despite technological interests in neuronal information processing attributes, serious application of quantum computational approaches toward study of adaptive cybernetic-like neuron behavior and physiology remains disappointingly slow, except as it may broadly relate to more-or-less controversial debates over the statistical mechanics nature of consciousness, decision making, and other psychological states and functions of humans and animals (cf. Beck and Eccles, 1992; Hameroff, 1994, 2012; Tegmark, 2000; Schwartz et al., 2005; Khrennikov, 2009; Pothos and Busemeyer, 2013a,b). The strange properties of quantum mechanics, such as superposition, entanglement, interference, and tunneling (Box 1), can be harnessed to enhance the information storage capacity, processing speed, and fault tolerance of man-made computational systems (cf. Nielsen and Chuang, 2000). Over recent decades, quantum information theorists have steadily identified and adapted quantum computational constructs believed to outperform the classical universal Turing machine (Feynman, 1982; Deutsch, 1985), supported by the strong Church–Turing thesis to be the upper limit for powerful computational devices obeying classical information theory and physicochemical laws. Actual physical quantum computers are only now moving out of proof-of-concept stage due to gradual progress in innovating suitable, if not optimal, device architectures, such as optical lattices, ion traps, nuclear magnetic resonators, quantum dots, and other technologies (e.g., Vandersypen et al., 2001; DiCarlo et al., 2009; Politi et al., 2009; Johnson et al., 2011). Nonetheless, algorithms built from quantum gates and circuits offer exciting practical, though often intuitively difficult, ways for obtaining performance characteristics better than those exhibited by classical processors. For example, several general classes of quantum algorithms based on Shor's quantum Fourier transform (Shor, 1994), the Deutsch–Jozsa algorithm, and Grover's quantum algorithm (Grover, 1996) are known. Through a series of quantum logic gates, Shor's quantum Fourier transform enables a fast two-register eigenvalue phase-estimation procedure to be executed on eigenstates of a unitary operator put into quantum superposition. Phase-estimation subroutines, in turn, serve as modules for other algorithms that exponentially decrease the number of operations required to solve important problems, such as related order-finding and hidden-subgroup problems, judged intractable with classical computers. Alternately, Grover's quantum algorithm, also termed Grover's quantum search algorithm, the quantum search algorithm, or the fast search algorithm, reaches only root-rate or quadratic operating improvements when compared to classical algorithms searching or counting elements of unstructured databases. This single-register algorithm initializes the search field containing target solutions into a uniform superposition state via a quantum transformation. A quantum subroutine called the Grover's operator or iteration then conditionally shifts or rotates the phase of certain computational bases until search solutions become found.
Box 1. Glossary of terminology.
Bell Basis States or Einstein–Podolsky–Rosen Pairs
Named respectively after John Bell and Albert Einstein, Nathan Rosen, and Boris Podolsky, these four orthonormal quantum states, spanning the two-qubit state space, form an essential computational basis for many fundamentally useful applications of quantum information theory. The states or pairs are: |ψ〉00 = (|00〉 + |11〉)/21/2, |ψ〉01 = (|01〉 + |10〉)/21/2, |ψ〉10 = (|00〉 − |11〉)/21/2, |ψ〉11 = (|01〉 − |10〉)/21/2. Quantum entanglement between the two qubits of a state permits secure cryptographic protocols, such as quantum teleportation, and compressed information encoding and storage, such as superdense coding and quantum memory.
Church–Turing Limit
Upper computational bound of efficiency for classical computers independently determined by Alonzo Church and Alan Turing. The Church–Turing limit emerges from the Church–Turing thesis or conjecture, which equates functions computable on a Turing machine with those computable by an algorithm. The strong limit is believed to subtend allowable complexity of computations performed by quantum computers, as captured in David Deutsch's rigorous conceptualization of universal quantum computers.
Eigenstates, Eigenvalues, and Eigenspaces
An eigenstate or eigenvector, |v〉, is a nonzero state in a state space operated on by a linear function L, so that L|v〉 = ω|v〉 with complex eigenvalue ω. Eigenstates and eigenvalues are ascertained from the characteristic function, c(λ) = det|L − λI|, where det is the determinant function. The eigenspace of ω, a subset of the state space on which L acts, is the set of eigenstates with the eigenvalue ω.
Entropic Uncertainty Principle
Information or entropy principle first derived by Iwo Bialynicki-Birula and Jerzy Mycielski and by David Deutsch from Werner Heisenberg's uncertainty principle. The principle is formally expressed in the strong condition as H(Q) + H(R) ≥ 2 log2[1/f(Q, R)], where H(Q) and H(R) are the Shannon entropies of respective spectrally decomposed measurements Q and R of quantum state |ψ〉 with probability distributions p(q) and p(r) and maximum fidelity or inner product f(Q, R) = maxq,r|〈q|r〉| between eigenvectors |q〉 and |r〉. As with Heisenberg's version involving the standard deviation of observables, the entropic uncertainty principle places an upper bound on attainable knowledge about quantum systems.
Hadamard Transformation
An important step for quantum parallel computing, the Hadamard transformation applies the Hadamard gate n times to n input qubits to initialize the data register of a quantum information system into superposition, so that multiple values of an index integer x can be simultaneously analyzed by a single function f. Common notation for the Hadamard transform is H⊗n.
Hermitian Operator
A linear operator, also known as a self-adjoint operator, imposed on a vector space V. For a Hermitian operator L, there is a unique linear operator L† acting on V, so that an adjoint or conjugate vector |v〉† exists for every |v〉 in V. That is, L = L†, |v〉 = |v〉†, and LL† = L†L when L is normal.
Landauer's Principle
Principle postulated by Rolf Landauer to define the relationship between energy and computation. Landauer improved earlier ideas of Leó Szilárd, John von Neumann, and other theorists to concretize the minimum amount of energy/information consumed during irreversible operations. Although Landauer's principle applies generally to energy/information dissipated as heat from work, it is usually placed into the context of memory erasure. For example, for a biological or technological computer with exhausted finite memory capacity, it is necessary to erase information for further computations. Landauer's principle states at least kB Tln2 of energy, where kB is Boltzmann's constant and T is ambient temperature in degrees Kelvin, must be transferred to the environment for erasure of one bit of information. The corresponding entropy rendering of Landauer's principle may be written without variable T.
Quantum Gates and Circuits
Logic gates and circuits constructed to perform operations based on quantum mechanics and information theory. Popular unitary single-qubit gates in matrix form include, for instance, the quantum Identity gate, the quantum NOT or Pauli , Pauli , and quantum Flip or Pauli gates, the Hadamard gate, and the Phase gate. These and other gates may be assembled into quantum circuits, such as multiple-qubit controlled-NOT, controlled-Phase, controlled-Swap or Fredkin, and Toffoli gates, also used to transform input qubits. The above single-qubit gates establish with other quantum gates a discrete subset of logical primitives (i.e., gates and/or circuits) capable of unitary transformation and of emulating any other transformation to approximate computational universality.
Quantum Mechanical Properties
Statistical wave-particle features of quantum mechanical systems, such as quantum superposition, entanglement, interference, and tunneling, not observed for deterministic classical Newtonian physical or Shannon informational systems. Quantum superposition describes the linear combination or addition of state or vector solutions to Schrödinger's wave equation (or other quantum state equation permutations). When superposed states are indistinguishable, they are said to be entangled. Quantum interference is the disruption of state or vector (e.g., a wave or particle) spacetime trajectories. And quantum tunneling is the transition of one state to another without surmounting classical energy barriers required for transformation in classical physics. Such probabilistic effects are useful for development of information technologies and additional purposes.
Quantum Networks
Technological and biological networks whose connectivity tends to obey either Bose-Einstein or Fermi-Dirac quantum statistics rather than classical Maxwell-Boltzmann statistics. The strength of each network node is described as a separate fitness or energy level and nodal links take on the identity of particle states functioning under associative-like preferential attachment rules. In such cases, control parameter T (i.e., local absolute temperature), which dictates system behavior, is often replaced with a computational annealing parameter, such as space, time, or the “critical tunneling field strength.” Quantum networks may display the network analogs of Bose-Einstein condensation and the Pauli exclusion principle depending on statistical parameters. In addition, rate of state transitions or computational decisions in a quantum network follows nonlinear first-order Arrhenius kinetics associated with quantum tunneling, also making it a computational or network analog of the physical phenomenon. These properties of quantum networks strongly compare with networks capable of certain associative forms of learning and memory, such as Hebbian-type learning dependent upon mutually weighted nodal or synaptic strengths.
Schrödinger Wave Function
A solution to Erwin Schrödinger's wave equation used to describe the statistical nature of eigenstates that exhibit wave-particle duality. The wave function gives the probable energy of a wave in a 4D spacetime interval. Each wave is associated with a respective wave number related to wavelength or an energy level known as a quantum. Because the wave equation is additive, the distribution of wave numbers or energy levels occurring over the spacetime interval may be combined into a mixed or superposed wave packet. Pure states are represented by a single wave number or quantum.
Unitary Operator
A mathematical operation performed on a state space that satisfies the identity operator by being normal, having a spectral decomposition (i.e., capable of being reduced to additive components), and preserving the inner product of two vectors, such as a unitary phase shift of 180° from state or vector |0〉 to |1〉 or |1〉 to |0〉 residing on the unit circle or the unit 3D sphere—the Bloch sphere.
Universal Turing Machine
An idealized computational machine with unbounded memory belonging to a class of devices introduced by Alan Turing, the universal Turing machine is one of the most powerful classical computers conceived and serves as model to examine issues of computational complexity. All Turing machines are prototype modern programmable computers capable of executing algorithmic routines of different complexity. They consist of four essential components: (1) a microprocessor-like finite state control that coordinates computing action, (2) a program, (3) a memory tape, and (4) a read-write tape head that points to the tape location currently accessible for read-write operations. Unlike other Turing machines, the only variable component maintained by the universal Turing machine is the initial contents of the tape. Such a configuration is deceivably powerful and enables the universal Turing machine to emulate or simulate the processing of all other Turing machines, even more powerful ones.
Similar processing advantages arising from quantum mechanics may exist for natural computations performed by live biological systems, particularly at the level of single cells and their subcellular components. Mounting evidence from decades of analytical and experimental research continues to oppose the conventional tenet that quantum mechanical phenomena exert, at best, trivial influences over bioprocesses (cf. Davies, 2004). Criticisms still tend to concentrate on the capacity of biological systems to settle or cohere into a quantum regime long enough to accomplish quantum computation (cf. Tegmark, 2000; Davies, 2004; Reimers et al., 2009; Wolynes, 2009; Trevors and Masson, 2010). However, issues regarding quantum decoherence, the collapse of the Schrödinger wave function into a single classical or macroscopic state due to thermodynamic processes involving a system and its environment, are less problematic for cellular enzymatic processes reliant on small, thermally-shielded protein reaction sites and/or on local temperature gradients which can force cellular substrate from decoherent to coherent activity (cf. Davies, 2004). Considering these factors, a number of substrate essential for cellular computations are already associated with quantum performance characteristics, such as cytoskeletal lattices (Hameroff, 1994; Matsuno, 2006; Craddock et al., 2009), photosynthetic protein complexes (Hu et al., 1998; Sener et al., 2005), the citric acid cycle (Matsuno, 2006)and metabolism (Demetrius, 2003), molecular ratchets (Matsuno, 1999, 2006; McFadden and Al-Khalili, 1999; Patel, 2001; Cooper, 2009), molecule folding (Gutin et al., 1996; Cieplak and Hoang, 2003), synaptic boutons and vesicles (Beck and Eccles, 1992; Schwartz et al., 2005), long-range enzymatic activity (Fröhlich, 1968, 2004; see Reimers et al., 2009 for a dissenting view), odorant receptors (Turin, 1996; Brookes et al., 2007; Solov'yov et al., 2012), and second-messenger cascades (Clark, 2010a,b,c,d, 2011, 2012b). Quantum effects at both informational and physical degrees of freedom thus seem to appear in every major aspect of cell structure and function, from sensory transduction to gene expression to cellular metabolism to cell motility (Clark, 2011, 2012b,c). However, one of many significant questions remaining to be answered is whether or not neurons are capable of emulating levels of quantum computational performance to optimize the fitness of cellular decisions during both normal and challenged cytophysiological states. Experimental and theoretical findings concerning aneural ciliate heuristic-guided social behaviors tantalizingly imply that all eukaryotic cells equipped with cellular machinery for fast autocatalytic intracellular Ca2+ signaling and response regulation may execute quantum-efficient algorithms to select and implement appropriate response strategies to better cope with changing ambient and homeostatic conditions (Clark, 2010a,b,c,d, 2011, 2012b, 2013a). To partly address this issue for neurons, I argue in the present Hypothesis and Theory article that intracellular store-operated Ca2+ release offers a suitable and common mechanism for widespread biological evolution and expression of Grover's quantum algorithm in cellular life. I begin with brief reviews of intracellular store-operated Ca2+ release in neurons and the basic facets of Grover's quantum algorithm. I then narrow my discussion to highlight correspondences between a mathematical fire-diffuse-fire model of intracellular store-operated Ca2+ release and Grover's quantum algorithm, followed by an unprecedented, if preliminary, parameterization of the fire-diffuse-fire model to fit Grover's quantum algorithm operating specifications. Lastly, I contemplate testable model predictions and the ecological and evolutionary impact that a cellular version of Grover's quantum algorithm may have for healthy and diseased neurons and the organisms to which they are invested.
Intracellular Ca2+ Dynamics and Response Regulation in Neurons
Extensive varieties of functional Ca2+ channels, transporters, and exchangers are expressed by eukaryotic cells. Each protein type can be directly or indirectly involved in cellular response-regulatory pathways and/or Ca2+ homeostasis. The main classes of Ca2+ channels, transporters, and exchangers across animal phylogeny rely on mechanosensitive [e.g., transient receptor potential (TRP) compression and stretch receptors], ATP-dependent [e.g., sarcoplasmic-endoplasmic-reticulum (SERCA) and plasma-membrane ATPase (PMCA) Ca2+ uptake/extrusion pumps), ion-gated (e.g., Ca2+/H+ and Na+/Ca2+ exchangers)], voltage-gated (e.g., L-, N-, P/Q-, R-, and T-type receptors), ligand-gated [e.g., inositol 1,4,5-trisphosphate (IP3), ryanodine (Ry), and N-methyl-D-aspartate receptors (NMDA)], and peptidergic porin (e.g., aquaporins) mechanisms (Clark, 2013b; Clark and Eisenstein, 2013; Clark et al., 2013; Dolphin, 2006; Foskett et al., 2007). The majority of known selective or nonselective Ca2+ channel, transporter, and exchanger systems are well identified and studied for a range of differentiated animal cell types, such as neurons and myocytes. With respect to neurons (Figure 1, left panel), scientific attention is frequently given to those Ca2+-permeable or -activating proteins, such as L- and N-type voltage-gated channels, ligand-gated NMDA receptors (NMDARs) and α-amino-3-hydroxy-5-methyl-4-isoxazolepropionicacid receptors (AMPARs), and metabotropic glutamate receptors (GPCRs), critical for the induction and/or maintenance of certain forms of synaptic structural and transmission plasticity (cf. Franks and Sejnowski, 2002; Bear, 2003; Malenka and Bear, 2004; Iino, 2006; Cohen and Greenberg, 2008; Levitan, 2008; Yashiro and Philpot, 2008; Okamoto et al., 2009; Catterall, 2010; Selvaraj et al., 2010; Castillo et al., 2011; Fioravante and Regehr, 2011; Hartmann et al., 2011; Wright and Vissel1, 2012). However, these same and additional proteins are also instrumental, for example, in experience-independent cytokine and chemokine immunological responses, gene expression, cellular trafficking, and homeostasis (cf. Clark, 2013b; Clark and Eisenstein, 2013; Foskett et al., 2007), when extracellular Ca2+ influx and/or triggered IP3-dependent store-operated intracellular Ca2+-induced Ca2+ reactions (CICRs) help control endosome transport, membrane remodeling, and up- and downregulation of metabolic and catabolic processes. In classic scenarios of facilitated and depressed glutamatergic synaptic function, respectively known as long-term potentiation (LTP) and depression (LTD), extracellular Ca2+ enters the post-synaptic cell through activated NMDARs during the induction phase of plasticity. Ca2+ loading in dendritic spines often evokes either LTP or LTD in a concentration-dependent manner, with higher and lower levels of Ca2+ tending to respectively produce LTP and LTD (cf. Malenka and Bear, 2004). As free Ca2+ diffuses in spines and perhaps other cell compartments, various Ca2+-dependent messenger systems become activated and contribute to the induction and maintenance phases of plasticity. Signal transduction by Ca2+ and its sensors/binding proteins, such as calmodulin and calcinurins, stimulate cascading enzymatic activity from calcium-calmodulin kinase II (CaMKII) and IV, nitric oxide synthase, protein kinase C, tyrosine kinase Src, mitogen-activated protein kinase, and other molecular complexes that lead to enduring changes through post-synaptic CREB-dependent transcription and immediate early gene activation, post-synaptic receptor synthesis, transport, and distribution, pre- and post-synapse geometry, and pre-synaptic vesicular transport and docking at transmitter release zones (cf. Malenka and Bear, 2004). Since the number and spatial distribution of Ca2+-dependent LTP and LTD events can quickly exhaust NMDAR transients, LTP and LTD must be supported by store-operated CICRs (cf. Malenka and Bear, 2004; Verkhratsky, 2005). The initial requirements of Ca2+ loading to excite CICRs for expression of LTP and LTD differ according to the frequency of post-synaptic stimulation, whether LTP or LTD develops, and the type of neuron in which they occur. However, it is now accepted that IP3 receptor (IP3R)-mediated CICRs assist in directing response regulation under physiological constraints of neuronal synaptic transmission and plasticity.
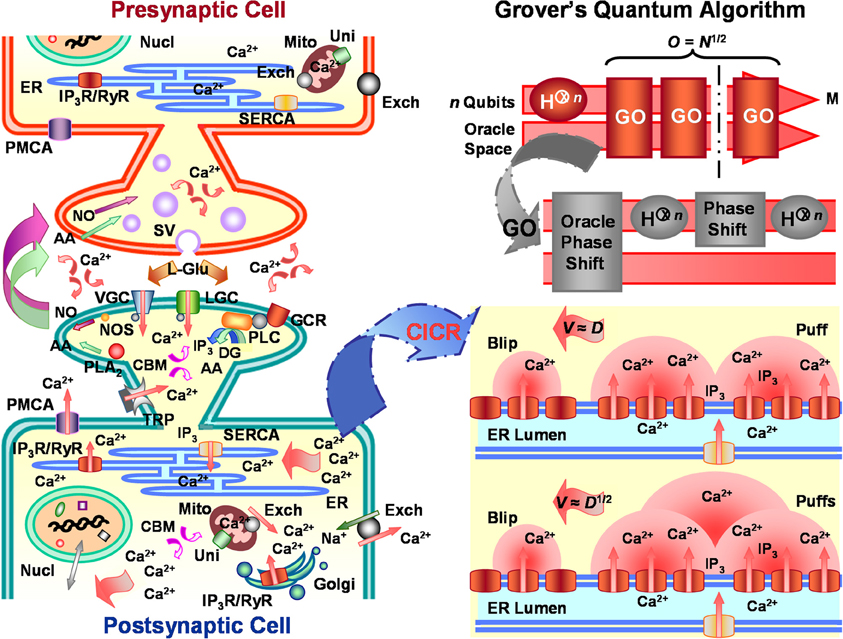
Figure 1. Calcium-induced calcium reactions (CICRs) emulate Grover's quantum algorithm in neuronal information processing. Left panel portrays major characteristic substrate (e.g., receptors, organelles, etc.) involved in Ca2+-mediated response regulation of arbitrary glutamatergic neurons, including, but not limited to, substrate critical for synaptic plasticity, cellular energetics, immunoprotection, homeostasis, gene expression, biosynthesis, molecular trafficking, cytoskeletal organization, and cell fate. Similar mechanisms affect both pre- and post-synaptic neurons, but, for descriptive purposes, post-synaptic cell activity is emphasized. Ca2+ entry into the post-synaptic neuron through voltage-gated receptor (VGC), ligand-gated receptor (LGC), and transient potential receptor (TRP) channels and stimulated inositol 1,4,5-trisphosphate (IP3) production by activated G-protein coupled receptors (GCR) help initiate cytosolic CICRs from integral IP3 receptors (IP3R) located along the endoplasmic reticulum (ER) membrane. CICRs may cause traveling waves of varying velocities and patterns which emulate search routines capable of eliciting/suppressing appropriate response regulation from different cellular compartments. Lower right panel illustrates CICR saltatory and continuous waves. Saltatory Ca2+ waves and the information they carry conduct at velocities (V) proportional to the classical Ca2+ diffusion coefficient (D). Whereas, faster continuous Ca2+ waves and the information they transmit move at velocities proportional to the square-root of the classical Ca2+ diffusion coefficient. Coefficient D of continuous waves for either intercluster or intracluster diffusion is assumed to be up to orders of magnitude greater than that for saltatory waves. The quadratic disparity in the velocities of saltatory and continuous waves corresponds to the root-rate increase of information processing by Grover's quantum algorithm over classical algorithms. Upper right panel shows schematic of Grover's quantum algorithm. The algorithm takes as input n qubits, upon which it performs Hadamard transformations (H⊗n) and Grover's operation (GO) to find a target m of M solutions stored in database N. Regardless of whether one or more consultations of the Oracle are needed, Grover's quantum algorithm finds the target solution within O = N1/2 algorithmic steps or operations O. Additional abbreviations: arachidonic acid (AA), Ca2+ binding molecule (CBM), Ca2+ uniporter (Uni), diacylgycerol (DG), Golgi apparatus (Golgi), L-glutamate (L-Glu), nucleus (Nucl), mitochondria (Mito), nitric oxide (NO), nitric oxide synthase (NOS), phospholipase A2 (PLA2), phospholipase C (PLC), plasma-membrane Ca2+ ATPase (PMCA), ryanodine receptor (RyR), sarcoplasmic-endoplasmic-reticulum Ca2+ ATPase (SERCA), Na+/Ca2+ exchanger (Exch), synaptic vesicle (SV).
IP3Rs and Cytophysiology of CICRs in Neurons and Other Differentiated Animal Cells
Four integral 310-kDA tetrameric IP3R isoforms, all permeable to certain mono- and divalent cations, especially Ca2+, are expressed by animals (cf. Taylor et al., 2004; Foskett et al., 2007; Taylor and Tovey, 2010). Three of these isoforms, types 1 through 3, are encoded in vertebrate genomes (Patel et al., 1999; Taylor et al., 1999). Invertebrate genomes encode the remaining receptor isoform closely related to IP3R type 1 (Iwasaki et al., 2002; Ionescu et al., 2006). Except for structurally and functionally similar polymorphic ryanodine receptors (RyRs), IP3Rs are the foremost ion pore responsible for nonmitochondrial store-operated Ca2+ release in animal cells, including neurons. Receptors concentrate in the membrane of the ER (e.g., Ross et al., 1989; Otsu et al., 1990; Ferreri-Jacobia et al., 2005), the principle calcium storage site of most cells, but are also located in the nuclear envelope, Golgi apparatus, secretory vesicles, and plasma membrane of various differentiated cell types (Ross et al., 1989; Tanimura et al., 2000; Dellis et al., 2006). In mammalian brain, where IP3Rs are very rich in the cerebellum (Supattapone et al., 1988; Furuichi et al., 1989; Sharp et al., 1999) and hippocampus (Furuichi et al., 1993, 1994; Sharp et al., 1993), greater heterogeneity in intracellular distribution occurs for receptor isoforms. IP3R type 1, the most abundant isoform in brain, resides in dendrites, cell bodies, axons, and synaptic terminals of cerebellar Purkinje cells, while being largely confined to soma and proximal dendrites in other neurons (Ryugo et al., 1995; Dent et al., 1996; Sharp et al., 1999). The IP3R type 3, in contrast, is localized to neuropil and neuronal terminals (Sharp et al., 1999). Consistent with receptor distributions, IP3Rs act as a prominent signal interface between the ER and most other organelles, including mitochondria, to directly and indirectly affect cell processes (cf. Ponce-Dawson et al., 1999; Strier et al., 2003; Coombes et al., 2004; Taylor et al., 2004; Fraiman et al., 2006; Foskett et al., 2007; Solovey and Ponce-Dawson, 2010; Taylor and Tovey, 2010). Importantly, large observed variations in receptor structural identity may predictably correspond to an equally large functional diversity with subtle developmental and physiologic consequences for specific IP3R-populated organs and tissues. However, receptor types likely provide complementary and redundant substrate for intracellular Ca2+ signaling. Redundancy may be apparent in small observed divergences in agonist binding affinities across receptor types (cf. Foskett et al., 2007; Clark et al., 2013). Without significant variance in agonist sensitivity, separate isoforms are unable to titrate Ca2+-dependent physiological responses to differential cytosolic ligand concentrations. Moreover, channel phosphorylation and protein interactions tend to cause similar respective allosteric modification of heterotrophic ligand binding regardless of receptor type (cf. Foskett et al., 2007; Clark et al., 2013).
Well studied for oocyte development, myocardial activity, and cerebellar cortex neural output, IP3R-mediated ER Ca2+ release aids, for example, in regulating protein and lipid biosynthesis, cell energetics, stress responses, cell fate and death, synaptic plasticity, and immunoprotection (cf. Clark and Eisenstein, 2013). The complex spatiotemporal information conveyed in Ca2+ signals is highly dependent upon IP3 production by phospholipase C (PLC)-β and -γ, distribution and activation/inhibition properties of IP3Rs, uptake and storage of Ca2+ in the ER and other reservoirs, and influences over Ca2+ diffusion (cf. Clark and Eisenstein, 2013). The ER membrane encompasses a cisternal space that occupies about 10% of cell volume and importantly harbors cotranslational proteins, lipids, and divalent ions, such as Ca2+. ER-membrane-bound Ca2+ ATPases (e.g., sarcoplasmic-endoplasmic-reticulum Ca2+ ATPase) sequester free cytosolic Ca2+ in the ER lumen, where it stays free or becomes attached to buffers. Estimates of total luminal Ca2+ concentrations are as high as 1 mM. The fraction of unbound luminal Ca2+ ranges from 100 to 700 μM (Montero et al., 1995; Bygrave and Benedetti, 1996; Pinton et al., 1998; Alvarez and Montero, 2002; Bassik et al., 2004; Palmer et al., 2004; Verkhratsky, 2005). Although ER Ca2+ modulates IP3R function from the luminal side via interactions with channel sensor domains, cobinding of IP3 and Ca2+ to cytosolic sites opens the gated IP3R channel in a concentration-dependent manner, driving passive Ca2+ flux down its electrochemical gradient and into the cytosol. In IP3 concentrations ranging between 100 nM and 1 μM that continuously saturate receptor binding sites for IP3, Ca2+ generally excites and blocks IP3R activity in respective low (e.g., ~50 nM–1 μM) and high (e.g., >10 μM) concentrations (cf. Foskett et al., 2007). Changes in IP3R conformation and pore permeability occur due to IP3 and Ca2+ allosteric interactions that dissociate suppressor, calmodulin, and gatekeeper receptor regions, repositioning the transmembrane gate and activating Ca2+ conductance (cf. Foskett et al., 2007; Clark and Eisenstein, 2013). In absence of IP3 binding, low-affinity binding of cytosolic Ca2+ to one of two calmodulin heads occludes the ion channel as calmodulin crosslinks with suppressor and gatekeeper regions of adjacent receptor subunits. The receptor lumen stays closed and inactive when only cytosolic IP3 binds to receptor sites. Depending on recording preparations, receptor type, and other factors, Ca2+ conductance and current through single channels have been electrophysiologically measured at around 10–125 pS and 0.1–0.5 pA, respectively, (cf. Foskett et al., 2007). Maximum mean duration of IP3R opening tends to be no more than 15 and 40 ms for respective vertebrate and invertebrate receptor types (cf. Foskett et al., 2007). The lengths of these periods are independent of agonist concentrations. But the durations of subsequent prolonged refractory or reversible inactivation periods are determined by agonist concentrations. Frequency of channel activity and graded Ca2+ mobilization are thus primarily due to cytoplasmic ligand levels, with additional regulation by nucleotides, phosphorylation, redox states, and protein interactions.
Stimulation of an individual or several IP3Rs evokes a spatially discrete Ca2+ release usually termed a blip (Figure 1, lower right panel). Blips are the most elemental Ca2+ release event (cf. Foskett et al., 2007; Solovey and Ponce-Dawson, 2010). Quantal release creates a microdomain of high cytosolic Ca2+ concentration that can exceed 100 μM near the opening of an activated channel (Naraghi and Neher, 1997; Rios and Stern, 1997; Neher, 1998). Once a 10-μM Ca2+ threshold is reached, free cytosolic Ca2+ begins to exert inhibitory feedback control over all-or-none openings of surrounding IP3Rs. Inhibitory control of IP3Rs is proportionally tuned by presence of local IP3 concentrations, which interfere with the ability of Ca2+ to bind to low-affinity sites. Furthermore, rapid buffering by both mobile and immobile Ca2+ traps often limit diffusion of free cytosolic Ca2+ to a radius no greater than 5 μm from the source channel (Allbritton et al., 1992). Buffers alone are typically insufficient to quench a Ca2+ release event involving multiple adjacent receptors. But beyond the distance of 5 μm, cytosolic Ca2+ concentrations, homeostatically regulated by transporters, exchangers, and porins, steeply decline from 1 μM to ~50 nM without widespread Ca2+ mobilization (Naraghi and Neher, 1997; Rios and Stern, 1997; Neher, 1998). Since IP3Rs organize in autocatalyst-linked clusters on the ER membrane, a larger coordinated Ca2+ release event, commonly called a puff or spark, can be initiated following a blip (cf. Ponce-Dawson et al., 1999; Strier et al., 2003; Coombes et al., 2004; Fraiman et al., 2006; Foskett et al., 2007; Solovey and Ponce-Dawson, 2010). Puffs occur as Ca2+ from the blip diffuses and binds to neighboring inactive IP3Rs already docked by IP3 (Figure 1, lower right panel), an autocatalytic event referred to as a CICR or fire-diffuse-fire reaction (cf. Yao et al., 1995; Ponce-Dawson et al., 1999; Strier et al., 2003; Coombes et al., 2004; Taylor et al., 2004; Fraiman et al., 2006; Guisoni and de Oliveira, 2006; Shuai et al., 2006; Foskett et al., 2007; Bruno et al., 2009; Smith and Parker, 2009; Ur-Rahman et al., 2009; Solovey and Ponce-Dawson, 2010; Taylor and Tovey, 2010). Single IP3Rs are typically separated by 10–20 nm within a cluster of perhaps 50 receptors covering a maximum ER-membrane surface area of 400 nm2 in some cells (Shuai et al., 2006; Bruno et al., 2009; Ur-Rahman et al., 2009). Individual clusters can be separated by regular or irregular distances of up to around 2 μm (Yao et al., 1995). Though cytosolic Ca2+ binding proteins may alter Ca2+ transport in the vicinity of a receptor channel cluster, the interchannel distances are too short to prevent most ions from diffusing. Therefore, when an estimated 20 to 35 IP3Rs become simultaneously bound with coligands, Ca2+ puffs arise (Shuai et al., 2006; Bruno et al., 2009; Smith and Parker, 2009). As mentioned earlier, this autocatalytic coupling of clustered receptors forms local and global cellular networks or lattices that can generate either small- or large-scale mobilization of Ca2+. Irregularities in spatial organization of IP3R clusters together with channel coupling associated with CICRs produce assorted intracellular Ca2+ signals. The amplitude, frequency, and velocity of signals vary according to cytosolic Ca2+ buffer concentrations, feedforward excitation of IP3Rs via possible high affinity Ca2+ binding, feedback inhibition of IP3Rs via possible low affinity Ca2+ binding, and crosstalk with additional messenger systems (cf. Clark, 2011, 2012b), such as cAMP pathways (e.g., Siso-Nadal et al., 2009). Puffs may trigger global Ca2+ waves as cellular conditions promote sustained CICRs. Waves can oscillate, extinguish, and travel throughout different cell compartments as saltatory, continuous, or anisotropic fronts. The spatiotemporal variability of blips, puffs, and large-scale waves suggests a high degree of specificity is achieved for intracellular Ca2+ signaling, reducing the likelihood of corruption and loss of transmitted information content by noisy intracellular processes (cf. Clark, 2011, 2012b, 2013a). In many respects then, the behavior of neuronal CICRs conforms to fundamental principles and attributes of (classical and quantum) search algorithms and patterns used to efficiently find and execute various kinds of appropriate cellular responses to extracellular and/or intracellular stimuli (Clark, 2010a,b,c,d, 2011, 2012a,b, 2013a; Clark and Eisenstein, 2013).
Description of Grover's Quantum Algorithm
Before entering into discussion on the relationship between CICRs and Grover's quantum algorithm, I now identify basic specifications of Grover's quantum algorithm through a short primer of information and computational theory. In standard quantum information theory and computation, the classical bit originated by Shannon (1948a,b) is replaced with the quantum bit or qubit, a concept and term, respectively credited to Weisner (1983) and Schumacher (1995). Qubits are information units that may be transmitted, transformed, stored, and measured. The possible states of a single qubit in Dirac notation are the orthonornal unit vectors or basis (eigen)states and which span a two dimensional vector, state, or Hilbert space. States |0〉 and |1〉 correspond to classical bit states of 0 and 1. However, unlike classical bits, these states may form an indefinite linear combination or superposition: |ψ〉 = a|0〉 + b|1〉, where variables a and b are complex numbers called vector amplitudes (cf. Nielsen and Chuang, 2000). By way of a common example useful to later exposition of Grover's quantum algorithm, states |0〉 and |1〉 forming the unique quantum supposition (|0〉 − |1〉)/21/2 have respective amplitudes 1/21/2 and −1/21/2. If qubit states remain linearly independent, then any measurement or eigenvalue m on the system |ψi〉 via arbitrary Hermitian measurement operators Mi ≡ |ψi〉 〈ψi| and M0 = I − ∑i ≠ 0 |ψi〉 〈ψi|, where I is the identity matrix , will decompose into a single pure state |0〉 or |1〉 with respective probabilities |a|2 and |b|2, so that measurement probability pi = 〈ψi|Mi|ψi〉 = |a|2 + |b|2 = 1 (cf. Nielsen and Chuang, 2000). Conversely, in agreement with the entropic uncertainty principle, an informational analog to Heisenberg's uncertainty principle, indistinguishable or nonorthonormal quantum states cannot be measured with certitude because of variances inherent in observables. As one may expect, these concepts become slightly more complicated in instances of composite or joint systems—those involving two or more qubits. Although the full implications of composite systems go beyond the scope of this article, it is important to introduce some content on the subject for future consideration. Take two entangled component systems, each respectively described by superposition states |ψi〉 = (|0〉 + |1〉)/21/2 and |ψj〉 = (|0〉 − |1〉)/21/2. The state space of such a bipartite system is defined by the tensor product |ψi〉 ⊗ |ψj〉 = |ψ〉10 = (|00〉 − |11〉)/21/2, yielding, in the present case, the third Bell basis state or Einstein–Podolsky–Rosen pair. Composite quantum information systems, such as the four Bell basis states or Einstein–Podolsky–Rosen pairs, play significant roles in superdense coding, information encryption, error diagnosis and correction, and other aspects of quantum computation, including execution of quantum algorithms (cf. Nielsen and Chuang, 2000).
As previously noted, quantum computational methods entail use of specialized quantum gates and circuits to form algorithms that manipulate qubits to purposefully arrive at some goal state, much as would be accomplished for classical bits operated on by classical logic gates and circuits. Purposes may include, for instance, finding correct solutions to difficult or classically intractable factorization, ordering, counting, and search problems. Now imagine a quintessential large database or map of salient landmarks, such as cities (or, as will be detailed below, rate-limiting parameters for selective spatiotemporal chemical diffusion patterns). Using a classical search algorithm to discover the shortest route n among all possible routes N through every city on the map, a dilemma known as the Hamiltonian cycle decision problem, requires N total operations O or algorithmic steps [i.e., O(N)]. The same search problem may be accelerated to O(N1/2) with Grover's quantum algorithm and its unique Grover's operator (Grover, 1996) (Figure 1, upper right panel). Typical uses of Grover's quantum algorithm search register entries i = {in|n = 0, …, N − 1} indexed to actual elements n of N. This convention is created so that the database can be conveniently set to N = 2n bits of storage, with a subset M = 1 ≤ M ≤ N = {im|m = 1 ≤ m ≤ N − 1} of exact solutions. Another convention enlists a function θ that accepts as input an integer x = i valued over the range 0 to N − 1. The function returns results θ(x) = 1 or θ(x) = 0 when a solution m is or is not obtained, respectively. Given these constraints, Grover's operator consists of four distinct sequential procedures (cf. Nielsen and Chuang, 2000): (1) application of the Oracle, (2) application of the Hadamard transformation, (3) application of a conditional phase shift, and (4) application of the Hadamard transformation. The operator first samples inputs from the initial equally weighted superposition state generated by the efficient Hadamard transform, H⊗n, then it labels problem solutions through the unitary action of the Oracle:
where |x〉 represents the index-register qubit set to |0〉 and (|0〉 − |1〉)/21/2 is the single Oracle qubit which assists in flipping or phase-shifting |x〉 only when θ(x) returns 1 as a result. A second Hadamard transformation is utilized following the Oracle call to place labeled qubits into superposition. From this state, a conditional phase shift, |x〉 → − (− 1)θ(x)|x〉, becomes executed for all basis states not equal to |0〉. The final Hadamard transformation again puts the register qubit into superposition for possible further Oracle summons in the event a target solution is not located, although successful search attempts may require no more than one Oracle call.
Correspondence between CICRs and Grover's Quantum Algorithm
If modifiable operation of linked intracellular Ca2+ release sites and associated affector/effector systems function as quantum-like computational networks for response regulation, as reported by Clark (2010a,b,c,d, 2011, 2012a,b, 2013a), then reaction-diffusion equations should reveal classical and quantum properties of search algorithms and of search patterns selectively applied to those networks. One such reaction-diffusion equation, the simple fire-diffuse-fire model of Ca2+ propagation, defines Ca2+ waves by the following evolution equation (Ponce-Dawson et al., 1999):
where [Ca2+](x, t) is the average concentration of calcium in directions perpendicular to the direction x of propagation, δ(ζ) is the δ function, H(ζ) is the Heavyside step function (and not the Hadamard transform), D is the classical Ca2+ diffusion coefficient, d is the (mean) distance between Ca2+ release sites, ti is the first time the ith Ca2+ release site reaches threshold value, σ is the total number of Ca2+ ions released per storage site, and τ is the period that receptors remain open to release Ca2+ in a single event. Notably, the evolution equation and parameters for this sort of model are general enough to fit conditions stipulating IP3R clusters or individual IP3Rs as Ca2+ release sites (cf. Guisoni and de Oliveira, 2006; Solovey and Ponce-Dawson, 2010), with corresponding changes in intersite distances, timescales, and released Ca2+ concentrations. The dynamics of the equation additionally rely on two dimensionless parameters, Γ and β (Ponce-Dawson et al., 1999), with:
where σ/d3 is the concentration of Ca2+ released and [Ca2+]T and [Ca2+]b are respective threshold and basal concentrations of Ca2+, and
Parameter Γ of Equation 3 acts as a multiplicative variable governing the ease of starting a Ca2+ wave, the velocity at which it will travel, and, therefore, the effectiveness of the wave to effect response regulation. Whereas, the value of parameter β of Equation 4 defines whether a Ca2+ wave propagates with a slow saltatory, fast continuous, or intermediate mixed front. As chemical processes, such as the duration of Ca2+ mobilization or degree of Ca2+ buffer overload, become rate-limiting over interstore distances, β ≫ 1 and Ca2+ waves transition from saltatory to continuous waves (Figure 1, lower right panel). Moreover, saltatory wave propagation travels at a rate proportional to the Ca2+ diffusion coefficient, v ≈ (D/d)g−1Γ, where g−1 is an inverse function (Ponce-Dawson et al., 1999). In contrast, the velocity of continuous waves is proportional to the square-root of the Ca2+ diffusion coefficient, v ≈ (D/τ)1/2f−1Γ, where f−1 is an inverse function (Ponce-Dawson et al., 1999). When continuous waves have sufficiently large Γ, wave velocity approximates the Luther equation, v = α(D/τ)1/2 with α = Γ1/2. The equations for wave velocity should not be misleading, as continuous waves are often faster than saltatory ones (cf. Izu et al., 2001). (Noted exceptions include the large-scale completely homogenous fertilization waves of oocytes.) If the value of D is the same for both saltatory and continuous waves and τ is much larger for continuous waves, then saltatory Ca2+ waves would always transmit at faster speeds. But when compared to saltatory waves, continuous waves well exceed buffering capacities of slow and fast Ca2+-buffer species and display far greater diffusion coefficients and shorter intersite diffusion times (cf. Strier et al., 2003) for both intercluster and intracluster models of diffusion for constant small d. The effect of overcoming buffering capacity on continuous wave velocity may be also amplified by diminution of τ on the order of one to two magnitudes to the ms timescale (cf. Izu et al., 2001; Strier et al., 2003; Foskett et al., 2007), which differs from τ given by Ponce-Dawson et al. (1999). In either situation of saltatory or continuous waves, wave conduction generally fails for small D (e.g., <10 μm2/s), large d (e.g., d > 3 μm), and extremely small or large Γ (cf. Keizer et al., 1998; Ponce-Dawson et al., 1999; Strier et al., 2003). These values reflect significant differences in the physiological roles of saltatory and continuous Ca2+ waves (e.g., Keizer et al., 1998), with the former believed to inhibit local and global cellular responses via Ca2+-wave conduction failure and CICR blockade and the latter believed to evoke and integrate a range of local and global cellular responses through complex spatiotemporal patterns and widespread delivery of information throughout the cell. Fire-diffuse-fire models of Ca2+ propagation are remarkably robust, explaining the diffusive characteristics of store-operated Ca2+ regulation in a generous variety of eukaryotic cell types, including oocytes, cardiac myocytes, and neurons (e.g., Ponce-Dawson et al., 1999; Strier et al., 2003; Coombes et al., 2004; Timofeva and Coombes, 2004; Fraiman et al., 2006; Guisoni and de Oliveira, 2006; Thul et al., 2007; Solovey and Ponce-Dawson, 2010; Bressloff, 2014).
Importantly, the leading edge of intracellular Ca2+ gradients passing between separate receptor clusters is relatively slow, being experimentally recorded to typically travel at velocities ranging from 20 to 70 μm/s (Jaffe, 1993). Some reports, however, indicate continuous longitudinal waves can approach an astonishing 6000 μm/s in live cells (Miura et al., 1999). In any event, when N and D are numerically related (Clark, 2010a, 2012b), the quadratic disparity between the speeds (i.e., intersite-travel time) of saltatory and continuous Ca2+ waves appears consistent with expression of a square-root quantum algorithm that increases target searches, such as searching for the most appropriate response to external and/or internal stimuli, in living cells beyond the bounds of classical algorithms (Clark, 2010a,b, 2011, 2012b) (Figure 1, lower and upper right panels). In the algorithmic (rather than strictly physicochemical) sense, the properties of classical Ca2+ diffusion effectively describe a phenomenological basis for Grover's quantum algorithm (cf. Clark, 2010a,b). A physicochemical manifestation of quantum mechanics via a quantum diffusion term is unnecessary to produce quantum-efficient algorithm searches, a result perhaps counterintuitive for most biophysicists since diffusive processes may be classical, quantum, or semiclassical/semiquantum in nature. At biologically relevant subsecond times, warm temperatures, and micrometer scales described for the conditions of Ca2+ fire-diffuse-fire reactions (cf., Ponce-Dawson et al., 1999), quantum diffusive processes produce minor effects without thermodynamic shielding, such as in the case of bacterial photosynthetic reaction cores (Hu et al., 1998; Sener et al., 2005), or pump-process energy transfer, such as in the possible case of actomyosin polymerization (Matsuno, 1999). Neither thermodynamic shielding nor pump-process constraints must occur for initiation and maintenance of classical fire-diffuse-fire reactions. The diffusion coefficient or diffusivity, D, in Equations 2 and 4 is a purely classical parameter generally derived from Fick's laws and the Einstein-Smoluchowski relation as D = μkBT, where μ is particle mobility or the inverse drag coefficient, kB is Boltzmann's constant, and T is temperature in degrees Kelvin (cf. Clark, 2012b). This equation, via the Einstein-Sutherland relation, becomes the Einstein-Stokes equation in one dimension, D = kBT/2πηr, and in three dimensions, D = kBT/6πηr, for spherical particles of radius r moving through a fluid of viscosity η at a low Reynolds number. If the density of the diffusing material affects D, then the diffusion equation is nonlinear and D is taken to be variable (cf. Clark, 2012b). When independent of thermodynamic influences, D = h/4πm, where h is Planck's constant and m is the mass of the diffusing particle. The latter definition of the diffusion coefficient is quantum mechanical (cf. Clark, 2012b). One may draw direct comparison of these sorts of effects with the operation of closely related technological quantum networks performing search functions (e.g., Bianconi and Barabási, 2001; Bianconi, 2002a,b, 2003; Stella et al., 2005; Clark, 2010b,c,d, 2011, 2012a,b, 2013a). In such instances, observed statistical quantum-like outcomes, often referred to as quantum mechanical analogs, emerge from weighted macroscale computational networks and their parameters capable of both classical and quantum behavior. For technological systems (Bennett, 2003; Ladyman et al., 2007) and individual cells (Clark, 2010b,c,d, 2011, 2012b, 2013a; Bérut et al., 2012; Mehta and Schwab, 2012), this behavior is consistent with Landauer's principle of energy/information transfer. Similar to computational network analogs of quantum behavior, the classical Ca2+ diffusion coefficient might instantiate a computational analog of quantum mechanical systems without actually residing in a physicochemical quantum regime.
Although the physical expression of the diffusion coefficient should be entertained, it must be stressed that in some sense any reflection is superfluous with respect to application of Grover's quantum algorithm. The reason for this, as indicated in the previous paragraph, is that a relationship between N and D seems apparent (and will be established in below sections). The variable N represents the total number of search elements queried by Grover's quantum algorithm. Its value is neither quantum nor classical! Therefore, D needs to be neither quantum nor classical to effect Grover's quantum algorithm in a cellular system! That is, what makes Grover's quantum algorithm quantum in nature is its action on a search field, not necessarily the properties of the search field itself. In view that classical diffusion terms satisfy the quadratic improvements needed for Grover's quantum algorithm, it is interesting that search selectivity by such an algorithm in single cells may be enhanced, instead of being damped, by diffusion barriers sometimes causing unstable Ca2+ gradients. Anisotropic patterns of Ca2+ diffusion due to free cytosolic chaperons and buffers (Chen et al., 2008, 2009) and frequency and amplitude modulated Ca2+ liberation (De Pitta et al., 2008, 2009) have been reported to help improve the specificity of encoding sensory information transmitted by intracellular Ca2+ cascades. Intracellular spaces are filled with Ca2+ traps, such as immobile binding sites. Though traps reduce the effective diffusion coefficient below expected values for free diffusion, propagation of information can move faster than single particle diffusion (Pando et al., 2006). The storage and retrieval of that information is expected to be further refined by recursive phosphorelays affecting Ca2+ permeability to extracellular sources and subsequent reactivation CICRs (Clark, 2010a,b,c,d, 2011, 2012a,b, 2013a). Collectively, these findings should be put into local and global contexts of mixed and continuous wave fronts rather than taken to mean that spatiotemporal patterns of ineffectual punctuate store-operated Ca2+ emissions or unreliable saltatory Ca2+ waves serve as useful media to convey information vital to response regulation (cf. Keizer et al., 1998). These events likely rather function as wave guides that direct mixed or continuous waves to specific target locations within cell compartments.
Parameterizing the Neuronal Fire-Diffuse-Fire Model for Grover's Quantum Algorithm
The superficial similarity between variables N and D in quadratic processing efficiency encourages mathematical treatment that supplants analogy and parameterizes the Ca2+ fire-diffuse-fire model to more precisely fit specifications of Grover's quantum algorithm (Clark, 2011, 2012b). Because the model captures local dynamics of individual IP3R permeability, which inherently control the evolution of collective wave behavior within and across networked IP3R clusters, Grover's quantum algorithm may be reduced to the scale of a single receptor channel, as opposed to receptor clusters or an entire ER membrane of receptors. This convention has several attractive qualities. First, an inability to make quantum measurements due to quick decoherence rates of superposed states becomes a negligible confound for quantum logic operators the physical size of tetrameric protein channels (cf. Beck and Eccles, 1992; Gutin et al., 1996; Turin, 1996; Cieplak and Hoang, 2003; Davies, 2004; Brookes et al., 2007; Solov'yov et al., 2012). Second, uncovering (or framing) a reasonable search goal and associated parameters becomes more conceptually manageable. In regard to both issues, the natural inclination would be to perhaps equate N from the previous example of the Hamiltonian cycle decision problem to the total number of possible spatiotemporal patterns of chemical diffusion needed to evoke a proper IP3R-mediated neuronal response to external and/or internal perturbation, with the target solution being the shortest chain or route of networked receptor clusters across the entire or a circumscribed area of the ER membrane surface. While this decision-problem situation correctly assumes that some or all receptor clusters can be activated as a collective search routine to evoke an arbitrary desired cell response, it challenges the spatiotemporal limits of superposed (physical and not network-analog) quantum states needed to execute Grover's quantum algorithm, since each state embodies a long-range networked pattern of catalyst-linked receptor clusters (e.g., minimally greater than 2 or 4 μm) and, consequently, probably surpasses Wigner's mass-time uncertainty for periodic mechanical processes (cf. Wigner, 1957, 1981; Reimers et al., 2009). The mechanism and processing efficiency of this kind of emergent search algorithm likely would be characteristically (physicochemically) classical in nature. Whereas, the almost instantaneous and continuous chemical diffusion in an approximate 10- to 20-nm distance between two activation-primed IP3Rs (Shuai et al., 2006; Bruno et al., 2009; Smith and Parker, 2009) avoids violating Wigner-type quantum boundaries (cf. Pešić, 1993; Schwartz et al., 2005) and yields suitable conditions for expression of a quantum algorithm. Moreover, in terms of second messenger reaction-diffusion cascades and response regulation, stochastic punctate intracluster spatial patterns of diffusion often play significant roles in spark and wave initiation and are complemented by intermediate and overloaded ion-concentration magnitudes, which help force activation gradients, fast conduction velocities, and stable propagation to initiate cell responses (cf. Keizer et al., 1998; Izu et al., 2001; Strier et al., 2003; Chen et al., 2008, 2009; Solovey and Ponce-Dawson, 2010). Stipulating individual IP3Rs, and their quantum-mechanical small reaction sites and gating kinetics (cf. Ahern et al., 2009; Chan et al., 2010; Pitt et al., 2010; Li et al., 2013), as the computational apparatus of Grover's quantum algorithm allows one then to resolve the search problem to finding the shortest time or fastest rate m taken to reach and autocatalytically activate a neighboring receptor from among a database N of all possible time and activation outcomes (Table 1). Given slower intracluster saltatory Ca2+ waves have high propagation and response-regulation failure rates (e.g., Guisoni and de Oliveira, 2006; Solovey and Ponce-Dawson, 2010), target solutions will be elements of the set M of fast intracluster continuous Ca2+ waves. Such a query is idealized by the search for the maximum Ca2+ diffusion coefficient Dmax, which, in integer form spanning the range of possible integer diffusion coefficients, bears likeness to N. However, as individual IP3Rs do not actually detect diffusion coefficients, the search must be conducted over a “register” indexing each different D with a concentration-dependent parameter biologically associated with D and germane to IP3R reaction kinetics.

Table 1. Comparison of major Ca2+ fire-diffuse-fire model and Grover's quantum algorithm parameters.
To make the present exposition more explicit and amenable with the previous coverage of Grover's quantum algorithm, I now mathematically define critical variables N, M, and D (Table 1), giving fuller attention to physical descriptions of the Grover's quantum algorithm workspaces and operators in subsequent paragraphs (Figure 1, upper right panel). As before, N = {nj|j = 0, …, ∞}, but, as will be determined below, is realistically a finite interval with respect to reaction-diffusion parameters. Elements nj of N are indexed with register entries i = {in|n = 0, …, N − 1}, with a subset M = 1 ≤ M ≤ N = {im|m = 1 ≤ m ≤ N − 1} of exact solutions to the search problem. Algebraic manipulation of Equation 4 yields the general definition of the classical Ca2+ diffusion coefficient:
However, fluctuations in loading of cytosolic Ca2+ buffering systems and, more appreciably, choice of rate-limiting parameters (inter-IP3R) d2, τ, and σ for the fire-diffuse-fire model make the diffusion coefficient variable. Sharper definitions of D may be obtained from the wave velocity equations for saltatory Ca2+ waves, v = (D/d)g−1Γ, and continuous Ca2+ waves, v = (D/τ)1/2f−1Γ. It follows that the respective diffusion coefficients for saltatory and continuous Ca2+ waves are:
with DSmin > 0 and DSmax ≪ DCmin, and
with DCmin ≫ 0, DSmax and DCmax ≪ ∞. Setting Dmax = 0 ≤ Dmax ≤ DCmax = {Dnj|j = 0, …, DCmax} and considering the one-to-one discrete mapping Dmax onto N, Dmax → N, M therefore transforms into the subset DC = DSmax ≪ M ≤ N = {im|m = DSmax ≪ m ≤ N − 1} of all correct solutions involving only intracluster continuous Ca2+ wave fronts. A major result from this interpretation is that, in order to arrive at a solution m = DC, quadratic and exponential speed-ups in respective algorithmic search time and wave velocity must coexist, with a maximum algorithmic search time of O(Dmax/DC)1/2 and wave velocity of vC = v2S! In addition, Equations 6 and 7 are especially useful for purposes of implementing Grover's quantum algorithm, since they are inversely proportional to dimensionless parameter Γ rather than β. As shown in Equation 3, reliance upon Γ permits Ca2+ diffusion coefficients to be indexed to physiologically pertinent ratios involving Ca2+ concentrations liberated by IP3R-dependent store operation and free cytosolic Ca2+ concentrations sensed by multiaffinity IP3R cytosolic Ca2+ binding sites. So that, index values of register entries i corresponding to Dmax and DC may be practically redefined by substituting Equation 5 into Equations 6 and 7, then solving for Γ for separate saltatory and continuous Ca2+ wave forms:
with ΓSmin > 0 and ΓSmax ≪ ΓCmin, and
with ΓCmin ≫ 0, ΓSmax and ΓCmax ≪ ∞. Therefore, index i = {in|n = 0, …, N − 1} = Γmax = {in|n = 0, …, ΓCmax} and solution subset index iM = {im|m = ΓCmin ≤ m ≤ ΓCmax}. Remember also from earlier reviewed content that Grover's quantum algorithm employs a function θ that accepts as input an integer x = i valued over the range 0 to N − 1. The function returns results θ(x) = 1 or θ(x) = 0 when a solution m is or is not acquired, respectively. In parameterizing the fire-diffuse-fire model for Grover's quantum algorithm, elements of the index set i yielding θ(x) = 1 readily signify the solution subset iM = {im|m = ΓCmin ≤ m ≤ ΓCmax} for intracluster continuous Ca2+ waves, whereas elements of the index set i yielding θ(x) = 0 signify the incorrect-solution or failure subset iF = {if|f = 0 ≤ f < ΓCmin} for all intracluster noncontinuous Ca2+ waves, including saltatory and possibly mixed Ca2+ wave fronts.
With key fire-diffuse-fire model parameters written in terms of Grover's quantum algorithm, candidate physicochemical substrate for algorithm operators can be next identified to a first approximation using known IP3R molecular biology and function (Figure 2). Grover's quantum algorithm, as previously mentioned, requires five distinct sequential procedures. The first of these steps, in notation consistent with the fire-diffuse-fire model, is application of the Hadamard transformation, H⊗nj, which prepares the algorithm in an initial equally weighted superposition state . Such a state presumes that a single IP3R acting as Grover's quantum algorithm is capable of simultaneously detecting any probable index values Γmax = {in} marking Dmax = {Dnj} and associated with x, the variable denoting a successful or unsuccessful search for shortest times or fastest rates m needed for store-released concentrations of free cytosolic Ca2+ to continuously diffuse and autocatalytically activate a nearest neighbor receptor and, thereby, ensure fast cellular response regulation. Furthermore, IP3R molecular regions and all other substrate effecting the superposition interrogate the superposition state with interaction-free measurements to maintain the superposition state until a solution is determined (e.g., Hosten et al., 2006). This computational feat is, of course, accomplished via inferential measurement of Dmax via measurement of index Γmax inherent in the operation of IP3Rs. Although IP3Rs may switch between four different conformational states, the inactivated IP3-bound IP3R conformation is perfectly suited for the initial superposition state of Grover's quantum algorithm because all saltatory and continuous waves affiliated with Γmax retain equal probabilities of manifesting (Figure 2).
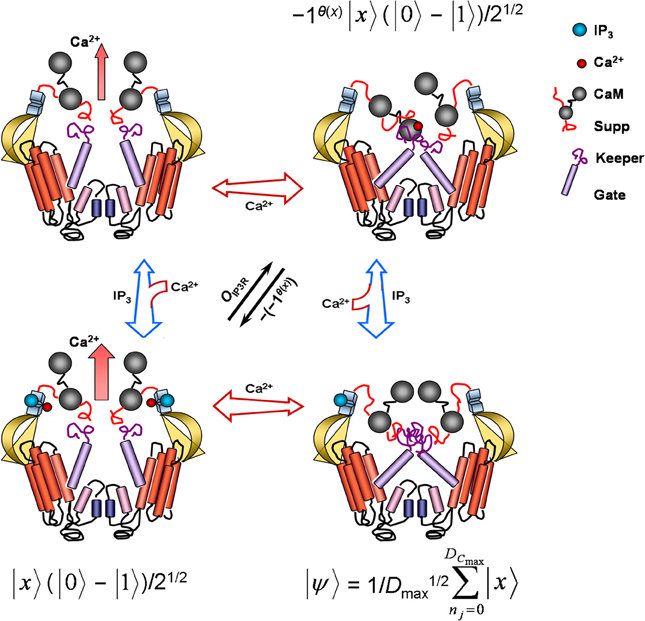
Figure 2. Model of conformation, ion permeability, and corresponding Grover's quantum-algorithm function of an inositol 1,4,5-trisphosphate receptor channel (IP3R). Each cross-section contains two of four complete IP3R subunits. When only cytosolic IP3 (blue sphere) binds, the receptor lumen stays closed and inactive. Cobinding of cytosolic IP3 and Ca2+ (red sphere) to separate high-affinity sites proximal to the IP3-binding domain dissociates suppressor (Suppr), calmodulin (CaM), and gatekeeper (Keeper) regions, repositioning the transmembrane gate (Gate) and activating Ca2+ conductance. In absence of IP3 binding, low-affinity binding of cytosolic Ca2+ to one of two calmodulin heads occludes the ion channel as calmodulin crosslinks with suppressor and gatekeeper regions of adjacent receptor subunit. No ligand binding is accompanied by a small leaking Ca2+ conductance. Free cytosolic proteins, nucleotides, and other substances can facilitate or impair IP3R gating by interacting with the IP3 binding-core, suppressor, and gate-keeper regions. Free endoplasmic-reticulum proteins and Ca2+ may also further modulate pore activity (not shown) via selectivity filters (small blue cylinders) located near pore helices (small rose cylinders). In the superposition state |ψ〉, the IP3R samples all possible index values Γmax marking Dmax, returning an output x denoting a successful or unsuccessful search for shortest times or fastest rates m needed for store-released concentrations of free cytosolic Ca2+ to continuously diffuse and autocatalytically activate a nearest neighbor receptor. This superposition state may be regarded indefinitely stable in saturating IP3 concentrations. A phase shift by OIP3R reversibly inactivates the receptor channel with high free cytosolic Ca2+ concentrations. Another subsequent phase shift reactivates the channel, confirming solution m has been found. See Equation 10 and relevant text for additional details. IP3R conformation representations adapted from Clark and Eisenstein (2013) with permission.
After initializing the IP3R into this IP3-saturated superposition state, which may remain indefinitely so in saturating IP3 concentrations, the final four steps of Grover's quantum algorithm involve execution of Grover's operator—application of the Oracle, a second Hadamard transformation, a conditional phase shift, and the last Hadamard transformation. Grover's operator may be expected to sample |ψ〉 and to then mark problem solutions through the unitary action of the IP3R Oracle:
where again |x〉 denotes the index-register qubit set to |0〉 (i.e., all if values, including value 0 for the inactivated IP3-bound IP3R conformation) and (|0〉 − |1〉)/21/2 is the superposed IP3R-Oracle qubit. The IP3R Oracle phase-shifts |x〉 only when θ(x) returns 1 as a result. Function θ(x), accordingly, may be thought of as the low- and high-affinity Ca2+ binding sites located at the cytosolic end of the IP3R emulating Grover's quantum algorithm (Figure 2). Recall that IP3R activity demonstrates a bell-shaped response profile to cytoplasmic Ca2+ levels. Ca2+ generally excites and blocks IP3Rs in respective low (e.g., ~50 nM–1 μM) and high (e.g., >10 μM) concentrations. Low Ca2+ concentrations capable of inducing sustained Ca2+ waves bind to high-affinity binding sites, changing cation-pore permeability by repositioning the transmembrane gate and activating Ca2+ conductance. In contrast, very low or very high Ca2+ levels keep the IP3R in a closed state. Ca2+ binding sites operating as θ(x) return 1 upon ion-pore opening and otherwise return 0 as a result. Coincident with θ(x) action and all-or-none IP3R stimulation, the IP3R Oracle labels |x〉 by flipping the state from |1〉 to |0〉. Isolating the Oracle's operation to a particular IP3R molecular region and function presents some conceptual difficulties. Arguments could be made for cytoplasmic and ER-lumen channel sensors which detect the presence of cations ions and IP3R interactions with nucleotides, proteins, and other substrate. Regardless, as noted above, once an IP3R becomes active, respective high quantal Ca2+ release exceeding 10 μM near the opening of the same channel begins to cause reversible autoinhibition, presumably via low-affinity Ca2+ binding sites located proximal to IP3R cytoplasmic terminus. Inactivation may last longer than the open-channel period τ. Such an effect is tantamount to the |x〉 phase shift produced by the Oracle of Grover's quantum algorithm (Figure 2). Furthermore, channel inactivation spans the entire Γmax index set, placing the IP3R into another superposition state |ψ〉, as expected from application of the second Hadamard transformation. When IP3R inactivation is finally reversed to a fully excited Ca2+-permeable state, the conditional phase shift, |x〉 → − (− 1)θ(x)|x〉, has been performed for all basis states not equal to |0〉. The last Hadamard transformation puts the register qubit into an equally weighted superposition for possible future Oracle summons. Since τ can be accurately determined to be greater than the time of intersite Ca2+ diffusion for continuous waves (Strier et al., 2003; Solovey and Ponce-Dawson, 2010) and since the IP3R-Oracle phase shift of |x〉 only serves to emphasize timescale differences implicit in Γ of saltatory and continuous Ca2+ waves, the IP3R-mediated fire-diffuse-fire model simulating Grover's quantum algorithm will find target m indexed to im with quadratic improvement in search efficiency. Together, steps 3 to 5 of Grover's quantum algorithm may be expressed as:
where I is the identity matrix (cf. Nielsen and Chuang, 2000). The overall effectiveness of arriving at a solution involving a fast intracluster continuous Ca2+ wave predictably grants neurons better opportunities to initiate local and global response regulation for a variety of necessities.
Testable Predictions and Significance of Grover's Quantum Algorithm for Other CICR Models
A fundamental prediction of the above analytical treatment unaddressed by standard classical interpretations is that, for an individual IP3R-based Grover's quantum algorithm to arrive at a solution m = DC upon sensing/actuating Γmax with multiaffinity IP3R cytosolic Ca2+ binding sites and gating kinetics, quadratic and exponential speed-ups in respective algorithmic search time and wave velocity must coexist, with a maximum algorithmic search time of O(Dmax/DC)1/2 and wave velocity of vC = v2S. If these constraints are not met, algorithm-processing capabilities will approach a classical algorithm taking O(Dmax/DS) time. After only quick inspection, the velocity equations for saltatory, vS = (D/d)g−1Γ, and continuous waves, vC = (D/τ)1/2f−1Γ, may falsely imply to readers that a quantum-search result is impossible. Indeed, the arguments of Ponce-Dawson et al. (1999), for instance, enforce the idea that (global or intercluster) stable saltatory wave propagation is the fastest mode of transmission, at least for oocyte maturation. That conclusion heavily relies on the condition of τS < τC, where receptor-channel open duration τC might be one to two orders of magnitude larger than τS. This type of variation in receptor open time is not experimentally reported for IP3Rs, which tend to be open for a fixed period between 15 and 40 ms depending on receptor subtype irrespective of Ca2+ wave propagation mode (Foskett et al., 2007; Clark and Eisenstein, 2013). And, if τ is instead calculated to be the rise time of Ca2+ concentration across a local grouping of channels contributing to a release event, the divergence between τS and τC can be expected to be no more than one magnitude for most neuronal Ca2+ waves. Taking these aspects into consideration and utilizing examples of experimentally realistic parameter values (e.g., Izu et al., 2001; Strier et al., 2003; Foskett et al., 2007; Clark and Eisenstein, 2013) for d = 2 μm between IP3R clusters, D = 190 μm2/s for continuous waves, D = 15 μm2/s for saltatory waves, and τ = 0.04 s for both continuous and saltatory waves, it becomes apparent continuous waves (β = 1.9, v ≈ (D/τ)1/2 ≈ 69 μm/s) can exceed saltatory wave (β = 0.15, v ≈ D/d ≈ 7.5 μm/s) velocity by greater than a power of 2. Despite being a simple example, these values underscore the plausibility of fast continuous Ca2+ waves displaying characteristics consistent with those predicted by the Grover's quantum-algorithm model. Importantly, the version of the fire-diffuse-fire model used in the present article assumes deterministic channel refractivity and instantaneous buffering for σ without specification of Ca2+ store re-uptake or extracellular extrusion (cf. Ponce-Dawson et al., 1999). Fast and slow Ca2+ buffering and Ca2+ extrusion and sequestration, such as that parameterized in stochastic models (e.g., Coombes and Timofeeva, 2003; Coombes et al., 2004; Keener, 2006), will decelerate and even quench wave propagation, especially lower concentration saltatory waves. But the impact buffering has on wave-conduction modality and velocity is further dependent on model selection. For instance, in the rapid-Ca2+-buffering approximation with or without slow re-uptake (e.g., Strier et al., 2003), the fire-diffuse-fire model further becomes susceptible to error when describing saltatory-wave evolution. Continuous waves, however, largely overcome buffering capacity, even more so when a massive wave-induction event occurs, such as calcium overload from extracellular sources or large ER mobilization. These sorts of effects predictably serve to increase Γ, effective diffusion, wave velocity, and thus fast stable Ca2+ wave search patterns at scales of receptor clusters or larger ER membrane surface areas supported by the Grover's quantum-algorithm model. In situations where waves are quenched or annihilated through Ca2+ buffers, re-uptake, or other factors (Keizer et al., 1998; Thul et al., 2007), the affected area will act as a wave guide to direct the (stochastic or deterministic) initiation and movements of subsequent waves, including planar, spiral, and oscillatory wave profiles capable of sending and storing distinct types of cellular information. With respect to these contexts (cf. Falcke, 2003a), future detailed numerical examination of parameters is needed to identify the continuum limits of fire-diffuse-fire saltatory and continuous wave dynamics and their relation to expression of Grover's quantum algorithm at different scales of CICR organization. As a special case of percolation Ca2+-release/-diffusion universality (cf. Timofeva and Coombes, 2004; Solovey and Ponce-Dawson, 2010), fire-diffuse-fire models conform to different spatiotemporal scales. The Grover's quantum algorithm model, in its conceptual form as a single IP3R operator, is best understood through local CICRs conducting at the scale of single receptor clusters, so that the model may reside in a quantum regime at both thermodynamic and informational degrees of freedom. For local or intracluster wave propagation mode and velocity, where d = 20 nm, the set of above (valid) values for global (i.e., intercluster) continuous and saltatory waves yield respective local (intracluster) continuous waves of β = 19000 with v ≈ 69 μm/s and β = 1500 with v ≈ 19 μm/s. The large values for β indicate conditions supporting saltatory waves at a global scale do not necessarily ensure presence of saltatory waves for intracluster dimensions. Thus, although the algorithm searches for and finds optimal solution m, the boundary between local and global waves needs to be better resolved through numerical examination of Γmax—the critical Grover's quantum-algorithm index of effective diffusion and solution m.
Though a computationally tractable term containing many essential traits, employing the deterministic threshold-dependent Γmax unsatisfactorily weakens the explanatory power of the current model in regard to channel gating kinetics and quantum molecular action underlying formation and interrogation of superposition states, such as |ψ〉. Resolution of state boundaries for the IP3R Grover's quantum-algorithm model therefore should be perfected by redefining Γmax and, naturally, constituent Γ to include buffering, re-uptake, and gating kinetics terms, as is done with more complex wave-evolution equations (e.g., Strier et al., 2003; Timofeva and Coombes, 2004; Thul et al., 2007). Deterministic (DeYoung and Keizer, 1992) and probabilistic (Falcke, 2003b) mathematical models of single IP3R behavior offer richer accounts of the dynamic range expected for channel activity, wave profiles, feedback control, and search patterns inherent in different channel reaction kinetics and structural configurations (Figure 2). Accordingly, Equation 3 may be restated, for benefit of future investigations, as:
Variables Φ1, Φ2, and Φ3 quantify changes in point-source store-operated Ca2+ emission through respective release, re-uptake, and buffering kinetics relative to threshold activation kinetics, ([Ca2+]ωti − [Ca2+]ωt0), with [Ca2+]ωti, [Ca2+]ωt0 = [Ca2+]T − [Ca2+]b. The role of molecular dynamics in channel state is evident in each Φ (cf. DeYoung and Keizer, 1992; Falcke, 2003b); Φ1 = CER/C(FMOpO + FL)([Ca2+]ER − [Ca2+]C), Φ2 = FU[Ca2+]2C/[Ca2+]2C + A2, and Φ3 = KB[Ca2+]C[B]C, where CER/C is the ratio of Ca2+ in ER and cytoplasmic volumes, FMO is maximum outward IP3R Ca2+ flux, FL is IP3R Ca2+ leak flux, FU is maximum ER Ca2+ uptake, pO is the probability of IP3R-channel opening, A is the ER-uptake-activation constant, KB is the Ca2+-buffer-binding constant, [Ca2+]ER and [Ca2+]CF are free ER and cytoplasmic Ca2+ concentrations, and [B]C is the free Ca2+ buffer concentration. While the complexity of these equations may be increased, addition of the open-channel-probability term,
where KCaI is the dissociation constant for IP3R channel inhibition, KIP31 and KIP32 are IP3 dissociation constants, and KCaA is the dissociation constant for IP3R channel activation, gives a much stronger framework for molecular considerations. For example, a consequence of the new Γ formulation is that the initialized index-register qubit becomes . Vector |100〉 is the molecular configuration of composite IP3R binding subunits for each IP3R monomer (Mn) primed for channel activation and Ca2+ conductance. The first, second, and third vector columns of |100〉 represent the respective (saturated) occupied IP3-biding subunit (i.e., 1), the unoccupied high-affinity Ca2+-binding subunit (i.e., 0), and the unoccupied low-affinity Ca2+-binding subunit (i.e., 0). When multiqubit-controlled function θ(x) = 1 = |110〉, the high-affinity subunit binds Ca2+, making the IP3R permeable to cations. The IP3R Grover's operator, also acting as a multiqubit operator through coligand channel gating kinetics, as earlier conjectured, then labels |x〉 by flipping the final two or all column values in conjunction with saturating- or subsaturating-IP3, Ca2+-dependent channel inactivation. The operators's rate and probability of flipping between 0 and 1 for each column and of finding target solution m is expectedly proportional to percent saturation of [Ca2+]C for high- and low-affinity Ca2+-binding subunits and, therefore, proportional to index ΓC, DC, and vC.
The IP3R-based Grover's quantum algorithm of CICR behavior and Ca2+-mediated cellular response regulation thus imparts greater comprehensiveness than possible with traditional single receptor, intracluster, and intercluster models. For instance, above quantum depictions of the IP3R conformational state vector |x〉 uniquely permits study of computationally efficient subcellular superdense coding (Clark, 2010c), quantum learning and memory (Clark, 2010a,b,c,d, 2011, 2012a,b, 2013a; Liu et al., 2013), quantum error diagnosis and correction (Clark, 2010c, 2013a), and quantum encryption (Clark, 2010c, 2013a, in press). Recalling the discussion on the third Bell state, (|00〉 − |11〉)/21/2, the IP3R Grover's quantum-algorithm model may be extended to quantum coupling between two nearest neighbor IP3-saturated activation-primed receptor channels R1 and R2. For R1 and R2, each in superposition state , the entangled bell bases may be deemed bidirectional coupling factors, such as Ca2+ sensitivity, shared between receptors and imposed by level of cytoplasmic modulator (e.g., ATP) saturation on coligand-dependent IP3R allostery (Foskett et al., 2007; Clark and Eisenstein, 2013), where R1 and R2 each possess one unique highly correlated complimentary Bell-state qubit. R1, depending on the action of multiqubit-operators θ and Grover's iteration, may send classical information intrinsic to Γ to R2 in the form of two-bit strings, such as 00 indicating neither sets of Ca2+ binding sites are occupied, 10 indicating only the set of high-affinity Ca2+ binding sites are occupied, or 01 indicating only the set of low-affinity Ca2+ binding sites are occupied. By employing the decoding gate matching R1's classical signal, R2 can decode the superdense signal sent from R1 with less computational expenditure and superior acquired content than possible with classical information processing (cf. Nielsen and Chuang, 2000)1. Not only does this interpretation of channel conformational state and channel-channel communication agree with the IP3R Grover's quantum algorithm and CICR cytophysiology, it also establishes conditions for, among other phenomena, the expression of quantum-molecular memory storage and retrieval at levels of single IP3Rs and IP3R clusters. Since only three of four IP3R monomers must be activated for channel opening, the revised definition of |x〉 implies, in a manner like Ventura and Martinez (1999), single IP3Rs must maintain or remember Mn!/(Mn − 1)! = 4 superposed combinations of: (1) initial activation-primed conformational patterns |100〉 for about 19 ms or less to finish θ (x)-labeling before IP3 dissociates from its IP3R binding subunit, (2) θ(x)-transformed conformational patterns |110〉 for about 600 ms or less to finish the Oracle call before Ca2+ dissociates from its high-affinity IP3R binding subunits, and (3) Oracle-transformed conformational patterns |101〉 or |001〉 for about 5 s or less to finish the algorithm's final phase shift before Ca2+ dissociates from its low-affinity IP3R binding subunits (DeYoung and Keizer, 1992). These superposition states, embedded in |ψ〉, have spatiotemporal estimates well within quantum-decoherence bounds calculated for macromolecules located in live cells constrained by physiologically salient environments (cf. Gutin et al., 1996; McFadden and Al-Khalili, 1999; Cieplak and Hoang, 2003; Davies, 2004) and are experimentally testable by molecular dynamics and CICR simulation as well as bioassays involving wildtype and selectively mutated IP3R isoforms reconstituted in planar lipid bilayers. Although coverage of larger memory structures, such as that formed by multiply coupled IP3R intracluster patterns, is beyond the scope of this article, the same concepts presented for individual IP3Rs are scalable to intracluster dimensions and organization.
Relevance of Grover's Quantum Algorithm for Healthy and Diseased Neurons
In preceding sections, a fire-diffuse-fire model capable of explaining intracluster activity of individual IP3Rs was identified and analytically parameterized as a candidate mechanism for a natural neuronal form of Grover's quantum algorithm. Model accuracy fundamentally depends upon the sensitivity of IP3Rs to physiological parameters characterizing Ca2+-channel molecular structure and function as well as scalable quantum-level gains in classical Ca2+ diffusion rates, Ca2+ wave propagation, and appropriate fast cellular response regulation. Computations made by the IP3R algorithm infer search target solutions for fast classical Ca2+ diffusion rates via interrogation of index variable Γmax associated with detectable free cytosolic Ca2+ concentrations and properties of IP3R channel conductance. Collectively, these features of the model allow the algorithm to operate within quantum computational and thermodynamic regimes without concern of incurring statistical mechanics measurement problems, such as decoherence of processed superposed eigenstates. The model nevertheless yields only a computational first-approximation of Grover's quantum algorithm and needs future refinement by applying sophisticated: (1) relativistic quantum physicochemistry theory to aptly match IP3R protein structure and function with the workspaces and operators of Grover's quantum algorithm, and (2) fire-diffuse-fire or lattice-percolation mathematical treatments of intracluster IP3R activity and CICR dynamics to fully address aspects of reaction-diffusion stochasticity and cytosolic Ca2+ buffering (cf. Izu et al., 2001; Strier et al., 2003; Guisoni and de Oliveira, 2006; Solovey and Ponce-Dawson, 2010). With respect to the latter topic, the present model becomes particularly relevant during actuation of intracellular compartmental Ca2+ loading from interstitial and intracellular cation sources. Even as a preliminary construct, the model implies contexts coincident with moderate to massive fluxes of Ca2+ through cation-permeable integral cell membrane pores and gated channels, such as during synaptic plasticity (Malenka and Bear, 2004), microbial pathogen attack (Clark, 2013b; Clark and Eisenstein, 2013; Clark et al., 2013), pathological oxidative stress (Bénédicte et al., 2012; Clark, 2012c), and neurological disease and aging (Verkhratsky, 2005; Bezprozvanny and Mattson, 2008; Stutzmann and Mattson, 2011), will assist in driving neurons to accelerate response regulation to quantum-level efficiency through induction of stable local and possibly subsequent global continuous Ca2+ waves. From a physiological perspective, dramatic increases in Ca2+ wave velocity and signal transduction at either intracluster or intercluster physical dimensions are impressive and attainable for a all sorts of differentiated eukaryotic cells (cf. Izu et al., 2001), requiring a maximum algorithmic search time of O(Dmax/DC)1/2 and wave velocity of vC = v2S to be realized. However, whether it is activated by stochastic blips of high Ca2+-conductance or deterministic cellular Ca2+ loading, a neuronal version of Grover's quantum algorithm, just like that proposed for other eukaryotic cells, figures to promote advantageous subcellular superdense coding (Clark, 2010c), quantum learning and memory (Clark, 2010a,b,c,d, 2011, 2012a,b, 2013a; Liu et al., 2013), quantum error diagnosis and correction (Clark, 2010c, 2013a), and quantum encryption (Clark, 2010c, 2013a, in press).
Equally significant, the quantum computational value of a receptor-scale Grover's quantum algorithm also can be expected to contribute to surprising classical information processing over much longer intracellular distances and times common to global, multicompartmental Ca2+ signaling. This expectation, unaccounted for by standard (stochastic or deterministic) CICR models, agrees with expression of three-agent quantum teleportation over communication channels transmitting classical bits via the information content of Γ, a circumstance, as described in the above section, that exposes superdense coding and quantum molecular memory for IP3R systems. Limited evidence suggests digital representation of cellular processing is encoded, transmitted, and stored by free intracellular Ca2+ (Plieth, 2005), CaMKII holoenzyme (Hameroff et al., 2010), and other Ca2+-related substrate broadly distributed across affector-effector systems. Individual molecules conveying bitwise information may form higher-order bytes at large concentrations and/or with molecular complexes, such as that reported for six-domain CaMKII encoding of microtubule lattices (Hameroff et al., 2010). Expression of an IP3R-based Grover's quantum algorithm, which may serve as a quantum amplifier and router, supports an estimated forty-fold boost in classical information processing by networked Ca2+ release sites through buffer-dependent superadditive Ca2+ wave densities and velocities (cf. Izu et al., 2001). Such effects presumably enhance operational traits of, for example, signal coincidence detection and integration, bidirectional synaptic plasticity, gene expression, immunodefenses, growth and tropisms, protein modification and transport, cytoskeletal polymerization, endosome formation and other cell functions by rapidly selecting, ordering, and/or counting optional local response regulation choices. The impact on neuronal cyctoskeleton operation alone attests to favorable cascading effects governing geometry of dendritic spines and synaptic cleft widths, intracellular molecular and vesicular trafficking, membrane repair, synaptogenesis, neurite growth, and efficacious synaptic transmission (e.g., Malenka and Bear, 2004; Verkhratsky, 2005; Bezprozvanny and Mattson, 2008; Craddock et al., 2010; Priel et al., 2010; Dent et al., 2011). Using archetypal glutamatergic neurons (e.g., Verkhratsky, 2005; Hagenston and Bading, 2011), which are exquisitely sensitive to fluctuations in intracellualar Ca2+ homeostasis, one can readily extrapolate how the IP3R-based Grover's quantum algorithm figures to help execute ER-dependent signal amplification and integration in healthy cell states of all neurons (Clark, 2012b). Unlike spontaneous punctate store-operated Ca2+ emissions observed for every eukaryotic cell or environmentally triggered massive store-operated Ca2+ overload observed for certain cell types (e.g., oocytes), large temporary elevation of Ca2+ microdomain concentrations following post-synaptic Ca2+ entry through activated NMDARs initiates widespread and differential response regulation in dendritic, somal, and axonal compartments. The amount and spread of inward Ca2+ current is too small to effect most transduction processes. Instead, NMDAR-mediated Ca2+ entry stimulates secondary Ca2+ release from intracellular stores. Information processed by NMDAR-dependent Ca2+ cascades is augmented by glutamate diffusion to extrasynaptic GPCRs responsible for intracellular IP3 generation. Compared to RyRs, IP3Rs tend to have greatest density in ER membranes located in the soma and dendritic shafts of neurons, where coligand IP3 may exert maximum influence (cf. Stutzmann and Mattson, 2011). Thus, an IP3R Grover's quantum algorithm likely guides heterosynaptic activity as well as kinase-induced (e.g., CaMKII and IV) gene transcription and protein synthesis accompanying longer-term structural plasticity, chiefly that of LTP (cf. Fitzjohn and Collingridge, 2002), rather than vesicular events particular to shorter-term presynaptic paired-pulse and post-tetanic facilitation. The algorithm ensures synaptic plasticity maintenance and nuclear response regulation by selecting the best target solutions for fast classical Ca2+ diffusion rates, stable continuous Ca2+ wave modes, and, consequently, activation of kinase and other messenger pathways via detectable free cytosolic Ca2+ concentrations and properties of IP3R channel conductance.
However, the appearance of a quantum-efficient search algorithm in the function of neurons or, for that matter, any other cell type need not necessarily guarantee evolutionary and/or ecological benefit for the cell that implements the algorithm and the host to which the cell belongs. Indeed, viral, bacterial, fungal, and protozoal infectious agents, including, among other pathogens, Human Immunodeficiency Virus type 1 and Trypanosoma parasites, that selfishly coopt neuron intracellular Ca2+ systems can use the algorithm to optimize timing and effectiveness of infection stages against barriers to invasion, pathogenesis, proliferation, and release. While most pathogens deploy well-timed Ca2+-dependent trophic and deleterious strategies, such as genomically encoded proteins and lipopolysacchrides, to exploit host-cell physiology, infected neurons are unusually susceptible to metabolic distress, apoptosis, and additional harmful effects leading to host cognitive impairments (Clark, 2013b; Clark and Eisenstein, 2013; Clark et al., 2013). Similarly, an uninfected, but diseased or aging, neuron can diminish its own cell performance by speeding-up the selection and execution of cellular response regulation incompatible with cell or host survival. Good examples involve neurodegenerative Parkinson's and Alzheimer's diseases, where ER-mediated deficits play major roles in disease severity and progression (cf. Stutzmann and Mattson, 2011). In the case of Alzheimer's disease, persistent upregulation of intracellular Ca2+ concentrations are known to commence and accelerate synaptic loss and amyloid plaque disposition, manifest pathocytological characteristics of the disease. While the excitotoxic nature of Ca2+ dysregulation in Alzheimer's disease is well understood, the exact causes are not (Stutzmann and Mattson, 2011; Popugaeva and Bezprozvanny, 2013). Recent and somewhat controversial evidence indicates that IP3R activation by presenilins, protein products of autosomal inherited mutated genes PS1 and PS2 linked to early onset Alzheimer's disease, may be a major contributing factor. The corresponding heightened IP3R-mediated Ca2+ mobilization means implementation of IP3R Grover's quantum algorithm drives diseased, injured, and/or aging neurons toward faster catastrophic failure than would be otherwise possible with classical response regulation. Hence, the delicate balance between beneficial and detrimental uses of a neuronal version of Grover's quantum algorithm demands thorough theoretical and empirical scrutiny of cellular conditions governing the algorithm's application in both healthy and diseased states.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
1. ^In this example of Bell state |κ〉 10 = (|00〉 + |11〉)/21/2, the first |00〉 and second |11〉 qubits respectively denote equilibrium and high Ca2+ sensitivity induced by saturating and supersaturating free cytoplasmic ATP. R1, which possesses the first qubit of coupling factor |κ〉10, applies θ(x) = 1 = |x〉 = |110〉, interacts |x〉 with its half of the coupling factor, and transmits classical bit-string 10 via Γ. R2, which possesses the second qubit of coupling factor |κ〉10, will next employ its half of the coupling factor and associated quantum-flip gate, θ(x) = 0 → 1 = |x〉 = |110〉, to recover information about the conformational state |x〉 of R1 and initiate its own Grover's operator. This computational scenario, resilient to error, is equivalent to three-agent quantum teleportation transpiring over classical communication channels (cf. Nielsen and Chuang, 2000).
References
Adamatzky, A. (2010). Physarum Machines: Computers from Slime Mould. Singapore: World Scientific Publishing Company.
Ahern, C. A., Eastwood, A. L., Dougherty, D. A., and Horn, R. (2009). An electrostatic interaction between TEA and an introduced pore aromatic drives spring-in-the-door inactivation in Shaker potassium channels. J. Gen. Physiol. 134, 461–469. doi: 10.1085/jgp.200910260
Allbritton, N. L., Meyer, T., and Stryer, L. (1992). Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science 258, 1812–1815. doi: 10.1126/science.1465619
Alvarez, J., and Montero, M. (2002). Measuring [Ca2+] in the endoplasmic reticulum with aequorin. Cell Calcium 32, 251–260. doi: 10.1016/S0143416002001860
Bassik, M. C., Scorrano, L., Oakes, S. A., Pozzan, T., and Korsmeyer, S. J. (2004). Phosphorylation of Bcl-2 regulates ER Ca2+ homeostasis and apoptosis. EMBO J. 23, 1207–1216. doi: 10.1038/sj.emboj.7600104
Baumgardner, J., Acker, K., Adefuye, O., Crowley, S. T., Deloache, W., Dickson, J. O., et al. (2009). Solving a Hamiltonian path problem with a bacteria computer. J. Biol. Eng. 3:11. doi: 10.1186/1754-1611-3-11
Bear, M. F. (2003). Bidirectional synaptic plasticity: from theory to reality. Philos. Trans. R. Soc. B 358, 649–655. doi: 10.1098/rstb.2002.1255
Beck, F., and Eccles, J. C. (1992). Quantum aspects of brain activity and the role of consciousness. Proc. Natl. Acad. Sci. U.S.A. 89, 11357–11361. doi: 10.1073/pnas.89.23.11357
Bénédicte, O., Dolores, D. P., and Mounia, C. (2012). “Mitochondrial calcium signalling: Role in oxidative phosphorylation diseases,” in Bioenergetics, ed K. B. Clark (Rijeka: InTech), 29–62.
Bennett, C. H. (2003). Notes on Landauer's principle, reversible computation, and Maxwell's demon. Stud. Hist. Philos. Mod. Phys. 340, 501–510. doi: 10.1016/S1355-2198(03)00039-X
Bérut, A., Arakelyan, A., Petrosyan, A., Ciliberto, S., Dilenschneider, R., and Lutz, E. (2012). Experimental verification of Landauer's principle linking information and thermodynamics. Nature 483, 187–189. doi: 10.1038/nature10872
Bezprozvanny, I., and Mattson, M. P. (2008). Neuronal calcium mishandling and the pathogenesis of Alzheimer's disease. Trends Neurosci. 31, 454–463. doi: 10.1016/j.tins.2008.06.005
Bianconi, G. (2002a). Growing Cayley trees described by a Fermi distribution. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 66:036116. doi: 10.1103/PhysRevE.66.036116
Bianconi, G. (2002b). Quantum statistics in complex networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 66:056123. doi: 10.1103/PhysRevE.66.056123
Bianconi, G. (2003). Size of quantum networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 67:056119. doi: 10.1103/PhysRevE.67.056119
Bianconi, G., and Barabási, A.-L. (2001). Bose-Einstein condensation in complex networks. Phys. Rev. Lett. 86, 5632–5635. doi: 10.1103/PhysRevLett.86.5632
Bressloff, P. C. (2014). “Calcium waves and sparks,” in Waves in Neural Media: From Single Neuron to Network Fields (New York, NY: Springer), 137–181.
Brookes, J., Hartoutsiou, F., Horsfield, A., and Stoneham, A. (2007). Could humans recognize odor by phonon assisted tunneling? Phys. Rev. Lett. 98:038101. doi: 10.1103/PhysRevLett.98.038101
Bruno, L., Ventura, A. C., Dargan, S., and Ponce-Dawson, S. (2009). Quantifying calcium fluxes underlying calcium puffs in xenopus laevis oocytes. Cell Calcium 47, 273–286. doi: 10.1016/j.ceca.2009.12.012
Bygrave, F. L., and Benedetti, A. (1996). What is the concentration of calcium ions in the endoplasmic reticulum? Cell Calcium 19, 547–551. doi: 10.1016/S0143-4160(96)90064-0
Castillo, P. E., Chiu, C. Q., and Carroll, R. C. (2011). Long-term synaptic plasticity at inhibitory synapses. Curr. Opin. Neurobiol. 21, 328–338. doi: 10.1016/j.conb.2011.01.006
Catterall, W. A. (2010). Signaling complexes of voltage-gated sodium and calcium channels. Neurosci. Lett. 486, 107–116. doi: 10.1016/j.neulet.2010.08.085
Chan, J., Yamazaki, H., Ishiyama, N., Seo, M.-D., Mal, T. K., Michikawa, T., et al. (2010). Structural studies of inositol 1,4,5-trisphosphate receptor: coupling lingand binding to channel gating. J. Biol. Chem. 285, 36092–36099. doi: 10.1074/jbc.M110.140160
Chen, W., Levine, H., and Rappel, W. J. (2008). A mathematical analysis of second messenger compartmentalization. Phys. Biol. 5:46006. doi: 10.1088/1478-3975/5/4/046006
Chen, W., Levine, H., and Rappel, W. J. (2009). Compartmentalization of second messengers in neurons: a mathematical analysis. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 80:041901. doi: 10.1103/PhysRevE.80.041901
Cieplak, M., and Hoang, T. X. (2003). Universality classes in folding times of proteins. Biophys. J. 84, 475–488. doi: 10.1016/S0006-3495(03)74867-X
Clark, K. B. (2010a). Origins of learned reciprocity in solitary ciliates searching grouped ‘courting’ assurances at quantum efficiencies. BioSystems 99, 27–41. doi: 10.1016/j.biosystems.2009.08.005
Clark, K. B. (2010b). Bose-Einstein condensates form in heuristics learned by ciliates deciding to signal “social” commitments. BioSystems 99, 167–178. doi: 10.1016/j.biosystems.2009.10.010
Clark, K. B. (2010c). On classical and quantum error-correction in ciliate mate selection. Commun. Integr. Biol. 3, 374–378. doi: 10.4161/cib.3.4.11974
Clark, K. B. (2010d). Arrhenius-kinetics evidence for quantum tunneling in microbial “social” decision rates. Commun. Integr. Biol. 3, 540–544. doi: 10.4161/cib.3.6.12842
Clark, K. B. (2011). “Live soft-matter quantum computing,” in Computer Search Algorithms, ed E. C. Salander (Hauppauge: Nova Science Publishers Inc), 1–24.
Clark, K. B. (2012a). Social biases determine spatiotemporal sparseness of ciliate mating heuristics. Commun. Integr. Biol. 5, 3–11. doi: 10.4161/cib.18337
Clark, K. B. (2012b). Bioreaction quantum computing without quantum diffusion. NeuroQuantology 10, 646–654. doi: 10.14704/nq.2012.10.4.574
Clark, K. B. (2012c). “Preface,” in Bioenergetics, ed K. B. Clark (Rijeka: InTech), IX–XIX. doi: 10.5772/2083
Clark, K. B. (2013a). Ciliates learn to diagnose and correct classical error syndromes in mating strategies. Front. Microbiol. 4:229. doi: 10.3389/fmicb.2013.00229
Clark, K. B. (2013b). Biotic activity of Ca2+-modulating nontraditional antimicrobial and -viral agents. Front. Microbiol. 4:381. doi: 10.3389/fmicb.2013.00381
Clark, K. B. (in press). Evolution of affective and linguistic disambiguation under social eavesdropping pressures. Behav. Brain Sci.
Clark, K. B., and Eisenstein, E. M. (2013). Targeting host store-operated Ca2+ release to attenuate viral infections. Curr. Top. Med. Chem. 13, 1916–1932. doi: 10.2174/15680266113139990128
Clark, K. B., Eisenstein, E. M., and Krahl, S. E. (2013). Calcium antagonists: a ready prescription for treating infectious diseases? Curr. Top. Med. Chem. 13, 2291–2305. doi: 10.2174/15680266113136660161
Cohen, S., and Greenberg, M. E. (2008). Communication between the synapse and the nucleus in neuronal development, plasticity, and disease. Annu. Rev. Cell Dev. Biol. 24, 183–209. doi: 10.1146/annurev.cellbio.24.110707.175235
Coombes, S., Hinch, R., and Timofeeva, Y. (2004). Receptors, sparks and waves in a fire-diffuse-fire framework for calcium release. Prog. Biophys. Mol. Biol. 85, 197–216. doi: 10.1016/j.pbiomolbio.2004.01.015
Coombes, S., and Timofeeva, Y. (2003). Sparks and waves in a stochastic fire-diffuse-fire model of Ca2+ release. Phys. Rev. E 68:021915. doi: 10.1103/PhysRevE.68.021915
Cooper, W. G. (2009). Evidence of transciptase quantum processing implies entanglement and decoherence of superposition proton states. BioSystems 97, 73–89. doi: 10.1016/j.biosystems.2009.04.010
Craddock, T. J., Tuszynski, J. A., Priel, A, and Freedman, H. (2010). Microtubule ionic conduction and its implications for higher cognitive function. J. Integr. Neurosci. 9, 103–122. doi: 10.1142/S0219635210002421
Craddock, T. J. A., Beauchemin, C., and Tuszynnski, J. A. (2009). Information processing mechanisms in microtubules at physiological temperature: model predictions from experimental tests. BioSystems 97, 28–34. doi: 10.1016/j.biosystems.2009.04.001
Daniel, R., Rubens, J. R., Sarpeshkar, R., and Lu, T. K. (2013). Synthetic analog computation n living cells. Nature 497, 619–623. doi: 10.1038/nature12148
Davies, P. C. W. (2004). Does quantum mechanics play a non-trivial role in life? BioSystems 78, 69–79. doi: 10.1016/j.biosystems.2004.07.001
Dellis, O., Dedos, S. G., Tovey, S. C., Taufiq Ur, R., Dubel, S. J., and Taylor, C. W. (2006). Ca2+ entry through plasma membrane IP3 receptors. Science 313, 229–233. doi: 10.1126/science.1125203
Demetrius, L. (2003). Quantum statistics and allometric scaling of organisms. Physica A 322, 477–490. doi: 10.1016/S0378-4371(03)00013-X
Dent, E. W., Merriam, E. B., and Hu, X. (2011). The dynamic cytoskeleton: backbone of dendritic spine plasticity. Curr. Opin. Neurobiol. 21, 175–181. doi: 10.1016/j.conb.2010.08.013
Dent, M. A., Raisman, G., and Lai, F. A. (1996). Expression of type 1 inositol 1,4,5-trisphosphate receptor during axogenesis and synaptic contact in the central and peripheral nervous system of developing rat. Development 122, 1029–1039.
De Pitta, M., Volman, V., Levine, H., and Ben-Jacob, E. (2009). Multimodal encoding in a simplified model of intracellular calcium signaling. Cogn. Process. 10, S55–S70. doi: 10.1007/s10339-008-0242-y
De Pitta, M., Volman, V., Levine, H., Pioggia, G., De Rossi, D., and Ben-Jacob, E. (2008). Coexistence of amplitude and frequency modulations in intracellular calcium dynamics. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 77:060903. doi: 10.1103/PhysRevE.77.030903
Deutsch, D. (1985). Quantum theory, the Church-Turing Principle and the universal quantum computer. Proc. R. Soc. Lond. A 400, 97. doi: 10.1098/rspa.1985.0070
DeYoung, G. W., and Keizer, J. (1992). A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc. Natl. Acad. Sci. U.S.A. 89, 9895–9899. doi: 10.1073/pnas.89.20.9895
DiCarlo, L., Chow, J. M., Gambetta, J. M., Bishop, L. S., Johnson, B. R., Schuster, D. I., et al. (2009). Demonstration of two-qubit algorithms with a superconducting quantum processor. Nature 460, 240. doi: 10.1038/nature08121
Dolphin, A. C. (2006). A short history of voltage-gated calcium channels. Br. J. Pharm. 147, S56–S62. doi: 10.1038/sj.bjp.0706442
Ehrenfeucht, A., Harju, T., Petre, I., Prescott, D. M., and Rozenberg, G. (2003). Computation in Living Cells: Gene Assembly in Ciliates. Berlin: Springer.
Falcke, M. (2003a). Deterministic and stochastic of intracellular calcium waves. New J. Phys. 5, 1–96. doi: 10.1088/1367-2630/5/1/396
Falcke, M. (2003b). On the role of stochastic channel behavior in intracellular Ca2+ dynamics. Biophys. J. 84, 42–56. doi: 10.1016/S0006-3495(03)74831-0
Ferreri-Jacobia, M., Mak, D.-O. D., and Foskett, J. K. (2005). Translational mobility of the type 3 inositol 1,4,5-trisphosphate receptor Ca2+ release channel in endoplasmic reticulum membrane. J. Biol. Chem. 280, 3824–3831. doi: 10.1074/jbc.M409462200
Feynman, R. P. (1982). Simulating physics with computers. Int. J. Theor. Phys. 21, 467–488. doi: 10.1007/BF02650179
Fioravante, D., and Regehr, W. G. (2011). Short-term forms of presynaptic plasticity. Curr. Opin. Neurobiol. 21, 269–274. doi: 10.1016/j.conb.2011.02.003
Fitzjohn, S. M., and Collingridge, G. L. (2002). Calcium stores and synaptic plasticity. Cell Calcium 32, 405–411. doi: 10.1016/S0143416002001999
Foskett, J. K., White, C., Cheung, K.-H., and Mak, D.-O. D. (2007). Inositol trisphosphate receptor Ca2+ release channels. Physiol. Rev. 87, 593–658. doi: 10.1152/physrev.00035.2006
Fraiman, D., Pando, B., Dargan, S., Parkery, I., and Ponce-Dawson, S. (2006). Analysis of puff dynamics in oocytes: Interdependence of puff amplitude and interpuff interval. Biophys. J. 90, 3897–3907. doi: 10.1529/biophysj.105.075911
Franks, K. M., and Sejnowski, T. J. (2002). Complexity of calcium signaling in synaptic spines. Bioessays 24, 1130–1144. doi: 10.1002/bies.10193
Friedland, A. E., Lu, T. K., Wang, X., Shi, D., Church, G., and Collins, J. J. (2009). Synthetic gene network that count. Science 324, 1199–1202. doi: 10.1126/science.1172005
Fröhlich, H. (1968). Long-range coherence and energy storage in biological systems. Int. J. Quantum Chem. 2, 641–649. doi: 10.1002/qua.560020505
Fröhlich, H. (2004). Evidence for coherent excitation in biological systems. Int. J. Quantum Chem. 23, 1589–1595. doi: 10.1002/qua.560230440
Furuichi, T., Furutama, D., Hakamata, Y., Nakai, J., Takeshima, H., and Mikoshiba, K. (1994). Multiple types of ryanodine receptor/Ca2+ release channels are differentially expressed in rabbit brain. J. Neurosci. 14, 4794–4805.
Furuichi, T., Simon-Chazottes, D., Fujino, I., Yamada, N., Hasegawa, M., Miyawaki, A., et al. (1993). Widespread expression of inositol 1,4,5-trisphosphate receptor type 1 gene (Insp3r1) in the mouse central nervous system. Receptors Channels 1, 11–24.
Furuichi, T., Yoshikawa, S., Miyawaki, A., Wada, K., Maeda, N., and Mikoshiba, K. (1989). Primary structure and functional expression of the inositol 1,4,5-trisphosphate-binding protein P400. Nature 342, 32–38. doi: 10.1038/342032a0
Goñi-Moreno, A., Amos, M., and de la Cruz, F. (2013). Multicellular computing using conjugation for wiring. PLoS ONE 8:e65986. doi: 10.1371/journal.pone.0065986
Grillner, S. (2006). Biological pattern generation: the cellular and computational logic of networks in motion. Neuron 52, 751–766. doi: 10.1016/j.neuron.2006.11.008
Grover, L. K. (1996). “A fast quantum mechanical algorithm for database search,” in Proceedings of the 28th Annual ACM Symposium on the Theory of Computing (New York, NY: AMC Press).
Guisoni, N., and de Oliveira, M. J. (2006). Calcium dynamics on a stochastic reaction-diffusion lattice model. Phys. Rev. E. 74:061905. doi: 10.1103/PhysRevE.74.061905
Gutin, A. M., Abkevich, V. I., and Shakhnovich, E. I. (1996). Chain length scaling of protein folding time. Phys. Rev. Lett. 77, 5433–5436. doi: 10.1103/PhysRevLett.77.5433
Hagenston, A. M., and Bading, H. (2011). Calcium signaling in synapse to nucleus communication. Cold Spring Harb. Perspect. Biol. 3:a004564. doi: 10.1101/cshperspect.a004564
Hameroff, S. (2012). How quantum brain biology can rescue conscious free will. Front. Integr. Neurosci. 6:93. doi: 10.3389/fnint.2012.00093
Hameroff, S. A. (1994). Quantum coherence in microtubules: a neural basis for emergent consciousness. J. Conscious. Stud. 1, 98–118.
Hameroff, S. R., Craddock, T. J., and Tuszynski, J. A. (2010). “Memory bytes” – molecular match for CaMKII phosphorylation encoding of microtubule lattices. J. Integr. Neurosci. 9, 253–267. doi: 10.1142/S0219635210002482
Hartmann, J., Henning, H. A., and Konnerth, A. (2011). mGluR1/TRPC3-mediated synaptic transmission and calcium signaling in mammalian central neurons. Cold Spring Harb. Perspect. Biol. 3:a006726. doi: 10.1101/cshperspect.a006726
Hosten, O., Rakher, M. T., Barreiro, J. T., Peters, N. A., and Kwiat, P. G. (2006). Counterfactual quantum computation through quantum interrogation. Nature 439, 949–952. doi: 10.1038/nature04523
Hu, X., Damjanović, A., Ritz, T., and Schulten, K. (1998). Architecture and mechanism of the light-harvesting apparatus of purple bacteria. Proc. Natl. Acad. Sci. U.S.A. 95, 5935–5941. doi: 10.1073/pnas.95.11.5935
Iino, M. (2006). Ca2+-dependent inositol 1,4,5-trisphosphate and nitric oxide signaling in cerebellar neurons. J. Pharmacol. Sci. 100, 538–544. doi: 10.1254/jphs.CPJ06006X
Ionescu, L., Cheung, K. H., Vais, H., Mak, D.-O. D., White, C., and Foskett, J. K. (2006). Graded recruitment and inactivation of single InsP3 receptor Ca2+-release channels: implications for quantal Ca2+ release. J. Physiol. 573, 645–662. doi: 10.1113/jphysiol.2006.109504
Iwasaki, H., Chiba, K., Uchiyama, T., Yoshikawa, F., Suzuki, F., Ikeda, M., et al. (2002). Molecular characterization of the starfish inositol 1,4,5-trisphosphate receptor and its role during oocyte maturation and fertilization. J. Biol. Chem. 277, 2763–2772. doi: 10.1074/jbc.M108839200
Izu, L. T., Wier, W. G., and Balke, C. W. (2001). Evolution of cardiac calcium waves from stochastic calcium sparks. Biophys. J. 80, 103–120. doi: 10.1016/S0006-3495(01)75998-X
Jaffe, L. (1993). Classes and mechanisms of calcium waves. Cell Calcium 14, 736–745. doi: 10.1016/0143-4160(93)90099-R
Ji, W., Shi, H., Zhang, H., Sun, R., Xi, J., Wen, D., et al. (2013). A formalized design process for bacterial consortia that perform logic computing. PLoS ONE 8:e57482. doi: 10.1371/journal.pone.0057482
Johnson, M. W., Amin, M. H., Gildert, S., Lanting, T., Hamze, F., Dickson, N., et al. (2011). Quantum annealing with manufactured spins. Nature 473, 194–198. doi: 10.1038/nature10012
Karafyllidis, I. G. (2012). Quantum gate circuit model of signal integration in bacterial quorum sensing. IEEE/ACM Trans. Comput. Biol. Bioinform. 9, 571–579. doi: 10.1109/TCBB.2011.104
Keener, J. P. (2006). Stochastic calcium oscillations. Math. Med. Biol. 23, 1–25. doi: 10.1093/imammb/dql002
Keizer, J., Smith, G. D., Ponce-Dawson, S., and Pearson, J. E. (1998). Saltatory propagation of Ca2+ waves by Ca2+ sparks. Biophys. J. 75, 595–600. doi: 10.1016/S0006-3495(98)77550-2
Khrennikov, A. (2009). Quantum-like model of cognitive decision making and information processing. BioSystems 95, 179–187. doi: 10.1016/j.biosystems.2008.10.004
Koch, C., and Segev, I. (2000). The role of single neurons in information processing. Nat. Neurosci. 3, 1171–1177. doi: 10.1038/81444
Ladyman, J., Presnell, S., Short, A. J., and Groisman, B. (2007). The connection between logical and thermodynamic irreversibility. Stud. Hist. Philos. Mod. Phys. 38, 58–79. doi: 10.1016/j.shpsb.2006.03.007
Landauer, R. (1961). Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 5:183. doi: 10.1147/rd.53.0183
Levitan, E. S. (2008). Signaling for vesicle mobilization and synaptic plasticity. Mol. Neurobiol. 37, 39–43. doi: 10.1007/s12035-008-8014-3
Li, C., Enomoto, M., Rossi, A. M., Seo, M.-D., Rahman, T., Stathopulos, P. B., et al. (2013). caBP1, a neuronal Ca2+ sensor protein, inhibits inositol trisphosphate receptors by clamping intersubunit interactions. Proc. Natl. Acad. Sci. U.S.A. 110, 8507–8512. doi: 10.1073/pnas.1220847110
Liu, C. Y., Chen, C., Chang, C. T., and Shih, L. M. (2013). Single-hidden-layer feed-forward quantum neural network based on Grover learning. Neural Netw. 45, 144–150. doi: 10.1016/j.neunet.2013.02.012
Malenka, R. C., and Bear, M. F. (2004). LTP and LTD: An embarrassment of riches. Neuron 55, 5–21. doi: 10.1016/j.neuron.2004.09.012
Matsuno, K. (1999). Cell motility as an entangled quantum coherence. BioSystems 51, 15–19. doi: 10.1016/S0303-2647(99)00009-X
Matsuno, K. (2006). Forming and maintaining a heat engine for quantum biology. BioSystems 85, 23–29. doi: 10.1016/j.biosystems.2006.02.002
McAdams, H. H., and Arkin, A. (2000). Towards a circuit engineering discipline. Curr. Biol. 10, R318–R320. doi: 10.1016/S0960-9822(00)00440-1
McAdams, H. H., and Shapiro, L. (1995). Circuit simulation of genetic networks. Science 269, 650–656. doi: 10.1126/science.7624793
McFadden, J., and Al-Khalili, J. A. (1999). Quantum mechanical model of adaptive mutations. BioSystems 50, 203–211. doi: 10.1016/S0303-2647(99)00004-0
Mehta, P., and Schwab, D. J. (2012). Energetic costs of cellular computation. Proc. Natl. Acad. Sci. U.S.A. 109, 17978–17982. doi: 10.1073/pnas.1207814109
Miura, M., Boyden, P. A., and ter Keurs, H. E. (1999). Ca2+ waves during triggered propagated contractions in intact trabeculae. Determinants of the velocity of propagation. Circ. Res. 84, 1459–1468. doi: 10.1161/01.RES.84.12.1459
Monod, J., and Jacob, F. (1961). General conclusions: telenomic mechanisms in cellular metabolism, growth, and differentiation. Cold Spring Harb. Symp. Quant. Biol. 26, 389–401. doi: 10.1101/SQB.1961.026.01.048
Montero, M., Brini, M., Marsault, R., Alvarez, J., Sitia, R., Pozzan, T., et al. (1995). Monitoring dynamic changes in free Ca2+ concentration in the endoplasmic reticulum of intact cells. EMBO J. 14, 5467–5475.
Naraghi, M., and Neher, E. (1997). Linearized buffered Ca2+ diffusion in microdomains and its implications for calculation of [Ca2+] at the mouth of a calcium channel. J. Neurosci. 17, 6961–6973.
Neher, E. (1998). Vesicle pools and Ca2+ microdomains: new tools for understanding their roles in neurotransmitter release. Neuron 20, 389–399. doi: 10.1016/S0896-6273(00)80983-6
Nielsen, M. A., and Chuang, I. L. (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press.
Norris, V., Zemirline, A., Amar, P., Audinot, J. N., Ballet, P., Ben-Jacob, E., et al. (2011). Computing with bacterial constituents, cells and populations: from bioputing to bactoputing. Theory Biosci. 130, 211–228. doi: 10.1007/s12064-010-0118-4
Okamoto, K., Bosch, M., and Hayashi, Y. (2009). The roles of CaMKII and F-actin in the structural plasticity of dendritic spines: a potential molecular identity of a synaptic tag? Physiology 24, 357–366. doi: 10.1152/physiol.00029.2009
Otsu, H., Yamamoto, A., Maeda, N., Mikoshiba, K., and Tashiro, Y. (1990). Immunogold localization of inositol 1,4,5-trisphosphate (InsP3) receptor in mouse cerebellar Purkinje cells using three monoclonal antibodies. Cell Struct. Funct. 15, 163–173. doi: 10.1247/csf.15.163
Palmer, A. E., Jin, C., Reed, J. C., and Tsien, R. Y. (2004). Bcl-2-mediated alterations in endoplasmic reticulum Ca2+ analyzed with an improved genetically encoded fluorescent sensor. Proc. Natl. Acad. Sci. U.S.A. 101, 17404–17409. doi: 10.1073/pnas.0408030101
Pando, B., Ponce-Dawson, S., Mak, D.-O. D., and Pearson, J. E. (2006). Messages diffuse faster than messengers. Proc. Natl. Acad. Sci. U.S.A. 103, 5338–5342. doi: 10.1073/pnas.0509576103
Patel, A. J. (2001). Why genetic information processing could have a quantum basis. J. Biosci. 26, 145–151. doi: 10.1007/BF02703638
Patel, S., Joseph, S. K., and Thomas, A. P. (1999). Molecular properties of inositol 1,4,5-trisphosphate receptors. Cell Calcium 25, 247–264. doi: 10.1054/ceca.1999.0021
Pinton, P., Pozzan, T., and Rizzuto, R. (1998). The Golgi apparatus is an inositol 1,4,5-trisphosphate-sensitive Ca2+ store, with functional properties distinct from those of the endoplasmic reticulum. EMBO J. 17, 5298–5308. doi: 10.1093/emboj/17.18.5298
Pitt, S. J., Funnell, T. M., Sitsapesan, M., Venturi, E., Rietdorf, K., Ruas, M., et al. (2010). TPC2 is a novel NAADP-sensitive Ca2+ release channel, operating as a dual sensor of luminal pH and Ca2+. J. Biol. Chem. 285, 35039–35046. doi: 10.1074/jbc.M110.156927
Plieth, C. (2005). Calcium: just another regulator in the machinery of life? Ann. Bot. 96, 1–8. doi: 10.1093/aob/mci144
Politi, A., Matthews, J. C., and O'Brien, J. L. (2009). Shor's quantum factoring algorithm on a photonic chip. Science 325, 1221. doi: 10.1126/science.1173731
Ponce-Dawson, S., Keizer, J., and Pearson, J. E. (1999). Fire-diffuse-fire model of dynamics of intracellular calcium waves. Proc. Natl. Acad. Sci. U.S.A. 96, 6060–6063. doi: 10.1073/pnas.96.11.6060
Popugaeva, E., and Bezprozvanny, I. (2013). Role of endoplasmic reticulum Ca2+ signaling in the pathogenesis of Alzheimer's disease. Front. Mol. Neurosci. 6:29. doi: 10.3389/fnmol.2013.00029
Pothos, E. M., and Busemeyer, J. R. (2013a). Can quantum probability provide a new direction for cognitive modeling? Behav. Brain Sci. 36, 255–274. doi: 10.1017/S0140525X12001525
Pothos, E. M., and Busemeyer, J. R. (2013b). Quantum principles in psychology: the debate, the evidence, and the future. Behav. Brain Sci. 36, 310–327. doi: 10.1017/S0140525X12003226
Priel, A., Tuszynski, J. A., and Woolf, N. J. (2010). Neural cytoskeleton capabilities for learning and memory. J. Biol. Phys. 36, 3–21. doi: 10.1007/s10867-009-9153-0
Reimers, J. R., McKemmish, L. K., McKenzie, R. H., Mark, A. E., and Hush, N. S. (2009). Weak, strong, and coherent regimes of Fröhlich condensation and their applications to terahertz medicine and quantum consiousness. Proc. Natl. Acad. Sci. U.S.A. 106, 4219–4224. doi: 10.1073/pnas.0806273106
Rios, E., and Stern, M. D. (1997). Calcium in close quarters: microdomain feedback in excitation-contraction coupling and other cell biological phenomena. Annu. Rev. Biophys. Biomol. Struct. 26, 47–82. doi: 10.1146/annurev.biophys.26.1.47
Ross, C. A., Meldolesi, J., Milner, T. A., Satoh, T., Supattapone, S., and Snyder, S. H. (1989). Inositol 1,4,5-trisphosphate receptor localized to endoplasmic reticulum in cerebellar Purkinje neurons. Nature 339, 468–470. doi: 10.1038/339468a0
Ryugo, D. K., Pongstaporn, T., Wright, D. D., and Sharp, A. H. (1995). Inositol 1,4,5-trisphosphate receptors: immunocytochemical localization in the dorsal cochlear nucleus. J. Comp. Neurol. 358, 102–118. doi: 10.1002/cne.903580107
Schwartz, J. M., Stapp, H. P., and Beauregard, M. (2005). Quantum physics in neuroscience and psychology: a neurophysiological model of mind-brain interaction. Philos. Trans. R. Soc. B 360, 1309–1327. doi: 10.1098/rstb.2004.1598
Selvaraj, S., Sun, Y., and Singh, B. B. (2010). TRPC channels and their implications for neurological diseases. CNS Neurol. Disord. Drug Targets 9, 94–104. doi: 10.2174/187152710790966650
Sener, M. K., Jolley, C., Ben-Shem, A., Fromme, P., Nelson, N., Croce, R., et al. (2005). Comparison of the light-harvesting networks of plant and cyanobacterial photosystem I. Biophys. J. 89, 1630–1642. doi: 10.1529/biophysj.105.066464
Shannon, C. E. (1938). A symbolic analysis of relay and switching circuits. Trans. Am. Inst. Electr. Eng. 57, 713–723. doi: 10.1109/T-AIEE.1938.5057767
Shannon, C. E. (1948a). A mathematical theory of communication. Bell System Tech. J. 27, 379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x
Shannon, C. E. (1948b). A mathematical theory of communication. Bell System Tech. J. 27, 623–656. doi: 10.1002/j.1538-7305.1948.tb00917.x
Sharp, A. H., McPherson, P. S., Dawson, T. M., Aoki, C., Campbell, K. P., and Snyder, S. H. (1993). Differential immunohistochemical localization of inositol 1,4,5-trisphosphate- and ryanodine-sensitive Ca2+ release channels in rat brain. J. Neurosci. 13, 3051–3063.
Sharp, A. H., Nucifora, F. C. Jr., Blondel, O., Sheppard, C. A., Zhang, C., Snyder, S. H., et al. (1999). Differential cellular expression of isoforms of inositol 1,4,5-triphosphate receptors in neurons and glia in brain. J. Comp. Neurol. 406, 207–220.
Shor, P. W. (1994). “Algorithms for quantum computation: Discrete logarithms and factoring,” in Preceedings of the 25th Annual Symposium on Foundations of Computer Science (Los Alamitos, CA: IEEE Press).
Shuai, J., Rose, H. J., and Parker, I. (2006). The number and spatial distribution of IP3 receptors underlying calcium puffs in xenopus oocytes. Biophys. J. 91, 4033–4044. doi: 10.1529/biophysj.106.088880
Siso-Nadal, F., Fox, J. J., Laporte, S. A., Hebert, T. E., and Swain, P. S. (2009). Cross-talk between signaling pathways can generate robust oscillations in calcium and cAMP. PLoS ONE 4:e7189. doi: 10.1371/journal.pone.0007189
Smith, I. F., and Parker, I. (2009). Imaging the quantal substructure of single IP3R channel activity during Ca2+ puffs in intact mammalian cells. Proc. Natl. Acad. Sci. U.S.A. 106, 6404–6409. doi: 10.1073/pnas.0810799106
Solovey, G., and Ponce-Dawson, S. (2010). Intra-cluster percolation of calcium signals. PLoS ONE 5:e8997. doi: 10.1371/journal.pone.0008997
Solov'yov, I. A., Chang, P. Y., and Schulten, K. (2012). Vibrationally assisted electron transfer mechanism of olfaction: myth or reality? Phys. Chem. Chem. Phys. 14, 13861–13871. doi: 10.1039/c2cp41436h
Stella, L., Santoro, G. E., and Tosatti, E. (2005). Optimization by quantum annealing: lessons from simple cases. Phys. Rev. B 72:014303. doi: 10.1103/PhysRevB.72.014303
Strier, D. E., Ventura, A. C., and Ponce-Dawson, S. (2003). Saltatory and continuous calcium waves and the rapid buffering approximation. Biophys. J. 85, 3575–3586. doi: 10.1016/S0006-3495(03)74776-6
Stutzmann, G. E., and Mattson, M. P. (2011). Endoplasmic reticulum Ca2+ handling in excitable cells in health and disease. Pharmacol. Rev. 63, 700–727. doi: 10.1124/pr.110.003814
Supattapone, S., Worley, P. F., Baraban, J. M., and Snyder, S. H. (1988). Solubilization, purification, and characterization of an inositol trisphosphate receptor. J. Biol. Chem. 263, 1530–1534.
Szilárd, L. (1929). Uber die entropieverminderung in einen thermodynamischen system bei eingriffen intelligenter wesen. Z. Phys. 53, 840–856. doi: 10.1007/BF01341281
Tanimura, A., Tojyo, Y., and Turner, R. J. (2000). Evidence that type I, II, III inositol 1,4,5-trisphosphate receptors can occur as integral plasmamembrane proteins. J. Biol. Chem. 275, 27488–27493. doi: 10.1074/jbc.M004495200
Taylor, C. W., da Fonseca, P. C. A., and Morris, E. P. (2004). IP3 receptors: the search for structure. Trends Biochem. Sci. 29, 210–219. doi: 10.1016/j.tibs.2004.02.010
Taylor, C. W., Genazzani, A. A., and Morris, S. A. (1999). Expression of inositol trisphosphate receptors. Cell Calcium 26, 237–251. doi: 10.1054/ceca.1999.0090
Taylor, C. W., and Tovey, S. C. (2010). IP3 receptors: toward understanding their activation. Cold Spring Harb. Perspect. Biol. 2:a004010. doi: 10.1101/cshperspect.a004010
Tegmark, M. (2000). The importance of quantum decoherence in brain processes. Phys. Rev. E 61, 4194–4206. doi: 10.1103/PhysRevE.61.4194
Thul, R., Smith, G. D., and Coombes, S. (2007). A biodomain threshold model of propagating calcium waves. J. Math. Biol. 56, 435–463. doi: 10.1007/s00285-007-0123-5
Timofeva, Y., and Coombes, S. (2004). Directed percolation in a two-dimensional stochastic fire-diffuse-fire model. Phys. Rev. E Nonlin. Soft Matter Phys. 70:062901. doi: 10.1103/PhysRevE.70.062901
Turin, L. (1996). A spectroscopic mechanism for primary olfactory reception. Chem. Senses 21, 773–791. doi: 10.1093/chemse/21.6.773
Turing, A. M. (1936). On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. 2-42, 230.
Ur-Rahman, T., Skupin, A., Falcke, M., and Taylor, C. W. (2009). Clustering of IP3 receptors by IP3 retunes their regulation by IP3 and Ca2+. Nature 458, 655–659. doi: 10.1038/nature07763
Vandersypen, L. M. K., Steffen, M., Breyta, G., Yannoni, C. S., Sherwood, M. H., and Chuang, I. L. (2001). Experimental realization of Shor's quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887. doi: 10.1038/414883a
Ventura, D., and Martinez, T. (1999). “A quantum associative memory based on Grover's algorithm,” in Proceedings of the International Conference on Artificial Neural Networks and Genetic Algorithms, eds A. Dobnikar, N. C. Steele, D. W. Pearson, and R. F. Albrecht (Vienna: Springer-Verlag), 22–27. doi: 10.1007/978-3-7091-6384-9_5
Verkhratsky, A. (2005). Physiology and pathophysiology of the calcium store in the endoplasmic reticulum of neurons. Physiol. Rev. 85, 201–279. doi: 10.1152/physrev.00004.2004
Wigner, E. P. (1957). Relativistic invariance and quantum phenomena. Rev. Mod. Phys. 29, 255–268. doi: 10.1103/RevModPhys.29.255
Wigner, E. P. (1981). “Review of the quantum mechanical measurement problem,” in Quantum Optics, Experimental Gravity, and Measurement Theory, eds P. Meystre and M. O. Scully (New York, NY: Plenum Press), 43–63.
Wolynes, P. G. (2009). Some quantum weirdness in physiology. Proc. Natl. Acad. Sci. U.S.A. 106, 17247–17248. doi: 10.1073/pnas.0909421106
Wright, A., and Vissel1, B. (2012). The essential role of AMPA receptor GluA2 subunit RNA editing in the normal and diseased brain. Front. Mol. Neurosci. 5:34. doi: 10.3389/fnmol.2012.00034
Yao, Y., Choi, J., and Parker, I. (1995). Quantal puffs of intracellular Ca2+ evoked by inositol trisphosphate in xenopus oocytes. J. Physiol. 482, 533–553.
Keywords: biotechnology, calcium-induced calcium reactions (CICRs), cellular decision making, classical and quantum computation, inositol 1,4,5-trisphosphate receptors (IP3Rs), intracellular calcium, neuronal plasticity, quantum molecular networks and memory
Citation: Clark KB (2014) Basis for a neuronal version of Grover's quantum algorithm. Front. Mol. Neurosci. 7:29. doi: 10.3389/fnmol.2014.00029
Received: 15 January 2014; Accepted: 31 March 2014;
Published online: 17 April 2014.
Edited by:
Andreas Vlachos, Goethe University Frankfurt, GermanyReviewed by:
Peter Jedlicka, Goethe University, GermanyGillian Queisser, Goethe Center for Scientific Computing, Germany
Copyright © 2014 Clark. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kevin B. Clark, 4229 SE Harney Street, Portland, OR 97206-0941, USA e-mail: kbclarkphd@yahoo.com
 Kevin B. Clark
Kevin B. Clark