- 1Department of Physiology and Pharmacology “V. Erspamer”, Sapienza Università di Roma, Rome, Italy
- 2Molecular Pathology, Istituto Neurologico Mediterraneo (IRCCS), Parco Tecnologico, Pozzilli, Italy
Nicotinic acetylcholine receptors (nAChRs) are cation-selective ligand-gated ion channels exhibiting variable Ca2+ permeability depending on their subunit composition. The Ca2+ permeability is a crucial functional parameter to understand the physiological role of nAChRs, in particular considering their ability to modulate Ca2+-dependent processes such as neurotransmitter release. The rings of extracellular and intracellular charged amino acid residues adjacent to the pore-lining TM2 transmembrane segment have been shown to play a key role in the cation selectivity of these receptor channels, but to date a quantitative relationship between these structural determinants and the Ca2+ permeability of nAChRs is lacking. In the last years the Ca2+ permeability of several nAChR subtypes has been experimentally evaluated, in terms of fractional Ca2+ current (Pf, i.e., the percentage of the total current carried by Ca2+ ions). In the present study, the available Pf-values of nAChRs are used to build a simplified modular model describing the contribution of the charged residues in defined regions flanking TM2 to the selectivity filter controlling Ca2+ influx. This model allows to predict the currently unknown Pf-values of existing nAChRs, as well as the hypothetical Ca2+ permeability of subunit combinations not able to assemble into functional receptors. In particular, basing on the amino acid sequences, a Pf > 50% would be associated with homomeric nAChRs composed by different α subunits, excluding α7, α9, and α10. Furthermore, according to the model, human α7β2 receptors should have Pf-values ranging from 3.6% (4:1 ratio) to 0.1% (1:4 ratio), much lower than the 11.4% of homomeric α7 nAChR. These results help to understand the evolution and the function of the large diversity of the nicotinic receptor family.
Introduction
Ca2+ ions are able to permeate through the cation-selective pentameric nicotinic acetylcholine receptors (nAChRs; Katz and Miledi, 1969; Bregestovski et al., 1979; Eusebi et al., 1980; for review see Fucile, 2004). This Ca2+ entry pathway plays relevant physiopathological roles, for instance positively modulating neurotransmitter release in neuronal presynaptic terminals (Wonnacott, 1997) or damaging the muscle endplates in patients with slow-channel congenital myasthenic syndromes (Engel et al., 2003). For these reasons the quantification of the amount of Ca2+ flowing through a particular nAChR subtype is a relevant goal to understand its functional role and the physiological consequences of its activation. The very first methodological approach to quantitatively determine the ion channel Ca2+ permeability was based on the measurement of the reversal potential shift upon changes in [Ca2+]o, and then calculating the PCa/PNa ratio using the Goldman-Hodgkin-Katz constant field assumptions (Lewis, 1979). A second experimental approach was later introduced by Erwin Neher and his group in the early 90's, basing on the possibility to simultaneously record transmembrane currents with the Patch-Clamp techniques and the [Ca2+]i changes with fluorescence microscopy (Zhou and Neher, 1993; Neher, 1995), and leading to the direct measurement of the fractional Ca2+ current, usually indicated as Pf and representing the percentage of the total current carried by Ca2+ ions. A careful comparison of the two methods (Burnashev et al., 1995) indicated that the second one was more advisable, being independent from the constant field assumptions, not always respected in real ion channels. In the last two decades the Ca2+ permeability of several nAChRs has been characterized in terms of Pf, using the Neher's methodological approach (see references in Table 2 and in Fucile, 2004). These studies highlighted a large variability of Ca2+ permeability, with Pf-values ranging from 1.5% (human α4β4; Lax et al., 2002) to 22% (rat α9α10; Fucile et al., 2006b), and raise questions about the physiological meaning and the structural determinants of this large spectrum. In particular, seminal studies have clearly indicated a fundamental role of charged amino acid rings flanking the transmembrane region TM2, for single-channel conductance (Imoto et al., 1988), cation selectivity (Corringer et al., 1999), and Ca2+ permeation (Bertrand et al., 1993). It is widely known and accepted that these highly conserved charged residues, when mutated, may profoundly alter the ion selectivity filter of nAChRs, leading to significant changes of ion permeability (Bertrand et al., 1993; Corringer et al., 1999). Despite this long established knowledge, the possibility to quantitatively relate the Ca2+ permeability to the presence of charged residues in key positions is lacking. Though in theory it is possible to build a molecular model to simulate the channel energy profile and numerically calculate the Ca2+/Na+ flow ratio for each distinct nAChR subtype (Song and Corry, 2009), this approach would be extremely onerous. In this study the sum of the electrical charges present in different regions of the channels have been considered as modular components of the selectivity filter and quantitatively analyzed, with the aim to understand the contribution of each region to the Ca2+ influx through nAChRs, and to build a quantitative model able to predict Pf-values from the amino acid sequences of nAChR subunits.
Methods
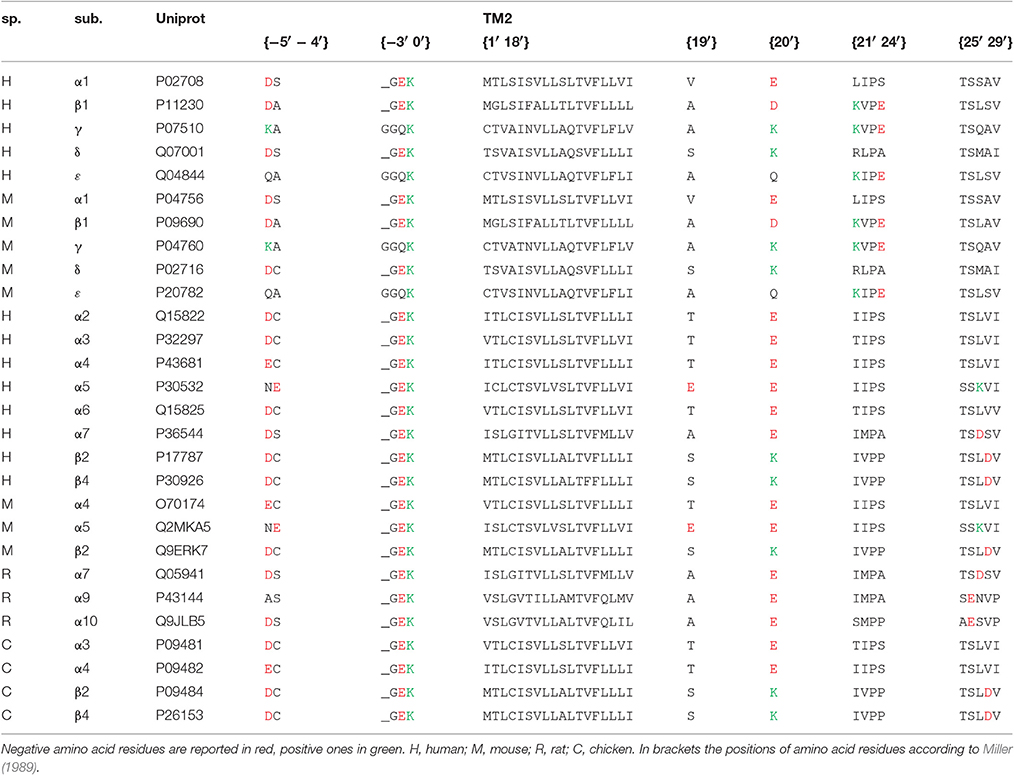
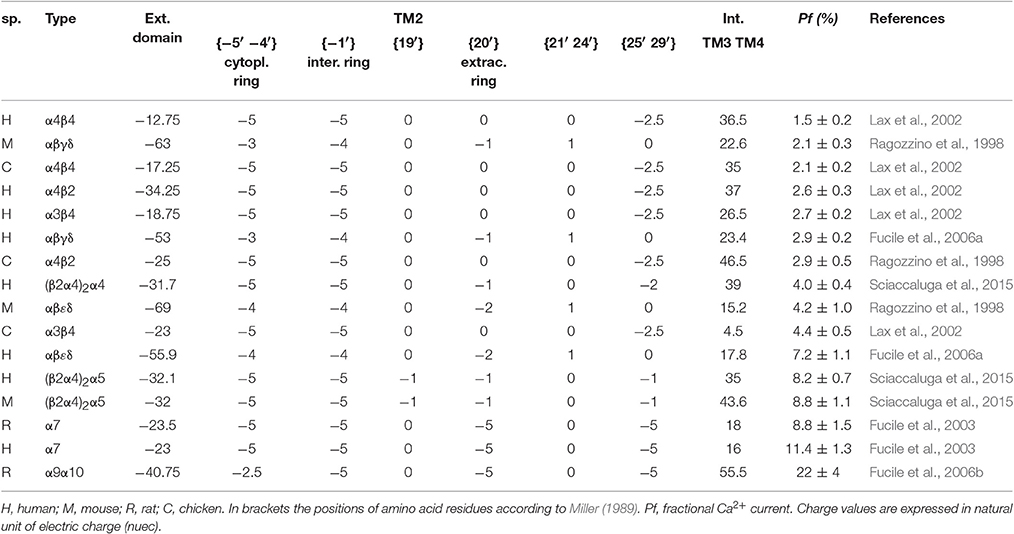
The amino acid sequences of all nicotinic subunits considered in this study have been obtained by the Uniprot website, and all the Uniprot accession numbers are given in Table 1. For each pentameric subunit assembly considered, the sum of electrical charges arising from negative (aspartate, glutamate) and positive (arginine, histidine, lysine) residues has been calculated in different portions of the channel. In particular each histidine was considered contributing +0.1 in the extracellular solution (pH 7.4) or +0.4 in the intracellular one (pH 7.0). The channel sections considered in the study were: (1) the extracellular region, composed by both N- and C-terminal side of the five subunits; (2) the intracellular region between TM3 and TM4 transmembrane regions; (3) the {−5′ −4′} positions in the intracellular side of TM2 (where 0′ is the conserved lysine residue immediately preceding TM2, according to Miller, 1989); (4) the {−1′} position; (5) the {19′} position in the extracellular side of TM2; (6) the {20′} position; (7) the {21′–24′} positions; (8) the {25′–29′} positions. The fractional Ca2+ current (Pf, i.e., the percentage of the total current carried by Ca2+ ions) values were obtained from previous measurements made in our laboratory, in the same (or very similar) experimental conditions (for details see references in Table 2). When considering experiments in which the transfection of two subunits could result in the coexpression of two alternative stoichiometry, the mean charge distribution has been used. All the information used to build the model are reported in Table 1 (subunits) and in Table 2 (assembled receptors).
Fitting Procedure
To evaluate the contribution of charged amino acids placed in different region of nicotinic subunits to the Ca2+ permeability of distinct nAChRs, a very simple methodological approach has been followed. In the presence of a single energy barrier ΔG, if all other parameters are fixed (membrane potentials, temperature), and if the flowing ions are present only at the outside of the membrane at fixed concentration, the flowing current will be proportional to e−ΔG/RT (Hille, 2001).
In these conditions,
where the term CCa is constant when ion concentrations, potential and temperature are fixed, and ΔGCa is the energy barrier value for Ca2+ ions.
The same relation is valid for Na+ fluxes:
Given that, when Na+ and Ca2+ are the only permeant ions, by definition
then
With a strong oversimplification, the term ΔGCa – ΔGNa has been substituted by a weighted sum of the electric charges (Δqi) associated to the negative (glutamate, aspartate) and positive (lysine, arginine, histidine) amino acids present in 1, 2, 3, or 5 (n) different regions of the nicotinic subunits. Furthermore, the constant ratio CNa/CCa has been substituted by a single constant const. Thus, Pf data have been fitted with the following equation:
For each fit the R2-value has been reported, and the predicted Pf-values have been compared with the real ones. The const and ki-values obtained by fitting the charge distribution in the five out the eight regions were then used to predict the Pf-values of several pentameric subunit combination giving rise to unreal or existing nicotinic receptors. The natural unit of electrical charge (nuec) has been used as charge unit throughout the paper.
Results
The first aim of this study was to verify if the Ca2+ permeability of 16 different nAChRs (measured in terms of fractional Ca2+ current, Pf) correlated with the local distribution of the electrical charges associated to the amino acid sequences of their subunits (Table 1). The first region analyzed was the extracellular domain composed by both the large N-terminal and the short C-terminal segments. A net negative charge characterizes the extracellular domains of all nAChRs, with a clear segregation of muscle receptors, exhibiting a stronger negativity comprised between −50 and −70, while in all other nAChRs the charge sum was comprised between −10 and −40 (Table 2 and Figure 1A). By contrast, in the intracellular regions composed by the five segments between transmembrane helices TM3 and TM4, there was a large prevalence of positive charges (Table 2 and Figure 1B), likely contributing to interaction sites with intracellular negative molecules. Linear regressions were used to estimate the correlation between observed Pf and charge values, and the resulting coefficients and statistics indicated for both intracellular and extracellular regions the absence of any correlation. These portions of the receptor-channel were no longer considered for further analysis in the present study. Then the charges near the TM2 helices were analyzed to look for significant correlations with Ca2+ permeability. Six distinct locations were chosen, forming two intracellular rings, i.e., position {−5′ −4′}, and the position {−1′}, or four extracellular rings: position {19′}; position {20′}; position {21′ 24′}; position {25′ 29′}. It is worth to note some characteristic features of the charge distribution described in Tables 1, 2 and in Figure 1: (a) in position {20′} α subunits always exhibit a negative charge, while positive charges are present in most non-α subunits; (b) position {19′} exhibits a negative charge only when an α5 subunit is present; (c) the charge distribution of position {−1′} and position {21′ 24′} are overlapping, yielding the same linear regression results, due to the fact that the muscle receptors in both position exhibit a one-unit more positive charge than all other receptors. This last observation makes the two positions redundant, and in the following analysis only position {−1′} will be considered. The data and the regressions reported in Figures 1C–H clearly indicated significant negative correlations when considering charges in position {20′} (Figure 1F) or in position {25′29′} (Figure 1H), with p < 0.05 for angular coefficients. In other positions the linear regressions still yielded negative angular coefficients, supporting the notion that in general the increase of the overall negative charge corresponds to an enhancement of Ca2+ fluxes, with the only exception of position {−5′ −4′}.
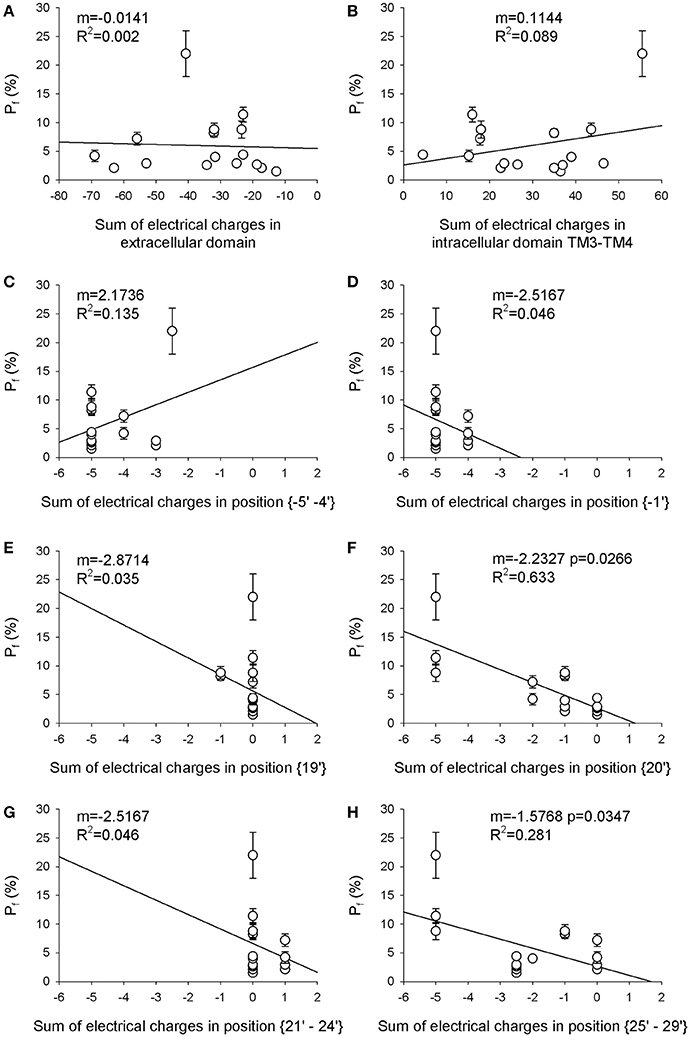
Figure 1. Electrical charge in the TM2 extracellular ring (position 20′) is the main determinant of Ca2+ permeability. The sum of the electrical charges associated with charged amino acids in eight different regions of each nAChR reported in Table 1 has been calculated and plotted against the Pf-value of the same nAChR. (A) extracellular domain; (B) intracellular domain between TM3 and TM4; (C) position {−5′ −4′} (where 0′ is the conserved lysine residue immediately preceding TM2, according to Miller, 1989); (D) position {−1′}; (E) position {19′}; (F) position {20′}; (G) position {21′–24′}, (H) position {25′–29′}. In each panel the angular coefficient m of the linear regression is reported, expressed in nuec−1, as well as the R2-value, to evaluate the fit. Please note the significant linear correlations reported in (F) for position {20′}, and in (H) for position {25′–29′}, with the indicated p-values.
The second aim of this study was to quantitatively estimate the contribution of the charges distributed in different receptor regions to the nAChR Ca2+ permeability, to have a better understanding of the structural determinants of this relevant physiological parameter, and to try to build a simple model allowing to predict the effect of different subunit compositions or mutations on the Pf-value. Thus, a progressive multidimensional fitting procedure was adopted (for details see Section Methods), in which the sigmoidal function described by Equation (5) was used to best fit the 16 known Pf-values, starting using as independent variable the sum of electrical charges in position {20′}, where it was observed the most significant correlation. Successive fit procedures used the electrical charges present in two or more positions as independent variables, progressively choosing the positions giving the higher R2-values. In Figure 2 the sigmoidal curves best fitting the Pf-values are plotted using as abscissa the weighted sum of the charges in different receptor regions, where the ki constant were derived from the fitting procedure. For each fit the comparison between observed and predicted Pf-values is reported. As expected from the linear regression analysis, the best monodimensional fit was obtained using the position {20′} data as independent variable (Figure 2A). However, this charge distribution alone is not able to explain large differences in Ca2+ permeability. When adding a second independent variable, the best result was obtained with position {−5′ −4′}, differently from what could be expected from linear analysis. This effect may be due to the similar pattern of charge-receptor association exhibited by both position {20′} and position {25′ 29′} (Figures 1F,H), not really helping to discriminate between different receptors. By contrast, the introduction of the data of position {−5′ −4′} clearly helped to discriminate between highly Ca2+ permeable nAChRs (e.g., α7 vs. α9α10 nAChRs; Figure 2B). The best fit result in terms of statistical significance was obtained with three independent variables, i.e., the charge distributions of position {20′}, position {−5′ −4′} and position {19′} (Figure 2C). Including all these data, the Pf of α5-containing nAChRs were much better accounted for, the R2-value was strongly enhanced and all the ki constants were statistically significant (p < 0.05, see legend of Figure 2 for details). However, several subunit combinations present distinct charge patterns in the other locations, thus a final fit based on all five independent regions was made, providing the best correlation between observed and predicted Pf-values (Figure 2D; R2 = 0.95).
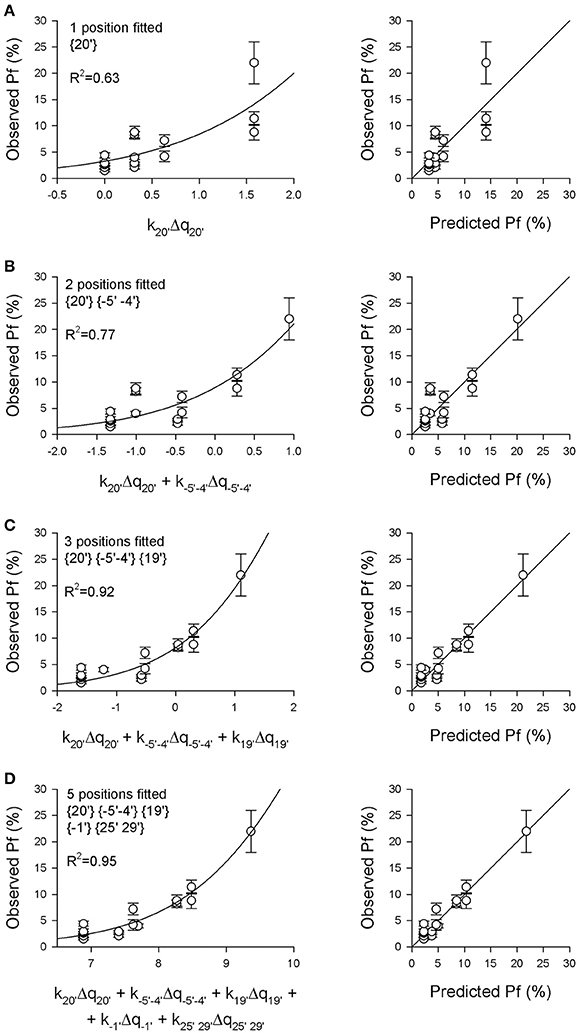
Figure 2. The Pf-values of 16 different nAChRs are predicted by a model based on the charge distributions in five distinct pore regions. The experimentally measured Pf-values reported in Table 2 were plotted against the weighted sum of the electrical charges Δqi present in different pore regions, as indicated, with the multiplicative ki-values allowed to vary in order to best fit the data, according to Equation (see Section Methods for details). (A) Best fit of Pf-values (left) and comparison between observed and predicted Pf-values (right), using as independent variable only the electrical charge present in the extracellular position {20′}, representing the main determinant of Ca2+ permeability (const = 29.5, p = 0.0029; k20′ = −0.316, p = 0.0003). (B) The charge distributions in position {20′} and in the intracellular position {−5′ −4′} were used as independent variables (const = 10.2, p = 0.0501; k20′ = −0.321, p = 0.0001; k−5′−4′ = 0.266, p = 0.013). (C) The charge distributions in positions {20′}, {−5′ −4′} and {19′} were used as variables (const = 11.2, p = 0.0084; k20′ = −0.3806, p < 0.0001; k−5′−4′ = 0.3197, p = 0.0002; k19′ = −1.260, p = 0.0002). Note the substantial improvement of the fit adding the charges in position {19′} to the analysis, which now takes into account the negative glutamate residue present in α5 subunits in this position. (D) The electrical charges of the five indicated positions were used as variables (const = 41917, p = 0.82; k20′ = −0.5654, p = 0.0134; k−5′−4′ = 0.3521, p < 0.0001; k19′ = −0.0798, p = 0.90; k−1′ = −1,975, p = 0.0816; k25′ 29′ = 0.491, p = 0.1598). Note the high R2-value and the excellent agreement between observed and predicted Pf-values.
The resulting ki constants values, reported in Table 3, were then used to weight the relative contribution of each position and to build a simple modular model linking the electrical charges present in the examined amino acid rings to a Pf-value. In this way it was possible to predict the hypothetical Pf-values of several combinations of human subunits which are not able to assemble into functional nAChRs in living cells (in red in Table 3), but also of existing receptors whose Ca2+ permeability has not yet experimentally measured (in green in Table 3). The proposed model indicates very high Pf-values (>50%) for homomeric nAChRs constituted by α subunits (from α1 to α6), all lacking the five negative charges in position {25′ 29′} in the α7 subunit, which determine for this last receptor the reduction to 10.4%. Interestingly, if the charges in position {−1′} are removed, as for α7E237A, the Pf-value is 0.0, exactly as expected from the direct measure of Ca2+ permeability reported for this mutated nAChR (Bertrand et al., 1993). The model has been applied to the α7β2 nAChRs (Wu et al., 2016), which may be expressed with different subunit ratios. The higher the number of β2 subunits, the lower the Ca2+ permeability, due to the increasing positivity in position {20′}. Other heteromeric combination are reported, with higher values for combinations with α5 subunit. Thus, the proposed model suggests a dramatically high Ca2+ permeability for non-existing homomeric nAChRs likely eliminated during evolution, describes the effect on Ca2+ permeability of known mutations, and allows to reasonably predict the Pf-values of physiologically relevant heteromeric nAChRs.
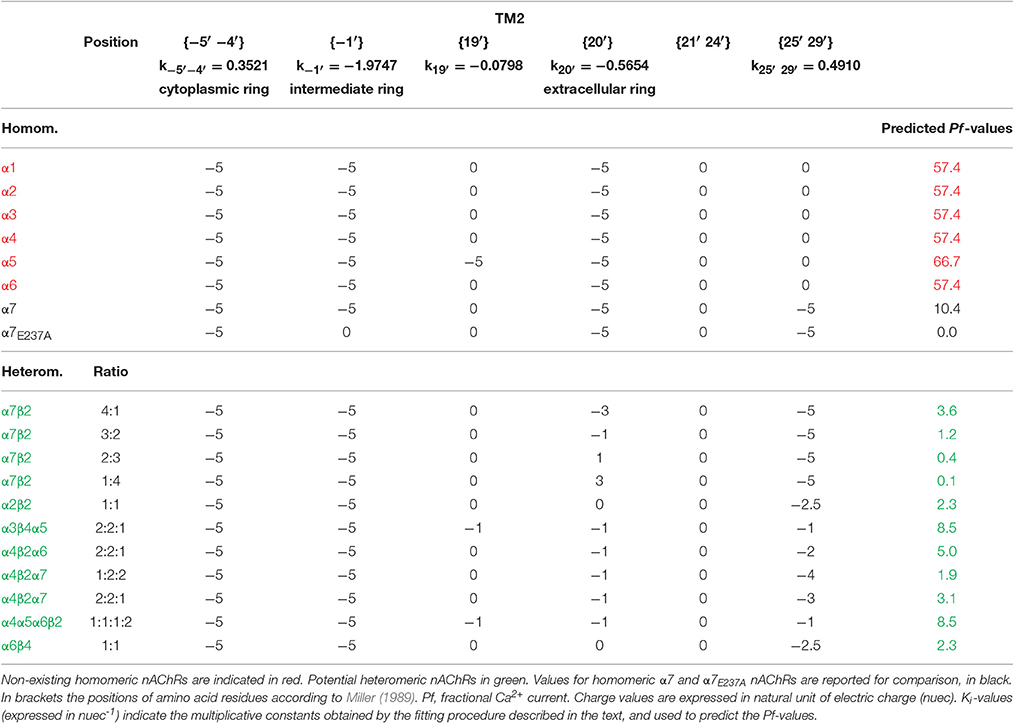
Table 3. Charge distribution and predicted Pf-values of human nAChRs with different subunit composition.
Discussion
The main results of this study are represented by an improved picture of the functional relations between the distribution of electrical charges and Ca2+ fluxes in nAChRs and the availability of a new simple model to predict Pf-values associated to any (possible or impossible) pentameric combination of nicotinic subunits. Relating known Pf-values to the charge spatial design of the corresponding nAChRs provided several observations.
First, the Ca2+ permeability of these receptors does not depend on the total amount of charge present in the large extracellular or intracellular domains. All extracellular domains have an overall negative charge, with muscle nAChRs exhibiting the most negative values in this region. The extracellular overall negative charge may be functionally relevant for agonist binding, assembly, posttranslational modification, and interactions with extracellular molecular apparatus, in particular for muscle nAChRs which cooperate with a large number of molecular components at the endplate (Witzemann et al., 2013), but there is no evidence of a role in shaping Ca2+ permeability. This finding becomes relevant when considering that Ca2+ permeability of nAChRs can be modulated by extracellularly applied drugs, such as verapamil or salbutamol (Piccari et al., 2011), which in theory could act in the large extracellular nAChR vestibule. Analogously, though all intracellular domains formed by the five TM3-TM4 segments exhibit overall positive charges, hosting interactions sites for cytoplasmic factors (Stokes et al., 2015), there is no correlation between Pf-values and the amount of electrical charges present at this location.
By contrast, significant relationships between Ca2+ permeability and charged residues are evident when considering the regions closer to TM2: in particular the best linear correlation is observed in the extracellular ring, in position {20′}, where increasing negativity is significantly linked to higher Pf-values. Interestingly, although a similar relation is evident also in residues slightly farther in respect to TM2, in position {25′ 29′}, in the model arising from the fitting procedure this two regions appear to differently contribute to the Ca2+ permeability: negative residues in position {20′}enhance it, while those in position {25′ 29′} reduce it. The same kind of inverse relation is present also in the cytoplasmic ring (position {−5′ −4′}). These results confirm for nAChRs the observation that negatively charged sites may either facilitate Ca2+ flow, reducing the electrostatic energy profile for divalent cations, or counteract it, in particular if the negative residues represent a high affinity Ca2+ binding site in which Ca2+ itself may produce a long lasting electrical repulsion for other incoming divalent cations (Yang et al., 1993).
Other charge distributions are extremely conserved: in particular, both at the intermediate ring and at position {21′ 24′}) only muscle nAChRs exhibit a slight less negative charge than all other receptors. In the intermediate ring a reduction of the negative charge is associated to reduced Pf-values, as strongly confirmed by α7E237A homomeric nAChR: this mutation has been shown to abolish Ca2+ permeability (Bertrand et al., 1993) and consistently the present model reports only for this mutated nAChRs a zero Pf-value.
The α5 subunit presents a unique feature: it is the only nicotinic subunit to host a negative residue in position {19′} and a positive one in position {25′ 29′}, both conferring high Ca2+ permeability to α5* nAChRs. A hypothetical α5 homomeric nAChR would exhibit, according to this model, the highest calculated Pf-value, and the replacement by an α5 subunit of any other α subunit in a heteromeric nAChR always enhance Ca2+ permeability. This finding is of relevant physiological interest, given the role of α5* nAChRs in modulating the self-administration of nicotine and the overall use of tobacco (Fowler et al., 2011). The polymorphic variant α5D398N, associated with a higher incidence of smoking and lung cancer (Bierut et al., 2008), does not affect the Ca2+ permeability of these receptors, but appears to be differently modulated by Ca2+ in the cytoplasmic domain (Sciaccaluga et al., 2015). Given the high Ca2+ permeability, an attractive hypothesis is that Ca2+ may modulate the same α5* nAChRs which it flows through, with the α5D398N subunit dysfunctional in this process, leading to less nicotine aversion (Frahm et al., 2011) and increased nicotine self-administration.
All these observations confirm and summarize several previous reports concerning the role of charged amino acids in some of the regions considered in this study (Bertrand et al., 1993; Corringer et al., 1999; Tapia et al., 2007; Sciaccaluga et al., 2015), and allow a comprehensive description of the different selectivity filters exhibited by distinct nAChRs. In summary, it is possible to group nAChRs in three functional categories: Na+-selective; Ca2+-selective; non-selective between Na+ and Ca2+. The last ones, in fixed conditions, allow the flow of Ca2+ and Na+ ions with the same probability, and should exhibit, in 2 mM [Ca2+]i and 140 mM [Na+]i, a Pf-value of 2.8%, due to the relative abundance of the two ions. Indeed, many heteromeric nAChRs exhibit Pf around this value (see Table 2). Ca2+-selective nAChRs favor Ca2+ over Na+ due to a complex organization of the charges placed in strategic positions: (i) an increased negativity in the immediate intra- and extra-cellular proximity of the channel pore (positions {−1′}, {19′}, and {20′}), with a mechanism similar to the selectivity filter of voltage-gated Ca2+ channels (Yang et al., 1993); (ii) a decreased negativity in farther intra- and extra-cellular positions ({−5′ −4′} and {25′ 29′}). The vice-versa is true for Na+-selective nAChRs, as for instance α7E237A or α4β4. In Figure 3 the spatial distributions of charged amino acid residues has been shown for several paradigmatic nAChRs, with upward arrows indicating positions in which higher negativity implies higher Ca2+ permeability.
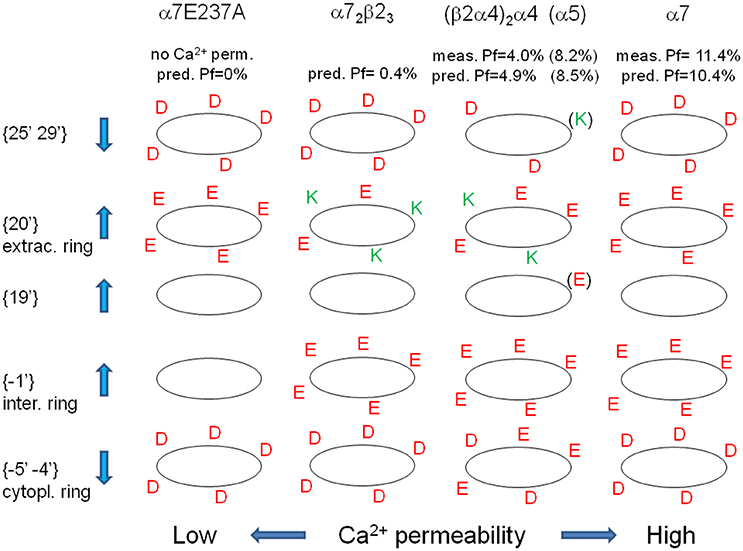
Figure 3. Spatial distribution of charged amino acid residues in the proximity of the channel pore, for different nAChRs. For the indicated nAChRs the distribution of positive (green) and negative (red) amino acid residues is reported for each distinct TM2-flanking regions. Up- and down-wards arrows indicate rings in which higher negativity is associated with higher or lower Ca2+ permeability, respectively. In brackets the residues present if an α5 subunit replace an α4 subunit, yielding a strong increase in Ca2+ permeability. For each nAChR measured and predicted Pf-values are reported (in brackets for α5-contaning nAChRs).
The analysis of the predicted Pf-values reported in Table 3 leads to interesting observations. First, the surprisingly high Ca2+ permeability of all nAChRs ideally formed by non-existing homomeric combinations of different α subunits. All these values are much higher than the Pf observed and predicted for homomeric α7 nAChR, suggesting that the exclusion of these receptors could be due to evolutionary processes opposing excessive Ca2+ entry and excitotoxicity. In contrast with the usual association “α7-high Ca2+ permeability,” this subunit appears to be the α subunit less able to create the conditions for large Ca2+ fluxes through nAChRs, and exactly for this reason it could have been allowed by evolution to form homomeric receptors. This hypothesis is supported also by model predictions in which α7 substitutes for a different α subunit in heteromeric nAChRs, as for α4(β2)2(α7)2 vs. (α4β2)2α4 (Pf-values of 1.9 vs. 4.0%, respectively). In this view, the insertion in heteromeric neuronal nAChRs of β2 or β4 subunits together with α2, α3, α4, or α6 appears a protective process, adding positive lysine residues instead of negative ones in the extracellular ring (position {20′}). The same role of “Ca2+ limiter” is played by β2 subunit in heteromeric nAChRs containing α7 subunits: decreasing the ratio α7:β2 considerably lowers the Pf-values of the corresponding nAChRs, suggesting distinct physiological roles for different subunit combinations forming these recently described heteromeric receptors (Wu et al., 2016).
The predictive model presented in this study is based on a strongly oversimplified interpretation of the distribution of charged amino acid residues in selected regions of the receptor-channels, and presents clear limitations. First, it is well-known that the nAChR Ca2+ permeability depend also on uncharged residues (Di Castro et al., 2007), and the geometry of the pore, highly relevant for ion-ion and ion-amino acid interactions, has been weakly taken into account, with a literature-based but still arbitrary regional partition. A deeper analysis should use molecular dynamics techniques to numerically build, for each individual nAChR, a proper model taking into account all the interactions able to modulate Ca2+ fluxes, in an extremely complex picture.
Furthermore, in the present study the overall extracellular distribution of charged amino acids did not appear to affect Ca2+ fluxes through nAChRs, but a single acid residue in the extracellular domain has been shown to strongly decrease the Ca2+ permeability of α7 nAChR (rat aspartate 44, corresponding to human aspartate 42; Colón-Sáez and Yakel, 2014), clearly indicating the a more complex analysis would be necessary.
Despite all these known limitations, the present simple approach led to a surprisingly good description of the relation between charge distribution and Pf-values, strongly indicating that the amount of negative charges in strategic intracellular and extracellular TM2-flanking regions represents the main determinant of nAChR Ca2+ permeability.
This study might be useful as a starting point to build future more sophisticated models, to plan future experimental studies on poorly described heteromeric nAChRs (see Table 3), and to give hints to evaluate the Ca2+ permeability of other receptor-channels, as for instance the highly relevant insect nAChRs, representing the major target for several insecticides (Dupuis et al., 2012) and never described in terms of Pf. Furthermore, in the future this approach could be useful to analyze other classes of ligand-gated channels, such as ionotropic glutamate receptors, whose Ca2+ permeability play a major role in synaptic plasticity and in neurodegenerative processes. The knowledge of the molecular mechanisms regulating Ca2+ entry through ion channels represents the first step to understand how to modulate it, in particular when and where the excessive accumulation of intracellular Ca2+ endangers cell health and survival.
Author Contributions
SF designed, wrote and approved this study, and agrees to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Bertrand, D., Galzi, J. L., Devillers-Thiéry, A., Bertrand, S., and Changeux, J. P. (1993). Mutations at two distinct sites within the channel domain M2 alter calcium permeability of neuronal alpha 7 nicotinic receptor. Proc. Natl. Acad. Sci. U.S.A. 90, 6971–6975. doi: 10.1073/pnas.90.15.6971
Bierut, L. J., Stitzel, J. A., Wang, J. C., Hinrichs, A. L., Grucza, R. A., Xuei, X., et al. (2008). Variants in nicotinic receptors and risk for nicotine dependence. Am. J. Psychiatry 165, 1163–1171. doi: 10.1176/appi.ajp.2008.07111711
Bregestovski, P. D., Miledi, R., and Parker, I. (1979). Calcium conductance of acetylcholine-induced endplate channels. Nature 279, 638–639. doi: 10.1038/279638a0
Burnashev, N., Zhou, Z., Neher, E., and Sakmann, B. (1995). Fractional calcium currents through recombinant GluR channels of the NMDA, AMPA and kainate receptor subtypes. J. Physiol. 485, 403–418. doi: 10.1113/jphysiol.1995.sp020738
Colón-Sáez, J. O., and Yakel, J. L. (2014). A mutation in the extracellular domain of the α7 nAChR reduces calcium permeability. Pflugers Arch. 466, 1571–1579. doi: 10.1007/s00424-013-1385-y
Corringer, P. J., Bertrand, S., Galzi, J. L., Devillers-Thiéry, A., Changeux, J. P., and Bertrand, D. (1999). Mutational analysis of the charge selectivity filter of the alpha7 nicotinic acetylcholine receptor. Neuron 22, 831–843. doi: 10.1016/S0896-6273(00)80741-2
Di Castro, A., Martinello, K., Grassi, F., Eusebi, F., and Engel, A. G. (2007). Pathogenic point mutations in a transmembrane domain of the epsilon subunit increase the Ca2+ permeability of the human endplate ACh receptor. J. Physiol. 579, 671–677. doi: 10.1113/jphysiol.2007.127977
Dupuis, J., Louis, T., Gauthier, M., and Raymond, V. (2012). Insights from honeybee (Apis mellifera) and fly (Drosophila melanogaster) nicotinic acetylcholine receptors: from genes to behavioral functions. Neurosci. Biobehav. Rev. 36, 1553–1564. doi: 10.1016/j.neubiorev.2012.04.003
Engel, A. G., Ohno, K., Shen, X. M., and Sine, S. M. (2003). Congenital myasthenic syndromes: multiple molecular targets at the neuromuscular junction. Ann. N.Y. Acad. Sci. 998, 138–160. doi: 10.1196/annals.1254.016
Eusebi, F., Miledi, R., and Takahashi, T. (1980). Calcium transients in mammalian muscles. Nature 284, 560–561. doi: 10.1038/284560a0
Fowler, C. D., Lu, Q., Johnson, P. M., Marks, M. J., and Kenny, P. J. (2011). Habenular α5 nicotinic receptor subunit signalling controls nicotine intake. Nature 471, 597–601. doi: 10.1038/nature09797
Frahm, S., Slimak, M. A., Ferrarese, L., Santos-Torres, J., Antolin-Fontes, B., Auer, S., et al. (2011). Aversion to nicotine is regulated by the balanced activity of β4 and α5 nicotinic receptor subunits in the medial habenula. Neuron 70, 522–535. doi: 10.1016/j.neuron.2011.04.013
Fucile, S. (2004). Ca2+ permeability of nicotinic acetylcholine receptors. Cell Calcium 35, 1–8. doi: 10.1016/j.ceca.2003.08.006
Fucile, S., Renzi, M., Lax, P., and Eusebi, F. (2003). Fractional Ca2+ current through human neuronal α7 nicotinic acetylcholine receptors. Cell Calcium 34, 205–209. doi: 10.1016/S0143-4160(03)00071-X
Fucile, S., Sucapane, A., and Eusebi, F. (2006b). Ca2+ permeability through rat cloned α9-containing nicotinic acetylcholine receptors. Cell Calcium 39, 349–355. doi: 10.1016/j.ceca.2005.12.002
Fucile, S., Sucapane, A., Grassi, F., Eusebi, F., and Engel, A. G. (2006a). The human adult subtype ACh receptor channel has high Ca2+ permeability and predisposes to endplate Ca2+ overloading. J. Physiol. 573, 35–43. doi: 10.1113/jphysiol.2006.108092
Hille, B. (2001). Ion Channels of Excitable Membranes. 3rd Edn. Sunderland: Sinauer Associates, Inc.
Imoto, K., Busch, C., Sakmann, B., Mishina, M., Konno, T., Nakai, J., et al. (1988). Rings of negatively charged amino acids determine the acetylcholine receptor channel conductance. Nature 335, 645–648. doi: 10.1038/335645a0
Katz, B., and Miledi, R. (1969). Spontaneous and evoked activity of motor nerve endings in calcium Ringer. J. Physiol. 203, 689–706. doi: 10.1113/jphysiol.1969.sp008887
Lax, P., Fucile, S., and Eusebi, F. (2002). Ca2+ permeability of human heteromeric nAChRs expressed by transfection in human cells. Cell Calcium 32, 53–58. doi: 10.1016/S0143-4160(02)00076-3
Lewis, C. A. (1979). Ion-concentration dependence of the reversal potential and the single channel conductance of ion channels at the frog neuromuscular junction. J. Physiol. 286, 417–445. doi: 10.1113/jphysiol.1979.sp012629
Miller, C. (1989). Genetic manipulation of ion channels: a new approach to structure and mechanism. Neuron 2, 1195–1205. doi: 10.1016/0896-6273(89)90304-8
Neher, E. (1995). The use of fura-2 for estimating Ca buffers and Ca fluxes. Neuropharmacology 34, 1423–1442. doi: 10.1016/0028-3908(95)00144-U
Piccari, V., Deflorio, C., Bigi, R., Grassi, F., and Fucile, S. (2011). Modulation of the Ca2+ permeability of human endplate acetylcholine receptor-channel. Cell Calcium 49, 272–278. doi: 10.1016/j.ceca.2011.03.002
Ragozzino, D., Barabino, B., Fucile, S., and Eusebi, F. (1998). Ca2+ permeability of mouse and chick nicotinic acetylcholine receptors expressed in transiently transfected human cells. J. Physiol. 507, 749–757. doi: 10.1111/j.1469-7793.1998.749bs.x
Sciaccaluga, M., Moriconi, C., Martinello, K., Catalano, M., Bermudez, I., Stitzel, J. A., et al. (2015). Crucial role of nicotinic α5 subunit variants for Ca2+ fluxes in ventral midbrain neurons. FASEB J. 29, 3389–3398. doi: 10.1096/fj.14-268102
Song, C., and Corry, B. (2009). Role of acetylcholine receptor domains in ion selectivity. Biochim. Biophys. Acta 1788, 1466–1473. doi: 10.1016/j.bbamem.2009.04.015
Stokes, C., Treinin, M., and Papke, R. L. (2015). Looking below the surface of nicotinic acetylcholine receptors. Trends Pharmacol. Sci. 36, 514–523. doi: 10.1016/j.tips.2015.05.002
Tapia, L., Kuryatov, A., and Lindstrom, J. (2007). Ca2+ permeability of the (α4)3(β2)2 stoichiometry greatly exceeds that of (α4)2(β2)3 human acetylcholine receptors. Mol. Pharmacol. 71, 769–776. doi: 10.1124/mol.106.030445
Witzemann, V., Chevessier, F., Pacifici, P. G., and Yampolsky, P. (2013). The neuromuscular junction: Selective remodeling of synaptic regulators at the nerve/muscle interface. Mech. Dev. 130, 402–411. doi: 10.1016/j.mod.2012.09.004
Wonnacott, S. (1997). Presynaptic nicotinic ACh receptors. Trends Neurosci. 20, 92–98. doi: 10.1016/S0166-2236(96)10073-4
Wu, J., Liu, Q., Tang, P., Mikkelsen, J. D., Shen, J., Whiteaker, P., et al. (2016). Heteromeric α7β2 nicotinic acetylcholine receptors in the brain. Trends Pharmacol. Sci. 37, 562–574. doi: 10.1016/j.tips.2016.03.005
Yang, J., Ellinor, P. T., Sather, W. A., Zhang, J. F., and Tsien, R. W. (1993). Molecular determinants of Ca2+ selectivity and ion permeation in L-type Ca2+ channels. Nature 366, 158–161. doi: 10.1038/366158a0
Keywords: fractional Ca2+ current, ion selectivity, nicotinic subunits, charged amino acids, nicotine dependence
Citation: Fucile S (2017) The Distribution of Charged Amino Acid Residues and the Ca2+ Permeability of Nicotinic Acetylcholine Receptors: A Predictive Model. Front. Mol. Neurosci. 10:155. doi: 10.3389/fnmol.2017.00155
Received: 31 March 2017; Accepted: 08 May 2017;
Published: 29 May 2017.
Edited by:
Piotr Bregestovski, Aix-Marseille University, FranceReviewed by:
Jerrel Yakel, National Institute of Environmental Health Sciences (NIH), United StatesAlexey Rossokhin, Research Center of Neurology, Russia
Copyright © 2017 Fucile. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sergio Fucile, sergio.fucile@uniroma1.it
 Sergio Fucile
Sergio Fucile