Functional significance of complex fluctuations in brain activity: from resting state to cognitive neuroscience
David Papo- Computational Systems Biology Group, Center for Biomedical Technology, Universidad Politécnica de Madrid, Madrid, Spain
Behavioral studies have shown that human cognition is characterized by properties such as temporal scale invariance, heavy-tailed non-Gaussian distributions, and long-range correlations at long time scales, suggesting models of how (non observable) components of cognition interact. On the other hand, results from functional neuroimaging studies show that complex scaling and intermittency may be generic spatio-temporal properties of the brain at rest. Somehow surprisingly, though, hardly ever have the neural correlates of cognition been studied at time scales comparable to those at which cognition shows scaling properties. Here, we analyze the meanings of scaling properties and the significance of their task-related modulations for cognitive neuroscience. It is proposed that cognitive processes can be framed in terms of complex generic properties of brain activity at rest and, ultimately, of functional equations, limiting distributions, symmetries, and possibly universality classes characterizing them.
Introduction
Ideally, cognitive psychology aims at providing a description of the space of cognitive processes, the nature of each of them, and the way they interact. Cognitive processes are unobservable regimes of an underlying dynamical system. However, they can be reconstructed by considering that sequences of observable quantities, sampled during the execution of controlled cognitive tasks, are the output of this system.
In behavioral studies, the underlying system is construed as a black box function, with given tasks, supposed to summon given cognitive processes, as inputs, and observable behavioral performance as outputs.
Typically, a quantitative description of cognitive processes consists in calculating means and standard deviations of trial-averaged performance measures, implicitly assuming an underlying Gaussian distribution (which is completely described by its first two moments), and statistical independence of the various trials.
However, the results of numerous behavioral studies [see (Kello et al., 2010) for a review] cannot be reconciled with Gaussian distribution functions. Power-law distributions and temporal scaling have consistently been found for relatively short time series (~102–103 time points) (Gilden, 2001) of inter-trial fluctuations in performance levels, although finer temporal scales have also been considered, particularly for motor tasks (Cabrera and Milton, 2002; Diniz et al., 2011).
Behavioral scaling laws contain important information about cognitive function, viz. on how (non observable) components of cognition interact (Holden et al., 2009). For instance, power-law scaling of trial-to-trial performance variations has been taken to arise from multiplicative interactions among interdependent processes, suggesting that the mechanisms through which processes interact to give rise to cognitive performance may be no less fundamental than single components' functioning principles (Holden et al., 2009; Ihlen and Vereijken, 2010).
The scaling properties appear to be modulated in a task-specific way. For example, increasing task difficulty accelerates the transition from 1/f to white noise in decision-making time series (Correll, 2008; Grigolini et al., 2009).
Cognitive function is naturally understood as originating from brain activity, and quantitatively characterized in terms of the brain properties associated with the execution of given cognitive tasks. Cortical activity adds spatial and temporal scales unavailable in behavioral studies, so that scaling can be assessed within single process realizations.
The brain generates fluctuations with complex scaling properties (Novikov et al., 1997; Linkenkaer-Hansen et al., 2001; Gong et al., 2002, 2007; Freeman et al., 2003; Bianco et al., 2007; Suckling et al., 2009; Freyer et al., 2009), even in the absence of exogenous perturbations or changes in parameters controlling its activity. Only few experimental studies (Linkenkaer-Hansen et al., 2004; Popivanov et al., 2006; Buiatti et al., 2007; Bhattacharya, 2009; He et al., 2010; Ciuciu et al., 2011, 2012; Zilber et al., 2012) investigated the scaling properties of task-related brain activity, or their relationship with behavioral ones (Monto et al., 2008; Palva et al., 2013; Kello, 2013).
The aetiology and functional meaning of brain fluctuation scaling have been discussed at length. For example, the presence of spatial and temporal inverse-power law correlations is often taken to suggest that the brain lives near a second order phase transition, a condition optimizing information processing and storage, and dynamic response (Chialvo, 2010).
Here, instead, we discuss ways in which fluctuation properties can be used as metrics making cognitive function observable.
A Random Walk Around Brain Activity's Space
To garner a physical intuition of the meaning of brain fluctuations one can think of brain activity as the motion of a random walker making steps of size x at given times t, or, in the continuous limit, of a diffusing macroscopic particle in a complex high-dimensional space, subject to viscous friction, with a time scale τm, and driven by an additive random force with a characteristic time τη (Hsu and Hsu, 2009).
The relationship between τm and τη determines how the system evolves in this complex space, including traveled distances, velocity, degree to which the space is visited, time to reach a given target point, system's memory of its own trajectory within the landscape, relationship between spontaneous and task-related activity, and ultimately how microscopic fluctuations renormalize to give rise to observable macroscopic statistical properties (Papo, 2013b).
If spontaneous fluctuations were Markovian, with Gaussian δ-correlated noise, and τη « τm, the particle would undergo normal diffusion: the step length would be taken from the Maxwell-Boltzmann equilibrium distribution, and the mean-square distance (MSD) traveled by the particle would scale linearly with time 〈|x(t)|2〉 ~ t. Under general conditions, the first passage time from a prescribed phase space domain would be characterized by a universal distribution, independent of the jump length distribution (Sparre Andersen, 1953). For t » τm, the temporal autocorrelation of velocity fluctuations would behave as C(τ) ~ exp(−t/τm), with a unique characteristic time τm. The dynamics would hop without memory from one configuration to another, eventually visiting the whole phase space.
However, the properties of observed brain fluctuations are inconsistent with the Markovian approximation (Fraiman and Chialvo, 2012). Spontaneous fluctuations show temporal and spatial scale-free statistics (Novikov et al., 1997; Linkenkaer-Hansen et al., 2001; Gong et al., 2002; Stam and de Bruin, 2004; Expert et al., 2010; van de Ville et al., 2010). The MSD scales as 〈 |x(t)|2〉 ~ t2ν with ν ≠ 1/2, so that its diffusion is anomalous, and indeed even strongly anomalous (Suckling et al., 2009; Ciuciu et al., 2011, 2012; Zilber et al., 2012), with the q-th moments scaling as 〈|x(t)|q〉 ~ tqν(q), with ν(q) ≠ const (Castiglione et al., 1999). Appropriately rescaled average temporal fluctuations collapse onto universal scaling functions (Sherrington, 2010; Friedman et al., 2012; Shriki et al., 2012).
Exponential relaxation is replaced by complex scaling, e.g., of a Mittag-Leffler type (Bianco et al., 2007), with stretched exponential relaxation at microscopic scales (t < τ), and inverse power-law scaling C(τ) ~ τ−α, for t » τ, so that, for α ≤ 1, the correlation time τC = ∫ξ0C(t)dt diverges, leading to a scale-free process with memory. The system undergoes ageing (Bianco et al., 2007): correlations are time-inhomogeneous, with a dependence on the time of application of a given field, history-dependent (Sherrington, 2010), and weakly non-ergodic (Bianco et al., 2007), as some phase space region may take extremely long times to be visited (Bouchaud, 1992).
Activity shows statistical and dynamical intermittency: on the one hand, although large-scale fluctuations are approximately Gaussian, non-Gaussian fluctuations appear at higher frequencies (Freyer et al., 2009). On the other hand, activity is characterized by alternating laminar and turbulent phases (Gong et al., 2007; Allegrini et al., 2010, 2011).
Understanding Brain Fluctuations
The statistical and dynamical properties of brain fluctuations contain information on the structure of the functional space within which brain dynamics evolves, and on the style, as it were, with which brain dynamics explores its dynamic repertoire (Ghosh et al., 2007; Deco et al., 2011; Betzel et al., 2012).
From Single Steps to Complete Walks
Scaling laws indicate that the walker takes steps of all sizes, from local to extremely long jumps.
More importantly, probability distributions contain information on how observable large-scale outcomes arise from the interactions of many small-scale processes (Frank, 2009). Observed probability distributions can be thought of as reproducible macroscopic features emerging from the sum of highly fluctuating individual elements. It is natural to see this sum as representing the temporal aggregation of fluctuations within a given time-window.
The central limit theorem (CLT) ensures that the limit distribution of the sum of a large number of random variables is a stable law. The law is Gaussian if the variables are independent and have finite variance. For correlated or infinite variance fluctuations, the CLT ought to be generalized, and the stable law is not Gaussian but Lévy. Importantly, in the latter the largest term is of approximately the same order of magnitude of the sum, indicating that extreme events dominate the underlying process (Laguës and Lesne, 2008).
From a dynamical view-point, the CLT accounts for normal diffusion and the time dependence of the MSD (or the walker's position), while generalized CLTs result in anomalous diffusion, which differs both in relaxation speed, and in the probability distribution's shape, even at very long times.
Probability distributions can be seen as resulting from the iteration of some action on them. For instance, stable laws are fixed points of the convolution operation. Somehow equivalently, fluctuation distributions can be understood as asymptotic behaviors emerging as the system is coarse-grained and rescaled (Hochberg and Pérez-Mercader, 2003). Scale-free distributions are fixed points of a renormalization flow, and universality classes are their basins of attraction. The surface comprising the models flowing into the same fixed point separates the space into phases, corresponding to different macroscopic phenomenologies (Laguës and Lesne, 2008). Universality can be understood in terms of relevant and irrelevant operators, depending on the consequence they have on the statistical behavior (Laguës and Lesne, 2008).
Probability distributions can also be seen as solutions to specific problems expressed e.g., by differential equations (Barenblatt and Zel'dovich, 1972). For instance, probability distributions are solutions of the Fokker-Planck equation of evolution of the particle's transition probabilities, under given information constraints (Jaynes, 1957). For the linear diffusion equation, the solution is a time-evolving spatial Gaussian probability function maximizing the Shannon entropy. Correlated anomalous diffusion is governed by a nonlinear Fokker-Planck equation whose exact stationary solutions are probability distributions maximizing Tsallis generalized entropy (Borland, 1998).
Emergence of Structure: Memory, Temporal Order, and Non-Locality
Correlations are propagators, whose characteristic length ξ constitutes an active time window within which all points are somehow related to each other.
A Markovian system has perfectly elastic almost instantaneous relaxation and no memory: the time axis tends to be infinitely fragmented, so that activities of overall duration L are temporally disordered (L » ξ).
Brain fluctuations' loss of scale separation allows microscopic randomness to renormalize and become macroscopically detectable (Grigolini et al., 1999): correlated driving noise and cross-scale relationships produce temporally ordered structures (L ~ ξ), so that activity at a given time point is temporally non-local, and not easily divorced from that occurring within the scaling range.
With temporal scaling, fluctuations no longer have a characteristic time; more than to a multiplicity of scales {τi}, the emphasis shifts to some relationship between them. The brain's functional heterogeneity introduces a spatial distribution of time scales {σi} inducing a structure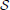 
. Eventually, the studied dynamics is a field ϕ(, t) ∈ Φ, where Φ = {ϕ} is a space of systems, endowed with a spatio-temporal structure { 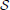* ℜ}, with arbitrarily complex topological properties (Zaslavsky, 2002), and which can become observable through a wealth of collective state variables X ∈ X.
The structure {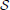 * ℜ} is a dynamical system in the space of fields ϕ, relating representations of the process at different scales (Friedrich et al., 2000; Bacry et al., 2001; Longo et al., 2012). For instance, at any given scale λ within the scaling range, the probability P(x, t) that the particle traveled a distance x at time t can be thought of as the convolution of the distribution PΛ(x, t) at the coarsest scale Λ and a probability distribution G(.), not necessarily a power-law (Chainais et al., 2005), expressing the relationships across time scales (Castaing et al., 1990). For scale-invariant processes, P(x, t) = t−ν
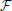(x/tν), G collapses into a single point, and is simply the scaling exponent ν. Scale invariance breakdown indicates that P(x, t) is specified by a complex spectrum of scaling exponents.
The set of renormalization operators is endowed with some structure, e.g., a multiplicative semi-group structure, and a covariance property comparable to that of tensors under the action of rotations, with scale invariance replacing Galilean invariance and fractal geometry the Euclidean one (Lesne, 2008a). In turn, scaling laws can be seen as the statistical properties prescribed by the symmetries of a (semi)group on the time-scale space (Borgnat et al., 2003).
Altogether, the presence of complex fluctuations allows treating brain activity as a physical object, defining subparts, and relationships among them, and ultimately using theoretical physics tools such as functional analysis and algebra to characterize them.
Velocity and Operational Time
The presence of scaling can be interpreted in dynamical terms in various ways.
Furthermore, the Lamperti transform establishes a bijective correspondence between self-similar processes on ℝ+ and stationary processes on ℝ (Flandrin et al., 2003). Self-similar solutions reflect a uniform propagation regime (Barenblatt and Zel'dovich, 1972), and the system can be seen as moving at constant velocity, given by the scaling exponent (Sornette, 2004), whereas the breakdown of exact self-similarity indicates that the propagator is not time-stationary.
The scaling properties also define an intrinsic time of the process. This can be seen by considering that the random walk of brain activity has a waiting-time distribution (WTD) between jumps scaling as a power-law. The WTD defines an internal operational time, which can grow sub- or super-linearly with physical time (Sokolov and Klafter, 2005). Without multiplicative interactions, operational and physical time coincide. Multiplicative cross-scale interactions bias the WTD so that, local probability densities become time-dependent and intermittent, and time translational invariance is broken (Crisanti and Ritort, 2003). The observed Mittag-Leffler fluctuation distribution (Bianco et al., 2007) may in fact stem from the process intermittent subordination with internal time.
Dynamical Regimes and Fluctuation Dissipation Relations
Brain fluctuation properties help relating two only seemingly antagonistic aspects of brain activity: spontaneous and task-induced brain activity. For Gaussian δ-correlated fluctuations, the fluctuation-dissipation theorem (FDT) ensures that the system's integrated response χ(t, t′) at time t to an external field applied at time t′ and the autocorrelation function CX(t, t′) of the unperturbed system are linked by the temperature T of the bath with which the system is in equilibrium (Kubo, 1966). Translated in terms of brain activity, the FDT would establish an equivalence between stimulus-evoked and spontaneous brain fluctuation correlations (Papo, 2013c).
Complex multiscale fluctuations suggest that thermalization happens simultaneously at widely different timescales, so that the FDT in its classical form is not expected to hold (West et al., 2008). For systems with the type of intermittency observed for brain activity, the linear response is anomalous even with simple stimuli (Silvestri et al., 2009; Allegrini et al., 2010). The way the FDT is violated and the ingredients necessary to recover it can be used in various ways as descriptors of brain activity.
First, the properties of ongoing fluctuations define the form of the generalized FDT holding for brain activity and, in fine, the way stimulus information is transferred to the brain. The presence of correlated noise affects the particle's transport properties and corresponding dynamics (Machura and łuczka, 2010), and information transfer is maximized when stimuli and brain fluctuations display similar scaling properties (Allegrini et al., 2007; West and Grigolini, 2010; Aquino et al., 2011). Moreover, scaling exponents mark dynamical transitions between qualitatively different response regimes (Burov and Barkai, 2008).
Second, the nature of FDT violation helps understanding at what scales correlations and memory start playing a role, and correctly characterizing the underlying dynamics by specifying the additional degrees of freedom necessary to recover Markovianity (Zwanzig, 2001).
Finally, effective temperatures, i.e., what a thermometer responding on the time scale at which the system slowly reverts to equilibrium would measure, which may be used to derive a generalized FDT (Cugliandolo et al., 1997), constitute intrinsic time scales of the system. Fluctuations ultimately identify a spatial distribution of scale-dependent relationships between spontaneous and stimulus-induced brain activity, quantifying the extent to which each scale deviates from equilibrium (Papo, 2013a). This reflects the fact that a path realizes qualitatively different diffusion processes at different temporal and the spatial scales.
Task-Related Modulations
Because most complex scaling properties are presumably generic, psychologists are primarily interested in the extent to which cognitive activity may affect them. Furthermore, precisely because they are generic, task-induced modulations of these properties represent powerful descriptors of the underlying processes.
Cross-Overs and Symmetry Changes
Numerous cognitive tasks have been shown to modulate the scaling exponents of brain fluctuation probability functions (Linkenkaer-Hansen et al., 2004; Popivanov et al., 2006; Buiatti et al., 2007; He et al., 2010; Ciuciu et al., 2011, 2012; Zilber et al., 2012). Task demands also appear to enhance data collapse and universality of brain fluctuations (Bhattacharya, 2009).
Cognitive demands may push brain activity toward the basin of attraction of adaptively advantageous probability distributions. Cognitive function would be tantamount to designing a driving noise function making the system's stationary distribution equal a desired target one. Moreover, insofar as power laws are solutions of functional equations, rather than frequency or amplitude modulators, cognitive processes may be conceptualised as operators acting upon the functional form of brain activity.
A still poorly explored possibility is that these modulations represent cross-overs between universality classes. This would allow classifying observed cognitive function as operators acting on symmetries (Lübeck, 2004). Renormalization flows would represent generalized dynamic pathways within the functional space, and universality classes a partition of this space, quantifying robustness with respect to control parameter variations (Lesne, 2008a,b).
Whether and how cognitive demands act on brain activity's symmetries is a deserving matter (Freeman and Vitiello, 2006; Buice and Cowan, 2009). For instance, the transition from mono- to multifractal distributions has been reported at the late stages of various fracture phenomena (de Arcangelis and Herrmann, 1989; Kapiris et al., 2004). However, whether spontaneous activity is temporally scale-free (van de Ville et al., 2010) or breaks down scale invariance (Ciuciu et al., 2011, 2012; Wink et al., 2012; Zilber et al., 2012) is still an open debate. Existing discrepancies may stem from the order parameter used to evaluate scaling, e.g., whether it is local or has prominent spatial extension, as heterogeneity and disorder may directly affect the scaling exponents.
The shrinking of the multifractal spectrum associated with performance of cognitive tasks may amount to selecting a set of complex patterns from the available repertoire, or to modifying the rate at which these patterns are re-edited across the system (Kenet et al., 2003; Betzel et al., 2012). On the other hand, stimuli drive neural activity away from criticality (Kohen-Kashi Malina et al., 2013), an action reminding the interruption of ageing caused by an external field forcing a glassy material (Kranz et al., 2010). In this sense, one may interpret multifractality as a sign of ageing (Allegrini et al., 2004).
Steering Within the Phase Space
As they modulate the temporal scaling of fluctuations, cognitive demands affect the temporal organization of brain activity and the corresponding operational time.
The observable outcome could come in the form of a modulation of cross-over scales, e.g., the time scales at which fluctuations start converging to a Gaussian distribution, varying the likelihood of large scale events (Mantegna and Stanley, 1994), the length interval over which activity can be considered a Markov process, the time scale of the transition from microscopic to macroscopic dynamics (Aquino et al., 2007), or the degree of non-ergodicity, corresponding to different ways of visiting the state space (Lomholt et al., 2013).
Furthermore, stimulus-induced modulations of temporal correlations may induce phase transitions in first-passage times (Carretero-Campos et al., 2012) and in response regimes (Burov and Barkai, 2008), and may influence fluctuations' transition to scaling, while endogenous activity likely affects the WTD scaling properties (Aquino et al., 2011).
Finally, cognitive demands may bias either the probabilities or the occurrence times of the walker's jumps (Allegrini et al., 2004), and therefore the operational time associated with a given process.
Conclusions
We addressed the question of whether and how brain fluctuations help describing non observable cognitive processes.
That observed behavior is a product of brain activity is a matter of general consensus. Here, we further proposed that the former can be described in terms of the generic properties of the latter, such as scaling regimes and their basins of attraction, symmetries (not only scale invariance), FDT violations. Ultimately, it is tempting to conceive of observed behavior as a macroscopic property emerging from the renormalization of microscopic brain fluctuations.
Such characterization of the action of cognitive demands on brain activity affords a wealth of order parameters through which activity becomes observable, each representing a cut, in different dimensions and scales, of the same underlying space. More generally, it allows a conceptualization whereby cognitive processes operate upon the structure of brain activity, producing effects observable from various perspectives (e.g., structural or dynamical). Eventually, this shapes a functional space for which internal structure, and transition and combinatory rules can be extracted.
Finally, it is important to warn that these descriptions do not unambiguously characterize the aetiology of fluctuation properties, as similar scaling properties may stem from qualitatively different generators (Magdziarz et al., 2009; Meroz et al., 2013; Thiel et al., 2013) which may be difficult to distinguish with a finite amount of data (Grigolini, 2008).
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgment
The author acknowledges the support of MINECO (FIS2012-38949-C03-01).
References
Allegrini, P., Bellazzini, J., Bramanti, G., Ignaccolo, M., Grigolini, P., and Yang, J. (2004). Scaling breakdown: a signature of aging. Phys. Rev. E 66:015101. doi: 10.1103/PhysRevE.66.015101
Allegrini, P., Bologna M., Fronzoni, L., Grigolini, P., and Silvestri, L. (2010). Experimental quenching of harmonic stimuli: universality of linear response theory. Phys. Rev. Lett. 103:030502. doi: 10.1103/PhysRevLett.99.010603
Allegrini, P., Bologna, M., Grigolini, P., and West, B. J. (2007). Fluctuation-dissipation theorem for event-dominated processes. Phys. Rev. Lett. 99:010603. doi: 10.1103/PhysRevLett.99.010603
Allegrini, P., Menicucci, D., Paradisi, P., and Gemignani, A. (2010). Fractal complexity in spontaneous EEG metastable-state transitions: new vistas on integrated neural dynamics. Front. Physiol. 1:128. doi: 10.3389/fphys.2010.00128
Allegrini, P., Paradisi, P., Menicucci, D., Bedini, R., Gemignani, A., and Fronzoni, L. (2011). Noisy cooperative intermittent processes: from blinking quantum dots to human consciousness. J. Phys. Conf. Ser. 306:012027. doi: 10.1088/1742-6596/306/1/012027
Aquino, G., Bologna, M., West, B. J., and Grigolini, P. (2011). Transmission of information between complex systems: 1/f resonance. Phys. Rev. E 83:051130. doi: 10.1103/PhysRevE.83.051130
Aquino, G., Grigolini, P., and West, B. J. (2007). Linear response and fluctuation-dissipation theorem for non-poissonian renewal processes. Europhys. Lett. 80:10002. doi: 10.1209/0295-5075/80/10002
Bacry, E., Delour, J., and Muzy, J. F. (2001). Multifractal random walk. Phys. Rev. E 64:026103. doi: 10.1103/PhysRevE.64.026103
Barenblatt, G. I., and Zel'dovich, Y. B. (1972). Self-similar solutions as intermediate asymptotics. Annu. Rev. Fluid Mech. 4, 285–312. doi: 10.1146/annurev.fl.04.010172.001441
Betzel, R. F., Erickson, M. A., Abell, M., O'Donnell, B. F., Hetrick, W. P., and Sporns, O. (2012). Synchronization dynamics and evidence for a repertoire of network states in resting EEG. Front. Comput. Neurosci. 6:74. doi: 10.3389/fncom.2012.00074
Bhattacharya, J. (2009). Increase of universality in human brain during mental imagery from visual perception. PLoS ONE 4:e4121. doi: 10.1371/journal.pone.0004121
Bianco, S., Ignaccolo, M., Rider, M. S., Ross, M. J., Winsor, P., and Grigolini, P. (2007). Brain, music, and non-Poisson renewal processes. Phys. Rev. E 75, 061911.
Borgnat, P., Amblard, P. O., and Flandrin, P. (2003). Invariances D'échelles Brisées et Accroissements Stationnaires. Paris: Colloque GRETSI-03.
Borland, L. (1998). Microscopic dynamics of the nonlinear Fokker-Planck equation: a phenomenological model. Phys. Rev. E 57, 6634–6642. doi: 10.1103/PhysRevE.57.6634
Bouchaud, J.-P. (1992). Weak ergodicity breaking and aging in disordered systems. J. Phys. I France 2, 1705–1713. doi: 10.1051/jp1:1992238
Buiatti, M., Papo, D., Baudonnière, P. M., and van Vreeswijk, C. (2007). Feedback modulates the temporal scale-free dynamics of brain electrical activity in a hypothesis testing task. Neuroscience 146, 1400–1412. doi: 10.1016/j.neuroscience.2007.02.048
Buice, M. A., and Cowan, J. D. (2009). Statistical mechanics of the neocortex. Prog. Biophys. Mol. Biol. 99, 53–86. doi: 10.1016/j.pbiomolbio.2009.07.003
Burov, S., and Barkai, E. (2008). Critical exponent of the fractional Langevin equation. Phys. Rev. Lett. 100:070601. doi: 10.1103/PhysRevLett.100.070601
Cabrera, J. L., and Milton, J. G. (2002). On-off intermittency in a human balancing task. Phys. Rev. Lett. 89:158702. doi: 10.1103/PhysRevLett.89.158702
Carretero-Campos, C., Bernaola-Galván, P., Ivanov, P.Ch., and Carpena, P. (2012). Phase transitions in the first-passage time of scale-invariant correlated processes. Phys. Rev. E 85:011139.
Castaing, B., Gagne, Y., and Hopfinger, E. J. (1990). Velocity probability density functions of high Reynolds number turbulence. Physica D 46, 177–200. doi: 10.1016/0167-2789(90)90035-N
Castiglione, P., Mazzino, A., Muratore-Ginanneschi, P., and Vulpiani, A. (1999). On strong anomalous diffusion. Physica D 134, 75. doi: 10.1016/S0167-2789(99)00031-7
Chainais, P., Riedi, R., and Abry, P. (2005). On non scale invariant infinitely divisible cascades. IEEE Trans. Inf. Theory 51, 1063–1083. doi: 10.1109/TIT.2004.842570
Ciuciu, P., Abry, P., Rabrait, C., and Wendt, H. (2011). Log wavelet leaders cumulant based multifractal analysis of EVI fMRI time series: evidence of scaling in ongoing and evoked brain activity. IEEE J. Sel. Top. Appl. 2, 929–943. doi: 10.1109/JSTSP.2008.2006663
Ciuciu, P., Varoquaux, G., Abry, P., Sadaghiani, S., and Kleinschmidt, A. (2012). Scale-free and multifractal time dynamics of fMRI signals during rest and task. Front. Physiol. 3:186. doi: 10.3389/fphys.2012.00186
Correll, J. (2008). 1/f noise and effort on implicit measures of bias. J. Pers. Soc. Psychol. 94, 48–59. doi: 10.1037/0022-3514.94.1.48
Crisanti, A., and Ritort, F. (2003). Violation of the fluctuation–dissipation theorem in glassy systems: basic notions and the numerical evidence. J. Phys. A Math. Gen. 36, R181–R290. doi: 10.1088/0305-4470/36/21/201
Cugliandolo, L. F., Dean, D. S., and Kurchan, J. (1997). Fluctuation-dissipation theorems and entropy production in relaxational systems. Phys. Rev. Lett. 79, 2168–2171. doi: 10.1103/PhysRevLett.79.2168
de Arcangelis, L., and Herrmann, H. J. (1989). Scaling and multiscaling laws in random fuse networks. Phys. Rev. B 39, 2678.
Deco, G., Jirsa, V. K., and McIntosh, A. R. (2011). Emerging concepts for the dynamical organization of resting-state activity in the brain. Nat. Rev. Neurosci. 12, 43–56. doi: 10.1038/nrn2961
Diniz, A., Wijnants, M. L., Torre, K., Barreiros, J., Crato, N., Bosman, A. M., et al. (2011). Contemporary theories of 1/f noise in motor control. Hum. Mov. Sci. 30, 889–905. doi: 10.1016/j.humov.2010.07.006
Expert, P., Lambiotte, R., Chialvo, D. R., Christensen, K., Jensen, H. J., Sharp, D. J., et al. (2010). Self-similar correlation function in brain resting-state functional magnetic resonance imaging. J. R. Soc. Interface 8, 472–479. doi: 10.1098/rsif.2010.0416
Flandrin, P., Borgnat, P., and Amblard, P. O. (2003). From stationarity to self-similarity, and back: variations on the lamperti transformation. Lect. Notes Phys. 621, 88–117. doi: 10.1007/3-540-44832-2_5
Fraiman, D., and Chialvo, D. R. (2012). What kind of noise is brain noise: anomalous scaling behavior of the resting brain activity fluctuations. Front. Physiol. 3:307. doi: 10.3389/fphys.2012.00307
Frank, S. A. (2009). The common patterns of nature. J. Evol. Biol. 22, 1563–1585. doi: 10.1111/j.1420-9101.2009.01775.x
Freeman, W. J., Holmes, M. D., Burke, B. C., and Vanhatalo, S. (2003). Spatial spectra of scalp EEG and EMG from awake humans. Clin. Neurophysiol. 114, 1053–1068. doi: 10.1016/S1388-2457(03)00045-2
Freeman, W. J., and Vitiello, G. (2006). Nonlinear brain dynamics as macroscopic manifestation of underlying many-body field dynamics. Phys. Life Rev. 3, 93–118. doi: 10.1016/j.plrev.2006.02.001
Freyer, F., Aquino, K., Robinson, P. A., Ritter, P., and Breakspear, M. (2009). Bistability and Non-Gaussian fluctuations in spontaneous cortical activity. J. Neurosci. 29, 8512–8524. doi: 10.1523/JNEUROSCI.0754-09.2009
Friedman, N., Ito, S., Brinkman, B. A., Shimono, M., DeVille, R. E., Dahmen, K. A., et al. (2012). Universal critical dynamics in high resolution neuronal avalanche data. Phys. Rev. Lett. 108:208102. doi: 10.1103/PhysRevLett.108.208102
Friedrich, R., Peinke, J., and Renner, C. (2000). How to quantify deterministic and random influences on the statistics of the foreign exchange market. Phys. Rev. Lett. 84, 5224–5227. doi: 10.1103/PhysRevLett.84.5224
Ghosh, A., Rho, Y., McIntosh, A. R., Kötter, R., and Jirsa, V. K. (2007). Noise during rest enables the exploration of the brain's dynamic repertoire. PLoS Comput. Biol. 4:e1000196. doi: 10.1371/journal.pcbi.1000196
Gilden, D. L. (2001). Cognitive emission of 1/f noise. Psychol. Rev. 108, 33–56. doi: 10.1037/0033-295X.108.1.33
Gong, P., Nikolaev, A. R., and van Leeuwen, C. (2002). Scale-invariant fluctuations of the dynamical synchronization in human brain electrical activity. Neurosci. Lett. 336, 33–36. doi: 10.1016/S0304-3940(02)01247-8
Gong, P., Nikolaev, A. R., and van Leeuwen, C. (2007). Intermittent dynamics underlying the intrinsic fluctuations of the collective synchronization patterns in electrocortical activity. Phys. Rev. E 76, 011904.
Grigolini, P. (2008). Complexity and generalized exponential relaxation: memory versus renewal. Int. J. Bifurcat. Chaos 9, 2709–2716. doi: 10.1142/S0218127408021920
Grigolini, P., Aquino, G., Bologna, M., Lukoviæ, M., and West, B. J. (2009). A theory of 1/f noise in human cognition. Physica A 388, 4192–4204. doi: 10.1016/j.physa.2009.06.024
Grigolini, P., Rocco, A., and West, B. J. (1999). Fractional calculus as a macroscopic manifestation of randomness. Phys. Rev. E 59, 2603–2613. doi: 10.1103/PhysRevE.59.2603
He, B. J., Zempel, J. M., Snyder, A. Z., and Raichle, M. E. (2010). The temporal structures and functional signi?cance of scale-free brain activity. Neuron 66, 353–369. doi: 10.1016/j.neuron.2010.04.020
Hochberg, D., and Pérez-Mercader, J. (2003). The renormalization group and fractional Brownian motion. Phys. Lett. A 296, 272–279. doi: 10.1016/S0375-9601(02)00290-6
Holden, J. G., Van Orden, G. C., and Turvey, M. T. (2009). Dispersion of response times reveals cognitive dynamics. Psychol. Rev. 116, 318–342. doi: 10.1037/a0014849
Hsu, D., and Hsu, M. (2009). Zwanzig-Mori projection operators and EEG dynamics: deriving a simple equation of motion. PMC Biophys. 2:6. doi: 10.1186/1757-5036-2-6
Ihlen, E. A. F., and Vereijken, B. (2010). Interaction-dominant dynamics in human cognition: Beyond 1/fα fluctuation. J. Exp. Psychol. Gen. 139, 436–463. doi: 10.1037/a0019098
Jaynes, E. T. (1957). Information theory and statistical mechanics. Phys. Rev. 106, 620–630. doi: 10.1103/PhysRev.106.620
Kapiris, P. G., Eftaxias, K. A., and Chelidze, T. L. (2004). Electromagnetic signature of prefracture criticality in heterogeneous media. Phys. Rev. Lett. 92, 065702. doi: 10.1103/PhysRevLett.92.065702
Kello, C. T. (2013). Critical branching neural networks. Psychol. Rev. 120, 230–254. doi: 10.1037/a0030970
Kello, C. T., Brown, G. D., Ferrer-I-Cancho, R., Holden, J. G., Linkenkaer-Hansen, K., Rhodes, T., et al. (2010). Scaling laws in cognitive sciences. Trends Cogn. Sci. 14, 223–232. doi: 10.1016/j.tics.2010.02.005
Kenet, T., Bibitchkov, D., Tsodyks, M., Grinvald, A., and Arieli, A. (2003). Spontaneously emerging cortical representations of visual attributes. Nature 425, 954–956. doi: 10.1038/nature02078
Kohen-Kashi Malina, K., Jubran, M., Katz, Y., and Lampl, I. (2013). Imbalance between excitation and inhibition in the somatosensory cortex produces postadaptation facilitation. J. Neurosci. 33, 8463–8471. doi: 10.1523/JNEUROSCI.4845-12.2013
Kranz, T., Sperl, M., and Zippelius, A. (2010). Glass transition for driven granular fluids. Phys. Rev. Lett. 104:225701. doi: 10.1103/PhysRevLett.104.225701
Kubo, R. (1966). The fluctuation-dissipation theorem. Rep. Progr. Phys. 29, 255–284. doi: 10.1088/0034-4885/29/1/306
Lesne, A. (2008a). “Regularization, renormalization, and renormalization groups: relationships and epistemological aspects,” in Vision of Oneness, eds I. Licata and A. Sakaji (Rome: Aracne), 121–154.
Lesne, A. (2008b). Robustness: confronting lessons from physics and biology. Biol. Rev. Camb. Philos. Soc. 83, 509–532. doi: 10.1111/j.1469-185X.2008.00052.x
Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M., and Ilmoniemi, R. (2001). Long-range temporal correlations and scaling behavior in human oscillations. J. Neurosci. 15, 1370–1377.
Linkenkaer-Hansen, K., Nikouline, V. V., Palva, J. M., Kaila, K., and Ilmoniemi, R. (2004). Stimulus-induced change in long-range temporal correlations and scaling behaviour of sensorimotor oscillations. Eur. J. Neurosci. 19, 203–211. doi: 10.1111/j.1460-9568.2004.03116.x
Lomholt, M. A., Lizana, L., Metzler, R., and Ambjörnsson, T. (2013). Microscopic origin of the logarithmic time evolution of aging processes in complex systems. Phys. Rev. Lett. 110:208301. doi: 10.1103/PhysRevLett.110.208301
Longo, G., Montévil, M., and Pocheville, A. (2012). From bottom-up approaches to levels of organization and extended critical transitions. Front. Physiol. 3:232. doi: 10.3389/fphys.2012.00232
Lübeck, S. (2004). Universal scaling behavior of non-equilibrium phase transitions. arXiv:cond-mat/0501259v1. doi: 10.1142/S0217979204027748
Machura, L., and łuczka, J. (2010). Transport driven by biharmonic forces: impact of correlated thermal noise. Phys. Rev. E 82:031133. doi: 10.1103/PhysRevE.82.031133
Magdziarz, M., Weron, A., Burnecki, K., and Klafter, J. (2009). Fractional brownian motion versus the continuous-time random walk: a simple test for subdiffusive dynamics. Phys. Rev. Lett. 103:180602. doi: 10.1103/PhysRevE.85.011139
Mantegna, R., and Stanley, E. (1994). Stochastic process with ultraslow convergence to a Gaussian: the truncated Lévy flight. Phys. Rev. Lett. 73, 2946–2949. doi: 10.1103/PhysRevLett.73.2946
Meroz, Y., Sokolov, I. M., and Klafter, J. (2013). Test for determining a subdiffusive model in ergodic systems from single trajectories. Phys. Rev. Lett. 110:090601. doi: 10.1103/PhysRevLett.110.090601
Monto, S., Palva, S., Voipio, J., and Palva, J. M. (2008). Very slow EEG fluctuations predict the dynamics of stimulus detection and oscillation amplitudes in humans. J. Neurosci. 28, 8268–8272. doi: 10.1523/JNEUROSCI.1910-08.2008
Novikov, E., Novikov, A., Shannahoff-Khalsa, D., Schwartz, B., and Wright, J. (1997). Scale-similar activity in the brain. Phys. Rev. E 56, R2387–R2389. doi: 10.1103/PhysRevE.56.R2387
Palva, J. M., Zhigalov, A., Hirvonen, J., Korhonen, O., Linkenkaer-Hansen, K., and Palva, S. (2013). Neuronal long-range temporal correlations and avalanche dynamics are correlated with behavioral scaling laws. Proc. Natl. Acad. Sci. U.S.A. 110, 3585–3590. doi: 10.1073/pnas.1216855110
Papo, D. (2013a). Measuring brain temperature without a thermometer. Front. Physiol. 5:124. doi: 10.3389/fphys.2014.00124
Papo, D. (2013b). Time scales in cognitive neuroscience. Front. Physiol. 4:86. doi: 10.3389/fphys.2013.00086
Papo, D. (2013c). Why should cognitive neuroscientists study the brain's resting state? Front. Hum. Neurosci. 7:45. doi: 10.3389/fnhum.2013.00045
Popivanov, D., Stomonyakov, V., Minchev, Z., Jivkova, S., Dojnov, P., Jivkov, S., et al. (2006). Multifractality of decomposed EEG during imaginary and real visual-motor tracking. Biol. Cybern. 94, 149–156. doi: 10.1007/s00422-005-0037-5
Sherrington, D. (2010). Physics and complexity. Phil. Trans. R. Soc. A 368, 1175–1189. doi: 10.1098/rsta.2009.0208
Shriki, O., Alstott, J., Carver, F., Holroyd, T., Henson, R. N., Smith, M. L., et al. (2012). Neuronal avalanches in the resting MEG of the human brain. J. Neurosci. 33, 7079–7090. doi: 10.1523/JNEUROSCI.4286-12.2013
Silvestri, L., Fronzoni, L., Grigolini, P., and Allegrini, P. (2009). Event-driven power-law relaxation in weak turbulence. Phys. Rev. Lett. 102:014502. doi: 10.1103/PhysRevLett.102.014502
Sokolov, I. M., and Klafter, J. (2005). From diffusion to anomalous diffusion: a century after Einstein's Brownian motion. Chaos 15:026103. doi: 10.1063/1.1860472
Sornette, D. (2004). Critical Phenomena in Natural Sciences, Chaos, Fractals, Self-Organization and Disorder: Concepts and Tools. 2nd Edn, Heidelberg: Springer Series in Synergetics.
Sparre Andersen, E. (1953). On the fluctuations of sums of random variables. Math. Scand. 1, 263–285.
Stam, C. J., and de Bruin, E. A. (2004). Scale-free dynamics of global functional connectivity in the human brain. Hum. Brain Mapp. 22, 97–109. doi: 10.1002/hbm.20016
Suckling, J., Wink, A. M., Bernard, F. A., Barnes, A., and Bullmore, E. (2009). Endogenous multifractal brain dynamics are modulated by age, cholinergic blockade and cognitive performance. J. Neurosci. Methods 174, 292–300. doi: 10.1016/j.jneumeth.2008.06.037
Thiel, F., Flegel, F., and Sokolov, I. M. (2013). Disentangling sources of anomalous diffusion. Phys. Rev. Lett. 111:010601. doi: 10.1103/PhysRevLett.111.010601
van de Ville, D., Britz, J., and Michel, C. M. (2010). EEG microstate sequences in healthy humans at rest reveal scale-free dynamics. Proc. Natl. Acad. Sci. U.S.A. 107, 18179–18184. doi: 10.1073/pnas.1007841107
West, B. J., Geneston, E. L., and Grigolini, P. (2008). Maximizing information exchange between complex networks. Phys. Rep. 468, 1–99. doi: 10.1016/j.physrep.2008.06.003
West, B. J., and Grigolini, P. (2010). The living matter way to exchange information. Med. Hypotheses 75, 475–478. doi: 10.1016/j.mehy.2010.04.028
Wink, A. M., Bullmore, E., Barnes, A., Bernard, F., and Suckling, J. (2012). Monofractal and multifractal dynamics of low frequency endogenous brain oscillations in functional MRI. Hum. Brain Mapp. 29, 791–801. doi: 10.1002/hbm.20593
Zaslavsky, G. M. (2002). Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 371, 461–580. doi: 10.1016/S0370-1573(02)00331-9
Keywords: scaling, multifractals, ageing, weak ergodicity breaking, symmetry, fluctuation-dissipation theorem, cognitive neuroscience, resting state
Citation: Papo D (2014) Functional significance of complex fluctuations in brain activity: from resting state to cognitive neuroscience. Front. Syst. Neurosci. 8:112. doi: 10.3389/fnsys.2014.00112
Received: 16 April 2014; Accepted: 26 May 2014;
Published online: 11 June 2014.
Edited by:
Lucilla De Arcangelis, Second University of Naples, ItalyReviewed by:
Paolo Allegrini, Consiglio Nazionale delle Ricerche, ItalyAntonio De Candia, University of Naples, Italy
Copyright © 2014 Papo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David Papo, Computational Systems Biology Group, Center for Biomedical Technology, Universidad Politécnica de Madrid, Calle Ramiro de Maeztu, 7, 28040 Madrid, Spain e-mail: papodav@gmail.com