- 1Institute for Signal Processing, University of Lübeck, Lübeck, Germany
- 2German Research Center for Artificial Intelligence (DFKI), Lübeck, Germany
Moving microphones allow for the fast acquisition of sound-field data that encode acoustic impulse responses in time-invariant environments. Corresponding decoding algorithms use the knowledge of instantaneous microphone positions for relating the dynamic samples to a positional context and solving the involved spatio-temporal channel estimation problem subject to the particular parameterization model. Usually, the resulting parameter estimates are supposed to remain widely unaffected by the Doppler effect despite the continuously moving sensor. However, this assumption raises issues from the physical point of view. So far, mathematical investigations into the actual meaning of the Doppler effect for such dynamic sampling procedures have been barely provided. Therefore, in this paper, we propose a new generic concept for the dynamic sampling model, introducing a channel representation that is explicitly based on the instantaneous Doppler shift according to the microphone trajectory. Within this model, it can be clearly seen that exact trajectory tracking implies exact Doppler-shift rendering and, thus, enables unbiased parameter recovery. Further, we investigate the impact of non-perfect trajectory data and the resulting Doppler-shift mismatches. Also, we derive a general analysis scheme that decomposes the microphone signal along with the encoded parameters into particular subbands of Doppler-shifted frequency components. Finally, for periodic excitation, we exactly characterize the Doppler-shift influences in the sampled signal by convolution operations in the frequency domain with trajectory-dependent filters.
1 Introduction
Dynamic measurement procedures are capable of acquiring entire sound-field information by use of only one non-stop moving microphone. Due to their low effort in hardware and calibration compared to stationary approaches, such continuous techniques are ideally suited to gather fast estimates of acoustic impulse responses (AIRs) within expanded listening areas. Prominent examples of AIRs are head-related impulse responses (HRIRs), room impulse responses (RIRs), and binaural room impulse responses (BRIRs). Adequate estimates of AIR fields are essential for various applications related to multichannel equalization and cross-talk cancellation, sound-field analysis, auralization, and audio reproduction, e.g., for virtual and augmented reality systems (Benesty et al., 2008).
An analytical method for the reconstruction of AIRs along linear and circular microphone trajectories has been presented in (Ajdler et al., 2007). Here, a specially designed input signal is needed, and the speed of the microphone must be constant and is restricted to an upper limit. Quite different from usual AIR measurements, the excitation signal must not contain all audio frequencies, but only a certain subset in order to avoid overlapping frequency shifts. The omitted frequencies are essentially generated through the Doppler effect. Beyond that method, dynamic approaches are typically based on estimates from linear equations that model the convolution of involved AIRs and excitation sequences, and relate them to the samples acquired at instantaneously varying microphone positions. In one group of such methods, the spatio-temporal dependencies are simplified and impulse responses at steadily changing positions are considered as time-varying systems whose coefficients are tracked by adaptive filtering concepts (Haykin, 2001). This setup is well-known from acoustic echo cancellation (Sondhi, 1967; Benesty et al., 2006), and, combined with controlled surroundings and trajectories, it is also suitable for the fast acquisition of HRIRs (Enzner, 2008; He et al., 2018).
More recently, a new group of dynamic techniques have emerged, where the continuously acquired sound-field samples are directly embedded into a spatio-temporal context (Hahn and Spors, 2016; Katzberg et al., 2017b, 2018, 2021; Hahn et al., 2017; Hahn and Spors, 2017; Hahn and Spors, 2018; Urbanietz and Enzner, 2020). Here, the measurement model is explicitly multidimensional, with a moving microphone that collects uniform samples in the time domain and, in general, non-uniform samples at varying points in the spatial domain. Thus, such techniques inherently require positional information based either on a controlled pre-defined trajectory or a tracking of the microphone positions (Katzberg et al., 2022). The method by Urbanietz and Enzner (2020) uses a spatial Fourier basis for the angular reconstruction of HRIRs from continuous-azimuth recordings and shows more accurate performance than an adaptive-filter-based solution. In (Hahn and Spors, 2016), perfect-sequence excitation (Stan et al., 2002) is used for the orthogonal expansion of impulse responses, in order to describe the dynamic spatio-temporal sampling by notional static sampling processes of single expansion coefficients. This method simplifies the problem to pure interpolation in space. It has been investigated for reconstructing RIRs (Hahn and Spors, 2017; Hahn and Spors, 2018) and BRIRs (Hahn et al., 2017) along circular trajectories. In (Katzberg et al., 2017b), a versatile framework has been presented that allows for RIR reconstruction at off-trajectory positions within cubical volumes. To achieve this, the sound field is parameterized by modeling virtual grid points in space, and dynamic samples are understood as the result of bandlimited interpolation on that grid using sampled sinc-function approximations. In practice, the corresponding inverse problem is most likely ill-posed or even underdetermined. Therefore, in (Katzberg et al., 2018; Katzberg and Mertins, 2022), a strategy has been proposed that exploits sparse Fourier representations and applies principles of compressed sensing (CS) (Candès et al., 2006). Recently, the dynamic framework subject to sinc-function related parameters has been generalized to a formulation, where arbitrary spatial basis functions cover expanded target volumes (Katzberg et al., 2021). Based on this, a physical perspective has been provided for representing dynamic sound-field samples in terms of spherical solutions to the acoustic wave equation (Katzberg et al., 2021).
For the measurement methods where a non-stop moving microphone collects sound-field data to AIRs, the Doppler effect will always be present in the sampled signal. The dynamic approaches considering the spatio-temporal context rely on the assumption that the occurring Doppler shifts are at least partly covered by the sampling model, as long as the microphone signal at the particular receiving times is connected to the instant positions in space. However, for all the existing frameworks, the implication between positional tracking and Doppler-shift rendering is not directly apparent from the mathematical model. Therefore, in this paper, we introduce a new interpretation of the dynamic sampling procedure from the Doppler perspective.
First, in Section 2, we briefly outline the basic differences in the mathematical models between stationary and dynamic sound-field measurement strategies. Then, in Section 3, we develop an equivalent Doppler-domain concept from which one can easily see that exact tracking of the microphone trajectory inherently allows for the exact tracking of the involved and unknown Doppler shifts in the frequency domain. The proposed representation explicitly describes the instantaneous interferences of the Doppler effect during the dynamic observation process. This can be used to estimate the underlying sound-field parameters without any Doppler bias, provided that the acoustic properties of the surroundings remain constant during the measurement sessions. In Section 4, we analyze the case of non-perfect positional tracking and describe the resulting Doppler-shift mismatches in the mathematical model. We derive structured expressions for the corresponding error terms and adapt stability guarantees and error bounds for both least-squares and CS-based solutions. In Section 5, the Doppler-based channel representation is exploited to provide a spatio-temporal filtering scheme that can be employed for decomposing the Doppler-shifted microphone signal into particular subbands. This allows us to reconstruct low-frequency content in cases where the wideband recovery problem is ill-conditioned. Considering periodic excitation, Section 6 shows how the proposed concept enables us to directly relate the Doppler shifts in the measured signal to trajectory-dependent filters that spread spectral sound-field characteristics across adjoining frequency bins. Finally, in Section 7, we demonstrate the key points of the Doppler framework on experimental data.
2 Dynamic sound-field sampling procedures
Assuming a fixed environment with several reflecting surfaces and constant atmospheric conditions, the propagation of the sound signal s(t) inside the target area
where s(t) originates at a fixed source position xS∉Ω subject to the global time
By coupling the spatial dimensions to the time dimension, the dynamic sound field along the trajectory
where
2.1 Stationary sampling schemes
Measuring the sound-field signal (1) leads to stationary sampling schemes, where R microphones provide temporal samples with high acquisition rates fs at uniform points tn = n/fs
where f(c, x) are sampled basis functions for the interpolation inside Ω according to a spatialization model (e.g., sampled plane waves),
with ηr(n) comprising the measurement noise and parameterization errors. Parameter decoding may be achieved by solving the inverse problem given a controlled excitation sequence s(n) and calibrated sampling positions xr. Adequate estimates of γ(c, l) from the corresponding system of linear equations may be used for the sound-field reconstruction according to (3). The reconstruction along the delay time m is simple due to high temporal sampling rates fs ≥ 2fcut of the microphones, effortlessly achievable for practical cutoff frequencies fcut. Note that, of course, stationary microphones allow for decoupling the multidimensional sampling problem (4). So, in practice, estimates of h(xr, m) are calculated first by solving the deconvolution problem for each microphone position separately, and then the parameters γ(c, l) are recovered from the remaining linear interpolation equations of the form
2.2 Dynamic sampling schemes
For the sampling of the dynamic sound pressure (2), measurement procedures with moving microphones can be used that generate samples at uniform points in time and, generally, at continuously varying and non-uniform positions in space. As temporal sampling implies spatial sampling in such setups, only one microphone measuring along an appropriate trajectory
By employing the identical parameterization model as in (3), the spatio-temporal AIR sampled (non-uniformly) along the trajectory
Accordingly, the particular sound-field parameters γ(c, l) are encoded in samples of (2) subject to
where
In fact, it turns out that all spatio-temporal sampling procedures with moving microphones as outlined in Section 1 are based on the sampling model (6), generally involving non-uniformly sampled basis functions
In (Urbanietz and Enzner, 2020), for example, the sound-field parameters γ(c, l) are HRIRs themselves, spatially expanded by circular harmonics of maximum order Q. This is equivalent to the choices f(c, ϕ(n)) = ej(c−Q)ϕ(n) and
In this paper, we introduce a mathematical framework exploiting a representation by
3 Doppler-shift model for dynamic channels
In dynamic approaches, the sound signal sampled by the moving microphone is always affected by the Doppler effect. This raises the question about the impact of the involved Doppler shifts on the estimates of the sound-field parameters. Numerical and real-word experiments to the dynamic approaches outlined in Section 1 indicate that the positional tracking of the microphone allows for the Doppler-shift tracking in the dynamic signal, and, in turn, for uncorrupted parameter estimates. Thus, the key of these dynamic techniques lies in the tracking or controlling of the receiver trajectory, e.g., by using a robot-guided microphone, or by performing a circular trajectory at constant speed and measuring the round-trip time of the moving microphone. However, from the mathematical perspective, such implicit Doppler-shift rendering by use of positional data may not be straightforwardly comprehensible from a general spatio-temporal signal description in line with (6). In order to close this conceptual gap, we propose a more intrinsic channel interpretation for the dynamic sampling model.
3.1 General model for Doppler-shifted sound observations
For a general analytical description of interfering Doppler shifts, we use a doubly-dispersive signal model and adopt the concept of Doppler-variant impulse responses and transfer functions (Bello, 1963). Such Doppler-domain representations are well-known from time-varying channels in wireless systems (Haykin and Liu, 2010; Hlawatsch and Matz, 2011; Grami, 2016), e.g., for underwater acoustic communications (Li and Preisig, 2007; Zeng and Xu, 2012).
For the moment, let us disregard the spatial context in (2). Accordingly, the dynamic time signal
with h(t, τ) being the time-variant impulse response. The Fourier transforms of h(t, τ) along the particular dimensions yield, respectively, the Doppler-variant impulse response
which contains the variable ν denoting the Doppler shift, the time-variant transfer function
with angular frequency
The time-variant impulse response in (7) may be interpreted as the time-varying contribution from a continuum of scattering paths. By using the inverse Fourier transform of
In (11), we can see that the signal arriving at the moving receiver is composed of a weighted superposition of time-delayed and frequency-shifted replicas of the source sequence s(t). The weighting
with
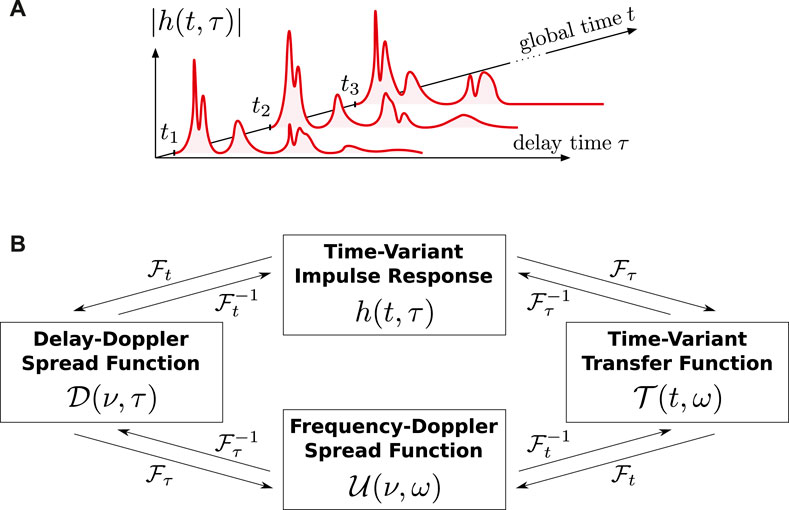
Figure 1. Linear time-variant channel impulse response. (A) Outline of considered dimensions and (B) particular frequency representations, where
3.2 Spatial parameterization of the time-variant transfer function
In (12), the term
where A(ρ, ω) is a continuum of sound-field parameters subject to the variable ρ that constitutes a continuum of possible spatial variations for x ∈ Ω due to multipath arrivals, and f(ρ, x) are appropriate spatial basis functions. The reverberant field H(x, ω) represents solutions to the Helmholtz equation for a Dirac impulse excitation at τ = 0. In the following descriptions, H(x, ω) is considered as the spatial transfer function from the static sound source to the receiver position x.
Doppler shifts can be represented in terms of the (unknown) acoustic field (13) with fixed initial and boundary conditions. By introducing the spatial context subject to H(x, ω), we rewrite the dynamic signal (12) as
where
As a result,
3.3 Examples of Doppler-aware spatialization concepts
Using plane-wave basis functions is probably the most intuitive way to represent Doppler-based sound-field observations and to calculate frequency shifts due to a moving receiver. In existing, physics-heavy literature, complex acoustics in dynamic and fluctuating environments are typically described in terms of plane-wave expressions (Morse and Ingard, 1986; Ostashev and Wilson, 2019). Corresponding simplified examples are given in Section 3.3.1 for special steady-state scenarios. Then, two specific implementations of the spatio-temporal transfer function
3.3.1 Plane waves
First, let us consider the Doppler effect for the simplest scenario with an ideal free-field environment having no reflective surfaces and a linearly moving microphone. For a stationary source that emits sound of the single angular frequency ω and a receiver that moves at constant speed v0 and constant angle ψ in relation to the direction of the wave front, the shifted frequency
with the constant scaling factor ζ = v0 cos(ψ)/c0 and the sound velocity c0. For the special cases ψ = 0, ψ = π, and ψ = ± π/2, the receiver is moving along, opposed, and orthogonal to the wave propagation, respectively. In (17), the sensed frequency
where
For non-linear receiver trajectories, the Doppler effect can be described in terms of a time-varying velocity vector v(t) (Ostashev and Wilson, 2019). The sensed, so-called instantaneous frequency is given by
where
with the constants
By comparing (19) and (20) with (18), it is straightforward to see that phase modulations in terms of relative receiver locations induce frequency modulations according to the Doppler effect. Moreover, by choosing appropriate constants τb and db, the observed Doppler-shifted frequencies can be represented subject to the particular sound-field characteristics, i.e., solutions to the acoustic wave equation for the involved initial and boundary conditions. Convenient constants are τb = 0 and db = x0, with x0 being the initial position of the receiver subject to the global coordinate system. By knowing the absolute trajectory
Based on (19), (20), dynamic free-field observations of sound from a stationary broadband source can be easily expressed as modulated plane waves. For a simplified scenario that regards the global steady-state sound field Hst(x, ω) = S(ω)H(x, ω) (and allows for dropping the delay dimension τ), a moving receiver observes the superposing, trajectory-dependent wave forms
where ejωt is the fundamental temporal solution to the homogeneous wave equation,
Let us finally consider a dynamic receiver that is moving arbitrarily within a reverberant LTI scene. Multiple sound scattering paths lead to multiple angles of arrival within the source-free target volume Ω. Therefore, the dynamically observed sound field comprises multiple interfering Doppler shifts. This can be modeled on the basis of (21), e.g., by extending the wave vector to the dependency on a continuum of scatterers and introducing a corresponding integral. A more elegant description is given by
where S2 denotes the surface of the unit sphere and
3.3.2 Spherical harmonics
Using the Jacobi-Anger expansion (Colton and Kress, 2019), the continuous plane-wave representation (22) can also be cast into a series of standing waves in radial direction with a set of infinite but countable coefficients (Fazi et al., 2012). This leads to a spherical-harmonic representation of the received signal and is basically equivalent to the dynamic model proposed in (Katzberg et al., 2021).
In (Katzberg et al., 2021), the multi-frequency AIR field subject to the delay-time variable τ is modeled as
where the position vector x◦ ∈ Ω of the receiver is given in spherical coordinates x◦ = [r,θ,ϕ]T, with radius r ∈ [0, rmax], polar angle θ ∈ [0, π], and azimuth angle ϕ ∈ [0, 2π). The Helmholtz-based wave field representation by analogy with (13) is chosen according to
with
As a result, the acoustic transfer function becomes connected with an actual spatio-temporal meaning. It is equivalent to the dynamically shaped spherical-wave field observed in the Doppler domain along the receiver trajectory
3.3.3 Spatial Fourier bases
The AIR-field reconstruction problem can also be interpreted as the classical bandlimited-interpolation task, which involves sinc-function based interpolation filters in multiple separable dimensions subject to Cartesian coordinates. For this, actually no explicit sound propagation model is needed. The assumption of a sound signal with maximum frequency ωcut allows for the sampling-theory inspired parameterization of the wave field according to
where
is the continuous spectrum of the spatially sampled sound field, equidistantly provided along a three-dimensional grid in space at sampling intervals Δξ for ξ ∈ {x, y, z},
Following the pure sampling-theory perspective, the transfer-function representation in the sense of (15) can be written as
with Γc = {k : |k| ≤ ωcut/c0} denoting the set of spatial target frequencies in the baseband,
Note that this uniform-grid approach, with expressions adopted from classical sampling and reconstruction ideas, is, in fact, closely connected with plane-wave representations such as the ones from Section 3.3.1.
For the physical conditions considered, the dispersion relation (Ostashev and Wilson, 2019; Pierce, 2019) obeys the spectral relationship
3.4 General system of linear equations for broadband parameters
After having provided particular parameterization examples in Section 3.3, let us continue with describing the measurement equations for the more general signal formulation from Section 3.2.
The measurement along the trajectory
where
is the short-time Fourier transform of the sampled source sequence s(n). By modeling a discrete sound-field approximation of (13) for sampled frequencies ωl = 2πfsl/L, the sampled Doppler domain reads
and the Doppler-shifted microphone signal is
with A(c, l) being a finite number of
Let us highlight the direct link to the abstract formulation (6) that has been initially introduced for outlining existing dynamic sampling models. Substituting (28) into the Doppler-based measurement equation given by (27) yields
This emphasizes the relationship to the spatio-temporal AIR along the measurement trajectory in terms of the Fourier transform
This yields both a delay-based representation by a(c, m) (equivalent to using
In summary, it can be stated that the Doppler effect in the dynamically acquired signal
where
the matrices
the vectors
and
and the vector concatenation
Note that the spectrum of the real-valued sound field is conjugate symmetric which can be exploited for reducing the effective number of parameters and saving computational cost. In practice, of course, there will be the usual sampling artifacts due to the measurement within finite observation windows in time and space. Also, the microphone dynamics demand a little amount of oversampling (which is usual either way), since the Doppler effect affects the highest frequencies that fall beyond the cutoff frequency of the anti-aliasing prefilter in case the microphone moves toward the source.
4 Non-ideal microphone tracking
Given perfect positional tracking of the moving microphone, the relative motion function
4.1 Perturbation model
For non-perfect microphone tracking, the positional errors lead to inconsistencies between the real-world Doppler effect and the frequency shifts performed within the signal model. Mathematically, this erroneous mapping of Doppler shifts can be expressed by a perturbation on the sampling matrix according to
with the multiplicative noise term
with deviations given by
where
and specifies the multiplicative noise as
4.2 Sensitivity considerations for Doppler-shift mismatches
The structured perturbation matrix (35) allows us to provide stability conditions and error bounds for sound-field estimates that are based on noisy trajectory data, i.e., Doppler-shift mismatches. For this, existing perturbation theory can be adapted, which is demonstrated in the following for both the least-squares and CS cases.
First, let us consider the effects of positional perturbations in
where ‖ ⋅‖F denotes the Frobenius norm, and, following (35),
The bound (36) does not necessarily remain finite as
which guarantees that
Now, we consider the solution of the linear least-squares problem to (34),
Let us assume a compatible linear system with vanishing model error,
with
According to the conditions (38) attached to ϵ, the performance guarantee (39) requires an accuracy of the microphone tracking that satisfies
Regarding CS-based strategies, Doppler-shift mismatches can be seamlessly incorporated into the perturbation model from (Herman and Strohmer, 2010). For simplicity, let us assume a strictly K-sparse parameter vector a having the support size ‖a‖0 = |{i : ai ≠ 0}| ≤ K ≪ P. Also, let us assume a sampling matrix
where the total perturbation obeys
The worst-case relative perturbations are quantified by
where
or, vice versa, for Doppler-shift errors in
we can set the absolute noise parameter
with
and guarantee the stability of the basis pursuit solution according to
where the well-behaved factor μ ≥ 0 is defined by
and, similar to the least-squares case, they ensure for any k ≤ 2K that
5 Subband analysis in Doppler domain
For extensive target regions and wide-ranging bandwidths, the linear system (33) with the parameter set in a might become too large for practical applications due to limitations in computational power and memory. For example, by considering a spherical volume with radius rmax, the number of parameters required for the spatialization at ωl is
5.1 Spatio-temporal filtering in Doppler domain
Isolating distinct subbands of temporal frequencies by applying conventional bandpass filtering to the microphone signal is not feasible. The measured position is varying over time since the microphone is supposed to move. It is easy to see that applying a digital bandpass filter
Nevertheless, let us consider linear-phase FIR filters
with operator
Our model (45) implies that the time-domain convolution between the measured signal
Using the substitutions
Defining
where the sum over
5.2 Subband decomposition in Doppler domain
Similar to the broadband case in Section 3.4, the frequency-based spatialization model (29) can be applied to the bandpass filtered signal (45), which allows for representing the isolated Doppler-shifted frequencies
with
representing the subband AIR in the sampled Doppler domain and
where the band interleaving margins αℓ and βℓ are chosen according to the maximum expected Doppler shift, which can be approximated by knowing the microphone trajectory and using (17). The Doppler margins ensure that there is no measured signal component in
5.3 System of linear equations for subband parameters
In comparison with (33), we can now shrink the broadband parameter vector
that describes the subband case (46) with the reduced number of parameters
Caused by the interfering Doppler shifts and the non-ideal bandpass filters, the full information on a single discrete frequency l might be spread over neighbouring subbands (cf. Section 7.1; Figure 3). According to the complete signal decomposition (44), the entire frequency information is composed of
with
5.4 III-conditioning and subband improvements
Beside the ability of the subband approach to divide a large-scale broadband problem into many small-size subtasks that can be solved in parallel, some further numerical benefits are obtained for finding suitable and robust solutions to the inverse problem. This is highlighted in the following considerations.
5.4.1 Number of unknown parameters
For larger bandwidths and larger target regions, arbitrary microphone trajectories lead to a linear system (33) that will be ill-posed or even underdetermined with high probability unless an excessive number of spatially dense samples are acquired. This is essentially due to the exploding number of spatially dense sound-field parameters required to represent the dynamically coupled samples by broadband wave fields in spacious areas. For example, the uniform-grid model from Section 3.3.3 comprises at least (Δξ = πc0/ωcut)
parameters to be estimated for recovering field information at temporal frequency ωl inside a D-dimensional cubical region Ωcub of size
The overall linear system (33) models the typical broadband measurement case where the moving microphone acquires sound-field samples at the rate fs for a spectrally flat excitation signal emitted by a controlled loudspeaker source. Thus, choosing the uniform-grid model for example, the spatio-temporal recovery of AIRs with duration (L − 1)fs involves
In the light of the previous considerations, a decomposition of the overall linear system (33) is desirable. There are two strategies to divide the large-scale problem into smaller problems: the spectral decomposition of the global bandwidth [ω0, ωL−1] and the spatial decomposition of the measurement region Ω into multiple subareas with smaller extent. The feasibility of spatial decomposition will be highly dependent on both the microphone trajectory and the spatialization model, and, thus, is not further considered in this paper. However, the proposed subband filtering scheme provides a useful and general tool for the spectral signal and parameter decoupling in the presence of Doppler shifts. It can be used to solve smaller subproblems where only subsets of frequency parameters according to (47) are active.
5.4.2 Singular values
The subband approach solves the inverse problem by use of
with the sets
and ai denoting the i-th element in a. Since Vℓ ⊆ V, it follows
Hence, the condition number of the subband sampling matrix satisfies
Compared to the broadband case, the subband formulation typically yields a shrunken range between singular values, most likely for Pℓ ≪ P. This improves the matrix condition and, therefore, the robustness of the estimates and the theoretical error bounds in the sense of (39).
For a broadband sampling matrix
where
where J = P − Pℓ is the number of dropped columns due to the subband formulation. Especially for low-frequency subbands that require only a small number of spatial parameters, Pℓ ≪ P and J in (52) becomes very large, so that the subband solution by analogy with (51) is most likely more robust.
For M < P, the broadband measurement matrix
which states that each submatrix constructed by no more than K columns has its singular values in the interval
6 Frequency analysis in Doppler domain
Having a moving microphone, the decoupling of single temporal frequencies by applying conventional Fourier analysis to the measured signal is not possible. Due to the receiver motion within the multipath environment, spectral characteristics are actually spread over multiple frequency components (frequency dispersion). The range of this spectral broadening is measured by the so-called Doppler spread, which, in our case, increases for higher velocities of the microphone. For the subband design in Section 5, the extent of frequency spreading is taken into consideration by the frequency set (47), where αℓ and βℓ are simple worst-case bounds for the Doppler spread according to the maximum expected microphone speed. In this section, we derive trajectory-dependent filters that exactly characterize the frequency dispersion in the sampled microphone signal. The knowledge of the receiver trajectory allows for calculating these filters and describing frequency components in the dynamically observed signal by frequency-spread versions of the particular sound-field parameters.
6.1 Spatio-spectral spreading due to dynamic observations
As demonstrated in Section 3, the dynamic signal model (2) can be seamlessly embedded into the concept of Doppler-variant impulse responses and transfer functions, which is often used in wireless-communications literature. Let us adapt the notation in (2) accordingly, i.e.,
where the subscript indicates the temporal context to the trajectory. In (53), the signal multiplication subject to t translates to the convolutive frequency representation
where
In comparison to (14), where the sound-pressure observation is given in the time domain, (55) displays the Fourier correspondence of the dynamic signal subject to the global time variable t. This reveals the convolutional coupling of the frequency variables ω and ν due to the receiver movement.
6.2 Spatial parameterization of the Doppler-variant transfer function
Similar to (15), the trajectory-shaped spreading function in (55) can be represented subject to the particular spatialization model of the time-invariant sound-field characteristics, i.e.,
with the trajectory-dependent filters
constructed by the Fourier transform of the particularly evaluated basis functions. In Figure 2, we summarize the parameter-based relationships between the four fundamental system functions that describe the dynamic channel as introduced in Section 3.1 with direct connections to the receiver trajectory. Note that the parameterized domains in Figure 2 are equivalent to the four domains in Figure 1. Substituting (56) into (55) yields the representation
that describes the dynamically observed frequencies in terms of the sound-field parameters A(ρ, ω) and their trajectory-dependent smearing due to
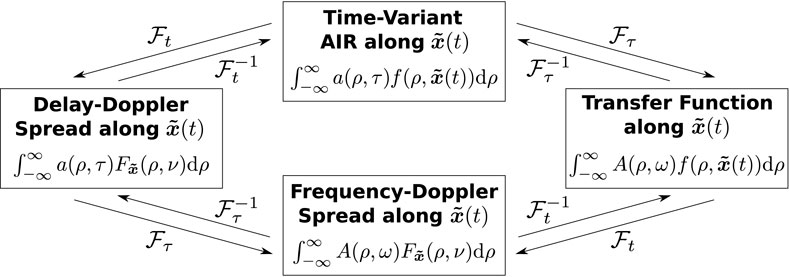
Figure 2. Representation of the four domains in Figure 1 subject to shaped parameters. The effective time-variance of the dynamic receiver channel is fully attributed to trajectory-shaped (filtered) versions of fixed sound-field parameters a(ρ, τ) and A(ρ, ω), respectively.
6.3 Sampled frequency spreading for periodic excitation
For obtaining a sampled analogy to (57), let us consider the periodic excitation
by use of a deterministic sequence
Based on (31), we define the short-time segment
of length L obtained from rectangular windowing of the microphone signal for window indices
with the discrete Fourier transform of the sequence
the (spatially) windowed Doppler-variant impulse response
shaped by the particular trajectory segment, and the corresponding transfer function
modeling the frequency spread in the sampled signal due to the moving microphone. Taking the discrete Fourier transform of both sides of (60) yields
which clearly describes the resulting frequency shifts in the short-time Fourier representation
6.4 Frequency-spreading filters due to moving microphones
The discrete spatialization model (29) allows for the sampled Doppler-variant representation
subject to the finite set of sound-field parameters A(c, l) and the trajectory-dependent FIR filters
for the specific choice of spatial basis functions. Substituting (62) into (61) finally reveals the short-time Fourier representation
of the dynamic sampling model (30) in terms of the frequency-spreading filters
and
respectively, with (65) being actually dissolved into a short-time Fourier representation of the stationary sampling concept (4) for L-periodic excitation.
Similar to the subband procedure proposed in Section 5, the short-time Fourier analysis (64) could be used to set up a recovery strategy that decomposes the dynamic broadband problem (33) into multiple subproblems of narrow frequency ranges. In fact, this is straightforward for sufficiently slow trajectories which allow for approximations
7 Experiments and results
In this section, we demonstrate the key points of the introduced Doppler framework on the basis of experimental data and specifically chosen examples of parameterization models.
7.1 Doppler-spread visualizations
Let us first consider unrealistic toy examples with extreme receiver velocities for clear visualizations of both the Doppler shifts between dynamic subbands
Four experiments were carried out with different trajectory mean velocities of 5 km/h, 50 km/h, 100 km/h, and 200 km/h. The spherical-harmonic parameterization from Section 3.3.2 was selected for the dynamic reconstruction. Accordingly, the spatially embedded transfer function sampled along
with
The absolute values of the recovered subband parameters A[ℓ]((v, q), l) arranged in aℓ are depicted in Figure 3 in reference to the four numerical experiments with various microphone velocities. The parameters are successively concatenated first along the spatial (v, q)-dimensions and then along l with increasing frequency. Dotted lines indicate the vector indices where the defined cutoffs are reached. In Figure 3, the Doppler effect can be clearly observed in terms of subband-overlapping broadening of frequency-based parameters, especially with regard to higher frequencies and faster measurement trajectories. In case of 5 km/h, the subband of Doppler interfered frequencies in
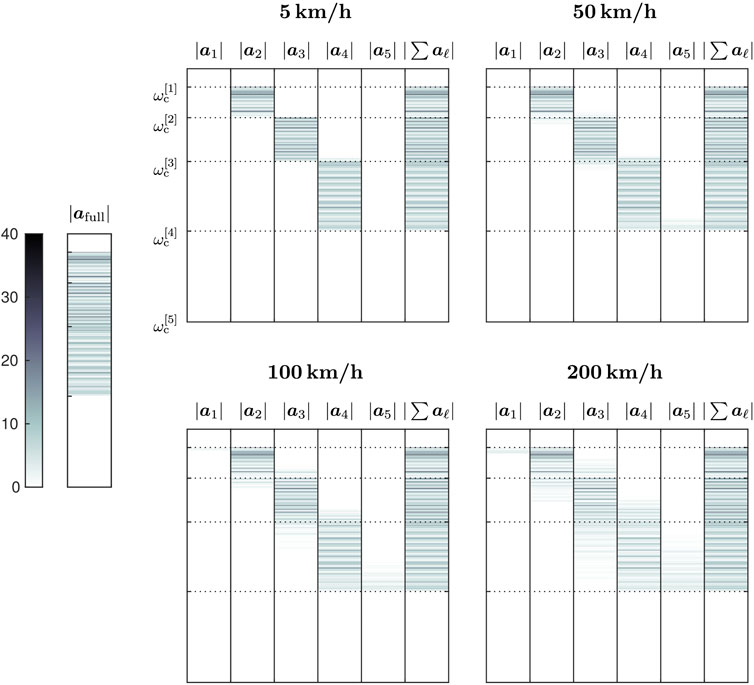
Figure 3. Magnitudes of spherical-harmonic parameters in vector |afull| recovered from the broadband formulation in comparison to the magnitudes in |aℓ|, ℓ ∈ {1 …, 5}, recovered from the subband decomposition scheme for several trajectory velocities. Higher velocities induce a visible spreading of frequency information over different subbands.
By using the Doppler analysis scheme from Section 6, Figure 4 depicts several examples of the underlying frequency-spreading filters
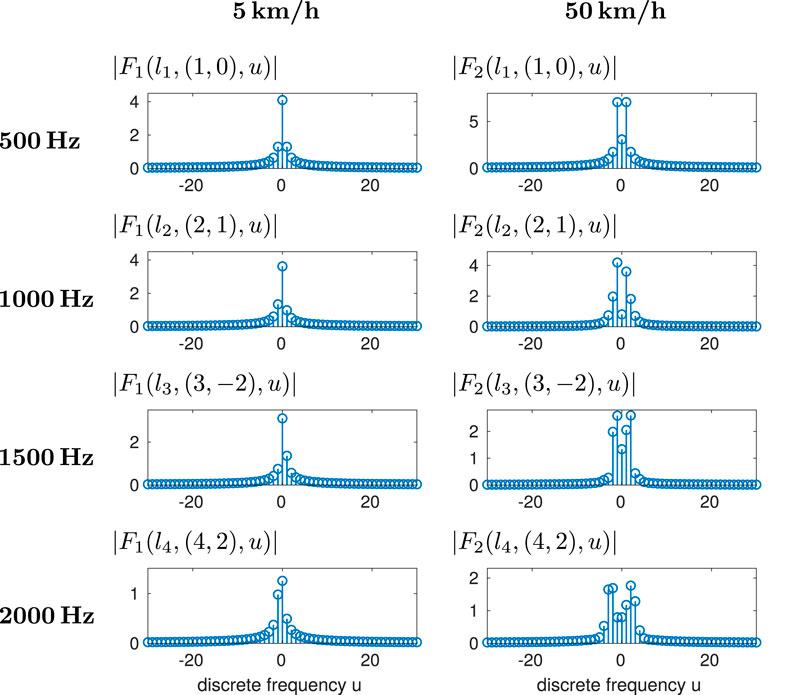
Figure 4. Lower- and higher-frequency examples (rows) of trajectory-dependent filters causing the Doppler spreading for two different trajectory velocities (columns). The range of the Doppler spread is defined by the effective filter length. It increases for higher frequencies and higher velocities.
7.2 Doppler misalignment due to noisy trajectory data
Inaccuracies in the positional tracking of the microphone result in Doppler-shift discrepancies as introduced in Section 4. The subband decoupling scheme from Section 5 may increase the robustness against noisy trajectory data, especially regarding low-frequency parameter estimates as highlighted in Section 5.4. For demonstrating such sensitivity relationships, we carried out numerical experiments in twenty simulated room scenarios, randomly chosen according the uniform distribution of box-shaped dimensions [2 m; 10 m]3 and reverberation times T60 ∈ [0.2 s; 0.35 s]. In each environment, both the source position and the location of the considered measurement plane were randomly selected. Impulse responses were limited to length L = 4095. Recordings of an omnidirectional microphone were simulated at fs = 12 kHz along planar Lissajous trajectories
The grid approach from Section 3.3.3 was combined with aspects from theoretical acoustics and used for CS-based sound-field recovery (Katzberg et al., 2018; Katzberg and Mertins, 2022). Regarding the experiments with two-dimensional trajectories on planar target regions, the discretized sound-field model on a finite Gx × Gy grid reads
where
As error measure for the overall sound-field reconstruction involving G grid AIRs, the mean normalized system misalignment
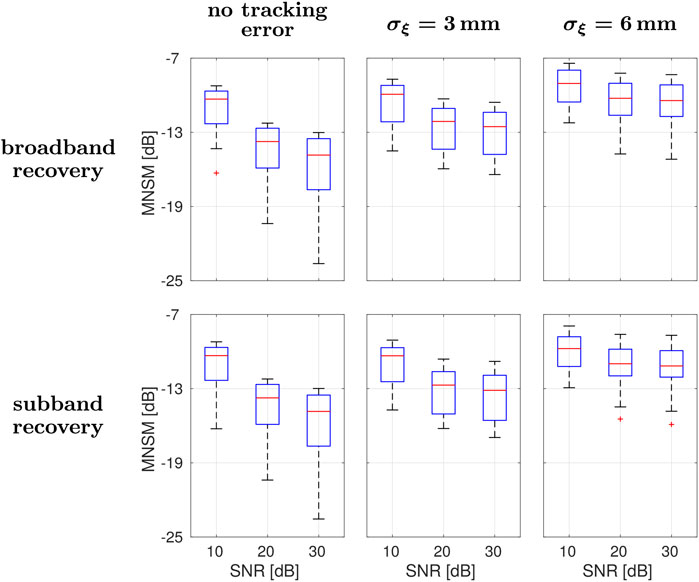
Figure 5. Errors of AIR parameters obtained from the broadband (first row) and subband formulations (second row) for various microphone SNRs and different levels of tracking inaccuracies (columns).
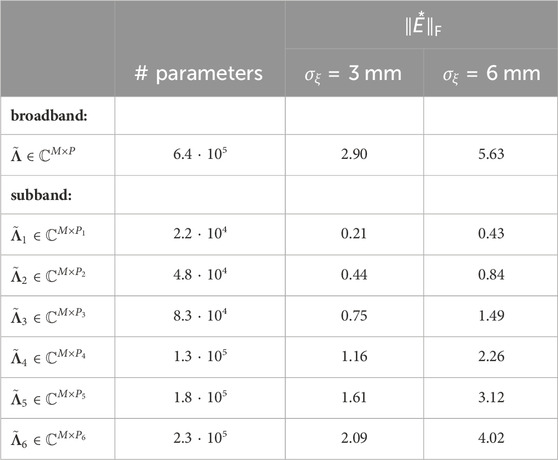
Table 1. Comparison of parameter numbers for the broadband and subband strategies, and evaluation of matrix perturbations due to positional deviations of σξ = 3 mm and σξ = 6 mm, respectively.
While the recovery performances are essentially equal for noiseless trajectory data, the subband scheme improves the robustness against the trajectory discrepancies compared to the standard broadband approach. For σξ = 6 mm, its performance gain is about 1 dB on average (Figure 5). For visualizing the effects of positional inaccuracies, the magnitudes of two particular frequency-spreading filters F1((κx, κy), u) are presented in Figure 6 given a true trajectory segment and its noisy version: for filters such as F1((10, 10), u) pointing to rather higher spatial frequencies (and, thus, also to higher temporal frequencies), the resulting Doppler mismatches are typically more considerable. To analyze frequency-based recovery performances, we apply the mean energy spectral density of the error
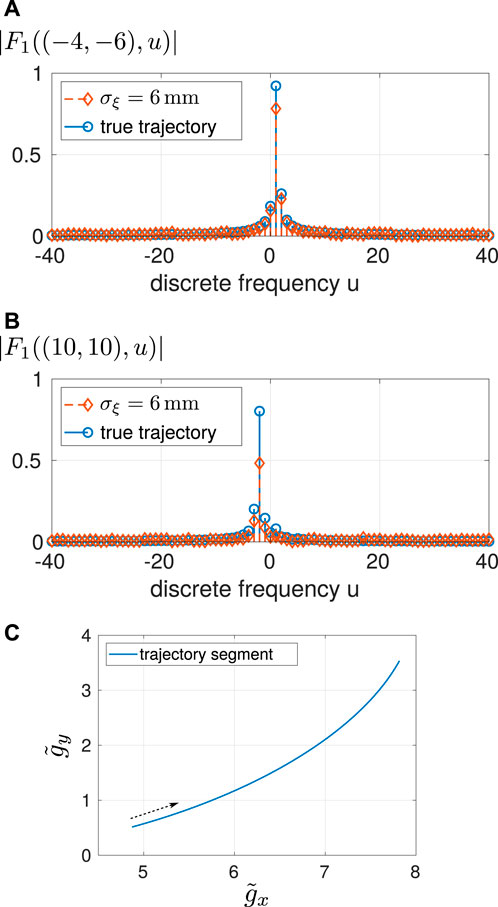
Figure 6. Outline of mismatched and true Doppler-spreading filters F1((κx, κy), u) for discrete-frequency pairs of (A) (κx, κy) = (−4, − 6) and (B) (κx, κy) = (10, 10). The underlying true trajectory segment is depicted in (C), where the arrow indicates the direction of microphone motion. Note that there is an intuitive filter interpretation due to the applied uniform-grid model (cf. Section 3.3.3). For example, F1((10,10), u) can be considered to render the trajectory-dependent Doppler effect for a virtual plane wave arriving from direction [−1, − 1], i.e., it basically shifts the sound-field parameters to lower frequencies as can be seen from (B).
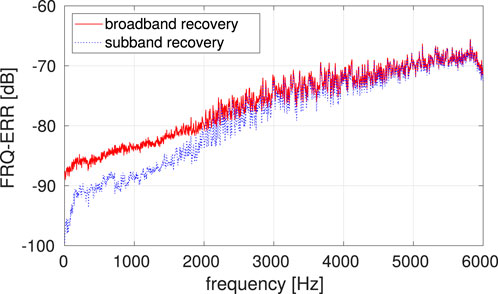
Figure 7. Frequency-dependent errors of recovered sound-field parameters. The subband approach allows for improved reconstructions especially at low frequencies.
8 Conclusion
In this work, we formulated a Doppler-based framework that reveals the frequency-spreading effects in dynamic sound-field sampling procedures. It has been shown that the exact positional tracking of a moving microphone allows for the exact rendering of underlying Doppler shifts in the acquired signal. As it turned out, the involved frequency shifts are directly connected with the sampling of spatial basis functions subject to the microphone trajectory. For the practically relevant case of tracking inaccuracies, we described the resulting impact on the inverse problem in terms of mismatches between true and inaccurately modeled Doppler shifts. Such mismatches lead to a multiplicative perturbation model, for which we provided sensitivity considerations regarding least-squares and CS-based estimates. Also, a subband analysis scheme has been derived, which enables us to split the presented Doppler model for broadband measurements into a number of smaller subproblems that consider particular frequency bands. This allows for parallelizing the computational effort and for obtaining faster reconstructions with improved robustness against the trajectory errors, especially regarding lower frequencies. Further, we provided a reasonable concept for the (short-time) Fourier analysis of the dynamic measurement signal. Due to the continuously moving microphone, this yields an actually spatio-temporal Fourier description, dimensionally coupled by the performed trajectory. In this representation, the included Doppler spreads can be explicitly characterized by a series of trajectory-dependent FIR filters.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
FK: Writing–original draft. MM: Writing–review and editing. AM: Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work has been supported in part by the German Research Foundation under Grant No. ME 1170/10-2.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ajdler, T., Sbaiz, L., and Vetterli, M. (2006). The plenacoustic function and its sampling. IEEE Trans. Signal Process. 54, 3790–3804. doi:10.1109/tsp.2006.879280
Ajdler, T., Sbaiz, L., and Vetterli, M. (2007). Dynamic measurement of room impulse responses using a moving microphone. J. Acoust. Soc. Am. 122, 1636–1645. doi:10.1121/1.2766776
Allen, J., and Berkley, D. (1979). Image method for efficiently simulating small-room acoustics. J. Acoust. Soc. Am. 65, 943–950. doi:10.1121/1.382599
Bah, B., and Tanner, J. (2010). Improved bounds on restricted isometry constants for Gaussian matrices. SIAM J. Matrix Anal. Appl. 31, 2882–2898. doi:10.1137/100788884
Bello, P. (1963). Characterization of randomly time-variant linear channels. IEEE Trans. Commun. Syst. 11, 360–393. doi:10.1109/tcom.1963.1088793
Benesty, J., Huang, Y., Chen, J., and Naylor, P. A. (2006). “Adaptive algorithms for the identification of sparse impulse responses,” in Topics in acoustic echo and noise control. Editors E. Hänsler, and G. Schmidt (Berlin: Springer), 125–153.
J. Benesty, M. Sondhi, and Y. Huang (2008). Springer handbook of speech processing (Germany: Springer).
Candès, E., Romberg, J., and Tao, T. (2006). Stable signal recovery from incomplete and inaccurate measurements. Commun. Pure Appl. Math. 59, 1207–1223. doi:10.1002/cpa.20124
Colton, D., and Kress, R. (2019). Inverse acoustic and electromagnetic scattering theory. 4 edn. Germany: Springer.
Enzner, G. (2008). Analysis and optimal control of LMS-type adaptive filtering for continuous-azimuth acquisition of head related impulse responses. Proc. IEEE Int. Conf. Acoust. Speech, Signal Process., 393–396. doi:10.1109/ICASSP.2008.4517629
Fazi, F. M., Noisternig, M., and Warusfel, O. (2012). Representation of sound fields for audio recording and reproduction. Proc. Acoust., 859–865.
Golub, G. H., and Van Loan, C. F. (2013). Matrix computations. 4 edn. United States: Johns Hopkins University Press.
Hahn, N., Hahne, W., and Spors, S. (2017). Dynamic measurement of binaural room impulse responses using an optical tracking system. Proc. Int. Conf. Spat. Audio., 16–21. doi:10.1109/WASPAA.2017.81700241
Hahn, N., and Spors, S. (2016). Comparison of continuous measurement techniques for spatial room impulse responses. Proc. Eur. Signal Process. Conf., 1638–1642. doi:10.1109/EUSIPCO.2016.7760526
Hahn, N., and Spors, S. (2017). Continuous measurement of spatial room impulse responses using a non-uniformly moving microphone. IEEE Workshop Appl. Signal Process. Audio Acoust, 205–208.
Hahn, N., and Spors, S. (2018). Simultaneous measurement of spatial room impulse responses from multiple sound sources using a continuously moving microphone. Proc. Eur. Signal Process. Conf., 2194–2198. doi:10.23919/EUSIPCO.2018.8553532
S. Haykin, and K. J. R. Liu (2010). Handbook on array processing and sensor networks (New York: Wiley).
He, J., Ranjan, R., Gan, W.-S., Chaudhary, N. K., Hai, N. D., and Gupta, R. (2018). Fast continuous measurement of HRTFs with unconstrained head movements for 3D audio. J. Audio Eng. Soc. 66, 884–900. doi:10.17743/jaes.2018.0050
Herman, M., and Strohmer, T. (2010). General deviants: an analysis of perturbations in compressed sensing. IEEE J. Sel. Top. Signal Process. 4, 342–349. doi:10.1109/jstsp.2009.2039170
F. Hlawatsch, and G. Matz (2011). Wireless communications over rapidly time-varying channels (USA: Academic Press).
Katzberg, F., Maass, M., and Mertins, A. (2021). Spherical harmonic representation for dynamic sound-field measurements. Proc. IEEE Int. Conf. Acoust. Speech, Signal Process., 426–430. doi:10.1109/ICASSP39728.2021.9413708
Katzberg, F., Maass, M., Pallenberg, R., and Mertins, A. (2022). Positional tracking of a moving microphone in reverberant scenes by applying perfect sequences to distributed loudspeakers. Proc. Int. Workshop Acoust. Signal Enhanc. doi:10.1109/IWAENC53105.2022.9914709
Katzberg, F., Mazur, R., Maass, M., Koch, P., and Mertins, A. (2017a). Multigrid reconstruction of sound fields using moving microphones. Proc. Workshop Hands-free Speech Commun. Microphone Arrays, 191–195. doi:10.1109/HSCMA.2017.7895588
Katzberg, F., Mazur, R., Maass, M., Koch, P., and Mertins, A. (2017b). Sound-field measurement with moving microphones. J. Acoust. Soc. Am. 141, 3220–3235. doi:10.1121/1.4983093
Katzberg, F., Mazur, R., Maass, M., Koch, P., and Mertins, A. (2018). A compressed sensing framework for dynamic sound-field measurements. IEEE/ACM Trans. Audio, Speech, Lang. Process. 26, 1962–1975. doi:10.1109/taslp.2018.2851144
Katzberg, F., and Mertins, A. (2022). “Sparse recovery of sound fields using measurements from moving microphones,” in Compressed sensing in information processing. Editors G. Kutyniok, H. Rauhut, and R. J. Kunsch (Germany: Springer), 377–411.
Knopp, T., Biederer, S., Sattel, T., Weizenecker, J., Gleich, B., Borgert, J., et al. (2009). Trajectory analysis for magnetic particle imaging. Phys. Med. Biol. 54, 385–397. doi:10.1088/0031-9155/54/2/014
Li, W., and Preisig, J. C. (2007). Estimation of rapidly time-varying sparse channels. IEEE J. Ocean. Eng. 32, 927–939. doi:10.1109/joe.2007.906409
Moreau, S., Daniel, J., and Bertet, S. (2006). 3D sound field recording with higher order ambisonics - objective measurements and validation of a 4th order spherical microphone. Proc. 120th Conv. Audio Eng. Soc. (Conv. Paper 6857).
Ostashev, V. E., and Wilson, D. K. (2019). Acoustics in moving inhomogeneous media. 2 edn. United States: CRC Press.
Peterson, P. M. (1986). Simulating the response of multiple microphones to a single acoustic source in a reverberant room. J. Acoust. Soc. Am. 80, 1527–1529. doi:10.1121/1.394357
Pierce, A. D. (2019). Acoustics: an introduction to its physical principles and applications. Germany: Springer.
Rafaely, B. (2005). Analysis and design of spherical microphone arrays. IEEE Trans. Speech Audio Process 12, 135–143. doi:10.1109/tsa.2004.839244
Rife, D. D., and Vanderkooy, J. (1989). Transfer-function measurement with maximum-length sequences. J. Audio Eng. Soc. 37, 419–444.
Sondhi, M. (1967). An adaptive echo canceller. Bell Syst. Tech. J. 46, 497–511. doi:10.1002/j.1538-7305.1967.tb04231.x
Stan, G.-B., Embrechts, J.-J., and Archambeau, D. (2002). Comparison of different impulse response measurement techniques. J. Audio Eng. Soc. 50, 249–262.
Stewart, G. W. (1977). On the perturbation of pseudo-inverses, projections and linear least squares problems. SIAM Rev. 19, 634–662. doi:10.1137/1019104
Thompson, R. C. (1972). Principal submatrices IX: interlacing inequalities for singular values of submatrices. Linear Algebra Appl. 5, 1–12. doi:10.1016/0024-3795(72)90013-4
Urbanietz, C., and Enzner, G. (2020). Direct spatial-Fourier regression of HRIRs from multi-elevation continuous-azimuth recordings. IEEE/ACM Trans. Audio, Speech, Lang. Process. 28, 1129–1142. doi:10.1109/taslp.2020.2982291
Välimäki, V., and Laakso, T. (2000). Principles of fractional delay filters. Proc. IEEE Int. Conf. Acoust. Speech, Signal Process., 3870–3873. doi:10.1109/ICASSP.2000.860248
Vasquez, F. G., and Mauck, C. (2018). Approximation by Herglotz wave functions. SIAM J. Appl. Math. 78, 1283–1299. doi:10.1137/17m1144234
Wedin, P.-Å. (1973). Perturbation theory for pseudo-inverses. BIT Numer. Math. 13, 217–232. doi:10.1007/bf01933494
Williams, E. G. (1999). Fourier acoustics – sound radiation and nearfield acoustical holography. United States: Academic Press.
Keywords: sound field, moving microphone, Doppler effect, Doppler spreading function, wave equation, acoustic impulse response
Citation: Katzberg F, Maass M and Mertins A (2024) Doppler frequency analysis for sound-field sampling with moving microphones. Front. Sig. Proc. 4:1304069. doi: 10.3389/frsip.2024.1304069
Received: 28 September 2023; Accepted: 24 January 2024;
Published: 10 April 2024.
Edited by:
Thomas Dietzen, KU Leuven, BelgiumReviewed by:
Nara Hahn, University of Southampton, United KingdomAlbert Prinn, Fraunhofer Insititute for Integrated Circuits (IIS), Germany
Copyright © 2024 Katzberg, Maass and Mertins. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fabrice Katzberg, Zi5rYXR6YmVyZ0B1bmktbHVlYmVjay5kZQ==
†Present address: Marco Maass, German Research Center for Artificial Intelligence (DFKI), Lübeck, Germany
 Fabrice Katzberg
Fabrice Katzberg Marco Maass
Marco Maass Alfred Mertins
Alfred Mertins