1
Integrative Neuroscience Laboratory, Physics Department, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires Buenos Aires, Argentina
2
Computer Science Department, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires Buenos Aires, Argentina
Free-word association has been used as a vehicle to understand the organization of human thoughts. The original studies relied mainly on qualitative assertions, yielding the widely intuitive notion that trajectories of word associations are structured, yet considerably more random than organized linguistic text. Here we set to determine a precise characterization of this space, generating a large number of word association trajectories in a web implemented game. We embedded the trajectories in the graph of word co-occurrences from a linguistic corpus. To constrain possible transport models we measured the memory loss and the cycling probability. These two measures could not be reconciled by a bounded diffusive model since the cycling probability was very high (16% of order-2 cycles) implying a majority of short-range associations whereas the memory loss was very rapid (converging to the asymptotic value in ∼7 steps) which, in turn, forced a high fraction of long-range associations. We show that memory loss and cycling probabilities of free word association trajectories can be simultaneously accounted by a model in which transitions are determined by a scale invariant probability distribution.
“Apart from the studies to be reported here, there have been a few, if any, systematic attempts to subject meaning to quantitative measurement. There are probably several reasons for this even in a period of intense objectivity in psychology: For one thing, the term “meaning” seems to connote, from most psychologists at least, something inherently nonmaterial, more akin to “idea” or “soul” than to observable stimulus and response, and therefore to be treated like the other “ghosts” that J.B. Watson dispelled form psychology”.
In their seminal work Osgood et al. (1957)
argued that the semantic space could be quantitatively measured determining a number of principal semantic axes. Each concept could then be mapped to a vector in this high-dimensional semantic space. For instance, it is relatively easy to position the concepts “mouse”, “dog” and “house” in the size-axis. While this approach resulted in a metric which could successfully predict performance in various experiments, it had theoretical and practical problems (Lund and Burgess, 1996
): the determination of the principal axis from objective grounds
1
and the number of subjective judgments required, which is proportional to the number of axes.
These two problems were solved at once deriving the high-dimensional semantic space from a lexical co-occurrence matrix (Deerwester et al., 1990
; Lund and Burgess, 1996
). The main assumption for this derivation is that semantic proximity can be inferred by analyzing the statistical regularities in a text corpus. For instance, if the word “giraffe” is mentioned in a text, it is likely that the words, “neck”, “zebra” and “zoo” (which are semantically related) will also be mentioned. The conditional probabilities of co-occurrence (i.e. the probability of finding “dog” given that “cat” was mentioned) are thus likely to determine a good measure of semantic proximity. Lund and Burgess demonstrated this relation determining that: (1) Near neighbors in the co-ocurrence space correspond to related meanings (2) Clusters in this space corresponded to semantic categories and (3) Similarity in co-occurrence space determined the effect on RT in a semantic priming experiment.
This result was in line with prior evidence which had shown a correlation between frequency of co-occurrence and free-word association probabilities (Spence and Owens, 1990
), since the associative structure of words plays a central role in recall (Bousfield, 1953
; Jenkins et al., 1958
; Deese, 1959
, 1965
), cued recall (Nelson et al., 1992
), and recognition (Nelson et al., 2001
). Recently, Steyvers and colleagues showed that free word-association metrics (Nelson et al., 1999
; Steyvers et al., 2004
) performed better than corpus based metrics to predict human performance in various experiments of semantic memory.
Assuming that the semantic space has been fully characterized, how should a model of retrieval and free-association be determined from this space? The underlying hypothesis of most current studies is that memory retrieval and word-association result from a propagation process (concept spreading) in semantic space where the high-dimensional neighborhood surrounding each word is something akin to a semantic field (Collins and Loftus, 1975
; McClelland and Jenkins, 1991
; Burgess and Lund, 1994
; Cancho, 2001
; Sigman and Cecchi, 2002
; Cancho and Sole, 2003
; Steyvers and Tenenbaum, 2005
).
In this framework, meanings which are not directly connected, can be related through long chains of semantic relationships (for instance the sequence lion → feline → tiger → stripes). These semantic trajectories can be reconstructed from association pairs as the minimal path linking non-connected words (Dijkstra, 1959
; Nelson and Zhang, 2000
). Previous research has explicitly shown that the indirect associative strengths play a role in cued recall (Nelson and Zhang, 2000
) and recognition (Nelson et al., 2001
). Also, the inclusion of indirect associations in a measure for associative strength significantly helped in predicting recognition memory performance (Steyvers et al., 2004
).
This evidence taken together is thus quite consistent with the idea that word-association and memory retrieval involve the navigation in a semantic graph. However no previous study has explicitly tested this hypothesis by generating long-chains (trajectories) of word-associations and exploring how these trajectories embed in a co-occurrence graph. Here we set to achieve this task.
We measured, for free-word association trajectories, the memory loss (how many word-associations are needed to loose a trace of the original seed in the chain) and the cycling probability (the probability that after n associations the trajectory returns to the original word). As we will show later, these two measures taken together provide strong constraints of possible navigation models.
We show that the simplest hypothesis – that free-word association corresponds to a diffusion process, i.e. a random-walk where the probability of associating two meanings is a normally distributed (gaussian) function of the distance between word pairs – is inconsistent with the data. We then show that a transportation process based on scale invariant probabilities – where most associations relate proximal neighbors and a few associations establish long-range relations – provides an accurate description of free-word association trajectories.
Word association trajectories where collected implementing an online game. The game had a very simple structure. Upon registering, each player received a word (the seed of the trajectory) and was instructed to send the first associated word to any other player in the game (for a more detailed description see Materials and Methods). One association after the other, a chain of associations is formed. Here we’d like to stress that each word of the trajectory is dependent only on the previous one (and some internal state of the player). The game was open for 2 months and generated 1299 trajectories of mean length 30.
We embedded these trajectories in a weighted graph, which was built based on standard methodology of co-occurrence of words in a large text corpus (Church and Hanks, 1990
; Steyvers et al., 2004
). The strength of the link between words j and k is determined by the conditional probability of finding word k given that word j occurred at a distance of less than 10 words. Note that the conditional probability is not symmetric and thus the graph is directed.
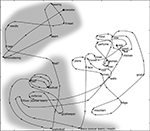
As an example, we show a segment of a representative trajectory (see Figure 1
). For illustration purposes only, we represent this trajectory in a 2D projection which was constructed using a combination of a fuzzy clustering algorithm (Hotta et al., 2003
) and a Sammon projection (Sammon, 1969
) (see Materials and Methods).
Figure 1. The plane corresponds to the Sammon projection of a subgraph of the word co-occurrence graph. This classification revealed two distinct clusters which can be mapped to semantic categories. Within this space, word-association trajectories are confined to clusters with a highly cyclic structure. A fraction of the jumps link words of distinct clusters. *(pelota and bola are synonyms of the word ball in Spanish).
The segment of the trajectory starts on the word “Egg” (marked with a star) and ends on “Sweater” (marked with a square). Some aspects of the topology of the trajectory – which we will later quantify over the statistics of all trajectories – are evident in this example.
First, most transitions of the trajectory resulted from a short step (i.e. an association between two words which are close to each other). Second, for several consecutive associations, the trajectory is confined to a neighborhood (cluster) of word space. Third, within each cluster, cycles are very prominent. Indeed, the most frequent are order-2 cycles, i.e. two words with an exceedingly high reciprocal return probability. (e.g. ball–soccer–ball… | man–woman–man…). Finally, in some sporadic instances – a word association results in a long jump, relating two words of distinct clusters.
We next quantify this qualitative observations. For each pair of words, we define, from the statistics of the written corpus, the displacement between word k and word j as Δ(k, j) = A−1/P(j |k) where A is the normalization constant A = Σ∀k,j1/P(j |k) (see Materials and Methods). This measure is often referred as a distance. However, note that Δ is not formally a distance since Δ(k, j) ≠ Δ(j, k) and thus is not symmetric.
The ensemble of trajectories {Ti} is a list of sequences. Ti is a sequence of words 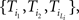 where Li is the length of the trajectory Ti. We define < Δ(n)> as the average of
where Li is the length of the trajectory Ti. We define < Δ(n)> as the average of 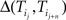 – the displacement between word
– the displacement between word 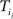 and word
and word 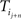 – over all possible such pairs in each trajectory and over all trajectories. The second measure which we will use to constrain transport models is the cycling probability, simply defined as the fraction of trajectories which return to the original word after n steps).
– over all possible such pairs in each trajectory and over all trajectories. The second measure which we will use to constrain transport models is the cycling probability, simply defined as the fraction of trajectories which return to the original word after n steps).
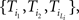 where Li is the length of the trajectory Ti. We define < Δ(n)> as the average of
where Li is the length of the trajectory Ti. We define < Δ(n)> as the average of 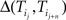 – the displacement between word
– the displacement between word 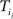 and word
and word 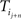 – over all possible such pairs in each trajectory and over all trajectories. The second measure which we will use to constrain transport models is the cycling probability, simply defined as the fraction of trajectories which return to the original word after n steps).
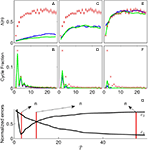
– over all possible such pairs in each trajectory and over all trajectories. The second measure which we will use to constrain transport models is the cycling probability, simply defined as the fraction of trajectories which return to the original word after n steps).We observed that the displacement increased monotonically with the number of steps, reflecting the loss of the memory trace after the concatenations of a series of word associations (Figure 2
A, x-marks). This progression reached an asymptotic value of about 0.75. This value is lower than 1 (the mean displacement between two words) indicating that the words which occurred more frequently in the game were closer to the rest of the graph than less-frequent words.
Figure 2. In the upper part we present simulations of the kernel (blue) and exponential (green) models for different values of their parameter (K and 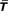 ). (A) and (B) are simulations for a small value of the parameters K = 6,
). (A) and (B) are simulations for a small value of the parameters K = 6, 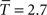 . The cyclic structure is reproduced correctly but the diffusion is too slow. In (E) and (F), the converse case is presented (K = 60,
. The cyclic structure is reproduced correctly but the diffusion is too slow. In (E) and (F), the converse case is presented (K = 60, 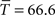 ) now the diffusive behavior is captured correctly but the cyclic structure is not. (C) and (D) correspond to intermediate values (K = 18,
) now the diffusive behavior is captured correctly but the cyclic structure is not. (C) and (D) correspond to intermediate values (K = 18, 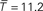 ). These values are chosen as to minimize
). These values are chosen as to minimize 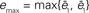 but the result is not satisfactory. In (G) we present the normalized errors
but the result is not satisfactory. In (G) we present the normalized errors 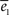 and
and 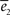 for the exponential model. Here it is clearly seen that the regions in parameter space which correctly adjust the displacement and cyclic structure are complementary.
for the exponential model. Here it is clearly seen that the regions in parameter space which correctly adjust the displacement and cyclic structure are complementary.
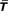 ). (A) and (B) are simulations for a small value of the parameters K = 6,
). (A) and (B) are simulations for a small value of the parameters K = 6, 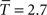 . The cyclic structure is reproduced correctly but the diffusion is too slow. In (E) and (F), the converse case is presented (K = 60,
. The cyclic structure is reproduced correctly but the diffusion is too slow. In (E) and (F), the converse case is presented (K = 60, 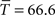 ) now the diffusive behavior is captured correctly but the cyclic structure is not. (C) and (D) correspond to intermediate values (K = 18,
) now the diffusive behavior is captured correctly but the cyclic structure is not. (C) and (D) correspond to intermediate values (K = 18, 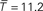 ). These values are chosen as to minimize
). These values are chosen as to minimize 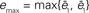 but the result is not satisfactory. In (G) we present the normalized errors
but the result is not satisfactory. In (G) we present the normalized errors 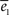 and
and 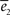 for the exponential model. Here it is clearly seen that the regions in parameter space which correctly adjust the displacement and cyclic structure are complementary.
for the exponential model. Here it is clearly seen that the regions in parameter space which correctly adjust the displacement and cyclic structure are complementary.The cycling probability also showed a clear pattern (see Figure 2
B x-marks). There was a very marked parity effect (even number of steps showed a much higher cycling probability) modulated by an overall exponential decrease. The parity effect indicates that the cyclic structure is dominated by order-2 cycles, i.e. segments of the form dog–cat–dog–… are very frequent in trajectories of word-association. Also note that the probability of finding a order-2 cycle is very high (around 0.16, indicating that about 1/6 of the words return to the original starting point after a pair of word associations by two different players). The fact that we do not find order-1 cycles simply shows that subjects follow the instruction of not repeating the presented word.
These two curves which characterize the displacement and the structure of cycles of the trajectories will become our yardstick to evaluate generative models for word-association. We describe such models in the framework of a first order Markov process where each word represents a state and a model is completely determined by specifying the transition probabilities between states. We iterate this procedure, starting in the same words which were used as seeds in the experiment, to simulate the trajectories (see Materials and Methods for more details) based on different transport models. We then measure the displacement and cycling probability functions of the simulated trajectories and confront them to the experimental data.
We first explored the simplest spreading model (a Kernel model) in which the transition probability from any given word is a step function. Let {1…N} be the sorted list of neighbours of a word [according to the weights Δ(k, j)], then the probability distribution in this set for the Kernels model is:

where p(i) is the probability of jumping to the ith closest neighbor. The limiting behaviors of this model are quite easy to understand. K = 1 corresponds to perseveration – only associating to the closest word in the graph. Whenever two words are reciprocally the closest neighbours (which happens often but not always since the graph is not symmetric) the trajectory gets locked up in a cycle. Thus, in this limit cycles are very prominent and the displacement rarely converges to the mean displacement value. The other limiting case corresponds to K = N (the number of nodes in the graph) in which transitions are made completely at random. In this situation cycles are extremely rare (order 1/N) and the displacement function is flat and equal to the mean displacement. We explored – using a least squares metric – whether intermediate values could adjust the cycles and displacement function, thus validating the model and serving as a measure of the degree of randomness of word associations.
The goodness of the fit is measured by the normalized squared errors defined as: 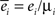 , where ei is the sums of the squared error for the displacement (i = 1) and cycles’ (i = 2) curves respectively. The
, where ei is the sums of the squared error for the displacement (i = 1) and cycles’ (i = 2) curves respectively. The 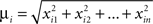 are normalization factors (xij are data points of curve i).
are normalization factors (xij are data points of curve i).
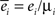 , where ei is the sums of the squared error for the displacement (i = 1) and cycles’ (i = 2) curves respectively. The
, where ei is the sums of the squared error for the displacement (i = 1) and cycles’ (i = 2) curves respectively. The 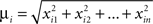 are normalization factors (xij are data points of curve i).
are normalization factors (xij are data points of curve i).The cycles and displacement functions can be well fitted individually but with drastically different parameters as can be seen in Figures 2
A,B,E,F (in blue). The best fit for cycles corresponds to K = 6 (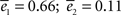 ), which could have simply been predicted as discussed previously by the return probability. The best fit for displacement corresponds to a much larger value of K [K = 60 (
), which could have simply been predicted as discussed previously by the return probability. The best fit for displacement corresponds to a much larger value of K [K = 60 (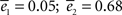 )]. We could not find intermediate values of K which could adjust simultaneously the two curves.
)]. We could not find intermediate values of K which could adjust simultaneously the two curves.
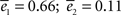 ), which could have simply been predicted as discussed previously by the return probability. The best fit for displacement corresponds to a much larger value of K [K = 60 (
), which could have simply been predicted as discussed previously by the return probability. The best fit for displacement corresponds to a much larger value of K [K = 60 (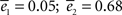 )]. We could not find intermediate values of K which could adjust simultaneously the two curves.
)]. We could not find intermediate values of K which could adjust simultaneously the two curves.The previous model only incorporated proximity in the co-occurrence graph in a discrete manner, assigning a uniform probability to the K closest words. We explored whether weighting this associations in a continuous manner could yield better results, exploring the best fits for a model (Exponential model) in which the transition probabilities follow an exponential function of Δ(k, j) according to:

where A is just a normalization constant and T can be seen as the “temperature” of the system – i.e the degree of stochasticity. In this model T plays a role comparable to that of K in the previous model, with the analogies K = 1 (T → 0) for perseveration and K = N (T → ∞) for random behavior. The limit cases are indeed identical.
As in the previous model, we found two different parameter values which could explain reasonably well the cycle and the displacement functions (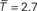
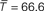 where the bar denotes that T is normalized by the mean Δ of the graph). However, as observed with the Kernel model, we could not find a single parameter which could explain correctly both functions simultaneously. The values of
where the bar denotes that T is normalized by the mean Δ of the graph). However, as observed with the Kernel model, we could not find a single parameter which could explain correctly both functions simultaneously. The values of 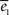 and
and 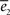 for the exponential model are plotted in Figure 2
G. From the graph it becomes evident that the minima do not overlap and thus both curves cannot be adjusted correctly for any parameter value. An attempt to plot an intermediate value – one which minimizes
for the exponential model are plotted in Figure 2
G. From the graph it becomes evident that the minima do not overlap and thus both curves cannot be adjusted correctly for any parameter value. An attempt to plot an intermediate value – one which minimizes 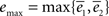 – is also not satisfactory (Figures 2
C,D). A very similar result is obtained for the Kernel model.
– is also not satisfactory (Figures 2
C,D). A very similar result is obtained for the Kernel model.
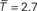
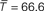 where the bar denotes that T is normalized by the mean Δ of the graph). However, as observed with the Kernel model, we could not find a single parameter which could explain correctly both functions simultaneously. The values of
where the bar denotes that T is normalized by the mean Δ of the graph). However, as observed with the Kernel model, we could not find a single parameter which could explain correctly both functions simultaneously. The values of 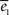 and
and 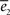 for the exponential model are plotted in Figure 2
G. From the graph it becomes evident that the minima do not overlap and thus both curves cannot be adjusted correctly for any parameter value. An attempt to plot an intermediate value – one which minimizes
for the exponential model are plotted in Figure 2
G. From the graph it becomes evident that the minima do not overlap and thus both curves cannot be adjusted correctly for any parameter value. An attempt to plot an intermediate value – one which minimizes 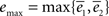 – is also not satisfactory (Figures 2
C,D). A very similar result is obtained for the Kernel model.
– is also not satisfactory (Figures 2
C,D). A very similar result is obtained for the Kernel model.While we did not explore this exhaustively, it is qualitatively easy to understand that any model in which the probabilities of associations are confined to a finite kernel (weighted by any function of distance) cannot explain the cycles and displacement function simultaneously.
The probability of second order cycles is equal to 1/K (if each word can be associated to K words, then the probability of returning to the original word is 1/K), this imposes a small and confined value for K. On the contrary, the displacement function, which shows a relatively fast convergence to the asymptotic value, determines that the number of neighbors (K in the kernel model, or effective neighbors for the exponential model) has to be of ∼60. Thus, word association cannot be explained by a simple bounded diffusive model. This is in agreement with the intuition which emerged from our original example in which we observed that while most associations were constrained to a local kernel in a semantic cluster, a few associations were long-range, linking words from different clusters.
One possible way to achieve this in the simulation is to implement the previous models, adding a small probability of producing random jumps. This approach works – i.e. it is possible to fit both the displacement and cycles curve, however it comes at the cost of introducing an additional parameter (the random-jump probability).
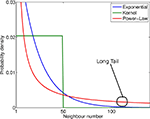
A better solution is to consider a scale-invariant, power-law probability distribution. This distribution is long-tailed, as compared with exponential or step function (see Figure 3
for a comparison of the three models). The ratio of small and long-range jumps is determined by the exponent of the power-law which is the unique parameter in this model. Thus, in the power-law model, the transition probabilities would then be:

Figure 3. Comparison between the three probability distributions (for illustration purposes only). Notice the long tail of the power-law compared with the other two functions.
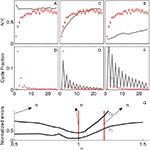
This model also exhibits similar limiting regimes for α → 0 and α → ∞ as is depicted in Figures 4
A,B,E,F. For small values of α (Figures 4
A,B) transitions are made completely at random, hence, the displacement is essentially flat and there are virtually no cycles. Conversely, for large values of α (Figures 4
E,F), trajectories are dominated by cycles and diffusion is very slow. However, in the power-law model, it is possible to find an intermediate value for α which correctly fits both curves (see Figures 4
C,D). In Figure 4
G we plot the normalized errors for both curves, this time both minima occur for the same parameter value which corresponds to α = 0.99 ± 0.05.
Figure 4. In the upper part we present simulations of the power-law model for different values of the parameter (α). (A) and (B) are simulations for a small value of α (0.1). Note that jumps are made completely at random, hence, the displacement is essentially flat and there are virtually no cycles. In (E) and (F), the converse case is presented (α = 1.2) and we observe that trajectories are dominated by cycles and diffusion is very slow. (C) and (D) correspond to the best fit for the power law model (α = 0.99 ± 0.5). In the lower part (G) we present the normalized errors 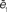 and
and 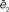 for the power-law model. As opposed to what happened in both the kernel and exponential model, here the minima of the errors for the two curves coincide.
for the power-law model. As opposed to what happened in both the kernel and exponential model, here the minima of the errors for the two curves coincide.
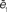 and
and 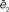 for the power-law model. As opposed to what happened in both the kernel and exponential model, here the minima of the errors for the two curves coincide.
for the power-law model. As opposed to what happened in both the kernel and exponential model, here the minima of the errors for the two curves coincide.It should be noted that the distribution of displacements of the simulation of the model depends both on the α of the model and on the distribution of weights in the graph. This can be understood with a simple example: In a graph in which all nodes have only one neighbor with Δ = 1, all transitions would correspond to Δ = 1 regardless of the transport model. We simulated the power-law model (with α = 0.99) and calculated the distribution of displacement of direct associations (between consecutive words of the simulated trajectories). This resulted in a power-law distribution with an exponent of −1.29 ± 0.05. This is consistent with the measured distribution of displacements of word-associations in the experiment, which also yielded a power-law distribution with an exponent of −1.27 ± 0.03. The fact that α ∼ 1 means that the best way in which to transverse the graph – as to best emulate free-word association – is according to the conditional probabilities alone. Indeed, from the definition, Δ(k, j) ∝ 1/p(j |k) and in the power-law model p(k → j) ∝ Δ−α then if α = 1, p(k → j) ∝ p(j |k). This means that there is no need to alter the probabilities extracted from the corpus in any way.
We performed a free-word association experiment in a web based game. Players passed words to each other in such a way that the associated word of a player was the to-be associated word of another and so on. This resulted in a large number of sequences of associated words, for instance: “sound → light → shadow → tree → wood”.
Our main objective and motivation was to determine whether these sequences could be explained in terms of trajectories in a semantic graph. Trajectories in a graph are often referred as “tourist walks” or simply as “walks” (Lima et al., 2001
).We investigated which transport rules, i.e. the algorithm by which the tourist walks the graph, generated trajectories which matched two important statistical indicators of the experimental sequences; the speed of displacement in the graph and the cycling probability.
Doing so required solving two issues in conjunction: the transport model and the structure of the underlying semantic graph. Our approach was to work with a unique graph, derived from the co-occurrence matrix of a large text corpus. Our results are certainly dependent on this choice. Had we constructed the semantic graph based on co-occurrences in fluid speech, or derived it from relations in a thesaurus, the results obtained may be different. In this sense, our study explores specifically the relation between the regularities in written text and in free-word associations.
Another specific aspect of this study is that subjects are aware only of the previous word and thus the trajectories are Markovian. Previous psychological experiments have studied consecutive associations made by the same subject (Palermo and Jenkins, 1964
) which constitute a non-Markovian process where words are produced with large memory window. Since also in written corpora words and sentences are generated in a non-Markovian way (it is the same subject that produces a long stream of text) it may seem that single-subject generated sequences may be a more appropriate comparison. However, long trajectories of free word association by single subjects are subject to other constraints, such as fatigue, semantic satiation (Jakobovits, 1962
). Thus, to avoid the effect of such factors, we decided to explore here a comparatively simpler situation in which each word depends – apart from internal states – only on the previous word of the sequence.
We showed that a walk based on a bounded diffusive model algorithm results in trajectories which cannot match the experimental sequences, regardless of the parameter choice (i.e. independently of the diffusion coefficient). On the contrary, walking the graph based on a power-law distribution of association can accurately match the experimental sequences. The critical aspect of this algorithm is that it walks to a close node in the graph with very high probability and, in a small but significant number of cases, it associates (walks to) words which are far in the graph.
This transport organization is reminiscent of Lévy flights, a process in which most transitions are short-range, as in a diffusive random-walk, and a small fraction of transitions are arbitrarily long jumps (Levy, 1925
). Levy flights are characterized by a power-law distribution with an exponent ranging between −1 and −3 [p ∝ x−α; α ∈ (1, 3)]. This has a very concise implication: the mean (the average step size) is finite but the variance (the progressive dispersion) is infinite. We found that the probability distribution of associations measured experimentally and of the best fitting model corresponded to power laws whose exponents were respectively −1.29 ± 0.05 and −1.27 ± 0.03 which are within the Lévy-flight range. However, the semantic graph is bounded and thus both the mean and the variance remain finite.
Deterministic tourist walks have been explored in a thesaurus derived network (Kinouchi et al., 2002
; Motter et al., 2002
). In these studies, the main parameter is the memory of the walker. The walker moves according to the following rule: go to the nearest site that has not been visited in the preceding N time steps. After a transient, trajectories drift to cycles of a length which is determined by the memory of the walker. If the walker has no memory (only of the present, it cannot stay in the same word) trajectories converge to 2-order cycles as, for instance, in the sequence: “translation → conversion → change → alter → change → …”. Thus excursions are not ergodic and 2-order cycles act as attractors. Colloquially, this can be interpreted as an erosion process where the semantic richness of a meaning collapses after a few iterations to a synthetic pair of words which are representative of the semantic category.
Word-association trajectories showed a trace of this phenomenon. First, Δ(n) remained smaller than the mean distance in the graph, even after many iterations, indicating that trajectories are not ergodic. Second, 2-order cycles were very prominent and dominated the cycling probability function as indicated by the parity effect. A crucial difference between deterministic thesaurus and free-word associations trajectories is that the latter are more stochastic and thus trajectories escape this cycles. For instance, a quite peculiar sequence which shows this effect was “madre → padre → madre → padre → madre → loca”.
Thus, as observed qualitatively in Figure 1
, word associations are for the most part confined to small semantic clusters and are thus very stereotyped and cyclic. In a few instances they result in long-range transitions which link different semantic clusters.
Of course – as discussed in the preceding paragraphs – the notion of close or distant is completely determined by the structure of the graph. Thus it is possible that long-range jumps can indeed be explained including further links to the graph, for instance relating phonologically similar words, and that under this constructions, the trajectories could remain purely local.
While this surely plays an important role, we tentatively suggest that, as suggested in Figure 1
, long-range associations stem from polysemous words which relate – through their multiple meanings – different semantic clusters. For instance, one example shown in Figure 1
is the word “Boca” (mouth in Spanish) which also refers to the most popular Argentinean football club Boca Juniors, thus linking sports concepts to body parts. The role of polysemous words bridging different semantic clusters is consistent with an observation from a complementary study, in which we found that polysemous words act as hubs of a semantic graph derived from Wordnet (Fellbaum et al., 1998
; Sigman and Cecchi, 2002
) and with the theoretical proposal which suggests that polysemy may be crucial for metaphoric thinking, imagery, and generalization (Lakoff and Johnson, 1980
).
In summary, We embedded this trajectories in a graph of word co-occurrences obtained from a large corpus of text, using this strategy to compare the highly structured linguistic texts with the more random trajectories of free word association. We observed that these trajectories could not be accounted by a purely bounded diffusive model, since different aspects of the statistics could not be reconciled in the same model. We showed that transitions exhibiting a scale-free behavior, could account quite accurately for the observed empirical distributions. This was in good agreement with the qualitative observation: word associations are, for the most part, confined to small semantic clusters and are thus very stereotyped and cyclic. In a few instances they result in long-range transitions – that are probably more prominent in polysemous words – which link different semantic clusters.
Generation of the Corpus Based-Metrics
The corpus was composed of uncopyrighted books, written in Spanish, from the Gutenberg Project
2
as well as all articles from local newspaper “La Nacion” that appeared between years 2000 and 2008. All texts were cleaned, removing any HTML code or headers that they may contain. They were also stripped from accents and diaeresis (á, é, í, ó, ú, ü). This was done in order to capture very common misspellings (accents are frequently omitted specially in online text). Evidently this comes at the cost of confusing two words that differ only in accentuation (e.g. te and té). The whole Corpus contained around 53 million words.
We then proceeded to count word co-occurrences within a window size of 10 words. This allowed us to estimate the conditional probability of finding a word A given that another word B is present “nearby”. Specifically this was done by measuring the frequency of co-occurrence of words A and B divided by the frequency of appearance of word B within the window size. This fraction gives a measure of how strongly linked two words are. We also defined the displacement between word A and B as the multiplicative inverse of the aforementioned conditional probability. It may happen – and is often the case – that two words never appear together. This would result in a null conditional probability and thus, an infinite displacement. One way to solve this problem would be to construct a new graph G where the element Gij corresponds to the value of the shortest path between words i and j in the original ill-defined graph. In this new graph every possible displacement would be finite (provided the original graph is connected). We have tried this approach and found it to be unsatisfactory. The reason is that we must select the subset of words for which we will compute the paths (doing the calculation including all the different words in the corpus is computationally out of our reach). Evidently the graph G is strongly dependant on which words are included in the subset. For that reason we decided to calculate all displacements in the original graph, not taking into account infinite jumps. These represent about 20% of all first order associations and increase monotonically with the order of the jump.
All the cleaning, counting and other text handling algorithms were programmed in PERL and are readily available
3
.
Acquisition of Word Association Data
The free association game was programmed using a combination of HTML, PHP and JavaScript. The data were recorded in a MySQL open source database. The site was divided in three major parts only two of which were visible to the players. The first one was where new players could register to play in the game. They had to write down their name and email address where they received a confirmation of their registration and the instructions to play the game.
The second and main part of the site was the personal page, where each player could see how many new words they had received and send their associations to other players. Once in a while they were given the choice to send the same association to two different players, thus bifurcating the trajectory. This means that some associations belong to more than one trajectory. The probability of bifurcation could be controlled dynamically to regulate the total traffic of words in the game. Upon registration each player would receive a “seed” word from a closed list of 20 nouns. Once a player had answered all of his/her words, they could steal words from lagging players or see a snapshot of a past trajectory. A ranking of the most responding players was also kept available to all the subjects. All this was done for motivation purposes. Non responding players were given first a yellow and then a red card (which entailed the termination of their account). Every couple of days an email was sent reminding players how many unanswered words they had.
A third part of the site was not visible to players and served as a “backdoor” to monitor the development of the game. From there the experimenter could check the activity of each player or the game as a whole, send reminders, yellow and red cards and set the probability of bifurcation of trajectories.
The game was open for 2 months and generated over 11,000 associations from 120 players.
2D Projection of the Trajectory
A first dimensionality reduction was achieved applying a fuzzy clustering algorithm (Hotta et al., 2003
) which led to seven significant clusters. This clustering algorithm works directly with weights instead of distances and does not assume the matrix to be symmetric. It is thus suitable for applications involving directed graphs. After applying the algorithm each word can be positioned in a 7-dimensional space, where each coordinate is determined by the degree of membership to each cluster. This was further reduced to a two dimensional Sammon projection (Sammon, 1969
). This plane optimizes the correlation between the pair-wise distances of the projection and the original higher dimensional space.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
We thank the Argentinean newspaper “La Nacion” for allowing us to use their online material to generate a Corpus as well as the Gutenberg Project. The participants of the XX Neurotaller for playing the game during the meeting which resulted in the original data for this manuscript. This research was funded by the Human Frontiers Science Program, by the SECYT and a CONICET fellowship to MEC.
- ^ A formally similar problem was faced by John Wilkins, when he set to determine – “a general language, organizing and covering all human ideas”. His analytical language was organized in a tree-like structure based on categories, further divided in sub-categories and so on. Each word indicated the position of a concept in a tree and thus meaning could be extracted without prior knowledge. As Borges (1997) mentions in ‘El idioma analítico de Wilkins’, a fundamental theoretical problem with Wilkins’ approach is the determination of the categories. “Having defined Wilkins’ procedure, we must examine a problem that is impossible or at least difficult to postpone: the value of the [forty] genera which are the basis of the language”.
- ^ http://www.gutenberg.org
- ^ http://neurociencia.df.uba.ar/
Fellbaum, C., Al-Halimi, R., Berwick, R. C., Burg, J. F. M., Chodorow, M., Fellbaum, C., Grabowski, J., Harabagiu, S., Hearst, M. A., Hirst, G., Jones, D. A., Kazman, R., Kohl, K. T., Landes, S., Leacock, C., Miller, G. A., Miller, K. J., Moldovan, D., Nomura, N., Priss, U., Resnik, P., St-Onge, D., Tengi, R., van de Riet R. P., and Voorhees, E. (1998). WordNet: An Electronic Lexical Database. Cambridge, MA, MIT Press.
Steyvers, M., Shiffrin, R., and Nelson, D. (2004). Word association spaces for predicting semantic similarity effects in episodic memory. Cognitive psychology and its applications: Festschrift in honor of Lyle Bourne, Walter Kintsch, and Thomas Landauer. Washington, DC, American Psychological Association.