1
Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany
2
Wellcome Trust Centre for Neuroimaging, UCL, London, UK
In this paper, we suggest that perception could be modeled by assuming that sensory input is generated by a hierarchy of attractors in a dynamic system. We describe a mathematical model which exploits the temporal structure of rapid sensory dynamics to track the slower trajectories of their underlying causes. This model establishes a proof of concept that slowly changing neuronal states can encode the trajectories of faster sensory signals. We link this hierarchical account to recent developments in the perception of human action; in particular artificial speech recognition. We argue that these hierarchical models of dynamical systems are a plausible starting point to develop robust recognition schemes, because they capture critical temporal dependencies induced by deep hierarchical structure. We conclude by suggesting that a fruitful computational neuroscience approach may emerge from modeling perception as non-autonomous recognition dynamics enslaved by autonomous hierarchical dynamics in the sensorium.
Although there have been tremendous advances in the development of algorithms and devices that can extract meaningful information from their environment, we seem still far away from building machines that perceive as robustly and as quickly as our brains. For example, in artificial speech recognition, Deng et al. (2006)
summarize current technology with: ‘The machine would easily break if the users were to speak in a casual and natural style as if they were talking with a friend.’ The situation is similar in machine vision: Although highly specialized recognition devices exist; e.g., for face recognition (Tan et al., 2006
; Zhao et al., 2003
), there is no generally accepted computational principle for robust perception.
In artificial speech recognition, the conventional approach is to approximate the acoustic expression of speech by hidden Markov models (Bilmes, 2006
; O’Shaughnessy, 2008
). This scheme and its variants do not seem, by construction, to capture efficiently the long-range temporal and contextual dependencies in speech (O’Shaughnessy, 2008
). However, a novel approach is emerging that suggests a fundamental computational principle: the idea is to model fast acoustic features of speech as the expression of comparatively slow articulator movement (Deng et al., 2006
; King et al., 2007
; McDermott and Nakamura, 2006
). These models describe speech as a hierarchy of dynamic systems, where the lowest (fastest) level generates auditory output. Although this approach, due to its complexity, is still at an early stage of development, the premise is that hierarchical dynamics may provide valuable constraints on speech recognition. These could make artificial speech recognition systems more robust, in relation to conventional approaches, which do not embody hierarchical constraints efficiently. In the visual domain, similar hierarchical models have been considered for making inference on dynamic human behavior, such as those used in robot-human interaction or surveillance technology (Kruger et al., 2007
; Moeslund et al., 2006
; Oliver et al., 2004
; Robertson and Reid, 2006
; Saenko et al., 2005
; Yam et al., 2004
).
The question we address in this paper is whether these developments in hierarchical, trajectory-based perception models point to a computational principle which can be implemented by the brain. In Kiebel et al. (2008)
we developed a simple recognition system, based on a specific functional form of hierarchical dynamics. We reprise the approach here to show it affords schemes for perception that are both robust to noise and can represent deep hierarchical structure in the sensory streams.
We consider three constraints on perception that the brain has to contend with. The first is that our environment and sensations are dynamic processes. This places computational demands on the speed of recognition and makes perception, at first glance, more formidable than recognizing static scenes or objects. However, a dynamic environment has temporal structure and regularities, which can be learned and may be beneficial for robust perception.
The second constraint is that the brain performs perception online, because it has no access to future sensory input and cannot store the details of past sensations (we assume here that the brain does not have the equivalent of computer memory, which could faithfully store the sensory stream for off-line processing). This means that transient sensory information must be used to represent the dynamic state of the environment. This constraint renders perception distinct from other analyses of time-series data, where timing is not critical and stored data can be analyzed off-line.
The third constraint is that we assume that the perception conforms to the free-energy principle (FEP); i.e., the perceptual system dynamically minimizes its free-energy and implicitly makes inferences about the causes of sensory input (Friston et al., 2006
). To minimize its free-energy, the agent uses a generative model of how the environment produces sensory input. This formulation leads to the question ‘what generative model does the brain use?’ (Dayan et al., 1995
; Lee and Mumford, 2003
). Here, we will review and discuss a hierarchical model for perception, where higher levels (further away from sensory input) encode the shape of attractors which contain faster, lower level dynamics (Kiebel et al., 2008
). Previously we have shown in simulations, that this hierarchical model enables agents to recognize states causing sensory input, at two time scales. In this paper, we focus on the implications of hierarchical attractor models for artificial agents, for example speech recognition devices, and real brains. In particular, we introduce neurocomputational models of perception that emerge when one describes the dynamics of two systems (the environment and the agent) that are coupled via sensory input.
In the following, we summarize a generative model based on a hierarchy of attractors and its variational inversion. In Kiebel et al. (2008)
, we used simulations to show that the inversion of these models shows a range of features which reproduce experimental findings in systems neuroscience. Here, we relate this model to research in artificial speech recognition.
A Model of Perceptual Inference
Human speech perception has been construed as the output of a multi-level hierarchical system, which must be decoded at different time-scales (Chater and Manning, 2006
; Poeppel et al., 2008
). For example, while a spoken sentence might only last for seconds, it also conveys information about the speaker’s intent (an important environmental cause) that persists over much longer time-scales. To illustrate these points, we will simulate the recognition of birdsongs. We use this avian example to illustrate that communication entails (i) embedding information at various time-scales into sound-waves at a fast time-scale and (ii) that the recipient must invert a hierarchical dynamic model to recover this information. Our objective is to show that communication can be implemented using hierarchical models with separation of temporal scales. In the following, we describe a two-level system that can generate sonograms of synthetic birdsong and serves as a generative model for perception of these songs.
There is a large body of theoretical and experimental evidence that birdsongs are generated by dynamic, nonlinear and hierarchical systems (Glaze and Troyer, 2006
; Sen et al., 2001
; Vu et al., 1994
; Yu and Margoliash, 1996
). Birdsong contains information that other birds use for decoding information about the singing bird. It is unclear which features birds use to extract this information; however, whatever these features are, they are embedded in the song, at different time-scales. For example, at a long time-scale, another bird might simply register the duration of a song, which might belie the bird’s fitness. At short time-scales, the amplitude and frequency spectrum of the song might reflect attributes of the bird or imminent danger.
A Generative Birdsong Model
In Kiebel et al. (2008)
, we described a system of two coupled Lorenz attractors, whose output was used to construct a sonogram and associated sound wave, which sounds like a series of chirps. The key point of this model is that, when generating output, the states of a Lorenz attractor at a slower time scale act as control parameters for another Lorenz attractor at a faster time scale. The model can be expressed as
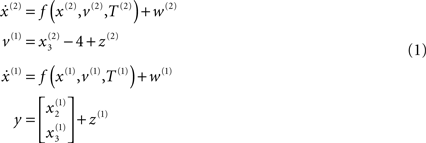
where, v(i) represent inputs to level i (or outputs from level i + 1), which perturb the possibly autonomous dynamics among that level’s states x(i). The nonlinear function f encodes the equations of motion of the Lorenz system:
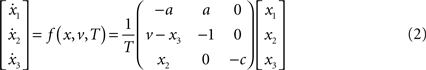
For both levels, we used a = 10 (the Prandtl number) and c = 8/3. The parameter T controls the speed at which the Lorenz attractor evolves; here we used T(1) = 0.25 s and T(2) = 2 s; so that the dynamics at the second level are an order of magnitude slower than at the first. At the second-level we used a Rayleigh number; v(2) = 32. We coupled the fast to the slow system by making the output of the slow system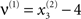 
the Rayleigh number of the fast system. The Rayleigh number is effectively a control parameter that determines whether the autonomous dynamics supported by the attractor are fixed point, quasi-periodic or chaotic (the famous butterfly shaped attractor). The sensory signals generated are denoted by y, which comprises the second and third state of x(1) (Eq. 1). We will call the vectors x(i) hidden states, and the scalar v(1) the causal state, where superscripts indicate model level and subscripts refer to elements. At each level we modeled Gaussian noise on the causes and states (w(i) and z(i)) with a log-precision (inverse variance), of eight (except for observation noise z(1), which was unity). We constructed the sonogram (describing the amplitude and frequency of the birdsong) by making 
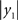the amplitude and y2 the frequency (scaled to cover a spectrum between 2 and 5 kHz). Acoustic time-series (which can be played) are constructed by an inverse windowed Fourier transform. An example of the system’s dynamics and the ensuing sonogram are shown in Figures 2
A,B. The software producing (and playing) these dynamics and the sonogram can be downloaded as Matlab 7.7 (Mathworks) code (see software note).
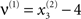the Rayleigh number of the fast system. The Rayleigh number is effectively a control parameter that determines whether the autonomous dynamics supported by the attractor are fixed point, quasi-periodic or chaotic (the famous butterfly shaped attractor). The sensory signals generated are denoted by y, which comprises the second and third state of x(1) (Eq. 1). We will call the vectors x(i) hidden states, and the scalar v(1) the causal state, where superscripts indicate model level and subscripts refer to elements. At each level we modeled Gaussian noise on the causes and states (w(i) and z(i)) with a log-precision (inverse variance), of eight (except for observation noise z(1), which was unity). We constructed the sonogram (describing the amplitude and frequency of the birdsong) by making 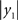the amplitude and y2 the frequency (scaled to cover a spectrum between 2 and 5 kHz). Acoustic time-series (which can be played) are constructed by an inverse windowed Fourier transform. An example of the system’s dynamics and the ensuing sonogram are shown in Figures 2
A,B. The software producing (and playing) these dynamics and the sonogram can be downloaded as Matlab 7.7 (Mathworks) code (see software note).This model can be regarded as a generative or forward model that maps states of the singing bird to sensory consequences (i.e., the sonogram). For human listeners, the resulting song sounds like a real birdsong. Given a generative model of birdsong, we can generate (different) songs and ask: How could a synthetic bird recognize these songs?
The online inversion of this forward model; i.e., the online reconstruction of the hidden and causal states, corresponds to perception or mapping from the sonogram to the underlying states of the singing bird. In this example, perception involves the online estimation of states at the fast and slow level. Although, at the fast first-level, two of the states (those controlling amplitude and frequency of the acoustic input) are accessed easily, the third 
describes a completely hidden trajectory. It is important to estimate this state correctly because it determines the dynamics of the others (see Eq. 2). Model inversion also allows the listening bird to perceive the slowly varying hidden states at the second level, x(2), which cannot be heard directly but must be inferred from fast sensory input. The second-level hidden states encode the high-order structure of the song by specifying the shape of the attractor at the first level. The ensuing inversion problem is difficult to solve because the bird can only infer states at both levels through the nonlinear, continuous and stochastic dynamics of the Lorenz attractor at the first level.
describes a completely hidden trajectory. It is important to estimate this state correctly because it determines the dynamics of the others (see Eq. 2). Model inversion also allows the listening bird to perceive the slowly varying hidden states at the second level, x(2), which cannot be heard directly but must be inferred from fast sensory input. The second-level hidden states encode the high-order structure of the song by specifying the shape of the attractor at the first level. The ensuing inversion problem is difficult to solve because the bird can only infer states at both levels through the nonlinear, continuous and stochastic dynamics of the Lorenz attractor at the first level.Perception Using Variational Inversion
In Kiebel et al. (2008)
, we showed how inversion of this hierarchical model can be implemented using the free-energy principle (Friston et al., 2006
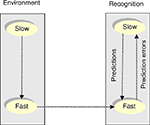
). This variational online inversion can be conceptualized as shown in Figure 1
. The environment, here a synthetic bird, generates output using a hierarchical system with coupled slow and fast dynamics (Eqs 1 and 2). This generates sensory input that is recognized by the receiving bird. It does this by passing top-down messages (predictions) and bottom-up messages (prediction errors) between the levels of its generative model. When top-down messages from the first level predict sensory input, the hidden and causal states of the generative model become representations of the corresponding states of the singing bird and perceptual inference is complete. For mathematical details, we refer the interested reader to Friston et al. (2008)
.
Figure 1. Birdsong generation and its recognition using variational inversion. Environment (left): In this two-level birdsong model, sonograms are generated by the autonomous, coupled dynamics of two Lorenz attractors (see Eqs 1 and 2). The states of the first Lorenz attractor evolve at a slow time scale and act as control parameters for the faster Lorenz attractor. Perception system (right): The implicit variational dynamic inversion is a recurrent message passing scheme, where top-down predictions are sent from the slow level to the fast level, while the fast level receives sensory input and generates bottom-up prediction errors. The resulting recognition dynamics are non-autonomous and try to ‘mirror’ the environmental dynamics.
Simulations of Birdsong Perception
Here, we describe the result of a single simulation to show that the online inversion can successfully recognize songs and track the trajectories of the states at all levels. In Friston and Kiebel (2009) and Kiebel et al. (2008)
we present more simulations, and discuss and relate them to perception, categorization and omission responses in the brain. In Figure 2
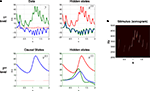
A we plot the hidden and causal states, which produce sensory output corresponding to synthetic birdsong generation. One can see immediately that the two levels have different time-scales due to their different rate constants (Eqs 1 and 2). The resulting sonogram is shown in Figure 2
B.
Figure 2. Data and states, over 2 s, generated by a two-level birdsong model. (A) At the first level, there are two outputs (i.e., sensory data) (left: blue and green solid line) and three hidden states of a Lorenz attractor (right: blue, green, and red solid line). The second level is also a Lorenz attractor that evolves at a time-scale that is one magnitude slower than the first. At the second level, the causal state (left: blue solid line) serves as control parameter (Rayleigh number) of the first-level attractor, and is governed by the hidden states at the second level (right: blue, green, and red solid line). The red dotted lines (top left) indicate the observation error on the output. (B) Sonogram (time-frequency representation) constructed from model output. High intensities represent time-frequency locations with greater power.
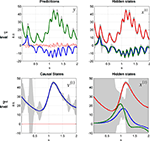
The results of online inversion (i.e., song recognition) are shown in Figure 3
. At the first level, the uncertainty about the states was small, as indicated by narrow 90% confidence intervals, shown in grey. At the second level, the system tracks the hidden and causal states veridically. However, as these variables are inferred through the sensory data, uncertainty about the hidden state reaches, intermittently, high values. The uncertainty about the hidden states at the second-level is very high, because these variables can only be inferred via the causal state v(1). In particular, note the increased period of uncertainty at about 0.3 s, at both levels. This uncertainty is caused by the hidden state of the first-level switching between the ‘wings’ of the Lorenz attractor. At this point, the hidden state at the first level is less identifiable than when it is on the outer reaches of a wing. This is because of nonlinearities in the generative model, which mean, at this point, the motion of the state is a weaker function of the states per se. This uncertainty (i.e., will the state cross to the other wing or not?) is part of inference.
Figure 3. Dynamic online inversion of the data presented in Figure 2
. Observed data (see Figure 2
) are now shown as black, dotted lines, and the model predictions as solid, coloured lines. The 90% confidence interval around the conditional means is shown in grey. The prediction error (i.e. difference between observation and model prediction) is indicated by red dotted lines.
In summary, these results show that the hierarchical model can not only generate birdsong dynamics but, using the free-energy principle, it can be used as a generative model to decode incoming sensory input with relatively high precision. Critically, at the second level, the decoding (listening) bird infers hidden states that evolve slowly over time. This is an important result because the values of the hidden states at the second level specify the attractor manifold, and therefore the trajectory of states at the first. In other words, one location in state space at the higher level specifies a sequence of states at the lower. Moreover, because the states at the second level also follow a slowly varying trajectory, the attractor manifold at the first level keeps changing slowly over time. It is this slow modulation of the first-level manifold that expresses itself in the variations of the fast moving first-level state, which enable the perception to track hidden trajectories at the second level.
A key aspect of this model rests on the nonlinearity of the generative model. This is because the only way for slowly varying causes to be expressed as faster consequences is through nonlinear mechanisms (Eq. 2). It is this nonlinearity that allows high-level states to act as control parameters to reconfigure the motion of faster low-level states. If the equations of motion at each level were linear in the states, each level would simply convolve its supraordinate inputs with an impulse response function. This precludes the induction of faster dynamics because linear convolutions can only suppress various frequencies. However, the environment is nonlinear, where long-term causes may disclose themselves through their influence on the dynamics of other systems. To predict the ensuing environmental trajectories accurately, top-down effects in the agent’s generative model must be nonlinear too. We suggest that this principle of separation of time scales in a nonlinear hierarchy is not only used in avian but also in human communication, because both birdsong and speech share the common feature that information is transmitted via rapidly modulated sound waves. In the following, we will review evidence which suggests that human speech can be appropriately modeled and recognized by a hierarchy of attractors.
Artificial Speech Recognition
How are our simulations related to artificial perception systems that solve ‘real-world’ recognition tasks? Here, we focus on artificial speech recognition (ASR) but note that there are similar modeling initiatives in other areas of artificial perception; e.g., vision (Moeslund et al., 2006
; Oliver et al., 2004
; Yam et al., 2004
).
An intuitive approach to speech recognition is to consider speech as a sequence of phonemes; i.e., speech sounds are like ‘beads on a string’, which form syllables, words and sentences (Ostendorf, 1999
). The idea here is that when one knows the ‘single beads’, one just needs to read out the sentence. This intuition leads naturally to models that treat speech as a sequence of states, which can be recognized, given the auditory input, using hidden Markov models (Bilmes, 2006
; O’Shaughnessy, 2008
). However, speech does not seem to work like this: Speech exhibits all kinds of contextual effects, at various time-scales, leading to cross-temporal dependencies. For example, co-articulation induces a dependence of the acoustic expression of speech-sounds on the sound’s temporal neighbors (Browman and Goldstein, 1992
). These temporal dependencies introduce a tremendous amount of variations in the ‘single beads’. In conventional hidden Markov models these can be modeled by increasing the number of states and parameters, which can lead to serious model identification issues: Various reviews discuss why the hidden Markov model and its extensions, as conventionally used in ASR, are probably not appropriate to model and recognize speech with human-like performance (Bilmes, 2006
; King et al., 2007
; O’Shaughnessy, 2008
).
Although ignored as a main-stream modeling assumption in the ASR field, the acoustic stream is the consequence of hidden state-space trajectories: the vocal tract (VT) dynamics, i.e. tongue, mouth and lips and other VT components, generate articulatory gestures, which are understood to be the basic elements of speech (Browman and Goldstein, 1997
; Deng et al., 2006
; Liberman and Whalen, 2000
; McDermott and Nakamura, 2006
). A novel modeling approach, which seems to be emerging from the ASR field, focuses on two crucial points: First, the specification of a generative hierarchical speech model for recognition, which models VT dynamics as hidden trajectories. Second, these VT dynamics form speech ‘gestures’, whose perception is the goal of artificial speech recognition. There are many interesting variants of this approach, e.g. (Deng et al., 2006
, 2007
; Hofe and Moore, 2008
; King et al., 2007
; Livescu et al., 2007
; McDermott and Nakamura, 2006
; Rose et al., 1996
; Saenko et al., 2005
).
Such hierarchical generative models place fast acoustics at the lowest level, whereas (various levels of) VT dynamics causing the acoustics through top-down influences (Deng et al., 2006
). Importantly, VT dynamics tend to be slower than the changes in acoustics they cause and the function which maps VT to acoustic dynamics can be highly nonlinear. Naturally, development of these generative models is slow because of their complexity and the ongoing development of novel schemes for inverting dynamic nonlinear hierarchical models. It may be that recent developments (Friston et al., 2008
) in the inversion of these models, particularly in a neurobiological setting (Friston, 2008a
), may play a useful role in the recognition of generative speech models used in ASR.
We have suggested that a simple model of birdsong perception, motivated by computational neuroscience and ongoing developments in artificial speech recognition share a critical feature: Generative models for human and avian communication seem to be based on a hierarchy of dynamical systems, where high levels display slow variations and provide contextual guidance for lower faster levels. The principle of hierarchical inference, using appropriate inversion schemes, with separation of time-scales, could be an inherent part of the computations that underlie successful artificial recognition of human action and behavior.
A hierarchical inference has several implications for cortical structure as well as for artificial and human perception. For cortical structure, these are:
• Cortical areas are organized hierarchically (Felleman and Van Essen, 1991
; Fuster, 2004
).
• Macroscopic neuroanatomy recapitulates hierarchical separation of time-scales; see Kiebel et al. (2008)
for a discussion of the evidence that the cortex is organized as an anatomic-temporal hierarchy.
• Extrinsic forward connections convey prediction error (from superficial pyramidal cells) and backward connections mediate predictions, based on hidden and causal states (from deep pyramidal cells) (Friston, 2005
; Mumford, 1992
; Sherman and Guillery, 1998
).
In the following we discuss the implications for artificial and human perception.
A Computational Principle for Perception
The conjecture that the brain inverts hierarchical generative models may lead to a deeper understanding of the computational principles behind perception. As described above, a hierarchical approach has also been adopted in the engineering and artificial perception literature (Deng et al., 2006
; Kim et al., 2008
; Moeslund et al., 2006
; Yam et al., 2004
). It is worth noting that these developments seem to have made minimal reference to neuroscience but were driven by the insight that conventional non-hierarchical models do not capture the deep hierarchical structure of sensory data (Bilmes, 2006
; Deng et al., 2006
; Oliver et al., 2004
).
What are the advantages and disadvantages of using hierarchical models as the basis of artificial perception? A clear disadvantage is that, for real-world applications like speech recognition, the dynamics of movements may take complicated forms, at various time scales. It is therefore not surprising that the best working solutions for artificial speech recognition rather rely on learning large numbers of free parameters in less constrained models (McDermott and Nakamura, 2006
). In addition, the inversion of nonlinear stochastic hierarchical dynamic models is a non-trivial challenge (Budhiraja et al., 2007
; Friston et al., 2008
; Judd and Smith, 2004
). However, in principle, hierarchical dynamics can be parameterized by rather low-dimensional systems, in comparison to the high-dimensional sensory stream. This means that relatively few parameters are required to track acoustic trajectories. This might make dynamic speech identifiable, leading to robust perception schemes. Interestingly, for speech, prior research has already investigated the dynamics of articulation but is embraced with reluctance by the artificial speech recognition field (McDermott and Nakamura, 2006
).
A hierarchical model may also be useful in robust perception of motor behavior, because human movements seem to be more invariant than the sensory features which they cause (Todorov and Jordan, 2002
). This means that movements, which are on a comparatively slower time-scale than their sensory expressions, may be expressed naturally at a higher level in hierarchical models. This is consistent with neuroscience findings that higher cortical levels show invariance over greater time scales than lower levels (Giese and Poggio, 2003
; Hasson et al., 2008
; Koechlin and Jubault, 2006
). Furthermore, the relative slowness of human movements, in comparison to consequent variations in the sensory stream, may also enable the prediction of fast sensory features, increasing the robustness of perception (King et al., 2007
; Yam et al., 2004
). We have demonstrated this by showing that a hierarchical scheme can out-perform a non-hierarchical scheme, see Figure 5 in Kiebel et al. (2008)
.
In addition, speech trajectories could be modelled at time-scales beyond single speech-sounds and syllables, e.g. covering words and sentences. At this level, long-range hierarchical and cross-temporal dependencies are subject of active research in computational linguistics and natural language (Bengio et al., 2003
; Huyck, 2009
; Smits, 2001
). The inversion of models with temporal hierarchies may provide a framework for computational models of language processing. For example, they are in a position to explain how uncertainty about the meaning of the early part of a sentence is resolved on hearing the end: i.e., increases in conditional certainty about hidden states, based on current sensory input confirms their predictions. In other words, the long-range or deep temporal dependencies in speech might lend themselves to hierarchical temporal modelling. The resulting inference, using serial speech input, may appear to be non-serial because decisive evidence for hidden states at different levels arrives at different times. To our knowledge, a fully dynamical hierarchical scheme that maps from sound waves to the semantics is still beyond the current abilities of artificial speech recognition (Deng et al., 2006
).
Simple Network Operations
Although the variational inversion of hierarchical dynamic models might appear too unwieldy for a simple theory of perception, the actual operations needed to implement recognition dynamics are rather simple (Friston et al., 2008
). By ‘simple’ we mean that all operations are instantaneous and just involve message-passing among neurons in a network and associative plasticity of their connections. This renders the approach neurobiologically plausible. The message-passing scheme is not the only possible implementation, there may be others, each with their own approximations and simplifications to compute the free energy. Irrespective of the optimization scheme used, the requisite update equations are determined by the generative model, which is specified by the likelihood and priors. This means that the identification of the brain’s generative model of the environment is the key to understanding perception (Friston, 2008a
; Rao and Ballard, 1999
; Yuille and Kersten, 2006
).
The variational inversion using generative models is just a recipe to construct a system of differential equations, which recognize sensory input, i.e., optimise a free-energy bound on the log evidence for some model. This means the scheme shares many formal similarities with dynamical systems used in computational neuroscience to describe neuronal systems (Rabinovich et al., 2006
). As noted by one of our reviewers, it may be that such schemes have evolved to exploit natural or universal phenomena that appear when dynamical systems are coupled (Breakspear and Stam, 2005
). Indeed, in an evolutionary setting, the emergence of efficient coupled dynamical systems that optimise free-energy may exploit these phenomena. For example, coupled nonlinear systems naturally evolve towards a synchronous state, even with relatively weak coupling. It would be very interesting if these synchronised states could be associated with optimised free-energy states that are mandated by perception in particular and the free-energy principle in general.
In short, the variational approach entails finding a dynamic system (the generative model), which describes the generation of sensory input. Variational learning principles are then applied to derive differential equations, which decode hidden states from sensory input. The use of generic inversion systems as proposed in Friston et al. (2008)
enables one to focus on the first challenge, which may be informed by the study of coupled dynamical systems, in a more general setting.
Coupling Between Time-Scales
The variational inversion of temporal hierarchies describes how fast sensory input can influence inferred states at slow time-scales. There are recent studies that suggest this sort of coupling may be a generic feature of coupled dynamical systems: Fujimoto and Kaneko describe how to exploit a bifurcation cascade to couple slow high-level states to fast low-level dynamics. Crucially, they find that coupling is seen only in a narrow regime of time-scale ratios, around two to three (Fujimoto and Kaneko, 2003a
,b
). As shown in Kiebel et al. (2008)
, dynamical systems based on variational inversion schemes operate in a broader regime: one can construct systems where fast dynamics influence slow dynamics at much higher time-scale ratios. In the present work, we use a ratio of eight, which is beyond the limit identified by Fujimoto and Kaneko (2003b)
. However, dynamics based on variational inversion have a natural lower limit on the time-scale ratio: When the ratio approaches one, the changes in the manifold of the fast system, caused by the slow system, evolve nearly as fast as the states themselves. This means that the changes in the manifold cannot be separated from the dynamics of the states. This suggests that robust inversion of temporal hierarchies rests on a separation of temporal scales, which may impose a lower bound on the relative time-scales.
Although we have not emphasized it in this paper, the fact that one can formulate the inversion of dynamic models with deep or hierarchical temporal structure as a dynamical system rests on recent technical advances in Bayesian filtering (Friston, 2008b
; Friston et al., 2008
). In brief, these advances use generalised coordinates of motion to represent the trajectories of hidden states. Generalised coordinates cover position, velocity acceleration etc. Although this increases the number of implicit hidden states it greatly simplifies inversion, in comparison with conventional schemes like particle and extended Kalman filtering. This simplification reduces filtering (i.e., inversion) to a gradient descent, which can be implemented in a neurobiologically plausible fashion. The use of generalised coordinates is formally similar to temporal embedding in the characterisation of dynamical systems: Taken’s theorem (Takens, 1981
) states that it is possible to embed (i.e. geometrically represent) the structure of a vector-field in a higher dimensional space. This means that one can reconstruct the structure of the manifold, on which dynamics unfold, by using a Taylor expansion of the vector-field. This is very close to the idea of projecting the system into generalized coordinates. In essence, this projection allows the observer to encode the structure of the flow-field at each point in time.
A General Mechanism for Perception and Action in the Brain?
In a recent paper, we reviewed some compelling experimental evidence for temporal hierarchies in the brain. We argued that these hierarchies may reflect a general form of generative models that the brain uses to recognize causes beyond the temporal support of elemental percepts (e.g., formants in audition and biological motion in vision, Kiebel et al., 2008
). We have shown previously that the inversion of these generative models lead to robust and accurate inferences about the causes of sensory input. Hierarchical models are approximations to the environmental processes that generate sensory data (Todorov et al., 2005
); so one might ask why evolution selected temporal hierarchies? Intuitively, there is something fundamentally correct about generative models based on temporal hierarchies; in the sense that the content of our sensorium changes more quickly than its context. However, for communication and biological motion there may be additional reasons to suppose temporal hierarchies afford just the right model; this is because our brains may use the same architecture to generate and recognise movements (Kilner et al., 2007
). This means that, during co-evolution with our conspecifics, temporal hierarchies may have been subject to selective pressure, precisely because they enable generation and recognition of communicative stimuli over multiple time-scales (i.e., with deep temporal structure) (Rauschecker and Scott, 2009
; von Kriegstein et al., 2008
).
Perception Mirrors the Environment
The role of non-autonomous recognition dynamics is to mirror or track autonomous dynamics in the environment. If this tracking is successful, the recognition system ‘inherits’ the dynamics of the environment and can predict its sensory products accurately. This inheritance is lost when the sensory input becomes surprising, i.e. is not predicted by perception. In this case, the recognition system uses prediction error to change the predictions and make sensory input unsurprising again. This heuristic explains how the agent’s dynamics manage to switch rapidly between different attractor regimes. This switching, e.g. see Figure 3
in Kiebel et al. (2008)
, is caused by the interplay between the system’s attempt to minimize surprise (which is bounded by free-energy) and (surprising) sensory input.
Identification of the Environmental Model
Explicit modeling of environmental dynamics and their inversion may be a useful approach to model perception for several reasons: most current research in computational neuroscience focuses on modeling a single neuronal system, which generates neuronal dynamics just as the brain does. This ‘single system’ approach, which does not model the environmental dynamics explicitly, is very useful for identifying neuronal mechanisms and relating them to applied sensory input and neuronal or behavioral observations (Rabinovich et al., 2006
). However, this approach does not address how these neuronal mechanisms (and not others) come about in the first place.
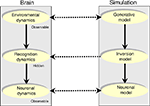
An alternative approach may be to model neuronal dynamics ‘from scratch’: Such a full forward model would comprise three components: (i) A model of the environment with autonomous dynamics, which, using the free-energy principle, prescribes (ii) non-autonomous recognition dynamics, which are implemented by (iii) neuronal dynamics (Figure 4
, left panel). In other words, appropriate models of the environment may be requisite to make strong predictions about observed neuronal dynamics. Given the complexity and detail of neuronal dynamics, one might argue that the identification of appropriate environmental models is a daunting task. However, the ‘dual-system’ approach of modeling both environment and the brain would essentially rephrase the question ‘How does the brain work?’ to ‘What is a good model of the environment that discloses how the brain works?’ (see, e.g., Chiel and Beer, 1997
; Proekt et al., 2008
). This approach has the advantage that environmental models, which cannot be inverted, disqualify themselves and are unlikely to be used as generative models by the brain. For example, in artificial speech recognition, the conventional hidden Markov model has been found difficult to invert for casual speech. Moreover, this model is also a poor generative model of speech, i.e. speech generated by this model yields barely intelligible speech (McDermott and Nakamura, 2006
). Given that one can identify appropriate models of the environment; e.g., for audiovisual speech, the recognition performance can be directly compared to human performance. Furthermore, one could use established model selection schemes to evaluate environmental models in the context of their neuronal inversion (Friston et al., 2008
). This dual-system modeling approach may also allow one to ask whether simulated recognition produces the same kind of predictions and prediction errors as humans, e.g. when exposed to sensory input that induces the McGurk effect (Cosker et al., 2005
). Such experiments would enable us to explain the McGurk effect and similar perception phenomena in a causal fashion, as the consequence of our brains’ generative environmental model. In addition, one may be able to couple simulated recognition dynamics with models of neuronal dynamics and relate these to observed neuronal dynamics (Figure 4
, right). This would enable us to make predictions about observed neuronal responses under specific assumptions about the generative model used by the brain, and how neuronal dynamics implement recognition.
Figure 4. Modeling neuronal dynamics caused by environmental dynamics. Brain system (left): In this dual-system model, neuronal dynamics (bottom) correspond to inversion or recognition dynamics (middle) induced by environmental dynamics (top). We assume that the environmental and neuronal dynamics can be partially observed, while the recognition dynamics are hidden. Simulated system (right): The full generative model of neuronal dynamics; starting with environmental dynamics, which specify recognition dynamics, which predict neuronal dynamics.
The value of this dual-system approach is that neuroscience and artificial perception have a common interest in these models (Scharenborg, 2007
). Not only would such an integrative approach provide a constructive account of brain function, at multiple levels of description, but also enable machines to do real-world tasks, (see, e.g., Rucci et al., 2007
) for a spatial localization example at the interface between artificial perception, robotics and neuroscience.
We have demonstrated that the recognition of environmental causes from sensory input can be modeled as the inversion of dynamic, nonlinear, hierarchical, stochastic models. We have discussed relevant developments in artificial perception, which suggest that perception models the environment as a hierarchy of autonomous systems, evolving at various time-scales, to generate sensory input. In this view, the computational principles of perception may be accessed by considering variational inversion of these models.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
SJK is funded by the Max Planck Society. KJF and JD are funded by the Wellcome Trust. We thank Katharina von Kriegstein for valuable comments and discussions. We also thank the two reviewers for their helpful and constructive comments.
All procedures described in this note have been implemented as Matlab (MathWorks) code. The source code is freely available in the Dynamic Expectation Maximization (DEM) toolbox of the Statistical Parametric Mapping package (SPM8) at http://www.fil.ion.ucl.ac.uk/spm/
.
Livescu, K., Cetin, O., Hasegawa-Johnson, M., King, S., Bartels, C., Borges, N., Kantor, A., Lal, P., Yung, L., Bezman, A., Dawson-Haggerty, S., Woods, B., Frankel, J., Magimai-Doss, M., and Saenko, K. (2007). Articulatory feature-based methods for acoustic and audio-visual speech recognition: Summary from the 2006 JHU summer workshop. 2007 Proc. IEEE Int. Conf. Acoust. Speech Signal Process. IV(Pts 1–3), 621–624.