- SBILab (Signal Processing and Bio-Medical Imaging Lab), Deptt. of ECE (Electronics and Communication Engineering), Indraprastha Institute of Information Technology (IIIT)-Delhi, New Delhi, India
Hyperspectral imaging (HSI) is useful in many applications, including healthcare, geosciences, and remote surveillance. In general, the HSI data set is large. The use of compressive sensing can reduce these data considerably, provided there is a robust methodology to reconstruct the full image data with quality. This article proposes a method, namely, WTL-I, that is mutual information-based wavelet transform learning for the reconstruction of compressively sensed three-dimensional (3D) hyperspectral image data. Here, wavelet transform is learned from the compressively sensed HSI data in 3D by exploiting mutual information across spectral bands and spatial information within the spectral bands. This learned wavelet basis is subsequently used as the sparsifying basis for the recovery of full HSI data. Elaborate experiments have been conducted on three benchmark HSI data sets. In addition to evaluating the quantitative and qualitative results on the reconstructed HSI data, performance of the proposed method has also been validated in the application of HSI data classification using a deep learning classifier.
1 Introduction
Hyperspectral imaging (HSI) is an image acquisition method that combines optical spectroscopy and optical imaging. The HSI image/data set consists of a set of images captured in a large number of spectral bands. In HSI, radiation intensity measurements are acquired in many spectral bands of the electromagnetic spectrum as opposed to only three spectral bands of red, green, and blue bands in the conventional imaging systems. Thus, each pixel in hyperspectral images also contains spectral information along the third dimension of the data cube (Chang, 2003). Of late, HSI applications have been extended from remote sensing (Schowengerdt, 2006; Khoshsokhan et al., 2019b; Yu et al., 2022) to healthcare, astronomy, pharmaceuticals, geosciences (Geladi, 2007), mineralogy (Bajorski, 2012), agriculture (Xie et al., 2013), military remote surveillance (Chen et al., 2012), and landform classification (Prasad et al., 2012).
With advances in acquisition techniques in HSI, the amount of hyperspectral data has seen a rapid surge that poses challenges in data transmission and data storage. This problem has led researchers to explore solutions for efficient data acquisition and transmission systems, particularly compressive sensing (CS) methods that work at sub-Nyquist rates. Compressive sensing of data leads to under-determined set of linear equations that need to be solved to recover the full data. In general, optimization frameworks are utilized with constraints such as sparsity of the signal in some transform domains to recover a unique solution from infinite possible solutions of the under-determined set of equations.
For a specific hyperspectral data set, the task may be to perform classification (Yu et al., 2022), band selection (Shang et al., 2021), unmixing (Khoshsokhan et al., 2019a; Khoshsokhan et al., 2019b), or reconstruction. This article proposes a novel reconstruction framework for the compressively sensed hyperspectral data set. Optimization frameworks for compressive sensing-based reconstruction involve minimization of a loss function under some predefined constraints on the characteristics of signals. For example, a loss function involving total variation (TV) and nuclear norm constraints was minimized by Golbabaee and Vandergheynst (2012b). These two constraints, respectively, capture the piece-wise smoothness (due to spatial correlation) and low-rank structure of the HSI data. However, this approach (Golbabaee and Vandergheynst, 2012b) ignores the spectral correlation in HSI. Similarly, the l2,1 norm is optimized by Golbabaee and Vandergheynst (2012a) to exploit the spectral and spatial correlation along with the nuclear norm to capture the low-rank structure in HSI. A downside of this method is the assumption of same sparsity support for all the bands that limits the complete utilization of the spectral similarity. To overcome this limitation, the Manhattan distance-based function along with TV norm and nuclear norm has been used in Zhang and Zhang (2018) to capture the spectral correlation, spatial correlation, and the low-rank property. There have also been attempts to model the sparsity structure in the signals that lead to better reconstruction performance (Chen et al., 2014; Zhang et al., 2015). For example, a re-weighted Laplace prior is used in Zhang et al. (2015) to learn the structure of the sparse coefficients. In fact, all the aforementioned methods (Golbabaee and Vandergheynst, 2012a; Chen et al., 2014; Zhang et al., 2015; Zhang and Zhang, 2018) utilized a predefined dictionary as the sparsifying basis. The sparsification level of a signal depends on the sparsifying bases. One basis can provide more sparsification than the other, depending on the structure of the signal. Hence, it is more intuitive to employ a learned dictionary (Aharon et al., 2006; Ravishankar and Bresler, 2011). In Zhang et al. (2016), a blind dictionary approach is presented to learn a structured dictionary directly from the samples obtained through the measurement matrix. This approach also takes into consideration the sparsity structure of the data. Again, these methods (Zhang et al., 2015; Zhang et al., 2016) exploit only the spectral correlation without utilizing the spatial correlation in the HSI.
The proposed method uses a data-dependent sparsifying basis that characterizes the spectral and spatial sparsity of the HSI data. The sparsifying basis required in compressive sensing applications is actively being learned via transform learning (TL) or blind dictionary learning (DL) (Ravishankar and Bresler, 2015) because it adapts to signals of interest and performs better than discrete cosine transform (DCT) or discrete wavelet transform (DWT) in CS. However, the optimization framework of blind compressive sensing with joint learning of transform basis and its coefficients is generally non-convex with no closed-form solution. This leads to computationally expensive solutions. Before the emergence of dictionary learning approaches (Yaghoobi et al., 2009; Ataee et al., 2010), wavelets were a preferred choice as the sparsifying basis in a number of applications. This is due to the availability of a number of wavelet bases, where one can choose the basis of interest for an application. Furthermore, the ability to design a wavelet basis motivated researchers to learn wavelets for signals of interest (Sweldens, 1996; Gupta et al., 2005a; Gupta et al., 2005b; Ansari and Gupta, 2015), instead of trying different wavelets in an application. In the recent past, compactly supported wavelets have been learned for one-dimensional (1D) signals in the application of compressively transmitted ECG signals for telemedicine (Ansari and Gupta, 2019), for natural images (Ansari and Gupta, 2018b), for the reconstruction of compressively sensed images (Ansari and Gupta, 2016), and for non-separable 2-dimensional (2D) wavelet learning (Ansari et al., 2016). Similarly, a lifting framework of rational wavelet learning has been proposed (Ansari and Gupta, 2018a). While the traditional TL or DL requires learning a large number of parameters, wavelet transform learning (WTL) requires learning wavelet filter coefficients that are significantly less than dictionary learning. Thus, a small number of parameters are required to be learned with wavelet transform learning compared to the traditional transform learning or dictionary learning. This leads to computationally efficient learning of the basis using a small data size. However, so far, to the best of our knowledge, no work has been done to learn wavelets for hyperspectral images.
In this study, we applied the wavelet transform learning (WTL) approach in HSI imaging and proposed closed-form solutions for WTL from HSI data. We proposed wavelet transform learning for 3D HSI images, where the method for 2D images (Ansari and Gupta, 2017) is used for transform learning in the x − y spatial plane and a new information theory-based method is proposed to learn the wavelet transform along the spectral direction. Since the partial canonical sensing identity (PCI) sensing matrix is significantly simple and time-efficient compared to the Gaussian and Bernoulli sensing matrices, although with slightly inferior performance by approximately 2 dB (Ansari and Gupta, 2017), we used PCI sensing matrix-based HSI data recovery. Furthermore, we utilized recently proposed multi-level L-pyramid wavelet decomposition (Ansari and Gupta, 2017) that provides better performance on images. The salient contributions of the work are as follows:
1) We proposed an information theory-based method of wavelet transform learning (WTL) for 3D HSI images that exploits information of spatial and spectral directions. To the best of our knowledge, this is the first work on wavelet transform learning for hyperspectral images.
2) We proposed an integrated framework of data recovery and wavelet transform learning, where the WTL is learned from the compressively sensed data.
3) We utilized multi-level L-pyramid wavelet decomposition that yields better performance than the traditional multi-level wavelet decomposition.
4) We carried out extensive tests on three benchmark HSI datasets to evaluate the performance of the proposed methodology.
5) We also validated the method on the application of deep learning based classification. The proposed method is observed to perform better than the two state-of-the-art CS-based reconstruction methods in HSI.
2 Methods
The proposed WTL-I method (Figure 1) is a joint data recovery and wavelet transform learning method for the compressively sensed 3D HSI data. The work pipeline contains two stages for wavelet transform learning and the third stage for data recovery. The performance is assessed in terms of reconstruction accuracy. Furthermore, the quality of reconstructed images is evaluated in the application of HSI data classification using deep learning classifier. Better classification results are obtained on the images reconstructed via the proposed WTL-I method compared to those reconstructed via other methods. The complete workflow of this work is shown in Figure 1.
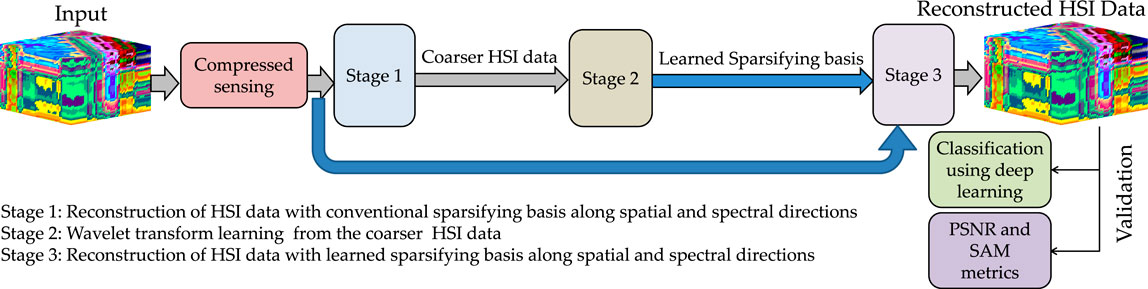
FIGURE 1. Complete workflow. The proposed method consists of three steps: 1) reconstruction of coarser HSI data with conventional sparsifying basis, 2) learning of the sparsifying basis from this coarser HSI data, and 3) using the learned sparsifying basis to reconstruct the HSI data. Finally, the quality of reconstructed HSI data is evaluated via standard reconstruction metrics and via an application.
2.1 Stage 1: Coarser HSI Data Recovery
In this stage, we recovered a coarser estimate of the HSI data from compressively (partially) sensed measurement data. The HSI data is a 3D data, as shown in Figure 6. Separable orthogonal Daubechies wavelet transform (namely, dB4 with filter length 8) is used as the sparsifying transform for each spectral band of the HSI data set for the recovery of compressively sensed data. Thus, each spectral band of HSI data is recovered separately. For example, compressively sensed data of the kth spectral band is represented in the vector form as xk = Φkyk, where yk denotes the original data required to be recovered and Φk denotes the sensing matrix. The partial canonical identity (PCI) sensing matrix Φk, as suggested by Ansari and Gupta (2017), is constructed separately for each of the kth band as follows. First, Φk is initialized to an identity matrix. Next, rows of Φk, which correspond to pixel positions not available in xk, are dropped. For example, let us say that the pixel at the second position of yk is not sensed and hence is not available in xk. Then the second row of the identity matrix will be dropped. Next, the basis pursuit (BP) optimization method is used to recover the signal
where Ψ corresponds to any standard wavelet. We used orthogonal dB4 wavelet in stage 1. The coarser approximation of the signal is obtained as
2.2 Stage-2: Wavelet Transform Learning for Individual Spectral Bands
We used the signal reconstructed in the previous step to learn wavelet for each of the spectral band using the method presented in Ansari and Gupta (2017). For the sake of completeness, the method is presented in brief.
First, we converted a given kth spectral band image into two 1D signals: one with column-wise scanning and another with row-wise scanning (refer to Figure 2). Next, wavelet is learned for row space and column space separately using the two signals constructed before. Thus, we learned a separable wavelet transform for each of the spectral bands. To illustrate the process of learning, let us first consider column-wise vector for any spectral band. We required learning a 2-channel wavelet system, as shown in Figure 3.

FIGURE 2. (A) Column-wise serpentine scanning. (B) Row-wise serpentine scanning as proposed in Ansari and Gupta (2017).
This is done by using the lifting framework, as shown in Figure 4. First, the analysis wavelet filter is learned in the predict stage, followed by the synthesis wavelet filter in the update stage, as follows:
1) Predict Stage: The filters are initialized with F0(z) = 1, F1(z) = z, G0(z) = 1, and G1(z) = z−1, in Figure 3. This is called the lazy wavelet. Next, the predict stage filter P(z) is required to be learned. For this, the coarser version of original signal
where * is the convolution operator and Lp is the length of the predict stage filter p[n] with its Z-transform given by P(z) = Z{p[n]}. For good prediction, a sample (here, odd indexed) should be predicted from its immediate past and immediate future neighbors that requires a careful choice on the predict stage filter provided by Theorem 1 of Ansari and Gupta (2017). Here, the signal
where A is the convolution matrix consisting of even and odd indexed samples of
where ′ denotes the transpose operation. We substituted (4) in (5) and (6) to update the analysis high-pass and synthesis low-pass filters and obtain new filters

FIGURE 4. Steps of lifting: split, predict, and update. (A) Wavelet decomposition; (B) wavelet reconstruction as proposed in Ansari and Gupta (2017).
Thus, we notice that the predict step modifies the high-pass filter of the analysis end and low-pass filter of the synthesis end.
2) Update Stage: In the update stage, update polynomial Q(z) is learned. To achieve this, we wrote the output of the upper subband signal using the lower subband signal,
where q[n] is the time domain description of the update stage filter Q(z). Filter q[n] is chosen such that the elements of the upper branch are updated using its nearest neighbors. The corresponding structure for q[n] is provided by Theorem 2 of Ansari and Gupta (2017). This subband signal
With the assumption that the variations in horizontal or the vertical direction of any spectral band image are slow, signal
From (7) and (8), it is clear that
Thus, we learned the wavelet for one of the directions of the kth spectral band. The aforementioned method of learning wavelet for 1D signals is applied on row-scanned and column-scanned signal of the kth spectral band image and corresponding wavelet is learned for the row space and the column space separately. This process is repeated to learn two-dimensional separable wavelet for each of the spectral band image.
2.3 Stage 3: Learning Wavelet for the Spectral Direction Using the Mutual Information of Spectral Band Images
The mutual information (MI) measures the mutual dependence between two random variables. It is a quantitative measure to ascertain the amount of information that can be obtained about one random variable by observing the other random variable. The concept can be extended to 1D signals or images and is computed using the entropy of a random variable as explained next.
The entropy represents the expected randomness or the information contained in a random variable X as follows:
Similarly, the joint entropy between two random variables X and Y is represented as follows:
The mutual information (MI) between two random variables X and Y is given as follows:
For two images, A and B, (14) can be represented as follows (Pluim et al., 2003):
where p(a), p(b), and p(a, b) are the probabilities of random variables of images A and B and can be estimated with histogram method. MI represents the information that A contains about B and can be used to measure the similarity between two images (Viola and Wells, 1995; Wells et al., 1996; Russakoff et al., 2004). For hyperspectral images, mutual information finds application in band selection (Amankwah, 2015), classification (Champa et al., 2020), segmentation (Lin and Zhang, 2020), and features reduction (Islam et al., 2020).
In this work, we proposed to utilize mutual information between spectral bands of an HSI image to learn a sparsifying wavelet for the spectral direction. Similar to the theory of learning a sparsifying basis for the spatial direction, a basis is required to be learned for the spectral dimension. It requires to capture the best/compact representation of the information contained in all the bands of the HSI image. MI between the bands can efficiently help to design such as basis because it captures the inter-band information. To the best of our knowledge, this is the first work to propose the use of an inter-band MI matrix for learning the wavelet sparsifying basis for the spectral direction.
Consider a data cube Ym×n×l. We created a mutual information matrix ρl×l such that (i, j) entry records the mutual information between the ith and the jth band. Specifically, ith row of ρl×l has mutual information of ith band with all the bands. In this way, we obtained a symmetric matrix with diagonal containing the mutual information between the same bands. This matrix is able to capture the similarity between the bands. We used this matrix as an image and learn the sparsifying basis for the spectral direction using the method outlined in Subsections 2.1 and 2.2. Since the matrix is symmetric, both the row-scanned and the column-scanned signals yield the same wavelet. Figure 5 shows the coefficients of dB4 wavelet, DCT, and the learned wavelet for a single pixel’s intensities along different spectral bands. It is evident that the learned wavelet provides better sparsity than both DCT and a standard wavelet dB4.
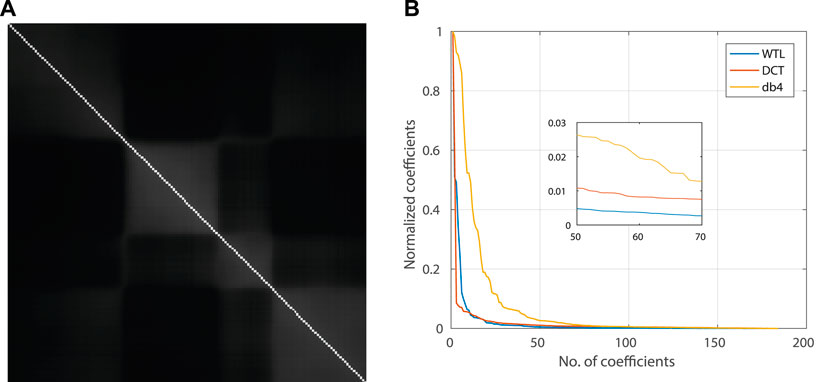
FIGURE 5. (A) Mutual information (MI) matrix for the data set “Urban”: a symmetric matrix with highest value along the diagonal that represents MI between same bands. The proposed WTL-I framework utilizes the MI matrix for the spectral direction. (B) Sparsification with DCT and the learned wavelet. A sparser signal has faster decaying coefficients such that the majority of total energy is accumulated in a fewer number of coefficients. The normalized coefficients are obtained by normalizing each coefficient with the maximum-value coefficient. Wavelet transform learning (WTL) with the MI matrix for the spectral direction provides more sparsification than the fixed DCT and db4 basis. Results are shown for a single pixel along the spectral direction.
2.4 HSI Data Reconstruction Using Learned Wavelet
The workflow of the proposed WTL-I method is shown in Figure 1. First, the coarser version of full HSI data is constructed from the compressively sensed data using a standard wavelet. Next, from this coarser signal, sparsifying basis
where
3 Materials
We have used three hyperspectral images for experiment purpose. As a preprocessing step, we removed noisy channels from all the HSI. We assumed a channel to be noisy if its pixels contain noisy or no information about the underlying material. Salinas (Salinas Dataset, 2019) scene is captured by AVIRIS over Salinas Valley, California. It has 224 bands and 512 × 217 pixels. We removed the noisy channels and crop the image to obtain a final image of size 200 × 200 × 184. Urban (Urban Dataset, 2019) scene has 307 × 307 pixels with each pixel corresponding to 2 × 2-m2 area and 210 bands in 400–2500 nm wavelength range. This image is preprocessed to remove the noisy channels and finally cropped to have a size of 200 × 200 × 160. Jasper Ridge (Jasper Ridge Dataset, 2019) scene has 512 × 614 pixels with 224 channels in 380–2500 nm wavelength range. A simpler version of this data set with size 100 × 100 × 198 is also available. A cropped version of this image with size 96 × 96 × 192 is considered for experiments. The sample band for these data sets is shown in Figure 6.

FIGURE 6. Hyperspectral images used in experiments. (A) Urban, (B) Jasper Ridge, (C) Salinas, (E) 90th band of Urban, (F) 30th band of Jasper Ridge, and (G) 40th band of Salinas.
4 Results and Discussion
Experiments are carried out to validate the proposed method. Results are obtained by using different sparsifying basis to optimize (16). The notations of different sparsifying basis used in this work are as follows:
• db-D: Daubechies orthogonal (“db4”) wavelet along the spatial dimensions and DCT along the spectral dimension.
• db-db: “db4” along all the dimensions.
• D-D: DCT along all the dimensions.
• WTL-D: learned wavelet transform along the spatial dimensions and DCT along the spectral dimension.
• WTL-I: learned wavelet transform along all the dimensions, where the spectral dimension’s wavelet is learned using mutual information of spectral bands.
The multi-level L-pyramid wavelet decomposition strategy (Ansari and Gupta, 2017), as shown in Figure 7 is used for each of the kth spectral band.
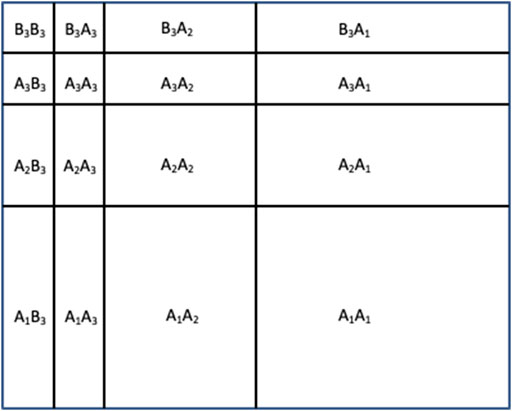
FIGURE 7. Multi-level wavelet decomposition of image using the 3-level L-pyramid wavelet decomposition as proposed in Ansari and Gupta (2017) Notations: (A) denotes Highpass filtering and (B) denotes lowpass filtering.
4.1 Performance Metrics
To evaluate the quality of reconstructed images, the peak signal-to-noise ratio (PSNR) (Peng et al., 2014) and spectral angle mapper (SAM) (Peng et al., 2014) are used as the performance metrics. the PSNR is expressed in decibels and is used to measure the quality of the reconstructed image based on mean squared error. It is defined as the ratio of the maximum power of the signal to the power of noise corrupting the signal.
SAM represents the average angle between spectral vectors of the reconstructed image and reference image at each spatial position. PSNR increases, while SAM decreases as a reconstructed image approaches closer to the original image.
4.2 Impact of Sensing Matrices
Traditionally, Gaussian and Bernoulli measurement matrices are used in hyperspectral compressed sensing. However, due to their unstructured nature, they have high computational complexity (Do et al., 2012). To overcome this, we used partial canonical identity (PCI) sensing matrix as suggested in Ansari and Gupta (2017). The PCI sensing matrix is used for each of the kth spectral band.
For reconstruction with the PCI sensing matrix, we required sensing only few pixel positions, unlike Gaussian and Bernoulli matrices, where a linear combination of all pixels is captured, and hence, all the pixels are required to be sensed. Thus, PCI reduces the time complexity as well as the memory requirement of the algorithm. To validate this point, we used the PCI sensing matrix as a measurement matrix and compared its performance with Gaussian and Bernoulli measurement matrices in terms of reconstruction accuracy and time complexity, as shown in Figure 8.
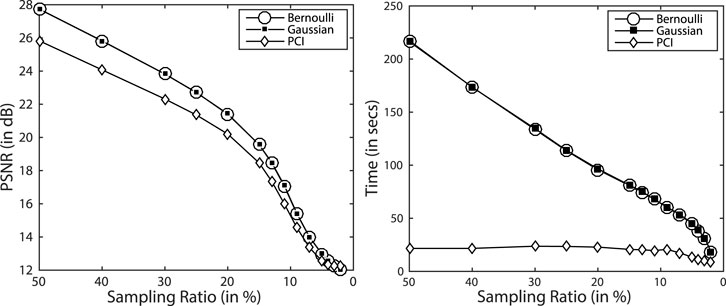
FIGURE 8. Reconstruction accuracy (A) and time complexity (B) with different measurement matrices for the data set “Urban.” db-D is used as the sparsifying basis to generate these results. Reported values are obtained by averaging values across all the bands. PCI provides similar SNR but with significantly reduced time complexity.
Results in Figure 8 indicate that the reconstruction accuracy with the PCI sensing matrix lags behind performance with Gaussian and Bernoulli sensing matrices only by
4.3 Comparison of Different Methods
The proposed WTL-I method or the learned sparsifying basis is compared in a number of ways in terms of reconstruction accuracy. First, we compared the proposed WTL-D and WTL-I methods with db-db, db-D, and D-D sparsifying basis. We also compared the performance of WTL-D and WTL-I with two existing state-of-the-art methods: 1) re-weighted Laplace prior-based hyperspectral compressive sensing (RLPHCS) (Zhang et al., 2015) and 2) structured sparsity-based blind compressive sensing (SSHBCS) (Zhang et al., 2016).
4.3.1 Reconstruction With Different Sparsifying Basis
We compared the reconstruction performance of different methods mentioned before at different sampling ratios (SR). The range is chosen to emphasize the reconstruction accuracy at lower sampling ratios.
Table 1 presents the PSNR of the reconstructed images with different methods at different SR. The WTL-D and WTL-I lead at lower SR as well as higher SR, where the performance margin is higher at lower SR. This is due to the exploitation of the underlying signal structure by the learned sparsifying basis. Also, WTL-I performs best with WTL-D performing second best at majority of the SRs. This observation proves the advantage of using learned sparsifying for spatial and spectral directions.
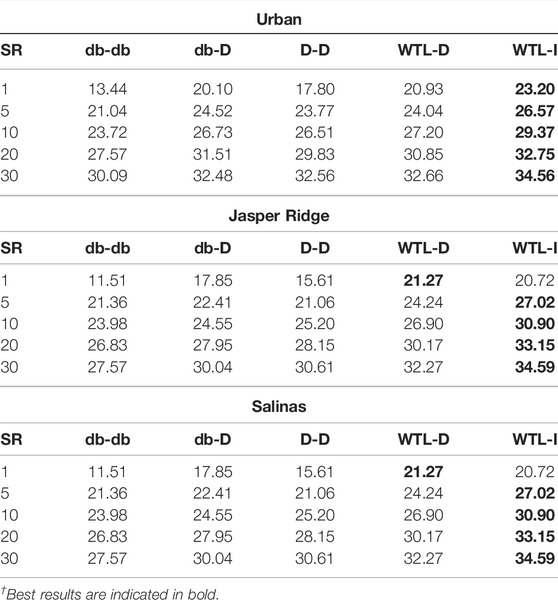
TABLE 1. PSNR of reconstructed HSI with different sparsifying basis at different sampling ratios and 20 db SNR (best results are highlighted).
We have also presented visually one of the reconstructed bands of Salinas data set (band number 20th). The reconstruction is carried out at 5% SR and 20 db SNR and resultant image is shown in Figure 9. Even at such low SR, WTL-D and WTL-I are able to capture a relatively large number of fine details as compared to those reconstructed with other wavelets. This result is consistent with the relatively higher PSNR of WTL-D and WTL-I observed in Table 1.

FIGURE 9. Reconstruction of 20th band of data set Salinas with different sparsifying basis at 20 db SNR and 5% SR. (A) Original band, (B) db-db, (C) db-D, (D) D-D, (E) WTL-D, and (F) WTL-I.
Experiments are also performed to show reconstruction performance in noisy scenarios (Figure 10). The Gaussian noise of varying variance is added to the original image to obtain different SNR (10 − 20 db). It is observed that WTL-I is leading other sparsifying basis in the reconstruction performance of images corrupted at all the noise levels considered. Although WTL-D is also performing better than the other basis, it is lagging in a few cases. In conclusion, learned sparsifying basis, specifically, when learned in both spatial and spectral dimensions perform better at low SR as well as at high noise levels.
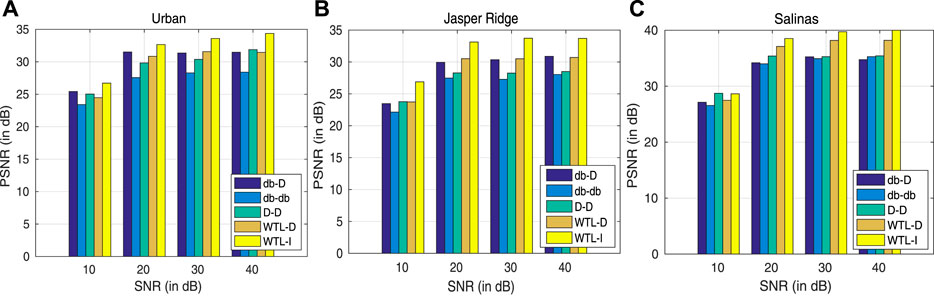
FIGURE 10. PSNR for reconstruction with different sparsifying basis at different noise levels. (A) Urban, (B) Jasper Ridge, and (C) Salinas. Results are shown at 20% SR.
4.3.2 Comparison With Prior-Based Methods
We have already established that learned sparsifying basis provide better recovery of compressively sensed HSI data than different combinations of conventional basis. Now, we will compare the performance of WTL-D and WTL-I with two other methods, RLPHCS (Zhang et al., 2015) and SSHBCS (Zhang et al., 2016). We have used the codes provided by (Zhang et al., 2015) and (Zhang et al., 2016) to generate the results with these methods. Table 2 shows the PSNR of the reconstructed images at 20 db SNR. For image Urban, SSHBCS is leading the RLPHCS at almost all the SR. But, for image Jasper Ridge, RLPHCS is slightly leading the SSHBCS and for image Salinas, RLPHCS is leading the SSHBCS by a good margin. For all the images, learned sparsifying basis based methods are leading the other two methods by a large margin at lower SR and higher SR. We also calculated the SAM of the reconstructed images (Figure 11). The same pattern is observed with SAM, where WTL-D and WTL-I lead other two methods, particularly at lower SR. From PSNR and SAM metrics, it is observed that wavelet transform learning based approach provides better recovery of compressively sensed HSI data than the state-of-the-art methods RLPHCS and SSHBCS.
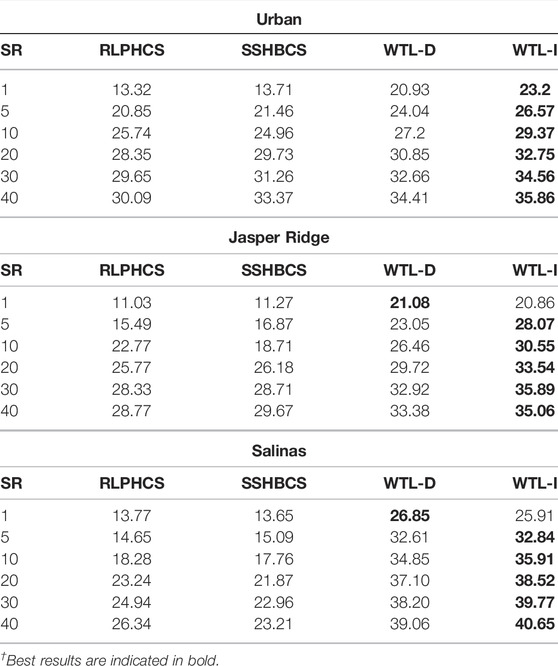
TABLE 2. PSNR of reconstructed HSI with WTL-D, WTL-I, SSHBCS, and RLPHCS (best results are highlighted). The noise level is 20 dB.
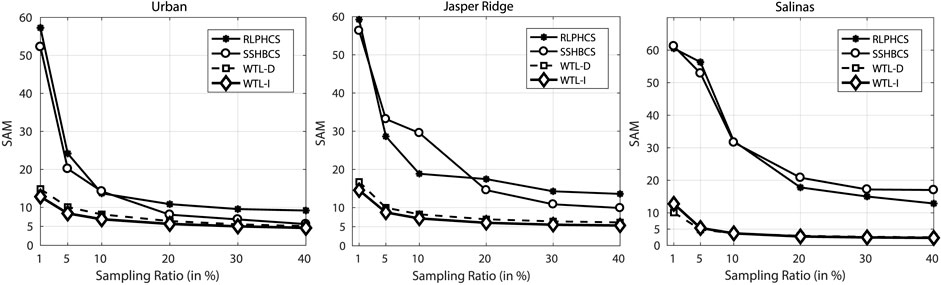
FIGURE 11. Reconstruction performance comparison of WTL-D, WTL-I, SSHBCS, and RLPHCS in terms of SAM for data sets: (A) Urban, (B) Jasper Ridge, and (C) Salinas. Results are generated for images corrupted with noise, having an SNR of 20 dB.
The reconstructed image with these methods is shown in Figure 12. The reconstruction is carried out at 5% SR and 25 db SNR. For image Urban, SSHBCS and RLPHCS have suppressed the pixel intensities in the reconstructed image. WTL-D and WTL-I, on the other hand, have generated an image that resembles the original image considerably. Also, among WTL-D and WTL-I, WTL-I reconstruct the image much closer to the original image. Same pattern is observed for the image “Salinas” with WTL-I performing better than the other methods. For image Jasper Ridge, the reconstruction is not satisfactory with either of the methods. We have also computed the PSNR and SAM of reconstructed images at different noise levels. These results are shown in Table 3 and Figure 13. Results indicate that WTL-D and WTL-I lead the other two methods at all noise levels.

FIGURE 12. Reconstruction using different methods: (from top to bottom) 110th band of image “Urban,” 55th band of image “Salinas,” and 10th band of image “Jasper-Ridge.” (A) Original band, (B) SSHBCS, (C) RLPHCS, (D) WTL-D, and (E) WTL-I. Results are shown at 5% SR and 25 dB SNR.
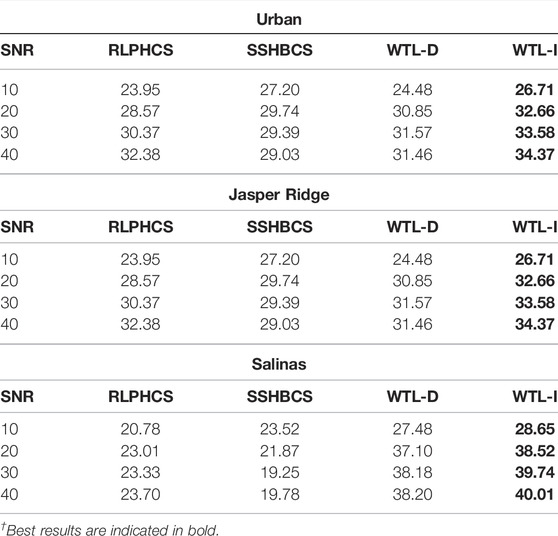
TABLE 3. PSNR of reconstructed images with SSHBCS, RLPHCS, WTL-D, and WTL-I at different noise levels and 20% SR (best results are highlighted).
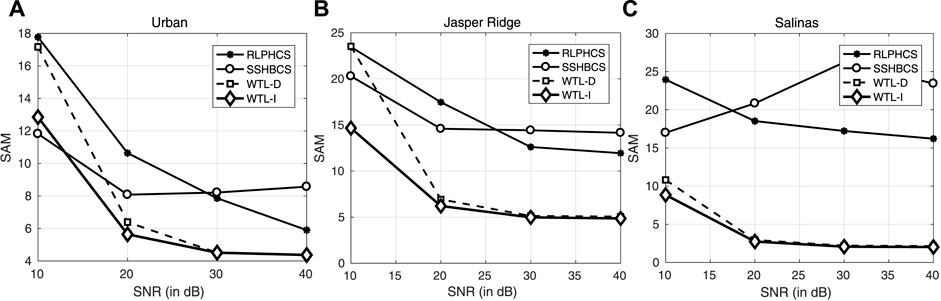
FIGURE 13. Comparative performance of SSHBCS, RLPHCS, WTL-D, and WTL-I in terms of SAM at different noise levels in CS-based recovery of HSI data: (A) Urban, (B) Jasper Ridge, (C) Salinas. Results are generated at 20% SR.
5 Validation of WTL-I in the Application of HSI Classification
Convolutional neural networks (CNNs) (LeCun et al., 2004; Jarrett et al., 2009; Krizhevsky et al., 2012; Simonyan and Zisserman, 2015; He et al., 2016; Gehlot et al., 2020a; Gehlot et al., 2021; Goyal et al., 2021; Gupta et al., 2021) have been used successfully in various applications to achieve satisfactory performance (Goswami et al., 2020; Gehlot et al., 2020b; Gupta et al., 2020; Gehlot and Gupta, 2021). Here, we have used a CNN-based classifier (Figure 14) to ascertain the quality of HSI data set reconstructed with different methods. To achieve this, we performed pixel-wise classification of the original image and the reconstructed images, and compared these images with the ground truth. Results for an accurately reconstructed image must not deviate much from the ground truth. The image Salinas is used for this purpose due to availability of its ground truth. This image is reconstructed at 25 dB SNR and 25% SR. We have used Salinas data set of size 512 × 216 × 184. This size is chosen to retain all the classes of the data set as cropping might remove some classes. Also, for comparison, we chose four different methods: SSHBCS, RLPHCS, WTL-D, and WTL-I.
5.1 Training Procedure
Figure 14 shows the CNN architecture used for classification. The stride used is two for convolutional layers and one for pooling layers. We performed the training using the original data set. As a preprocessing step, we extracted mean normalized patches of size 13 × 13 for all the classes which are then given as an input to the CNN. Adagrad optimizer with learning rate .01 and batch size of 100 is used to train the CNN. The experiments are carried out using Nvidia GeForce GTX 1080 GPU and Tensorflow 1.8 deep learning library. Once the model is trained, we used it to classify the original hyperspectral image and the reconstructed image. Both qualitative results and quantitative results are reported to evaluate the classification performance.
5.2 Results
We performed the classification of original image and reconstructed image using the trained model (Figure 15). It is observed that the model is performing well and classification performance of the original image matched the ground truth approximately. Some portions of the original image were classified perfectly, but a few pixels were misclassified in some regions. It is observed that the images reconstructed using SSHBCS (Figure 15C) and RLPHBCS (Figure 15D) are deviating considerably from the ground truth. On the other hand, the images reconstructed using the learned wavelet sparsifying basis performs considerably better and yielded approximately the same results as the original image (Figure 15E).

FIGURE 15. Classification of image Salinas using the trained model. The images are reconstructed at 20% SR and 20 db SNR (A) ground truth. (B) Classification of original image. Classification of image reconstructed with (C) SSHBCS, (D) RLPHCS, and (E) WTL-I.
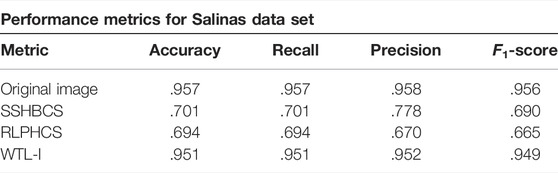
We can also verify aforementioned results using the performance metrics. Table 4 shows the performance metric results on both the datasets. It is observed that for the data set Salinas, original image and the image reconstructed by WTL-I has almost same values for all the metrics, while RLPHBCS and SSHBCS are lagging by a large margin.
The lower performance of RLPHCS and SSHBCS might be due to the fact that they are exploiting only the spatial correlation and not the spectral correlation. On the contrary, the proposed approach is able to utilize spatial as well as spectral correlation. Also, WTL-I performs better that WTL-D. This is due to the application of learned sparsifying basis in all the three directions unlike WTL-D, which is using DCT as the sparsifying basis in the spectral direction instead of learning a basis from the information in the spectral direction. The leading performance of WTL-I also highlights the capability of mutual information matrix to capture the spectral correlation. The sparsifying basis learned with this matrix is performing better than the conventional basis (dB4 or DCT). To summarize, learned sparsifying basis applied in all the directions is able to better capture the spatial and spectral correlation and hence, performs better.
6 Conclusion
In this article, we proposed and validated wavelet transform learning based method, namely, WTL-I, for the 3D HSI data set and used it successfully in an inverse image problem of compressive sensing-based reconstruction. We learned the sparsifying basis for the spectral direction using the mutual information between different spectral bands. We used a partial canonical identity (PCI) sensing matrix for CS-based reconstruction of hyperspectral images in place of existing Gaussian or Bernoulli sensing matrices as former performs much faster and hence is suitable for real-time time-bound reconstruction-based applications. Even at as low as 5% sampling ratio, the quality of recovery of the HSI data is noteworthy. We also used CNN to perform pixel-wise classification (leading to segmentation of HSI data) that demonstrated the superior reconstruction capability of the WTL-I method.
Data Availability Statement
The study utilizes the datasets publicly available at https://rslab.ut.ac.ir/data.
Author Contributions
AG, NA, and SG contributed to the method formulation. NA and SG contributed to the implementation and experiments. AG and SG prepared the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
SG would like to thank the University Grants Commission (UGC), govt. of India, for the UGC-Junior Research Fellowship and UGC-Senior Research Fellowship.
References
Aharon, M., Elad, M., and Bruckstein, A. (2006). K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Trans. Signal. Process. 54, 4311–4322. doi:10.1109/tsp.2006.881199
Amankwah, A. (2015). Spatial Mutual Information Based Hyperspectral Band Selection for Classification. ScientificWorldJournal 2015, 630918. doi:10.1155/2015/630918
Ansari, N., Gupta, A., and Duggal, R. (2016). Design of Image Matched Non-separable Wavelet Using Convolutional Neural Network. arXiv preprint arXiv:1612.04966.
Ansari, N., and Gupta, A. (2017). Image Reconstruction Using Matched Wavelet Estimated from Data Sensed Compressively Using Partial Canonical Identity Matrix. IEEE Trans. Image Process. 26, 3680–3695. doi:10.1109/tip.2017.2700719
Ansari, N., and Gupta, A. (2016). “Joint Framework for Signal Reconstruction Using Matched Wavelet Estimated from Compressively Sensed Data,” in 2016 Data Compression Conference (DCC), Snowbird, UT, 30 March-1 April 2016 (IEEE), 580. doi:10.1109/dcc.2016.87
Ansari, N., and Gupta, A. (2018a). M-RWTL: Learning Signal-Matched Rational Wavelet Transform in Lifting Framework. IEEE Access 6, 12213–12227. doi:10.1109/access.2017.2788084
Ansari, N., and Gupta, A. (2015). “Signal-Matched Wavelet Design via Lifting Using Optimization Techniques,” in 2015 IEEE International Conference on Digital Signal Processing (DSP), Singapore, 21-24 July 2015, 863–867. doi:10.1109/icdsp.2015.7251999
Ansari, N., and Gupta, A. (2018b). “Statistical Learning of Rational Wavelet Transform for Natural Images,” in 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (IEEE), 4679–4683. doi:10.1109/icassp.2018.8462583
Ansari, N., and Gupta, A. (2019). WNC-ECGlet: Weighted Non-Convex Minimization Based Reconstruction of Compressively Transmitted ECG Using ECGlet. Biomed. Signal Process. Control. 49, 1–13. doi:10.1016/j.bspc.2018.10.005
Ataee, M., Zayyani, H., Babaie-Zadeh, M., and Jutten, C. (2010). “Parametric Dictionary Learning Using Steepest Descent,” in 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, 14-19 March 2010 (IEEE), 1978–1981. doi:10.1109/icassp.2010.5495278
Bajorski, P. (2012). Target Detection under Misspecified Models in Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 5, 470–477. doi:10.1109/JSTARS.2012.2188095
Berg, E. V. D., and Friedlander, M. P. (2015). A Solver for Large-Scale Sparse Reconstruction. SPGL1 package.
Berg, E. V. D., and Friedlander, M. P. (2008). Probing the Pareto Frontier for Basis Pursuit Solutions. SIAM J. Scientific Comput. 31, 890–912. doi:10.1137/080714488
Champa, A. I., Mahedy Hasan, S. M., Rahman, M. A., and Rabbi, M. F. (2020). “Hybrid Technique for Classification of Hyperspectral Image Using Quadratic Mutual Information,” in 2020 IEEE Region 10 Symposium (TENSYMP), Dhaka, Bangladesh, 5-7 June 2020, 933–936. doi:10.1109/tensymp50017.2020.9230817
Chang, C.-I. (2003). Hyperspectral Imaging: Techniques for Spectral Detection and Classification. New York: Plenum Publishing Co..
Chen, C., Li, Y., and Huang, J. (2014). Forest Sparsity for Multi-Channel Compressive Sensing. IEEE Trans. Signal Process. 62, 2803–2813. doi:10.1109/TSP.2014.2318138
Chen, Y., Nasrabadi, N. M., and Tran, T. D. (2012). “Kernel Sparse Representation for Hyperspectral Target Detection,” in 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, 22-27 July 2012, 7484–7487. doi:10.1109/IGARSS.2012.6351901
Do, T. T., Gan, L., Nguyen, N. H., and Tran, T. D. (2012). Fast and Efficient Compressive Sensing Using Structurally Random Matrices. IEEE Trans. Signal. Process. 60, 139–154. doi:10.1109/tsp.2011.2170977
Gehlot, S., Gupta, A., and Gupta, R. (2021). A CNN-Based Unified Framework Utilizing Projection Loss in Unison with Label Noise Handling for Multiple Myeloma Cancer Diagnosis. Med. Image Anal. 72, 102099. doi:10.1016/j.media.2021.102099
Gehlot, S., Gupta, A., and Gupta, R. (2020a). “EDNFC-Net: Convolutional Neural Network with Nested Feature Concatenation for Nuclei-Instance Segmentation,” in CASSP 2020 - 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4-8 May 2020, 1389–1393. doi:10.1109/icassp40776.2020.9053633I
Gehlot, S., Gupta, A., and Gupta, R. (2020b). SDCT-AuxNet : DCT Augmented Stain Deconvolutional CNN with Auxiliary Classifier for Cancer Diagnosis. Med. Image Anal. 61, 101661. doi:10.1016/j.media.2020.101661
Gehlot, S., and Gupta, A. (2021). “Self-Supervision Based Dual-Transformation Learning for Stain Normalization, Classification Andsegmentation,” in Machine Learning in Medical Imaging. Editors C. Lian, X. Cao, I. Rekik, X. Xu, and P. Yan (Cham: Springer International Publishing), 477–486. doi:10.1007/978-3-030-87589-3_49
Geladi, H. G. P. (2007). Techniques and Applications of Hyperspectral Image Analysis. New Jersey: Wiley.
Golbabaee, M., and Vandergheynst, P. (2012a). “Hyperspectral Image Compressed Sensing via Low-Rank and Joint-Sparse Matrix Recovery,” in 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, 25-30 March 2012, 2741–2744. doi:10.1109/icassp.2012.6288484
Golbabaee, M., and Vandergheynst, P. (2012b). “Joint Trace/TV Norm Minimization: A New Efficient Approach for Spectral Compressive Imaging,” in 2012 19th IEEE International Conference on Image Processing, Orlando, FL, September 30-October 3, 2012, 933–936. doi:10.1109/icip.2012.6467014
Goswami, S., Mehta, S., Sahrawat, D., Gupta, A., and Gupta, R. (2020). Heterogeneity Loss to Handle Intersubject and Intrasubject Variability in Cancer. arXiv preprint arXiv:2003.03295.
Goyal, P., Mulleti, S., Gupta, A., and Eldar, Y. C. (2021). “Duras: Deep Unfolded Radar Sensing Using Doppler Focusing,” in ICASSP 2021-2021 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, 6-11 June 2021 (IEEE), 4070–4074. doi:10.1109/icassp39728.2021.9414967
Gupta, A., Duggal, R., Gehlot, S., Gupta, R., Mangal, A., Kumar, L., et al. (2020). GCTI-SN: Geometry-Inspired Chemical and Tissue Invariant Stain Normalization of Microscopic Medical Images. Med. Image Anal. 65, 101788. doi:10.1016/j.media.2020.101788
Gupta, A., Jain, J., Poundrik, S., Shetty, M. K., Girish, M., and Gupta, M. D. (2021). “Interpretable Ai Model-Based Predictions of Ecg Changes in Covid-Recovered Patients,” in 2021 4th International Conference on Bio-Engineering for Smart Technologies (BioSMART), Paris/Créteil, December 8-10, 2021 (IEEE), 1–5. doi:10.1109/biosmart54244.2021.9677747
Gupta, A., Joshi, S. D., and Prasad, S. (2005a). A New Approach for Estimation of Statistically Matched Wavelet. IEEE Trans. Signal. Process. 53, 1778–1793. doi:10.1109/tsp.2005.845470
Gupta, A., Joshi, S. D., and Prasad, S. (2005b). A New Method of Estimating Wavelet with Desired Features from a Given Signal. Signal. Process. 85, 147–161. doi:10.1016/j.sigpro.2004.09.008
He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep Residual Learning for Image Recognition,” in IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, 27-30 June, 2016, 770–778. doi:10.1109/cvpr.2016.90
Islam, R., Ahmed, B., and Hossain, A. (2020). Feature Reduction of Hyperspectral Image for Classification. J. Spat. Sci., 1–21. doi:10.1080/14498596.2020.1770137
Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. (2009). “What Is the Best Multi-Stage Architecture for Object Recognition?” in IEEE International Conference on Computer Vision, ICCV, Kyoto, September 29-October 2 2009, 2146–2153.
[Dataset] Jasper Ridge Dataset (2019). Available at: http://lesun.weebly.com/hyperspectral-data-set.html (Accessed 03 25, 2019).
Khoshsokhan, S., Rajabi, R., and Zayyani, H. (2019a). Clustered Multitask Non-Negative Matrix Factorization for Spectral Unmixing of Hyperspectral Data. J. Appl. Rem. Sens. 13, 1–13. doi:10.1117/1.jrs.13.026509
Khoshsokhan, S., Rajabi, R., and Zayyani, H. (2019b). Sparsity-Constrained Distributed Unmixing of Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 12, 1279–1288. doi:10.1109/JSTARS.2019.2901122
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “Imagenet Classification with Deep Convolutional Neural Networks,” in Advances in Neural Information Processing Systems, Nevada, December 03-08, 2012, 1097–1105.
LeCun, Y., Huang, F., and Bottou, L. (2004). “Learning Methods for Generic Object Recognition with Invariance to Pose and Lighting,” in Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, June 27-July 2, 2004.
Lin, L., and Zhang, S. (2020). Superpixel Segmentation of Hyperspectral Images Based on Entropy and Mutual Information. Appl. Sci. 10 (4), 1261. doi:10.3390/app10041261
Peng, Y., Meng, D., Xu, Z., Gao, C., Yang, Y., and Zhang, B. (2014). “Decomposable Nonlocal Tensor Dictionary Learning for Multispectral Image Denoising,” in IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, 23-28 June 2014, 2949–2956. doi:10.1109/cvpr.2014.377
Pluim, J. P. W., Maintz, J. B. A., and Viergever, M. A. (2003). Mutual-Information-Based Registration of Medical Images: A Survey. IEEE Trans. Med. Imaging 22, 986–1004. doi:10.1109/TMI.2003.815867
Prasad, S., Li, W., Fowler, J. E., and Bruce, L. M. (2012). Information Fusion in the Redundant-Wavelet-Transform Domain for Noise-Robust Hyperspectral Classification. IEEE Trans. Geosci. Remote Sensing 50, 3474–3486. doi:10.1109/TGRS.2012.2185053
Ravishankar, S., and Bresler, Y. (2015). Efficient Blind Compressed Sensing Using Sparsifying Transforms with Convergence Guarantees and Application to Magnetic Resonance Imaging. SIAM J. Imaging Sci. 8, 2519–2557. doi:10.1137/141002293
Ravishankar, S., and Bresler, Y. (2011). MR Image Reconstruction from Highly Undersampled K-Space Data by Dictionary Learning. IEEE Trans. Med. Imaging 30, 1028–1041. doi:10.1109/tmi.2010.2090538
Russakoff, D. B., Tomasi, C., Rohlfing, T., and Maurer, C. R. (2004). “Image Similarity Using Mutual Information of Regions,” in Computer Vision - ECCV 2004, Prague, Czech Republic, May 11-14, 2004 (Springer Berlin Heidelberg), 596–607. doi:10.1007/978-3-540-24672-5_47
[Dataset] Salinas Dataset (2019). Available at: http://www.ehu.eus/ccwintco/index.php?title=Hyperspectral_Remote_Sensing_Scenes#Salinas (Accessed 10 10, 2018).
Schowengerdt, R. A. (2006). Remote Sensing: Models and Methods for Image Processing. Third Edition. Orlando, FL, USA: Academic Press.
Shang, X., Song, M., Wang, Y., Yu, C., Yu, H., Li, F., et al. (2021). Target-Constrained Interference-Minimized Band Selection for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sensing 59, 6044–6064. doi:10.1109/TGRS.2020.3010826
Simonyan, K., and Zisserman, A. (2015). “Very Deep Convolutional Networks for Large-Scale Image Recognition,” in International Conference on Learning Representations, California, May 7-9, 2015.
Sweldens, W. (1996). The Lifting Scheme: A Custom-Design Construction of Biorthogonal Wavelets. Appl. Comput. Harmonic Anal. 3, 186–200. doi:10.1006/acha.1996.0015
[Dataset] Urban Dataset (2019). Available at: http://lesun.weebly.com/hyperspectral-data-set.html (Accessed 03 25, 2019).
Viola, P., and Wells, W. M. (1995). “Alignment by Maximization of Mutual Information,” in Proceedings of IEEE International Conference on Computer Vision, Cambridge, MA, 20-23 June 1995, 16–23. doi:10.1109/ICCV.1995.466930
Wells, W. M., Viola, P., Atsumi, H., Nakajima, S., and Kikinis, R. (1996). Multi-Modal Volume Registration by Maximization of Mutual Information. Med. Image Anal. 1, 35–51. doi:10.1016/s1361-8415(01)80004-9
Xie, X., Li, Y. X., Li, R., Zhang, Y., Huo, Y., Bao, Y., et al. (2013). Hyperspectral Characteristics and Growth Monitoring of rice (Oryza Sativa) under Asymmetric Warming. Int. J. Remote Sensing 34, 8449–8462. doi:10.1080/01431161.2013.843806
Yaghoobi, M., Daudet, L., and Davies, M. E. (2009). Parametric Dictionary Design for Sparse Coding. IEEE Trans. Signal. Process. 57, 4800–4810. doi:10.1109/tsp.2009.2026610
Yu, C., Liu, C., Song, M., and Chang, C.-I. (2022). Unsupervised Domain Adaptation with Content-Wise Alignment for Hyperspectral Imagery Classification. IEEE Geosci. Remote Sensing Lett. 19, 1–5. doi:10.1109/lgrs.2021.3126594
Zhang, L., Wei, W., Zhang, Y., Shen, C., van den Hengel, A., and Shi, Q. (2016). Dictionary Learning for Promoting Structured Sparsity in Hyperspectral Compressive Sensing. IEEE Trans. Geosci. Remote Sensing 54, 7223–7235. doi:10.1109/tgrs.2016.2598577
Zhang, L., Wei, W., Zhang, Y., Tian, C., and Li, F. (2015). “Reweighted Laplace Prior Based Hyperspectral Compressive Sensing for Unknown Sparsity,” in IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, 7-12 June 2015, 2274–2281. doi:10.1109/cvpr.2015.7298840
Keywords: compressive sensing, hyperspectral images, matched wavelet, wavelet transform learning, reconstruction
Citation: Gehlot S, Ansari N and Gupta A (2022) WTL-I: Mutual Information-Based Wavelet Transform Learning for Hyperspectral Imaging. Front. Sig. Proc. 2:854207. doi: 10.3389/frsip.2022.854207
Received: 13 January 2022; Accepted: 16 March 2022;
Published: 02 May 2022.
Edited by:
Marco Cagnazzo, Télécom ParisTech, FranceReviewed by:
Hadi Zayyani, Qom University of Technology, IranKe Gu, Beijing University of Technology, China
Copyright © 2022 Gehlot, Ansari and Gupta. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Anubha Gupta, YW51YmhhQGlpaXRkLmFjLmlu
 Shiv Gehlot
Shiv Gehlot Anubha Gupta
Anubha Gupta