- 1Department of Computer Science, The University of Sheffield, Sheffield, United Kingdom
- 2National Center for Radiation Protection and Computational Physics, Italian Institute of Health, Rome, Italy
- 3Department of Biomedical Science, The University of Sheffield, Sheffield, United Kingdom
- 4Neuroscience Institute, The University of Sheffield, Sheffield, United Kingdom
Echo state networks (ESNs) are a powerful form of reservoir computing that only require training of linear output weights while the internal reservoir is formed of fixed randomly connected neurons. With a correctly scaled connectivity matrix, the neurons’ activity exhibits the echo-state property and responds to the input dynamics with certain timescales. Tuning the timescales of the network can be necessary for treating certain tasks, and some environments require multiple timescales for an efficient representation. Here we explore the timescales in hierarchical ESNs, where the reservoir is partitioned into two smaller linked reservoirs with distinct properties. Over three different tasks (NARMA10, a reconstruction task in a volatile environment, and psMNIST), we show that by selecting the hyper-parameters of each partition such that they focus on different timescales, we achieve a significant performance improvement over a single ESN. Through a linear analysis, and under the assumption that the timescales of the first partition are much shorter than the second’s (typically corresponding to optimal operating conditions), we interpret the feedforward coupling of the partitions in terms of an effective representation of the input signal, provided by the first partition to the second, whereby the instantaneous input signal is expanded into a weighted combination of its time derivatives. Furthermore, we propose a data-driven approach to optimise the hyper-parameters through a gradient descent optimisation method that is an online approximation of backpropagation through time. We demonstrate the application of the online learning rule across all the tasks considered.
1 Introduction
The high inter-connectivity and asynchronous loop structure of Recurrent Neural Networks (RNNs) make them powerful techniques for processing temporal signals [1]. However, the complex inter-connectivity of RNNs means that they cannot be trained using the conventional back-propagation (BP) algorithm [2] used in feed-forward networks, since each neuron’s state depends on other neuronal activities at previous times. A method known as Back-Propagation-Through-Time (BPTT) [3], which relies on an unrolling of neurons’ connectivity through time to propagate the error signal to earlier time states, can be prohibitively complex for large networks or time series. Moreover, BPTT is not considered biologically plausible as neurons must retain memory of their activation over the length of the input and the error signal must be propagated backwards with symmetric synaptic weights [4].
Many of these problems can be avoided using an alternative approach: reservoir computing (RC). In the subset of RC networks known as Echo State networks, a fixed “reservoir” transforms a temporal input signal in such a way that only a single layer output perceptron needs to be trained to solve a learning task. The advantage of RC is that the reservoir is a fixed system that can be either computationally or physically defined. Since it is fixed it is not necessary to train the reservoir parameters through BPTT, making RC networks much simpler to train than RNNs. Furthermore, the random structure of a RC network renders the input history over widely different time-scales, offering a representation that can be used for a wide variety of tasks without optimising the recurrent connectivity between nodes.
Reservoirs have biological analogues in cerebellum-like networks (such as the cerebellum, the insect mushroom body and the electrosensory lobe of electric fish), in which input signals encoded by relatively few neurons are transformed via “expansion re-coding” into a higher-dimensional space in the next layer of the network, which has many more neurons than the input layer [5–8]. This large population of neurons (granule cells in the cerebellum; Kenyon cells in the mushroom body) acts as a reservoir because their input connectivity is fixed and learning occurs only at their output synapses. The principal neurons of the “reservoir” can form chemical and electrical synapses on each other (e.g., Kenyon cells: [9–11]), analogous to the recurrent connectivity in reservoir computing that allows the network to track and transform temporal sequences of input signals. In some cases, one neuronal layer with recurrent connectivity might in turn connect to another neuronal layer with recurrent connectivity; for example, Kenyon cells of the mushroom body receive input from olfactory projection neurons of the antennal lobe, which are connected to each other by inhibitory and excitatory interneurons [12, 13]. Such cases can be analogised to hierarchically connected reservoirs. In biological systems, it is thought that transforming inputs into a higher-dimensional neural code in the “reservoir” increases the associative memory capacity of the network [5]. Moreover, it is known that for the efficient processing of information unfolding in time, which requires networks to dynamically keep track of past stimuli, the brain can implement ladders of neural populations with hierarchically organised “temporal receptive fields” [14].
The same principles of dimensional expansion in space and/or time apply to artificial RC networks, depending on the non-linear transformation of the inputs into a representation useful for learning the task at the single linear output layer. We focus here on a popular form of RC called Echo State Networks [15], where the reservoir is implemented as a RNN with a fixed, random synaptic connection matrix. This connection matrix is set so the input “echoes” within the network with decaying amplitude. The performance of an Echo State Network depends on certain network hyper-parameters that need to be optimised through grid search or explicit gradient descent. Given that the dependence of the network’s performance on such hyper-parameters is both non-linear and task-dependent, such optimisation can be tedious.
Previous works have studied the dependence of the reservoir properties on the structure of the random connectivity adopted, studying the dependence of the reservoir performance on the parameters defining the random connectivity distribution, and formulating alternatives to the typical Erdos-Renyi graph structure of the network [16–18]. In this sense, in [17] a model with a regular graph structure has been proposed, where the nodes are connected forming a circular path with constant shortest path lengths equal to the size of the network, introducing long temporal memory capacity by construction. The memory capacity has been studied previously for network parameters such as the spectral radius (ρ) and sparsity; in general memory capacity is higher for ρ close to one and low sparsity, but high memory capacity does not guarantee high prediction [19, 20]. ESNs are known to perform optimally when at the “edge of criticality” [21], where low prediction error and high memory can be achieved through network tuning.
More recently, models composed of multiple reservoirs have gathered the attention of the community. From the two ESNs with lateral inhibition proposed in [22], to the hierarchical structure of reservoirs first analyzed by Jaeger in [23], these complex architectures of multiple, multilayered reservoirs have shown improved generalisation abilities over a variety of tasks [23–25]. In particular, the works [26, 27] have studied different dynamical properties of such hierarchical structures of ESNs, while [28] have proposed hierarchical (or deep) ESNs with projection encoders between layers to enhance the connectivity of the ESN layers. The partitioning (or modularity) of ESNs was studied by [29], where the ratio of external to internal connections was varied. By tuning this partitioning performance can be increased on memory or recall tasks. Here we demonstrate that one of the main reasons to adopt a network composed by multiple, pipelined sub-networks, is the ability to introduce multiple timescales in the network’s dynamics, which can be important in finding optimal solutions for complex tasks. Examples of tasks that require such properties are in the fields of speech, natural language processing, and reward driven learning in partially observable Markov decision processes [30]. A hierarchical structure of temporal kernels [31], as multiple connected ESNs, can discover higher level features of the input temporal dynamics. Furthermore, while a single ESN can be tuned to incorporate a distribution of timescales with a prefixed mode, optimising the system hyper-parameters to cover a wide range of timescales can be problematic.
Here, we show that optimisation of hyper-parameters can be guided by analysing how these hyper-parameters are related to the timescales of the network, and by optimising them according to the temporal dynamics of the input signal and the memory required to solve the considered task. This analysis improves performance and reduces the search space required in hyper-parameter optimisation. In particular, we consider the case where an ESN is split into two sections with different hyper-parameters resulting in separate temporal properties. In the following, we will first provide a survey of timescales in ESNs before presenting the comparative success of these hierarchical ESNs on three different tasks. The first is the non-linear auto-regressive moving average 10 (NARMA10) task which requires both memory and fast non-linear transformation of the input. Second, we explore the performance of the network in a reconstruction and state “perception” task with different levels of external white noise applied on the input signal. Finally, we apply the hierarchical ESN to a permuted sequential MNIST classification task, where the usual MNIST hand written digit database is serialised and permuted as a 1 dimensional time-series.
2 Survey of Timescales in Echo State Networks
We begin by describing the operations of an ESN and present a didactic survey of their inherent timescales, which will be drawn upon in later sections to analyze the results.
As introduced in the previous section, an ESN is a recurrent neural network and the activity,
where
The timescales of this dynamical system are closely linked to the specific structure of
Considering that the eigenvalues
This corresponds to a rescaling of value
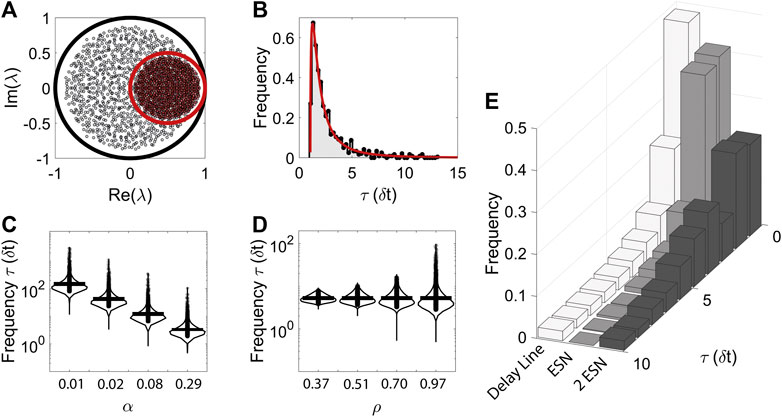
FIGURE 1. The analysis of the timescales of the system in the linear regime can guide the search for the optimal values of the hyper-parameters α and ρ. (A): Translation and scaling of the eigenvalues of the system due to the presence of the leakage factor. (B): Example of distribution of timescales, computed analytically (red line) and computationally (black points) estimated from the eigenvalues of
When the connectivity matrix,
Importantly we note that while the eigenvalues are uniformly distributed over the unit circle, the timescales are not due to the inverse relationship between them. The resulting distribution of the linearised system, shown in Figure 1B (red line), is in excellent agreement with the numerically computed distribution for a single ESN (black points + shaded area).
The analytical form of the distribution, together with Eq. 5, allows us to explicitly derive how changes in α and ρ affect the network timescales. Notably we can obtain analytical expression for the minimum, maximum and most probable (peak of the distribution) timescale:
where Eqs. 8 and 7 can be derived directly from Eq. 5, while Eq. 9 follows from maximisation of Eq. 6. As expected, α strongly affects all these three quantities; interestingly, though, α does not influence the relative range of the distribution,
2.1 Hierarchical Echo-State Networks
Different studies have proposed alternatives to the random structure of the connectivity matrix of ESNs, formulating models of reservoirs with regular graph structures. Examples include a delay line [17], where each node receives and provides information only from the previous node and the following one respectively, and the concentric reservoir proposed in [18], where multiple delay lines are connected to form a concentric structure. Furthermore, the idea of a hierarchical architecture of ESNs, where each ESN is connected to the preceding and following one, has attracted the reservoir computing community for its capability of discovering higher level features of the external signal [34]. Figure 2 schematically shows the architecture for (A) a single ESN, (B) 2 sub-reservoir hierarchical ESN for which the input is fed into only the first sub-reservoir which in turn feeds into the second and (C) a parallel ESN, where two unconnected sub-reservoirs receive the same input. These hierarchical ESNs are identical to the 2 layer DeepESN given by [27]. A general ensemble of interacting ESNs can be described by
where the parameters have the similar definitions as in the case of a single ESN in Eq. 1. The index k indicates the network number and
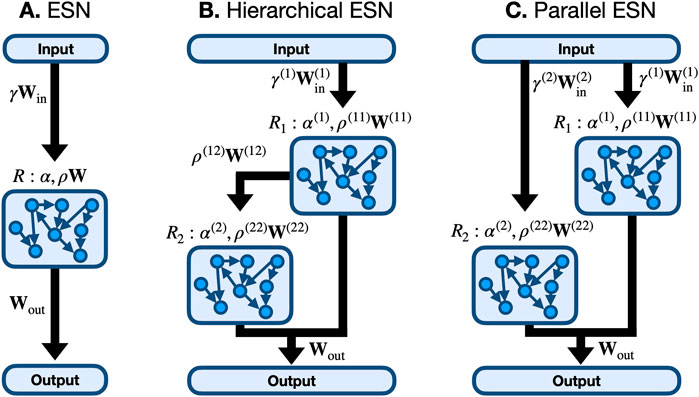
FIGURE 2. Single and hierarchical echo-state network (ESN) architectures. (A): A single ESN with internally connected nodes with a single set of hyper-parameters α and ρ. (B): A hierarchical ESN composed of 2 connected reservoirs where the input is fed into reservoir one only and the connection is unidirectional from R1 to R2, which is identical to the 2 layer DeepESN of [27]. (C): A parallel (or unconnected hierarchical) ESN where the network is partitioned into 2 reservoirs, R1 and R2, which each receive the input and provide output but have distinct hyper-parameters.
In Figure 1E we show examples of the timescale distributions of the corresponding linearised dynamical systems for different ESN structures, from the simple delay line model to the higher complexity exhibited from two hierarchical ESNs. In order from left to right, the histograms of timescales are for a delay line, a single ESN, and two ESNs (whether hierarchically connected or unconnected; see below for clarification). All the models share an ESN with
Yet, the spectrum of the eigenvalues of the linearised system is only partially informative of the functioning and capabilities of an ESN. This is clearly demonstrated by the fact that a hierarchical and a parallel ESN share the same spectrum in the linear regime. Indeed, for a hierarchical ESN, whose connectivity matrix of the linearised dynamics is given by:
it is easy to demonstrate that every eigenvalue of
It is interesting to note, in this respect, that the success of the hierarchical ESN is generally achieved when the leakage term of the first reservoir is higher than the leakage term of the second (or, in other words, when the first network has much shorter timescales). Such observation opens the way to an alternative route to understand the functioning of the hierarchical structure, as the first reservoir expanding the dimensionality of the input and then feeding the enriched signal into the second network. Indeed, in the following, we will show how, in a crude approximation and under the above condition of a wide separation of timescales, the first ESN extracts information on the short term behavior of the input signal, notably its derivatives, and the second ESN integrates such information over longer times.
We begin with the (continuous time) linearized dynamics of a Hierarchical ESN given by
where, for simplicity, we have reabsorbed the
The neuron activity can be projected on to the left eigenvector of each of the
where
where
By applying this approximation to Eq. 18, and by defining the diagonal matrix of characteristic times
The coefficients of this series are equivalent to taking successive time derivatives in Fourier space, such that
which can be inserted into Eq. 17 to give
Thus the second ESN integrates the signal with a linear combination of its derivatives. In other words, the first reservoir expands the dimensionality of the signal to include information regarding the signal’s derivatives (or, equivalently in discretized time, the previous values assumed by the signal). In this respect, Eq. 23 is key to understanding how the hierarchical connectivity between the two reservoirs enhances the representational capabilities of the system. The finite-difference approximation of the time derivatives appearing in Eq. 23 implies that a combination of past values of the signal appears, going back in time as much as the retained derivative order dictates.
2.2 Online Learning of Hyper-Parameter
Selecting the hyper-parameters of such systems can be challenging. Such selection process can be informed by the knowledge of the natural timescales of the task/signal at hand. Alternatively one can resort to a learning method to optimise the parameters directly. The inherent limitation of these methods is the same as learning the network weights with BPTT: the whole history of network activations is required at once. One way to by-pass this issue is to approximate the error signal by considering only past and same-time contributions, as suggested by Bellec et al. [4] in their framework known as e-prop (see also [36]), and derive from this approximation an online learning rule for the ESN hyper-parameters. Following their approach, we end up with a novel learning rule for the leakage terms of connected ESNs that is similar to the rule proposed by Jaeger et al. [32] but extended to two hierarchical reservoirs. The main learning rule is given by:
where
where
where
3 Results
The following sections are dedicated to the study of the role of timescales and the particular choices of α and ρ in various tasks, with attention on networks composed by a single ESN, 2 unconnected ESNs and 2 hierarchical ESNs. The number of trainable parameters in each task for the different models will be preserved by using the same total number of neurons in each model. The results analyzed will be consequently interpreted through the analysis of timescales of the linearised systems.
3.1 NARMA10
A common test signal for reservoir computing systems is the non-linear auto-regressive moving average sequence computed with a 10 step time delay (NARMA10) [37, 38]. Here we adopt a discrete time formalism where
where
The task of reconstructing the output of the NARMA10 sequence can be challenging for a reservoir as it requires both a memory (and average) over the previous 10 steps and fast variation with the current input values to produce the desired output. A typical input and output signal is shown in Figure 3A and the corresponding auto-correlation function of the input and output in B. Since the input is a random sequence it does not exhibit any interesting features but for the output the auto-correlation shows a clear peak at a delay of 9
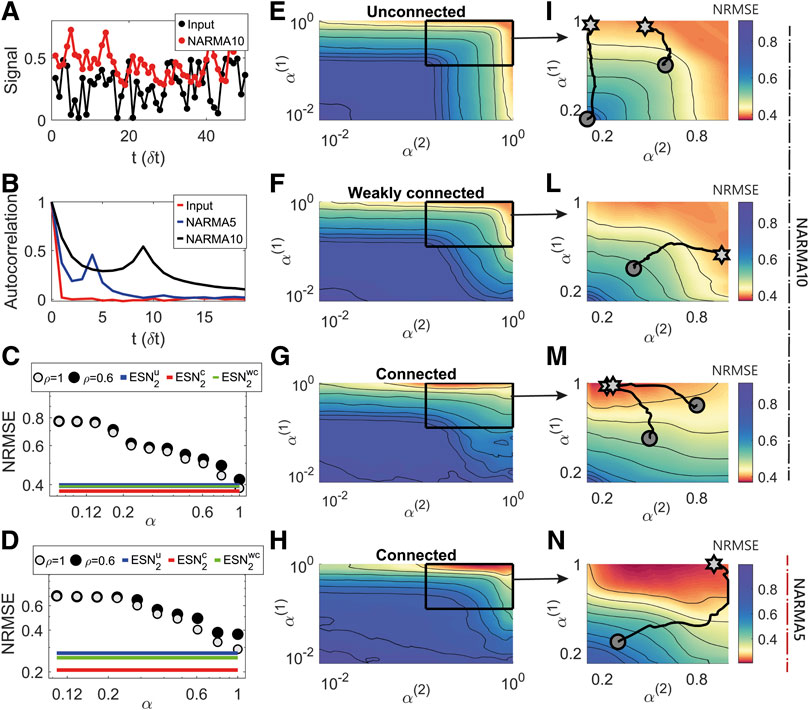
FIGURE 3. Performance of single or hierarchical ESNs on the NARMA10 and NARMA5 task. (A): Example input signal (black) and desired output (red) for the NARMA10 task. (B): The auto-correlation function of the (black) input (red) NARMA10 and (blue) NARMA5 desired output signals, showing a second peak at about 9 delay steps for the NARMA10 and 4 for the NARMA5. (C): The NRMSE for a single ESN for with
This regression task is solved by training a set of linear output weights to minimise the mean squared error (MSE) of the network output and true output. The predicted output is computed using linear output weights on the concatenated network activity
where
where
where
To test the effectiveness of including multiple time-scales in ESNs, we simulate first a single ESN with

TABLE 1. Table of the hyper-parameters adopted in the online learning process. η is the learning rate in each case, while
Figures 3E–G and I–M show the NRMSE depending on
Figure 3C shows the relative performance of the single ESN to the minimum values for the unconnected (
To further investigate the effect of the inherent timescale of the task on the timescales we performed a similar analysis on the NARMA5 task. Figures 3H,L show the NRMSE surface for the strongly connected case. The minimum error occurs at
In this theoretical task where the desired output is designed a priori, the memory required and the consequent range of timescales necessary to solve the task are known. Consequently, considering the mathematical analysis in Section 2.1, and that for hierarchical ESNs the timescales of the first ESN should be faster than those of the second Figure 3), the best-performing values of the leakage terms can be set a priori without the computationally expensive grid search reported in Figures 3E–L. However, it can be difficult to guess the leakage terms in the more complex cases where the autocorrelation structure of the signal is only partially informative of the timescales required.
This problem can be solved using the online learning approach defined through Eq. 24. In this case, learning is accomplished through minibatches and the error function can be written explicitly as
where
3.2 A Volatile Environment
We now turn to study the reservoir performance on a task of a telegraph process in a simulated noisy environment. The telegraph process
The transition probabilities of the second signal are fixed and symmetric such that
The probabilities
The input signal corresponds to
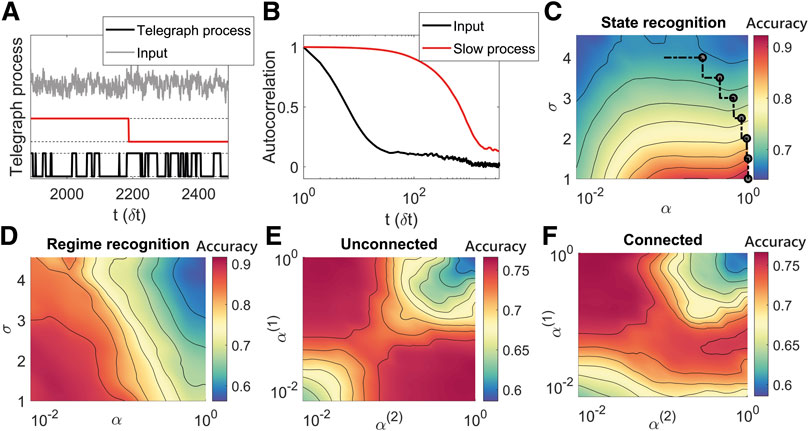
FIGURE 4. The best structure and parameters of the model depend on the specific environment considered, that is different values of the additive noise in the input signal, and on the specific desired output. (A): Example of input signal and of its generative processes, which have a faster and a slower dynamic respectively. When the slower process (red line) is up (down), the other signal is in a regime where the average time in the zero (one) state is greater than the average time spent in the other state. The input signal (gray line) corresponds to the faster process (black line) with additional white noise. (B): Auto-correlation structure of the two generative processes. (C): The accuracy surface for a single ESN on the state recognition sub-task for varying level of noise (σ) and leakage rate of the network showing that for increasing levels of noise a lower leakage rate is needed to determine the state. The line shows the trajectory of α using the online learning method when the strength of the noise is changed. (D): The accuracy for a single ESN on the regime recognition sub-task for varying noise and leakage rate. In this case the low leakage rate is preferred for all values of noise. (E): Accuracy surface for the state recognition sub-task for an unconnected hierarchical ESN showing how either of the leakage rates must be low while the other is high. (F): Accuracy surface for the regime recognition sub-task for a hierarchical ESN showing the first reservoir must have a high leakage rate and the second a low leakage rate.
Panels C and D of Figure 4 show the performance of a single ESN when it is tasked to reconstruct the processes
Finally, panels E and F of Figure 4 show the accuracy of two unconnected (E) and connected (F) reservoirs when the network has to classify the state and the regime of the input signal at the same time. In this case, the desired output corresponds to a four dimensional signal that encodes all the possible combinations of states and regimes; for instance, when the signal is in the state one and in the regime one, we would require the first dimension of the output to be equal to one and all other dimensions to be equal to zero, and so on. The best performance occurs when one leakage term is high and the other one is low and in the range of significant delays of the auto-correlation function. This corresponds to one network solving the regime recognition and the other network solving the state recognition. For the unconnected reservoirs, it does not matter which reservoir has high vs. low leakage terms, reflected by the symmetry of Figure 4E, while for the connected reservoirs, the best performance occurs when the first reservoir has the high leakage term and the second the low leakage terms, see Figure 4F, similar to Figure 3. Both two-reservoir networks can achieve accuracy 0.75, but the single ESN can not solve the task efficiently, since it cannot simultaneously satisfy the need for high and low αs, reporting a maximum performance of about 0.64.
The path reported in panel C of Figure 4 and all panels in Figure 5 show the application of the online training algorithm in this environment. The values of the hyper-parameters adopted in the optimisation process through the Adam optimiser are the same as in Section 3.1, where we used a slower learning rate and a higher first momentum on the leakage terms in comparison to the values adopted for the output weights. The line of panel C (Figure 4) shows the online adaptation of α for a simulation where the external noise increases from one to four with six constant steps of 0.5 equally spaced across the computational time of the simulation. The result shows how the timescales of the network decrease for each increase in σ, depicted with a circle along the black line. The path of online adaptation reports a decrease of the α value for noisier external signals. This result occurs because as the signal becomes noisier (σ rises), it becomes more important to dampen signal fluctuations. This result also shows that the online algorithm can adapt in environments with varying signal to noise ratio. Figure 5 shows the online training of
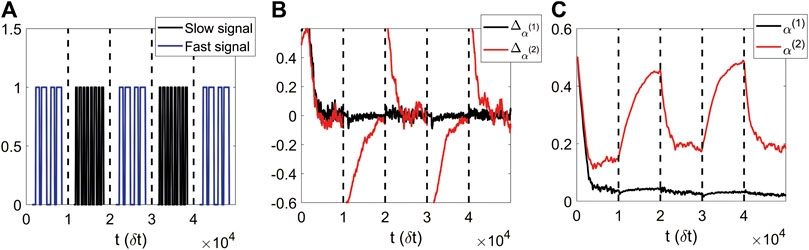
FIGURE 5. The online training of the leakage terms can adapt to the changing environment, that is the signal probabilities are increased or decreased periodically. (A): Scheme of the change of the values of probabilities, where high probabilities of switching are referred to as fast phase of the telegraph process, while low probabilities as slow phase. (B): Running average of the gradients of
3.3 Permuted Sequential MNIST
The Permuted Sequential MNIST (psMNIST) task is considered a standard benchmark for studying the ability of recurrent neural networks to understand long temporal dependencies. The task is based on the MNIST dataset, which is composed of
where m is the minibatch index,
where sigm stands for sigmoid activation function. We then repeat the simulation for two different time frames of sampling for each different model, that is a single ESN and a pair of unconnected or connected ESNs, as in the previous sections.
The two values of M used are 28 and 196, corresponding to a sampling of 28 and 4 previous representations of the network respectively. Of course, a higher value of M corresponds to a more challenging task, since the network has to exploit more its dynamic to infer temporal dependencies. We note, however, that none of the representation expansions used can guarantee a good understanding of the temporal dependencies of the task, or in other words, can guarantee that the system would be able to discover higher order features of the image, considering that these features depend on events that could be distant in time.
In Figure 6 we again analyze the performance of two connected or unconnected ESNs varying
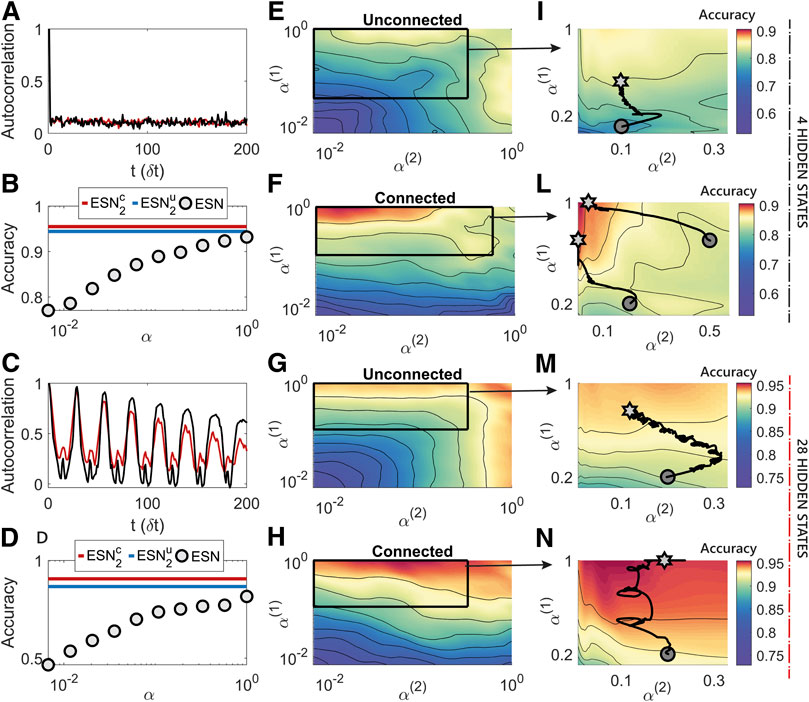
FIGURE 6. The additional non linearity added by the hierarchical reservoir structure is responsible for a relevant modification and increase of the performance surface. (A,C): Auto-correlation structure of the MNIST dataset for two examples of digits, where each pixel is presented one after the other (C), and auto-correlation structure of the data after the random permutation (A). The oscillatory trend in C reflects the form of the written digits, when this is seen one pixel after the other. The auto-correlation function of the permuted data is low, but not negligible, for all the temporal steps, showing the necessity to have a wide repertoire of timescales in the interval corresponding to the image size. (B,D): Accuracy of a single ESN for various α values compared the maximum accuracy of the hierarchical ESNs with 4 hidden states (B) or 28 hidden states (D). (E–F): case with low sampling frequency of the ESNs which corresponds to a higher demand of internal memory in the reservoir. While the best region of accuracy for the unconnected reservoirs is characterised by intermediate values of the leakage factors, the hierarchically connected network structure reports the best performance when the second network has slower dynamics. (G–H): The utilisation of a high sampling frequency alleviates the need for long term memory, and the reservoirs prefer the regions with fast timescales. In both cases analyzed, the additional complexity of the hierarchical model leads to a considerable boost in performance. (I–N): Paths (black line, starting from the circle and ending in the star) that describe the online changes of the leakage terms achieved through the online training algorithm in a zoomed region of the performance surface of
As in the other simulations, we found that the values of ρ corresponding to the best performance was approximately one, which maximises the range of timescales and the memory available in the network. Figures 6E,F shows the case with
This relatively simple behavior of the dependence of the accuracy on the setting of the hyper-parameters changes in the cases of two connected ESNs, whose additional complexity corresponds to a considerable increase in the performance. Figure 6H reports how the network prefers a regime with a fast timescale in the first reservoir and a intermediate timescale in the second, which acts as an additional non-linear temporal filter of the input provided by the first network. The need of memory of events distant in time is emphasised in 6F, where the best performing network is composed by reservoirs with fast and slow dynamics respectively. The performance boost from the panels E–G to the ones F-H has only two possible explanations: first, the timescales of the second network are increased naturally thanks to the input from the first reservoir; second, the connections between the two reservoirs provide an additional non-linear filter of the input that can be exploited to discover higher level features of the signal. Thus, we can conclude once again that achieving high performance in applying reservoir models requires 1) additional non-linearity introduced through the interconnections among the reservoirs and 2) an appropriate choice of timescales, reflecting the task requirements in terms of external signal and memory.
Panels I, L, M and N show the application of the online training of αs for the various cases analyzed. In the psMNIST task we found that the major difficulties in the application of an iterative learning rule on the leakage terms are: the possibility to get trapped in local minima, whose abundance can be caused by the intrinsic complexity of the task, the intrinsic noise of the dataset, the randomness of the reservoir and of the applied permutation; the high computational time of a simulation that exploits an iterative optimisation process on
Finally, we note how the best accuracy of 0.96 reached throughout all the experiments on the psMNIST is comparable to the results obtained by recurrent neural networks trained with BPTT, whose performance on this task are analyzed in [42] and can vary from 0.88 to 0.95. In comparison to recurrent structures trained through BPTT, a network with two interacting ESNs provide a cheap and easily trainable model. However, this comparison is limited by the necessity of recurrent neural networks to carry the information from the beginning to the end of the sequence, and to use the last temporal state only or to adopt attention mechanisms.
4 Conclusion
In summary, ESNs are a powerful tool for processing temporal data, since they contain internal memory and time-scales that can be adjusted via network hyper-parameters. Here we have highlighted that multiple internal time-scales can be accessed by adopting a split network architecture with differing hyper-parameters. We have explored the performance of this architecture on three different tasks: NARMA10, a benchmark composed by a fast-slow telegraph process and PSMNIST. In each task, since multiple timescales are present the hierarchical ESN performs better than a single ESN when the two reservoirs have separate slow and fast timescales. We have demonstrated how choosing the optimal leakage terms of a reservoir can be aided by the theoretical analysis in the linear regime of the network, and by studying the auto-correlation structure of the input and/or desired output and the memory required to solve the task. The theoretical analysis developed needs to be considered as a guide for the tuning of the reservoir hyper-parameters, and in some specific applications it could be insufficient because of the lack of information about the nature of the task. In this regard, we showed how to apply a data-driven online learning method to optimise the timescales of reservoirs with different structures, demonstrating its ability to find the operating regimes of the network that correspond to high performance and to the best, task-dependent, choice of timescales. The necessity of adopting different leakage factors is emphasised in the case of interactive reservoirs, whose additional complexity leads to better performance in all cases analyzed. Indeed, the second reservoir, which acts as an additional non linear filter with respect to the input, is the perfect candidate to discover higher temporal features of the signal, and it consequently prefers to adopt longer timescales in comparison to the first reservoir, which has instead the role of efficiently representing the input. We believe such hierarchical architectures will be useful for addressing complex temporal problems and there is also potential to further optimise the connectivity between the component reservoirs by appropriate adaptation of the online learning framework presented here.
Data Availability Statement
Publicly available datasets were analyzed in this study. This data can be found here: http://yann.lecun.com/exdb/mnist/. The code for this study is available from: https://github.com/LucaManneschi/EchoStatesNetwork.
Author Contributions
All the authors contributed to the paper conceptually and to the writing of the article. EV proposed the original concept of the paper. LM, ME, GG, PD, EV contributed to the design of the case studies and to the analysis of the results. LM and ME designed and performed the simulations.
Funding
EV and AL acknowledge the support from a Google Deepmind Award. EV and ME were funded by the Engineering and Physical Sciences Research Council (Grant No. EP/S009647/1). EV was also supported by EPSRC (Grant Nos. EP/S030964/1 and EP/P006094/1). PD and GG were supported by the European Union Horizon 2020 Research and Innovation program under the FET Flagship Human Brain Project (SGA2 Grant agreement No. 785907 and SGA3 Grant agreement No. 945539). AL was supported by the European Research Council (639489) and the Biotechnology and Biological Sciences Research Council (BB/S016031/1).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fams.2020.616658/full#supplementary-material.
References
1. Ludik, J, Prins, W, Meert, K, and Catfolis, T. A comparative study of fully and partially recurrent networks. Proc Int Conf Neural Netw (1997). 1(ICNN’97):292–7. doi:10.1109/ICNN.1997.611681
2. Rumelhart, DE, Hinton, GE, and Williams, RJ. Technical Report. Learning internal representations by error propagation. California Univ San Diego La Jolla Inst for Cognitive Science (1985).
3. Werbos, PJ. Backpropagation through time: what it does and how to do it. Proc IEEE (1990). 78:1550–60. doi:10.1109/5.58337
4. Bellec, G, Scherr, F, Subramoney, A, Hajek, E, Salaj, D, Legenstein, R, et al. A solution to the learning dilemma for recurrent networks of spiking neurons. Nat Commun (2020). 11:3625. doi:10.1038/s41467-020-17236-y
5. Marr, D. A theory of cerebellar cortex. J Physiol (1969). 202:437–70. doi:10.1113/jphysiol.1969.sp008820
6. Farris, SM. Are mushroom bodies cerebellum-like structures? Arthropod Struct Dev (2011). 40:368–79. doi:10.1016/j.asd.2011.02.004
7. Laurent, G. Olfactory network dynamics and the coding of multidimensional signals. Nat Rev Neurosci (2002). 3:884–95. doi:10.1038/nrn964
8. Warren, R, and Sawtell, NB. A comparative approach to cerebellar function: insights from electrosensory systems. Curr Opin Neurobiol (2016). 41:31–7. doi:10.1016/j.conb.2016.07.012
9. Takemura, SY, Aso, Y, Hige, T, Wong, A, Lu, Z, Xu, CS, et al. A connectome of a learning and memory center in the adult Drosophila brain. eLife (2017). 6:5643. doi:10.7554/eLife.26975
10. Zheng, Z, Lauritzen, JS, Perlman, E, Robinson, CG, Nichols, M, Milkie, D, et al. A complete electron microscopy volume of the brain of adult Drosophila melanogaster. Cell (2018). 174:730–43. doi:10.1016/j.cell.2018.06.019
11. Liu, Q, Yang, X, Tian, J, Gao, Z, Wang, M, Li, Y, et al. Gap junction networks in mushroom bodies participate in visual learning and memory in Drosophila. eLife (2016). 5:e13238. doi:10.7554/eLife.13238
12. Shang, Y, Claridge-Chang, A, Sjulson, L, Pypaert, M, and Miesenböck, G. Excitatory local circuits and their implications for olfactory processing in the fly antennal lobe. Cell (2007). 128:601–12. doi:10.1016/j.cell.2006.12.034
13. Olsen, SR, and Wilson, RI. Lateral presynaptic inhibition mediates gain control in an olfactory circuit. Nature (2008). 452:956–60. doi:10.1038/nature06864
14. Yeshurun, Y, Nguyen, M, and Hasson, U. Amplification of local changes along the timescale processing hierarchy. Proc Natl Acad Sci U S A (2017). 114:9475–80. doi:10.1073/pnas.1701652114
15. Jaeger, H. The “echo state” approach to analysing and training recurrent neural networks-with an erratum note. Bonn, Germany: German National Research Center for Information Technology GMD Technical Report (2001). 148:13.
16. Deng, Z, and Zhang, Y. Collective behavior of a small-world recurrent neural system with scale-free distribution. IEEE Trans Neural Netw (2007). 18:1364–75. doi:10.1109/tnn.2007.894082
17. Rodan, A, and Tino, P. Minimum complexity echo state network. IEEE Trans Neural Netw (2010). 22:131–44. doi:10.1109/TNN.2010.2089641
18. Bacciu, D, and Bongiorno, A. Concentric esn: assessing the effect of modularity in cycle reservoirs. In: 2018 International Joint Conference on Neural Networks (IJCNN); 2018 July 8–13; Rio, Brazil (IEEE) (2018), 1–8.
19. Farkaš, I, Bosák, R, and GergeĬ, P. Computational analysis of memory capacity in echo state networks. Neural Netw (2016). 83:109–20. doi:10.1016/j.neunet.2016.07.012
20. Marzen, S. Difference between memory and prediction in linear recurrent networks. Phys Rev E (2017). 96:032308. doi:10.1103/PhysRevE.96.032308
21. Livi, L, Bianchi, FM, and Alippi, C. Determination of the edge of criticality in echo state networks through Fisher information maximization. IEEE Trans Neural Netw Learn Syst (2018). 29:706–17. doi:10.1109/TNNLS.2016.2644268
22. Xue, Y, Yang, L, and Haykin, S. Decoupled echo state networks with lateral inhibition. Neural Netw (2007). 20:365–76. doi:10.1016/j.neunet.2007.04.014
23. Jaeger, H. Technical Report. Discovering multiscale dynamical features with hierarchical echo state networks. Bremen, Germany: Jacobs University Bremen (2007).
24. Gallicchio, C, Micheli, A, and Pedrelli, L. Deep echo state networks for diagnosis of Parkinson’s disease (2018a). arXiv preprint. Available from: https://arxiv.org/abs/1802.06708 (Accessed February 19, 2018).
25. Malik, ZK, Hussain, A, and Wu, QJ. Multilayered echo state machine: a novel architecture and algorithm. IEEE Trans Cybernetics (2016). 47:946–59. doi:10.1109/TCYB.2016.2533545
26. Gallicchio, C, and Micheli, A. Echo state property of deep reservoir computing networks. Cogn Comp (2017). 9:337–50. 10.1007/s12559-017-9461-9
27. Gallicchio, C, Micheli, A, and Pedrelli, L. Design of deep echo state networks. Neural Netw (2018b). 108:33–47. doi:10.1016/j.neunet.2018.08.002
28. Ma, Q, Shen, L, and Cottrell, GW. Deepr-esn: a deep projection-encoding echo-state network. Inf Sci (2020). 511:152–71. doi:10.1016/j.ins.2019.09.049
29. Rodriguez, N, Izquierdo, E, and Ahn, YY. Optimal modularity and memory capacity of neural reservoirs. Netw Neurosci (2019). 3:551–66. doi:10.1162/netn_a_00082
30. Szita, I, Gyenes, V, and Lőrincz, A. Reinforcement learning with echo state networks. In: International Conference on Artificial Neural Networks; December 5–8, 2006; Athens, Greece (Springer) (2006). 830–9.
31. Hermans, M, and Schrauwen, B. Recurrent kernel machines: computing with infinite echo state networks. Neural Comput (2012). 24:104–33. doi:10.1162/NECO_a_00200
32. Jaeger, H, Lukoševičius, M, Popovici, D, and Siewert, U. Optimization and applications of echo state networks with leaky-integrator neurons. Neural Netw (2007). 20:335–52. doi:10.1016/j.neunet.2007.04.016
34. Gallicchio, C, Micheli, A, and Pedrelli, L. Deep reservoir computing: a critical experimental analysis. Neurocomputing (2017). 268:87–99. doi:10.1016/j.neucom.2016.12.089
35. Sun, X, Li, T, Li, Q, Huang, Y, and Li, Y. Deep belief echo-state network and its application to time series prediction. Knowl Based Syst (2017). 130:17–29. doi:10.1016/j.knosys.2017.05.022
36. Manneschi, L, and Vasilaki, E. An alternative to backpropagation through time. Nat Mach Intell (2020). 2:155–6. doi:10.1002/mp.14033
37. Atiya, AF, and Parlos, AG. New results on recurrent network training: unifying the algorithms and accelerating convergence. IEEE Trans Neural Networks (2000). 11:697–709. doi:10.1109/72.846741
38. Goudarzi, A, Banda, P, Lakin, MR, Teuscher, C, and Stefanovic, D. A comparative study of reservoir computing for temporal signal processing (2014). arXiv preprint. Available from: https://arxiv.org/abs/1401.2224 (Accessed January 10, 2014).
39. Lukoševičius, M, and Jaeger, H. Reservoir computing approaches to recurrent neural network training. Computer Science Review (2009). 3:127–49. doi:10.1016/j.cosrev.2009.03.005
40. Schaetti, N, Salomon, M, and Couturier, R. Echo state networks-based reservoir computing for mnist handwritten digits recognition. In: 2016 IEEE Intl Conference on Computational Science and Engineering (CSE) and IEEE Intl Conference on Embedded and Ubiquitous Computing (EUC) and 15th Intl Symposium on Distributed Computing and Applications for Business Engineering (DCABES); 2016 August 24–26; Paris, France (IEEE) (2016). 484–91.
41. Manneschi, L, Lin, AC, and Vasilaki, E. Sparce: sparse reservoir computing (2019). arXiv preprint. Available at: https://arxiv.org/abs/1912.08124 (Accessed December 4, 2019).
Keywords: reservoir computing (RC), echo state network (ESN), timescales, hyperparameter adaptation, backpropagation through time
Citation: Manneschi L, Ellis MOA, Gigante G, Lin AC, Del Giudice P and Vasilaki E (2021) Exploiting Multiple Timescales in Hierarchical Echo State Networks. Front. Appl. Math. Stat. 6:616658. doi: 10.3389/fams.2020.616658
Received: 12 October 2020; Accepted: 29 December 2020;
Published: 17 February 2021.
Edited by:
Andre Gruning, University of Surrey, United KingdomReviewed by:
Petia D. Koprinkova-Hristova, Institute of Information and Communication Technologies (BAS), BulgariaIgor Farkaš, Comenius University, Slovakia
Copyright © 2021 Manneschi, Ellis, Gigante, Lin, Del Giudice and Vasilaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Eleni Vasilaki, ZS52YXNpbGFraUBzaGVmZmllbGQuYWMudWs=
†These authors share senior authorship
 Luca Manneschi
Luca Manneschi Matthew O. A. Ellis
Matthew O. A. Ellis Guido Gigante
Guido Gigante Andrew C. Lin
Andrew C. Lin Paolo Del Giudice
Paolo Del Giudice Eleni Vasilaki
Eleni Vasilaki