PoV: An Efficient Voting-Based Consensus Algorithm for Consortium Blockchains

Introduction

Information on the Internet is transparent and untrustworthy that hackers can tamper with its authenticity. Therefore, traditional Internet transaction data requires a third-party trusted organization to vouch for its correctness (Khalil and Gervais, 2017). The security risk of online trading is that once the third-party platform collapses, the guarantee of trust it provides becomes invalid. Based on cryptography instead of trust, the blockchain is an essential technology for reliably transmitting and securely storing transaction data. It enables any mutually agreed parties to generate transactions directly without the involvement of third-party intermediaries. Furthermore, there is almost no single point of failure in the blockchain system. Various machine nodes around the world collaborate to store data on the blockchain, making it “Stable,” “Trustworthy,” and “Immutable.” These features endow the information on the Internet with a trusted value. Therefore, the blockchain is considered as the most promising technology to drive the transition from “Information Internet” to “Value Internet.”

The blockchain originates from a unique way to store data in the system of cryptocurrencies such as Bitcoin (Dinh et al., 2018). It can hold all historical data, transaction records, and other related information in the past by using a self-referencing blockchain data storage structure. A significant amount of data is stored in a Peer-to-Peer distributed network (Puthal et al., 2018) and is encapsulated into a series of data blocks using cryptography. Each data block contains the essential identification information (Hash) of the previous block in the chain structure so that all the blocks are linked chronologically to become a globally distributed log record (Bhattacharya et al., 2018). If hackers want to tamper with a particular piece of data in a block, they need to recalculate the block and all subsequent block information. One of the blockchain’s critical technologies is the consensus algorithm that makes tampering with data almost impossible for attackers in computational difficulty. Combining distributed storage, cryptography, consensus algorithm and peer-to-peer transmission (Kiyomoto et al., 2017), the blockchain technology forms spontaneous self-development in the decentralized environment.

Generally, the blockchain is divided into three types: public, private and consortium blockchain (Buterin, 2015). The public blockchain suffers from various restrictions in different countries because of its transparency, untraceable traits and weak controllability. As a compromise between the private and the public blockchain, the consortium blockchain has the advantage of realizing “partial decentralization” between some existing institutions, making the consortium of them efficient and fair. From the fact that numerous international financial giants have participated in the R3 CEV blockchain project (Khan et al., 2017), financial institutions seem to be inclined to the application scenarios of the consortium blockchains.

From the perspective of management, the introduction of the consortium blockchain is a massive innovation for the multi-party cooperation model. Its disintermediation nature makes it no longer require a powerful organization to coordinate members. The consortium has functions of information sharing and data clearing by maintaining a distributed shared ledger and realizes a system that can be jointly managed by multiple parties. On the other hand, from the perspective of performance efficiency, the consortium blockchain enables the members to provide external services, respectively, with no need for third-party trusted organizations to act as service agents, thus avoiding single-point attacks. At the same time, the absence of third-party intermediary agents dramatically reduces the system’s operating cost. Specifically, it reduces the overhead of forwarding and integrating system messages technically and the fee of third-party intermediary services. Therefore, the research on consensus algorithms especially used in the consortium blockchain has become indispensable. The purpose of the consensus algorithms is to achieve two key features of the public ledger. The first is consistency, that is, after removing the k latest blocks of the blockchain (k is the security parameter of the blockchain), the blockchains of honest nodes can be prefixed by each other. The second is activity, that is, the transactions uploaded by the honest user, must appear in the ledger of all other honest nodes after a certain period of time (Liu et al., 2018).

Currently, consensus algorithms designed for the consortium blockchains are inefficient due to a considerable amount of time and energy consumed for block production and safety performance. Researchers have designed different consensus algorithms as the tradeoff to make consistency in distributed systems. The traditional Practical Byzantine Fault Tolerance (PBFT) (Castro and Liskov, 1999) achieves consistency through multi-phase commit and validation, but with high communication cost and poor scalability. Delegated Byzantine Fault Tolerance (dBFT) (Zhang, 2014) resolves the scalability problem but suffers from a maximum of 33% Byzantine representative nodes. The BA⋆ algorithm achieves lightweight execution by eliminating state sharing between steps and still tolerates up to 33% malicious computing power because of the characteristics of BFT algorithms. This paper proposes a consensus algorithm that makes clever use of the characteristics of the consortium blockchains. A final block is generated by the voting result, which optimizes transaction validation time and throughput of the system.

Our goal is to design a high-performance consensus algorithm with specific security capabilities for consortium blockchains – a voting-based consensus called proof of vote (PoV). We regard the core nodes, which monitor and verify the production of blocks by voting, as the logical central cluster of the entire network (the geographical locations of different consortium nodes could be around the world). To maintain independence, a professional team, which is elected by the core nodes, is responsible for packing blocks. The separation of voting rights and bookkeeping rights guarantees fairness within the consortium, which promotes the growth of the consortium. Our contributions are as follows:

(1) We propose a new type of consensus algorithm called PoV for the consortium blockchain, where the members of the consortium work together to make “decentralized” arbitration.

(2) Through the theoretical analysis of correctness and security, we prove that PoV can achieve eventual consistency and limited partition tolerance. With negligible energy consumption, it merely needs to make sure that more than half of the core nodes and at least one bookkeeping node stay credibly and hard-working so that PoV can function correctly.

(3) To evaluate the performance of the consensus algorithm, we implement PoV on the distributed system. We also compare the performance between PoV and BFT-SMART through the dynamic adjustment of network scales.

Related Work

The PoW consensus mechanism (Wright, 2008) is the most successful consensus mechanism in the Bitcoin blockchain. Participants accept the longest chain as the historical transaction data of the system and try to extend it to contribute to the longest chain. At the same time of great success, PoW also has some shortcomings. The most serious drawback is its limited throughput and long transaction validation time. Also, PoW has a “51% power attack,” when the attacker’s hash computing power exceeds 51%, it may lead to double payment and loss of security. GHOST (Sompolinsky and Zohar, 2013) uses blocks on the sidechain to achieve high transaction rates on the basis of Bitcoin. Bitcoin-NG (Eyal et al., 2016) adopts the trust model of Bitcoin and improves scalability by breaking down the consensus operation of Bitcoin into leadership election and transaction serialization. Specter (Sompolinsky et al., 2016) improves performance by using DAG instead of the chain structure and allows miners to generate blocks simultaneously. PoW-based consensus has disadvantages as intensive power consumption, no external utility, and easy to lead to centralization, which stimulates the development of a new kind of PoX consensus protocol. Based on PoS consensus, Ouroboros (Kiayias et al., 2017) randomly selects a subset of stakeholders as participants in an epoch. Snow-White (Bentov et al., 2016) uses the leader-election mechanism similar to PoS, where the target value is determined by the stake of each participant. PoS-based consensus is efficient, but at the expense of security (Wang et al., 2018). Intel PoET (Intel Corporation, 2018) uses the trusted enclave in Intel SGX, where participants request wait times and choose the chip with the shortest wait time as the leader. REM (Zhang et al., 2017) uses the SGX to generate a random number and look for a value less than the current difficulty.

In efficiency-driven blockchains with few nodes, BFT-based algorithms are also considered as consensus algorithms. The Hyperledger Fabric version 0.6 adopted PBFT, but due to the limitation of the communication complexity, it is no longer supported in version 1.0 and later. BFT-SMART (Bessani et al., 2014) is similar to PBFT, but with increased reliability and modularity, as well as flexible programming interfaces. However, these BFT-based consensus algorithms have an inherent problem of high traffic complexity of O(N²) that greatly limits the size of the system.

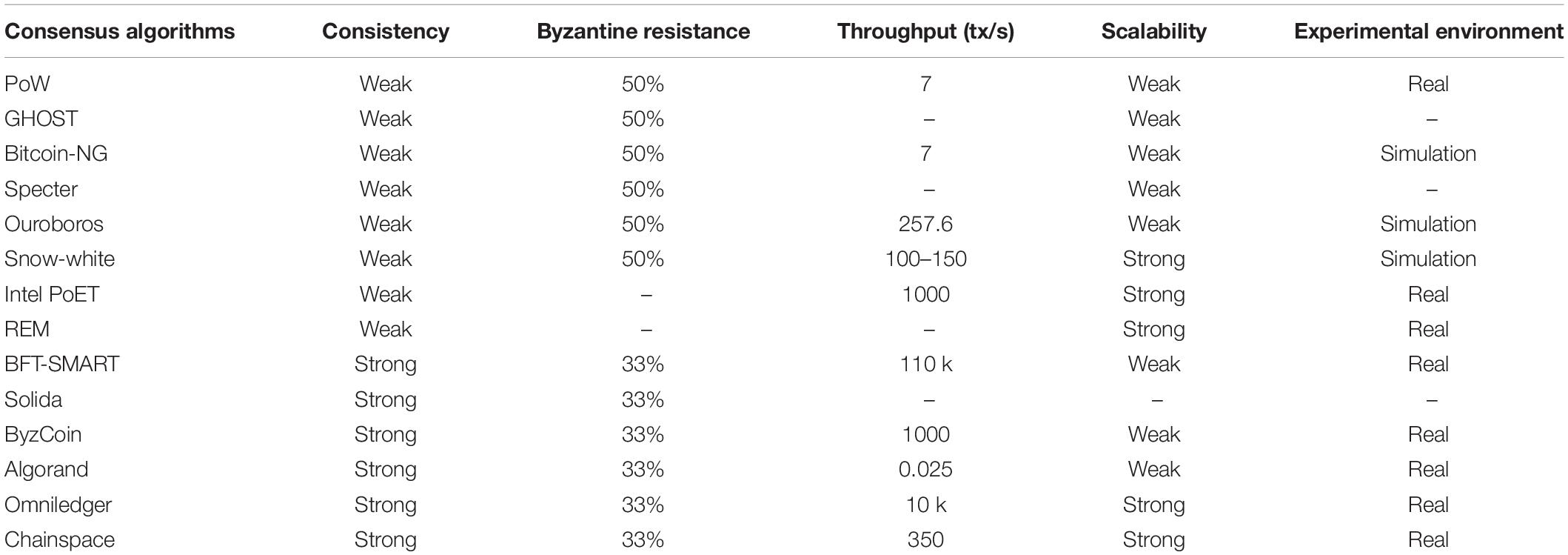
Single consensus protocols have disadvantages such as low performance, weak consistency, and poor fault tolerance. Inspired by Pass and Shi’s research (Pass and Shi, 2016), Ittai et al. adopted a hybrid consensus network model and proposed a blockchain protocol based on reconfigurable Byzantine consensus Solida (Abraham et al., 2018). In ByzCoin (Kogias et al., 2016), the committee is a dynamic window formed by recent miners, with each miner’s voting right proportional to the number of blocks it mines in the current window. Algorand (Gilad et al., 2017) uses encryption lottery to select committee members from candidates. Committee members further implement the BA^∗ consensus protocol and attach the necessary information to the message for other members to check their identity. Omniledger (Kokoris-Kogias et al., 2018) is composed of an identity blockchain and multiple shards. All verifiers are divided into different groups by RandHound protocol for verification and consensus. Chainspace (Al-Bassam et al., 2017) abstracts the details of reconfiguring the committee and uses smart contracts to determine the committee’s node allocation strategy. In Peercensus (Decker et al., 2016), consensus committee members agree on whether a node can be accessed over the network, which determines whether a node can join the committee. Comparative details are shown in Table 1. The proposed PoV is also based on the idea of mixed consensus. It optimizes the traffic complexity of single BFT-based consensus algorithms to O(3N_c) and achieves great scalability when the number of nodes is over 100.

TABLE 1

Table 1. Detailed comparison of blockchain consensus mechanisms.

Problem

Application Scenario

The consensus algorithm designed in this paper is oriented to the consortium blockchain scenario. The consortium blockchain usually runs between different institutions or organizations with secure connections. By eliminating the need for third-party management and intermediation costs, it can reduce the cost of communication and synchronization between organizations and increase the efficiency of business collaboration. The original intention of the consortium blockchain is to bring different organizations together to achieve the synergistic value of strong relevance and decentralization within the consortium, thus completing the “partial decentralization” of the consortium blockchain system (Treleaven et al., 2017). The consortium blockchain generally has strict identity licensing restrictions. More importantly, consortium members, as service providers in the system, jointly provide services to the outside world and need to have sufficient control over the data and operation. In the event of an abnormal situation, the consortium can initiate a regulatory mechanism through negotiation, and implement specific governance measures to track and punish the malicious attackers, or to make further compensation for the data damage caused to reduce losses.

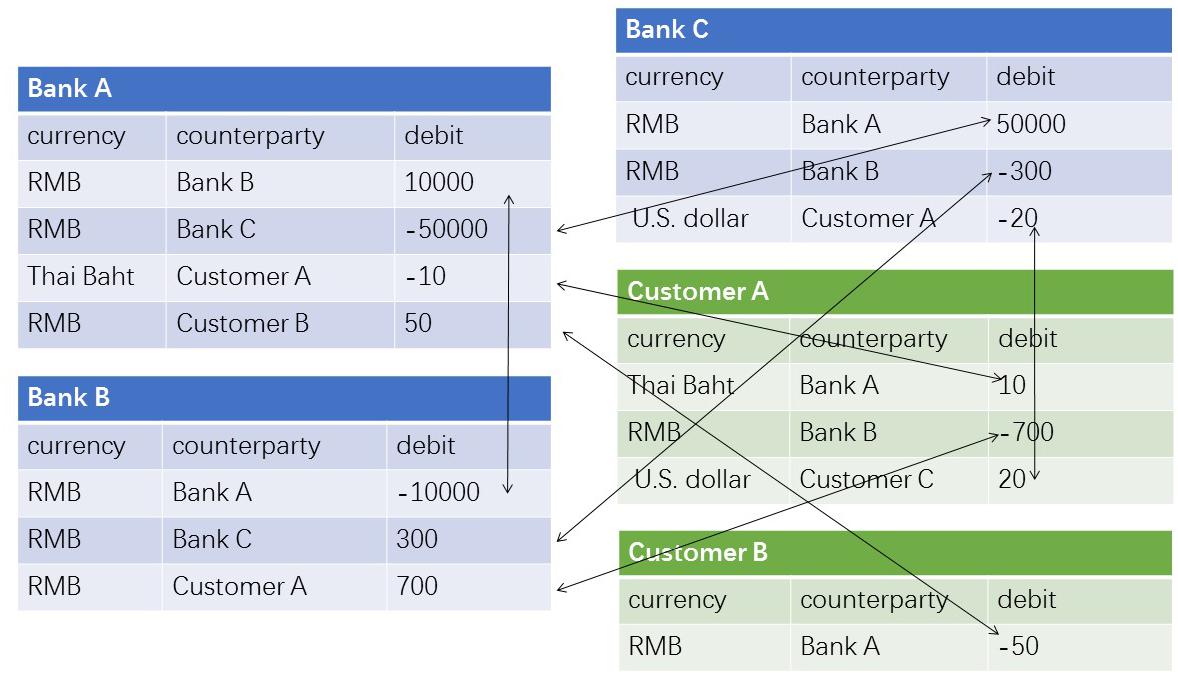
We describe the necessity of the consortium blockchain from a simple scenario, assuming that there are three banks (Bank A, Bank B, Bank C) and two customers (Customer A, Customer B) in the system. Figure 1 shows the traditional accounting methods: each bank has its account table. Different banking systems work differently, and the same transaction exists in two different tables. As a result, verification and liquidation of funds become complicated.

FIGURE 1

Figure 1. Traditional accounting method.

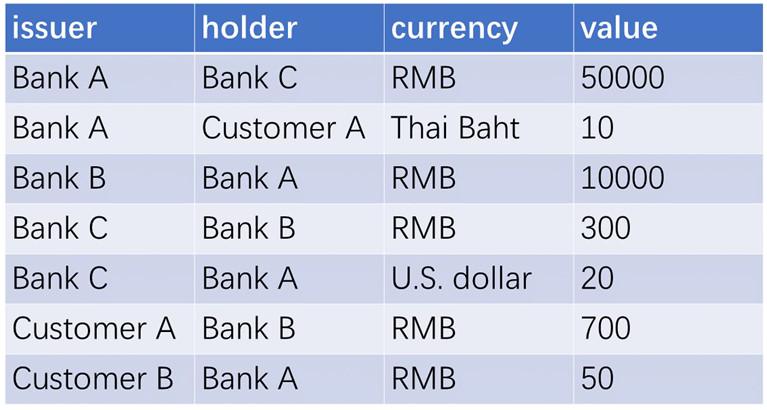
The blockchain technology can quickly solve the above problem by recording all the transactions in a super form with only one distributed ledger. As shown in Figure 2, every bank easily obtains their respective data from this super form. Then the problem is the ownership of the distributed ledger. This blockchain system is a typical consortium blockchain scenario. The banks are still the fund managers, and the customers enjoy the service of this system. In this case, “partially decentralized” means that the banks will form a coalition committee as the center of the entire system, which needs to realize the decentralization among the banks.

FIGURE 2

Figure 2. Distributed ledger of the blockchain.

Problem Definition

As a proposed consensus algorithm, PoV is expected to satisfy the following characteristics in the consortium blockchain:

(1) Consistency: The blockchain data copies in all nodes should be able to reach a final consistent state and offer a unified external service. PoV has consensus termination and only requires one block to realize the final validation and make transactions tamper-resistant.

(2) Availability: The consensus algorithm should make the services provided by the system consistently available. For each operation request, the system should respond within a limited time. PoV ensures that the operation of the consensus process can also produce blocks in limited time under proper parameter settings.

(3) Partition Tolerance: The distributed system should guarantee the provision of services when the system fails in any network partition. PoV can make a certain degree of partition tolerance with certain security assumptions.

(4) Efficient: The throughput expressed as the total number of transactions ∑|tx_h| processed per unit time, should be as large as possible.

Threat Model

In the case where a node may be attacked and become an adversary, we assume that attackers have controlled some (less than half) of the core consortium nodes. The system can tolerate less than 50% of the core nodes attacked. Adversaries may forge transactions or act like a normal one. The network may be partitioned. However, the adversary cannot crack and forge the signatures.

Security Assumptions

The PoV algorithm is based on the following assumptions:

Hypothesis 1: Assume time synchronization for all core member nodes. Since these core nodes are in the same consortium, the NTP (Network Time Protocol), which is a networking protocol for clock synchronization between computer systems over packet-switched, variable-latency data networks, can help to guarantee time synchronization above the millisecond level.

Hypothesis 2: Assume that all core member nodes are trusted and more than half of these core nodes work regularly. As a core node in the consortium blockchain, it will use an operating system and configuration with a higher security defense factor. Under normal circumstances, the core member will not attack the system separately. If so, the system will expel the lousy node. Moreover, the remaining core members repair the damage to the system, so all the core consortium nodes are considered credible. Each core member node may have an internal cluster of an enterprise. The internal consistency [may be achieved by Paxos (Gafni and Lamport, 2000)] of the cluster guarantees synchronization and provides uninterrupted external service. Therefore, it is unlikely that the core consortium nodes will fail to work. Even so, PoV can tolerate no more than half of the consortium nodes failing to work or partitioned, which will be analyzed later in the security analysis part.

Hypothesis 3: Assume that there is at least one bookkeeping node working honestly to satisfy the consistency of the algorithm. This assumption is entirely valid for the setting that the core member node can also serve as the bookkeeping node. We will analyze this in the final consistency analysis part.

Hypothesis 4: Assume that the system is partitioned, and at least one of the partitions still satisfies the above hypothesis 1–3.

Proof of Vote

In this section, we present a novel consensus algorithm called PoV. As we have mentioned in the application scenario part, banks can recruit a bookkeeping team in the network through voting. Ordinary nodes join the team spontaneously. Then they take turns randomly to write to the ledger, but each writing must be validated by most of the banks to ensure its security. According to Hypothesis 2, the bank nodes are trustworthy. As long as more than 50% of bank nodes work correctly, the system can produce the right result through the consensus process. This scenario can explain the basic idea of PoV.

Role Definition

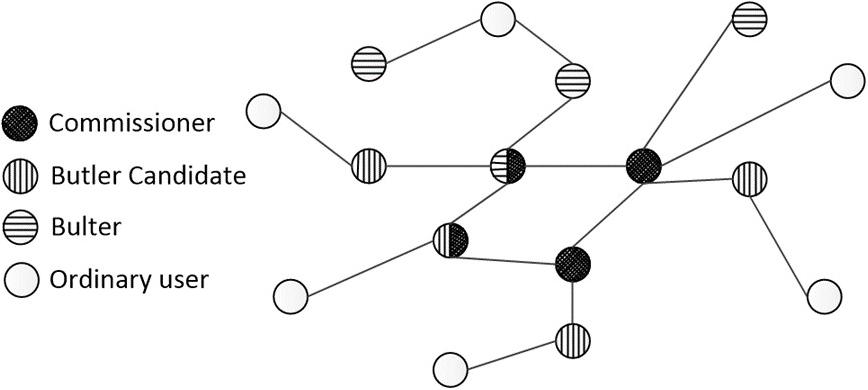
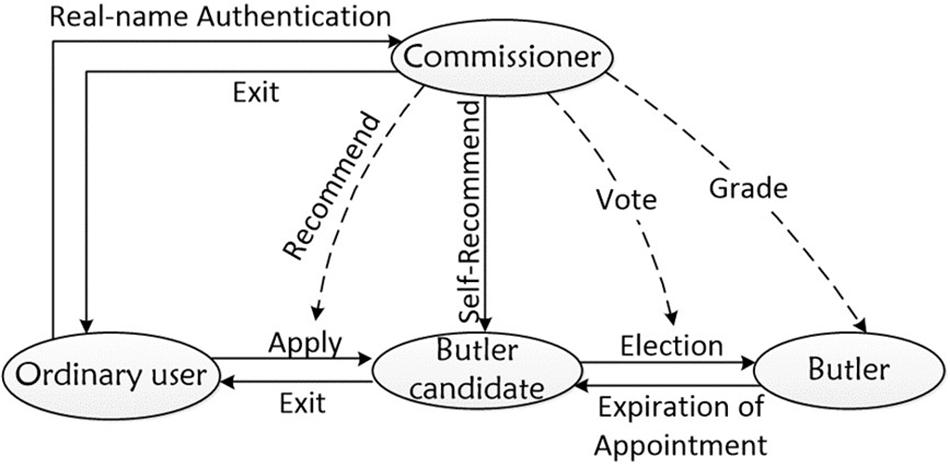
Figure 3 shows four roles in PoV: commissioner, butler, butler candidate, and ordinary user.

FIGURE 3

Figure 3. Four roles in the PoV network.

Commissioner

Several enterprises or institutions from different regions of the world form a consortium committee and maintain a consortium blockchain system together. A commissioner is one of the members of the consortium committee and may be assumed any other roles. In the consortium system, a new commissioner must be accepted by the proposed consortium law and represented by a node working in the consortium blockchain network. Commissioners have the right to recommend, vote for and evaluate the butlers. They are also obligated to verify and forward blocks and transactions. Different consortiums can set different voting rights according to the shares, which can be reflected in the proportion of the signature of the commissioners. In this paper, each commissioner has the same rights and obligations and is of equal standing. Blocks generated in the blockchain network will be broadcast to all commissioners for verification. When a block has majority votes, the block will be marked as valid and added to the blockchain. The result of voting represents the will of all commissioners.

Butler

Butlers specialize in producing blocks. The number of butler nodes is limited. We design the butler role to separate the voting and bookkeeping right. Commissioners are in charge of voting and butlers are responsible for producing blocks, namely, bookkeeping. Butlers are like the miners in the Bitcoin, but they do not need to waste computing power to snatch the right of producing blocks, and they are randomly appointed to produce a block by the consensus rule. A butler should gather transactions from the network, pack them into a block, and sign it. Becoming a butler takes two steps:

(1) Register as a butler candidate.

(2) Win an election for the butler.

The commissioners vote for butler candidates to elect the butler team. The butlers take turns to generate blocks in random order during the tenure and accept re-election after the expiration of their term of office. A node can be a commissioner and a butler at the same time.

Butler Candidate

As the number of butlers is limited, commissioners can elect butlers only from butler candidates through voting. If butler candidates lose in the election, they can stay online, and wait for the next election. There are three steps to apply for a butler candidate:

(1) Register a user account in the consortium system and request to be a butler candidate.

(2) Submit a recommendation letter signed by at least one commissioner. The recommendation letter is similar to the invitation code, generated by the commissioner via calling a function of asymmetric encryption. The private key is used to encrypt the recommended letter to prevent forgery.

(3) Pay the deposit to become a butler candidate.

Commissioners can retain dual roles as commissioners and butler candidates so that they can recommend themselves to become butler candidates.

Ordinary User

Ordinary users can join or exit the network at any time without being authorized. They can also see the whole consensus process while accepting the service of the system. In the process of block generation, ordinary users have the right to submit transactions and the obligation to participate in the process of block forwarding.

Figure 4 shows the relationship between the four roles.

FIGURE 4

Figure 4. The conversion of the four roles.

Consensus Process

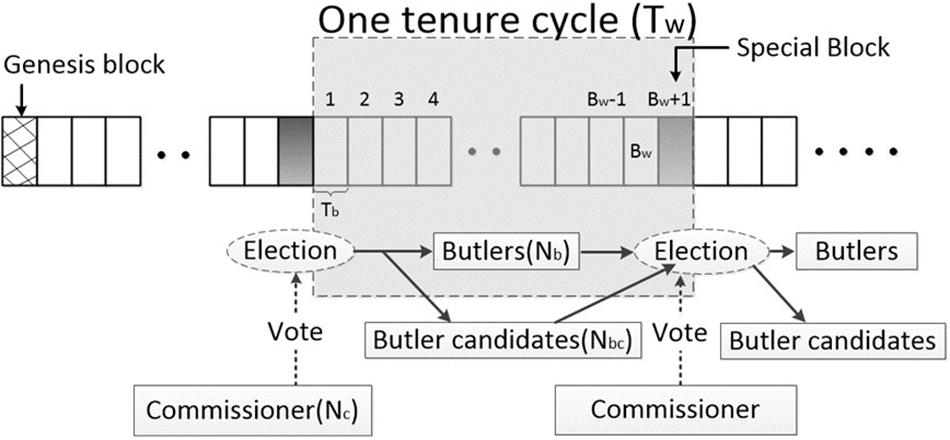
We denote the number of commissioners as N_c, the number of butlers as N_b, the number of butler candidates as N_bc, and the number of ordinary users as N_o. Since a node may have multiple identities, the total number of all roles is N_all, and satisfies N_all ≤ N_c + N_b + N_bc + N_o, where N_b is a constant. In each tenure, we assign each butler a number ranging from 0 to N_b − 1. The number of butler candidates N_bc is usually larger than the number of butlers N_b. If N_bc < N_b, that is, there are insufficient bulter candidates, the butlers will be assigned multiple numbers to make the system function properly. For example, when N_b = 8 and N_bc = 6, the system assigns the numbers from 0 to 7 to the butlers {B₁, B₂, B₃, B₄, B₅, B₆, B₁, B₂} sequentially. The butler B₁ and B₂, as the two butlers with the most votes, can achieve two butler numbers, respectively.

We suppose the butler’s tenure is T_w, and in each tenure, there are B_w + 1 valid blocks generated, the last of which is a special block including the butlers’ election results and related information. A block must collect at least $\lfloor \frac{N_c}{2}\rfloor +1$ signatures from different commissioners to become a valid block. A butler is required to generate a valid block within the allotted time, which is the packing cycle T_b. Figure 5 shows a consensus model of one tenure cycle.

FIGURE 5

Figure 5. Consensus model of one tenure cycle.

A round of consensus means that a butler generates a valid block. There are totally B_w + 1 rounds of consensus in each round of tenure, with B_w + 1 valid blocks generated. At the end of each round of consensus, the butler calls a function to generate a random number R, 0 ≤ R ≤ N_b. Then the butler whose number is equal to R is assigned responsibility for generating a block in the next round of consensus. If no valid block is generated in the T_b time, the (R + 1)^th butler will re-generate the block and let R = R + 1 mod N_b. If at least one butler works normally, the network will finally reach consensus. Because at most one block can receive majority signatures in one packing cycle T_b, each valid block has finality, and the blockchain will not bifurcate.

The (B_w + 1)^th block generated in the tenure is the special block. The incumbent butlers and butler candidates run for new butlers of the next tenure in this round of consensus. Each commissioner gives a vote list, and eventually, the top N_b candidates will win the election. Election results and related information will be written into this special block. After this special block generated, the current butlers officially retired, and the new butlers start working in the new tenure.

Block Generation

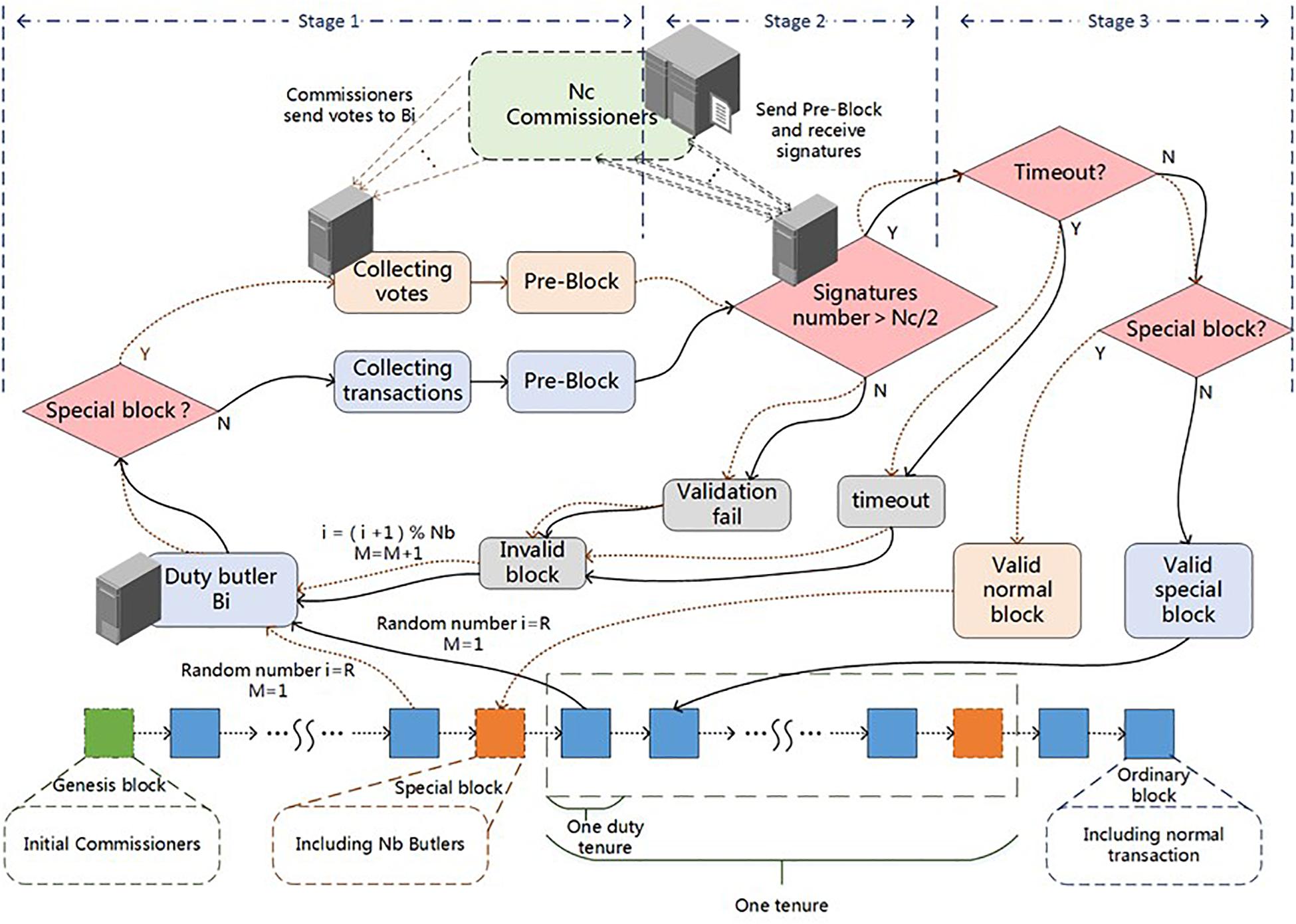
There are three types of blocks in the network, the ordinary block, the special block and the genesis block. Figure 6 shows the generation process of these three blocks.

FIGURE 6

Figure 6. Block generation process.

Ordinary Block Generation

A round of consensus may take M packing cycles (T_b). If the butler B_i fails to generate a valid block within T_b time, the permissions of this block’s production will be handed over to the butler B_i+1. The total time for a round of consensus T_c is M × T_b, which means that there are M − 1 invalid blocks have been abandoned in this consensus. When M ≤ N_b, generating a valid block contains the following steps:

S1 The ordinary users create transactions with their signatures attached. At the same time, they receive transactions, verify their validity, and forward the valid transactions to other commissioners and butlers.

S2 The butlers monitor transactions and store valid transactions into their local pool. All butlers and the commissioners in the network periodically synchronize their NTP time.

S3M = 1, R = GetPreviousBlockRandomNum(). If this is the first block of the tenure, then the previous block is the last valid special block of the previous tenure. If this consensus is to produce the genesis block (the first block of the blockchain), thenR defaults to 0.

S4 The duty butlerB_i (i = R) takes out some transactions from the local pool, packs them into a pre-block, and sends the pre-block to all commissioners. The cutoff time of this block isT_cut = GetPreviousBlockComfirmTime() + M × T_b.

S5 After receiving a pre-block, the commissioners verify its validity, and if they agree on the block’s production, then send their signature on this pre-block and current timestamp back to the butler.

S6 After collecting at least$\lfloor \frac{{\mathbf{N}}_{\mathbf{c}}}{\mathbf{2}}\rfloor +1$ signatures from different commissioners, the duty butler serializes the received signatures into a string in ascending order of its timestamp and attaches it to the Pre-Header. After that, it calculatesR = GetPreviousBlockRandomNum() and adds theR-value and the block time (the maximum value in the timestamp list returned by the commissioners) to form the Final-Header. If the block time is beforeT_cut, the duty butler will update its signature in the Pre-Header to prove its work. Jump to S8.

S7 If the time has exceededT_cut, this block will become an invalid block. LetR = (R + 1)modN_b andM = M + 1. Jump to S4.

S8 After generating a valid block, butlerB_R sends the Final-Header to all commissioners and then releases the block to other nodes. Once more than half of the commissioners confirm receipt of the valid block, the block enters the legal state in the system and has final confirmation.

S9 After receiving the valid block, the butlers and commissioners delete the included transactions from their local pool, obtain the random numberR and begin the next round of consensus.

Special Block Generation

The last block in a tenure cycle aims to complete an election for the butler team in the next tenure. The process is similar to that of an ordinary block:

P1 The commissioner generates a sequence from the list of the current butlers and butler candidates to form a vote, and sends it to the duty butler.

P2 The commissioners and the current butlers receive votes from all commissioners and put them into their local pool.

P3 The duty butler judges whether the number of voting transactions collected exceeds half of the number of commissioners. If so, perform P4–P8 to generate a new special block; if not, continue to wait until a timeout and be replaced by another duty butler.

P4–P8 Similar to S4–S8 of the ordinary block generation, the special block also needs commissioners’ signature and finally reaches a consensus. The difference with the ordinary block is that the special block contains voting transactions, but not ordinary data transactions. After counting, the topN_b nodes will win the election and become new butlers of the next tenure.

P9 After the production of the special block, the butlers of the current tenure are relieved of their office and delete the relevant voting transactions in the local pool.

Genesis Block Generation

The genesis block is the most special block in the consortium blockchain, with a height of 0. It contains the initial consortium nodes and the first batch of butler nodes’ information, which lays the foundation for subsequent blocks. The process of its generation is as follows:

T1 The primary commissioner nodes of the consortium communicate with each other to confirm online. Each node has an address hash. The member with the smallest hash value (as a proxy commissioner) is responsible for generating the genesis block.

T2 The primary commissioner sends the transaction of updating to the commissioner to the proxy commissioner.

T3 The commissioners who also want to be butler candidates submit identity change transactions. After receiving these transactions, the commissioners put them into their local pool.

T4 The commissioner selects at leastK candidate addresses for butlers from their local pool, serializes these addresses into a vote, signs it, and sends to the proxy commissioner.

T5 After counting the voting information, the proxy commissioner integrates all the transactions to generate a pre-block and sends it to all commissioners. When the proxy commissioner receives the signatures of the pre-block from all commissioners (this step confirms that all commissioners can communicate with each other, which means the consortium blockchain network has been established), the genesis block can be released. This process is similar to S4–S8 of generating an ordinary block.

T6 After all the commissioners receive the genesis block, they delete the unconfirmed transactions in the local pool.

Implicit 2PC

In S4–S8 of ordinary block generation, we use the modified two-phase commit to ensure the unique legality of the block. The duty butler needs to run a round of “Prepare-Ready-Propose-(Confirm)” two-phase commit process to complete the final confirmation of the block. “Prepare-Ready” is the process in which the butler sends the pre-block to the commissioners and receives their signatures. It is a necessary stage for block generation. “Propose-(Confirm)” refers to the stage in which the block is released and confirmed after finally generated. Since the system is in time synchronization with NTP, in a certain period, only one duty butler can legally perform block generation and a two-phase commit process. To improve the performance of the algorithm under the premise of ensuring correctness, “Propose-(Confirm)” is simplified to the process of releasing blocks, and the Confirm process is implicitly reflected in the process of consensus operation. Therefore, the communication complexity of PoV is O(3N_c), which is only affected by the number of commissioner nodes N_c.

Generation of Random Number

Each block generates a random number that determines who will be the next duty butler in a random manner. The random number generation algorithm is as follows:

Suppose the duty butler has received signatures and timestamps from K commissioners, which are represented by ⟨C_time(i), C_sign(i)⟩ (0 ≤ i < K, $\lfloor \frac{N_c}{2}\rfloor <K\le N_c$). Then the duty butler will sort them in ascending order of C_time, so C_time(K−1) is the largest. Compute R_source = C_time(K−1) ⊕ C_sign(K−1).

Denote the function of taking the last 32 bits of the string as SubStringEnd32(string), so R is:

$$R=StrToInt\left(SubStringEnd32\left(Hash\left(R_{source}\right)\right)\right)mod{N}_b.$$

Since the value of each block header is unpredictable, we can obtain a variable R_source and a random number R, preventing the possibility that butlers may unite to get more income by making R-values appear in a specific pattern.

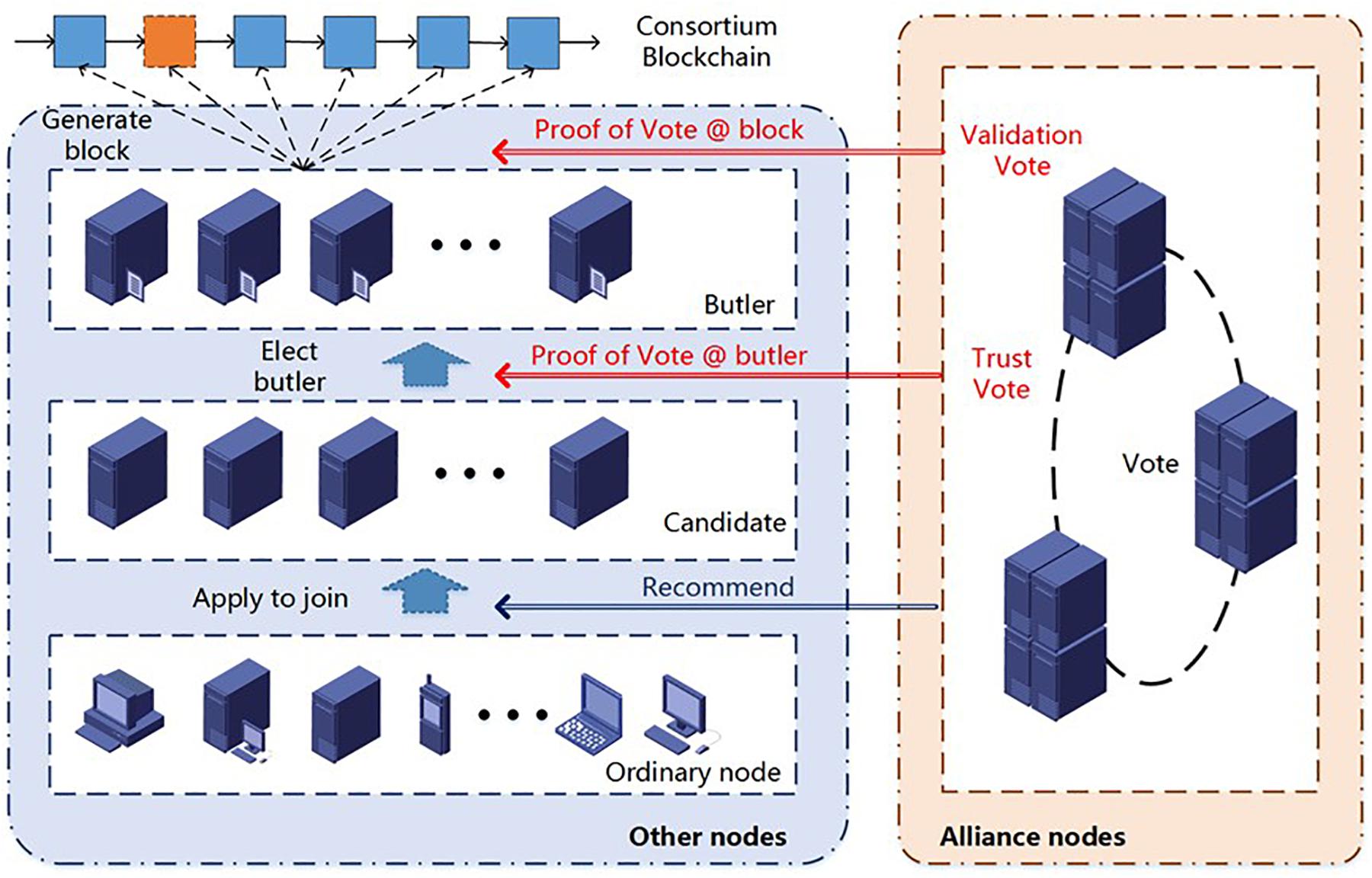
Voting Process

The idea of “proof of vote” is reflected in the design of the consensus mechanism by two kinds of votes shown in Figure 7. The first one is voting for block production, and the second one is voting for the butler team. The commissioners vote by returning their signatures.

FIGURE 7

Figure 7. Two kinds of proof of vote.

Proof of Vote on Blocks

The butler B_i generates a block and sends it to all commissioners. If a commissioner agrees to produce this block, it encrypts the block header and the timestamp and returns the signature and the timestamp to the butler B_i. If the butler B_i receives at least $\lfloor \frac{N_c}{2}\rfloor +1$ signatures within the predefined time, the block is valid. Otherwise, the block is invalid and will be reproduced by the butler B_i+1.

Proof of Vote on Butlers

During the last round of consensus in the tenure, the commissioners send the signed voting transactions to the duty butler B_i. After collecting and counting the votes, it generates a special block containing election results and related records. Then the butler B_i will send this block to all commissioners for validation.

The commissioners’ voting information is a combination of two kinds of tickets:

(1) Score tickets: Every commissioner holds a list of butler candidates’ scores, and the commissioner selects a candidate sequence with high scores.

(2) Designated tickets: The commissioner sets a specific selection of candidates with consideration of human factors, or sets a random candidate selection, which increases the butler’s mobility.

Excitation Mechanism

The butler candidates can give up his identity at any time. When it exists, a butler candidate retrieves its deposit. However, a butler cannot regain its deposit if it applies to exit from the network during its tenure.

Both parties need to pay some transaction fees for the transaction, as a reward for the butler’s packaging the transaction into the block. Specifically, each commissioner maintains a list of butler candidates and evaluates their behaviors. The scoring rules include:

(1) Each time the commissioner passes and signs a block, it will give the corresponding duty butler extra points; otherwise, its score will reduce.

(2) When the butler is offline and has missed the block production, its score will be cleared, which means that when the butler is online, he needs to start scoring again.

A butler may have different scores recorded by different commissioners. The score represents the degree of trust from a commissioner and also becomes one of the grounds for voting. After a whole tenure ends, butlers and butler candidates will receive rewards from the consortium based on the number of valid blocks they have generated so that they can be motivated to take the job, work honestly, and stay online for a long time.

Performance Proof and Analysis

We propose a complete consensus algorithm in this paper based on a voting mechanism for the consortium blockchain. Most of the current consensus algorithms choose to sacrifice some performance for security. Based on the credible characteristics of the consortium nodes and the appropriate consensus decision, PoV can significantly reduce the delay of blockchain transaction validation while ensuring the correctness of the algorithm, thus improving the performance of the consortium blockchain. With the assumptions stated in Section 2, PoV meets the following three conditions (Pritchett, 2008):

(1) Consistency: Proof of vote has a consensus termination, and only one block confirmation is required to achieve final validation and non-destructive modification of transactions.

(2) Availability: Proof of vote can ensure that the butlers output valid blocks smoothly and continuously under the appropriate parameter settings. For each operation request of the users, the system can always return a result within a limited time.

(3) Partition Tolerance: Proof of vote can achieve a certain degree of partition tolerance in the case where a partition contains more than half of the commissioners and at least one honest butler.

Security

Theorem 4.1: As long as more than $\lfloor \frac{N_c}{2}\rfloor +1$ commissioners are working effectively, blocks are safe and legal.

Proof: We use reduction to absurdity and assume that illegal blocks can be adequately validated. Because a butler must collect more than $\lfloor \frac{N_c}{2}\rfloor +1$ signatures to produce a valid block, and the number of active commissioners is higher than $\lfloor \frac{N_c}{2}\rfloor +1$, the active commissioners will not sign the illegal block. So the number of signatures of the illegal block is at most $\lfloor \frac{N_c}{2}\rfloor$. Therefore, this assumption is failed, and the original proposition is correct.

Consistency

Lemma 4.2: When a Block_h with height h is valid in the system, it indicates that the transactions in {Block₀, Block₁, …, Block_h−1} have the final consistency and cannot be tampered with.

Proof: We use mathematical induction. When h = 0, Block₀ is the genesis block. The proxy commissioner generates it and ensures that each member node is signed to recognize it so that each commissioner will hold the same genesis block.

When h = 1, a valid Block₁ appears in the system, indicating that more than half of the commissioners have verified the signatures of ${\text{Block}}_1^{\prime }$s pre-block, which means that there is a set C containing more than half of the commissioners, and each commissioner in C has Block₀. Each commissioner in the system has already saved the same genesis block, which means the final consistency of the transactions in Block₀. That is, when h = 1, the lemma is established.

When h = k + 1, and a valid Block_{k + 1} appears in the system, it means that the Final-Header in Block_{k + 1} contains more than half of the commissioners’ signatures. That is to say, there is a set C′ containing more than half of the commissioners, and each commissioner of C′ has checked and signed the pre-block of Block_{k + 1}. Therefore, every commissioner of C′ must have the same and effective Block_k. When the assumption is correct, all commissioners in C′ have the same {Block₀, Block₁,…, Block_k−1}, so all commissioners in C′ have the same {Block₀, Block₁, …, Block_k}.

In conclusion, Lemma 4.2 is true for all h.

Availability

To get rewards after winning the election, butlers must maintain the maximum online time, work honestly and fulfill the responsibility of producing block within the allotted time.

Lemma 4.3: The butler team will effectively produce blocks and become more and more reliable.

Proof: If block production does not consistent with the system rules, the block cannot pass the commissioners’ verification, and the butler’s scores will reduce. As a result, its probability of getting a vote will be lower in the election. Defeat in the election makes the butler lose the opportunity of producing blocks as well as getting rewards. Evidence shows that it is difficult for the butler who attempts to create illegal blocks to succeed in the election or gain any profit. Reliable butlers are more likely to win the election, and the system will become more reliable.

The reliability of the butler is controllable, and we can adjust the authenticity of the butlers’ work with two parameters: the number of votes K and the butler’s income B.

First of all, we analyze the number of votes K by each commissioner. According to the rules of voting, in each round of the election, N_b butlers will be selected from N_bc butler candidates by N_c commissioners. By establishing a mathematical model, we study the minimum number of votes K, which is the simplest, time-saving, fair and reasonable voting rule.

Without the consideration of the impact of the scoring mechanism, we assume that the votes are random without any abandonment, and each commissioner has K tickets, then the probability of each candidate to get a vote is $\frac{K}{N_{bc}}$. The voting activity subjects to the binomial distribution principle. The probability that a butler candidate j gets X votes is:

$$P_j\left(X\right)=\frac{N_c!}{X!\left(N_c-X\right)!}{\left(\frac{K}{N_{bc}}\right)}^X{\left(1-\frac{K}{N_{bc}}\right)}^{N_c-X}.(1)$$

To make the results of the voting more impartial, we hope that the average number of votes that an elected butler can receive exceeds $\frac{N_c}{2}$. So, we can figure out the probability of the above event:

$$P_1{}_j={\sum }_{i=\frac{N_c}{2}}^{N_c}\frac{N_c!}{i!\left(N_c-i\right)!}{\left(\frac{K}{N_{bc}}\right)}^i{\left(1-\frac{K}{N_{bc}}\right)}^{N_c-i}.(2)$$

For the purpose to select N_b butlers among N_bc candidates, the probability of a candidate’s success in the election is:

$$P_2{}_j=\frac{N_b}{N_{bc}}.(3)$$

$$P_1{}_j=P_2{}_j.(4)$$

According to Equations (2) and (3), the minimum K-value satisfying Equation (4) is the optimal number of votes.

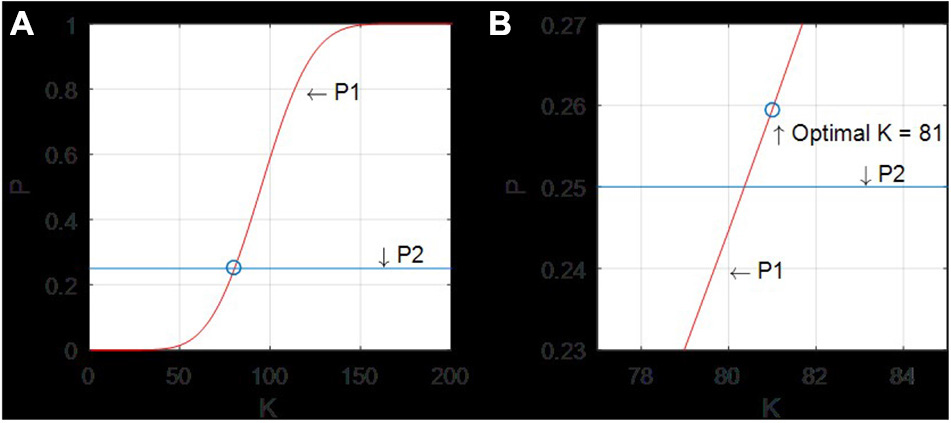
For example, we set N_c = 20, N_b = 50, N_bc = 200, and draw the image of $P_1{}_j$ and $P_2{}_j$. The abscissa is K, and the ordinate is the probability. We get optimal K from the curve intersection of $P_1{}_j$ and $P_2{}_j$.

As shown in Figure 8, when the optimal K = 81, each commissioner can submit 81 votes, and the number of votes that received by the butler who wins the election is probably exceeded half the number of commissioners, which means that the elected butlers can get more than half of the commissioners’ recognition. In this way, the results can be recognized by the majority of commissioners, so that the results of the vote are more scientific and impartial. When PoV is applied to different systems, K can be figured out by changing the values of N_c, N_b and N_bc.

FIGURE 8

Figure 8. Distribution map of $P_1{}_j$ and $P_2{}_j(N_c=20,N_b=50,N_{bc}=200).$ (A) Original map and (B) magnified map.

Introduce a scoring mechanism. A butler who has worked reliably will get a higher score, so an honest butler is more likely to receive score tickets during the election, and each commissioner could grade each butler independently (Section “Problem”). We rewrite the Equation (1) as:

$$P_3{}_j={\sum }_{i=\frac{N_c}{2}}^{N_c}\frac{N_c!}{i!\left(N_c-i\right)!}{\left(\frac{K}{N_{bc}}+{\mathrm{\alpha }}_j\right)}^i{\left(1-\frac{K}{N_{bc}}-{\mathrm{\alpha }}_j\right)}^{N_c-i},$$

$$-\frac{K}{N_{bc}}<{\mathrm{\alpha }}_j<1-\frac{K}{N_{bc}}.(5)$$

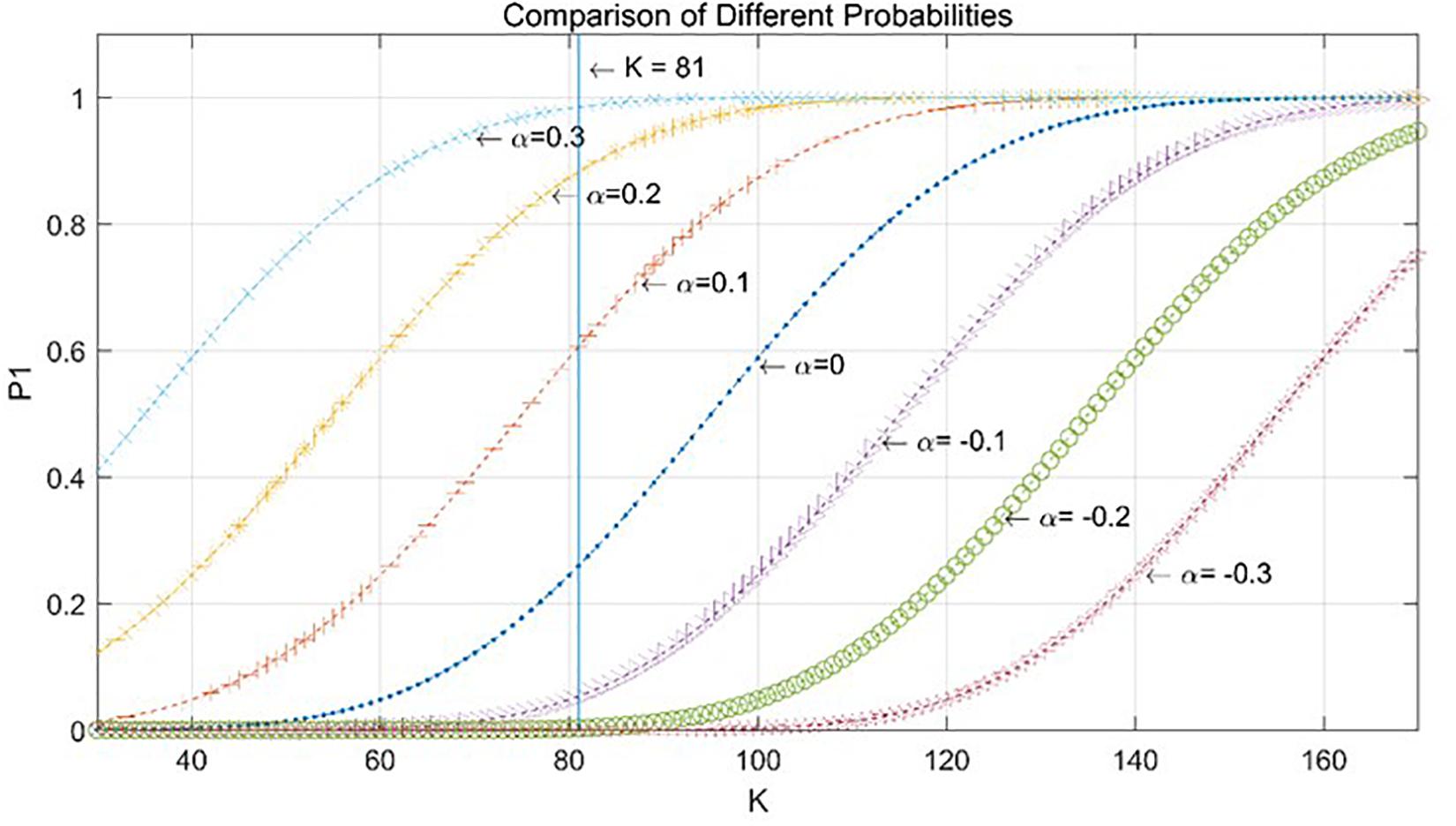
α_j > 0 means that the candidate has a higher probability to be voted by commissioners on account of a higher score. α_j > 0 represents the candidate has a lower chance of getting votes than average.

By setting up α_j=−0.3,−0.2,−0.1, 0, 0.1, 0.2, 0.3, we can compare the probability distributions of different situations. The results are shown in Figure 9.

FIGURE 9

Figure 9. Comparison of probabilities with different α_j.

As shown in Figure 9, when K is a fixed value, the more reliable the butler works, the higher the score the butler can get during the tenure. Therefore, the butler has a higher probability of getting the votes as a candidate and is more likely to win the election.

The second parameter is the butler’s benefit. In one tenure cycle, a candidate j has the probability of $\frac{N_b}{N_{bc}}$ being elected to be a butler. After becoming a butler, the butler has the probability of $\frac{1}{N_b}$ to pack a block at each packing cycle. We indicate p_j as the probability of packing a valid block.

$$p_j=\frac{1}{N_{bc}}.$$

Assuming that a reward for a block is B_j, we define the average energy cost of a single packing cycle as e_j. After n cycles, the total cost is e_j × n. We also define an event E_jk that the butler candidate j successfully wins the election and producing a valid block k (k = 1, 2, ⋯, n).

$$E_{jk}=\{\begin{array}{cc}\hfill 1,\hfill & \hfill p_j,\hfill \\ \hfill 0,\hfill & \hfill 1-p_j.\hfill \end{array}(k=1,2,\mathrm{\cdots },n)$$

E_jk subjects to an identical independent distribution (iid). The total rewards that butler j can receive after n packing cycles are:

$$R_j=\sum _{k=1}^n{E}_{jk}\times B_j-e_j\times n.$$

R_j follows a binomial distribution with the mean indicated as:

$$\mathrm{\mu }\left(R_j\right)=n\times p_j\times B_j-e_j\times n.$$

A butler candidate will survive only if μ(R_j) < 0, i.e.,

$$B_j<\frac{e_j}{p_j}{N}_{bc}\times e_j.(6)$$

In conclusion, considering the scoring mechanism and voting mechanism, butlers trying to ruin the system will fail to release blocks and thus receive a negative grade. Therefore, the probability that bad butlers or candidates win the election is below the average. If the system has a more substantial number of candidates than the expected number, unreliable candidates will quit the network because their meager rewards are unable to compensate for their energy cost. Equations (4) and (6) can be criteria for quality and quantity control of candidates.

Partition Tolerance

Lemma 4.4: In the case of operating in a partitioned network, PoV only needs one partition to satisfy the conditions that more than half of the commissioners operate normally and at least one butler works honestly, and the algorithm can continue to serve.

Proof: According to the block generation process, the accountability of the butler who cannot work honestly will be handed over to the next butler. In the case of a network partition, if a partition contains more than half of the online commissioners and at least one honest butler, the bookkeeping rights will eventually be transferred to the honest butler, and half of the commissioners sign the block. Therefore the partition will continue to operate the consensus process and produce blocks. The number of commissioners in other partitions is less than half, and the consensus process will be continually looping through the process of replacing the butler and failing to generate new blocks.

Transaction Finality

Lemma 4.5: Proof of vote will not “fork” in the case of partitioning.

Proof: If the network is split into two completely separate partitions: Partition A and Partition B, A∩B = ∅. As long as the number of commissioners in one of the partitions satisfies $\left|A\right|\le \lfloor \frac{N_c}{2}\rfloor +1$ or $\left|B\right|\le \lfloor \frac{N_c}{2}\rfloor +1$, and there is at least one butler who works honestly, according to Lemma 4.4, the blocks in the partition can still be efficiently generated. Suppose partition A satisfies these two conditions. In the Partition B, even if the block can be successfully packaged by the butler, it is impossible to obtain enough verification signatures. Therefore, it is impossible to have a new chain in the Partition B. Thus, PoV allows partitioning without forking.

Selfish Mining

Selfish mining has different forms in different consensus algorithms (Sapirshtein et al., 2016). In summary, it is a behavior that undermines consensus fairness to gain higher profits without compromising the correctness of the system. In the process of PoV consensus, there is the possibility of selfish mining attacks due to the incentive mechanism.

In this part, we will discuss a possible selfish mining attack in PoV—R-Collision. Although the previous legal block specifies the next duty butler by the R-value, there is a way to increase the possibility that current duty butler will continue to serve as the next duty butler.

R-collision: According to the random number generation method in the section “Problem,” if the duty butler is a selfish mining attacker, it is possible to select different combinations of signatures to obtain different R-values. This process is called “R-collision.” If there is an attacker’s number in the optional R-value, the attacker can become the next duty butler to earn revenue. At a very low probability, an attacker may occupy the role of a duty butler for a long time.

We modeled the process of the “R-collision.” Since the election process is independent of the process of generating the random number R, we will not analyze whether the attacker can successfully be elected as a butler. Assume that the current butler set is B = {B₀, B₁, B₂, ⋯, B_Nb−1}, and the number of generated blocks is B_w + 1. The tenure of every butler is T = {t₀, t₁, ⋯, t_i,}. Assume that attacker f has been elected as a butler and has come to its duty cycle, f ∈ B, and the duty butler’s number is B_f. The signature set received by B_f after generating the pre-block in the current duty cycle is Q_f ∈ {,⟨C_time(k), C_sign(k)⟩,} (0 ≤ k < N_c, C_time(k) ≤ C_time(k + 1)). Considering the worst case, the attacker B_f can collect the signatures of all the commissioners every time, and Q_f is sorted in ascending order of C_time. We set $Q_f{}_1\left(k\right)$ to represent a subset of Q_f and contain only one element, i.e., $Q_f{}_1\left(k\right)=\left\{⟨\text{C\_time}\left(k\right),\text{C\_sign}\left(k\right)⟩\right\}$, and set $Q_f{}_n(k,m)$ also to be a subset of Q_f (0 < n ≤ m−k), representing to choose n elements from $Q_f{}_{m-k}(k,m)$ = ⟨C_time(k),C_sign(k)⟩,⋯,⟨C_time(m),C_sign(m)⟩.

If B_f needs to generate a valid block, the effective combination of “R-collision” is $Q_f{}_n(1,k)\cup Q_f{}_1\left(k+1\right)$, $\lfloor \frac{N_c}{2}\rfloor <n\le N_c$. The best strategy for “R-collision” attacks for B_f is first to pick a $Q_f{}_1\left(k+1\right)$ that satisfies $k\ge \lfloor \frac{N_c}{2}\rfloor$ in Q_f as the signature of the largest C_time in the signature list that can be written to the final block. Then B_f selects n signatures from $Q_f{}_k(1,k)$ to form $Q_f{}_n(1,k)$. This means that the C_time of the elements in $Q_f{}_n(1,k)$ is less than that in $Q_f{}_1\left(k+1\right)$. This strategy guarantees that the number of signatures in the commissioners’ signature list of the final block $\left|Q_f{}_n(1,k)\cup Q_f{}_1\left(k+1\right)\right|=n+1\ge \lfloor \frac{N_c}{2}\rfloor +1$, and the maximum value of C_time can be specified as the C_time value of $Q_f{}_1\left(k+1\right)$.

Therefore, the duty butler (attacker) B_f can specify the value of $Q_f{}_1\left(k+1\right)$ to get the result set of different “R-collision,” ℜ_f={R₁, R₂, R₃,}. Since $\lfloor \frac{N_c}{2}\rfloor \le \text{k}<k+1<N_c$, there are at most $\lceil \frac{N_c}{2}\rceil$ possibilities for the value of $Q_f{}_1\left(k+1\right)$, that is, B_f can have $\lceil \frac{N_c}{2}\rceil$ chances to recalculate the random number R to get an R = f, so $\left|{\Re }_f\right|=\lceil \frac{N_c}{2}\rceil$. We define P(R−collisionsuccess) as the possibility that B_f can get the expected value of R = f from ℜ_f.

Each time B_f recalculates the random number R, R ∈ {0, 1, 2, ⋯, N_b − 1}, the probability that R is precisely equal to f is $p=\frac{1}{N_b}$. Whether each R in ℜ_f is f is an independent event Y_l:

$$Y_l=\{\begin{array}{cc}\hfill 1,\hfill & \hfill p,\hfill \\ \hfill 0,\hfill & \hfill 1-p.\hfill \end{array}(l=1,2,,n,n=\lceil \frac{N_c}{2}\rceil )$$

We take Y_l as an identical independent distribution (iid), Y_l obeys 0 - 1 distribution, E(Y_l) = p, D(Y_l) = p(1−p). Assume:

$$X_n=\sum _{l=1}^n{Y}_l.$$

According to the additive of the binomial distribution, we know that X_nB(n,p)where X_n represents the total number of R = f in the set. According to the central limit theorem of the binomial distribution – the De Moivre-Laplace theorem, the limit distribution of mutually independent random variables is the standard normal distribution, namely:

$$\underset{n\to }{lim}P(\frac{X_n-np}{\sqrt{np\left(1-p\right)}}\le x)=\mathrm{\varnothing }\left(x\right).$$

When n is sufficiently large (in the normal approximation of the binomial distribution, “n is sufficiently large” is generally considered to be n ≥ 50), there is an approximation:

$$X_{n}N(np,np\left(1-p\right)).$$

Therefore, the probability that the total number of R = f in ℜ_f is less than 1 is the probability of failure of “R-collision.”

If the probability of completing a selfish mining attack (R-collision) is less than 0.01, a selfish mining attack can be considered as a small probability event, where the relationship between the number of butlers N_b and the number of commissioners N_c can be calculated by using relevant probability calculation methods.

By establishing a three-dimensional model of “R-collision,” the influence of the number of butlers and the number of commissioners on safety can be quantitatively analyzed. The following model is established in Matlab:

$$\begin{array}{c}\hfill x=N_c\hfill \\ \hfill y=N_b\hfill \end{array}\}\Rightarrow z=P\left(R-\mathrm{collosion}\mathrm{fail}\right)=\mathrm{\varnothing }\left(\frac{1-np}{\sqrt{np\left(1-p\right)}}\right),$$

$$n=\lceil \frac{N_c}{2}\rceil ,p=\frac{1}{N_b}.$$

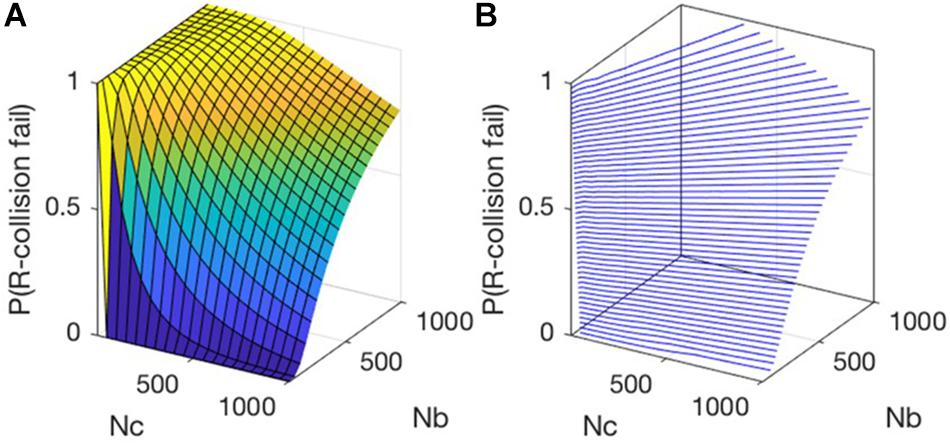
Figure 10A shows that when N_c is fixed, the larger N_b is, the bigger probability of “R-collision” failure, and the lower the success rate of selfish mining attack, the higher the safety. The contour plot in Figure 10B shows that the contour lines are linearly distributed, which means that when N_c and N_b are in a specific proportional relationship, the size of P(R−collosion fail) can be kept constant. When the ratio of N_b and N_c is higher than a particular fixed value, P(R−collosion fail) must be higher than an absolute value.

FIGURE 10

Figure 10. The probability of R-collision failure. (A) Three-dimensional map and (B) contour map.

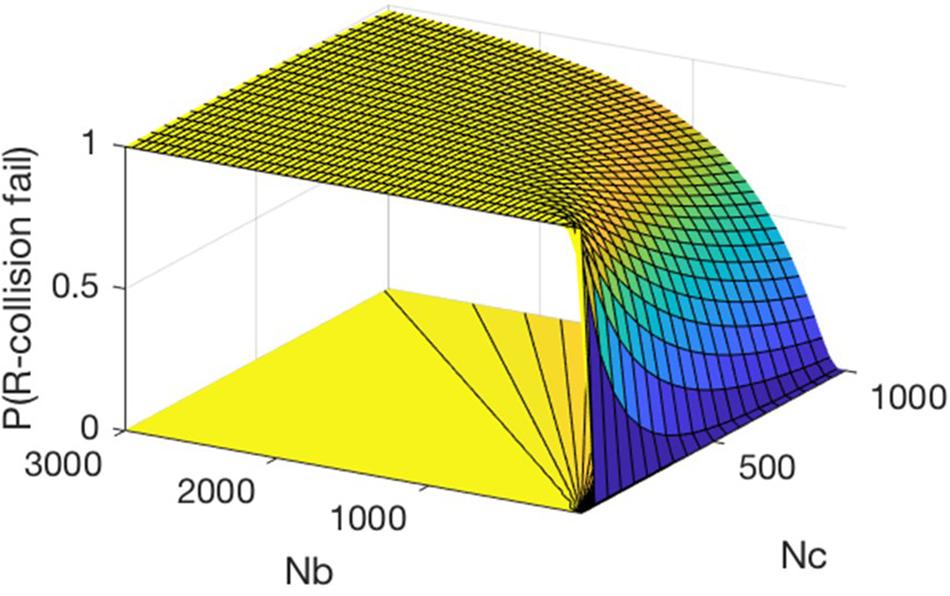
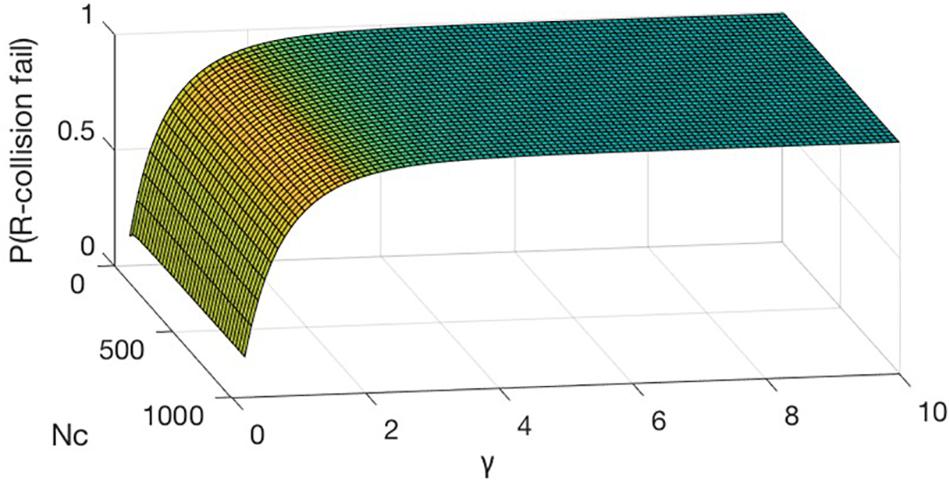
We project the contour map of the 3D chart onto the xoy plane in Figure 11. It shows that when $\frac{N_b}{N_c}$ is greater than $\frac{1000}{300}$, P(R−collosion fail) is close to 1.

FIGURE 11

Figure 11. The probabilities of R-collision fail vary with N_b and N_c.

Let $\mathrm{\gamma }=\frac{N_b}{N_c}$, we build the following model in Matlab. The 3D model is shown in Figure 12.

FIGURE 12

Figure 12. The probabilities of R-collision fail vary with γ and N_c.

$$\begin{array}{c}\hfill x=N_c\hfill \\ \hfill y=\mathrm{\gamma }=\frac{N_b}{N_c}\hfill \end{array}\}\Rightarrow z=P\left(R-\mathrm{collosion}\mathrm{fail}\right)$$

$$=\mathrm{\varnothing }\left(\frac{1-np}{\sqrt{np\left(1-p\right)}}\right),$$

$$n=\lceil \frac{N_c}{2}\rceil ,p=\frac{1}{N_b}=\frac{1}{\mathrm{\gamma }{N}_c}.$$

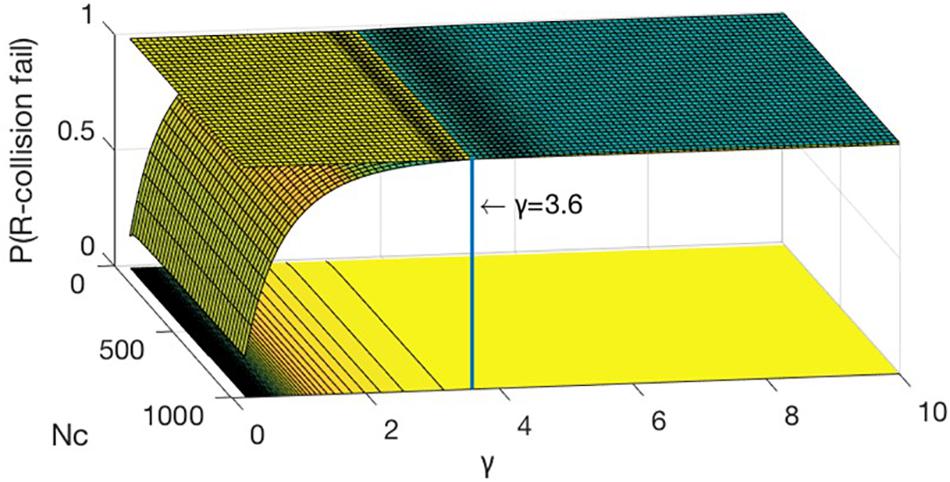
As seen from Figure 12, regardless of how N_c changes, P(R−collosion fail) always increases as γ increases. Furthermore, as shown in Figure 13, we plot the contour map contour on the xoy plane and add a cross section (z = 0.99) to intersect the model map, and found that γ of the boundary line is equal to 3.6. So far, the model fully verified that when the number of $\mathrm{\gamma }=\frac{N_b}{N_c}\ge 3.6$, P(R−collosion fail) ≥ 0.99. Therefore, selfish mining can be a small probability event, by which time the system is safe to some extent.

FIGURE 13

Figure 13. The probabilities of R-collision fail 0.99.

Experiments

We have implemented PoV of C++ code. To test the performance of our consensus algorithm, this section will compare the throughput of PoV and a state-of-art algorithm, BFT-SMART in an actual distributed environment.

Theoretical Model

Our experimental environment is based on the simple theoretical model: there are L servers each connected directly to a router in the network. The N commissioner nodes are evenly distributed among the L servers, and each commissioner node can also serve as the butler. Suppose the server has sufficient memory and CPU resources, and the total transmission bandwidth between the servers is a fixed value band. Since the server has great internal bandwidth and extremely high CPU processing speed, we only consider the process of node communication between different servers. Define the message header size as M, the signature size as S, the pre-block header size of PoV as H, the transaction size as T, and the maximum number of transactions in a block as K.

Generating a PoV block contains three steps of communication. First, the duty butler sends the pre-block message to all the commissioners, and the communication data in this step is the total pre-block message data sent by the duty butler to the $\left(\frac{L-1}{L}\times N\right)$ nodes on other servers. The maximum traffic and time required are:

$$dat{a}_1=\left(M+H+T\times K\right)\times N\times \frac{L-1}{L},$$

$$t_1=\frac{dat{a}_1}{band}=\frac{\left(M+H+T\times K\right)\times N\times \left(L-1\right)}{L\times band}.$$

Then all the commissioners return their signature messages to the duty butler. The maximum traffic and time required are:

$$dat{a}_2=\left(M+S\right)\times N\times \frac{L-1}{L},$$

$$t_2=\frac{dat{a}_2}{band}=\frac{\left(M+S\right)\times N\times \left(L-1\right)}{L\times band}.$$

Finally, the duty butler sends the Final-Header to all the commissioners, which mainly contains the Pre-Header and the received signatures of the commissioners. The maximum traffic and time required are:

$$dat{a}_3=\left(M+H+S\times N\right)\times N\times \frac{L-1}{L},$$

$$t_3=\frac{dat{a}_3}{band}=\frac{\left(M+H+S\times N\right)\times N\times \left(L-1\right)}{L\times band}.$$

Therefore, the maximum numbers of transactions per second (TPS) processed by PoV is:

$$TPS=\frac{K}{t_1+t_2+t_3}$$

$$=\frac{K\times L\times band}{\left[3M+2H+T\times K+S\times \left(N+1\right)\right]\times N\times \left(L-1\right)}.$$

Take M = 266Bytes, S = 1340Bytes, H = 7455Bytes, T = 264Bytes, K = 8000 and band = 1Gbps as an example, the theoretical throughput of PoV is:

$$TPS=\frac{4\times {10}^5\times L}{\left(0.852N+0.000536N^2\right)\left(L-1\right)}.(8)$$

Experimental Results

We conduct our experiments on five servers (HUAWEI FusionServer 2288 V5) connected to the same router, each with 128G of memory and Intel Xeon Silver 4116 Processor. Each PoV tenure can generate six PoV blocks, including five ordinary blocks and a special block. Table 2 shows their performance variation in the system with different scales.

TABLE 2

Table 2. Proof of vote’s and BFT-SMART’s theoretical and experimental throughout.

The experimental results show that the actual performance trend of PoV accord with the theoretical values. When the number of nodes is more than 100, the throughput of PoV declines gently, and its descending speed is lower than that of BFT-SMART. Compared with BFT-SMART, PoV has better efficiency and scalability.

Since the butler nodes are mainly responsible for the message transmission in the PoV algorithm, in system design, the butler nodes are usually required to have certain bandwidth conditions, combined with some excitation mechanism, so that they have a higher probability of getting block rewards.

Discussion

The security guarantee of PoW-based consensus algorithms greatly hinders the improvement of performance. Compared with the PoW-based consensus algorithms, PoV only needs one block to confirm the tamper-proof transaction, which ensures that the improvement of its performance is not limited by security. Compared with BFT-based consensus algorithms, PoV’s communication complexity is only O(3N_c), which is only affected by the number of committee nodes, and can theoretically achieve better performance.

In terms of energy consumption, PoV does not require a lot of computation, nor does it facilitate the emergence of ASICS. Therefore, the use of PoV consensus in the consortium blockchain can avoid unnecessary energy waste.

In addition, PoV consensus supports regular rotation of consensus nodes, which can greatly avoid distributed single point of failure and prevent the system from being controlled by attackers for a long time. At the same time, PoV is subject to the control of all committee nodes. In the establishment of a real blockchain system, the government and regulatory agencies can participate in the supervision properly by cooperating with the appropriate audit layer. If there is an illegal transaction that needs to be changed, a special modification transaction can be issued with the consent of more than half of the committee members through government consultation to correct the existing wrong data. Therefore, PoV can not only adapt to the top-down regulation but also adapt to the bottom-up modification of the blockchain system, with flexible supervision.

However, the main limitation of PoV is the need to dynamically change the waiting time of the butlers based on network conditions. If the waiting time is too short, the butlers will not be able to collect enough transactions into the block, resulting in low throughput. On the contrary, if the waiting time is too long, it will lead to the failure to complete the consensus within the specified time, triggering the timeout mechanism, which will lead to the drop in the throughput. In our implementation, we adjust the waiting time to a suitable size as 5 s for an excellent performance.

Conclusion and Future Work

In summary, this paper proposes a new type of consortium-oriented consensus algorithm—PoV and proves its performance by experimenting in a distributed environment. Based on the idea of voting by the consortium members, PoV’s design relies on the credibility difference between the core nodes and other nodes in the consortium blockchain. We define four roles in the PoV model. The algorithm introduces the butler role and the butler candidate role to achieve the rotation of the consensus nodes and establishes a voting mechanism to ensure that the consensus results need to be verified by the majority of the commissioners. This kind of consensus process separates voting rights and bookkeeping rights, which achieves decentralized management among consortium members. PoV utilizes the trusted environment of the commissioner nodes to ensure its security and guarantees privacy based on the cryptography foundation of the blockchain technology. It requires only one block to confirm the finality with almost negligible power consumption. Compared with traffic complexity O(N²) of BFT-based algorithms, PoV has just the complexity of O(3N_c) and achieves a great improvement when the number of nodes is over 100.

Our future work lies in optimizing PoV consensus in subsequent practical system development. In our current design, it is a consensus algorithm of principle and may have problems at the system level, such as modular design and parallel processing. Our other future work is the balance between privacy protection and regulation in our blockchain system with PoV consensus. We initially plan to combine the GDPR-Blockchain Compliant architecture design of IEEE (Lima, 2018) to store the sensitive data in the off-chain trusted database, and only the pointer and digest of the data will be stored on the chain.

Author Contributions

KL and HL contributed conception and design of the study. HW wrote the first draft of the manuscript and participated in the experiment. All authors contributed to manuscript revision, read and approved the submitted version.

Funding

This work was supported by ZTE University Funding, National Keystone R&D Program of China (No. 2017YFB0803204), National Natural Science Foundation of China (NSFC) (No. 61671001), PCL Future Regional Network Facilities for Large-scale Experiments and Applications (No. PCL2018KP001), GuangDong Key Program (No. GD2019B010137001), and Shenzhen Research Programs (Nos. JSGG20170824095858416, JCYJ20190808155607340, and JCYJ20170306092030521).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This manuscript is further research and expansion on the previous work (Li et al., 2017). In comparison with the previous work, we remove the signature process of the NTP server in the previous work, which can become a bottleneck of the system. The timestamp of the commissioner is added in the process of its signature, which is equivalent to making the trusted commissioner node concurrently serve as the distributed NTP server. We also upgrade the random number algorithm in the consensus process and analyze its ability to resist selfish mining attacks. We also add comparative experiments in an actual distributed environment. We thank Jiansen Huang and Yongjie Bai for their significant contributions to experimental testing and analysis.

References

Abraham, I., Malkhi, D., Nayak, K., Ren, L., and Spiegelman, A. (2018). “Solida: a blockchain protocol based on reconfigurable Byzantine consensus,” in Proceedings of the 21st International Conference on Principles of Distributed Systems, OPODIS 2017 [25] (Leibniz International Proceedings in Informatics, LIPIcs; Vol. 95), eds J. Aspnes, J. Leitao, A. Bessani, and P. Felber (Wadern: Schloss Dagstuhl- Leibniz-Zentrum fur Informatik GmbH, Dagstuhl Publishing). doi: 10.4230/LIPIcs.OPODIS.2017.25

CrossRef Full Text | Google Scholar

Al-Bassam, M., Sonnino, A., Bano, S., Hrycyszyn, D., and Danezis, G. (2017). “Chainspace: a sharded smart contracts platform,” in Proceedings of the Network and Distributed System Security Symposium (NDSS), Sydney, NSW.

Google Scholar

Bentov, I., Pass, R., and Shi, E. (2016). Snow white: provably secure proofs of stake. IACR Cryptol. ePrint Arch. 2016:919.

Google Scholar

Bessani, A., Sousa, J., and Alchieri, E. E. P. (2014). “State machine replication for the masses with BFT-SMART,” in Proceedings of 44th Annual IEEE/IFIP International Conference on Dependable Systems and Networks, DSN 2014, Atlanta, GA.

Google Scholar

Bhattacharya, R., White, M., and Beloff, N. (2018). “A blockchain based peer-to-peer framework for exchanging leftover foreign currency,” in Proceedings of IEEE Computing Conference, London, July 2017 (London: IEEE), 1431–1435.

Google Scholar

Buterin, V. (2015). On Public and Private Blockchains. Ethereum Blog, Crypto Renaissance Salon. Available online at: https://blog.ethereum.org/2015/08/07/on-public-and-private-blockchains/ (accessed August 6, 2015).

Google Scholar

Castro, M., and Liskov, B. (1999). Practical Byzantine fault tolerance. OSDI 99, 173–186. doi: 10.2196/10163

PubMed Abstract | CrossRef Full Text | Google Scholar

Decker, C., Seidel, J., and Wattenhofer, R. (2016). “Bitcoin meets strong consistency,” in Proceedings of the 17th International Conference on Distributed Computing and Networking, Singapore.

Google Scholar

Dinh, T. T. A., Liu, R., Zhang, M., Chen, G., Ooi, B. C., and Wang, J. (2018). Untangling blockchain: a data processing view of blockchain systems. IEEE Transact. Knowl. Data Eng. 30, 1366–1385. doi: 10.1109/tkde.2017.2781227

CrossRef Full Text | Google Scholar

Eyal, I., Gencer, A. E., Sirer, E. G., and van Renesse, R. (2016). “Bitcoin-Ng: a scalable blockchain protocol,” in Proceedings of the 13th USENIX Symposium on Networked Systems Design and Implementation, Santa Clara, CA, 45–59.

Google Scholar

Gafni, E., and Lamport, L. (2000). “Disk paxos,” in Proceedings of the International Conference on Distributed Computing, Berlin, 330–344. doi: 10.1007/3-540-40026-5_22

CrossRef Full Text | Google Scholar

Gilad, Y., Hemo, R., Micali, S., Vlachos, G., and Zeldovich, N. (2017). “Algorand: scaling Byzantine agreements for cryptocurrencies,” in Proceedings of the 26th Symposium on Operating Systems Principles, Shanghai, 51–68.

Google Scholar

Intel Corporation. (2018). Hyperledger Sawtooth. Available online at: https://sawtooth.hyperledger.org/ (accessed October 15, 2018).

Google Scholar

Khalil, R., and Gervais, A. (2017). “Revive: rebalancing off-blockchain payment networks,” in Proceedings of the 24th ACM SIGSAC Conference on Computer and Communications Security, CCS 2017, Dallas, TX, USA (New York, NY: Association for Computing Machinery), 439–453.

Google Scholar

Khan, C., Lewis, A., Rutland, E., Wan, C., Rutter, K., and Thompson, C. (2017). A distributed-ledger consortium model for collaborative innovation. Computer 50, 29–37. doi: 10.1109/mc.2017.3571057

CrossRef Full Text | Google Scholar

Kiayias, A., Russell, A., David, B., and Oliynykov, R. (2017). “Ouroboros: a provably secure proof-of-stake blockchain protocol,” in Proceedings of the 37th Annual International Cryptology Conference (Cham: Springer).

Google Scholar

Kiyomoto, S., Rahman, M. S., and Basu, A. (2017). “On blockchain-based anonymized dataset distribution platform,” in Proceedings of the 15th International Conference on Software Engineering Research, Management and Applications (London: IEEE), 85–92.

Google Scholar

Kogias, E. K., Jovanovic, P., Gailly, N., Khoffi, I., Gasser, L., and Ford, B. (2016). “Enhancing bitcoin security and performance with strong consistency via collective signing,” in Proceedings of the 25th USENIX Security Symposium, New York, NY, 279–296.

Google Scholar

Kokoris-Kogias, E., Jovanovic, P., Gasser, L., Gailly, N., Syta, E., and Ford, B. (2018). “OmniLedger: a secure, scale-out, decentralized ledger via sharding,” in Proceedings of the 2018 IEEE Symposium on Security and Privacy, San Francisco, CA, 583–598.

Google Scholar

Li, K., Li, H., Hou, H., Li, K., and Chen, Y. (2017). “Proof of vote: a high-performance consensus protocol based on vote mechanism & consortium blockchain,” in Proceedings of the 2017 IEEE 19th International Conference on High Performance Computing and Communications; IEEE 15th International Conference on Smart City; IEEE 3rd International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Bangkok, 466–473.

Google Scholar

Lima, C. (2018). Blockchain-GDPR Privacy by Design: How Decentralized Blockchain Internet Will Comply With GDPR Data Privacy. Piscataway, NJ: IEEE Blockchain Standards.

Google Scholar

Liu, Y., Liu, J., and Yu, H. (2018). Research on blockchain consensus: comparison of typical schemes. Zte Technol. J. 24, 6–11.

Google Scholar

Pass, R., and Shi, E. (2016). Hybrid Consensus: Efficient Consensus in the Permissionless Model. Cryptology ePrint Archive: Report 2016/917. Available oline at: https://eprint.iacr.org/2016/917 (accessed February 16, 2017).

Google Scholar

Pritchett, D. (2008). BASE: an acid alternativ. ACM Queue 6, 48–55.

Google Scholar

Puthal, D., Malik, N., Mohanty, S. P., Kougianos, E., and Yang, C. (2018). The Blockchain as a decentralized security framework [future directions]. IEEE Consum. Electron. Mag. 7, 18–21. doi: 10.1109/mce.2017.2776459

CrossRef Full Text | Google Scholar

Sapirshtein, A., Sompolinsky, Y., and Zohar, A. (2016). “Optimal selfish mining strategies in bitcoin,” in Financial Cryptography and Data Security. FC 2016. Lecture Notes in Computer Science, Vol. 9603, eds J. Grossklags and B. Preneel (Berlin: Springer), 515–532.

Google Scholar

Sompolinsky, Y., Lewenberg, Y., and Zohar, A. (2016). SPECTRE: a fast and scalable cryptocurrency protocol. IACR Cryptol. ePrint Arch. 2016:1159.

Google Scholar

Sompolinsky, Y., and Zohar, A. (2013). Accelerating bitcoin’s transaction processing. fast money grows on trees, not chains. IACR Cryptol. ePrint Arch. 2013:881.

Google Scholar

Treleaven, P., Brown, R. G., and Yang, D. (2017). Blockchain technology in finance. Computer 50, 14–17. doi: 10.1109/mc.2017.3571047

CrossRef Full Text | Google Scholar

Wang, L., Qin, B., and Qiao, X. (2018). Development and security of blockchain consensus mechanism. Zte Technol. J. 24, 12–16.

Google Scholar

Wright, C. S. (2008). Bitcoin: A Peer-to-Peer Electronic Cash System. Available online at: https://ssrn.com/abstract=3440802 (accessed August 21, 2008).

Google Scholar

Zhang, E. (2014). A Byzantine Fault Tolerance Algorithm for Blockchain. White paper. Available online at: https://docs.neo.org/docs/en-us/basic/whitepaper.html

Google Scholar

Zhang, F., Eyal, I., Escriva, R., Juels, A., and van Renesse, R. (2017). “REM: resource-efficient mining for blockchains,” in Proceedings of the 26th USENIX Security Symposium, Vancouver, BC, 1427–1444.

Google Scholar