Uncertainties
Ground Motion Definition
Earthquake events and realized earthquake ground motions are extremely uncertain even with the present knowledge, and it is not easy to predict forthcoming events precisely both in time and frequency (Anderson and Bertero, 1987; Takewaki et al., 1991; 2013; 2011a; Conte et al., 1992; Ariga et al., 2006; Minami et al., 2013; Çelebi et al., 2014). For example, recently reported near-field ground motions (Northridge 1994, Kobe 1995, Turkey 1999, and Chi–Chi, Taiwan 1999), the Mexico Michoacan motion 1985, and the Tohoku motion 2011, had some peculiar characteristics that could not have been predicted. It is also true that civil, mechanical, and aerospace engineering structures are often subjected to disturbances with inherent uncertainties due mainly to their “low rate of occurrence.” Worst-case analysis (Drenick, 1970; Shinozuka, 1970; Takewaki, 2006/2013; Elishakoff and Ohsaki, 2010), combined with proper information based on reliable physical data, is expected to play an important role in avoiding difficulties caused by such uncertainties. Approaches based on the concept of “critical excitation” seem promising.
There are various buildings in a city (Figure 1A). Each building has its own natural period and its idiosyncratic structural properties. Earthquakes trigger various kinds of ground motions in the city. The relation of the building’s natural period with the predominant period of the induced ground motion may lead to disastrous phenomena, as many observations from past historical earthquakes have demonstrated. Once a large earthquake occurs, some building codes are typically upgraded, but such makeshift efforts never resolve all issues and new damage problems have occurred even recently. In order to overcome this problem, a new paradigm has to be posed. In my view, the concept of “critical excitation,” and structural design based upon it, could become a powerful new paradigm. Critical excitation methods were pioneered by Drenick (1970) and Shinozuka (1970). Just as the investigation of limit states of structures plays an important role in the specification of allowable response and performance levels of structures during disturbances, the clarification of critical excitations for a given (group of) structure(s) can provide structural designers with useful information for determining excitation parameters.
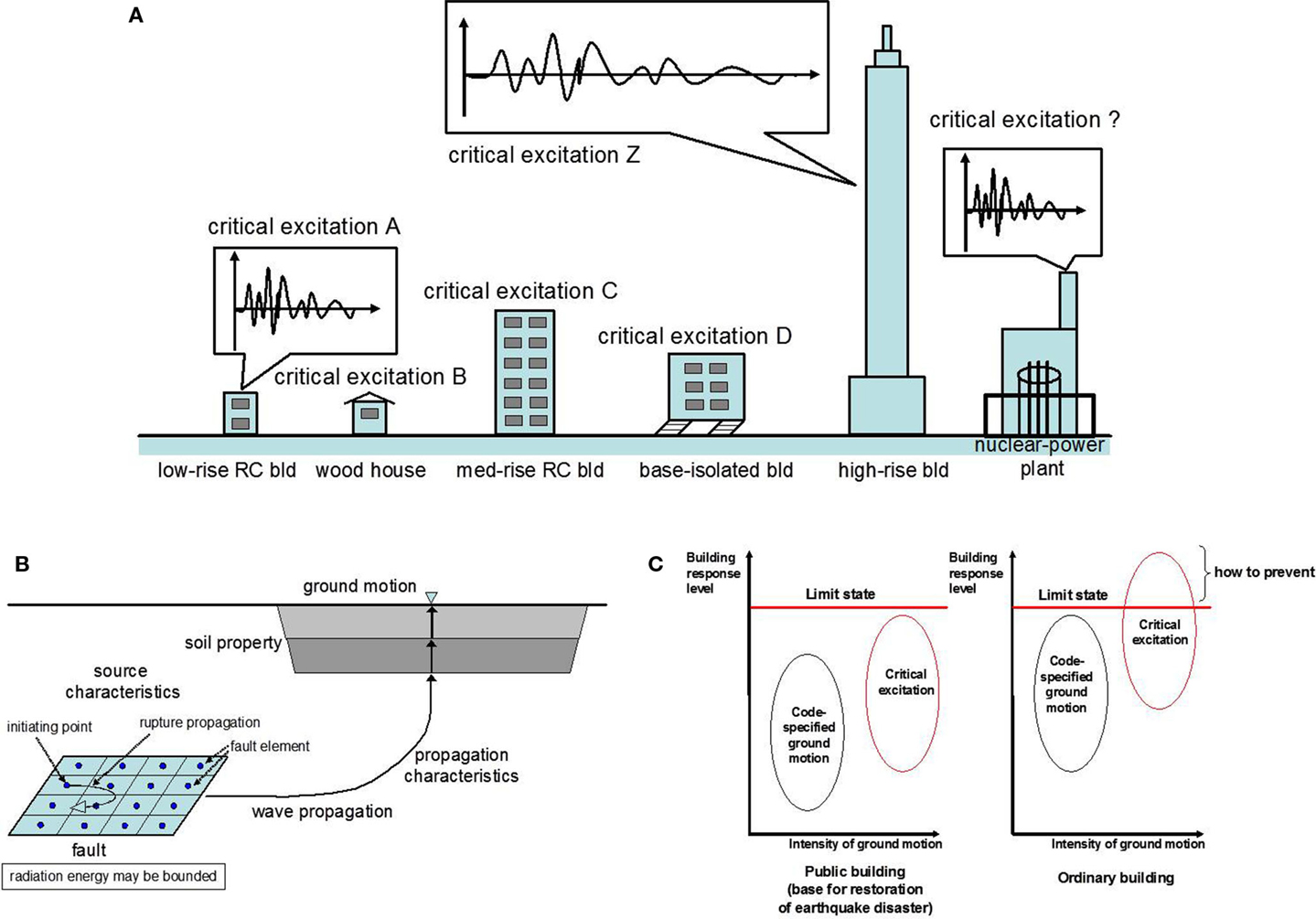
Figure 1. (A) Critical excitation for each building and facility (Takewaki, 2008a), (B) earthquake ground motion depending on fault rupture mechanism, wave propagation and surface ground amplification, etc. (Takewaki, 2006/2013), (C) relation of critical excitation with code-specified ground motion in public and ordinary buildings (Takewaki, 2006/2013).
After Drenick and Shinozuka’s pioneering work (1970), versatile researches have been developed (Iyengar and Manohar, 1985; 1987; Pirasteh et al., 1988; Srinivasan et al., 1992; Manohar and Sarkar, 1995; Pantelides and Tzan, 1996; Tzan and Pantelides, 1996; Takewaki, 2000; 2001a;b; 2008a; Abbas and Manohar, 2002; Fujita et al., 2010a; Moustafa and Takewaki, 2010a;b; Moustafa et al., 2010; Moustafa, 2011; Takewaki et al., 2012). Details of critical excitation methods are given in Takewaki (2006/2013).
In the case where influential active faults are known during the design stage of a structure (especially an important structure), the effects of these active faults should be taken into account through the concept of critical excitation. While influential active faults are not necessarily known in advance, virtual or scenario faults and their energy can be predefined, especially for the design of important and socially influential structures. It is believed that earthquakes have an upper bound on magnitude (Strasser and Bommer, 2009). The combination of worst-case analysis (Takewaki, 2004; 2005) with appropriate specification of energy levels (Boore, 1983) derived from the analysis of various factors, e.g., the fault rupture mechanism and earthquake occurrence probability, enables more robust and reliable seismic-resistant design methods (Figure 1B). The appropriate setting of energy levels or information used in the worst-case analysis is important, and more research should be conducted on this subject.
In other words, the earthquake energy radiated from the fault has an upper bound (Trifunac, 2008). The problem is to find the most unfavorable ground motion for a (group of) building(s) (Figure 1A) (Takewaki et al., 2013). A ground motion displacement spectrum or acceleration spectrum has been proposed at the rock surface depending on the seismic moment, distance from the fault, etc. (Figure 1B) (Boore, 1983). Such spectra may have uncertainties. One possibility or approach is to specify the acceleration or velocity power while allowing variability of the spectrum (Takewaki and Tsujimoto, 2011; Takewaki et al., 2013).
The problem of ground motion variability is very important and difficult. Code-specified design ground motions are usually constructed by taking past observations and probabilistic insights into account. However, as stated above, uncertainties in the occurrence of earthquakes (or ground motions), fault rupture mechanisms, wave propagation mechanisms, ground properties, etc., cause much difficulty in defining reasonable design ground motions, especially for important buildings in which damage or collapse has to be avoided absolutely (see Figure 1C) (Anderson and Bertero, 1987; Geller et al., 1997; Stein, 2003; Takewaki, 2006/2013).
A long-period ground motion has been observed in Japan recently (Takewaki et al., 2011a). This type of ground motion is reported to require large seismic demands on such structures as high-rise buildings, base-isolated buildings, oil tanks, etc., which have a long natural period. This large seismic demand is induced by the resonance between the long-period ground motion and the long natural period of these constructed facilities. To the best of the author’s knowledge, a promising approach is to shift the natural period of the building and add damping to the building by taking full advantage of technologies via seismic control (Takewaki, 2009). However, it is also understood that seismic control is still under development, while sufficient time is necessary to respond to uncertain ground motions. It is hoped that the approach of critical excitation methods (Takewaki et al., 2013) will help the development of new seismic-resistant design methods of buildings for such unpredicted or unpredictable ground motions. Critical excitation problems for fully non-stationary excitation models [see, for examples, Conte and Peng (1997), Fang and Sun (1997)] and critical excitation problems for elastic–plastic responses subjected to those excitations seem to be challenging problems.
As for response combination by multiple actions, Menun and Der Kiureghian (2000a;b) discussed the evaluation methods of envelopes for seismic response vectors. The normal stress in a structural member under combined loading of axial and bending actions may be one example. This problem is related to interval analysis (Fujita and Takewaki, 2011a;b) and its further development is warranted.
Structural Parameter Specification
Structural control with passive dampers has a successful history in mechanical and aerospace engineering, probably because these fields usually deal with predictable external loading and environments with little uncertainty. This technique is also supported by various methods of structural health monitoring (Takewaki et al., 2011b). However, in civil engineering, the situation is different (Housner, 1997; Soong and Dargush, 1997; Srinivasan and McFarland, 2000; Cheng et al., 2008; Takewaki, 2009). Building and civil structures are often subjected to severe earthquake ground motions, wind disturbances, and other external loading with large uncertainties (Takewaki, 2006/2013). It is therefore inevitable to take these uncertainties into account in structural design and its application to actual structures.
Interval analysis [see, for example, Moore (1966), Alefeld and Herzberger (1983), Qiu (2003), Chen and Wu (2004), Chen et al. (2009)] in terms of uncertain structural parameters is an effective tool for evaluating the sustainability of buildings in earthquake-prone countries. The number of combinations of uncertain structural parameters increases exponentially, but this difficulty can be overcome by introducing a sensitivity analysis or Taylor series expansion.
The critical combination of interval parameters is found by introducing an assumption of “inclusion monotony” as well as sensitivity information from Taylor series expansion. It has been demonstrated that the proposed method is useful for the development of the concept of sustainable building design under uncertain structural-parameter environments.
The concept of sustainable building design under uncertain structural-parameter environments is illustrated in Figure 2A. The member stiffness and strength of buildings are uncertain due to various factors resulting from randomness, material deterioration, temperature dependence, etc. The damping coefficients of structural members and/or passive dampers may also be uncertain (Takewaki and Ben-Haim, 2005). Several kinds of methods have been proposed to describe this uncertainty (Ben-Haim and Elishakoff, 1990; Ben-Haim et al., 1996; Ben-Haim, 2001/2006). The time variation of Young’s modulus and damping coefficients are shown in Figure 2A as representative examples. Karbhari and Lee (2009) discuss the service life estimation and extension of civil engineering structures from the viewpoints of material deterioration. These member and/or damper uncertainties lead to response variability of buildings under earthquake ground motions. Efficient and reliable methods are desired for predicting the upper bound of such building response.
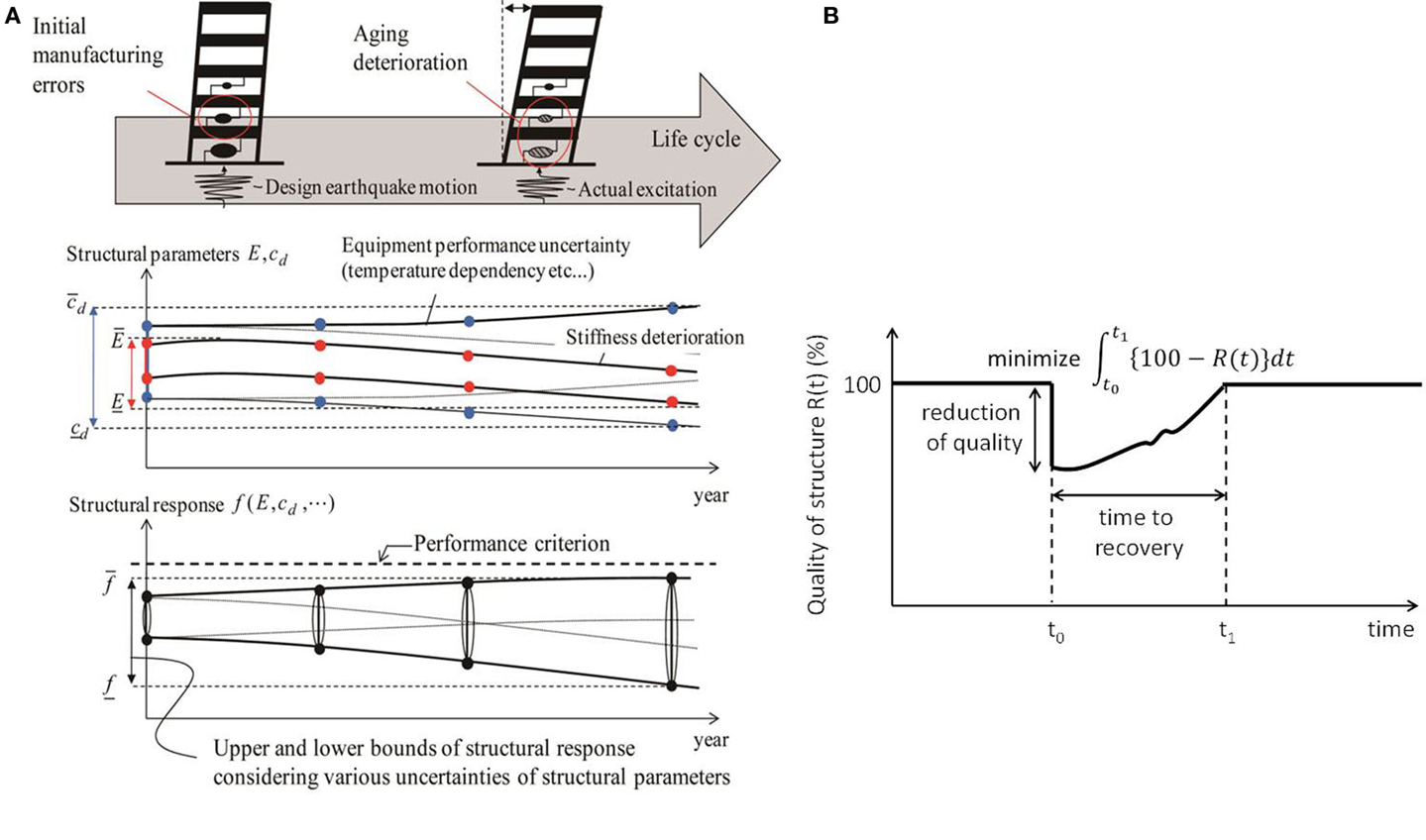
Figure 2. (A) Sustainable design concept considering varied structural performance caused by various uncertainties of structural parameters (Fujita and Takewaki, 2011b), (B) example of earthquake resilience measure.
As stated above, interval analysis in terms of uncertain structural parameters is an effective tool for evaluating the response variability and the sustainability of buildings in earthquake-prone countries. The number of combinations of end-points of uncertain structural parameters increases exponentially, while the evaluation of the upper and lower bounds of the objective function requires elaborate manipulation. It has been shown that this difficulty can be overcome by introducing the sensitivity or Taylor series expansion analysis.
Recently, various kinds of problems with uncertain parameters have been dealt with (Kanno and Takewaki, 2006; Takewaki, 2008b; Fujita and Takewaki, 2011a;b; 2012; Takewaki and Fujita, 2014).
Unpredicted Phenomena
In recent years, unexpected phenomena in earthquake engineering have proved to be possible in a real world: for example, resonance of building vibration to ground motion in Mexico (1985) and Tohoku (2011), pulse-type ground motion in Northridge (1994) and Kobe (1995), large fault displacement in Chi–Chi (1999), giant tsunami, long-period long-duration ground motion, and soil liquefaction under smaller vibration level with longer duration in Tohoku (2011). The effects by torsional response of buildings with eccentricity and soil-structure interaction under rather soft ground may cause further unpredicted phenomena.
Because super high-rise buildings in megacities in Japan had never been shaken intensively by so-called long-period ground motions before March 11, 2011, the response of high-rise buildings to such long-period ground motions is one of the most controversial subjects and issues in the field of earthquake-resistant design in Japan (Takewaki et al., 2012; 2011a). Ground motions with large levels of velocity response spectrum in a broad frequency range including the period of 5–10 s is called the long-period ground motion. It is worth noting that most of high-rise and super-high-rise buildings in Japan have never been designed based on careful recognition of such issue. The analysis of possibility of occurrence of long-period ground motions should be investigated in more detail. The inspection of deep ground profiles may be absolutely necessary (Takewaki et al., 2011a, 2012; 2013).
Smart prediction and preparedness are extremely important and suitable for responding to such unexpected phenomena and for addressing issues related to earthquake engineering.
Strategy for Uncertainties
Worst-Case Analysis
A significance of critical excitation is supported by its broad perspective. In general, there are two classes of buildings in a city. One is the important buildings, which play an important role during disastrous earthquakes. The other is ordinary buildings. The former should not be damaged during earthquakes, while some partial damage is acceptable for the latter, especially under critical excitation that is larger than code-specified design earthquakes (see Figure 1C). The concept of critical excitation may enable structural designers to make ordinary buildings more seismic-resistant (Takewaki, 2006/2013; Takewaki et al., 2012). The worst-case analysis is also characterized by the word of “Anti-optimization” (Elishakoff and Ohsaki, 2010). While the design of minimum cost corresponds to the design of minimum response for limited materials and a specified input, the design obtained by the anti-optimization means the design of maximum response for variable inputs.
Structural Control and Health Monitoring
While structural control is a promising and smart tool for sustainable building design (Fujita et al., 2010b), it is also true that a lot of uncertainties should be quantified for reliable implementation of these techniques (Takewaki and Ben-Haim, 2005). The sustainable building design under uncertain structural-parameter environment may be one of the most challenging issues in the building structural engineering. Even if all the design constraints are satisfied at the initial construction stage, some responses to external loadings (earthquakes, strong winds, etc.) may ultimately come to violate them over service life due to randomness, material deterioration, temperature dependence, etc. To overcome such difficulties, response evaluation methods for uncertain structural-parameter environments are needed. By predicting the response variability accurately, the elongation of service life of buildings may be possible.
Enhancement of Earthquake Resilience
Bruneau and Reinhorn (2006) discussed the earthquake resilience of building structures and infrastructures. They defined “the resilient structures” as (1) those with small collapse probability, (2) those with reduced consequences from failures in terms of lives lost, damage, and negative economic and social consequences, (3) reduced time to recovery. Figure 2B shows the temporal variation of performance and functionality of a structure after an earthquake. The requirements of (2) and (3) may be understood so that the minimization of the time integral of the reduction of quality, (100-Quality), corresponds to the upgrade of the resilience of the structure. They proposed four resilience measures; (1) robustness, (2) redundancy, (3) resourcefulness, (4) rapidity.
Concluding Remarks
There exist aleatory and epistemic uncertainties in the seismic structural design under earthquake ground motions. The aleatory uncertainty represents the uncertainty related to inherent randomness of a phenomenon, which cannot be reduced by the advancement of research and the epistemic uncertainty means the uncertainty concerned with knowledge which can be reduced by the development of research. While uncertainties in modeling earthquake ground motions seem to include both aleatory and epistemic uncertainties because of their extremely small probability of occurrence, uncertainties in modeling structural properties of buildings seem to contain mostly aleatory uncertainties based on the rapid advance of research in this field (although compared to the nature and level of input uncertainties). It is desired to narrow the region of epistemic uncertainties both in modeling earthquake ground motions and structural properties. Worst-case analysis, structural control and health monitoring, and introduction of the concept of earthquake resilience may be promising strategies for overcoming such unavoidable uncertainties.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abbas, M., and Manohar, C. S. (2002). Investigations into critical earthquake excitations within deterministic and probabilistic frameworks. Earthq. Eng. Struct. Dyn. 31, 813–832. doi: 10.1002/eqe.124.abs
Alefeld, G., and Herzberger, J. (1983). Introduction to Interval Computations. New York: Academic Press.
Anderson, J. C., and Bertero, V. V. (1987). Uncertainties in establishing design earthquakes. J. Struct. Eng. ASCE 113, 1709–1724. doi:10.1061/(ASCE)0733-9445(1987)113:8(1709)
Ariga, T., Kanno, Y., and Takewaki, I. (2006). Resonant behavior of base-isolated high-rise buildings under long-period ground motions. Struct. Des. Tall Spec. Build. 15, 325–338. doi:10.1002/tal.298
Ben-Haim, Y. (2001/2006). Infomation-Gap Decision Theory: Decisions Under Severe Uncertainty. London: Academic Press.
Ben-Haim, Y., Chen, G., and Soong, T. T. (1996). Maximum structural response using convex models. J. Eng. Mech. ASCE 122, 325–333. doi:10.1061/(ASCE)0733-9399(1996)122:4(325)
Ben-Haim, Y., and Elishakoff, I. (1990). Convex Models of Uncertainty in Applied Mechanics. Amsterdam: Elsevier.
Boore, D. M. (1983). Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra. BSSA 73, 1865–1894.
Bruneau, M., and Reinhorn, A. (2006). “Overview of the resilience concept,” in Proc. 8th US Nat. Conf. on Earthq. Eng., San Francisco.
Çelebi, M., Okawa, I., Kashima, T., Koyama, S., and Iiba, M. (2014). Response of a tall building far from the epicenter of the 11 March 2011 M9.0 Great East Japan earthquake and aftershocks. Struct. Des. Tall Spec. Build. 23, 427–441. doi:10.1002/tal.1047
Chen, S. H., Ma, L., Meng, G. W., and Guo, R. (2009). An efficient method for evaluating the natural frequency of structures with uncertain-but-bounded parameters. Comput. Struct. 87, 582–590. doi:10.1016/j.compstruc.2009.02.009
Chen, S. H., and Wu, J. (2004). Interval optimization of dynamic response for structures with interval parameters. Comput. Struct. 82, 1–11. doi:10.1016/j.compstruc.2003.09.001
Cheng, F. Y., Jiang, H., and Lou, K. (2008). Smart Structures: Innovative Systems for Seismic Response Control. CRC Press.
Conte, J. P., and Peng, B. F. (1997). Fully nonstationary analytical earthquake ground motion model. J. Eng. Mech. ASCE 123, 15–24. doi:10.1061/(ASCE)0733-9399(1997)123:1(15)
Conte, J. P., Pister, K. S., and Mahin, S. A. (1992). Nonstationary ARMA modeling of seismic motions. Soil Dyn. Earthq. Eng. 11, 411–426. doi:10.1016/0267-7261(92)90005-X
Drenick, R. F. (1970). Model-free design of aseismic structures. J. Eng. Mech. Div. ASCE 96, 483–493.
Elishakoff, I., and Ohsaki, M. (2010). Optimization and Anti-Optimization of Structures Under Uncertainty. London: Imperial College Press.
Fang, T., and Sun, M. (1997). A unified approach to two types of evolutionary random response problems in engineering. Arch. Appl. Mech. 67, 496–506. doi:10.1007/s004190050134
Fujita, K., Moustafa, A., and Takewaki, I. (2010a). Optimal placement of viscoelastic dampers and supporting members under variable critical excitations. Earthq. Struct. 1, 43–67. doi:10.12989/eas.2010.1.1.043
Fujita, K., Yamamoto, K., and Takewaki, I. (2010b). An evolutionary algorithm for optimal damper placement to minimize intestorey-drift transfer function. Earthq. Struct. 1, 289–306. doi:10.12989/eas.2010.1.3.289
Fujita, K., and Takewaki, I. (2011a). An efficient methodology for robustness evaluation by advanced interval analysis using updated second-order Taylor series expansion. Eng. Struct. 33, 3299–3310. doi:10.1016/j.engstruct.2011.08.029
Fujita, K., and Takewaki, I. (2011b). Sustainable building design under uncertain structural-parameter environment in seismic-prone countries. Sustain. Cities Soc. 1, 142–151. doi:10.1016/j.scs.2011.07.001
Fujita, K., and Takewaki, I. (2012). Robust passive damper design for building structures under uncertain structural parameter environments. Earthq. Struct. 3, 805–820. doi:10.12989/eas.2012.3.6.805
Geller, R. J., Jackson, D. D., Kagan, Y. Y., and Mulargia, F. (1997). Earthquakes cannot be predicted. Science 275, 1616. doi:10.1126/science.275.5306.1616
Housner, G., Bergman, L. A., Caughey, T. K., Chassiakos, A. G., Claus, R. O., Masri, S. F., et al. (1997). Special issue, structural control: past, present, and future. J. Eng. Mech. ASCE 123(9), 897–971.
Iyengar, R. N., and Manohar, C. S. (1985). “System dependent critical stochastic seismic excitations,” in M15/6, Proc. of the 8th Int. Conf. on SMiRT, Brussels.
Iyengar, R. N., and Manohar, C. S. (1987). Nonstationary random critical seismic excitations. J. Eng. Mech. ASCE 113, 529–541. doi:10.1061/(ASCE)0733-9399(1987)113:4(529)
Kanno, Y., and Takewaki, I. (2006). Sequential semidefinite program for maximum robustness design of structures under load uncertainties. J. Optim. Theory Appl. 130, 265–287. doi:10.1007/s10957-006-9102-z
Karbhari, V. M., and Lee, L. S.-W. (2009). “Vibration based damage detection techniques for structural health monitoring of civil infrastructure systems,” in Chapter 6 in Structural Health Monitoring of Civil Infrastructure Systems, ed. V. M. Karbhari and F. Ansari (Cambridge: CRC Press/Woodhead Publishing), 177–212.
Manohar, C. S., and Sarkar, A. (1995). Critical earthquake input power spectral density function models for engineering structures. Earthq. Eng. Struct. Dyn. 24, 1549–1566. doi:10.1002/eqe.4290241202
Menun, C., and Der Kiureghian, A. (2000a). Envelopes for seismic response vectors: I theory. J. Struct. Eng. ASCE 126, 467–473. doi:10.1061/(ASCE)0733-9445(2000)126:4(474)
Menun, C., and Der Kiureghian, A. (2000b). Envelopes for seismic response vectors: II application. J. Struct. Eng. ASCE 126, 474–481. doi:10.1061/(ASCE)0733-9445(2000)126:4(474)
Minami, Y., Yoshitomi, S., and Takewaki, I. (2013). System identification of super high-rise buildings using limited vibration data during the 2011 Tohoku (Japan) earthquake. Struct. Control Health Monit. 20, 1317–1338. doi:10.1002/stc.1537
Moustafa, A. (2011). Damage-based design earthquake loads for single-degree-of-freedom inelastic structures. J. Struct. Eng. ASCE 137, 456–467. doi:10.1061/(ASCE)ST.1943-541X.0000074
Moustafa, A., and Takewaki, I. (2010a). Critical characterization and modeling of pulse-like near-fault strong ground motion. Struct. Eng. Mech. 34, 755–778. doi:10.12989/sem.2010.34.6.755
Moustafa, A., and Takewaki, I. (2010b). Deterministic and probabilistic representation of near-field pulse-like ground motion. Soil Dyn. Earthq. Eng. 30, 412–422. doi:10.1016/j.soildyn.2009.12.013
Moustafa, A., Ueno, K., and Takewaki, I. (2010). Critical earthquake loads for SDOF inelastic structures considering evolution of seismic waves. Earthq. Struct. 1, 147–162. doi:10.12989/eas.2010.1.2.147
Pantelides, C. P., and Tzan, S. R. (1996). Convex model for seismic design of structures: I analysis. Earthq. Eng. Struct. Dyn. 25, 927–944. doi:10.1002/(SICI)1096-9845(199609)25:9<927::AID-EQE594>3.0.CO;2-H
Pirasteh, A. A., Cherry, J. L., and Balling, R. J. (1988). The use of optimization to construct critical accelerograms for given structures and sites. Earthq. Eng. Struct. Dyn. 16, 597–613. doi:10.1002/eqe.4290160410
Qiu, Z. P. (2003). Comparison of static response of structures using convex models and interval analysis method. Int. J. Numer. Methods Eng. 56, 1735–1753. doi:10.1002/nme.636
Shinozuka, M. (1970). Maximum structural response to seismic excitations. J. Eng. Mech. Div. ASCE 96, 729–738.
Soong, T. T., and Dargush, G. F. (1997). Passive Energy Dissipation Systems in Structural Engineering. Chichester: John Wiley & Sons.
Srinivasan, A. V., and McFarland, D. M. (2000). Smart Structures: Analysis and Design. Cambridge: Cambridge University Press.
Srinivasan, M., Corotis, R., and Ellingwood, B. (1992). Generation of critical stochastic earthquakes. Earthq. Eng. Struct. Dyn. 21, 275–288. doi:10.1002/eqe.4290210401
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Stein, R. S. (2003). Earthquake conversations. Sci. Am. 288, 72–79. doi:10.1038/scientificamerican0103-72
Strasser, F. O., and Bommer, J. J. (2009). Large-amplitude ground-motion recordings and their interpretations. Soil Dyn. Earthq. Eng. 29, 1305–1329. doi:10.1016/j.soildyn.2009.04.001
Takewaki, I. (2000). Optimal damper placement for critical excitation. Probab. Eng. Mech. 15, 317–325. doi:10.1016/S0266-8920(99)00033-8
Takewaki, I. (2001a). A new method for nonstationary random critical excitation. Earthq. Eng. Struct. Dyn. 30, 519–535. doi:10.1002/eqe.21
Takewaki, I. (2001b). Critical excitation for elastic-plastic structures via statistical equivalent linearization. Probab. Eng. Mech. 17, 73–84. doi:10.1016/S0266-8920(01)00030-3
Takewaki, I. (2004). Bound of earthquake input energy. J. Struct. Eng. ASCE 130, 1289–1297. doi:10.1061/(ASCE)0733-9445(2004)130:9(1289)
Takewaki, I. (2005). Bound of earthquake input energy to soil-structure interaction systems. Soil Dyn. Earthq. Eng. 25, 741–752. doi:10.1016/j.soildyn.2004.11.017
Takewaki, I. (2006/2013). Critical Excitation Methods in Earthquake Engineering, 1st and 2nd Edn. London: Elsevier.
Takewaki, I. (2008a). “Critical Excitation Methods for Important Structures”, Invited as a Semi-Plenary Speaker. Southampton: EURODYN.
Takewaki, I. (2008b). Robustness of base-isolated high-rise buildings under code-specified ground motions. Struct. Des. Tall Spec. Build. 17, 257–271. doi:10.1002/tal.350
Takewaki, I. (2009). Building Control with Passive Dampers: Optimal Performance-Based Design for Earthquakes. Singapore: John Wiley & Sons Ltd.
Takewaki, I., and Ben-Haim, Y. (2005). Info-gap robust design with load and model uncertainties. J. Sound Vib. 288, 551–570. doi:10.1016/j.jsv.2005.07.005
Takewaki, I., Conte, J. P., Mahin, S. A., and Pister, K. S. (1991). A unified earthquake-resistant design method for steel frames using ARMA models. Earthq. Eng. Struct. Dyn. 20, 483–501. doi:10.1002/eqe.4290200508
Takewaki, I., and Fujita, K. (2014). “Robust control of building structures under uncertain conditions,” in Encyclopedia of Earthquake Engineering, eds M. Beer, E. Patelli, I. Kougioumtzoglou, and I. Siu-Kui (Berlin, Heidelberg: Springer-Verlag).
Takewaki, I., Fujita, K., and Yoshitomi, S. (2013). Uncertainties in long-period ground motion and its impact on building structural design: case study of the 2011 Tohoku (Japan) earthquake. Eng. Struct. 49, 119–134. doi:10.1016/j.engstruct.2012.10.038
Takewaki, I., Moustafa, A., and Fujita, K. (2012). Improving the Earthquake Resilience of Buildings: The Worst Case Approach. London: Springer.
Takewaki, I., Murakami, S., Fujita, K., Yoshitomi, S., and Tsuji, M. (2011a). The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 31, 1511–1528. doi:10.1016/j.soildyn.2011.06.001
Takewaki, I., Nakamura, M., and Yoshitomi, S. (2011b). System Identification for Structural Health Monitoring. Southampton: WIT Press.
Takewaki, I., and Tsujimoto, H. (2011). Scaling of design earthquake ground motions for tall buildings based on drift and input energy demands. Earthq. Struct. 2, 171–187. doi:10.12989/eas.2011.2.2.171
Trifunac, M. D. (2008). Energy of strong motion at earthquake source. Soil Dyn. Earthq. Eng. 28, 1–6. doi:10.1039/c4sm00280f
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: earthquake engineering, uncertainty, ground motion, structural parameter, interval analysis, robustness, redundancy
Citation: Takewaki I (2015) Beyond uncertainties in earthquake structural engineering. Front. Built Environ. 1:1. doi: 10.3389/fbuil.2015.00001
Received: 23 October 2014; Accepted: 04 February 2015;
Published: 18 February 2015.
Edited by:
Nikos D. Lagaros, National Technical University of Athens, GreeceReviewed by:
Sameh Samir F. Mehanny, Cairo University, EgyptCopyright: © 2015 Takewaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence:dGFrZXdha2lAYXJjaGkua3lvdG8tdS5hYy5qcA==
 Izuru Takewaki
Izuru Takewaki