- Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyoto, Japan
A theory of earthquake input energy to building structures under single impulse is useful for disclosing the property of energy transfer function. This property shows that the area of the energy transfer function is constant irrespective of natural period and damping of building structures. However, single impulse may be unrealistic from a certain viewpoint because the frequency characteristic of input cannot be expressed by this input. In order to resolve such issue, a double impulse is introduced in this paper. The frequency characteristic of the Fourier amplitude of the double impulse is found in an explicit manner and a critical excitation problem is formulated with an interval of two impulses as a variable. The solution to that critical excitation problem is derived. An upper bound of the earthquake input energy is then derived by taking full advantage of the property of the energy transfer function that the area of the energy transfer function is constant. The relation of the double impulse to the corresponding one-cycle sinusoidal wave as a representative of near-fault pulse-type waves is also investigated.
Introduction
In the history of seismic resistant design of building structures, the earthquake input energy has played an important role together with deformation and acceleration (for example, Housner, 1959, 1975; Berg and Thomaides, 1960; Housner and Jennings, 1975; Zahrah and Hall, 1984; Akiyama, 1985; Ohi et al., 1985; Uang and Bertero, 1990; Leger and Dussault, 1992; Fajfar and Vidic, 1994; Kuwamura et al., 1994; Riddell and Garcia, 2001; Trifunac et al., 2001; Takewaki, 2004a,b; Trifunac, 2008). While deformation and acceleration can predict and evaluate the performance of a building structure mainly for serviceability, the energy can evaluate the performance of a building structure mainly for safety. Especially, energy is appropriate for describing the performance of building structures of different sizes in a unified manner because energy is a global index different from deformation and acceleration as local indices.
Compared with most of the previous works dealing with time histories, the earthquake input energy is formulated here in the frequency domain (Lyon, 1975; Ordaz et al., 2003; Takewaki, 2004a,b, 2005a,b; Takewaki and Fujita, 2009; Kojima et al., 2015) to enable the derivation of bound of earthquake input energy, which is useful for the design of building structures under uncertain conditions. Another advantageous feature to introduce the upper bound of input energy is to avoid the infinite numerical integration required in the frequency-domain formulation (Kojima et al., 2015). When the structure becomes stiffer, the contribution from higher excitation frequencies is not negligible (a smaller time increment is required in the time domain). In such a case, the avoidance of the infinite numerical integration in the frequency domain may be useful.
A theory of earthquake input energy to building structures under single impulse has been shown to be useful for disclosing the property of energy transfer function (Takewaki, 2004a). This property means that the area of the energy transfer function is constant. The property of the energy transfer function similar to the case of a simple single-degree-of-freedom (SDOF) model has also been clarified for a swaying-rocking model. By using this property, the mechanism of earthquake input energy to the swaying-rocking model including the soil amplification has been made clear under the input of single impulse (Kojima et al., 2015). However, single impulse may be unrealistic because the frequency characteristic of input cannot be expressed by this input. In order to resolve such issue, double impulse is introduced in this paper.
The double impulse represents a simplified version of near-fault pulse-type waves. For this class of ground motions, many useful research works have been conducted. Mavroeidis and Papageorgiou (2003) investigated the characteristics of this class of ground motions in detail and proposed some simple models (for example, Gabor wavelet and Berlage wavelet). Xu et al. (2007) employed a kind of Berlage wavelet and applied it to the performance evaluation of passive energy dissipation systems. Takewaki and Tsujimoto (2011) used the Xu’s approach and proposed a method for scaling ground motions from the viewpoints of drift and input energy demand. Takewaki et al. (2012) employed a sinusoidal wave for pulse-type waves. In this paper, a one-cycle sinusoidal wave is employed as a representative of near-fault pulse-type waves and is compared with the double impulse.
The frequency characteristic of the Fourier amplitude of the double impulse is found in an explicit manner and a critical excitation problem is formulated with an interval of two impulses as a variable. The solution to that critical excitation problem is then derived. An upper bound and a narrower upper bound of the earthquake input energy are derived by taking full advantage of the property of the energy transfer function that the area of the energy transfer function is constant. The narrower upper bound enables the evaluation of the upper bound of the earthquake input energy without infinite integration. Only a linear elastic response of an SDOF model is considered here for the introduction of the frequency-domain approach.
Earthquake Input Energy in Frequency Domain
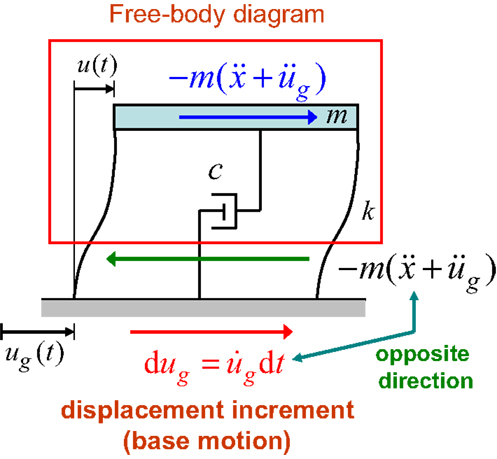
Consider a damped linear SDOF system of mass m, stiffness k, and damping coefficient c as shown in Figure 1. Let , h = c/(2 Ωm), and x denote the undamped natural circular frequency, the damping ratio, and the displacement of the mass relative to the ground, respectively. The time derivative is denoted by an over-dot. The input energy to this SDOF system by a unidirectional ground acceleration from t = 0 to t = t0 (end of input) can be defined by the work made by the ground on the structural system and is expressed by
The term indicates the inertial force with minus sign and is equal to the sum of the restoring force kx of the spring and the damping force cẋ of the dashpot in the system. Integration by parts of Eq. (1) provides
If the initial and terminal conditions are expressed by at t = 0 and at t = 0 and t = t0, the input energy can be reduced to the following form:
It is known (Page, 1952; Lyon, 1975; Ordaz et al., 2003; Takewaki, 2004a,b, 2005a,b; Takewaki and Fujita, 2009; Kojima et al., 2015) that the input energy per unit mass can also be expressed in the frequency domain by use of Fourier and inverse Fourier transformations.
where HV(ω; Ω, h) is the velocity transfer function defined by and F(ω) = − Re[HV(ω; Ω, h)]/π. and are the Fourier transforms of and , respectively. The function F(ω) is called the “energy transfer function” from the expression of Eq. (4). The symbol i denotes the imaginary unit. The velocity transfer function HV(ω; Ω, h) can be expressed explicitly by
The energy transfer function F(ω) can then be expressed by
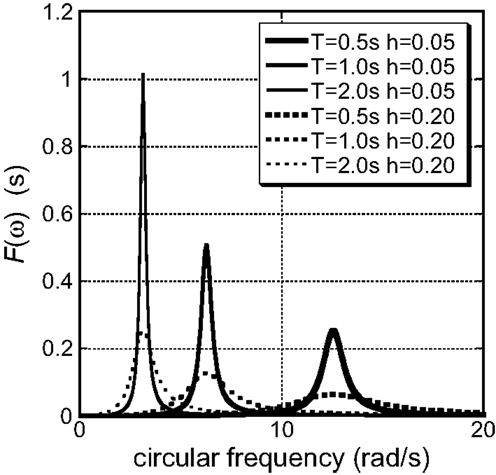
Equation (4) indicates that the earthquake input energy to a damped linear elastic SDOF system does not depend on the phase property of input motions and this fact is well known (Page, 1952; Lyon, 1975; Kuwamura et al., 1994; Ordaz et al., 2003; Takewaki, 2004a,b, 2005a,b; Takewaki and Fujita, 2009; Kojima et al., 2015). It can also be understood from Eq. (4) that the function F(ω) defined in Eq. (6) plays an important role in the evaluation of the earthquake input energy and may have some influence on the investigation of constancy property of the earthquake input energy for structures with various model parameters (natural period and damping ratio). The functions F(ω) for various natural periods T = 0.5, 1.0, 2.0 s and damping ratios h = 0.05, 0.20 are plotted in Figure 2. It is noteworthy that the area of F(ω) can be proved to be constant regardless of Ω and h. This fact for any damping ratio has already been pointed out by Ordaz et al. (2003). Its proof has been presented by Takewaki (2004a) and the property is shown in the following section.
Property of Energy Transfer Function
Consider the earthquake input energy to the SDOF model subjected to single impulse with = V, where δ(t) is the Dirac delta function. From Eq. (4), this earthquake input energy in a normalized form can be evaluated by
Equation (7) can be proved by taking into account that single impulse with = V is equivalent to the impulsive loading with the initial velocity of V in time domain (Takewaki, 2004a). Another proof may be possible with the help of the residue theorem (Ordaz et al., 2003; Takewaki, 2004a). This property of Eq. (7) will be used effectively in deriving the upper bounds of input energy subjected to double impulse in the Section “Bounds of Earthquake Input Energy to SDOF System Subjected to Double Impulse.”
Double Impulse Input
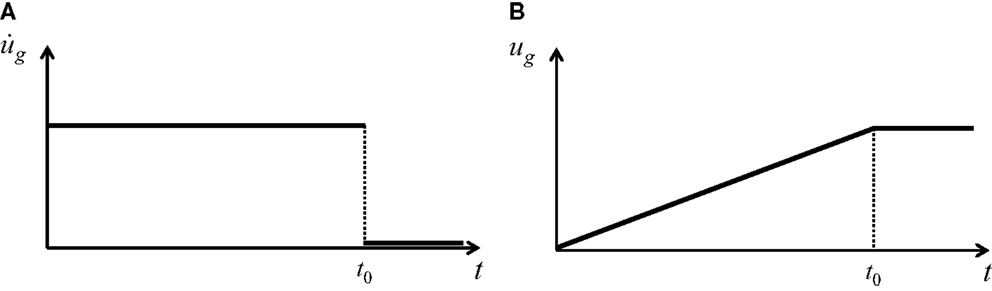
Consider a ground motion acceleration as double impulse, as shown in Figure 3A, expressed by
where V is the given initial velocity and t0 = π/ω0 (ω0: interval circular frequency) is the time interval between two impulses. The comparison with the corresponding one-cycle sinusoidal wave is also plotted in Figure 3A. The application of the double impulse and one-cycle sinusoidal wave to an actual recorded ground motion (NS-component at Kobe University during 1995 Hyogoken-Nanbu earthquake) is shown in Figure 3B. It can be observed that a one-cycle sinusoidal wave of a predominant period 1.2 s can be a good substitute of a part of this recorded ground motion. The corresponding velocity and displacement of such double impulse are plotted in Figure 4. The Fourier transform of can be derived as
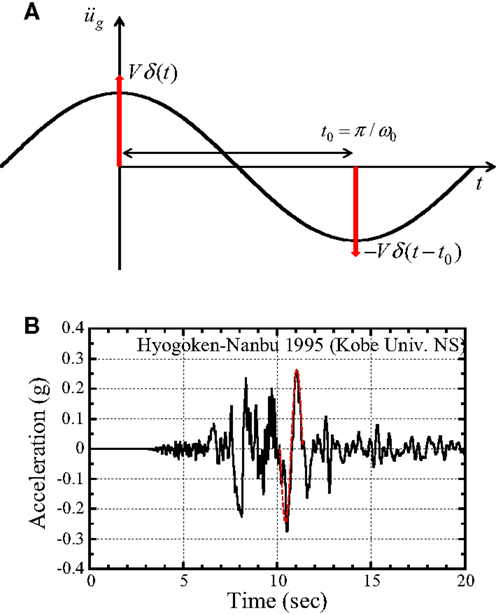
Figure 3. Earthquake ground motion acceleration as double impulse: (A) comparison with the corresponding one-cycle sinusoidal wave, (B) application to actual recorded ground motion.
The squared Fourier amplitude of the double impulse can then be computed as
Earthquake Input Energy by Double Impulse and the Corresponding Critical Excitation Problem
The substitution of Eq. (10) into Eq. (4) leads to
The critical excitation problem (Drenick, 1970; Takewaki, 2001a, 2013; Abbas and Manohar, 2002; Moustafa et al., 2010) can be formulated as
[Critical Excitation Problem]: Find the double impulse interval t0 for the fixed double impulse velocity V so as to maximize the earthquake input energy EI/(mV2).
By using F(ω) = 0 at ω = 0, ω →∞ and the integration by parts,
it can be shown that
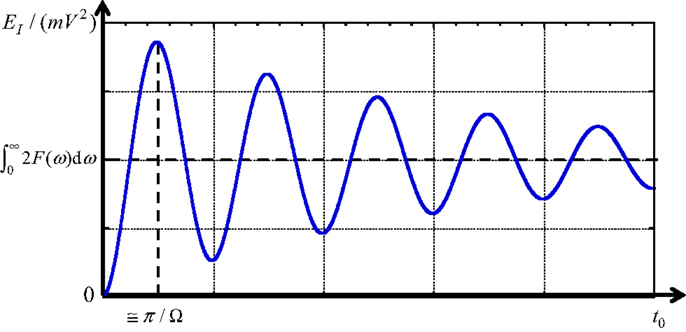
Then, the normalized earthquake input energy EI/(mV2) with respect to t0 can be sketched as shown in Figure 5. The wavy property comes from the timing of the correspondence of peaks of the energy transfer function F(ω) and the normalized squared Fourier amplitude (2 − 2cosω t0) of the double impulse shown in Figure 6.
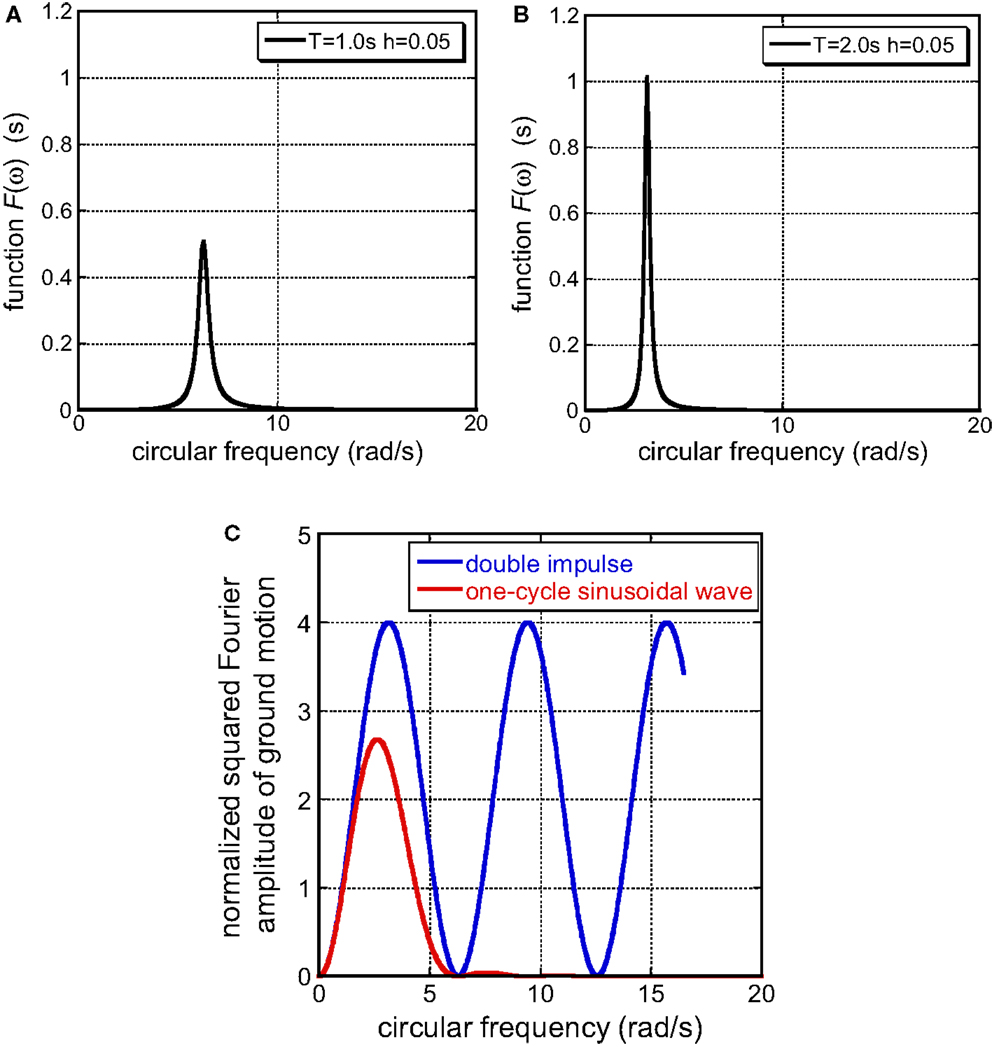
Figure 6. Relation of energy transfer function with normalized squared Fourier amplitude of double impulse: (A) energy transfer function with T = 1.0 s, h = 0.05, (B) energy transfer function with T = 2.0 s, h = 0.05, (C) normalized squared Fourier amplitude of double impulse [t0 = 1.0 s] and the corresponding one-cycle sinusoidal wave.
The condition to characterize the critical value t0 maximizing the earthquake input energy can be described as
This is the stationarity condition and the condition is expressed more explicitly by expanding the manipulation in Eq. (13) as follows.
The solution to the present critical excitation problem can be obtained as the first peak of EI/(mV2) as shown in Figure 5.
Figures 6A–C show two examples of the relation of energy transfer function with the normalized squared Fourier amplitude of ground motion (double impulse: t0 = 1.0 s). The normalized squared Fourier amplitude of the corresponding one-cycle sinusoidal wave is also plotted in Figure 6C. The normalization has been done for the square V2 of velocity amplitude. It can be understood that the double impulse is a good substitute of a one-cycle sinusoidal wave except the amplitude within a certain range. Since the first peak plays an important role as shown later (see “Numerical Example”), this limited correspondence is sufficient for the present formulation. It is further observed that the one-cycle sinusoidal wave exhibits a frequency characteristic slightly shorter than that for the double impulse. This is because, zero initial conditions of velocity and displacement are used for the one-cycle sinusoidal wave and the period of velocity and displacement waves become slightly shorter than that of the acceleration.
Bounds of Earthquake Input Energy to SDOF System Subjected to Double Impulse
Uncertainties exist in the Fourier amplitude of the double impulse. For example, the value V in Eq. (8) may be uncertain. If the value V becomes smaller, its Fourier amplitude can be bounded by the original one. It is therefore meaningful to discuss the upper bound of the earthquake input energy to the SDOF system.
Consider the bounds of the scaled earthquake input energy defined by Eq. (11). Since the energy transfer function F(ω) in Eq. (6) is usually positive, it is sufficient to discuss the envelope function of .
Let and denote the upper bound and the proposed narrower upper bound of the earthquake input energy using a narrower bound of Fourier amplitude (see Figure 7). and can then be derived as follows:
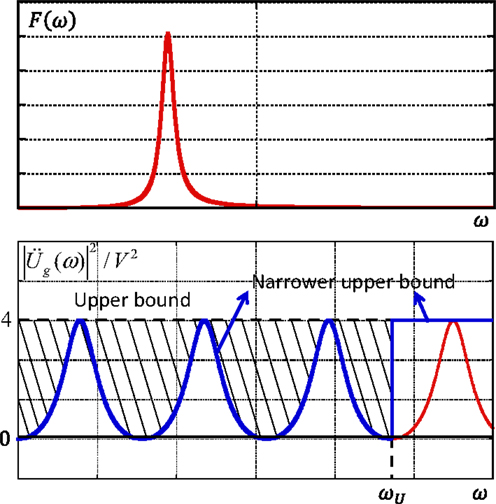
Figure 7. Energy transfer function and squared Fourier amplitude of double impulse for upper bound and narrower upper bound.
In Eq. (15b), ωU denotes the upper limit of circular frequency for computation of integration shown in Figure 7. The term {4 − (2 − 2cosω t0)} in Eq. (15b) indicates the shaded portion in Figure 7. The validity of inequality in Eq. (15b) can be proven by the property of F(ω) as a positive function and the relation 0 ≤2 −2 cos ω t0 ≤ 4. The positivity of F(ω) can be shown from the fact that, if some parts of F(ω) are negative, it contradicts the positivity of the energy consumption (total input energy) in the SDOF model subjected to an infinitely long sinusoidal ground motion expressed by a Dirac delta function at the corresponding frequency. Equation (15b) enables the evaluation of the upper bound of the scaled earthquake input energy without infinite integration by taking full advantage of Eq. (7).
Numerical Example
The validity of the solution to the critical excitation problem shown in the Section “Double Impulse Input” and the accuracy of the upper bound derived in the Section “Earthquake Input Energy by Double Impulse and the Corresponding Critical Excitation Problem” are demonstrated here. The accuracy of the frequency-domain formulation in the computation of earthquake input energy was demonstrated by Ordaz et al. (2003) and Takewaki (2004b) through the comparison with the result by the time-domain formulation.
Figure 8 shows the normalized input energy EI/(mV2) with respect to t0 for the SDOF model of Ω = 2π rad/s and h = 0.05 under the double impulse and the corresponding one-cycle sinusoidal wave. The principal property for the one-cycle sinusoidal wave can be captured by the double impulse except the amplitude (i.e., the critical period of the one-cycle sinusoidal wave can be obtained within a good approximation). The amplitudes depend on the normalization of both inputs and their difference does not cause any difficulty because the principal objective is to obtain the critical period of the one-cycle sinusoidal wave and the critical interval of the double impulse. In addition, a slightly shorter period characteristic can be observed for the one-cycle sinusoidal wave. This phenomenon results from the fact explained in Figure 6. It should be noted that the SDOF structural model is fixed as explained just before, and the interval of the double impulse is varied for finding the critical interval. During the variation of the interval, the velocity amplitude V is kept constant. Such a treatment of variation of the interval may be difficult for recorded ground motions because the amplitude of acceleration has to be changed depending on the interval for the constant velocity amplitude. It can be observed that EI/(mV2) exhibits the maximum value approximately at t0 = 0.5 s because π/Ω = 0.5 (Ω = 2π rad/s) in this model and certainly converges to , i.e., 1. From the practical point of view, t0 should be set between 0.25 and 2 s in order to express the characteristic period between 0.5 and 4 s of pulse-type waves.
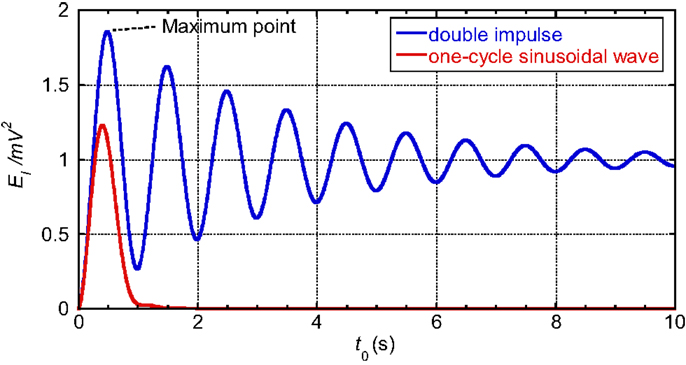
Figure 8. Normalized input energy EI/(mV2) with respect to t0 for Ω = 2π rad/s and h = 0.05 under double impulse and the corresponding one-cycle sinusoidal wave.
Figure 9 illustrates the convergence of EI/(mV2) with respect to ωmax, the upper bound of circular frequency for numerical integration. It can be understood that ωmax = 20 rad/s is almost sufficient for the estimation of the maximum value, which occurs approximately at t0 = 0.5 s in this case. On the other hand, ωmax = 100 rad/s is necessary for the estimation of the local minimum value, which occurs approximately at t0 = 1.0 s. This difference may result from the fact that, while the error is relatively large at the local minimum point, the error is relatively small at the maximum point. Since only the maximum point is meaningful, the large setting of ωmax for the local minimum value of earthquake input energy does not cause any problem.
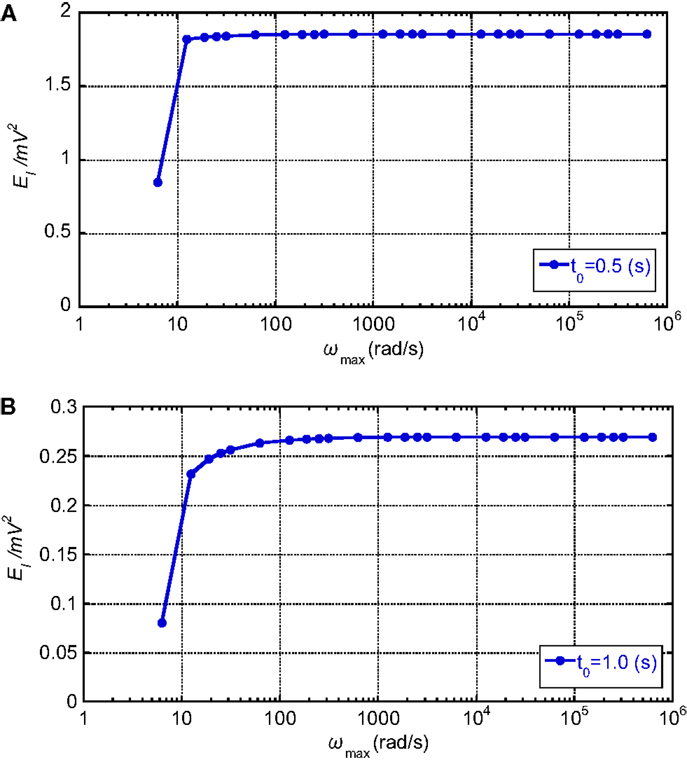
Figure 9. Convergence of EI/(mV2) with respect to ωmax, the upper bound of circular frequency for numerical integration. (A) t0 = 0.5 s. (B) t0 = 1.0 s.
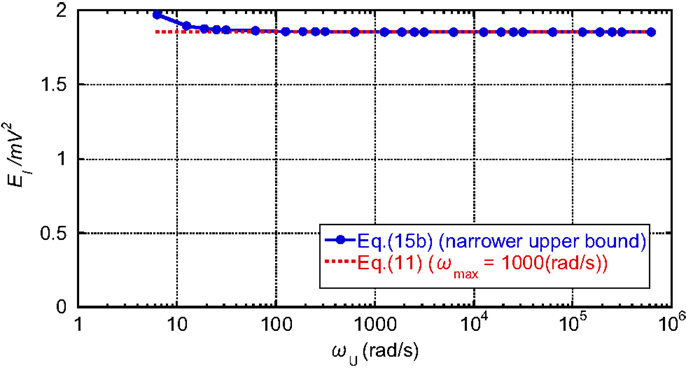
Figure 10 presents the comparison of the narrower upper bound given by Eq. (15b) with the exact one by Eq. (11). The parameters are Ω = 2π rad/s, h = 0.05, and ωmax = 1000 rad/s. The upper bound given by Eq. (15a) is 2.0. It can be observed that, as ωU (upper limit circular frequency for numerical integration) becomes larger than 20 rad/s, the narrower upper bound given by Eq. (15b) converges rapidly to the exact one by Eq. (11). About the triple of the fundamental natural circular frequency [Ω = 2π rad/s in this case] seems to be sufficient for practical computation.
Conclusion
The conclusions may be summarized as follows:
(1) When the ground motion is white-like (constant Fourier amplitude spectrum), the input energy to the structure is constant regardless of the natural period and damping ratio of the structure, i.e., input energy constant property. This input corresponds to single pulse. The input energy constant property can be proved by considering the physical meaning of the constant Fourier spectrum of the input ground motion in the time domain, i.e., the input of initial velocity at zero time.
(2) Double impulse is more realistic because the input frequency characteristic can be introduced. A critical excitation problem with an interval of two impulses as a variable can be formulated in the frequency domain and the solution to that critical excitation problem can be derived by drawing the graph of the normalized earthquake input energy with respect to the interval of two impulses. The solution to the present critical excitation problem can be obtained as the first peak of the normalized earthquake input energy.
(3) An upper bound and a narrower upper bound of the earthquake input energy to a SDOF model under double impulse input can be derived by taking full advantage of the property of the energy transfer function that the area of the energy transfer function is constant (input energy constant property) and introducing the envelope function in the Fourier transform of the double impulse input. The narrower upper bound enables the evaluation of the upper bound of the normalized earthquake input energy without infinite integration.
(4) Numerical examples demonstrate that the double impulse represents a one-cycle sinusoidal wave as an approximation of near-fault ground motions and can capture the critical property of near-fault ground motions (i.e., the critical period of the one-cycle sinusoidal wave can be obtained within a good approximation). Furthermore, the proposed upper bound of earthquake input energy can converge to an exact value as the upper limit of frequency ωU for numerical integration becomes larger.
Only elastic structures have been treated for simple presentation of the theory and the present method takes advantage of the energy transfer function approach, which can be used for elastic structures. An equivalent linearization technique (Caughey, 1960; Roberts and Spanos, 1990; Takewaki, 2001b) may be promising for inelastic structures. This formulation will be presented in the future.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Part of the present work is supported by the Grant-in-Aid for Scientific Research of Japan Society for the Promotion of Science (No. 24246095, No. 15H04079). This support is greatly appreciated.
References
Abbas, A. M., and Manohar, C. S. (2002). Investigations into critical earthquake load models within deterministic and probabilistic frameworks. Earthquake Eng. Struct. Dyn. 31, 813–832. doi: 10.1002/eqe.124.abs
Akiyama, H. (1985). Earthquake Resistant Limit-State Design for Buildings. Tokyo: University of Tokyo Press.
Berg, G. V., and Thomaides, T. T. (1960). “Energy consumption by structures in strong-motion earthquakes,” in Proceedings of 2nd World Conference on Earthquake Engineering, Tokyo, 681–696.
Caughey, T. K. (1960). Random excitation of a system with bilinear hysteresis. J. Appl. Mech. 27, 649–652. doi:10.1115/1.3644077
Fajfar, P., and Vidic, T. (1994). Consistent inelastic design spectra: hysteretic and input energy. Earthquake Eng. Struct. Dyn. 23, 523–537. doi:10.1002/eqe.4290230505
Housner, G. W. (1975). “Measures of severity of earthquake ground shaking,” in Proc. of the US National Conf. on Earthquake Engineering, Ann Arbor, MI, 25–33.
Housner, G. W., and Jennings, P. C. (1975). “The capacity of extreme earthquake motions to damage structures,” in Structural and Geotechnical Mechanics: A Volume Honoring N.M.Newmark, ed. W. J. Hall (Englewood Cliff, NJ: Prentice-Hall), 102–116.
Kojima, K., Sakaguchi, K., and Takewaki, I. (2015). Mechanism and bounding of earthquake energy input to building structure on surface ground subjected to engineering bedrock motion. Soil Dyn. Earthquake Eng. 70, 93–103. doi:10.1016/j.soildyn.2014.12.010
Kuwamura, H., Kirino, Y., and Akiyama, H. (1994). Prediction of earthquake energy input from smoothed Fourier amplitude spectrum. Earthquake Eng. Struct. Dyn. 1994, 1125–1137. doi:10.1002/eqe.4290231007
Leger, P., and Dussault, S. (1992). Seismic-energy dissipation in MDOF structures. J. Struct. Eng. 118, 1251–1269. doi:10.1061/(ASCE)0733-9445(1992)118:5(1251)
Mavroeidis, G. P., and Papageorgiou, A. S. (2003). A mathematical representation of near-fault ground motions. Bull. Seismol. Soc. Am. 93, 1099–1131. doi:10.1785/0120020100
Moustafa, A., Ueno, K., and Takewaki, I. (2010). Critical earthquake loads for SDOF inelastic structures considering evolution of seismic waves. Earthquake Struct. 1, 147–162. doi:10.12989/eas.2010.1.2.147
Ohi, K., Takanashi, K., and Tanaka, H. (1985). A simple method to estimate the statistical parameters of energy input to structures during earthquakes. J. Struct. Construct. Eng. Archi. Inst. Jpn. 347, 47–55.
Ordaz, M., Huerta, B., and Reinoso, E. (2003). Exact computation of input-energy spectra from Fourier amplitude spectra. Earthquake Eng. Struct. Dyn. 32, 597–605. doi:10.1002/eqe.240
Riddell, R., and Garcia, J. E. (2001). Hysteretic energy spectrum and damage control. Earthquake Eng. Struct. Dyn. 30, 1791–1816. doi:10.1002/eqe.93
Roberts, J. B., and Spanos, P. D. (1990). Random Vibration and Statistical Linearization. New York, NY: Wiley.
Takewaki, I. (2001a). A new method for nonstationary random critical excitation. Earthquake Eng. Struct. Dyn. 30, 519–535. doi:10.1002/eqe.21
Takewaki, I. (2001b). Probabilistic critical excitation for MDOF elastic-plastic structures on compliant ground. Earthquake Eng. Struct. Dyn. 30, 1345–1360. doi:10.1002/eqe.66
Takewaki, I. (2004a). Bound of earthquake input energy. J. Struct. Eng. 130, 1289–1297. doi:10.1061/(ASCE)0733-9445(2004)130:9(1289)
Takewaki, I. (2004b). Frequency domain modal analysis of earthquake input energy to highly damped passive control structures. Earthquake Eng. Struct. Dyn. 33, 575–590. doi:10.1002/eqe.361
Takewaki, I. (2005a). Bound of earthquake input energy to soil-structure interaction systems. Soil Dyn. Earthquake Eng. 25, 741–752. doi:10.1016/j.soildyn.2004.11.017
Takewaki, I. (2005b). Frequency domain analysis of earthquake input energy to structure-pile systems. Eng. Struct. 27, 549–563. doi:10.1016/j.engstruct.2004.11.014
Takewaki, I. (2013). Critical Excitation Methods in Earthquake Engineering, 2nd Edn. Oxford: Elsevier.
Takewaki, I., and Fujita, K. (2009). Earthquake input energy to tall and base-isolated buildings in time and frequency dual domains. J. Struct. Des. Tall Spec. Build. 18, 589–606. doi:10.1002/tal.497
Takewaki, I., Moustafa, A., and Fujita, K. (2012). Improving the Earthquake Resilience of Buildings: The Worst Case Approach. London: Springer.
Takewaki, I., and Tsujimoto, H. (2011). Scaling of design earthquake ground motions for tall buildings based on drift and input energy demands. Earthquake Struct. 2, 171–187. doi:10.12989/eas.2011.2.2.171
Trifunac, M. D. (2008). Energy of strong motion at earthquake source. Soil Dyn. Earthquake Eng. 28, 1–6. doi:10.1039/c4sm00280f
Trifunac, M. D., Hao, T. Y., and Todorovska, M. I. (2001). On Energy Flow in Earthquake Response. Report CE 01-03. University of Southern California, Los Angeles.
Uang, C. M., and Bertero, V. V. (1990). Evaluation of seismic energy in structures. Earthquake Eng. Struct. Dyn. 19, 77–90. doi:10.1002/eqe.4290190108
Xu, Z., Agrawal, A. K., He, W.-L., and Tan, P. (2007). Performance of passive energy dissipation systems during near-field ground motion type pulses. Eng. Struct. 29, 224–236. doi:10.1016/j.engstruct.2006.04.020
Keywords: earthquake input energy, double impulse, critical excitation method, energy transfer function, upper bound of input energy
Citation: Kojima K, Fujita K and Takewaki I (2015) Critical double impulse input and bound of earthquake input energy to building structure. Front. Built Environ. 1:5. doi: 10.3389/fbuil.2015.00005
Received: 08 April 2015; Accepted: 14 May 2015;
Published: 05 June 2015
Edited by:
Nikos D. Lagaros, National Technical University of Athens, GreeceReviewed by:
Chara C. Mitropoulou, National Technical University of Athens, GreeceAlfredo Camara, City University London, UK
Copyright: © 2015 Kojima, Fujita and Takewaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Izuru Takewaki, Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyotodaigaku-Katsura, Nishikyo, Kyoto 615-8540, Japan,dGFrZXdha2lAYXJjaGkua3lvdG8tdS5hYy5qcA==
 Kotaro Kojima
Kotaro Kojima Kohei Fujita
Kohei Fujita Izuru Takewaki
Izuru Takewaki