- Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyoto, Japan
The multiple impulse input is introduced as a substitute of the long-duration earthquake ground motion, mostly expressed in terms of harmonic waves, and a closed-form solution is derived of the elastic–plastic response of a single-degree-of-freedom structure under the “critical multiple impulse input.” Since only the free vibration appears under such multiple impulse input, the energy approach plays an important role in the derivation of the closed-form solution of a complicated elastic–plastic response. It is shown that the critical inelastic deformation and the corresponding critical input frequency can be captured depending on the input level by the substituted multiple impulse input in the form of original and modified input sequence. The validity and accuracy of the proposed theory are investigated through the comparison with the response analysis to the corresponding sinusoidal input as a representative of the long-duration earthquake ground motion.
Introduction
There are several types of earthquake ground motions. One is a near-fault ground motion, which is getting much interest recently, another is a random ground motion, which is represented by El Centro NS etc., and the other is a long-duration, long-period ground motion, which was observed rather recently [see Takewaki et al. (2011, 2012)]. The effects of near-fault ground motions on structural response have been investigated extensively (Bertero et al., 1978; Hall et al., 1995; Sasani and Bertero, 2000; Alavi and Krawinkler, 2004; Mavroeidis et al., 2004; Kalkan and Kunnath, 2006, 2007; Xu et al., 2007; Rupakhety and Sigbjörnsson, 2011; Yamamoto et al., 2011; Khaloo et al., 2015; Vafaei and Eskandari, 2015). The fling-step and forward-directivity are widely recognized as special keywords to characterize such near-fault ground motions (Mavroeidis and Papageorgiou, 2003; Bray and Rodriguez-Marek, 2004; Kalkan and Kunnath, 2006; Mukhopadhyay and Gupta, 2013a,b; Zhai et al., 2013; Hayden et al., 2014; Yang and Zhou, 2014). Especially, Northridge earthquake in 1994, Hyogoken-Nanbu (Kobe) earthquake in 1995, and Chi-Chi (Taiwan) earthquake in1999 raised special attention to many earthquake structural engineers.
The fling-step and forward-directivity inputs have been characterized by two or three wavelets. For this class of ground motions, many useful research works have been conducted. Mavroeidis and Papageorgiou (2003) investigated the characteristics of this class of ground motions in detail and proposed some simple models (e.g., Gabor wavelet and Berlage wavelet). Xu et al. (2007) employed a kind of Berlage wavelet and applied it to the performance evaluation of passive energy dissipation systems. Takewaki and Tsujimoto (2011) used the Xu’s approach and proposed a method for scaling ground motions from the viewpoints of drift and input energy demand. Takewaki et al. (2012) employed a sinusoidal wave for pulse-type waves.
Most of the previous works on the near-fault ground motions deal with the elastic response because the number of parameters (e.g., duration and amplitude of pulse, ratio of pulse frequency to structure natural frequency, and change of equivalent natural frequency for the increased input level) to be considered on this topic is many and the computation itself of elastic–plastic response is quite complicated.
In order to tackle such important but complicated problem, the double impulse input was introduced by Kojima and Takewaki (2015a) as a substitute of the fling-step near-fault ground motion and a closed-form solution of the elastic–plastic response of a structure by the “critical double impulse input” is derived. It was shown that, since only the free vibration appears under such double impulse input, the energy approach plays an important role in the derivation of the closed-form solution of a complicated elastic–plastic response. It was also shown that the maximum inelastic deformation can occur either after the first impulse or after the second impulse depending on the input level. The validity and accuracy of the proposed theory are investigated through the comparison with the response analysis result to the corresponding one-cycle sinusoidal input as a representative of the fling-step near-fault ground motion. The amplitude of the double impulse was modulated so that its maximum Fourier amplitude coincides with that of the corresponding one-cycle sinusoidal input. The extension of the theory for the fling-step near-fault ground motion to the forward-directivity near-fault ground motion was made by Kojima and Takewaki (2015b).
It was pointed by Takewaki (1996, 1997) that, when considering the upper bound of response to the random earthquake ground motions, it is appropriate to introduce the response spectrum method and the bounding theories [see Takewaki (1996, 1997)].
The closed-form or nearly closed-form solutions of the elastic–plastic earthquake response have been obtained so far only for the steady-state response to sinusoidal input or the transient response to an extremely simple sinusoidal input (Caughey, 1960a,b; Roberts and Spanos, 1990; Liu, 2000). In this article, the following motivation is raised. If a long-duration ground motion can be represented by a multiple impulse, the elastic–plastic response (continuation of free vibrations) can be derived by an energy approach without solving directly the differential equation (equation of motion). The input of impulse is expressed by the instantaneous change of velocity of the structural mass. A closed-form expression of plastic-deformation amplitude is derived by using an energy approach. An approximate expression of residual displacement is also provided by using the multiple impulse.
In the earthquake-resistant design, the resonance is a key word and it has been investigated extensively. While the resonant equivalent frequency has to be computed for a specified input level by changing the excitation frequency in a parametric manner in dealing with the sinusoidal input (Caughey, 1960a,b; Iwan, 1961, 1965a,b; Roberts and Spanos, 1990; Liu, 2000), no iteration is required in the proposed method for the multiple impulse. This is because the resonant equivalent frequency can be obtained directly without the repetitive procedure. In the multiple impulse, the analysis can be done without the input frequency (timing of impulses) before the second impulse is input. The resonance can be proved by using energy investigation and the timing of the second and third impulses can be characterized as the time with zero restoring force. The maximum elastic–plastic response after impulse can be obtained by equating the initial kinetic energy computed by the initial velocity to the sum of hysteretic and elastic strain energies. It should be pointed out that only critical response (upper bound) is captured by the proposed method and the critical resonant frequency can be obtained automatically for the increasing input level of the multiple impulse.
Figure 1 shows an actual resonant response of a super high-rise building in Osaka, Japan, during the 2011 off the Pacific coast of Tohoku earthquake. This phenomenon clearly indicates the necessity and requirement of consideration of response under long-duration ground motion.
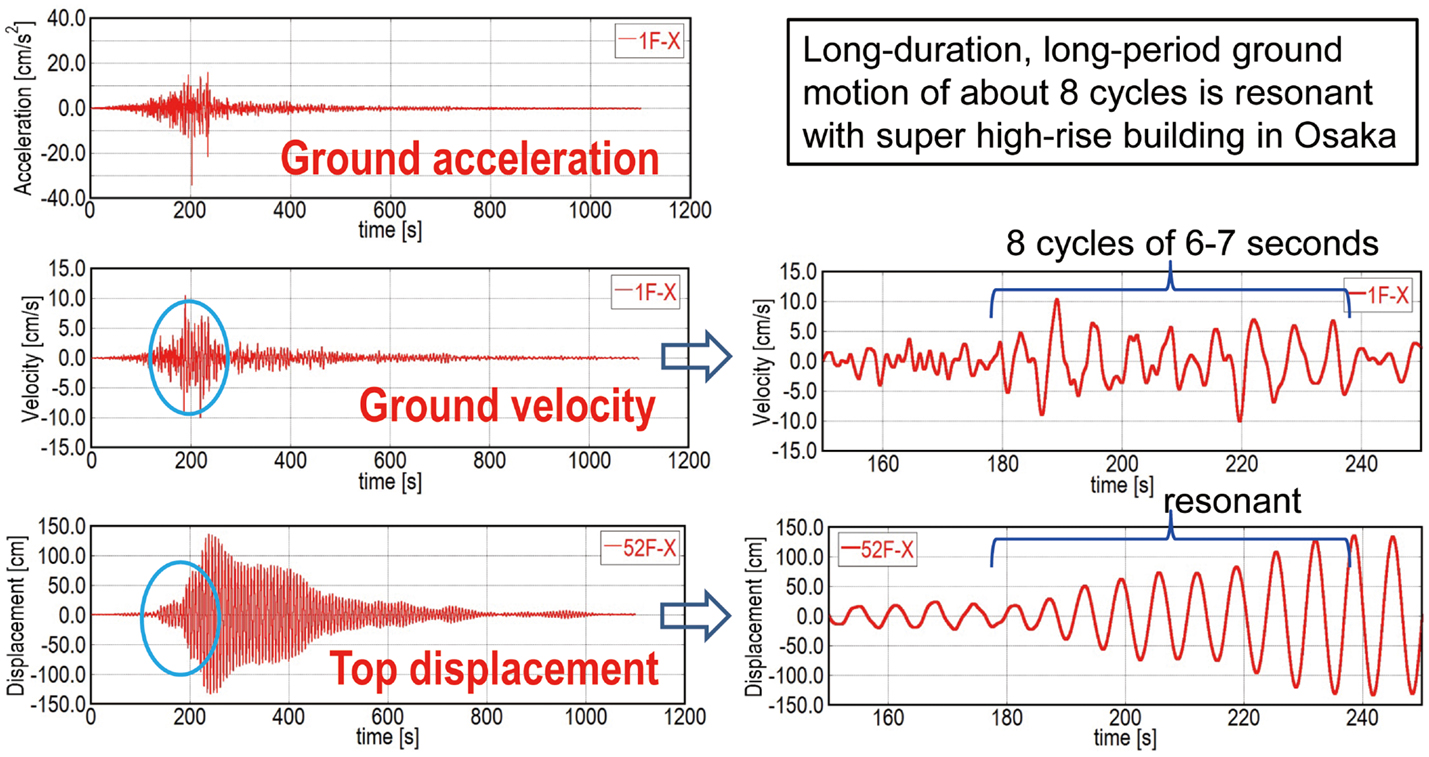
Figure 1. Resonant response of a super high-rise building in Osaka, Japan, during the 2011 off the Pacific coast of Tohoku earthquake under long-duration, long-period ground motion (Takewaki et al., 2011, 2012).
Multiple Impulse Input
It has been shown that the fling-step input (fault-parallel) of the near-fault ground motion can be represented by a one-cycle sinusoidal wave, and the forward-directivity input (fault-normal) of the near-fault ground motion can be expressed by a series of three sinusoidal wavelets (Kalkan and Kunnath, 2006; Khaloo et al., 2015). In the works by Kojima and Takewaki (2015a,b), it was demonstrated that these typical near-fault ground motions can be simplified by a double impulse (Kojima et al., 2015) and a triple impulse. This is because the double impulse and triple impulse have a simple characteristic and a straightforward expression of the response can be expected even for elastic–plastic responses based on an energy approach to free vibrations. Furthermore, the double impulse and triple impulse enabled us to describe directly the critical timing of impulses (resonant frequency), which is not easy for the sinusoidal and other inputs without a repetitive procedure (Caughey, 1960a,b; Iwan, 1961, 1965a,b).
Consider a ground acceleration as the multiple impulse, as shown in Figure 2A, expressed by
where V is the given initial velocity and t0 is the time interval between two consecutive impulses. Its velocity and displacement are shown in Figure 2A. In view of the realistic point of view, the following modified multiple input is introduced and treated principally in this article (see Figure 2B).
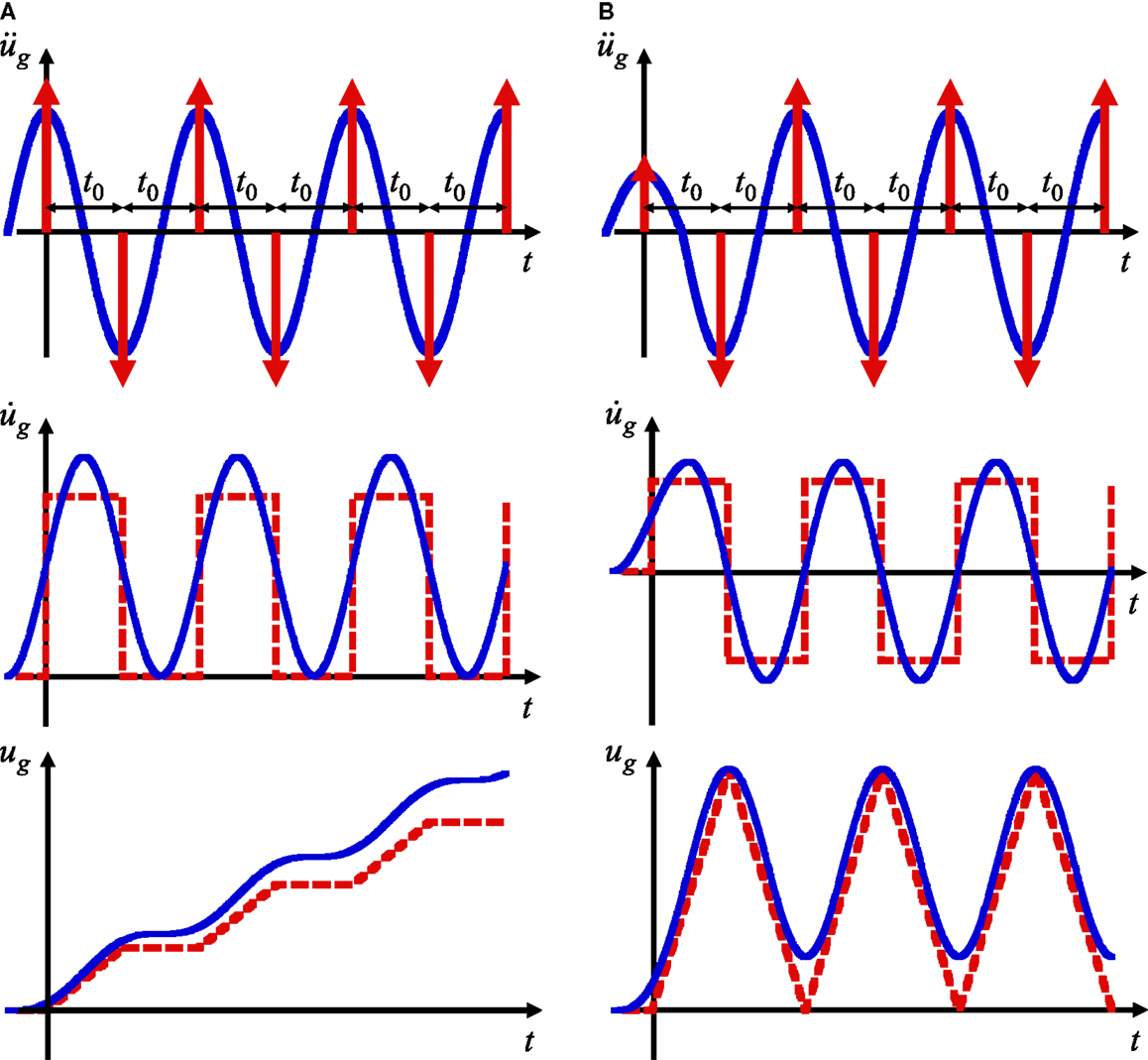
Figure 2. Long-duration earthquake ground motion in terms of sinusoidal waves and the corresponding multiple impulse: (A) multiple impulse with equal magnitude and (B) multiple impulse with smaller magnitude of first impulse.
The comparison with the corresponding multicycle sinusoidal wave as a representative of the long-duration earthquake ground motion input is plotted in Figure 2B. The corresponding velocity and displacement of such multiple impulse and sinusoidal wave are also plotted in Figure 2B. It can be understood that the multiple impulse is a good approximation of the corresponding sinusoidal wave even in the form of velocity and displacement. However, the correspondence in the response should be discussed carefully. This will be conducted later (see Section: Maximum Elastic–Plastic Deformation of SDOF System Subjected to Multiple Impulse; Figure 5).
Figure 3A shows the Input Sequence 1 (original input with equal interval) corresponding to Figure 2B. The points of impulses in the force–deformation relation converge to two points. On the other hand, Figure 3B presents the Input Sequence 2 (critical timing with residual deformation). The acting points of impulses in the force–deformation relation indicate the points with zero restoring force. It can be found that the time interval between the first and second impulses is different from those between the later consecutive two impulses. It is interesting to note that, if we consider the case as shown in Figure 3C, we can set the residual displacement to zero by changing the magnitude of the first impulse. It is also interesting that, if we employ the critical timing in Figure 3B [criticality can be shown by the same reason as proved in Appendix in Kojima and Takewaki (2015a)] as the timing of the multiple impulse in Figure 3A, the acting points of impulses in the force–deformation relation converge to two points with zero restoring force. This fact supports the significance of introducing the Input Sequence 2 in order to find the critical interval of the multiple impulse for the Input Sequence 1 without repetition. This is the most original aspect in this article.
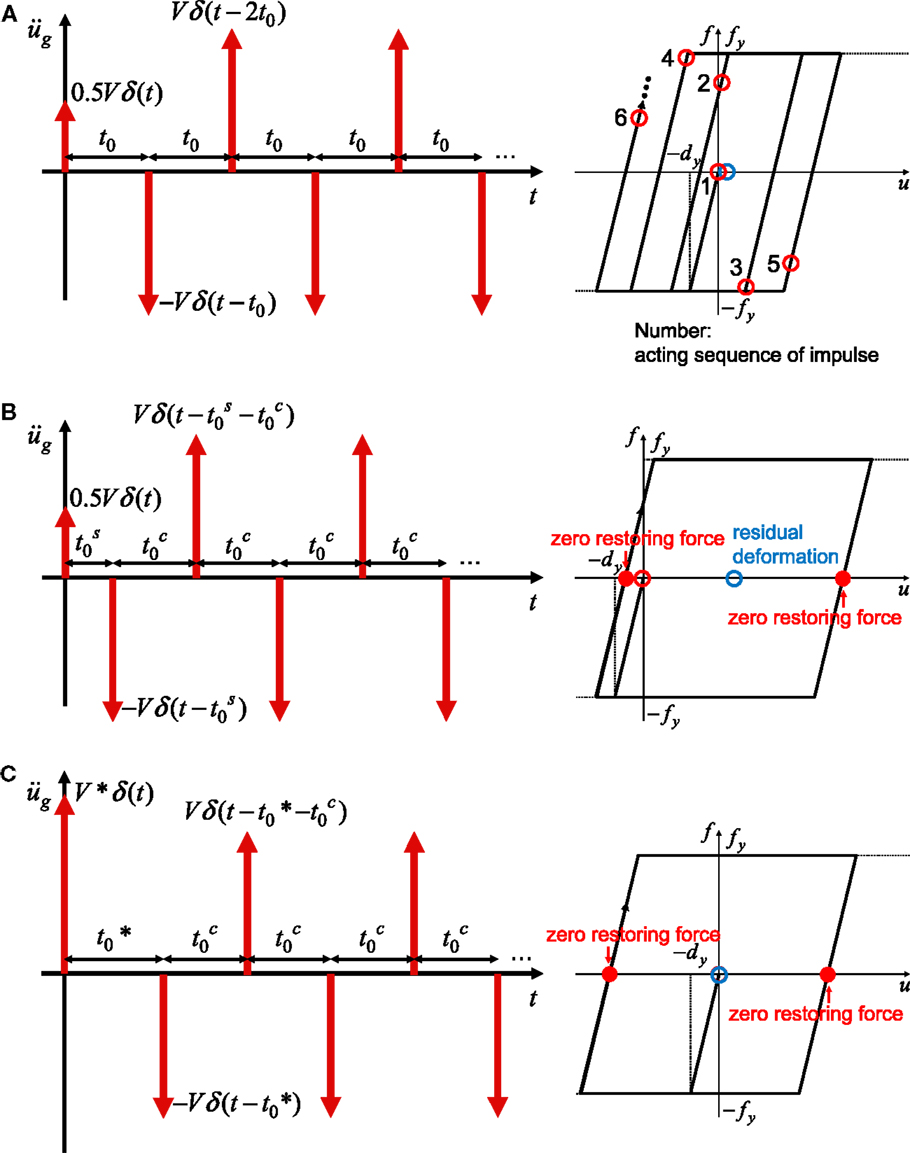
Figure 3. Three input sequences: (A) Input Sequence 1: multiple impulse input with equal interval; (B) Input Sequence 2: multiple impulse input with modification of first impulse timing; (C) Input Sequence 3: multiple impulse input with modification of first impulse timing and first impulse amplitude.
The Fourier transform of of the multiple impulse input (Input Sequence 1 expressed by Eq. 1b) can be derived as
The absolute value of Eq. 2 leads to
SDOF System
Consider an undamped elastic–perfectly plastic single-degree-of-freedom (SDOF) system of mass m and stiffness k. The yield deformation and yield force are denoted by dy and fy. Let u, and f denote the undamped natural circular frequency, the displacement of the mass relative to the ground (deformation of the system), and the restoring force of the model, respectively. The time derivative is denoted by an over-dot. In Section “Maximum Elastic–Plastic Deformation of SDOF System Subjected to Multiple Impulse,” these parameters will be dealt with in a non-dimensional or normalized form to derive the relation of permanent interest between the input and the elastic–plastic response. However, numerical parameters will be introduced partially in Sections “Maximum Elastic–Plastic Deformation of SDOF System Subjected to Multiple Impulse” and “Accuracy Check by Time-History Response Analysis Subjected to the Corresponding Multicycle Sinusoidal Input” to demonstrate an example of actual parameters.
Maximum Elastic–Plastic Deformation of SDOF System Subjected to Multiple Impulse
Non-Iterative Determination of Critical Timing and Critical Plastic Deformation by Using Modified Input Sequence
Consider Input Sequence 1 in Figure 3A at first. If the SDOF system is elastic, the critical timing t0 is half the natural period of the SDOF system. However, if the SDOF system goes into a plastic region, the critical set of input amplitude and input frequency (timing of impulse) has to be computed iteratively. This situation is the same for the multicycle sinusoidal wave (Caughey, 1960a,b; Iwan, 1961, 1965a,b).
In order to overcome this difficulty, consider Input Sequence 2 in Figure 3B, which introduces a modified input (only the timing between the first and second impulses is modified so that the second impulse is given at the zero restoring force). Input Sequence 2 is based on the assumption that, if the steady state exists in which the impulse is given at zero restoring-force timing, impulse provides the maximum steady-state plastic deformation. This assumption is verified by giving the critical timing obtained from Input Sequence 2 to Input Sequence 1. In other words, if the critical timing obtained from Input Sequence 2 is given to Input Sequence 1, the timing of impulse converges to zero restoring-force timing. This verification is also supported by the one-to-one correspondence between the input amplitude and its critical timing of impulses (impulses have to be given at zero restoring-force points). It is also possible to derive the Input Sequence 3 and its response with zero residual displacement (see Figure 3C).
The elastic–plastic response to the multiple impulse can be described by the continuation of free vibrations.
The maximum deformation after the first impulse is denoted by umax 1 and that after the second impulse is expressed by umax 2 as shown in Figure 4. The input of each impulse is expressed by the instantaneous change of velocity of the structural mass. Such response can be derived by an energy approach without solving directly the differential equation (equation of motion). The kinetic energy given at the initial stage (the time of the first impulse) and at the time of the second impulse is transformed into the sum of the hysteretic energy and the strain energy corresponding to the yield deformation. By using this rule, the maximum deformation can be obtained in a simple manner.
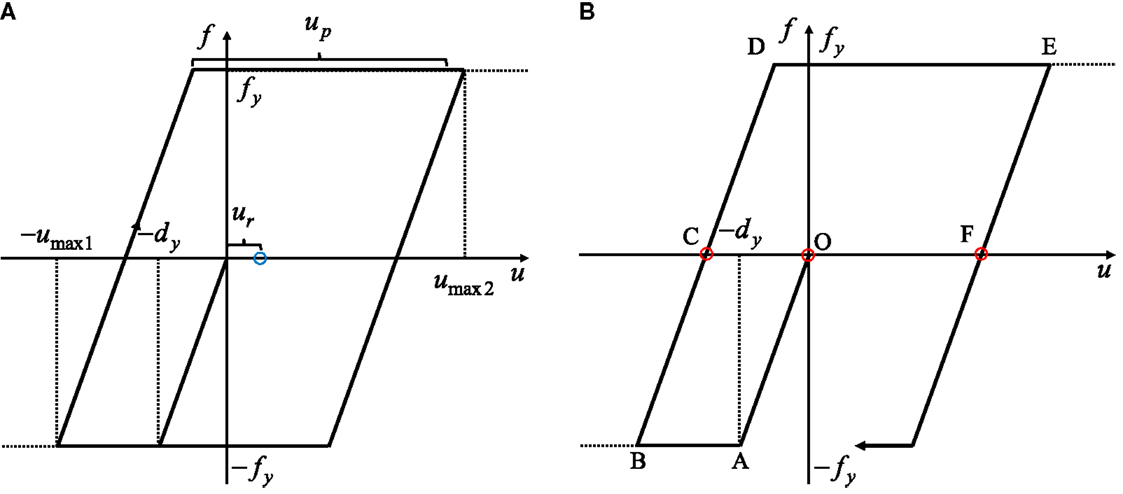
Figure 4. Definition of response quantities and response transition: (A) schematic diagram of deformation quantities in force–deformation relation and (B) transition of response process and impulse timing (Input Sequence 2).
It should be emphasized that, while the resonant equivalent frequency has to be computed for a specified input level by changing the excitation frequency in a parametric manner in dealing with the sinusoidal input (Caughey, 1960a,b; Iwan, 1961, 1965a,b; Roberts and Spanos, 1990; Liu, 2000; Moustafa et al., 2010), no iteration is required in the proposed method for the multiple impulse. This is because the resonant equivalent frequency [resonance can be proved by using energy investigation: see Appendix in Kojima and Takewaki (2015a)] can be obtained directly without the repetitive procedure. As a result, the timing of the second impulse can be characterized as the time with zero restoring force.
Only critical response (upper bound) is captured by the proposed method and the critical resonant frequency can be obtained automatically for the increasing input level of the multiple impulse. One of the original points in this article is the introduction of the concept of “critical excitation” in the elastic–plastic response (Drenick, 1970; Abbas and Manohar, 2002; Takewaki, 2002, 2007; Moustafa et al., 2010). Once the frequency and amplitude of the critical multiple impulse are computed, the corresponding multicycle sinusoidal motion as a representative of the long-duration earthquake ground motion can be identified.
Let us explain the evaluation method of umax 1 and umax 2. The plastic deformation after the first impulse is expressed by up1 and that after the second impulse is denoted by up2. There are three cases to be considered depending on the yielding stage (Kojima and Takewaki, 2015a). Let Vy(= ω1 dy) denote the input level of velocity of the impulse at which the SDOF system at rest just attains the yield deformation after the impulse of such velocity.
Consider the case where the model goes into the yielding stage even after the first impulse. This case corresponds to (CASE 3) in the problem of double impulse (Kojima and Takewaki, 2015a). Figure 4A shows the schematic diagram of the response in this case. umax 1 can be obtained from the following energy conservation law.
On the other hand, umax 2 can be computed from another energy conservation law.
where vc is characterized by and up2 is characterized by umax 2 + (umax 1 − dy) = dy + up2. In other words, umax 2 can be obtained from
As in the above case, the velocity V induced by the second impulse is added to the velocity vc introduced by the first impulse (the maximum velocity during the unloading stage). Although only CASE 3 in the double impulse (Kojima and Takewaki, 2015a) has been considered here, CASE 2 (yielding only after the second impulse) can be treated by replacing vc in Eqs 5, 6 by 0.5V.
Figure 5 shows the plot of the plastic deformation amplitude up (up2 in this case) and the residual deformation ur, shown in Figure 4A, with respect to the input level V/Vy for Input Sequence 1 and 2. While the plastic deformation amplitude is the same for Sequence 1 and 2, the residual deformations are different. This results from the difference in the initial disturbances in Input Sequence 1 and 2.
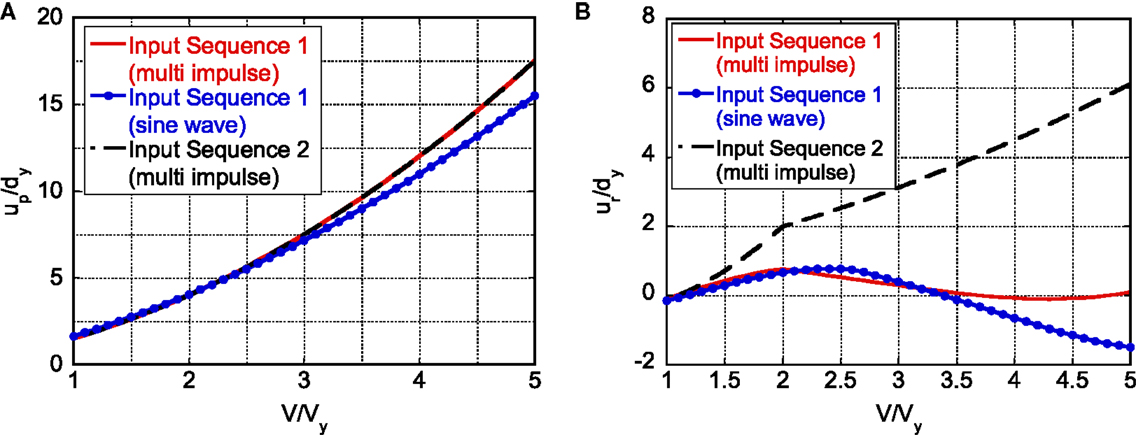
Figure 5. Comparison of response among Input Sequence 1 (multiple impulse), Input Sequence 1 (sine wave), and Input Sequence 2 (multiple impulse): (A) plastic deformation amplitude and (B) residual deformation.
Determination of Critical Timing of Impulses
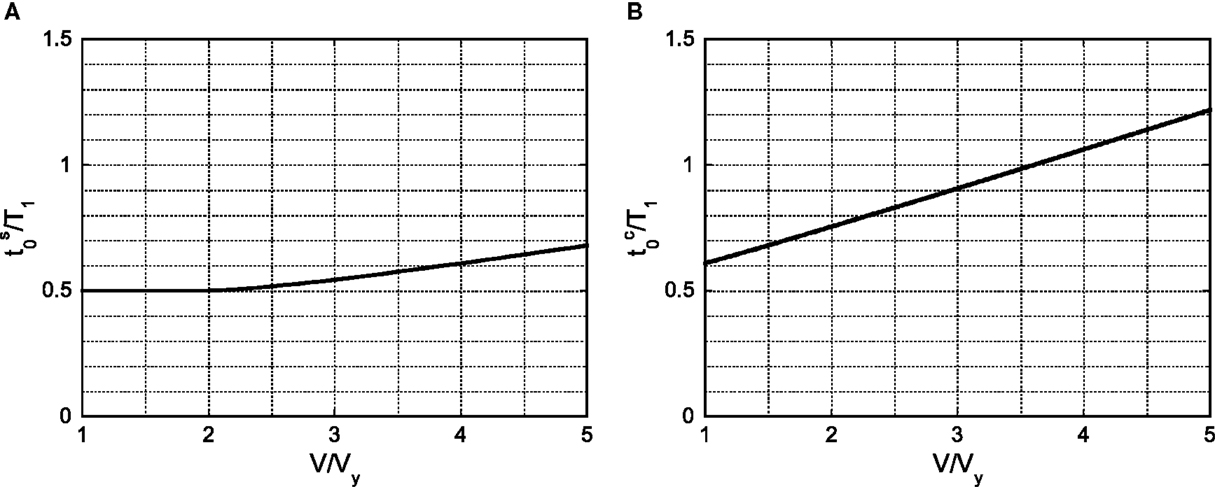
Consider the Input Sequence 2 in this section. The time between two consecutive impulses can be obtained by solving the differential equations (equations of motion) and substituting the continuation conditions at the transition points. The time between the first and second impulses and the time between two consecutive impulses after the second impulse can be expressed as follows:
where tOA, tAB, tBC, tCD, tDE, and tEF are the times between two consecutive transition points shown in Figure 4B. If V/Vy < 2,
In Eqs 8a–f, denotes V/Vy.
Figures 6A,B present the normalized timing and with respect to the input level. These timings coincide with the time intervals between the points with zero restoring force (see Figure 4). It can be observed that the timing is delayed due to plastic deformation as the input level increases. It seems noteworthy to state again that only the critical response giving the maximum value of up/dy is sought by the proposed method and the critical resonant frequency is obtained automatically without repetition for the increasing input level of the multiple impulse. One of the original points in this article is the tracking of the critical elastic–plastic response.
Correspondence of Responses between Input Sequence 1 (Original One) and Input Sequence 2 (Modified One)
Figures 7 and 8 show the time histories of relative displacement (relative to base motion), relative velocity, restoring force, and the force–deformation relation under Input Sequence 1 with for V/Vy = 2 and V/Vy = 3, respectively. In Figures 7 and 8, ω1 = 2π(rad/s)(T1 = 1.0 s) and dy = 0.16 m are used. Since the steady state is very sensitive to the time increment in the time-history response analysis using an elastic–perfectly plastic model, the time increment has been chosen as 1.0 × 10−6 s. In fact, an elastic–perfectly plastic model was not treated in most works (Caughey, 1960a,b; Iwan, 1961, 1965a,b) for its difficult treatment. It should be noted that the impulse timing is the critical one obtained by using the Input Sequence 2. The circles in Figures 7 and 8 indicate the acting points of impulses. It can be observed that, although some irregularities appear at first, the response converges to a state with the timing of impulse at zero restoring-force point irrespective of the input level.
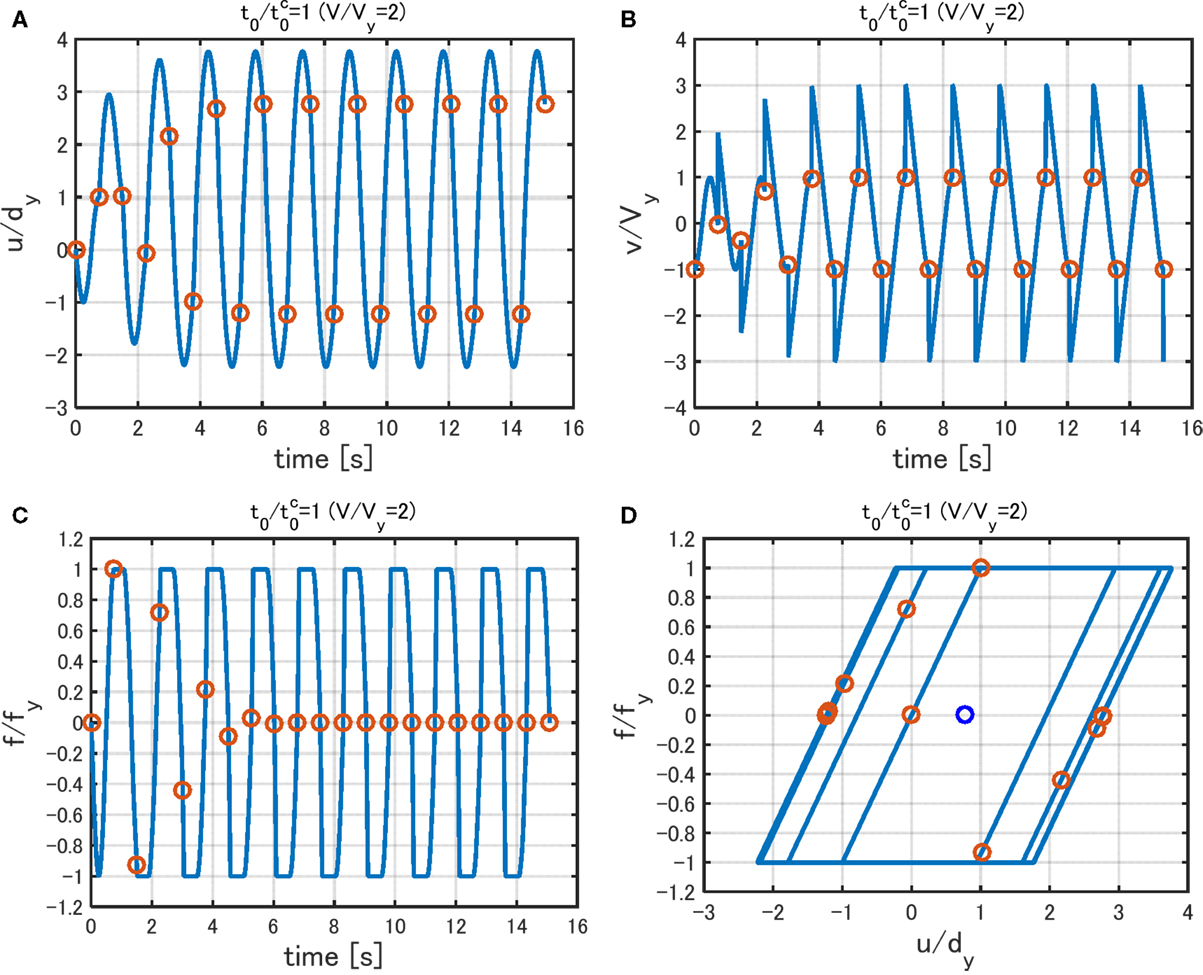
Figure 7. Response to Input Sequence 1 for V/Vy= 2 (impulse timing is the critical one obtained by using the Input Sequence 2): (A) displacement, (B) velocity, (C) restoring force, and (D) force–deformation relation.
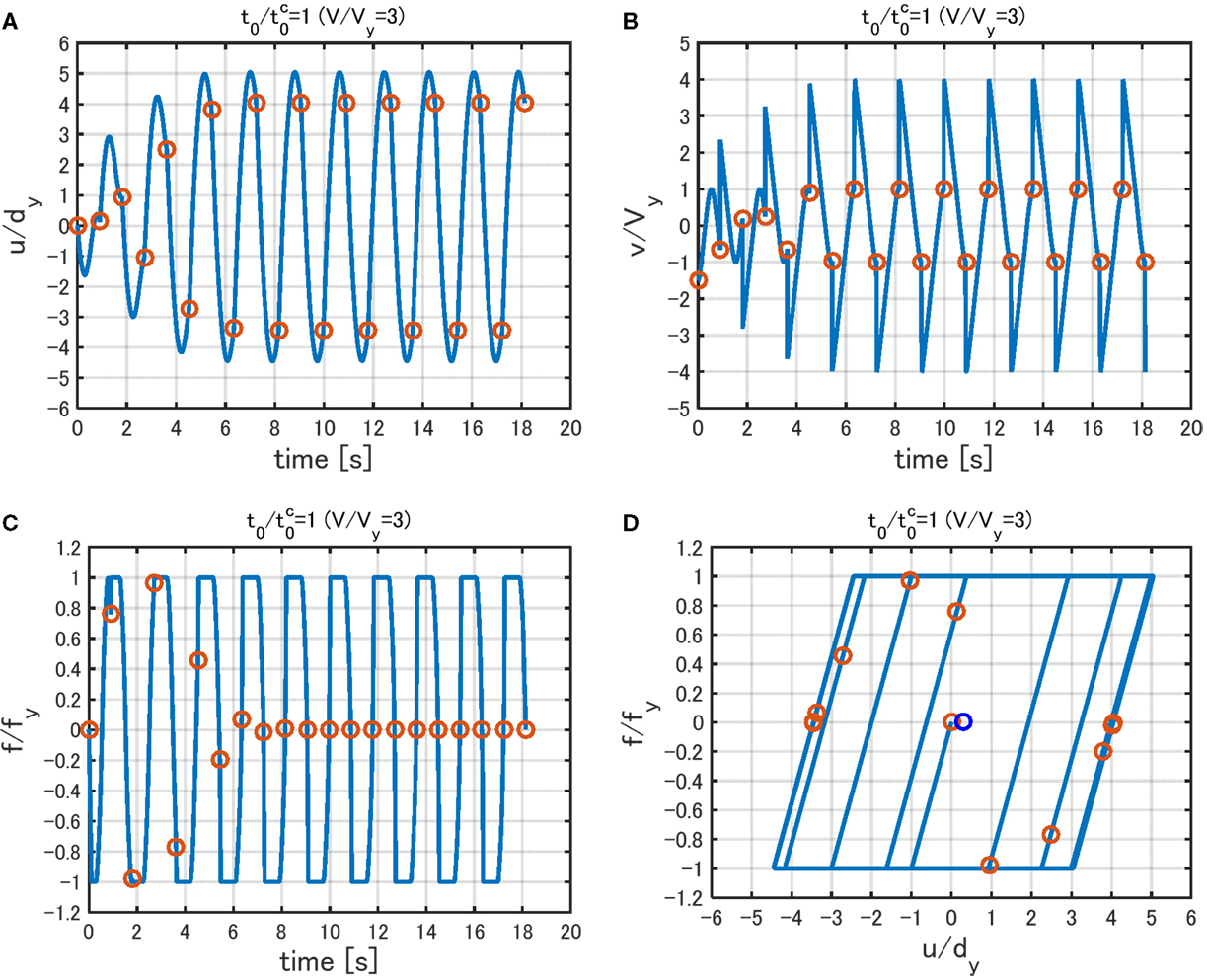
Figure 8. Response to Input Sequence 1 for V/Vy= 3 (impulse timing is the critical one obtained by using the Input Sequence 2): (A) displacement, (B) velocity, (C) restoring force, and (D) force–deformation relation.
Figure 9 summarizes the force–deformation relation under the multiple impulse of Input Sequence 1 with the time interval for two input levels V/Vy = 2, 3. While in Figures 7 and 8 only the case of is treated, three cases of time intervals are dealt with in Figure 9. It can be confirmed that the response converges to a steady state irrespective of the impulse timing and certainly gives the maximum plastic deformation amplitude up. This demonstrates the validity of introducing the Input Sequence 2 for finding the critical timing of multiple impulse even for the Input Sequence 1.
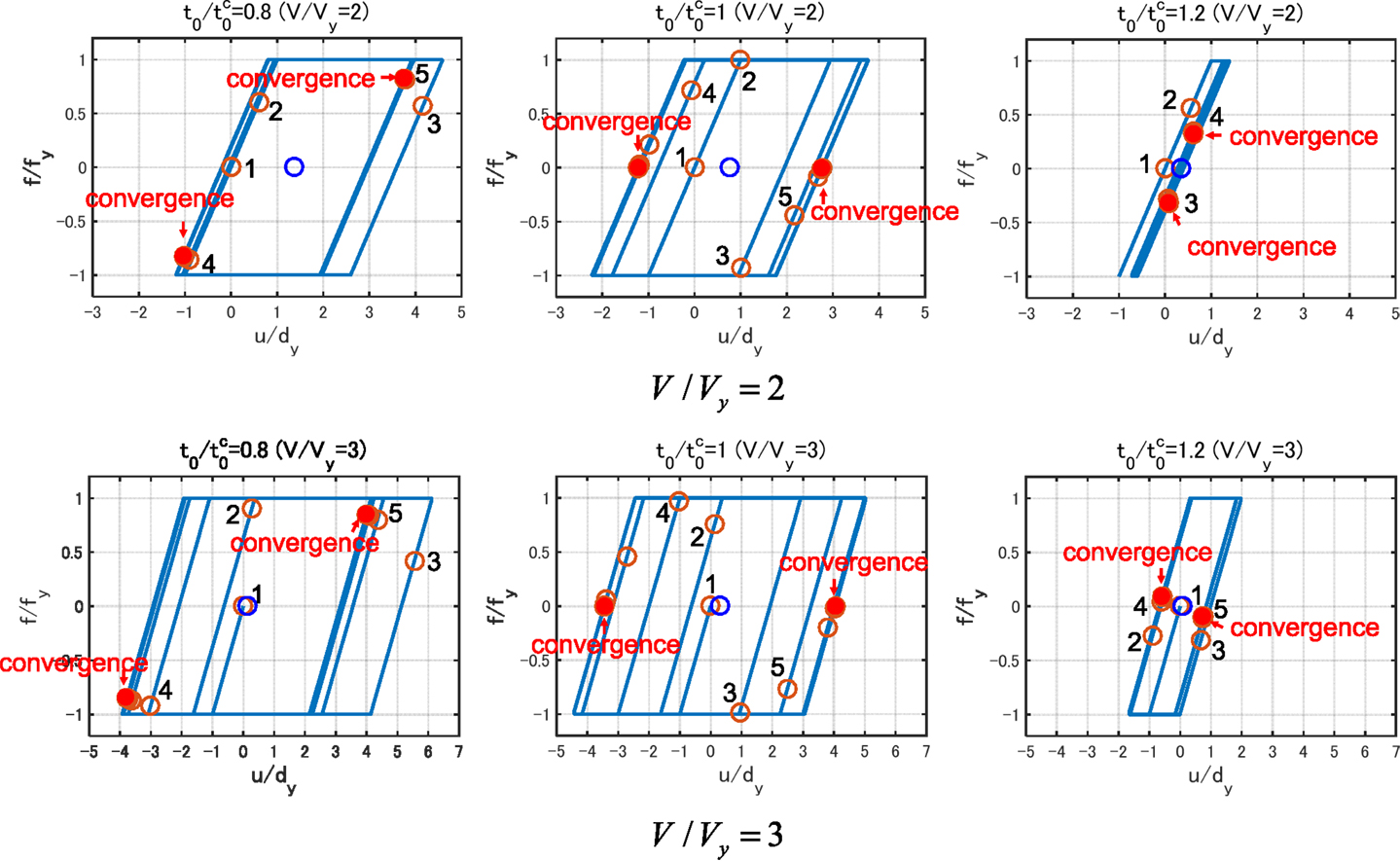
Figure 9. Response to Input Sequence 1 for three impulse timings with two input levels V/Vy= 2, 3 (Number beside circle: acting sequence of impulse).
On the other hand, Figures 10 and 11 show the time histories of relative displacement (relative to base motion), relative velocity, restoring force, and the force–deformation relation under Input Sequence 2 for V/Vy = 2 and V/Vy = 3, respectively. In Figures 10 and 11, ω1 = 2π(rad/s)(T1 = 1.0 s) and dy = 0.16 m are used. It can be observed that the realized response exhibits a steady state from the initial stage and corresponds to a state with the timing of impulse at zero restoring-force point irrespective of the input level. The critical timing of multiple impulse computed by Eq. 7b can be obtained without repetition and can be used as the critical timing even for the Input Sequence 1.
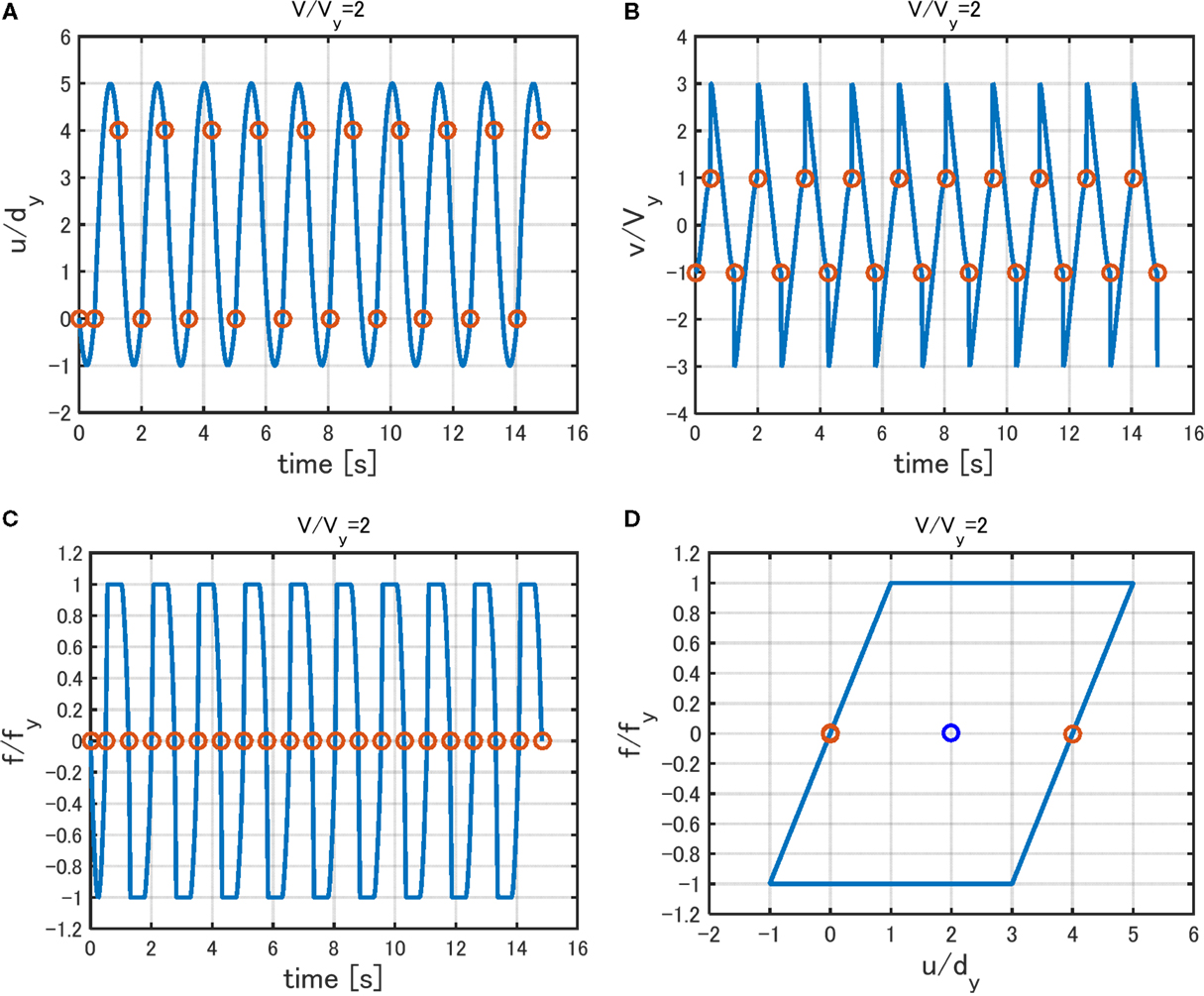
Figure 10. Response to Input Sequence 2 for V/Vy= 2: (A) displacement, (B) velocity, (C) restoring force, and (D) force–deformation relation.
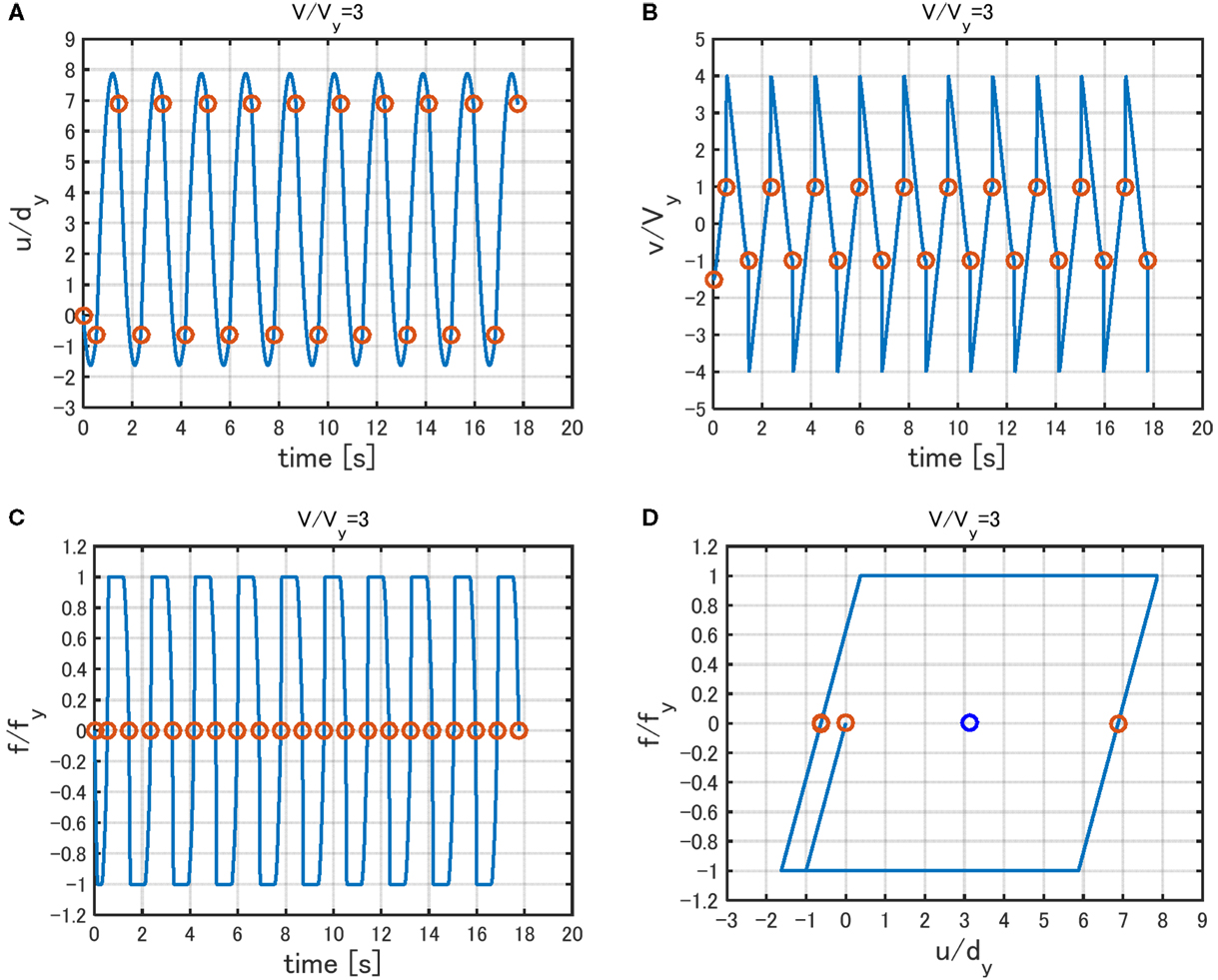
Figure 11. Response to Input Sequence 2 for V/Vy= 3: (A) displacement, (B) velocity, (C) restoring force, and (D) force–deformation relation.
Accuracy Check by Time-History Response Analysis Subjected to the Corresponding Multicycle Sinusoidal Input
In order to investigate the accuracy of using the multiple impulse (Input Sequence 1) as a substitute of the corresponding multicycle sinusoidal wave (representative of the long-duration ground motion input), the time-history response analysis of the elastic–plastic SDOF model under the multicycle sinusoidal wave has been conducted.
In the evaluation procedure, it is important to adjust the input level of the multiple impulse and the corresponding multicycle sinusoidal wave. This adjustment is made by using the equivalence of the maximum Fourier amplitude and a modification based on the response equivalence at some points with different input levels.
Figures 12A,B illustrate the comparison of the ground displacement and velocity between the multiple impulse and the corresponding multicycle sinusoidal wave for the input level V/Vy = 3 In Figures 12A,B, ω1 = 2π(rad/s)(T1 = 1.0 s) and dy = 0.16 m are used. The amplitude of the sinusoidal wave has been amplified by 1.15 after both Fourier amplitudes of the sinusoidal wave and the multiple impulse are adjusted (10 cycles). This amplification factor 1.15 has been set based on the response equivalence at some points with different input levels. It should be remarked that the information on critical timing shown in Figure 6 is incorporated in Figure 12.
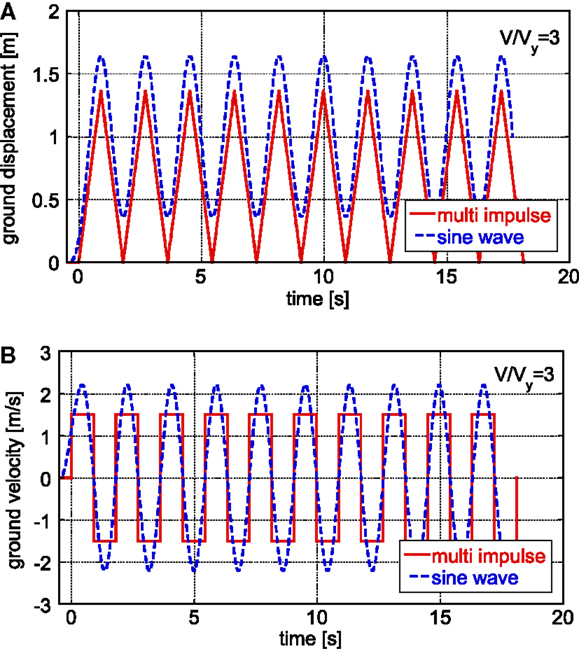
Figure 12. Comparison of ground displacement and velocity between the multiple impulse and the corresponding multicycle sinusoidal wave for the input level V/Vy= 3: (A) displacement, (B) velocity.
Figure 5 presents the comparison of the maximum plastic deformation up/dy and the residual displacement ur/dy of the elastic–plastic structure under the multiple impulse and the corresponding multicycle sinusoidal wave with respect to the input level. It can be seen that the multiple impulse provides a fairly good substitute of the multicycle sinusoidal wave in the evaluation of the maximum plastic deformation up/dy if the amplitudes of both inputs are adjusted appropriately. Although the residual displacement exhibits a rather good correspondence between the multiple impulse (Input Sequence 1) and the corresponding multicycle sinusoidal wave, the Input Sequence 2 shows somewhat larger residual displacement. However, since the Input Sequence 2 is used mainly for getting the critical timing, this discrepancy does not cause any problem.
Figure 13 shows the comparison of displacement responses to the multiple impulse (Input Sequence 1) and the corresponding sinusoidal wave for V/Vy = 2, 3 and In Figure 13, ω1 = 2π(rad/s)(T1 = 1.0 s) and dy = 0.16 m are used. It should be noted that the phase lag has been adjusted for ease in comparison. The ground displacement and velocity of the corresponding sinusoidal wave for V/Vy = 3 are shown in Figure 12. It can be observed that, although a slight difference exists in the first cycle, both responses show a fairly good correspondence in the steady state. If desired, the residual displacement can be evaluated from Figure 5B. As is well known, the residual displacement is sensitive to the irregularity in the input in the case of the elastic–perfectly plastic system. This issue is beyond the scope of this article.
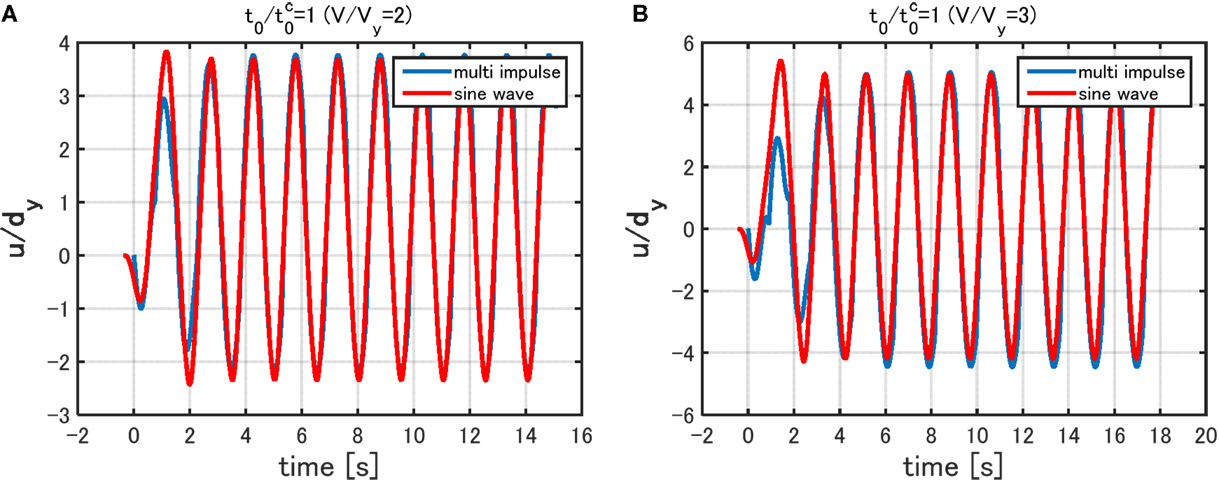
Figure 13. Comparison of responses to multiple impulse and sinusoidal wave (phase lag has been adjusted): (A) V/Vy= 2 and (B) V/Vy = 3.
Proof of Critical Timing
Figure 14 shows the normalized plastic deformation amplitude up/dy with respect to timing of multiple impulse input for various input levels V/Vy = 1, 2, 3, 4, 5 (Input Sequence 1). It can be confirmed that the critical timing derived from the Input Sequence 2 provides the critical case even under Input Sequence 1. Repetitive appearance of peaks with the same amplitude indicates the existence of multiple solutions. However, the lowest timing is meaningful from the viewpoint of occurrence possibility of such ground motion with long duration. It is noted that the peak at the value of t0 larger than ) implies the action of the second impulse after the point with zero restoring force. As the input level becomes smaller, the value attaining the peak becomes larger.
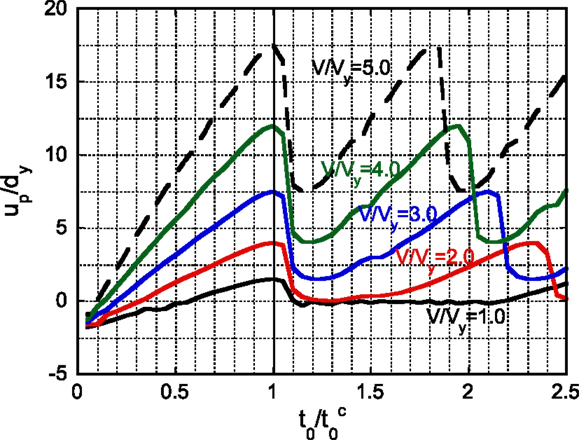
Figure 14. Plastic deformation amplitude with respect to timing of multiple impulse input for various input levels (Input Sequence 1).
Conclusion
The conclusions may be summarized as follows:
(1) The multiple impulse input has been introduced as a substitute of the long-duration earthquake ground motion, mostly expressed in terms of harmonic waves, and a closed-form solution has been derived of the elastic–plastic response of an SDOF structure under the critical multiple impulse input. It should be mentioned that the critical elastic–plastic response is treated mainly in this article.
(2) While the critical set of input amplitude and input frequency (timing of impulse) have to be computed iteratively for the multicycle sinusoidal wave that can be obtained directly without iteration for the multiple impulse input by introducing a modified version (only the timing between the first and second impulses is modified so that the second impulse is given at the zero restoring force). The resonance has been proved by using energy investigation, and it has been made clear that the critical timing of the multiple impulses can be characterized as the time with zero restoring force. This decomposition of input amplitude and input frequency has overcome the long-time difficulty in finding the resonant frequency without repetition. This is one of the most original contributions in this article.
(3) It has been shown that, since only the free vibration appears in such multiple impulse input, the energy approach plays an important role in the derivation of the closed-form solution of a complicated elastic–plastic critical response. In other words, the energy approach enables the derivation of the maximum critical elastic–plastic seismic response without solving the differential equation (equation of motion). In this process, the input of impulse is expressed by the instantaneous change of velocity of the structural mass. The maximum elastic–plastic response after impulse can be obtained by equating the initial kinetic energy computed by the initial velocity to the sum of hysteretic and elastic strain energies. It has been shown that the critical inelastic deformation and the corresponding critical input frequency can be captured by the substituted multiple impulse input depending on the input level. This is the second one of the most original contributions in this article.
(4) The validity and accuracy of the proposed theory have been investigated through the comparison with the response analysis result to the corresponding multicycle sinusoidal input as a representative of the long-duration earthquake ground motion. It has been made clear that, if the adjustment of both inputs is made by using the equivalence of the Fourier amplitude and a modification based on the response equivalence at some points with different input levels, the maximum elastic–plastic deformation to the multiple impulse exhibits a good correspondence with that to the multicycle sinusoidal wave.
(5) While the previous approaches (Caughey, 1960a,b; Iwan, 1961, 1965a,b) are aimed at constructing an equivalent linear structural model to an unchanged input (sinusoidal input) in order to enable the simple approximate computation of complicated elastic–plastic responses, the present article is aimed at finding an equivalent input model for an unchanged exact elastic–plastic model. The most significant difference between two approaches is that, while the previous approaches require the repetition both in the computation of equivalent model parameters for one input frequency and the computation of the resonant frequency giving the maximum response, the present approach does not require any repetition in the computation of the critical input timing (resonant frequency) and the critical response. The present approach also enables the computation of the steady-state response for an elastic–perfectly plastic model which cannot be treated by the previous approaches.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Part of the present work is supported by the Grant-in-Aid for Scientific Research of Japan Society for the Promotion of Science (No.15H04079). This support is greatly appreciated.
References
Abbas, A. M., and Manohar, C. S. (2002). Investigations into critical earthquake load models within deterministic and probabilistic frameworks. Earthq. Eng. Struct. Dyn. 31, 813–832. doi:10.1002/eqe.124.abs
Alavi, B., and Krawinkler, H. (2004). Behaviour of moment resisting frame structures subjected to near-fault ground motions. Earthq. Eng. Struct. Dyn. 33, 687–706. doi:10.1002/eqe.370
Bertero, V. V., Mahin, S. A., and Herrera, R. A. (1978). Aseismic design implications of near-fault San Fernando earthquake records. Earthq. Eng. Struct. Dyn. 6, 31–42. doi:10.1002/eqe.4290060105
Bray, J. D., and Rodriguez-Marek, A. (2004). Characterization of forward-directivity ground motions in the near-fault region. Soil Dyn. Earthq. Eng. 24, 815–828. doi:10.1016/j.soildyn.2004.05.001
Caughey, T. K. (1960a). Sinusoidal excitation of a system with bilinear hysteresis. J. Appl. Mech. 27, 640–643. doi:10.1115/1.3644077
Caughey, T. K. (1960b). Random excitation of a system with bilinear hysteresis. J. Appl. Mech. 27, 649–652. doi:10.1115/1.3644077
Hall, J. F., Heaton, T. H., Halling, M. W., and Wald, D. J. (1995). Near-source ground motion and its effects on flexible buildings. Earthq. Spectra. 11, 569–605. doi:10.1193/1.1585828
Hayden, C. P., Bray, J. D., and Abrahamson, N. A. (2014). Selection of near-fault pulse motions. J. Geotechnical Geoenvironmental Eng. 140, doi:10.1061/(ASCE)GT.1943-5606.0001129
Iwan, W. D. (1961). The Dynamic Response of Bilinear Hysteretic Systems. Pasadena, CA: California Institute of Technology.
Iwan, W. D. (1965a). The steady-state response of a two-degree-of-freedom bilinear hysteretic system. J. Appl. Mech. 32, 151–156. doi:10.1115/1.3625711
Iwan, W. D. (1965b). “The dynamic response of the one-degree-of-freedom bilinear hysteretic system,” in Proceedings of the Third World Conference on Earthquake Engineering, Vol. II. 783–796.
Kalkan, E., and Kunnath, S. K. (2006). Effects of fling step and forward directivity on seismic response of buildings. Earthq. Spectra 22, 367–390. doi:10.1193/1.2192560
Kalkan, E., and Kunnath, S. K. (2007). Effective cyclic energy as a measure of seismic demand. J. Earthq. Eng. 11, 725–751. doi:10.1080/13632460601033827
Khaloo, A. R., Khosravi1, H., and Hamidi Jamnani, H. (2015). Nonlinear interstory drift contours for idealized forward directivity pulses using “modified fish-bone” models. Adv. Struct. Eng. 18, 603–627. doi:10.1260/1369-4332.18.5.603
Kojima, K., Fujita, K., and Takewaki, I. (2015). Critical double impulse input and bound of earthquake input energy to building structure. Front. Built Environ. 1:5. doi:10.3389/fbuil.2015.00005
Kojima, K., and Takewaki, I. (2015a). Critical earthquake response of elastic-plastic structures under near-fault ground motions (part 1: fling-step input). Front. Built Environ. 1:12. doi:10.3389/fbuil.2015.00012
Kojima, K., and Takewaki, I. (2015b). Critical earthquake response of elastic-plastic structures under near-fault ground motions (part 2: forward-directivity input). Front. Built Environ. 1:13. doi:10.3389/fbuil.2015.00013
Liu, C.-S. (2000). The steady loops of SDOF perfectly elastoplastic structures under sinusoidal loadings. J. Mar. Sci. Technol. 8, 50–60.
Mavroeidis, G. P., Dong, G., and Papageorgiou, A. S. (2004). Near-fault ground motions, and the response of elastic and inelastic single-degree-freedom (SDOF) systems. Earthq. Eng. Struct. Dyn. 33, 1023–1049. doi:10.1002/eqe.391
Mavroeidis, G. P., and Papageorgiou, A. S. (2003). A mathematical representation of near-fault ground motions. Bull. Seism. Soc. Am. 93, 1099–1131. doi:10.1785/0120020100
Moustafa, A., Ueno, K., and Takewaki, I. (2010). Critical earthquake loads for SDOF inelastic structures considering evolution of seismic waves. Earthq. Struct. 1, 147–162. doi:10.12989/eas.2010.1.2.147
Mukhopadhyay, S., and Gupta, V. K. (2013a). Directivity pulses in near-fault ground motions – I: Identification, extraction and modeling. Soil Dyn. Earthq. Eng. 50, 1–15. doi:10.1016/j.soildyn.2013.02.017
Mukhopadhyay, S., and Gupta, V. K. (2013b). Directivity pulses in near-fault ground motions – II: estimation of pulse parameters. Soil Dyn. Earthq. Eng. 50, 38–52. doi:10.1016/j.soildyn.2013.02.017
Roberts, J. B., and Spanos, P. D. (1990). Random Vibration and Statistical Linearization. New York, NY: Wiley.
Rupakhety, R., and Sigbjörnsson, R. (2011). Can simple pulses adequately represent near-fault ground motions? J. Earthq. Eng. 15, 1260–1272. doi:10.1080/13632469.2011.565863
Sasani, M., and Bertero, V. V. (2000). “Importance of severe pulse-type ground motions in performance-based engineering: historical and critical review,” in Proceedings of the Twelfth World Conference on Earthquake Engineering (Auckland, New Zealand).
Takewaki, I. (1996). Design-oriented approximate bound of inelastic responses of a structure under seismic loading. Comput. Struct. 61, 431–440. doi:10.1016/0045-7949(96)00086-7
Takewaki, I. (1997). Design-oriented ductility bound of a plane frame under seismic loading. J. Vib. Control 3, 411–434. doi:10.1177/107754639700300404
Takewaki, I. (2002). Robust building stiffness design for variable critical excitations. J. Struct. Eng. 128, 1565–1574. doi:10.1061/(ASCE)0733-9445(2002)128:12(1565)
Takewaki, I. (2007). Critical Excitation Methods in Earthquake Engineering, 2nd Edn in 2013. Oxford: Elsevier.
Takewaki, I., Moustafa, A., and Fujita, K. (2012). Improving the Earthquake Resilience of Buildings: The Worst Case Approach. London: Springer.
Takewaki, I., Murakami, S., Fujita, K., Yoshitomi, S., and Tsuji, M. (2011). The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 31, 1511–1528. doi:10.1016/j.soildyn.2011.06.001
Takewaki, I., and Tsujimoto, H. (2011). Scaling of design earthquake ground motions for tall buildings based on drift and input energy demands. Earthq. Struct. 2, 171–187. doi:10.12989/eas.2011.2.2.171
Vafaei, D., and Eskandari, R. (2015). Seismic response of mega buckling-restrained braces subjected to fling-step and forward-directivity near-fault ground motions. Struct. Des. Tall Spec. Build. 24, 672–686. doi:10.1002/tal.1205
Xu, Z., Agrawal, A. K., He, W.-L., and Tan, P. (2007). Performance of passive energy dissipation systems during near-field ground motion type pulses. Eng. Struct. 29, 224–236. doi:10.1016/j.engstruct.2006.04.020
Yamamoto, K., Fujita, K., and Takewaki, I. (2011). Instantaneous earthquake input energy and sensitivity in base-isolated building. Struct. Des. Tall Spec. Build. 20, 631–648. doi:10.1002/tal.539
Yang, D., and Zhou, J. (2014). A stochastic model and synthesis for near-fault impulsive ground motions. Earthq. Eng. Struct. Dyn. 44, 243–264. doi:10.1002/eqe.2468
Keywords: earthquake response, critical input, critical response, elastic–plastic response, ductility factor, long-duration ground motion, resonance, multiple impulse
Citation: Kojima K and Takewaki I (2015) Critical input and response of elastic–plastic structures under long-duration earthquake ground motions. Front. Built Environ. 1:15. doi: 10.3389/fbuil.2015.00015
Received: 29 July 2015; Accepted: 02 September 2015;
Published: 15 September 2015
Edited by:
Nikos D. Lagaros, National Technical University of Athens, GreeceReviewed by:
Johnny Ho, The University of Queensland, AustraliaPeng Pan, Tsinghua University, China
Copyright: © 2015 Kojima and Takewaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Izuru Takewaki, Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyotodaigaku-Katsura, Nishikyo, Kyoto 615-8540, Japan,dGFrZXdha2lAYXJjaGkua3lvdG8tdS5hYy5qcA==
 Kotaro Kojima
Kotaro Kojima Izuru Takewaki
Izuru Takewaki