Effect of Planar Impact Modeling on the Pounding Response of Base-Isolated Buildings

During strong earthquake excitations, base-isolated buildings may collide, either with the surrounding moat wall or with adjacent buildings if the available clearance is exceeded. This undesirable possibility has been recently investigated by several researchers, adopting various types of force-based impact models. Evidently, an important issue that arises regarding such numerical studies is the way of taking into account potential impacts. This paper parametrically investigates the effects of impact modeling characteristics on the computed overall peak response of a base-isolated building that experiences structural pounding. Specifically, the Kelvin–Voigt impact model and various other modifications of this linear viscoelastic impact model are considered in the conducted analyses. In order to efficiently conduct this investigation, a specially developed software is used. The results indicate that the excitation’s and isolator’s characteristics do not significantly influence the variation in the normalized peak response of the superstructure. In contrast, the impact parameters can have a significant effect on the superstructures’ peak accelerations with overestimations up to 70%. In general, the normalized peak response ratios of the interstory drifts tend to increase as the available seismic gap and the coefficient of restitution decrease, although the magnitude of the deviations is within 5%, which can be considered insignificant.

Introduction

Seismic isolation is widely considered as an efficient earthquake-resistant design technology to improve the seismic performance of structures (Skinner et al., 1993; Naeim and Kelly, 1999; Komodromos, 2000). Although base isolation decreases the possibility of damage to a building, it induces large relative displacements at the isolation level due to the increased flexibility. To accommodate the expected large relative displacements, a wide seismic gap must be provided, as a clearance, around the building. This requirement imposes a practical constraint for the utilization of seismic isolation, considering that there are often certain restrictions to the size of the available clearance around seismically isolated buildings, hereafter referred to as seismic gap, especially in cases of retrofitting existing buildings in densely populated urban areas. Therefore, a reasonable concern is the risk of structural pounding with the surrounding moat wall or adjacent structures during very strong earthquakes and the potential consequences from such undesired incidents.

Earthquake-induced structural pounding on base-isolated structures has been studied by several researchers during the last few years. Nagarajaiah and Sun (2001) observed that the response of the base-isolated Fire Command and Control Building in Los Angeles during the 1994 Northridge earthquake was significantly amplified due to the occurrence of impact in one direction, eradicating the effectiveness of base isolation in that direction. Malhotra (1997) and Tsai (1997) examined the response of a base-isolated structure pounding against the surrounding moat wall. The superstructure was idealized as a rigid shear beam structure colliding on an adjacent retaining wall modeled as a spring element. Matsagar and Jangid (2003) investigated the seismic pounding of a multi-story building supported on various base isolation systems during impact with adjacent structures, while impacts were assumed to happen only at the base of the building with the moat wall. Komodromos et al. (2007) and Komodromos (2008) investigated, through parametric studies, the effects of poundings of a base-isolated building with the surrounding moat wall, revealing the potentially detrimental effects of structural impact on the effectiveness of seismic isolation. Limited research works have been conducted considering three-dimensional (3D) earthquake-induced structural pounding, apparently because of the involved complexities and the consequently excessive computational cost. Pant and Wijeyewickrema (2012, 2014) studied seismic pounding of a typical four-story base-isolated building with retaining walls at its base, using 3D finite element analyses. More recently, Polycarpou et al. (2014) presented a novel methodology for simulating earthquake-induced pounding of buildings that are modeled as 3D multi-degree-of-freedom systems.

A critical aspect in numerical simulations of structural pounding is the impact model that is employed and the values of the associated parameters, which may affect the computed results, regarding the peak responses of the simulated structures. In most research studies on structural pounding, force-based impact models are used, exerting impact forces to the colliding structures whenever their seismic gaps are exceeded. Anagnostopoulos (1988), Jankowski (2005), Komodromos et al. (2007), Ye et al. (2009a), Mahmoud and Jankowski (2011), Pant and Wijeyewickrema (2012), and others (Muthukumar and DesRoches, 2006; Ye et al., 2009b; Barros et al., 2013; Liu et al., 2014; Naderpour et al., 2016) have proposed various methodologies using either a linear or a non-linear impact spring together with an energy dissipation mechanism to model structural pounding.

This paper describes five different impact models that have been proposed in the relevant scientific literature and compares their relative performances through dynamic analyses of a typical five-story seismically isolated building, which is subjected to a set of strong near-fault ground motions. Simulation results are presented while varying several parameters, such as the size of the seismic gap and impact characteristics. The majority of the numerical studies already published in the scientific literature, use a fixed set of impact and structural parameters and they do not parametrically investigate their influence on the overall dynamic response. Therefore, the objective of this research work is to investigate how the peak seismic response of base-isolated buildings during pounding may be affected by the type of the incorporated impact model. A numerical study on the deviation of the peak absolute floor accelerations and interstory deflections during poundings is presented, considering as base values the peak responses predicted by the classical linear viscoelastic (Kelvin–Voigt) impact model, which is the most commonly used model.

Modeling and Simulation Details

It is common practice in numerical simulations to consider structural impacts using force-based approaches, also known as penalty methods. These methods allow some penetration between the colliding structures, which can be justified by local deformability at the contact point. Specifically, contact springs are automatically formed as soon as an impact is detected, kept active while the colliding bodies remain in contact and removed once the bodies are detached from each other. At each time step, the penetration depth, δ(t), is used together with the stiffness of the contact spring to assess, according to the adopted impact model, the contact forces that should be applied to the structures in contact. In this research work, five impact models that have been proposed in the relevant scientific literature are used, in order to investigate the relative effect of the impact model selection on the computed peak seismic response considering pounding incidences.

Assessment of the Impact Force during Collision between Structures

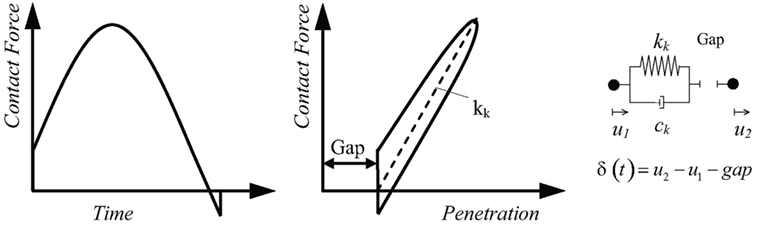
The classical Kelvin–Voigt, or viscoelastic, model is the commonly used impact model to calculate the impact force generated between two colliding structures. The Kelvin–Voigt model consists of a linear elastic spring and a viscous damper, acting in parallel, in order to simulate the energy loss at the contact point, as shown in Figure 1. The forces in the contact element can be calculated through the equation:

$F_{\text{imp}}\left(t\right)=k_{\text{k}}\cdot \mathrm{\delta }\left(t\right)+c_{\text{k}}\cdot \dot{\mathrm{\delta }}\left(t\right)$ (1)

where k_k is the impact (spring) stiffness, c_k is the impact viscous damping coefficient, and $\dot{\mathrm{\delta }}\left(t\right)$ is the relative velocity between the colliding bodies in contact at time t. Anagnostopoulos (1988) has provided the following analytical formulas that associate the dashpot constant, c_k, with the coefficient of restitution, e, of two impacting masses:

$c_{\text{k}}=2\cdot {\mathrm{\xi }}_{\text{k}}\sqrt{k_{\text{k}}\frac{m_1\cdot m_2}{m_1+m_2}},{\mathrm{\xi }}_{\text{k}}=-\frac{\ln e}{\sqrt{{\mathrm{\pi }}^2+{\left(\ln e\right)}^2}}$ (2)

FIGURE 1

Figure 1. The Kelvin–Voigt (linear viscoelastic) impact model.

In the above formulas, m₁ and m₂ are the masses of the two bodies, while e represents the coefficient of restitution, which accounts for the energy loss during impact and is defined as the ratio of the relative velocity between the colliding bodies after and before impact (0 < e ≤ 1).

The viscous impact damper of the Kelvin–Voigt element dissipates energy throughout the approach and restitution phases, but in reality, most of the energy dissipation takes place during the approach period, while less energy is dissipated during the restitution phase. Furthermore, this model exhibits an initial jump in the impact force values due to the viscous damping term, while the damping force at the end of the restitution phase causes negative (i.e., tensile/adhesive) contact forces that pull the colliding bodies together, which is unrealistic for most structural materials. However, due to its simplicity, this model has been widely used to simulate structural pounding (Anagnostopoulos and Spiliopoulos, 1992; Jankowski et al., 1998; Zhu et al., 2002).

The unrealistic presence of tensile forces after the detachment of the colliding bodies can be rectified through a slight adjustment of the linear viscoelastic impact model, as proposed by Komodromos et al. (2007). The modified viscoelastic impact model prevents the tensile forces assuming some permanent plastic deformations, by zeroing the impact force when the contact is lost at the end of the restitution phase of the impact, which increases the corresponding seismic gap. Therefore, the pounding force can be computed as:

$F_{\text{imp}}\left(t\right)=\left\{\begin{array}{cc}{k}_{\text{k}}\cdot \mathrm{\delta }\left(t\right)+c_{\text{k}}\cdot \dot{\mathrm{\delta }}\left(t\right)\hfill & \text{for\hspace{0.17em}}{F}_{\text{imp}}\left(t\right)\ge 0\hfill \\ 0\hfill & \text{for\hspace{0.17em}}{F}_{\text{imp}}\left(t\right)<0\hfill \end{array}\right.$ (3)

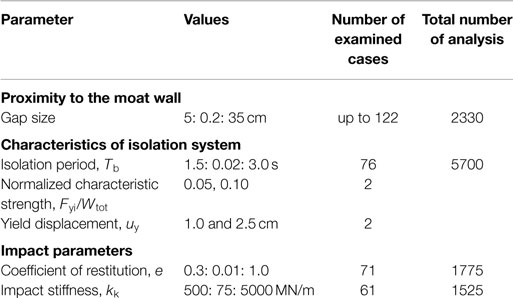
Ye et al. (2009a) proposed a different modification to the Kelvin–Voigt impact model, as shown in Figure 2, noting that the Kelvin–Voigt model cannot reasonably reflect the physical nature of structural pounding. The proposed model preserves the convenience in determining the linear impact spring stiffness, while the damping coefficient ${\widehat{c}}_k$ and the damping constant ${\widehat{\mathrm{\xi }}}_{\text{k}}$ are given by the following equations:

${\widehat{c}}_k={\widehat{\mathrm{\xi }}}_{\text{k}}\cdot \dot{\mathrm{\delta }}\left(t\right),{\widehat{\mathrm{\xi }}}_{\text{k}}=\frac{3}{2}\cdot \frac{k_{\text{k}}\left(1-e\right)}{e\cdot v_{\text{imp}}}$ (4)

where v_imp is the relative impact velocity of the colliding masses just before impact. However, relevant previous studies reveal that the utilization of this model does not always avoid the appearance of tensile forces immediately before separation (Pant et al., 2010; Mavronicola et al., 2015). The existence of tensile forces is possible due to the activation of the dashpot element, which by definition is included in the restitution phase of contact.

FIGURE 2

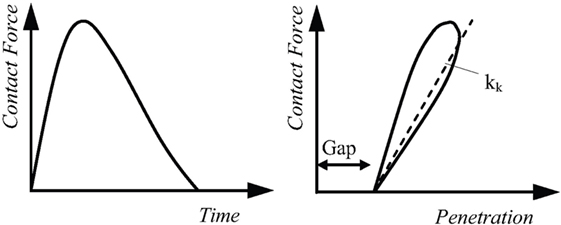
Figure 2. The modified linear viscoelastic impact model proposed by Ye et al. (2009a).

More recently, variations in the Kelvin–Voigt model have been proposed for modeling the seismic pounding between reinforced concrete moment-resisting frame buildings (Figure 3). The main difference from the classical Kelvin–Voigt model lies on the usage of a dashpot, in parallel with the impact spring, that is activated only during the approach period, in which most of the energy is dissipated. The equation that provides the impact force is written as follows:

$F_{\text{imp}}\left(t\right)=\left\{\begin{array}{cc}{k}_{\text{k}}\cdot \mathrm{\delta }\left(t\right)+c_{\text{k}}\cdot \dot{\mathrm{\delta }}\left(t\right)\hfill & \text{for\hspace{0.17em}}\dot{\mathrm{\delta }}\left(t\right)>0\hfill \\ 0\hfill & \text{for\hspace{0.17em}}\dot{\mathrm{\delta }}\left(t\right)\le 0\hfill \end{array}\right.$ (5)

FIGURE 3

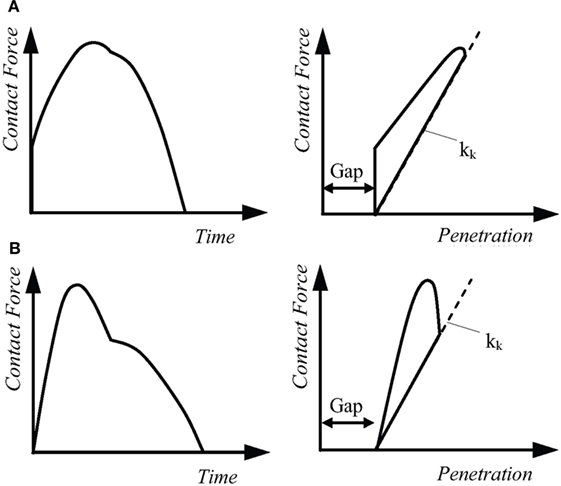
Figure 3. The modified linear viscoelastic impact model proposed by (A) Mahmoud and Jankowski and (B) Pant and Wijeyewickrema.

Mahmoud and Jankowski (2011) and Jankowski and Mahmoud (2015) proposed the incorporation of a modified linear viscoelastic impact model, as presented in Figure 3A, in which the damping term is activated only during the approach period of collision, and the impact element’s damping is defined by Eq. 2. However, the analytical formula between the impact damping ratio and the coefficient of restitution was reassessed in order to satisfy the relation between the post-impact and the prior-impact relative velocities, as follows:

${\mathrm{\xi }}_{\text{k}}=\frac{1-e^2}{e\left(e\left(\mathrm{\pi }-2\right)+2\right)}$ (6)

The relations between the coefficient of restitution and the impact damping ratio for both the linear and the modified linear viscoelastic models were further examined in this study. It was shown that the usage of the modified linear viscoelastic model without the tensile force produces comparable results to those obtained using the linear viscoelastic model.

Another variation in the Kelvin–Voigt model was proposed by Pant and Wijeyewickrema (2012) for the seismic pounding between reinforced concrete moment-resisting frame buildings, Figure 3B. The proposed linear viscoelastic model, in which the damping term is activated only during the approach phase of the collision, aimed to overcome the negative value of the pounding force that occurs just before separation and has no physical resemblance to structural impacts. The following formulas are used for the damping coefficient and the damping ratio, respectively:

${\bar{c}}_{\text{k}}={\bar{\mathrm{\xi }}}_{\text{k}}\cdot \dot{\mathrm{\delta }}\left(t\right),{\bar{\mathrm{\xi }}}_{\text{k}}=\frac{3}{2}\cdot \frac{k_{\text{k}}\left(1-e^2\right)}{e^2\cdot v_{\text{imp}}}$ (7)

Two different approaches can be identified herein for the simulation of the impact damping force. In the Kelvin–Voigt model and the modified Versions proposed by Komodromos et al. and Mahmoud and Jankowski, the viscous component of the impact force acts at a constant damping coefficient. The effect of time-dependent damping coefficient has been incorporated in the models of Ye et al. and Pant and Wijeyewickrema, where ξ and subsequently ${\bar{c}}_{\text{k}}$ become functions of the impact velocity. Figure 4A shows the evolution of the damping ratio as a function of the coefficient of restitution for the five models considered in this study. As mentioned previously, the models of Ye et al. and Pant and Wijeyewickrema have a velocity-dependent damping ratio and for comparison purposes only the curves that correspond to a k_k/v_imp = 1 are considered. It is obvious that each model leads to a significantly different damping ratio that will eventually lead to variations among the dissipated energies during impact. Furthermore, it should be noted that, in general, a k_k/v_imp = 1 is on the lower end of practical values. Larger values will tend to shift the curves of the two models to the right, but the general observations will persist.

FIGURE 4

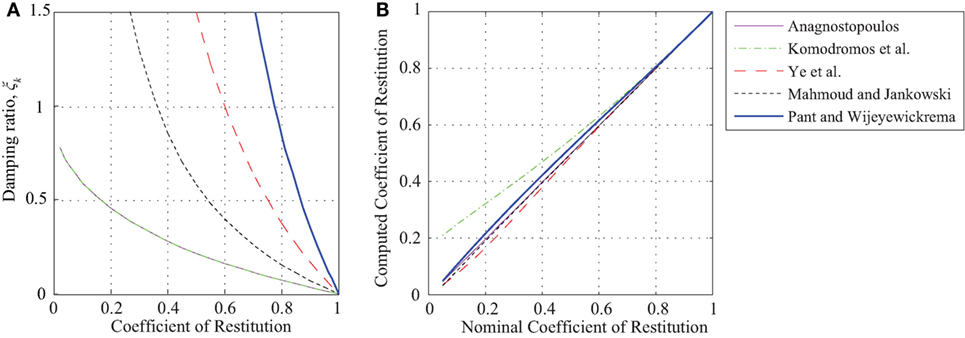
Figure 4. (A) Damping ratio vs. coefficient of restitution for the five models considered herein and (B) comparison between the nominal and computed coefficient of restitution.

In this work, two colliding masses and a range of values of the coefficient of restitution are used in order to assess the accuracy of the aforementioned impact models. For each predefined value of the coefficient of restitution, each of the impact models is used to perform an impact simulation, compute the impact velocity after impact and, thus, the corresponding computed value for the coefficient of restitution. Figure 4B compares the prespecified (nominal) and the computed values for the impact models under consideration, which ideally should coincide. The results show that the assumption of a direct relationship between the impact velocity and the penetration is reasonable for prespecified coefficients of restitution larger than 0.5. As the coefficient of restitution approaches 1.0, it should be noted that all five models converge to the linear elastic contact model with impact stiffness k_k. For most practical purposes, considering that the coefficient of restitution for structural impact varies within the range of 0.5–0.75 (Jankowski, 2005), the accuracy of the proposed formulas is satisfactory.

Modeling of Seismically Isolated Buildings Considering Poundings

In this study, the dynamic analyses of the simulated building, taking into account structural pounding, are performed in two dimensions, while the superstructure of the seismically isolated building is modeled as a shear-type structure mounted on LRBs with one lateral degree-of-freedom at each floor and the masses lumped at the floor levels, as shown in Figure 5A. Pounding is assumed to happen between the moat wall and the base floor, which is the most common case of structural impact for a base-isolated building due to the expected large relative displacements at the isolation level. The seismically isolated MDOF system is subjected to horizontal components of near-fault ground motions, while it is assumed that the superstructure maintains a linear elastic behavior during the induced earthquake excitations.

FIGURE 5

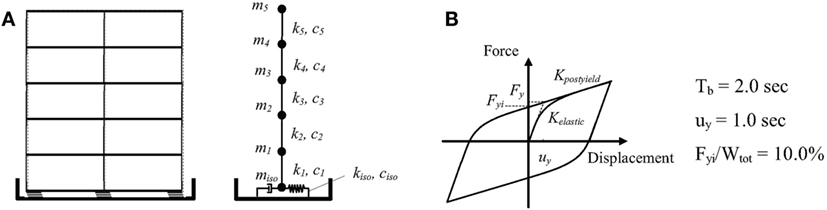
Figure 5. (A) Configuration of a five-story seismically isolated building and (B) smooth bilinear inelastic model for the behavior of the seismic isolation system.

A typical five-story base-isolated building, with 340 tons lumped mass at each floor level and a roof mass of 250 tons, is used in the simulations, while a finite seismic gap on either of its sides is considered in order to compare the estimations of the peak structural responses using the five afore-described impact models. An additional mass of 340 tons is assumed to be lumped at the seismic isolation level. Each story has a horizontal stiffness of 600 MN/m, whereas a viscous damping ratio equal to 2.0% is assumed for the superstructure. In the performed simulations, the Bouc–Wen, a smooth bilinear inelastic model, is used for simulating the response of the seismic isolators (Mavronicola and Komodromos, 2014). For the LRBs, an isolation period based on the post-yield stiffness of 2.0 s, a normalized characteristic strength F_yi/W_tot = 0.10 and a yield displacement equal to 1.0 cm, Figure 5B, were considered unless otherwise stated. For all performed dynamic analyses, the values 1.0, 0.5, 0.5, and 2 are adopted for the Bouc–Wen models’ parameters A, β, γ, and n, respectively. In addition to the hysteretic damping of the isolation system, a 5.0% viscous damping ratio is also considered.

In order to effectively perform the necessary numerical simulations required for this investigation, an extendable software has been developed, using an object-oriented programing approach and the Java programing language. The software uses an algorithm that combines the solution of the equations of motion, using the unconditionally stable Newmark’s method, and the solution of the differential equation governing the behavior of the Bouc–Wen for the LRBs, based on the implicit Runge–Kutta method with a fixed time step. The time interval for solving the equations of motion has been set to 2.0 × 10⁻⁵ s.

Parametric Studies and Numerical Results

A parametric study has been performed in order to examine the effects of the excitation characteristics on the dynamic response of the simulated base-isolated building during pounding. Table 1 shows the five near-fault ground motions that have been used. The selected seismic accelerograms have been taken from the PEER Pacific Earthquake Engineering Research Center (2011) and are expected to induce large displacements to the seismically isolated building, since they are characterized by low-frequency content, which is one of the most decisive factors for the occurrence of pounding in such structures.

TABLE 1

Table 1. Earthquake records that have been used in the performed simulations.

The various cases that have been examined in this parametric study are presented in Table 2. Certain influencing parameters are intentionally varied in order to assess how their values may affect the effectiveness of the seismic isolation during poundings. Furthermore, the effect of using different impact models for the calculation of the impact forces on the overall seismic response during pounding is also examined in this section. Specifically, more than 11,300 non-linear time–history analyses have been performed, considering the 5 aforementioned impact models.

TABLE 2

Table 2. Examined cases in the parametric study (initial value: step: final value).

Effect of the Gap Size and the Characteristics of the Earthquake Excitation

The seismic gap width is systematically varied in the range of 5–35 cm with a step of 0.2 cm, in order to investigate its effect on the overall response. The five-story base-isolated building is analyzed under the selected near-fault ground motions, while the moat wall is assumed to be present, with the same seismic gap, on both sides of the building. The linear viscoelastic model and its modifications that have been proposed in the literature are used to compare the peak response of the building due to poundings with the surrounding moat wall. The impact stiffness is considered to be 2500 MN/m, the coefficient of restitution is taken as 0.7 for all cases, while the mass of the surrounding moat wall is set to 500 tons. The stiffness parameters of all models are assumed to be the same, for consistency (Muthukumar and DesRoches, 2004; Ye et al., 2009a; Pant et al., 2010; Mate et al., 2012; Khatiwada et al., 2014).

Figure 6 presents the peak floor accelerations and the maximum interstory drifts of the base-isolated building using the records from Loma Prieta and Northridge earthquakes as a function of the seismic gap width, considering the classical Kelvin–Voigt model using the formula provided by Anagnostopoulos for the estimation of the impact damping coefficient. It is apparent that the most severe peak floor accelerations occur at the base level where poundings occur. Subsequently, the maximum interstory deflections occur at the 1–0 interface. The simulation results indicate that both peak absolute acceleration and interstory drifts of the building increase significantly due to structural impact, reaching values that are several times the corresponding peak response values without pounding. It is also observed that the dynamic structural response is, in general, amplified as the seismic gap reduces. However, this increase is not monotonic with local maxima to exist that are correlated with structural and earthquake characteristics.

FIGURE 6

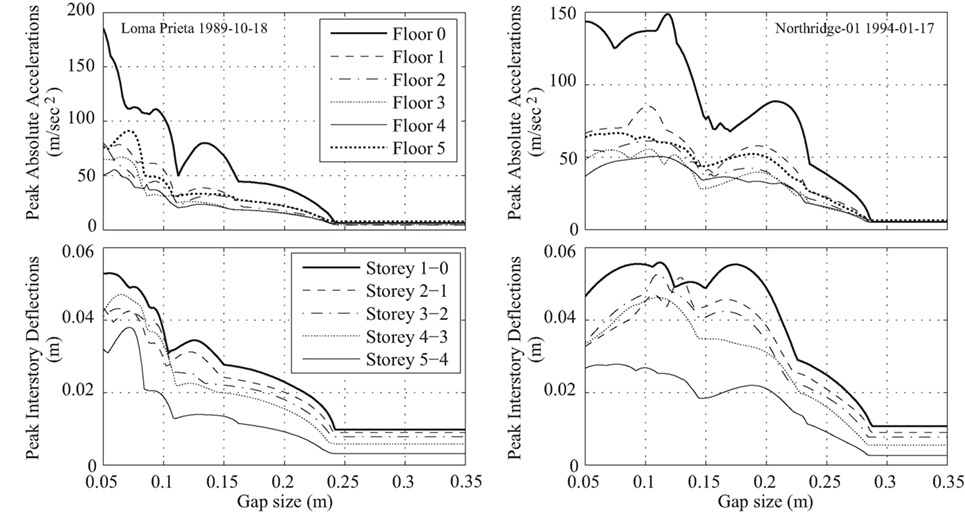
Figure 6. Peak floor response of the five-story base-isolated building due to poundings with the moat wall in terms of the width of the seismic gap considering the classical Kelvin–Voigt model.

The variation in the peak response amplification (absolute floor accelerations and interstory deflections) due to the characteristics of the excitation and the peak impact velocities are provided in Figure 7, where the envelope of the peak response is plotted for all considered excitations. The amplification factor is defined as the ratio of the maximum response among all floors of the building when poundings occur, divided by the corresponding maximum response values without poundings. It is observed that, in general and for a range of values of the seismic gap near the maximum induced displacement, i.e., the critical gap size, the response is decreasing rapidly with the increase of the gap size. The differences between the peak response curves for each ground motion are large. This indicates that the frequency content and the predominant frequencies are the most important characteristics of the seismic excitations, influencing greatly the peak response during poundings. Overall, the five impact models that have been examined provide similar trends for the peak response of the superstructure. Additionally, for a seismic gap 15% smaller than the maximum unobstructed relative displacement under each one of the selected near-fault ground motions, the amplification of the peak interstory drifts is similar. Furthermore, it is observed that the trends of peak impact velocities at the base (third column of Figure 7) are very similar to the corresponding peak absolute floor acceleration of the seismically isolated building, indicating that the amplification of the response due to impact is proportional to the impact velocity. It is also observed that the maximum impact velocity is relatively consistent between the impact models that are considered. It should be noted that the maximum force generated during impact (hereafter referred to as peak impact force) may not be related to the maximum impact velocity.

FIGURE 7

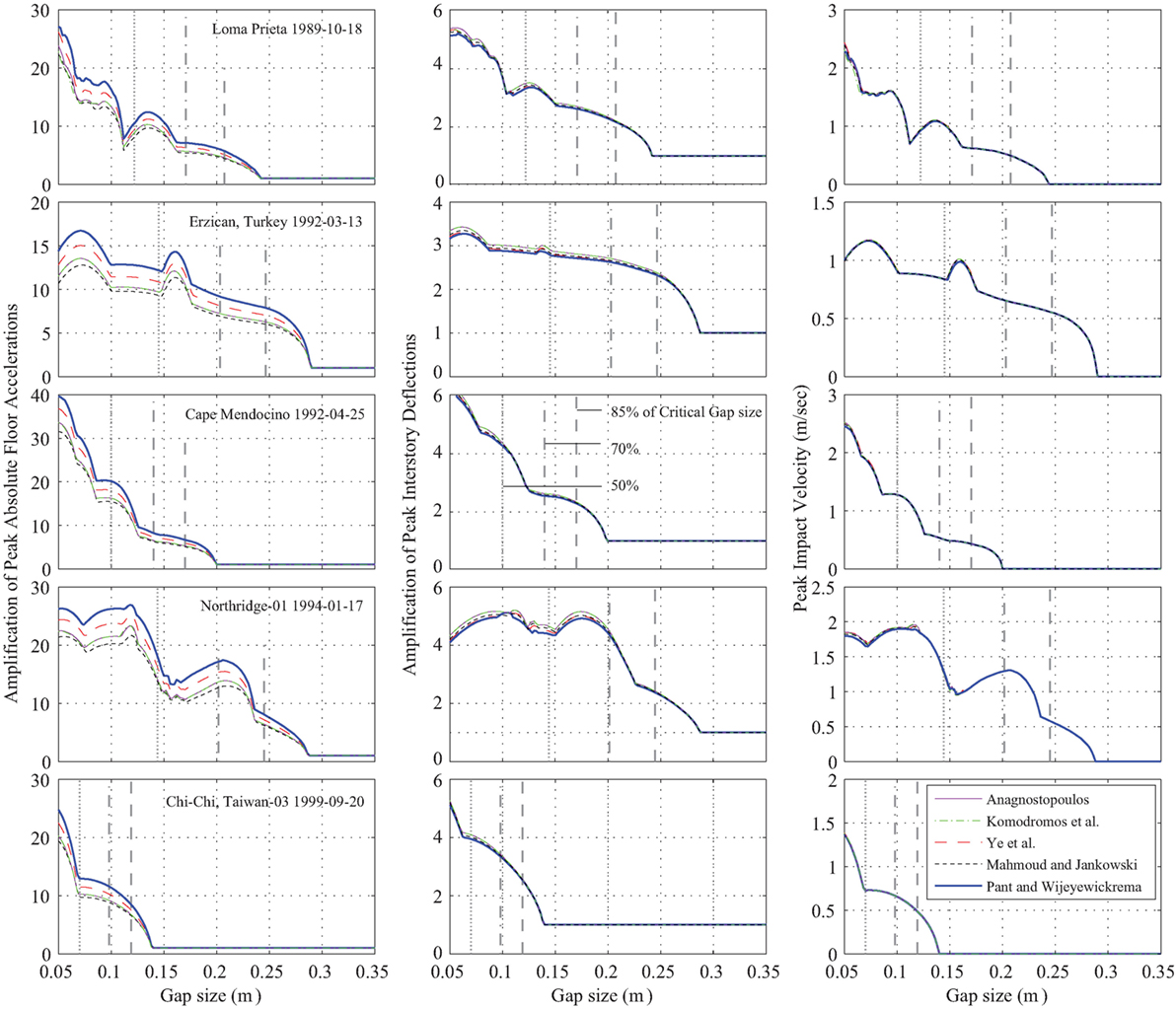
Figure 7. Peak (floor accelerations and interstory deflections) responses amplification and peak impact velocity of the base-isolated building, in terms of the width of the seismic gap.

In order to more easily compare the results among the five impact models, all peak responses are normalized with respect to the classical Kelvin–Voigt model. The linear viscoelastic model using the formula provided by Anagnostopoulos for the estimation of the impact damping coefficient has been considered as a base model due to its wide usage in numerical simulations. Figure 8 presents the normalized peak absolute floor accelerations (first column), showing that the Kelvin–Voigt impact model and the modified linear viscoelastic model proposed by Komodromos et al., in which a permanent deformation is allowed, lead to almost identical responses. In general, the peak floor accelerations are underestimated at about 5% when the contact element proposed by Mahmoud and Jankowski, is used with respect to the linear viscoelastic impact model. On the other hand, normalized response ratios are, in general, kept at values higher than 1.0, indicating overestimation around 10 and 25% when the contact elements proposed by Ye et al. and the Pant and Wijeyewickrema, respectively, are used. It is interesting to note that the response deviation remains almost constant. The differences in the peak floor accelerations predicted by the various models appear to relate with their capacity to either overestimate or underestimate, with respect to the Kelvin–Voigt model, the peak impact force.

FIGURE 8

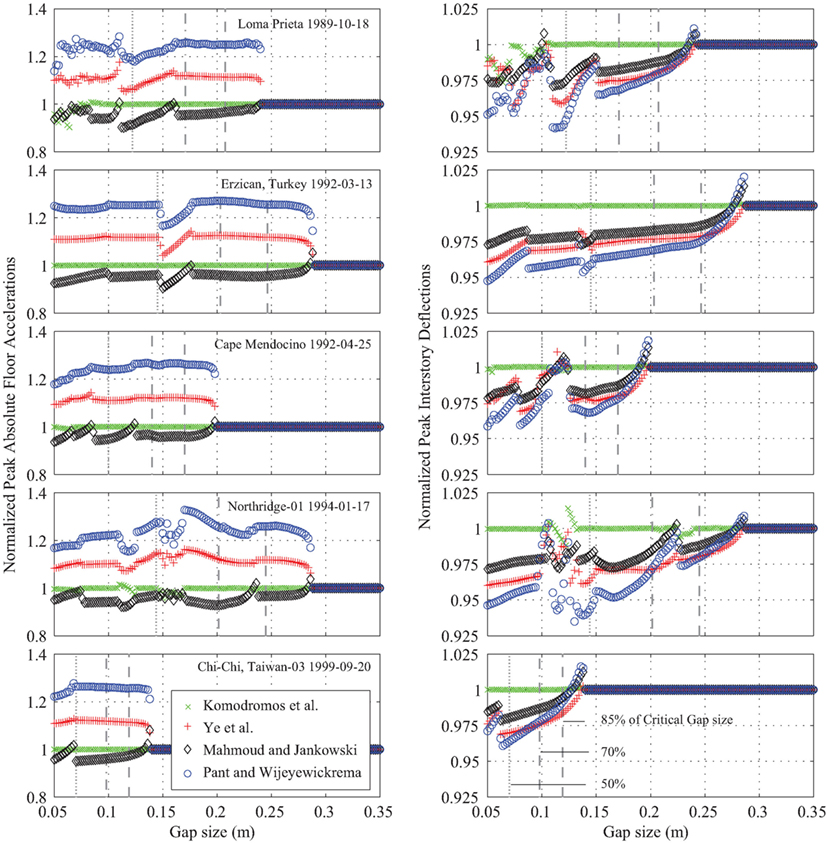
Figure 8. Peak (floor accelerations and interstory deflections) response using the modified linear impact models, normalized to the corresponding peak response obtained using the classical Kelvin–Voigt model in terms of the width of the seismic gap.

It is observed that the values of the maximum interstory deflections calculated through the Kelvin–Voigt model and the modified Version proposed by Komodromos et al. are essentially equal. While the peak interstory deflections are, in general, underestimated when the impact models proposed by the Ye et al., Mahmoud and Jankowski, and Pant and Wijeyewickrema are used, compared to the corresponding peak responses computed using the classical Kelvin–Voigt model. In general, the underestimation of the peak response while using the aforementioned modified models tends to increase as the width of the seismic gap reduces. The underestimation of the response for seismic gap widths 20% smaller than the maximum base drifts, for each earthquake record appears to fall within a range of 1.0–3.0% for all modified linear impact models. Such an underestimation of the response can be considered as insignificant. These responses are in line with the capacity of the models to dissipate energy in various extends, as indicated in Figure 4A; the higher the dissipation capacity, the lower the interstory deflections.

Effect of the Isolation System Characteristics

In order to investigate the effect of the isolation characteristics on the amplification of the peak response, the smooth Bouc–Wen model is used for the isolation system with an isolation eigenperiod, T_b, which approximates the post-yield fundamental eigenperiod of the base-isolated building, varies between 1.5 and 3.0 s. For all considered cases, a non-linear time–history analysis has been performed for the simulated MDOF base-isolated building for different combinations of the normalized characteristic strength (0.05 and 0.10) and the isolators’ yield displacements (1.0 and 2.5 cm). The impact parameters considered are those that have been used in the previous subsection.

Figure 9 presents the peak response amplifications considering the classical Kelvin–Voigt model, for all excitations considering gap size equal to 20 cm and assuming equal gaps on both sides of the buildings. The simulation results indicate that there is a substantial increase of the response amplification in the case of normalized characteristic strength equal to 5%, and, in general, the response amplification increases rapidly with the increase of the isolation period. It should be noted that a gap size of 20 cm is sufficient to avoid any structural pounding during the Chi–Chi earthquake; therefore, the amplification factors remain constant at 1.0. As already discussed, the more restricted the available seismic gap compared to the maximum unobstructed displacement under each one of the selected near-fault ground motions the higher the response amplification. Therefore, the previous finding can be justified considering that with the increase of the normalized characteristic strength the isolation system becomes relatively stiff, and the bearing displacement decreases, while the relative bearing displacements are higher for higher values of the isolation period.

FIGURE 9

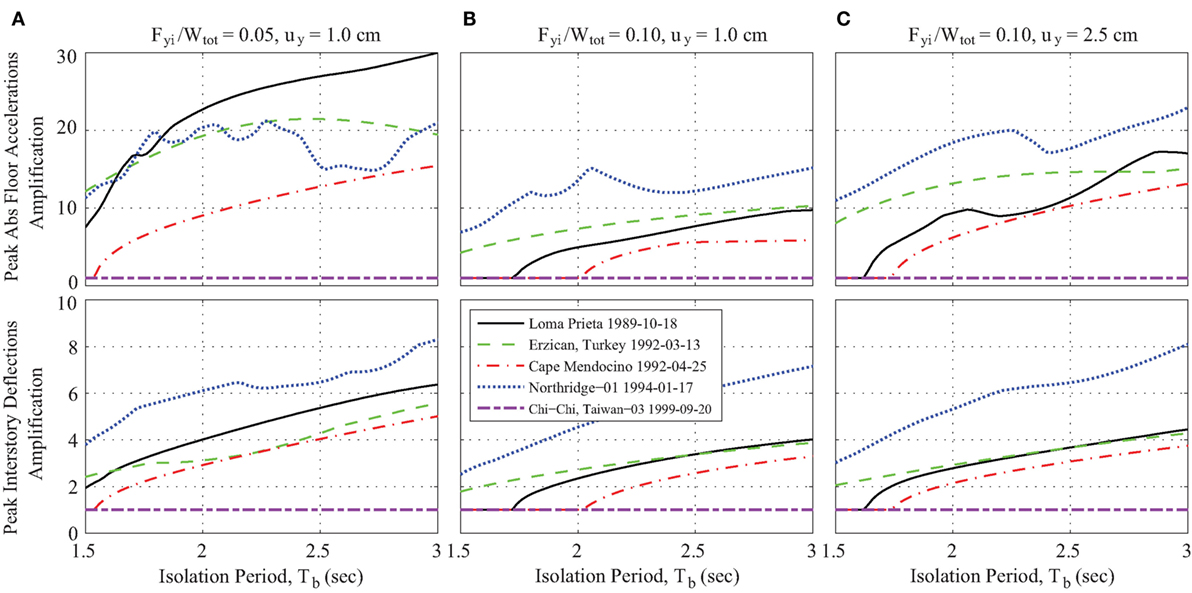
Figure 9. Amplifications of the peak floor accelerations and interstory deflections in terms of the period of isolation system considering the classical Kelvin–Voigt model with a 20-cm gap size at both sides using various seismic isolation systems. (A) F_yi/W_tot = 0.05 and u_y = 1.0 cm, (B) F_yi/W_tot = 0.10 and u_y = 1.0 cm and (C) F_yi/W_tot = 0.10 and u_y = 2.5 cm.

Moreover, the case of having isolator yield displacement equal to 2.5 cm is examined, and the results are illustrated in Figure 9C. In general, it is observed that the response amplification reaches higher values compared to the corresponding response amplification considering yield displacement of 1.0 cm for the isolation system, as shown in Figure 9A. Previous studies showed that the bearing displacement presents a marginal increasing trend with the increase of the isolator yield displacements (Matsagar and Jangid, 2004). Therefore, the results suggest that the earthquake characteristics in combination with the characteristics of the seismic isolation system and the difference between the available seismic gap and the maximum relative displacements of the building for each earthquake record seem to play a significant role in the severity of the structural impact and its consequences.

The amplifications of the peak floor accelerations and interstory deflections, using the four aforementioned modifications of the impact models, normalized with respect to the corresponding peak responses computed with the classical Kelvin–Voigt impact model are provided in Figures 10 and 11, respectively. The variation in the normalized responses under the selected near-fault excitations is presented for different values of the normalized characteristic strengths and the isolators’ yield displacements, in terms of the seismic isolation period.

FIGURE 10

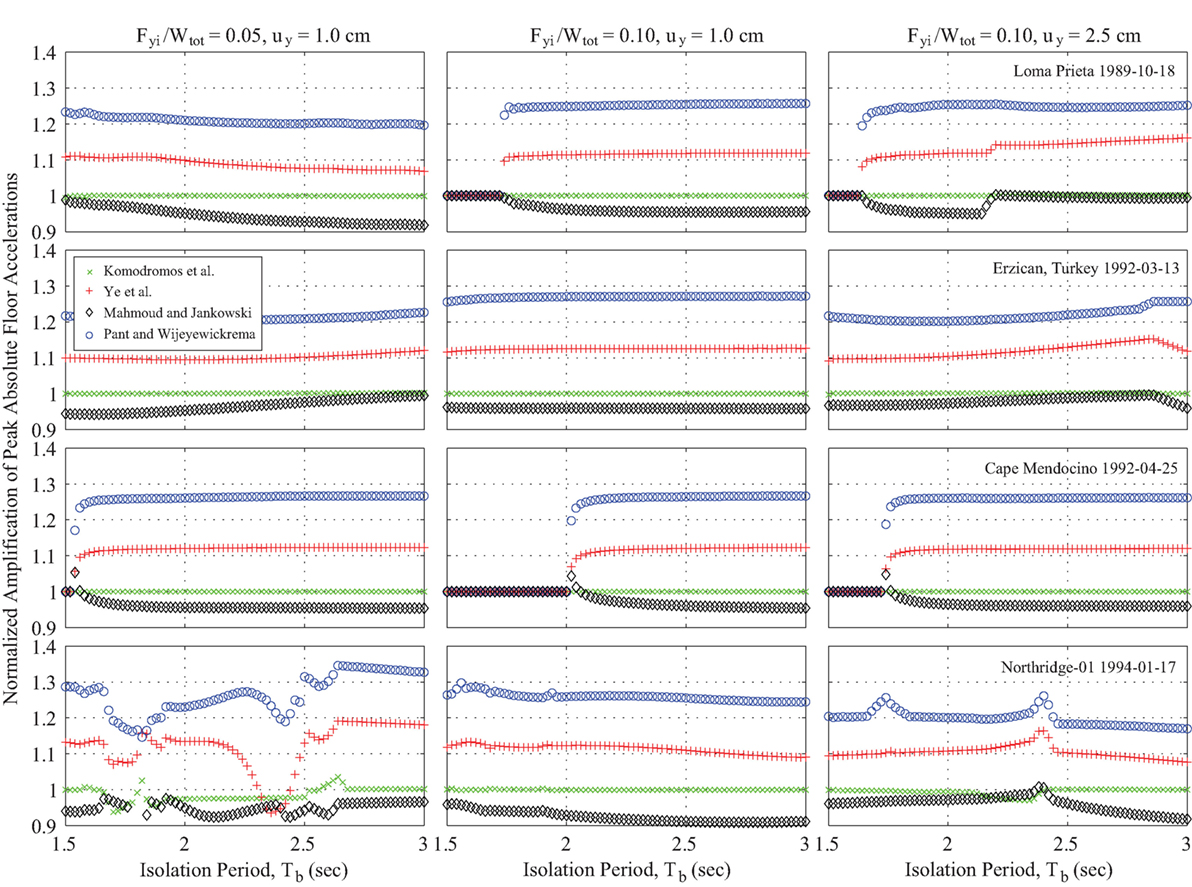
Figure 10. Peak absolute floor accelerations using the modified linear impact models, normalized to the corresponding peak response obtained using the Kelvin–Voigt model, in terms of the isolation period.

FIGURE 11

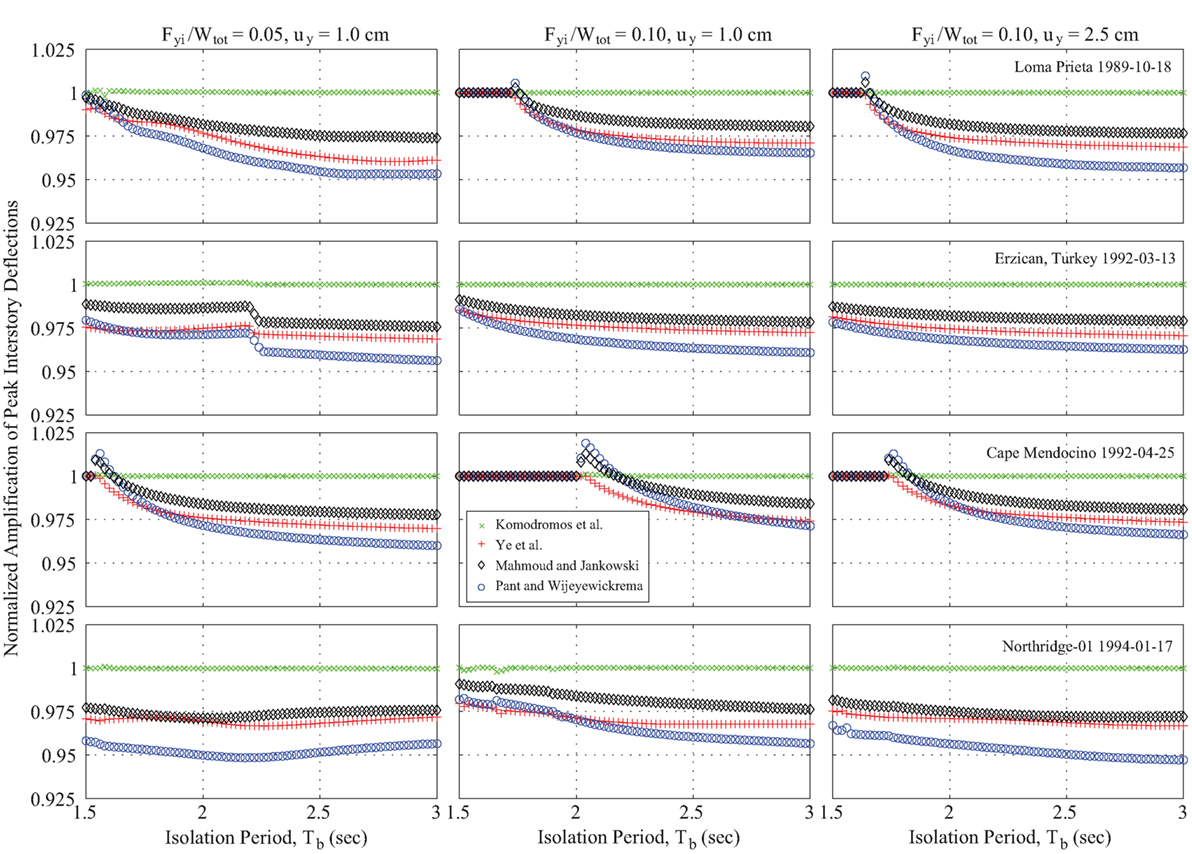
Figure 11. Peak interstory deflections, using the modified linear impact models, normalized to the corresponding peak response obtained using the Kelvin–Voigt model, in terms of the isolation period.

The plots of Figure 10 indicate that the seismic isolation period, the normalized characteristic strength, and the yield displacement of the isolation system do not considerably influence the normalized peak floor acceleration. Furthermore, the normalized peak response ratios are not affected by the difference between the available gap size and the maximum response displacement of the corresponding MDOF system. Additionally, the Kelvin–Voigt impact model and the modified linear viscoelastic model proposed by Komodromos et al. lead to almost identical responses for the absolute floor accelerations, while when the contact element proposed by Mahmoud and Jankowski is used, the response is slightly underestimated compared to the former two models. On the other hand, the peak response obtained using Ye et al. and the Pant and Wijeyewickrema models are much higher than those obtained using the classical Kelvin model, fluctuating around 10 and 25%, respectively.

The variations in the normalized interstory deflections for various isolators’ characteristics are shown in Figure 11. The peak responses considering the classical Kelvin–Voigt model and the contact elements proposed by Komodromos et al. are, in general, identical to each other. Interestingly, the simulation results indicate that the underestimation of the normalized peak interstory drifts considering the rest of the impact models tend to increase as the isolation period increases. The results indicate that the difference between the seismic gap and the maximum displacement of the corresponding MDOF system influence the variation in normalized interstory deflections.

Effect of the Impact Parameters

In order to examine the effect of the values of the impact stiffness and the coefficient of restitution on the computed peak seismic responses of the base-isolated building during poundings, another series of parametric studies is performed. For this investigation, the five-story base-isolated building is simulated, assuming a seismic gap 15% smaller than the maximum unobstructed relative displacement at the isolation level under each one of the selected near-fault ground motions, in order to ensure the occurrence of structural pounding. The impact stiffness, k_k, of the linear impact spring is varied in the range of 500–5000 kN/mm, assuming a coefficient of restitution equal to 0.7. In addition, the coefficient of restitution is varied between 0.5 and 1.0, while the impact stiffness for the linear viscoelastic impact models is set to 2500 kN/mm. The pounding force between the moat walls is modeled using each of the five afore-described impact models.

Figure 12 presents the impact incidences obtained from the time–history analysis carried out for the Loma Prieta ground motion considering the five different impact models for various impact parameters. For this particular excitation, it should be noted that the first impact incidence delivers the peak responses. As shown in the first row of Figure 12, the coefficient of restitution does not influence considerably the peak impact force for the Kelvin–Voigt model and the model proposed by Komodromos et al. in order to eliminate the tensile forces during detachment. On the other hand, the peak impact force as computed while using the recommended modifications by Ye et al., Mahmoud and Jankowski, and Pant and Wijeyewickrema depends significantly on the coefficient of restitution. The computed results indicate that the contact element proposed by Mahmoud and Jankowski exhibits a high initial jump, especially for lower values of the coefficient of restitution, upon impact. The authors have acknowledged that the modified formula is inferior to the original formulation in all their studied cases and recommend the original formula for use in the study of structural poundings (Mahmoud and Jankowski, 2011).

FIGURE 12

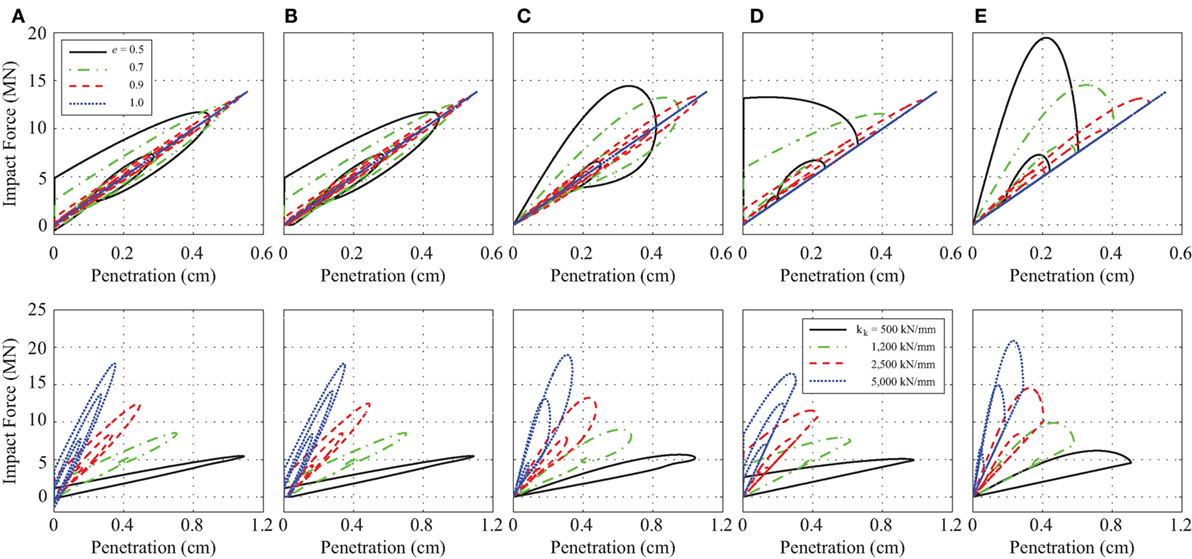
Figure 12. Comparison of the impact forces, under the Loma Prieta ground motion, considering the (A) classical Kelvin–Voigt, (B) Komodromos et al., (C) Ye et al., (D) Mahmoud and Jankowski, and (E) Pant and Wijeyewickrema impact models, for various impact parameters.

Furthermore, the results highlight the significant influence of the impact stiffness on the peak impact force due to pounding with the adjacent moat wall, as shown in the second row of Figure 12. In general, large peak forces are coupled with higher values of the impact stiffness and small deformations across all impact models. It is apparent that the models proposed by Ye et al. and Pant and Wijeyewickrema produce significantly higher magnitude impact forces than the classical linear viscoelastic impact model, mainly due to the damping of the contact elements. The enclosed areas between the loading and unloading curves of an impact force vs. indentation curve define the amount of energy dissipated during impact. Comparison of the amount of dissipated energy during impact reveals that the dissipated energy during impact that is computed by the modified contact models proposed by Ye et al., Mahmoud and Jankowski, and Pant and Wijeyewickrema is higher than the dissipated energy during impact computed by the classical Kelvin–Voigt model.

The variation in the amplification of peak floor accelerations and peak interstory deflections of the five-story base-isolated building that are computed considering the classical Kelvin–Voigt model in terms of the two impact parameters is now discussed. The peak response amplification of the five-story base-isolated building in terms of the coefficient of restitution under five ground motions is presented in Figure 13A. It is observed that the amplification of the peak floor accelerations shows a marginal increasing trend with a slight increase of the coefficient of restitution, reaching their maximum values when the impact becomes purely elastic. In general, the excitation characteristics influence considerably the magnitude of the amplification due to poundings.

FIGURE 13

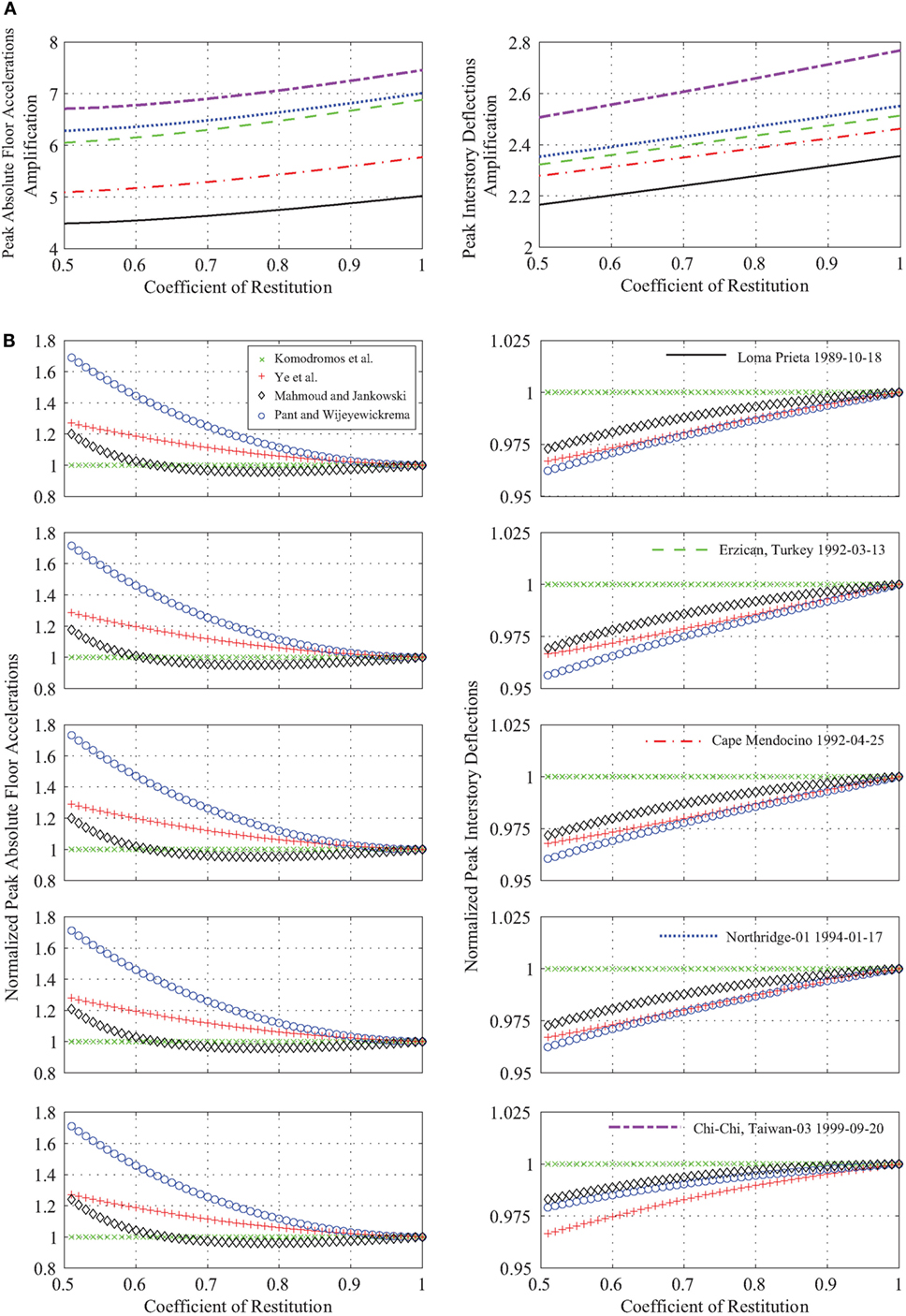
Figure 13. (A) Amplifications of peak responses while considering the Kelvin–Voigt contact element under the five ground excitations and (B) normalized peak responses while considering the four other impact models, in terms of coefficient of restitution, e, under the five ground excitations.

Figure 13B shows the normalized peak response of the four modified impact models with respect to the classical Kelvin–Voigt model, with the same usage of the line-types as those used in the plots of Figure 13A, regarding the imposed earthquake excitation. The results indicate that the modification proposed by Komodromos et al. does not significantly change the peak structural response. On the other hand, the peak floor acceleration ratios, as estimated using the Mahmoud and Jankowski contact element, are overestimated for coefficient of restitutions lower than 0.65 with an increasing tendency, reaching values up to about 20% for e = 0.5. For e between 0.65 and 1.0, the response is slightly underestimated. It should be noted that the range of underestimation depends on the values of the impact stiffness, something that is further investigated in the following paragraphs. Furthermore, using Ye et al. and Pant and Wijeyewickrema models lead to a significant overestimation of the peak absolute floor acceleration, i.e., of the magnitude of 1.7 and 1.3 for e = 0.5, respectively, as the coefficient of restitution influences more significantly the peak impact forces derived from those models than those derived from the classical Kelvin–Voigt model. Furthermore, the development of higher impact forces during collision leads to more severe peak floor accelerations. The capacity of the models to generate different magnitudes of peak forces during impact is evidenced in Figure 12.

Moreover, the peak interstory deflections computed using the models proposed by Ye et al., Mahmoud and Jankowski, and Pant and Wijeyewickrema lead to an underestimation of the response up to 4% with respect to the corresponding peak responses computed using the classical Kelvin–Voigt model. This can be justified by considering that the corresponding amount of dissipated energy in the Kelvin–Voigt model for a given coefficient of restitution is the lowest among all modified models. For all cases, the underestimation of the peak interstory deflections tends to decrease with the increase of the value of the coefficient of restitution.

The peak absolute floor accelerations due to pounding of the base-isolated building with the moat wall under each one of the five selected near-fault ground motions, which are presented in Figure 14A, tend to increase for higher values of the impact stiffness, as it is varied from 500 to 5000 kN/mm. This finding suggests that the value of the impact stiffness should not be much higher than the stiffness of the superstructure in order to avoid large peak floor accelerations, which can be destructive for sensitive equipment that may be housed in the building, upon impact. Hence, potential incorporation of a flexible material with low impact stiffness between the building and the adjacent walls, which may act as a collision bumper, could be an effective measure to minimize the detrimental effects of impacts, under certain circumstances. Furthermore, the peak interstory drift amplifications increase rapidly when the impact stiffness increases up to the value of 650–800 kN/mm, while for the rest of the examined range, the amplifications of the peak response remain almost insensitive to this parameter. The simulation results also reveal that the excitation characteristics influence considerably the amplification of the peak response.

FIGURE 14

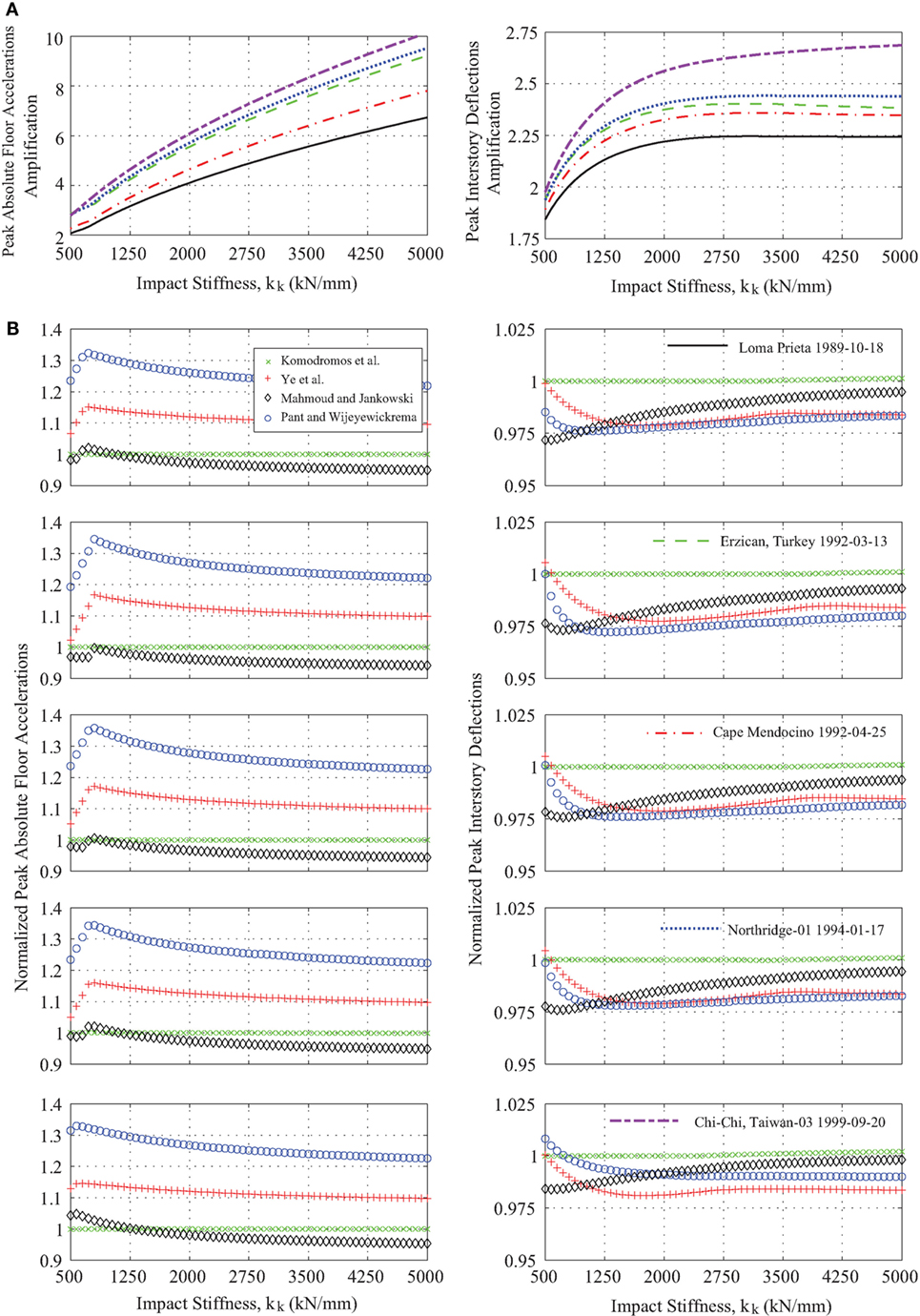
Figure 14. (A) Amplifications of peak responses while considering the Kelvin–Voigt contact element under the five ground excitations and (B) normalized peak responses while considering the four other impact models, in terms of the varying impact stiffness, k_k under the five ground excitations.

Figure 14B depicts the normalized peak responses computed using the five modified impact models, while considering as reference the classical linear viscoelastic model. The results indicate that using the Ye et al. and Pant and Wijeyewickrema models lead to an overestimation of the peak absolute floor accelerations, as the magnitudes of the contact forces during impact are much higher in those cases, while the response is slightly underestimated when model of Mahmoud and Jankowski is used for the structural pounding. The computed results indicate that the overestimation of the amplification of the response tends to increase up to 15 and 33%, for the Ye et al. and Pant and Wijeyewickrema models, followed by an exponential-type trend that tends to 10 and 20% increases, respectively. An examination of the response for each floor showed that the kinks appearing in the variation of the normalized peak floor acceleration relate to an interchange between the floors that dominate the global structural response. More specifically, for low k_k values, the top floor appears to deliver the peak floor acceleration, whereas k_k increases the response is dominated by the base floor accelerations, which relates to the level of impact with the moat wall. It should be noted that the variation in the normalized floor accelerations depends on the impact parameters, but does not seem to be sensitive to the characteristics of the excitation. Regarding the peak interstory drifts obtained considering the four modifications of the classical linear viscoelastic impact model, it was found that the computed peak interstory drifts are relatively underestimated, up to 2.5%, compared to the corresponding peak responses computed while using the classical Kelvin–Voigt impact model.

Conclusion

The seismic performance of a base-isolated building pounding against the surrounding moat wall has been evaluated using near-fault pulse-like ground motions. Four recently proposed variations in the classical linear viscoelastic impact model have been compared considering as a base model the classical Kelvin–Voigt model. The relative performance of the base-isolated structure has been evaluated based on the peak absolute floor accelerations and interstory drifts. The presented results refer to a typical five-story base-isolated building with specific structural characteristics under different cases of gap sizes and characteristics of the isolators, as well as different impact parameters, subjected to a range of different near-fault excitations. From the trends of the computed results of this study, the following conclusions have been drawn.

• The impact model proposed by Mahmoud and Jankowski aimed at eliminating the tensile force just before separation of the colliding bodies, while reassessing the relationship between ξ_k and e. However, after this improvement, the sudden jump at the beginning of impact still appears in the model.

• The minor modification proposed by Komodromos et al. for the linear viscoelastic model does not influence considerably the peak response values.

• The maximum impact forces obtained using the impact models proposed by Ye et al. and Pant and Wijeyewickrema are much higher than those obtained using the classical linear viscoelastic model with the formulas provided by Anagnostopoulos, leading to a relative overestimation of the peak absolute floor accelerations.

• The absolute floor accelerations for all modified models appear to be a function of the impact stiffness and the coefficient of restitution investigated within this study. When either the impact stiffness or the coefficient of restitution is reduced, the deviations of the peak response tend to increase.

• The maximum interstory deflections of the building are, in general, slightly underestimated when the modified impact models are used. Those response deviations are related with the capacity of the models to dissipate energy in various extends and, in general, tend to increase as the available gap size and the coefficient of restitution decrease.

• Both the characteristics of the seismic excitation and the properties of the isolators do not seem to influence the variation in the normalized peak responses.

Author Contributions

PP developed the original numerical tool. EM carried out literature review, extended the developed software, and run parametric analysis. PK supervised the study. All authors analyzed the results and contributed to the manuscript at all stages.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Anagnostopoulos, S. A. (1988). Pounding of buildings in series during earthquakes. Earthq. Eng. Struct. Dyn. 16, 443–456. doi: 10.1002/eqe.4290160311

CrossRef Full Text | Google Scholar

Anagnostopoulos, S. A., and Spiliopoulos, K. V. (1992). An investigation of earthquake induced pounding between adjacent buildings. Earthq. Eng. Struct. Dyn. 21, 289–302. doi:10.1002/eqe.4290210402

CrossRef Full Text | Google Scholar

Barros, R. C., Naderpour, H., Khatami, S. M., and Mortezaei, A. (2013). Influence of seismic pounding on RC buildings with and without base isolation system subject to near-fault ground motions. J. Rehabil. Civ. Eng. 1, 39–52.

Google Scholar

Jankowski, R. (2005). Non-linear viscoelastic modelling of earthquake-induced structural pounding. Earthq. Eng. Struct. Dyn. 34, 595–611. doi:10.1002/eqe.434

CrossRef Full Text | Google Scholar

Jankowski, R., and Mahmoud, S. (2015). Earthquake-Induced Structural Pounding. Cham: Springer International Publishing.

Google Scholar

Jankowski, R., Wilde, K., and Fujino, Y. (1998). Pounding of superstructure segments in isolated elevated bridge during earthquakes. Earthq. Eng. Struct. Dyn. 27, 487–502. doi:10.1002/(SICI)1096-9845(199805)27:5<487:AID-EQE738>3.0.CO;2-M

CrossRef Full Text | Google Scholar

Khatiwada, S., Chouw, N., and Butterworth, J. W. (2014). A generic structural pounding model using numerically exact displacement proportional damping. Eng. Struct. 62–63, 33–41. doi:10.1016/j.engstruct.2014.01.016

CrossRef Full Text | Google Scholar

Komodromos, P. (2000). Seismic Isolation for Earthquake Resistant Structures. Southampton: WIT Press.

Google Scholar

Komodromos, P. (2008). Simulation of the earthquake-induced pounding of seismically isolated buildings. Comput. Struct. 86, 618–626. doi:10.1016/j.compstruc.2007.08.001

CrossRef Full Text | Google Scholar

Komodromos, P., Polycarpou, P. C., Papaloizou, L., and Phocas, M. C. (2007). Response of seismically isolated buildings considering poundings. Earthq. Eng. Struct. Dyn. 36, 1605–1622. doi:10.1002/eqe.692

CrossRef Full Text | Google Scholar

Liu, Y., Liu, W.-G., Wang, X., He, W.-F., and Yang, Q.-R. (2014). New equivalent linear impact model for simulation of seismic isolated structure pounding against moat wall. Shock Vib. 2014, 10. doi:10.1155/2014/151237

CrossRef Full Text | Google Scholar

Mahmoud, S., and Jankowski, R. (2011). Modified linear viscoelastic model of earthquake-induced structural pounding. Iran. J. Sci. Technol. 35, 51–62.

Google Scholar

Malhotra, P. K. (1997). Dynamics of seismic impacts in base-isolated buildings. Earthq. Eng. Struct. Dyn. 26, 797–813. doi:10.1002/(SICI)1096-9845(199708)26:8<797:AID-EQE677>3.0.CO;2-6

CrossRef Full Text | Google Scholar

Mate, N. U., Bakre, S. V., and Jaiswa, O. R. (2012). “Comparative study of impact simulation models for linear elastic structures in seismic pounding,” in 15th World Conference on Earthquake Engineering (Lisbon).

Google Scholar

Matsagar, V. A., and Jangid, R. S. (2003). Seismic response of base-isolated structures during impact with adjacent structures. Eng. Struct. 25, 1311–1323. doi:10.1016/S0141-0296(03)00081-6

CrossRef Full Text | Google Scholar

Matsagar, V. A., and Jangid, R. S. (2004). Influence of isolator characteristics on the response of base-isolated structures. Eng. Struct. 26, 1735–1749. doi:10.1016/j.engstruct.2004.06.011

CrossRef Full Text | Google Scholar

Mavronicola, E., and Komodromos, P. (2014). On the response of base-isolated buildings using bilinear models for LRBs subjected to pulse-like ground motions: sharp vs. smooth behaviour. Earthq. Struct. 7, 1223–1240. doi:10.12989/eas.2014.7.6.1223

CrossRef Full Text | Google Scholar

Mavronicola, E., Polycarpou, P. C., and Komodromos, P. (2015). “The effect of modified linear viscoelastic impact models in the pounding response of a base-isolated building with adjacent structures,” in 5th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering (Crete Island).

Google Scholar

Muthukumar, S., and DesRoches, R. (2004). “Evaluation of impact models for seismic pounding,” in 13th World Conference on Earthquake Engineering (Vancouver, BC).

Google Scholar

Muthukumar, S., and DesRoches, R. (2006). A Hertz contact model with non-linear damping for pounding simulation. Earthq. Eng. Struct. Dyn. 35, 811–828. doi:10.1002/eqe.557

CrossRef Full Text | Google Scholar

Naderpour, H., Barros, R. C., Khatami, S. M., and Jankowski, R. (2016). Numerical study on pounding between two adjacent buildings under earthquake excitation. Shock Vib. 2016, 9. doi:10.1155/2016/1504783

CrossRef Full Text | Google Scholar

Naeim, F., and Kelly, J. M. (1999). Design of Seismic Isolated Structures: From Theory to Practice. Hoboken, NJ: John Wiley & Sons Inc.

Google Scholar

Nagarajaiah, S., and Sun, X. (2001). Base-isolated FCC building: impact response in Northridge earthquake. J. Struct. Eng. 127, 1063–1075. doi:10.1061/(ASCE)0733-9445(2001)127:9(1063)

CrossRef Full Text | Google Scholar

Pant, D. R., and Wijeyewickrema, A. C. (2012). Structural performance of a base-isolated reinforced concrete building subjected to seismic pounding. Earthq. Eng. Struct. Dyn. 41, 1709–1716. doi:10.1002/eqe.2158

CrossRef Full Text | Google Scholar

Pant, D. R., and Wijeyewickrema, A. C. (2014). Performance of base-isolated reinforced concrete buildings under bidirectional seismic excitation considering pounding with retaining walls including friction effects. Earthq. Eng. Struct. Dyn. 43, 1521–1541. doi:10.1002/eqe.2409

CrossRef Full Text | Google Scholar

Pant, D. R., Wijeyewickrema, A. C., and Ohmachi, T. (2010). “Seismic pounding between reinforced concrete buildings: a study using two recently proposed contact element models,” in 14th European Conference on Earthquake Engineering (Ohrid).

Google Scholar

PEER Pacific Earthquake Engineering Research Center. (2011). Ground Motion Database. Available at: http://peer.berkeley.edu/peer_ground_motion_database

Google Scholar

Polycarpou, P. C., Papaloizou, L., and Komodromos, P. (2014). An efficient methodology for simulating earthquake-induced 3D pounding of buildings. Earthq. Eng. Struct. Dyn. 43, 985–1003. doi:10.1002/eqe.2383

CrossRef Full Text | Google Scholar

Skinner, R. I., Robinson, W. H., and McVerry, G. H. (1993). An Introduction to Seismic Isolation. West Sussex: John Wiley & Sons Ltd.

Google Scholar

Tsai, H. C. (1997). Dynamic analysis of base-isolated shear beams bumping against stops. Earthq. Eng. Struct. Dyn. 26, 515–528. doi:10.1002/(SICI)1096-9845(199705)26:5<515:AID-EQE654>3.0.CO;2-C

CrossRef Full Text | Google Scholar

Ye, K., Li, L., and Zhu, H. (2009a). A modified Kelvin impact model for pounding simulation of base-isolated building with adjacent structures. Earthq. Eng. Eng. Vib. 8, 433–446. doi:10.1007/s11803-009-8045-4

CrossRef Full Text | Google Scholar

Ye, K., Li, L., and Zhu, H. (2009b). A note on the Hertz contact model with nonlinear damping for pounding simulation. Earthq. Eng. Struct. Dyn. 38, 1135–1142. doi:10.1002/eqe.883

CrossRef Full Text | Google Scholar

Zhu, P., Abe, M., and Fujino, Y. (2002). Modelling three-dimensional non-linear seismic performance of elevated bridges with emphasis on pounding of girders. Earthq. Eng. Struct. Dyn. 31, 1891–1913. doi:10.1002/eqe.194

CrossRef Full Text | Google Scholar