Centrifuge Testing and Seismic Response Analysis for Uplift Behavior of Spread Foundation Structures on Rock

Introduction

When spread foundation structures on rock are subjected to large seismic motions, significant uplift may occur. Uplift behavior during an earthquake is an important consideration in the seismic designs of a building for ensuring safety (e.g., nuclear power-related facilities).

Many experimental or analytical studies on this problem have been conducted previously. For the seismic design of a nuclear power plant, analytical studies on non-linear rocking behavior have been conducted [e.g., Muto and Kobayashi (1979), Yamada and Kawamura (1984), Shimomura (1988), Yano et al. (1991), and Nakamura et al. (2016)]. Moreover, experimental studies using shaking table or centrifugal tests have been conducted [e.g., Yano et al. (1983), Hangai et al. (1986, 1987), Ishikawa et al. (2007), Imamura et al. (2014), and Imamura et al. (2013)]. There are analytical and experimental studies on other types of buildings too [e.g., Midorikawa et al. (2009), Ishihara et al. (2009), and Nakamura et al. (2014)].

However, few studies have investigated significant uplift behavior. Thus, in this work, experimental and analytical studies are conducted for understanding the uplift behavior of spread foundation structures on bedrock for accumulation of basic research data on this problem.

First, centrifugal loading tests for determining the uplift behavior of spread foundation structures are conducted. The parameter of the experiment is embedding condition, so that effect of embedded to uplift behavior is confirmed. Second, a simulation analysis of centrifugal load testing, with the aim of verifying the analytical accuracy of uplift behavior evaluation by using a three-dimensional FE Model of a spread foundation structure built on bedrock, is conducted. The analytical results of the simulation are compared with the experimental results to clarify any differences and determine modeling requirements for maintaining analytical accuracy in three-dimensional FE models using joint elements.

Centrifugal Test

Centrifugal Model

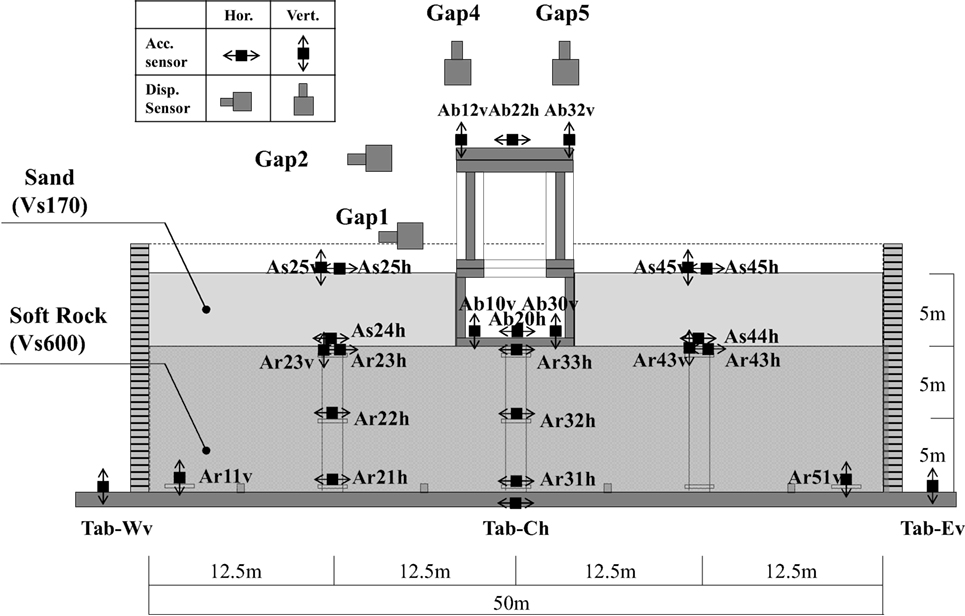
Centrifugal testing was carried out using a centrifugal acceleration field of 50 G and a laminar shear container to consider two separate cases. Case 1 involved the model shown in Figure 1 in a “non-embedded condition”; i.e., after the subsurface layer (labeled as “sand”) had been removed. In Case 2, the prototype scale model was kept in the “embedded” condition depicted in Figure 1. Figure 2A shows a diagram of the entire structural model, and Figure 2B is a photograph of the structural model.

FIGURE 1

Figure 1. Model foundation outline (centrifuge acceleration: 50 G, real conversion, embedded).

FIGURE 2

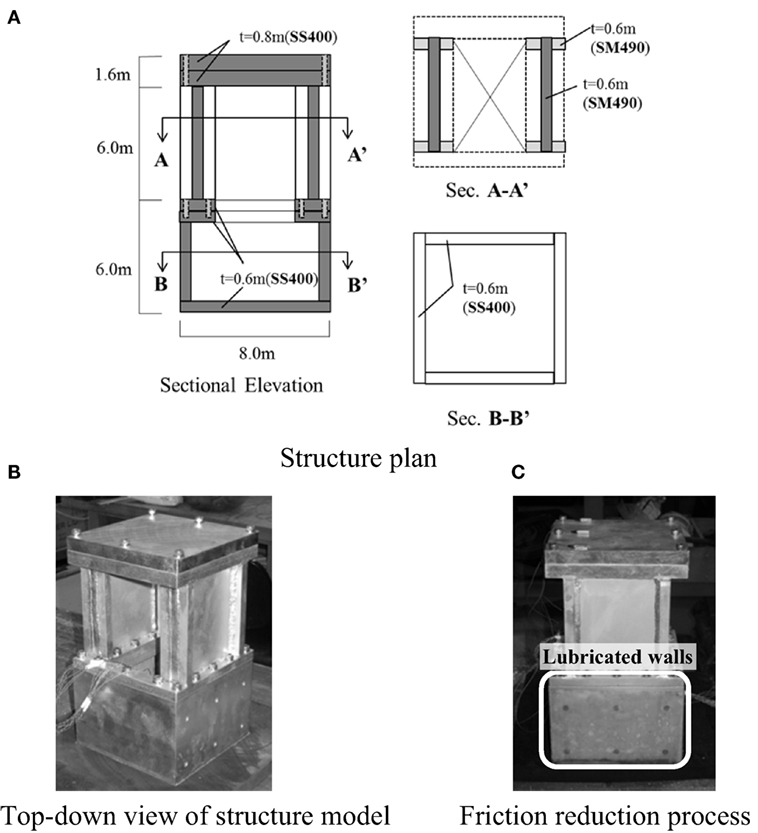
Figure 2. Structure model. (A) Structure plan, (B) top-down view of structure model, and (C) friction reduction process.

The model structure had a foundation width of 8 m × 8 m, a height from its base of 13.6 m (the footing depth in the embedded case was 5 m), and the average contact pressure of the structure was 400 kN/m². The structure consisted of an underground portion (1F), an above-ground portion (2F), and dead weight tonnage (RF), with each being manufactured from welding steel (SS400, SM490) and connected by bolts. The original model was planned as a rigid body with a center of gravity 6.7 m from the base of the foundation and a primary natural frequency of 25 Hz (real conversion).

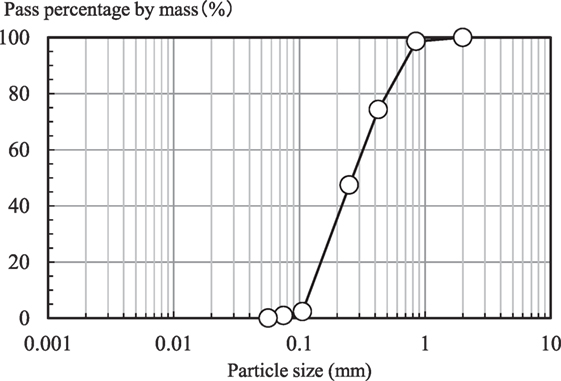
The soil was made up of a rock-bearing stratum of cement-treated soil and a subsurface layer of Iide silica sand 4–7 (a dry, well-graded sand).

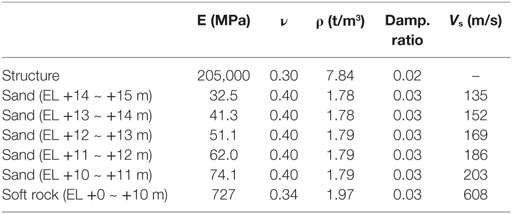
To manufacture the load-bearing stratum, cement-treated soil was produced by mixing Iide silica sand 6 with Kaolin clay to a 4:1 ratio by weight. To this was added an amount of blast furnace B-type cement equivalent to 6.125% of the dry weight of the mixture and water amounting to 28.7% of the dry weight. The resulting cement-treated soil had a wet weight of p_t = 1.967 g/cm³ and an unconfined compression strength of qf = 830 kN/mm². The constants for its elastic wave speed (P wave, S wave) were V_p = 1,259 m/s and V_s = 608 m/s, or ν = 0.340.

The same load-bearing stratum was used for Cases 1 and 2. The subsurface layer was developed using a dehydrated sand mixture of Iide 4–7, the particle size distribution of which is shown in Figure 3 (p_s = 2.646 g/cm³; e_max = 0.845; e_min = 0.485; relative density, D_r = 100%; p_d = 1.782 g/cm³). For the confining pressure of the subsurface layer under the assumed centrifugal field (K₀ = 0.5), the wave speed (S) results derived from bender elements by using triaxial test equipment were around V_s = 135–205 m/s. Using the confining pressure at the average depth of the surface foundation (GL – 2.5 m) increases this to about 170 m/s.

FIGURE 3

Figure 3. Particle size distribution of subsurface layer (Iide silica sand 4–7).

Profile Side Contact Conditions

As mentioned earlier, Case 1 represents a “non-embedded” condition in which there is no subsurface layer, whereas Case 2 is an “embedded” condition in which there is a subsurface layer. Although the 1F outer wall in Case 2 is in contact with the subsurface layer, this test assumes that this outer wall is not subjected to any shear resistance. To create these “frictionless” conditions, silicon grease (Shinetsu KS-63G) was applied to the 1F outer wall, and 0.3 mm-thick membrane sheets were pasted onto the four walls. According to Tatsuoka et al. (1984), this treatment reduces the coefficient of friction to μ < 0.02. Figure 2C is a photograph showing the boundary treatment condition of the 1F outer wall.

Measurement Plan

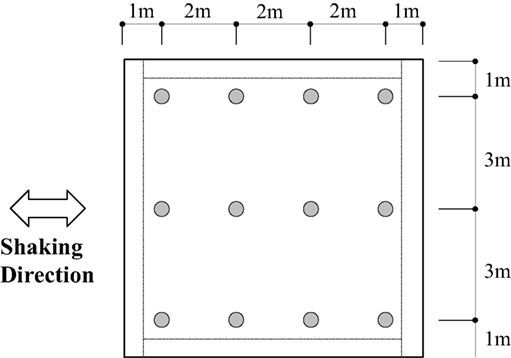
The measuring instruments used in testing (Figure 1) were accelerometers and earth pressure gages installed at the base of the foundation, and contactless gap sensors for determining displacement. A sampling speed of 100 Hz was used with real conversion. Figure 4 shows the position of the earth pressure gages that were installed at the base of the foundation to measure the ground contact ratio.

FIGURE 4

Figure 4. Configuration of earth pressure gages on underside of structure model.

Input Seismic Motion

To generate seismic motion, an L2 earthquake wave-in notification (Kobe register) was used as an input wave (2E). As with any shaking table experiment using a centrifugal field, it was necessary to stipulate a compound wave (E + F) made up of the input wave and rebound waves at the bottom of the laminar shear container. To achieve this, an earthquake response analysis was implemented according to a one-dimensional wave motion theory that does not take into account the structural model, from which compound waves in the laminar shear container were drawn up. Once the input signal was adjusted to reproduce this compound wave, the maximum acceleration of input motion is set to 300 cm/s².

Figure 5 shows the history of the input wave (2E) and compound wave (E + F) at the bottom of the laminar shear container over time. The acceleration response spectrum of the input wave and compound wave at the base of the foundation are also shown. The period of controlled excitation (0.25–2.0 s) is indicated by arrows.

FIGURE 5

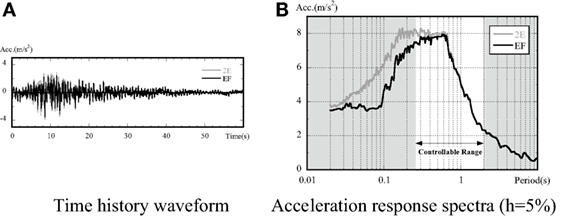
Figure 5. Input acceleration to excitation. (A) Time history waveform and (B) acceleration response spectra (h = 5%).

Experimental Result Summary

Figure 6 shows the experimental results for the no embedding case. The values of ground contact ratios were calculated by dividing the contact area with the total foundation area based on the values obtained from earth pressure gages installed on the underside of the structure. Moreover, in this figure, time history response and maximum or minimum response values are shown. In the no embedding case, the minimum ground contact ratio was 25.0%. Furthermore, at the top of the structure, the maximum horizontal displacement was 113 mm, the maximum horizontal acceleration was 605 cm/s², and the maximum vertical acceleration was 878 cm/s². From ground contact ratio over time, it was confirmed that uplift occurs immediately after shaking starts. Then, at approximately 15 s, significant uplift occurred, and the ground contact ratio was 25%. With this significant uplift, the horizontal displacement and acceleration amplitude also increased significantly, and the period of these response waves was long term. Moreover, significant uplift-induced vertical motions occurred.

FIGURE 6

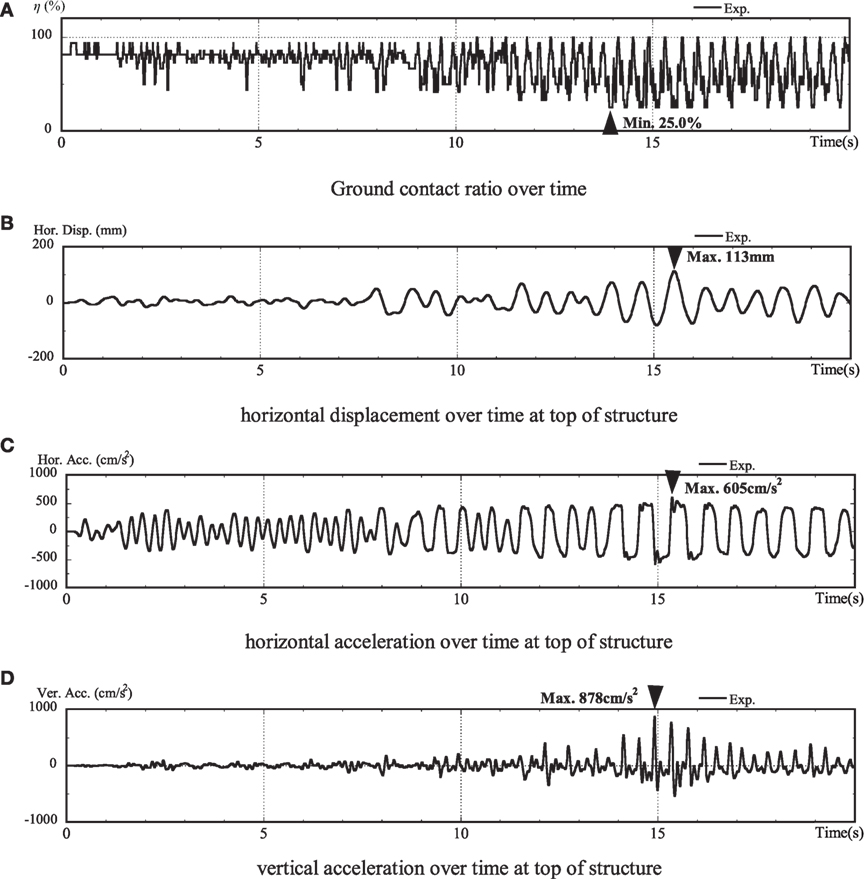
Figure 6. Experimental results (no embedding). (A) Ground contact ratio over time, (B) horizontal displacement over time at top of structure, (C) horizontal acceleration over time at top of structure, and (D) vertical acceleration over time at top of structure.

Figure 7 shows the experimental results for the embedded case. In the embedded case, the minimum ground contact ratio was 37.5%. Furthermore, at the top of the structure, the maximum horizontal displacement was 65.4 mm, the maximum horizontal acceleration was 520 cm/s², and the maximum vertical acceleration was 370 cm/s². The response values of the embedded case were lower than those for the no embedding case. It is assumed that this is due to the embedded effect. From ground contact ratio over time, as well as the no embedding case, uplift occurs immediately after shaking starts. Then, at approximately 12 s, significant uplift occurred, and the ground contact ratio was 37.5%. Moreover, with the increase in uplift, all response values increased.

FIGURE 7

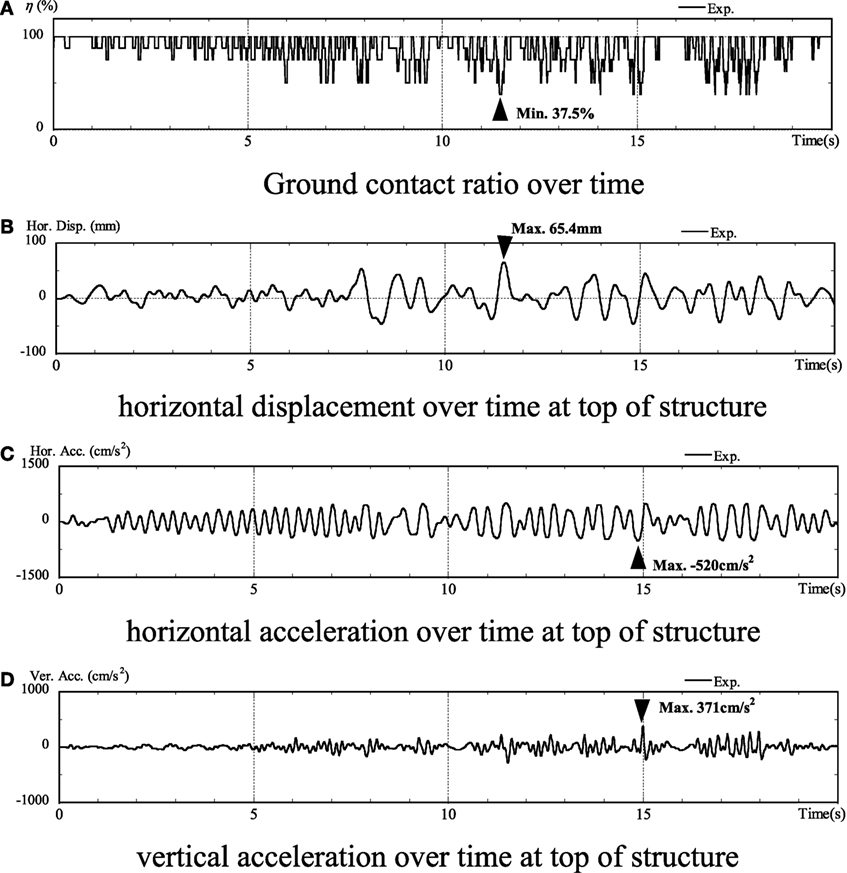
Figure 7. Experimental results (embedded). (A) Ground contact ratio over time, (B) horizontal displacement over time at top of structure, (C) horizontal acceleration over time at top of structure, and (D) vertical acceleration over time at top of structure.

Analysis Conditions

Model Overview

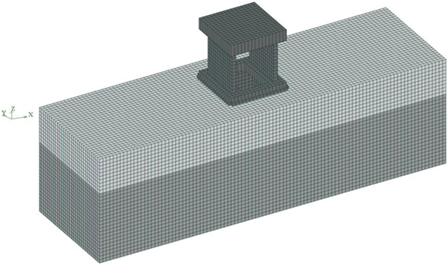
Figure 8 shows a top-down view of the embedded analysis model used in Case 1 drawn at prototype scale. The soil was modeled as eight solid elements (integral points: 2 × 2 × 2), while the structure was modeled as four node-plate elements (integral points: 2 × 2). Each was treated as a linear element by using physical properties corresponding to the test results shown in Table 1. Proportional stiffness damping was used, along with a reference frequency of 1 Hz.

FIGURE 8

Figure 8. Top-down view of analytical model (embedded).

TABLE 1

Table 1. Components of foundation and structure.

The foundation was modeled at horizontal intervals of 50 m relative to the laminar shear container, and vertical intervals of 10 m from the bottom of the foundation. The mesh partition was maintained at no more than 1/5 of the 20 Hz wavelength of the V_s (160 m/s) for the subsurface layer (i.e., no more than 160/20/5 = 1.6 m) and was set up so as to partition the foundation of the structure into 16 separate sections (0.5 m pitch). This same mesh partition was used for the mesh partitions of the structure, the details of which were modeled after adding modifications of ±0.25 m. The embedded model had the largest number of nodes and elements, with 90,000 of each.

A repeat boundary condition was used at the side of the soil, while a fixed boundary was used at the bottom of the soil. The weight of the frame of the laminar shear container was not taken into account.

Boundary Conditions between the Foundation and the Structure

The foundation uplift behavior was evaluated by setting up a joint element between the underside of the structure and the soil. Joint elements are almost “rigid” in response to compression but have no stiffness in response to tension (Nakamura et al., 2007). These need to be set up, so that during contact they have sufficient rigidity in the shear direction, but no rigidity during separation in the tensile direction. The validity of using a joint element has been verified through comparison with the Green Function Method in Nakamura et al. (2016). An almost “rigid” joint element is one with a stiffness 100× that calculated by vibration admittance theory (VA).

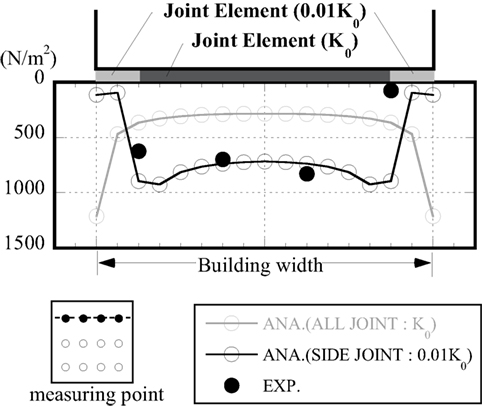
Figure 9 shows one example of the comparison between experimental measurements of the initial stress distribution in the foundation underside and the analysis values. Note that the end stress tended to be smaller in the experimental measurements when compared with the contact pressure occurring at the end in the analytical results, which used a basic value for the rigidity of all joint components.

FIGURE 9

Figure 9. Initial compressive stress distribution.

By lowering the basic value used for the rigidity of the joint component of the 1 m outer circumference (2 elements) to 1/100, the initial contact pressure of the outer circumference was reduced to more closely to conform to the experimental data. The reason for this may be because the process of increasing gravity on the soil and structure at the start of the experiment results in some non-linearity in the load-bearing stratum (the cement-treated soil) due to the large initial stress occurring at the edge of the foundation.

The joint elements in the embedded model were also set up on the sides, but because the experimental conditions were designed to make the coefficient of friction on the sides close to 0, rigidity in the shear direction was set at close to 0. The rigidity in the normal direction was set to the same value as the joint element below the structure, and detachment in the normal vector direction was not taken into account.

Input Seismic Motion

The acceleration history of the seismic motion input was measured in both the horizontal and vertical directions. The horizontal acceleration was inputted as Tab-Ch in Figure 1, while the vertical acceleration was inputted through the average acceleration of Tab-Wv and Tab-Ev. The seismic motion input for the experimental results was passed through a high-cut filter process (8–14 Hz), because high peaks were observed in the high oscillation range that fell outside of the guaranteed performance frequency range of the centrifugal load equipment. Analysis was carried out from the start of the earthquake until 20 s had elapsed.

Other Analytical Conditions

The Newmark-β method was used in the integral method; and to maintain analytical stability in the non-linear areas, such as resettling after uplift, a value attenuation of β = 0.6, y = 0.3025 was used. The time increment used for analysis was set at 0.002 s, while the output time increment was set at 0.01 s.

Verifying Simulation Accuracy

This section verifies the analytical accuracy of the simulation analysis implemented using the analytical conditions described in Section “Analysis Conditions” and also considers the limits to its analytical accuracy. As described in Section “Input Seismic Motion,” strong peaks were observed in the high oscillation component of the experimental results, and so a high-cut filter process (8–14 Hz) was carried out in this section to allow for direct comparison.

Non-Embedded Condition

A comparison of the experiment and analysis results for the non-embedded condition is shown in Figure 10. The items compared here over time are the ground contact ratio, the horizontal displacement for the top of the structure, the horizontal acceleration, the vertical acceleration, and the acceleration response spectrum for the top of the structure (h = 5%).

FIGURE 10

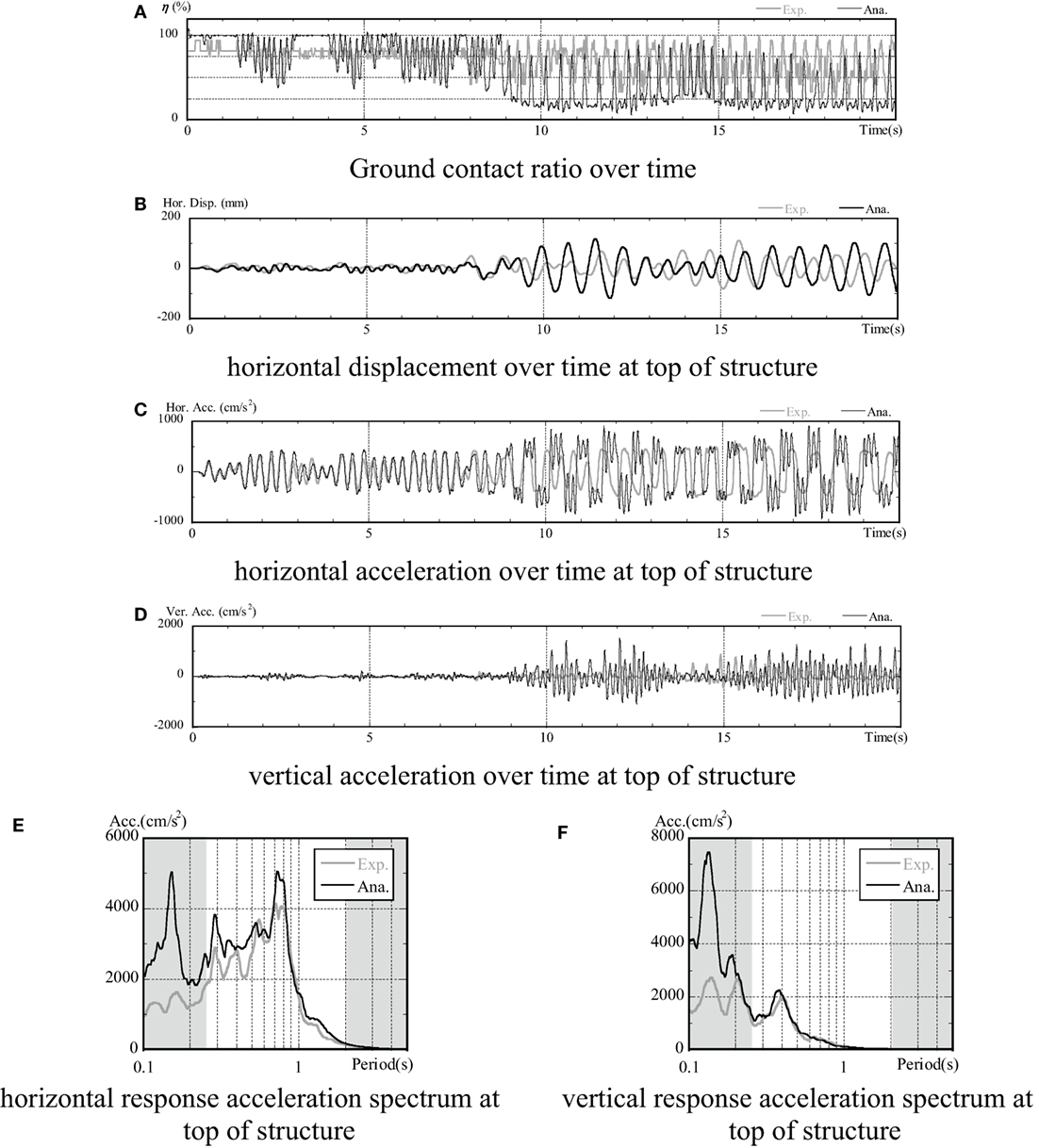
Figure 10. Comparison of experimental and analysis results (no embedding). (A) Ground contact ratio over time, (B) horizontal displacement over time at top of structure, (C) horizontal acceleration over time at top of structure, (D) vertical acceleration over time at top of structure, (E) horizontal response acceleration spectrum at top of structure, and (F) vertical response acceleration spectrum at top of structure.

The ground contact ratio values were calculated as the contact area divided by the total foundation area based on the values obtained from the earth pressure gages installed on the underside of the structure. In the analysis, it was calculated based on the vertical stress of the joint elements installed between the structure and the soil. The acceleration response spectrum was filled out, as shown in Figure 5, except for the frequency bands for which the credibility of the equipment load could be maintained.

In verifying the history of the ground contact ratio with time (a), it was found that the experiments and analysis correspond favorably to each other until 9 s in. However, disparities arise beyond this point and the analysis tends to give smaller values than the experiment (i.e., the uplift is higher in the analysis values). The ground contact ratio in the analysis results is generally 25% lower, but even when the analysis produces values of <25%, the experimental results did not produce equally low ground contact ratios.

A divergence between the experimental and analytical results also occurred with the time histories of (b) horizontal displacement, (c) horizontal acceleration, and (d) vertical acceleration. In each of these cases, the results match up until about 9 s, after which disparities arise in that the analysis results tend to overestimate the extent and period of response. The analysis results therefore tend to overestimate uplift behavior, matching the trend seen with (a) ground contact ratio. With regard to the (c) horizontal acceleration, although high oscillation waves were confirmed to occur at the peak time for acceleration, this may simply be a secondary mode excitation that occurs during major uplift, as pointed out in prior literature (Ishihara et al., 2009).

The acceleration response spectra shown in (e) and (f) (drawn up from waveforms of h = 5%, 0–20 s) confirm that the analytical and experimental results correspond well at frequency ranges that are guaranteed by the centrifuge equipment. The differences in response and period in the time history of the waves did not have a major effect on the spectrum values, but the analysis results were found to exceed some experimental results.

Embedded Condition

A comparison of the experimental and analysis results for the embedded condition are shown in Figure 11. Note that the items compared were the same as for the non-embedded condition.

FIGURE 11

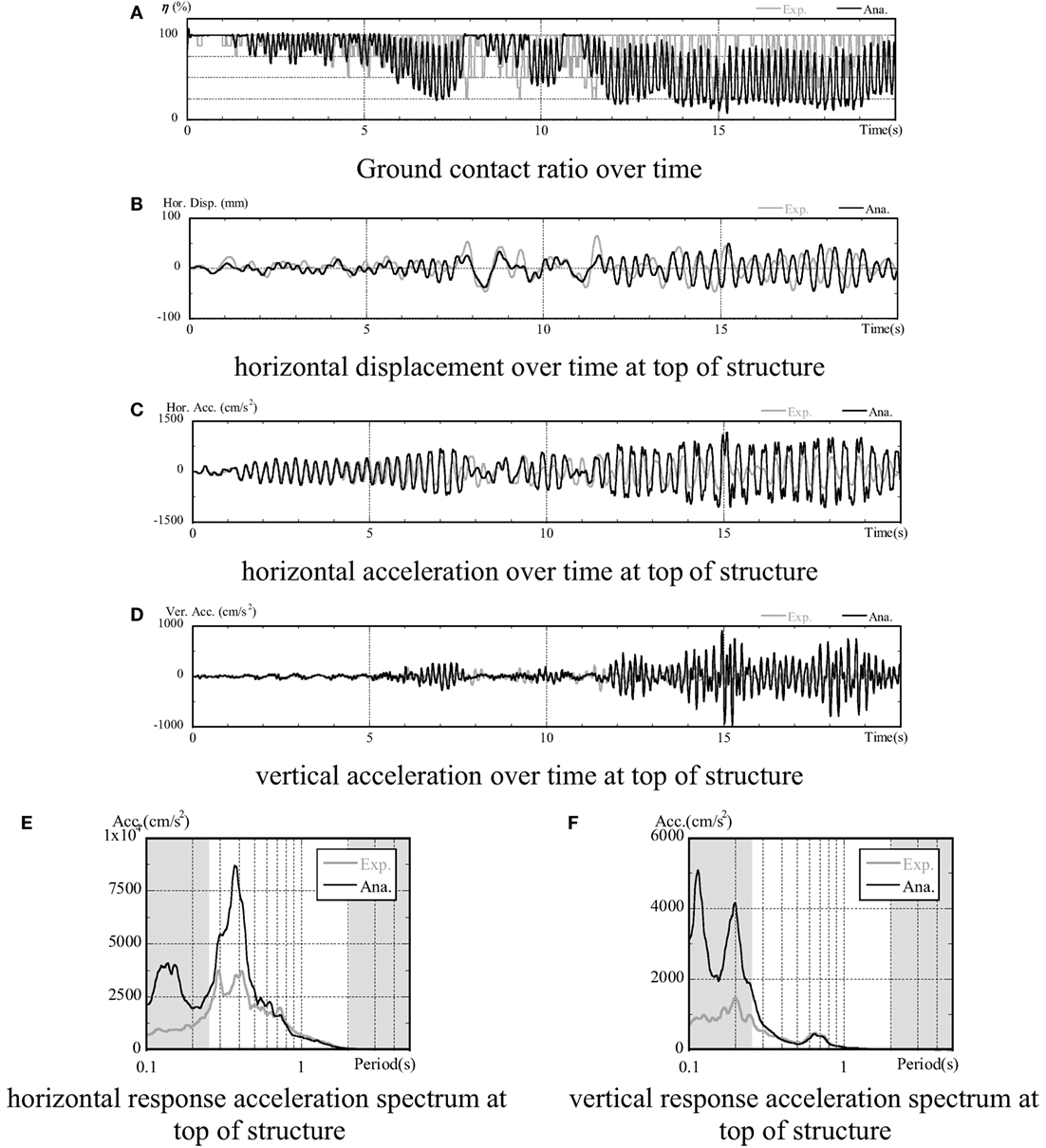
Figure 11. Comparison of experimental and analysis results (embedded). (A) Ground contact ratio over time, (B) horizontal displacement over time at top of structure, (C) horizontal acceleration over time at top of structure, (D) vertical acceleration over time at top of structure, (E) horizontal response acceleration spectrum at top of structure, and (F) vertical response acceleration spectrum at top of structure.

In verifying the time history of the ground contact ratio for the embedded condition, the analysis results were found to fall below the estimated accuracy limit of 25% at around 8 s and after 12 s. At this point, the two sets of results diverged in a similar manner to that seen in the non-embedded condition, with the analysis results tending to be lower. However, the results in this case generally matched until reaching 25%. With the (b) horizontal displacement, (c) horizontal acceleration, and (d) vertical acceleration at the top of the structure, discrepancies once again arose when the ground contact ratio fell below 25%. Thus, although the results were matched up until around 8 s, disparities started to arise beyond this that resulted in the analysis results tending to overestimate the extent and period of response (in other words, to overestimate the uplift). With the acceleration waveform for the embedded condition (c), high oscillation waveforms were confirmed to occur during uplift when the ground contact ratio fell below 25%.

The comparison between the acceleration response spectra in (e) and (f) (drawn up from a wave form h = 5%, 0–20 s) revealed a relatively large variation between the analytical and experimental results, with the analytical results producing overestimations. This also had an effect on the acceleration response spectra when evaluating uplift in the embedded condition. However, as shown in Figure 12, the discrepancy in the spectra was small in the first 0–8 s, during which time the disparity in ground contact ratio was also small. The analysis spectrum values, on the other hand, had high accuracy in the region in which the ground contact ratio was above 25%.

FIGURE 12

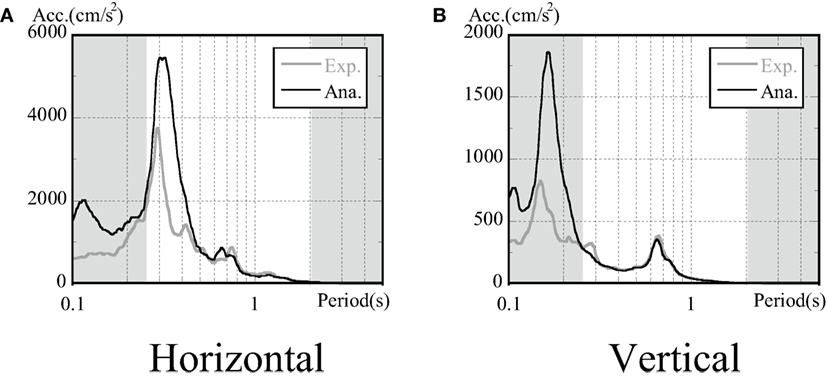
Figure 12. Comparison of acceleration response spectra at top of structure (embedded, 0–8 s). (A) Horizontal and (B) vertical.

Limits of Analysis Model

This section considers the reason why the ground contact ratio determined by the FE model established in this paper gets smaller in comparison to the experimental values as the uplift increases.

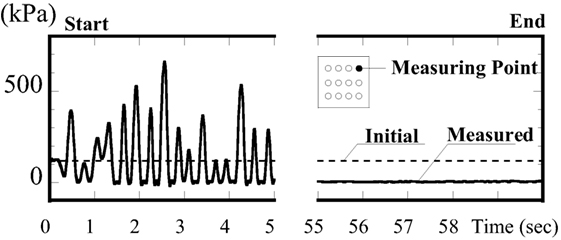
As pointed out in the literature (Nakamura et al., 2014), the discrepancy between the analysis and experimental results may be explained by local non-linear transformations in the ground. That is, although the contact pressure in the experiment increases inversely when the area of ground occupied by the building is smaller, local non-linear transformations in the soil may occur. Figure 13 shows the values recorded by the earth pressure gages in an embedded condition, which clearly suggests that the initial stress is released and residual deformations remain in the ground. However, visual inspection after the experiment failed to confirm that any such residual deformation actually occurs. Any local non-linearity in the ground during the experiment is therefore thought to be small, as any local non-linear transformations should be accompanied by a sinking of the structure, as shown in Figure 14. If this produced the same rotational deformation, it would lead to an increase in the ground contact area. This kind of phenomenon did occur in the experiments and, thus, may have led to the ground contact ratio being smaller in the analysis results because of using the linear soil model.

FIGURE 13

Figure 13. Comparison of earth pressure gage readings during excitation.

FIGURE 14

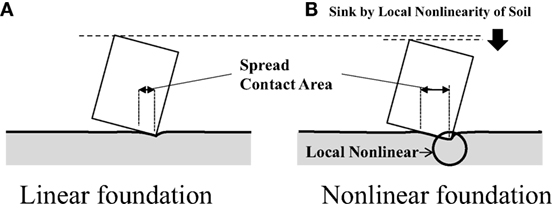
Figure 14. Effects of foundation non-linearity on uplift behavior. (A) Linear foundation and (B) non-linear foundation.

Conclusion

In this work, experimental and analytical studies were conducted for clarifying the significant uplift behavior of spread foundation structures built on bedrock for accumulation of basic research data on uplift behavior. Through this study, the following insights were obtained:

(1) From the centrifugal test, the effect of embedding on the significant uplift behavior of structures is confirmed. The uplift of embedded building is smaller than that of non-embedded building. Because of low uplift, the horizontal and vertical responses of embedded buildings were lower than those of non-embedded buildings.

(2) If established analytical conditions are used, then regardless of whether the structure is embedded, the experimental and analytical results match if the ground contact ratio is no <25%.

(3) Disparities occur between the experimental and analytical results if the ground contact ratio is <25%. Moreover, in this region, an analysis will tend to indicate higher displacement and acceleration responses than the experimental results.

Author Contributions

TS participated in the design of this study and drafted the manuscript. YO contributed for a planning of the centrifuge testing. TH conducted the centrifuge testing. SA contributed for a planning of the analytical condition. NY performed the simulation analysis. NN participated in the design and coordination of this study. All authors read and approved the final manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Hangai, Y., Akino, K., Ohta, H., Miura, K., Koyanagi, Y., Kakuta, T., et al. (1986). “Model tests on base mat uplift of reactor building part. 1–6,” in Architectural Institute of Japan, Summaries of Technical Papers of Annual Meeting, Hokkaido, B, 971–982.

Google Scholar

Hangai, Y., Akino, K., Ogata, T., Imazawa, T., Miura, K., Kakuta, T., et al. (1987). “Field tests on base mat uplift of reactor building part. 1–6,” in Architectural Institute of Japan, Summaries of Technical Papers of Annual Meeting, Kinki, B, 219–230.

Google Scholar

Imamura, A., Hashimoto, T., Suzuki, Y., Adachi, N., and Sako, Y. (2013). Uplift behavior of spread foundation structures on sand and clay deposit, Architectural Institute of Japan. J. Struct. Constr. Eng. 692, 1759–1768. doi: 10.3130/aijs.78.1759

CrossRef Full Text | Google Scholar

Imamura, A., Hashimoto, T., Suzuki, Y., Adachi, N., and Sako, Y. (2014). Uplift behavior of spread foundation structures embedded in clay ground, Architectural Institute of Japan. J. Struct. Constr. Eng. 705, 1625–1635. doi:10.3130/aijs.79.1625

CrossRef Full Text | Google Scholar

Ishihara, T., Midorikawa, M., and Azuhata, T. (2009). Modal properties and free vibration of uplifting behavior of multistory building modeled as uniform shear-beam, Architectural Institute of Japan. J. Struct. Constr. Eng. 640, 1055–1061. doi:10.3130/aijs.74.1055

CrossRef Full Text | Google Scholar

Ishikawa, T., Okutani, T., Kawasato, T., Fujimori, T., Akimoto, M., Imazuka, Y., et al. (2007). “A experimental study on the seismic soil-structure interaction by centrifuge large shear box shaking table tests part. 1–2,” in Architectural Institute of Japan, Summaries of Technical Papers of Annual Meeting, Kyushu, B-2, 127–130.

Google Scholar

Midorikawa, M., Sudo, T., Asato, T., Azuhata, T., and Ishihara, T. (2009). Three-dimensional seismic response of ten-story steel frames with yielding base plates allowed to uplift. J. Struct. Constr. Eng. 637, 495–502. doi:10.3130/aijs.74.495

CrossRef Full Text | Google Scholar

Muto, K., and Kobayashi, T. (1979). Nonlinear rocking analysis of nuclear reactor buildings: simultaneous horizontal and vertical earthquake inputs, Architectural Institute of Japan. J. Struct. Constr. Eng. 276, 69–77.

Google Scholar

Nakamura, N., Kashima, K., Ikeda, S., Suzuki, T., Kamoshita, N., Mizobuchi, T., et al. (2014). “Horizontal Load Capacity of Middle-high-rise RC Building with Multi-story Shear Wall Considering Uplift Behavior part16: Earthquake Response Analysis Considering Soil Nonlinearity” in Architectural Institute of Japan, Summaries of Technical Papers of Annual Meeting, Hokkaido, Structural II, 1031–1032.

Google Scholar

Nakamura, N., Inoda, K., Suzuki, T., and Matsumoto, K. (2016). Study on Induced Vertical Motion due to Basemat Uplift of Building during Severe Earthquake, Architectural Institute of Japan. J. Struct. Constr. Eng. 719, 525–535. doi:10.3130/aijs.81.525

CrossRef Full Text | Google Scholar

Nakamura, N., Ino, S., Kurimoto, O., and Miake, M. (2007). An estimation method for basement uplift behavior of NPP building. Nucl. Eng. Design 237, 1275–1287. doi:10.1016/j.nucengdes.2006.10.010

CrossRef Full Text | Google Scholar

Shimomura, S. (1988). Dynamic Interactions between Structure and Foundation Taking into Account Foundation Uplift [Dissertation]. Tokyo: Nihon University.

Google Scholar

Tatsuoka, F., Molenkamp, F., Torii, T., and Hino, T. (1984). Behavior of lubrication layers of platens in element tests. Soils Found. 24, 113–128. doi:10.3208/sandf1972.24.113

CrossRef Full Text | Google Scholar

Yamada, M., and Kawamura, S. (1984). A study on uplift of base mat: response analysis of rigid model under three directional motions, Architectural Institute of Japan. J. Struct. Constr. Eng. 340, 32–39.

Google Scholar

Yano, A., Sato, M., Hara, A., Naito, Y., Kanechika, M., and Hori, H. (1983). “Shaking table test and analysis about dynamic uplift problem using a rigid building model on the elastic ground: part 1–4,” in Architectural Institute of Japan Summaries of Technical Papers of Annual Meeting, Structural, Hokuriku, 755–762.

Google Scholar

Yano, A., Naito, Y., and Horikoshi, S. (1991). Dynamic analysis on uplift of buildings using an FEM model with nonlinear connecting elements: simulation for comparison with shaking table tests, Architectural Institute of Japan. J. Struct. Constr. Eng. 427, 87–98.

Google Scholar