- 1Department of Building Civil and Environmental Engineering, Concordia University, Montreal, QC, Canada
- 2Department of Architecture and Built Environment, The University of Nottingham, Nottingham, UK
The ever-increasing demand for heating in different sectors, along with more preventative regulations on greenhouse emissions, has forced different countries to seek new alternatives to heat buildings such as district heating system (DHS). Although rudiments of DHSs can be observed over the centuries, it was not widely implemented until last two decades when the DHS became a strategy to design more energy-efficient way of heating the buildings. This paper suggests a new approach in categorizing DHSs based on their geographical location, scale, heat density, and end-user demand. Furthermore, this paper reviews system and component modeling approaches with a focus on DHS load prediction. Main limitations of the existing methods are also addressed and discussed with a comprehensive review of the recent studies. Finally, the state of the art in optimization of the different DHSs has been reviewed and categorized based on their objective functions and the techniques used for solving optimization problems (deterministic and heuristic).
Introduction
The global population will exceed 9.7 billion by 2050 (United Nations, 2013), which will lead to approximately 70% increase in the number of households from 1.9 billion in 2010 to 3.2 billion in 2050 (I.E. Agency, 2012). Residential and commercial buildings account for about 40% and 26%, respectively, of total energy consumption in U.S. and European households (Mertens, 2013; I.E. Agency, 2012). About 38% and 36% of U.S. and EU carbon dioxide (CO2) emissions are also associated with these buildings. Moreover, several unwanted side effects, such as urban heat island, are associated with the drastic increase in urbanization (Mirzaei, 2015; Mirzaei et al., 2015). Thus, these statistics emphasize the necessity of a global objective to reduce the CO2 emission by half by 2050, which is described as the goal of the Energy Technology Perspectives 2012 roadmap (EIA, 2011). This calls for increased efforts and market uptake from the building sector to reach the ambitious goal of net-zero energy buildings (NZEB) by 2050 given the 50% rise in energy demand predicted by the current consumption trajectory. Another example is European Union obligation in 9% reduction in energy use by 2016 based on 2006/32/EC directive (European Parliament, 2006). The European countries are also committed to increase the share of renewable energy sources to 20% by 2020 (P.H.A.F.S. Committee on Environment, 2011).
Different strategies in energy production, conversion, and user-side demand have been proposed to conserve energy in the building sector, i.e., increasing the energy efficiency of buildings with refurbishment technologies such as thermal insulation, double and triple glazing, solar shadings, cavity wall, reflective coating windows, efficiency enhancement, the functionality performance of HVAC equipment, integrating renewable strategies such as BIPV and solar collectors, utilizing natural ventilation. In addition to these technologies, one of the viable solutions is to improve the energy efficiency in buildings, which can be accomplished by using district heating system (DHS) (International District Energy Association, 2014; http://www.districtenergy.org/what-is-district-energy).
Traditional DHSs are generally used for residential space heating and domestic hot water, which are accounting for the largest share of energy consumption in buildings (International District Energy Association, 2014; http://www.districtenergy.org/what-is-district-energy). Other advantages of DH are known as the improvement of resource and energy management and also reduction in the user-side costs, including operation, maintenance, and safety expenses (Rezaie and Rosen, 2012). Moreover, flexibility and safety in selection of the energy source such as biomass and geothermal energy instead of fossil fuels, which dominates the current heat market, is another attractive option of the DHSs (Hepbasli, 2010; Akhtari et al., 2014).
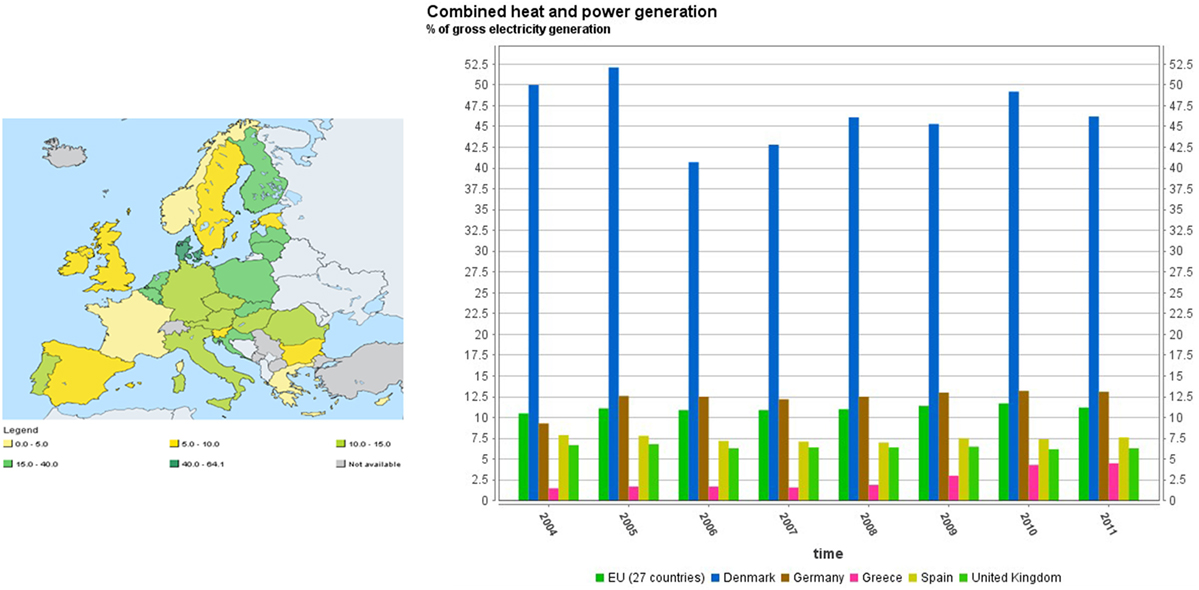
Despite the well-known advantages of DHS, its market share around the world is still very low while only about 6000 DHSs exist in European Union with the market share of about 13% (Figure 1). Besides many social, economic, and technological issues revolving around worldwide implementation of DHSs, the predominant reason for neglecting such systems is the lack of suitable tools to design, analyze, and optimize them (Connolly et al., 2014).
Apart from such issues, one of the major limitations of DHS is lower thermal comfort, especially in older DHSs where occupants have very little control over the water temperature (International District Energy Association, 2014; http://www.districtenergy.org/what-is-district-energy). In denser urban regions, which expanding the DHS distribution network should follow the rules of the municipality, existing infrastructure, such as roads, water/sewage distribution networks, and city layout in some cases, are the common barriers against the optimal expansion of DHSs.
The discussed advantages and limitation in DHSs has persuaded the communities to move toward the implementation of novel ideas and strategies in energy sharing and management of DHSs. The new strategies are mainly focused on combining renewable energy, use of storage technologies, and establishing a linkage between heating and electricity systems to significantly reduce the dependency on the fossil fuel resources (International District Energy Association, 2014; http://www.districtenergy.org/what-is-district-energy). One of the major challenges toward the design of such systems is associated with lack of available tools, which can effectively model and optimize DHSs.
To shed more light on the recent achievements in modeling and optimization of DHSs, this paper aims to summarize the current state of the art. Thus, various definitions of DHS are first provided followed by the molding approaches utilized to investigate the performance of these systems. Eventually, modeling and optimization of DHS studies based on different climates, scales, energy sources, and implemented tools are further summarized in this paper.
Complexity Level of District Heating Systems
In general, a DHS consists of a heat source, a network of users, and a distribution network. The complexity of a DHS varies in accordance with various parameters as stated below (Sakawa et al., 2002; Weber et al., 2007):
(a) Number of utilized technologies: one of the complexities of design and optimization of the DHSs is the number of technologies available to be utilized in addition to the type of the heat source system. For example, in DHSs with geothermal energy source, the system could operate with the organic fluid instead of water (Weber et al., 2007), while in case of having heat sink close to the DHS, the heat pump is more favorable. Moreover, a combination of sources can be used in DHS, while other renewable source of energies can be integrated to the system (Sakawa et al., 2002; Weber et al., 2007).
(b) Number of end-users: one of the main concerns in designing a district heating is the number and variety of the users connected to the system. A DHS located in a municipal area serves a variety of residential, commercial, and industrial buildings with different demand levels (Pirouti et al., 2013).
(c) Temporal profile: different types of users connected to a system demand their own operating temperature and profiles (Weber et al., 2007). For example, the heat demand profile for industrial users will be effected less by seasonal changes during a year, meaning that their required end-use temperature is higher compared with residential users (Buoro et al., 2014).
(d) Spatial concerns: in addition to the coordinate of all users, the layout of a city, in which a DHS is planned, plays a key role in design of distribution network. For example, interception with municipal infrastructures should be avoided when a network is designed. Other factors such as soil quality, topology of the region, and type of the users could similarly affect the design of a DHS (Weber et al., 2007; Ben Hassine and Eicker, 2013).
Classification of District Heating Systems
In general, a DHS can be categorized based on five main parameters including geographical conditions, scale of the DHS, heat density of the DHS, the level of end-user demands, and type of heat sources.
Geographical Conditions
Geographical considerations, namely climatic conditions and energy source accessibility, will impact the overall design of a DHS. In particular, a DHS close to Northern latitudes with a colder climate requires higher rate of heat transfer per unit area compared to the DHS closer to the equatorial line with a warmer climate for similar types of buildings (Dalla Rosa and Christensen, 2011). This higher amount of heat transfer in DHSs can be reached either by increasing the mass flow rate of the fluid or by increasing the operational temperature of the system, which consequently increases the distribution heat loss of the system due to the higher operational fluid temperature (Hassine and Eicker, 2011).
Energy sources accessibility is a function of geographical and geological variation and, therefore, impacts the design considerations of a DHS. Investigating the distribution of different energy resources for different geographical locations addresses the accessibility of at least one of the main sources of renewable energy at any region. For example, comparison of the solar (Huld and Pinedo-Pascua, 2012) and wind map of Europe (see text footnote 1) shows that region with lower solar intensity have higher wind speeds and vice versa (Figure 2). Specifically, Scandinavian region has one of the lowest solar intensities while it is exposed to the highest wind speed in Europe.
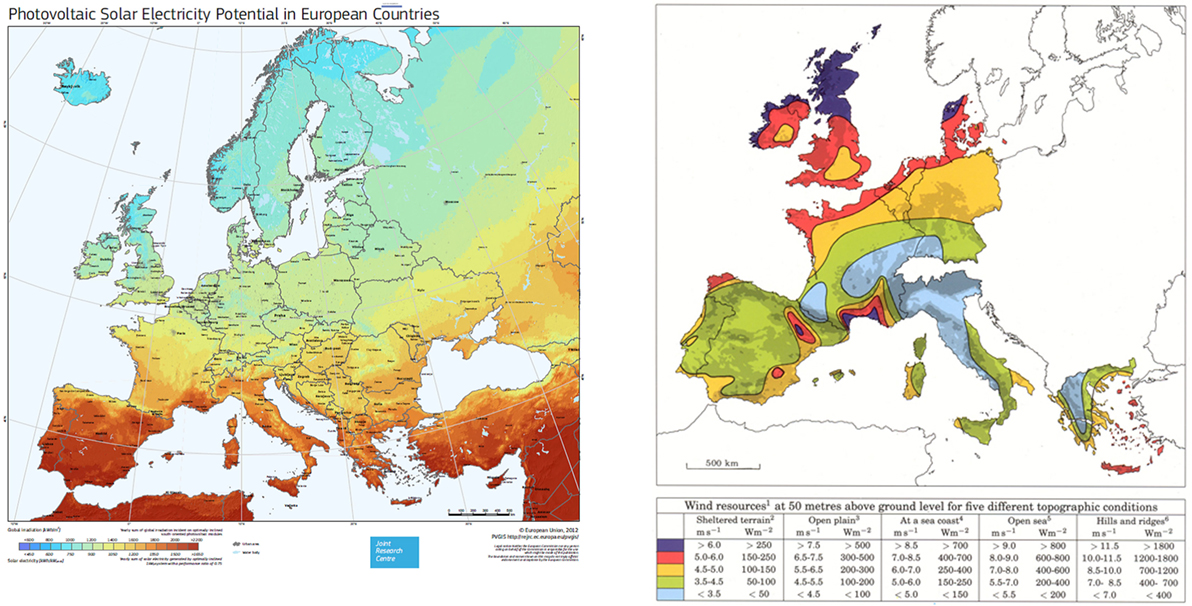
Figure 2. (Left) solar map of Europe (right) wind map of Europe1 (Huld and Pinedo-Pascua, 2012).
Scale
Scale of a DHS plays a significant role in performance of such systems as the influential parameter in design stage varies in accordance with the scale. From the spatial point of view, DHS can be designed as a small, medium, or large system (Figure 3).
Small-scale DHS is referred to a network of users in which the distance from the heat source is in the order of magnitude of less than few hundreds of meter (Weber et al., 2007). In fact, the associated temperature and pressure drops are relatively low due to the short length of the pipelines in the distribution system (Hurtig, 2010). DHSs in the level of multi-residential buildings are more likely known as small systems with a relatively low temperature drop.
The distance between the heat source and the users is mainly assumed to be from 200 to 300 m in the medium-scale DHS (Weber et al., 2007; Dalla Rosa and Christensen, 2011; Ancona et al., 2014). In general, these systems are formed as a close-loop network of buildings linked together with a piping system. Similar to the small-scale DHSs, pressure drop is a significant element in design of such systems, whereas for older generation or higher operating fluid temperature systems, the heat loss is substantial and should be considered at the design stage (Hassine and Eicker, 2011; Nuytten et al., 2013).
Large-scale DHS, mostly known as community size DHSs, consists of many users and a longer pipeline network compared with the latter groups. Due to longer length of the pipes in distribution network, the heat loss is considerably significant and accounts for up to 15% of the total energy delivered by the system (Hassine and Eicker, 2011; Xing et al., 2012).
Heat Density
Linear heating density of a network (LHD) is defined based on the ratio of its total annual heating demand over trench length (Reidhav and Werner, 2008):
where Qtotal is the total annual heating demand of the DHS, and L is the total trench length of the distribution network.
Based on this definition, higher LHD means higher heat density of the network or users with a higher annual demand. In systems with higher heat density, the importance of the heat loss is less significant (Nuytten et al., 2013), and thus the system is designed only based on the hydraulic equilibrium. The economic and environmental threshold for the LHD of different networks are varied from 1 MWh/m for DHSs with biomass heat source to 0.2 MWh/m for combined heat and power (CHP)-based systems (Reidhav and Werner, 2008; Nuytten et al., 2013).
End-User Demand
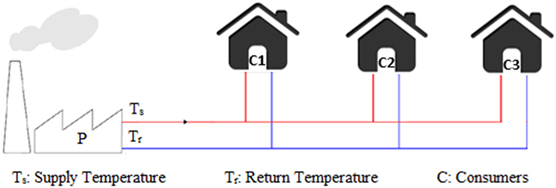
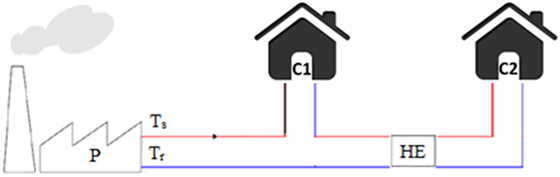
Residential buildings utilize lower end-use temperatures for heating while industrial users require higher fluid temperatures. This means that the demand level of users in a network results in different arrangement of the DHS (Buoro et al., 2014). One arrangement is to design a network based on the maximum demanded temperature (Pirouti et al., 2013), while another option is to use a multi-loop network with different operational temperatures associated with each of them. Multi-loop networks further interact with each other through sets of heat exchangers (Figure 4). This implies that the main loop operates with the maximum temperature while secondary loops operate at lower temperatures in order to satisfy the temperature requirements of all users (Hassine and Eicker, 2011; Ben Hassine and Eicker, 2013).
Heat Source Type
In general, heat sources are categorized as permanent and non-permanent types. In the permanent heat sources, the heat generation continuously exceeds the heat demand of the network where in the non-permanent sources the generation profile fluctuates during the time. In the latter scenarios, the generation mainly does not match with the user demand profile, and therefore another energy source is mostly integrated to meet the peak demand of the system.
Combined heat and power, geothermal, and biomass sources are known as permanent source (Hlebnikov and Siirde, 2009; Noussan et al., 2014; Sartor et al., 2014). On the other hand, convertible renewable sources into thermal energy such as wind and solar energy with high rate of fluctuations are categorized as non-permanent sources. Moreover, heat storage systems can be integrated into DHSs to store the surplus of generated heat at their off-peak time to be later utilized at the peak time of the DHS (Avila-Marin et al., 2013; Nuytten et al., 2013).
Component Modeling of District Heating System
Accurate modeling and design of each DHS’s component plays an important role in its efficacy and efficiency. This section investigates various techniques employed to model DHS’s components.
Heat Source
In general, heat sources in DHSs are modeled based on their efficiency and heat generation output. A minimum efficiency index has been defined depending on the type of the heat source. For example, the primary energy saving index (PES) has been defined to evaluate the efficiency of a CHP heat source (Noussan et al., 2014):
where CHP Hη is the heat efficiency in cogeneration production, Ref Hη is the efficiency in separated heat generation, CHP Eη is the electricity efficiency in cogeneration production, and Ref Hη is the efficiency in separated electricity generation.
The minimum value of the PES for CHP heat sources with the nominal size of smaller than 1 MW should be a positive value while this value is more than 0.1 for sources above 1 MW (Noussan et al., 2014). Same types of indices have been defined for other type of heat sources (Hepbasli, 2005).
End-User Profile
Accurate prediction of the energy demand profile of users in smaller time interval such as hourly basis can affect the efficiency of a network as well as its optimization procedure (Ortiga et al., 2007). The DHS modeling of the users’ network consists of two levels: understanding of the heating demand profiles of the users in order to define the total load required for the network and calculation of a heat exchanger for each user.
Since building heterogeneity in each district system is elevated, particularly in the urban setting, and each building has its own properties and corresponding demand profile, determining the model which could predict the demand profile of the entire district with acceptable accuracy, is essential. In general, there are different methods suggested to model and predict this demand. Many of these methods predict the energy demand of a building in terms of its maximum energy demand, while others predict the actual profile of the building in smaller intervals such as an hourly basis.
Regardless of the method used, the heating demand profile of each user consists of three major parts, including physical and environmental characteristics of a building (i.e., R-value, infiltration rate, ambient air temperature, solar radiation, and humidity), human-related factors or social behavior of the occupants, and random factors that account for uncertainties. Different techniques have been suggested in the literature in order to predict the demand profile of the users considering one or all of the above factors including historical approaches (Dotzauer, 2002; Ortiga et al., 2007), deterministic, and times series predictive methods (Eriksson, 2012).
Historical Methods
These methods use historical data obtained from both demand and supply sides to model the demand profile of the system.
Heating Degree Day
Heat loss in buildings is proportional to the difference between indoor and outdoor ambient temperature. This concept is used in the development of the Heating Degree Day method (HDD) (Day, 2006):
Here, the overall heat loss coefficient is determined based on the infiltration rate and the summation of the UA value for all different envelope assemblies of the building. The infiltration rate can be defined either as an average or hourly rate (Day, 2006).
Online and free historical weather data are mainly assumed as reliable sources to obtain the HDD method (Verda et al., 2012; Pirouti et al., 2013).2,3 This method is widely used for modeling of small buildings in which the main source of heat loss is unclear in their envelope. Al-Homoud (2001) compares this method with another historical method known as the Bin method. Unlike the degree day method, the bin method is mainly used for larger scale buildings in which the internal load generation has a higher effect, rendering the degree day method unfeasible. In both cases, the main concern in modeling is the outdoor air condition of the buildings and the average envelope thermal resistance. The fact that factors such as the social behavior of occupants and the thermal mass of the buildings have not been taken into account result in predominantly poorly accurate findings (Dotzauer, 2002). Furthermore, the low frequency of available data results in inaccurate outcomes.
Energy Use Intensity and Load Factor
Energy use intensity (EUI) and load factor (LF) is another technique to estimate the users demand profile, whereby the historical supply data are provided. EUI is the rate of energy use per unit area (Sharp, 1996), and LF is the ratio of energy consumption over the maximum possible energy generation of the supply side (Dalla Rosa and Christensen, 2011; Dalla Rosa et al., 2012):
Knowing the EUI and LF of different users4 results in calculation of the total energy and peak heating demand required for each consumer. The supply energy demand calculates the annual average LF per area of different users. Mainly, the values are accessible based on region or reference archetype (see text footnotes 3 and 4). Barnaby and Spitler (2005) used this method for load prediction based on different users’ sector of the DHS and added them together to predict the users’ heating demand profile. One of the main problems with this method is associated with non-existence of separated factors for ambient conditions.
Measurements
Measurement campaigns can provide reliable inputs to be inserted as the end-user demand profile of DHS (Sanaei and Nakata, 2012; Nuytten et al., 2013; Wang et al., 2013; Noussan et al., 2014). Achieving a high frequency dataset, however, is not always a feasible option due to the extensive cost of the equipment and time-consuming procedure.
Archetype Building
Another type of the widely used historical methods is prototype or archetype buildings. In this method, buildings with a same occupancy type are divided into subcategories, while a reference building is defined for each building. The demand profile of other buildings located in each category is later defined based on the reference building with some adjustment. The number of building categories used in this method and the number of adjustments required for modeling the demand profiles are the key parameters of the prototype method. The most commonly utilized technique is the regression method. Lara et al. (2015) used the linear regression method in order to define the useful parameter that can be employed as an input data for modeling of school buildings, whereas Filippin et al. (2013) used a multivariate regression method in evaluating the heating demand profile of a residential sector.
Deterministic Methods
Deterministic methods, also referred as simulation-based models, use the mathematical representation of the physical behavior of the buildings. Based on the volume of the used information, deterministic methods can be categorized into two major subdivisions, such as complex or software-based simulation models, which use different simulation software that takes into account all the different parameters affecting the demand profile of a building and simplified models, which basically simplify the level of the calculations taken into the account.
Complex Models
Energy simulation software, such as Energy Plus (Crawley et al., 2001) and TRNSYS (University of Wisconsin—Madison, Solar Energy Laboratory and Klein, 1979), is broadly used for modeling various type of buildings. Although they yield highly accurate demand profiles, the main disadvantage of these models is their dependency on data quantity and high computational cost for modeling each building (Ortiga et al., 2007; de Guadalfajara et al., 2012; Guadalfajara et al., 2014). For small-scale systems consisting of a limited number of buildings, using the comprehensive method can increase the accuracy of the simulation. Nonetheless, providing the data and time required for modeling of many buildings in a city-wide scale is very extensive. The example of complex modeling is a work by Zhang et al. (2015, 2014) where a comprehensive method was utilized to model the demand profile of 95,817 buildings in Westminster, UK.
Simplified Models
Simplified methods are adapted when the adaption of the comprehensive method is relatively extensive for a large-scale community. These methods simplify physical characteristics of the buildings in order to predict their demand profile. For example, Kim et al. (2014) considered the parameters including shape, orientation, and occupancy type in the modeling of the end-users’ profile. They used the average energy required per square meter of a dwelling area of a building based on its monthly/yearly outdoor design temperature. In order to take into account the shape and orientation of the building, new sets of coefficients were introduced: (1) the ratio of the outdoor surface to volume of the building (the shape factor) and (2) the orientation relative to the south (orientation factor) (de Guadalfajara et al., 2012). Wang and Xu (2006) used a simplified physical method to predict the demand profile load within which they also included the effect of thermal mass on load prediction by means of a genetic algorithm. Results obtained from their simulations illustrate a good correlation with actual data for a residential building, which has a lower internal heat gain density. Inversely, this method is unsuitable for larger buildings with higher internal heat gain density.
Predictive Time-Series Methods
The predictive time-series methods rely on the mathematical curve fitting relations in order to predict the demand profile of the users.
Predictive Models
Different predictive models have been suggested for modeling the demand profile, including classical approaches [i.e., time-series ARMA models, regression (Lei and Hu, 2009; Yun and Steemers, 2011; Guadalfajara et al., 2014), Kalman filter] and artificial intelligence (AI) methods [i.e., artificial neural network algorithms (ANN) (Hippert et al., 2001) and fuzzy neural network (FNN)] (Gross and Galiana, 1987).
ARMA Type. ARMA time-series predict the profile of the end-user by implementation of a linear combination between the previous value of the demand along with previous and current values of the noise (Gross and Galiana, 1987):
where Yp(t) represents the day and the normal weather condition for the design day, and Y(t) indicates the effect of deviation from the normal weather pattern.
With slight difference from the general form, different kinds of ARMA-type models can be developed, e.g., Box-Jenkins (Tang et al., 1991), time series (Amjady, 2001), and ARIMA (Lee and Ko, 2011).
Kalman Filter. Similar to other predictive methods, this technique estimates the value of the variables for future time steps (t + Δt) based on the values of the variables at its current time step (t). In order to make the best estimation, Kalman filter determine the best variable set, which minimizes the source function using the residual sequence method. In each step, the Kalman filter will check the difference between the measurements and the model output and chose the variable set to minimize the difference. Since the deviation from the measurement can be positive or negative, two different sets of residual sequences could be assumed for the system, such as residual for the hot side and residual for the cold side of the profile (Palsson, 1993).
Artificial Intelligence
Using predictive methods, such as artificial intelligence, is another approach to predict the demand profiles of the building. The most common artificial intelligence methods used in the field of load prediction are ANN, FNN, and Support Vector Machine (SVM). The ANN has been widely used in research for predicting the load particularly in forecasting the electricity consumption of buildings (Zhang et al., 1998). In most of the cases, ANN shows higher prediction performance compared with other simulation-based methods. This higher accuracy with the ANN method is usually due to its higher adaptability, as it considers the social parameters in load prediction due to the integration of real case data into the system training (Zhang et al., 1998; Hippert et al., 2001). Despite the high accuracy of the predictive methods, their main drawbacks are the over-fitting problem as well as the data requirements for the training proposes. Providing accurate, comprehensive archives of data for ANN is one of the main drawbacks of this method. In cases where the data archive used for training the system is small, using the SVM methods (Chen et al., 2004) shows a better performance. However, only a scarce number of studies were conducted using SVM in the last few years; hence, the information regarding the utilization of this model is limited.
Limitations of the Current Models
The main limitations of the methods have been used in prediction of the demand profile of the DHS could be addressed as below:
• Feasibility of expanding one model to the entire district level: the first limitation of the presented methods is related to the limitation of these models in prediction of the total energy consumption of the entire district. Especially, in case of a larger district system that the heterogeneity of the buildings is elevated, this problem becomes more amplified. For instance, HDD should be only used for prediction of the small residential buildings while the Bin method is more suitable for larger buildings with much higher internal heat generation density. As a result, an archetype method with a combination of these methods should be used to predict the total energy load of the entire network.
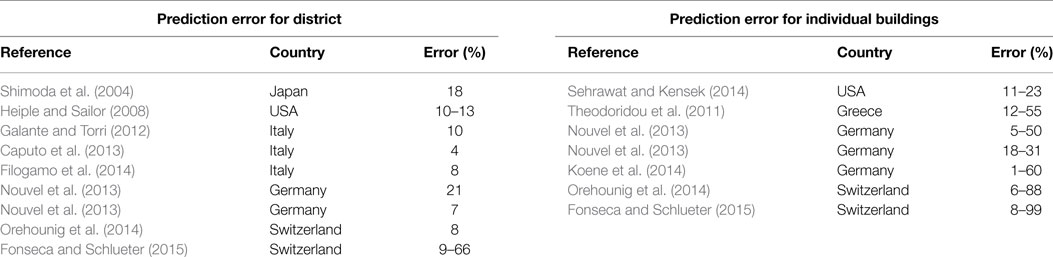
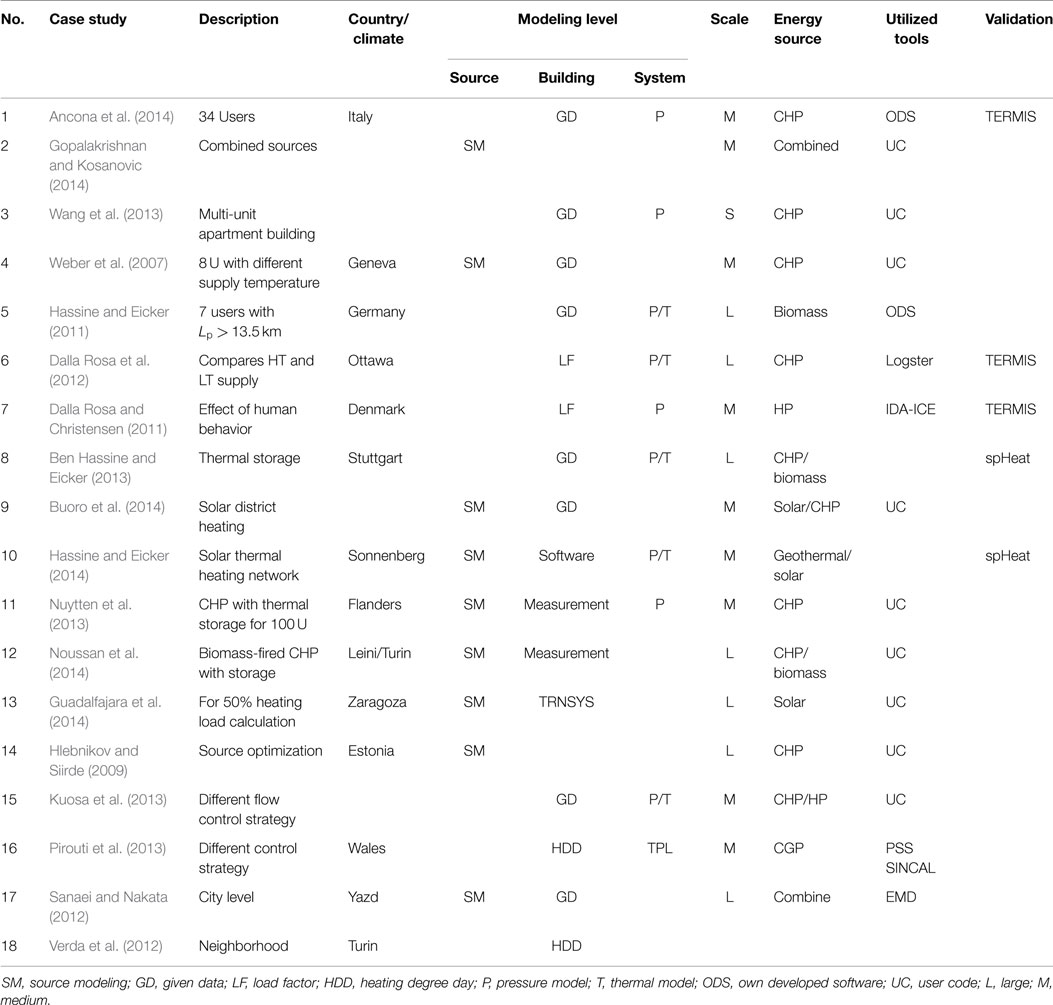
• Type of prediction: another limitation of the presented works is the type of prediction. Most of the presented methods have been adapted to predict the total energy consumption. Even though at the design stage, DHSs are designed based on the total energy consumption and the maximum peak demand of the system, detail profile of the network is further required in order to improve the efficiency of the system and enhancing the energy distribution management. Table 1 summarizes different prediction methods that have been used to predict the consumption load of DHSs.
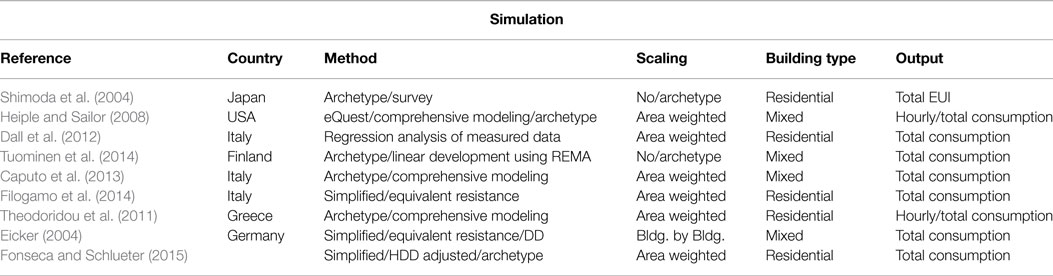
Table 1. Summary of the method has been used for load prediction in DHS and type of building stocks.
As illustrated in Table 1 most of the works that have been done only focused on the total energy consumption of the networks and not the detail profile.
• Accuracy: accuracy of the prediction is the next limitation of the previous models. In case of load prediction for district systems, two different types of errors could be defined; the first type is the error associated with the entire district model, while the second one is associated with the modeling at the building level. As illustrated in Table 2 the simulation error is mainly much lower at the district level in comparison with the building level 1, which is mainly related to behavior of the users.
• Computational time: the computational time of the stock modeling is one of the major limitations of the current DHS models.
Energy Distribution Network
A distribution network of a DHS is mainly designed in accordance with the scale of the system, geographical considerations, type of the users, and utilized heat generations sources. Besides the role of the distribution network in linking the generation side with the demand side of the cycle and defining the inter communication between different components of the system, the distribution network has an effect on the energy consumption of the system as well. In general, the total energy required to be fed to the system is equal to:
where Q is the total energy consumption of the DHS, Qi is the demand profile of each user, and Qloss is the heat loss of the system. Since most distribution networks work within a specific temperature range, the heat loss from the system could be considered as a function of the size of the network and not a function of time. As a result, the total energy requirement of the system is equal to the summation of the profiles of different users in addition to the heat loss per network length. Since the DHS is type of the hydronic system, the modeling technique to design the distribution system can be either based on hydraulic or thermal equilibrium.
Hydraulic Equilibrium
The distribution system in the DHS works based on the transferring of heat through a heated fluid, and therefore, it should be designed based on the requirements of the hydraulic system regardless of the flow rate and energy level of the fluid.
Mass Flow Balance
The mass flow balance could be written for each point of the system as follows (Ben Hassine and Eicker, 2013; Kuosa et al., 2014):
where Qin is the mass flow rate enter the point, Qout is the mass flow rate exit the point, and Quser is the mass flow rate required by the utility. Depending on the type of the system, such as an open or closed loop, Quser could be considered as 0. It is important to note that the system and network are assumed to be leak free without any loss of the fluid mass.
Energy Balance
In the mass flow balance techniques, the energy balance could be written between any two points in the system as below (Ancona et al., 2014):
where ΔHij represents the energy loss between points i and j; Hi and Hj are, respectively, the energy content of the fluid at points i and j. Considering the DHS as a closed system and without any loss in the liquid mass, the energy loss in the system could be written as a correlation to the pressure loss in the system represented in two different ways:
In the distribution pressure loss, the friction loss due to viscous effect, generated by the pipe surface, is the governing parameter. The hydraulic diameter of the pipe, mass flow rate of the system, and roughness of the pipe surface are the parameters affecting the distribution pressure loss of the system (Kuosa et al., 2014). Additionally, in concentrated pressure loss, head loss due to fittings and changes in diameter of the pipe are taken into the account (Ancona et al., 2014).
Thermal Equilibrium
Thermal equilibrium can be represented as either a steady-state or dynamic equation. DHS with operational temperature lower than 70°C or with low heat propagation (well insulated) can be represented as a steady-state system. Inversely, DHS operating with higher temperatures than 110°C or with high heat propagation can be considered as dynamic system (Madsen et al., 1994; Lund et al., 2014). The thermal model could be written based on two major sources of the temperature drop in the system, including temperature drop across the users and due to the heat loss in the system. The temperature drop across the users can be modeled based on a simple convection heat transfer equation (Dahm, 1999; Wang et al., 2013):
where Q is the amount of the energy required by the system, U is the heat transfer coefficient, and ΔT is the temperature drop across the users.
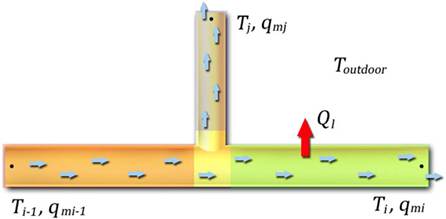
On the other side, the temperature drop due to heat loss in the system occurs in both longitudinal and radial directions. Longitudinal heat loss is along the system between different locations, whereas radial heat loss occurs in the surrounding environment. Both types of the heat transfer in the system could simply be modeled by using the enthalpy balance between any two points (Hassine and Eicker, 2011; Kuosa et al., 2013):
where is the convective heat flow, is the radial heat flow and could be expressed as below:
where k is the radial heat transmission coefficient and qm is the flow rate. By replacing the and in the Eq. 12, the temperature at any point can be calculated as follows (Figure 5):
where Cp is heat capacity, Tn is the temperature, Δt is the time step, and mi is the mass of the water.
Based on the definition of the , one of the main factors influencing the amount of heat loss is the earth’s temperature. In systems with a higher operating temperature, higher differences in temperature could result in higher amounts of the heat loss in the system. Similarly, increased heat losses in a system could result in increased surrounding temperatures over time, and consequently decreasing the heat loss over time.
Holistic Modeling of District Heating System
Physical and black box models are the approaches conducted in holistic modeling of the DHS (Palsson, 2000). The network has been considered as a whole package in the black box models where individual design of the components is disregarded. The whole system is then modeled by techniques such as the transfer function or ANN (Yabanova and Keçebas, 2013). One the other hand, in physical models, each component of the DHS has been designed separately and as a set of equations describing the flow and pressure losses of that element. Arsene et al. (2004) categorized the physical modeling as the link flow (Q), the loop corrective flow (ΔQ), the nodal heads (H), and finally the mixed node-loop approaches.
Due to a high number of the elements that need to be taken into consideration, solving such a system can be computationally expensive. Therefore, numerical approaches have been widely developed for solving the system of equations of the hydraulic distribution networks. Some of these approaches are categorized by Arsene as:
• Numerical minimization method, finding the minimum value of the non-linear function subjected to linear constrained;
• Hardy-Cross method, solving the system of non-linear equations (Chenoweth and Crawford, 1974);
• Newton–Raphson method, solving the system of non-linear equations (Donachie, 1974);
• Linear theory method, solving the system of non-linear equations (Collins and Johnson, 1975).
Based on the simplicity of the input data, the number of equations and size of the matrix of the equations (Calí and Borchiellini, 2002; Hassine and Eicker, 2011) as well as the accuracy of the results, the most frequent used method is a combination of Newton–Raphson and nodal head methods (Arsene et al., 2004; Hassine and Eicker, 2011). Due to weak convergence of the nodal equation algorithm for networks with low flow rate, another approach has been suggested by Arsene et al. (2004) called the loop equation method, which is again a combination of a loop corrective and Newton–Raphson methods.
Further to the above mentioned studies, several commercial software have been developed based on the loop equation method using the graph theory, such as TERMIS5 or SpHeat (Eicker, 2004). Table 3 summarizes some of the current DHS modeling studies.
Optimization of District Heating System
Different optimization methods have been developed in order to decrease the heat loss as well as the cost associated with operation and construction of the DHSs. Among various used methods, mathematical methods based on continuous or discrete variables, generic algorithm, neural network, and fuzzy logic systems are widely implemented techniques. Based on the defined type of the objective function, the DHS optimization is mainly formed on the basis of a single objective function or multi-objective functions. While most single variable function will be solved using the deterministic numerical methods, the multi-objective functions use either weighted factors or pareto-front approaches. In the weighted factor approach, importance factor is fitted to different objectives of the optimization problem, based on the trial-and-error approach, to convert the multi-objective function to single objective problem, which provides a numerical solution for the problem. The following chart shows different deterministic methods for the numerical optimization approaches.
where the optimization problem can be defined as (Caputo et al., 2013):
where the objective function f (x, y) is subjected to the set of constraints. h(x, y) = 0 defines performance of the system, and g(x, y) ≤ 0 stands for feasible plan of the system. Moreover, two different types of variables could be defined for MIP problems; the continuous variable (x), representing the state variable and the discrete variable (y) with the value of 0 and 1, representing the assignment of the equipment of a sequential task to the system.
Optimization algorithms consist of both continuous and discrete variables where they furthermore characterized as mixed-integer linear programing (MILP) if all the equations are linear or mixed-integer non-linear programing (MINLP) if one of the equations is non-linear. In the cases of having no discrete variable, the optimization algorithm can be addressed with linear programing and non-linear programing (Biegler and Grossmann, 2004).
The schematic of the optimization process, presented in Eq. 17, serves as a basis of several optimization tools, which have been developed for optimization of the DHSs, e.g., general optimization toolboxes such as MATLAB or GenOpt (Attia et al., 2013), customized DHS optimization tools such as FreeOpt (Akhtari et al., 2014), cost-associated optimization tools with the thermal electrical load of the system such as STEFaN (Connolly et al., 2014), network pipe size and routing optimization tool such as MODEST(Model for Optimization of Dynamic Energy System with Time-Dependent and Boundary Condition), the system investment, and operational cost optimization at both supply and demand level (Henning, 1999).
Regardless of the type of optimizing algorithm, the main objective of such models is to minimize the operational cost, investment cost, and heat demand of the system in addition to minimizing the environmental impacts such as CO2 emission (Lu et al., 2014). Table 4 summarizes some of the recent DHSs optimization studies.
Conclusion
In this paper, the state of the art of modeling and optimization of DHSs is reviewed and limitations of the previous works have been summarized. One of the major limitations of the existing works is addressed as the procedure that could be used in predicting the demand load of the entire district network. In general, there are different methods suggested to model and predict the demand profile in DHSs. Many of these methods predict the energy demand of a building in terms of its maximum value, while others predict the actual profile of the system in a smaller interval such as an hourly basis. This limitation becomes more important in case of larger DHSs in which building heterogeneity is elevated. Table 1 summarizes the different approaches that have been used in predicting the load of the DHSs. It was concluded that most of the utilized approaches are only applicable to one type of building.
Also, the accuracy of the predictions of previous works has been addressed in Table 2. Since most of the existing models do not take into consideration the effect of the occupants’ behavior in their modeling, the accuracy of the prediction, particularly at the building level, is much lower in the previous works. In contrast, the accuracy significantly increases when the entire DHS is considered. This phenomenon can be observed in previous works focused on DHSs with similar building types. Since more than one building is involved in the profile prediction of an entire district network, their demand profiles overlap and therefore compensate the accumulated error in the load prediction; this process significantly increases prediction accuracy.
In terms of the distribution network, the existing works has been categorized in three levels, small size, mid-size, and large systems. This categorization has been summarized in Table 3. Even though in the mid-size and large size networks, there is a higher heat loss ratios, thermal insulation of the distribution network is suggested to be a major drawback; however, for the newer DHS generations, working with lower temperature, this loss can be embedded as an into the demand load. Regarding the state of the art of the optimization methods, Table 4 provides a summary on the basis of their objective functions.
Author Contributions
BT, first author. PM, second supervisor. AB, collaborator. FH, first supervisor.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to express their gratitude to Concordia University for supporting this research through the Concordia Research Chair program.
Footnotes
- ^European Wind Atlas. Copyright © 1989 by Risø National Laboratory, Roskilde, Denmark. http://www.wasp.dk/dataandtools#wind-atlas__european-wind-atlas
- ^Degree Days Weather Data for Energy Professionals. Available at: http://www.degreedays.net/
- ^Energy Use Data Handbook. (2013). Available at: http://oee.nrcan.gc.ca/publications/statistics/handbook2010/handbook2013.pdf
- ^Commercial & institutional consumption of energy survey summary. (2008). Available from: http://oee.nrcan.gc.ca/publications/statistics/cices08/pdf/cices08.pdf
- ^Termis District Energy Optimization Software. Available at: http://software.schneider-electric.com/products/termis/
References
Åberg, M., and Henning D. (2011). Optimisation of a Swedish district heating system with reduced heat demand due to energy efficiency measures in residential buildings. Energy Policy 39, 7839–7852. doi:10.1016/j.enpol.2011.09.031
Akhtari, S., Sowlati, T., and Day, K. (2014). Economic feasibility of utilizing forest biomass in district energy systems – a review. Renew. Sustain. Energ. Rev. 33, 117–127. doi:10.1016/j.rser.2014.01.058
Al-Homoud, M. S. (2001). Computer-aided building energy analysis techniques. Build. Environ. 36, 421–433. doi:10.1016/S0360-1323(00)00026-3
Amjady, N. (2001). Short-term hourly load forecasting using time-series modeling with peak load estimation capability. IEEE Trans. Power. Syst. 16, 498–505. doi:10.1109/59.962429
Ancona, M. A., Bianchi, M., Branchini, L., and Melino, F. (2014). District heating network design and analysis. Energy Procedia 45, 1225–1234. doi:10.1016/j.egypro.2014.01.128
Arsene, C. T. C., Bargiela, A., and Al-Dabass, D. (2004). Modelling and simulation of water systems based on loop equations. Int. J. Simulat. 5, 61–72.
Attia, S., Hamdy, M., O’Brien, W., and Carlucci, S. (2013). Assessing gaps and needs for integrating building performance optimization tools in net zero energy buildings design. Energy Build. 60, 110–124. doi:10.1016/j.enbuild.2013.01.016
Avila-Marin, A. L., Fernandez-Reche, J., and Tellez, F. M. (2013). Evaluation of the potential of central receiver solar power plants: configuration, optimization and trends. Appl. Energy 112, 274–288. doi:10.1016/j.apenergy.2013.05.049
Barnaby, C. S., and Spitler, J. D. (2005). Development of the residential load factor method for heating and cooling load calculations. ASHRAE Transact. 111.
Ben Hassine, I., and Eicker, U. (2013). Impact of load structure variation and solar thermal energy integration on an existing district heating network. Appl. Therm. Eng. 50, 1437–1446. doi:10.1016/j.applthermaleng.2011.12.037
Biegler, L. T., and Grossmann, I. E. (2004). Retrospective on optimization. Comp. Chem. Eng. 28, 1169–1192. doi:10.1016/j.compchemeng.2003.11.003
Buoro, D., Casisi, M., De Nardi, A., Pinamonti, P., and Reini, M. (2013). Multicriteria optimization of a distributed energy supply system for an industrial area. Energy 58, 128–137. doi:10.1016/j.energy.2012.12.003
Buoro, D., Pinamonti, P., and Reini, M. (2014). Optimization of a distributed cogeneration system with solar district heating. Appl. Energy 124, 298–308. doi:10.1016/j.apenergy.2014.02.062
Calí, M., and Borchiellini, R. (2002). District heating networks calculation and optimization. Encycl. Life Support Syst. 2.
Caputo, P., Costa, G., and Ferrari, S. (2013). A supporting method for defining energy strategies in the building sector at urban scale. Energy Policy 55, 261–270. doi:10.1016/j.enpol.2012.12.006
Chen, B.-J., Chang, M.-W., and Lin, C.-J. (2004). Load forecasting using support vector machines: a study on EUNITE competition 2001. IEEE Trans. Power Syst. 19, 1821–1830. doi:10.1109/TPWRS.2004.835679
Collins, A. G., and Johnson, R. L. (1975). Finite-element method for water-distribution networks. J. Am. Water Works Assoc. 385–389.
Connolly, D., Lund, H., Mathiesen, B. V., Werner, S., Möller, B., Persson, U., et al. (2014). Heat Roadmap Europe: combining district heating with heat savings to decarbonise the EU energy system. Energy Policy 65, 475–489. doi:10.1016/j.enpol.2013.10.035
Crawley, D. B., Lawrie, L. K., Winkelmann, F. C., Buhl, W. F., Huang, Y. J., Pedersen, C. O., et al. (2001). EnergyPlus: creating a new-generation building energy simulation program. Energy Build. 33, 319–331. doi:10.1016/S0378-7788(00)00114-6
Dall, O. G., Galante, A., and Torri, M. (2012). A methodology for the energy performance classification of residential building stock on an urban scale. Energy Build. 48, 211–219. doi:10.1016/j.enbuild.2012.01.034
Dalla Rosa, A., and Christensen, J. E. (2011). Low-energy district heating in energy-efficient building areas. Energy 36, 6890–6899. doi:10.1016/j.energy.2011.10.001
Dalla Rosa, A., Boulterb, R., Churchb, K., and Svendsen, S. (2012). District heating (DH) network design and operation toward a system-wide methodology for optimizing renewable energy solutions (SMORES) in Canada: a case study. Energy 45, 960–974. doi:10.1016/j.energy.2012.06.062
Day, T. (2006). Degree-Days: Theory and Application. London: The Chartered Institution of Building Services Engineers, 106.
de Guadalfajara, M., Lozano, M. A., and Serra, L. M. (2012). Evaluation of the potential of large solar heating plants in Spain. Energy Procedia 30, 839–848. doi:10.1016/j.egypro.2012.11.095
Dobersek, D., and Goricanec, D. (2009). Optimisation of tree path pipe network with nonlinear optimisation method. Appl. Therm. Eng. 29, 1584–1591. doi:10.1016/j.applthermaleng.2008.07.017
Dotzauer, E. (2002). Simple model for prediction of loads in district-heating systems. Appl. Energy 73, 277–284. doi:10.1016/S0306-2619(02)00078-8
Eicker, U. (2004). POLYCITY-Europäische Energieforschung für Kommunen. Solares Bauen. Sonderheft der Sonnenenergie.
Eriksson, N. (2012). Predicting Demand in District Heating Systems a Neural Network Approach. Uppsala: Uppsala University.
European Parliament. (2006). Directive 2006/32/EC of the European Parliament and of the Council of 5 April 2006. Off. J. Eur. Union 45, 64–85.
Falke, T., Krengel, S., Meinerzhagen, A.-K., and Schnettler, A. (2016). Multi-objective optimization and simulation model for the design of distributed energy systems. Appl. Energy. doi:10.1016/j.apenergy.2016.03.044
Filippin, C., Ricard, F., and Larsen, S. F. (2013). Evaluation of heating energy consumption patterns in the residential building sector using stepwise selection and multivariate analysis. Energy Build. 66, 571–581. doi:10.1016/j.enbuild.2013.07.054
Filogamo, L., Peri, G., Rizzo, G., and Giaccone, A. (2014). On the classification of large residential buildings stocks by sample typologies for energy planning purposes. Appl. Energy 135, 825–835. doi:10.1016/j.apenergy.2014.04.002
Fonseca, J. A., and Schlueter, A. (2015). Integrated model for characterization of spatiotemporal building energy consumption patterns in neighborhoods and city districts. Appl. Energy 142, 247–265. doi:10.1016/j.apenergy.2014.12.068
Galante, A., and Torri, M. (2012). A methodology for the energy performance classification of residential building stock on an urban scale. Energy Build. 48, 211–219. doi:10.1016/j.enbuild.2012.01.034
Gopalakrishnan, H., and Kosanovic, D. (2014). Economic optimization of combined cycle district heating systems. Sustainable Energy Technol. Assess. 7, 91–100. doi:10.1016/j.seta.2014.03.006
Gross, G., and Galiana, F. D. (1987). Short-term load forecasting. Proc. IEEE 75, 1558–1573. doi:10.1109/PROC.1987.13927
Guadalfajara, M., Lozano, M. A., and Serra, L. M. (2014). Comparison of simple methods for the design of central solar heating plants with seasonal storage. Energy Procedia 48, 1110–1117. doi:10.1016/j.egypro.2014.02.124
Hassine, I. B., and Eicker, U. (2011). “Simulation and optimization of the district heating network in Scharnhauser Park,” in Proceedings of 2nd Polygeneration Conference, 2nd Edn (Tarragona: ECP).
Hassine, I. B., and Eicker, U. (2011). Simulation and optimization of the district heating network in Scharnhauser Park, in Proceedings of 2nd Polygeneration Conference (2nd ECP), 30 (Tarragona), 2011–2011.
Hassine, I. B., and Eicker, U. (2014). Control aspects of decentralized solar thermal integration into district heating networks. Energy Procedia 48, 1055–1064. doi:10.1016/j.egypro.2014.02.120
Heiple, S., and Sailor, D. J. (2008). Using building energy simulation and geospatial modeling techniques to determine high resolution building sector energy consumption profiles. Energy Build. 40, 1426–1436. doi:10.1016/j.enbuild.2008.01.005
Henning, D., Amiri, S., and Holmgren, K. (2006). Modelling and optimisation of electricity, steam and district heating production for a local Swedish utility. Eur. J. Oper. Res. 175, 1224–1247. doi:10.1016/j.ejor.2005.06.026
Henning, D. (1999). Optimisation of Local and National Energy Systems. Development and Use of the MODEST Model.
Hepbasli, A. (2005). Thermodynamic analysis of a ground-source heat pump system for district heating. Int. J. Energy Res 29, 671–687. doi:10.1002/er.1099
Hepbasli, A. (2010). A review on energetic, exergetic and exergoeconomic aspects of geothermal district heating systems (GDHSs). Energy Convers. Manag. 51, 2041–2061. doi:10.1016/j.enconman.2010.02.038
Hippert, H. S., Pedreira, C. E., and Souza, R. C. (2001). Neural networks for short-term load forecasting: a review and evaluation. IEEE Trans. Power Syst. 16, 44–55. doi:10.1109/59.910780
Hlebnikov, A., and Siirde, A. (2009). Optimization of Narva district heating network and analysis of competitiveness of Oil Shale CHP building in Narva. Oil Shale 26, 269–282. doi:10.3176/oil.2009.3S.09
Hurtig, J. (2010). Report-Evaluation of a Small Scale District Heating System in Ullared, Sweden. Halmstad University, School of Business and Engineering (SET), Biological and Environmental Systems (BLESS), Energiteknik.
Huld, T., and Pinedo-Pascua, I. (2012). Photovoltaic Solar Electricity Potential in European Countries. Italy: European Commission. Available at: http://re.jrc.ec.europa.eu/pvgis/cmaps/eu_cmsaf_opt/PVGIS-EuropeSolarPotential.pdf
Keçebaş, A., and Yabanova, İ (2012). Thermal monitoring and optimization of geothermal district heating systems using artificial neural network: a case study. Energy Build. 50, 339–346. doi:10.1016/j.enbuild.2012.04.002
Keçebas, A., Ali Alkan, M., Yabanova, İ, and Yumurtacł, M. (2013). Energetic and economic evaluations of geothermal district heating systems by using ANN. Energy Policy 56, 558–567. doi:10.1016/j.enpol.2013.01.039
Kim, E.-J., Plessis, G., Hubert, J.-L., and Roux, J.-J. (2014). Urban energy simulation: simplification and reduction of building envelope models. Energy Build. 84, 193–202. doi:10.1016/j.enbuild.2014.07.066
Koene, F. G., Bakker, L. G., Lanceta, D., and Narmsara, S. (2014). “Simplified building models of districts,” in Proceedings of BauSIM (Aachen, Germany).
Kuosa, M., Kontu, K., Mäkilä, T., Lampinen, M., and Lahdelma, R. (2013). Static study of traditional and ring networks and the use of mass flow control in district heating applications. Appl. Therm. Eng. 54, 450–459. doi:10.1016/j.applthermaleng.2013.02.018
Kuosa, M., Aalto, M., El Haj Assad, M., Mäkilä, T., Lampinen, M., and Lahdelma, R. (2014). Study of a district heating system with the ring network technology and plate heat exchangers in a consumer substation. Energy Build. 80, 276–289. doi:10.1016/j.enbuild.2014.05.016
Lara, R. A., Pernigotto, G., Cappelletti, F., Romagnoni, P., and Gasparella, A. (2015). Energy audit of schools by means of cluster analysis. Energy Build. 95, 160–171. doi:10.1016/j.enbuild.2015.03.036
Lee, C.-M., and Ko, C.-N. (2011). Short-term load forecasting using lifting scheme and ARIMA models. Expert Syst. Appl. 38, 5902–5911. doi:10.1016/j.eswa.2010.11.033
Lei, F., and Hu, P. (2009). “A baseline model for office building energy consumption in hot summer and cold winter region,” in International Conference on Management and Service Science. MASS’09 (IEEE), 1–4.
Li, J., Xiao, X., Boukouvala, F., Floudas, C. A., Zhao, B., Du, G., et al. (2016a). Data-driven mathematical modeling and global optimization framework for entire petrochemical planning operations. AIChE J. 62, 3020–3040. doi:10.1002/aic.15220
Li, L., Mu, H., Li, N., and Li, M. (2016b). Economic and environmental optimization for distributed energy resource systems coupled with district energy networks. Energy 109, 947–960. doi:10.1016/j.energy.2016.05.026
Lu, H., Alanne, K., and Martinac, I. (2014). Energy quality management for building clusters and districts (BCDs) through multi-objective optimization. Energy Convers. Manag. 79, 525–533. doi:10.1016/j.enconman.2013.12.051
Lund, H., Werner, W., Wiltshire, R., Svendsen, S., Thorsen, J. E., Hvelplund, F., et al. (2014). 4th Generation District Heating (4GDH): integrating smart thermal grids into future sustainable energy systems. Energy 68, 1–11. doi:10.1016/j.energy.2014.02.089
Madsen, H., Sejling, K., Søgaard, H. T., and Palsson, O. P. (1994). On flow and supply temperature control in district heating systems. Heat Recov. Syst. CHP 14, 613–620. doi:10.1016/0890-4332(94)90031-0
Mertz, T., Serra, S., Henon, A., and Reneaume, J. M. (2016). A MINLP optimization of the configuration and the design of a district heating network: academic study cases. Energy. doi:10.1016/j.energy.2016.07.106
Mertens, R. (2013). Manual for Statistics on Energy Consumption in Households. Luxembourg: Publications Office of the European Union. Available from: http://ec.europa.eu/eurostat/documents/3859598/5935825/KS-GQ-13-003-EN.PDF/baa96509-3f4b-4c7a-94dd-feb1a31c7291
Mirzaei, P. A. (2015). Recent challenges in modeling of urban heat island. Sustain. Cities Soc. 19, 200–206. doi:10.1016/j.scs.2015.04.001
Mirzaei, P. A., Olsthoorn, D., Torjan, M., and Haghighat, F. (2015). Urban neighborhood characteristics influence on a building indoor environment. Sustain. Cities Soc. 19, 403–413. doi:10.1016/j.scs.2015.07.008
Noussan, M., Abdin, G. C., Poggio, A., and Roberto, R. (2014). Biomass-fired CHP and heat storage system simulations in existing district heating systems. Appl. Therm. Eng. 71, 729–735. doi:10.1016/j.applthermaleng.2013.11.021
Nouvel, R., Schulte, C., Eicker, U., and Coors, V. (2013). CityGML-based 3D city model for energy diagnostics and urban energy policy support. IBPSA World 2013, 1–7.
Nuytten, T., Claessens, B., Paredis, K., Van Bael, J., and Six, D. (2013). Flexibility of a combined heat and power system with thermal energy storage for district heating. Appl. Energy 104, 583–591. doi:10.1016/j.apenergy.2012.11.029
Orehounig, K., Mavromatidis, G., Evins, R., Dorer, V., and Carmeliet, J. (2014). “Predicting energy consumption of a neighbourhood using building performance simulations,” in Building Simulation and Optimization (London, England).
Ortiga, J., Bruno, J. C., Coronas, A., and Grossman, I. E. (2007). Review of optimization models for the design of polygeneration systems in district heating and cooling networks. Comp. Aided Chem. Eng. 24, 1121–1126. doi:10.1016/S1570-7946(07)80211-2
P.H.A.F.S. Committee on Environment. (2011). Implementation of the Energy and Climate Package. Brussel: European Parliament – National Parliaments.
Palsson, H. (2000). Methods for Planning and Operating Decentralized Combined Heat and Power Plants in Riso National Laboratory. Roskilde, Denmark: Technical University of Denmark.
Palsson, O. P. (1993). Stochastic Modeling, Control and Optimization of District Heating System. Ph.D. thesis, DTU, Lyngby Denmark.
Pirouti, M., Bagdanavicius, A., Ekanayake, J., Wu, J., and Jenkins, N. (2013). Energy consumption and economic analyses of a district heating network. Energy 57, 149–159. doi:10.1016/j.energy.2013.01.065
Reidhav, C., and Werner, S. (2008). Profitability of sparse district heating. Appl. Energy 85, 867–877. doi:10.1016/j.apenergy.2008.01.006
Rezaie, B., and Rosen, M. A. (2012). District heating and cooling: review of technology and potential enhancements. Appl. Energy 93, 2–10. doi:10.1016/j.apenergy.2011.04.020
Sakawa, M., Kato, K., and Ushiro, S. (2002). Operational planning of district heating and cooling plants through genetic algorithms for mixed 0–1 linear programming. Eur. J. Oper. Res. 137, 677–687. doi:10.1016/S0377-2217(01)00095-9
Sanaei, S. M., and Nakata, T. (2012). Optimum design of district heating: application of a novel methodology for improved design of community scale integrated energy systems. Energy 38, 190–204. doi:10.1016/j.energy.2011.12.016
Sartor, K., Quoilin, S., and Dewallef, P. (2014). Simulation and optimization of a CHP biomass plant and district heating network. Appl. Energy 130, 474–483. doi:10.1016/j.apenergy.2014.01.097
Sehrawat, P., and Kensek, K. (2014). “Urban energy modeling: GIS as an alternative to BIM,” in Proceedings of ASHRAE/IBPSA Conference.
Sharp, T. (1996). “Energy benchmarking in commercial office buildings,” in Proceedings of the ACEEE, (Mankato: Minnesota State University).
Shimoda, Y., Fujii, T., Morikawa, T., and Mizuno, M. (2004). Residential end-use energy simulation at city scale. Build Environ. 39, 959–967. doi:10.1016/j.buildenv.2004.01.020
Söderman, J. (2007). Optimisation of structure and operation of district cooling networks in urban regions. Appl. Thermal Eng. 27(16), 2665–2676.
Tang, Z., de Almeida, C., and Fishwick, P. A. (1991). Time series forecasting using neural networks vs. Box-Jenkins methodology. Simulation 57, 303–310. doi:10.1177/003754979105700508
Theodoridou, I., Papadopoulos, A. M., and Hegger, M. (2011). A typological classification of the Greek residential building stock. Energy Build. 43, 2779–2787. doi:10.1016/j.enbuild.2011.06.036
Tuominen, P., Holopainen, R., Eskola, L., Jokisalo, J., and Airaksinen, M. (2014). Calculation method and tool for assessing energy consumption in the building stock. Building Env. 75, 153–160. doi:10.1016/j.buildenv.2014.02.001
United Nations. (2013). World Population Prospects the 2012 Revision, Key Findings and Advance Tables, ESA/P/WP. New York: United Nations.
University of Wisconsin—Madison, Solar Energy Laboratory, and Klein, S. A. (1979). TRNSYS, a Transient System Simulation Program. Solar Energy Laboratory, University of Wisconsin—Madison.
Verda, V., Baccinoa, G., Sciacovellia, A., and Russo, S. L. (2012). Impact of district heating and groundwater heat pump systems on the primary energy needs in urban areas. Appl. Therm. Eng. 40, 18–26. doi:10.1016/j.applthermaleng.2012.01.047
Wang, J., Zhou, Z., and Zhao, J. (2016). A method for the steady-state thermal simulation of district heating systems and model parameters calibration. Energy Convers. Manag. 120, 294–305. doi:10.1016/j.enconman.2016.04.074
Wang, S., and Xu, X. (2006). Simplified building model for transient thermal performance estimation using GA-based parameter identification. Int. J. Thermal. Sci. 45, 419–432. doi:10.1016/j.ijthermalsci.2005.06.009
Wang, W., Cheng, X., and Liang, X. (2013). Optimization modeling of district heating networks and calculation by the Newton method. Appl. Therm. Eng. 61, 163–170. doi:10.1016/j.applthermaleng.2013.07.025
Weber, C., Maréchal, F., and Favrat, D. (2007). “Design and optimization of district energy systems,” in 10th International Symposium on District Heating and Cooling, eds P. Valentin and A. Paul Serban (Hanover: Elsevier), 1127–1132.
Wright, J. A., Loosemore, H. A., and Farmani, R. (2002). Optimization of building thermal design and control by multi-criterion genetic algorithm. Energy and Buildings 34, 959–972.
Xing, Y., Bagdanavicius, A., Lannon, S., Pirouti, M., and Bassett, T. (2012). “Low temperature district heating network planning with focus on distribution energy losses,” in International Conference on Applied Energy ICAE 2012 (Suzhou, China).
Yabanova, I., and Keçebas, A. (2013). Development of ANN model for geothermal district heating system and a novel PID-based control strategy. Appl. Therm. Eng. 51, 908–916. doi:10.1016/j.applthermaleng.2012.10.044
Yun, G. Y., and Steemers, K. (2011). Behavioural, physical and socio-economic factors in household cooling energy consumption. Appl. Energy 88, 2191–2200. doi:10.1016/j.apenergy.2011.01.010
Zhang, G., Eddy Patuwo, B., and Hu, M. Y. (1998). Forecasting with artificial neural networks: the state of the art. Int. J. Forecast. 14, 35–62. doi:10.1016/S0169-2070(97)00044-7
Zhang, Y., Soga, K., Choudhary, R., and Bains, S. (2015). “GSHP application for heating and cooling at ‘City Scale’ for the city of westminster,” in Proceedings World Geothermal Congress, Melbourne.
Keywords: district, heating, modeling, optimization, energy
Citation: Talebi B, Mirzaei PA, Bastani A and Haghighat F (2016) A Review of District Heating Systems: Modeling and Optimization. Front. Built Environ. 2:22. doi: 10.3389/fbuil.2016.00022
Received: 29 June 2016; Accepted: 13 September 2016;
Published: 04 October 2016
Edited by:
Taehoon Hong, Yonsei University, South KoreaCopyright: © 2016 Talebi, Mirzaei, Bastani and Haghighat. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Parham A. Mirzaei, cGFyaGFtLm1pcnphZWlfYWhyYW5qYW5pQG5vdHRpbmdoYW0uYWMudWs=
 Behrang Talebi
Behrang Talebi Parham A. Mirzaei
Parham A. Mirzaei Arash Bastani1
Arash Bastani1 Fariborz Haghighat
Fariborz Haghighat