- Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyoto, Japan
An innovative hybrid control building system of multiple isolation and connection is proposed and investigated using both time history and input energy responses for various types of ground motions together with transfer functions. It is concerned that the seismic displacement response at the base-isolation layer of the existing base-isolated buildings may extremely increase under long-period and long-duration ground motions, which are getting great attention recently. In order to enhance the seismic performance of those base-isolated buildings, a novel hybrid system of multiple isolation and building connection is proposed and compared with other structural systems such as an independent multiple isolation system, a hybrid system of base isolation and building connection. Furthermore, the robustness of seismic responses of the proposed hybrid system for various types of ground motion is discussed through the comparison of various structural systems including non-hybrid systems. Finally, the optimal connection damper location is investigated using a sensitivity-type optimization approach.
Introduction
Recently, the concept of resilience is becoming very popular in the field of earthquake structural engineering (Bruneau and Reinhorn, 2006; Takewaki et al., 2012). In order to enhance the earthquake resilience of building structures, it is desired through advanced design methodologies to make building structures safe for a broader class of earthquake ground motions (Amadio et al., 2003; Kobori, 2004, Takewaki et al., 2012, 2013; Takewaki, 2013). Since earthquake ground motions seem highly uncertain, it appears difficult to predict the forthcoming events within an allowable accuracy in time, space, and character (Takewaki et al., 2011, 2012, 2013; Takewaki, 2013). In addition, because the building structural properties (especially the properties of advanced buildings systems, such as base-isolation systems and passive control system) are not deterministic (Ben-Haim, 2006) and the consideration of their variation is inevitable in the seismic-resistant design of building structures, the concepts of robustness and redundancy are becoming also very important. In fact, it is mandatory in Japan to take into account the variability of structural properties of isolators and dampers in the design of base-isolated buildings and passively controlled buildings. In such design procedure, the worst combination of structural properties of isolators and dampers is investigated as a key concept (Ben-Haim, 2006; Elishakoff and Ohsaki, 2010, Takewaki et al., 2012), and all the design conditions are investigated for this worst case.
While various base-isolated buildings have been developed recently as an effective building system for pulse-type ground motions with non-resonant frequency contents (Jangid and Datta, 1994; Hall et al., 1995, Heaton et al., 1995; Jangid, 1995, Jangid and Banerji, 1998; Kelly, 1999, Naeim and Kelly, 1999; Jangid and Kelly, 2001, Morales, 2003; Takewaki, 2005, Li and Wu, 2006; Hino et al., 2008, Takewaki, 2008; Takewaki and Fujita, 2009), their resilience for earthquakes is not necessarily proved for long-period ground motions with the characteristic period of 5–8 s (Irikura et al., 2004; Kamae et al., 2004, Ariga et al., 2006). This is because the resonance of the base-isolated buildings to the long-period ground motions may cause catastrophic outcomes (Hashimoto et al., 2015). The long-period ground motions with the characteristic period of 5–8 s were of great interest in the structural design of base-isolated buildings and super high-rise buildings since the Tokachi-oki earthquake in 2003 and were demonstrated as a key critical input for such buildings during the 2011 Tohoku earthquake. The resonances of a large oil tank during the Tokachi-oki earthquake in 2003 and base-isolated buildings and super high-rise buildings during the 2011 Tohoku earthquake with long-period ground motions are very famous in the field of structural design of those structures. On the other hand, it is also true that, while building structures including passive energy dissipating systems are effective for long-duration and long-period ground motions (Takewaki, 2007; Patel and Jangid, 2011, Takewaki et al., 2011, 2012; Kasagi et al., 2015), they are not necessarily resilient for pulse-type ground motions. The resolution of these two issues is greatly desired in the field of seismic-resistant and control design (Koo et al., 2009; Petti et al., 2010, Karabork, 2011).
In this paper, a new hybrid passive control building system is proposed in which a multiple isolation building model (Pan et al., 1995; Becker and Ezazi, 2016, Fujita et al., 2016) is connected to another non-isolated building (free wall) with oil dampers. A similar type of connected buildings without isolation and another type of base-isolated buildings with connection have been designed and constructed by Obayashi Corporation and Shimizu Corporation in Japan as an apartment house with a car parking tower (Murase et al., 2013; Kasagi et al., 2016). However, buildings with such new system (multiple isolation and building connection model) have never been proposed and constructed so far. It is demonstrated here that the present hybrid passive building control system is effective both for pulse-type ground motions and long-duration, long-period ground motions. It is also made clear from the energy analysis that although the connecting dampers in the hybrid system are not effective for a pulse-type wave, those are effective for a long-duration, long-period wave. Finally, it is also demonstrated that the present hybrid passive control building system has high redundancy and robustness for a broad range of disturbances and an optimal connecting damper location can be found using a sensitivity-type optimization approach.
Hybrid Control System Using Multiple Isolation and Building Connection
Proposed Building Model and Other Comparable Models
Consider a 40-story reinforced concrete building, as shown in Figure 1, which includes two isolation stories and is connected to a reinforced concrete free wall of 26 stories (a RC wall system) at some floor levels by using oil dampers. The isolators used in this study are considered to be linear. This hybrid system can be regarded as an extension of the previously proposed hybrid system (Murase et al., 2013) consisting of a base-isolated building and a connected free wall.
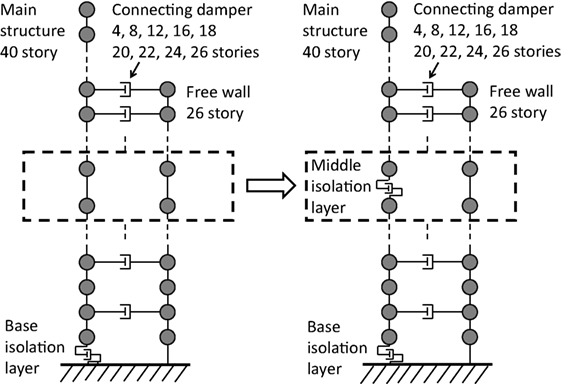
Figure 1. Transformation of base-isolated and building connection model into multiple isolation and building connection model.
The oil dampers for building connection are installed at 4, 8, 12, 16, 18, 20, 22, 24, and 26th floor levels. The floor mass of the main building is 1.7 × 106 kg at each floor and that of the free wall is 2.2 × 105 kg. The base-isolation floor mass (also middle-isolation story floor mass) is larger than other floor mass and is set to 5.1 × 106 kg. The story height is 3.5 m in all the stories.
The superstructure of the main building (base-isolated building) is designed so as to have the fundamental natural period of 3.0 s and a straight fundamental mode for a fixed base model. However, the story stiffnesses at several stories near the top have been modified (slightly increased) so as to restrain the larger response near the top. On the other hand, the free wall is designed so as to have the fundamental natural period of 0.63 s and a straight fundamental mode. In the proposed hybrid model (multiple isolation and building connection model), the 20th story is replaced by the middle-story isolation system. The stiffness of the middle-story isolation system is designed to have two-thirds of the base-isolation system so that the deformation component of the middle-story isolation system has the same deformation component of the base-isolation system in the lowest mode.
The fundamental natural periods of the base-isolated model and the multiple isolation model are 6.79 and 8.36 s, respectively. On the other hand, the fundamental natural periods of the base-isolated and building connection model and the multiple isolation and building connection model are 6.73 and 8.31 s, respectively. The horizontal stiffness of the isolation story can be regarded as the equivalent stiffness after consideration of the P-delta effect. The structural damping ratio of the superstructure (stiffness-proportional damping) is set to 0.03, and the damping coefficient of the base-isolation story in the base-isolated and building connection model has been set so as for the damping ratio of the base-isolation story for a rigid superstructure to be 0.15. The damping coefficient of the middle-isolation story in the multiple isolation and building connection model is the same as the damping coefficient of the base-isolation story in the base-isolated and building connection model. The interconnection oil dampers are allocated uniformly to the above-mentioned floors (damping coefficient 2.16 × 106 Ns/m), and the approximate lower-mode damping ratio for a rigid free wall is set to 0.15 under non-modal-coupling approximation. Therefore, an approximate fundamental damping ratio of the base-isolated and building connection model is 0.30.
In this paper, five building models as shown in Figure 2 are considered for the comparison of earthquake responses. The five models are the multiple isolation and building connection model (proposed model), the base-isolated and building connection model, the building connection model without isolation, the multiple isolation model without building connection (Pan et al., 1995; Becker and Ezazi, 2016, Fujita et al., 2016), and the base-isolated model without building connection.
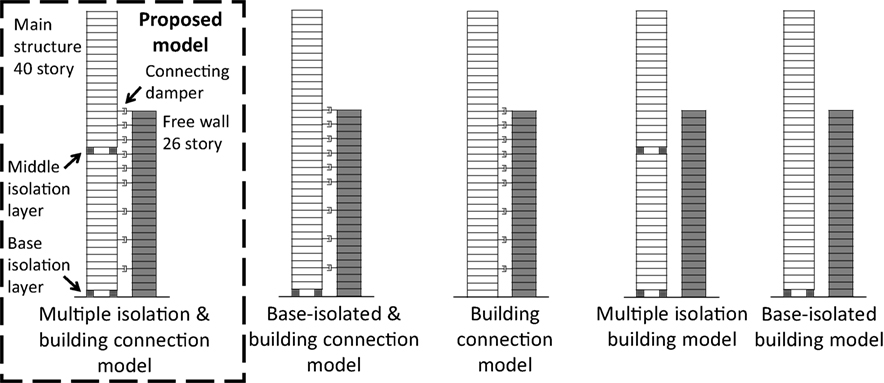
Figure 2. Multiple isolation and building connection model (proposed model), base-isolated and building connection model, building connection model, multiple isolation building model, and base-isolated building model.
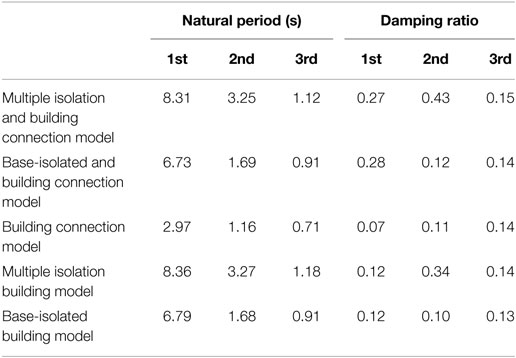
Natural Frequencies and Damping Ratios of Proposed Building Model and Other Comparable Models
Table 1 shows the first to third natural periods of various building models to be considered here and the first to third damping ratios of those models. These values have been computed by the complex eigenvalue analysis. It can be observed that the fundamental natural period of the proposed building model becomes longer compared to the comparable base-isolated and building connection model. It can also be found that while the building connection makes the fundamental natural period slightly shorter than the corresponding non-connection models, the effect is small.
As for damping ratios, the fundamental damping ratio of the base-isolated and building connection model becomes 0.28 and is close to the setting value of 0.30 in the previous section. In addition, the fundamental damping ratio of the proposed building model has almost the same value as the base-isolated and building connection model. A remarkable point is that the second damping ratio of the proposed building model is 0.43 and is increased from the base-isolated and building connection model.
Transfer Functions of Isolation Story Deformation and Top Acceleration
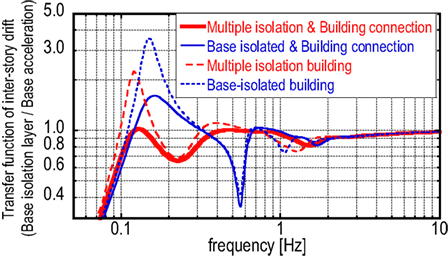
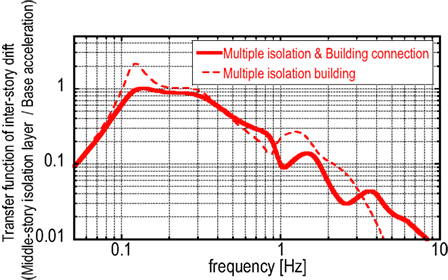
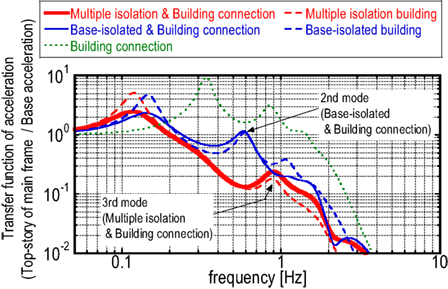
It may be possible to characterize the dynamic properties of a structural model by using a transfer function to the base input. Figure 3 shows the transfer function of inter-story drift (base-isolation layer/base acceleration) for the proposed building model (multiple isolation and building connection model), the base-isolated and building connection model, the multiple isolation model without interconnection, and the base-isolated building model without interconnection. On the other hand, Figure 4 presents the transfer function of inter-story drift (middle-story isolation layer/base acceleration) for the proposed building model (multiple isolation and building connection model) and the multiple isolation model without interconnection. Furthermore, Figure 5 illustrates the transfer function of top-story acceleration of the main structure in the proposed building model (multiple isolation and building connection model), the base-isolated and building connection model, the multiple isolation model without interconnection, the base-isolated building model without interconnection, and the building connection model (without isolation).
It can be observed that the transfer function of the proposed building system possesses lower values in a broader frequency range compared to other comparable building systems. In particular, the inter-story drifts of the base-isolation story and the middle-isolation story at the fundamental natural frequency have been reduced greatly together with the top-story acceleration of the main multiple isolation building at higher natural frequencies. However, compared with both the base-isolated building model and the base-isolated and building connection model, the inter-story drift of the base-isolation story has been increased a little bit in the frequency range slightly larger than the second natural frequency (0.31 Hz).
Earthquake Responses of Proposed Building Model and Other Comparable Models
In this section, the earthquake responses of the proposed building model and the other comparable models are shown for the pulse-type ground motions and long-period, long-duration ground motions. Based on these results, the robustness of the proposed building model is demonstrated.
Input Ground Motions
Consider an artificial pulse-type ground motion (He, 2003; Xu et al., 2007, He and Agrawal, 2008). The velocity wave of the artificial pulse-type ground motion can be expressed by
where ωP is the input circular frequency corresponding to the input period Tp. Tp = 1.0 s is used, and n = 1, a = 2.51 1/s, and CP = 6.7 m/s are specified for wave generation in comparison with the JMA Kobe NS (1995).
On the other hand, consider an artificial long-period, long-duration ground motion (Takewaki and Tsujimoto, 2011). The velocity wave of the artificial long-period, long-duration ground motion can be described by
where ωL is the input circular frequency. Two parameters TL1 = 2π/ωL1 = 6.8 s (corresponding to the fundamental natural period of the base-isolated building) and TL2 = 2π/ωL2 = 8.4 s (corresponding to the fundamental natural period of the multiple isolation building) are specified. The amplitude CL = 0.2 m/s is set in comparison with the Tomakomai EW (2003).
On the other hand, as the representative recorded ground motions, the JMA Kobe NS (1995) and the Tomakomai EW (2003) have been chosen. The JMA Kobe NS (1995) has been amplified so that the maximum velocity attains 0.5 m/s, which is the specified level in Japan for an intensive design earthquake ground motion.
The acceleration records of these selected ground motions are shown in Figure 6 and the displacement, velocity, acceleration response spectra (damping ratio = 0.3), and the energy spectra are shown in Figures 7A–D. The energy spectra have been obtained from the following relation:
where M denotes the total mass and E is the total input energy.
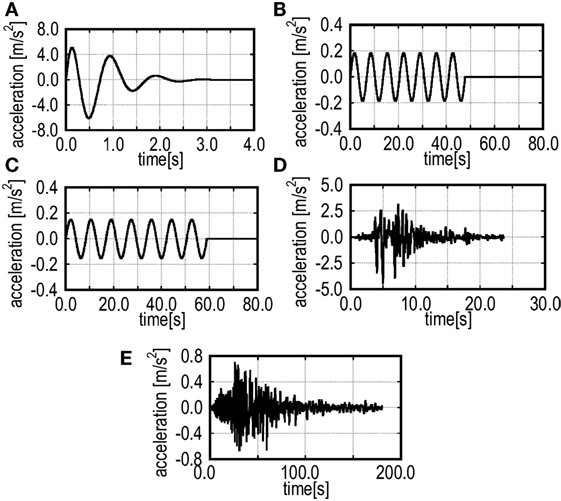
Figure 6. Input ground motions: (A) artificial pulse-type ground motion (Tp = 1.0 s), (B) artificial long-period, long-duration ground motion (6.8 s), (C) artificial long-period, long-duration ground motion (8.4 s), (D) JMA Kobe NS (level 2: 0.5 m/s), and (E) Tomakomai EW (2003).
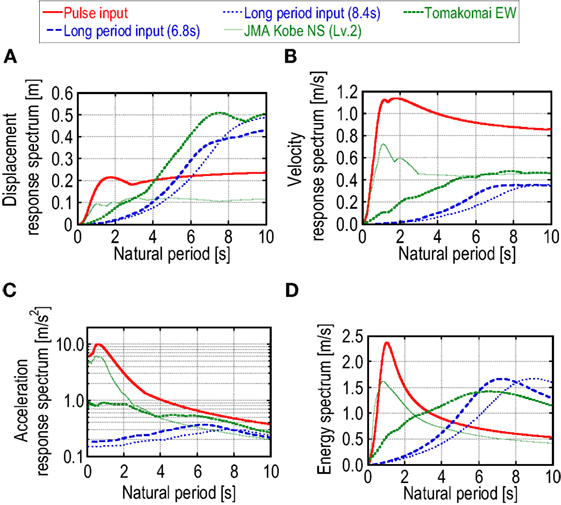
Figure 7. Various spectra of five ground motions: (A) displacement response spectra, (B) velocity response spectra, (C) acceleration response spectra, and (D) energy spectra.
Maximum Response of Proposed Building Model and Other Comparable Models under Several Earthquake Ground Motions
The maximum horizontal displacements under the artificial long-period, long-duration ground motion (6.8 s), the artificial long-period, long-duration ground motion (8.4 s), the Tomakomai EW (2003), the artificial pulse-type ground motion, and the JMA Kobe NS (1995) are shown in Figure 8. On the other hand, the maximum accelerations under these ground motions are illustrated in Figure 9. Figures 8A–C and 9A–C in these figures are for the long-period, long-duration ground motions, and Figures 8D,E and 9D,E are for the pulse-type ground motions.
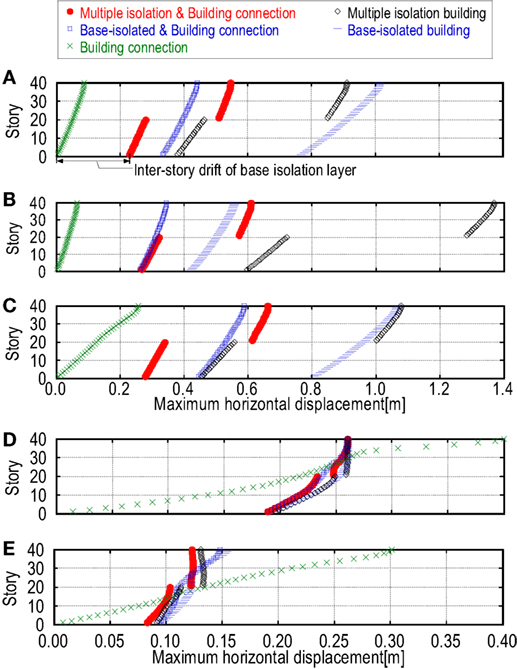
Figure 8. Maximum horizontal displacements under various ground motions: (A) artificial long-period, long-duration ground motion (6.8 s), (B) artificial long-period, long-duration ground motion (8.4 s), (C) Tomakomai EW (2003), (D) artificial pulse-type ground motion, and (E) JMA Kobe NS (1995).
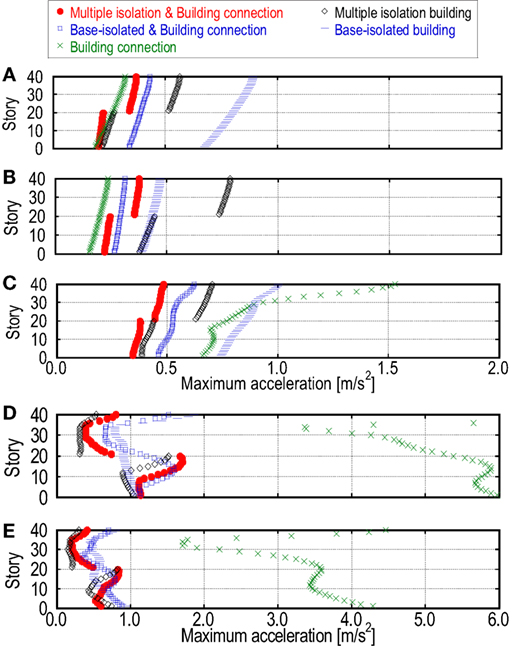
Figure 9. Maximum top-story accelerations under various ground motions: (A) artificial long-period, long-duration ground motion (6.8 s), (B) artificial long-period, long-duration ground motion (8.4 s), (C) Tomakomai EW (2003), (D) artificial pulse-type ground motion, and (E) JMA Kobe NS (1995).
It can be observed from Figures 8 and 9 that the proposed building system is effective both for pulse-type ground motions and long-period, long-duration ground motions. This indicates the high robustness of the proposed building system for various kinds of ground motion. In particular, the story drifts of the base-isolation story and the middle-isolation story exhibit the value of half or two-thirds of the corresponding values of the comparable building systems (base-isolated and building connection model, multiple-isolation building model) under the long-period, long-duration ground motions. Furthermore, the acceleration of the proposed building system can be reduced effectively under the long-period, long-duration ground motions compared to the comparable building systems (base-isolated building model, multiple-isolation building model).
Energy Response of Proposed Building Model and Other Comparable Models under Several Earthquake Ground Motions
In this section, the energy responses of the proposed building model and other comparable models are shown for the pulse-type ground motions and long-period, long-duration ground motions. In particular, the effect of the energy consumption at the connected dampers on the response is investigated in detail.
Figure 10 shows the time histories of energy response of the proposed building model and the building connection model (without isolation) under the artificial pulse-type ground motions. The input energy, total damping energy, kinetic energy, and damping energy at the connected dampers are plotted in this figure.
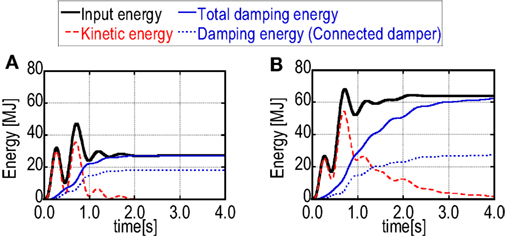
Figure 10. Energy response of the proposed building model and other comparable model under the artificial pulse-type earthquake ground motion: (A) proposed model (multiple isolation and building connection model) and (B) building connection model (without isolation).
On the other hand, Figure 11 presents the time histories of energy response of the proposed building model and the multiple isolation building model (without connection) under the artificial long-period, long-duration ground motion (8.4 s).
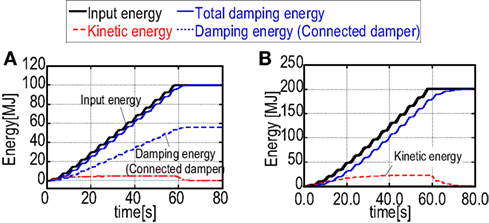
Figure 11. Energy response of the proposed building model and other comparable model under the artificial long-period, long-duration earthquake ground motion (8.4 s): (A) proposed building model and (B) multiple isolation building model (without connection).
It can be observed that the proposed building system has a larger value of the ratio of the energy consumption in the connected dampers to the overall energy consumption compared to other comparable building systems. This leads to the effective reduction of the vibration energy in the main building. The remarkable reduction of the vibration energy in the main building has also been observed also under the long-period, long-duration ground motions.
Robustness of Proposed Building Model and Other Comparable Models under Several Earthquake Ground Motions
Figure 12 shows the response variability (inter-story drift of base-isolation layer, inter-story drift of middle-story isolation layer, inter-story drift of non-isolation story of the main structure, base shear, overturning moment at the base) in the proposed building model and other comparable models under various ground motions.
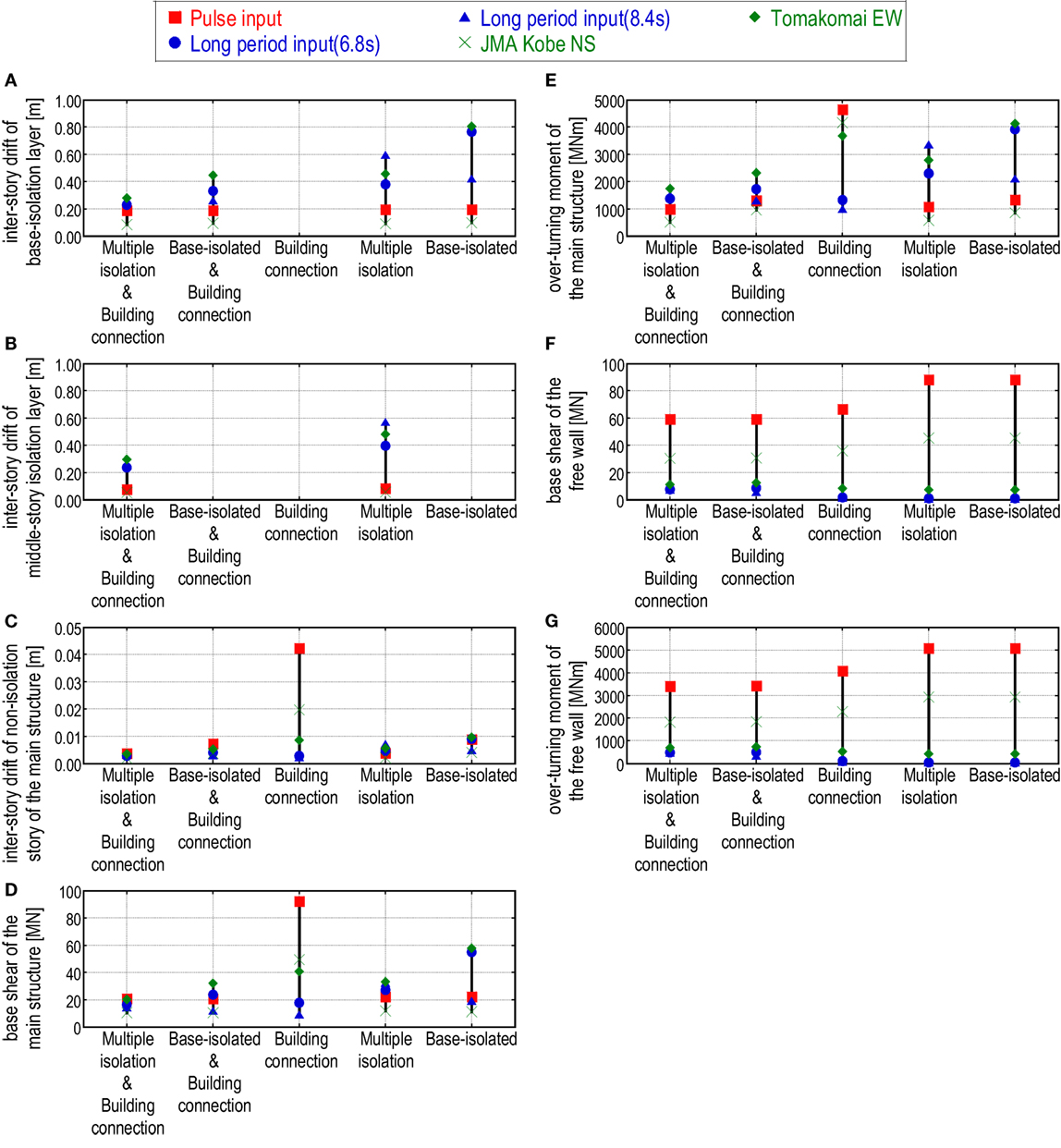
Figure 12. Response variability of proposed building model and other comparable models under various earthquake ground motions: (A) inter-story drift of base-isolation layer, (B) inter-story drift of middle-story isolation layer, (C) inter-story drift of non-isolation story of the main structure, (D) base shear of the main structure, (E) base overturning moment of the main structure, (F) base shear of the free wall, and (G) base overturning moment of the free wall.
It can be observed from Figures 12A,B that the proposed building system exhibits a good performance in the inter-story drift of the base-isolation layer and the middle-story isolation layer, especially for long-period ground motions which are critical to the base-isolation system. The good performance can be observed also in the non-isolation story drift, base shear, and overturning moment at the base (Figures 12C–E). A small response variability in the proposed building system can also be understood from Figures 12A–D.
It can be observed from Figures 12F,G that the base shear and base overturning moment in the free wall of the proposed building system under the pulse-type ground motions exhibit almost equivalent or smaller values compared to the other comparable building systems. On the other hand, while these values become slightly larger under the long-period, long-duration ground motions, no serious problem occurs because those response values are relatively small compared to those response values under the pulse-type ground motions.
Summary of Response and Robustness Analysis
Table 2 shows the summary of the response characteristics of the proposed building model and other comparable models under representative two-type ground motions. As stated above, the proposed building system exhibits a good performance for the pulse-type ground motion keeping the allowable response to the long-period, long-duration ground motions. For long-period, long-duration ground motions, the largest response was selected.
Optimization of Connection Damper Location
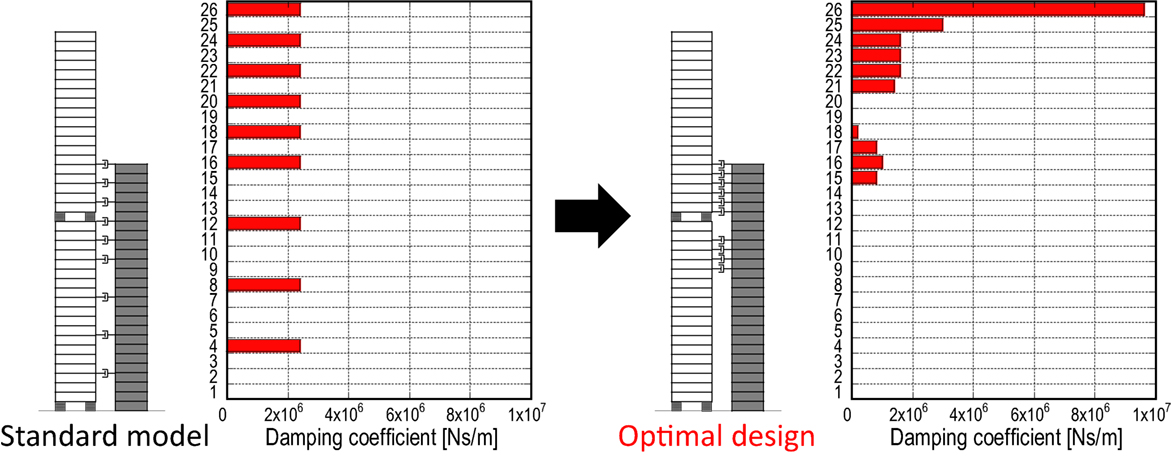
The effective connection damper location is an interesting issue. In order to find the optimal location, the maximization of the area of the energy transfer function (Takewaki, 2007) for the connection dampers is adopted as the objective function. This quantity indicates the energy absorbed in the connection dampers under an ideal white noise-like input. A sensitivity analysis is employed as the optimization method. The initial design is the model without connection damper, and the optimization is terminated at the stage where the total quantity of damping coefficients reaches the total quantity for the standard model with a uniform damping coefficient 2.16 × 106 Ns/m.
Figure 13 shows the result of the optimization. It can be found that the effective dampers are located at several stories above and below the middle-isolation story (20th story) and larger quantities are allocated to the upper side. The objective function (area of the energy transfer function for connection dampers) was maximized from 2.12 × 107 Ns3/m (standard model) to 2.35 × 107 Ns3/m. Table 3 presents the comparison of the first three natural periods and damping ratios. It can be observed that the fundamental natural period of the optimal design is shorter than that of the standard model and the lowest mode damping ratio of the optimal design is larger than that of the standard model.
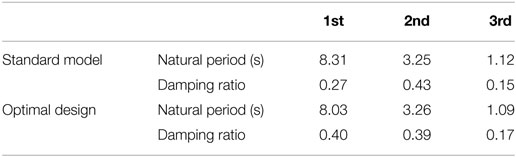
Table 3. Comparison of the first three natural periods and damping ratios between the standard model and the optimal design.
The position of the middle-story isolation may be an interesting theme in the response reduction. This will be discussed in the future.
Conclusion
The following conclusions have been derived.
(1) A new hybrid passive control building system has been proposed, in which a multi-isolation (double-isolation) building is connected to another non-isolated building (free wall) with oil dampers.
(2) It was demonstrated that the transfer function of the proposed building system possesses lower values in a broader frequency range compared to other comparable building systems. In particular, the story drifts of the base-isolation story and the middle-isolation story in the fundamental natural frequency have been reduced greatly together with the top-story acceleration of the main multi-isolation building at higher natural frequencies. However, the story drift of the base-isolation story at the second natural frequency has been increased a little bit.
(3) It has been shown that the proposed building system is effective both for pulse-type ground motions and long-period, long-duration ground motions. This indicates the high robustness of the proposed building system for various kinds of ground motions. In particular, the story drifts of the base-isolation story and the middle-isolation story exhibit the value of half or two-thirds of the corresponding values of the comparable building systems (base-isolated and building connection model, multiple-isolation building model) under the long-period, long-duration ground motions. Furthermore, the acceleration of the proposed building system can be reduced effectively under the long-period, long-duration ground motions compared to the comparable building systems (base-isolated building model, multiple-isolation building model).
(4) From the viewpoint of energy response, it has been shown that the proposed building system has a larger value of the ratio of the energy consumption in the connected dampers to the overall energy consumption compared to other comparable building systems. This leads to the effective reduction of the vibration energy in the main building. The remarkable reduction of the vibration energy in the main building has also been observed also under the long-period, long-duration ground motions.
(5) The response reduction in the base-isolation story of the proposed system has been achieved by the distributed placement of dampers in the middle-isolation story and connection system. The realization of the larger ratio of the fundamental natural periods between the main building and the free wall has made the proposed system effective. On the other hand, the installation of dampers at the non-isolated inter-stories is not effective because of the small inter-story drift in the base-isolated (or multiple-isolation) buildings.
(6) The story shear and overturning moment in the free wall of the proposed building system under the pulse-type ground motions exhibit smaller values compared to the other comparable building systems. While these values become a slightly larger under the long-period, long-duration ground motions, no problem occurs because those response values are relatively small compared to those response values under the pulse-type ground motions.
(7) The effective connection damper location can be found by introducing the energy transfer function for the connection damper as an objective function and using a sensitivity analysis. The effective dampers are located at several stories above and below the middle-isolation story (20th story), and larger quantities are allocated to the upper side.
In introducing the proposed system, a cost issue should be resolved. When base-isolation systems were developed and introduced in 1980s, the cost issue was discussed in detail. However, the benefits obtained from such new systems resolved that issue. Furthermore, as the number of constructions of buildings using such new systems becomes large, the cost is becoming lower gradually. In addition, the property of the proposed system as a highly robust system for a broad type of earthquake ground motions seems to be preferred, especially in the current situation that the properties of earthquake ground motions are highly uncertain and unpredictable.
Author Contributions
M Taniguchi formulated the problem, conducted the computation, and wrote the paper. KF helped the computation and discussed the results. M Tsuji discussed the results. IT supervised the research and wrote the paper.
Funding
Part of the present work is supported by the Grant-in-Aid for Scientific Research (KAKENHI) of Japan Society for the Promotion of Science (No. 15H04079). This support is greatly appreciated.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Amadio, C., Fragiacomo, M., and Rajgelj, S. (2003). The effects of repeated earthquake ground motions on the non-linear response of SDOF systems. Earthq. Eng. Struct. Dyn. 32, 291–308. doi: 10.1002/eqe.225
Ariga, T., Kanno, Y., and Takewaki, I. (2006). Resonant behavior of base-isolated high-rise buildings under long-period ground motions. Struct. Des. Tall Spec. Build. 15, 325–338. doi:10.1002/tal.298
Becker, T., and Ezazi, A. (2016). Enhanced performance through a dual isolation seismic protection system. Struct. Des. Tall Spec. Build. 25, 72–89. doi:10.1002/tal.1229
Ben-Haim, Y. (2006). Information-Gap Decision Theory: Decisions under Severe Uncertainty. London: Academic Press.
Bruneau, M., and Reinhorn, A. (2006). “Overview of the resilience concept,” in Proc. of the 8th US National Conference on Earthquake Engineering. San Francisco, CA.
Elishakoff, I., and Ohsaki, M. (2010). Optimization and Anti-Optimization of Structures under Uncertainty. London: Imperial College Press.
Fujita, K., Miura, T., Tsuji, M., and Takewaki, I. (2016). Experimental study on influence of hardening of isolator in multiple isolation building. Front. Built Environ. 2:12. doi:10.3389/fbuil.2016.00012
Hall, J. H., Heaton, T. H., Halling, M. W., and Wald, D. J. (1995). Near-source ground motion and its effect on flexible buildings. Earthq. Spectra 11, 569–605. doi:10.1193/1.1585828
Hashimoto, T., Fujita, K., Tsuji, M., and Takewaki, I. (2015). Innovative base-isolated building with large mass-ratio TMD at basement. Int. J. Future Cities Environ. 1, 9. doi:10.1186/s40984-015-0007-6
He, W. L. (2003). Smart Energy Dissipation Systems for Protection of Civil Infrastructures from Near-Field Earthquakes. Ph.D. dissertation, The City Univ. of New York, New York.
He, W. L., and Agrawal, A. K. (2008). Analytical model of ground motion pulses for the design and assessment of seismic protective systems. J. Struct. Eng. 134, 1177–1188. doi:10.1061/(ASCE)0733-9445(2008)134:7(1177)
Heaton, T. H., Hall, J. H., Wald, D. J., and Halling, M. W. (1995). Response of high-rise and base-isolated buildings in a hypothetical MW 7.0 blind thrust earthquake. Science 267, 206–211. doi:10.1126/science.267.5195.206
Hino, J., Yoshitomi, S., Tsuji, M., and Takewaki, I. (2008). Bound of aspect ratio of base-isolated buildings considering nonlinear tensile behavior of rubber bearing. Struct. Eng. Mech. 30, 351–368. doi:10.12989/sem.2008.30.3.351
Irikura, K., Kamae, K., and Kawabe, H. (2004). “Importance of prediction of long-period ground motion during large earthquakes,” in Annual Conference of the Seismological Society of Japan, Poster Session, Fukuoka (in Japanese).
Jangid, R. S. (1995). Optimum isolator damping for minimum acceleration response of base-isolated structures. Aust. Civil Eng. Trans. 37, 325–331.
Jangid, R. S., and Banerji, P. (1998). Effects of isolation damping on stochastic response of structures with nonlinear base isolators. Earthq. Spectra 14, 95–114. doi:10.1193/1.1585990
Jangid, R. S., and Datta, T. K. (1994). Non-linear response of torsionally coupled base isolated structure. J. Struct. Eng. 120, 1–22. doi:10.1061/(ASCE)0733-9445(1994)120:1(1)
Jangid, R. S., and Kelly, J. M. (2001). Base isolation for near-fault motions. Earthq. Eng. Struct. Dyn. 30, 691–707. doi:10.1002/eqe.31
Kamae, K., Kawabe, H., and Irikura, K. (2004). “Strong ground motion prediction for huge subduction earthquakes using a characterized source model and several simulation techniques,” in Proceedings of the13th WCEE (Vancouver).
Karabork, T. (2011). Performance of multi-storey structures with high damping rubber bearing base isolation systems. Struct. Eng. Mech. 39, 399–410. doi:10.12989/sem.2011.39.3.399
Kasagi, M., Fujita, K., Tsuji, M., and Takewaki, I. (2015). Effect of nonlinearity of connecting dampers on vibration control of connected building structures. Front. Built Environ. 1:25. doi:10.3389/fbuil.2015.00025
Kasagi, M., Fujita, K., Tsuji, M., and Takewaki, I. (2016). Automatic generation of smart earthquake-resistant building system: hybrid system of base-isolation and building-connection. Heliyon 2, 2. doi:10.1016/j.heliyon.2016.e00069
Kelly, J. M. (1999). The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 28, 3–20. doi:10.1002/(SICI)1096-9845(199901)28:1<3::AID-EQE801>3.3.CO;2-4
Kobori, T. (2004). Seismic-Response-Controlled Structure (New Edition). Tokyo: Kajima Publisher. (in Japanese).
Koo, J.-H., Jang, D.-D., Usman, M., and Jung, H.-J. (2009). A feasibility study on smart base isolation systems using magneto-rheological elastomers. Struct. Eng. Mech. 32, 755–770. doi:10.12989/sem.2009.32.6.755
Li, H.-N., and Wu, X.-X. (2006). Limitations of height-to-width ratio for base-isolated buildings under earthquake. Struct. Des. Tall Spec. Build. 15, 277–287. doi:10.1002/tal.295
Morales, C. A. (2003). Transmissibility concept to control base motion in isolated structures. Eng. Struct. 25, 1325–1331. doi:10.1016/S0141-0296(03)00084-1
Murase, M., Tsuji, M., and Takewaki, I. (2013). Smart passive control of buildings with higher redundancy and robustness using base-isolation and inter-connection. Earthq. Struct. 4, 649–670. doi:10.12989/eas.2013.4.6.649
Pan, T. C., Ling, S. F., and Cui, W. (1995). Seismic response of segmental buildings. Earthq. Eng. Struct. Dyn. 24, 1039–1048. doi:10.1002/eqe.4290240708
Patel, C. C., and Jangid, R. S. (2011). Dynamic response of adjacent structures connected by friction dampers. Earthq. Struct. 2, 149–169. doi:10.12989/eas.2011.2.2.149
Petti, L., Giannattasio, G. M., De Iuliis, M., and Palazzo, B. (2010). Small scale experimental testing to verify the effectiveness of the base isolation and tuned mass dampers combined control strategy. Smart Struct. Syst. 6, 57–72. doi:10.12989/sss.2010.6.1.057
Takewaki, I. (2005). Uncertain-parameter sensitivity of earthquake input energy to base-isolated structure. Struct. Eng. Mech. 20, 347–362. doi:10.12989/sem.2005.20.3.347
Takewaki, I. (2007). Earthquake input energy to two buildings connected by viscous dampers. J. Struct. Eng. 133, 620–628. doi:10.1061/(ASCE)0733-9445(2007)133:5(620)
Takewaki, I. (2008). Robustness of base-isolated high-rise buildings under code-specified ground motions. Struct. Des. Tall Spec. Build. 17, 257–271. doi:10.1002/tal.350
Takewaki, I. (2013). Critical Excitation Methods in Earthquake Engineering, 2nd Edn. Amsterdam: Elsevier Science.
Takewaki, I., and Fujita, K. (2009). Earthquake input energy to tall and base-isolated buildings in time and frequency dual domains. Struct. Des. Tall Spec. Build. 18, 589–606. doi:10.1002/tal.497
Takewaki, I., Fujita, K., and Yoshitomi, S. (2013). Uncertainties in long-period ground motion and its impact on building structural design: case study of the 2011 Tohoku (Japan) earthquake. Eng. Struct. 49, 119–134. doi:10.1016/j.engstruct.2012.10.038
Takewaki, I., Moustafa, A., and Fujita, K. (2012). Improving the Earthquake Resilience of Buildings: The Worst Case Approach. London: Springer.
Takewaki, I., Murakami, S., Fujita, K., Yoshitomi, S., and Tsuji, M. (2011). The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 31, 1511–1528. doi:10.1016/j.soildyn.2011.06.001
Takewaki, I., and Tsujimoto, H. (2011). Scaling of design earthquake ground motions for tall buildings based on drift and input energy demands. Earthq. Struct. 2, 171–187. doi:10.12989/eas.2011.2.2.171
Keywords: multiple isolation, building connection for control, hybrid passive control system, robustness, redundancy, optimal damper location
Citation: Taniguchi M, Fujita K, Tsuji M and Takewaki I (2016) Hybrid Control System for Greater Resilience Using Multiple Isolation and Building Connection. Front. Built Environ. 2:26. doi: 10.3389/fbuil.2016.00026
Received: 22 August 2016; Accepted: 27 September 2016;
Published: 10 October 2016
Edited by:
Nikos D. Lagaros, National Technical University of Athens, GreeceReviewed by:
Naohiro Nakamura, Hiroshima University, JapanTao Wang, China Earthquake Administration, China
Vasile-Mircea Venghiac, “Gheorghe Asachi” Technical University of Iaşi, Romania
Copyright: © 2016 Taniguchi, Fujita, Tsuji and Takewaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Izuru Takewaki dGFrZXdha2lAYXJjaGkua3lvdG8tdS5hYy5qcA==
 Masaki Taniguchi
Masaki Taniguchi Kohei Fujita
Kohei Fujita Masaaki Tsuji
Masaaki Tsuji Izuru Takewaki
Izuru Takewaki