- Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyoto, Japan
In order to identify physical model parameters of a high-rise building, a new story stiffness identification method is presented based on a shear-bending model and the identification function. Although a shear building model may be the simplest conventional model for representing tall buildings, the system identification (SI) method using that model is not necessarily appropriate. This is because the influence of bending deformation is predominant in such high-rise buildings. For this reason, a shear-bending model is used where the shear and bending stiffnesses are unknown. In the previous researches using the shear-bending model, it was difficult to identify the bending stiffnesses stably and reliably. In this paper, to overcome such instability of bending stiffness identification of the shear-bending model, a new SI algorithm using both the shear model and the shear-bending model is presented. The proposed SI algorithm is based on the observation that the fundamental-mode shape of the identified shear model is similar to that of the shear-bending model identified in the previous SI method. In order to verify the advanced SI method, two different 20-story building models are investigated in the numerical simulations. From the results of the simulations, both the shear and bending stiffnesses of the shear-bending model are identified reliably and stably in the proposed SI method.
Introduction
The structural health monitoring has been studied and applied to many engineering fields, such as civil, mechanical, and aerospace structures, for the evaluation of the structural safety and the decision-making to operate the objective structures (Boller et al., 2009; Takewaki et al., 2011). In the structural health monitoring, the system identification (SI) methodologies play a key role in identifying mechanical properties of structures. It is well recognized that the modal-parameter SI and physical-parameter SI are two major branches in the field of SI. Much interest is focused on the modal-parameter SI, which can provide the overall mechanical properties of a structural system and has a stable characteristic. On the other hand, the physical-parameter SI is important from the different point of view that the physical parameters, e.g., stiffness or damping coefficient of the structural model, can be obtained directly, and this is quite effective for the damage detection. Although the physical-parameter SI is preferred in the structural health monitoring, its development is limited due to the requirement of multiple measurements or the necessity of complicated manipulation (Hart and Yao, 1977; Udwadia et al., 1978; Shinozuka and Ghanem, 1995; Takewaki and Nakamura, 2000, 2005; Brownjohn, 2003; Nagarajaiah and Basu, 2009; Takewaki et al., 2011; Zhang and Johnson, 2013).
As one of limited works on physical-parameter SI, Takewaki and Nakamura (2000) introduced a special SI formulation based on the work by Udwadia et al. (1978). In that method, the stiffness and damping coefficient at a specific story of a shear building model (S model) can be identified directly from the floor acceleration records just above and below the target story using the so called identification function (IDF). However, in the SI method proposed by Takewaki and Nakamura (2000, 2005), there exists a difficulty in applying to actual recorded data, e.g., microtremors, due to the small signal/noise (SN) ratio in the low frequency range. Furthermore, an S model is not necessarily appropriate for representing the structural property of high-rise buildings with large aspect ratios due to the influence of bending deformation. The former problem has been a major and most difficult problem in the field of the physical-parameter SI method, where the limit value evaluation of the transfer function for ω → 0 is needed. The Auto-Regressive with eXogenous (ARX) model with constraints on the ARX parameters has been introduced by Maeda et al. (2011) to eliminate the noise effect. By applying the ARX model to transfer functions, the difficulty in the evaluation of limit value for a small SN ratio data has been avoided. On the other hand, the latter problem has been tackled by expanding the SI algorithm to the shear-bending model (SB model) (Minami et al., 2013; Fujita et al., 2013). Since the bending deformation of the high-rise building is correlated with floor rotations, the SB model is expected to be an appropriate simplified structural model to analyze the actual high-rise building. However, the identification of bending stiffness in the SB model is unstable in the previous SI method. In the SI method using the SB model (Minami et al., 2013; Fujita et al., 2013), when the horizontal floor accelerations just above and below the target story can be used from the first story to the top story, it is needed to determine the ratio of the bending stiffness to the shear stiffness at each floor by applying optimization algorithms. Therefore, the identified results may depend on the initial-value selection of the stiffness ratio. Furthermore, the IDF (Takewaki and Nakamura, 2000) is included in the stiffness evaluation. Since this formulation is also used in this paper, the equations for stiffness evaluation using the IDF will be referred in the next section. One of the reasons of the stability problem in the previous SI method is caused by the accuracy of the evaluation of the IDF from the measured data. Although the ARX model is applied to raw data, the limit value of the IDF may vary in various numbers of orders of the ARX model. In summary, the difficulty in the previous proposed SI method may result from the initial-value dependence problem in identifying the unknown parameters and the accuracy problem in the evaluation of the IDFs.
In this paper, in order to enhance the applicability of the proposed SI method using the SB model, the difficulty in the limit manipulation of the transfer function is overcome by introducing the filter design method using a quantitative index in terms of the ARX model parameters. Furthermore, a statistical evaluation method in the limit manipulation for the IDF is presented where the specification of the number of orders of the ARX model is not needed. These proposed procedures on the filter design and the selection of the number of orders of the ARX model can provide the limit value of the IDF in a relatively stable manner without any further manipulation. By enhancing the accuracy of the evaluation of the IDF, the influence of the initial values on the identification stability can be improved. Formulations to evaluate the bending stiffnesses are presented using both an S model and an SB model. It is shown that these formulations are also effective to stabilize the identification. The proposed method can be applied to the input of earthquake ground motions or microtremors. For numerical verification of the advanced SI method, the present method is applied to stiffness identification of high-rise buildings under microtremors. As shown in the numerical simulations, the advanced SI method can provide reliable stiffness identification results, which may be effective in the structural health monitoring, e.g., the evaluation of the structural performance of high-rise buildings in the operating term or after an earthquake.
System Identification Using Shear-Bending Building Model
In this section, the theoretical formulation of the SI method using the SB model is briefly introduced. Since the formulations for the SI method using the SB model introduced in Takewaki and Nakamura (2000, 2005), Kuwabara et al. (2013), and Minami et al. (2013) are also important in the present SI method, some related equations based on the stiffness identification method are presented here to apply for the identification of the SB model. In the previous SI method using the SB model, there exists a stability problem of the identification of bending stiffnesses due to various uncertainties in the determination of the identification parameters. On the other hand, the advanced SI method is mainly aimed at overcoming this difficulty to obtain more reliable stiffness identification results and apply the advanced SI method to the actual health monitoring of high-rise buildings.
Formulation of Stiffness Identification of Shear-Bending Model
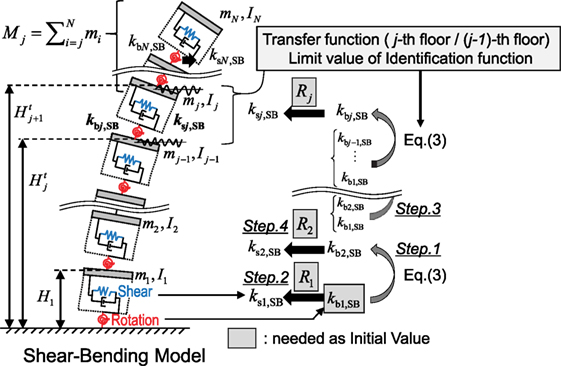
In a high-rise building due to the influence of bending deformation on the interstory drift, the SB model can be regarded as an appropriate model. Consider an N-story SB model as shown in Figure 1. Let mj, Ij, Hj, , ksj,SB, and kbj,SB denote the mass, the moment of inertia, the story height, the floor height from the ground, the story shear stiffness, and the bending stiffness of the j-th story, respectively. Since the frequency-domain approach is appropriate in the present formulation, all the governing equations subjected to the ground motion are expressed in the frequency domain by
where M, C, and K denote the mass, damping, and stiffness matrices of the SB model, and “i” denote the imaginary unit. U(ω) is the Fourier transform of u(t) described as
where uj(t) and ϕj(t) are the horizontal displacement and floor rotation angle of the SB model. In Eq. 1 is the influence coefficient vector defined by {1, ⋯, 1, 0, ⋯, 0}.
The IDF in terms of the transfer function between the floor responses at j-th story and ( j − 1)-th story has been proposed by Takewaki and Nakamura (2000, 2005). It has been proved theoretically that the limit value of the IDF for ω → 0 becomes the shear stiffness of the shear building model (S model). Based on the concept of the SI method using the IDF theory, the theoretical formulation of the physical-parameter SI method using the SB model has been proposed (Kuwabara et al., 2013; Minami et al., 2013). In those SI methods, the bending and shear stiffnesses of the SB model can be derived from the following equations with the stiffness ratio Rj = kbj,SB/ksj,SB.
where fj(ω) is called the IDF and is defined by
In the previous paper (Minami et al., 2013), the inverse of the function in Re{} in Eq. 5 was defined as the IDF. In Eqs 3 and 5, and is the transfer function.
From Eqs 3 and 4, the shear and bending stiffnesses are identified sequentially from the first story. In this procedure, the bending stiffness at the first story and the stiffness ratio Rj( j = 1, 2, ⋯, N) are unknown parameters. These unknown parameters are necessary to identify by applying the conventional optimization algorithm. The objective function fobj evaluated in the optimization is defined by
where ωobs,i and ωide,i, are the natural circular frequencies derived from observed data and those derived by the eigenvalue analysis of the identified SB model. Depending on the optimization algorithm, the influence of the selection of the initial value may cause unstable identification. In the present SI method, these initial values are determined by introducing a random searching technique. A detailed explanation will be presented in numerical simulations.
The SI method using the SB model is summarized in Figure 1. The IDFs at all stories are also necessary to identify the stiffness of the building. Even though the simultaneous measurement of all floor responses is needed in the conventional physical-parameter SI method, the IDF derived in Eq. 5 can be evaluated only from the simultaneous recorded data at j-th story and ( j − 1)-th story. From the view point of the measurement system installation, this advantage enables the practical application of the proposed SI method to the existing high-rise building.
Evaluation of Limit Value of Identification Function Using ARX Model
In the previous SI method based on the IDF as formulated in Eq. 3, the limit manipulation of the IDF for ω → 0 was needed. However, when the IDFs are evaluated from the raw recorded data, e.g., the microtremor measurement, the IDFs become unstable and exhibit a large variability in the low frequency range due to the measurement noise. In order to eliminate the influence of these noises, the ARX model as a time-domain model has been introduced (Takewaki and Nakamura, 2009; Takewaki et al., 2011; Minami et al., 2013). By using ARX parameters, the transfer function Gj,j−1(ω) can be described as
where NARX, , and are the number of orders of the ARX model and the ARX parameters of the polynomial estimation between input and output, respectively. The limit value of the transfer function Gj,j−1(ω) for ω → 0 can be derived by the Taylor series expression of Gj,j−1(ω) as described by
From the structural investigations that the j-th floor and ( j − 1)-th floor move identically at ω → 0, and the transfer function Gj,j−1(ω) should not have a linear term of ω, the following relations can be derived as
These constraints are also considered in the determination of the ARX parameters. By substituting Eqs 9 and 10 into Eq. 8, and then substituting this into Eq. 5, the limit value of the IDF can be derived finally using , the real part of A2, as
where can be expressed in terms of the ARX parameters (Kuwabara et al., 2013). This formulation in terms of the ARX model is also used in the present SI method. However, there still exists a difficulty in the determination of NARX in the application to the proposed SI method. Since the evaluation of the limit value of IDF is included in Eq. 3, it is important to clarify the influence of the estimation error of the ARX model on the stiffness identification.
Instability of Identification of Bending Stiffness
In the previous researches (Kuwabara et al., 2013; Minami et al., 2013; Ikeda et al., 2014, 2015), the bending stiffness kb1,SB at the first story and the stiffness ratio Rj( j = 1, 2, …, N) at all stories are unknown parameters to be identified. In order to identify these unknown parameters, it is needed to minimize a certain objective function by applying an optimization algorithm. By using identified parameters, the shear and bending stiffnesses of the SB model can be obtained sequentially in Eqs 3 and 4. In those previous researches, the error of the natural frequencies of the identified SB model from the observed ones was employed as an example of the objective function. However, due to the initial-value dependence problem in the optimization algorithm and the inaccuracy of the evaluation of the limit value of the IDF, the identified stiffnesses of the SB model exhibit a large variability compared with the specified values. Especially for the bending stiffnesses, when the objective function is given by the error of the natural frequencies, the insensitivity of the bending stiffness to the natural frequencies becomes a major problem and causes unstable identification results.
Development of Reliable Evaluation Method of Limit Value of Identification Function
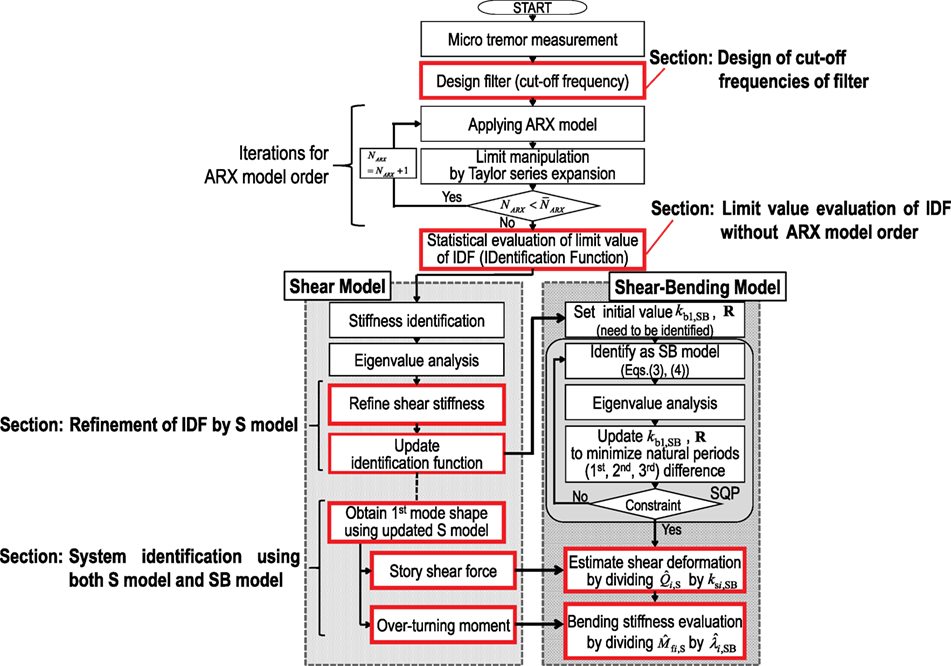
In the previous stiffness identification method using the SB model, there still exists a problem of instability in the identification of bending stiffnesses. In order to overcome this difficulty, it seems important to enhance the reliability of the limit value evaluation of the IDF for ω → 0. In the previous SI method, the number of orders of the ARX model and the cut-off frequencies of the filtering were determined by a trial-and-error approach. The variability of the limit value of IDF may result from these reasons.
In this section, a reasonable filtering design method is presented first. After applying the ARX model to time series data processed by the proposed filters, a statistical evaluation method for the limit value of the IDF is proposed where the selection of the number of orders of ARX model is not necessary.
Design of Cut-Off Frequencies of Filter
It is well known that the application of the filter to raw data can help eliminating the noise and improving the accuracy of the transfer function evaluation in the ARX model. In the conventional filters, such as low-pass, band-pass, high-pass filters, the cut-off frequencies are the important parameters of those filters. A band-pass filter is used in the advanced SI method. In order to obtain stable identification results, appropriate cut-off frequencies are recommended to be determined in accordance with the proposed quantitative index. From the observation of the theoretical transfer function which can be derived by the equation of dynamic equilibrium in frequency domain, the gradient of the transfer function in terms of circular frequency becomes a positive value in the frequency range from 0 to the fundamental natural frequency of the objective building. In this paper, the following accuracy rate function FTF,j is proposed based on the above observation.
where sgn() is a mathematical function which gives −1 for the negative argument and 1 for the positive argument. Therefore, gsgn,j(ωi) can be used as a Boolean data type function where the case that the gradient of the real part of transfer function at ω = ωi becomes a positive value is true and the case that the gradient of the real part of transfer function at ω = ωi becomes a negative value is false. In Eq. 12, Nα denotes the element number in the frequency domain from 0 to the upper bound frequency to evaluate FTF,j. The upper bound frequency is determined as the fundamental natural circular frequency of the objective building which can be obtained easily from the microtremor measurement.
Figure 2 presents examples to explain the relationship between the real part of transfer function Re{Gj,j−1(ωi)} and gsgn,j(ω) ( j = 1, 5, 10, 15, 20) of a 20-story SB model under microtremor (see Microtremor Ground Motion). The structural properties of the SB model are shown in Section “Numerical Examples.” In Figure 2A, the real part of the transfer function evaluated by using the ARX model (NARX = 150) is compared with that derived theoretically from the equations of motion. Furthermore, the transfer function estimated in the conventional manner from the ratio of an ensemble average of the cross spectrum to that of the power spectrum of the raw data is described. As mentioned before, only the value of the transfer function for ω → 0 is needed to identify stiffnesses. As observed in Figure 2, gsgn,j(ωi) of the theoretical transfer function becomes a constant value in the lower frequency domain than the fundamental natural circular frequency. In the transfer function estimated from raw data, gsgn,j(ωi) becomes false in some frequencies and the limit value of the transfer function seems to be unstable. On the other hand, gsgn,j(ωi) of the transfer function derived by the ARX model indicates an accurate fitness of the transfer function with the theoretically given transfer function. However, gsgn,1(ωi) for NARX = 150 becomes false in the most frequency domain. This indicates that the fitness of the transfer function is not good. Therefore, to determine the cut-off frequencies of the filter, gsgn,j(ωi) should be evaluated for various numbers of orders of the ARX model.
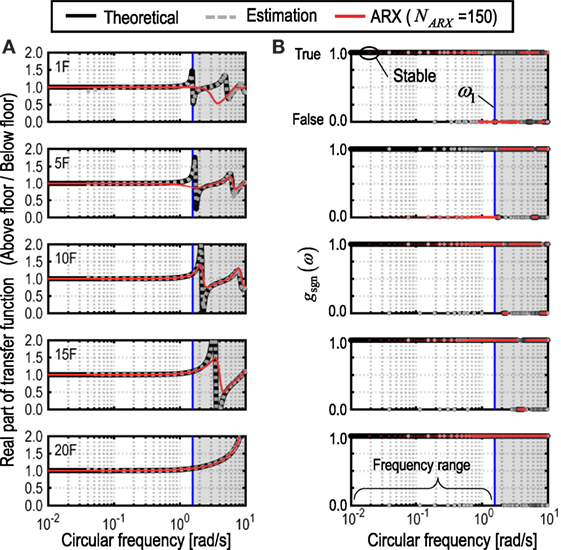
Figure 2. Application of quantitative index to determine filtering parameters. (A) Real part of transfer function and (B) Boolean data type function in Eq. 12b.
The variations of the gradient of the real part of transfer function are presented in Figure 3 for various numbers of orders of the ARX model (21 ≤ NARX ≤ 300) with and without using the band-pass filter, respectively. In this figure, the domain where becomes 0, i.e., the gradient of the real part of transfer function is negative, is emphasized in red marker.
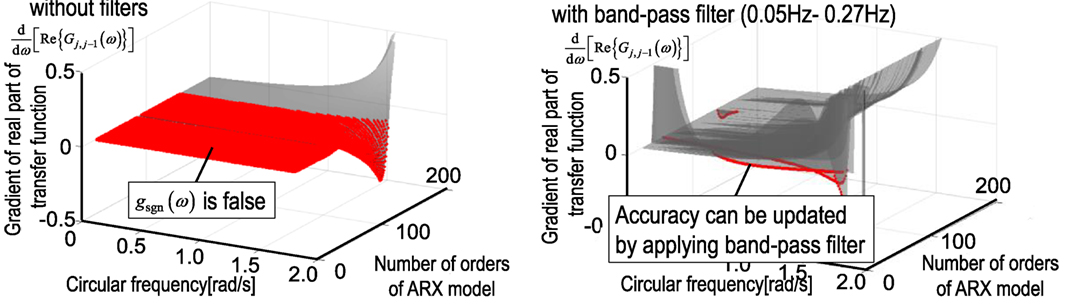
Figure 3. Comparison of gradient of real part of transfer function d[Re{Gj,j−1(ωi)}]/dω with and without filter.
Limit Value Evaluation of Identification Function without Determination of Number of Orders of ARX Model
In applying the ARX model to the SI to reduce the noise influence, it is generally important to determine the number of orders of the ARX model. In the previous SI method using the SB model, the ARX model was introduced to evaluate the limit value of the IDF in Eq. 10. However, since the number of orders of the ARX model was determined by trial and error calculations, the accuracy of the identification may depend on the experiences of structural engineers. Therefore, it seems difficult to obtain stable identification results in the previous SI method. In this paper, the limit value of the IDF is determined by a statistical approach, where various numbers of orders of the ARX model are applied in the parametric calculation.
Figure 4 shows an example of the evaluation of the limit value of the IDF ( j = 1, 5, 15, 20) in a 20-story building model under microtremor (see Microtremor Ground Motion). Figure 4A indicates the variation of the limit value of the IDF with respect to number of orders of the ARX model. Figure 4B shows the cumulative distribution of the limit value of the IDF corresponding to the result shown in Figure 4A. As shown in Figure 4A, the limit value of the IDF cannot be evaluated stably in the small number of orders of the ARX model especially in the lower stories. Since the IDF is derived from the transfer function between the floor responses just above and below the target story, the reliable identification of the limit value of the IDF at the lower stories can be performed through the wide range calculations in the number of orders. This is because the number of degrees of freedom of the substructure of the objective building becomes larger at the lower stories when the floor response at the below of the current story is regarded as the input to the substructure. Although the instability in the estimation of the limit value of the IDF in terms of the ARX model is shown in Figure 4A, the limit value of the IDF is determined by the mean value statistically obtained in the cumulative distribution in the proposed SI method.
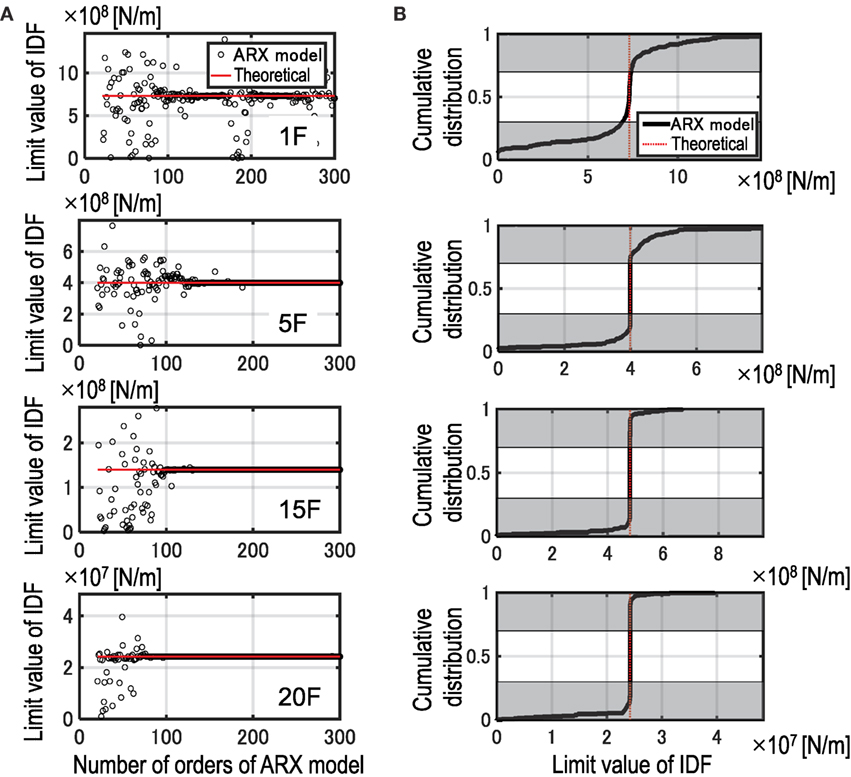
Figure 4. Limit value evaluation of identification function without selection of number of orders of ARX model: (A) variation of limit value of IDF and (B) cumulative distribution of limit value of IDF.
As mentioned above, an unstble domain, where the limit value of the IDF varies in the small number of orders of the ARX model, becomes larger at lower stories. If the number of stories of the object building is higher than the current example, the variability of the limit value of the IDF would be larger. Therefore, it is needed to calculate the limit value of the IDF in a larger number of orders of the ARX model. It is recommended that the range of the number of orders of the ARX model to inspect the limit value of IDF is changed in the lower story and higher story, respectively.
Refinement of Identification Function by Shear Model
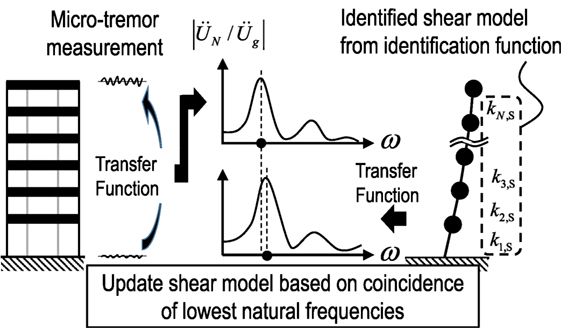
Since the stiffness of the S model is derived directly from the limit value of the IDF in the previous SI method, the fundamental natural frequency of the identified S model does not necessarily coincide with the observed lowest natural frequency. This difference of the fundamental natural frequency indicates that there still exists an estimation error in the limit value of the IDF. While, due to the difference of the identification algorithm using the conventional optimization calculation in the SB model, the fundamental natural frequency of the identified SB model can be obtained as almost the same value of observed one. Therefore, in the present identification method, the limit value of the IDF is refined through an optimization procedure where the objective function is defined as an error of the fundamental natural frequencies between observed one and identified one. Figure 5 illustrates the concept of update of the IDF using the S model.
System Identification Using Both Shear Model and Shear-Bending Model
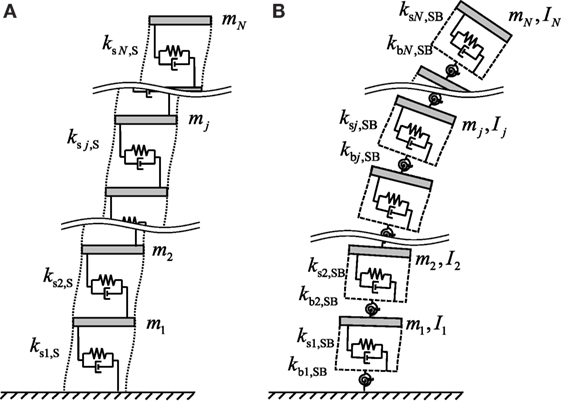
In this section, a new approach for the stable identification of bending stiffnesses is presented. The proposed method is based on the observation that the fundamental natural frequencies and the first-mode shapes of the identified S model are similar to those of the identified SB model. By combining the modal information from the identified S model in the SI method using the SB model, the bending stiffness of the SB model can be evaluated without depending on the identification algorithm based on the IDF.
Consider an N-story S model and an SB model as shown in Figure 6. Let mi denote the i-th mass of the S model and the SB model and let Ii denote the i-th mass moment of inertia of the SB model. Those are given as known parameters. The story stiffnesses of the S model can be derived from the theory using the IDF. After the shear stiffnesses of the S model are refined as shown in previous section (see Refinement of Identification Function by Shear Model), the story shear force in the free vibration of the first mode can be derived using the fundamental natural frequency and the first-mode shape of the S model as
where and Uj,S denote the fundamental natural circular frequency and the first-mode shape of the S model. In the following formulation, the hat above symbol, such as , denotes the estimation from the S model. The shear deformation in the i-th story of the SB model can be estimated by dividing by shear stiffness ksi,SB of the SB model.
where the shear stiffness ksi,SB of the SB model can be derived by the previous identification method. From this estimation, the interstory drift caused by the floor rotation of the SB model in the free vibration of the first mode can be obtained as
where is the interstory drift of the SB model in the free vibration of the first mode. The absolute floor rotation angle can be obtained by dividing by floor height Hi. Since the absolute floor rotation angle is the cumulative sum of the interstory floor rotation angle, the interstory floor rotation angle can be derived as
Considering the rotational equilibrium equation, the product of and kbi,SB becomes the overturning moment at the i-th floor level. The overturning moment of the first mode can also be obtained from the identified S model as
Finally, the bending stiffness of the SB model can be derived as
Figure 7 shows the diagram of the formulation for the evaluation of bending stiffnesses of the SB model using the identified S model. The flowchart of the proposed stiffness identification method is summarized in Figure 8.
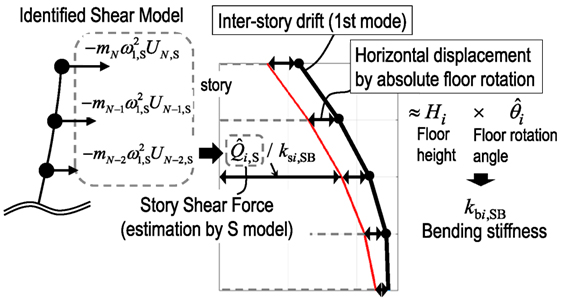
Figure 7. Identification of bending stiffness using first-mode shapes of shear model and shear-bending model.
Numerical Examples
Shear-Bending Model Parameters
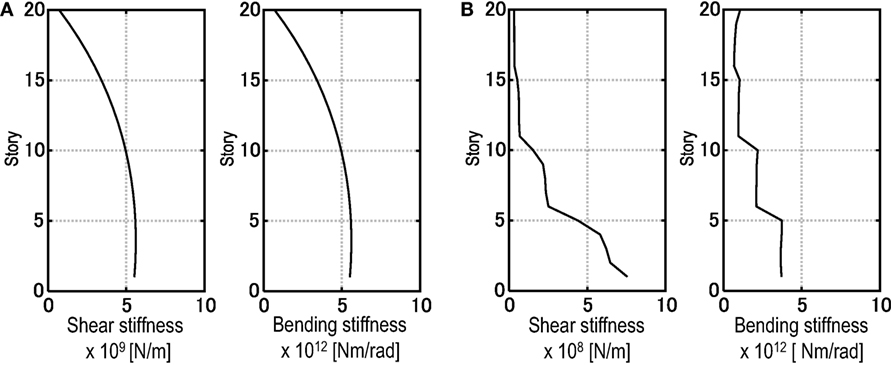
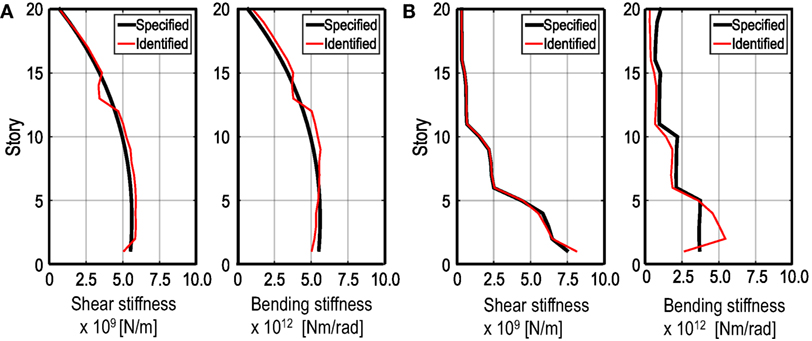
In order to verify the validity and stability of the advanced SI method, the time history responses of two different 20-story SB models, called Models A and B, have been simulated numerically and applied as the recorded data. The shear and bending stiffnesses of Model A are given as follows. First, the S model is used and its shear stiffnesses are determined so as to have a specified fundamental natural frequency and a specified interstory drift of the first-mode shape. The first-mode distribution of interstory drifts is given by a trapezoidal shape where the first story is 1.0 and top story is 0.7. This shear stiffnesses of the S model are used as the shear stiffnesses of the SB model. Second, the bending stiffnesses are given by the product of the specified stiffness ratio and obtained shear stiffnesses. The stiffness ratio is defined as the ratio of the bending stiffness to the shear stiffness. The structural properties of Model A are summarized in Table 1. In Model A, the stiffness ratio is given as uniform in all stories. On the other hand, the shear and bending stiffnesses of Model B are provided by referring to the 20-story plane-frame building model. From the relationship between the static external force and nodal displacement of the frame model, the equivalent shear and bending stiffnesses of the shear-bending model can be derived. The mass at each story is 220 × 103 kg in Model B. The story height and structural damping ratio are the same as Model A. Figure 9 shows the shear and bending stiffness of Models A and B.
Microtremor Ground Motion
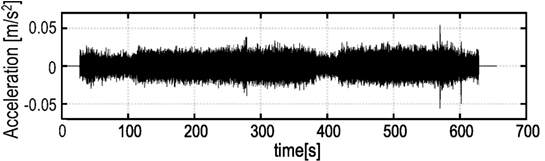
The actual microtremor ground motion measured in the Disaster Prevention Research Institute of Kyoto University in 2013 is applied as the base input in following numerical simulations. Figure 10 shows an example of the measured microtremor on the ground. In the numerical simulations, the band-limited white noise data is added to each floor response to take into account the influence of the measurement noise. The noise data are given independently at each floor in time domain. The ratio of root mean square (RMS) of the added noise to that of the floor responses without noise is given as 5% in all stories.
Stiffness Identification Using Theoretically Given Identification Function
In order to demonstrate the validity of the identification algorithm using both the S model and the SB model, the stiffness identifications of both Models A and B using the theoretical IDFs are investigated. The theoretical IDF can be derived from the dynamic equilibrium equation in the specified SB model. When the limit value of the IDF is provided as known parameters or identified parameters, there still exists the initial-value dependence problem in the identification procedure, where the bending stiffness in the first story and the stiffness ratio distribution for all stories are unknown parameters to identify. In order to overcome the initial-value dependence problem, a random search technique is introduced to obtain an appropriate combination of these unknown parameters as an initial value.
Figure 11 shows the minimization of the function in Eq. 6 for various initial values of the first story bending stiffness and the stiffness ratio by random search. The stiffness ratios are varied from 500 to 5000 in the Model A, and from 500 to 10,000 in the Model B. The stiffness ratio is assumed to be constant in all stories in the random searching. The error of the natural frequencies from the first mode to the third mode is used as the objective function defined in Eq. 6. As shown in Figure 11, the initial value of the bending stiffness in the first story can be selected from the combination which makes the objective function minimum. However, since the variation of the objective function is relatively small when the bending stiffness in the first story becomes larger than the specified bending stiffness, it may be difficult to determine an appropriate initial value depending on the structural properties.
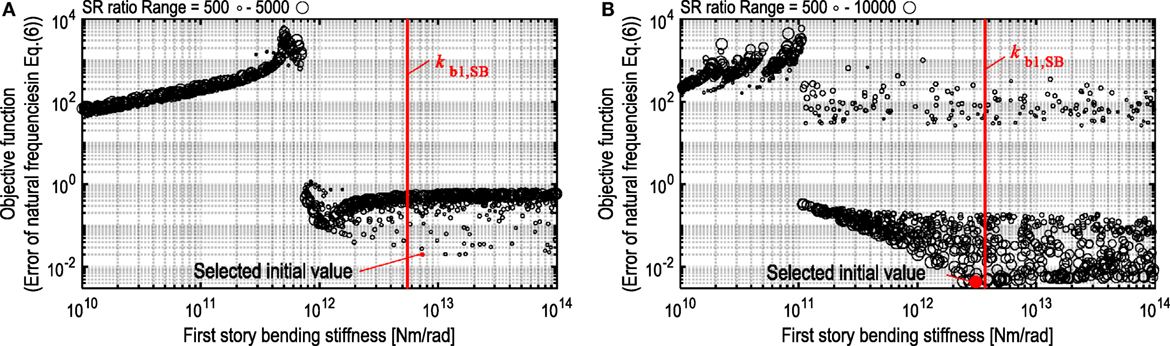
Figure 11. Minimization of function in Eq. 6 for various initial values of first story bending stiffness and stiffness ratio by random search: (A) Model A and (B) Model B.
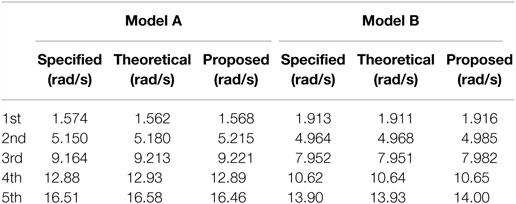
Figure 12 shows the identified shear and bending stiffnesses using the given IDF theoretically and the obtained initial values in Figure 11. The bending stiffnesses derived by the proposed identification method using both the S model and the SB model are compared with that by the previous SI method. From these figures, when the limit value of the IDF can be obtained in an accurate manner, the advanced SI method can provide reliable identification results. Table 2 shows the comparison of the natural frequencies (1st, 2nd, 3rd, 4th, and 5th modes) of the specified SB model with those derived by an eigenvalue analysis of the identified SB model.
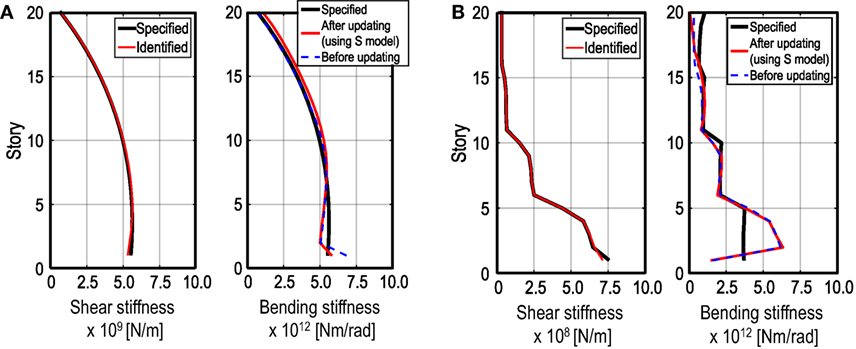
Figure 12. Stiffness identification using theoretical identification function of SB model: (A) Model A and (B) Model B.
Stiffness Identification Using Estimated Identification Function
In the application of the advanced SI method to actual buildings, it seems impossible to obtain the theoretical IDF. Therefore, it is important to enhance the accuracy of the estimation of the IDF. In this section, the stiffness identification is implemented by using numerically simulated structural response data including noise influence.
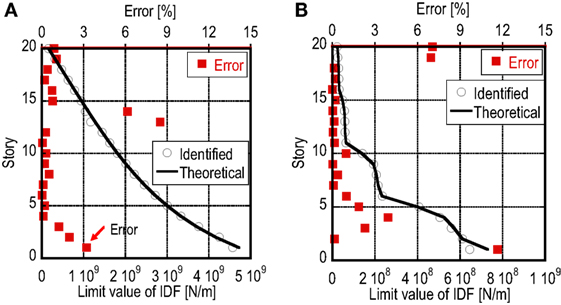
Figure 13 presents the comparison of the identified limit value with a theoretical one . In addition, the error of the identified limit value is also shown in these figures. It can be observed that the error defined by the following formula becomes relatively large in the lower stories.
Figure 14 shows the identified shear and bending stiffnesses using the estimated limit values of the IDF. It can be observed that there exist some differences in the identified stiffnesses compared with the specified stiffnesses. This difference may be related with the estimation error of the limit value of the IDF. As seen in Figure 14, the bending stiffnesses can be identified within an allowable accuracy by improving the accuracy of the limit value evaluation. The natural frequencies obtained by the eigenvalue analysis of the identified SB model are summarized in Table 2. In this table, the theoretical natural frequencies indicate that those values are derived from the identification results using theoretical IDF values. It can be seen that the SB model identified by the proposed procedures can provide accurate natural frequencies even in higher modes.
Discussion
In the numerical verification presented above, two different 20-story SB models have been identified. As shown in Figure 13, although the estimation error in the limit value of the IDF becomes large at some stories, i.e., the maximum error is 8.5% at the 13th-story in Model A and 11.6% at the first story in Model B, the identified shear and bending stiffnesses of the SB models are relatively accurate. Compared with the shear stiffness, the identified bending stiffness distribution is a little different from the specified distribution as shown in Figure 14. However, the natural frequencies from the first to fifth modes coincide well between the specified model and the identified model. This is because the bending stiffness of the SB model may have little influence on the lower natural frequencies.
The number of stories of the building is limited to the 20th story in this paper. In order to investigate the applicability of the advanced SI method to any number of stories, especially for buildings higher than the current verification, it is needed to inspect how accurately the limit value of the IDF can be estimated by this framework in the future study. Furthermore, when the building height is higher than the current model, the influence of the soil type and wind loadings on the stiffness identification should be investigated in more detail. It was reported that the SI method using the S model and the IDF for microtremor input on relatively soft soil can provide a reliable results (Fujita et al., 2015). On the other hand, the theoretical formulation to decrease the influence of the wind loading on the identification was studied by Koyama et al. (2015) for rather low-rise buildings. The theoretical formulations by Koyama et al. (2015) showed that the term of the floor mass can be included in the IDF as a compensated term for considering the influence of wind loading. The applicability to higher buildings should be discussed in more detail in the future.
Conclusion
The following conclusions have been derived.
(1) As an advanced stiffness identification method based on the shear-bending model (SB model), a new practical approach has been presented using both a shear model (S model) and a SB model to overcome the stability problem in the identification process in the previous SI method for the SB model. A practical advantage of the proposed method applied to actual buildings is that only simultaneous measurements at floors just above and below of the target inspecting story are needed to identify the structural properties, i.e., story stiffnesses. The IDF derived from such measurement is a powerful solution to identify the building using the S model. However, the stability problem in the identification, especially for the bending stiffness of the SB model, may come from the initial-value dependence problem in the optimization procedure and the inaccurate limit value evaluation of the IDF at ω = 0. The proposed practical procedure can resolve these problems by applying the reasonably designed filters and ARX model.
(2) The cut-off frequencies of the filters, e.g., high-pass or band-pass filters, have been determined by the proposed quantitative index guaranteeing the accuracy of the estimation of transfer functions. This quantitative index can provide the fitness of the estimated transfer function. Furthermore in the proposed identification method, the limit value of the IDF is statistically evaluated without selecting the number of orders of the ARX model. These practical procedures are helpful to evaluate the limit value of the IDF within certain accuracy. The accuracy of the limit value of the IDF can also be improved by modifying the fundamental natural frequency of the identified S model so as to be equal to the observed lowest natural frequency. This new approach to use the result of the identification of the S model is effective to implement the stable identification for the SB model.
(3) The theoretical formulations in the stiffness identification method using both the S model and SB model have been presented to evaluate the bending stiffness. This formulation is based on the assumption that the first-mode shape of the identified SB model should be similar to that of the identified S model. From the first mode of the identified S model, a shear force and an overturning moment in the first mode can be estimated. The bending stiffness of the SB model can then be obtained by substituting these estimated values into the equilibrium equation in the first mode.
Author Contributions
KF carried out the theoretical and numerical analysis. IT supervised the theoretical analysis.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Part of the present work is supported by the Grant-in-Aid for Scientific Research (KAKENHI) of Japan Society for the Promotion of Science (No. 16K18184, 15H04079). This support is greatly appreciated. Part of the numerical example was conducted by Mr. R. Koyama. His support is greatly appreciated.
References
Boller, C., Chang, F.-K., and Fujino, Y. (eds) (2009). Encyclopedia of Structural Control and Health Monitoring, Vol. 1–5. Chichester, UK: Wiley.
Brownjohn, J. M. W. (2003). Ambient vibration studies for system identification of tall building. Earth Eng. Struct. Dyn. 32, 71–95. doi:10.1002/eqe.215
Fujita, K., Ikeda, A., Shirono, M., and Takewaki, I. (2013). “System identification of high-rise buildings using shear-bending model and ARX model: experimental investigation,” in Proc. of ICEAS13 in ASEM 13, September 8–12, Jeju, Korea, 2803–2815.
Fujita, K., Ikeda, A., and Takewaki, I. (2015). Application of story-wise shear building identification method to actual ambient vibration. Front. Built Environ. 1:2. doi:10.3389/fbuil.2015.00002
Hart, G. C., and Yao, J. T. P. (1977). System identification in structural dynamics. J. Eng. Mech. Div. 103, 1089–1104.
Ikeda, A., Fujita, K., and Takewaki, I. (2014). Story-wise system identification of actual shear building using ambient vibration data and ARX model. Earthq. Struct. 7, 1093–1118. doi:10.12989/eas.2014.7.6.1093
Ikeda, A., Fujita, K., and Takewaki, I. (2015). Reliability of system identification technique in super high-rise building. Front. Built Environ. 1:11. doi:10.3389/fbuil.2015.00011
Koyama, R., Fujita, K., and Takewaki, I. (2015). Influence of wind disturbance on smart stiffness identification of building structure using limited micro-tremor observation. Struct. Eng. Mech. 56, 293–315. doi:10.12989/sem.2015.56.2.293
Kuwabara, M., Yoshitomi, S., and Takewaki, I. (2013). A new approach to system identification and damage detection of high-rise buildings. Struct. Control Health Monit. 20, 703–727. doi:10.1002/stc.1486
Maeda, T., Yoshitomi, S., and Takewaki, I. (2011). Stiffness-damping identification of buildings using limited earthquake records and ARX model. J. Struct. Constr. Eng. 666, 1415–1423. doi:10.3130/aijs.76.1415 (in Japanese)
Minami, Y., Yoshitomi, S., and Takewaki, I. (2013). System identification of super high-rise buildings using limited vibration data during the 2011 Tohoku (Japan) earthquake. Struct. Control Health Monit. 20, 1317–1338. doi:10.1002/stc.1537
Nagarajaiah, S., and Basu, B. (2009). Output only modal identification and structural damage detection using time frequency & wavelet techniques. Earthq. Eng. Eng. Vib. 8, 583–605. doi:10.1007/s11803-009-9120-6
Shinozuka, M., and Ghanem, R. (1995). Structural-system identification II: experimental verification. J. Eng. Mech. 121, 265–273. doi:10.1061/(ASCE)0733-9399(1995)121:2(265)
Takewaki, I., and Nakamura, M. (2000). Stiffness-damping simultaneous identification using limited earthquake records. Earth. Eng. Struct. Dyn. 29, 1219–1238. doi:10.1002/1096-9845(200008)29:8<1219::AID-EQE968>3.0.CO;2-X
Takewaki, I., and Nakamura, M. (2005). Stiffness-damping simultaneous identification under limited observation. J. Eng. Mech. 131, 1027–1035. doi:10.1061/(ASCE)0733-9399(2005)131:10(1027)
Takewaki, I., and Nakamura, M. (2009). Temporal variation of modal properties of a base-isolated building during an earthquake. J. Zhejiang Univ. Sci. A 11, 1–8.
Takewaki, I., Nakamura, M., and Yoshitomi, S. (2011). System Identification for Structural Health Monitoring. UK: WIT Press.
Udwadia, F. E., Sharma, D. K., and Shah, P. C. (1978). Uniqueness of damping and stiffness distributions in the identification of soil and structural systems. J. Appl. Mech. 45, 181–187. doi:10.1115/1.3424224
Keywords: system identification, high-rise building, shear-bending model, microtremor input, ARX model, identification function
Citation: Fujita K and Takewaki I (2016) Advanced System Identification for High-Rise Building Using Shear-Bending Model. Front. Built Environ. 2:29. doi: 10.3389/fbuil.2016.00029
Received: 27 September 2016; Accepted: 31 October 2016;
Published: 21 November 2016
Edited by:
Solomon Tesfamariam, University of British Columbia, CanadaCopyright: © 2016 Fujita and Takewaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kohei Fujita, Zm0uZnVqaXRhQGFyY2hpLmt5b3RvLXUuYWMuanA=
 Kohei Fujita
Kohei Fujita Izuru Takewaki
Izuru Takewaki