Project Discrepancies in Roadway Construction and Preservation: A Statistical Analysis of Public–Private Partnership Contract Types in the US

At the planning stage of a roadway construction or preservation project, public agencies face a crucial challenge; to adopt and implement the appropriate contractual framework that can minimize the anticipated project discrepancies, on the basis of project-specific conditions. Focusing on public–private partnerships (PPPs), a deeper understanding of the factors that affect each type of discrepancy can assist public agencies in thoroughly evaluating and comparing PPP options. This paper seeks to provide an empirical but comprehensive analysis on PPP-specific project discrepancies, by identifying influential factors that significantly affect cost savings, cost overrun, change orders, and time delays in roadway projects. Using data from 645 PPP projects implemented in the USA between 1996 and 2011, seven popular PPP contracting approaches in the USA were considered in the analysis, and a number of random parameters linear and non-linear statistical models were estimated by PPP approach. The results demonstrate that PPP-specific attributes such as project cost, size, types of constituent activities, and expected duration have mixed effects on the occurrence and the magnitude of each type of discrepancy.

Introduction

Over the last decades, public agencies have been facing challenges in constraining expenditure for new transportation infrastructure projects or for the preservation of the aging infrastructure. This has led to innovative and cost-efficient technological advancements, which has in turn motivated the development of alternative funding methods that combine the public sector’s experience with the private entities’ capital investment and risk undertaking. Public–private partnerships (PPPs) for roadway construction and preservation constitute a rapidly growing type of synergy (contractual agreement) formed between public agencies and private sector entities (Engel et al., 2011). In fact, more than 46 billion dollars were disbursed between 1990 and 2010 in the USA for transportation PPP projects (Rall et al., 2010), while over 150 billion euros were allocated to PPP transportation projects in the European Union between 2000 and 2015 (Tomasi, 2016). Despite the widespread use of PPPs, the majority of public agencies have yet to determine a comprehensive decision making framework with respect to appropriate PPP type selection for a given transportation project. The need for such framework is corroborated by the frequent presence of critical project cost and time discrepancies during the implementation phase of PPP contracts.

Project cost and time discrepancies constitute contractual aberrations of high interest to both public and the private entities, and typically include cost overrun, cost savings, change orders, and time delays (Bordat et al., 2004). Previous research has been devoted on the investigation of the influential factors for each of the aforementioned project discrepancies, independently of the PPP type. The goal of this paper is to provide a comprehensive comparison of the parameters affecting contract discrepancies of popular PPP types, such as cost-plus-time (A + B),¹ performance-based contracting (PBC),² incentives/disincentives (I/D),³ design–build–operate–maintain (DBOM),⁴ lane rentals,⁵ and warranties⁶ (Mallet, 2008; Anastasopoulos et al., 2010a; Papajohn et al., 2010).

The identification of discrepancy- and PPP-specific relationships (i.e., identification of parameters specific to each discrepancy and PPP type) aims to assist transportation agencies in deciding whether a particular PPP type is appropriate for a specific roadway construction or preservation project, in terms of minimizing discrepancies and maximizing benefits.

Review of Past Work

A significant amount of past research in PPP projects for roadway construction and preservation has focused on the identification of factors affecting cost savings, cost overrun, time delays, and change orders (Rowland, 1981; Hester et al., 1991; Majid and McCaffer, 1998; Jacoby, 2001; Ellis and Thomas, 2003; Fimpong et al., 2003; Flyvbjerg et al., 2003; Bordat et al., 2004; Odeck, 2004; Assaf and Al-Hejji, 2006; Gkritza and Labi, 2008; Anastasopoulos et al., 2010a,b,c, 2011, 2014; Serag et al., 2010; Ambituuni, 2011; Irfan et al., 2011; Cantarelli et al., 2012). For example, Odeck (2004) formulated a regression framework to investigate the factors affecting cost overrun in roadway construction projects and found that small-scale projects are more vulnerable to cost overrun. The effect of the project size along with other significant contract attributes on cost savings and cost overrun was also investigated by Anastasopoulos et al. (2010b, 2011, 2014), using data for different activity types and multiple PPP types. These studies identified the project duration as a major influential factor for the cost overrun or cost savings. Cost overrun was also examined with respect to the successive phases of the project development, with the stage between the decision for the project implementation and the beginning of the construction works being critical for the cost overrun (Cantarelli et al., 2012).

Time delay is another factor that results in project discrepancies, especially in long-term transportation projects. For example, Bordat et al. (2004) found that approximately 12% of the contracts let by the Indiana Department of Transportation between 1996 and 2001, had an approximate delay of 115 days. Majid and McCaffer (1998) considered several groups of factors related to project planning and development (e.g., labor, equipment, material, control, etc.) and identified and ranked 25 main causes that can result in non-excusable delays. A number of studies (Ellis and Thomas, 2003; Fimpong et al., 2003; Assaf and Al-Hejji, 2006; Ambituuni, 2011; Irfan et al., 2011) identified several factors as significant causes of time delays in highway construction projects, such as design errors, impact of weather, unpredicted site conditions, modifications in the design and the scope of the project, inefficient planning and scheduling procedures, poor technical performance, and deadline contract type, to name a few.

Finally, change orders in transportation projects pertain to modifications in the project’s scope, in terms of additional requirements, amount, time, and design method alterations. Several linear regression, discrete outcome, and count data modeling techniques have been used to identify possible influential factors that can affect change orders, such as the construction complexity of the project, site conditions, the project’s final cost, the difference between the initial cost estimation (by the agency) and the winning bid amount, design deficiencies, and weather conditions (Rowland, 1981; Hester et al., 1991; Jacoby, 2001; Anastasopoulos et al., 2010c; Serag et al., 2010).

Method and Approach

Two approaches are considered for the investigation of project discrepancies for roadway construction and preservation by PPP type. To explore the factors that affect the extent of project discrepancies for each PPP type, linear regression models are estimated for the percentage of cost savings and cost overrun, count data (Poisson) models are estimated for the change orders frequency, and hazard-based duration models are estimated for the time delay. At the pre-planning phase, many transportation agencies are as well interested in identifying factors affecting the likelihood that a project will incur project discrepancies (Gkritza and Labi, 2008; Anastasopoulos et al., 2010a, 2014). To that end, the likelihood of cost savings, cost overrun, change orders, and time delay occurrence is investigated, through the use of binary logit and probit models. Next, an overview of the methodological approaches is presented.

The percentage of cost savings, %CS_ki, and cost overrun, %CO_ki, for a project i performed under contract type k, are, respectively, calculated as follows:

$\%C{S}_{ki}=100\times [(C{B}_{ki}-C{A}_{ki})/\text{}C{B}_{ki}],$ (1)

and

$\%C{O}_{ki}=100\times [(C_{Fki}-C_{WBki})/\text{}{C}_{WBki}],$ (2)

where CB_ki is the final contract cost performed under traditional contracting (which is typically based on the amount of work being measured and paid for on agreed rates for various work items), CA_ki is the final contract cost of the project (including the same work items and project characteristics) performed under the PPP approach, C_WBki is the winning bid cost of the project, and C_Fki is the final project cost upon its completion and delivery to the agency. For the two dependent variables, %CS_ki and %CO_ki, the linear regression model can be specified as:

$\%C{S}_{ki}={\mathrm{\beta }}_{CSki}+{\mathrm{\beta }}_{CS}{\mathbf{\text{X}}}_{CSki}+{\mathrm{\epsilon }}_{CSki},$ (3)

and

$\%C{O}_{ki}={\mathrm{\beta }}_{COki}+{\mathrm{\beta }}_{CO}{\mathbf{\text{X}}}_{COki}+{\mathrm{\epsilon }}_{COki},$ (4)

where β_CSki and β_COki are constant terms, β_CO and β_CS are vectors of estimable parameters, X_CSki and X_COki are vectors of explanatory parameters, ε_CSki and ε_COki, are the disturbance terms, and all other terms as previously defined. With regard to the estimation of the vectors of parameters, the most common approach for the regression context is the ordinary least squares estimation (for an example, see Anastasopoulos et al., 2015). However, in order to account for unobserved heterogeneity across the observations, random parameters are introduced in model estimation, thus the maximum likelihood estimation method is adopted herein. Specifically, the log-likelihood functions, for the two dependent variables, are specified as (Washington et al., 2011):

$LL=-\frac{I}{2}\text{ln}(2\mathrm{\pi })-\frac{I}{2}\text{ln}({\mathrm{\sigma }}^2)-\frac{1}{2{\mathrm{\sigma }}^2}{(\%C{S}_{ki}-{\mathbf{\text{X}}}_{CSki}{\mathrm{\beta }}_{CS})}^{\mathrm{{\rm T}}}(\%C{S}_{ki}-{\mathbf{\text{X}}}_{CSki}{\mathbf{\beta }}_{CS})$ (5)

$LL=-\frac{I}{2}\text{ln}(2\mathrm{\pi })-\frac{I}{2}\text{ln}({\mathrm{\sigma }}^2)-\frac{1}{2{\mathrm{\sigma }}^2}{(\%C{O}_{ki}-{\mathbf{\text{X}}}_{COki}{\mathrm{\beta }}_{CO})}^{\mathrm{{\rm T}}}(\%C{O}_{ki}-{\mathbf{\text{X}}}_{COki}{\mathrm{\beta }}_{CO})$ (6)

where I is the number of observations, σ² is the variance of the normally distributed error terms, and all other terms are as previously defined. The maximization of the log-likelihood function yields the best specified parameter estimates of the linear regression model.

Given that a project time delay has occurred, the length of the delay can be statistically modeled as duration data using hazard-based duration modeling methods. To model the conditional probability of a project delay terminating at time t (under the condition that it has not terminated until then), a hazard function that accounts for the effect of explanatory variables is specified as (Washington et al., 2011):

$h\left(t|\mathbf{\text{X}}\right)=h_0\left(t\right)\text{exp}\left(-\mathrm{\beta }\mathbf{\text{X}}\right),$ (7)

where h₀(t) is the baseline hazard (denoting the hazard when all elements of the explanatory variables vector are zero), and all other terms as previously defined. The underlying hazard function in Eq. 5 can take various parametric forms, such as Exponential, Weibull, and Log-logistic (Anastasopoulos et al., 2012, 2017). For model estimation, all three parametric forms were explored, and the Weibull model provided the best statistical fit (in terms of goodness-of-fit measures, such as log-likelihood function at convergence, McFadden pseudo-R², and Akaike Information criteria). For the Weibull model, with parameters λ > 0 and P > 0, the density function is (Washington et al., 2011):

$f(t)=\mathrm{\lambda }P{(\mathrm{\lambda }t)}^{P-1}\text{exp}\left[-{(\mathrm{\lambda }t)}^P\right]$ (8)

and the baseline hazard in Eq. 5 becomes:

$h\left(t\right)=\mathrm{\lambda }P{\left(\mathrm{\lambda }t\right)}^{P-1}.$ (9)

The Weibull model yields monotonically increasing or decreasing (over time) hazard functions, on the basis of the estimable Weibull parameter P. If P is greater than one, the hazard monotonically increases with the delay duration, indicating that the probability of a project delay terminating at time t increases over time; the opposite is observed, if P is less than one, since the hazard function monotonically decreases with the delay duration, indicating that the probability of a project delay terminating at time t decreases over time. For the estimation of the vector of parameters β, a maximum likelihood estimation method is adopted.

The frequency of change orders can be modeled using count data modeling approaches, such as the Poisson and negative binomial models, and their zero-inflated counterparts (Anastasopoulos et al., 2010c). For model estimation, all count data modeling techniques were explored, and the Poisson model gave the best overall statistical fit (in terms of goodness-of-fit measures, such as log-likelihood function at convergence, ρ², Vuong statistic, and Akaike Information criteria). For the Poisson model, the probability, P(n_i), of contract, i, to incur n change orders is (Washington et al., 2011):

$P\left(n_i\right)=\frac{\text{exp}\left(-{\mathrm{\lambda }}_i\right){\mathrm{\lambda }}_i^{n_i}}{n_i!},$ (10)

where λ_i = exp(βX_i) is the expected number of change orders, and all other terms as previously defined. For model estimation, a maximum likelihood estimation method was employed, with the corresponding log-likelihood function being defined as:

$LL(\mathrm{\beta })=\underset{i=1}{\overset{I}{{\displaystyle \mathrm{\Sigma }}}}\left[-\text{exp}(\mathrm{\beta }{\mathbf{{\rm X}}}_i)+y_i\mathrm{\beta }{\mathbf{{\rm X}}}_i-LN(y_i!)\right]$ (11)

where y_i is the frequency of change orders with expected value E(y_i) = λ_i, and all other terms as previously defined. Since there is not dispersion in the data, the maximum likelihood estimates of the Poisson model yield unbiased and consistent parameters.

For the likelihood of cost savings, cost overrun, change orders, and time delay occurrence, binary (since only two outcomes are considered: discrepancy and non-discrepancy occurrence) logit and probit models can be used (Washington et al., 2011). The fundamental difference between the two logit and probit approaches arises from the assumed distribution of the error terms. For the logit specification, the disturbances are assumed to be Gumbel-extreme value Type I distributed, whereas, for the probit specification, the disturbances are assumed to be normally distributed. The binary logit outcome probabilities are thus defined as (Washington et al., 2011):

$P_{ki}\left(D\right)=\frac{1}{1+\text{exp}\left[-\left({\mathrm{\beta }}_D{\mathbf{\text{X}}}_{D_{ki}}\right)\right]},$ (12)

and the binary probit outcome probabilities as:

$P_{ki}\left(D\right)=\mathrm{\Phi }\left[\frac{{\mathrm{\beta }}_D{\mathbf{\text{X}}}_{D_{ki}}-{\mathrm{\beta }}_{ND}{\mathbf{\text{X}}}_{N{D}_{ki}}}{\mathrm{\sigma }}\right],$ (13)

where P_ki(D) is the probability of observation, i, in PPP approach, k, incurring a discrepancy, D, or no discrepancy, ND, in terms of cost savings, cost overrun, time delay, or change orders, Φ(.) is the standardized cumulative normal distribution, and σ is a scaling parameter (which is typically set to one) that determines the discrete outcomes. For the estimation of the parameter vectors β_D and β_ND, standard maximum likelihood estimation methods are used (Washington et al., 2011). Specifically, for the probit model specification, the log-likelihood function is:

$LL={\displaystyle \sum _{i=1}^I\left[{\mathbf{\beta }}_D{\mathbf{\text{X}}}_{D_{ki}}-LN{{\displaystyle \mathrm{\Sigma }}}_{\forall J}\text{exp}({\mathbf{\beta }}_{JD}{\mathbf{\text{X}}}_{J{D}_i})\right]};$ (14)

whereas, for the logit model specification, the log-likelihood function is defined as:

$LL=\underset{i=1}{\overset{N}{{\displaystyle \mathrm{\Sigma }}}}({\mathrm{\delta }}_{Di}LN\mathrm{\Phi }\left(\frac{{\mathrm{\beta }}_D{\mathbf{\text{X}}}_{D_{ki}}-{\mathrm{\beta }}_{ND}{\mathbf{\text{X}}}_{N{D}_{ki}}}{\mathrm{\sigma }}\right)+(1-{\mathrm{\delta }}_{Di})LN\mathrm{\Phi }\left(\frac{{\mathrm{\beta }}_D{\mathbf{\text{X}}}_{D_{ki}}-{\mathrm{\beta }}_{ND}{\mathbf{\text{X}}}_{N{D}_{ki}}}{\mathrm{\sigma }}\right))$ (15)

where δ_Di is equal to 1 if the observation i incurs a discrepancy, D, or zero otherwise, N denotes the number of observations, and the other terms are as previously defined.

To account for unobserved heterogeneity—a common misspecification issue—the effect of the parameters of the aforementioned modeling schemes is allowed to vary across the observations, through the use of random parameters modeling. This is an important consideration, as if unobserved heterogeneity is not addressed, the parameter estimates can be erroneous, the inferences inconsistent, and the forecasts inaccurate (Washington et al., 2011; Russo et al., 2014; Anastasopoulos, 2016; Anastasopoulos and Mannering, 2016; Mannering et al., 2016; Sarwar et al., 2016, 2017). In random parameters modeling, the coefficients become:

${\mathrm{\beta }}_n=\mathrm{\beta }+{\mathrm{\omega }}_n,$ (16)

where β_n is a vector of estimable parameters, and ω_n is a randomly distributed term (for example, a normally distributed term with mean zero and variance σ²). Under this consideration, β_n is a vector of individual parameters across observations, with its variation to be described by a density function—also referred as mixing distribution—q(β|ω), where ω refers to a vector of parameters of the density distribution (Greene, 2007; Washington et al., 2011; Anastasopoulos et al., 2012). To address the added complexity by the inclusion of random parameters in the computation of outcome probabilities, a simulation-based maximum likelihood estimation approach is employed. Specifically, various values of βs are drawn from the density function q(β|ω) and are used for the computation of the logit (or probit) outcome probabilities, as shown in Eqs 12 and 13. Numerous iterations of the same procedure provide the corresponding simulated probabilities, which are, in turn, introduced in the simulated log-likelihood function (Washington et al., 2011). As far as the sampling technique of β values from the mixing distribution is concerned, the technique of Halton draws (Halton, 1960) is employed, which can provide efficient probability approximations, by limiting the number of draws to the smallest possible extent; the non-random selection of draws provide more robust estimates, as compared to the use of purely random draws (see Bhat, 2003; Train, 2003; Washington et al., 2011, for further details on the simulation approach). For model estimation, 200 Halton draws are used, which have been shown to yield stable and accurate parameter estimates (Bhat, 2003; Milton et al., 2008; Anastasopoulos et al., 2016). For the functional form of the parameter density function, normal, Weibull, lognormal, uniform, and triangular distributions were considered in model estimation, and the normal distribution yielded the best specified model results, in terms of statistical fit. It should be noted that a parameter is considered as random when the mean and the SD of the parameter density function are statistically different from zero, at a pre-specified level of confidence (at a 0.90 level of confidence herein).

Empirical Setting

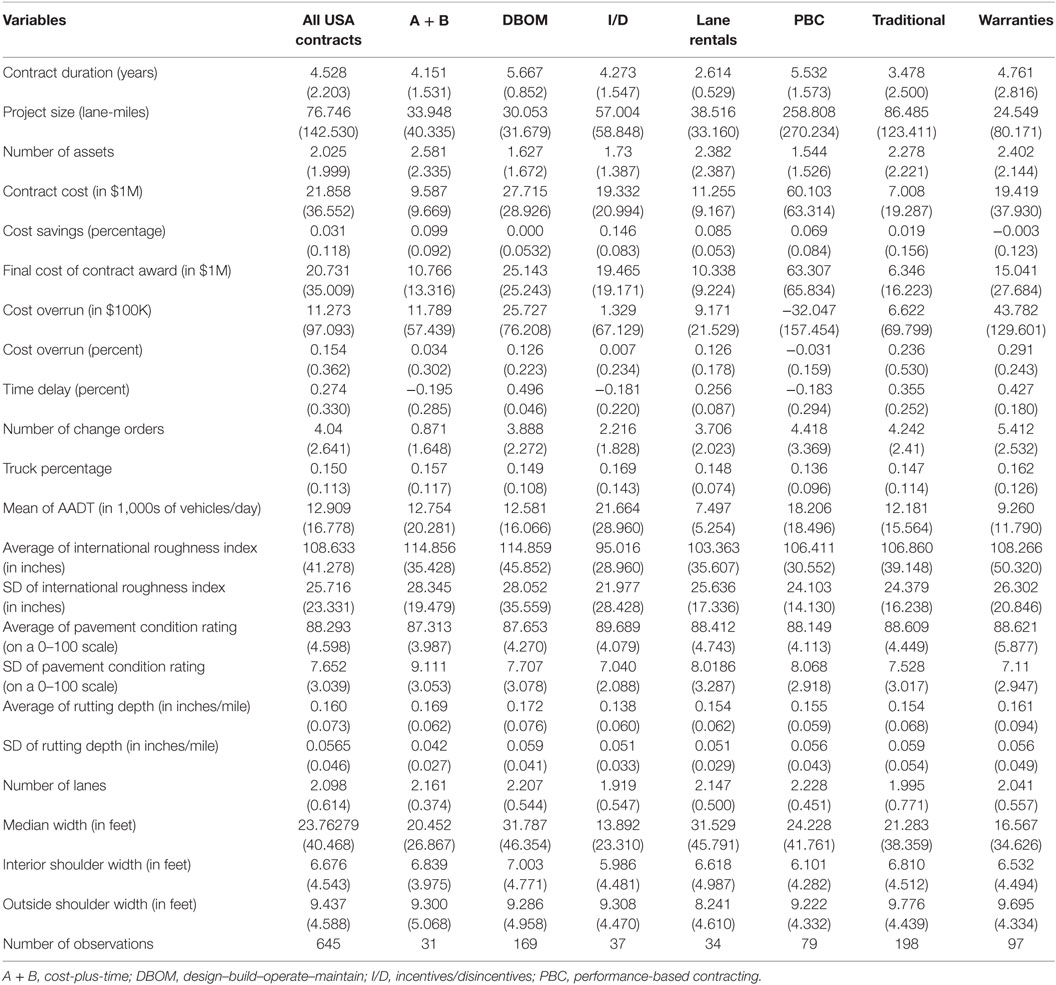
To identify the factors that affect the extent and likelihood of project discrepancies, cost- and project-specific data are used. These data have been published in previous studies (Anastasopoulos et al., 2010a, 2011; Nahidi, 2015; Nahidi et al., 2015; Sarwar and Anastasopoulos, 2016a,b) and have since been extended to include new information, in terms of the number of contracts and of the independent variables (i.e., pavement, traffic safety, and operations characteristics). Specifically, the data include information for 645 PPP contracts implemented in the USA between 1996 and 2011. In addition to traditional outsourcing contracts, six popular PPP types are represented in the data, namely, cost-plus-time (A + B), PBC, I/D, DBOM, lane rentals, and warranties. These data also include cost and time-related information (contract cost, bid cost, number of bids, cost savings, cost overrun/underrun, time delay, number of change orders and associated costs, etc.); contract duration (and extension); roadway functional classification and roadway geometrics (segment length, number of lanes, median and shoulder attributes, drainage rating, and horizontal/vertical alignment characteristics); pavement characteristics (roughness, rutting depth, and pavement condition rating); traffic characteristics (annual average daily traffic, level of service, and truck traffic); weather conditions (precipitation and temperature); and number of assets (constructed or preserved) included in the contract. In addition, these data contain information about the scope and activity type of the project (e.g., construction, repair, maintenance, and management activities), as well as the asset type (e.g., pavements, bridges, roadway cross-section elements, traffic infrastructure, landscape, and emergency facilities). Table 1 presents descriptive statistics of key variables. For a detailed description of the dataset, see Nahidi (2015) and Nahidi et al. (2015).

TABLE 1

Table 1. Descriptive statistics of key variables (average values, with SDs in parentheses).

Model Estimation Results

Tables 2–9 present the estimation results of the best model specifications (several variables and variable combinations were explored, and the ones that provided the best overall statistical fit—in terms of goodness-of-fit measures—are presented herein), along with their goodness-of-fit measures, for the extent and likelihood of project discrepancies by PPP type. The subsequent sections provide a brief discussion of the model estimation results for each discrepancy type. Note that, for brevity, key results (including only a few random parameters) are discussed in detail.

TABLE 2

Table 2. Random parameters linear regression model estimation results for cost savings percentage (t-stats in parentheses).

TABLE 3

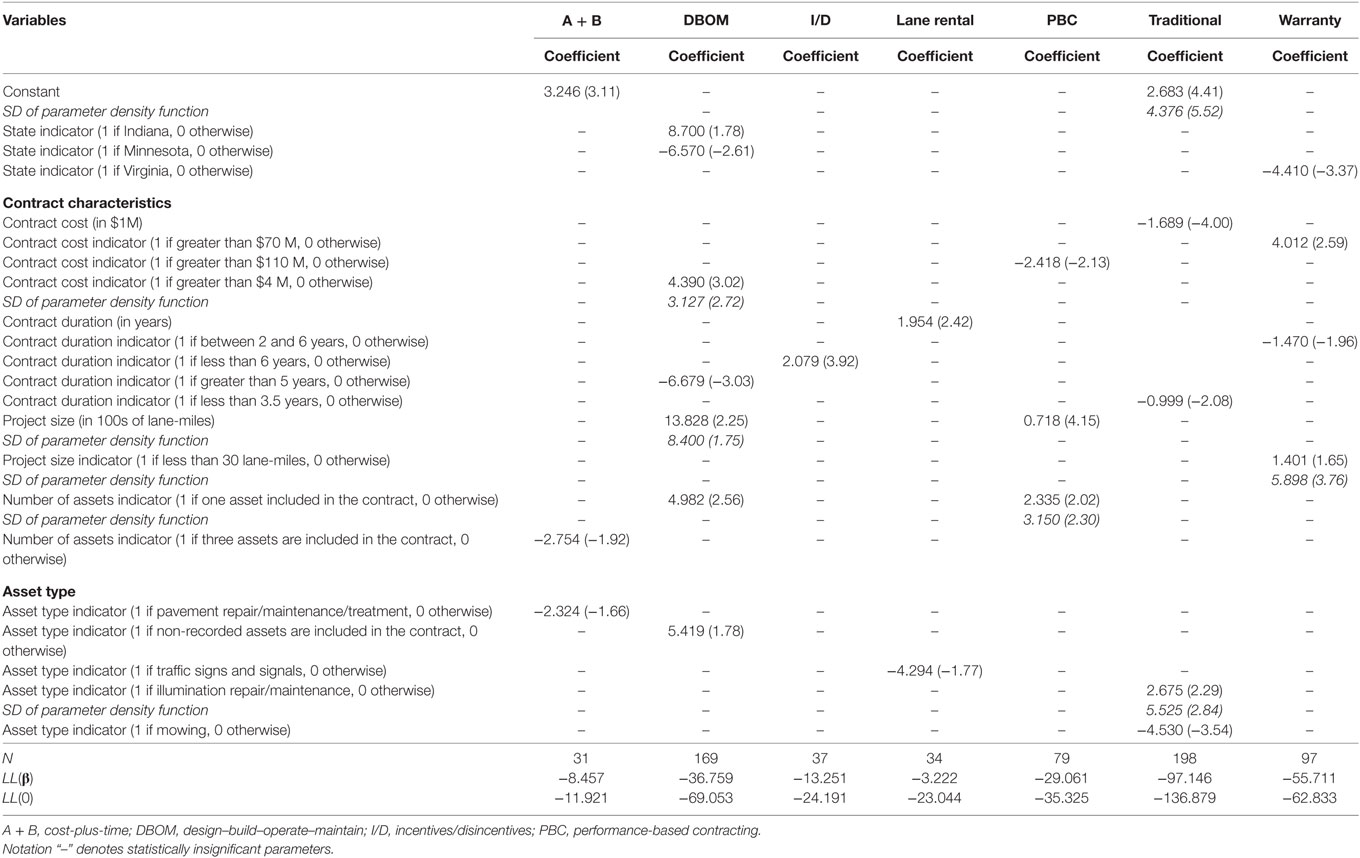
Table 3. Random parameters binary logit model estimation results for cost savings occurrence (t-stats in parentheses).

TABLE 4

Table 4. Random parameters linear regression model estimation results for cost overrun percentage (t-stats in parentheses).

TABLE 5

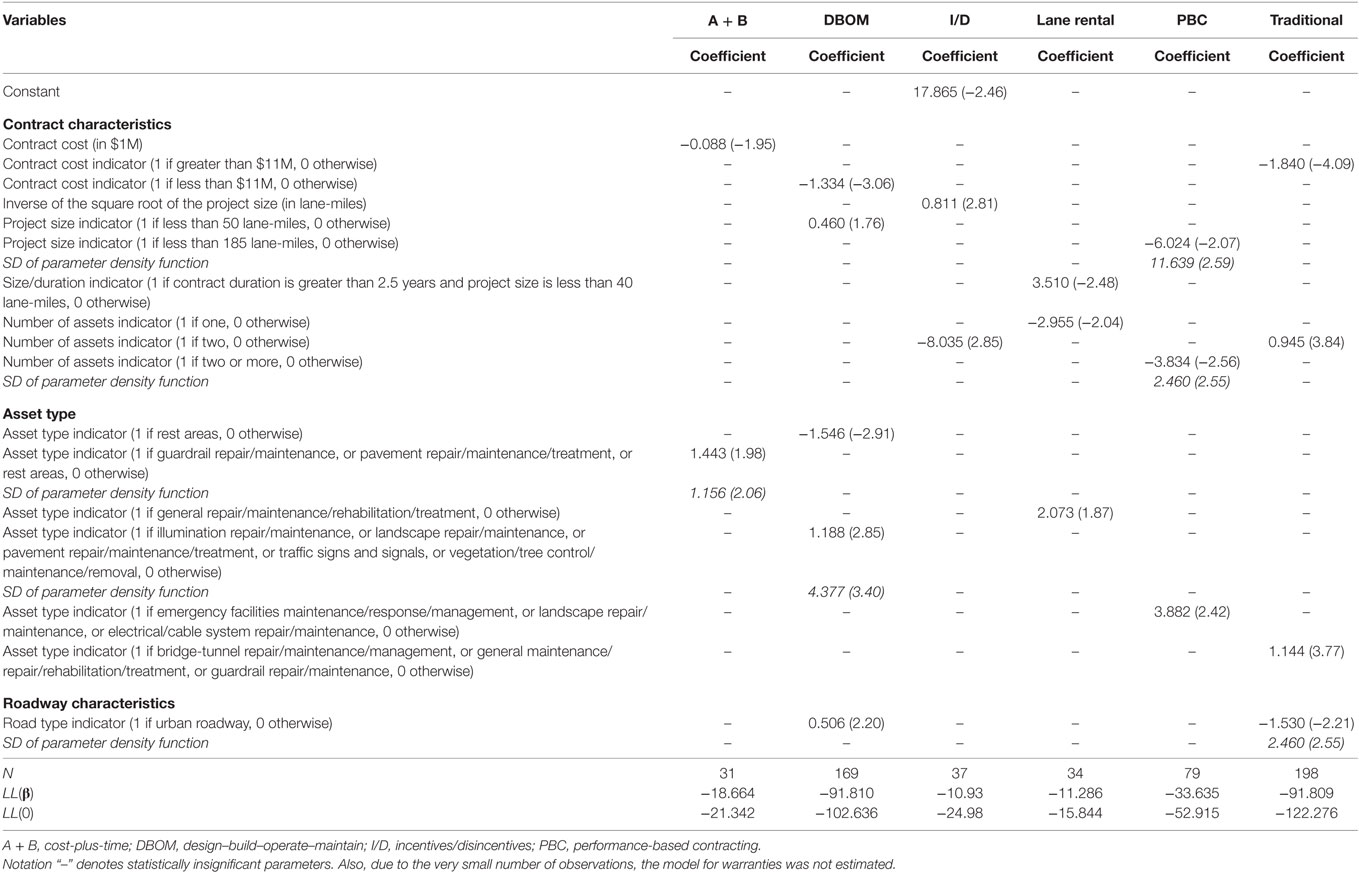
Table 5. Random parameters binary probit model estimation results for cost overrun occurrence (t-stats in parentheses).

TABLE 6

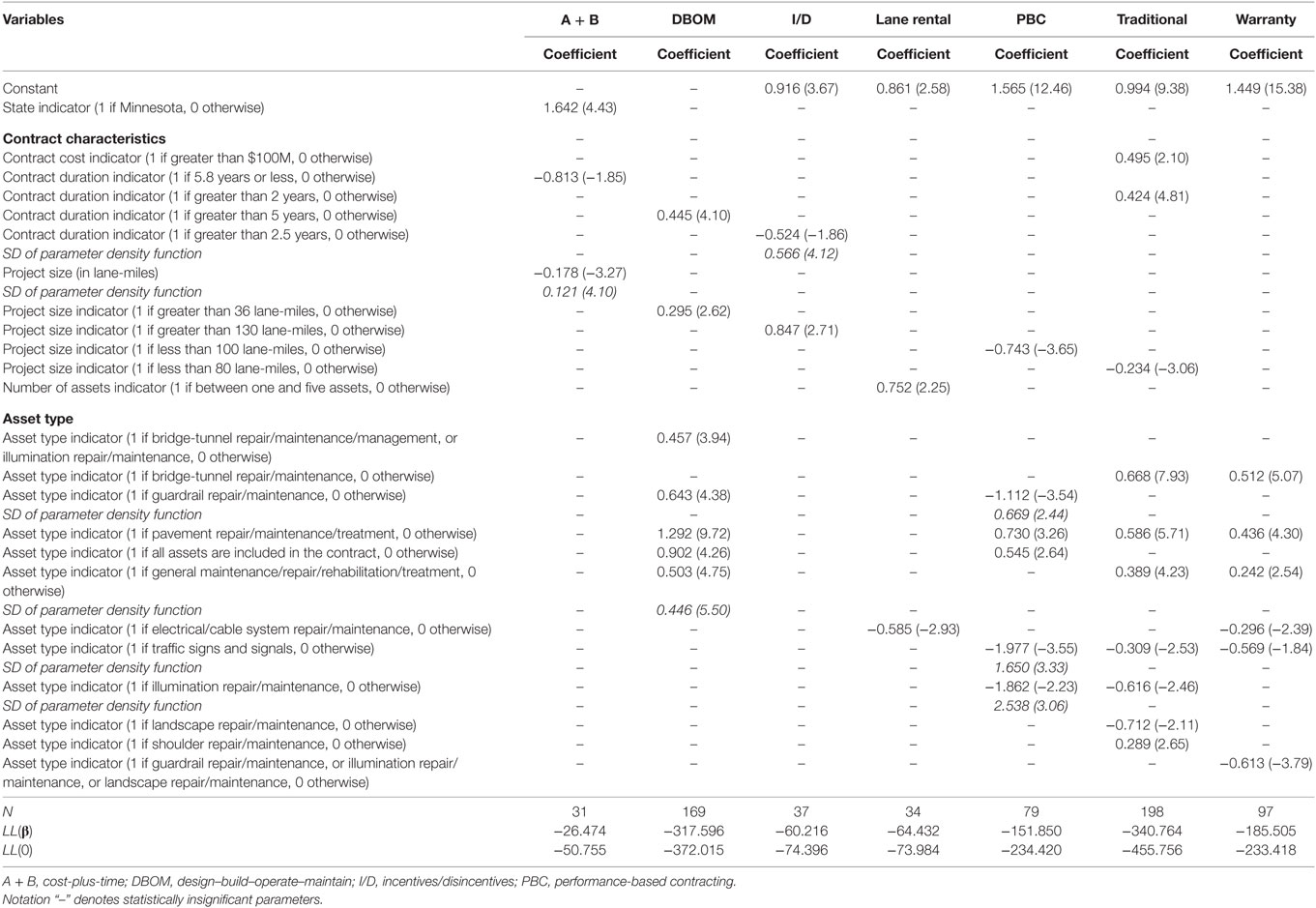
Table 6. Random parameters Poisson model estimation results for change orders frequency (t-stats in parentheses).

TABLE 7

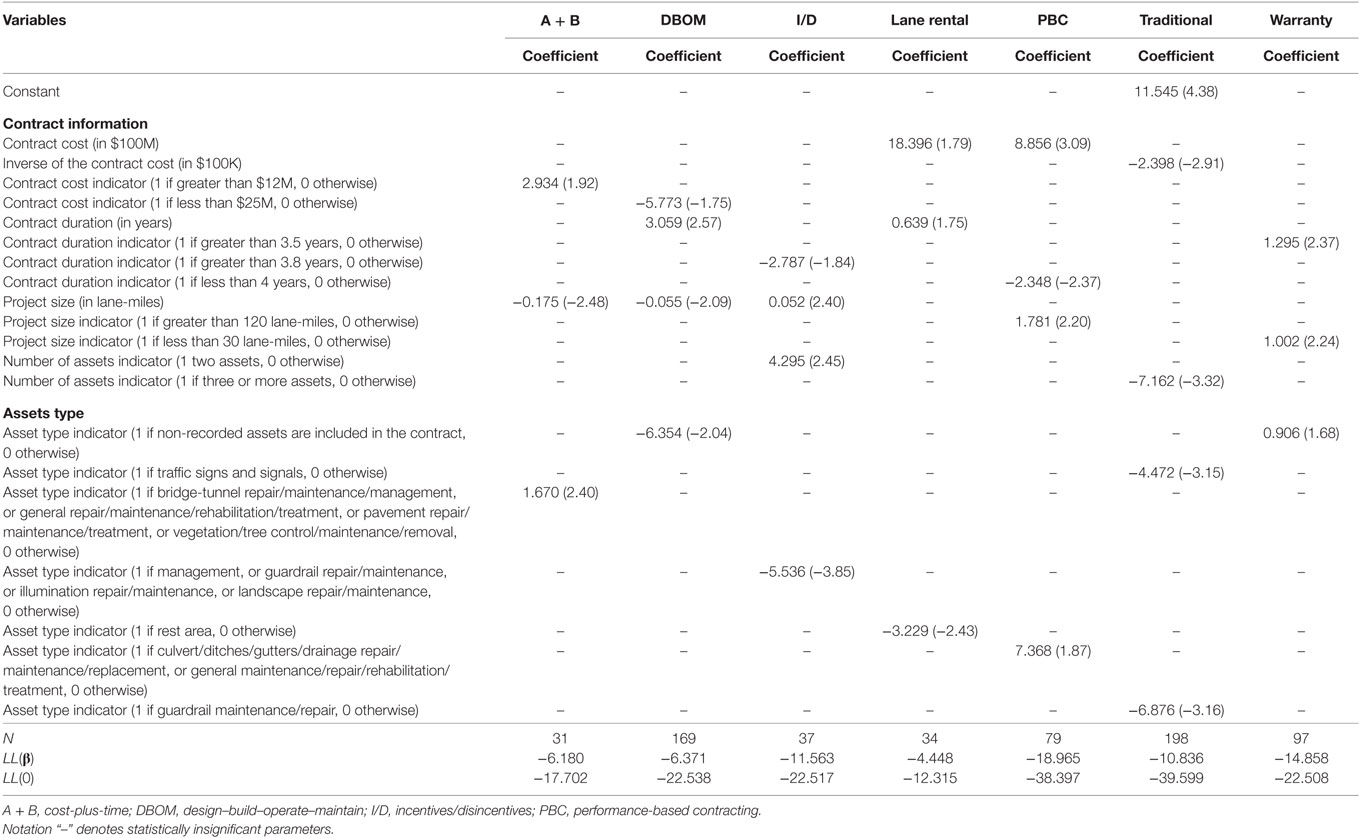
Table 7. Binary logit model estimation results for change orders occurrence (t-stats in parentheses).

TABLE 8

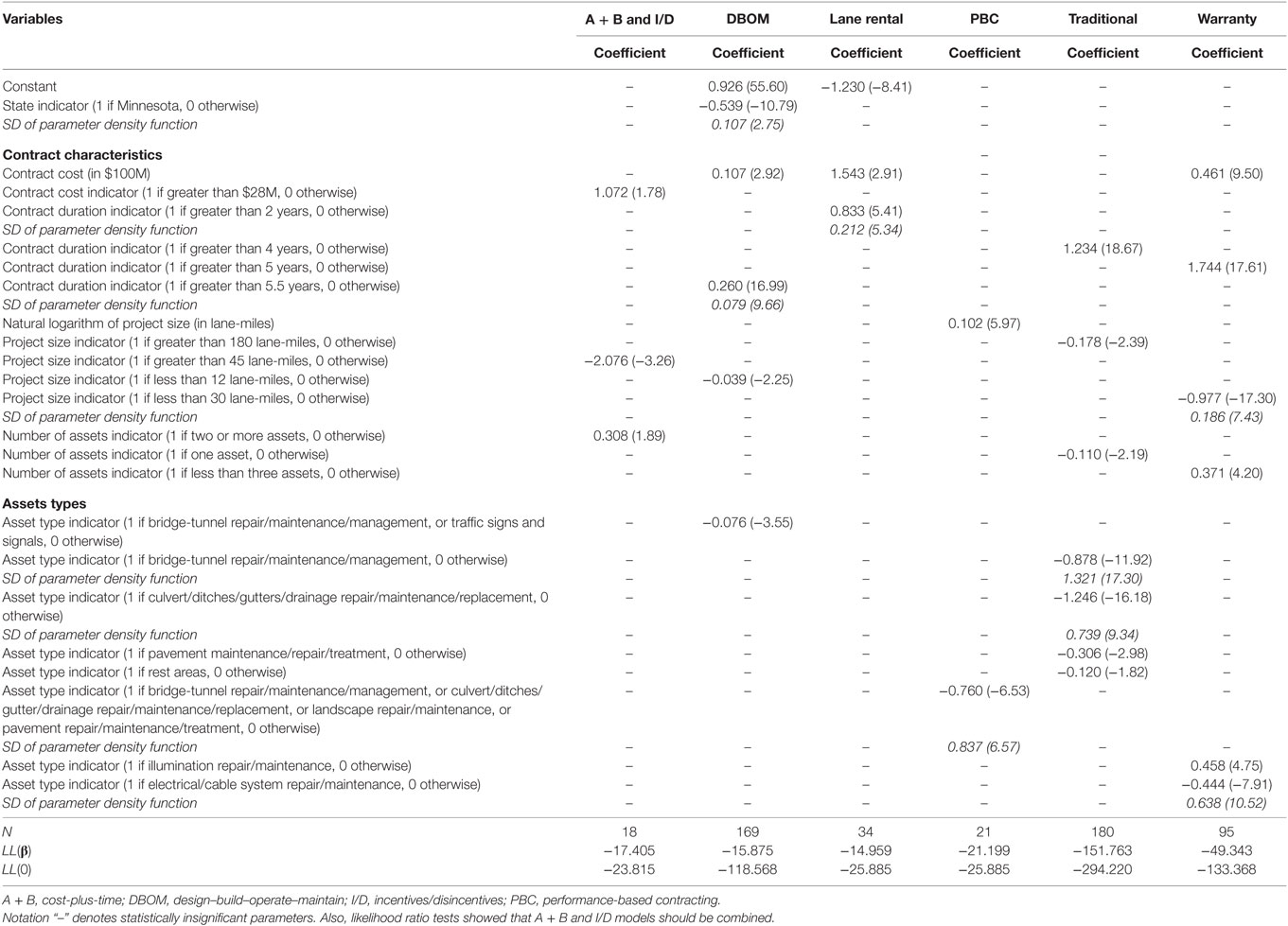
Table 8. Random parameters duration (Weibull) model estimation results for time delay (t-stats in parentheses).

TABLE 9

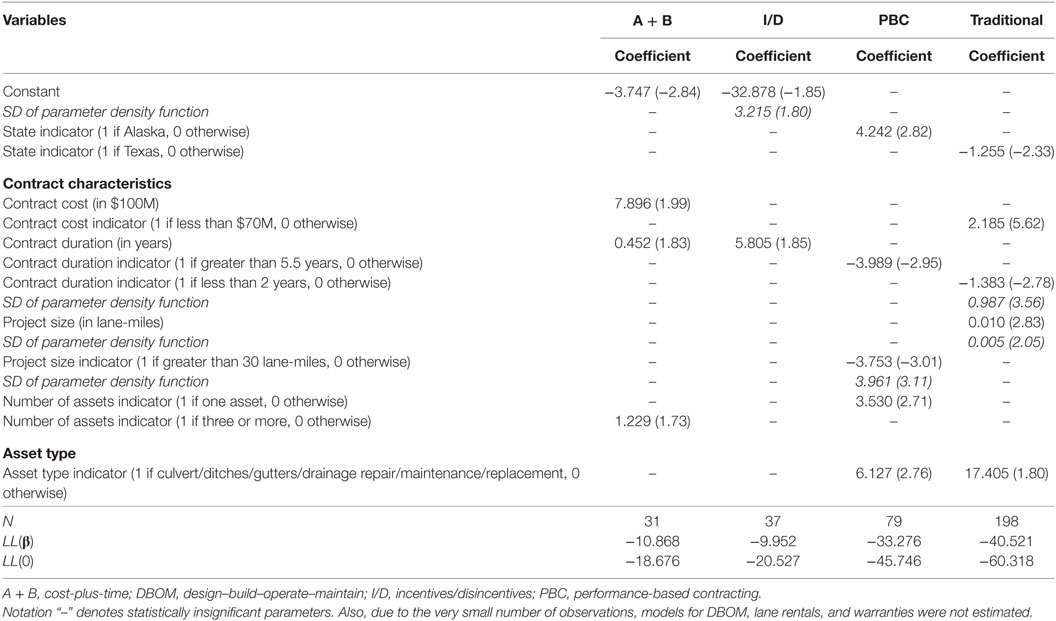
Table 9. Random parameters binary logit model estimation results for time delay occurrence (t-stats in parentheses).

Cost Savings

Tables 2 and 3 presents the model estimation results of the random parameters linear regression and binary logit models, for the percentage and likelihood of cost savings, respectively. The results show that project size (in terms of outsourced lane-miles) has mixed effects on cost savings. For example, large size projects decrease the percentage of cost savings for DBOM, I/D, and warranties; while, they decrease the percentage of cost savings for 72% of A + B contracts (for 28% of these contracts, they increase the cost savings), and for 68% of PBCs (for 32% they increase the cost savings for PBCs). Contract duration is also found to be an influential factor. Contracts with duration of more than 2 years decrease cost savings for warranties, traditional, DBOM, and A + B contracts. Cost savings percentage is as well affected by the number of outsourced assets, with three or more outsourced assets generally reducing cost savings. The findings are in line with the literature (Anastasopoulos et al., 2010b,d, 2014).

Furthermore, the results show that high cost contracts (with a total final cost exceeding $11.5M) increase cost savings for DBOM, while low-cost contracts (with a total final cost of $600K or less) increase cost savings for lane rentals. The activity type also plays a significant role in cost savings. For example, pavement related activities (such as pavement repair, maintenance, and treatment) increase the percentage of cost savings under DBOM contracts; while cross-section specific activities (such as culvert, ditches, gutters, or drainage repair, maintenance, or replacement; or mowing, vegetation, or tree control maintenance or removal) increase cost savings for lane rentals and PBCs. On the contrary, activities such as culvert, ditches, gutters or drainage repair, maintenance or replacement, and guardrail repair, reduce cost savings for I/Ds, while mowing and litter removal reduce cost savings for warranties. These findings are in line with previous studies (Anastasopoulos et al., 2010d, 2014).

Turning to the results of the random parameters (mixed) binary logit models, the likelihood of cost savings occurrence is affected by a number of location-specific factors. For example, warranties and DBOM contracts in Virginia and Minnesota, respectively, are more likely to incur loss; while, DBOM contracts in Indiana are more likely to incur cost savings. Interestingly, the likelihood of cost savings occurrence for DBOM, I/D, and warranties decreases, when the contract duration increases; whereas the opposite effect is observed for lane rentals.

Moreover, project size (in terms of lane-miles) is found to significantly affect the likelihood of cost savings occurrence. Large size DBOM, PBC, and traditional projects are more likely to incur cost savings; while, short size (less than 30 lane-miles) warranty projects are more likely to incur cost savings. The contract cost is found to have mixed effects on the likelihood of cost savings occurrence. For example, PBC contracts exceeding $110M in final cost are less likely to incur cost savings, whereas, high cost warranties (greater than $70M) and medium- to low-cost DBOM ($4M or less) are more likely to incur cost savings. The results also show that PBC and DBOM contracts with only one outsourced activity are more likely to incur cost savings. This finding likely captures the effect of smaller projects, which are typically less prone to cost and time discrepancies.

With respect to the specific activity types included in the contract, mowing is found to reduce the likelihood of cost savings occurrence in traditional contracts. This is an indication that mowing may favor outsourcing under a different PPP option, as, for example, PBC (Anastasopoulos et al., 2010d). Pavement maintenance or rehabilitation activities for A + B contracts are likely to reduce the likelihood of cost savings occurrence. At the same time, illumination repair and maintenance for warranty contracts has mixed effects on the likelihood of cost savings occurrence. These findings are in accordance with previous research (Anastasopoulos et al., 2010d, 2014).

Cost Overrun

Tables 4 and 5 present the model estimation results of the random parameters linear regression and binary probit models, for the percentage and likelihood of cost overrun, respectively. As with the cost savings models, the results show that project size (in terms of outsourced lane-miles) has mixed effects on cost overrun. For instance, large size PBC projects reduce cost overrun; whereas, for 86 and 30% of A + B and warranties, respectively, large size projects increase cost overrun (while, for the remaining 14 and 70% of A + B and warranties, respectively, large size projects reduce cost overrun). The results also show that contract duration (measured in years) has mixed effects on I/D and PBC cost overrun. Long duration contracts (greater than 4 years) reduce PBC cost overrun for the majority (66%) of the contracts and increase it for the minority (34%) of the contracts, while, as the contract duration increases, I/D cost overrun decreases for 88% of the contracts and increases for the remaining 12%. Contract cost is also found to have mixed effects on cost overrun. As the PBC and A + B final cost increases, cost overrun also increases in 72% of PBC and 93% of A + B contracts, and decreases for the remaining 28 and 7% of these contracts, respectively. Whereas an increase in I/D final cost is found to constantly reduce cost overrun for all contracts.

Moving to the effect of the number of activities and activity types on cost overrun, A + B and traditional contracts with one or three activities, respectively, increase cost overrun for 88 and 91% of the contracts, and reduce it for the remaining 12 and 9% of the contracts, respectively. In contrast, DBOM contracts with less than three activities increase the cost overrun, but the magnitude of the increase varies across the contracts. Crack/pothole sealing and repair, or emergency facilities maintenance and repair, are found to increase cost overrun for 77% of warranty contracts, and reduce it for the remaining 23%—possibly capturing location-specific heterogeneity, whereas pavement repair, maintenance, or treatment reduce cost overrun of warranty contracts. This result is intuitive, considering the wide use of warranties for pavement work (Bordat et al., 2004). Another interesting finding pertains to bridge and tunnel repair, maintenance or management (activities that are both expensive and comprehensive), which are found to decrease the DBOM and I/D cost overrun. In such large projects, contractors are likely overbidding, to account for minor change orders or other factors that can possibly lead to cost overrun. On the contrary, contractors may infrequently underestimate low-cost activities (e.g., electrical cable and system maintenance, guardrail repair and maintenance, landscape, and illuminations repair and maintenance, to name a few), and bid lower to get the award. To that end, the results show that such low-cost activities generally increase cost overrun.

As far as the likelihood of cost overrun occurrence is concerned, the estimation results of the random parameters (mixed) binary probit models show that the final cost of the contract has mixed effects on the outcome probabilities. Traditional contracts with a final cost of $11M or greater are less likely to incur cost overrun; DBOM contracts with a final cost of less than $11M are less likely to incur cost overrun; and as the final cost of A + B contracts increases, the likelihood of cost overrun decreases. Examining the impact of project size (in terms of lane-miles), the results show that for DBOM, I/D, and lane rentals, shorter size projects are more likely to incur cost overrun. While, for 70% of PBC contracts with less than 185 lane-miles, the likelihood of cost overrun occurrence decreases, and increases for the remaining 30%.

Activity type also plays an important role in determining the likelihood of cost overrun occurrence, with pavement and guardrail repair and maintenance increasing the cost overrun likelihood in 90% of A + B contracts, and decreasing it for the remaining 10%. In addition, bridge-tunnel activities, and general maintenance, repair, and rehabilitation, are found to generally increase the likelihood of cost overrun occurrence. DBOM contracts implemented in urban areas are less likely to incur cost overrun for their majority (73% of contracts), and more likely for a small minority (27%) of contracts—likely picking up region-specific heterogeneity. It should be noted that warranty contracts are found to be generally associated with a higher cost overrun likelihood, as compared to the other PPP types.

Change Orders

Tables 6 and 7 presents the model estimation results of the random parameters Poisson and binary logit models, for the frequency and likelihood of change orders, respectively. The results show that a variety of factors affect the frequency and likelihood of change orders occurrence. For example, A + B contracts in Minnesota have a higher change orders frequency, which is possibly capturing the effect of unobserved factors, such as design errors or weather conditions. The duration of the contract also plays an important role in change orders occurrence. A + B contracts with a duration of 5.8 years (derived as the mean A + B contract duration plus 1 SD) or less have a lower change orders frequency; traditional and DBOM contracts with a duration of 2 or more and 5 or more years, respectively, have a higher change orders frequency; and I/D contracts with a duration of 2.5 years or greater have a lower change orders frequency for 82% of the contracts, and a higher for the remaining 18%. Project size (in lane-miles) has varying effects on change orders occurrence, due to the unique attributes of each PPP type. As the A + B project size increases, the change orders frequency decreases for 93% of the contracts, and increases for the remaining 7%; however, DBOM, I/D, PBC, and traditional large size projects are likely to incur higher change orders frequency. With respect to activity types, bridge-tunnel, guardrail, pavement, and general repair and maintenance are all found to increase change orders frequency for PPP contracts. However, assets related to repair, maintenance and treatment of the electrical cable system, illumination, landscape, traffic signs, and signals are found to decrease the change orders frequency.

The binary logit model estimation results show that large size (in terms of lane-miles) A + B, DBOM, and warranty projects are less likely to incur change orders, while, for the remaining of the PPP types, large size projects are more likely to incur change orders. In a similar fashion, the likelihood of change orders occurrence increases with the project’s cost (as the cost increases, the likelihood of change orders occurrence also increases). For most of the PPP types, longer contracts in terms of duration (in years) are more likely to incur change orders. Activities such as illumination maintenance and repair, litter removal, vegetation or tree control, maintenance and removal, traffic signs and signals, guardrail repair, and maintenance and rest areas, are all found to generally decrease the likelihood of change orders occurrence for I/D, lane rentals, traditional, and warranty contracts. On the other hand, activities such as bridge-tunnel repair, maintenance and management, pavement repair, maintenance and treatment, culvert, ditches gutter and drainage system repair, maintenance, let under A + B and PBC, are more likely to incur change orders.

Time Delay

Tables 8 and 9 presents the model estimation results of the random parameters Weibul hazard-based duration and binary logit models, for the duration and likelihood of time delay, respectively. Project size (measured in lane-miles) is found to have various effects on the duration of time delay. For warranties, PBC, and DBOM contracts, an increase in the size of the project increases time delay; however, under some PPP types, such as A + B, I/D, and traditional contracts, large size projects reduce time delay. Furthermore, time delay is intuitively affected by the contract duration, with a contract duration increase resulting in successive increases in time delay. This result is likely capturing the effect of larger projects, which can frequently be more comprehensive, and for which a minor change in the project’s original scope is likely to result in time delay. With respect to the effect of contract final cost, contracts with higher final costs are intuitively found to have greater time delay (Bordat et al., 2004; Anastasopoulos et al., 2012). The number of activities and activity types are also crucial in determining the duration of time delay. With the exception of warranties, contracts with three or more activities increase the duration of time delay for all other PPP types. At the same time, activities such as bridge-tunnel, culvert, ditches, gutters and drainage system repair, and maintenance decrease the duration of time delay. These findings are in line with past research (Anastasopoulos et al., 2010a).

The random parameters (mixed) binary logit model estimation results of time delay occurrence show that, for the majority of the PPP types, comprehensive contracts with long duration, large size (in lane-mile terms), and high cost are more likely to incur time delay. In addition, A + B contracts with two or more assets are more likely to incur time delay; while, PBC contracts with two or more assets are less likely to incur time delay. With respect to the contract location, traditional contracts in Texas are less likely to incur time delay; in contrast, PBC contracts in Alaska are more likely to incur time delay. This result may be capturing weather or region-specific heterogeneity. Activity type is another important determinant of the likelihood of time delay occurrence, with contracts that include culvert, ditches, gutters and drainage repair, maintenance and replacement activities, being more likely to incur time delay. As a final point, all warranty, lane rental, and DBOM contracts are found to have higher likelihood of time delay occurrence.

Summary and Conclusion

This paper seeks to provide an empirical analysis of the influence of contract, project, and roadway characteristics on common project discrepancy types (cost savings, cost overrun, change orders, and time delay), for popular roadway construction and preservation PPP contract types [traditional outsourcing, cost-plus-time (A + B), DBOM, I/D, lane rentals, PBC, and warranties]. The presented comprehensive statistical modeling framework allows the identification of factors that affect both the extent (typically used by transportation agencies in the planning phase) and the likelihood (frequently used by transportation agencies in the pre-planning phase) of project discrepancies, while accounting for unobserved factors that can vary systematically across the observations (i.e., unobserved heterogeneity). The factors that affect the extent of project discrepancies for each PPP type, are statistically modeled with random parameters linear regression models (for the cost savings and cost overrun percentages), with random parameters count data (Poisson) models (for the change orders frequency), and with random parameters hazard-based duration (Weibull) models (for the time delay duration). While random parameters (mixed) binary logit and probit models are estimated to investigate the factors affecting the likelihood of cost savings, cost overrun, change orders, and time delay occurrence.

Table 10 provides a qualitative overview of the various factors affecting the extent and the likelihood of project discrepancies, by PPP type. Although the analysis does not aim to yield explicit guidelines regarding the adoption of the most appropriate PPP type, it has the potential to provide significant insights with regard to the effectiveness of each PPP type, in the context of different project discrepancies and several contract- and project-specific characteristics. The model estimation results show that contracts with longer duration generally incur lower cost savings and have lower cost savings occurrence likelihood. Longer contract duration also results in cost overrun, time delay, and change orders increase. For most of the PPP types (A + B, DBOM, PBC, and I/D), large size projects incur a reduction in cost savings, and an increase in cost overrun and time delay; while, for DBOM, PBCs, and traditional contracts, large size projects incur an increase in change orders frequency. Furthermore, in cases of high contract cost, DBOM, I/D, and warranties are found to increase cost savings; the opposite holds for lane rentals, PBCs, and traditional contracts. The number and type of assets (constructed or preserved) included in a contract also play an important role in project discrepancies by PPP type. A general finding is that contracts with many assets incur lower cost savings, and higher cost overrun and time delay. On the other hand, the activity types have varying effects on project discrepancies for each PPP type. For example, activities such as guardrail, shoulder repair and maintenance, traffic signs and signals, and electrical and cable repair and maintenance, perform better (in terms of cost savings, cost overrun, change orders, and time delay) when they are let under lane rentals. In contrast, crack and pothole sealing, and pavement repair and maintenance, perform better (in terms of cost related discrepancies) when they are let under warranties. In addition, contracts with generally low-cost activities (such as mowing, vegetation, tree control, or landscape repair and maintenance) perform better when they are let either under lane rentals or warranties. Whereas, contracts with many and variable activities such as general management, or bridge repair and maintenance, perform better (in terms of most project discrepancies) when they are let under PBC.

TABLE 10

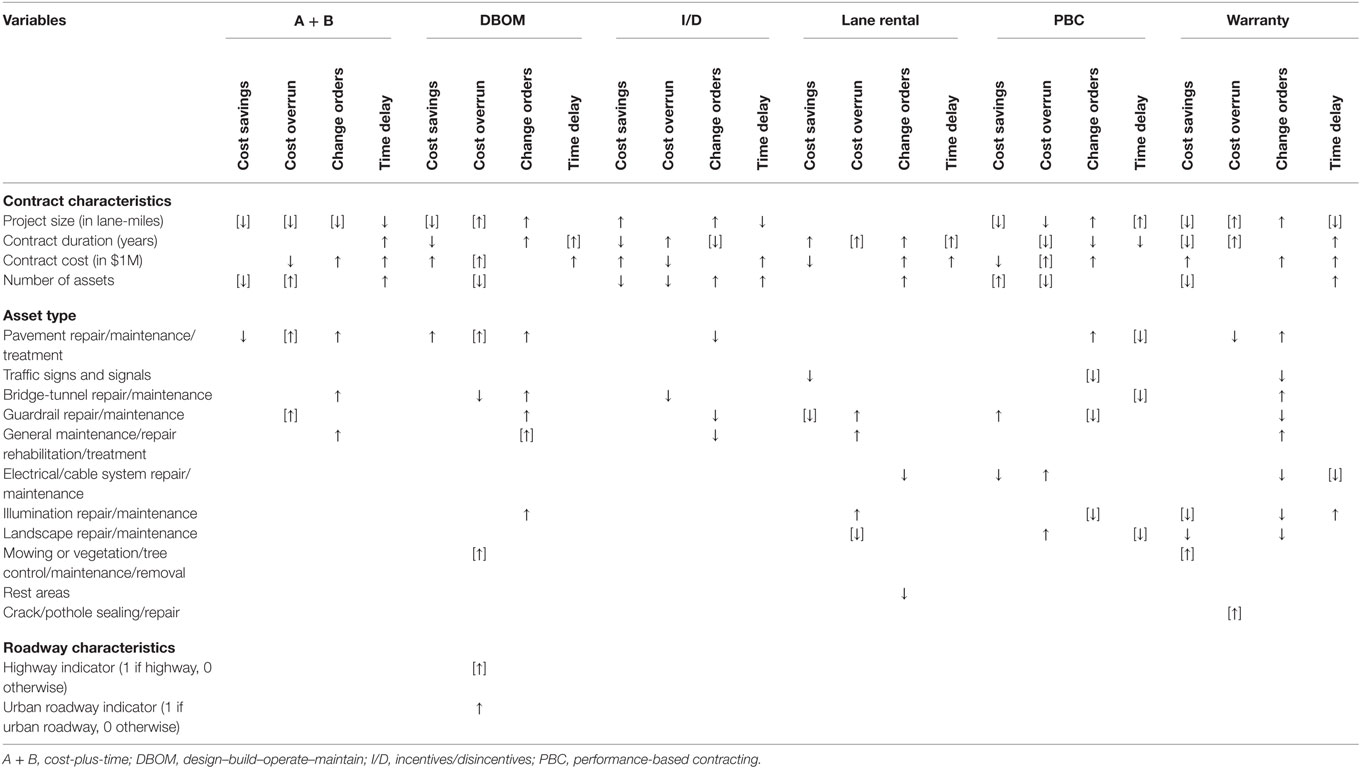
Table 10. Summary of the variable effect on the project discrepancies by public–private partnership type (brackets reveal mixed effects).

In an overall assessment, large-scale roadway projects (in terms of size, duration, cost and number of assets included) may favor the adoption of PBC or I/D; on the contrary, roadways projects associated with tighter deadlines or with activities requiring high level of expertise may be better accomplished under the DBOM or the warranty contractual approaches. The latter PPP types involve significant risk transfer to the contractors, which might act as incentive toward the minimization of cost- or time-related discrepancies. However, these general findings should be carefully assessed by Public Agencies and contractors in conjunction with various location-, time-, and detailed project-specific factors, which introduce considerable heterogeneity in the decision making process.

Unlike previous studies that have investigated project discrepancies separately and—to a large extent—irrespective of the PPP type, this study provides a comprehensive framework that allows identification of various project, contract, and roadway characteristics for all project discrepancies and some of the most popular PPP types. In this context, the selection of an appropriate PPP type for a given transportation (construction or preservation) project at the planning or pre-planning phase, can be informatively supported by the attributes of the factors that are likely to affect each (separately) or all (collectively) of the project discrepancy types.

In all, this empirical study should be viewed as an incremental step toward the development of decision-making guidelines for the adoption of various PPP types, as a function of project discrepancies and several contract, project, and roadway characteristics. Extension of this work could include the collection of PPP contracts from existing regions or from regions not explored in the current study, and development of more robust statistical models with a greater number of observations. The simultaneous statistical modeling—as a system of equations—of the extent of the four different project discrepancy types could also serve as a direction for future work, as it would possibly account for common unobserved factors underlying in the error terms (in the form of cross-equation error correlation).

Author Contributions

All authors contributed in the preparation and the completion of the submitted paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

The research work presented in this paper was supported by the Region 2 UTRC (Project No 49997-42-25). The contents of this paper reflect the views of the authors, who are responsible for the facts and the accuracy of the data presented herein. The contents do not necessarily reflect the official views or policies of any agency, nor do the contents constitute a standard, specification, or regulation.

Footnotes

1. ^Under the cost-plus-time contracting method, Agencies employ the initial construction/maintenance cost and the total project duration, as fundamental criteria for awarding the project to the contractor (Choi et al., 2013; Anastasopoulos et al., 2014).
2. ^Performance-based contracting (PBC) constitutes a more flexible method for contractors, since only the required—in the final stage—physical conditions of the project are specified in the contracting agreement; thus, the evaluation of the final project deliverables, in terms of several pre-agreed performance standards, constitutes the basic criterion for the payment of the contractor (Anastasopoulos et al., 2014).
3. ^Incentives/Disincentives (I/D) provide monetary awards to contractors for early project completion, and discourage delays or unsubstantiated extensions through imposing penalties.
4. ^In the design-build-operate-maintain approach, the contractor undertakes the processes of designing, constructing, operating and preserving the roadway (over a pre-specified period of time), with the public entity holding the ultimate ownership of the infrastructure (Abdel-Aziz, 2007).
5. ^Over the last years, lane rentals are primarily preferred for projects with ongoing operation of the roadway, throughout the entire project duration. Specifically, the contractor is charged with an additional cost in order to “rent” existing lanes or shoulders, in an effort to reduce the total project duration (Anastasopoulos et al., 2014).
6. ^Warranties introduce contractor’ responsibilities for possible deficiencies or inconsistencies with the pre-determined performance standards of the project; therefore, the contractor is strongly encouraged to deliver a high-quality infrastructure, in order to minimize the anticipated maintenance or rehabilitation cost, during the warranty period (Singh et al., 2007).

References

Abdel-Aziz, A. M. (2007). A survey of the payment mechanisms for transportation DBFO projects in British Columbia. Constr. Manage. Econ. 25, 529–543. doi:10.1080/01446190601161465

CrossRef Full Text | Google Scholar

Ambituuni, A. (2011). “Causes of project delay and cost overrun, and mitigation approach,” in Presented to the Robert Gordon University in Partial Fulfillment of the Award of MSc Project Management (Aberdeen, UK).

Google Scholar

Anastasopoulos, I., Anastasopoulos, P. Ch., Agalianos, A., and Sakellariadis, L. (2015). Simple method for real-time seismic damage assessment of bridges. Soil Dyn. Earthquake Eng. 78, 201–212. doi:10.1016/j.soildyn.2015.07.005

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch. (2016). Random parameters multivariate tobit and zero-inflated count data models: addressing unobserved and zero-state heterogeneity in accident injury-severity rate and frequency analysis. Anal. Methods Accid. Res. 11, 17–32. doi:10.1016/j.amar.2016.06.001

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., Fountas, G., Sarwar, M. T., Karlaftis, M., and Sadek, A. (2017). Transport habits of travelers using new energy type modes: a random parameters hazard-based approach of travel distance. Transp. Res. C. doi:10.1016/j.trc.2017.01.017

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., Haddock, J., and Peeta, S. (2014). Cost overrun in public-private partnerships: toward sustainable highway maintenance and rehabilitation. ASCE J Constr. Eng. Manage. 140, 04014018. doi:10.1061/(ASCE)CO.1943-7862.0000854

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., Islam, M., Volovski, M., Powell, J., and Labi, S. (2011). Comparative evaluation of public-private partnerships in roadway preservation. Transp. Res. Rec. 2235, 9–19. doi:10.3141/2235-02

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., Labi, S., Bhargava, A., and Mannering, F. L. (2012). Empirical assessment of the likelihood and duration of highway project time delays. J. Constr. Eng. Manage. 138, 390–398. doi:10.1061/(ASCE)CO.1943-7862.0000437

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., Labi, S., McCullouch, B. G., Karlaftis, M. G., and Moavenzadeh, F. (2010a). Influence of highway project characteristics on contract type selection: an empirical assessment. J. Infrastruct. Syst. 16, 323–333. doi:10.1061/(ASCE)IS.1943-555X.0000035

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., Florax, R., Labi, S., and Karlaftis, M. G. (2010b). Contracting in highway maintenance and rehabilitation: are spatial effects important? Transp. Res. A Policy Prac. 44, 136–146. doi:10.1016/j.tra.2009.12.002

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., Labi, S., Bhargava, A., Bordat, C., and Mannering, F. L. (2010c). Frequency of change orders in highway construction using alternate count-data modeling methods. ASCE J. Constr. Eng. Manage. 136, 886–893. doi:10.1061/(ASCE)CO.1943-7862.0000198

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., McCullouch, B., Gkritza, K., Mannering, F. L., and Sinha, K. C. (2010d). Cost savings analysis of performance-based contracts for highway maintenance operations. ASCE J. Infrastruct. Syst. 16, 251–263. doi:10.1061/(ASCE)IS.1943-555X.0000012

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., and Mannering, F. L. (2016). The effect of speed limits on drivers’ choice of speed: a random parameters seemingly unrelated equations approach. Anal. Methods Accid. Res. 10, 1–11. doi:10.1016/j.amar.2016.03.001

CrossRef Full Text | Google Scholar

Anastasopoulos, P. Ch., Sarwar, M. T., and Shankar, V. (2016). Safety-oriented pavement performance thresholds: accounting for unobserved heterogeneity in a multi-objective optimization and goal programming approach. Anal. Methods Accid. Res. 12, 35–47. doi:10.1016/j.amar.2016.10.001

CrossRef Full Text | Google Scholar

Assaf, S. A., and Al-Hejji, S. (2006). Causes of delay in large construction projects. Int. J. Project Manage. 24, 349–357. doi:10.1016/j.ijproman.2005.11.010

CrossRef Full Text | Google Scholar

Bhat, C. R. (2003). Simulation estimation of mixed discrete choice models using randomized and scrambled Halton sequences. Transp. Res. B 37, 837–855. doi:10.1016/S0191-2615(02)00090-5

CrossRef Full Text | Google Scholar

Bordat, C., McCullouch, B. G., Labi, S., and Sinha, K. C. (2004). An Analysis of Cost Overruns and Time Delays of INDOT Projects. Publication no. FHWA/IN/JTRP-2004/7, SPR-2811. Washington, DC: Transportation Research Board.

Google Scholar

Cantarelli, C. C., Molin, E. J. E., van Wee, B., and Flyvbjerg, B. (2012). Characteristics of cost overruns for Dutch transport infrastructure projects and the importance of the decision to build and project phases. Transp. Policy 22, 49–56. doi:10.1016/j.tranpol.2012.04.001

CrossRef Full Text | Google Scholar

Choi, S., Kim, D., Han, S., and Kwak, Y. (2013). Conceptual cost-prediction model for public road planning via rough set theory and case-based reasoning. ASCE J. Constr. Eng. Manage. 139, 04013026. doi:10.1061/(ASCE)CO.1943-7862.0000743

CrossRef Full Text | Google Scholar

Ellis, R. D., and Thomas, H. R. (2003). “The root causes of delays in highway construction,” in 82nd Annual Meeting of the Transportation Research Board (Washington, DC: Transportation Research Board).

Google Scholar

Engel, E., Fischer, R., and Galetovic, A. (2011). Public-Private Partnerships to Revamp US Infrastructure. Washington, DC: Hamilton Policy Brief, Brookings Institution.

Google Scholar

Fimpong, Y., Oluwoye, J., and Crawford, L. (2003). Causes of delay and cost overrun in construction of ground water project in developing countries: Ghana as a case study. Intern. J. Project Manage. 21, 321–326. doi:10.1016/S0263-7863(02)00055-8

CrossRef Full Text | Google Scholar

Flyvbjerg, B., Shamris Holm, M. K., and Buhl, S. L. (2003). How common and how large are cost overruns in transport infrastructure projects? Transp. Rev. 23, 71–88. doi:10.1080/01441640309904

CrossRef Full Text | Google Scholar

Gkritza, K., and Labi, S. (2008). Estimating cost discrepancies in highway contracts: multistep econometric approach. J. Constr. Eng. Manage. 134, 953–962. doi:10.1061/(ASCE)0733-9364(2008)134:12(953)

CrossRef Full Text | Google Scholar

Greene, W. (2007). Limdep, Version 9.0. Plainview, NY: Econometric Software, Inc.

Google Scholar

Halton, J. (1960). On the efficiency of certain quasi-random sequences of points in evaluating multi-dimensional integrals. Numerische Mathematik 2, 84–90. doi:10.1007/BF01386213

CrossRef Full Text | Google Scholar

Hester, W. T., Kuprenas, J. A., and Chang, T. C. (1991). Construction Changes and Change Orders: Their Magnitude and Impact. Source Document 66. Austin, TX: Construction Industry Institute, The University of Texas at Austin.

Google Scholar

Irfan, M., Khurshid, M. B., Anastasopoulos, P. Ch, Labi, S., and Moavenzadeh, F. (2011). Planning-stage estimation of highway project duration on the basis of anticipated project cost, project type, and contract type. Int. J. Project Manage. 29, 78–92. doi:10.1016/j.ijproman.2010.01.001

CrossRef Full Text | Google Scholar

Jacoby, C. (2001). Report on Supplemental Agreement Reasons, AASHTO FHWA Project Cost Overrun Study. Washington, DC: Federal Highway Administration, U.S. Department of Transportation.

Google Scholar

Majid, M. A., and McCaffer, R. (1998). Factors of non-excusable delays that influence contractors’ performance. J. Manage. Eng. 14, 42–49. doi:10.1061/(ASCE)0742-597X(1998)14:3(42)

CrossRef Full Text | Google Scholar

Mallet, W. J. (2008). Public-Private Partnerships in Highway and Transit Infrastructure. Rep. RL34567. Washington, DC: Congressional Research Service.

Google Scholar

Mannering, F. L., Shankar, V., and Bhat, C. R. (2016). Unobserved heterogeneity and the statistical analysis of highway accident data. Anal. Methods Accid. Res. 11, 1–16. doi:10.1016/j.amar.2016.04.001

CrossRef Full Text | Google Scholar

Milton, J. C., Shankar, V., and Mannering, F. L. (2008). Highway accident severities and the mixed logit model: an exploratory empirical analysis. Accid. Anal. Prev. 40, 260–266. doi:10.1016/j.aap.2007.06.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Nahidi, S. (2015). Evaluation of Public-Private Partnership Contract Types for Roadway Construction, Maintenance and Rehabilitation. [Master’s Thesis], University at Buffalo, The State University of New York, Buffalo, NY.

Google Scholar

Nahidi, S., Androutselis, T., Golshani, N., Sarwar, M. T., Eker, U., Anastasopoulos, P. Ch., et al. (2015). “Evaluation of public-private partnership contract types for roadway construction and preservation,” in Technical Report for the University Transportation Research Center-Region II, Project Number 49997-42-25 (Buffalo, NY: University at Buffalo, The State University of New York).

Google Scholar

Odeck, J. (2004). Cost overruns in road construction—what are their sizes and determinants? Transp. Policy 11, 43–53. doi:10.1016/S0967-070X(03)00017-9

CrossRef Full Text | Google Scholar

Papajohn, D., Cui, Q., and Bayraktar, M. E. (2010). Public-private partnerships in US transportation: research overview and a path forward. J. Manage. Eng. 27, 126–135. doi:10.1061/(ASCE)ME.1943-5479.0000050

CrossRef Full Text | Google Scholar

Rall, J., Reed, J. B., and Farber, N. J. (2010). Public-Private Partnerships for Transportation: A Toolkit for Legislators. Washington, DC: National Conference of State Legislatures. Available at: http://www.ncsl.org/documents/transportation/PPPTOOLKIT.pdf

Google Scholar

Rowland, H. J. (1981). The Causes and Effects of Change Orders on the Construction Process. [MS thesis], Georgia Institute of Technology, Atlanta, GA.

Google Scholar

Russo, B., Savolainen, P., Schneider, W., and Anastasopoulos, P. Ch. (2014). Comparison of factors affecting injury severity in angle collisions by fault status using a random parameters bivariate ordered probit model. Anal. Methods Accid. Res. 2, 21–29. doi:10.1016/j.amar.2014.03.001

CrossRef Full Text | Google Scholar

Sarwar, M. T., and Anastasopoulos, P. Ch. (2016a). A three-stage least squares analysis of post-rehabilitation pavement performance. Transp. Res. Rec. 2589, 97–109. doi:10.3141/2589-11

CrossRef Full Text | Google Scholar

Sarwar, M. T., and Anastasopoulos, P. Ch. (2016b). The effect of long term non-evasive pavement deterioration on accident injury-severity rates: a seemingly unrelated and multivariate equations approach. Anal. Methods Accid. Res. 13, 1–15. doi:10.1016/j.amar.2016.10.003

CrossRef Full Text | Google Scholar

Sarwar, M. T., Anastasopoulos, P. Ch., Ukkusuri, S., Murray-Tuite, P., and Mannering, F. L. (2016). A statistical analysis of the dynamics of household hurricane-evacuation decisions. Transportation 1–20. doi:10.1007/s11116-016-9722-6

CrossRef Full Text | Google Scholar

Sarwar, M. T., Anastasopoulos, P. Ch, Golshani, N., and Hulme, K. F. (2017). Grouped random parameters bivariate probit analysis of perceived and observed aggressive driving behavior: a driving simulation study. Anal. Methods Accid. Res. 13, 52–64. doi:10.1016/j.amar.2016.12.001

CrossRef Full Text | Google Scholar

Serag, E., Oloufa, A., Malone, L., and Radwan, E. (2010). Model for quantifying the impact of change orders on project cost for US roadwork construction. J. Constr. Eng. Manage. 136, 1015–1027. doi:10.1061/(ASCE)CO.1943-7862.0000206

CrossRef Full Text | Google Scholar

Singh, P., Oh, J. E., Labi, S., and Sinha, K. C. (2007). Cost-effectiveness evaluation of warranty pavement projects. J. Constr. Eng. Manage. 133, 217–224. doi:10.1061/(ASCE)0733-9364(2007)133:3(217)

CrossRef Full Text | Google Scholar

Tomasi, M. (2016). “Public private partnerships in member states,” in Presented at the Tenth Meeting of the Network of Public Finance Economists in Public Administration (Brussels, Belgium: European Commission, DG ECFIN). Available at: http://ec.europa.eu/economy_finance/events/2016/20160302-pfn/index_en.htm

Google Scholar

Train, K. (2003). Discrete Choice Methods with Simulation Cambridge, UK: Cambridge University Press.

Google Scholar

Washington, S., Karlaftis, M., and Mannering, F. L. (2011). Statistical and Econometric Methods for Transportation Data Analysis, 2nd Edn. Boca Raton, FL: Chapman and Hall/CRC.

Google Scholar