- 1Department of Architecture and Urban Engineering, Ritsumeikan University, Kusatsu, Japan
- 2Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyotodaigaku-Katsura, Kyoto, Japan
A method of physical parameter system identification (SI) is proposed here for three-dimensional (3D) building structures with in-plane rigid floors in which the stiffness and damping coefficients of each structural frame in the 3D building structure are identified from the measured floor horizontal accelerations. A batch processing least-squares estimation method for many discrete time domain measured data is proposed for the direct identification of the stiffness and damping coefficients of each structural frame. Although previous researches on the SI of 3D building structures are limited to a class of structures with regular eccentricity, this article removes this limitation. Advantageous features of the proposed identification method are that it is unnecessary to specify the stiffness eccentricities (location of the center of stiffness) before identification, and the identification of all stiffness and damping parameters can be performed simultaneously. The reliability and accuracy of the proposed method are demonstrated by numerical simulations.
Introduction
A new physical parameter system identification (SI) theory is proposed in this article for three-dimensional (3D) building structures with in-plane rigid floors in which the stiffness and damping coefficients of each structural frame in the 3D building structure are identified from the measured floor horizontal accelerations. Research on physical parameter SI of 3D building structures with eccentricity is very limited (for example, Omrani et al., 2012). This is because there are many parameters to be identified in 3D building structures. The approach by Omrani et al. (2012) is based on the statistical analysis, and the quantity of eccentricity is assumed to be known. On the other hand, advantageous features of the proposed identification method are that it is unnecessary to specify the stiffness eccentricities (location of center of stiffness) before identification, and the identification of all stiffness and damping parameters can be performed simultaneously.
Recently, the business continuity plan (BCP) has been discussed academically and practically with great interest in the construction and operating management of various built environments. Unexpected hazards experienced during the last few decades made BCP a key subject, and many significant attempts on BCP have been made. It is recognized worldwide that the structural health monitoring plays a key role in BCP.
The structural health monitoring has a long history in many engineering fields, such as civil, mechanical, and aerospace engineering (Boller et al., 2009; Takewaki et al., 2011). The SI methodologies play a key role in the structural health monitoring. It is commonly understood that the modal parameter SI and physical parameter SI are two principal branches in the field of SI. Historically great concern has been directed to the modal parameter SI (Hart and Yao, 1977; Agbabian et al., 1991; Nagarajaiah and Basu, 2009), which can provide the overall mechanical properties of a structural system and has a stable characteristic. On the other hand, the physical parameter SI has another merit from the different point of view that the physical parameters, e.g., stiffness and/or damping coefficient of the structural model, can be obtained directly, and this is quite effective for the damage detection. In spite of the fact that the physical parameter SI is preferred in the structural health monitoring, its advancement is limited due to the strict requirement of multiple measurements or the necessity of complicated manipulation (Hart and Yao, 1977; Udwadia et al., 1978; Shinozuka and Ghanem, 1995; Takewaki and Nakamura, 2000, 2005; Brownjohn, 2003; Nagarajaiah and Basu, 2009; Takewaki et al., 2011; Zhang and Johnson, 2013a,b; Johnson and Wojtkiewicz, 2014; Wojtkiewicz and Johnson, 2014).
In the field of physical parameter SI, Nakamura and Yasui (1999) developed a direct method using a least-squares method. They discussed a damage detection problem for steel buildings, which were severely damaged during the Hyogoken-Nanbu earthquake in 1995. However, their approach requires many measurement points and components. Therefore, it can be used only for one-dimensional shear-type building models. On the other hand, Takewaki and Nakamura (2000) were looking for a smart identification method and introduced a unique SI formulation based on the pioneering work devised by Udwadia et al. (1978). In the method demonstrated by Udwadia et al. (1978), the stiffness and damping coefficient at a given story of a shear building model (S model) can be identified directly from the floor acceleration records just above and below the target story using the so-called identification function. However, in the SI method proposed by Takewaki and Nakamura (2000, 2005), there exists an issue to be overcome in applying to actual data, e.g., microtremors, due to the small signal/noise (SN) ratio in the low frequency range (Ikeda et al., 2014, 2015; Fujita et al., 2015). Furthermore, an S model is not necessarily a suitable model of high-rise buildings with large aspect ratios due to the influence of building overall bending deformation. The former problem has been a major and most difficult problem in the field of the physical parameter SI method where the limit value evaluation of the transfer function for is needed. The autoregressive with exogenous (ARX) model with constraints on the ARX parameters has been introduced by Maeda et al. (2011), Kuwabara et al. (2013), and Minami et al. (2013) to avoid the difficulty caused by the noise. By applying the ARX model to transfer functions, the difficulty in the evaluation of limit value for a small SN ratio data has been avoided. On the other hand, the latter problem has been tackled by expanding the SI algorithm to the shear-bending model (Fujita et al., 2013; Minami et al., 2013).
To develop a hybrid method of the modal parameter SI and physical parameter SI, some researchers proposed a reliable SI method in which the physical parameters are identified from the preidentified modal parameters (Hjelmstad et al., 1995). However, it needs a deeper consideration of the relation between the physical parameters and the modal parameters together with the detailed theoretical investigation on inverse problem formulation (Hjelmstad, 1996).
As another effective approach, the SI method using Kalman filter or extended Kalman filter was developed many years ago (Hoshiya and Saito, 1984). Although the approach is general and can consider noise issues appropriately, it requires strong mathematical backgrounds, and simple use may be difficult. Recently, an approach to the SI based on the Bayesian updating is developing very fast (Boller et al., 2009). The procedure of simple application of this approach to actual problems is desired.
A method of physical parameter SI is proposed here for 3D building structures with in-plane rigid floors. A batch processing least-squares estimation method for many discrete time domain measured data is proposed for the direct identification of the stiffness and damping coefficients of each structural frame in the 3D building structure. The reliability and accuracy of the proposed method are demonstrated by numerical simulations.
Model for Identification and Equations of Motion
Consider an N-story 3D shear building model, as shown in Figure 1A, with in-plane rigid horizontal floors. Each story of this model has four vertical plane frames parallel to the x or y axis. It is unnecessary that the vertical plane frames exist in the common plane through all stories. The locations of these four frames in the nth story are denoted by as shown in Figure 1B, and the locations of the center of mass in the nth story are denoted by . Each vertical plane frame is a shear-type model and consists of a stiffness element and a viscous damping element. Let and denote the horizontal stiffnesses and damping coefficients, respectively, of four vertical plane frames in the nth story. The advantage of the present model is that the specification of the location of the center of stiffness is unnecessary. The center of stiffness is determined automatically after the identification of horizontal stiffnesses of the vertical frames. On the other hand, the masses are concentrated at the corners of the plan. Let denote the mass located at the intersection of frame and frame (see Figure 1B).
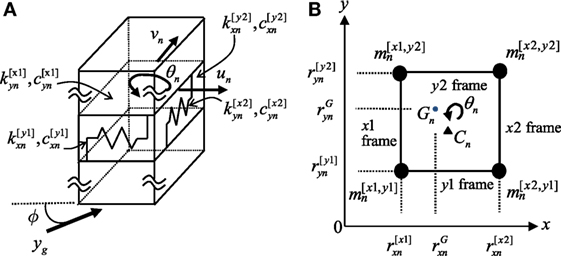
Figure 1. Three-dimensional shear building model with four vertical plane frames subjected to inclined horizontal ground motion: (A) overview and (B) plan.
This building model is subjected to the horizontal ground acceleration in the direction angle ϕ from the x-axis. Let denote the horizontal displacements of the center of mass in the x and y directions and the angle of floor rotation around the vertical axis in the nth story.
Let denote the frame displacements in the x-direction in the ith story and let denote the frame displacements in the y-direction in the ith story (see Figure 1B). These displacements can be expresses as
where
A more detailed explanation can be found in Figures 2 and 3.
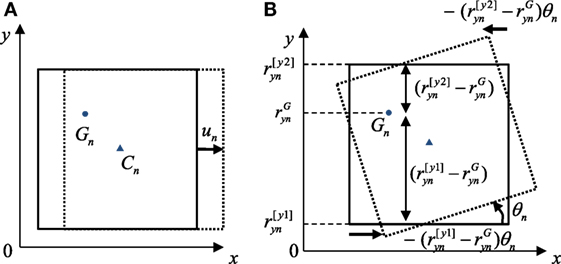
Figure 2. Definition of displacements: (A) x-direction displacement without rotation and (B) x-direction displacement due to rotation around center of mass.
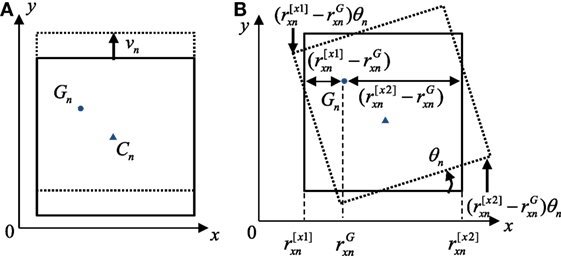
Figure 3. Definition of displacements: (A) y-direction displacement without rotation and (B) y-direction displacement due to rotation around center of mass.
Let M, C, and K denote the stiffness, damping, and stiffness matrices, respectively, of this model. The equations of motion of this 3D building structure can be expressed by
The vectors r and y are defined by
The mass matrix M is obtained as
where
The mass mi and the mass moment of inertia mri in the ith story can be expressed as
On the other hand, the stiffness matrix K can be expressed by
where
In Eq. 10, xx, xr, rx, yy, yr, ry, and rr should be substituted in the suffix {a}. and are the element stiffness matrix of N × N in which defined below exists as the only non-zero terms in (i − 1, i) rows and (i − 1, i) columns.
where
Finally, the damping matrix C is assumed to be proportional to the stiffness matrix and expressed as
where h is the lowest-mode damping ratio and ω is the fundamental natural circular frequency.
Formulation of Direct SI
In this section, a new formulation of direct SI is presented. An advantageous feature of the proposed identification method is that it is unnecessary to specify the stiffness eccentricities (location of center of stiffness) before identification.
Assume that and are measured. More specifically assume that and are measured. As an example, it is sufficient to measure the x and y-direction absolute accelerations at the diagonal two edges at all floors in Figure 1B in addition to the x and y-direction absolute accelerations at the base. Then, and y(t) can be integrated numerically.
By transforming the equations of motion into the equations in terms of unknown parameters, i.e., stiffness and damping coefficients, the following relations are derived.
where
and in Eq. 19 are the element coefficient matrices of N × N. x, y, and r are substituted in the suffix {a} and x1, x2, y1, and y2 are substituted in the suffix {b}. defined below exists as the only non-zero terms in (i − 1, i) rows and ith column of .
As for , u,ν, and θ are replaced by , , and , respectively. In Eq. 16, Z(t) is defined by
The errors in Eq. 16 derived from the equations of motion can be expressed by
The sum of the squares of the errors ε(t) during the time duration from t1 to t2 can be expressed by
The differential of E with respect to Θ provides
The least-squares estimation method incorporating the batch processing (Takewaki and Nakamura, 2010) provides the parameters Θ, which minimize the error E.
It is important to note that the identification of all stiffness and damping parameters can be performed simultaneously.
Numerical Example
Examples without Noise
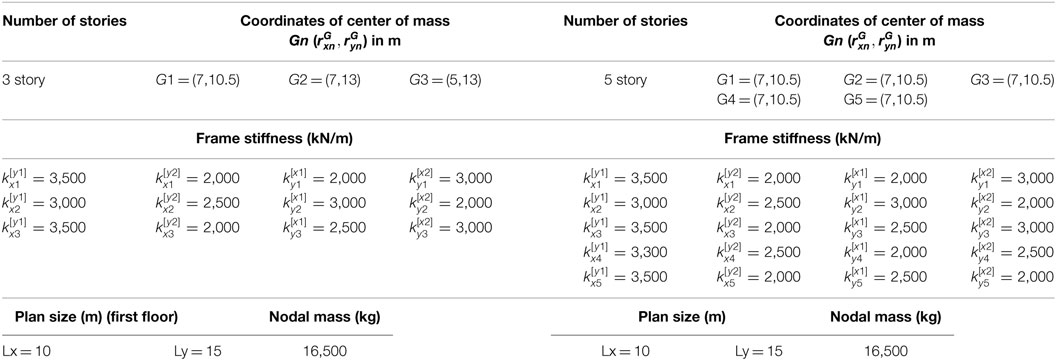
To verify the validity and accuracy of the proposed method, a three-story model and a five-story model as shown in Figures 4 and 5, respectively, have been used. The three-story model has storywise different plans and the five-story model has a storywise common plan. The model parameters are shown in Table 1. The damping ratio in the lowest mode is assumed to be 0.02. As an input ground motion, El Centro NS 1940 as shown in Figure 6 has been used and input in the direction angle ϕ = π∕4. The data during 10(s) from the beginning were used for identification. The time history responses of these two models have been simulated numerically using the Newmark-beta method. The time increment is 0.02 s.
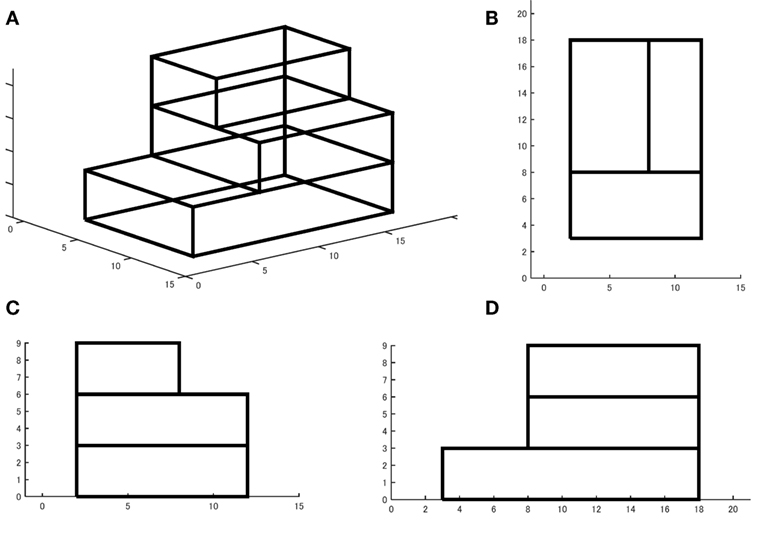
Figure 4. Three-story model with storywise different plans: (A) overview, (B) plan, (C) side view 1, and (D) side view 2.
Figure 7 shows the correspondence between the given stiffness and damping coefficients and the identified values in the three-story model. On the other hand, Figure 8 presents the correspondence between the given stiffness and damping coefficients and the identified values in the five-story model. The horizontal axis illustrates the location of the stiffness and damping parameters, e.g., x1(1F) indicates and x2(1F) indicates . It can be observed that the proposed identification method has a reliable accuracy in both the stiffness and the damping.
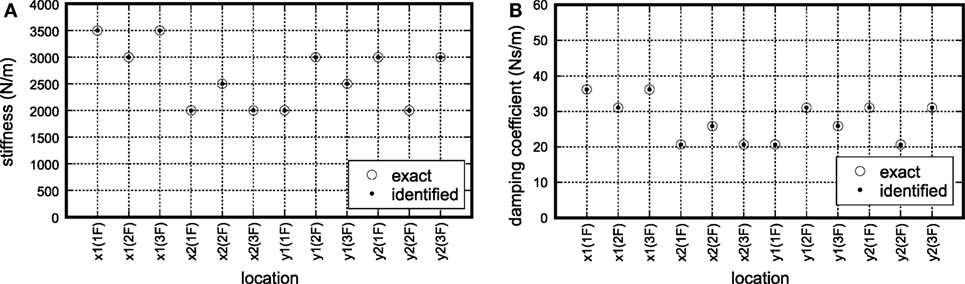
Figure 7. Accuracy of identification without noise (three-story model): (A) stiffness and (B) damping coefficient.
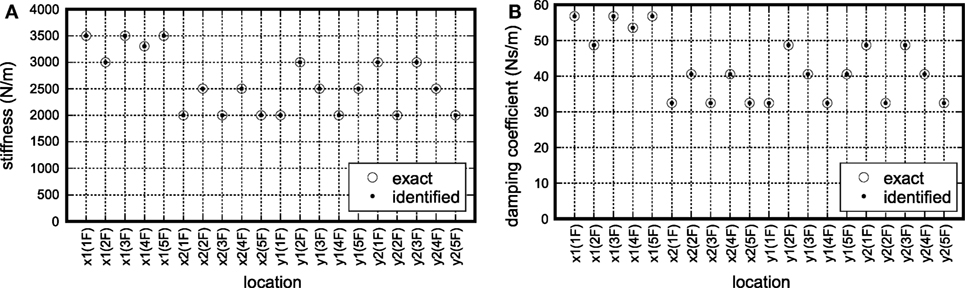
Figure 8. Accuracy of identification without noise (five-story model): (A) stiffness and (B) damping coefficient.
To investigate the effect of the input direction of ground motions on the identification accuracy, ϕ = 0, π/5 were used in addition to ϕ = π/4. It has been confirmed that the sufficient accuracy is maintained regardless of the input motion direction. As for the effect of the location of data window used for identification on the identification accuracy, no remarkable effect has been observed except during the short duration at the beginning. Furthermore, it has been found that the duration longer than 2 s is sufficient.
Examples with Noise
To investigate the effect of noise on the accuracy of identification (Koyama et al., 2015), noises have been added to the input and response values simulated without noise. The noise was produced by using a band-limited white noise with the frequency range 0.075–150 (rad/s). Different independent noises were added to the original input and response data (acceleration, velocity, and displacement) simulated without noise. Root mean square values were employed to quantify the noise level, and the data during 10(s) from the beginning were used for identification.
Figure 9 shows the plot of story stiffness and damping coefficient with respect to the noise level in the three-story model. It can be observed that, although the accuracy of stiffness degrades gradually for the increase of noise, the order of accuracy degradation in damping is larger. This phenomenon corresponds well with the well-recognized knowledge in the field of SI (Takewaki and Nakamura, 2005; Boller et al., 2009; Takewaki et al., 2011). Furthermore, although most of stiffnesses become smaller with the increase of noise level, some damping coefficients become smaller and others become larger.
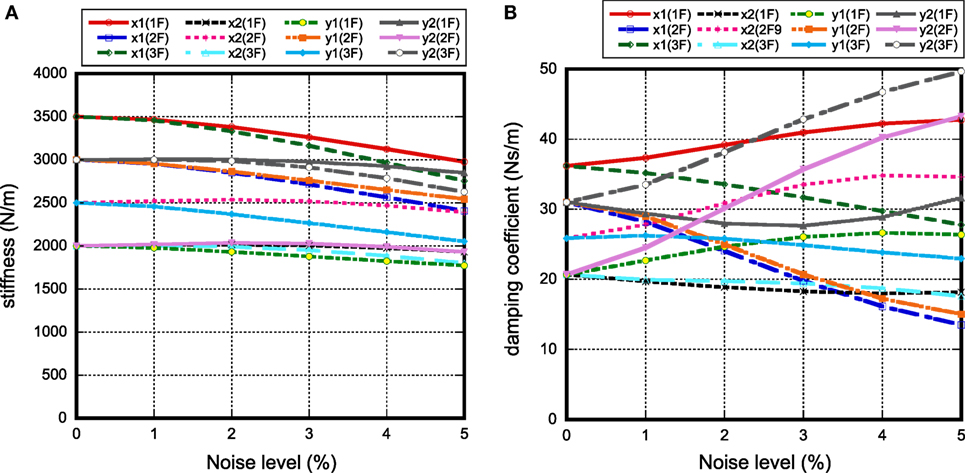
Figure 9. Influence of noise level on accuracy of identification of stiffness and damping in three-story model: (A) stiffness and (B) damping coefficient.
Extension to Model with In-Plane Flexible Floor
Since the present theory has flexibility and generality (treatment of each vertical frame as independent stiffness and damping element), it can be extended to 3D building structures with in-plane flexible floors by specifying the in-plane flexibility of floors. There are four degrees of freedom in each story (four horizontal degrees of freedom). The four degrees of freedom in each story are related by introducing the in-plane shear stiffness of flexible floors. Because the batch processing least-squares estimation method explained in Section “Formulation of Direct SI” does not depend on the number of degrees of freedom and the number of parameters to be identified, a similar formulation may be possible for the model with in-plane flexible floors. This formulation will be presented in the future.
Conclusion
A method of physical parameter SI has been proposed for 3D building structures in which the stiffness and damping coefficients of each structural frame in the building structure are identified from the measured floor horizontal accelerations. The following conclusions have been derived.
(1) A batch processing least-squares estimation method for many discrete measured data has been proposed for the direct identification of the stiffness and damping coefficients of each story. A model with in-plane rigid floors has been used as the model for the physical parameter SI. Advantageous features of the proposed identification method are that it is unnecessary to specify the stiffness eccentricities (location of center of stiffness) before identification, and the identification of all stiffness and damping parameters can be performed simultaneously.
(2) Numerical simulations have been conducted for three-story and five-story 3D building structures with different mass and stiffness eccentricities. It has been demonstrated that, irrespective of the condition of mass and stiffness eccentricities, the proposed method is reliable and accurate in noise-free models. On the other hand, the identification accuracy degrades gradually as the noise level increases. However, a certain accuracy level can be maintained by limiting the level of noise.
Author Contributions
KS formulated the problem, conducted the computation, and wrote the paper. SY supervised the research, helped the computation, and wrote the paper. IT supervised the research and wrote the paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer SC and the handling editor declared their shared affiliation, and the handling editor states that the process nevertheless met the standards of a fair and objective review.
Funding
Part of the present work is supported by the Grant-in-Aid for Scientific Research (KAKENHI) of Japan Society for the Promotion of Science (No. 15H04079) and Sumitomo Rubber Industries, Co. This support is greatly appreciated.
References
Agbabian, M. S., Masri, S. F., Miller, R. K., and Caughey, T. K. (1991). System identification approach to detection of structural changes. J. Engng. Mech. 117, 370–390. doi: 10.1061/(ASCE)0733-9399(1991)117:2(370)
Boller, C., Chang, F.-K., and Fujino, Y. (eds) (2009). Encyclopedia of Structural Control and Health Monitoring, Vol. 1–5. Chichester, UK: Wiley.
Brownjohn, J. M. W. (2003). Ambient vibration studies for system identification of tall building. Earth. Eng. Struct. Dyn. 32, 71–95. doi:10.1002/eqe.215
Fujita, K., Ikeda, A., Shirono, M., and Takewaki, I. (2013). “System identification of high-rise buildings using shear-bending model and ARX model: experimental investigation,” in Proc. of ICEAS13 in ASEM13, September 8-12 (Jeju, Korea), 2803–2815.
Fujita, K., Ikeda, A., and Takewaki, I. (2015). Application of story-wise shear building identification method to actual ambient vibration. Front. Built Env. 1:2. doi:10.3389/fbuil.2015.00002
Hart, G. C., and Yao, J. T. P. (1977). System identification in structural dynamics. J. Engng. Mech. Div. 103, 1089–1104.
Hjelmstad, K. D. (1996). On the uniqueness of modal parameter estimation. J. Sound Vib. 192, 581–598. doi:10.1006/jsvi.1996.0205
Hjelmstad, K. D., Banan, M. R., and Banan, M. R. (1995). On building finite element models of structures from modal response. Earthq. Engng. Struct. Dyn. 24, 53–67. doi:10.1002/eqe.4290240105
Hoshiya, M., and Saito, E. (1984). Structural identification by extended Kalman filter. J. Engng. Mech. 110, 1757–1770. doi:10.1061/(ASCE)0733-9399(1984)110:12(1757)
Ikeda, A., Fujita, K., and Takewaki, I. (2014). Story-wise system identification of actual shear building using ambient vibration data and ARX model. Earthq. Struct. 7, 1093–1118. doi:10.12989/eas.2014.7.6.1093
Ikeda, A., Fujita, K., and Takewaki, I. (2015). Reliability of system identification technique in super high-rise building. Front. Built Env. 1:11. doi:10.3389/fbuil.2015.00011
Johnson, E., and Wojtkiewicz, S. (2014). Efficient sensitivity analysis of structures with local modifications. II: transfer functions and spectral densities. J. Engng. Mech. 140. doi:10.1061/(ASCE)EM.1943-7889.0000769
Koyama, R., Fujita, K., and Takewaki, I. (2015). Influence of wind disturbance on smart stiffness identification of building structure using limited micro-tremor observation. Struct. Eng. Mech. 56, 293–315. doi:10.12989/sem.2015.56.2.293
Kuwabara, M., Yoshitomi, S., and Takewaki, I. (2013). A new approach to system identification and damage detection of high-rise buildings. Struct. Control Health Monitoring 20, 703–727. doi:10.1002/stc.1486
Maeda, T., Yoshitomi, S., and Takewaki, I. (2011). Stiffness-damping identification of buildings using limited earthquake records and ARX model. J. Struct. Construct. Eng. 666, 1415–1423. doi:10.3130/aijs.76.1415
Minami, Y., Yoshitomi, S., and Takewaki, I. (2013). System identification of super high-rise buildings using limited vibration data during the 2011 Tohoku (Japan) earthquake. Struct. Control Health Monitoring 20, 1317–1338. doi:10.1002/stc.1537
Nagarajaiah, S., and Basu, B. (2009). Output only modal identification and structural damage detection using time frequency & wavelet techniques. Earthq. Eng. Eng. Vib. 8, 583–605. doi:10.1007/s11803-009-9120-6
Nakamura, M., and Yasui, Y. (1999). Damage evaluation of a steel structure subjected to strong earthquake motion based on ambient vibration measurements. J. Struct. Construct. Eng. 517, 61–68. doi:10.3130/aijs.64.61_1
Omrani, R., Hudson, R. E., and Taciroglu, E. (2012). Story-by-story estimation of the stiffness parameters of laterally-torsionally coupled buildings using forced or ambient vibration data: I. Formulation and verification. Earthq. Eng. Struct. Dyn. 41, 1609–1634. doi:10.1002/eqe.1192
Shinozuka, M., and Ghanem, R. (1995). Structural-system identification II: experimental verification. J. Eng. Mech. 121, 265–273. doi:10.1061/(ASCE)0733-9399(1995)121:2(265)
Takewaki, I., and Nakamura, M. (2000). Stiffness-damping simultaneous identification using limited earthquake records. Earthq. Eng. Struct. Dyn. 29, 1219–1238. doi:10.1002/1096-9845(200008)29:8<1219::AID-EQE968>3.0.CO;2-X
Takewaki, I., and Nakamura, M. (2005). Stiffness-damping simultaneous identification under limited observation. J. Eng. Mech. 131, 1027–1035. doi:10.1061/(ASCE)0733-9399(2005)131:10(1027)
Takewaki, I., and Nakamura, M. (2010). Temporal variation of modal properties of a base-isolated building during an earthquake. J. Zhejiang Univ.-SCIENCE A 11, 1–8. doi:10.1631/jzus.A0900462
Takewaki, I., Nakamura, M., and Yoshitomi, S. (2011). System Identification for Structural Health Monitoring. UK: WIT Press.
Udwadia, F. E., Sharma, D. K., and Shah, P. C. (1978). Uniqueness of damping and stiffness distributions in the identification of soil and structural systems. J. Appl. Mech. 45, 181–187. doi:10.1115/1.3424224
Wojtkiewicz, S., and Johnson, E. (2014). Efficient sensitivity analysis of structures with local modifications. I: time domain responses. J. Engng. Mech. 140. doi:10.1061/(ASCE)EM.1943-7889.0000768
Zhang, D., and Johnson, E. (2013a). Substructure identification for shear structures I: substructure identification method. Struct. Control Health Monitoring 20, 804–820. doi:10.1002/stc.1497
Keywords: system identification, torsional response, general eccentricity, batch processing least-squares method, physical parameter identification
Citation: Shintani K, Yoshitomi S and Takewaki I (2017) Direct Linear System Identification Method for Multistory Three-dimensional Building Structure with General Eccentricity. Front. Built Environ. 3:17. doi: 10.3389/fbuil.2017.00017
Received: 16 January 2017; Accepted: 27 February 2017;
Published: 20 March 2017
Edited by:
Nikos D. Lagaros, National Technical University of Athens, GreeceReviewed by:
Stavros Chatzieleftheriou, National Technical University of Athens, GreecePeng Pan, Tsinghua University, China
Copyright: © 2017 Shintani, Yoshitomi and Takewaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Izuru Takewaki, dGFrZXdha2lAYXJjaGkua3lvdG8tdS5hYy5qcA==
 Kenichirou Shintani
Kenichirou Shintani Shinta Yoshitomi
Shinta Yoshitomi Izuru Takewaki
Izuru Takewaki