Sensing and Monitoring for Stadium Structures: A Review of Recent Advances and a Forward Look

Catbas, Fikret Necati; Celik, Ozan; Avci, Onur; Abdeljaber, Osama; Gul, Mustafa; Do, Ngoan Tien

doi:10.3389/fbuil.2017.00038

REVIEW article

Front. Built Environ., 08 August 2017

Sec. Structural Sensing, Control and Asset Management

Volume 3 - 2017 | https://doi.org/10.3389/fbuil.2017.00038

Sensing and Monitoring for Stadium Structures: A Review of Recent Advances and a Forward Look

$\r\nFikret Necati Catbas*$ Fikret Necati Catbas¹*

Ozan Celik¹

Onur Avci²

Osama Abdeljaber²

Mustafa Gul³ $Ngoan Tien Do\r\n$ Ngoan Tien Do⁴

¹Department of Civil, Environmental and Construction Engineering, University of Central Florida, Orlando, FL, United States
²Department of Civil and Architectural Engineering, College of Engineering, Qatar University, Doha, Qatar
³Department of Civil and Environmental Engineering, University of Alberta, Donadeo Innovation Centre for Engineering, Edmonton, AB, Canada
⁴Department of Civil and Environmental Engineering, University of Alberta, Markin/CNRL Natural Resources Engineering Facility, Edmonton, AB, Canada

Stadiums like those used for sporting or concert events are distinct from other civil engineering structures due to several different characteristics. Some challenges mainly originate from the interaction with the human factor, as stadiums are subjected to both synchronized and random motion of large crowds. The investigations in the literature on this topic clearly state that stadiums designs are in urgent need of more reliable load quantification and modeling strategies, deeper understanding of structural response, generation of simple but efficient human–structure interaction models, and more accurate criteria for vibration acceptability. Although many esthetically pleasing and technologically advanced stadiums have been designed and constructed using structurally innovative methods, recent research on this field still calls for less conservative and more realistic designs. This article aims to highlight the recent advances in this field and to provide a follow-up to the literature review covering until 2008 (Jones et al., 2011a) on vibration serviceability of stadiums structures. The article will also discuss new sensing and monitoring techniques on load-time history measurements and their regeneration, as well as crowd motion, stadium health monitoring, and human comfort analysis. Operational effects of crowds on the dynamic properties are also discussed. The article concludes with a forward look on the recommended work and research for dynamic assessment of stadiums.

Introduction

Stadiums (plural of stadium, also used as stadia) are designed with the intent to hold large number of people. Over the years, stadiums have become an integral part of the building and entertainment sectors, functioning as the main location for large social events and as a significant resource for revenue. With the recent population growth and expansion of the entertainment industry, demand for such structures has increased dramatically, resulting in the need for new designs capable of accommodating even larger crowds. However, these new designs must also satisfy the architectural and esthetic considerations, which call for a trade off in strength in return for slender structures, such as long cantilevers, which are preferred for better lines of sight (Figure 1). The slenderness of long cantilevers resides in their length along with the mass of the crowd they are accommodating and their synchronized motion. Being constructed as such, the structural components might be stressed to critical limits for serviceability and even safety. Stadium utilization for concerts and various events other than sports games might be more critical as coordinated crowds can excessively excite the structures to critical levels.

FIGURE 1

Figure 1. Architectural and structural details of a stadium.

The real nature of crowd excitation and its accurate representation are still yet to be adequately understood. The current guidance and codes provide solutions that need to be improved for this problem (Canadian Commission on Building and Fire Codes, 2006; ISO/TC 98/SC 2, 2007; IStructE/DCLG/DCMS Joint Working Group, 2008). The construction of typical structures, such as buildings, must comply with the related design codes, which require the structure to maintain safety and serviceability. However, random coordinated motions induced by occupying crowds on flexible structures need a more comprehensive assessment. Many effects that could normally be neglected for ordinary structures become increasingly important under high occupancy because of occupant-mass ratio and crowd-induced forces. Structural parameters in this case are variable and uncertain.

A widely accepted procedure for vibration serviceability problem is to evaluate the system as a three-step framework (input/excitation/source—system/path/structure—output/response/receiver) (ISO/TC 98/SC 2, 2007; Jones et al., 2011a). The input is simply the characterization of loading caused by humans. This part plays a crucial role in the problem since the output generated by the system greatly depends on the correct measurement of the loading. There has been a great deal of research on human-induced load modeling in both civil engineering and biomechanics. The approaches are narrowed down to estimation of jumping and bobbing of individuals since these are the extreme cases to be considered in stadiums especially when they are synchronized. Methods of direct mathematical representation provide an easily applicable procedure, yet it is still too simplistic as they are composed of fitting combinations of transcendental functions (mostly Fourier series). The second approach is to use the measurement of real-life force–time histories as an input and then implement mathematical functions to recreate the measured histories. The downside of this approach is the inability to distinguish similar responses from the structure due to possible alterations in mass, stiffness, and damping. Both methods ignore the sophisticated nature of the actual behavior, such as time lags between each loading sequences or peak-to-peak variations. An accurate expansion of these simplified models to crowd motion has not been achieved yet. In the last decade, there has been valuable research on this part of the problem by proposing stochastic modeling methods for individual loading which are deemed to be more reliable (Ellis and Ji, 2004; Racic and Pavic, 2010b; Racic and Brownjohn, 2011).

The structural systems of stadiums show significant variations especially in mass, stiffness, and damping. These variations are the product of several factors: the uneven distribution of the crowd occupying the structure, the inherent capability of the human body to absorb energy, the interactions between people, and also the motion differences within their own body (posture and reaction to different events). The main approach in understanding these structures is to develop a reliable monitoring system and to identify suitable methods for accurately estimating the modal parameters. This is crucial since the findings will be used in nearly every stage of the assessment; such as the validation of newly developed load and human–structure models, the construction and fine tuning of finite element models, and to develop a holistic understanding of the empty and occupied structure. Of all the varying modal parameters in vibration serviceability of stadiums, damping is the most uncertain and therefore will be the most challenging to estimate (Avci, 2016). It is known that the greatest contribution to damping occurs when the crowd is completely passive; however, it is difficult to decide on what portion of the crowd can be considered passive as well as which posture of that passive crowd has the most effect on damping.

The response of stadium structures can be measured in the form of acceleration, strain, displacement, etc. These responses are then used to estimate the structure’s behavior. The most important aspect of the output in the vibration serviceability problem is the relationship between the measured quantities combining serviceability and human comfort. Although there are several measures indicated in standards to quantify perception levels, these methods provide insufficient explanations on the calculation of these values. The available methods do not avoid disparities of perception from person to person, either. They also lack the ability to perform controlled experiments to create serious discomfort levels.

Background and Issues

A comprehensive and detailed report on the issues of the stadium serviceability is presented in a very well-organized literature review (Jones et al., 2011a). This review identifies several important areas still in need of research: codes and guidance, individual and crowd load modeling, human–structure interaction, prediction of dynamic structural properties, and acceptability of vibrations.

Canadian guidance (Canadian Commission on Building and Fire Codes, 2006) provides a simple procedure for dynamic assessment of stadium structures. Loading is defined with mathematical functions and the acceleration response of the structure is estimated as a function of loading and modal properties of the structure. This model does not accurately describe the human effect on the structure because it underestimates the responses that occur during real events. ISO guidance (ISO/TC 98/SC 2, 2007) provides crowd-loading models based on statistical treatment of many experimental studies. Loading models are modified with factors to account for crowd’s coordinated motion and the damping values are provided only for empty structures. A detailed vibration serviceability criterion is also defined. However, the ISO model’s criteria for damping and vibration acceptability are not met in reality. Joint Working Group (IStructE/DCLG/DCMS Joint Working Group, 2008) in the UK defines crowd loading as the superposition of different measurements from individuals. The model assumes that the superposition process will include the interaction between individuals. It also necessitates the use of reduced space model with two or more degrees of freedom to represent human–structure interaction.

An accurate expression of dynamic forces influencing grandstands is complicated. The first issue arises due to the inherent nature of the human body to absorb or give energy, which alters damping (Ellis and Ji, 1994; Brownjohn, 2001; Racic and Pavic, 2010a). It gets further complicated when the focus is expanded from individual activities to the entire crowd, which introduces factors such as the active/passive spectator ratios and their interactions within or with the structure. The human body has been modeled as combination of mass spring systems by various researchers as a simple model to simulate the subparts that are connected with joints (Ellis and Ji, 1997; Wei and Griffin, 1998; Brownjohn, 2001; Zheng and Brownjohn, 2001; Mansfield and Griffin, 2002; Sim et al., 2006). One detailed approach by biodynamicists has been to model the human body with more than 20 degrees of freedom. This approach will surely be more accurate but such higher degrees of freedom are not feasible to implement in crowd behavior modeling. Either individually or with crowd, occupants have multiple significant effects on the structure such as the change in damping (Lenzen, 1966; Ebrahimpour et al., 1991; Ellis and Ji, 1997; Brownjohn and Zheng, 2001; Brownjohn, 2001) and frequency (Sachse et al., 2004). The change in damping is an issue that continues to be difficult to estimate as it is dependent on various factors of the human body such as postures and seating positions. This has been supported in references above with clear changes in damping and frequency.

Regarding the human–structure interaction, the most suitable models have been shown to be mass spring damper systems acting together. Early works of this model represents the human body and structure system as two connected individuals with one degree of freedom (Sachse et al., 2002, 2004). Other models then expand this model by representing the passive and active crowds as additional degree of freedoms attached to the structure. While some studies use more complicated higher degrees of freedom (Sim et al., 2006), the others choose to simplify down to only three DOFs representing the structure, the active and the passive occupants acting together. It is stated that higher degree of freedoms considering both active and passive occupants are more likely to match the measured values.

All models that represent both individual loading and crowd-structure interaction have limitations and present their own unique advantages and disadvantages. According to the current literature, some of them appear to be converging on simulation or experimental results (Jones et al., 2011a). Nevertheless, there is still a need for additional research to verify the effectiveness of these models against the data collected from real-life grandstands.

Modal testing and structural identification of grandstands are other areas that require further in-depth study. These studies are crucially important, as they will provide adequate information to be input to numerical and analytical models. There are several studies that solely focus on the performance of these structures (Reynolds and Pavic, 2002, 2006; Reynolds et al., 2004, 2005, 2007; Prasenjit et al., 2005; Caprioli et al., 2006b, 2009; Peeters et al., 2007; Cigada et al., 2008a,b; Jones and Reynolds, 2009; Catbas et al., 2011; Sazak et al., 2011). The examples in literature are generally restricted to certain sections that are believed to be critical. In these studies, the sensors are distributed in a way that they capture the most significant modes. In most cases, output only in-service data is used together with operational modal analysis (OMA). It is known that structural dynamic parameters significantly change due to the level of occupancy as the general behavior is like an interconnected mass spring and damper systems. The excitation applied by active audience through jumping/bobbing/bouncing, and the status of the passive audience, either sitting or standing straight (or simply with bent knees), may induce significant shifts in the values of frequency and damping.

Current Practices and Advancements

Sensing/Monitoring of Individuals and Crowd for Load Estimation

Accurate determination of design loads is the first step to create an optimum serviceability design. Almost all different sorts of loads that can be encountered in human–structure interaction problems are explained therein (Racic et al., 2009b; Jones et al., 2011a). Of all different types of human loading, bouncing and jumping with their synchronized and long period applicability are viewed to be the most critical cases (Yao et al., 2006; Sim et al., 2008; Georgiou et al., 2015). The dynamic effects of these two loadings on the structures, as it is pointed out by design guidelines, need to be assessed to determine if the vertical resonant frequencies of the structures fall below 8.5 Hz. This limit is based on the observation that higher Fourier harmonics of jumping load between the jumping and bobbing frequencies of 1.5–3.5 Hz are capable of generating critical structural response. Nevertheless, these guidelines are still far away from providing explicit and reliable methods for crowd loading. Besides, recreating realistic measured individual force–time histories is still an issue due to the variations in motion within a subject’s (intrasubject) body. The need for clarification of these uncertainties has been the motivation of the research on load modeling. Recent research is concentrated mainly on the improvement of conventionally recreated force–time history measurements and relatively new image-based techniques.

Load-Time History Measurements

In general, dynamic force measurements are made by utilizing load cells or force plates that are capable of generating force signals during the “contact phase” and “aerial phase” of jumping or bobbing. A novel example of this measurement technique can be seen in a laboratory raked grandstand model that is used to capture full force–time histories via embedded force plates within the structure (Comer et al., 2010, 2013). The grandstand is capable of accommodating 15 test subjects. The stand is supported by air springs and driven using linear actuators (Figure 2). This setup allows the structure to behave in two different modes namely “rigid” and “floating,” which allows the dynamic response to vary between 2.8 and 23 Hz. The real-time control techniques allow the researchers to test various structures and understand human–structure interaction, group coordination levels, and acceptability limits of vibrations.

FIGURE 2

Figure 2. The grandstand rig and the air spring assembly. Reprinted from (Comer et al., 2010) with permission from Springer.

However, use of force plates brings some concerns such as (1) having small dimensions (~0.6 m × 0.4 m) that require controlled jumping which is quite tough when the subject is to jump at higher frequencies, therefore having distorted ground reaction force (GRF) patterns and (2) giving inaccurate results when mounted on a flexibly moving structure such as grandstand for the reason that additional inertial forces contribute to the measurements (Perry, 1992; AMTI, 2008; Racic et al., 2011).

To remedy these problems regarding conventional methods, a preliminary novel load (bouncing/jumping, walking, and running)—GRF estimation study based on motion tracking is proposed (Racic et al., 2009a) rendering “free field” measurements possible without the necessity of traditional laboratory restricted tests. The body of a test subject is subdivided into 15 major body segments, which are then instrumented with markers at their connection points modeled as spherical hinges (Figure 3).

FIGURE 3

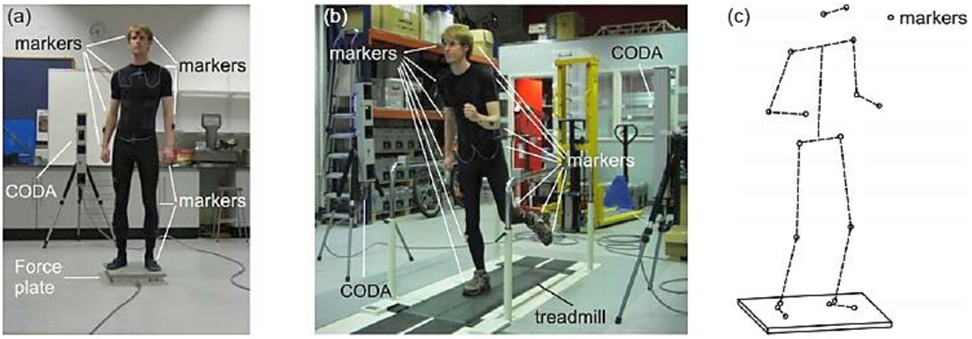
Figure 3. (A) Data markers on the subject, (B) walking and running, and (C) human body model and arrangement of markers. Reprinted from (Racic et al., 2009a).

Position of the markers is tracked down by video-based optoelectronic technology at 200 Hz, and accelerations are derived to be used in the estimation of GRF through Eq. 1:

F_{GR} = \sum_{i = 1}^{s} m_{i} (a_{i} - g)

(1)

where m_i and a_i are mass and acceleration of the center of the mass of the ith body segment, and s is the total number of segments. Calculated GRFs are then validated by the direct measurements using an instrumented treadmill that is embedded in the ground. The results seem quite promising in capturing three harmonics of jumping records in frequency domain (up to 15 Hz) especially for extreme loads (bouncing/jumping) commonly encountered in crowd dynamics (Figure 4).

FIGURE 4

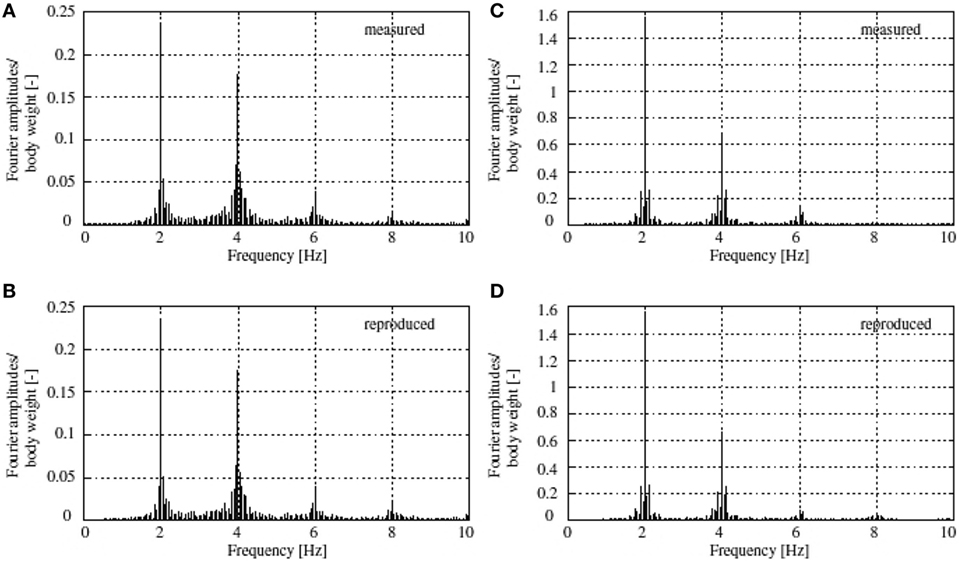
Figure 4. Comparison between directly measured and reproduced (A,B) bouncing and (C,D) jumping forces in the frequency domain. Each Fourier amplitude was derived from a single 20-s long force signal without the use of averaging. Reprinted from (Racic et al., 2010a) with permission from Elsevier.

The same method is validated in other studies by the same researchers (Racic et al., 2010a, 2011). The test subjects perform the same test (without force plate measurements) both separately and together at three frequencies: 2, 2.2, and 2.5 Hz but with identical conditions on a simply supported floor stripe whose modal characteristics are known from previous modal analysis. Generated force histories via tracking of visual data marker during jumping phase of subjects are input into the computer model and are compared with those acquired through direct acceleration measurements from the floor stripe. The results show a good match between the measured vibration responses and those calculated from the corresponding SDOF model using the recreated forces. The proposed method is suggested to be applied on many different applications of human-induced vibrations such as grandstands, and footbridges to be explored in more depth in terms of practicality and accuracy especially in the existence of a large number of time-dependent force records. As shown in the previous study, a database of different loadings can be generated to further create stochastic load models. However, the real-life applications of data markers require the test subjects to stand in a prescribed certain line to fully capture the three dimensional motion. Therefore, for field measurements where exists a high density of crowd, this method does not seem to be really feasible.

This problem is remedied by contactless sensing via the use of computer vision techniques. The earliest works of this kind include tracking the prominent body parts (mainly the face) of people by segmentation and looking at their correlation in consecutive images to estimate the loads applied to grandstands by large crowds (Hoath et al., 2007). Inspired by some early works on contour detection (Beucher and Lantuejoul, 1979; Blake and Isard, 1998) and Bayesian clustering methods for crowd tracking (Brostow and Cipolla, 2006), researchers use an easier method specifying each tracked segment with a rectangle for estimating jumping and bobbing pattern on a laboratory grandstand. The results are not quite satisfying for the following reasons: (1) run time for the tracking algorithm being too long since the amount of data is large and (2) method not being sensitive enough to rapid changes in tracking the objects. Similarly, other trials focus on motion measurement of people and the patterns of their behavior in terms of velocity amplitude and frequency through either simulation in a computer-controlled environment (Caprioli et al., 2008a, 2011) or utilizing off the shelf regular or thermal imaging cameras on a portion of a real grandstand (Caprioli et al., 2006a; Cigada and Zappa, 2006). A well-known family of algorithms called as digital image correlation (DIC) commonly referred to as particle image velocimetry is used in these studies. The application includes dividing the image into different fixed sized rectangular areas called regions of interest (ROIs) and tracking the displacement of the most similar regions in the consecutive images. Since the elapsed time between consecutive images is known, the displacement and average velocity field as well as acceleration time histories could be acquired. Detailed analyses on some uncertainties regarding the technique such as the size of the ROIs and the resolution of the images are carried out via 2D and three dimensional (3D) image processing. In conclusion, a minimum limit for a successful image-based study in terms of acquisition and analysis for grandstands is proposed. The proposed limits are 400 mm × 400 mm minimum ROI size that is equal or higher than 8 × 8 pixels and a conversion factor from pixels to millimeters of 22 mm/pixel or less. Utilization of the technique and recommendations for uncertainties are validated with scaled down images of a real stadium (Caprioli et al., 2008b) having shaker-controlled dummies and a real small crowd jumping (Caprioli et al., 2011) in another study. A promising contactless measurements method captures the displacement and acceleration information from a real-life event where a group of people in various sizes demonstrates jumping activities. The novelty of the study lies within the adaptive nature of the algorithm to non-stationary changes as illumination changes, object deformation. The results are compared with data marker tracking system and wireless accelerometers that can be attached on the human body (Feng et al., 2014).

After several preliminary trials of DIC algorithm applications, a promising step-up toward the load estimation is achieved relying on the experiments done at a section of an instrumented real-life grandstand (Jones et al., 2011b). The aim is to generate loading functions based on the developed acceleration time histories. Regarding the large number of occupants, poor image resolution, and perspective issues, it is chosen to work only on a small portion of the grandstand (Figure 5) and with root mean square (RMS) of what values, thereby mitigating the noise problem. The application, as before, includes dividing the image into different fixed sized rectangular ROIs and tracking the displacement of the most similar region in the consecutive images.

FIGURE 5

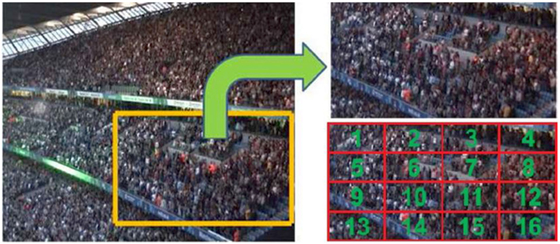
Figure 5. The analyzed portion of the grandstand and 16 regions of interest. Reprinted from (Jones et al., 2011b) with permisson from Springer.

Since the elapsed time between consecutive images is known, the velocity field and average velocity time histories along with their RMS_tot could be acquired as in Eq. 2:

{RMS}_{tot} (t_{k}) = \sqrt{\frac{\sum_{i = 1}^{N} {({RMS}_{i} (t_{k}))}^{2}}{N}}

(2)

where N is the number of ROIs and RMS_i (t_k) is the RMS value at time t_k for the ith ROI within the considered area. One problem corrupting the images with unexpected spikes in estimated measurement histories is photo-camera flashes blinking. The problem is overcome by looking at the Kurtosis coefficient of numerical velocity history differences in consecutive images and eventually eliminating the undesirable peaks.

Acceleration values to be used in the generation of forcing functions are found by multiplying RMS_tot(mm/s) by a coefficient 2πf where f = 2.1 Hz that is found via autocorrelation step of DIC driven by the frequency of a popular song beat played during the game. Multiplying the accelerations with the apparent estimated mass of the crowd, force histories are obtained. Generated forcing functions are then used in a FE model of the real stadium with modal space approximation approach. The acquired responses come out much more similar to measured responses than those of calculated by utilizing the forcing functions given in current codes and guidance.

Another vision-based approach renders measurement of jumping and bobbing loads on a crowd and on the field by making use of the same family of DIC algorithms (Mazzoleni and Zappa, 2012). Despite the idea of expanding an individual forcing to the entire crowd, the proposed method uses the motion of the crowd directly for generating forcing functions. The preliminary verifications for the method is performed by comparing the measured DIC data with the data coming from both accelerometers installed on a single-test subject and dynamometric platform where the subject is jumping and bobbing within the frequency range of 1.5–3.5 Hz (0.1 Hz intervals). The estimation of vertical-induced loads are obtained by the sum of acceleration and body mass multiplication of body parts and they show a reasonable match with high correlation compared to measured quantities (Figure 6). The level of discrepancy is also evaluated based on the difference between the experimental results from the method and the directly measured values by looking at the spectrums. None of the differences exceed 15%. The real-life experiments involved small groups, varying in number (1, 4, and 8 people) and mass (65, 260, and 600 kg), that were required to jump at frequencies: 2.1, 2.3, and 2.5 Hz. The crowds were located at either 1/2 or 1/3 span portions of the stadium where an experimental modal analysis (EMA) was carried out utilizing a moving mass to extract frequency response functions (FRFs) of the system. The structural vibrations were found by multiplying the force spectrum extracted via DIC with the FRFs acquired from previous EMA test. Figure 7 shows the comparison of measured and computed structural accelerations with a reasonable coherence.

FIGURE 6

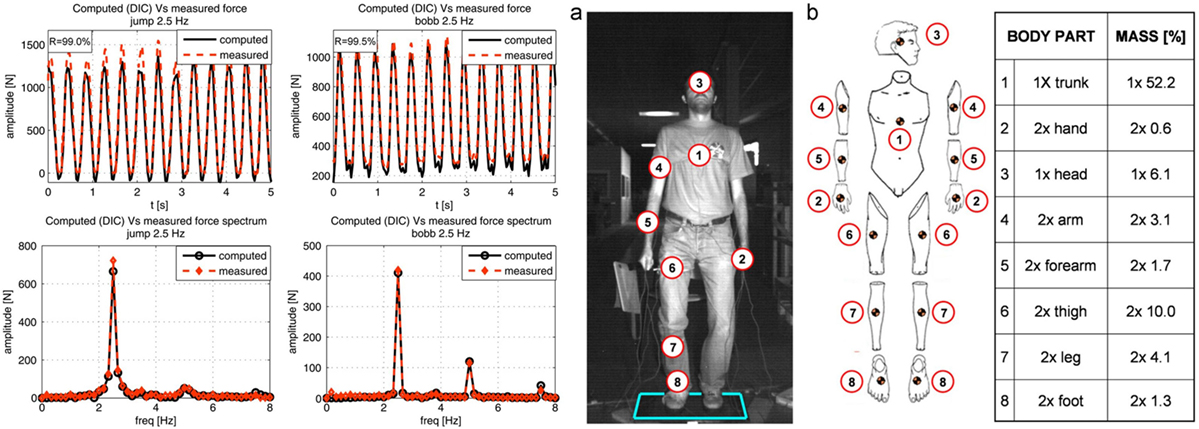
Figure 6. Comparison between measured and estimated forces for both jumping and bobbing tests at 2.5 Hz; results in both time and frequency domain. Reprinted from (Mazzoleni and Zappa, 2012) with permission from Elsevier. (A) Locations of accelerometers on human body; (B) Mass distribution over different body parts.

FIGURE 7

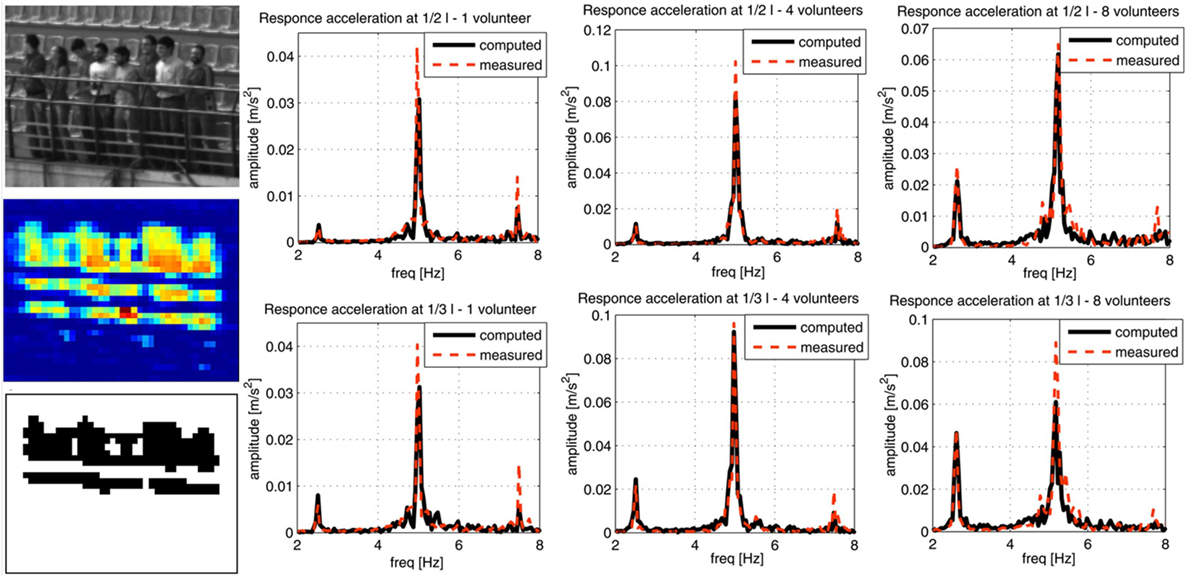
Figure 7. Comparison between measured and computed structural acceleration; tests at 2.5 Hz. Reprinted from (Mazzoleni and Zappa, 2012) with permission from Elsevier.

Regeneration of Force Recordings

A reliable design considering the motion of a crowd requires an accurate representation of loading histories. The common fitting approaches used for load measurements via force plates or load cells at higher sampling rates either in time or frequency domain have now proven to be inaccurate and deficient for the following reasons: (1) real forcing functions are non-identical and not perfectly periodic, (2) fitting functions or Fourier series are incapable of representing the original forcing signals, and (3) it suggests overly conservative designs due to excessive level of vibrations calculated in return. It has been shown by various researchers (Newland, 1993; Brownjohn et al., 2004) that walking and jumping loads are not perfectly periodic and are narrow-band phenomenon (intrasubject variation) by evincing the leakage around higher harmonics and frequently varying phase lags (Figure 8).

FIGURE 8

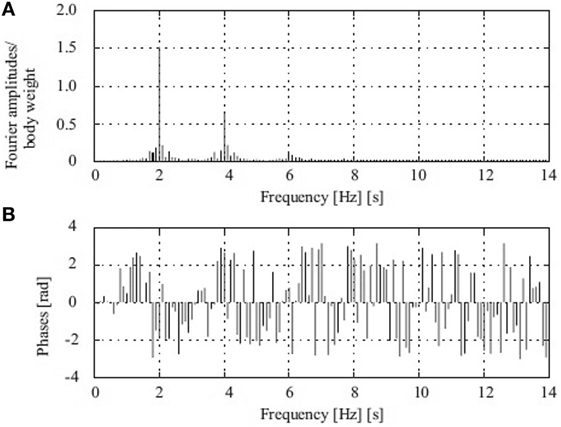
Figure 8. Fourier (A) amplitudes and (B) phase lags up to 14 Hz derived from 10 s of the force record due to a single person jumping at 2 Hz. Reprinted from (Racic and Pavic, 2009) with permission from ASCE.

This knowledge necessitates a more advanced modeling strategy considering the altered morphology, variability of both peak-to-peak intervals and amplitudes of real jumping records. Although there has been studies toward the solution of the problem by utilizing probability distributions to model frequency and Fourier coefficients of jumping pulses (Ellis and Ji, 2004; Kasperski and Agu, 2005), these are insufficient to reflect the true random nature of the problem. The consideration of peak-to-peak timing and amplitude variations are mainly observed through an autoregression model (Sim et al., 2008). Recognizing that the preceding jumps are dependent on each other with an addition of normally distributed error each time, autoregression model is constructed upon two statistics namely mean delay (between the beat and the corresponding jump) and phase scatter (deviation about the mean). However, measured and generated force recordings do not closely match along the full frequency band except for the first two dominant harmonics. This is due to the reason that cosine-squared functions could only fit smooth shaped jumping pulses that are not always the case for different jumping frequencies. Figure 9 illustrates commonly encountered jumping pulse shapes classified as double-peaked, merging, and single-peaked (Sim, 2006). It should be noted that the consecutive pulses belonging to the same jumping frequency also change their shape.

FIGURE 9

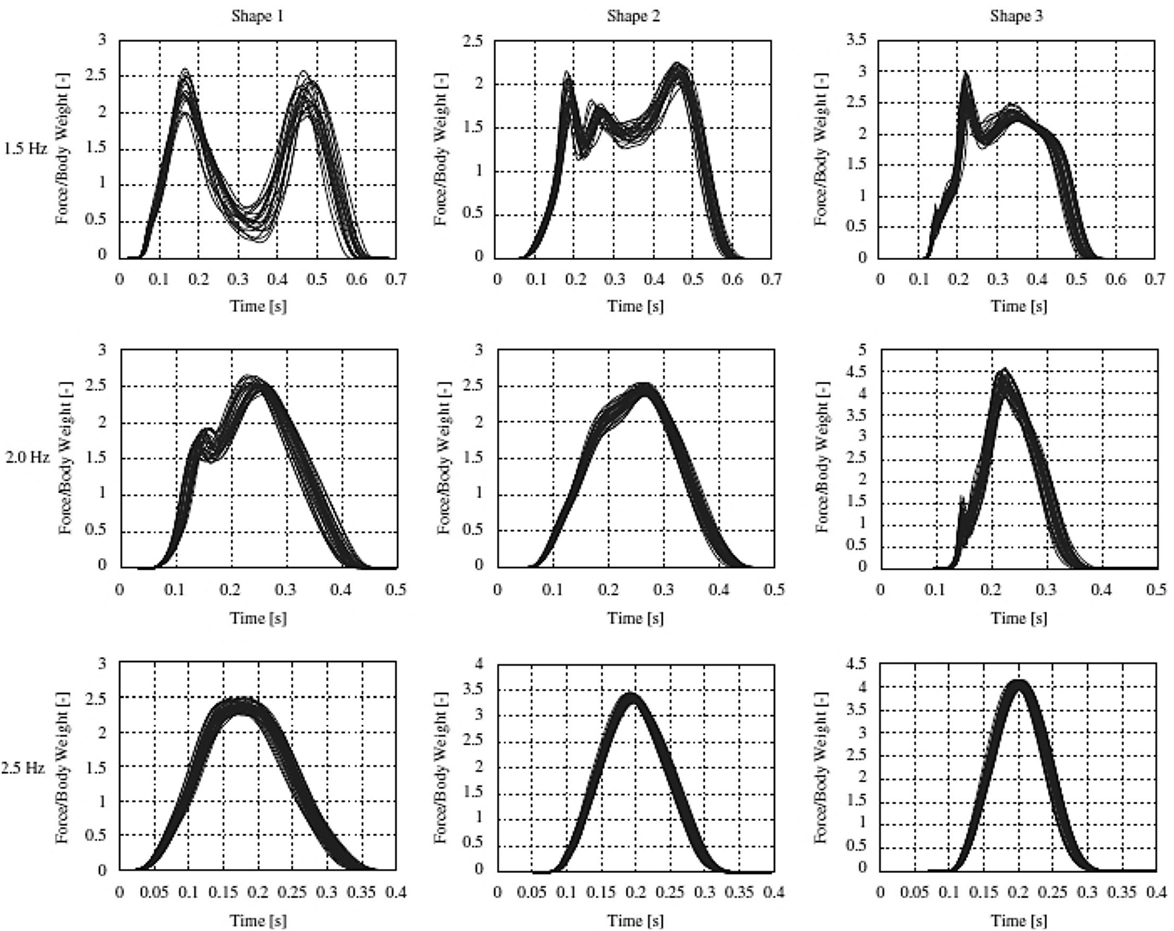
Figure 9. Examples of different shapes of measured force traces due to jumping at 1.5, 2, and 2.5 Hz. Reprinted from (Racic and Pavic, 2010b) with permission from Elsevier.

In a series of recent studies by the same researchers, all these variations in peak-to-peak timing and amplitude and inadequate modeling issues seem to be mostly resolved with a novel approach (Racic and Pavic, 2009, 2010a; Racic et al., 2010b). Through stochastic processes, researchers are able to create a model that considers the lack of symmetry of the single-peaked shapes by fitting Gaussian functions. They also achieve in representing local irregularities by increasing the number of Gaussians in the sum covering high-frequency content of Fourier amplitude spectra. As to developing the model, measured force records serve for acquiring regression coefficients ρ₀ and ρ₁ reflecting the correlation between period T_i and weight normalized impulses I_w,i calculated through Eq. 3:

I_{w, i} = \frac{1}{mg} \sum_{i = 1}^{n} F_{i} Δ t, Δ t = \frac{1}{f_{s}}

(3)

where m_i is the body mass, g is acceleration of gravity, F_i is the force magnitude of the pulse, f_s is the sampling rate, and n is the total number of pulses.

Then, the regression model can be expressed with an error ΔI_w,i modeled as Gaussian noise following a normal distribution as in Eq. 4:

I_{w, i} = ρ_{1} T_{i} + ρ_{0} + Δ I_{w, i} .

(4)

The real novelty of the method dwells in the ability to generate force–time histories utilizing a closed-loop trajectory in three dimensional space (r, θ, z) laying on a unit circle in the (r, θ) plane. Figure 10 shows an arbitrary individual pulse that can be modeled as a sum of Gaussians around a cylinder by making use of Eq. 5:

Z_{i} (θ) = \sum_{r = 1}^{f_{s} / 2} A_{i r} e^{- \frac{{(θ - θ_{r})}^{2}}{2 β_{r}^{2}}}, θ \in [0, 2 π]

(5)

where, A_ir is height of the rth Gaussian peak, θ_r = ω_it_r is the fixed angle with time positions of the Gaussian peaks t_r, β_r = ω_ib_r controls the width with the factors b_r. Simply, changing the angular frequency around unit circle will correspond to the variation of jump-by-jump intervals, whereas tracing the trajectory will provide different size and shapes of jumping pulses. This regeneration process is based on the assumption that the duration of the jumping cycle does not influence the general shape of the unity normalized pulses. Comparison of measured and generated near-periodic jumping force–time histories can be seen in Figure 11.

FIGURE 10

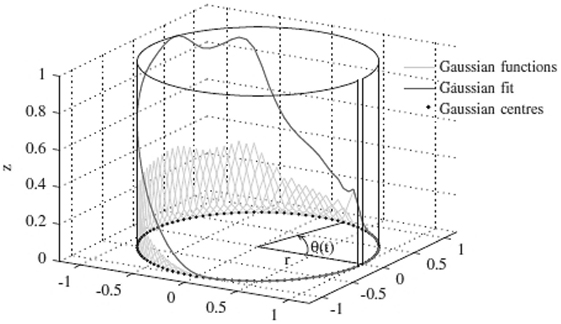
Figure 10. Trajectory of Gaussians in three dimensional space. Reprinted from (Racic and Pavic, 2010b) with permission from Elsevier.

FIGURE 11

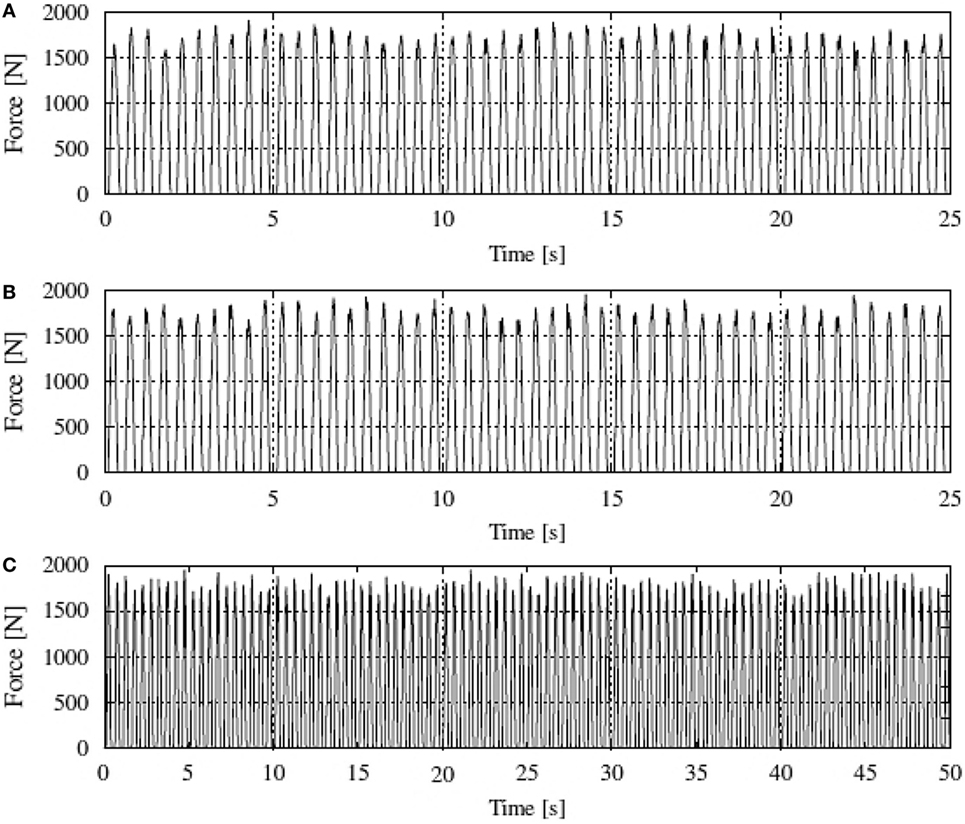
Figure 11. (A) Measured and examples of synthetic force signals when (B) N = 50 and (C) N = 100. Jumping rate is 2 Hz. Reprinted from (Racic and Pavic, 2010b) with permission from Elsevier.

Researchers expand their findings by developing a stochastic jumping load database. 825 measured force signals for the rates between 1.7 and 2.5 Hz are synthetically regenerated utilizing the new method. Considering that each synthetic recording is unity scaled, a vast majority of amplitudes for each recording can be acquired simply incorporating mass distributions for any human population of concern. This novel method seems to reflect the true nature of jumping loading more closely than any other proposed method as well as showing promising indices for the expansion to crowds.

Sensing/Monitoring of Stadiums

Monitoring of real-life stadium structures is crucial to understand the true nature of response of stadium structures. In general, the best approach to find the solution to a dynamic problem is to first conduct tests in a controlled laboratory environment and in most cases, this approach works well. However, the stadium serviceability presents several challenges for laboratory testing. Creation of a scaled down laboratory model with similar slenderness and flexibility requires the use of smaller sections and flexible connections. Because the excitation source is human, the loading case is extreme jumping or bobbing and the possibility of panic exists, the number of people would be limited down to several people. The cost of such planned constructions and acquiring the necessary space is also another obstacle to consider. These limitations bring up the question if the selected group of people would represent the similar nature of the real crowd. Several laboratory experiments of this nature have already been conducted, but this area of research still needs to be further explored.

It is obvious that the best resource to rely on is the data obtained from real events. Like the applications for dynamic assessment of any structure, conventional testing methods such as EMA and OMA are employed. Where field measurements and global behavior are concerned, the best conditions for testing are when the structure is in service, under ambient vibration or both. While field testing of stadiums is the most reliable approach, the following challenge needs to be taken into consideration. The scale of the structure is very large, and it is impractical to implement a full instrumentation network. One proposed solution is instead to focus on the sections that are expected to have the greatest amount of excitation. Another alternative is to use external artificial exciters; however, this is not as effective since each exciter can only affect the modes local to its position. A third solution is to utilize sensors to measure crowd motion. One disadvantage to this approach is that the applicable sensors are mostly limited to accelerometers, since it is not possible to place force plate sensors within the stadium. Thus, all these limitations necessitate long-term stadium monitoring to ensure that the effects of various extreme events are captured and that the monitoring accurately reveals the structure’s response to crowd behavior. Consequently, these factors entail creating a monitoring system that can collect data from a distance and from multiple structures.

Some notable techniques on data acquisition and storage have been observed in the literature. For instance, remote monitoring system is one technique that is quickly becoming an essential part of the monitoring network for stadiums. Remote sensing involves acquiring data from various sensors and surveillance cameras around the stadium and then storing it in a base station synchronously, where researchers can access it via ADSL broadband connection (Reynolds et al., 2004; Setareh, 2011).

Another promising technique is the utilization of either low-/high-resolution cameras or infrared cameras. Their use is becoming widespread because of their abilities to validate recorded data of crowd motion, distinguish the distribution of passive versus active people among the crowd (their ratios to be used in simulation), and assist in load modeling (as it is described throughout this text). One specific instance of camera utilization on determining mass ratios of active to passive people and type of dominant motion for a 3DOF human–structure model can be found in a study by Pavic and Reynolds (2008).

A more comprehensive study by Cigada et al. (2010) on the San Siro/Meazza Stadium proposed a new data acquisition strategy for structural health monitoring. Since the accurate assessment of crowd-induced vibrations requires continuous measurement, a large number of sensors, a sufficient sampling rate, and a storage base capable of holding vast amounts of data, the authors identified four items (sensors, network nodes, Ethernet network, and a “master” computer) that are vital to successful implementation. The master computer controls the whole system as shown in Figure 12. Figure 13A describes how the data gathered from multiple sensor channels are transmitted to a node with a fixed frame rate. A field programmable gate array controls the filtering and down sampling of the acquired data. A first input first output organizes the data that will be sent to the real-time controller, either for long distance transmission or storage. Although there are some problems with the synchronization process, the procedure minimizes the latency between nodes by utilizing a separate activation of the nodes from a central unit every 10 min (Figure 13B).

FIGURE 12

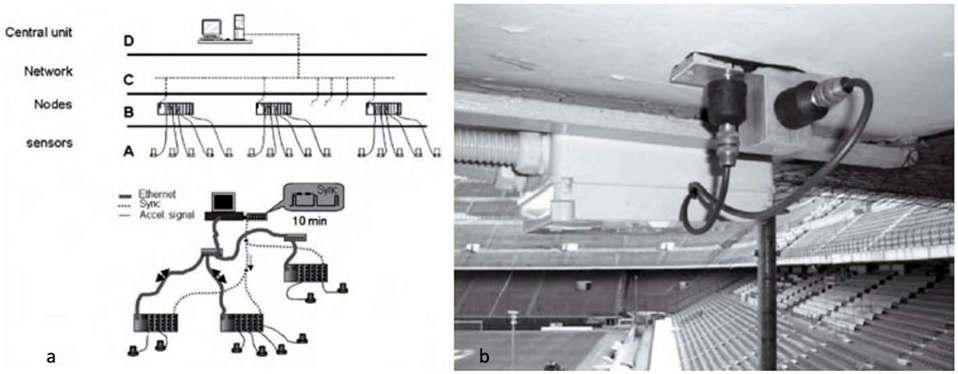
Figure 12. (A) Representation of the network system and (B) sensors deployed in the stadium. Reprinted from (Cigada et al., 2010).

FIGURE 13

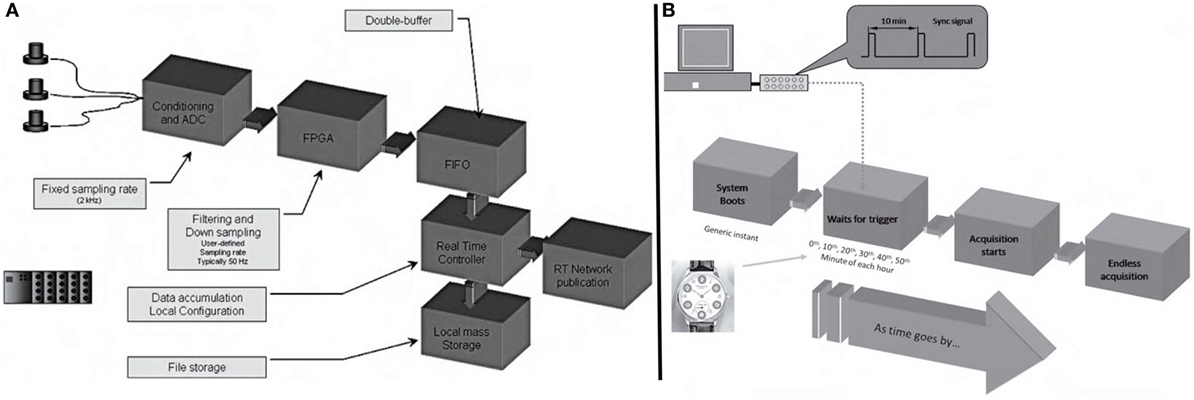
Figure 13. (A) Data acquisition and management logics and (B) synchronization logics. Reprinted from (Cigada et al., 2010).

Caprioli et al. (2009) shows a convenient way for maintaining a huge amount of data collected continuously from a real-life stadium by making use of RMS values that were calculated from vibration data of five different grandstands. The RMS data are used to classify the events as being more or less significant to be analyzed from those which do not have valuable information.

A new approach involving the use of cameras and similar analysis methods for contactless sensing of displacements reveals a new area to be studied and improved (Khuc and Catbas, 2016). In this study, the responses of a football stadium are investigated through the data collection from an experimental setup comprising of two LVDTs and four accelerometers that were attached to a retrofitted W16x40 steel beam of the stadium. The accuracy of the non-target vision-based monitoring method is then compared with the results from other displacement measurements and frequency identification tests.

Figure 14A depicts images captured by the camera and the installed displacement sensors of periods of intense crowd excitement throughout the football game. Figure 14B is the realization of a time window from a concurrent recording showing that both vision-based method and LVDT measurements virtually match.

FIGURE 14

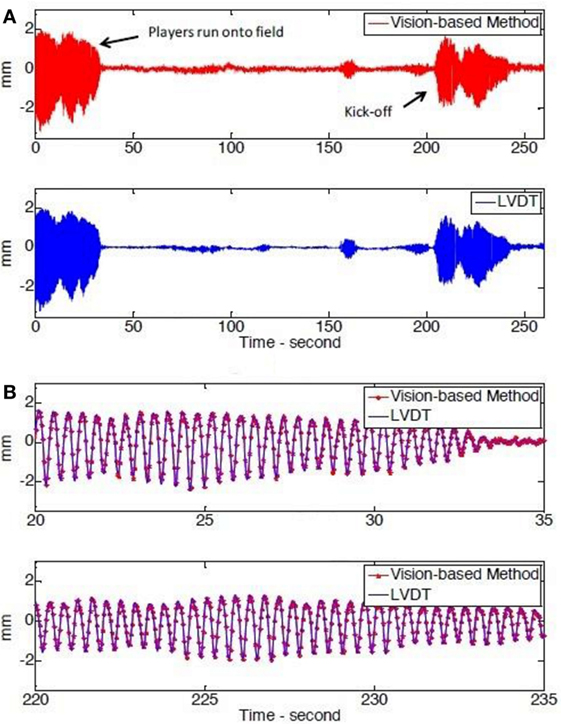
Figure 14. (A) test three displacement datasets and (B) two zoom—in windows from test 3. Reprinted from (Khuc and Catbas, 2016) with permission from John Wiley & Sons, Inc.

Continuing with the same study, a comparison on dynamic characteristics of the stadium is completed by comparing the extracted resonant frequencies coming from the vision-based displacement data with the frequencies extracted from the acceleration data. A reasonable match is acquired in three different frequencies under 10 Hz. This observation confirms the quality of vibration data acquired from the proposed method and enables a potential, easier to access complement for the most common sensors (LVDTs and accelerometers) deployed in SHM.

More efficient monitoring networks might be an alternative for a better investigation providing full scale implementation, especially if the behavior and contribution of additional peripheral members such as roofs or non-structural members are to be understood. Implementing a wired instrumentation monitoring system throughout the entirety of a large structure, such as a stadium, is simply impractical, expensive, time consuming, and labor intensive. Instead, wireless sensor networks (WSNs) can be used as an alternative. WSNs are easy to install, have low installation costs, and are capable of on-board computation and signal processing. This unique capability allows measured signals to be transformed into usable formats by each unit in the network before being transferred to the base station, reducing the amount of data to transfer and power consumed.

Although WSNs have their own challenges, these issues can be dramatically diminished by pairing them with other developments in technology. For instance, the time synchronization of large number of wireless sensors in the network is now reliably taken care of via time-synchronization protocols (Ganeriwal et al., 2003). Another challenge to consider is the power consumption of the wireless units, which requires routine replacement of batteries during long-term monitoring. A possible way to resolve this issue is to utilize power harvesting technologies—solar, wind, or vibrational energy converted to electrical energy—that can power the wireless sensing units renewably. Another solution for the power consumption problem is to compress data and to develop decentralized health monitoring algorithms for the on-board computational capabilities of wireless units.

An extensive study of a large-scale WSN implementation conducted by Shen et al. (2013) demonstrates the efficacy of this technology. The WSN was installed to monitor the National Stadium in China, generally known as the “Bird’s Nest,” which is very rigid structure. Various sensors (290 in total) that capture data concerning stress, displacement, acceleration, wind, and temperature were installed on the structure (Figure 15). The battery problem was addressed by using low-voltage and low-power microchips together with suitable energy management. The study employed independent radio frequency to reduce interference between different wireless network topologies. Based on the geometry and orientation of the structural members, a chain type network was chosen. The chain network allows for “dynamic addressing” which searches for weak connection routes and automatically replaces them with new, robust ones. This network topology is controlled by an algorithm developed with graphical user interface and is capable of rearranging topology, reassigning ID address, and artificially executing sampling.

FIGURE 15

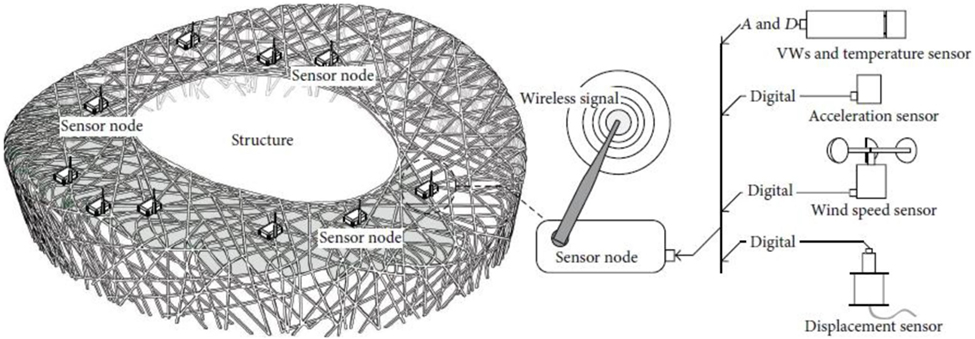
Figure 15. Wireless sensor network and multiple sensors for different measurements. Reprinted from (Shen et al., 2013).

Human–Structure Interaction

In stadium modeling, the most troublesome part of human–structure interaction, especially for assembly type structures, is the significant change in dynamic parameters due to crowd excitation. Based on preceding research, the mass ratio between the occupants and the structure itself, along with the slender characteristics of the structure (natural frequency range), are the most essential factors for determining whether to account for the effect of occupancy or not. Past observations reveal that this effect cannot be represented by only adding mass on the model, since the human body is contributed to the mass, damping, and stiffness of the structure through its inherent specifications and shifting postures. The phenomenon shows up as an increase or decrease in the recorded natural frequencies, as well as additional frequencies and highly altered damping. Intersubject and intrasubject have the ability to input or take away energy from the system, thus changing the dynamic behavior dramatically. Therefore, several additional conditions of the event need to be identified, such as what portion of the crowd is passive or active, what type of loading should be considered for the modeling of the active crowd (jumping, bobbing, or bouncing) and the degree of synchronization in their motions. The best approach so far, which shows a strong correlation between experimental and theoretical models, is to model the human–structure interaction as a mass spring damper system of three DOFs. The additional degree of freedoms are included to simulate structure, passive, and active crowds (Jones et al., 2011a). This approach is now known to provide more accurate results than most conservative approaches used in other studies (Pavic and Reynolds, 2008; Jones and Reynolds, 2009). Thus, implementation of this approach can be challenging and time consuming.

To better understand the effect of crowd excitation, there are several key issues to consider, such as the mass ratio of occupants to structure, distribution of the crowd, which portions of the crowd are active or passive, and the posture of the occupants. Salyards and Firman (2011) provide results from an experimental study by narrowing this investigation down to passive crowds and looking at their distribution, mass ratios, and different postures. In the study, groups ranging of 1–19 people (simulated various occupant-structures mass ratios) were required to stand with three different postures (standing straight up, standing with knees bent, and seated) on a composite slab, while it was being excited by an electromechanical shaker with a swept sine input. The experimental results were compared to a theoretical equivalent mass model. The data indicated that for a fixed number of people, the density of the crowd did not appear to influence the dynamic properties around the first natural frequency. However, as the mass ratio was increased, there was a decrease in the natural frequencies and an increase in damping ratios. Additionally, it was found that standing straight up or remaining seated resulted in the greatest increase in the natural frequency and standing with knees bent had the least impact. The same observations were also made for damping ratios (Noss and Salyards, 2012).

In a discussion by Salyards and Noss (2014), the experimental responses from the previously mentioned study were compared with those predicted by the British guidance “JWG” (2008). The guidance included models of two different crowd motion types: active standing (frequency of 2.3 Hz and 25% critical damping) and predominantly seated crowds (frequency of 5 Hz and 40% critical damping). The guidance’s experimental results on damping provided similar findings to those from Salyards and Noss’ study. However, there were variations in the results from a crowd standing with bent knees. Discrepancies are thought to stem from a person’s inability to maintain the same position for an extended time. An important discovery from the guidance and study is that the natural frequency affects both the damping ratio and posture. This discovery was made by varying the structural configuration but keeping the posture and mass ratio constant. The seated and standing JWG models are reported to underestimate the damping of the first mode resulting in unrealistic responses. This is a major problem since damping is a major factor in the vibration serviceability evaluation. Frequencies show mixed alterations in the form of increase, decrease, and addition of a second mode. The frequencies from the JWG model results are consistently less than experimentally acquired values. Salyards and Noss propose a new model that has the same SDOF implementation as in JWG, but instead has a 7.3 Hz frequency and 40% damping to fill the void point for standing passive crowds in JWG. Compared to the seated model, the proposed model has produced results that are more consistent with experimental findings.

Utilizing the same experimental program from the Salyards and Noss (structure, mass ratios, excitation, and experiment methodology), another study was conducted, this time including passive seated occupants. The experiment observed the effects of two different seating positions: the first position had the subjects seated with their back completely straight and arms resting on their legs and the second had the subjects lean forward while resting their elbows on their legs. From the study, it was observed that the damping ratio for a particular seated position did not always increase with the mass ratio. However, the damping ratio of the structure when it is occupied with different seated crowd size can increase the damping up to 13% and reducing the response as a result. This may mislead the designers to endorse the vibration serviceability of the structure that is normally unacceptable when empty. The dependence of damping ratio on the empty structure’s frequency and the occupant-structure mass ratio as it is found in Salyards and Noss (2014) is confirmed via observations.

An investigation by Harrison et al. (2008) examines the effects of a single subject on the alteration of structural mass and damping through jumping and bobbing on a perceptibly moving structure (Harrison et al., 2008). The investigation consisted of six different scenarios with varying mass and damping conducted on a special test rig whose natural frequency range and damping could be adjusted arbitrarily. The first observation made is that it is not possible to jump or bob near the resonance frequencies due to the excessive motion thus forcing the subject to adjust itself to the new frequency compatible with the given timing for a new jumping cycle. This effect appeared to diminish as the mass and damping ratios were increased separately. A new factor called “drop out” is defined as the minimum force at resonance divided by the value away from resonance where the force reaches its typical jumping level, to give an insight about the significance level of human–structure interaction on structures. Therefore, low values of the dropout factor indicate a deeper human–structure interaction, while a value close to “1” indicates negligible human–structure interaction. Further suggestions have been made on the reduction of dynamic load factors (DLFs) (Jones et al., 2011a), which are the magnitudes of sinusoidal harmonic force components in recreation of force–time histories. This reduction is observed to go up to 50% making DLF-based load modeling overly conservative and an idealized frequency-based simple methodology called “V-notch” curve to obtain dropout factors.

For a sample curve to be adopted in any guidance, a database including different jumping and bobbing rates as well as wide variety of mass and damping ratios need to be generated. Such a database could be used to create a versatile curve that better fits in performance design. DLF reduction is also realized in another study (Comer et al., 2013) in which 15 test subjects bob following a frequency range of 2–3.5 Hz on a specially built laboratory grandstand (Comer et al., 2007, 2010) simulator that has adjustable rigid and flexible support conditions. This study, in addition to the work done by Harrison et al. (2008), suggests that when the subjects adapt to new bobbing style it reduces the structural motion and hence the DLFs. This finding reveals two more possibilities to consider. The first is that the ability of the group absorbing energy from the system which is eliminated calculating the cycle-by-cycle average power of the system and the second is the group being able to supply energy in the system.

Some additional studies investigate the effects of four different seating types (e.g., a grandstand seat, a work desk chair, a swivel chair, and a rigid seat) occupied by subjects with various postures when coupled with changing occupant-structure mass ratios (Pedersen, 2008, 2009). Although previous studies generally agree that the human body should be modeled as a mechanical system with dampers and springs, which vibrates together with the structure mass, this study proposes that the human–seat–structure interaction would be a better model. This proposition was based on the fact that there is an increase in frequency when swivel chairs (flexible seats) are used, which is not present in scenarios involving rigid seats. Damping values are found to be dependent more on number of people rather than the posture and seat type.

Analysis of the Measured Data for Structural Identification and Human Comfort

Ensuring the successful identification of structures through experimental data will assist with:

• Understanding how a structure responds to the various types of crowd interaction (e.g., periods of intense motion; standing, sitting, and shifting postures; entering or leaving the stadium).

• Calculating appropriate values for structural parameters of finite element models that will be used to represent the true behavior of the actual structure.

• Measuring the accuracy of newly developed load and human–structure interaction models by comparing it to the finite element models and in-service response of the structure.

• Detecting any possible non-linearities that crowds induce in the system.

There are a few studies that address the performance of conventional identification methods for stadium service data (Prasenjit et al., 2005; Reynolds et al., 2005; Peeters et al., 2007). In these studies, different powerful OMA methods, such as Enhanced Frequency Domain Decomposition, Least Square Complex Exponential, Stochastic Subspace Identification (SSI-CVA, SSI-UPC, SSI-PC), Natural Excitation Technique, and Eigensystem Realization Algorithm, were used to analyze the data from common stadium conditions observed during a football game (Prasenjit et al., 2005; Reynolds et al., 2005). The different conditions that were observed were empty, crowd entering in, crowd seated, half-time, crowd leaving, and celebration due to a successful play. Two notable observations from the study were that dominant changes occurred in the frequency and damping values, and that the magnitude of the changes depended on the crowd configuration. The first observation was consistent with the findings from other literature. The study also revealed that the estimated parameters for each method were different, although the same data were used to estimate them. Based on the results from the study, it is suggested to use all possible different methods for creating reliable intervals and to complete a comprehensive identification study.

While it is suggested to use all possible methods to study a structure, not all methods may be applicable for stadiums. For instance, an OMA method may only be applied if several requirements are met, such as the whole frequency band must be excited, the structural system must be linear and time invariant, and most importantly, the excitation must be in the form of Gaussian random white noise. These requirements can be prohibitive for dynamic stadium analysis, since crowd movement can introduce dominant harmonic components into the system that transforms the excitation into colored noise. Additionally, the dynamic response parameters of the structure are not time invariant. In a finite-element modeling and updating study, it was observed that structural systems are possibly non-linear systems because of the large variability in measured damping values (Jones and Reynolds, 2009). In these cases, the use of current OMA techniques for stadiums problems could produce highly questionable data.

In light of research from 2008, it has been proven difficult to assess the extreme vibration levels on humans with the prescribed methods, current standards, and guidance for several reasons: (1) vibration levels are perceived differently from person to person and also from one location to another in the same structure, (2) spectators react differently depending on the type of the event, even though the same discomfort parameters are found for each event, and (3) each structure responds uniquely to crowd excitation. The current well-known and widely used assessment methodologies for vibration level measurements are “BS 6841” 1987, “ISO 2631-1” 1997, and “ISO 2631-2” 2003 (General Mechanical Engineering Committee, 1987; ISO/TC 108/SC 4, 1997, 2003). These standards were originally developed to evaluate human exposure to vibrations caused by operation of machinery and vehicles, but the same procedures were thought to be applicable to structures as well. The assessment measures used in these standards, such as RMS, running RMS, maximum transient vibration value (MTVV), fourth power vibration dose value (VDV), or root mean quad (RMQ), have slight differences in their calculations of measurement directions, subjects’ posture, application of frequency weightings, etc. Detailed information on the application of these measures have already been given in the review study by Jones et al. (2011a) mentioned above.

The research in the last decade has mainly focused on the application of health, perception, motion sickness, and comfort classification measures for sporting events (Salyards and Hanagan, 2007; Catbas and Gul, 2009; Catbas et al., 2011), concerts (Salyards et al., 2006; Caprioli and Reynolds, 2007), or a combination of both; and for a long-term monitoring (Caprioli and Vanali, 2009; Caprioli et al., 2009; Salyards and Hanagan, 2010; Cappellini et al., 2015). The following section intends to discuss some of the significant findings of this recent research and to indicate all critical research areas with somewhat consistent findings related to grandstands.

A psychophysical experimental method, called subjective scaling, was used to study an occupants’ comfort and perception levels, while either sitting or standing (Nhleko et al., 2009b). Comer et al. (2007) studied the often-confused relationship between human vibration perception and comfort levels through the use of a controlled occupied grandstand. Subjects were asked to stay on the grandstand as it was gradually excited with different RMS powered sine wave vibrations from 2 to 6 Hz. The subjects were then had to choose their subjective vibration perception and comfort levels from a bank of provided text descriptors. Their responses were then compared with frequency weighted acceleration of two particular standards namely “BS 6841” 1987 and “BS 6472” 1992 (General Mechanical Engineering Committee, 1992). Extreme perception levels seemed to be occurring before the actual discomfort was felt, thus making perception levels more important in serviceability assessments. Also, the serviceability data for grandstands are found to be below the limits given for transportation structures (BS6841) but significantly above the limits for buildings (BS 6472).

Following the same experimental psychophysical methodology, Nhleko et al. (2009b) proposed a new approach for perception assessment that considered the relation between human comfort and either the RMS of the normalized GRFs time history or the normalized foot point acceleration time history (Nhleko et al., 2009a). The study was originally motivated by the idea that the GRFs obtained with stationary measurements are different from those of a moving grandstand (Yao et al., 2006). The study consisted of 10 subjects of varying weight, who were asked to stand on force plates that were mounted on a grandstand’s floor while it was being excited. Then, their subjective responses were recorded. For frequencies of excitation lower than 2 Hz, GRF oscillations display the same characteristics as the grandstand oscillations. However, for frequencies greater than 2 Hz, GRF wave forms become inconsistent and almost non-linear in trend. This pattern indicates that the subjects were trying to adapt themselves to the new state of motion. At a frequency of 4 Hz, the subjects began to experience acute levels of discomfort. The study concluded with normalizing the GRF histories by gravity (meaning foot point acceleration), which revealed that the RMS values of normalized GRFs are more reliable for the assessment of human discomfort levels. GRF and RMS values were found to increase proportionally but were not necessarily proportional with increasing RMS values of the grandstand vibrations.

Although the weighting of acceleration record seemed to favor the calculation of primary assessment measure (RMS), the method’s outcomes are not drastically different from those of other methods. Reported RMS values are likely to vary within the time window that they are calculated; unfortunately, it is still unknown how long the duration should be. Although the evaluation via MTVV (derived from running RMS) is independent from duration and is mostly the case for grandstands considering the excessive vibration exceeding crest factor threshold, the information on the event causing the extreme values cannot be extracted. VDV and RMQ calculations experience the same problems. These alternative measures have not been given specific limits in the standards. However, VDV measures of perception can be made referring to a scale given in previous studies, which has proven to be the most reliable method among the others so far. In most cases, measures of perception or human discomfort levels from the measurement scale do not match with the actual, observed behavior of the occupants; raising questions of its appropriateness for application on grandstands.

Conclusion and Recommendations for Future Research

Taking the gaps of the existing knowledge on dynamic assessment of stadium structures into account, the developments and promising improvements at different stages of the problem are presented in light of the research that has been conducted in the last decade. The surveying of the current literature clearly states that significant improvements still need to be made. A summary of the review and future research suggestions are presented below.

Measurement and Sensing

A strong development made in load modeling is the utilization of visual data marker tracking and computer vision methods. The ability of data marker tracking to make accurate estimations makes it a promising alternative for measuring carried out on moving flexible structures. The use of image processing and computer vision techniques allows for completely contactless measurement of loads and has the following advantages: it is inexpensive, can track large numbers of people, and can be utilized in virtually every environment. This approach completely removes the need for laboratory measurements and implementation of mathematical fittings. It is also suitable for assessing both an individual’s induction on a system and a crowd’s. This is a huge improvement considering the expansion problem of individual load measurements to crowds.

Although it is claimed that the visual tracking method can make free field measurements without utilizing force plates, it still has some significant obstacles. Visual tracking methods are quite expensive to instrument large numbers of subjects with data markers in the field and it necessitates that the subjects remain in a prescribed line. This method is currently unable to track the motion of overlapping subjects.

The disadvantages of the computer vision and image processing based approaches are (1) it generates large amounts of data that are not feasible to be stored and analyzed for the long term, (2) cameras used to capture crowd motion cannot be placed in front of the crowd, (3) the lighting conditions and extraneous camera flashes may affect the results, and (4) cameras do not account for extraneous vibrations when recording. These problems are the motivation for further research on generating more efficient algorithms and on classification criteria for data to be stored based on the significance of the event. Creation of algorithms that are capable of counting and tracking multiple subjects through facial recognition might lead to more accurate response estimations and could assist with identification and isolation of passive and active members within the crowd.

Monitoring networks must become smarter and remotely controlled to handle the large size of stadium structures and maintain long-term monitoring of forces. The use of WSNs might be promising alternatives for full field implementations, since they are currently effective in monitoring portions of the stadium. Wireless networks could be applied to fairly underestimated members such as roofs (which are shown to have a dominant effect on global modes) and non-structural members in order to gain a better understanding of their behavior and of how to incorporate them into computer models.

Load Regeneration, Human–Structure Interaction, and Structural Identification

The stochastic load modeling approach is superior to the conventional half sine or Fourier series fitting methods because of its incredible abilities to replicate intra-personal variations and to reproduce force–time histories of variable length. Acquisition of every harmonics as in the original recordings with their spread over the spectral energy is factors that would prevent overestimations of responses. Stochastic load modeling has not been expanded from individual load modeling to crowd modeling. The next step is to generate synthetic histories by using data from a large variety of jumpers, bobbers at varying frequencies. These histories could then be condensed into a database that would later on let these excitations to be treated as a spectrum as in earthquake resistant design. Such a spectrum might easily be adopted in current guidance and used by designers.

Most of the studies from the last decade have generally focused on the damping and frequency alterations caused by the changes in the number of passive occupants, in their postures, and in their activities. The general observation that higher mass ratios yield a decrease in frequencies and an increase in damping ratios continues to be valid in general, although there are few exceptions that dispute this finding. Other studies claim that the changes in damping ratios depend on both posture and frequency.

All past experiments have been carried out under prescribed scenarios. At this time, there has still not been enough studies that have combined passive and active inter-personal effects, isolated them or incorporated them into the estimation process.

Operational modal analysis identification techniques that have been used so far give fairly approximate results but it a huge question remains whether the existing OMA methods are suitable to use for stadiums. The efficiency of the numerous identification methods still needs to be assessed. Newly developed methods in the scope of stadium monitoring should be introduced.

In future research, possible non-linearities of slender stadium structures, time-variant characteristics of the excitation, and existence of possible harmonics need serious investigation.

Vibration Serviceability

Of all the preceding research, the main point of discussion is on the applicability and compatibility of the operating machinery based standards for the grandstand serviceability problem; as the excitation type have different inherence compared to machinery based vibrations.

The idea of forming new type vibration serviceability limits, or the revision of existing ones to include human-induced excitation and building characteristics, is widely agreed upon, since the ones currently in use are incapable of accurately reflecting the true state. In the future, incorporation of more structures or event-based case studies can assist with the creation of a database and of more robust limit state measures.

Another possible area for investigation is the generation of a new assessment measure based on displacements of the structure that considers that vibration-based measures vary from person to person, are event dependent, and they are equally likely to create panic by visual inspection of the audience.

Author Contributions

FC—PI and leading investigator. OC—research assistant of FC. OA—leading researcher at Qatar University. OA—research assistant of OA. MG—leading researcher at University of Alberta. ND—research assistant of MG.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

The financial support for this research was provided by Qatar National Research Fund [QNRF (a member of Qatar Foundation)] via the National Priorities Research Program (NPRP), Project Number: NPRP 6-526-2-218. The statements made herein are solely the responsibility of the authors.

References

AMTI. (2008). AMTI User Manuals. Watertown, MA, USA: Advanced Mechanical Technology, Inc.