- 1Institute of Structural Analysis and Antiseismic Research, National Technical University of Athens, Athens, Greece
- 2Department of Civil Engineering and Energy Technology, Oslo and Akershus University College of Applied Sciences, Oslo, Norway
A new optimization concept is introduced which involves the optimization of non-linear planar shear buildings by using gradients based on equivalent linear structures, instead of the traditional practice of calculating the gradients from the non-linear objective function. The optimization problem is formulated as an equivalent linear system of equations in which a target fundamental eigenfrequency and equal dissipated energy distribution within the storeys of the building are the components of the objective function. The concept is applied in a modified Newton–Raphson algorithm in order to find the optimum stiffness distribution of two representative linear or non-linear MDOF shear buildings, so that the distribution of viscously damped and hysteretically dissipated energy, respectively, over the structural height is uniform. A number of optimization results are presented in which the effect of the earthquake excitation, the critical modal damping ratio, and the normalized yield inter-storey drift limit on the optimum stiffness distributions is studied. Structural design based on the proposed approach is more rational and technically feasible compared to other optimization strategies (e.g., uniform ductility concept), whereas it is expected to provide increased protection against global collapse and loss of life during strong earthquake events. Finally, it is proven that the new optimization concept not only reduces running times by as much as 91% compared to the classical optimization algorithms but also can be applied in other optimization algorithms which use gradient information to proceed to the optimum point.
Introduction
Optimization techniques play an important role in various occasions in structural design, where they can be used by engineers, decision makers, etc. to find the best possible solution. Optimization methods used for structural design can be classified into various categories, i.e., deterministic or stochastic (based on whether the model involves a fully specified or probabilistic formulation), constrained or unconstrained, local or global, etc. The objective of any structural optimization algorithm is to select among various possible design cases the optimum case which will minimize cost, maximize safety, and at the same time comply with the various design and construction constraints, if present.
In modern structural design for static and/or dynamic loading, it is intended to design structures that will partially respond in the inelastic range, since this design proves to be more economical. Especially in seismic design, inelastic behavior is acceptable within certain limits, determined by the tradeoff between structural safety and economy. Besides, many structures have resisted earthquakes during which much higher inertia forces were induced to them than their strength calculated through linear elastic force-based design. The concept of ductility was introduced to justify the latter and as a design tool for the former. These facts are realized by most current seismic design codes, mainly based on the traditional force-based design procedures, which take these effects into account by introducing modification factors to reduce seismic force and overstrength demands depending on the structural system and the ductility desired. However, both force-based and displacement-based design concepts are based only on the peak responses of a structure subject to an earthquake; the loading history or the time history of its response are not taken into account. The peak response does not provide enough information on how the structure has performed non-linearly during an earthquake ground motion; there are various quantities which accumulate within the structure, such as the plastic energy absorbed by the structural components. The latter is a good indication of the damage suffered by the structure, especially in reinforced concrete structures. Therefore, it should be understood that seismic design should be time-history dependent and not based only on peak response at specific time instances. Based on the above a new design method has appeared, based on the energy input and dissipation in structures, named Energy-Based Design (EBD). According to this method, an energy-dissipating mechanism has to be designed, which must have the ability to absorb greater amounts of energy than the input energy to a structure during strong ground motion, in order to ensure that the structure will efficiently resist earthquake motions.
Apart from the ductility of the construction material, the seismic performance of a structure is affected by its structural configuration and the distribution of strength and stiffness. Most collapses during or after past earthquakes have occurred to some extent due to incorrect structural configuration. The creation of soft storeys is a characteristic example of deficient structural behavior, where excessive ductility and drift are observed at a single floor of a building, leading to local collapse. Most buildings are designed according to the concept of equivalent static forces prescribed by seismic codes. The heightwise distribution of these forces results from the inherent assumption that the vibration modes of the structure are linear elastic. On the other hand, according to the EBD concept, it is assumed that the structure responds non-linearly; consequently the assumption of linear elastic modes does not lead to realistic calculation of equivalent force distributions of the structure, and thus does not necessarily ensure optimum seismic performance, or even safety.
In this study, a new iterative optimization algorithm of Newton type with line-search capabilities especially designed for structural optimization is presented and implemented for the optimum structural design in terms of the energy absorbed during an ensemble of seismic excitations. More specifically, the objective of the optimization process is to minimize the variation of the dissipated energy distribution along the height of a MDOF planar shear building, by finding the optimum distribution of storey stiffness and strength, for a prescribed fundamental (small strain) eigenperiod of the building. The optimization procedure is applied both for linear elastic and elastoplastic buildings. Based on the optimization results, the effects of different earthquakes, number of stories, and amount of viscous damping along the height of the building on the optimum strength distributions are investigated and discussed.
Literature Review
In most seismic design codes for buildings worldwide, the seismic effects on structures are taken into account in simplistic ways which refer to linear elastic structural models, or lateral force methods of analysis, e.g., CEN (1998), KBC (2009), International Code Council (ICC) (2006), UBC (1997), NZS1170 (2004), AIJ (1996). For example, in Part 1, section 4.3.3.2 of CEN (1998), the horizontal seismic force distributions to be applied for design are determined based on the elastic properties of the structure, or even on a triangular distribution of horizontal displacements. It is apparent that these force distributions usually do not lead to evenly distributed dynamic distress of building structures, and therefore attempts have been made in the past to calculate these distributions in an optimum way by enforcing that distress and damage are equidistributed among the storeys of a building.
A first approach is to apply the theory of uniform deformation to determine the optimum seismic forces (Moghaddam and Hajirasouliha, 2004). According to this concept, while in most conventional design cases the ductility demand will vary among the floors of a building, leading either to material partially working or to material less than required, it is enforced that the maximum inter-storey drift is uniformly distributed heightwise, and equal to the maximum allowable limit. Thus, the condition of uniform deformation results in optimum use of material. The uniform deformation theory has been successfully applied in various studies for optimum seismic design of shear buildings, either fixed base (Moghaddam and Hajirasouliha, 2006; Park and Medina, 2007; Hajirasouliha and Moghaddam, 2009; Hajirasouliha and Pilakoutas, 2012; Hajirasouliha et al., 2012) or with soil–structure interaction effects taken into account (Ganjavi and Hao, 2012, 2013).
Besides these, hysteretic energy dissipation in a structure during an earthquake is the key factor related to the amount of damage in it. A structure is considered to resist an earthquake ground motion provided that the energy input to the structure from the earthquake is lower than its energy absorption capacity. Following this, the EBD concept as well as the determination of elastic and/or hysteretic energy distributions were examined for MDOF systems (Berg and Thomaides, 1960; Penzien, 1960; Zahrah and Hall, 1982; Akiyama, 1985; Nakamura and Yamane, 1986; Léger and Dussault, 1992; Rodriguez, 1994; Nakashima et al., 1996; Connor et al., 1997). Chou and Uang (2003) presented a procedure for the distribution of seismic energy demand over the floors of a MDOF system solely by modal superposition of energy shapes, which are established from a static pushover analysis. Similar equivalent SDOF system concepts have also been used in the context of modal pushover analysis to estimate the hysteretic energy demand without the need for non-linear time-history analysis (Ghosh and Collins, 2006; Prasanth et al., 2008). Wang and Yi (2012) and Mezgebo (2015) proposed suitable hysteretic energy distributions for MDOF systems.
Apart from the above, it has been shown that the addition to the structure of dampers of various types leads to modification of the hysteretic energy or maximum inter-storey drift patterns. Optimum stiffness distribution along the building height has been proposed by Uetani et al. (2003). Optimum placement of oil, hysteretic, and inertial mass dampers in order to minimize the maximum inter-storey drift of the structure has been examined by Murakami et al. (2013). Detailed methods for addition of dampers in structures to optimize performance-based design for earthquakes can be found in Takewaki (2011).
Despite the large amount of the literature being concerned with hysteretic energy distributions in shear buildings, to the best of the authors’ knowledge, the investigation of the conditions for uniform distribution of hysteretic energy along the height of a shear building has not been yet addressed in the literature. Shargh and Hosseini (2010) and Shargh and Hosseini (2011) showed that it is possible to find an optimal stiffness distribution over the height of a linear elastic MDOF building to minimize the total seismic input energy, a ratio of which is the hysteretic energy responsible for structural damage. This optimum stiffness distribution results in minimum value of total dissipated hysteretic energy (Shargh et al., 2012).
Purpose of the Present Study
The issue of optimum seismic design of non-linear MDOF structures by modification of the stiffness and strength properties in order to achieve a uniform hysteretic energy dissipation pattern over the structure’s height requires the formulation of a theory of uniform hysteretic energy dissipation, similar to the theory of uniform deformation already used for optimum seismic design and presented in the previous section. It has been shown that according to the latter with decreasing lateral yield strength the ductility demand decreases and if the former becomes lower than a certain point this trend is reversed (Penzien, 1960). However, the variation of hysteretic energy demand with yield strength is not as obvious as the variation of ductility demand with yield strength; it also depends on additional factors such as the duration of the seismic event. This entails that more robust techniques than those used for the uniform deformation theory have to be used to find optimum structural properties for uniform hysteretic energy distributions. An attempt to develop a new powerful optimization technique is made in this study to solve the uniform hysteretic energy problem in MDOF systems, a problem that has not been solved yet, to the best of the author’s knowledge. Therefore, two main novelties are considered in this study:
• Formulation of the theory of uniform energy dissipation and optimum design of shear buildings according to the former, and
• Development of a new fast and robust energy-based optimization technique.
Numerical Modeling
Structural Model
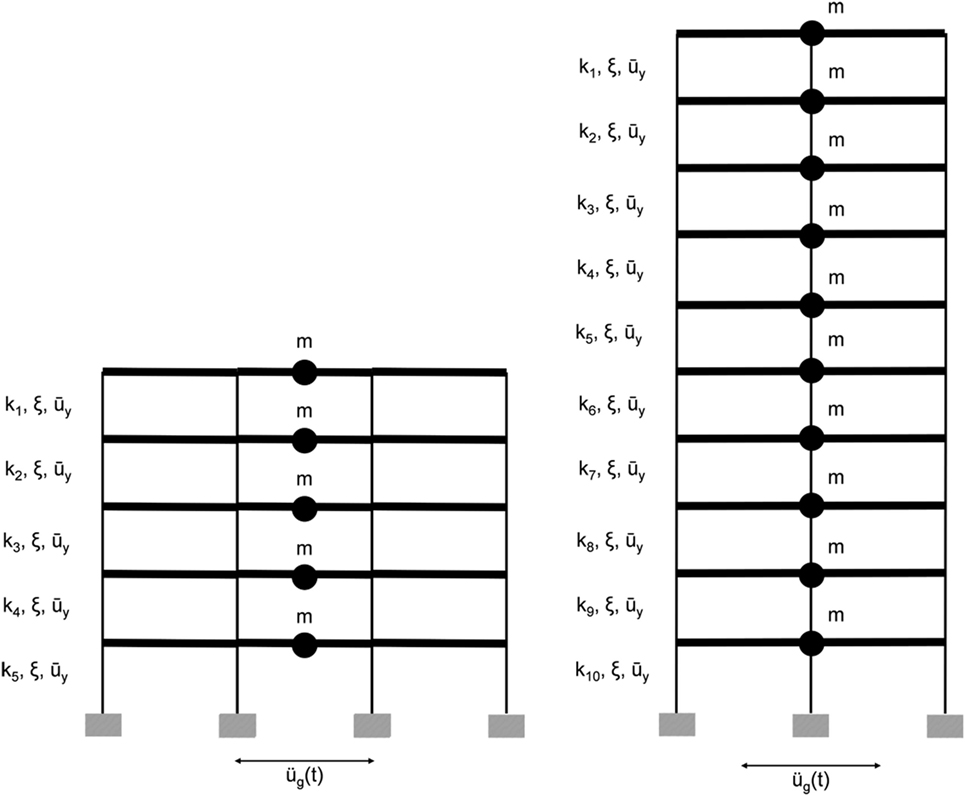
The most common model used for the dynamic response history analysis of building structures is the shear beam model. This system is represented by a viscously damped spring-mass system, where the mass is considered to be concentrated on each floor level and the storey shear force versus storey deflection relationship is presumed to be bilinear with a very low non-zero positive post-yield stiffness, so that the model responds effectively as elastic—perfectly plastic. The building deforms only in shear, since it is assumed that the floors are axially and flexurally rigid. Regularity with regards to the mass distribution along the height of a building is assumed and also it is presumed that changes in the stiffness distribution lead to negligible changes in the mass distribution (resulting from changes, e.g., in the cross section of the columns, etc.). Moreover, it is assumed that the floor masses move horizontally only within a vertical plane. Two MDOF systems are analyzed: one 5-storey building and one 10-storey building. For each of the two MDOF systems the height of the stories is assumed to be equal to 3 m and the mass per floor is assumed to be equal to 25,000 kg. For each building a realistic value of fundamental eigenfrequency f0 has been assumed; for the 5-storey building it is set equal to 2 Hz (corresponding to fundamental eigenperiod 0.5 s) and for the 10-storey building it is set equal to 1 Hz (corresponding to fundamental eigenperiod 1 s). The well-known rule of thumb that the fundamental eigenperiod of a building is equal to 0.1 s multiplied by the number of storeys was used. Both buildings are considered to be fixed at their base, whereas their behavior is assumed to be either linear or non-linear. Both linear and non-linear buildings have been examined in this study. Also, for the non-linear MDOF systems uniform non-dimensional yield displacement is assumed for all the floors, i.e., lateral stiffness is assumed as proportional to shear strength at each story. Damping is included through a classical damping matrix resulting from the superposition of the damping matrices of all linear elastic modes of the structures which have the same modal damping ratio. A number of horizontal seismic excitations are imposed at the base of the MDOF systems, resulting in their dynamic response. The two MDOF shear buildings analyzed are shown in Figure 1.
Several types of hysteresis models are employed in research and engineering practice to predict the response of steel and reinforced concrete members subjected to cyclic loading. Six of them have been presented by Decanini and Mollaioli (2001) who applied a methodology for the assessment of the seismic energy demands imposed in structures. To model the non-linear force-deformation behavior of shear buildings, the elastic-perfectly plastic constitutive model is chosen in this study. The elastoplastic model is chosen as a reference hysteretic model, since the introduction of a more sophisticated model of non-linear response would complicate the range of validity of the optimization results, subtracting thus from generality. The elastoplastic model is considered as the fundamental model of hysteretic behavior and furthermore it is easier to be compared with other models. The methodology introduced in the present study is virtually a general framework for the optimum design of shear buildings, opening thus the way for more specialized treatments of the problem using advanced structural constitutive models. Bilinear hysteretic behavior is simulated using two linear models, corresponding to the two branches of the hysteresis loop.
The basic idea is that each branch of the hysteresis may be described by an equation of the form fK = k(u − d), where fK is the restoring force, u is the displacement, and d, k are the equilibrium displacement and pre- or post-yield stiffness at the last application of the elastoplastic model. The restoring force is 0 when u = d. By suitable loops over the floors of the MDOF structure (counting from top to bottom of the shear building) and identification of transitions between the elastic loading, plastic loading, elastic unloading states, the inter-storey forces, and stiffnesses are calculated and passed to the time integration algorithm. An indicative one-cycle force-displacement diagram of the bilinear elastic model is shown in Figure 2. The elastic-perfectly plastic constitutive model used in this study is implemented as follows:
• (*) Form the square pre-yield stiffness matrix K from khi
• Find the eigenfrequencies ωi and eigenvectors φi of the linear elastic (pre-yield) structure with stiffness K and mass M for which the following relations hold:
and calculate the elastic pre-yield tangent damping matrix:
• (**)Read the values of u, and add a zero element to u, to account for the fixed base:
• for i from 1 to ndofs, where ndofs is the number of degrees of freedom (or storeys) of the structure, do the following:
• Compute the stiffness force of the current storey from k and d stored from previous application of the elastoplastic model [see step beginning with three asterisks (***) below]:
• Compute the yielding force level:
• Check for yielding or load reversal and update ki and di accordingly
• If ki = khi,i and and pK,i > py,i, the system has exceeded its positive yield force level. Update as follows:
• If ki = khi,i and and pK,i < py,i, the system has exceeded its negative yield force level. Update as follows:
• If ki = klo,i and , the system reloads from negative ultimate displacement or unloads from positive ultimate displacement. Update as follows:
• Update the global force vector:
• for i from 1 to ndofs find the elastoplastic forces of all storeys of the structure (with respect to its base):
• Add the contribution of linear elastic damping to the internal force:
• (***) Store k and d, and go back to the step beginning with an asterisk (*). Alternatively, store C, k and d, and go back to the step beginning with two asterisks (**).
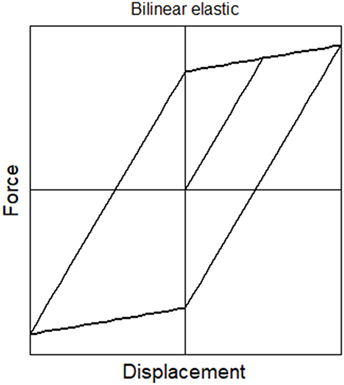
Figure 2. Force-displacement diagram showing one cycle of the bilinear elastic model used in this study.
The dimensionless inter-storey drift yield limit is considered to be uniform along the height of the MDOF shear building and is given by the equation:
where k is the pre-yield stiffness of a hypothetical SDOF system, uy is its yield limit, m is its mass, f0 is its fundamental eigenfrequency (which is considered equal to that of the building analyzed), and is the time history of the earthquake acceleration.
Time Integration Algorithm for Evaluation of Structural Response
The hysteretic energy demand can be accurately computed through a non-linear dynamic time-history analysis of the structure subjected to a given earthquake ground acceleration. For the dynamic response history analyses performed in this study, the family of non-linear direct time integration algorithms presented by Papazafeiropoulos et al. (2017) is used. This family of algorithms is described by the following basic relationships:
• The updates of displacement and velocity:
• The update of acceleration:
where
and
• The residual equivalent force, which becomes 0 if an iteration within an increment reaches equilibrium:
Any scheme of the aforementioned algorithm family needs 15 integration constants (of which 14 are independent) to be uniquely defined. See Papazafeiropoulos et al. (2017) for a complete list of known time integration schemes which are special cases of this family. The time integration algorithm used here has optimal numerical dissipation and dispersion and zero-order overshooting in displacement and velocity (U0-V0-Opt). In addition, equilibrium iterations are made within each increment by the use of a Newton–Raphson (N–R) procedure. The last updates the stiffness matrix at each iteration, until an equilibrium state is reached and the time integration algorithm proceeds to the next increment. It is possible, however, that during the iterations within an increment the algorithm does not converge, usually due to the fact that the stiffness of the structure changes abruptly between pre- and post-yielding state. In this case, the iterations are terminated and the last meaningful solution is accepted for equilibrium.
EBD Optimization Problem
The minimization of the deviation of the energy distribution along the height of a building is treated in this study as an unconstrained optimization problem, the components of which are described in detail in the following paragraphs.
Design Variables
The design variables of the optimization procedure are simply the stiffness of each storey of the two buildings under consideration, namely, for the 5-storey and 10-storey buildings there are 5 and 10 design variables, respectively. The various stiffness distributions encountered during the optimization process have to respect some upper and lower limits, to ensure that computations remain meaningful and that no premature termination of the process occurs. For the stiffness of each storey, an upper and a lower limit is imposed which remains constant during the optimization. Moreover, if at an iteration the new value of xk violates any of the upper and lower bounds, the step length is appropriately decreased by applying a line-search algorithm, so that the new value of xk lies within the upper and lower limits, whereas the Newton direction remains unchanged. This line-search algorithm is described in Section “Optimization Algorithm” below. The upper and lower bounds are equal to 1E9 and 1E6 N/m, respectively.
Objective Function
The objective of the optimization procedure employed in this study is to find the stiffness distribution that corresponds to uniform energy dissipation over the structural height, either in terms of energy dissipation due to viscous damping for linear elastic structures, or in terms of energy dissipation due to hysteresis for elastic-perfectly plastic structures. However, the enforcement of uniform energy dissipation alone does not lead to a unique stiffness/strength distribution of the structure; the magnitude of the energy dissipated has to be additionally determined. The latter is done by imposing that the structure will have a specific fundamental eigenfrequency f0 which controls the energy input in the structure. From the above it is concluded that the objective function has to be defined in a way that not only the distribution of the energy dissipation, but also the fundamental eigenfrequency of the structure have to be calculated as functions of the design variables (stiffness distribution along the height).
In this study the gradient of the objective function for elastic-perfectly plastic structures is defined as:
where the exponent q serves as a weighting factor between the energy distribution and the desired fundamental eigenfrequency of the building and is selected in a manner that maximizes the convergence rate of the optimization process. In this study, q is set equal to 10 for all optimization analyses. Here, yk is the vector of the hysteretically dissipated energy distribution along the height of the structure, is its mean value and ω0,k is the fundamental cyclic eigenfrequency of the structure having stiffness distribution xk. Analogous equation holds for the linear elastic structures:
where dk is the vector of the damped energy distribution along the structural height and its average. It must be noted here that the explicit definition of the objective function is not of interest here, since it does not have any physical meaning; only its gradient is considered, which becomes 0 at the point of optimum design.
Earthquakes Considered
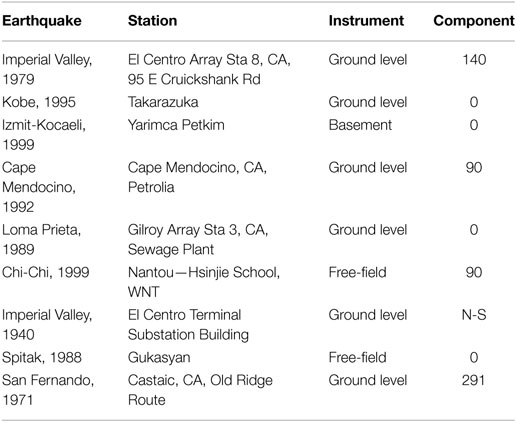
Nine earthquake records have been studied, which are the following: Imperial Valley (1979), Kobe (1995), Izmit-Kocaeli (1999), Cape Mendocino (1992), Loma Prieta (1989), Chi-Chi (1999), Imperial Valley (1940), Spitak (1988), and San Fernando (1971). More details about these earthquake records can be seen in Table 1.
Optimization Algorithm
In this study, a gradient optimization strategy is employed to find optimum stiffness (and strength) distributions at MDOF shear buildings. Gradient-based optimization methods search for a minimum of a scalar function fobj(xk) of a vector including the floor stiffnesses as design variables xk iteratively, by approximating the objective function by a Taylor series expansion around xk:
At each optimization step, a direction ek and a step length ak are calculated based on the current value of the stiffness distribution xk, and the latter as well as the objective function are updated based on the following equations:
The algorithm begins with a random initial stiffness distribution x0. The above process is repeated until the convergence criterion is satisfied, at which point the optimization algorithm terminates. The formal version of the Newton direction method involves a quadratic approximation of the objective function realized through the calculation of the Hessian matrix as follows:
where is the Jacobian. In this study, however, the above Newton direction is modified by adding a constant multiplied by the unity matrix, which is proved to stabilize the whole behavior of the optimization algorithm:
where is the modified Jacobian. Eq. 29 can be rewritten due to Eqs 23 and 24 as follows:
and
for elastic-perfectly plastic and linear elastic MDOF structures, respectively.
In this study, Eqs 30 and 31 are used for the computation of the modified Newton direction, without explicit consideration of the objective function fobj(xk). Note that the modified Jacobian of Eq. 30 is not a function of the hysteretically dissipated energy yk, but the damping energy of the equivalent linear elastic MDOF system dk. The equivalent linear elastic MDOF system of a given elastic-perfectly plastic MDOF system is defined as the latter with its yield limit set equal to infinity (i.e., the former is defined by the behavior of the latter for small strains). This new way of calculation of the Jacobian accelerates by far the optimization process of the non-linear MDOF system, despite the minor loss in accuracy that is associated with this option.
Given that the calculation of the derivative of the energy distribution requires the largest part of the total computational effort required for the optimization process, it is concluded that this new logic of gradient optimization of non-linear structures is vital for the reduction of the computational load. In addition, this rationale introduces the concept of optimization points found from non-linear structural response and directions found from equivalent linear structural response. The last concept can be applied not only in the case of Newton direction methods, but in many other types of optimization methods, utilizing either line searches or trust regions, such as steepest descent, conjugate gradient, subspace minimization, Broyden class algorithms, etc. In a future study, the authors will deal with how the aforementioned concept can be applied for improving the performance of such algorithms.
Two optimization procedures are implemented in this study. The first concerns the optimization of the linear elastic structure with respect to damping energy, using Eqs 31 and 26, whereas the second concerns the optimization of the elastic-perfectly plastic structure using Eqs 30 and 26. After having estimated the optimum stiffness distribution of the linear elastic structure, this distribution is used as the initial point for the optimization of the non-linear structure. The optimization procedure implemented in this study is as follows:
• Initialize:
• While the vector |rk|/|r| contains at least one value higher than tolr:
• Check if the hessian has to be updated. If yes, calculate it from the relation (35), else omit this step and proceed to the following steps:
• Solve for the quasi-Newton direction ek according to Eq. 30 or 31.
• Find a trial value for xk by assuming a unit step along the direction ek, using Eq. 36:
• If any value of the new vector xk+1 is not within the upper and lower limits ub and lb respectively:
• Perform line search for the step in the direction ek as follows:
• Adjust xk+1 for the next iteration according to Eq. 26.
• Calculate the new residual for the next iteration:
• Update the design variables and the iteration counter for the next iteration of the while loop:
Regarding the aforementioned optimization parameters, the values NRstab = −3E−6 and tolR = 0.01 are specified in this study. The optimization algorithm implemented in this study can be easily applied in the case of irregular structures and give proper optimum stiffness distributions, not only for linear, but also for non-linear shear buildings.
Typical Hysteretic Energy Distributions for Shear Buildings
Typical distributions of the energy dissipated due to hysteresis during elastoplastic response of the 5-storey and 10-storey buildings considered in this study are shown in Figure 3. It has been assumed that the buildings have uniform stiffness distributions along their height, which are scaled so that they correspond to fundamental eigenfrequencies equal to 2 and 1 Hz, respectively. As it has been often observed in practice, the largest amounts of energy are concentrated at the bottom floors of the buildings for all the earthquake records considered. At the top floors the energy is much lower, and sometimes becomes 0 (i.e., the upper floors do not participate as an energy absorption mechanism during seismic response). It is seen that generally the energy distributions vary non-linearly with height. The largest energy demand on the building is generally imposed by the Kobe (1995), Kocaeli (1999), and Chi-Chi (1999) earthquakes. Figure 3 shows clearly the reason for which the damages caused by an earthquake accumulate at the lower floors, and why soft storey mechanisms develop more often at these levels. This phenomenon is undesirable; there is the need to equidistribute the seismic energy absorbed by the building among all storeys, in order to exploit the construction material as much as possible, and maximize structural safety. This study tries to cover this need by proposing a new fast optimization algorithms which has already been presented in the previous sections.
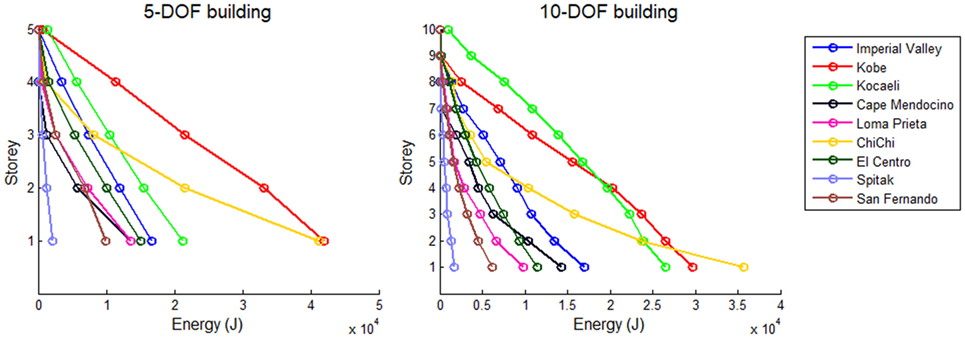
Figure 3. Distributions of energy dissipated due to hysteresis for the 5- and 10-storey shear buildings with uniform stiffness along their height, ξ = 5%, = 0.01 and fundamental eigenfrequencies 2 and 1 Hz, respectively, for various earthquake records.
Optimum Stiffness Distributions for Linear Structures
In this section, the optimum stiffness distributions are shown for the cases of the linear elastic versions of the 5-storey and 10-storey planar shear buildings considered in this study. The optimum stiffness distributions refer to the specific fundamental eigenfrequencies prescribed for both buildings (2 and, 1 Hz respectively) and various values of the critical damping ratio; uniformity of the dissipated energy due to viscous damping is enforced as has been already discussed. Apart from the optimum stiffness distributions, the effects of various factors are discussed in the next.
Effect of Earthquake Excitation on Optimum Stiffness and Energy Distributions
Two families of optimum stiffness distributions along with their corresponding damping energy distributions are shown in Figure 4 and Figure 5 for the 5-storey and 10-storey MDOF systems analyzed in this study, respectively. It seems that the optimum stiffness generally has a regular distribution, where the largest value is at the first storey and the lowest at the top storey.
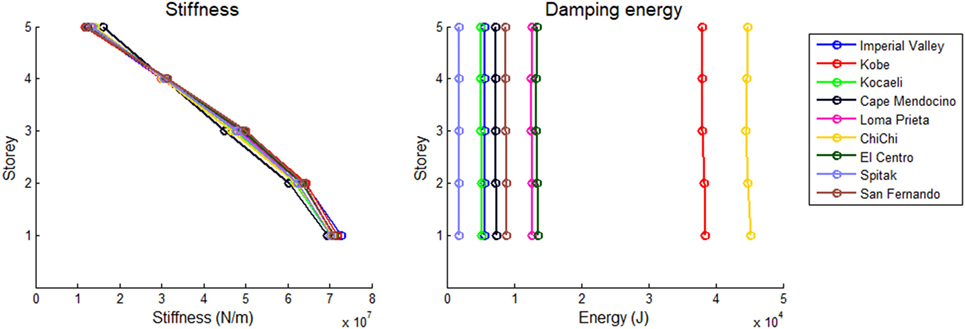
Figure 4. Optimum distributions of elastic stiffness and energy dissipated due to damping for the 5-storey shear building with ξ = 5% for various earthquake records.
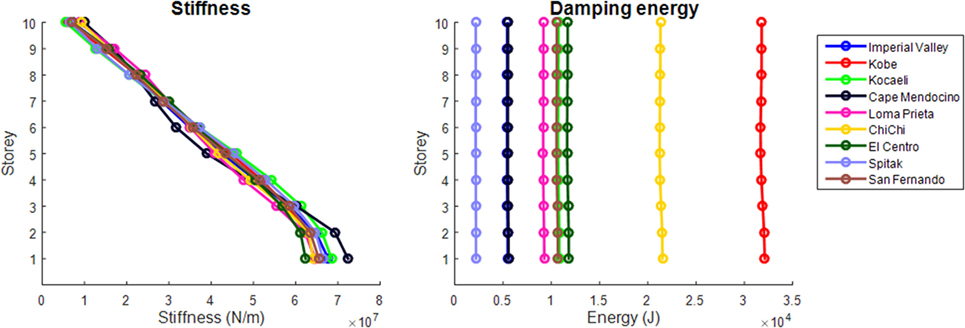
Figure 5. Optimum distributions of elastic stiffness and energy dissipated due to damping for the 10-storey shear building with ξ = 5% for various earthquake records.
Similar results with Figure 4 are presented in Figure 5, where the optimum stiffness and optimum damping energy distributions for the 10-storey shear building are shown. It is obvious that the stiffness distributions of the 10-storey MDOF systems are regular and have generally their largest value at the bottom of the structure and their lowest value at the top. The general observation is that the stiffness distribution which corresponds to uniform damping energy over the height of a shear building is generally independent of the earthquake motion with which the building is excited. By comparing Figure 5 with Figure 4, it can be stated that the stiffnesses of the 10-storey building are generally close to those of the 5-storey shear buildings. On the other hand, the energy distributions of the 10-storey building seem to be generally lower than those of the 5-storey building.
Effect of Modal Damping on Optimum Stiffness and Energy Distributions
In Figures 6 and 7 the effect of critical modal viscous damping ratio on the optimum distributions of stiffness and damping energy for both 5-storey and 10-storey systems considered in this study is illustrated. In Figures 6 and 7 results regarding the El Centro earthquake record are presented. It is apparent that the two shear buildings have nearly identical stiffness distributions for the various critical damping ratios in the case of the El Centro earthquake record. Regarding the damping energy distributions, it can be seen generally that as the damping ratio increases, the amount of the dissipated energy also increases. Apart from this, with increasing damping ratio, the difference between successive dissipated energy distributions of the 5-storey system and the 10-storey system becomes lower. Finally, another thing to be noted is that the energy distributions of the 5-storey building are generally larger than those of the 10-storey building.
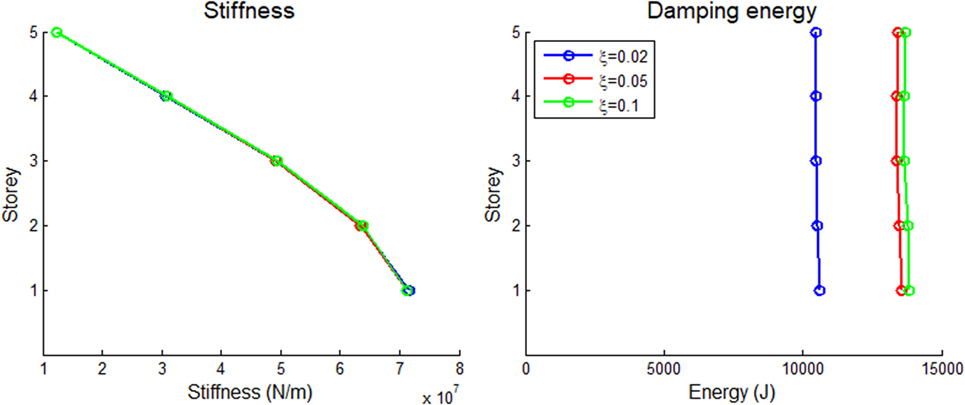
Figure 6. Optimum distributions of elastic stiffness and energy dissipated due to damping for the 5-storey shear building subject to the El Centro earthquake record for various critical modal damping ratios.
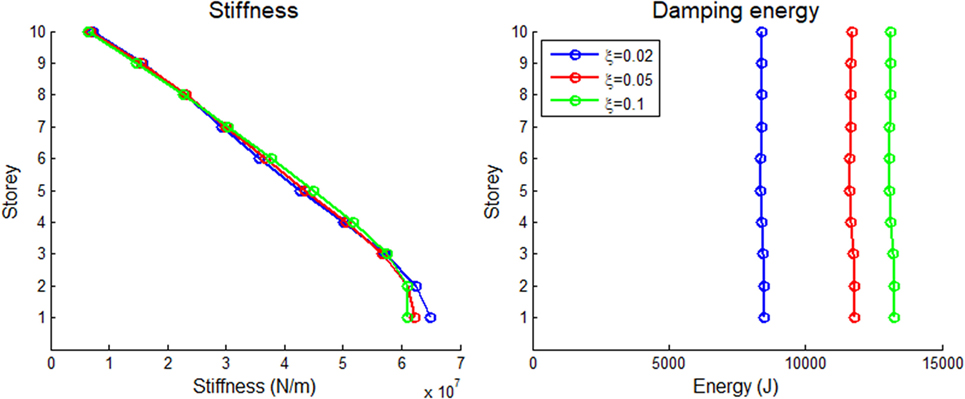
Figure 7. Optimum distributions of elastic stiffness and energy dissipated due to damping for the 10-storey shear building subject to the El Centro earthquake record for various critical modal damping ratios.
Optimum Stiffness Distributions for Elastic—Perfectly Plastic Structures
In this section, optimization results are presented for the elastic-perfectly plastic counterparts of the planar shear buildings considered in the previous section. Along with the critical modal damping ratio, an additional parameter is taken into account here, which is the normalized inter-storey drift yield limit, defined in Eq. 16. The fundamental eigenfrequencies of the two buildings remain the same as those in the linear elastic case: 2 and 1 Hz for the 5- and 10-storey building, respectively. The uniform normalized inter-storey drift yield limit is assumed to be and for the 5- and 10-storey building, respectively. It has to be noted here that the effective seismic force for which the structure will be designed can be easily calculated from the optimum stiffness distribution multiplied by the uniform yield inter-storey drift limit.
Effect of Earthquake Excitation on Optimum Stiffness and Energy Distributions
The optimum pre-yield stiffness distributions and its corresponding hysteretic energy distributions are shown in Figure 8, in the left and right subplots, respectively, for the 5-storey shear building considered in this study. It is observed that the stiffness distributions generally decrease from bottom to top, as was seen in the linear elastic case in Figure 4. It is noted that a general (quasi-linear) optimum stiffness distribution trend exists which is followed by the stiffness distributions for the various earthquake records considered, for both 5-storey and 10-storey buildings, perhaps with the slight exception of the Cape Mendocino (1992) and Loma Prieta (1989) earthquakes in the cases of 5- and 10-storey shear buildings, respectively. The general stiffness distribution trend can be used in each case for structural design, at least in the preliminary stage. Concerning the hysteretic energy distributions for optimum stiffness at the right subplot of the figure, it is seen that the hysteretic energy that is suffered by the two buildings in the case of Kobe (1995) earthquake appears to be the largest of all earthquakes. The Kobe (1995) earthquake yields also the largest damping energy distribution in the case of the linear elastic 10-DOF system with optimum stiffness distribution (Figure 5). The hysteretic energy distribution of the Spitak (1988) earthquake remains to be the lowest of all earthquakes for both buildings. The above results lead to the conclusion that there is some close relation between the linear viscous damping energy and elastoplastic hysteretic energy that is dissipated at the storeys of a shear building.
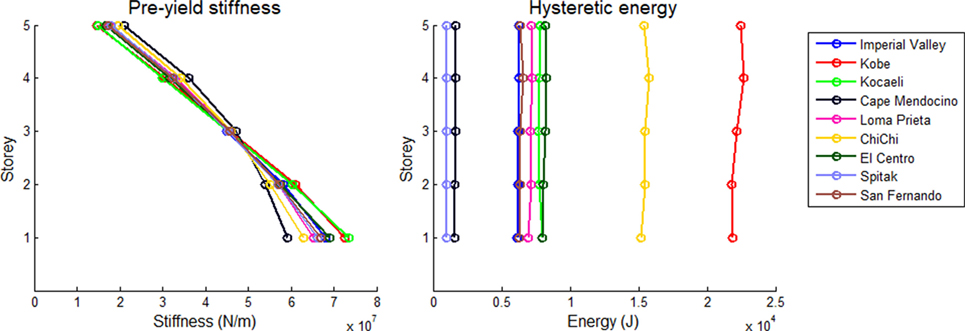
Figure 8. Optimum distributions of elastic pre-yield stiffness and energy dissipated due to hysteresis for the 5-storey shear building with ξ = 5%, = 0.1 for various earthquake records.
Figure 9 shows the optimum pre-yield stiffness distributions and their associated hysteretic energy distributions for the elastoplastically responding 10-storey shear building subject to various seismic excitations. It is seen that a general trend is again followed by the majority of the earthquakes considered. Regarding the energy distributions, it is seen again that the maximum hysteretic energy distribution occurs for the Kobe (1995) earthquake and the minimum for the Spitak (1988) earthquake. Additionally, the former is larger for the optimal 5-storey building than that for the optimal 10-storey building.
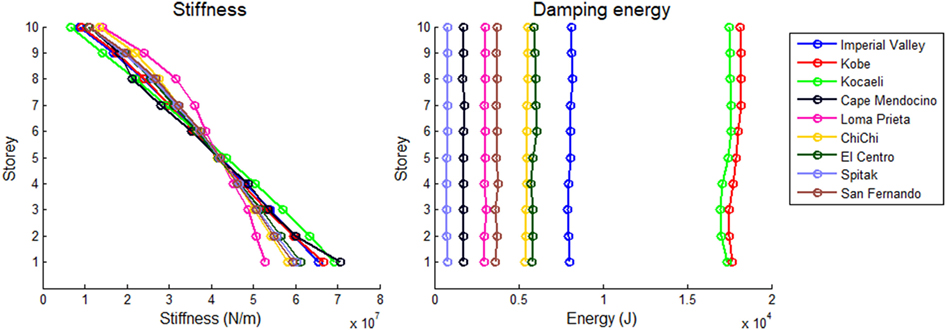
Figure 9. Optimum distributions of elastic pre-yield stiffness and energy dissipated due to hysteresis for the 10-storey shear building with ξ = 5%, = 0.04 for various earthquake records.
Effect of Critical Modal Damping Ratio on Optimum Stiffness and Energy Distributions
The effect of critical modal damping ratio on the optimum stiffness and energy distributions of the two shear buildings is shown in Figures 10 and 11 for the El Centro earthquake. It is observed that the various optimum stiffness distributions are nearly identical for the various cases of damping ratio, whereas it seems that as the damping ratio increases, the hysteretic energy distribution decreases. This can be explained by considering that the earthquake energy that is input to a shear building can be dissipated through either damping or hysteretic elastoplastic response. As the damping ratio increases, the energy dissipated through damping also increases. As a consequence of this, the portion of the input energy that is dissipated through hysteresis decreases. Apart from this, it is also observed that in all cases examined the 5-storey building has larger hysteretic energy distributions than the 10-storey building. Finally, the stiffness distributions for the 10-storey building are slightly lower than the corresponding distributions of the 5-storey building.
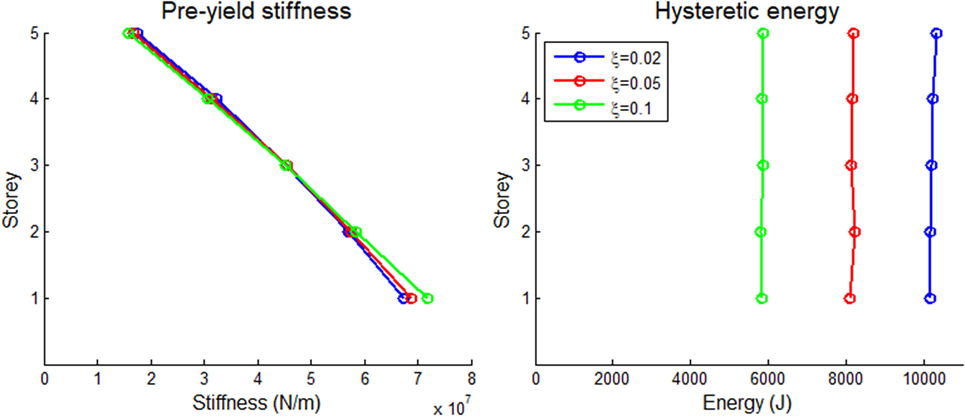
Figure 10. Optimum distributions of elastic pre-yield stiffness and energy dissipated due to hysteresis for the 5-storey shear building with = 0.1 subject to the El Centro earthquake record for various critical modal damping ratios.
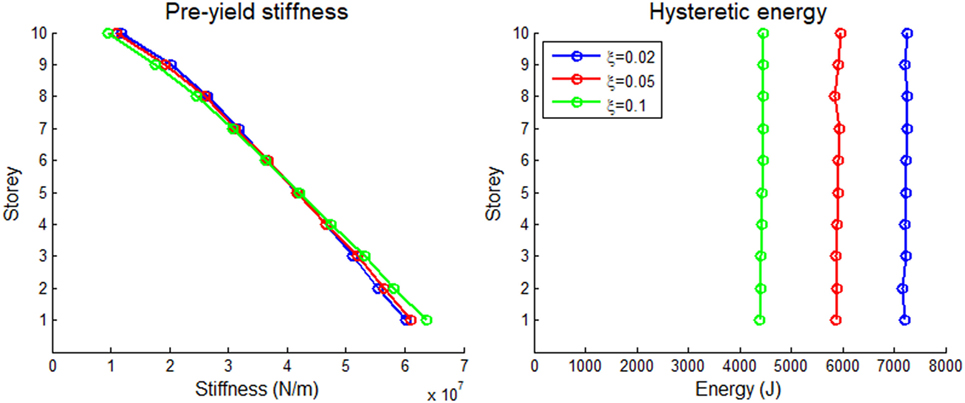
Figure 11. Optimum distributions of elastic pre-yield stiffness and energy dissipated due to hysteresis for the 10-storey shear building with = 0.04 subject to the El Centro earthquake record for various critical modal damping ratios.
Effect of Normalized Yield Inter-Storey Drift on Optimum Stiffness and Energy Distributions
The distribution of the normalized inter-storey drift yield limit at a shear building is another factor that affects profoundly its structural response in the elastoplastic regime. This parameter is taken to be uniform for all storeys, and is calculated based on Eq. 16. In Figures 12 and 13 the effect of this parameter is illustrated for the 5-storey and 10-storey shear building, respectively with ξ = 0.05, subject to the El Centro earthquake excitation. It is observed that the stiffness distributions are relatively close to each other both for 5-storey and for 10-storey buildings, for the two values of . This can be attributed to the fact that is uniform over the building height for both cases. Besides, the energy distributions show clearly that as decreases, the dissipated energy due to hysteresis increases, as is expected. This can be explained by the fact that as decreases, the structure responds at the perfectly plastic branch of the elastoplastic response for larger time intervals, and therefore, the effect of plasticity becomes greater, leading to larger hysteresis loops and thus increased hysteretic energies. Finally, it can be noted that the 5-storey building has slightly lower stiffness distributions and dissipates larger amounts of hysteretic energy than the 10-storey building.
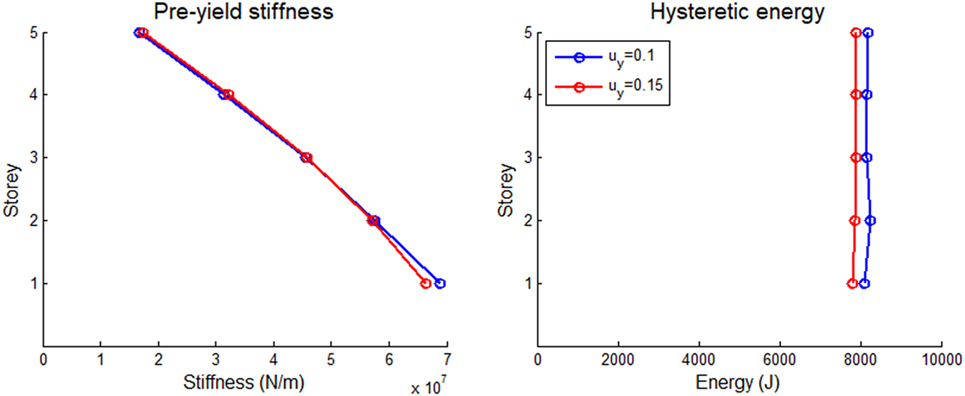
Figure 12. Optimum distributions of elastic pre-yield stiffness and energy dissipated due to hysteresis for the 5-storey shear building with ξ = 5% subject to the El Centro earthquake record for various normalized yield inter-storey drifts.
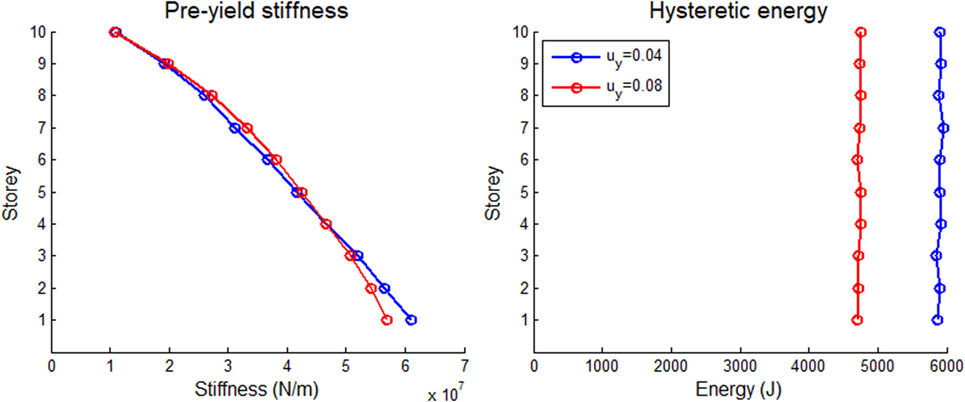
Figure 13. Optimum distributions of elastic pre-yield stiffness and energy dissipated due to hysteresis for the 10-storey shear building with ξ = 5% subject to the El Centro earthquake record for various normalized yield inter-storey drifts.
Effectiveness of the New Optimization Concept
For every new optimization algorithm, the question arises, how it increases the effectiveness, speed, etc. of the optimization process to which it is applied. The new optimization concept presented in this study can be applied for any energy-based optimization problem, and we need to see how the algorithm behaves for typical examples already presented in previous sections. In Figure 14 the evolution of the standard deviation of the hysteretic energy distribution is shown as a function of the normalized running time for the 5- and 10-storey shear buildings considered in this study with f0 = 2 Hz, ξ = 0.05, and f0 = 1Hz, ξ = 0.05, , respectively, subject to the El Centro earthquake record. The optimum stiffness and energy distributions for the two cases are shown in Figure 12 and 13. It is seen that the running times of the NR algorithm using linear derivatives are much lower than those with non-linear derivatives. The running time of each optimization problem is normalized with respect to the running time of the optimization algorithm using non-linear derivatives, hence the running time of the two non-linear derivative algorithms is set to unity (100%).
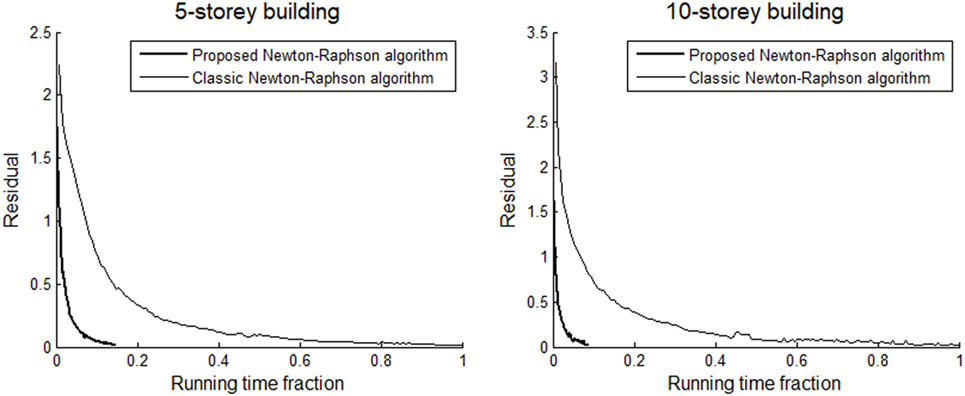
Figure 14. Evolution of the standard deviation of the hysteretic energy distributions during various optimization processes for the classic N–R optimization procedure and the proposed N–R optimization procedure, for 5- and 10-storey shear buildings with f0 = 2 Hz, ξ = 5%, y = 0.1 and f0 = 1 Hz, ξ = 5%, y = 0.04, respectively, subject to the El Centro earthquake record.
It is clearly seen that the novel optimization algorithm proposed in this study can be roughly as much as 11 times faster than the traditional NR for the 10-storey system and roughly seven times faster for the 5-storey system. For further increasing number of stories, the novel algorithm is expected to be even over 11 times faster than the ordinary NR, saving thus a great amount of computational effort. It has to be noted here that, for comparison purposes, the initial stiffness distributions with which the algorithms began were set to be identical for both sets of cases, and equal to the linear elastic optimum stiffness distributions shown in Figure 6 and 7 for ξ = 0.05. Since the algorithms begin from the same initial distribution to solve essentially the same problem (in terms of earthquake record and various structural properties), the differences in the running times and the general behavior are affected merely by the nature of the algorithm and its properties. The results of the optimization studies shown in Figure 14, are shown in Table 2.
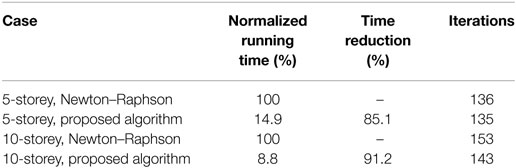
Table 2. Numerical results of the optimization processes the evolution of which is presented in Figure 14.
It is seen that, the proposed NR algorithm in this study, while it retains the number of iterations approximately at the same levels with the classic NR, it can reduce the execution time by as much as 85% in the case of the 5-storey building and by 91% in the case of the 10-storey building. The reduction in the running time is expected to increase for buildings with more storeys, or generally structures with more degrees of freedom. As a result, as the problem becomes more complicated, the proposed algorithm is expected to perform better compared to the classic NR method. Finally, it has to be pointed out that in both sets of cases, the final optimum stiffness distribution result was identical for both the classical NR method and the proposed optimization algorithm.
Conclusion
The main conclusions drawn from this study are the following:
• It is shown that there exist unique optimum stiffness distributions which correspond to equidistributed viscous damping and hysteretic energy dissipation for linear elastic and elastoplastic planar shear building structures, respectively.
• In addition, the optimum stiffness distribution for both elastic and elastoplastic shear buildings appears generally to have a quasi-linear shape (slightly curved), with the maximum value at the bottom floor and the minimum value at the top floor of the structure. This shape is generally independent of the earthquake excitation and offers the possibility for the development of simple methods for the calculation of the optimum stiffness distribution in shear buildings.
• Structural design based on the proposed approach is more rational and technically feasible compared to the uniform ductility concept, whereas it is expected to provide increased protection against global collapse and loss of life during strong earthquake events.
• It is finally proved that the novel concept of linear directions equipped with a stabilizer for optimization of non-linear problems, as applied for the modification of a simple full N–R method, leads to substantial computational savings, since, although the number of iterations required for convergence remains roughly the same, the running times can be reduced by a factor equal to 11. It is obvious that the new modified N–R algorithm is robust and efficient. The new concept presented in this study can be applied to other commonly used algorithms, which is the aim of future research to be conducted by the authors.
Author Contributions
GP had the research idea, drafted the article, did the data collection, and contributed in the numerical analysis of the numerical examples. VP contributed in the conception and design of the work and the data analysis and interpretation of the results. MP supervised the overall research work.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Akiyama, H. (1985). Earthquake-Resistant Limit-State Design for Buildings. Tokyo: University of Tokyo Press.
Berg, G. V., and Thomaides, S. S. (1960). “Energy consumption by structures in strong-motion earthquakes,” in Proceedings of the Second World Conference on Earthquake Engineering, Tokyo and Kyoto.
CEN. (1998). EN 1998-1: Eurocode 8, Design of Structures for Earthquake Resistance, Part 1. Brussels: European Committee for Standardization (CEN).
Chou, C. C., and Uang, C. M. (2003). A procedure for evaluating seismic energy demand of framed structures. Earthq. Eng. Struct. Dyn. 32, 229–244. doi: 10.1002/eqe.221
Connor, J. J., Wada, A., Iwata, M., and Huang, Y. (1997). Damage-controlled structures. I: preliminary design methodology for seismically active regions. J. Struct. Eng. 123, 423–431. doi:10.1061/(ASCE)0733-9445(1997)123:4(423)
Decanini, L. D., and Mollaioli, F. (2001). An energy-based methodology for the assessment of seismic demand. Soil Dyn. Earthq. Eng. 21, 113–137. doi:10.1016/S0267-7261(00)00102-0
Ganjavi, B., and Hao, H. (2012). A parametric study on the evaluation of ductility demand distribution in multi-degree-of-freedom systems considering soil–structure interaction effects. Eng. Struct. 43, 88–104. doi:10.1016/j.engstruct.2012.05.006
Ganjavi, B., and Hao, H. (2013). Optimum lateral load pattern for seismic design of elastic shear-buildings incorporating soil–structure interaction effects. Earthq. Eng. Struct. Dyn. 42, 913–933. doi:10.1002/eqe.2252
Ghosh, S., and Collins, K. R. (2006). Merging energy-based design criteria and reliability-based methods: exploring a new concept. Earthq. Eng. Struct. Dyn. 35, 1677–1698. doi:10.1002/eqe.602
Hajirasouliha, I., Asadi, P., and Pilakoutas, K. (2012). An efficient performance-based seismic design method for reinforced concrete frames. Earthq. Eng. Struct. Dyn. 41, 663–679. doi:10.1002/eqe.1150
Hajirasouliha, I., and Moghaddam, H. (2009). New lateral force distribution for seismic design of structures. J. Struct. Eng. 135, 906–915. doi:10.1061/(ASCE)0733-9445(2009)135:8(906)
Hajirasouliha, I., and Pilakoutas, K. (2012). General seismic load distribution for optimum performance-based design of shear-buildings. J. Earthq. Eng. 16, 443–462. doi:10.1080/13632469.2012.654897
International Code Council (ICC). (2006). International Building Code (IBC). Falls Church, VA. Available at: https://scholar.google.com/scholar_lookup?publication_year=2006&issue=2&author=+ICC&title=+International+Building+Code+
KBC. (2009). Ministry of Infrastructure and Transport, Sejong: Minister of Land, Transport and Maritime Affairs.
Léger, P., and Dussault, S. (1992). Seismic-energy dissipation in MDOF structures. J. Struct. Eng. 118, 1251–1269. doi:10.1061/(ASCE)0733-9445(1992)118:5(1251)
Mezgebo, M. G. (2015). Estimation of Earthquake Input Energy, Hysteretic Energy and Its Distribution in MDOF Structures. Syracuse, NY: Mebrahtom Gebrekirstos Mezgebo, Syracuse University.
Moghaddam, H., and Hajirasouliha, I. (2004). A new approach for optimum design of structures under dynamic excitation. Asian J. Civil Eng. 5, 69–84.
Moghaddam, H., and Hajirasouliha, I. (2006). Toward more rational criteria for determination of design earthquake forces. Int. J. Solids Struct. 43, 2631–2645. doi:10.1016/j.ijsolstr.2005.07.038
Murakami, Y., Noshi, K., Fujita, K., Tsuji, M., and Takewaki, I. (2013). Simultaneous optimal damper placement using oil, hysteretic and inertial mass dampers. Earthq. Struct. 5, 261–276. doi:10.12989/eas.2013.5.3.261
Nakamura, T., and Yamane, T. (1986). Optimum design and earthquake-response constrained design of elastic shear buildings. Earthq. Eng. Struct. Dyn. 14, 797–815. doi:10.1002/eqe.4290140508
Nakashima, M., Saburi, K., and Tsuji, B. (1996). Energy input and dissipation behaviour of structures with hysteretic dampers. Earthq. Eng. Struct. Dyn. 25, 483–496. doi:10.1002/(SICI)1096-9845(199605)25:5<483::AID-EQE564>3.0.CO;2-K
NZS1170. (2004). New Zealand Standard 1170. 5. 2004. Structural Design Actions, Part 5: Earthquake Actions. Wellington: Standards New Zealand (Ministry of Business, Innovation & Employment).
Papazafeiropoulos, G., Plevris, V., and Papadrakakis, M. (2017). A generalized algorithm framework for non-linear structural dynamics. Bull. Earthq. Eng. 15, 411–441. doi:10.1007/s10518-016-9974-8
Park, K., and Medina, R. A. (2007). Conceptual seismic design of regular frames based on the concept of uniform damage. J. Struct. Eng. 133, 945–955. doi:10.1061/(ASCE)0733-9445(2007)133:7(945)
Penzien, J. (1960). Dynamic response of elasto-plastic frames. Trans. Am. Soc. Civil Eng. 127, 1–13.
Prasanth, T., Ghosh, S., and Collins, K. R. (2008). Estimation of hysteretic energy demand using concepts of modal pushover analysis. Earthq. Eng. Struct. Dyn. 37, 975–990. doi:10.1002/eqe.802
Rodriguez, M. (1994). A measure of the capacity of earthquake ground motions to damage structures. Earthq. Eng. Struct. Dyn. 23, 627–643. doi:10.1002/eqe.4290230605
Shargh, F. H., and Hosseini, M. (2010). A study on the existence of an optimal distribution of stiffness over the height of mid-to high-rise buildings to minimize the seismic input energy. J. Appl. Sci. 10, 45–51. doi:10.3923/jas.2010.45.51
Shargh, F. H., and Hosseini, M. (2011). An optimal distribution of stiffness over the height of shear buildings to minimize the seismic input energy. J. Seismol. Earthq. Eng. 13, 25–32.
Shargh, F. H., Hosseini, M., and Daneshvar, H. (2012). An Optimal Distribution of Stiffness Over the Height of Buildings and Its Buildings and Its Influence on the Degree and Distribution of Earthquake Induced Damages and Distribution of Earthquake Induced Damages. Lisbon: Sociedade Portuguesa de Engenharia Sismica (SPES).
Takewaki, I. (2011). Building Control with Passive Dampers: Optimal Performance-Based Design for Earthquakes. New York, NY: John Wiley & Sons.
Uetani, K., Tsuji, M., and Takewaki, I. (2003). Application of an optimum design method to practical building frames with viscous dampers and hysteretic dampers. Eng. Struct. 25, 579–592. doi:10.1016/S0141-0296(02)00168-2
Wang, F., and Yi, T. (2012). A methodology for estimating seismic hysteretic energy of buildings. ASCE 2012 International Conference on Civil Engineering and Urban Planning, Yantai, 17–21.
Zahrah, T. F., and Hall, W. J. (1982). Seismic Energy Absorption in Simple Structures, University of Illinois Engineering Experiment Station. Champaign, IL: College of Engineering, University of Illinois at Urbana-Champaign.
Appendix: Notation
| ak | : | step length of update of xk at iteration k |
| C | : | damping matrix |
| d | : | equilibrium displacement |
| di | : | equilibrium displacement at degree of freedom i at the last application of the elastoplastic model |
| dk | : | damping energy distribution vector at iteration k of the optimization procedure |
| : | average of damping energy distribution at iteration k of the optimization procedure | |
| ek | : | direction of update of xk at iteration k |
| Ed | : | damping energy of a SDOF system |
| f | : | equivalent external loading vector due to seismic excitation imposed on the structure |
| : | effective force vector | |
| yk | : | hysteretic energy distribution vector at iteration k of the optimization procedure |
| : | average of hysteretic energy distribution at iteration k of the optimization procedure | |
| f0 | : | fundamental eigenfrequency of SDOF or MDOF structure for small deformations |
| fk | : | restoring force |
| fobj | : | objective function |
| g | : | residual equivalent force vector |
| I | : | unity matrix |
| Jk | : | Jacobian matrix (first derivative of energy distribution) at iteration k |
| k | : | iteration number or stiffness associated with a degree of freedom |
| khi | : | pre-yield stiffness vector |
| khi,i | : | pre-yield stiffness at degree of freedom i |
| ki | : | stiffness at degree of freedom i at the last application of the elastoplastic model |
| klo,i | : | post-yield stiffness at degree of freedom i |
| K | : | stiffness matrix |
| lb | : | lower bound of stiffness distribution xk |
| M | : | mass matrix |
| : | effective mass matrix | |
| m | : | lumped mass per storey of SDOF or MDOF systems |
| ndofs | : | number of degrees of freedom of the structure |
| NRstab | : | Newton–Raphson stabilizer constant for optimization procedure |
| pi | : | internal force due to stiffness at degree of freedom i |
| pK,i | : | internal force at degree of freedom i due to stiffness |
| pK,int,i | : | inter-storey force between degrees of freedom i and i + 1 due to stiffness |
| py,i | : | yield force at degree of freedom i |
| q | : | exponent of eigenfrequency ratio |
| r | : | initial value of residual for the optimization procedure |
| rk | : | residual at iteration k of optimization procedure |
| T0 | : | fundamental eigenperiod of SDOF or MDOF structure for small deformations |
| tolr | : | tolerance of |rk|/|r| |
| u | : | displacement |
| ub | : | upper bound of stiffness distribution xk |
| ui | : | displacement at degree of freedom i |
| : | velocity at degree of freedom i | |
| : | acceleration at degree of freedom i | |
| uy | : | yield displacement |
| uy,i | : | yield displacement at degree of freedom i. Yielding occurs if the inter-storey drift between degrees of freedom i and i + 1 exceeds uy,i. |
| : | dimensionless yield inter-storey drift | |
| W1 | : | time integration constant |
| : | earthquake ground acceleration | |
| xk | : | stiffness distribution at iteration k of optimization procedure |
| x0 | : | initial value of stiffness distribution to start optimization procedure |
| Δt | : | step of direct time integration scheme |
| λ1…λ5 | : | time integration constants |
| μ1…μ6 | : | time integration constants |
| ξ | : | ratio of critical viscous damping of the system, assumed to be unique for all stories of the structure |
| φi | : | ith fundamental eigenmode of structure |
| ω0,k | : | fundamental cyclic eigenfrequency of structure with stiffness distribution xk for small deformations |
| ωi | : | ith fundamental cyclic eigenfrequency of structure |
Keywords: optimization, non-linear, Newton–Raphson, shear building, stiffness distribution, energy dissipation
Citation: Papazafeiropoulos G, Plevris V and Papadrakakis M (2017) A New Energy-Based Structural Design Optimization Concept under Seismic Actions. Front. Built Environ. 3:44. doi: 10.3389/fbuil.2017.00044
Received: 06 June 2017; Accepted: 12 July 2017;
Published: 31 July 2017
Edited by:
Luigi Di Sarno, University of Sannio, ItalyReviewed by:
Fabrizio Mollaioli, Sapienza Università di Roma, ItalyAli Koçak, Yıldız Technical University, Turkey
Copyright: © 2017 Papazafeiropoulos, Plevris and Papadrakakis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: George Papazafeiropoulos, Z3BhcGF6YWZlaXJvcG91bG9zQHlhaG9vLmdy
 George Papazafeiropoulos
George Papazafeiropoulos Vagelis Plevris
Vagelis Plevris Manolis Papadrakakis1
Manolis Papadrakakis1