- State Key Laboratory for Disaster Reduction in Civil Engineering, Tongji University, Shanghai, China
With the trend of variable cross-sections for long-span bridges from truss-stiffened to quasi-streamlined, and then to multiple-box cross-section geometries, the importance of aeroelastic performance is becoming increasingly significant in wind-resistant design. This article shows that there is clearly insufficient qualitative as well as quantitative understanding of turbulence effects on bridge aerodynamics, particularly the mechanisms behind them. Although turbulence might help the stabilization of long-span bridges, and is thus not a conclusive parameter in wind-resistant design, turbulence effects on the aerodynamic and aeroelastic behaviors of a bridge need to be better understood because interaction between a bridge and turbulence always exists. This article also briefly introduces a newly developed multiple-fan wind tunnel that is designed to control turbulence to assist the study of turbulence effects.
Introduction
It goes without saying that innovations in structural systems, design methods, and construction techniques have played important roles in the realization of long-span bridges. Every increase in bridge span in the past has required scientific and technical innovations, among which the contributions from the wind-engineering field have become increasingly significant, because bridges become more wind sensitive with increase in span. The collapse of the Tacoma Narrows Bridge in 1940 boosted research in the field of bridge aerodynamics—aeroelastics, the study of which influenced the designs of all the world’s great long-span bridges built since that time. The Honshu–Shikoku project initiated in the 1960s comprised several long-span bridges including the famous Akashi Kaikyo Bridge, for which design against wind load and aeroelastic phenomena was one of the main concerns, and accelerated research on bridge aerodynamics. The Messina Crossing project, research on which dates back to the 1970s, also stimulated many innovative researches on nonlinear analysis methods for complex interaction phenomena occurring for long-span bridges in turbulent wind. All efforts made in the community of wind-resistant design of long-span bridges led to current sophisticated theory and comprehensive and integrated methods for wind-resistant design of long-span bridges, which guaranteed the safety and severability of long-span bridges constructed around the world (Ge and Xiang, 2008).
The significant contribution of aerodynamic research to the realization of long-span bridges can be easily seen from the revolution of bridge deck shape. It is well known that the Humber bridge, with a span of 1,410 m, completed in 1981 in the UK, played an important role in the historical development of suspension bridges because it is characterized by an aerodynamic section. However, the first example of a long-span bridge with this type of section was the bridge over the River Severn, UK, characterized by a main span of 988 m, which was completed in 1966 (Borri et al., 2013). For the design of the Humber Bridge, the depth of the deck was increased by 50% from that of the Severn Bridge to increase its torsional stiffness and thus avoid flutter at the design wind speed. The same design concept was followed for the Great Belt East Bridge with a main span of 1,624 m, built in Denmark in 1998. A streamlined section obtained by optimizing its wind performance by introducing wedge-shaped edge fairings was chosen. As many as 16 different trapezoidal box sections were tested to understand how modifications to the geometry could influence the bridge’s aerodynamic stability (Larsen and Gimsing, 1992). A series of studies on the aerodynamic performance of a twin box girder was carried out in China to meet the continuous need for creating long-span bridges and challenging the span limitation (Yang et al., 2015). A twin box girder solution was also chosen for the design of the 1,545-m long Kwangyang suspension Bridge in Korea, whose cross-sectional shape was optimized by section model tests at three different scales to maximize its aerodynamic stability and minimize its drag force (Kwon et al., 2008). Furthermore, a tri-cellular cross-section stiffened by several transverse beams was proposed for the Messina Strait Bridge because its exceptional span (main span 3,300 m long) required very high aerodynamic and aeroelastic performances. The improved stability achieved by this innovative solution was checked with a vast wind tunnel test campaign. Meanwhile, instead of a box solution, a classic truss-stiffened deck configuration with reduced aerodynamic performance was selected for the Akashi Kaikyo Bridge in Japan to reach the required performance level for flutter stability (critical wind speed higher than 78 m/s) (Miyata et al., 1988) and guarantee the required safety level for flutter instability. This was because the mid-span could not exceed 1,700 m if a closed-box deck solution was chosen. The options of perforated decks or laterally separated decks were not appropriate either because they provided insufficient torsional stiffness. Meantime the deck cross-sections of almost all long cable-stayed bridges were optimized from an aerodynamic point of view. The cross-section of the Sutong Bridge was chosen after various wind tunnel tests associated with aerodynamic instability (Chen et al., 2005). For the design of the Stonecutter Bridge, a twin box girder deck with a wide clear separation of 14.3 m was adopted, with which stability against flutter during both construction and in-service stages could be anticipated (critical 1-min wind speed higher than 95 m/s) (Larose et al., 2003). As shown above, without improved knowledge of bridge aerodynamics or advanced wind-resistant design methods considering the wind-structure interaction mechanism, it is impossible to realize long-span bridges.
However, it is difficult for the author to feel completely confident about the process of wind-resistant design of long-span bridges. The modern analytical framework for calculating or predicting wind-induced responses of a long-span bridge borrows the aerodynamic knowledge of an aerofoil with a streamlined body. However, the shape of many bridge decks is not streamlined. Furthermore, with bridges being more wind sensitive, several assumptions for analyzing bridge vibration such as small amplitude of vibration do not stand up, and the nonlinear features of bridge vibration are not ignorable anymore. Changes in stiffness, mass, and damping of bridges lead to new requirements in dealing with wind effects. Considerations for wind-resistant design of long bridges will have to be adjusted continuously as bridges become longer and more flexible by adding more terms or adjusting the values of parameters to describe the complicated and delicate interaction between air and bridge. Currently, wind-resistant performance of a long-span bridge is investigated mainly by wind tunnel experiments. From well-designed sectional or aeroelastic model tests to identify the static and aerodynamic parameters of bridge sections, safety against winds can be satisfactorily guaranteed. However, it must be noted that methods of assessing the stabilization of vortex-induced vibration or flutter of a bridge are sometimes built on trial and error. Also, there are a lot of unknown and uncertain issues in attempting to refine current methods for gust response analysis. In addition, the mechanisms of bridge vibration and vibration control lack sufficient physical understanding. It is believed that more fundamental researches on wind effects on bridges, in particular bridge aerodynamics, are necessary to facilitate physical understanding of the interaction between wind and bridge and thus make wind-resistant design more rational and reliable. Among the many problems that need to be solved, Reynolds number effect and turbulence effect are considered as important issues that add uncertainty in applying wind tunnel results to real structures.
Atmospheric turbulence comprises irregular air motions characterized by winds that vary in speed and direction. Shear-induced turbulence is mainly targeted when turbulence effects are concerned in the structural wind engineering field. Turbulence is characterized by chaotic property changes, including low momentum diffusion, high momentum convection, and rapid variation of pressure and flow velocity in space and time, and is considered the most important unsolved problem of classical physics. Therefore, turbulence problems are normally treated statistically rather than deterministically, although turbulence processes organize dynamic structures. The organized structure of turbulence such as a large-scale bulge of the atmospheric boundary layer that divide the whole turbulent boundary layer into turbulent and non-turbulent regions, longitudinal vortex, and other dynamic features were not explicitly considered. In addition to the chaos, turbulence is characterized by diffusivity, rotationality, three-dimensionality, and dissipation. Diffusivity is responsible for enhanced mixing and increased rates of mass, momentum, and energy transport. Rotationality and three-dimensionality are associated with vortex stretching, which is the core mechanism on which turbulence energy cascade relies. During vortex stretching, unsteady vortices appear on many scales and interact with each other, with an overall tendency for larger flow structures to break down into smaller structures, and this process continues until small scale structures are small enough that their kinetic energy can be transformed into heat, that is, to say, dissipates. Although turbulence is not a pure random process, first- and second-order turbulence statistics are often treated as representative parameters to illustrate the property of turbulence when quantitatively investigating their effects on flow–structure interaction.
Turbulence Effects
The previous studies on turbulence effects on VIV of a bridge deck generally led to a conclusion that turbulence has a strong effect on the synchronization mechanism, reducing oscillation amplitudes and in some instances even completely inhibiting them. However, Goswami et al. (1993) showed that the turbulence effect on the response amplitude of a circular cylinder in free vibration is negligible and remains virtually unchanged from the no-grid scenario. More studies on the turbulence effect on VIV seem necessary to achieve consistent understanding of the turbulence effect and the mechanism behind it.
Laneville and Parkinson (1971) investigated the influence of isotropic turbulence on the galloping behavior of rectangular cylinders, showing that the quasi-steady theory is still applicable if the static aerodynamic coefficients are measured in a turbulent flow with the same turbulence intensity. Turbulence was found to be able to suppress the galloping of a 2:1 rectangular cylinder with an elongated afterbody, but it did not affect the galloping of a square cylinder. However, for a 1:2 rectangular cylinder with a short afterbody, turbulence is found to foster instability.
It was reported a decrease of critical wind speed in turbulence for classical coupled flutter and no variation or small increase for torsional flutter. Davenport et al. (1971) found that turbulence raises the critical wind speed for coupled vertical-torsional flutter of flat-plate and truss-stiffened decks, although it only marginally postpones the onset of torsional instability for H-shaped plate-girder decks. It was also reported that turbulence can play either a destabilizing role if the critical mode is to act alone or a stabilizing role if it is coupled with other modes, because it fosters vibration energy transfer toward more stable modes.
Like flutter analysis, knowledge from the aeronautical field was referred in the initial stage of buffeting analysis for a bridge. Davenport (1962) published his theory of the dynamic response of structures to random excitation due to turbulence in the atmospheric boundary layer and applied it to a suspension bridge, showing that the fluctuating component has an effect as great as or greater than the mean wind, and that vertical vibrations due to the vertical component of turbulence may be as significant as horizontal action. The response of a bridge to turbulent wind is usually calculated by assuming the linear superposition of buffeting and self-excited forces and using the flutter derivatives measured in turbulent flow, although many studies have pointed out the necessity of considering coupled oscillation of bending and torsion to obtain good agreement with experimental results.
Generally, there have been relatively few studies on the turbulence effects on bridge aerodynamics, especially in the recent years. More experimental or numerical studies are necessary to obtain better understanding of turbulence effects. To achieve this goal, the turbulence-generation facilities that enable the studies should be developed first.
Turbulence Generation
Wind tunnel model testing is considered the most reliable approach to study wind effects on structures. The current wind load codes/standards are formulated under the premise that wind loads on structures are simulated in wind tunnels. Assuming that velocity fluctuations can be adequately modeled by stationary mean and turbulent flow properties, attempts to simulate an atmospheric flow in a wind tunnel have so far been confined to reproduction of statistical characteristics, including power spectra, vertical profiles of mean velocity and turbulence intensity, and sometimes coherence.
The well-known technique to create isotropic turbulence is to utilize turbulence grids, with which a homogeneous turbulence field can be anticipated. Currently, the most frequently used device to study turbulence effects of aerodynamics of a bluff body is still the turbulence grid. However, the inertia region in the spectrum of grid turbulence is usually too narrow compared with atmospheric turbulence or even does not exist. The turbulence Reynolds number is also too small. Modeling a high-turbulence Reynolds number flow by adding actuated devices in the tunnel have been tried by many researchers, because utilizing very large wind tunnels is usually impossible for the majority of the researchers. Specially designed devices that intentionally stimulate flow help increase the turbulence Reynolds number, or help in modeling some particular features of atmospheric turbulence. Makita (1991) developed a turbulence generator to model a homogeneous flow field with high-turbulence Reynolds number. Kobayashi et al. (1994) developed an active gust generator with arrays of plates and airfoils, which were controlled to control velocity fluctuations in the longitudinal and vertical directions, respectively. Diana et al. (2002) utilized an active turbulence generator to study the complex aerodynamic admittance role in buffeting response of a bridge deck.
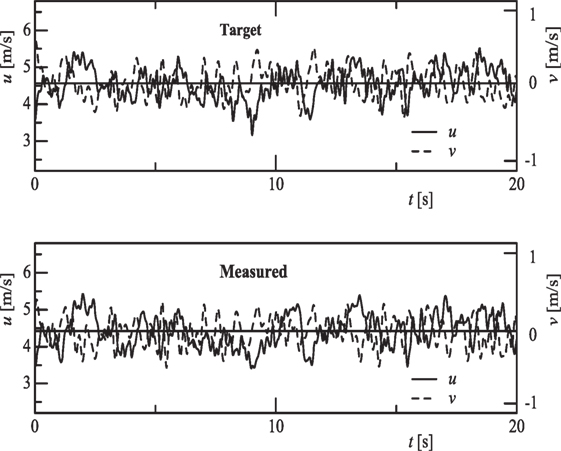
We considered that simulation of wind velocity history was of equal importance to reproduction of statistics. If “raw” wind velocity history can be reproduced, by which wind effects on structures are investigated, the obtained results would be more convincing. Longitudinal wind velocity is modeled by controlling the rotational speed of fans, while the vertical component is modeled by controlling the attack angle of the blades. Figure 1A illustrates an actively controlled multiple-fan (99 fans) wind tunnel installed at Miyazaki University, Japan (Cao et al., 2002). Figure 1B is a photo of a multi-fan (120 fans) wind tunnel of Tongji University, China, whose design concept followed that of the tunnel at Miyazaki University, Japan (Nishi and Miyagi, 1993), but the dynamic performance (frequency response) of the fans is improved, aiming at modeling high-frequency turbulence including transient wind. The 120 fans are arranged in a 12 × 10 matrix, and the test section is 1.8 m × 1.5 m. Figure 2 compares the time histories of longitudinal and vertical velocity components set as the target and those reproduced in the test section, the correlation of which is about 94%, implying a good modeling of the target velocity fluctuations.

Figure 1. Multiple-fan wind tunnels. (A) Miyazaki University tunnel (99 fans). (B) Tongji University tunnel (120 fans).
Conclusion
This article has reviewed phenomena of major concern in bridge aerodynamics: VIV, galloping, flutter, and buffeting, with particular attention to turbulence effects. It has been shown that both qualitative and quantitative understanding of turbulence effect, particularly the mechanism behind it, is clearly insufficient. Although turbulence might help the stabilization of long-span bridges and is thus not a conclusive parameter for wind-resistant design, turbulence effects on the aerodynamic, and aeroelastic behavior of a bridge must be better understood, because interaction between bridge and turbulence always exists. Advanced physical modeling of turbulence is being performed in Tongji University, but unfortunately, the interaction between generated turbulence with a bridge is being conducted, and this will be emphasized in future work.
Author Contributions
The first author is the corresponding author who designed the multiple-fan wind tunnel; the second author assisted the design.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer, AA, and handling editor declared their shared affiliation.
Funding
The author gratefully acknowledges the support of the National Natural Science Foundation of China (51720105005).
References
Borri, C., Bartoli, G., and Mannini, C. (2013). “The long way from Teddington 1963 to Cambridge 2013 through 50 years of bridge aerodynamics,” in Proc. of Fifty Years of Wind Eng., Sixth European and African Conference on Wind Engineering (Cambridge, UK).
Cao, S., Nishi, A., Kikugawa, H., and Matsuda, Y. (2002). Reproduction of wind velocity in a multiple fan wind tunnel. J. Wind Eng. Ind. Aerodyn. 90, 1719–1729. doi: 10.1016/S0167-6105(02)00282-9
Chen, A., You, Q., Zhang, X., Ma, R., and Zhou, Z. (2005). “Aerodynamic problems of a super-long span cable-stayed bridge,” in Proc. of the IABSE Symposium on Structures and Extreme Events, Jul. 11–15 (Lisbon, Portugal).
Davenport, A. G. (1962). Buffeting of a suspension bridge by storm winds. J. Str. Eng. 88(3), 233–268.
Davenport, A. G., Isyumov, N., and Miyata, T. (1971). “The experimental determination of the response of suspension bridges to turbulent wind,” in Proc. the International Conference on Wind Effects on Buildings and Structures, Tokyo, Japan, 1207–1219.
Diana, G., Bruni, S., and Cigada, A. (2002). Complex aerodynamic admittance role in buffeting response of a bridge deck. J. Wind Eng. Ind. Aerodyn. 90, 2057–2072. doi:10.1016/S0167-6105(02)00321-5
Ge, Y., and Xiang, H. (2008). Recent development of bridge aerodynamics in China. J. Wind Eng. Ind. Aerodyn. 96, 736–768. doi:10.1016/j.jweia.2007.06.045
Goswami, I., Scanlan, R. H., and Jones, N. P. (1993). Vortex-induced vibration of circular cylinders. J. Eng. Mech. 11, 2270–2287. doi:10.1061/(ASCE)0733-9399(1993)119:11(2270)
Kobayashi, H., Hatanaka, A., and Ueda, T. (1994). Active simulation of time histories of strong wind gust in a wind tunnel. J. Wind Eng. Ind. Aerodyn. 53, 315–330. doi:10.1016/0167-6105(94)90089-2
Kwon, S. D., Lee, S. H., Uejima, H., Lee, M. J., and Kim, J. (2008). “Aerodynamic design of Kwangyang suspension bridge with main span 1545m,” in Proc. of the 6th International Colloquium on Bluff Body Aerodynamics and Applications, Jul. 20–24 (Milan, Italy).
Laneville, A., and Parkinson, G. V. (1971). “Effects of turbulence on galloping of bluff cylinders,” in Proc. 3rd International Conference on Wind Effects on Buildings and Structures (Tokyo, Japan), 787–797.
Larose, G. L., Larsen, S. V., Larsen, A., Hui, M., and Jensen, A. G. (2003). “Sectional model experiments at high Reynolds number for the deck of a 1018m span cable-stayed bridge,” in Proc. of the 11th International Conference on Wind Engineering, Jun 2–5 (Lubbock, Texas), 373–380.
Larsen, A., and Gimsing, N. J. (1992). Wind engineering aspects of the east bridge tender project. J. Wind Eng. Ind. Aerodyn. 42, 1405–1416. doi:10.1016/0167-6105(92)90148-4
Makita, H. (1991). Realization of a large-scale turbulence field in a small wind tunnel. Fluid Dyn. Res. 8, 53–60. doi:10.1016/0169-5983(91)90030-M
Miyata, T., Okauchi, I., Shiraishi, N., Narita, N., and Narahira, T. (1988). Preliminary design considerations for wind effects on a very long-span suspension bridge. J. Wind Eng. Ind. Aerodyn. 29, 379–388. doi:10.1016/0167-6105(88)90176-6
Nishi, A., and Miyagi, H. (1993). Computer controlled wind tunnel. J. Wind Eng. Ind. Aerodyn. 4, 837–846. doi:10.1016/0167-6105(93)90360-Z
Keywords: active wind tunnel, turbulence effects, bridge aerodynamics, long-span bridges, turbulence modelling
Citation: Cao S and Cao J (2017) Toward Better Understanding of Turbulence Effects on Bridge Aerodynamics. Front. Built Environ. 3:72. doi: 10.3389/fbuil.2017.00072
Received: 05 October 2017; Accepted: 28 November 2017;
Published: 11 December 2017
Edited by:
Gregory Alan Kopp, University of Western Ontario, CanadaReviewed by:
Suren Chen, Colorado State University, United StatesAbul Fahad Akon, University of Western Ontario, Canada
Copyright: © 2017 Cao and Cao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shuyang Cao, c2h1eWFuZ0B0b25namkuZWR1LmNu
 Shuyang Cao
Shuyang Cao Jinxin Cao
Jinxin Cao