- Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyotodaigaku-Katsura, Nishikyo, Kyoto, Japan
An innovative hybrid control building system of base-isolation and building-connection has been proposed in the previous study. This system has two advantages, (i) to resist an impulsive earthquake input through the base-isolation system and (ii) to withstand a long-duration earthquake input through the building-connection system. A simple response evaluation method without the need of non-linear time–history response analysis is proposed here for this hybrid building system under a long-period and long-duration ground motion. An analytical expression is derived in the plastic deformation of an elastic–perfectly plastic single-degree-of-freedom (SDOF) model with viscous damping under the multi-impulse, which is the representative of long-period and long-duration ground motions. A transformation procedure of a base-isolation building-connection hybrid structural system into an SDOF model is proposed by introducing two steps, one is the reduction of the main base-isolated building to an SDOF system, and the other is the reduction of the connecting oil dampers supported on a free-wall to an oil damper with a newly introduced compensation factor on a rigid wall. Application of the analytical expression of the plastic deformation to the reduced SDOF model including the compensation factor on the connecting oil dampers enables the development of a simplified, but rather accurate response evaluation method. The time–history response analysis of the multi-degree-of-freedom model and the comparison with the proposed simplified formula make clear the accuracy and reliability of the proposed simplified response evaluation method.
Introduction
Resilience of infrastructures against natural disasters is becoming a key theme recently, and many earthquakes in the last few decades raised some issues which should be overcome for the continuing use of infrastructures in the field of earthquake structural engineering (Bruneau and Reinhorn, 2006; Takewaki et al., 2012). Bruneau and Reinhorn (2006) proposed four factors (robustness, redundancy, resourcefulness, and rapidity) as the principal elements of resilience. To take into account the earthquake resilience of building structures in the design stage, it is inevitable to make scenarios for building structures to resist devastating earthquakes without severe damage, which disturbs their continuing use (Amadio et al., 2003; Kobori, 2004; Takewaki et al., 2012, 2013; Takewaki, 2013). Since properties of earthquake ground motions are intrinsically uncertain, it seems difficult to predict the future events within an allowable accuracy in time, space, and character (Takewaki et al., 2011, 2012, 2013; Takewaki, 2013). Because the structural properties of buildings, especially in advanced buildings systems such as base-isolation systems and passive control systems are not certain (Ben-Haim, 2006) and the direct treatment of their variation is inevitable in the reliable seismic resistant design of building structures, the concepts of robustness and redundancy are becoming also very important. In fact, it is absolutely required in Japan to consider the uncertainties of structural properties of isolators and dampers in the design of base-isolated buildings and passively controlled buildings. In such design procedure, the worst combination of structural properties of isolators and dampers plays a key role for reliable design (Ben-Haim, 2006; Elishakoff and Ohsaki, 2010; Takewaki et al., 2012; Fujita et al., 2017; Kanno et al., 2017).
It appears that, if it is aimed at designing building structures with high resilience, base-isolation or structural control is inevitable. It is well recognized that, while base-isolated buildings are effective for pulse-type ground motions with predominant periods shorter than about 2 s or random earthquake ground motions without clear predominant period (Jangid and Datta, 1994; Hall et al., 1995; Heaton et al., 1995; Jangid, 1995; Jangid and Banerji, 1998; Kelly, 1999; Naeim and Kelly, 1999; Jangid and Kelly, 2001; Morales, 2003; Takewaki, 2005, 2008; Li and Wu, 2006; Hino et al., 2008; Takewaki and Fujita, 2009), their earthquake resilience is not clear for long-period ground motions with the characteristic period of 5–8 s (Irikura et al., 2004; Kamae et al., 2004; Ariga et al., 2006). The long-period ground motions with the characteristic period of 5–8 s have been argued in the structural design of base-isolated and super high-rise buildings since the Tokachi-oki earthquake in 2003 and have been treated as one of the most critical inputs for such buildings after the 2011 Tohoku earthquake. The long-period pulse with the clear period of 3 s and the large amplitude of velocity is under critical discussion in Japan after the Kumamoto earthquake in 2016. On the other hand, while building structures using passive energy dissipating systems are effective for long-duration and long-period ground motions (Takewaki, 2007; Patel and Jangid, 2011; Takewaki et al., 2011, 2012; Kasagi et al., 2015), they are not necessarily effective for pulse-type ground motions. This is because passive dampers requiring energy dissipation cannot withstand impulsive loading effectively. The overcome of these two difficult issues is of great concern in the field of earthquake-resistant and control design (Koo et al., 2009; Petti et al., 2010; Karabork, 2011).
In this article, an innovative hybrid passive control building system is treated in which a base-isolated building model is supported by (or connected to) another earthquake-resistant, non-isolated building (called free-wall) with oil dampers (Murase et al., 2013; Kasagi et al., 2016; Fukumoto and Takewaki, 2017). This innovative system has been developed by Obayashi Corporation and Shimizu Corporation in Japan as an apartment house with a car parking tower and has been actually constructed (Murase et al., 2013; Kasagi et al., 2016). It has been demonstrated that this hybrid passive building control system is effective and robust for different types of earthquake ground motions, i.e., pulse-type ground motions and long-period, long-duration ground motions. It has also been demonstrated using the energy analysis that, although the connecting oil dampers in the proposed hybrid system do not work effectively for pulse-type ground motions, those function effectively for long-period and long-duration ground motions. At the same time, it has also been clarified that this hybrid control system has a high degree of redundancy and robustness for a broad class of earthquake ground motions and an effective connecting damper location can be investigated using a sensitivity-type optimization approach (Taniguchi et al., 2016b; Tamura et al., 2017). However, only the time–history response analysis has been used for response evaluation and, if the non-linear response in the base-isolation story is taken into account, this response evaluation method requires heavy computational load.
Fujita et al. (2017) developed a new method of robustness evaluation for an elastoplastic base-isolated high-rise building considering simultaneous uncertainties of structural parameters. It has been shown that, by using the derived upper bound of the critical response to a double impulse, the robustness function (Ben-Haim, 2006), a measure of the robustness, of elastoplastic structures can be evaluated efficiently. However, it is difficult to derive a simple response evaluation method for a base-isolation building-connection hybrid structural system.
In this article, a simple response evaluation method using a single-degree-of-freedom (SDOF) model is proposed for a base-isolation building-connection hybrid structural system under a long-period and long-duration ground motion. An analytical expression is derived in the plastic deformation of an elastic–perfectly plastic SDOF model with viscous damping under the multi-impulse, which is the representative of long-period and long-duration ground motions. A transformation procedure of a base-isolation building-connection hybrid structural system into an SDOF model is proposed by introducing two steps, one is the reduction of the main base-isolated building to an SDOF system, and the other is the reduction of the connecting oil dampers supported on a free-wall to an oil damper with a compensation factor on a rigid wall. Application of the analytical expression of the plastic deformation to the reduced SDOF model including the compensation factor on the connecting oil dampers enables the development of a simplified, but rather accurate response evaluation method.
Analytical Expression of Maximum Response of Elastic–Perfectly Plastic SDOF Model with Viscous Damping Under Critical Multi-Impulse
Transformation of Long-Period and Long-Duration Ground Motion into Multi-Impulse Input
Kojima and Takewaki (2015b, 2017) showed that a long-period and long-duration ground motion can be well represented by a multi-impulse with an equal time interval as shown in Figures 1A,B (see also Application to Recorded Ground Motion). Figure 1A is a basic model with a common velocity amplitude, and Figure 1B is a realistic model with the half amplitude in the first impulse. The red arrow indicates the Dirac delta function. V is the given velocity (the input velocity level), and t0 is the equal time interval between two consecutive impulses. In terms of the Dirac delta function δ(t), the multi-impulse in Figure 1A can be expressed by the following equation:
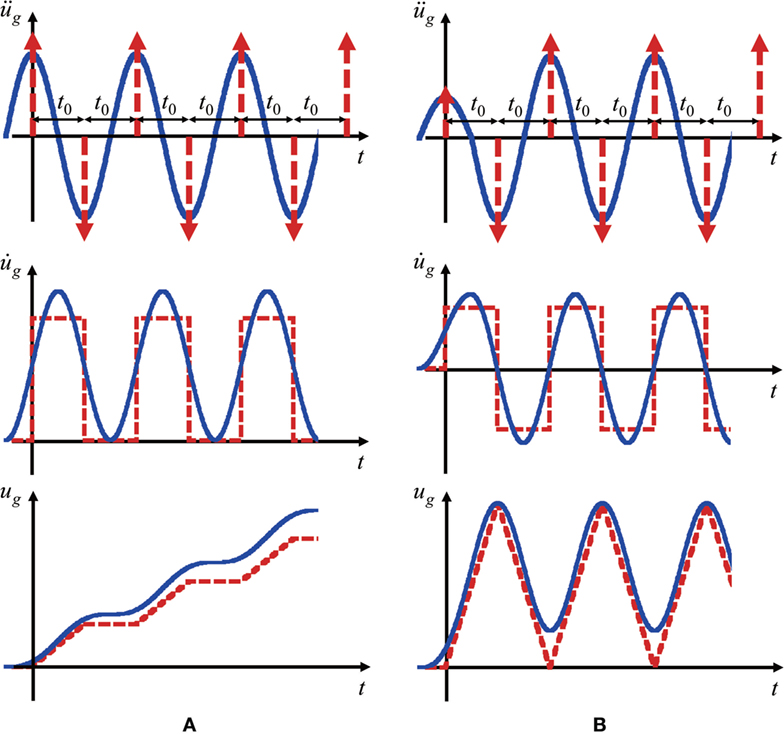
Figure 1. Multi-impulse input, (A) basic model and (B) realistic model with half amplitude in the first impulse and without gradual drift (Kojima and Takewaki, 2015b).
On the other hand, the multi-impulse in Figure 1B can be described by the following equation:
Elastic–Perfectly Plastic SDOF Model with Viscous Damping
Consider a viscously damped elastic–perfectly plastic SDOF model of mass m and stiffness k. The yield deformation and the yield force are denoted by dy and fy. Let , h, u, and f denote the undamped natural circular frequency, the damping ratio, the displacement of the mass relative to the ground (deformation of the system) and the restoring force of the model, respectively. Vy (≡ω1dy) denotes the input level of velocity of one impulse at which the undamped SDOF system at rest just attains the yield deformation after one impulse of such velocity and is used for normalizing the input velocity level. The time derivative is denoted by an over-dot.
Maximum Response of Elastic–Perfectly Plastic SDOF Model with Viscous Damping to Critical Multi-Impulse
An analytical expression of the plastic deformation is derived in this section for an elastic–perfectly plastic SDOF model with viscous damping to the critical multi-impulse. It should be emphasized that only the critical multi-impulse (resonant to the fundamental natural mode) is treated here which maximizes the plastic deformation for varied impulse timing. The criticality was demonstrated in the references (Kojima and Takewaki, 2015b; Kojima et al., 2017), and its detailed explanation will appear later in this section. Under such critical multi-impulse, the fundamental natural vibration mode governs most of the vibration component. This fact supports the validity of the modeling of a multi-degree-of-freedom (MDOF) model into an SDOF model. Since a residual deformation could exist in the elastic–perfectly plastic model and it is sensitive to the input motion, the plastic deformation is the focus of this article.
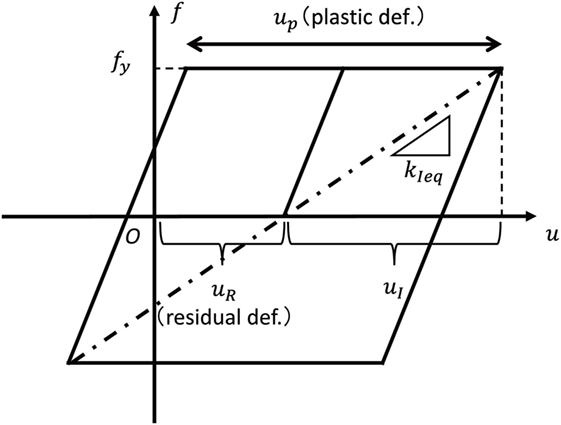
Figure 2 shows the spring and dashpot force–deformation relations of the elastic–perfectly plastic SDOF model with viscous damping to the critical multi-impulse. (a) Presents the restoring force–deformation relation and (b) indicates the damping force–deformation relation. The impulses in Figure 2 are two consecutive elements of the multi-impulse.
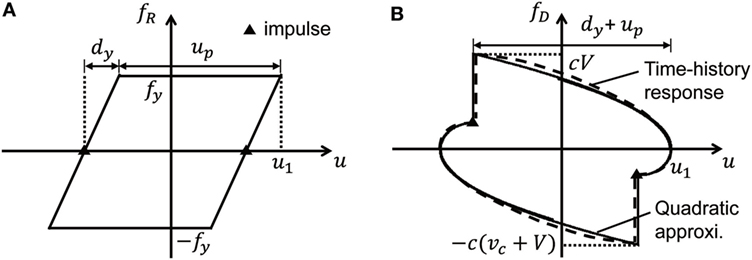
Figure 2. Spring and dashpot force–deformation relations of elastic–perfectly plastic single-degree-of-freedom (SDOF) model with viscous damping to critical multi-impulse, (A) restoring force–deformation relation and (B) damping force–deformation relation.
Kojima and Takewaki (2015a) showed that the critical timing of the second impulse corresponds to the zero restoring force in the first unloading stage in the case where an undamped elastic–perfectly plastic SDOF system is subjected to the double impulse. It was also demonstrated by Kojima and Takewaki (2015b) that this fact can be extended to the undamped elastic–perfectly plastic SDOF model subjected to the multi-impulse. Furthermore, this critical timing was confirmed by Kojima et al. (2017) for the damped elastic–perfectly plastic SDOF model subjected to the double impulse. Therefore, it is assumed here again that this critical timing is valid for the damped elastic–perfectly plastic SDOF model subjected to the multi-impulse. Under this assumption, an analytical expression of the plastic deformation is derived here.
It was shown by Kojima et al. (2017) that the maximum elastic–plastic responses of the damped SDOF model under the critical double impulse can be derived by an energy approach without solving directly the equation of motion. This approach is applied here to the damped elastic–perfectly plastic SDOF model subjected to the multi-impulse.
Let vc denote the velocity at the zero restoring-force timing, and let up denote the steady-state plastic deformation after one impulse. Since the response process in the unloading stage of the damped SDOF model under the critical multi-impulse is essentially the same as that of the damped SDOF model under the critical double impulse, vc derived in Kojima et al. (2017) can be used and expressed by the following equation:
As in Kojima et al. (2017) for the damped SDOF model under the critical double impulse, the damping force–deformation relation after one impulse is approximated by a quadratic function with the vertex (u, fD) = (u1, 0) and passing the point (u, fD) = (u1 − (up + dy), c(vc + V)) as shown in Figure 2B
The work done by the damping force can be obtained by integrating Eq. 4 from u = u1 − (up + dy) to u = u1
The energy balance law between the point of one impulse and the point attaining the maximum deformation can be expressed as follows by using Eq. 5
The left-hand side indicates the kinetic energy input at the timing of one impulse and the right-hand side presents the sum of the elastic strain energy, the dissipation energy by plastic deformation and the dissipation energy by viscous damping. From Eqs 3 and 6, the plastic deformation up can be expressed by the following equation:
MDOF Hybrid Model of Building-Isolation (Elastic–Perfectly Plastic Base-Isolation Story) and Building-Connection
Consider a 40-story base-isolated building connected to a 26-story free-wall for car parking by nc-story oil dampers (allocated to 4, 8, 12, 16, 18, 20, 22, 24, and 26th stories) as shown in Figure 3. The base-isolation story consists of natural rubber isolators, steel dampers, and oil dampers. This hybrid building system is modeled into the MDOF mass-spring-dashpot model as shown in Figure 3. For simple presentation, the super-structure has a common floor mass mU, and the free-wall has a common floor mass mF. The mass of the base-isolation story is denoted by mI, and the common damping coefficient of connecting oil dampers is denoted by c. Although the total restoring-force characteristic of the base-isolation story has a positive post-yield stiffness, the positive post-yield stiffness is neglected for simplicity. Therefore, the base-isolation story has an elastic–perfectly plastic restoring-force characteristic with viscous damping as shown in Figure 3 (Qi: story shear in the base-isolation story, ui: story deformation in the base-isolation story). kI, fy, and dyI indicate the initial elastic stiffness, the yield force and the yield deformation of the base-isolation story, respectively. Let Tup, Tsub, and cI denote the fundamental natural period of the main structure with fixed base-isolation story, the fundamental natural period of the free wall, and the damping coefficient of oil dampers in the base-isolation story. It is assumed that cI is given so that the damping ratio of oil dampers attains 0.15 for the equivalent stiffness kIeq of the base-isolation story at the base-isolation deformation uI = 0.4 m. The parameters of the base-isolation building-connection hybrid system are shown in Table 1.
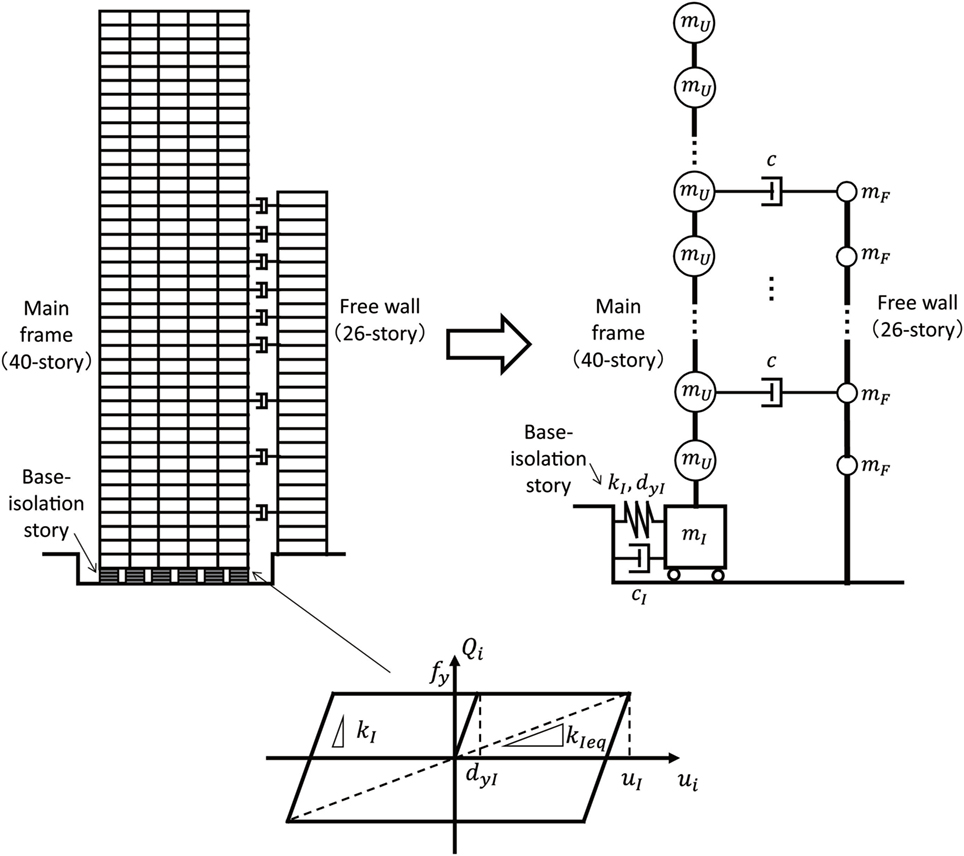
Figure 3. Base-isolation and building-connection hybrid system with elastic–perfectly plastic restoring force–deformation relation of base-isolation story and its modeling into multi-degree-of-freedom model.
Reduction of MDOF Model to SDOF Model
To use the analytical expression of the plastic deformation of the base-isolation story shown in Section “Analytical Expression of Maximum Response of ElasticâĂŞPerfectly Plastic SDOF Model with Viscous Damping under Critical Multi-Impulse,” the MDOF model shown in Figure 3 is reduced to an SDOF model. This model reduction consists of two parts. One is the reduction of the base-isolated building, and the other is the reduction of the connecting oil dampers.
In the base-isolated building, the upper structure is reduced to an SDOF model, and the reduced system of an SDOF super-structure and the base-isolation story is further reduced to the final SDOF model by neglecting the base-isolation mass, i.e., reduction using the series model.
On the other hand, in the reduction of the connecting oil dampers, it is necessary to take into account the effects of the free-wall height, the connecting oil damper location and the free-wall stiffness on the damping coefficient in the SDOF model. Since the number of stories with the connecting oil dampers (the common damping coefficient per floor is c) is nc, the total damping coefficient of the connecting oil dampers is ncc. When the modification factor is denoted by βd (see Figure 4), the compensated damping coefficient of the total connecting dampers can be expressed by the following equation:
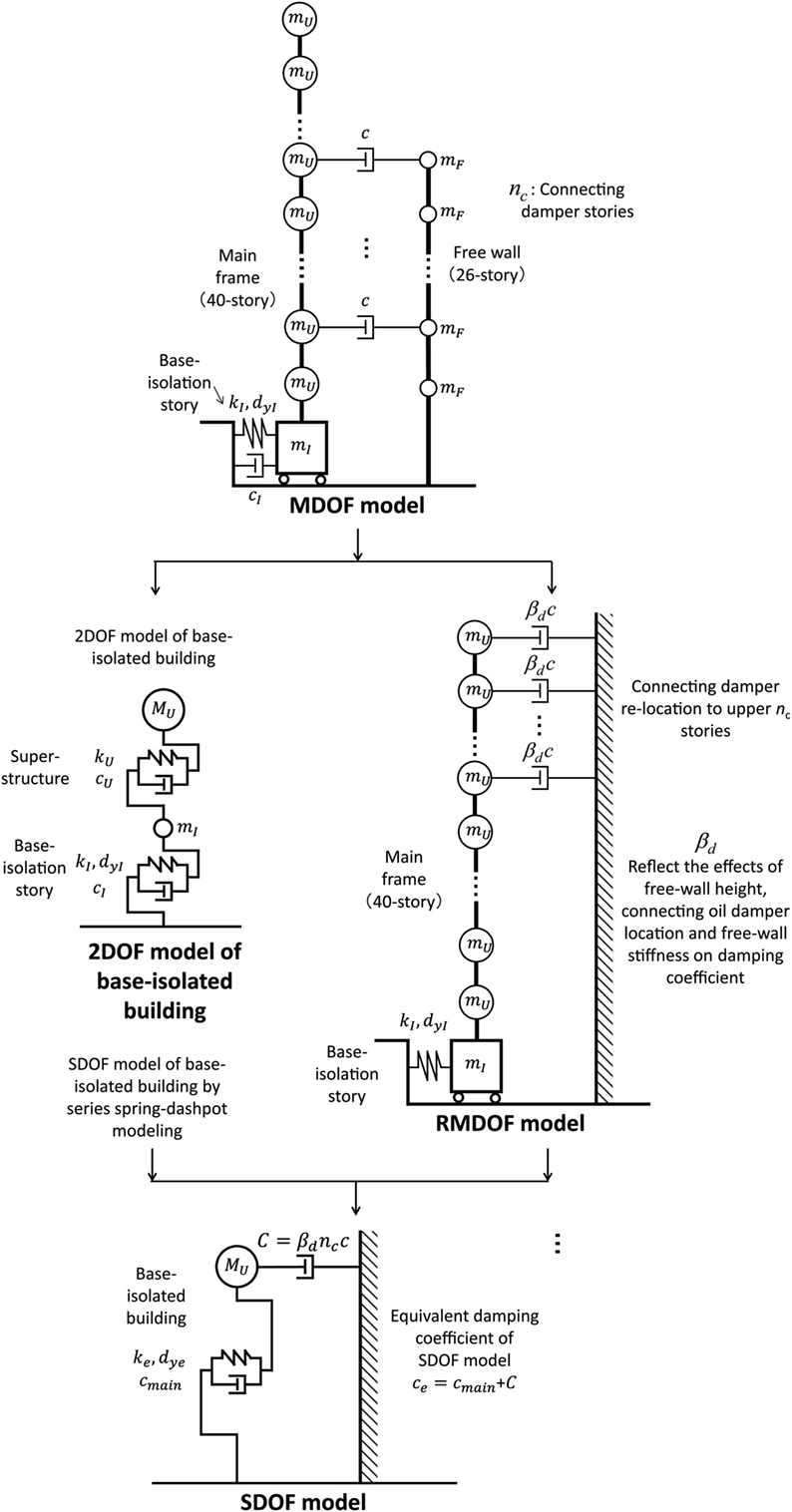
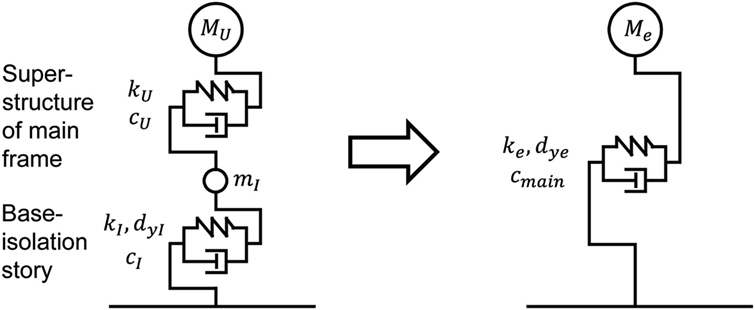
Figure 4. Modeling of multi-degree-of-freedom (MDOF) base-isolation and building-connection hybrid system into single-degree-of-freedom (SDOF) model.
The factor βd may include some effect of damper location. However it seems to reflect mainly the effect of flexibility of the free-wall. To determine βd, consider the virtual intermediate model, called the RMDOF model as shown in Figure 4, in which the connecting oil dampers with the damping coefficient βdc are concentrated to upper consecutive nc floors in the base-isolated building which is supported on a rigid wall by nc-floor oil dampers. The modification factor βd is determined by equating the lowest-mode damping ratios, by the complex modal analysis, between the RMDOF model and the MDOF model. In both RMDOF model and MDOF model, the equivalent stiffness kIeq of the base-isolation story is determined by conducting the repetitive computation of uI for convergence which will be explained later. It should also be remarked that the structural damping of the super-structure and the damping in the base-isolation story are neglected only in evaluating the damping ratios of the RMDOF model and the MDOF model for determination of βd.
It should be emphasized again that only the critical multi-impulse (resonant to the fundamental natural mode) is treated here. In this case, the fundamental natural vibration mode governs most of the vibration component in the present hybrid model. This fact supports the validity of the modeling of an MDOF model into an SDOF model.
Reduction of Base-Isolated Building to SDOF Model
The reduced 2DOF base-isolated building model is further reduced to the SDOF model in this section as shown in Figure 5. The super-structure mass MU of the 2DOF model is the summation of the super-structure masses. The super-structure stiffness and damping coefficient kU and cU of the 2DOF model are determined by the equivalence of the fundamental natural period and the lowest-mode damping ratio between the SDOF model with the fixed base-isolation story and the MDOF model.
Let Me, ke, dye, and cmain denote the mass, the initial stiffness, the yield deformation, and the damping coefficient of the reduced SDOF model of the base-isolated building.
In the case where the base-isolation story mass is negligible compared with the super-structure mass MU, Me can be regarded as follows:
In addition, if the base-isolation story mass is negligible compared with the super-structure mass MU, ke can be expressed in the following form by using a series spring modeling
Since the yield story shear forces are the same in the SDOF model and the 2DOF model with zero base-isolation story mass, the equivalent yield deformation of the SDOF model can be described by the following equation:
Let uI, uU, ue, and fy denote the base-isolation story displacement, the relative super-structure displacement, the displacement of the SDOF model, and the yield force in the base-isolation story.
Figure 6 shows the relation of the restoring force–deformation characteristic between the base-isolation story of the 2DOF model and the total SDOF model. It should be remarked that the plastic deformation dpe of the SDOF model is equal to the plastic deformation dpI of the base-isolation story in the 2DOF model due to the series modeling.
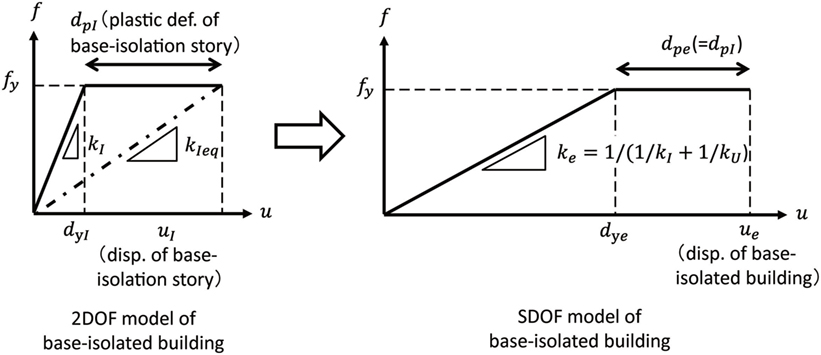
Figure 6. Relation of restoring force–deformation characteristic between base-isolation story of 2DOF model and total single-degree-of-freedom (SDOF) model.
Since the super-structure and the base-isolation story have different damping coefficients, the equivalent damping coefficient cmain of the SDOF model can be obtained by using the series complex spring modeling
where i is the imaginary unit and the natural circular frequency ωe of the SDOF model is defined by the following equation:
From Eqs 10, 12, and 13, cmain can be expressed by the following equation:
Reduction of Connecting Damper
As stated earlier, in the reduction of the connecting oil dampers, it is necessary to take into account the effects of the free-wall height, the connecting oil damper location and the free-wall stiffness on the damping coefficient in the SDOF model. It was confirmed that these effects can be taken into account properly by introducing the RMDOF model in which the connecting oil dampers with the compensated damping coefficient βdc are concentrated to the upper consecutive nc stories in the base-isolated building and the base-isolated building is supported on a rigid wall by nc-story oil dampers. The modification factor βd is determined by equating the lowest-mode damping ratios, by the complex modal analysis, between the RMDOF model (hR) and the MDOF model (hM)
As stated earlier, since only the critical multi-impulse (resonant to the fundamental natural mode) is treated here, the fundamental natural vibration mode governs most of the vibration component in the present hybrid model. For this reason, the equivalence of the lowest-mode damping ratio seems to provide a good correspondence of both models (RMDOF and MDOF). It should be remarked that the determination of the modification factor βd via Eq. 15 is difficult because some iterations are required. To avoid this iteration, we employ another procedure as shown in Figure 7. First of all, we compute the lowest-mode damping ratio hM for the MDOF model and also for the RMDOF model with ncc in place of βdncc. Then, if we assume the linearity of the lowest-mode damping ratio hR for the RMDOF model with respect to the total damping coefficient, we can obtain directly βd as from Figure 7.
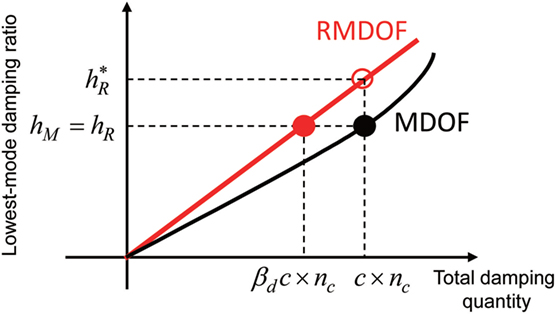
Figure 7. Procedure for determining βd without iteration using multi-degree-of-freedom (MDOF) and RMDOF models.
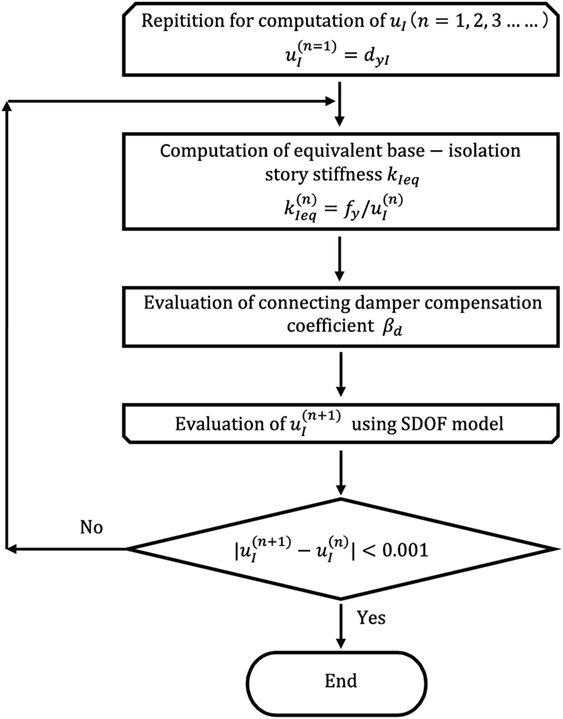
In both the RMDOF model and the MDOF model, the equivalent stiffness kIeq of the base-isolation story at the base-isolation deformation uI is adopted as the base-isolation story stiffness for the complex eigenvalue analysis as shown in Figure 8
In the evaluation of uI, a repetitive procedure is required as shown in Figure 9.
Numerical Investigation on Accuracy of Proposed Simple Response Evaluation Method Using SDOF Model
To investigate the accuracy of the proposed simple response evaluation method using the simplified SDOF model, three models with different numbers of stories of free-wall (26, 13, and 40) are considered. The fundamental natural period of the 13-story free-wall is 0.32 s and that of the 40-story free wall is 0.95 s in addition to 0.63 s of the 26-story free wall (Table 1). The base-isolated building is a 40-story model and four levels of the connecting oil dampers are considered (c = 1 × 106, 3 × 106, 5 × 106, and 7 × 106 Ns/m).
The MDOF model is a full model with the base-isolation story including the elastic–perfectly plastic restoring-force characteristic and the viscous damping due to oil dampers [see MDOF Hybrid Model of Building-Isolation (Elastic–Perfectly Plastic Base-Isolation Story) and Building-Connection for detail of the MDOF model]. The time–history response analysis is conducted for the critical multi-impulse. The critical timing of the multi-impulse has been determined by regarding the timing of the zero restoring force in the unloading process at the base-isolation story as the critical timing. This assumption comes from the fact of the SDOF model (Kojima and Takewaki, 2015a,b; Kojima et al., 2017) and the 2DOF model (Taniguchi et al., 2016a). The plastic deformation by the proposed SDOF model is computed by Eq. 7 and that by the SDOF model with βd = 1 (no compensation due to the effects of the free-wall height, the connecting oil damper location and the free-wall stiffness on the damping coefficient) is also computed by Eq. 7 for comparison.
Figure 10 shows the comparison of the plastic deformation in the base-isolation story with respect to the input level V/Vye of the multi-impulse between the full MDOF model (time–history response analysis) and the SDOF model (proposed simple evaluation method) for four levels of connecting dampers (free-wall: 26 stories). The result for the SDOF model with βd = 1 (without connecting damper compensation) has also been shown to demonstrate the influence of βd. It can be observed that, as the connecting oil damper quantity becomes larger, the proposed SDOF model including an appropriate βd exhibits a good performance.
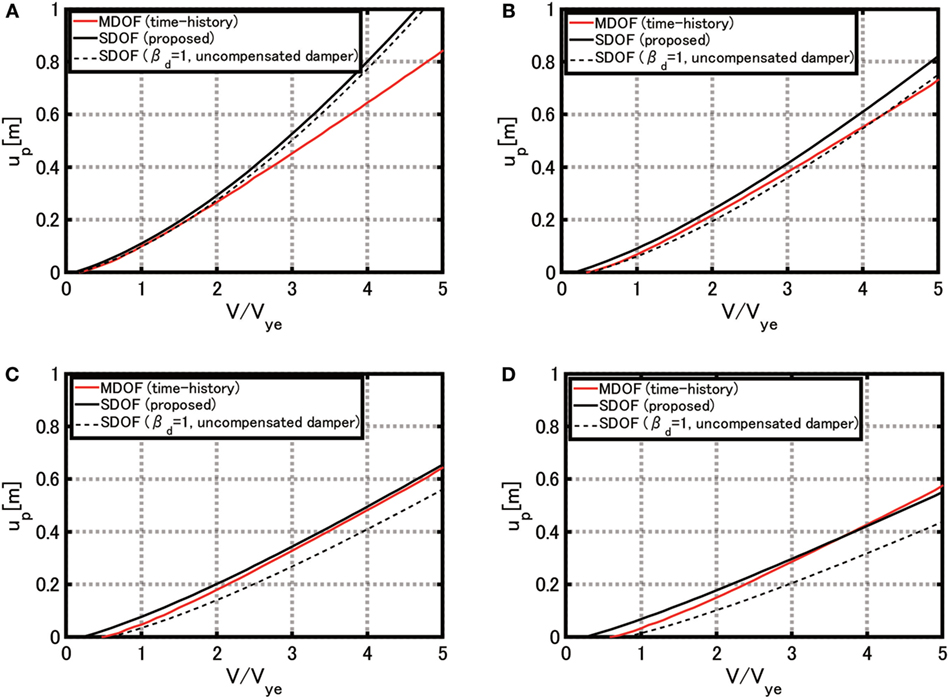
Figure 10. Comparison of plastic deformation in base-isolation story between multi-degree-of-freedom (MDOF) model (time–history response analysis) and single-degree-of-freedom (SDOF) model (simple evaluation method) for four levels of connecting dampers (free-wall: 26 stories), (A) c = 1 × 106 Ns/m, (B) c = 3 × 106 Ns/m, (C) c = 5 × 106 Ns/m, and (D) c = 7 × 106 Ns/m.
Figure 11 presents the similar figure for the 13-story free-wall model, and Figure 12 illustrates that for the 40-story free-wall model. It can be seen that, although a similar tendency exists in the 13-story free-wall model, the compensation effect of the connecting oil dampers by βd is not clear in the 40-story free-wall model.
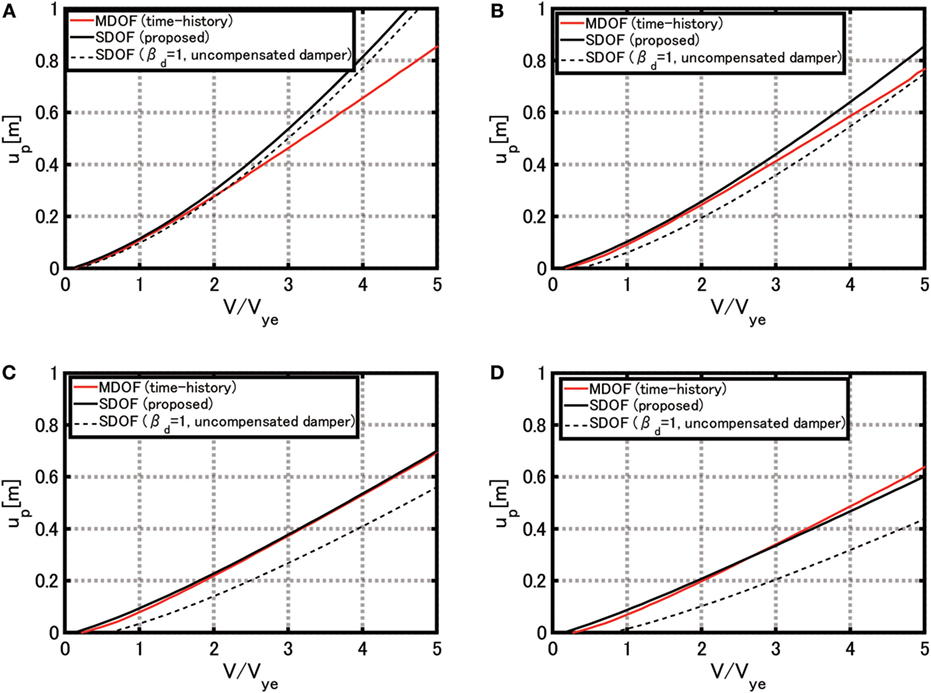
Figure 11. Comparison of plastic deformation in base-isolation story between multi-degree-of-freedom (MDOF) model (time–history response analysis) and single-degree-of-freedom (SDOF) model (simple evaluation method) for four levels of connecting dampers (free-wall: 13 stories), (A) c = 1 × 106 Ns/m, (B) c = 3 × 106 Ns/m, (C) c = 5 × 106 Ns/m, and (D) c = 7 × 106 Ns/m.
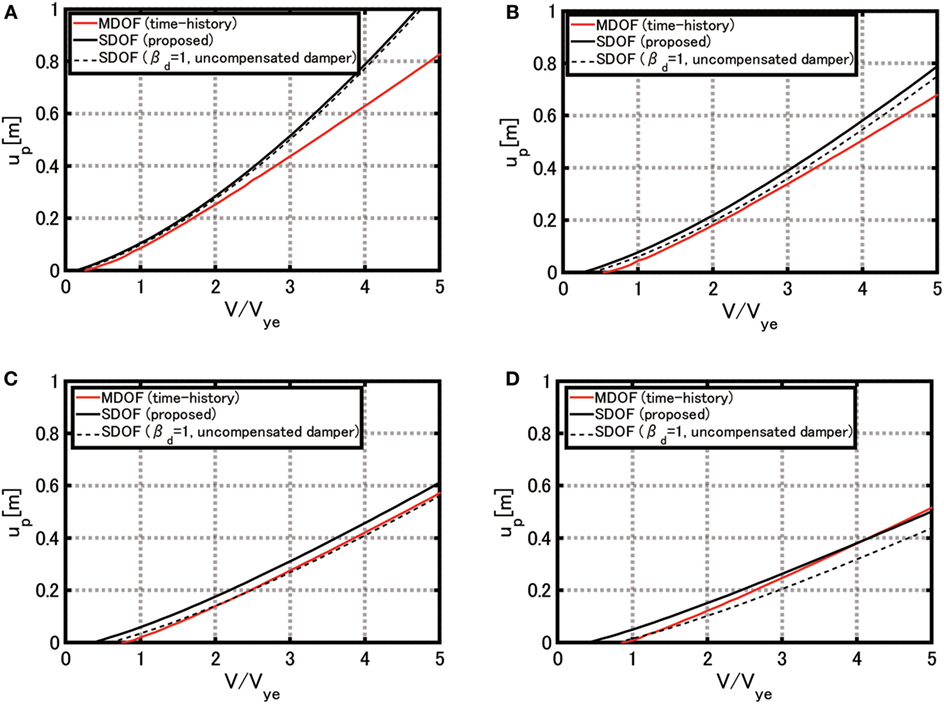
Figure 12. Comparison of plastic deformation in base-isolation story between multi-degree-of-freedom (MDOF) model (time–history response analysis) and single-degree-of-freedom (SDOF) model (simple evaluation method) for four levels of connecting dampers (free-wall: 40 stories), (A) c = 1 × 106 Ns/m, (B) c = 3 × 106 Ns/m, (C) c = 5 × 106 Ns/m, and (D) c = 7 × 106 Ns/m.
Figure 13 shows the maximum top relative displacement of the MDOF model with four levels of connecting dampers (c = 1 × 106, 3 × 106, 5 × 106, and 7 × 106 Ns/m) with respect to the input level V/Vye of the multi-impulse. It can be observed that the influence of the quantity of the connecting oil dampers on the maximum top relative displacement is rather small in a relatively large input level. In most of base-isolated buildings, the top relative displacement is not a critical response compared with the deformation of the base-isolation story. If necessary, a simple evaluation method using the proposed SDOF model will be developed.
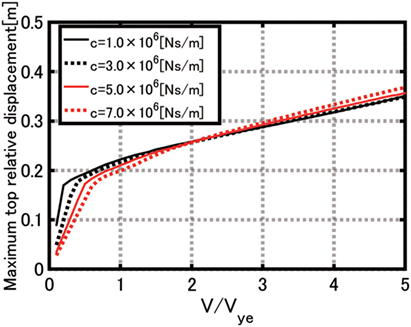
Figure 13. Maximum top relative displacement of multi-degree-of-freedom model with four levels of connecting dampers with respect to input level of multi-impulse.
Application to Near-Fault Ground Motion
In this article, a simplification into an SDOF model has been proposed under a long-period and long-duration ground motion. It may be useful to investigate the applicability of the proposed method to other types of ground motions, e.g., near-fault ground motions. Since it has been reported that the near-fault ground motions can be well represented by a double impulse, the accuracy of the proposed simple method using an SDOF model for such double impulse is investigated.
Figure 14 shows the comparison of the maximum deformation of the base-isolation story between the MDOF model and the SDOF model under the critical double impulse. The critical double impulse means the input maximizing the maximum deformation of the SDOF model for a varied impulse interval. It can be observed that, although a slight difference exists in the rather small input level, the accuracy of the proposed SDOF model is almost satisfactory.
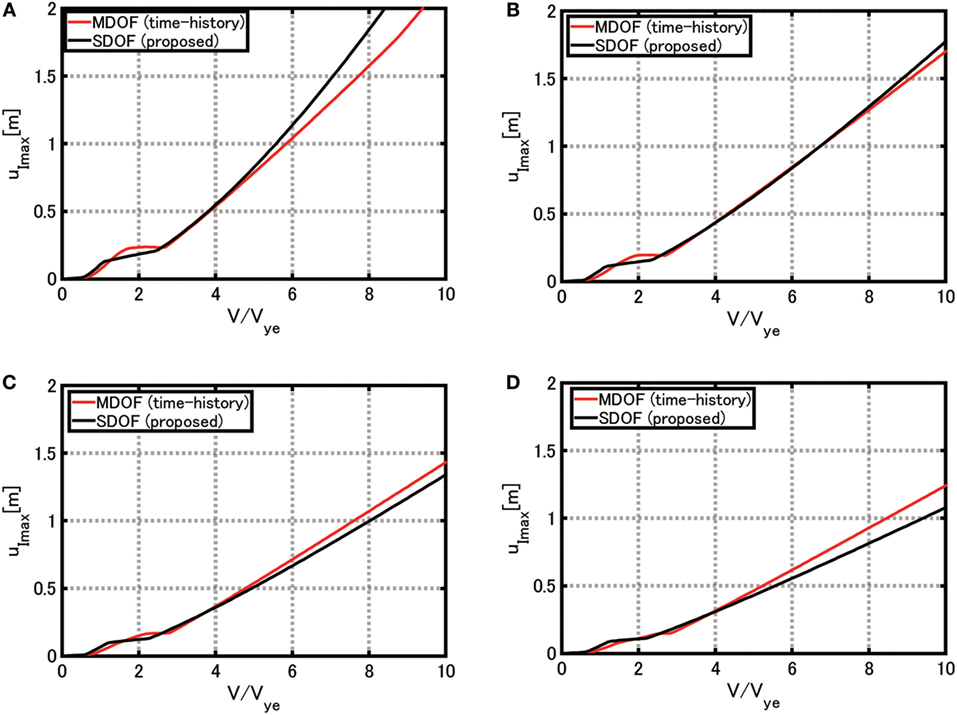
Figure 14. Comparison of maximum deformation of base-isolation story between multi-degree-of-freedom (MDOF) model and single-degree-of-freedom (SDOF) model, (A) c = 1 × 106 Ns/m, (B) c = 3 × 106 Ns/m, (C) c = 5 × 106 Ns/m, and (D) c = 7 × 106 Ns/m.
Application to Recorded Ground Motion
In Section “Numerical Investigation on Accuracy of Proposed Simple Response Evaluation Method Using SDOF Model,” only the multi-impulse was treated as an input. To show the applicability of the proposed simple response evaluation method using the multi-impulse to an actual earthquake ground motion, the Tomakomai EW motion (Tokachioki earthquake 2003) is used. This ground motion is well known as the first recorded famous one of a long-period, long-duration ground motion. The ground motion velocity wave is shown in Figure 15A together with the corresponding sinusoidal wave. The period of the sinusoidal wave is taken as 7 s, and the amplitude (0.285 m/s) is determined so that the three largest half waves are compatible in average with the sinusoidal wave.
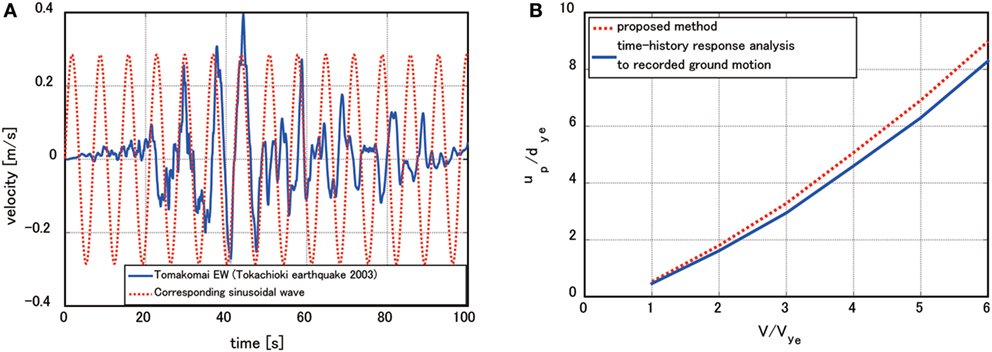
Figure 15. Application to recorded ground motion, (A) velocity wave of Tomakomai EW (Tokachioki earthquake 2003) and the corresponding sinusoidal wave, (B) comparison of the normalized plastic deformation in the base-isolation story with respect to the input level V/Vye of the multi-impulse between the time–history response analysis result and the result by the proposed simple evaluation method.
Figure 15B shows the comparison of the normalized plastic deformation in the base-isolation story with respect to the input level V/Vye of the multi-impulse between the time–history response analysis result and the corresponding one by the proposed simple evaluation method for the connecting damper level c = 5 × 106 Ns/m (free-wall: 26 stories). It should be noted that, since the velocity level V is fixed in this example, Vye is changed, i.e., ωe and dye are changed. This treatment is similar to the elastic–plastic response spectra introduced around 1960s (Veletsos et al., 1965).
Conclusion
A simple response evaluation method has been proposed for a base-isolation building-connection hybrid structural system under a long-period and long-duration ground motion. The following conclusions have been drawn.
(1) An analytical expression has been derived in the plastic deformation of an elastic–perfectly plastic SDOF model with viscous damping under a multi-impulse which is the representative of long-period and long-duration ground motions.
(2) A transformation procedure of a base-isolation building-connection hybrid structural system into an SDOF model has been proposed by introducing two steps, one is the reduction of the main base-isolated building to an SDOF model and the other is the reduction of the connecting oil dampers supported on a free-wall to the oil dampers with a compensation factor βd on a rigid wall.
(3) The comparison of the plastic deformation in the base-isolation story with respect to the input level V/Vye of the multi-impulse has been made between the full MDOF model (time–history response analysis) and the SDOF model (proposed simple evaluation method) for four levels of connecting dampers and three numbers (26, 13, and 40) of stories of the free-wall. The SDOF model with βd = 1 (without compensation) has also been shown for demonstrating the influence of βd. It has been observed that, as the connecting oil damper quantity becomes larger, the proposed SDOF model including an appropriate βd exhibits a good performance in the model with the number of stories of the free-wall (13 and 26). However, the compensation effect of the connecting oil dampers by βd is not clear in the 40-story free-wall model.
(4) In the evaluation of the maximum top relative displacement using the MDOF model with four levels of connecting dampers with respect to the input level V/Vye of the multi-impulse, the influence of the quantity of the connecting oil dampers on the maximum top relative displacement is rather small in a relatively large input level. In most base-isolated buildings, the top relative displacement is not a critical response compared with the deformation of the base-isolation story. If necessary, a simple evaluation method using the proposed SDOF model can be developed.
(5) The applicability of the proposed simplified method to other types of ground motions, i.e., near-fault ground motions, has been clarified. It has been observed that, although a slight difference exists in the rather small input level, the accuracy of the proposed SDOF model is almost satisfactory.
(6) The applicability of the proposed simplified method to a recorded ground motion has been investigated. It has been demonstrated that, if the adjustment of input level between the recorded long-duration ground motion and the sinusoidal motion is conducted appropriately, the proposed SDOF model provides a good estimation of plastic deformation in the base-isolation story.
Author Contributions
KH formulated the problem, conducted the computation, and wrote the article. KF helped the computation and discussed the results. MT discussed the results. IT supervised the research and wrote the article.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Funding
Part of the present work is supported by the JSPS KAKENHI (No. 15H04079 and 17K18922). This support is greatly appreciated. The authors are grateful to Mr. Kotaro Kojima for his contribution to a part of the derivation of the analytical expression.
References
Amadio, C., Fragiacomo, M., and Rajgelj, S. (2003). The effects of repeated earthquake ground motions on the non-linear response of SDOF systems. Earthq. Eng. Struct. Dyn. 32, 291–308. doi: 10.1002/eqe.225
Ariga, T., Kanno, Y., and Takewaki, I. (2006). Resonant behavior of base-isolated high-rise buildings under long-period ground motions. Struct. Des. Tall Spec. Build. 15, 325–338. doi:10.1002/tal.298
Ben-Haim, Y. (2006). Information-Gap Decision Theory: Decisions under Severe Uncertainty. London: Academic Press.
Bruneau, M., and Reinhorn, A. (2006). “Overview of the resilience concept,” in Proceedings of the 8th US National Conference on Earthquake Engineering, San Francisco.
Elishakoff, I., and Ohsaki, M. (2010). Optimization and Anti-Optimization of Structures under Uncertainty. London: Imperial College Press.
Fujita, K., Yasuda, K., Kanno, Y., and Takewaki, I. (2017). Robustness evaluation of elastoplastic base-isolated high-rise buildings subjected to critical double impulse. Front. Built Environ. 3:Article 31. doi:10.3389/fbuil.2017.00031
Fukumoto, Y., and Takewaki, I. (2017). Dual control high-rise building for robuster earthquake performance. Front. Built Environ. 3:Article 12. doi:10.3389/fbuil.2017.00012
Hall, J. H., Heaton, T. H., Halling, M. W., and Wald, D. J. (1995). Near-source ground motion and its effect on flexible buildings. Earthq. Spectra 11, 569–605. doi:10.1193/1.1585828
Heaton, T. H., Hall, J. H., Wald, D. J., and Halling, M. W. (1995). Response of high-rise and base-isolated buildings in a hypothetical MW 7.0 blind thrust earthquake. Science 267, 206–211. doi:10.1126/science.267.5195.206
Hino, J., Yoshitomi, S., Tsuji, M., and Takewaki, I. (2008). Bound of aspect ratio of base-isolated buildings considering nonlinear tensile behavior of rubber bearing. Struct. Eng. Mech. 30, 351–368. doi:10.12989/sem.2008.30.3.351
Irikura, K., Kamae, K., and Kawabe, H. (2004). “Importance of prediction of long-period ground motion during large earthquakes,” in Annual Conference of the Seismological Society of Japan, Poster Session (in Japanese), Fukuoka.
Jangid, R. S. (1995). Optimum isolator damping for minimum acceleration response of base-isolated structures. Aust. Civil Eng. Trans. 37, 325–331.
Jangid, R. S., and Banerji, P. (1998). Effects of isolation damping on stochastic response of structures with nonlinear base isolators. Earthq. Spectra 14, 95–114. doi:10.1193/1.1585990
Jangid, R. S., and Datta, T. K. (1994). Non-linear response of torsionally coupled base isolated structure. J. Struct. Eng. 120, 1–22. doi:10.1061/(ASCE)0733-9445(1994)120:1(1)
Jangid, R. S., and Kelly, J. M. (2001). Base isolation for near-fault motions. Earthq. Eng. Struct. Dyn. 30, 691–707. doi:10.1002/eqe.31
Kamae, K., Kawabe, H., and Irikura, K. (2004). “Strong ground motion prediction for huge subduction earthquakes using a characterized source model and several simulation techniques,” in Proceedings of the 13th WCEE, Vancouver.
Kanno, Y., Yasuda, K., Fujita, K., and Takewaki, I. (2017). Robustness of SDOF elastoplastic structure subjected to double-impulse input under simultaneous uncertainties of yield deformation and stiffness. Int. J. Non Linear Mech. 91, 151–162. doi:10.1016/j.ijnonlinmec.2017.02.013
Karabork, T. (2011). Performance of multi-storey structures with high damping rubber bearing base isolation systems. Struct. Eng. Mech. 39, 399–410. doi:10.12989/sem.2011.39.3.399
Kasagi, M., Fujita, K., Tsuji, M., and Takewaki, I. (2015). Effect of nonlinearity of connecting dampers on vibration control of connected building structures. Front. Built Environ. 1:Article 25. doi:10.3389/fbuil.2015.00025
Kasagi, M., Fujita, K., Tsuji, M., and Takewaki, I. (2016). Automatic generation of smart earthquake-resistant building system: hybrid system of base-isolation and building-connection. Heliyon 2, 2. doi:10.1016/j.heliyon.2016.e00069
Kelly, J. M. (1999). The role of damping in seismic isolation. Earthq. Eng. Struct. Dyn. 28, 3–20. doi:10.1002/(SICI)1096-9845(199901)28:1<3::AID-EQE801>3.0.CO;2-D
Kojima, K., Saotome, Y., and Takewaki, I. (2017). Critical earthquake response of SDOF elastic-perfectly plastic model with viscous damping under double impulse as substitute of near-fault ground motion. J. Struct. Constr. Eng. 735, 643–652. doi:10.3130/aijs.82.643
Kojima, K., and Takewaki, I. (2015a). Critical earthquake response of elastic-plastic structures under near-fault ground motions (part 1: fling-step input). Front. Built Environ. 1:Article 12. doi:10.3389/fbuil.2015.00015
Kojima, K., and Takewaki, I. (2015b). Critical input and response of elastic-plastic structures under long-duration earthquake ground motions. Front. Built Environ. 1:Article 15. doi:10.3389/fbuil.2015.00015
Kojima, K., and Takewaki, I. (2017). Critical steady-state response of SDOF bilinear hysteretic system under multi impulse as substitute of long-duration ground motions. Front. Built Environ. 3:Article 41. doi:10.3389/fbuil.2017.00041
Koo, J.-H., Jang, D.-D., Usman, M., and Jung, H.-J. (2009). A feasibility study on smart base isolation systems using magneto-rheological elastomers. Struct. Eng. Mech. 32, 755–770. doi:10.12989/sem.2009.32.6.755
Li, H.-N., and Wu, X.-X. (2006). Limitations of height-to-width ratio for base-isolated buildings under earthquake. Struct. Des. Tall Spec. Build. 15, 277–287. doi:10.1002/tal.295
Morales, C. A. (2003). Transmissibility concept to control base motion in isolated structures. Eng. Struct. 25, 1325–1331. doi:10.1016/S0141-0296(03)00084-1
Murase, M., Tsuji, M., and Takewaki, I. (2013). Smart passive control of buildings with higher redundancy and robustness using base-isolation and inter-connection. Earthq. Struct. 4, 649–670. doi:10.12989/eas.2013.4.6.649
Patel, C. C., and Jangid, R. S. (2011). Dynamic response of adjacent structures connected by friction dampers. Earthq. Struct. 2, 149–169. doi:10.12989/eas.2011.2.2.149
Petti, L., Giannattasio, G., De Iuliis, M., and Palazzo, B. (2010). Small scale experimental testing to verify the effectiveness of the base isolation and tuned mass dampers combined control strategy. Smart Struct. Syst. 6, 57–72. doi:10.12989/sss.2010.6.1.057
Takewaki, I. (2005). Uncertain-parameter sensitivity of earthquake input energy to base-isolated structure. Struct. Eng. Mech. 20, 347–362. doi:10.12989/sem.2005.20.3.347
Takewaki, I. (2007). Earthquake input energy to two buildings connected by viscous dampers. J. Struct. Eng. 133, 620–628. doi:10.1061/(ASCE)0733-9445(2007)133:5(620)
Takewaki, I. (2008). Robustness of base-isolated high-rise buildings under code-specified ground motions. Struct. Des. Tall Spec. Build. 17, 257–271. doi:10.1002/tal.350
Takewaki, I. (2013). Critical Excitation Methods in Earthquake Engineering, 2nd Edn. Amsterdam: Elsevier Science.
Takewaki, I., and Fujita, K. (2009). Earthquake input energy to tall and base-isolated buildings in time and frequency dual domains. Struct. Des. Tall Spec. Build. 18, 589–606. doi:10.1002/tal.497
Takewaki, I., Fujita, K., and Yoshitomi, S. (2013). Uncertainties in long-period ground motion and its impact on building structural design: case study of the 2011 Tohoku (Japan) earthquake. Eng. Struct. 49, 119–134. doi:10.1016/j.engstruct.2012.10.038
Takewaki, I., Moustafa, A., and Fujita, K. (2012). Improving the Earthquake Resilience of Buildings: The Worst Case Approach. London: Springer.
Takewaki, I., Murakami, S., Fujita, K., Yoshitomi, S., and Tsuji, M. (2011). The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 31, 1511–1528. doi:10.1016/j.soildyn.2011.06.001
Tamura, G., Taniguchi, M., Fujita, K., Tsuji, M., and Takewaki, I. (2017). Optimal damper placement in hybrid control system of multiple isolation and building connection. Int. J. Earthq. Impact Eng. 2, 67–87. doi:10.1504/IJEIE.2017.083718
Taniguchi, R., Kojima, K., and Takewaki, I. (2016a). Critical response of 2DOF elastic-plastic building structures under double impulse as substitute of near-fault ground motion. Front. Built Environ. 2:Article 2. doi:10.3389/fbuil.2016.00002
Taniguchi, M., Fujita, K., Tsuji, M., and Takewaki, I. (2016b). Hybrid control system for greater resilience using multiple isolation and building connection. Front. Built Environ. 2:Article 26. doi:10.3389/fbuil.2016.00026
Keywords: base-isolation, building-connection, hybrid control, passive control, long-period long-duration motion
Citation: Hayashi K, Fujita K, Tsuji M and Takewaki I (2018) A Simple Response Evaluation Method for Base-Isolation Building-Connection Hybrid Structural System under Long-Period and Long-Duration Ground Motion. Front. Built Environ. 4:2. doi: 10.3389/fbuil.2018.00002
Received: 12 October 2018; Accepted: 08 January 2018;
Published: 06 February 2018
Edited by:
Fabio Mazza, University of Calabria, ItalyReviewed by:
Christian Málaga-Chuquitaype, Imperial College London, United KingdomIvo Caliò, Università degli Studi di Catania, Italy
Copyright: © 2018 Hayashi, Fujita, Tsuji and Takewaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Izuru Takewaki, dGFrZXdha2lAYXJjaGkua3lvdG8tdS5hYy5qcA==
 Kohei Hayashi
Kohei Hayashi Kohei Fujita
Kohei Fujita Masaaki Tsuji
Masaaki Tsuji Izuru Takewaki
Izuru Takewaki