- 1School of Civil Engineering, National Technical University of Athens, Athens, Greece
- 2Department of Mathematics, University of Patras, Rio, Greece
The aim of this paper is to investigate the effects of hysteresis and negative stiffness on seismic response reduction. For this reason, the novel Hysteretic Nonlinear Energy Sink (HNES) is used as a passive vibration control device for seismic response mitigation. So far, HNES performance has been tested in shock mitigation and has proved to exhibit exceptional robustness and energy dissipation merits. Apart from a small mass and a nonlinear elastic spring of the Duffing oscillator (type-I NES), HNES is also comprised of a purely hysteretic and a linear elastic spring of potentially negative stiffness, connected in parallel. The Bouc-Wen model is used to describe the force produced by both the purely hysteretic and linear elastic springs. In this investigation, the response reduction of a primary two-degree-of-freedom model of a shear building is studied against a strong ground motion which is based on the 1999 Athens, Greece earthquake. The response reduction is achieved by using three optimized passive vibration control devices, i.e., an HNES, a type-I NES, and a traditional Tuned Mass Damper (TMD). The optimum configuration of each device is determined using Differential Evolution, a robust metaheuristic algorithm, using the maximum absolute displacement of the top floor as the objective function. Example problems are presented in order to assert that HNES behavior is vastly superior over both NES and TMD. Furthermore, the key advantage of HNES is its inherent insensitivity to drastic changes in the structural characteristics. In particular, it maintains a significant level of performance even if the column stiffness is reduced by half.
Introduction
The concept of passive vibration control by means of a mass damper was proposed by Watts as early as 1883 (Watts, 1883) and patented by Frahm (1909), who used the term “dynamic vibration absorber”. A classical engineering device implementing this concept is the Tuned Mass Damper (TMD), which is attached to a primary vibrating system in order to suppress undesirable vibrations. The device consists of a small mass m, a linear spring element k, and a viscous damper c and its natural frequency is tuned in resonance with the fundamental mode of the primary system. When tuned properly, a large amount of the structural vibrating energy is transferred from the primary system to the TMD and then dissipated by damping.
Since Den Hartog first proposed an optimal design theory for the TMD for an undamped single-degree-of-freedom (SDoF) structure (Hartog, 1956; see Figure 1), the TMD has been employed on a vast array of systems, with skyscrapers being among the most interesting ones (McNamara, 1977; Luft, 1979; Rana and Soong, 1998). Apart from buildings, recent studies also include the use of TMDs for vibration absorption in seismic or other forms of excitation of bridge structures (Debnath et al., 2016).
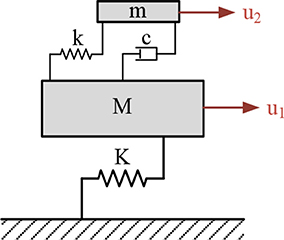
Figure 1. Schematic representation of a dynamic vibration absorber for an undamped SDoF system as suggested by Hartog (1956).
Even though TMDs are very efficient when tuned properly, they possess certain drawbacks. First, their efficacy is subject to errors in the initial estimate of the natural frequency. They are also rather sensitive to detuning (Rana and Soong, 1998; Weber and Feltrin, 2010), caused by common time-related processes, such as creep, or during a major seismic event due to the accumulated inelastic deformations of the structure. Researchers have attempted to mitigate their sensitivity by using alternative configurations, e.g., by stacking multiple TMDs together (Casciati and Giuliano, 2009) or by introducing active control elements, as in Active Mass Dampers (AMDs) (Soong et al., 1994). Nevertheless, little progress has been achieved regarding the detuning of a passive TMD device. In addition, a large oscillating mass is generally required in order to achieve significant vibration reduction, rendering its construction and placement rather difficult in real-life situations. Similarly, many researchers have investigated the implementation of other passive systems on vibration control, e.g., Han et al. (2006), Patel and Jangid (2011), Tani et al. (2017), and Taniguchi et al. (2016), including rocking controlled systems (Eatherton et al., 2010; Ma et al., 2010; Lu et al., 2017).
In light of the above, the use of essentially nonlinear (i.e., non-linearizable) attachments to the primary oscillating system has gained tremendous attention by researchers, as evidenced by numerous books and papers relevant to the subject that have proliferated over last few years. When properly designed, these attachments act, in essence, as Nonlinear Energy Sinks (NESs), i.e., they passively absorb energies generated by transient disturbances in the primary oscillating system to which they are weakly attached (Georgiadis et al., 2005). This broadband, one-way directed transfer of energy from the primary oscillator to the nonlinear attachment, termed Targeted Energy Transfer (TET), is realized in NESs of various designs (Vakakis et al., 2008). Apart from their performance, the most important advantage of NESs over TMDs is that the former do not need to be fine-tuned to a particular frequency, as they absorb energy at a wider range of frequencies (Boroson et al., 2017).
In total, seven types of NESs have been proposed so far. In Type I, II, and III, an essentially nonlinear cubic spring has been employed with linear (Type I and III) or nonlinear (Type II) damping (Gourdon et al., 2007; Quinn et al., 2008; Sapsis et al., 2009). In Type IV, a rotating NES has been introduced coupled to a primary linear oscillator (Gendelman et al., 2012; Sigalov et al., 2012), whereas Type V and VI designs are devoted to strongly nonlinear vibro-impact coupling (Georgiadis et al., 2005; Nucera et al., 2007; Lee et al., 2009). In Type VII, a negative stiffness element is employed (Al Shudeifat, 2014), which is proved to considerably enhance the NES performance for passive energy pumping and rapid local energy dissipation.
The introduction of both rate-independent hysteresis and negative stiffness into a Type I NES has recently been investigated in shock mitigation (Tsiatas and Charalampakis, 2018). The resulting NES, termed Hysteretic Nonlinear Energy Sink (HNES), has proved to exhibit exceptional robustness and energy dissipation merits. In this paper, three passive devices, i.e., an HNES, a type-I NES, and a TMD, are optimized for the seismic response mitigation of a two-degree-of-freedom shear building. In this respect, the resulting dynamical system is comprised of the primary linear structure and the passive vibration control device. The formulation of the dynamical system is general since it can produce the response of all cases considered based on the appropriate selection of its parameters. The optimum properties of each device that minimize the maximum absolute displacement of the top floor are determined using Differential Evolution, a robust metaheuristic algorithm. It is shown that the performance of HNES is vastly superior, while it maintains a significant performance level even when drastic changes in the structural characteristics occur.
Model Structure and Design Ground Motion
In this study, a two-degree-of-freedom model of a shear building is studied as example structure (Figure 2) in seismic mitigation. The model is based on one built for a physical experiment conducted in the Smart Structures Technology Laboratory at the University of Illinois at Urbana-Champaign and has been investigated in detail by Wierschem et al. (2011). The building is designed to have natural frequencies similar to those of a typical mid-rise steel structure and it is subjected to a band-limited white noise ground acceleration. Its structural properties are presented in Table 1, resulting in first and second natural frequencies of 1.63 and 4.56 Hz, respectively. The damping ratio of the structure is set at 2% for each mode which is again similar to that of a typical mid-rise steel structure (Wierschem et al., 2011).
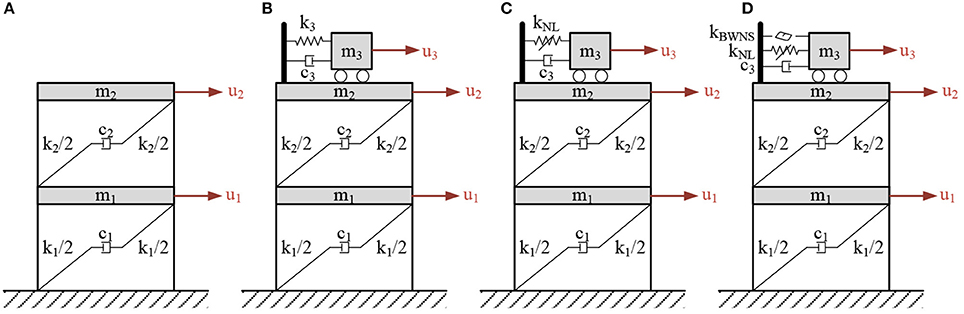
Figure 2. Structural configurations (A) unprotected structure (B) structure with TMD (C) structure with NES (D) structure with HNES.
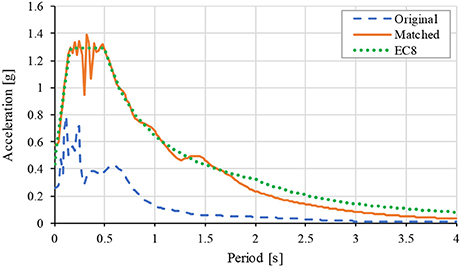
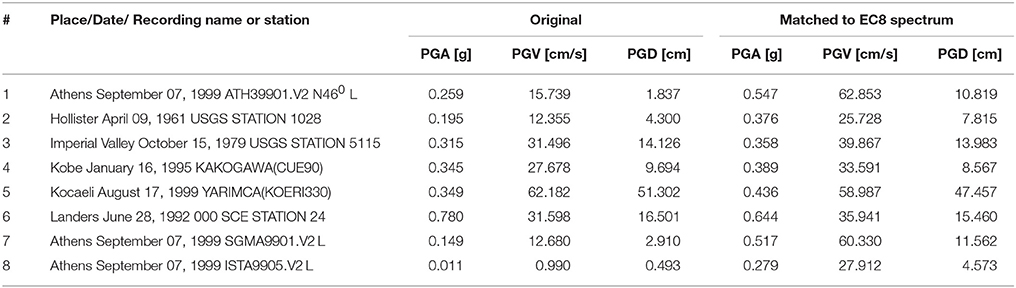
In this study, the design input is based on the ground acceleration record ATH39901. V2 L of the 1999 Athens earthquake occurred on September 7th in Greece, the country with the most intense seismic activity in Europe (Maniatakis and Spyrakos, 2012). The earthquake ground motion was obtained from the Institute of Engineering Seismology and Earthquake Engineering (ITSAK) (Theodulidis et al., 2004), and it was adjusted to match the EC8 Type-1 response spectrum, Soil class: Type B, PGA = 0.36 g and 2% damping ratio. The matching was performed based on the wavelets algorithm (Abrahamson, 1992; Hancock et al., 2006) using the SeismoMatch computer software (SeismoSoft., 2016). The original and matched spectra are shown in Figure 3.
Hysteretic Nonlinear Energy Sink (HNES)
The HNES employs a rate-independent hysteretic element, a linear elastic spring of potentially negative stiffness, a viscous damper and a cubic nonlinear spring (Tsiatas and Charalampakis, 2018). These are described in brief below.
Hysteretic Element
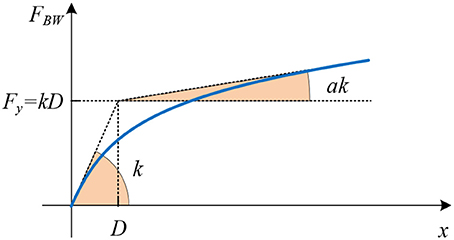
The Bouc-Wen model, introduced by Bouc (1967) and extended by Wen (1976), is employed to describe rate-independent hysteresis. The model utilizes internal (non-measurable) hysteretic variables which follow suitable differential equations. In a SDoF system, the hysteretic force is expressed by:
where, x(t) is the time history of the displacement, k > 0 is the initial stiffness, D > 0 is the yield displacement, and z(t) is a dimensionless hysteretic variable which is governed by the differential equation
in which n > 0 is the exponential parameter, governing the abruptness of transition between pre- and post-yield response, and sgn() is the signum function. Parameter a controls the ratio of post to pre-yield stiffness, while the dimensionless parameters A, β, and γ control the shape and size of the hysteretic loop (Charalampakis, 2010). For reasons of model consistency, the constraints A = β + γ = 1 are imposed which simplify the model without limiting its capabilities (Ma et al., 2004; Charalampakis and Koumousis, 2008; Charalampakis and Dimou, 2010; Charalampakis, 2015). As a result, z takes values in the range [−1,1], with ± 1 meaning full yield in the positive/negative direction.
Based on Equation (1), the model can be visualized as two springs connected in parallel, i.e., a linear elastic and a purely hysteretic spring, with:
and
respectively. The combined response is shown in Figure 4.
Negative Stiffness Element
The idea of employing negative stiffness springs, or “anti-springs,” for the absorption of oscillations, can be traced in aeronautical engineering and the innovative work by Molyneux (1957). This idea was extended significantly by Platus (1999). Apart from pre-compressed springs, the physical implementation of negative stiffness elements can be achieved by beams, slabs or shells in post-buckled arrangements, inverse pendulum systems, etc. Some interesting implementations of such non-linear isolation systems can be found in the works of Winterflood et al. (2002), Virgin et al. (2008), Liu et al. (2013), Antoniadis et al. (2015), and others.
Instead of introducing an additional negative stiffness element, a simplest approach has recently been proposed (Tsiatas and Charalampakis, 2018) which involves the already present linear elastic spring of the Bouc-Wen model. This spring can obtain negative stiffness for negative values of parameter a, leading to a true softening behavior which, however, is not related to damage of any kind. This approach allows for a seamless investigation of the HNES' behavior for both positive and negative values of a. In this regard, the stiffness of the Bouc-Wen model is indicated as kBWNS in Figure 2D, to indicate potentially negative stiffness.
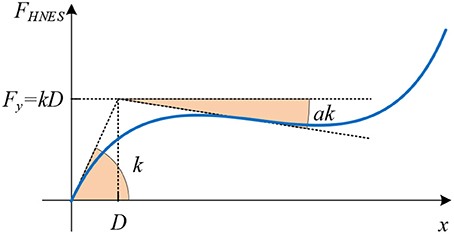
Combined Response
The HNES also includes a cubic nonlinear spring and a viscous damper, as in a Type-I NES. The combined response is shown in Figure 5. Note that the initial stiffness is always positive, which ensures stability in spite of the negative stiffness spring, as well as the cubic nonlinear element which can be used to restrict the stroke of HNES within feasible values.
Dynamical System
In this investigation, the optimum performance of three passive devices, i.e., an HNES, a type-I NES, and a TMD, is probed for the seismic response reduction of a two-degree-of-freedom shear building. In view of the above, the resulting dynamical system is comprised of the primary linear structure and the passive vibration control device. To visualize this, Figures 2B–D show the schematic representation of the dynamical systems describing the application of the three passive control devices (i.e., TMD, NES, and HNES) mounted atop of the two-degree-of-freedom shear building. Assuming now that ui is the displacement associated with mass mi, the equations of motion take the form:
where, üg is the ground acceleration and FS3 is the restoring force produced by each device. In case of a TMD, the restoring force is linear:
while in case of a type-I NES is nonlinear:
Examining the proposed novel HNES configuration (Tsiatas and Charalampakis, 2018), a Bouc-Wen type spring, described by Equations (1) and (2), is connected in parallel to the cubic nonlinear spring, producing a total restoring nonlinear force given by:
Equations (2), (5)–(7), and (10) can be cast in state-space form with zero initial conditions, as follows
The solution of the above nonlinear system is approached numerically using Runge-Kutta 4th−5th order integrator with adaptive time step, or any other time integration technique, e.g., (Katsikadelis, 2016). Based on the appropriate selection of its parameters, the system can produce the response of all cases shown in Figure 2. More in detail, for very small values of m3 one obtains the response of the unprotected structure; for kNL = 0 and a = 1 the cubic non-linear element, as well as the hysteretic spring of Bouc-Wen, are disabled, producing the response of a TMD; and, finally, for k3 = 0 the whole Bouc-Wen element is disabled, producing a type-I NES. By allowing these parameter values in the optimization procedure, the proposed HNES configuration is, therefore, able of producing a proper superset of responses with regard to both the TMD and type-I NES. It will be proved that the optimized HNES configuration indeed exhibits prodigious performance, with the additional advantage of insensitivity with respect to changes in the structural characteristics.
The Optimization Problem
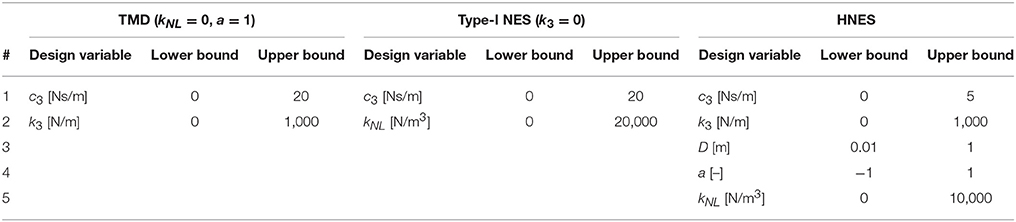
In this work, the maximum absolute displacement of the top floor is used as the objective function. Thus, the optimization problem is to minimize max|u2(t)| subject to the side constraints of the active design variables given in Table 2. In order to reduce the complexity of the optimization problem, the following parameters are known to have little sensitivity and were therefore fixed to reasonable values: n = 2 (smooth transition from elastic to post-elastic branch), β = γ = 0.5 (unloading branches are straight lines).
The optimum parameter values for all cases (Figures 2B, C) have been determined by a robust metaheuristic algorithm called Differential Evolution (DE). The algorithm was introduced by Storn and Price (1997) and makes no assumptions about the problem being optimized, which is therefore considered as a black box. An early version was initially conceived under the term “Genetic Annealing” (Price et al., 2005). The common version of DE, denoted “rand/1/bin,” assumes that a population of P individuals is randomly dispersed within the design space, as
where, Px,g is an array of P vectors (solutions); xi,g is a ND-dimensional vector representing a candidate solution; gmax is the maximum number of generations; i is an index for vectors, g is an index for generations, j is an index for design variables; and the parentheses indicate an array. At each generation g, a mutated population Pv,g is formed based on
where, r0, r1, and r2 are mutually exclusive random integers in {1, 2, …, P}, which are also different from index i; xr0,g is the base vector; and F is a scalar parameter of the algorithm. Note that after using Equation (14), design variables are reset to their respective bounds in case a mutated solution moves out of the initial design space. Next, a trial population Pu,g is assembled, consisting of individuals created from the parent and mutated populations, as
where, jrand is a random index in {1, 2, …, P} that ensures that at least one design variable will originate from the mutant vector vi,g; and Cr is a scalar parameter in the range [0,1]. The final step of the algorithm is a greedy selection criterion, which for minimization problems is expressed as:
The above-described common implementation usually demonstrates strong exploration capability and thus is more suitable for solving multimodal problems (Storn and Price, 1997). Following recommendations by Price et al. (2005), F = 0.5 was selected. Also, a high value of Cr = 0.9 is expected to perform well with non-separable functions. The population size is set as P = 50 for all problems.
Results and Discussion
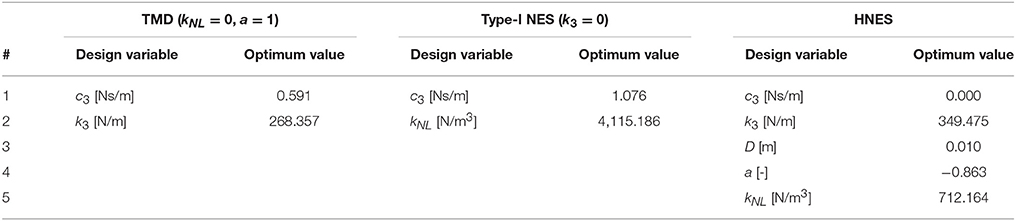
The best results of the optimum parameter values for the TMD, NES, and HNES devices are summarized in Table 3. The results were obtained out of 10 independent runs per device with different random seeds. Regarding HNES device, it is immediately noted that the optimization process guided toward the removal of the viscous damper (c3 = 0). In addition, the lower bound of the yield displacement D was selected at 0.01 m, which substantiates that a small yield force Fy = k3D has a beneficial effect.
Furthermore, the objective values (OV) of max|u2(t)| are tabulated in Table 4. Note that, HNES device achieves a reduction of 65.49%, i.e., more than double the reduction achieved with NES (30.71%) and almost three times the reduction achieved with TMD (23.63%), as compared to the response of the unprotected structure. HNES' great performance is evidenced by the negative value of the parameter a which indicates the presence of a negative stiffness spring. Tsiatas and Charalampakis (2018) have reached the same conclusion studying the behavior of HNES in shock mitigation.
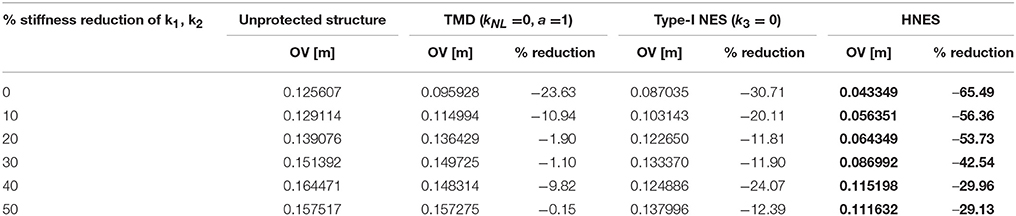
Table 4. Objective values (OV) of max|u2(t)| and percentage reduction with respect to the unprotected structure for the TMD, NES, and HNES devices (best values are shown in bold).
Subsequently, to account for potential deterioration effects during the life cycle of the structure, a stiffness reduction is imposed in both k1 and k2. Keeping the optimum parameters of Table 3, the calculated objective values indicate that HNES maintains a significant level of performance, e.g., it still achieves a 29.13% reduction even if the column stiffness is reduced by half. The observed behavior of HNES device is vastly superior as compared to both NES and certainly TMD devices.
Moreover, the time history responses of the model structure under all alternative protection systems are shown in Figure 6. It can be deduced that the structural displacements are significantly reduced using the proposed HNES device, in terms of both the maximum absolute value and overall (Figures 6A,B). The reduction factors are: 45.17% for max|u1(t)|; 65.49% for max|u2(t)|; 78.36% of RMS(u1); and 81.70% of RMS(u2). Figure 6C displays the acceleration of the top floor for the three devices considered. It is shown that the acceleration is comparable to that of the unprotected structure but only at the beginning of the event. As the event culminates, the HNES device rapidly diminishes the acceleration, with a reduction factor of RMS(ü2) equal to 61.55%.
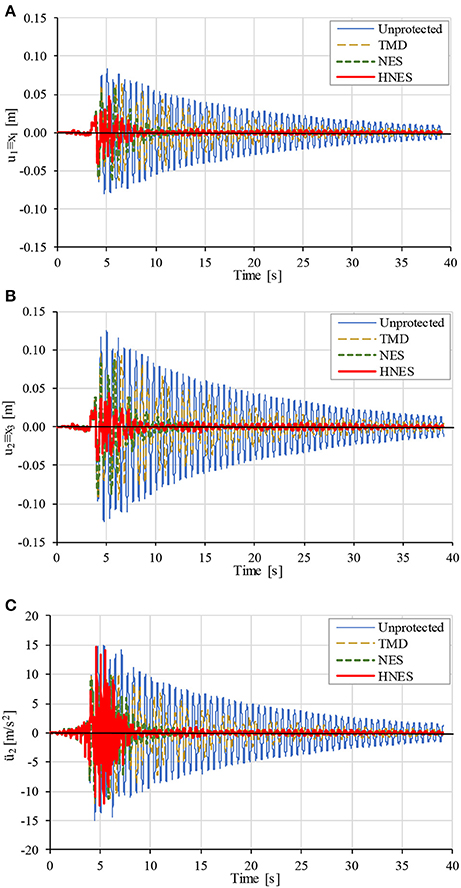
Figure 6. Time history responses of the model structure: (A) bottom floor displacement u1 (B) top floor displacement u2 (C) top floor acceleration ü2.
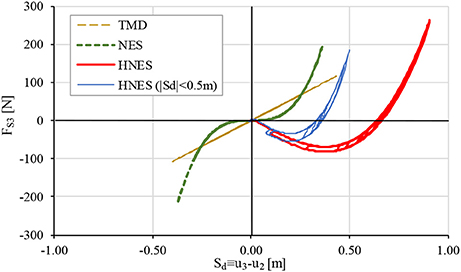
Figure 7 shows the restoring force FS3 produced by each passive control device (i.e., TMD, NES, and HNES) vs. the stroke displacement Sd = (u3 − u2), namely the displacement of the device relative to that of the top floor. What is interesting to notice is that the hysteretic loops of HNES are very shallow due to the small yield force, while the stroke requirements are increased but not unreasonable (max|Sd| = 0.91). If, however, a certain maximum level of Sd needs to be maintained, this can be taken into account in the optimization process as a constraint. For instance, the optimization results when the constraint |Sd| < 0.5 m is imposed are summarized in Table 5, and this case is also included in Figure 7. The constraint is met by means of a certain level of viscous damping as well as an increased nonlinear stiffness kNL. Due to this constraint, the performance of HNES has deteriorated as the reduction factor of max|u2(t)| drops to 43.66%, but this is still significantly better than both the NES and TMD. Note that the HNES response is displaced due to the negative stiffness spring and restoration to the initial position is required after the event.
Finally, the acceleration record set is extended with 5 well-known strong motion records, as well as 2 more records of the Athens 1999 earthquake taken from other stations. All records were adjusted to match the EC8 Type-1 response spectrum, as summarized in Table 6. Although the optimum parameters of Table 3 have been obtained solely using the first record, the HNES, in general, achieves significant results (Table 7). It is expected that optimization based on a larger set of strong motion recordings will improve the overall performance of HNES. This will be pursued in future research.
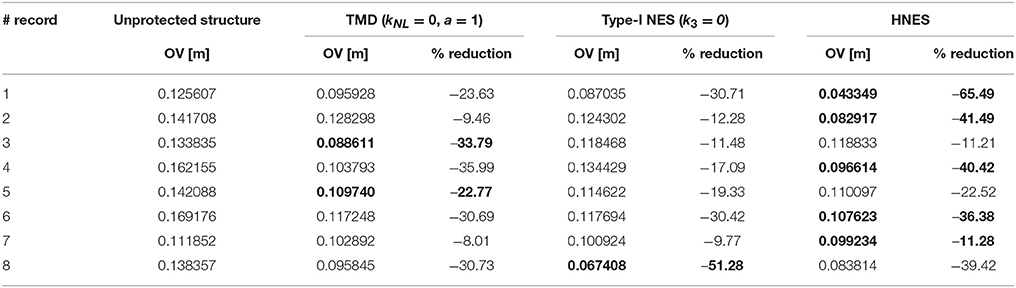
Table 7. Objective values of max|u2(t)| and percentage reduction with respect to the unprotected structure for the TMD, NES, and HNES devices for the extended accelerogram set (best values are shown in bold).
Conclusions—Future Research
In this paper, the beneficial effects of hysteresis and negative stiffness on seismic response reduction were presented. For this reason, the optimum performance of three passive devices, i.e., an HNES, a type-I NES, and a TMD, was probed in seismic mitigation of a two-degree-of-freedom shear building. The design input was the ground acceleration record of the 1999 Athens, Greece earthquake which was adjusted to match the EC8 Type-1 response spectrum (Soil class: Type B, PGA = 0.36 g and 2% damping ratio). Several numerical examples were presented in order to validate the prodigious behavior of HNES, over both NES, and TMD, and exemplify its salient features. The main conclusions that can be drawn from this investigation are as follows:
• In general, HNES surpassing performance lies in the dominant role of hysteresis in addition to the presence of negative stiffness spring.
• For the particular loading, HNES device achieves a reduction more than double of that achieved with NES device and almost three times the reduction achieved with TMD device, compared to the response of the unprotected structure.
• HNES exhibits an inherent insensitivity to drastic changes in the structural characteristics. In particular, it maintains a significant level of performance even if the column stiffness is reduced by half.
• In order to assess whether the obtained results are peculiar to the specific ground motion record or not, an extended acceleration record was utilized and the obtained results show that HNES performs satisfactorily although its configuration was determined solely using the first Athens record.
• The hysteretic loops of HNES are very shallow due to the small yield force, while the stroke requirement is increased, as compared to NES and TMD, but not unreasonable. If, however, a certain maximum level of stroke needs to be maintained, this can be taken into account in the optimization process as a constraint.
Bringing it all together, it is fair to say that using HNES for seismic response mitigation is very promising and certainly deserves attention. The following can be indicatively explored in future research:
• The use of other objective functions in optimization e.g., RMS of displacements, top floor acceleration, etc. as well as an extended accelerogram set for more robust results.
• Real-life implementation of HNES device.
Author Contributions
AC had the research idea, drafted the article, and contributed to the derivation of the numerical examples. GT contributed to the conception and design of the work, the theoretical analysis, and interpretation of the results.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Al Shudeifat, M. A. (2014). Highly efficient nonlinear energy sink. Nonlinear Dyn. 76, 1905–1920. doi: 10.1007/s11071-014-1256-x
Antoniadis, I., Chronopoulos, D., Spitas, V., and Koulocheris, D. (2015). Hyper-damping properties of a stiff and stable linear oscillator with a negative stiffness element. J. Sound Vib. 346, 37–52. doi: 10.1016/j.jsv.2015.02.028
Boroson, E., Missoum, S., Mattei, P.-O., and Vergez, C. (2017). Optimization under uncertainty of parallel nonlinear energy sinks. J. Sound Vib. 394, 451–464. doi: 10.1016/j.jsv.2016.12.043
Bouc, R. (1967). “Forced Vibrations of a Mechanical System with Hysteresis,” in Proceedings of the 4th Conference on Non-linear Oscillations (Prague).
Casciati, F., and Giuliano, F. (2009). Performance of multi-TMD in the towers of suspension bridges. J. Vib. Control 15, 821–847. doi: 10.1177/1077546308091455
Charalampakis, A. E. (2010). “Parameters of Bouc-Wen hysteretic model revisited,” in 9th HSTAM International Congress on Mechanics (Limassol, Cyprus).
Charalampakis, A. E. (2015). The response and dissipated energy of Bouc–Wen hysteretic model revisited. Arch. Appl. Mech. 85, 1209–1223. doi: 10.1007/s00419-014-0937-8
Charalampakis, A. E., and Dimou, C. K. (2010). Identification of Bouc–Wen hysteretic systems using particle swarm optimization. Comput. Struct. 88, 1197–1205. doi: 10.1016/j.compstruc.2010.06.009
Charalampakis, A. E., and Koumousis, V. K. (2008). On the response and dissipated energy of Bouc–Wen hysteretic model. J. Sound Vib. 309, 887–895. doi: 10.1016/j.jsv.2007.07.080
Debnath, N., Deb, S. K., and Dutta, A. (2016). Multi-modal vibration control of truss bridges with tuned mass dampers under general loading. J. Vib. Control 22, 4121–4140. doi: 10.1177/1077546315571172
Eatherton, M., Hajjar, J., Ma, X., Krawinkler, H., and Deierlein, G. (2010). “seismic design and behavior of steel frames with controlled rocking—Part I: concepts and Quasi-static subassembly testing,” in Structures Congress 2010 (Reston, VA: American Society of Civil Engineers), 1523–1533.
Gendelman, O. V., Sigalov, G., Manevitch, L. I., Mane, M., Vakakis, A. F., and Bergman, L. A. (2012). Dynamics of an eccentric rotational nonlinear energy sink. J. Appl. Mech. 79:11012. doi: 10.1115/1.4005402
Georgiadis, F., Vakakis, A. F., McFarland, D. M., and Bergman, L. A. (2005). Shock isolation through passive energy pumping caused by non-smooth nonlinearities. Int. J. Bifurc. Chaos 15, 1989–2001. doi: 10.1142/S0218127405013101
Gourdon, E., Alexander, N. A., Taylor, C. A., Lamarque, C. -H., and Pernot, S. (2007). Nonlinear energy pumping under transient forcing with strongly nonlinear coupling: theoretical and experimental results. J. Sound Vib. 300, 522–551. doi: 10.1016/j.jsv.2006.06.074
Han, S. J., Tsopelas, P., and Baz, A. (2006). Active/passive seismic control of structures. J. Earthq. Eng. 10, 509–526. doi: 10.1080/13632460609350607
Hancock, J., Watson-Lamprey, J., Abrahamson, N. A., Bommer, J. J., Markatis, A., McCoyh, E., et al. (2006). An improved method of matching response spectra of recorded earthquake ground motion using wavelets. J. Earthq. Eng. 10, 67–89. doi: 10.1080/13632460609350629
Katsikadelis, J. T. (2016). A new direct time integration method for the semi-discrete parabolic equations. Eng. Anal. Bound. Elem. 73, 181–190. doi: 10.1016/j.enganabound.2016.09.009
Lee, Y. S., Nucera, F., Vakakis, A. F., McFarland, D. M., and Bergman, L. A. (2009). Periodic orbits, damped transitions and targeted energy transfers in oscillators with vibro-impact attachments. Phys. D Nonlinear Phenom. 238, 1868–1896. doi: 10.1016/j.physd.2009.06.013
Liu, X., Huang, X., and Hua, H. (2013). On the characteristics of a quasi-zero stiffness isolator using Euler buckled beam as negative stiffness corrector. J. Sound Vib. 332, 3359–3376. doi: 10.1016/j.jsv.2012.10.037
Lu, L., Liu, X., Chen, J., and Lu, X. (2017). Seismic performance of a controlled rocking reinforced concrete frame. Adv. Struct. Eng. 20, 4–17. doi: 10.1177/1369433216645992
Ma, F., Zhang, H., Bockstedte, A., Foliente, G. C., and Paevere, P. (2004). Parameter analysis of the differential model of hysteresis. J. Appl. Mech. 71, 342–349. doi: 10.1115/1.1668082
Ma, X., Eatherton, M., Hajjar, J., Krawinkler, H., and Deierlein, G. (2010). “Seismic design and behavior of steel frames with controlled rocking—Part II: large scale shake table testing and system collapse analysis,” in Structures Congress 2010 (Reston, VA: American Society of Civil Engineers), 1534–1543.
Maniatakis, C. A., and Spyrakos, C. C. (2012). A new methodology to determine elastic displacement spectra in the near-fault region. Soil Dyn. Earthq. Eng. 35, 41–58. doi: 10.1016/j.soildyn.2011.10.005
Molyneux, W. G. (1957). Supports for Vibration Isolation. London: Ministry of Supply, Aeronautical Research Council, Technical Report CP-322.
Nucera, F., Vakakis, A. F., McFarland, D. M., Bergman, L. A., and Kerschen, G. (2007). Targeted energy transfers in vibro-impact oscillators for seismic mitigation. Nonlinear Dyn. 50, 651–677. doi: 10.1007/s11071-006-9189-7
Patel, C. C., and Jangid, R. S. (2011). Dynamic response of adjacent structures connected by friction damper. Earthquakes Struct. 2, 149–169. doi: 10.12989/eas.2011.2.2.149
Platus, D. L. (1999). “Negative-stiffness-mechanism vibration isolation systems,” in International Society for Optics and Photonics, eds E. A. Derby, C. G. Gordon, D. Vukobratovich, P. R. Yoder Jr, and C. H. Zweben (Denver, CO), 98–105.
Price, K. V., Storn, R. M., and Lampinen, J. A. (2005). Differential Evolution : A Practical Approach to Global Optimization. Berlin; Heidelberg: Springer-Verlag.
Quinn, D. D., Gendelman, O., Kerschen, G., Sapsis, T. P., Bergman, L. A., and Vakakis, A. F. (2008). Efficiency of targeted energy transfers in coupled nonlinear oscillators associated with 1:1 resonance captures: Part I. J. Sound Vib. 311, 1228–1248. doi: 10.1016/j.jsv.2007.10.026
Rana, R., and Soong, T. T. (1998). Parametric study and simplified design of tuned mass dampers. Eng. Struct. 20, 193–204. doi: 10.1016/S0141-0296(97)00078-3
Sapsis, T. P., Vakakis, A. F., Gendelman, O., Bergman, L. A., Kerschen, G., and Quinn, D. D. (2009). Efficiency of targeted energy transfers in coupled nonlinear oscillators associated with 1:1 resonance captures: Part II, analytical study. J. Sound Vib. 325, 297–320. doi: 10.1016/j.jsv.2009.03.004
SeismoSoft (2016). SeismoMatch - A Computer Program for Spectrum Matching of Earthquake Records. Available online at: www.seismosoft.com.
Sigalov, G., Gendelman, O. V., Al Shudeifat, M. A., Manevitch, L. I., Vakakis, A. F., and Bergman, L. A. (2012). Resonance captures and targeted energy transfers in an inertially-coupled rotational nonlinear energy sink. Nonlinear Dyn. 69, 1693–1704. doi: 10.1007/s11071-012-0379-1
Soong, T. T., Reinhorn, A. M., Aizawa, S., and Higashino, M. (1994). Recent structural applications of active control technology. J. Struct. Control 1, 1–21. doi: 10.1002/stc.4300010101
Storn, R. M., and Price, K. V. (1997). Differential Evolution – a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11, 341–359. doi: 10.1023/A:1008202821328
Tani, T., Maseki, R., and Takewaki, I. (2017). Innovative seismic response-controlled system with shear wall and concentrated dampers in lower stories. Front. Built Environ. 3:57. doi: 10.3389/fbuil.2017.00057
Taniguchi, M., Fujita, K., Tsuji, M., and Takewaki, I. (2016). Hybrid control system for greater resilience using multiple isolation and building connection. Front. Built Environ. 2:26. doi: 10.3389/fbuil.2016.00026
Theodulidis, N., Kalogeras, I., Papazachos, C., Karastathis, V., Margaris, B., Papaioannou, C., et al. (2004). HEAD 1.0: A Unified HEllenic Accelerogram Database. Seismol. Res. Lett. 75, 36–45. doi: 10.1785/gssrl.75.1.36
Tsiatas, G. C., and Charalampakis, A. E. (2018). A new Hysteretic Nonlinear Energy Sink (HNES). Commun. Nonlinear Sci. Numer. Simul. 60, 1–11. doi: 10.1016/j.cnsns.2017.12.014
Vakakis, A. F., Gendelman, O. V., Bergman, L. A., McFarland, D. M., Kerschen, G., and Lee, Y. S. (2008). Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems, I and II. Springer.
Virgin, L. N., Santillan, S. T., and Plaut, R. H. (2008). Vibration isolation using extreme geometric nonlinearity. J. Sound Vib. 315, 721–731. doi: 10.1016/j.jsv.2007.12.025
Watts, P. (1883). On a method of reducing the rolling of ships at sea. Trans. Inst. Nav. Archit. 24, 165–190.
Weber, B., and Feltrin, G. (2010). Assessment of long-term behavior of tuned mass dampers by system identification. Eng. Struct. 32, 3670–3682. doi: 10.1016/j.engstruct.2010.08.011
Wen, Y. K. (1976). Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 102, 249–263.
Wierschem, N. E., Spencer, B. F., Bergman, L. A., and Vakakis, A. F. (2011). “Numerical study of nonlinear energy sinks for seismic response reduction,” in The 6th International Workshop on Advanced Smart Materials and Smart Structures Technology (Dalian).
Keywords: nonlinear energy sink, tuned mass damper, seismic response mitigation, hysteresis, negative stiffness, Bouc-Wen model
Citation: Charalampakis AE and Tsiatas GC (2018) Effects of Hysteresis and Negative Stiffness on Seismic Response Reduction: A Case Study Based on the 1999 Athens, Greece Earthquake. Front. Built Environ. 4:23. doi: 10.3389/fbuil.2018.00023
Received: 14 December 2017; Accepted: 26 March 2018;
Published: 10 April 2018.
Edited by:
Solomon Tesfamariam, University of British Columbia, CanadaReviewed by:
Fabrizio Mollaioli, Sapienza Università di Roma, ItalyEhsan Noroozinejad Farsangi, Graduate University of Advanced Technology, Iran
Copyright © 2018 Charalampakis and Tsiatas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: George C. Tsiatas, Z3RzaWF0YXNAdXBhdHJhcy5ncg==
 Aristotelis E. Charalampakis
Aristotelis E. Charalampakis George C. Tsiatas
George C. Tsiatas