- 1ACE-Hellas, Athens, Greece
- 2College of Civil Engineering, Fuzhou University, Fuzhou, China
- 3Department of Civil Engineering and Architectural Science, Technical University of Bari, Bari, Italy
- 4Veltion Engineering and Applied Sciences Optimization Lab, Department of Structural Engineering, School of Civil Engineering, Institute of Structural Analysis & Antiseismic Research, National Technical University of Athens, Athens, Greece
The scope of the work is to detect the most appropriate damage index, able to provide a reliable description of the structural damage level. This damage index is used to formulate a performance-based design framework to be used as a design tool for achieving safer and more economic designs. This objective is achieved by comparing alternative structural systems that comply with the design demands in the most cost-efficient approach, i.e., those requiring less material volume for concrete and steel reinforcement. In this direction, design optimization problems for structural systems are defined for each damage index under consideration and the structural optimization problems at hand are solved by means of a popular metaheuristic search algorithm.
Introduction
Performance-based design (PBD) framework was presented throughout the past couple of decades, for designing structural systems exposed to non-deterministic earthquake loading conditions, aiming at increasing structural safety against earthquake hazard. In accordance to performance-based earthquake engineering the structures need to be able resisting various earthquake loading scenarios in a measurable fashion and sustaining potential damages corresponding to desirable performance levels (Vanzi et al., 2015). The contemporary PBD engineering state-of-practice, among others, can be found in US design codes such as FEMA-445 (2006), ASCE-41 (2006), ATC-58 (2009), and FEMA-P-58-1 (2012). Aiming to achieve the PBD engineering goals, these design guidelines suggest that in seismic-prone areas require implementing higher-order analysis methods for performing structural assessment and design of existing or new structural systems, respectively. Structural optimization can provide a highly-effective design framework, yet computationally intensive, exploiting the benefits provided by nonlinear dynamic or static analysis methods. Structural design optimization problems formulated on the basis of PBD frameworks became a topic of growing interest, over the last years, where interesting results have been reached. The progress in structural optimization has facilitated passing from design procedures of trial-and-error basis toward fully automatic ones using advanced design space exploration algorithms (Marano et al., 2009; Quaranta et al., 2014; Fiore et al., 2016a; Greco et al., 2016). Partly, this transition should be credited to metaheuristic search algorithms that last decades developed rapidly. These search algorithms are capable of dealing with optimization problems of high complexity. Furthermore, structural optimization matured from simple academic problems to become the core of contemporary design in case of extremely complicated structural systems (Marano and Greco, 2006; Marano et al., 2006, 2007, 2008; Lagaros, 2014a, 2018; Greco et al., 2015).
So far, many researchers have integrated the PBD concept into design optimization procedures for achieving better designs. Indicatively, Ganzerli et al. (2000) suggested a PBD optimization practice for reinforced concrete (RC) framed structures relying on mathematical programming search algorithms. Esteva et al. (2002) recommended a formulation for life-cycle cost (LCC) aiming to define optimized mechanical properties of structures subjected to earthquake risk. Li and Cheng (2003) presented a design concept based on damage reduction and was implemented into structural optimization problems and exhibited that this idea leads to improved designs with respect to structural performance in terms of both maximum interstory drift and life-cycle cost performance. Chan and Zou (2004) presented an improved approach for RC building structures subject to seismic loading aiming to improve elastic and inelastic interstory drifts into structural optimization problems. Liu et al. (2005) presented a design optimization approach for multiple-objectives using Genetic Algorithm (GA) for the case of steel framed structures taking into account various criteria; for two performance levels the resulting maximum interstory drift, material weight, and design complexity ones. Fragiadakis et al. (2006) presented PBD optimization practice for steel moment-resisting frames (MRFs) based on FEMA-350 (2000) probabilistic framework. An overview for the PBD framework state-of-the-art was presented by Foley et al. (2007) and implemented such a design framework into multiple-objective structural optimization problem formulations for single and multi-story steel framed structures having fully and partially restrained connections. European seismic code recommendations were assessed by Lagaros and Papadrakakis (2007), when adopted for designing 3D RC building structures, within a PBD multi-objective optimization concept. Aiming to deal with complex optimization problems, confidence levels were integrated with the objective criterion together with the material cost for various optimized design scenarios, the GA search algorithm was adopted by Rojas et al. (2007). Lagaros et al. (2010) presented an automated PBD approach that was implemented for designing RC building structures, examining the effect of infill walls, in this direction PBD approach alternatives were tested relying on non-linear static or dynamic analyses. In the work by Lagaros and Fragiadakis (2011) a comparative study is performed over the state-of-practice on nonlinear static analysis approaches, recommended by the European and US code provisions, were implemented within PBD optimization formulations; while aiming to examine the parameters that affect LCC estimation of structures, multi-objective LCC optimization problems were formulated by Mitropoulou et al. (2011).
The concept of defining the condition of structural loss using an engineering compatible quantity taking values on specific scale by means of a damage index (DI) is appealing due to its ease of implementation. So far several researchers have proposed several DIs for the case of RC or steel structural systems (i.e., Ghobarah, 2004; Estekanchi and Arjomandi, 2007). This work aims at exploring and assessing alternative designs, exhibiting a required performance monitored by a damage index, that comply with design codes according to the utmost economical way, i.e., having lower material volume requirements for concrete and steel reinforcement. In this direction, performance-based structural design optimization problems are formulated for various damage indices and the designs obtained are subsequently assessed under a set of seismic records properly selected. The main objective is to detect the most appropriate damage index, able to provide a reliable description of the structural damage level. This damage index is used to formulate a performance-based design framework to be used as a design tool for achieving safer and more economic designs. The resulting structural optimization problems are solved using a well-known metaheuristic optimization algorithm, namely the particle swarm optimization method, while the limit states implemented for the formulation of the performance-based design procedures, which describe the status of structural integrity, are based on calibrated values obtained from a former study of the authors (Mitropoulou et al., 2014).
Local and Global Damage Indices
Damage indices can be classified into two groups (Grigoriu, 1987): (a) DIs based on strength; and (b) those based on response. Strength-based DIs do not require response analyses (Shiga et al., 1982; Khashaee, 2005). However, they need to be calibrated with reference to observed damage based on rather large experimental databases. The performance of structures against seismic loading is generally correlated to the ability to sustain inelastic deformations (Resta et al., 2013), while experimental studies have shown that indices of structural performance (like ductility as well as others), which rely only on the fatigue concept of low-cycle, do not appear to offer an acceptable indicator for structural loss due to seismic loads (Banon and Veneziano, 1982). These observations are in agreement with the notion that brittle systems' failure is developed due to significant deformation demands, while ideal ductile structures' failure begun when inelastic deformations are observed repeatedly (Fiore et al., 2016b). Damage indices used to characterize the performance of structural systems that are not ideal ductile or brittle, need to consider for losses due to repeated and increased inelastic deformations (Park and Ang, 1985; Greco et al., 2017). Thus, more wide-ranging applicable and reliable indices are required to characterize structural performance.
According to Ghobarah et al. (1999) the DIs based on response are classified in three sets based on what DI accounts for: (a) maximum deformation (Mahin and Bertero, 1974; Saiidi and Sozen, 1981; Toussi and Yao, 1982; Roufaiel and Meyer, 1987; Powell and Allahabadi, 1988); (b) cumulative damage (Banon and Veneziano, 1982; Allahabadi and Powell, 1988); and (c) combination of cumulative damage and maximum deformation. In this work DIs accounting for both cumulative damage and maximum deformation are implemented. In particular, (i) the local DI by Park and Ang (1985), (ii) its alternative presented by Kunnath et al. (1992), (iii) local DI by Chung et al. (1987, 1989), (iv) together with the final and maximum softening DIs presented by DiPasquale and Çakmak (1987, 1988) are evaluated in the current study. For their implementation the local DIs are transformed into global ones by combining the local values of the DIs of the structural elements using weight coefficients.
Several damage indices account for the local damage induced to individual structural elements. Monitoring of local damage indices helps in the identification of the weak or vulnerable members that need to be rehabilitated. Nevertheless, it is not an easy task to obtain clear view for the structure's response provided the input earthquake record out of a list of members DIs. Currently, safety and residual strength of damaged structural systems rely on single or global DIs. The global ones are usually implemented for reliability studies, post-earthquake evaluation of structures, and performance-based design applications. Global DIs could be defined by combining local ones; the weighting scheme is the simplest approach for combining local damage indices (Kunnath et al., 1992). The weighting factors can predict the relative importance and/or the replacement cost of a structural element or part of the structure in preserving safety of the entire structure. However, employing weighted average procedures in order to define global DIs does not justify appropriately the concentration locally of the damages, does not distinguish between different structural elements, and might lead to misrepresentative conclusions. There are cases that for a few structural elements of the structural system to have undergone severe damage deprived of this being reflected in by a DI.
For the reasons described previously DIs expressed using weighting factors have not been considered; however, for purposes of completeness such DIs are briefly outlined below. Direct implementation of the damage model to the overall structural system, a single story frame or a structural member requires determining the corresponding overall structural system, story or member ultimate deformations. Nonlinear behavior is limited to plastic regions close to the structural joints; therefore, it is difficult to establish the relation between member, story or top story structural system deformations, with the rotations of the local plastic zone. Two other global and story damage indices were proposed (Kunnath et al., 1992), which are calculated using weighting factors, these factors rely on the hysteretic energy dissipated at story and component levels, respectively:
and
λi denotes the energy weight factor for story i; Ei represents the overall energy absorbed by the ith story or component, while nst and nel denote the total number of stories and components/elements, respectively.
Lower Bound Design of Structures
This work concerns the production of lower-bound optimized designs, which comply with design requirements by a cost-efficient means (i.e., those requiring less material volume for concrete and steel reinforcement) and subsequently to be compared. These designs are then used as the basis of comparison for identifying the best design procedure. Therefore, structural optimization problems are formulated and optimized designs obtained are subsequently evaluated.
Design of Reinforce Concrete Structures
Aiming to evaluate the performance of different designs of RC framed structures; structural optimization problems were formulated as below:
The design variables comprising of the dimensions of cross-sectional for groups of beams and columns considered for formulating the optimization problem are defined by vector s, F represents the feasible part of the design space where all serviceability and ultimate limit state design requirements implemented as constraint functions (i.e., the series of constraint functions ) are satisfied:
where RD represents the discrete design set where design vectors s take values. The structural materials cost CIN of the design is the objective function considered. Aiming to deal with the optimization problem the well-known metaheuristic search algorithm called as particle swarm optimization (PSO) method is implemented.
Swarm Intelligence
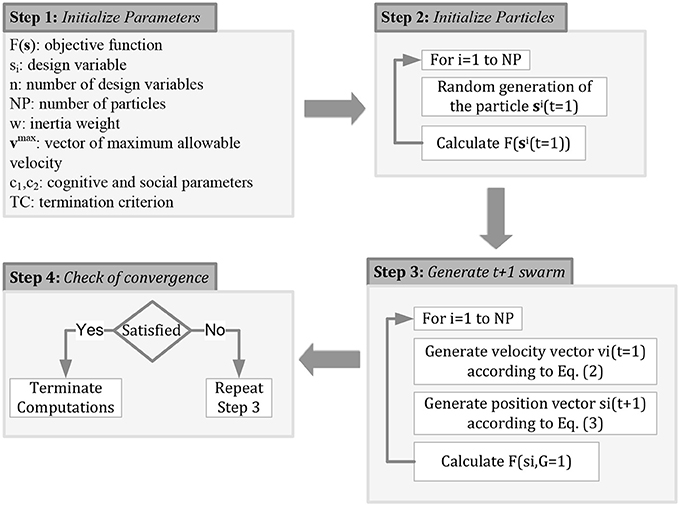
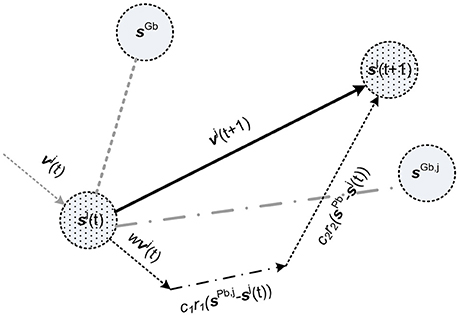
According to the optimization algorithm particle swarm (Kennedy and Eberhart, 1995), various design vectors collaborate. Every vector of unknowns is labeled as “particle” characterized by its velocity and position, both defined in the D-dimensional design domain, while a sum of particles constitutes the so termed “swarm.” During the search procedure where an optimized design vector is on the hunt, a particle “flies” in the design space of the problem. During the search procedure, velocity and position vectors are adjusted for every particle based on personal “experience” as well as that of the others (neighboring particles). Memorizing and tracking the best positions encountered construct particles' experience. PSO algorithm relies on joint search locally (self-experience) with global one (neighboring experience), trying to control exploitation with exploration. Every particle maintains its two basic characteristic vectors, i.e., velocity and position (or location), in the D-dimensional domain which are iterated as below:
vj(t) refers to the jth particle's velocity at time t, sj(t) denotes the jth particle's position vector at time t, the self-best location of jth particle is labeled as sPb, j, and the best position obtained globally is denoted with the vector sGb. Coefficients c1 and c2 denoted as acceleration ones, refer to the level of confidence with the best vector achieved by a specific particle (c1 is labeled as cognitive coefficient) and by entire swarm (c2 is denoted as social coefficient), respectively. Vectors r1 and r2 are composed by arbitrary elements distributed uniformly in [0,1]. Flowchart of Figure 1 describes the basic steps of PSO algorithm, while particle's motion indicatively for the case of the two-dimensional design space is depicted in Figure 2. The lower left dotted circle of Figure 2 represents present position vector sj(t) at time t, and the upper right dotted bold circle denotes new location vector sj(t+1) at time t+1. The means that the particle's transition into the D-dimensional search domain is affected by: (i) velocity vector vj(t); (ii) self-best found location vector (sPb, j); and (iii) swarm's global-best location achieved so far (sGb) is presented in Figure 2.
Damage Index-Based Design
In this work the performance degree are denoted in terms of structural deformation and cumulative energy, using different damage indices apart from maximum interstory drift that has been exclusively used in the past in PBD. More specifically Park and Ang DI and its reformed version as presented by Kunnath et al. (1992), as well as the Chung et al. DI, together with the final maximum and softening DIs suggested by DiPasquale and Çakmak (1988), have been considered for the definition of the performance levels. These five DIs account for cumulative damage and maximum deformation. These damage indices were calibrated in a recent study by the authors (Mitropoulou et al., 2014) relying on the crack openings' width. In particular, incremental dynamic analysis was employed for developing an archive of the DIs' values using a coarse modeling of structures employing column-beam 1D elements.
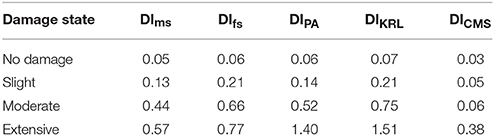
Six optimization problems are pursued within, following the PBD framework based on (i) interstory drift (DIθ), (ii) Park and Ang (DIPA); (iii) its alternative presented by Kunnath et al. (DIKRL); (iv) Chung et al. (DICMS); (v) maximum softening (DIms) as well as (vi) final softening (DIfs). Moreover, DIs statistical features were calculated implementing horizontal statistics combined with the method of maximum likelihood function together with a properly selected search technique. The values provided in Table 1 (Mitropoulou et al., 2014) represent calibrated damage states and they are used for defining the performance objective introduced in the proposed design framework.
Performance-Based Design
Several distinctive features for PBD seismic design procedure with respect to design procedures imposed by the prescriptive codes: (i) Permits structural engineers to select both appropriate seismic hazard level and the analogous performance of the structure, (ii) series of performance objectives are used for designing a structural system. PBD design procedure represents a design procedure relying on displacements where design measures and capacity demands are formulated considering displacements rather than using forces (Sullivan et al., 2003).
PBD implies that structural elements are selected, as well as the assessment; construction and maintenance studies are operated on the construction aiming to meet the purposes imposed by owners/users as well as society (Krawinkler and Miranda, 2004). When designing against seismic hazard, the aim is to construct structural systems having predictable performance capable to withstand seismic loading with measurable metrics. Hence, contemporary conceptual approach for structural design is that structural systems need to achieve performance objectives for several seismic levels varying in the rage of seismic event having low intensity and return period, to more damaging earthquake incidents having larger return periods. The contemporary state-of-practice for PBD structural engineering is offered by the various design codes (ASCE-41, 2006; FEMA-445, 2006; ATC-58, 2009; FEMA-P-58-1, 2012), that theoretically do not vary besides adopt techniques that represent the first significant difference with respect to prescriptive-based guidelines. Several of the contemporary design guidelines applied to design studies for new build structures can be considered as merely PBD ones, as these design guidelines combine all measures into a single level of performance, frequently the collapse prevention or life safety level. The definition of performance objectives represents the most important ingredient of a PBD seismic procedure.
DI-Based Design Concept for Safe and Economic Seismic Resistant Structures
The main scope of this step is to incorporate the DIs calibrated in a recent work by the authors into a performance-based design framework and to propose an innovative design concept leading to safe and economic earthquake resistant RC structures. For this purpose, the DIs selected in Mitropoulou et al. (2014) will be used to define different DI-based designs into structural optimization problems. The formulation of the DI-based concept can be stated as follows:
which represent the performance-based design constraints [denoted as gULT(s) in Equation 5]. The DI should be less or equal to the allowable upper bounds for a number of hazard levels (HL1, HL2,…,HLn) while i denotes the DI considered in the formulation (i = 1,2,…,m). The boundaries of the feasible part of the design space are defined using the calibrated values of the DIs defined in Mitropoulou et al. (2014) which are given in Table 2. Therefore, in order to identify the DI that represents better the structural behavior, various minimum initial material cost DI-based design optimization problems are formulated according to Equation (5), where the PBD checks are implemented according to Equation (9).
Numerical Tests
The objective of this work is to incorporate several damage indices examined in former study by the authors (Mitropoulou et al., 2014) into a performance-based design framework and to identify the best choice to be used for designing reinforced concrete structures.
Description of the Test Examples
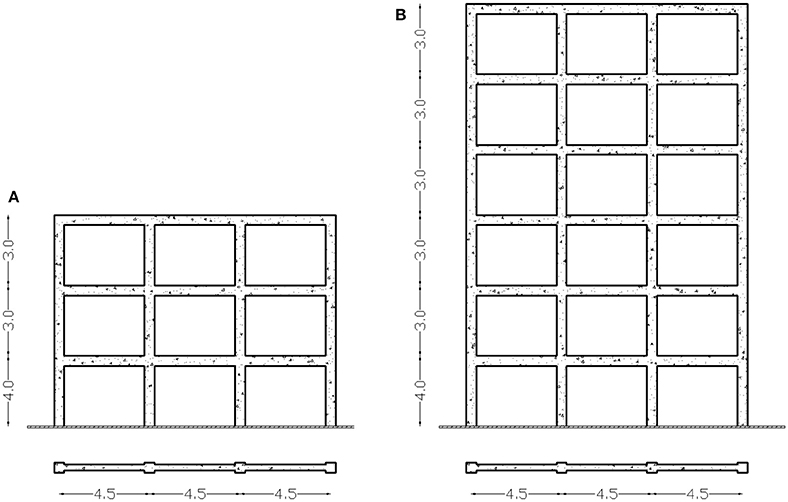
The two 2D RC moment resisting framed (MRF) building structures shown in Figure 3 have been taken into account aiming to study the effect of incorporating DI within the design framework of RC building structures. The foremost test example refers to a three-story concrete building while the second one is a six-story one. Class of concrete C20/25 and of steel S500 are assumed. The thickness of the slabs was taken equal to 15 cm for both test examples and their contribution to the moment of inertia of the beams through effective flange width is taken into account. Due to floor finishing-partitions permanent loading of 2 kN/m2 and moving one equal to 1.5 kN/m2, are applied further to the self-weight of beams and slabs, where an effective zone 10 × 15 m2 is considered for each story. The nominal imposed and permanent loads are combined using the load factors 1.50 and 1.35, respectively.
Columns and beams were simulated adopting the inelastic force-based fiber finite element. The simulation with this type of elements exhibits better accuracy than the plastic hinge formulation (Lagaros, 2014b). The structural analyses required in the framework the study were performed using OpenSEES (McKenna and Fenves, 2009) software. For steel reinforcement pure kinematic hardening bilinear material model was implemented, considering also geometric nonlinearities explicitly. The extended Kent-Park model as modified by Scott et al. (1982) was used for simulating concrete. Despite its relatively simple formulation, the specific model offers for acceptable forecasts of the needs for flexure-dominated RC members. The cyclic inelastic behavior of bars reinforcement was implemented with Menegotto-Pinto model (Menegotto and Pinto, 1973).
Analysis Procedure
During seismic structural design and/or assessment a wide-ranging earthquake events and multiple structural response levels are required for accounting the uncertainties that earthquake hazard introduces into performance-based earthquake engineering (PBEE) assessment or design. Methods implemented for PBEE assessment by means of nonlinear dynamic analyses are classified into single and multiple hazard level ones. Incremental dynamic analysis (IDA) and multi-stripe dynamic analysis (MSDA), their single and multicomponent (Lagaros, 2010) variants, represent the most appropriate ones. The numerical study performed consists of two stages, the optimization and the structural assessment ones, for both multi-stripe dynamic analysis (MSDA) was implemented for calculating the maximum inter-story drift.
Similar to IDA the purpose of MSDA studies is to form the relationship among earthquake intensity level and the correlative maximum structural performance. Earthquake ranking and performance of the structural system are defined through intensity measures (IM) and engineering demand parameters (EDP), correspondingly. MSDA implementation involves multiple inelastic dynamic analyses (stripes) executed in various spectral acceleration stages (see Figure 4 for the case of the final softening and Park and Ang designs). In every stripe various inelastic dynamic analyses are executed for the seismic records considered, all are scaled to specific spectral acceleration. The group of seismic records adopted for deriving each stripe should preferably be representative of the seismic hazard at specific spectral acceleration; nevertheless, although not necessarily always justified (e.g., Jalayer and Cornell, 2009), it is common to implement the same group of records for all spectral acceleration levels.
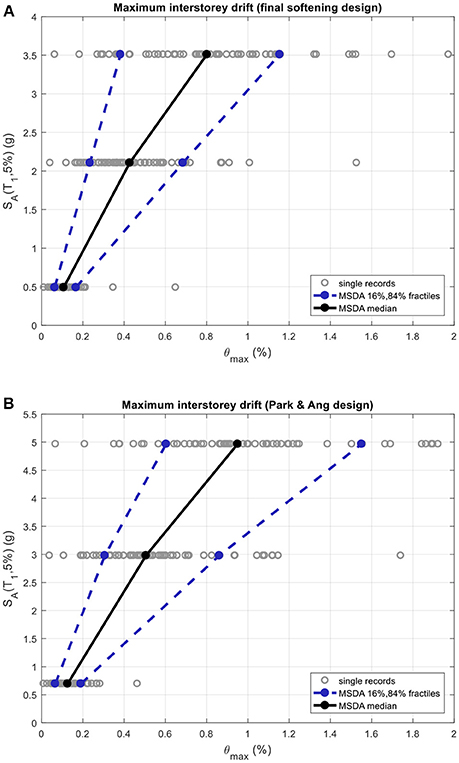
Figure 4. Three-story—multi-stripe dynamic analysis with reference to the maximum drift for (A) final softening and (B) Park and Ang designs.
Formulation of the Optimization Problems
The problem is expressed mathematically as single-objective minimization problem and is shown below:
subject to the constraints of Equation (9) (Quaranta et al., 2014; Fiore et al., 2016a). The total initial structural material cost C(s) is the objective criterion considered, and Ccl(s), Cb(s), Csl(s), and Cns(s) are the total material cost of columns, slabs, beams ,and nonstructural members, correspondingly. The ith DI for several hazard levels (HL1, HL2, …, HLn) should remain below the allowable upper bounds (). The limits of the feasible region are given in Table 2 (Mitropoulou et al., 2014). The PSO algorithm is adopted for dealing with the resulting structural design optimization problems. The boundaries for the maximum interstory drift were obtained by Ghobarah (2004).
The optimized design is computed by applying the PSO method with the following characteristic parameters for both test examples as suggested by the parametric study of Pedersen (2010): Number of particles NP is equal to 100, inertia weight w is equal to −0.6, cognitive and social parameters c1 is equal to −0.65 and c2 is equal to 2.65, respectively. Rectangular cross-sectional shape is adopted for both columns and beams, which are separated into different sets. The beams/columns dimensionality together with the longitudinal reinforcing bars represent the design parameters, which are allocated to every set of the beams/columns. The structural members (columns and beams) are divided in two sets for the three-story and three sets for the six-story test examples, resulting into five and seven design variables, respectively.
The optimized designs obtained are labeled as DDI = i associated with the damage index used (i–vi). The optimized designs obtained for different DI considerations with reference to steel and concrete material demands are shown in Tables 3, 4, respectively. According to Tables 3, 4 it looks that DDI = ms, DDI = fs, and DDI = CMS are leading to smaller columns for the three-storys but it does not apply to the six-story where DDI = θ is the one leading to smaller columns. With respect to beams, it looks that DDI = θ and DDI = CMS are leading to smaller beams for the three-stories and DDI = θ and DDI = KRL are leading ones for the six-story. Compared to design DDI = θ, it can be seen that, the initial material construction cost of the other five designs is increased by 23–145% for the three-story and by 26–75% for the six-story test example.
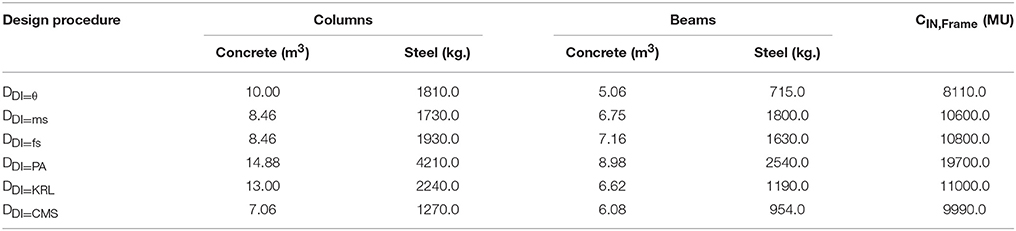
Table 3. Three-story test example: Concrete volume and steel weight corresponding to the optimized designs based on six DIs.
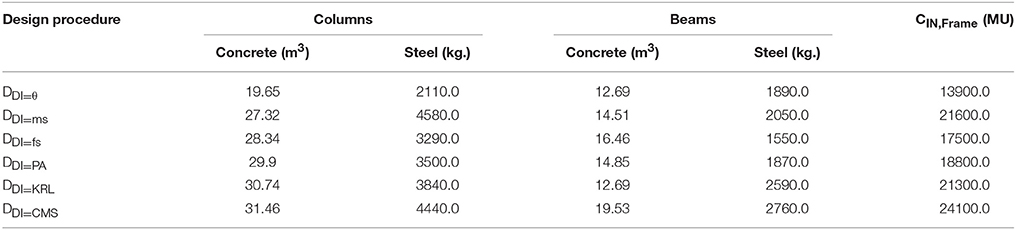
Table 4. Six-story test example: Concrete volume and steel weight corresponding to the optimized designs based on six DIs.
Assessment of the Optimized Designs
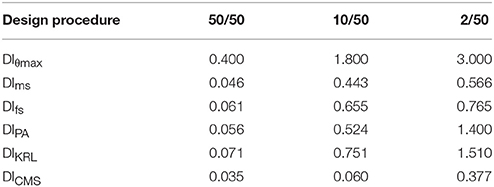
Aiming to evaluate the capacity of the optimized designs achieved by means of the six design PBD procedures described previously, a multi-stripe analyses is performed over a properly selected bin 100 natural records from the list of records provided in Mitropoulou et al. (2015). Seismic records were chosen from PEER (2010) database in agreement with the subsequent characteristics: (i) Records chosen in particular geographical zone (latitude 32–41°, longitude −124° to −115°). (ii) Magnitude (M) to be greater or equal to 5. (iii) Distance from the epicenter (R) is < 150 km. Figures 5, 6 depict the median values of maximum interstory drifts, maximum softening, final softening, Park and Ang damage index, Kunnath et al. damage index, and Chung et al. damage index. These quantities are obtained for three hazard levels namely 50/50, 10/50, and 2/50 (corresponding to probabilities of exceedance equal to 50, 10, and 2% in 50 years, respectively) and for the optimized designs achieved according to the design frameworks discussed above. Indicatively the multi-stripe analysis results for the three-story with reference to the maximum drift for final softening and Park and Ang designs that were used to derive the corresponding for these two designs median curves of Figure 5A are provided in Figure 4. In Figure 5A is represented the structural performance of the three-stories optimized designs (i.e., DIθmax, DIms, DIfs, DIPA, DIKRL, and DICMS) for the three hazard levels based only on maximum drift; the different lines are representing the different design.
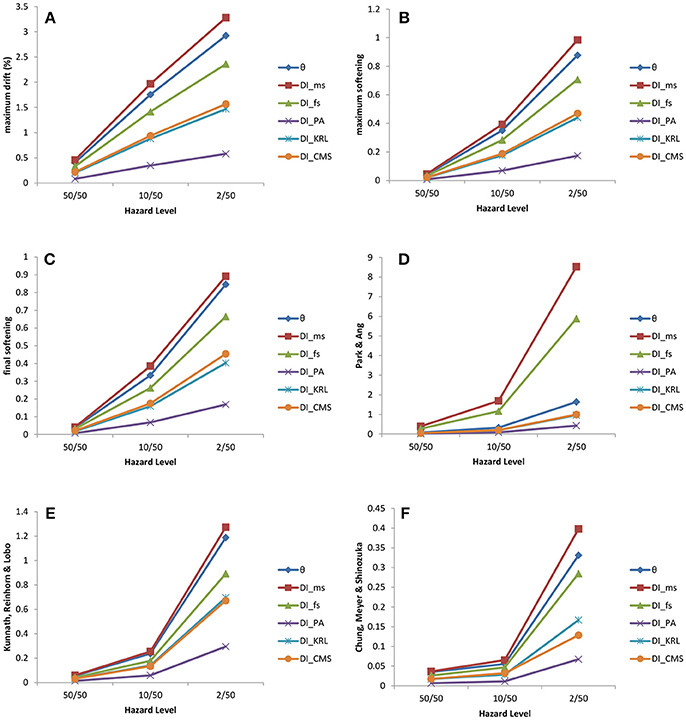
Figure 5. Three-story test example—performances of the optimized designs (i.e., DIθmax, DIms, DIfs, DIPA, DIKRL, and DICMS) for three hazard levels compared with respect (A) maximum drift, (B) maximum softening, (C) final softening, (D) Park and Ang damage index, (E) Kunnath et al. damage index, and (F) Chung et al. damage index.
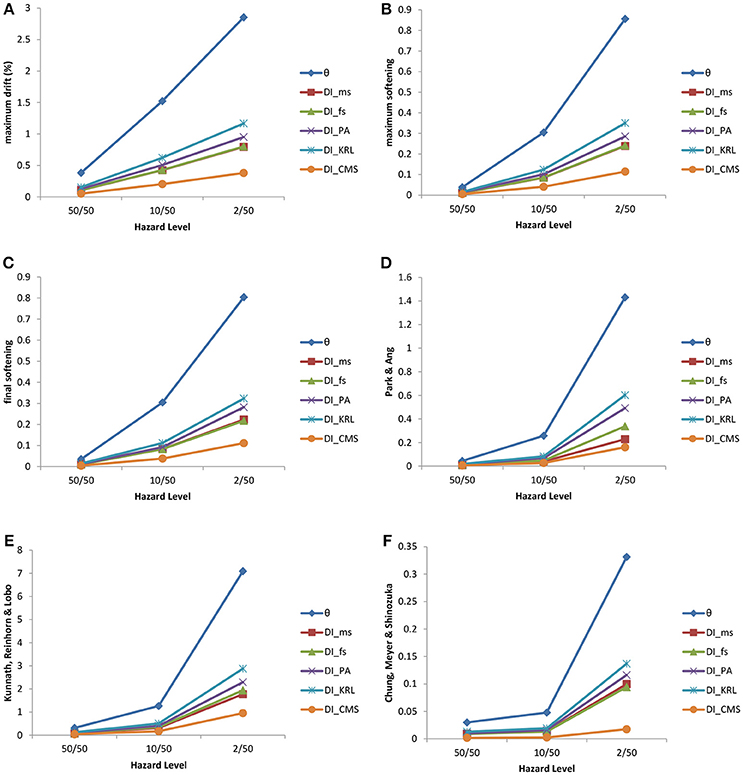
Figure 6. Six-story test example—performances of the optimized designs (i.e., DIθmax, DIms, DIfs, DIPA, DIKRL, and DICMS) for three hazard levels compared with respect (A) maximum drift, (B) maximum softening, (C) final softening, (D) Park and Ang damage index, (E) Kunnath et al. damage index, and (F) Chung et al. damage index.
The measure of the performance of one DI over the others is the structural performance achieved by each optimized design compared to the other ones, i.e., the design that has on average the better structural performance for all DIs. For the three-story test model it is the design obtained according to Park and Ang damage index that shows an overall better performance with reference to the six engineering demand parameters. On the other hand, for the six-story test model it is the design achieved according to Chung et al. damage index that exhibits the best performance, with reference to the six engineering demand parameter. Furthermore, for both test examples the maximum interstory drift appear to increase smoothly based on the abscissa escalation for all optimized designs in consideration of the hazard levels, while the structural behavior of the six designs is nonlinear with reference to the other damage indices. In general, it can be said that, for the two test examples considered, it is the Chung et al. damage index that shows an overall good performance with reference to the performance criteria considered. This is because for both test examples the designs obtained through the design formulation with the Chung et al. DI corresponds to the lower DI values, with reference to all six damage indices considered.
Conclusions
In this work we aim to incorporate a number of damage indices previously assessed by Mitropoulou et al. (2014) into a performance-based design framework and to identify the most suitable one for designing reinforced concrete framed structures. In this direction, structural optimization problems are formulated with performance-based design criteria corresponding to six damage indices for two reinforced concrete buildings.
An investigation was performed on the influence of these six damage indices incorporated into a performance-based design procedure. This was achieved by means of lower bound performance-based design. The ultimate objective was to compare lower-bound designs that satisfying in the most cost-efficient way the design code requirements, i.e., those requiring less material volume for concrete and steel reinforcement. The optimized designs obtained were subsequently assessed on the basis of their performance on a number of properly selected earthquakes with increasing intensity.
From the results obtained it was observed that, compared to design DDI = θ based on interstory drift, the initial construction cost of the other five designs is enlarged by 23–145% for the three-story test example and by 26–75% for the six-story one. It can also be concluded that for the two test examples considered it is the Chung et al. damage index that shows an overall good performance with reference to the performance criteria considered.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This research was supported by the OptArch project: Optimization Driven Architectural Design of Structures (No: 689983) belonging to the Marie Skłodowska-Curie Actions (MSCA) Research and Innovation Staff Exchange (RISE) H2020-MSCA-RISE-2015.
References
Allahabadi, R., and Powell, G. H. (1988). DRAIN-2DX User Guide. Technical Report No. UCB/EERC-88-06, Earthquake Engineering Research Center, University of California, Berkeley, CA.
ASCE-41 (2006). Seismic Rehabilitation of Existing Buildings. American Society of Civil Engineers ASCE/SEI Standard 41-06, Reston, VA.
ATC-58 (2009). Guidelines for Seismic Performance Assessment of Buildings. Applied Technology Council, Redwood City, CA.
Banon, H., and Veneziano, D. (1982). Seismic safety of reinforced members and structures. Earthq. Eng. Struct. Dyn. 10, 179–193. doi: 10.1002/eqe.4290100202
Chan, C.-M., and Zou, X.-K. (2004). Elastic and inelastic drift performance optimization for reinforced concrete buildings under earthquake loads. Earthq. Eng. Struct. Dyn. 33, 929–950. doi: 10.1002/eqe.385
Chung, Y. S., Meyer, C., and Shinozuka, M. (1987). Seismic Damage Assessment of Reinforced Concrete Members. Report NCEER-87-0022, National Center for Earthquake Engineering Research, State University of New York, Buffalo, NY.
Chung, Y. S., Meyer, C., and Shinozuka, M. (1989). Modelling of concrete damage. ACI Struct. J. 86, 259–271. doi: 10.1016/B978-012443341-0/50056-9
DiPasquale, E., and Çakmak, A. S. (1987). Detection and Assessment of Seismic Structural Damage. Report NCCER-87-O015, National Center for Earthquake Engineering Research State University of New York, Buffalo, NY.
DiPasquale, E., and Çakmak, A. S. (1988). Identification of the Serviceability Limit State and Detection of Seismic Structural Damage. Report NCEER-88-0022, National Center for Earthquake Engineering Research State University of New York, Buffalo, NY.
Estekanchi, H. E., and Arjomandi, K. (2007). Comparison of damage indexes in nonlinear time history analysis of steel moment frames. Asian J. Civil Eng. 8, 629–646. Available online at: http://www.sid.ir/En/Journal/ViewPaper.aspx?ID=103772
Esteva, L., Díaz-López, O., García-Pérez, J., Sierra, G., and Ismael, E. (2002). Life-cycle optimization in the establishment of performance-acceptance parameters for seismic design. Struct. Saf. 24, 187–204. doi: 10.1016/S0167-4730(02)00024-3
FEMA-350 (2000). Recommended Seismic Design Criteria for New Steel Moment-Frame Buildings. Federal Emergency Management Agency, Washington, DC.
FEMA-445 (2006). Next-Generation Performance-Based Seismic Design Guidelines, Program Plan for New and Existing Buildings. Federal Emergency Management Agency, Washington, DC.
FEMA-P-58-1. (2012). Seismic Performance Assessment of Building. Federal Emergency Management Agency, Washington, DC.
Fiore, A., Marano, G. C., Greco, R., and Mastromarino, E. (2016a). Structural optimization of hollow-section steel trusses by differential evolution algorithm. Int. J. Steel Struct. 16, 411–423. doi: 10.1007/s13296-016-6013-1
Fiore, A., Spagnoletti, G., and Greco, R. (2016b). On the prediction of shear brittle collapse mechanisms due to the infill-frame interaction in RC buildings under pushover analysis. Eng. Struct. 121, 147–159. doi: 10.1016/j.engstruct.2016.04.044
Foley, C. M., Pezeshk, S., and Alimoradi, A. (2007). Probabilistic performance-based optimal design of steel moment-resisting frames. I: formulation. J. Struct. Eng. 133, 757–766. doi: 10.1061/(ASCE)0733-9445(2007)133:6(757)
Fragiadakis, M., Lagaros, N. D., and Papadrakakis, M. (2006). Performance-based earthquake engineering using structural optimization tools. Int. J. Reliab. Saf. 1, 59–76. doi: 10.1504/IJRS.2006.010690
Ganzerli, S., Pantelides, C. P., and Reaveley, L. D. (2000). Performance-based design using structural optimization. Earthq. Eng. Struct. Dyn. 29, 1677–1690. doi: 10.1002/1096-9845(200011)29:1drd1<1677::AID-EQE986>3.0.CO;2-N
Ghobarah, A. (2004). “On drift limits associated with different damage levels,” in International Workshop on Performance-Based Seismic Design (Bled).
Ghobarah, A., Abou-Elfath, H., and Biddah, A. (1999). Response-based damage assessment of structures. Earthq. Eng. Struct. Dyn. 28, 79–104. doi: 10.1002/(SICI)1096-9845(199901)28:1 < 79::AID-EQE805>3.0.CO;2-J
Greco, R., Lucchini, A., and Marano, G. C. (2015). Robust design of tuned mass dampers installed on multi-degree-of-freedom structures subjected to seismic action. Eng. Optim. 47, 1009–1030. doi: 10.1080/0305215X.2014.941288
Greco, R., Marano, G. C., and Fiore, A. (2016). Performance–cost optimization of tuned mass damper under low-moderate seismic actions. Struct. Design Tall Spec. Build. 25, 1103–1122. doi: 10.1002/tal.1300
Greco, R., Marano, G. C., and Fiore, A. (2017). Damage-based inelastic seismic spectra. Int. J. Struct. Stabil. Dyn. 17:1750115. doi: 10.1142/S0219455417501152
Grigoriu, M. (1987). Damage Models for Seismic Analysis. Technical Report 87-4, Department of Structural Engineering, Cornell University, Ithaca, NY.
Jalayer, F., and Cornell, C. A. (2009). Alternative non-linear demand estimation methods for probability-based seismic assessments. Earthq. Eng. Struct. Dyn. 38, 951–972. doi: 10.1002/eqe.876
Kennedy, J., and Eberhart, R. (1995). “Particle swarm optimization,” in IEEE International Conference on Neural Networks (Piscataway, NJ), 1942–1948.
Khashaee, P. (2005). Damage-based seismic design of structures. Earthq. Spect. 21, 371–387. doi: 10.1193/1.1896366
Krawinkler, H., and Miranda, E. (2004). “Performance-based earthquake engineering,” in Earthquake Engineering: From Engineering Seismology to Performance-Based Earthquake Engineering, eds Y. Bozorgnia and Vitelmo V. Bertero (Boca Raton, FL: CRC Press), 9–59.
Kunnath, S. K., Reinhorn, A. M., and Lobo, R. F. (1992). IDARC Version 3.0: a Program for the Inelastic Damage Analysis of Reinforced Concrete Structures. Technical Report NCEER-92-0022, National Center for Earthquake Engineering Research, Buffalo, NY.
Lagaros, N. D. (2010). Multicomponent incremental dynamic analysis considering variable incident angle. J. Struct. Infrastruct. Eng. 6, 77–94. doi: 10.1080/15732470802663805
Lagaros, N. D. (2014a). A general purpose real-world structural design optimization computing platform. Struct. Multidiscip. Optim. 49, 1047–1066. doi: 10.1007/s00158-013-1027-1
Lagaros, N. D. (2014b). Risk assessment of steel and steel-concrete composite 3D buildings considering sources of uncertainty. Earthq. Struct. 6, 19–43. doi: 10.12989/eas.2014.6.1.019
Lagaros, N. D. (2018). The environmental and economic impact of structural optimization. Struct. Multidiscip. Optim. doi: 10.1007/s00158-018-1998-z. [Epub ahead of print].
Lagaros, N. D., and Fragiadakis, M. (2011). Evaluation of ASCE-41, ATC-40 and N2 static pushover methods based on optimally designed buildings. Soil Dyn. Earthq. Eng. 31, 77–90. doi: 10.1016/j.soildyn.2010.08.007
Lagaros, N. D., Naziris, I. A., and Papadrakakis, M. (2010). The influence of masonry infill walls in the framework of the performance-based design. J. Earthq. Eng. 14, 57–79. doi: 10.1080/13632460902988976
Lagaros, N. D., and Papadrakakis, M. (2007). Seismic design of RC structures: a critical assessment in the framework of multi-objective optimization. Earthq. Eng. Struct. Dyn. 36, 1623–1639. doi: 10.1002/eqe.707
Li, G., and Cheng, G. (2003). Damage-reduction-based structural optimum design for seismic RC frames. Struct. Multidiscip. Optim. 25, 294–306. doi: 10.1007/s00158-003-0299-2
Liu, M., Burns, S. A., and Wen, Y. K. (2005). Multiobjective optimization for performance-based seismic design of steel moment frame structures. Earthq. Eng. Struct. Dyn. 34, 289–306. doi: 10.1002/eqe.426
Mahin, S. A., and Bertero, V. V. (1974). Nonlinear seismic response evaluation - Charaima building. J. Struct. Eng. 100, 1225–1242.
Marano, G. C., and Greco, R. (2006). Damage and ductility demand spectra assessment of hysteretic degrading systems subject to stochastic seismic loads. J. Earthq. Eng. 10, 1–26. doi: 10.1080/13632460609350612
Marano, G. C., Greco, R., and Palombella, G. (2008). Stochastic optimum design of linear tuned mass dampers for seismic protection of high towers. Struct. Eng. Mech. 29, 603–622. doi: 10.12989/sem.2008.29.6.603
Marano, G. C., Quaranta, G., and Greco, R. (2009). Multi-objective optimization by genetic algorithm of structural systems subject to random vibrations. Struct. Multidiscip. Optim. 39, 385–399. doi: 10.1007/s00158-008-0330-8
Marano, G. C., Trentadue, F., and Greco, R. (2006). Optimum design criteria for elastic structures subject to random dynamic loads. Eng. Optim. 38, 853–871. doi: 10.1080/03052150600913028
Marano, G. C., Trentadue, F., and Greco, R. (2007). Stochastic optimum design criterion of added viscous dampers for buildings seismic protection. Struct. Eng. Mech. 25, 21–37. doi: 10.12989/sem.2007.25.1.021
McKenna, F., and Fenves, G.L. (2009). The OpenSees Command Language Manual - Version 2.0. Pacific Earthquake Engineering Research Centre, University of California, Berkeley, CA.
Menegotto, M., and Pinto, P. E. (1973). Method of analysis for cyclically loaded reinforced concrete plane frames including changes in geometry and non-elastic behaviour of elements under combined normal force and bending,” in IABSE Symposium on Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads (Lisbon), 15–22.
Mitropoulou, CCh., Lagaros, N. D., and Papadrakakis, M. (2011). Life-cycle cost assessment of optimally designed reinforced concrete buildings under seismic actions. Reliab. Eng. Syst. Saf. 96, 1311–1331. doi: 10.1016/j.ress.2011.04.002
Mitropoulou, CCh., Lagaros, N. D., and Papadrakakis, M. (2014). Numerical calibrations of damage indices. Adv. Eng. Softw. 70, 36–50. doi: 10.1016/j.advengsoft.2014.01.007
Mitropoulou, CCh., Lagaros, N. D., and Papadrakakis, M. (2015). Generation of artificial accelerograms for efficient life-cycle cost analysis of structures. Eng. Struct. 88, 138–153. doi: 10.1016/j.engstruct.2015.01.029
Park, Y. J., and Ang, A. H.-S. (1985). A mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 111, 722–739. doi: 10.1061/(ASCE)0733-9445(1985)111:4(722)
Pedersen, M. E. H. (2010). Good Parameters for Particle Swarm Optimization. Hvass Laborato-ries Technical Report no. HL1001, Southampton.
Powell, G. H., and Allahabadi, R. (1988). Seismic damage prediction by deterministic methods: concepts and procedures. Earthq. Eng. Struct. Dyn. 16, 719–734. doi: 10.1002/eqe.4290160507
Quaranta, G., Fiore, A., and Marano, G. C. (2014). Optimum design of prestressed concrete beams using constrained differential evolution algorithm. Struct. Multidiscip. Optim. 49, 441–453. doi: 10.1007/s00158-013-0979-5
Resta, M., Fiore, A., and Monaco, P. (2013). Non-Linear finite element analysis of masonry towers by adopting the damage plasticity constitutive model. Adv. Struct. Eng. 16, 791–803. doi: 10.1260/1369-4332.16.5.791
Rojas, H. A., Pezeshk, S., and Foley, C. M. (2007). Performance-based optimization considering both structural and nonstructural components. Earthq. Spectra 23, 685–709. doi: 10.1193/1.2754002
Roufaiel, M. S. L., and Meyer, C. (1987). Analytical modelling of hysteretic behaviour of RC frames. J. Struct. Eng. 113, 429–443. doi: 10.1061/(ASCE)0733-9445(1987)113:3(429)
Saiidi, M., and Sozen, M. A. (1981). Simple nonlinear seismic analysis of RC structures. J. Struct. Eng. 107, 937–952.
Scott, B. D., Park, R., and Priestley, M. J. N. (1982). Stress–strain behavior of concrete confined by overlapping hoops at low and high strain rates. ACI J. 79, 13–27.
Shiga, T., Shibata, A., and Hirosawa, M. (1982). “Outline of research on estimation of damages and repairs of the buildings damaged by the Miyagi-Ken-Oki earthquake, June, 1978,” in Seminar on Repair and Retrofit of Structures (Ann Arbor, MI), 147.
Sullivan, T. J., Calvi, G. M., Priestley, M. J. N., and Kowalsky, M. J. (2003). The limitations and performances of different displacement based design methods. J. Earthq. Eng. 7, 201–241. doi: 10.1080/13632460309350478
Toussi, S., and Yao, J. T. P. (1982). Hysteresis identification of existing structures. J. Eng. Mech. 109, 1189–1203. doi: 10.1061/(ASCE)0733-9399(1983)109:5(1189)
Keywords: performance-based design, structural optimization, damage indices, reinforced concrete structures, PSO algorithm
Citation: Mitropoulou CC, Marano GC and Lagaros ND (2018) Damage Index-Based Lower Bound Structural Design. Front. Built Environ. 4:32. doi: 10.3389/fbuil.2018.00032
Received: 17 April 2018; Accepted: 15 June 2018;
Published: 04 July 2018.
Edited by:
Vagelis Plevris, OsloMet—Oslo Metropolitan University, NorwayReviewed by:
Makoto Ohsaki, Kyoto University, JapanFrancesco Tornabene, Università degli Studi di Bologna, Italy
Flavia De Luca, University of Bristol, United Kingdom
Copyright © 2018 Mitropoulou, Marano and Lagaros. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nikos D. Lagaros, bmxhZ2Fyb3NAY2VudHJhbC5udHVhLmdy
 Chara Ch. Mitropoulou
Chara Ch. Mitropoulou Giuseppe C. Marano
Giuseppe C. Marano Nikos D. Lagaros
Nikos D. Lagaros