A Simple Rate-Independent Uniaxial Shape Memory Alloy (SMA) Model

Introduction

Throughout history, humanity has sought shelter from natural phenomena. Natural shelters, such as caves, were abandoned for artificial structures made of primitive materials, i.e., wood, stone, and brick. The building blocks were held in place by either sole gravity or by primitive paste. In the classical era, the Romans used opus caementicium, a pozzolanic concrete-like material, to build arches, vaults, and domes. Following a prolonged period of stagnation, new materials were introduced around 1800–1850 (i.e., cast iron and, later on, wrought iron and structural steel, as well as Portland cement), causing a revolution in the construction industry. Nowadays, the extensive use of high-strength steel and concrete, as well as the combination of them (as in composite structures), has led to an explosion in the capacity, performance, and size of structures that are feasible. Nevertheless, there is a consensus that, more or less, these materials have been fully exploited and groundbreaking development is unlikely to be observed.

Seeking the next revolution in the construction industry, researchers drew their attention to the so-called smart materials. These materials exhibit extraordinary properties, ranging from piezoelectricity and pH-sensitivity to magnetostriction and self-healing. A popular class of these materials, commonly known as Shape Memory Alloys (SMAs), exhibit physical and mechanical characteristics that allow their integration into structures. SMAs are capable of sustaining large inelastic strains that can be recovered by heating or unloading, depending on prior loading history. The origin of this unusual behavior is the ability of SMAs to undergo a first-order solid-solid diffusionless, and reversible phase change called martensitic transformation between a parent phase called austenite (A), stable at high temperature and low stress, and a product phase called martensite (M), metastable at low temperature and high stress (Olson and Cohen, 1982; Cisse et al., 2016). The martensitic transformation is at the origin of the two main effects observed in SMAs, namely the shape-memory effect and superelasticity.

Various innovative systems and devices, mainly using NiTi and Cu-based SMAs, have been developed for seismic energy absorption, damping control, structural retrofit. Several prototypes of SMA braces for the seismic protection of structures have been designed, numerically assessed and experimentally tested (Clark et al., 1995; Auricchio et al., 2006; Andrawes and DesRoches, 2007; Zhu and Zhang, 2008; Asgarian and Moradi, 2011). Hybrid devices, comprising of a combination of SMA and other components such as precompressed springs (Ma and Cho, 2008; Miller et al., 2012), or struts and steel tubes (Walter Yang et al., 2010) have been presented. Also, SMA-based isolation devices have been developed finding various applications on buildings or bridge structures (Krumme et al., 1995; Wilde et al., 2000). These devices exploit the hysteretic nature of SMA materials aiming to absorb structural vibrating energy and mitigate seismic effects. Gur and Mishra (2013) proposed a combination of steel-Teflon surface isolation device with superelastic SMA restrainers for energy dissipation and simultaneous minimization of isolator displacements and superstructure accelerations. Ozbulut and Hurlebaus (2010) introduced a sliding-type isolation system, optimally designed with the help of a multi-objective genetic algorithm, which consists of a steel Teflon sliding bearing and a NiTi SMA device, providing vertical load capacity, damping, and self-centering at the same time. Other applications of SMA materials in structural engineering include damping devices for bridge structures (Fujino et al., 1993; Ben Mekki and Auricchio, 2011; Torra et al., 2013), SMA-based structural connections in steel structures (Leon et al., 2001; Speicher et al., 2011; Fang et al., 2014) and reinforced concrete frames (Youssef et al., 2008; Muntasir Billah and Shahria Alam, 2012), structural retrofit of buildings and bridges (DesRoches and Delemont, 2002; Andrawes et al., 2010), use of SMA as reinforcement material in concrete structures (Deng et al., 2006; Zafar and Andrawes, 2013) as well as self-rehabilitation of structural elements (Li et al., 2006, 2008).

Obviously, proper modeling of the extraordinary behavior of SMAs is important and, thus, several models have been proposed in the literature. These can be broadly categorized into microscopic thermodynamic models, based on the Ginzburg-Landau theory or molecular dynamics; micro-macro models, based on micromechanics, micro-planes or micro-spheres; and macroscopic models, based on the theory of plasticity, thermodynamic potentials, finite strains or statistical physics (Cisse et al., 2016). For applications in structural engineering, however, uniaxial phenomenological models are of special interest as integration with existing reliable FEM codes, e.g., OpenSees (Mazzoni et al., 2006), is straightforward. Falling under this category, the Graesser-Cozzarelli model (Graesser and Cozzarelli, 1991), the Wilde-Gardoni-Fujino model (Wilde et al., 2000), and the Zhang-Zhu model (Zhang and Zhu, 2007) are examined herein in detail. Their parameters are examined concerning their physical representation, if any. This process reveals several limitations and drawbacks, most prominent of which is the large number of parameters and the unclear effect of specific parameters in the overall response. These are addressed in a unified manner in a new rate-independent model proposed herein. Finally, metaheuristic algorithms are employed for the identification of unknown parameter values. This process reveals valuable information regarding the relative sensitivity of the parameters as well as the mathematical consistency of the model.

Basic SMA Behavior

The primary forms of SMA behavior which are pertinent to the applications examined in this study are shown in Figure 1. In particular, Figure 1A shows the hysteretic loop observed at ambient temperatures T < M_f, where M_f is the temperature at which the microstructure of the material is fully martensitic. Although the loop strongly resembles the one observed in most conventional steels, the hysteretic mechanism is quite different. In steels, hysteresis in cyclic loading is due to dislocation glide but in SMAs it is due to twinning deformation of martensite that occurs by rotation, growth, and shrinkage of individual variants of martensite (Graesser and Cozzarelli, 1991). By application of sufficient strain, only one martensitic variant remains. This variant reverts to the original parent crystal orientation upon the application of heat, thus the term shape-memory effect.

FIGURE 1

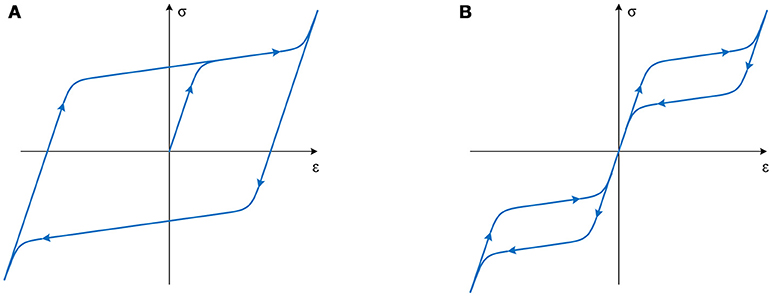
Figure 1. Schematic representation SMA behavior (A) twinning hysteresis (T < M_f), (B) superelasticity (T > A_f).

Figure 1B shows the hysteretic loop observed at ambient temperatures T > A_f, where A_f is the temperature at which the microstructure of the material is fully austenitic. This behavior exhibits two very important properties, i.e., energy dissipation and zero residual strain upon unloading, and thus it is termed superelastic. According to this, the stable austenitic microstructure is loaded elastically up to a threshold stress level, at which a transformation from austenite to martensite is initiated. The transformation is accompanied by the reduced modulus, as compared to the initial elastic loading, which strongly resembles the plastic yielding of steels. Gradually, the volume ratio of martensite is increased within the microstructure until it becomes dominant. Further loading of the now fully martensitic microstructure leads to elastic loading with a modulus smaller than the one of the elastic austenite, yet significantly higher than the one during transformation. Upon unloading, the inverse process is observed but at a significantly lower stress plateau. Ideally, the material returns to its exact original form (Graesser and Cozzarelli, 1991).

The Graesser-Cozzarelli Model

By modifying Ozdemir's model (Ozdemir, 1973), which is a particular case of the well-known Bouc-Wen hysteretic model (Bouc, 1967; Wen, 1976), Graesser and Cozzarelli (1991) proposed a one-dimensional phenomenological law to describe both twinning hysteresis and superelasticity, which is described by the following equations:

$\begin{array}{cc}\begin{array}{ccc}\dot{\sigma }& =& E\left[\dot{\epsilon }-\left|\dot{\epsilon }\right|{\left(\frac{\sigma -\beta }{Y}\right)}^n\right],\end{array}& (1)\end{array}$

$\begin{array}{cc}\begin{array}{ccc}\beta & =& E\alpha [{\epsilon }_{in}+f_T|\epsilon {|}^{c}erf(ā\epsilon )u(-\epsilon \dot{\epsilon })],\end{array}& (2)\end{array}$

where, (˙) = ordinary time derivative, σ = stress, ε = strain, β = backstress, E = initial elastic modulus, Y = yield stress, α = E_y/(E−E_y) = parameter controlling the post-elastic slope of the curve (E_y = post-elastic modulus), n = parameter controlling the abruptness of transition from the elastic to post-elastic branch, ε_in = ε−σ/E = inelastic strain, f_T, ā, c are model parameters, erf(·) is the error function defined by:

$\begin{array}{cc}erf(x)=\frac{2}{\sqrt{\pi }}{\displaystyle {\int }_x^0{e}^{-t^2}dt,}& (3)\end{array}$

and u(·) is the Heaviside step function defined by:

$\begin{array}{cc}u\left(x\right)=\{\begin{array}{l}1,x\ge 0\\ 0,x<0\end{array}& (4)\end{array}$

Note that parameter ā is used in Equation (2) to avoid confusion between parameters a and α in the original paper. Also, in Equation (1) the term (σ−β) may be negative, which is problematic when n takes real rather than integer values. This problem is addressed in a similar manner as in Zhang and Zhu (2007) in the proposed model which will be presented later.

Rate-Independency

The Graesser and Cozzarelli model is rate-independent, as is the Bouc-Wen model (Charalampakis and Koumousis, 2008b; Charalampakis, 2015). This means that in strain-controlled experiments, as the ones shown next, the same hysteretic loop will be traced irrespective of the rate of loading. In fact, the input does not even need to be sinusoidal; any input history with the specific sequence of local maxima and minima, i.e., 0 → ε_max → −ε_max → ε_max → …, will produce the same result.

Twinning Hysteresis

Twinning hysteresis in the Graesser and Cozzarelli model is observed by setting f_T = 0 in Equation (2). The base model shown in Figure 2A was used in the original paper (Graesser and Cozzarelli, 1991), where E = 28, 500 ksi; Y = 30ksi; α = 0.0197; n = 3. The input history is sinusoidal with ε_max = 0.016.

FIGURE 2

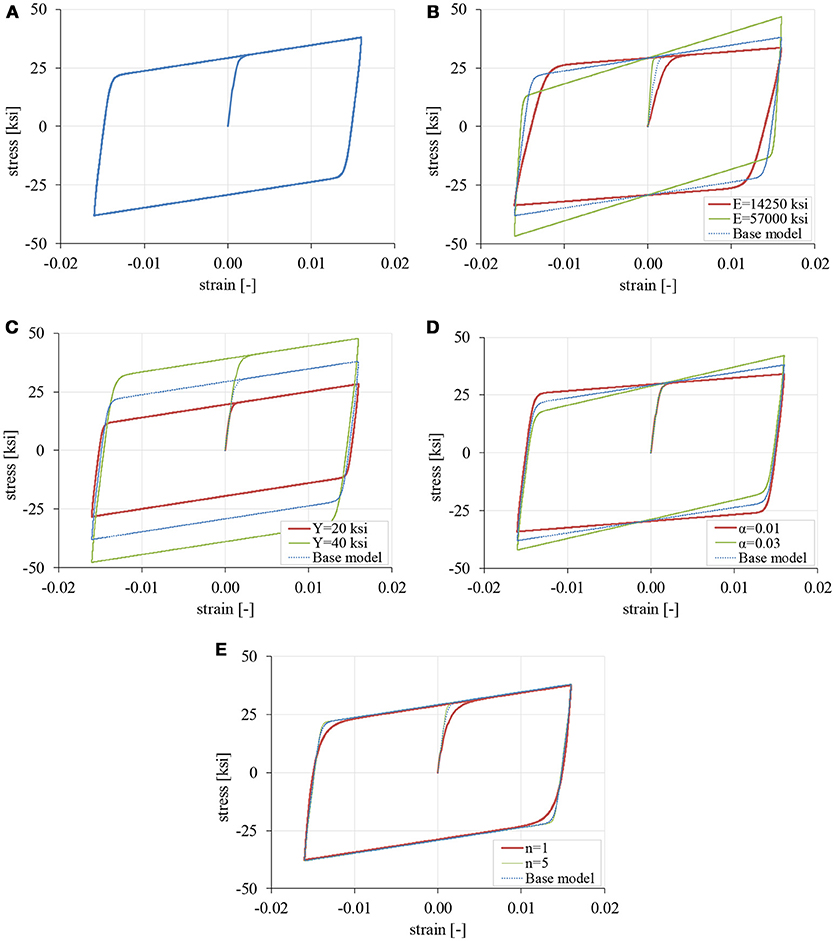
Figure 2. Twinning hysteresis (f_T = 0) with the Graesser-Cozzarelli model, (A) base model with E = 28,500 ksi, Y = 30 ksi, α = 0.0197, n = 3 (B) variation in E (C) variation in Y (D) variation in α (E) variation in n.

In Figure 2B, the effect of varying parameter E is shown. Apart from the initial stiffness, which is clearly controlled by E, the post-elastic stiffness E_y is also affected since E_y = αE /(1+α).

In Figure 2C the effect of varying parameter Y is examined. Obviously, Y controls the yield stress. Note that the term “yield stress” should be used rather loosely in our context. In SMA, it corresponds to the stress level at which stress induced phase transformation takes place in the material and has nothing to do with plastic deformation. Nevertheless, it will be used for reasons of simplicity.

In Figure 2D the effect of varying parameter α is shown. Clearly, α controls the post-elastic stiffness E_y without affecting the initial stiffness E.

In Figure 2E the effect of varying the exponential parameter n is shown. As is the case of the Bouc-Wen model, n controls the abruptness of transition between the initial (elastic) and post-elastic branches. Small values of n lead to a smooth transition and vice versa. Note that the sensitivity of the model with respect to this parameter becomes negligible when n ≥ 3. In the figure, the responses for n = 3 and n = 5 are practically the same.

Superelasticity

Superelasticity in the Graesser and Cozzarelli model is observed by setting f_T > 0 in Equation (2). The base model shown in Figure 3A was used in the original paper (Graesser and Cozzarelli, 1991), where E = 28,500 ksi; Y = 30 ksi; α = 0.0197; n = 3; f_T = 0.07; ā = 2,500; and c = 0.001. The input history is sinusoidal with ε_max = 0.016. In Figure 3B, the effect of varying parameter f_T is shown. It is observed that high values of f_T reduce the size of the energy-dissipating loops exhibited during the material transformations. Apparently, the sensitivity of the model with respect to f_T is high. In Figure 3C the effect of varying parameter ā is examined. As is the case with n, high values of ā do not alter the response significantly. For small values of ā, the response becomes smooth around the origin, yielding residual deformations upon unloading. In Figure 3D the effect of varying parameter c is shown. In general, the sensitivity of the model with respect to this parameter is very small. Figure 3E shows the variation of the quantity |ε|^c during the experiment. The responses for c = 0.001 and c = 0.00001 are practically the same, because |ε|^c ≅ 1 for ε ≠ 0. For c = 0.1, the graph of |ε|^c takes a form not radically different from the error function erf (·) used in the same expression, i.e., Equation (2). Thus, the response observed for c = 0.1, can also be obtained by appropriate values of f_T, n, and ā. To demonstrate this, the optimum values of f_T, n and ā have been obtained which produce a similar curve as the one with c = 0.1 (Figure 3F) using metaheuristics. In this regard, the term |ε|^c in Equation (2) is deemed redundant and will be removed in the proposed model which will be presented later.

FIGURE 3

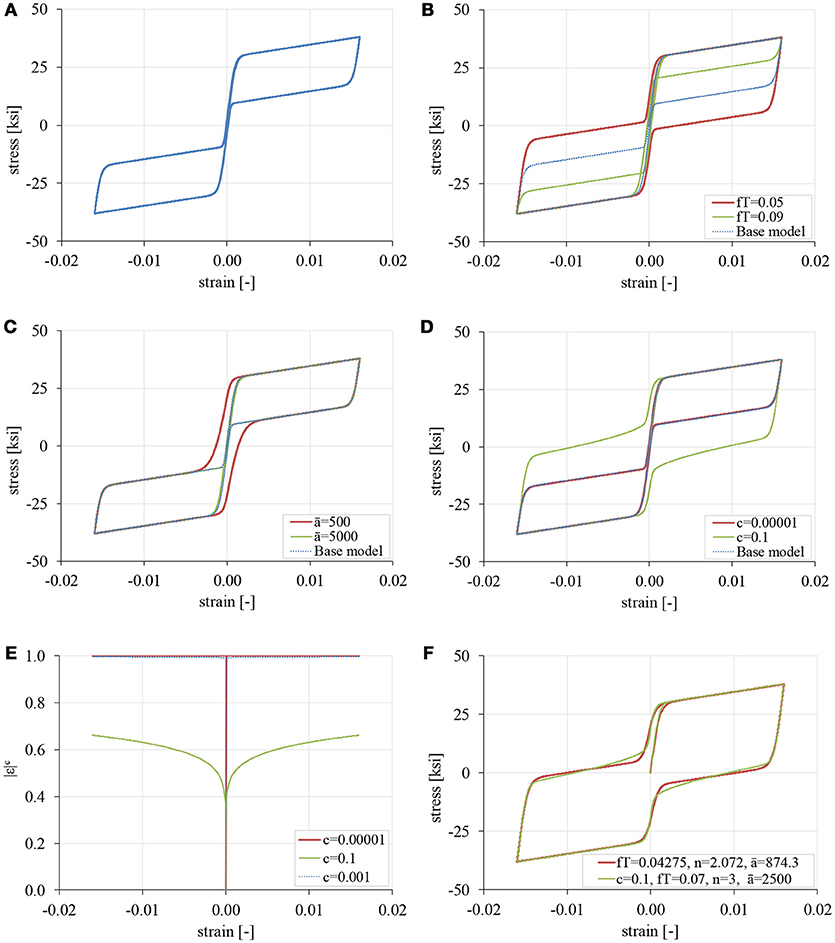
Figure 3. Superelasticity (f_T > 0) with the Graesser-Cozzarelli model, (A) base model with E = 28,500 ksi, Y = 30 ksi, α = 0.0197, n = 3, f_T = 0.07, ā = 2,500, c = 0.001 (B) variation in f_T (C) variation in $\bar{a}$ (D) variation in c, (E) value of |ε|^c for various values of c, (F) curve-fit of the response obtained with c = 0.1 by altering f_T, n, and ā only (c = 0).

Error Function

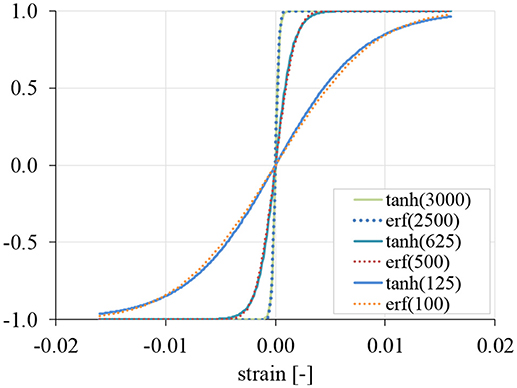
The final note on the Graesser-Cozzarelli model refers to the error function itself. As the evaluation of this function is cumbersome [see Equation (3)], its substitution with the hyperbolic tangent is proposed herein. The hyperbolic tangent is remarkably similar to the error function but more comfortable to evaluate, e.g., by using:

$\begin{array}{cc}\begin{array}{r}tanh(x)=1-\frac{2}{1+e^{2x}}.\end{array}& (5)\end{array}$

In Figure 4, the similarity of erf (āε) to tanh (âε) is illustrated. Three levels of strain coefficients, i.e., ā = {2, 500; 500; 100} are matched manually to â = {3, 000; 625; 125} to produce similar curves.

FIGURE 4

Figure 4. Comparison of the error and hyperbolic tangent functions.

The Wilde—Gardoni—Fujino Model

The Wilde-Gardoni-Fujino model (Wilde et al., 2000) is an extension of the Graesser-Cozzarelli model which takes into account the elastic behavior of the martensite which is activated after a particular strain level. The following equations describe it:

$\begin{array}{cc}\begin{array}{l}\begin{array}{ccc}\dot{\sigma }& =& E\left[\dot{\epsilon }-|\dot{\epsilon }|{\left(\frac{\sigma -\beta }{Y}\right)}^n\right]u_I(\epsilon )+E_m\dot{\epsilon }{u}_{II}(\epsilon )\end{array}\\ \begin{array}{c}+(3{\alpha }_1\dot{\epsilon }{\epsilon }^2+2{\alpha }_2\mathrm{sgn}(\epsilon )\dot{\epsilon }\epsilon +{\alpha }_3\dot{\epsilon })u_{III}(\epsilon ),\end{array}\end{array}& (6)\end{array}$

$\begin{array}{cc}\begin{array}{ccc}\beta & =& E\alpha [{\epsilon }_{in}+f_T|\epsilon {|}^{c}erf(ā\epsilon )u(-\epsilon \dot{\epsilon })],\end{array}& (7)\end{array}$

where the functions u_I (ε), u_II (ε), and u_III (ε) are given by:

$\begin{array}{cc}\begin{array}{rcl}{u}_I(\epsilon )& =& 1-u_{II}(\epsilon )-u_{III}(\epsilon ),\end{array}& (8)\end{array}$

$\begin{array}{cc}{u}_{II}\left(\epsilon \right)=\{\begin{array}{cc}1,& \left|\epsilon \right|\ge {\epsilon }_m\\ 0,& \text{otherwise}\end{array},& (9)\end{array}$

$\begin{array}{cc}{u}_{III}\left(\epsilon \right)=\{\begin{array}{cc}1,& \dot{\epsilon }\epsilon >0\text{ and }{\epsilon }_1<\left|\epsilon \right|<{\epsilon }_m\\ 0,& \text{otherwise }\end{array},& (10)\end{array}$

In this model, the response is divided into separate regions which are activated or deactivated by the flags described by Equations (8)–(10). The strain ε_m defines the point at which the transformation from austenite to martensite is completed. Beyond this strain, the response is linear elastic with modulus equal to E_m, due to the term $E_m\dot{\epsilon }{u}_{II}(\epsilon )$ in Equation (6). A smooth transition is achieved during loading only, due to the term activated by u_III (ε).

Although the model is capable of simulating the martensitic phase of the SMA, its usage is cumbersome. For instance, the coefficients a₁, a₂, and a₃ do not have physical representation and plausible value ranges are not easy to establish. As is the case with the Graesser-Cozzarelli model, the term (σ − β) may be negative, which is problematic when n takes real rather than integer values. Smooth transition between austenitic and martensitic phases can be realized with simpler and more elegant relations, as illustrated in the proposed model described later on.

The Zhang—Zhu Model

The Zhang-Zhu model (Zhang and Zhu, 2007) is a modification of the Wilde-Gardoni-Fujino model which aims to enhance the stability of numerical simulation and speed up the computation time. The following equations describe it:

$\begin{array}{cc}\begin{array}{l}\dot{\sigma }=E\left[\dot{\epsilon }-K\left(\epsilon \right)\left|\dot{\epsilon }\right|\mathrm{sgn}\left(\sigma -\beta \right){\left(\frac{\left|\sigma -\beta \right|}{Y}\right)}^n\right]u_I\left(\epsilon \right)\\ +E_m\dot{\epsilon }{u}_{II}\left(\epsilon \right)+\left(\text{}{E}_y\frac{{\epsilon }_m-\epsilon }{{\epsilon }_m-{\epsilon }_1}+E_m\frac{\epsilon -{\epsilon }_1}{{\epsilon }_m-{\epsilon }_1}\text{}\right)\dot{\epsilon }{u}_{III}\left(\epsilon \right),\end{array}& (11)\end{array}$

$\begin{array}{cc}\beta =E\alpha \left[{\epsilon }_{in}+f_{T}u\left(-\epsilon \dot{\epsilon }\right)sgn\left(\epsilon \right)g\left(\overline{a}{\epsilon }_{in}+sgn\left(\epsilon \right)b\right)\right],& (12)\end{array}$

where the functions u_I (ε), u_II (ε), u_III (ε), K(ε), g(t) are given by:

$\begin{array}{cc}\begin{array}{rcl}{u}_I(\epsilon )& =& 1-u_{II}(\epsilon )-u_{III}(\epsilon ),\end{array}& (13)\end{array}$

$\begin{array}{cc}{u}_{II}\left(\epsilon \right)=\{\begin{array}{l}1,\dot{\epsilon }\epsilon >0\text{ and }\left|\epsilon \right|\ge {\epsilon }_m\\ 0,\text{ otherwise}\end{array},& (14)\end{array}$

$\begin{array}{cc}{u}_{III}\left(\epsilon \right)=\{\begin{array}{cc}1,& \dot{\epsilon }\epsilon >0\text{ and }{\epsilon }_1<\left|\epsilon \right|<{\epsilon }_m\\ 0,& \text{otherwise}\end{array},& (15)\end{array}$

$\begin{array}{cc}K\left(\epsilon \right)=\{\begin{array}{cc}1,& \dot{\epsilon }\epsilon >0\\ u\left({\epsilon }_{in}\epsilon \right),& \text{otherwise}\end{array},& (16)\end{array}$

$\begin{array}{cc}\begin{array}{rcl}g(t)& =& 1-e^{-t^2},\end{array}& (17)\end{array}$

and the signum function is defined as

$\begin{array}{cc}\mathrm{sgn}\left(x\right)=\{\begin{array}{cc}1,& x>0\\ 0,& x=0\\ -1,& x<0\end{array}.& (18)\end{array}$

Note that parameters α, E, and n can take different values for loading and loading phases. Thus, the model contains up to fourteen parameters. The main improvements with respect to the Wilde-Gardoni-Fujino are the following:

• The problem with the potentially negative term (σ − β) has been addressed.

• The coefficients a₁, a₂, and a₃ have been replaced.

• The error function has been replaced.

The following, however, can be listed as disadvantages of the model:

• The number of parameters is high.

• Plausible value ranges are not provided for the parameters not having a physical representation.

• The response is still divided into many phases controlled with on/off flags.

Proposed Model

Based on the observations above, a simple rate-independent uniaxial phenomenological model is proposed herein which is described by the following terms:

$\begin{array}{cc}\dot{\sigma }=\left(1-s\left(\epsilon \right)\right)E\left[\dot{\epsilon }-\left|\dot{\epsilon }\right|\mathrm{sgn}\left(\sigma -\beta \right){\left(\frac{\left|\sigma -\beta \right|}{Y}\right)}^n\right]+s\left(\epsilon \right)E_m\dot{\epsilon },& (19)\end{array}$

$\begin{array}{cc}\beta =E\alpha [\epsilon -\sigma /E+f_T\tanh (ā\epsilon )u(-\epsilon \dot{\epsilon })],& (20)\end{array}$

$\begin{array}{cc}\begin{array}{r}s(\epsilon )=\frac{tanh(c(\left|\epsilon \right|-{\epsilon }_t))+1}{2},\end{array}& (21)\end{array}$

where, s(ε) is a smooth logistic function which yields 0 for |ε| ≪ ε_t and 1 for |ε| ≫ ε_t. Note that s(ε_t) = 0.5, i.e., at this level of strain the weights of the Graesser-Cozzarelli term and the elastic martensitic term in Equation (19) are equal. The coefficient c controls the abruptness of transition. For high values of c, the transition is abrupt, as evidenced by Figure 5A.

FIGURE 5

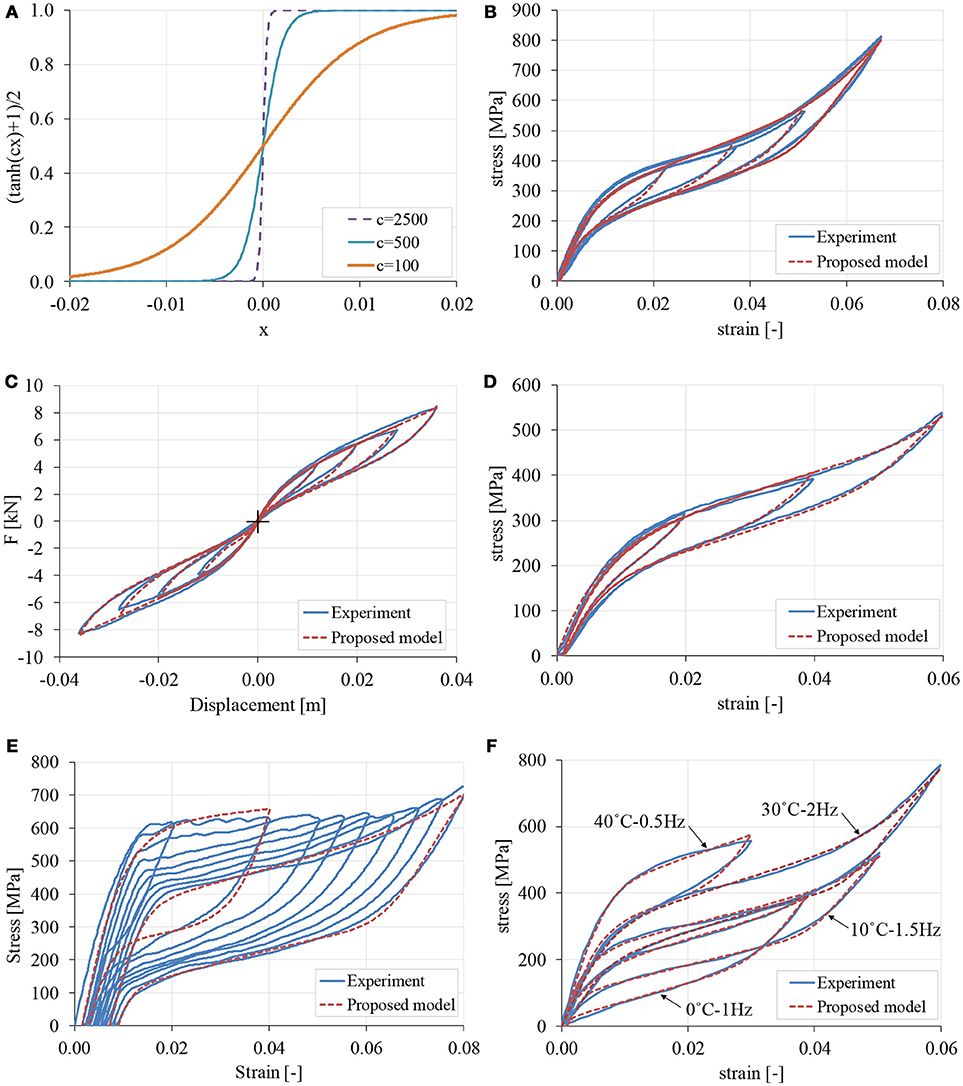
Figure 5. (A) Logistic function f (x) = (tanh (cx)+1)/2 for various values of coefficient c, and curve fit of the proposed model with experimental data obtained from (B) Zhang and Zhu (2007), (C) Zhuang et al. (2016), (D) Ozbulut et al. (2010), (E) Auricchio et al. (2003), (F) Ozbulut and Hurlebaus (2010).

In total, the model contains only nine parameters (E, Y, α, n, f_T, ā, E_m, ε_t, c) as opposed to the thirteen parameters of the Wilde-Gardoni-Fujino model (E, E_m, Y, α, n, f_T, c, ā, ε_m, ε₁, α₁, α₂, α₃) and the eleven to fourteen parameters of the Zhang-Zhu model (E_l, E_u, E_m, Y, E_Y, α_l, α_u, n_l, n_u, f_T, ā, ε_m, ε₁, b). A brief description of the model parameters and their effect on the overall response, based on the evidence examined earlier, is summarized in Table 1. The last three parameters refer to the martensitic phase.

TABLE 1

Table 1. Brief description of proposed model parameters and their effect on the overall response.

Despite its simplicity, the proposed model can accurately capture all the pertinent characteristics of the response curve. System identification based on metaheuristics produces excellent fit with experimental data obtained from the literature, as will be demonstrated. The optimum (best) parameter values were evaluated by Differential Evolution, a powerful metaheuristic algorithm (Storn and Price, 1997). The DE/rand/1/bin configuration was used with population size P = 50, F = 0.5 and C_r = 0.9. Ten independent runs were conducted with different random seeds. Each run was terminated after 20000 function evaluations. The sum of squares of the difference between the measured and the predicted time history of stress is used as the objective function to be minimized. Cast in discrete form, this function can be written as

$\begin{array}{cc}\begin{array}{r}OF(\text{p})={\sum (\sigma (t_i)-\hat{\sigma }(t_i|\text{p}))}^2,\end{array}& (22)\end{array}$

where p is the parameter vector.

In Figure 5B the case of tensional tests on cold-drawn nitinol wires with a diameter of 0.58 mm obtained from Zhang and Zhu (2007) is shown. A statistical analysis of the identified parameters is summarized in Table 2. It is noted that the initial side constraints are quite relaxed, yet the identification process was found to be straightforward. It is also observed that some parameters are very sensitive to the considered experimental data set, i.e., parameters ε_t, Y, E_m, f_T, and c, while the others are not so. In general, however, all runs were obviously guided to the same optimum region of the search space, which is a strong indication of a well-behaved model with uniquely defined parameters, each one with a distinct role in the response curve. If needed, the insensitive parameters can be accurately identified with other experiments which focus on the pertinent characteristics of the response curve, e.g., parameter E with a linear elastic experiment with small strains. Improved results can also be obtained by gradual tightening of the side constraints based on trial analyses, as in Charalampakis and Koumousis (2008a), but this lies beyond the scope of the present study and will be pursued in future research.

TABLE 2

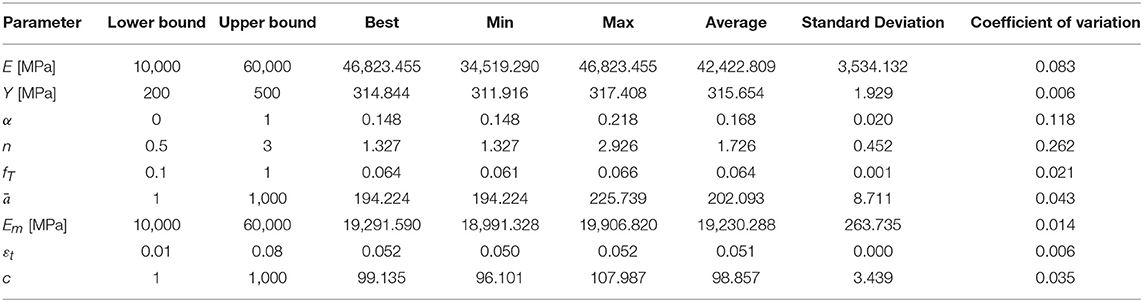
Table 2. Statistical analysis of identified parameters of the proposed model for the experimental data obtained from Zhang and Zhu (2007) shown in Figure 5B.

Figure 5C shows excellent fit in the case of the single SMA helical spring with hook-like ends obtained from Zhuang et al. (2016). Being phenomenological, the proposed model can be easily used with force-displacement curves instead of stress-strain curves, with the necessary semantic changes concerning parameters E and Y. By inspection, it is clear that the experimental data does not include any stress-induced martensitic phase. Therefore, the pertinent parameters (E_m, ε_t, c) cannot be identified. This fact is manifested clearly in the results of the identification, where the metaheuristic algorithm selects arbitrary values for these parameters in order to disable them (i.e., ε _t > 0.037, any E_m, and large c). In this specific case, we can use s(ε) = 0 instead of Equation (21), or repeat the experiment with a larger displacement to record martensitic phase data. A statistical analysis of the identified parameters is summarized in Table 3, where small coefficients of variation are observed.

TABLE 3

Table 3. Statistical analysis of identified parameters of the proposed model for the experimental data obtained from Zhuang et al. (2016) shown in Figure 5C.

Figure 5D shows an excellent fit for the case of NiTi SMA wires with a diameter of 1 mm. The data refers to the response of different strain levels at a frequency of 1 Hz and has been obtained from Ozbulut et al. (2010). A value of 0.005 has been subtracted from all strains to compensate for the lack of complete tautness. The wires have been trained with a set of 10 load cycles with a strain amplitude of 6% at 0.04 Hz. A statistical analysis of the identified parameters is summarized in Table 4, where, again, small coefficients of variation are observed.

TABLE 4

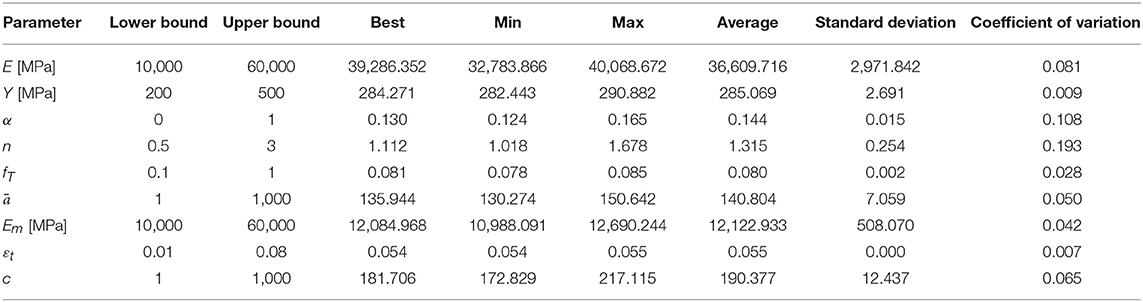
Table 4. Statistical analysis of identified parameters of the proposed model for the experimental data obtained from Ozbulut et al. (2010) shown in Figure 5D.

In Figure 5E, the experimental stress-strain response of an untrained commercial Ni-Ti wire with a diameter of 2.01 mm is shown. The loading cycles are characterized by an increasing value of the maximum elongation that varies from 2 to 8%. The data has been obtained from Auricchio et al. (2003), and an excellent fit can be observed for the second and last cycle, indicatively. Apparently, the values differ significantly, which is the result of the progressive decrement of the initial and final stress thresholds of the phase transformations during the training of a specimen (Auricchio et al., 2003). In similar fashion, in Figure 5F very good fit is observed for the experimental data obtained from Ozbulut and Hurlebaus (2010). The data refer to NiTi wires with a diameter of 1.5 mm which are subjected to tensile tests with various temperatures and strain rates. The identified model parameters for the latter cases are summarized in Table 5. By appropriate interpolation of model parameters, it may be possible that aspects which are not covered presently, such as strain-rate and temperature dependency, or training process, are taken into account. This, however, lies beyond the scope of the present study and will be pursued in future research.

TABLE 5

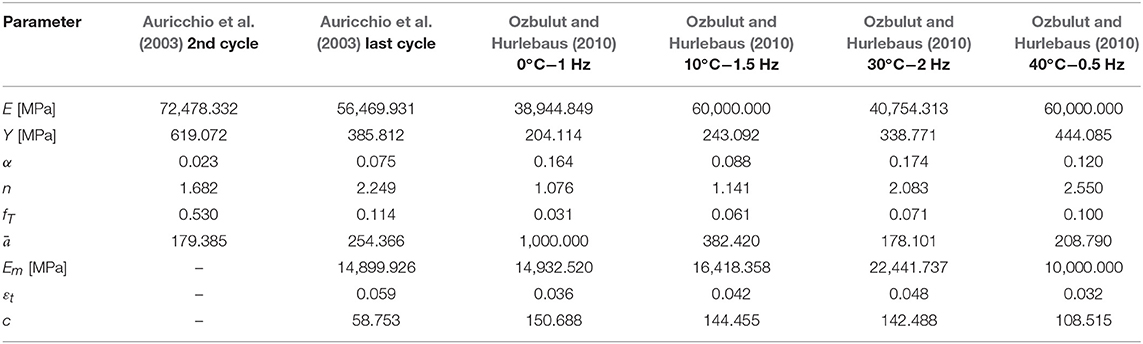
Table 5. Identified parameters of the proposed model for the experimental data shown in Figures 5E,F.

In order to demonstrate the advantages of the proposed model, the same identification procedure is applied to the Wilde-Gardoni-Fujino model with data obtained from Zhang and Zhu (2007). The results are summarized in Table 6, where great variability in parameter values and quality of solutions can be observed.

TABLE 6

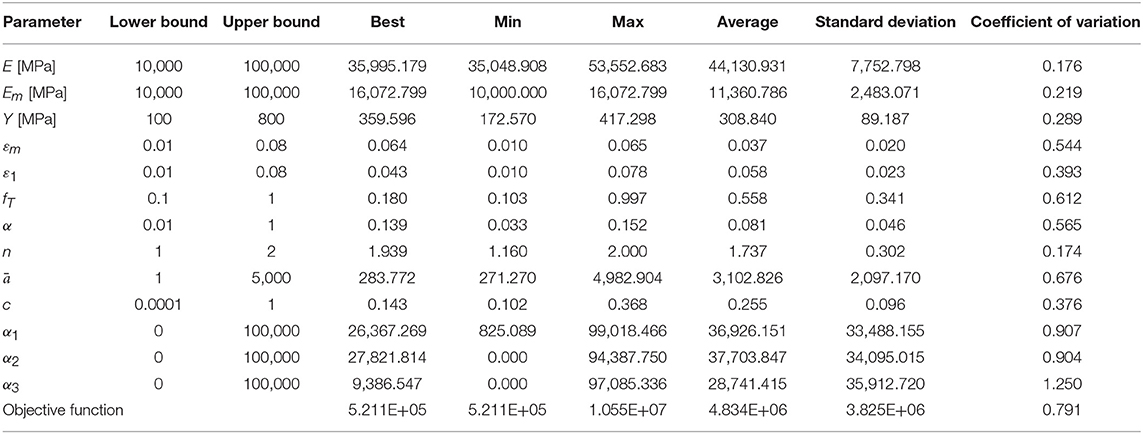
Table 6. Statistical analysis of identification results for the Wilde-Gardoni-Fujino model with data obtained from Zhang and Zhu (2007).

Conclusions

In this paper, three specific uniaxial phenomenological models commonly used for the description of a Shape Memory Alloy (SMA) behavior were examined in detail, and a new simple rate-independent model was proposed which addresses all issues in a unified manner. From the presented analysis and the numerical results, the following main conclusions can be drawn:

a) In total, the proposed model contains only nine parameters as opposed to the thirteen parameters of the Wilde-Gardoni-Fujino model and the eleven to fourteen parameters of the Zhang-Zhu model.

b) Despite its simplicity, the proposed model can accurately capture all the pertinent characteristics of the response curve.

c) For the proposed model, system identification based on metaheuristics produced excellent fit with experimental data obtained from the literature.

d) Apart from the best result, all runs produced quality solutions in the same region of the design space, and the identified parameters had small coefficients of variation. This is a strong indication of a well-behaved model, with uniquely defined parameters, each one with a distinct role in the response curve.

e) On the contrast, the application of the same identification process to the Wilde-Gardoni-Fujino model yielded significantly inferior results, i.e., great variability in parameter values and quality of solutions.

f) A significant advantage of the proposed uniaxial model is that it can be incorporated within a Finite Element code such as OpenSees straightforwardly.

Author Contributions

AC had the research idea, drafted the article, and contributed to the derivation of the numerical examples. GT contributed to the conception of the work and interpretation of the results. Both authors contributed to the writing of the manuscript.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor declared a shared affiliation, though no other collaboration, with one of the authors AC at time of review.

References

Andrawes, B., and DesRoches, R. (2007). Effect of hysteretic properties of superelastic shape memory alloys on the seismic performance of structures. Struct. Control Heal. Monit. 14, 301–320. doi: 10.1002/stc.159

CrossRef Full Text | Google Scholar

Andrawes, B., Shin, M., and Wierschem, N. (2010). Active confinement of reinforced concrete bridge columns using shape memory alloys. J. Bridg. Eng. 15, 81–89. doi: 10.1061/(ASCE)BE.1943-5592.0000038

CrossRef Full Text | Google Scholar

Asgarian, B., and Moradi, S. (2011). Seismic response of steel braced frames with shape memory alloy braces. J. Constr. Steel Res. 67, 65–74. doi: 10.1016/j.jcsr.2010.06.006

CrossRef Full Text | Google Scholar

Auricchio, F., Fugazza, D., and Desroches, R. (2006). Earthquake performance of steel frames with nitinol braces. J. Earthq. Eng. 10, 45–66. doi: 10.1080/13632460609350628

CrossRef Full Text | Google Scholar

Auricchio, F., Marfia, S., and Sacco, E. (2003). Modelling of SMA materials: training and two way memory effects. Comput. Struct. 81, 2301–2317. doi: 10.1016/S0045-7949(03)00319-5

CrossRef Full Text | Google Scholar

Ben Mekki, O., and Auricchio, F. (2011). Performance evaluation of shape-memory-alloy superelastic behavior to control a stay cable in cable-stayed bridges. Int. J. Non. Linear. Mech. 46, 470–477. doi: 10.1016/j.ijnonlinmec.2010.12.002

CrossRef Full Text | Google Scholar

Bouc, R. (1967). “Forced vibrations of a mechanical system with hysteresis,” in Proceedings of the 4th Conference on Non-Linear Oscillations (Prague).

Google Scholar

Charalampakis, A. E. (2015). The response and dissipated energy of Bouc–Wen hysteretic model revisited. Arch. Appl. Mech. 85, 1209–1223. doi: 10.1007/s00419-014-0937-8

CrossRef Full Text | Google Scholar

Charalampakis, A. E., and Koumousis, V. K. (2008a). Identification of Bouc–Wen hysteretic systems by a hybrid evolutionary algorithm. J. Sound Vib. 314, 571–585. doi: 10.1016/j.jsv.2008.01.018

CrossRef Full Text | Google Scholar

Charalampakis, A. E., and Koumousis, V. K. (2008b). On the response and dissipated energy of Bouc–Wen hysteretic model. J. Sound Vib. 309, 887–895. doi: 10.1016/j.jsv.2007.07.080

CrossRef Full Text | Google Scholar

Cisse, C., Zaki, W., and Ben Zineb, T. (2016). A review of constitutive models and modeling techniques for shape memory alloys. Int. J. Plast. 76, 244–284. doi: 10.1016/j.ijplas.2015.08.006

CrossRef Full Text | Google Scholar

Clark, P. W., Aiken, I. D., Kelly, J. M., Higashino, M., and Krumme, R. (1995). “Experimental and analytical studies of shape-memory alloy dampers for structural control,” in Proceedings Volume 2445, Smart Structures and Materials 1995: Passive Damping (San Diego, CA), 241–251. doi: 10.1117/12.208891

CrossRef Full Text | Google Scholar

Deng, Z., Li, Q., and Sun, H. (2006). Behavior of concrete beam with embedded shape memory alloy wires. Eng. Struct. 28, 1691–1697. doi: 10.1016/j.engstruct.2006.03.002

CrossRef Full Text | Google Scholar

DesRoches, R., and Delemont, M. (2002). Seismic retrofit of simply supported bridges using shape memory alloys. Eng. Struct. 24, 325–332. doi: 10.1016/S0141-0296(01)00098-0

CrossRef Full Text | Google Scholar

Fang, C., Yam, M. C. H., Lam, A. C. C., and Xie, L. (2014). Cyclic performance of extended end-plate connections equipped with shape memory alloy bolts. J. Constr. Steel Res. 94, 122–136. doi: 10.1016/j.jcsr.2013.11.008

CrossRef Full Text | Google Scholar

Fujino, Y., Warnitchai, P., and Pacheco, B. M. (1993). Active stiffness control of cable vibration. J. Appl. Mech. 60:948. doi: 10.1115/1.2901006

CrossRef Full Text | Google Scholar

Graesser, E. J., and Cozzarelli, F. A. (1991). Shape-memory alloys as new materials for aseismic isolation. J. Eng. Mech. 117, 2590–2608. doi: 10.1061/(ASCE)0733-9399(1991)117:11(2590)

CrossRef Full Text | Google Scholar

Gur, S., and Mishra, S. K. (2013). Multi-objective stochastic-structural-optimization of shape-memory-alloy assisted pure-friction bearing for isolating building against random earthquakes. Soil Dyn. Earthq. Eng. 54, 1–16. doi: 10.1016/j.soildyn.2013.07.013

CrossRef Full Text | Google Scholar

Krumme, R., Hayes, J., and Sweeney, S. (1995). “Structural damping with shape-memory alloys: one class of device,” in Proceedings Volume 2445, Smart Structures and Materials 1995: Passive Damping (San Diego, CA), 225–240. doi: 10.1117/12.208890

CrossRef Full Text | Google Scholar

Leon, R. T., DesRoches, R., Ocel, J., and Hess, G. (2001). “Innovative beam column connections using shape memory alloys,” in Proceedings Volume 4330, Smart Structures and Materials 2001: Smart Systems for Bridges, Structures, and Highways. Event: SPIE's 8th Annual International Symposium on Smart Structures and Materials (Newport Beach, CA), 227–237. doi: 10.1117/12.434122

CrossRef Full Text | Google Scholar

Li, H., Liu, Z. Q., and Ou, J. P. (2006). Behavior of a simple concrete beam driven by shape memory alloy wires. Smart Mater. Struct. 15, 1039–1046. doi: 10.1088/0964-1726/15/4/017

CrossRef Full Text | Google Scholar

Li, H., Liu, Z. Q., and Ou, J. P. (2008). Experimental study of a simple reinforced concrete beam temporarily strengthened by SMA wires followed by permanent strengthening with CFRP plates. Eng. Struct. 30, 716–723. doi: 10.1016/j.engstruct.2007.05.020

CrossRef Full Text | Google Scholar

Ma, H., and Cho, C. (2008). Feasibility study on a superelastic SMA damper with re-centring capability. Mater. Sci. Eng. A 473, 290–296. doi: 10.1016/j.msea.2007.04.073

CrossRef Full Text | Google Scholar

Mazzoni, S., McKenna, F., Scott, M. H., and Fenves, G. L. (2006). OpenSees Command Language Manual. Available online at: http://opensees.berkeley.edu/OpenSees/manuals/usermanual/OpenSeesCommandLanguageManualJune2006.pdf (Accessed July 18, 2018).

Miller, D. J., Fahnestock, L. A., and Eatherton, M. R. (2012). Development and experimental validation of a nickel–titanium shape memory alloy self-centering buckling-restrained brace. Eng. Struct. 40, 288–298. doi: 10.1016/j.engstruct.2012.02.037

CrossRef Full Text | Google Scholar

Muntasir Billah, A. H. M., and Shahria Alam, M. (2012). Seismic performance of concrete columns reinforced with hybrid shape memory alloy (SMA) and fiber reinforced polymer (FRP) bars. Constr. Build. Mater. 28, 730–742. doi: 10.1016/j.conbuildmat.2011.10.020

CrossRef Full Text | Google Scholar

Olson, G. B., and Cohen, M. (1982). Stress-assisted isothermal martensitic transformation: application to TRIP steels. Metall. Trans. A 13, 1907–1914. doi: 10.1007/BF02645934

CrossRef Full Text | Google Scholar

Ozbulut, O. E., and Hurlebaus, S. (2010). Evaluation of the performance of a sliding-type base isolation system with a NiTi shape memory alloy device considering temperature effects. Eng. Struct. 32, 238–249. doi: 10.1016/j.engstruct.2009.09.010

CrossRef Full Text | Google Scholar

Ozbulut, O. E., Roschke, P. N., Lin, P. Y., and Loh, C. H. (2010). GA-based optimum design of a shape memory alloy device for seismic response mitigation. Smart Mater. Struct. 19:065004. doi: 10.1088/0964-1726/19/6/065004

CrossRef Full Text | Google Scholar

Ozdemir, H. (1973). Nonlinear Transient Dynamic Analysis of Yielding Structure. Available online at: https://ci.nii.ac.jp/naid/10007658537/ (Accessed April 29, 2018).

Speicher, M. S., DesRoches, R., and Leon, R. T. (2011). Experimental results of a NiTi shape memory alloy (SMA)-based recentering beam-column connection. Eng. Struct. 33, 2448–2457. doi: 10.1016/j.engstruct.2011.04.018

CrossRef Full Text | Google Scholar

Storn, R. M., and Price, K. V. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11, 341–359. doi: 10.1023/A:1008202821328

CrossRef Full Text | Google Scholar

Torra, V., Auguet, C., Isalgue, A., Carreras, G., Terriault, P., and Lovey, F. C. (2013). Built in dampers for stayed cables in bridges via SMA. The SMARTeR-ESF project: a mesoscopic and macroscopic experimental analysis with numerical simulations. Eng. Struct. 49, 43–57. doi: 10.1016/j.engstruct.2012.11.011

CrossRef Full Text | Google Scholar

Walter Yang, C. S., DesRoches, R., and Leon, R. T. (2010). Design and analysis of braced frames with shape memory alloy and energy-absorbing hybrid devices. Eng. Struct. 32, 498–507. doi: 10.1016/j.engstruct.2009.10.011

CrossRef Full Text | Google Scholar

Wen, Y. K. (1976). Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 102, 249–263.

Google Scholar

Wilde, K., Gardoni, P., and Fujino, Y. (2000). Base isolation system with shape memory alloy device for elevated highway bridges. Eng. Struct. 22, 222–229. doi: 10.1016/S0141-0296(98)00097-2

CrossRef Full Text | Google Scholar

Youssef, M. A., Alam, M. S., and Nehdi, M. (2008). Experimental investigation on the seismic behavior of beam-column joints reinforced with superelastic shape memory alloys. J. Earthq. Eng. 12, 1205–1222. doi: 10.1080/13632460802003082

CrossRef Full Text | Google Scholar

Zafar, A., and Andrawes, B. (2013). Experimental flexural behavior of SMA-FRP reinforced concrete beam. Front. Struct. Civ. Eng. 7, 341–355. doi: 10.1007/s11709-013-0221-y

CrossRef Full Text | Google Scholar

Zhang, Y., and Zhu, S. (2007). A shape memory alloy-based reusable hysteretic damper for seismic hazard mitigation. Smart Mater. Struct. 16, 1603–1613. doi: 10.1088/0964-1726/16/5/014

CrossRef Full Text | Google Scholar

Zhu, S., and Zhang, Y. (2008). “Performance based seismic design of steel braced frame system with self-centering friction damping brace,” in Structures Congress 2008 (Reston, VA: American Society of Civil Engineers), 1–13.

Google Scholar

Zhuang, P., Xue, S., Nie, P., and Wang, W. (2016). Experimental and numerical study on hysteretic performance of SMA spring-friction bearings. Earthq. Eng. Eng. Vib. 15, 597–609. doi: 10.1007/s11803-016-0351-z

CrossRef Full Text | Google Scholar