Seismic Collapse Risk Assessment of Code-Conforming RC Moment Resisting Frame Buildings Designed With 2014 Canadian Standard Association Standard A23.3

Introduction

Collapse of buildings is identified as main contribution to injuries, casualties, and economic loss from past earthquakes (Porter, 2016). Current seismic design philosophy of Canadian and other countries, under rare earthquake events, focuses on buildings collapse prevention (DeVall, 2003; Haselton et al., 2011; Iervolino et al., 2017). In the current National Building Code of Canada (NBCC), reinforced concrete (RC) frame structures can be designed for two different ductility levels: ductile and moderately ductile (Mitchell et al., 2003; NBCC, 2010). The ductile and moderately ductile designs should have similar seismic performance under the site-specific design earthquake. However, the presence of unreinforced masonry infill (URM) infill walls, which is normally not considered in analysis and design process, may affect the performance and risk of collapse of infilled-RC frames in a severe earthquake to be greater or lesser than bare RC frames depending on the characteristics of URM infill walls (Mehrabi et al., 1996; Asteris et al., 2016; Sattar and Liel, 2016b). Thus, designing the buildings, by following a prescriptive design code, the collapse safety is uncertain (e.g., Burton and Deierlein, 2013; Jeon et al., 2015). In this paper, collapse risk of Canadian buildings is quantified, with seismicity of Vancouver, British Columbia, for the two ductility classes (ductile and moderately ductile) and with and without consideration of URM infill wall.

Various studies are reported on code-conforming RC moment-resisting frames (MRF). Haselton et al. (2011) implemented performance-based earthquake engineering (PBEE) approach to assess the collapse risk of ductile RC-MRF buildings designed according to ASCE 7-02 (ASCE 2002, 2005) and ACI 318-05 (2002). All models were developed using lumped-plasticity element to capture strength and stiffness degradation. Nonlinear dynamic analysis through incremental dynamic analysis (IDA) method was conducted to quantify collapse safety of 30 RC MRF varying from 1- to 20-stories. The collapse risk accounted for the effects of both record-to-record (RTR) variability and modeling uncertainty. The seismic assessment results show that the collapse probability of the buildings for the 2% in a 50-years hazard level, P(C|Sa_2/50), ranges from 3 to 20%. The mean annual frequency of collapse (λ_c) values range in 0.7 × 10⁻⁴ to 7.0 × 10⁻⁴ (i.e., probability of collapse in 50 years P_c = 0.4–3.4%). Koopaee et al. (2017) investigated the effect of ground motion selection method on seismic collapse fragility of 10-story RC MRF, representing mid-rise building, designed to New Zealand standard (NZS 1170.5, 2004; NZS 3101, 2006). In this study, fiber-based model was used to account the loss in vertical load carrying capacity of columns. Nonlinear dynamic analysis was carried out using multiple stripe analysis, using ground motion records selected at various hazard levels. The results indicate that the case study building has a 23% of P(C|Sa_2/50), which is higher than value reported in Haselton et al. (2011), particularly when comparing with average value estimated from 8- to 12-story RC frame buildings [i.e., P(C|Sa_2/50) = 17.5%]. This study found that considering loss of vertical load carrying capacity in structural model contributed to the higher value of collapse rate. Iervolino et al. (2017) quantified the seismic risk of code-conforming RC MRF buildings designed with the Italian NTC 2008 (Italian building code, 2008) design code. All the structures are designed for five sites with increasing seismic hazard. The results show that the RC MRF buildings considered in this study have λ_c between 1.0 × 10⁻⁵ and 8.47 × 10⁻⁵ and on average λ_c = 2.4 × 10⁻⁵ (i.e., P_c = 0.12%). The studies highlighted that as the site hazard level increases, the probability of collapse increases for all building systems.

Several studies focused on the seismic performance assessment of the RC frame with URM infill wall, which includes non-collapse or collapse, compared with bare RC frame buildings. Past earthquakes have indicated that most of the RC frame with URM infill wall buildings experiencing poor seismic performance (e.g., Zhao et al., 2009; Kam et al., 2010). Presence of URM infill wall can increase strength, stiffness and energy dissipation of the RC frame that lead to better seismic performance of buildings, but may introduced brittle or shear failure in the column due to interaction between infill and surrounding frame (e.g., Klingner and Bertero, 1978; Mehrabi et al., 1996; Stavridis et al., 2012; Stylianidis, 2012). The column shear failure is caused by the force from compressive diagonal strut in the URM infill wall. The columns shear failure can lead to a loss of the axial gravity load carrying capacity of the columns and typically occurs prior to flexural yielding of the columns at low drift levels (Burton and Deierlein, 2013). Neglecting columns shear failure due to the interaction between infill and surrounding frame in the seismic collapse assessment may lead to increase the uncertainty in the system response (Burton and Deierlein, 2013; Jeon et al., 2015; Sattar and Liel, 2016a). Therefore, a numerical modeling of infilled-RC frame that capable to simulate interaction between infill and frame and column shear failure is required to explicitly assess the collapse risk of RC frame with URM infill walls.

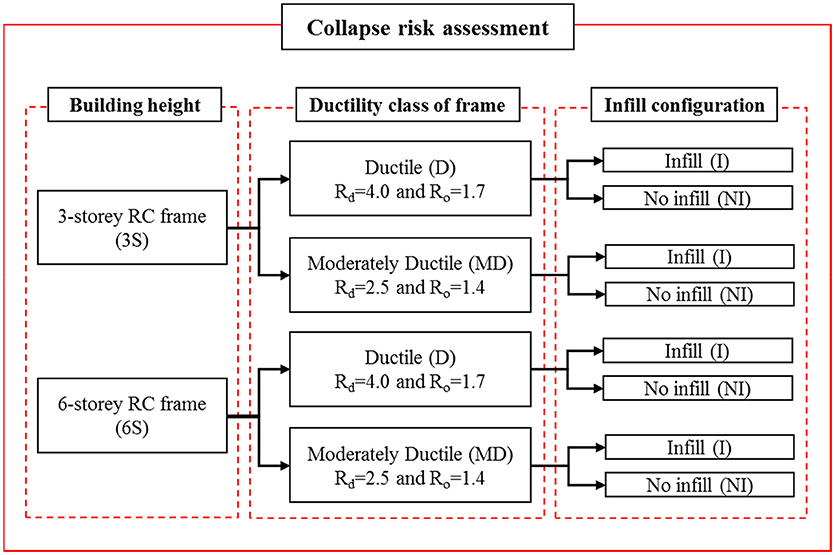
In this paper, the collapse risk assessment of code-conforming RC MRF buildings designed according to 2014 Canadian building code is carried out. The collapse assessments are conducted for ductile and moderately ductile RC MRF buildings. Figure 1 shows four set of building typologies considered in this study, which focusing on two different ductility class of RC MRF buildings with and without URM infill walls. The first step of this study is characterizing a set of typical structure by the archetypical buildings concepts. The selection of the archetypical structures is based on the FEMA P695 guidelines (FEMA-P695, 2009) to quantify the building's response and performance factor in the NBCC 2010 seismic design code. The details of the archetypical RC MRFs buildings with and without the masonry infill are outlined in sections Selection of Buildings: Characteristics and Configuration and Seismic Design Procedure. Next, the nonlinear structural analysis model is developed based on the selected building designs by considering the typical and critical failure modes of the structures as described in section Nonlinear Simulation Models: RC Frames and URM Infill Walls. Then, the ground motion is selected and scaled corresponded to a target seismic hazard level as discussed in section Ground Motion Selection. Next, the nonlinear model is used to simulate the response of the building until structural collapse through incremental dynamic analysis (IDA) [section Incremental Dynamic Analysis (IDA)]. Finally, as described in section Collapse Fragility Assessment, a collapse fragility curve is developed using IDA results. For this study, the seismic collapse risk assessment involves; (1) the evaluation of the median collapse capacity [g]; (2) the collapse margin ratio (CMR), (3) the mean annual frequency of collapse, λ_c, and (4) probability of collapse in 50 years.

FIGURE 1

Figure 1. Collapse risk assessment of RC frame framework.

Code-Conforming RC Frame Structures and Ground Motion Selection

Selection of Buildings: Characteristics and Configuration

For seismicity of Vancouver, BC, two sets of office building occupancy code-conforming RC MRF buildings (ductile and moderately ductile detailing) and building heights (3- and 6-stories) are designed. These buildings are founded on soft rock, which is the reference ground condition (class C) in the NBCC 2010. The Canadian code specifies that contribution URM infill wall is not considered in the design (DeVall, 2003). However, in this study, collapse risk assessment is carried for the RC building with and without consideration URM infill walls (Figure 2B). The building is regular in plan and elevation as shown in Figure 2. The RC office building considered has 7–6 m bays in N-S direction and 3 bays in the E-W direction consisting of 2–9 m and a bay (Figure 2). The story height for each level is 3.65 m. The following section explains the seismic design procedure and detailing according to the current NBCC and CSA A23.3-14 (CSA, 2014) standard provision, respectively.

FIGURE 2

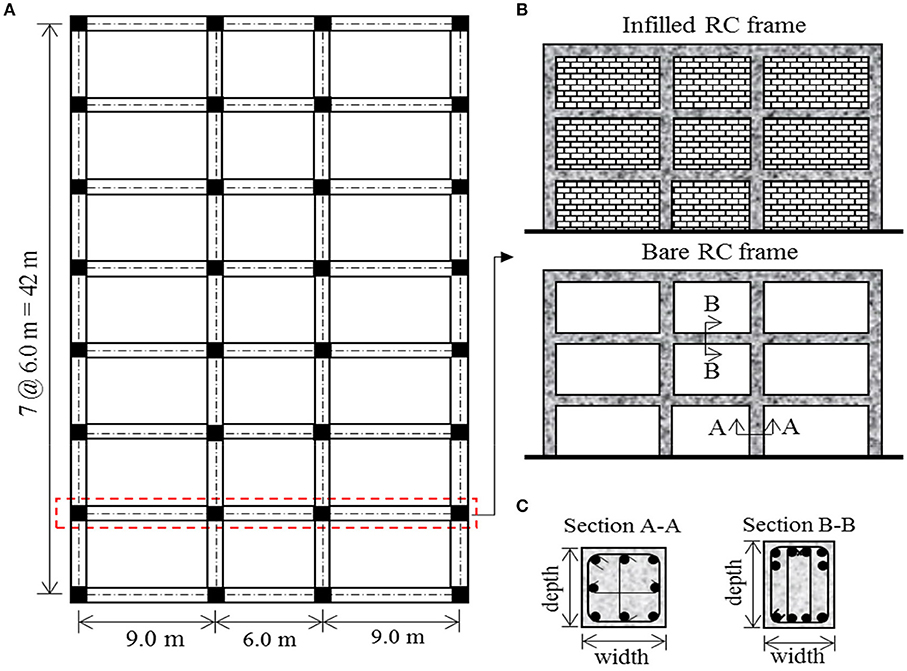
Figure 2. Code-conforming RC frame buildings; (A) Frame plan, (B) Frame elevations and types, and (C) typical columns and beams detailing.

Seismic Design Procedure

Each MRF RC building is designed based on the 2010 NBCC (NBCC, 2010) seismic design provision. The minimum design base shear force, of each studied building, was computed using the equivalent static force procedure, as (Mitchell et al., 2003):

$\begin{array}{ll}\text{V}=\frac{\text{S}({\text{T}}_{\text{a}}){\text{M}}_{\text{v}}{\text{I}}_{\text{E}}\text{W}}{{\text{R}}_{\text{d}}{\text{R}}_{\text{o}}}& (1)\end{array}$

where, S(T_a) is design spectral response acceleration expressed as a ratio of gravitational acceleration, g, at the design period T_a, M_v is the factor to account for higher mode effects, I_E is the earthquake importance factor, W is the building seismic weight including 25% of snow load, and R_d and R_o are the ductility-related and overstrength-related force modification factors. The empirical fundamental lateral period, T_a is given by${0.075\mathrm{\text{h}}}_{\text{n}}^{3/4}$, where h_n is height of building. However, since the dynamic fundamental periods usually greater than T_a value (more than 150%), therefore, the fundamental lateral period value used to select the design spectral response acceleration is taken as 1.5T_a.

The buildings are designed with importance factor, I_E = 1.0, on very dense soil and soft rock (Soil class C) and assumed fixed at ground level. Two different levels of ductility factors, which are ductile (R_d = 4.0 and R₀ = 1.7) and moderately ductile (R_d = 2.5 and R₀ = 1.4), are also considered (Mitchell et al., 2003). Since there is no eccentricity in the buildings, the effects of accidental torsional eccentricity is calculated by applying the lateral forces F_x at an accidental eccentricity of ±0.1D_nx = 4.245 m, where Dnx is a plan dimension of the building in the computed eccentricity direction that is perpendicular to the direction of seismic loading. The same floor plan is used at all levels as illustrated in Figure 2. Typical super imposed load values of 1.0, 0.5, 0.5 kN/m² are used as partition, mechanical services, and roofing material, respectively. The office floor live load of 2.4 kN/m² and snow load of 2.2 kN/m² are considered. Concrete compressive strength, ${f^{\prime }}_c$ and concrete modulus of elasticity, E_c was taken as 30 and 24,700 MPa, respectively. High yielding strength deformed rebar with yield strength, f_y = 400 MPa is used. The E-W moment resisting frame was chosen for the current study, as shown in Figure 2B. ETABS 2015, which has an option for current Canadian code CSA A23.14, is utilized to analyze and design three-dimensional structure system. The modal response spectrum analysis procedure including second order P-Delta effects is considered in the design.

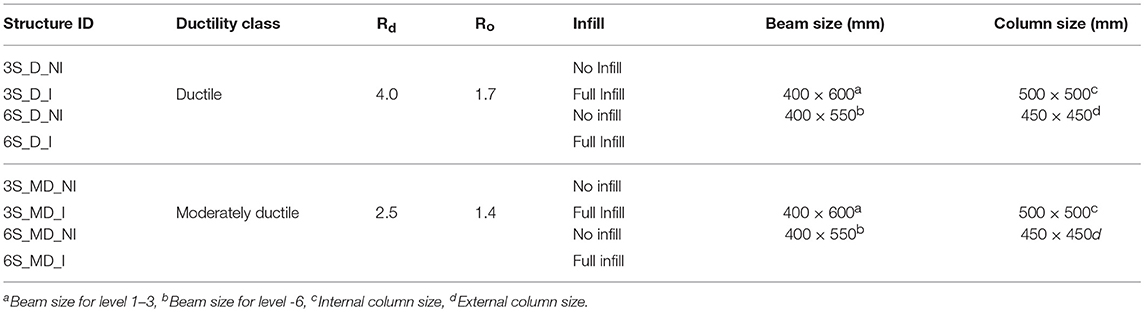
Table 1 provides a summary of the design characteristics for beams and columns. The interior and exterior column is 500 × 500 and 450 × 450 mm, respectively. The columns are assumed fixed at the base with ignoring soil-structure interaction. The beams of both the N-S and E-W frames are 400 mm wide × 600 mm deep for first three stories and 400 × 550 mm for other stories. The two-way slab floor system consists of a 210 mm thick slab. For the infilled-RC frame buildings, the URM infill walls are considered as a non-structural element and neglected in the structural design process. Thickness and compressive strength of infill panels are 150 mm and 6.9 MPa, respectively.

TABLE 1

Table 1. Summary of design characteristic of Ductile and Moderately Ductile RC frame.

Nonlinear Simulation Models: RC Frames and URM Infill Walls

A two-dimensional (2-D) models of code-conforming RC frame buildings with and without URM infill walls (Figure 3A) are developed using the Open System for Earthquake Engineering Simulation (OpenSees) software package (OpenSees, 2009). The 2-D model employs a leaning column to account for P-Δ effects. For the RC members, the model used lumped- plasticity element models and rigid beam-column joints zones. The lumped-plasticity model can be introduced using an elastic beam-column element with two zero-length elements at both element ends, as shown in Figure 3B. The zero length-elements are related to a rotational hinge model with a hysteretic response to represent the flexural behavior for the elements. The rotational hinge behavior is attached by the multiple uniaxial materials to display the moment-rotation or force-deformation relationship. This simulation approach is used for the collapse prediction to capture deterioration of the steel reinforcing bars due to the rebar buckling and low cyclic-fatigue, as well as to record the strength and stiffness deterioration in assessing the global collapse. In this study, Rayleigh damping model is used, which is a damping ratio of 5% is assigned to the first and third modes of the structure. For nonlinear dynamic analysis, the Newton algorithm is used to solve the system equations.

FIGURE 3

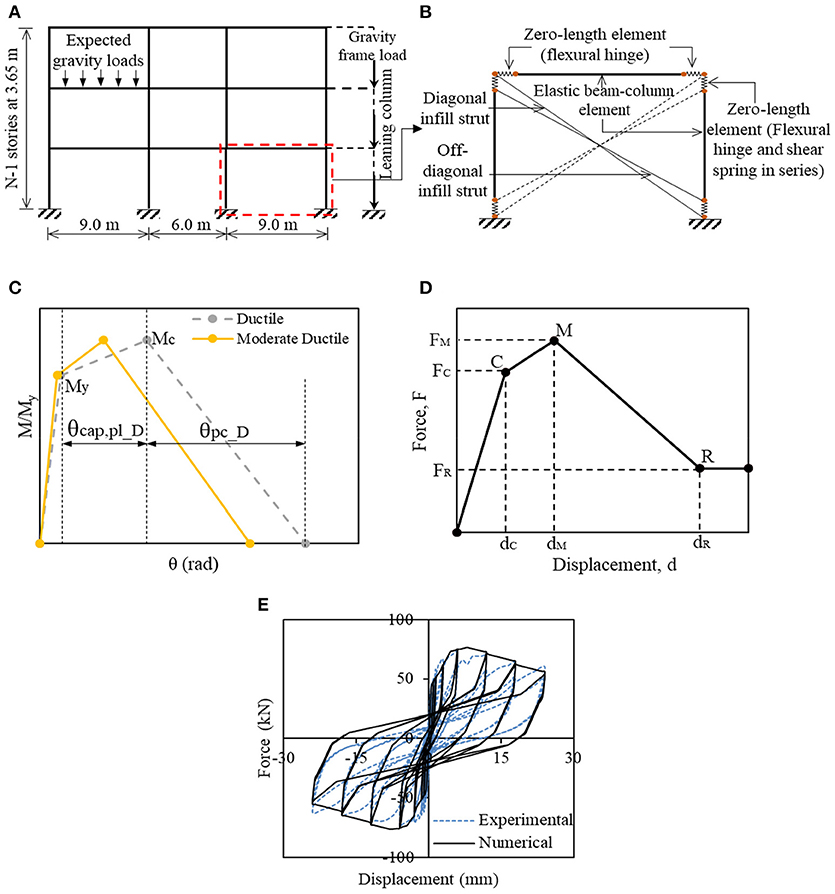
Figure 3. Schematic of RC frame modeling using lumped plasticity elements; (A) overview of overall model, (B) detail model for infilled—RC frame, (C) monotonic curve for RC frame member developed by Ibarra et al. (2005), (D) in-plane lateral force-displacement envelope model proposed by Decanini et al. (2014), and (E) hysteretic curve (cyclic behavior).

To describe the flexural behavior of the RC beam-column element, the most common OpenSees implementation of the peak oriented hysteretic model developed by Ibarra et al. (2005) (modIMKmodel), is adapted. This model captures four modes of cyclic deterioration, which includes; (1) the basic strength deterioration, (2) the post-capping strength deterioration, (3) the unloading stiffness deterioration, and (4) the accelerated reloading stiffness deterioration. The hysteretic model requires six key parameters: elastic stiffness (K_e), effective yield moment (M_y), strain hardening ratio (M_c/M_y), pre-capping rotation (θ_cap), post-capping rotation (θ_pc), and cyclic deterioration parameter (λ). The moment-rotation law (backbone) according to Ibarra et al. (2005) is illustrated in Figure 3C. All the parameters are obtained using the predictive equations and tools developed by Haselton et al. (2007). The M_y was calculated for each element from the sectional analysis.

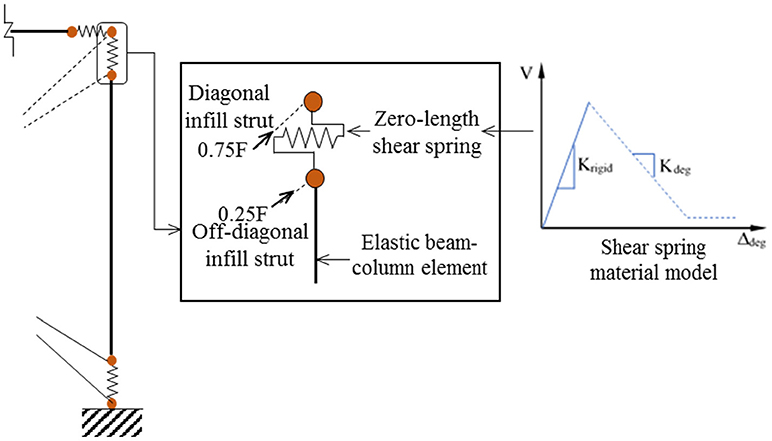
Analytical method to model infilled-frame buildings with consideration of shear failure are limited in the literature. Crisafulli and Carr (2007) developed a new macro model for the seismic response of infilled RC frames, which is can be modeled by four-node element. This model developed based on a multiple-strut formulation that includes two parallel off-diagonal struts and a special shear spring in each direction to account the diagonal tension failure and shear mechanism in the infill walls. Although the model capable to represent different type of failure modes in shear for URM infill wall, but the bending moment and shear forces of the surrounding frame not able to predict appropriately due to the simplicity of the model. Jeon et al. (2015) adopted a three-strut model developed by Chrysostomou et al. (2002) to assess seismic fragility of lightly RC frames with URM infills. Fiber-type displacement based model was used to capture the flexural response of the surrounding frame. Two off-diagonal struts and one central strut at each direction were employed to simulate the column shear failure. A contact length between the column and infill panel is computed by using Smith (1967) approach. Two types of column shear failure were considered: shear failure and flexure-shear failure. The column shear failure was simulated using two zero-length springs at the face of the beam and the flexure-shear mode the column shear strength model adopted from Sezen and Moehle (2004). For the flexure-shear failure has been modeled using a zero-length spring at center of the column incorporating with limit state model proposed by Elwood (2004). Burton and Deierlein (2013) applied a pair of central and off-diagonal compression-only strut at both direction with zero contact length to assess seismic performance of the non-ductile RC frame with URM infill walls. Lumped-plasticity model that can be introduced using an elastic beam-column with two zero-length elements at both ends is used to idealize beams and columns response. The flexure hinge and shear spring in series was introduced at top and bottom column to capture the column shear failure, and has been modeled based on the flexure-shear failure type that occurred after infill failure. Sattar and Liel (2016b) assessed the collapse risk of masonry-infilled RC frame buildings using the strut modeling enhanced by finite element (FE) analysis. Two struts in each direction were employed to simulate the column shear failure, which the contact length were determined through FE model response. This study also implemented lumped-plasticity model with spring in series at the top of column only. Burton and Deierlein (2013) and Sattar and Liel (2016a) also used similar approach developed by Sezen and Moehle (2004) to calculate the column shear strength. Although all studies applied similar approach to capture the response of strut and column shear failure, but the infilled-RC frame model developed by Burton and Deierlein (2013) is less sophisticated and able to simulate most of the seismic collapse mode of buildings. Therefore, in this study, the model and tools developed by Burton and Deierlein (2013) for the infilled-frame structures is adopted (Figure 3B).

A pair of off-diagonal strut, as presented in the Figure 3B, is used to capture shear failure due to the interaction between the column and the infill walls. As illustrated in Figure 4, zero-length shear springs model with a rigid softening material model is attached in series with the flexural hinges at the face of the columns. The column shear strength is calculated by using a model developed by Sezen and Moehle (2004). Whereas, the column shear deformation are obtained from the modeling parameter and acceptance criteria offered in Tables 6–8 of ASCE/SEI 41 (2007), which a proposed supplement to ASCE/SEI 41 developed by Elwood et al. (2007). Furthermore, this study assumed that collapse generated by axial column failure occur at ultimate shear deformation.

FIGURE 4

Figure 4. Spring model for column shear failure.

For the URM infill wall, an equivalent diagonal struts model is implemented to simulate the behavior of the masonry infill in terms of strength and stiffness. The performance of the masonry infill wall subjected to the in-plane effect is simulated by using two opposing pairs of the diagonal compression-only strut in each direction (Figure 3B). The monotonic backbone curve, shown in Figure 3D, proposed by Decanini et al. (2014) is applied to define the overall in-plane behavior of URM infill walls. The strength of the infill model is calculated using strength model proposed by Priestley and Calvi (1991) and Paulay and Priestley (1992). The distribution amount of force and stiffness of the strut are adopted from Chrysostomou (1991) who has investigated the force and stiffness distribution of central and off-diagonal strut of infilled-frame buildings using the principle of virtual displacements. The author founds that the maximum force distributed to the off-diagonal strut is ~25% of the total strut force. Thus, in this study, the stiffness proportion assigned to the central and off-diagonal strut are 75 and 25% of the total strut stiffness, respectively (Figure 4). The available elements and materials in the OpenSees are used to define the model. The selection of the most appropriate hysteretic model used to calculate and capture the strength, stiffness, and behavior of the URM infill walls is presented in Noh et al. (2017). Figure 3E shows the cyclic behavior of single-story infilled-frame by executing monotonic curves of RC frame member and infill wall, as illustrate in Figures 3C,D.

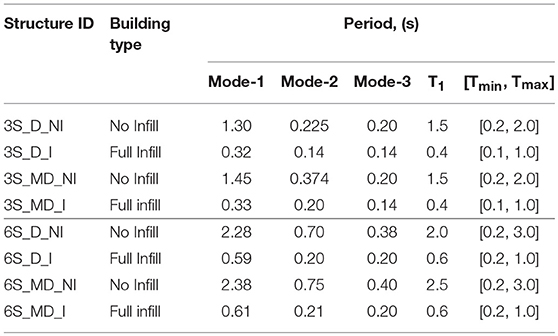
Table 2 presented the first three mode period of vibration obtaining through modal analysis conducted in OpenSees model. The dynamic fundamental period that calculated for the code-conforming RC frame models is based on the effective cracked stiffness of the structural members (Table 2). As shown in Table 2, the spectral acceleration at 1.5 s is selected and the time range used to select ground motion is between 0.2 and 2.0 for the 3-story building without infill. For the 3-story building with infill, the spectral acceleration is selected at 0.4 s. While for 6-story building without infill the spectral acceleration is selected at 2.0 and 2.5 s for ductile and moderately ductile, respectively, ranges from 0.2 to 3.0 s. The spectral acceleration at 0.6 s is selected for a 6-story building with infill, with ranges from 0.2 to 1.0 s. As reported in Table 2, the dynamic fundamental period obtained for same building height is not constant as suggested in the code provision. It is also observed that the fundamental period of the infilled-RC frame decreases due to the presence of URM infill wall. According to Banik and Halder (2016) the fundamental period of the RF frame buildings not only depends on the building height, but the fundamental period also influenced by effective stiffness properties of structural members, bay width, number of bays and support conditions.

TABLE 2

Table 2. First three fundamental periods of 3− and 6− story RC MRF buildings.

Ground Motion Selection

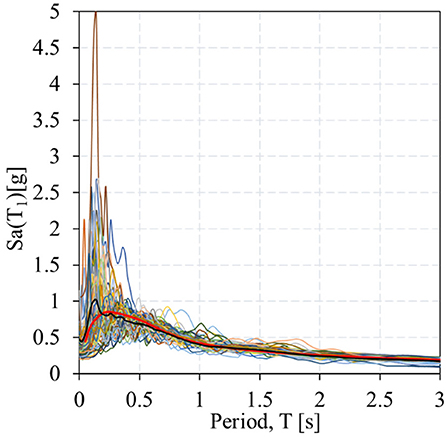
The RC buildings located in Vancouver, BC, Canada was considered due to its location and population and significant seismic activities (Onur et al., 2005; Atkinson and Goda, 2011). The selected building site consisting of very dense soil and soft rock site condition (Site class C) with the average shear-wave velocity in the upper 30 m (V_s30) between 360 and 760 m/s. S_a(T₁) of the buildings with 5% damping.

In order to perform the nonlinear dynamic analysis, a set of 50 ground motion records is selected based on the seismic hazard of interest. In this study, ground motion records were selected using the multiple conditions mean spectrum (CMS) method developed by Goda and Atkinson (2011). The selected ground motion records that follow same procedure reported in Tesfamariam et al. (2015) and (Tesfamariam and Goda (2015a,b), that considered three dominant sources of earthquake: shallow crustal, deep in-slab, and off-shore megathrust interface earthquakes type from the Cascadia subduction zone. Figure 5 shows an example of the ground motion records selected for 3S_D&MD_NI buildings with T₁ = 1.5 s.

FIGURE 5

Figure 5. Example of selected ground motion records for 3S_D&MD_NI (T₁ = 1.5 s).

Incremental Dynamic Analysis (IDA)

A series of nonlinear dynamic analyses is conducted through IDA to evaluate the seismic response and collapse fragility (Vamvatsikos and Cornell, 2002). The IDA was carried out based on multiple records of ground motions by increasing scale factor of each ground motion amplitude until cause sideways collapse. In this study, the IDA is implemented on eight RC MRF building models using 50 pairs of ground motion records selected based on the 2% PE in 50 years. Collapse is defined as the dynamic instability point when the maximum inter-story drift ratio of the buildings exceeds 0.10 (Haselton et al., 2007) and IDA curve transforms to horizontal line for each ground motion. The IDA curves provide a relationship between intensity measure level and maximum inter-story drift ratio.

In this assessment, collapse mechanisms due to column shear failure are not directly simulated in the analysis model. However, the columns are expected to experience critical shear failure when interacting with URM infill walls. Therefore, the shear critical failure modes, so-called non-simulated collapse mode, is evaluated by post-processing IDA result. In this process, force-based limit state check is applied to predict the median collapse drift ratio ($\widehat{\text{CDR}}$) at which critical shear failure will occur. The $\widehat{\text{CDR}}$ is defined using Equation (2) developed by Aslani and Miranda (2005),

$\begin{array}{ll}{\widehat{\text{C}\text{D}\text{R}}}_{\text{s}\text{h}\text{e}\text{a}\text{r}}=\frac{1}{ 0.26\left(\frac{\text{P}}{{\text{A}}_{\text{g}}{\text{f}}_{\text{c}}\prime {\text{ρ}}_{\text{sh}}}+25.4\right)}\ge \frac{1}{100}& (2)\end{array}$

where P is the axial load on the column, A_g is the gross cross-sectional area of the column, and ρ_sh is the transverse reinforcement ratio. The median CDR is calculated based on the properties of the column. The capacity of the deformation increases with decreasing axial load or more shear reinforcement.

Figures 6, 7 show IDA results for the 3- and 6-story RC MRF buildings. The circle marks on each IDA curve, in Figures 6C,D, 7C,D, shows the shear failure occurs predicted by Equation (2). For columns with ductile shear design and detailing, the predicted shear failure occurs at a $\widehat{\text{CDR}}$ between 0.0295 and 0.0339 rad, while for moderately ductile the predicted shear failure occurs at a $\widehat{\text{CDR}}$ between 0.0206 and 0.0275 rad. From the IDA results, the collapse fragility relationships, as described in the following section, are then developed to compute the median collapse capacity.

FIGURE 6

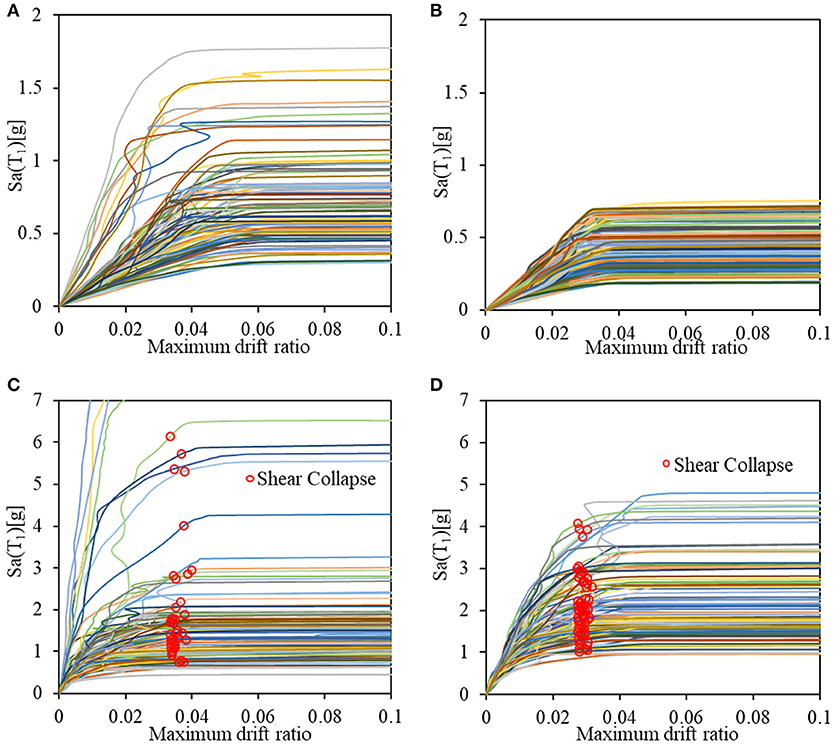
Figure 6. Incremental dynamic analysis curves for 3-story buildings; (A) 3S_D_NI, (B) 3S_MD_NI, (C) 3S_D_I, and (D) 3S_MD_I.

FIGURE 7

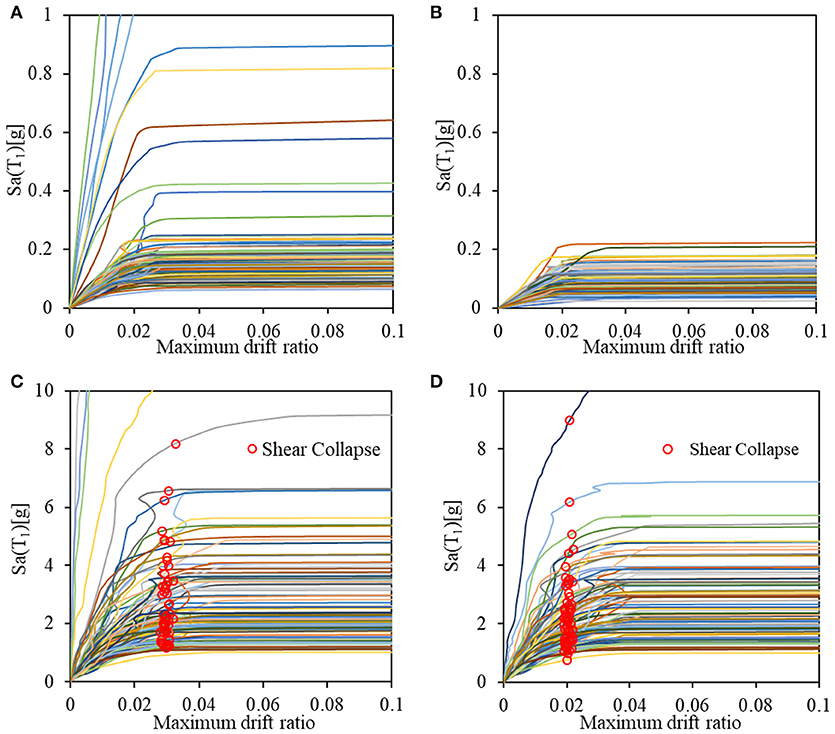
Figure 7. Incremental dynamic analysis curves for 6-story buildings; (A) 6S_D_NI, (B) 6S_MD_NI, (C) 6S_D_I, and (D) 6S_MD_I.

Collapse Fragility Assessment

Seismic collapse fragility curve shows the probabilistic relationship between the frequency of failure (collapse) of buildings and peak ground motion acceleration in an earthquake (Porter, 2017). In this study, a damage measure, which represents actual response of the building under seismic excitation, is based on maximum interstory drift (i.e., maximum interstory drift ratio is 0.1 for collapse). The collapse fragility curve that constructed based on the IDA results can be represented by a lognormal cumulative distribution function (Baker, 2015), as shown in Equation (3).

$\begin{array}{ll}\text{P}\left(\text{C| IM}=\text{x}\right)=\Phi \left(\frac{\text{ln }\left(\frac{\text{x}}{\mu }\right)}{\text{β}}\right)& (3)\end{array}$

where P(C|IM = x) is the probability that a ground motion with IM = x will cause the structure to collapse, Φ () is the standard normal cumulative distribution function, μ is the median of the fragility function and β is the standard deviation of lnIM (sometimes referred to as the dispersion of IM).

Figures 8A,B show the collapse fragility curves for 3- and 6-story RC MRF buildings derived from IDA and Equation (2). In this study, the collapse fragility assessment is also accounted for both record-to-record (RTR) variability and structural modeling (M) uncertainties for a comparison purposes. A modeling uncertainty of β_{ln, M} = 0.50 is assumed as suggested by Haselton and Deierlein (2007). The total uncertainty, β_{ln, Total} that account for both RTR and M is computed by using the square root of the sum of the squares (Equation 4),

$\begin{array}{ll}{\beta }_{\text{ln},\text{Total}}=\sqrt{{\beta }_{\text{l}\text{n},\text{R}\text{T}\text{R}}^2+{\beta }_{\text{l}\text{n},\text{M}}^2}& (4)\end{array}$

The dotted line is used to represent the RTR+M fragility curve. Figure 8 also illustrates the collapse fragility curve for RC MRF with and without consideration of shear failure, as shown by the solid and dashed curve, respectively.

FIGURE 8

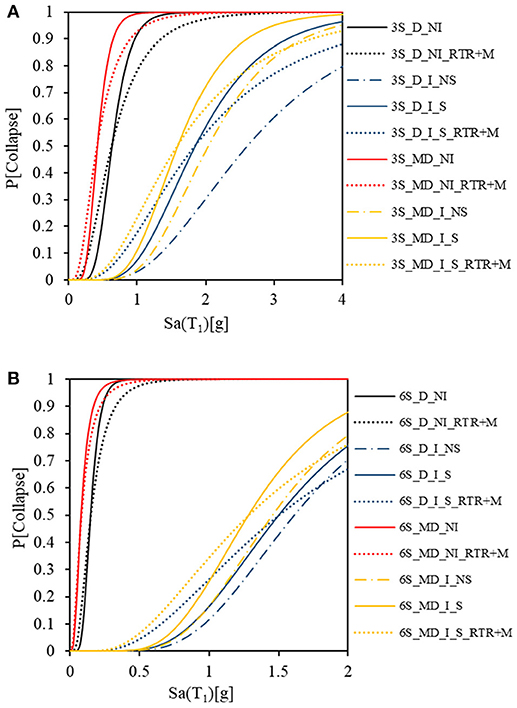
Figure 8. Fragility curves of (A) 3-story and (B) 6-story MRF RC frame with and without URM infill walls.

Based on these fragility curves, the collapse performance parameters, in terms of the median collapse capacity, can be obtained at the ground motion capacity with 50% of probability of reaching the collapse targets. The results in Figure 8 shows that the median collapse capacity for ductile bare RC MRF buildings ranging from 0.15 to 0.53 g, which is greater than the moderately ductile buildings varying from 0.08 to 0.41 g. Presence of URM infill walls on the RC MRF frame considered in this study increase the median collapse capacity by 66–90% and 74 and 94% for ductile and moderately ductile building, respectively, as compared to the bare RC MRF buildings. As shown in Figure 8, the collapse fragility capacity with consideration of shear failure significantly reduced by 8–30% compared to the sidesway collapse mechanism. Overall, the median collapse capacity decreases with increasing building height.

Median collapse capacity results are then expended to the evaluation of collapse median ratio (CMR). The CMR is evaluated by dividing the median collapse capacity of the structure by the ground motion intensity, S_MT. As recorded in Table 2, the ductile RC MRF buildings with and without URM infill walls induce higher CMR compared to moderately ductile RC MRF buildings, ranging from 0.65 to 2.25, and 0.45 to 1.92, respectively. Any CMR value that <1.0 indicates that the median collapse capacities are lower the S_MT and vice-versa.

Mean Annual Frequency of Collapse

The mean annual frequency of collapse in seismic risk assessment (Porter, 2017 and Ellingwood and Kinali, 2009) is given by:

$\begin{array}{ll}{\text{λ}}_{\text{c}}={\displaystyle {\int }_0^{\infty }}{\text{F}}_{\text{R}}(\text{x})\frac{\text{d}\text{H}(\text{x})}{\text{d}\text{x}}\text{d}\text{x}& (5)\end{array}$

where F_R(x) is the cumulative distribution function of seismic capacity of structural (collapse fragility curve), and dH(x) is the differential of the seismic hazard curve. Equation (5) can be expressed as

$\begin{array}{ll}{\text{λ}}_{\text{c}}=\sum \text{P}\left[\text{C}|\text{Q}=\text{x}\right]\text{P}\left[\text{Q}=\text{x}\right]& (6)\end{array}$

where P[Q = x] denote the seismic hazard and P[C|Q = x] represents the seismic fragility of a structure with collapse damage.

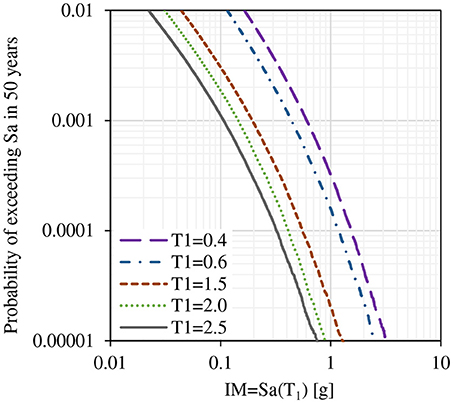
The ground motion hazard curves were selected at Vancouver, BC, Canada for site classification C and a period according to building model. Figure 9 shows the hazard curve for Vancouver at different periods.

FIGURE 9

Figure 9. Ground motion hazard curve for Vancouver for different periods on soil Class C.

The probability of collapse that will occur at least once in time, t (t = 50 years) is calculated using the following equation:

$\begin{array}{ll}\text{P}\left[\text{C in }t\text{ years}\right]=1-exp(-{\lambda }_c.t)& (7)\end{array}$

where λ_c is the expected value of collapse derived from Equation (5).

Seismic collapse assessment results for 3-and 6-story RC MRF buildings with and without URM infill walls, in terms of mean annual frequency of collapse and probability of collapse at 50 years, are reported in Table 3. Figure 10 shows the mean annual frequency of collapse of this study including results from different studies that used different code during seismic design process. Data in Table 3 also reported for both RTR and RTR+M uncertainties.

TABLE 3

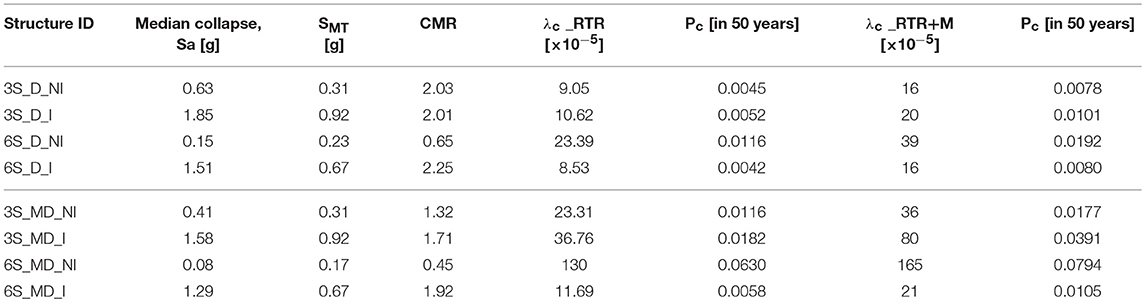
Table 3. Result of seismic collapse assessment for ductile and moderately ductile RC MRF with and without URM infill walls.

FIGURE 10

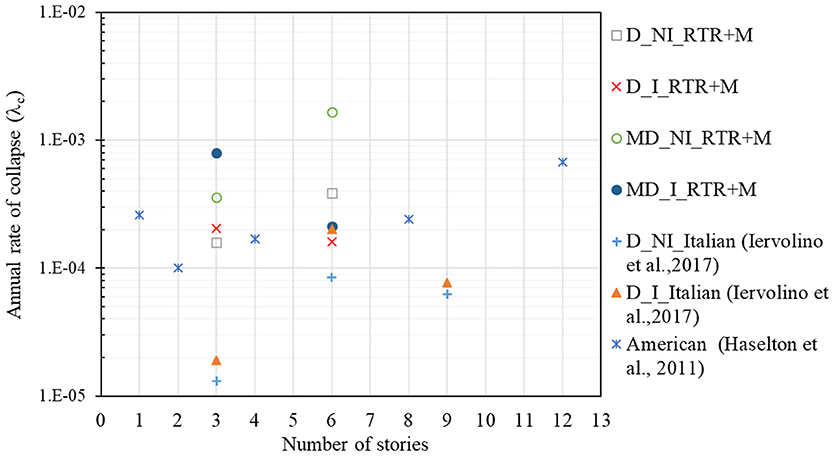
Figure 10. Mean annual frequency of collapse for ductile and moderately ductile RC MRF buildings with and without URM infill walls comparison with other building design codes.

As reported in Table 3 and illustrated in Figure 10, the mean annual frequency of collapse for ductile RC MRF buildings is between 16 and 39 × 10⁻⁵ with probability of collapse in 50 years ranging from 0.8 to 1.92%. For the moderately ductile RC MRF buildings, the calculated mean annual frequency of collapse is between 13 and 165 × 10⁻⁵ with probability of collapse in 50 years ranging from 1.05 to 7.94%. These results reveal that the seismic safety level is higher for the ductile RC MRF buildings than moderately ductile RC MRF buildings, due to the special detailing of reinforcement during design in increasing resistance for structural collapse.

Furthermore, this study also found that the 6-story bare RC MRF buildings have slightly higher mean annual frequency of collapse than the 3-story bare RC MRF building, which have ${\lambda }_c=39\text{ to }165\times {10}^{-5}$, corresponding to 1.92 to 7.94% probability of collapse in 50 years. This study observes that the increase in building height will increase the overall mass of the building that becomes dominant over the increase in the lateral stiffness. Moreover, this is due to lower spectral acceleration based on the hazard site for longer periods during building design stage, which in turn may affect the collapse capacity of the buildings.

Comparison of the bare RC MRF and RC MRF with URM infill walls buildings illustrates inconsistent results among infilled-RC MRF buildings. As observed, the 6-story RC MRF building with URM infill walls show lower collapse rate compared to the 6-story bare RC MRF buildings, ranging from 16 to 21 × 10⁻⁵. Whereas, the collapse rate of 3-story RC MRF with URM infill walls buildings are 20–80 × 10⁻⁵ illustrates higher collapse rate compared to the 3-story bare RC MRF buildings. The results of 6-story bare RC MRF buildings and 3-story RC MRF building with URM infill walls buildings are at least 2.5 and 1.2 times, respectively, to collapse compared to the 6-story RC MRF building with URM infill walls. Collapse performance of the RC MRF buildings with URM infill walls shows not uniform results may be effects of the geometric and material properties of the URM infill walls and surrounded frame. Besides, as the number of the stories increases, the inter-story drift ratios will be increased due to the increase in the building stiffness offered by the URM infill walls. Overall, this observation denotes that the RC MRF buildings with ductile design provide better collapse resistance and enhanced the safety of the buildings.

The results of mean annual frequency of collapse of ductile RC MRF buildings are further compared with studies conducted by Haselton et al. (2011) and Iervolino et al. (2017), whereby each building is designed based on different code provision that includes American code, and Italian code, respectively. For comparison purposes, the collapse assessment are evaluated by considering both record-to-record and modeling uncertainties. It can be observed that there is significant variation in the mean annual frequency of collapse for different designed buildings, which may due to the differences in design spectral, response reduction factors, site location, ground motion selection method, and structural configurations. As shown in Figure 10, RC frame building designed based on Canadian code have calculated mean annual rate of collapse between 1.6 and 3.9 × 10⁻⁴ whereas American code (Haselton et al., 2011) have calculated mean annual rate of collapse between 1 to 4.7 × 10⁻⁴. The mean annual rate of collapse for buildings designed based on Italian code ranging from 0.13 to 0.85 × 10⁻⁴. The range value of mean annual frequency of collapse for Canadian buildings is similar to the American buildings, which can considerably perceived to be within a reasonable range as reported in Haselton et al. (2011). In comparison, the buildings designed for Italian codes has significantly lower mean annual rate of collapse than the others buildings designed for Canadian and American codes. The decrease in collapse probability for Italian buildings is due to different response reduction factors during design process, site location and response history analysis. In addition, different approach to nonlinear dynamic analysis is adopted, where Canadian and American buildings assessed using IDA method whereas Italian buildings assessed using multiple stripe analysis method.

Discussion and Conclusion

This study evaluates the seismic collapse risk of two sets of code-conforming RC MRF buildings, considering ductile and moderately ductile design details, and with and without URM infill walls. The code-conforming RC MRF buildings were designed according to current Canadian seismic design code, NBCC 2010, and detailing, CSA A23.3-14. IDA method is used to perform nonlinear dynamic analysis. Collapse fragility relationships are developed from IDA results to represent the probability of building collapse as a function of ground motion intensity. The collapse mean annual frequency is determined by integrating seismic hazard and fragility function.

The results from this assessment identified that the mean annual frequency of collapse varied between 16 and 165 × 10⁻⁵ correspond to the collapse probabilities in 50 years from 1 to 7.9%. The ductile RC MRF buildings present better seismic collapse performance, for both 3- and 6- story buildings when compared to moderately ductile RC MRF buildings. These results are expected since the ductile RC MRF buildings are designed based on special reinforcement detailing with higher overstrength that importance to against structural collapse. It was observed that structural configuration may lead to different result of collapse probability at 50 years.

Seismic collapse assessments are also conducted to show the seismic performance over building height. Comparative studies between 3- and 6-story RC MRF buildings without infill demonstrate that as the building height increases, the calculated mean annual frequency of collapse is increases. This study would be useful to extend by investigating the influence of soil-structure interaction (SSI) effect, which this effect also may contribute to collapse risk. The collapse response is expected to be different for RC frame with SSI effect between building height and structural systems because the flexibility of the soil foundation reduces the overall stiffness of the structures that lead to expanding in the fundamental period of the system.

This study also investigated the influence of URM infill walls on the seismic collapse risk of buildings. A comparative study of this building system shows that the RC MRF buildings with URM infill walls are capable to resist higher ground motion of intensities. However, there is an inconsistency in term of collapse rate, whereby the 6-story RC MRF buildings have higher collapse rate when compared among the buildings considered. The presence of infill walls, in terms of material and geometric characteristic, and number of building story are considered as the main factors associated with these outcomes. A more comprehensive study of URM infill wall is recommended to enhance understanding on the overall contribution of infill wall to collapse safety by considering both in-plane and out-of-plane URM infill walls effect.

This study further compares the mean annual frequency of collapse of ductile RC MRF buildings for different codes. It has been observed that the RC MRF buildings designed by Canadian code is in reasonable range of collapse risk for buildings. Further, there is significant variation in the mean annual frequency of collapse of the building designed for Italian codes.

The results presented in this paper only focused on the low- to mid-rise buildings. However, the results obtained from this study are helpful to comprehend seismic safety level of current Canadian buildings. This study can be extended by considering the SSI effect and both in-plane and out-of-plane URM infill walls effect to obtain better understanding on the overall seismic collapse performance of buildings in Canada.

Author Contributions

NMN carried out this research under the supervision of ST.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The first author wishes to thank the financial support by Ministry of Higher Education (MoHE) Malaysia and study leave provided by Universiti Teknologi MARA (UiTM), Malaysia to undertake this research work at The University of British Columbia. The authors acknowledge the financial support through the Natural Sciences an Engineering Research Council of Canada (RGPIN-2014-05013) under the Discovery Grant programs.

References

Aslani, H., and Miranda, E. M. (2005). Probabilistic Earthquake Loss Estimation and Loss Disaggregation in Buildings. Blume TR 157, Stanford University, Palo Alto, CA.

Google Scholar

Asteris, P. G., Cavaleri, L., Di Trapani, F., and Sarhosis, V. (2016). A macro-modelling approach for the analysis of infilled frame structures considering the effects of openings and vertical loads. Struct. Infrastr. Eng. 12, 551–566. doi: 10.1080/15732479.2015.1030761

CrossRef Full Text | Google Scholar

Atkinson, G. M., and Goda, K. (2011). Effects of seismicity models and new ground motion prediction equations on seismic hazard assessment for four Canadian cities. Bull. Seismol. Soc. Am. 101, 176–189. doi: 10.1785/0120100093

CrossRef Full Text | Google Scholar

Baker, J. W. (2015). Efficient analytical fragility function fitting using dynamic structural analysis. Earthq. Spec. 31, 579–599. doi: 10.1193/021113EQS025M

CrossRef Full Text | Google Scholar

Banik, A., and Halder, L. (2016). Period formula for reinforced concrete buildings with infill walls. Appl. Mech. Mat. 857, 177–182. doi: 10.4028/www.scientific.net/AMM.857.177

CrossRef Full Text | Google Scholar

Burton, H., and Deierlein, G. (2013). Simulation of seismic collapse in non-ductile reinforced concrete frame buildings with masonry infills. J. Struct. Eng. 140:A4014016. doi: 10.1061/(ASCE)ST.1943-541X.0000921

CrossRef Full Text | Google Scholar

Chrysostomou, C. Z. (1991). Effects of Degrading Infill Walls on the Nonlinear Seismic Response of Two-Dimensional Steel Frames. Ph.D. dissertation, Department of Civil and Environmental Engineering, Cornell University, Ithaca, NY.

Chrysostomou, C. Z., Gergely, P., and Abel, J. F. (2002). A six-strut model for nonlinear dynamic analysis of steel infilled frames. Int. J. Struct. Stab. Dyn. 2, 335– 353. doi: 10.1142/S0219455402000567

CrossRef Full Text | Google Scholar

Crisafulli, F. J., and Carr, A. (2007). Proposed macro-model for the analysis of infilled frame structures. Bull. N. Z. Soc. Earthq. Eng. 40, 69–77.

Google Scholar

CSA (2014). Canadian Standards Association Design of Concrete Structures. CSA Standard Update Service. CSAA23.3-14. Mississauga, ON, Canada.

Decanini, L. D., Liberatore, L., and Mollaioli, F. (2014). Strength and stiffness reduction factors for infilled frames with openings. Earthq. Eng. Eng. Vib. 13, 437–454. doi: 10.1007/s11803-014-0254-9

CrossRef Full Text | Google Scholar

DeVall, R. (2003). Background information for some of the proposed earthquake design provisions for the 2005 edition of the National Building Code of Canada. Can. J. Civ. Eng. 30, 279–286. doi: 10.1139/l02-048

CrossRef Full Text | Google Scholar

Ellingwood, B. R., and Kinali, K. (2009). Quantifying and communicating uncertainty in seismic risk assessment. Struct. Safety 31, 179–187. doi: 10.1016/j.strusafe.2008.06.001

CrossRef Full Text | Google Scholar

Elwood, K. J. (2004). Modelling failures in existing reinforced concrete columns. Can. J. Civ. Eng. 31, 846–859. doi: 10.1139/l04-040

CrossRef Full Text | Google Scholar

Elwood, K. J., Matamoros, A. B., Wallace, J. W., Lehman, D. E., Heintz, J. A., Mitchell, A. D., et al. (2007). Update to ASCE/SEI 41 concrete provisions. Earthq. Spec. 23, 493–523. doi: 10.1193/1.2757714

CrossRef Full Text | Google Scholar

FEMA-P695 (2009). Recommended Methodology for Quantification of Building System Performance and Response Parameters. FEMA P695A, Prepared by the Applied Technology Council, Redwood, CA.

Goda, K., and Atkinson, G. M. (2011). Seismic performance of wood-frame houses in South-Western British Columbia. Earthq. Eng. Struct. Dyn. 40, 903–924. doi: 10.1002/eqe.1068

CrossRef Full Text | Google Scholar

Haselton, C. B., and Deierlein, G. G. (2007). Assessing Seismic Collapse Safety of Modern Reinforced Concrete Frame Buildings. PEER Report 2007/08, PEER Center, University of California, Berkeley, CA.

Haselton, C. B., Liel, A. B., Deierlein, G. G., Dean, B. S., and Chou, J. H. (2011). Seismic collapse safety of reinforced concrete buildings. I: Assessment of ductile moment frames. J. Struct. Eng. 137, 481–491. doi: 10.1061/(ASCE)ST.1943-541X.0000318

CrossRef Full Text | Google Scholar

Haselton, C. B., Liel, A. B., Taylor Lange, S., and Deierlein, G. G. (2007). Beam-Column Element Model Calibrated for Predicting Flexural Response Leading to Global Collapse of RC Frame Buildings. PEER Report 2007/03. PEER Center, University of California, Berkeley, CA.

Google Scholar

Ibarra, L. F., Medina, R. A., and Krawinkler, H. (2005). Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn. 34, 1489–1511. doi: 10.1002/eqe.495

CrossRef Full Text | Google Scholar

Iervolino, I., Spillatura, A., and Bazzurro, P. (2017). “RINTC Project: assessing the (implicit) seismic risk of code-conforming structures in Italy,” in 6th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering COMPDYN 2017 (Rhodes Island).

Google Scholar

Jeon, J. S., Park, J. H., and DesRoches, R. (2015). Seismic fragility of lightly reinforced concrete frames with masonry infills. Earthq. Eng. Struct. Dyn. 44, 1783–1803. doi: 10.1002/eqe.2555

CrossRef Full Text | Google Scholar

Kam, W. Y., Pampanin, S., Dhakal, R. P., Gavin, H., and Roeder, C. W. (2010). Seismic performance of reinforced concrete buildings in the September 2010 Darfield (Canterbury) earthquakes. Bull. N. Z. Soc. Earthq. Eng. 43, 340–350. Available online at: http://hdl.handle.net/10092/9006

Google Scholar

Klingner, R. E., and Bertero, V. V. (1978). Earthquake resistance of infilled frames. J. Struct. Div. 104, 973–989.

Google Scholar

Koopaee, M. E., Dhakal, R. P., and MacRae, G. A. (2017). Effect of ground motion selection methods on seismic collapse fragility of RC frame buildings. Earthq. Eng. Struct. Dyn. 46, 1875–1892. doi: 10.1002/eqe.2891

CrossRef Full Text | Google Scholar

Mehrabi, A. B., Benson Shing, P., Schuller, M. P., and Noland, J. L. (1996). Experimental evaluation of masonry-infilled RC frames. J. Struct. Eng. 122, 228–237. doi: 10.1061/(ASCE)0733-9445(1996)122:3(228)

CrossRef Full Text | Google Scholar

Mitchell, D., Tremblay, R., Karacabeyli, E., Paultre, P., Saatcioglu, M., and Anderson, D. L. (2003). Seismic force modification factors for the proposed 2005 edition of the National Building Code of Canada. Can. J. Civ. 30, 308–327. doi: 10.1139/l02-111

CrossRef Full Text | Google Scholar

NBCC (2010). National Building Code of Canada National Research Council of Canada. Ottawa, ON.

Noh, N. M., Liberatore, L., Mollaioli, F., and Tesfamariam, S. (2017). Modelling of masonry infilled RC frames subjected to cyclic loads: state of the art review and modelling with OpenSees. Eng. Struct. 150, 599–621. doi: 10.1016/j.engstruct.2017.07.002

CrossRef Full Text | Google Scholar

Onur, T., Ventura, C. E., and Finn, W. L. (2005). Regional seismic risk in British Columbia — damage and loss distribution in Victoria and Vancouver. Can. J. Civ. Eng. 32, 361–371. doi: 10.1139/l04-099

CrossRef Full Text | Google Scholar

OpenSees (2009). Open System for Earthquake Engineering Simulation Pacific Earthquake Engineering Research Center. University of California, Berkeley, CA. Available online at: http://opensees.berkeley.edu/

Paulay, T., and Priestley, M. J. N. (1992). Seismic Design of Reinforced Concrete and Masonry Buildings. New York, NY: John Wiley doi: 10.1002/9780470172841

CrossRef Full Text | Google Scholar

Porter, K. (2017). A Beginner's Guide to Fragility, Vulnerability, and Risk. Denver, CO: University of Colorado Boulder, 1–101.

Porter, K. A. (2016). Safe enough? A building code to protect our cities and our Lives. Earthq. Spec. 32, 677–695. doi: 10.1193/112213EQS286M

CrossRef Full Text | Google Scholar

Priestley, M. J. N., and Calvi, G. M. (1991). Towards a capacity-design assessment procedure for reinforced concrete frames. Earthq. Spec. 7, 413–437. doi: 10.1193/1.1585635

CrossRef Full Text | Google Scholar

Sattar, S., and Liel, A. B. (2016a). Seismic performance of nonductile reinforced concrete frames with masonry infill walls— I: development of a Strut Model Enhanced by Finite Element Models. Earthq. Spec. 32, 795–818. doi: 10.1193/90914EQS139M

CrossRef Full Text | Google Scholar

Sattar, S., and Liel, A. B. (2016b). Seismic performance of nonductile reinforced concrete frames with masonry infill walls—II: collapse assessment. Earthq. Spec. 32, 819–842. doi: 10.1193/091514EQS141M

CrossRef Full Text | Google Scholar

Sezen, H., and Moehle, J. P. (2004). Shear strength model for lightly reinforced concrete columns. J. Struct. Eng. 130, 1692–1703. doi: 10.1061/(ASCE)0733-9445(2004)130:11(1692)

CrossRef Full Text | Google Scholar

Smith, B. S. (1967). Methods for predicting the lateral stiffness and strength of multi-storey infilled frames. Build. Sci. 2, 247–257. doi: 10.1016/0007-3628(67)90027-8

CrossRef Full Text | Google Scholar

Stavridis, A., Koutromanos, I., and Shing, P. B. (2012). Shake-table tests of a three-story reinforced concrete frame with masonry infill walls. Earthq. Eng. Struct. Dyn. 41, 1089–1108. doi: 10.1002/eqe.1174

CrossRef Full Text | Google Scholar

Stylianidis, K. C. (2012). Experimental investigation of masonry infilled RC frames. Open Constr. Build. Technol. J. 6, 194–112. doi: 10.2174/1874836801206010194

CrossRef Full Text | Google Scholar

Tesfamariam, S., and Goda, K. (2015a). Seismic performance evaluation framework considering maximum and residual inter-story drift ratios: application to non-code conforming reinforced concrete buildings in Victoria, BC, Canada. Front. Built Environ. 1:18. doi: 10.3389/fbuil.2015.00018

CrossRef Full Text | Google Scholar

Tesfamariam, S., and Goda, K. (2015b). Loss estimation for non-ductile reinforced concrete building in Victoria, British Columbia, Canada: effects of mega-thrust Mw9-class subduction earthquakes and aftershocks. Earthq. Eng. Struct. Dyn. 44, 2303–2320. doi: 10.1002/eqe.2585

CrossRef Full Text | Google Scholar

Tesfamariam, S., Goda, K., and Mondal, G. (2015). Seismic vulnerability of reinforced concrete frame with unreinforced masonry infill due to main shock- aftershock earthquake sequences. Earthq. Spec. 31, 1427–1449. doi: 10.1193/042313EQS111M

CrossRef Full Text | Google Scholar

Vamvatsikos, D., and Cornell, A. C. (2002). Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 31, 491–514. doi: 10.1002/eqe.141

CrossRef Full Text | Google Scholar

Zhao, B., Taucer, F., and Rossetto, T. (2009). Field investigation on the performance of building structures during the 12 May 2008 Wenchuan earthquake in China. Eng. Struct. 31, 1707–1723. doi: 10.1016/j.engstruct.2009.02.039

CrossRef Full Text | Google Scholar