- 1Department of Architecture and Architectural Engineering, Graduate School of Engineering, Kyoto University, Kyoto, Japan
- 2Faculty of Design and Architecture, Kyoto Institute of Technology, Kyoto, Japan
An equi-spaced consecutive impulse input is treated as a simplified representative for a long-duration earthquake ground motion. The key property of such input can be captured approximately by using harmonic waves. An approximate closed-form solution is derived for the elastic-plastic response of a two-degree-of-freedom (2DOF) system under the “critical multiple impulse input” based on some assumptions. The 2DOF system is assumed to consist of an elastic-perfectly plastic restoring-force characteristic in the first story and a linear elastic restoring-force characteristic in the second story. The fact that only the free vibration emerges under such multiple impulse input enables the utilization of the energy approach in the derivation of the explicit expression for a complicated elastic-plastic response. The critical timing of the impulses is found to correspond to the zero restoring-force timing in the first story. The validation and accuracy check of the proposed theory are conducted by implementing the response analysis to the corresponding sinusoidal input as a representative of the long-duration earthquake ground motion. It is also demonstrated that the proposed theory can be applied to a base-isolated building with hysteretic property in the base-isolation story regardless of the number of stories of superstructures.
Introduction
Long-period, long-duration earthquake ground motions, which were not expected in the structural design of super high-rise buildings in 1970s, were observed during Mexico earthquake in 1985, Tokachi-oki earthquake in 2003, Chuetsu earthquake in 2004 and Tohoku earthquake in 2011 (Takewaki et al., 2011, 2012). Many seismic damages due to these earthquakes were observed. The ground motions with predominant period of about 2 s continued for more than 2 min during Mexico earthquake in 1985, and around 15-story buildings were collapsed by these long-period and long-duration ground motions (Beck and Hall, 1986). Oil storage tanks at Tomakomai were damaged by the sloshing phenomenon caused by the long-period ground motions during Tokachi-oki earthquake in 2003 (Hatayama et al., 2004; Aoi et al., 2008). In the 2004 Chuetsu earthquake, the long-period ground motions with the duration of more than 5 min were observed in Tokyo 150–200 km away from the epicenter, and elevator cables in high-rise buildings were damaged by the resonance with the long-period ground motions (Furumura and Hayakawa, 2007). Rather recently remarkable long-period, long-duration ground motions were observed in Tokyo and Osaka far from the epicenter during the Tohoku earthquake in 2011, and vibrations of high-rise buildings in Tokyo and Osaka continued for more than 10 min. Therefore, it is necessary to investigate the resonance phenomenon of high-rise buildings and base-isolation buildings to such long-period, long-duration ground motions. Repeated earthquake ground motions are another kind of long-duration input (Amadio et al., 2003; Fragiacomo et al., 2004). However, this kind of ground motions is not treated here.
Various researches on the steady-state response of elastic-plastic structures have been conducted since 1960s (Caughey, 1960a,b; Iwan, 1961, 1965a,b; Roberts and Spanos, 1990; Liu, 2000). Caughey (1960a) derived a resonance curve of a single-degree-of-freedom (SDOF) bilinear hysteretic system by using the equivalent linearization method based on a least squares approximation and Iwan (1961, 1965a) derived the exact solution for the steady-state response of an SDOF bilinear hysteretic system with a positive post-yield stiffness ratio under the harmonic wave and the square wave. Since his expression includes the transcendental equations, it is necessary to obtain the resonance curve numerically with repetition. Furthermore, an approximate theory for the steady-state response of 2-degree-of-freedom (2DOF) bilinear hysteretic system was derived by Iwan (1961, 1965b). However, it may be difficult to deal with the steady state of 2DOF bilinear hysteretic systems because of a difficulty in the iterative procedure for a complicated system with phase lag and a number of parameters to be considered in the transcendental equations. On the other hand, the transformation method of the one-cycle sinusoidal wave and the 1.5 cycle sinusoidal wave, which represent the main parts of the fling-step input (fault-parallel component) and the forward-directivity input (fault-normal component) of the near-fault ground motion, to double and triple impulses has been introduced and the closed-form solutions for the critical elastic-plastic responses under the double impulse and triple impulse have been derived by Kojima and Takewaki (2015a,b, 2016) and Kojima et al. (2017). The theory using the double impulse was extended to a 2DOF elastic-perfectly plastic system by Taniguchi et al. (2016), but only an expression for the upper bound of the critical elastic-plastic response was derived by taking into account the phase lag between the two masses of the system. A multiple impulse input has also been introduced as a substitute for a multi-cycle sinusoidal wave representing the main part of a long-period and long-duration ground motion, and a closed-form expression has been derived for the steady-state response of an SDOF elastic-perfectly plastic and bilinear hysteretic systems under the critical multiple impulse by Kojima and Takewaki (2015c, 2017). It has been demonstrated that the elastic-plastic response under such multiple impulse can be expressed by the continuation of free vibrations and a closed-form solution for the plastic deformation amplitude under the critical multi impulse can be obtained by using the energy balance law without solving the equation of motion directly.
In this paper, a closed-form solution for the critical steady-state response of an undamped SDOF elastic-perfectly plastic system under the critical multi impulse is extended to a 2DOF system and a closed-form expression is derived for the critical steady-state response of an undamped 2DOF elastic-perfectly plastic system under a multiple impulse as a good substitute for the long-duration ground motions. Furthermore, the critical non-linear response is investigated for a base-isolated building under such long-duration ground motion by using the proposed closed-form solution for the 2DOF system. The closed-form solution for the elastic-plastic response under the critical multi impulse can be obtained by introducing the approximation based on the results by time-history response analysis because it is difficult to derive the critical elastic-plastic response of the undamped 2DOF system by the energy balance law due to the phase lag of two masses. In this paper, the structural model is restricted to a simple model without viscous damping and the plastic deformation is concentrated in the first story. This is because the present paper proposes an analytical explicit approach for 2DOF models for the first time and it is intended to concentrate on a simple model. The steady state in which each impulse acts at the zero-restoring force timing in the first story is also assumed. The multiple impulse is introduced in section Multiple impulse input as substitute for long-duration ground motions. Then an approximate closed-form solution is derived in section Approximate closed-form solution for elastic-plastic steady-state response under critical multi impulse. The validity and accuracy of the approximations introduced here is investigated by time-history response analysis in section Verification of accuracy of approximation in steady state by time-history response analysis. The accuracy of the approximate closed-form solution is also investigated in section Numerical example and accuracy check of proposed closed-form solution through comparison with time-history response analysis result. The validity of the critical timing of the multiple impulse assumed in this paper is confirmed by time-history response analysis for the 2DOF elastic-perfectly plastic system under the multi impulse with various impulse time intervals in section Validity of critical timing. The proposed approximate solution is applied to base-isolated buildings in section Application of approximate closed-form solution to base-isolated building. Conclusions are summarized in section Conclusions.
It was found in the previous paper (Takewaki et al., 2017) that, when a 2DOF base-isolated building is transformed into an SDOF system and a closed-form solution for the critical elastic-plastic response of the SDOF system is applied to obtain the maximum deformation of the base-isolation story, it is necessary to select a transformation method from the two candidates, i.e., (i) the rigid super-structure approximation (low or middle-rise buildings), (ii) the series-spring approximation after ignorance of the base-isolation story mass (high-rise buildings), depending on the number of stories of the building. In contrast, the method proposed in this paper do not need to select the transformation methods and it enables a unified evaluation of the maximum deformation of the base-isolated story regardless of the number of stories. This advantage is an innovative point of the proposed method.
Multiple Impulse Input as Substitute for Long-Duration Ground Motions
Kojima and Takewaki (2015c, 2017) introduced the multiple impulse as a substitute for the multi-cycle sinusoidal wave representing the main part of long-duration ground motions (Takewaki and Tsujimoto, 2011). The multi impulse with the equal time interval, as shown in Figure 1, is expressed by the following equation.
where V is the given velocity allocated to masses or a mass by each impulse (the input velocity level), t0 is the time interval between two consecutive impulses, N is the number of impulses and δ(t) is the Dirac delta function. Considering the rising phase, the input velocity level of the first impulse is adjusted to 0.5 V. The ground acceleration, velocity and displacement of the multi impulse and the corresponding multi-cycle sinusoidal wave, which represents a long-duration ground motion, are shown in Figure 1A. It can be confirmed that the multiple impulse is a good approximate of the corresponding sinusoidal wave even in the form of velocity and displacement. To compare the response under the multiple impulse with that under the multi-cycle sinusoidal wave, it is important to adjust the input level of two inputs. The input levels of the multiple impulse and the multi-cycle sinusoidal wave are adjusted based on the equivalence of the maximum Fourier amplitude. The adjustment method is shown in the previous paper (Kojima and Takewaki, 2015c, 2017).
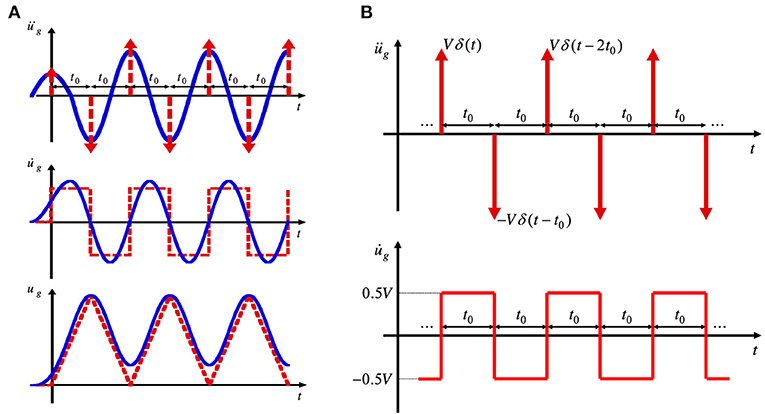
Figure 1. Multiple impulse and sine wave, (A) Correspondence of acceleration, velocity and displacement, (B) Acceleration and velocity of multiple impulse (Kojima and Takewaki, 2015c, 2017).
The Fourier transform of üg(t) of the multiple impulse can be derived as
Approximate Closed-Form Solution for Elastic-Plastic Steady-State Response Under Critical Multi Impulse
Undamped Two-Degree-Of-Freedom (2DOF) Elastic-Perfectly Plastic System
Consider a 2DOF system with the elastic-perfectly plastic restoring force-interstory drift characteristic only in the first story. The second story is assumed to be linear elastic. Let mi and ki denote the i-th story mass and stiffness, respectively. ui, di and fi denote the displacement of the i-th mass relative to the ground, the interstory drift of the i-th story and the restoring force in the i-th story, respectively. dy1 and fy1 = k1dy1 denote the yield deformation and the yield force, respectively, in the first story.
Steady-State Response Under Critical Multiple Impulse
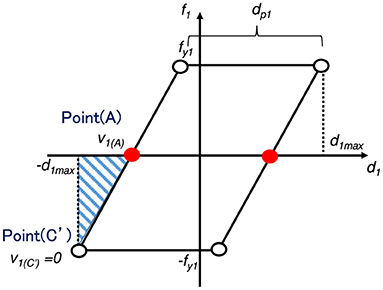
A steady-state response under the critical multiple impulse is assumed in which each impulse acts at the zero restoring-force timing in the first story. dp1 is the plastic deformation amplitude in the first story in the steady state. The critical multiple impulse means the impulse which maximizes dp1 for variable timing of impulses under a constant input velocity level V. The purpose of this paper is to obtain a closed-form solution for the plastic deformation amplitude dp1 in the first story under the critical multiple impulse. Figure 2 shows the steady state with the point symmetry in the restoring force-interstory drift relation. It is noted that dp1 is not affected by the existence of the residual deformation.
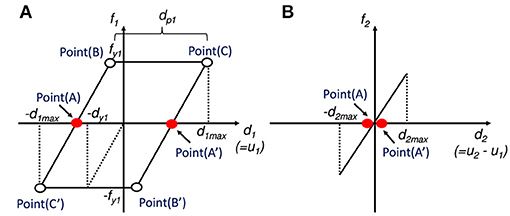
Figure 2. Transition points in first-story restoring force-interstory drift relation and second-story restoring force-interstory drift relation together with multiple impulse timing, (A) Restoring force-interstory drift relation in first story, (B) Restoring force-interstory drift relation in second story.
The following transition points are defined in the restoring force-interstory drift relation in the first story in the steady state.
Point (A): the acting point of each impulse at the zero restoring-force timing.
Point (B): the yielding point in the first story.
Point (C): the point attaining the maximum deformation d1max in the first story (the zero velocity point).
Points (A′), (B′), and (C′) in Figure 2 are defined to be point symmetric to the Points (A), (B), and (C). ui(A), vi(A), di(A) and i(A) denote the displacement of the mass in the i-th story relative to the ground, the velocity of the mass in the i-th story relative to the ground, the interstory drift of the i-th story, and the interstory velocity in the i-th story at Point (A), respectively. The relative displacement, the relative velocity, the interstroy drift and the inetrstory velocity in the i-th story at Points (B) and (C) are denoted by ui(B), vi(B), di(B), i(B) and ui(C), vi(C), di(C), i(C).
Approximation of Steady-State Response Based on Time-History Response Analysis Result
Kojima and Takewaki, 2015a,b,c derived the closed-form expressions for the critical elastic-plastic response under the double, triple and multi impulse by using the energy balance law between the acting point of each impulse and the point attaining the maximum deformation (the zero velocity point). However, it seems difficult to derive such closed-form solution for the elastic-plastic response of the 2DOF system under the critical multi impulse only by using the energy balance law due to the phase lag between two masses of the 2DOF system. To overcome this difficulty, the following four approximations are introduced to derive an approximate closed-form expression for the plastic deformation amplitude in the steady state. The following approximations are based on the time-history response analysis result, in which each impulse acts at the zero restoring-force timing in the first story.
Approximation (a): It is assumed that, between Point (C′) and Point (A), two energy balance laws hold independently in the first story and second story. The kinetic energy of the first-story mass at the zero restoring-force timing [Point (A)] just before the input of the impulse is equal to the elastic strain energy in the first story corresponding to the yield deformation at Point (C′), and the following approximate equation holds.
Approximation (b): It is assumed that the restoring force of the second story also becomes zero at Point (A), at which the restoring force of the first story, is zero and the following approximate equation holds.
Approximation (c): It is assumed that the interstory drift in the second story at Point (B), at which the interstory drift in the first story just attains the yield deformation, is zero and the following approximate equation holds.
Approximation (d): It is assumed that the velocity of the second story mass at Point (B) is equal to the velocity of the second story mass at Point (A) just after the input of each impulse. This assumption indicates the fact that the time interval between Point (A) and Point (B) is short and the amount of change of the deformation in the second story is small. The following approximate equation holds due to Approximation (d).
Approximate Closed-Form Expression for Steady-State Response of 2DOF Elastic-Perfectly Plastic System Under Critical Multiple Impulse
An approximate closed-form solution for the plastic deformation amplitude dp1 in the first story of the 2DOF elastic-perfectly plastic system under the critical multi impulse is derived by using the energy balance law and Approximations (a)–(d). The restoring force-interstory drift relations in the first and second stories in the steady state are shown in Figure 3.
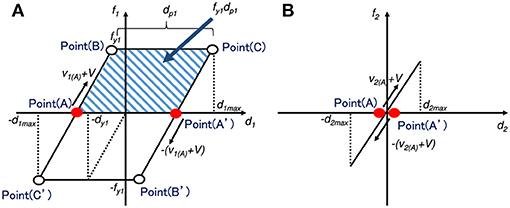
Figure 3. First- and second-story restoring force-interstory drift relations for evaluating the maximum deformation, (A) Restoring force-interstory drift relation in first story, (B) Restoring force-interstory drift relation in second story.
The energy balance law between Point (A) just after the input of each impulse and Point (A′) as shown in Figure 3 is obtained as follows.
The left-hand side of Equation (7) indicates the sum of the kinetic energy of each story mass and the elastic strain energy of the second story at Point (A) just after the input of each impulse. The right-hand side of Equation (7) indicates the sum of the kinetic energy of each mass at Point (A′), the elastic strain energy of the second story and the energy dissipated by the plastic deformation of the first story shown by the blue shaded area in Figure 3A.
In order to derive the plastic deformation amplitude dp1 in the first story in the steady state from Equation (7), it is necessary to obtain the velocities of v1(A) and v2(A) of the first- and second-story masses at Point (A). The derivation process of v1(A) and v2(A) is explained in below sections.
Velocity v1(A) of First-Story Mass at Point (A)
The velocity v1(A) of the first-story mass at Point (A) can be obtained approximately by using Approximation (a) () as follows.
where .
Velocity v2(A) of Second-Story Mass at Point (A)
The velocity v2(A) of the second-story mass at Point (A) is obtained next. The energy balance law between Point (C′) and Point (A) can be expressed by
The left-hand side of Equation (9) expresses the sum of the kinetic energy computed by the velocity v2(C) of the second-story mass at Point (C′) and the elastic strain energy of each story. On the other hand, the right-hand side of Equation (9) indicates the sum of the kinetic energies computed by the velocities v1(A) and v2(A) of the first- and second-story masses at Point (A) and the elastic strain energy in the second story. The following approximate equation can be obtained by substituting Equation (3) from Approximation (a) and Equation (4) from Approximation (b) into Equation (9).
Since the velocity v1(C) of the first-story mass is zero at Point (C) at which the first-story mass attains the maximum deformation, the velocity of the second-story mass is expressed by v2(C) = v1(C) + 2(C) = 2(C) and Equation (10) can be transformed into the following equation.
Consider the equations of motion for the free vibration between Point (B) and Point (C). At first,2(C), d2(C) are derived to obtain the velocity v2(A). The first story is in the loading stage (the plastic deformation stage) between Point (B) and Point (C). The equations of motion between Point (B) and Point (C) is expressed by
The following equation can be derived from Equations (12, 13) and d2 = u2 − u1.
where . The interstory drift and the interstory velocity in the second story at Point (B) are expressed by d2(B), 2(B) (= v2(B) − v1(B)), respectively, and the following equations can be obtained.
Equations (15) and (16) can be transformed into the following equations by introducing Approximation (c) (d2(B) ≃ 0).
where D1, D2, θ1 in Equations (17) and (18) are expressed by
The sum of the kinetic energy computed by the velocity of the second-story mass and the elastic strain energy in the second story at Point (C) is denoted by E, at which the first-story mass attains the maximum deformation. By substituting Equations (17) and (18) into Equation (11), E can be expressed by
where tBC denotes the time interval between Point (B) and Point (C).
Taniguchi et al. (2016) proved that the critical timing of the second impulse in the double impulse for a 2DOF system is the zero restoring-force timing in the first story. This is based on the theory that the increment of the kinetic energy by the second impulse is maximized at the critical timing. This critical timing is equal to the timing at which the sum of momentum of each story mass after the input of the second impulse is maximized. In this paper, for the multiple impulse input, the zero restoring-force timing in the first story is assumed as the critical timing of each impulse and the sum of momenta of the masses in the first and second stories (m1v1(A)+m2v2(A)) is also assumed to become the maximum at the critical timing. The validity of this assumption will be examined in Appendix. To obtain v2(A) which maximizes the sum of momenta of two masses just before the input of each impulse, it is also assumed that the sum of the kinetic energy and elastic strain energy E in the steady state is maximized at Point (C).
From Equation (22), the following equation can be obtained.
By substituting Equations (19) and (20) into Inequality (23), v2(A) maximizing the sum of the momenta of the first- and second-story masses can be obtained by using the following equation.
The interstory velocity 2(B) in the second story at Point (B) is expressed as follows by using v2(B) = v1(B) + 2(B) and Approximation (d) (v2(B) ≃ v2(A) + V).
Then v1(B) is derived to obtain v2(A) from Equations (24) and (25). The energy balance law between Point (A) and Point (B) can be expressed by
The left-hand side of Equation (26) expresses the sum of the kinetic energies of the masses at Point (A) just after the input of each impulse and the elastic strain energy in the second story. The right-hand side of Equation (26) expresses the sum of the kinetic energies of the masses and the first- and second-story elastic strain energies at Point (B). The following approximate equation can be obtained by substituting Equations (4), (5) and (6) obtained from Approximations (b), (c) and (d) into Equation (26).
Finally v1(B) can be obtained approximately from Equation (27).
By substituting Equations (25) and (28) into Equation (24), the following approximate equation can be obtained.
From Equation (29), v2(A) can be derived as follows.
Approximate Closed-Form Solution for Plastic Deformation Amplitude dp1 in Steady State
The plastic deformation amplitude dp1 can be derived from Equation (7).
By substituting the velocity v1(A) of the first-story mass and the velocity v2(A) of the second-story mass at Point (A), obtained approximately in sections Velocity v1(A) of mass of second story at Point (A) and Velocity v2(A) of mass of second story at Point (A), into Equation (31), the plastic deformation amplitude dp1 can be obtained approximately.
Verification of Accuracy of Approximation in Steady State by Time-History Response Analysis
The validity and accuracy of Approximations (a)–(d) introduced in section Approximate closed-form solution for elastic-plastic steady-state response under critical multi impulse are verified by using the time-history response analysis. These approximations are based on the time-history response analysis result and the parameters of the 2DOF system used for the time-history response analysis are set as follows. The masses in the first and second stories are , the fundamental natural period is T1 = 1.0[sec] and the ratio of the first-story stiffness to the second-story stiffness is k1 : k2 = 2 : 1. Therefore, the stiffnesses of the first and second stories are and . The yield deformation and the yield force in the first story are dy1 = 0.01[m] and , respectively. In this and following sections, each impulse acts at the zero restoring-force timing in the first story until the response converges to a steady state in the time-history response analysis in estimating the steady-state response. The validity of this method is investigated in section Validity of impulse timing. The time of computation in the time-history response analysis is 100[s] in order for the response to converge to a steady state and the time history response analysis results after 95[s], at which responses are sufficiently converged to a steady state, are shown in Figure 4. Although the closed-form solution of the 2DOF elastic-perfectly plastic system is derived in this paper, 0.001 × k1 as a post-yield stiffness of the first story is used in the time-history response analysis to make the steady-state maximum deformation in the first story point-symmetric with respect to the origin. The time increment is Δt = 1.0 × 10−3[sec].
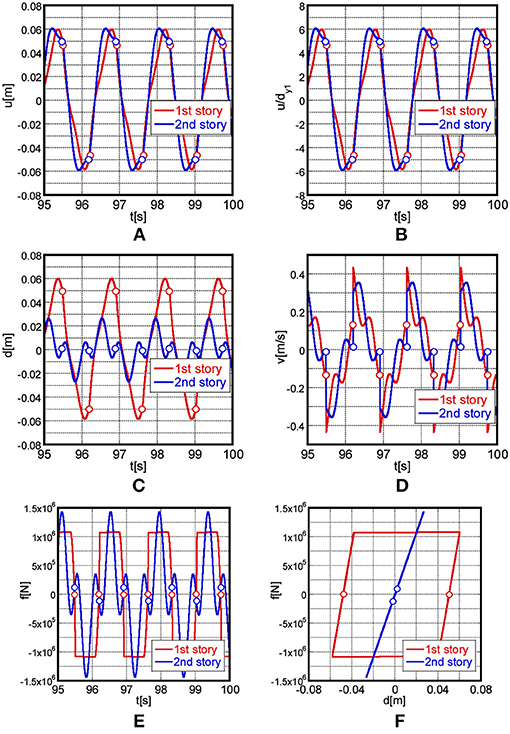
Figure 4. Time-history response of 2DOF elastic-perfectly plastic system under critical multiple impulse with V = 0.3 [m/s] by time-history response analysis, (A) Relative horizontal displacement, (B) Relative horizontal displacement (normalized by dy1), (C) Interstory drift, (D) Relative horizontal velocity, (E) Restoring force, (F) Restoring force-interstory drift relation.
Figures 4A–F show the time histories of the relative horizontal displacement, the relative horizontal displacement normalized by dy1, interstory drift, relative horizontal velocity, restoring force and restoring force-interstory drift relation in the first and second stories under the multi impulse with the input velocity level V = 0.3[m/sec] obtained by the time-history response analysis.
Approximation (a)
The validity of Approximation (a) is investigated first. Figure 5 shows a schematic diagram of the restoring force-interstory drift relation in the first story under the critical multi impulse. It is assumed that two energy balance laws hold independently in the first and second stories between Point (C′) and Point (A), and the kinetic energy of the first-story mass at Point (A) is equal to the elastic strain energy in the first story corresponding to the yield deformation at Point (C′). Figure 6 shows the comparison of the velocity v1(A) of the first-story mass at Point (A) obtained from Approximation (a) and that obtained by the time-history response analysis. It can be observed that v1(A) by Approximation (a) is a good approximate of the velocity v1(A) of the first-story mass at Point (A) as shown in Figure 6 and v1(A) can be obtained approximately by Equation (8).
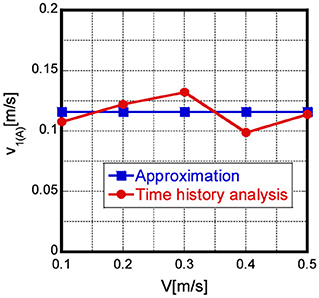
Figure 6. Comparison of velocity v1(A) of first-story mass at Point (A) derived from Approximation (a) and that obtained by time-history response analysis.
Approximation (b)
In this section, it is investigated whether the restoring force in the second story is approximately zero at the zero restoring-force timing in the first story. Figure 7 shows the time histories between Point (A) and Point (A′) of the restoring force in the first and second stories under the multiple impulse with the input velocity level V = 0.1, 0.3[m/sec] evaluated by the time-history response analysis. In Figure 7, it can be observed that the restoring force in the second story is almost zero at the zero restoring-force timing in the first story and d2(A) ≃ 0 can be derived.
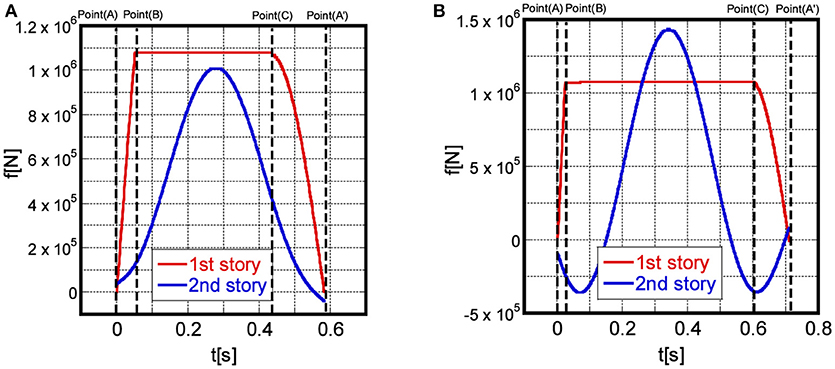
Figure 7. Time histories between Point (A) and Point (A′) of restoring force of first and second stories under critical multiple impulse with V=0.1, 0.3[m/s], (A) V=0.1[m/s], (B) V=0.3[m/s].
Approximation (c)
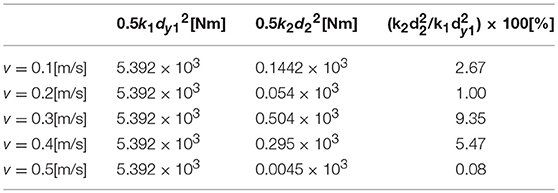
The validity of Approximation (c) is investigated next. It is assumed that the interstory drift at Point (B) is almost zero and the interstory drift in the second story at Point (B) is d2(B) ≃ d2(A) ≃ 0. This is because the time interval between Point (A) and Point (B) is small. In order to check the accuracy of Approximation (c), it is investigated that the elastic strain energy in the second story at Point (B) is sufficiently smaller than that in the first story at Point (B). The comparisons of the elastic strain energies in the first and second stories at Point (B) evaluated by the time-history response analysis for V = 0.1, 0.2, 0.3, 0.4, 0.5[m/sec] are summarized in Table 1. It can be observed from Table 1 that the elastic strain energy in the second story at Point (B) is sufficiently smaller than that in the first story at Point (B), and d2(B) ≃ 0 can be used in the derivation of an approximate closed-form solution for the steady-state response.
Approximation (d)
It is checked here that the velocity v2(B) of the second-story mass at Point (B) is approximately equal to the velocity of the second-story mass at Point (A) just after the input of each impulse. This is also based on the fact of the short time interval between Point (A) and Point (B). Figure 8 shows the time histories, between Point (A) and Point (A′), of the velocity of the second-story mass under the multiple impulse with the input velocity level V = 0.1, 0.3[m/sec] obtained by the time-history response analysis. It can be observed from Figure 8 that the velocity v2 of the second-story mass does not change much between Point (A) and Point (B), and therefore v2(B) ≃ v2(A) + V.
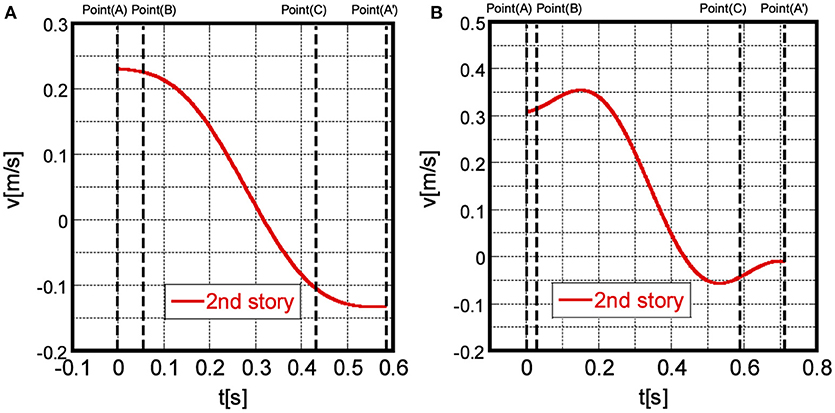
Figure 8. Time histories between Point (A) and Point (A′) of velocity of second-story mass under critical multiple impulse with V = 0.1, 0.3 [m/sec], (A) V = 0.1 [m/sec], (B) V = 0.3 [m/sec].
Numerical Example and Accuracy Check of Proposed Closed-Form Solution Through Comparison With Time-History Response Analysis Result
The accuracy of the approximate closed-form solution for the plastic deformation amplitude dp1 in the first story under the critical multiple impulse is verified through the comparison with that by the time-history response analysis. The fundamental natural period of the 2DOF system used in the time-history response analysis is T1 = 1.0[sec], the yield deformation in the first story is dy1 = 0.01[m], and the ratios of the masses and stiffnesses in the first and second stories are varied as follows (9 models).
(a) m1 : m2 = 1 : 1, k1 : k2 = 2 : 1 (m1 = m2 = 800 × 103[kg],
k1 = 1.0783 × 108[N/m], k2 = 5.3915 × 107[N/m])
(b) m1 : m2 = 1 : 1, k1 : k2 = 1 : 1 (m1 = m2 = 800 × 103[kg],
k1 = k2 = 8.2685 × 107[N/m])
(c) m1 : m2 = 1 : 1, k1 : k2 = 1 : 2 (m1 = m2 = 800 × 103[kg],
k1 = 7.2033 × 107[N/m], k2 = 1.4407 × 108[N/m])
(d) m1 : m2 = 1 : 2, k1 : k2 = 2 : 1 (m1 = 800 × 103[kg],
m2 = 1600 × 103[kg], k1 = 2.0125 × 108[N/m], k2 = 1.0063
× 108[N/m])
(e) m1 : m2 = 1 : 2, k1 : k2 = 1 : 1 (m1 = 800 × 103[kg],
m2 = 1600 × 103[kg], k1 = k2 = 1.4407 × 108[N/m])
(f) m1 : m2 = 1 : 2, k1 : k2 = 1 : 2 (m1 = 800 × 103[kg],
m2 = 1600 × 103[kg], k1 = 1.1787 × 108[N/m],
k2 = 2.3574 × 108[N/m])
(g) m1 : m2 = 2 : 1, k1 : k2 = 2 : 1 (m1 = 1600 × 103[kg],
m2 = 800 × 103[kg], k1 = 1.2633 × 108[N/m], k2 = 6.3165
× 107[N/m])
(h) m1 : m2 = 2 : 1, k1 : k2 = 1 : 1 (m1 = 1600 × 103[kg],
m2 = 800 × 103[kg], k1 = k2 = 1.0783
× 108[N/m])
(i) m1 : m2 = 2 : 1, k1 : k2 = 1 : 2 (m1 = 1600 × 103[kg],
m2 = 800 × 103[kg], k1 = 1.0063 × 108[N/m], k2 = 2.0125
× 108[N/m])
As shown before, each impulse acts at the zero restoring-force timing in the first story until the response converges to a steady state in the time-history response analysis to estimate the steady-state response assumed in section Approximate closed-form solution for elastic-plastic steady-state response under critical multi impulse. The steady state in which each impulse acts at the zero restoring-force timing in the first story is assumed in this section, and the validity of this assumption is investigated in next section. The plastic deformation amplitude is obtained by subtracting 2dy1 from the sum of the absolute values of the positive and negative maximum deformations after the response converges to the steady state.
Comparison of Proposed Closed-Form Solution and Time-History Response Analysis Result
Figures 9A–I (left-side) show the comparison between the approximate solution for the plastic deformation amplitude dp1 of models (a)-(i) under the critical multiple impulse with respect to the input velocity level V = 0.1, 0.2, 0.3, 0.4, 0.5[m/sec], and dp1 calculated by the time-history response analysis. It can be observed that the approximate solution can simulate the steady-state response under the critical multiple impulse with reasonable accuracy as an upper bound of the time-history response analysis result.
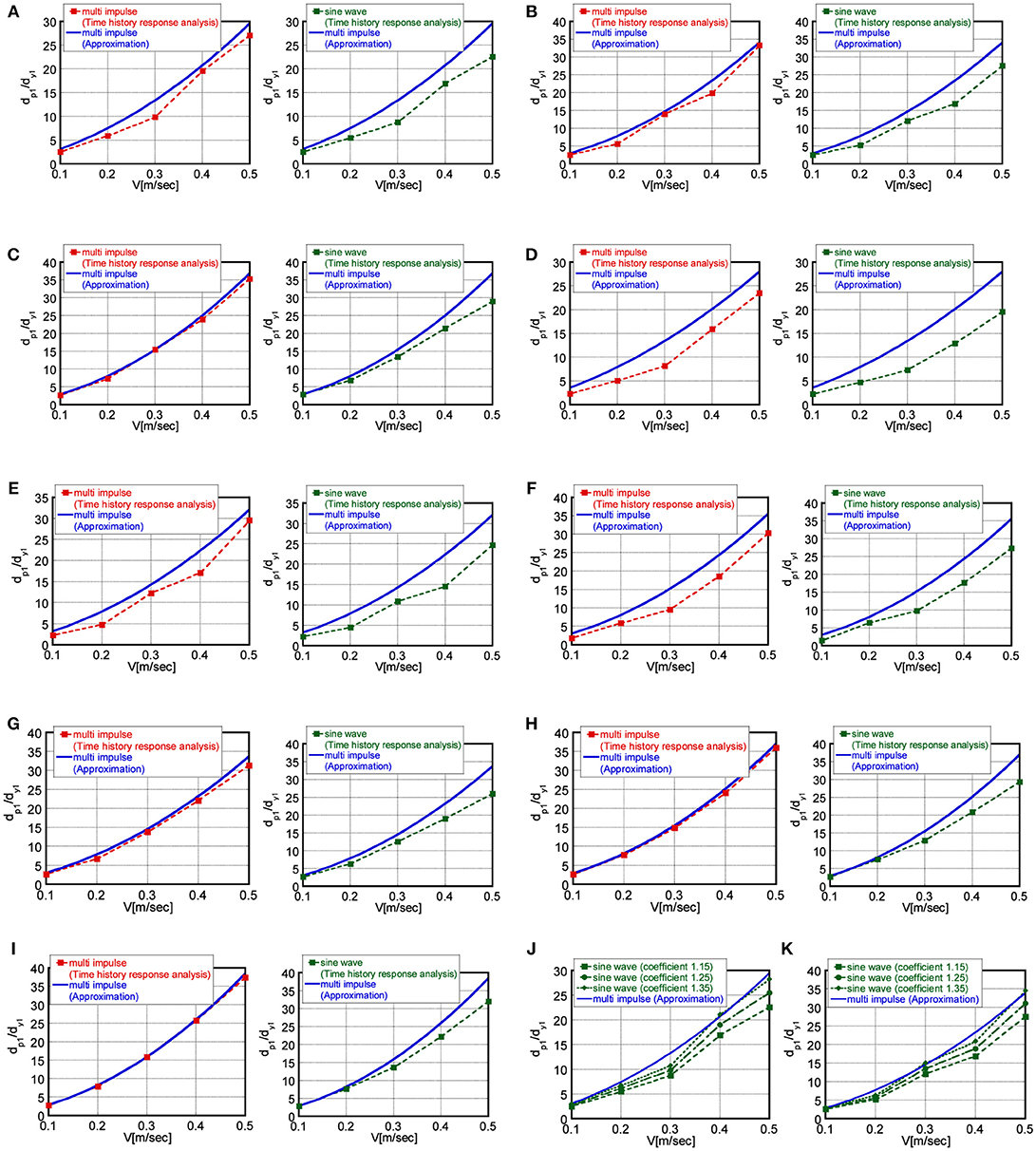
Figure 9. Comparison of plastic deformation amplitude under critical multiple impulse (approximate solution and time-history response analysis) and that under corresponding multi-cycle sinusoidal wave (time-history response analysis); (A) m1 : m2 = 1 : 1, k1 : k2 = 2 : 1, (B) m1 : m2 = 1 : 1, k1 : k2 = 1 : 1, (C) m1 : m2 = 1 : 1, k1 : k2 = 1 : 2, (D) m1 : m2 = 1 : 2, k1 : k2 = 2 : 1, (E) m1 : m2 = 1 : 2, k1 : k2 = 1 : 1, (F) m1 : m2 = 1 : 2, k1 : k2 = 1 : 2, (G) m1 : m2 = 2 : 1, k1 : k2 = 2 : 1, (H) m1 : m2 = 2 : 1, k1 : k2 = 1 : 1, (I) m1 : m2 = 2 : 1, k1 : k2 = 1 : 2, (J) m1 : m2 = 1 : 1, k1 : k2 = 2 : 1 (coefficient 1.15, 1.25, 1.35), (K) m1 : m2 = 1 : 1, k1 : k2 = 1 : 1 (coefficient 1.15, 1.25, 1.35).
Accuracy Check by Time-History Response Analysis Under Corresponding Multi-Cycle Sinusoidal Wave
The steady-state response under the critical multiple impulse is compared with the steady-state response under the corresponding multi-cycle sinusoidal wave to investigate the accuracy in using the multiple impulse as a substitute for the multi-cycle sinusoidal wave representing the main part of a long-duration earthquake ground motion.
The period Tl (the circular frequency ωl = 2π/Tl) of the corresponding multi-cycle sinusoidal wave is specified as Tl = 2t0, where t0 is the time interval between two consecutive impulses in the steady state evaluated by the time-history response analysis in section Comparison of proposed closed-form solution and time-history response analysis result. The acceleration amplitude Al of the corresponding multi-cycle sinusoidal wave is amplified by 1.15 after it is adjusted so that the maximum Fourier amplitude of the multi-cycle sinusoidal wave is equal to that of the multiple impulse. This adjustment method has been proposed for the SDOF elastic-perfectly plastic system in the previous paper (Kojima and Takewaki, 2015c). The procedure of using the equivalence of the maximum value of the Fourier amplitude of acceleration seems reasonable because the Fourier amplitude of acceleration means the velocity-related quantity of the input and is closely related to the input energy which plays a crucial role in the energy balance law in the proposed method. In addition, the coefficient 1.15 was introduced in the previous work (Kojima and Takewaki, 2015c) for fitting the maximum response amplitudes between the multiple impulse and the corresponding multi-cycle sine wave. This means that the adjustment property holds even in the 2DOF model with the same coefficient even though the plastic deformation is restricted only to the first story. The time incremental is Δt = 1.0 × 10−3[sec] and the number of cycles is 200 in the time-history response analysis.
Figures 9A–I (right-side) show the comparison between the plastic deformation amplitude dp1 of models (a)-(i) under the critical multiple impulse and that under the corresponding multi-cycle sinusoidal wave. It can be observed that the closed-form solution of the plastic deformation amplitude under the critical multiple impulse is an upper bound of that under the corresponding multi-cycle sinusoidal wave with reasonable accuracy. Although dp1 under the critical multiple impulse is relatively larger than that under the corresponding multi-cycle sinusoidal wave in the range V > 0.3[m/sec], this is due to the adjustment method. The multiplier 1.15 in the adjustment method has been set so that the plastic deformation amplitude of the SDOF elastic-perfectly plastic system under the critical multiple impulse corresponds to that under the multi-cycle sinusoidal wave in the range of normalized input velocity level V/Vy < 3. It is necessary to change the multiplier for adjustment in the larger range of V, in order to upgrade the correspondence between the steady-state response under the multiple impulse and that under the multi-cycle sinusoidal wave. For example, Figures 9J,K present the influence of the coefficient (1.15, 1.25, 1.35) multiplied on the multi-cycle sine wave. Figure 9J shows the comparison of the plastic deformation amplitude dp1 of model (a) and Figure 9K illustrates that of model (b). It can be observed that this coefficient influences much on the response and, as the coefficient becomes larger toward 1.35, the response under the magnified multi-cycle sine wave approaches to the plastic deformation amplitude under the critical multiple impulse. However, it should be noted that the fitting coefficient depends on the structural model and the input level. It should also be mentioned again that the coefficient 1.15 gives the upper bound of the response under the magnified multi-cycle sine wave in all structural models and in all input levels treated here.
Validity of Critical Timing
In this paper, it is assumed that the critical timing is the zero restoring-force timing in the first story and an approximate solution is derived. The validity of the critical timing is investigated in this section through the comparison with the result by the time-history response analysis in which each impulse acts at the zero restoring-force timing as in sections Verification of accuracy of approximation in steady state by time-history response analysis and Numerical example and accuracy check of proposed closed-form solution in comparison with time history response analysis result.
Verification by Time-History Response Analysis
The critical time interval is evaluated by varying the time interval t0 of the multiple impulse with constant input velocity level in the time-history response analysis. The plastic deformation amplitude is obtained by subtracting 2dy1 from the sum of the absolute values of the positive and negative maximum deformations after the response converges sufficiently to the steady state. The time incremental is [sec] and the number of impulses is 200 in the time-history response analysis. The time interval of the multiple impulse is varied with the increment of 0.005 s.
Figure 10 shows the comparison of the time interval calculated in section Comparison of proposed closed-form solution and time-history response analysis result and the critical time interval calculated in this section with respect to the input velocity level. The time intervals calculated by two methods correspond fairly well except for the case with V = 0.3[m/sec]. Figure 11 presents the restoring force-interstory drift relation in the first story under the multiple impulse with V = 0.3[m/sec] and t0 = 0.910[sec], which is the critical multiple impulse calculated by varying the time interval. The blank circles in Figure 11 show the impulse timing in the steady state, and it can be observed that each impulse acts at the zero restoring-force timing in the first story. Therefore, the zero restoring-force timing in the first story is a necessary condition for the critical multiple impulse for the 2DOF elastic-perfectly plastic system. It was also found that there are several time intervals which maximize the plastic deformation amplitude. Further investigation will be necessary.
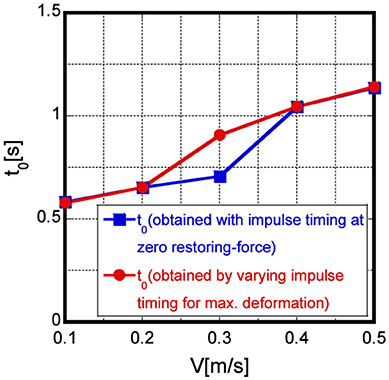
Figure 10. Comparison of critical time intervals for input level calculated with impulse timing at zero restoring force and varied for maximum deformation [Model (a)].
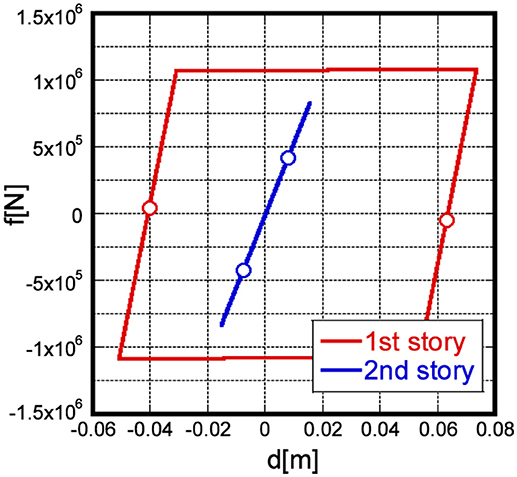
Figure 11. Restoring force-interstory drift of model (a) under multiple impulse with V = 0.3[m/sec] and t0 = 0.910[sec] maximizing dp1.
Figures 12A–I (left-side) show the comparison of the plastic deformation amplitude dp1 of models (a)-(i) obtained by the proposed approximate solution and that under the critical multiple impulse calculated by varying the time interval so as to maximize the plastic deformation amplitude. It can be observed from Figure 12 that the approximate solution can evaluate the plastic deformation amplitude dp1 in the first story under the critical multiple impulse with reasonable accuracy.
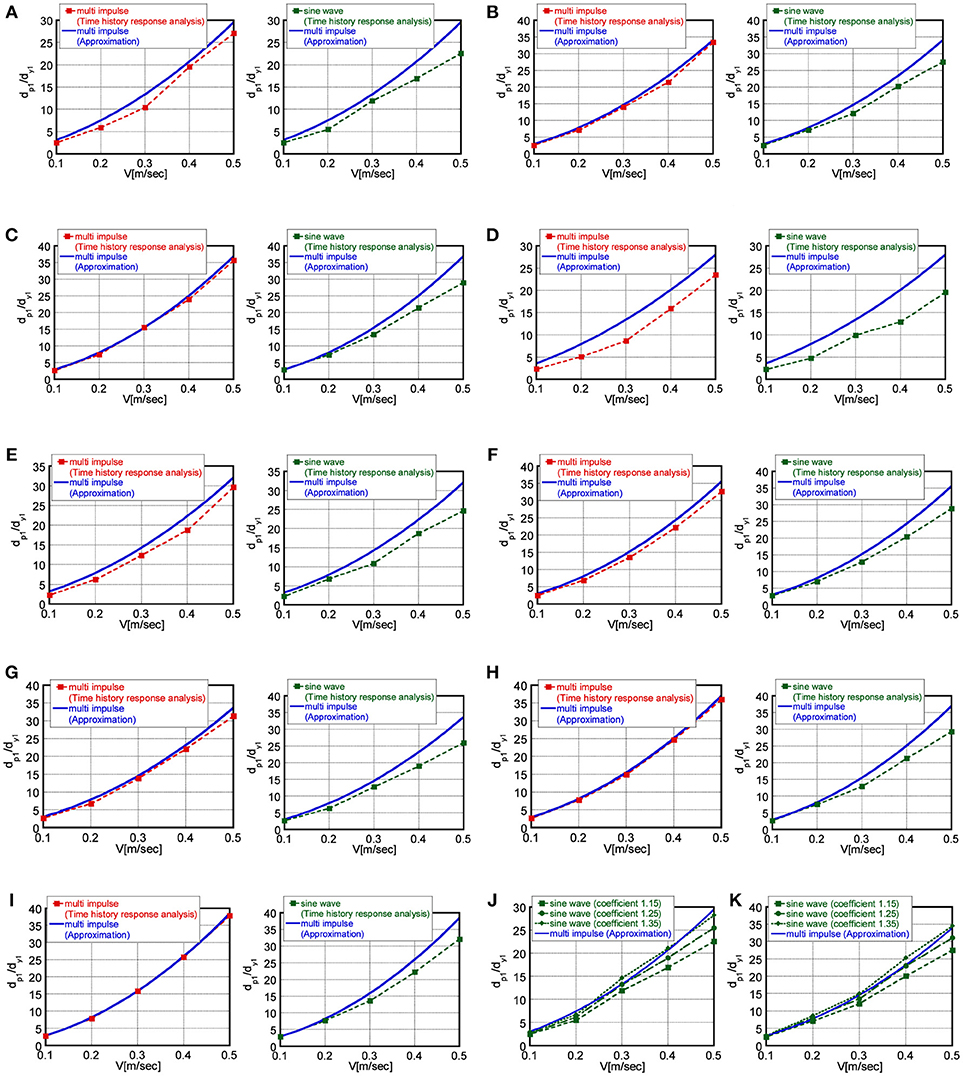
Figure 12. Comparison among plastic deformation amplitude under critical multiple impulse by approximate solution, that under critical multiple impulse calculated by varying time interval (time history response analysis) and that under corresponding multi-cycle sinusoidal wave (time history response analysis); (A) m1 : m2 = 1 : 1, k1 : k2 = 2 : 1, (B) m1 : m2 = 1 : 1, k1 : k2 = 1 : 1, (C) m1 : m2 = 1 : 1, k1 : k2 = 1 : 2, (D) m1 : m2 = 1 : 2, k1 : k2 = 2 : 1, (E) m1 : m2 = 1 : 2, k1 : k2 = 1 : 1, (F) m1 : m2 = 1 : 2, k1 : k2 = 1 : 2, (G) m1 : m2 = 2 : 1, k1 : k2 = 2 : 1, (H) m1 : m2 = 2 : 1, k1 : k2 = 1 : 1, (I) m1 : m2 = 2 : 1, k1 : k2 = 1 : 2, (J) m1 : m2 = 1 : 1, k1 : k2 = 2 : 1 (coefficient 1.15, 1.25, 1.35), (K) m1 : m2 = 1 : 1, k1 : k2 = 1 : 1 (coefficient 1.15, 1.25, 1.35).
Although the method used in sections Verification of accuracy of approximation in steady state by time-history response analysis and Numerical example and accuracy check of proposed closed-form solution in comparison with time-history response analysis result sometimes cannot calculate the critical steady-state response (this method sometimes calculates the local maximum value of dp1), the approximate closed-form solution can always evaluate the maximum steady-state elastic-plastic response under the critical multiple impulse.
Comparison of Steady-State Response Under Critical Multiple Impulse and That Under Corresponding Multi-Cycle Sinusoidal Wave
Figures 12A–I (right-side) show the comparison of the plastic deformation amplitude dp1 of models (a)-(i) under the critical multiple impulse obtained by the proposed approximate solution and that under the corresponding multi-cycle sinusoidal wave. The period of the multi-cycle sinusoidal wave is twice of the critical time interval calculated by varying the time interval in the previous section so as to maximize the plastic deformation amplitude. It can be observed from Figures 12A–I (right-side) that the approximate solution for the plastic deformation amplitude under the critical multiple impulse is an upper bound of that under the corresponding multi-cycle sinusoidal wave. Figures 12J,K present the influence of the coefficient (1.15, 1.25, 1.35) multiplied on the multi-cycle sine wave which were discussed in Figures 9J,K. Figure 12J shows the comparison of the plastic deformation amplitude dp1 of model (a) and Figure 12K illustrates that of model (b). It can be observed, as in Figures 9J,K, that this coefficient influences much on the response. In addition, as the coefficient becomes larger toward 1.35, the response under the magnified multi-cycle sine wave approaches to the plastic deformation amplitude under the critical multiple impulse. However, it should be remarked that the fitting coefficient depends on the structural model together with the input level and the coefficient 1.15 gives the upper bound of the response to the multi-cycle sine wave in all structural models and in all input levels treated here.
Application of Approximate Solution to Base-Isolated Building
The approximate closed-form solution for the plastic-deformation amplitude in the first story derived in section Approximate closed-form solution for elastic-plastic steady-state response under critical multi impulse is applied to base-isolated buildings with non-linear isolator.
Consider a base-isolated building which consists of an N-story superstructure and a non-linear base-isolation story. m0, k0, dy0 denote the mass, stiffness and yield deformation in the base-isolation story. The base-isolation story is assumed to consist of lead rubber bearings (or steel dampers and laminated natural rubber bearings), and modeled by a shear spring with an elastic-perfectly plastic restoring-force characteristic. The elastic-perfectly plastic restoring-force characteristic is used as the restoring-force characteristic in the base-isolation story here, although it is generally necessary to pay attention to the post-yield stiffness of the steel damper in the base-isolation story. The mass of each story in the superstructure is 200[ton] and the total mass of the superstructure is 200 × N[ton]. The stiffness in each story is determined so that the fundamental natural period of the superstructure with fixed base is 0.1 × N[sec]. The distribution of story stiffnesses is assumed to be the trapezoid distribution and the ratio of the stiffness of the bottom story to that of the top story is 2. The superstructure is assumed to be linear as in most of base-isolated buildings. The mass m0 of the base-isolation story is 600[ton], the stiffness k0 of the base-isolation story is set so that the fundamental natural period of the rigid superstructure on the base-isolation story is T1 = 1.0[sec], and the yield deformation of the base-isolation story is dy0 = 0.03[m].
Figure 13 shows the procedure for transforming the original base-isolated building into a 2DOF system. First, the original system is transformed into a three-degree-of-freedom (3DOF) system consisting of the base-isolated story, the upper half of the superstructure and the lower half of the superstructure. The superstructure is modeled by the two-degree-of-freedom system here to consider the higher mode of high-rise buildings. denote the mass and stiffness of the lower half of the superstructure and denote the mass and stiffness of the upper half of the superstructure. are set to 200 × 0.5N[ton], respectively. On the other hand, is determined based on the equivalence of the fundamental natural period and the fundamental natural mode. In order to obtain , the method reducing the multi-degree-of-freedom system into the lower multi-degree-of-freedom system based on the inverse formulation is used (Suzuki et al., 2009). Furthermore, the 3DOF system is transformed into the equivalent 2DOF system by neglecting the mass in the base-isolation story and considering the stiffnesses of the base-isolation story and the lower half of the superstructure as the series spring. The mass, stiffness and yield deformation in the first story of the equivalent 2DOF system are denoted by , respectively, and ke, dye can be obtained by
The proposed approximate solution for the steady-state response is applied to the equivalent 2DOF system, and the plastic-deformation amplitude of the base-isolation story can be obtained.
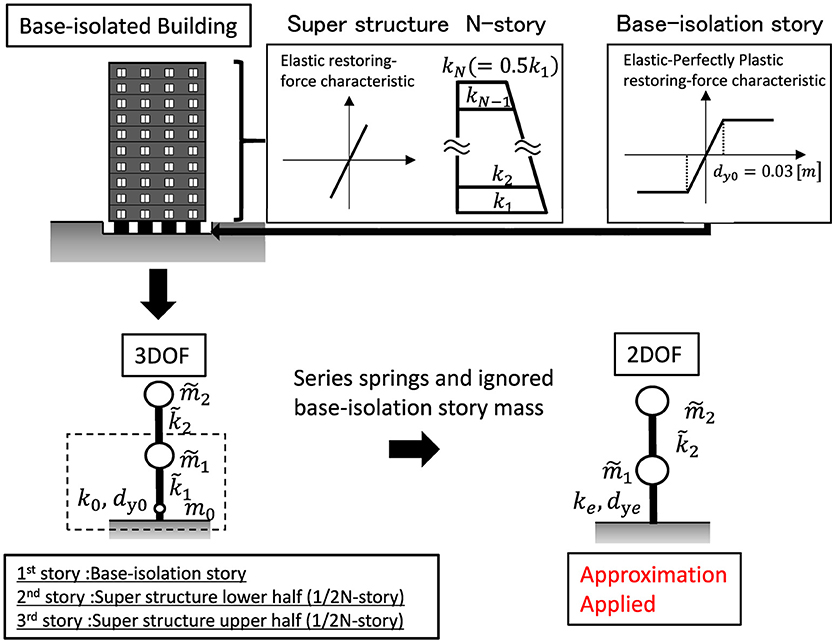
Figure 13. Procedure for transforming original base-isolated buildings into 2DOF elastic-perfectly plastic system.
Figure 14 shows the comparison of the plastic deformation amplitude in the base-isolation story by the proposed approximate solution for the equivalent 2DOF system and that by time-history response analysis for the original base-isolated building, for N = 10, 20, 30, 40. It can be observed from Figure 14 that the proposed method by using the equivalent 2DOF model and the approximate solution can evaluate the plastic deformation amplitude in the base-isolation story under the critical multiple impulse with reasonable accuracy. The proposed method enables a unified evaluation of the steady-state response in the base-isolation story regardless of the number of stories, although the different procedures depending on the number of stories were necessary in the previous method where the closed-form solution for the SDOF is applied to the base-isolated building (Takewaki et al., 2017).
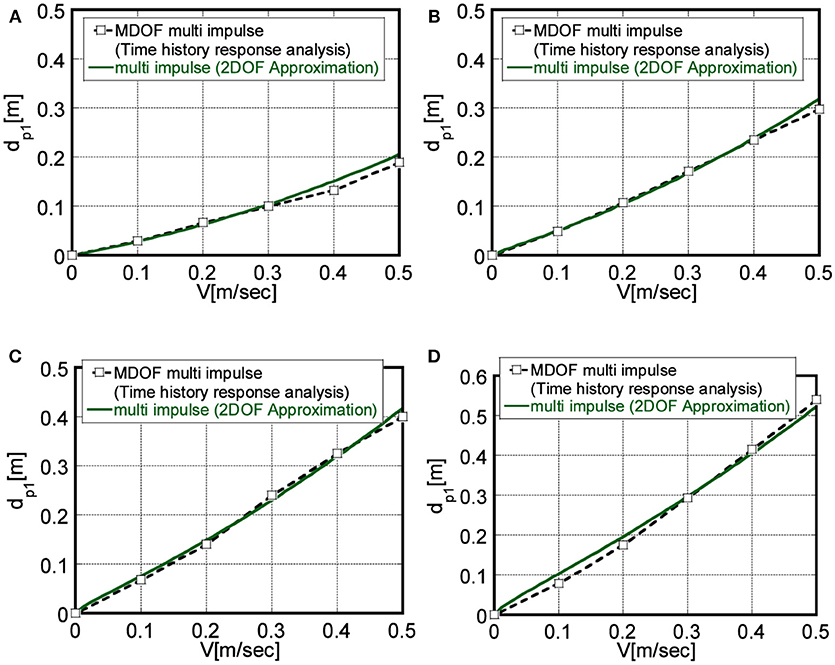
Figure 14. Comparison of plastic deformation amplitude of base-isolation story by approximate solution for 2DOF model and that by time-history response analysis for original model, (A) N = 10, (B) N = 20, (C) N = 30, (D) N = 40.
Conclusions
The critical non-linear response has been investigated for a 2DOF elastic-perfectly plastic system and a base-isolated building under a multiple impulse as a substitute for long-duration earthquake ground motions.
The conclusions may be summarized as follows.
(1) An approximate closed-form expression has been derived for the critical steady-state response of an undamped 2DOF elastic-perfectly plastic system under the critical multiple impulse as a substitute for long-duration ground motions. The steady state in which each impulse acts at the zero-restoring force timing in the first story is assumed and a closed-form solution for the plastic deformation amplitude under the critical multi impulse has been derived by introducing four approximations based on the result due to time history response analysis. This is because it is difficult to derive the critical elastic-plastic response of the undamped 2DOF system by the energy balance law due to the phase lag of two masses.
(2) The accuracy of the proposed approximate solution for the plastic deformation amplitude in the first story under the critical multiple impulse has been investigated through the comparison with the result of time-history response analysis in which each impulse acts at the zero-restoring force timing in the first story. The validity of the four approximations used in the derivation of the approximate solution has been investigated through the comparison with the time-history response analysis result.
(3) The validity of the multiple impulse as a substitute for the long-duration ground motion has been investigated through the comparison with the result for the steady-state response under the corresponding multi-cycle sinusoidal wave obtained by the time-history response analysis. It has been demonstrated that the closed-form solution of the plastic deformation amplitude under the critical multiple impulse is an upper bound of that under the corresponding multi-cycle sinusoidal wave and it is necessary to change the multiplier of adjustment in the larger range of V, to upgrade the correspondence between the steady-state response under the multiple impulse and that under multi-cycle sinusoidal wave.
(4) The validity of the critical timing of each impulse has been investigated by varying the time interval of the multiple impulse so as to maximize the plastic deformation amplitude. The critical timing of each impulse is the zero restoring-force timing in the first story, but there are several time intervals with which each impulse acts at the zero restoring-force timing. Therefore, the zero restoring-force timing in the first story is a necessary condition of the critical multiple impulse for the 2DOF system and there are several time intervals which maximize the steady-state response.
(5) A method using the approximate solution has been proposed to evaluate the critical steady-state response of a base-isolated building under a long-duration ground motion. The non-linear base-isolated building is first modeled by an N-degree-of-freedom system on the elastic-perfectly plastic shear spring representing the base-isolation story. Then the (N+1)-degree-of-freedom base-isolated building is transformed into the 3DOF system consisting of the reduced 2DOF superstructure and the base-isolation story. Finally, the 3DOF system is further transformed into the equivalent 2DOF system by neglecting the mass on the base-isolation story and considering the series spring assumption. The approximate solution for the 2DOF system derived in this paper has been applied to the equivalent 2DOF system to evaluate the plastic deformation amplitude in the base-isolation story. The accuracy of the proposed method has been investigated by the time-history response analysis for the original base-isolated building. It was demonstrated that the plastic deformation amplitude in the base-isolation story can be evaluated by the proposed method with reasonable accuracy. It was found in the previous paper (Takewaki et al., 2017) that, when a 2DOF base-isolation building is transformed into an SDOF system and the closed-form solution for the critical elastic-plastic response of an SDOF system is applied to obtain the maximum deformation of the base-isolation story, it is necessary to choose a transformation method based on (i) the rigid super-structure approximation (low and middle-rise buildings) and (ii) the ignorance of the base-isolation story mass and series-spring treatment (high-rise buildings), depending on the number of stories of buildings. In contrast, the proposed method using the 2DOF system does not need such selection of the transformation methods and it enables a unified evaluation of the maximum deformation in the base-isolated story regardless of the number of stories.
In this paper, a method for long-duration ground motions has been proposed. The applicability of the proposed method to the pulse-type input and the analysis of rocking motion of rigid bodies (Casapulla, 2015; Casapulla and Maione, 2017; Nabeshima et al., 2016) should be discussed in the future. However, the extension of the SDOF model to the 2DOF model causes a lot of difficulty and the treatment of irregular (or unsteady-state) responses due to the pulse-type impulse may need innovative ideas to overcome them.
Author Contributions
YS formulated the problem, conducted the computation, and wrote the paper. KK conducted the computation and discussed the results. IT supervised the research and wrote the paper.
Funding
Part of the present work is supported by KAKENHI of Japan Society for the Promotion of Science (No. 15H04079, 17J00407, 17K18922, 18H01584). This support is greatly appreciated.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Amadio, C., Fragiacomo, M., and Rajgelj, S. (2003). The effects of repeated earthquake ground motions on the non-linear response of SDOF systems. Earthq. Eng. Struct. Dyn. 32, 291–308. doi: 10.1002/eqe.225
Aoi, S., Honda, R., Morikawa, N., Sekiguchi, H., Suzuki, H., Hayakawa, Y., et al. (2008). Three-dimensional finite defference simulation of long-period ground motions for the 2003 Tokachi-oki, Japan, earthquake. J. Geophys. Res. 113:B07302, doi: 10.1029/2007JB005452
Beck, J. L., and Hall, J. F. (1986). Factors contributing to the catastrophe in Mexico City during the earthquake of September 19, 1985. Geophys. Res. Lett. 13, 593–596. doi: 10.1029/GL013i006p00593
Casapulla, C. (2015). On the resonance conditions of rigid rocking blocks. Int. J. Eng. Technol. 7, 760–771.
Casapulla, C., and Maione, A. (2017). Critical response of free-standing rocking blocks to the intense phase of an earthquake. Int. Rev. Civil Eng. 8, 1–10. doi: 10.15866/irece.v8i1.11024
Caughey, T. K. (1960a). Sinusoidal excitation of a system with bilinear hysteresis. J. Appl. Mech. 27, 640–643.
Caughey, T. K. (1960b). Random excitation of a system with bilinear hysteresis. J. Appl. Mech. 27, 649–652. doi: 10.1115/1.3644077
Fragiacomo, M., Amadio, C., and Macorini, L. (2004). Seismic response of steel frames under repeated earthquake ground motions. Eng. Struct. 26, 2021–2035. doi: 10.1016/j.engstruct.2004.08.005
Furumura, T., and Hayakawa, T. (2007). Anomalous propagation of long-period ground motions recorded in Tokyo during the 23 October 2004 Mw 6.6 Niigata-ken Chuetsu, Japan, Earthquake. Bull. of the Seism. Soc. Am. 97, 863–880. doi: 10.1785/0120060166
Hatayama, K., Zama, S., Nishi, H., Yamada, M., Hirokawa, Y, and Inoue, R. (2004). Long-period strong ground motion and damage to oil storage Tanks due to the 2003 Tokachi-oki earthquake, Zisin. J. Seismol. Soc. Japan 57, 83–103 doi: 10.4294/zisin1948.57.2_83 (in Japanese)
Iwan, W. D. (1961). The Dynamic Response of Bilinear Hysteretic Systems, Ph.D. Thesis, California Institute of Technology, Pasadena.
Iwan, W. D. (1965a). “The dynamic response of the one-degree-of-freedom bilinear hysteretic system,”in Proceedings of the Third World Conference on Earthquake Engineering, New Zealand.
Iwan, W. D. (1965b). The steady-state response of a two-degree-of-freedom bilinear hysteretic system. J. Appl. Mech. 32, 151–156. doi: 10.1115/1.3625711
Kojima, K., Saotome, Y., and Takewaki, I. (2017). Critical earthquake response of a SDOF elastic-perfectly plastic model with viscous damping under double impulse as a substitute of near-fault ground motion, J. Struct. Construct. Eng., 735, 643–652 (in Japanese) doi: 10.1002/2475-8876.10019.
Kojima, K., and Takewaki, I. (2015a). Critical earthquake response of elastic-plastic structures under near-fault ground motions (Part 1: Fling-step input). Front. Built Environ. 1:12. doi: 10.3389/fbuil.2015.00012
Kojima, K., and Takewaki, I. (2015b). Critical earthquake response of elastic-plastic structures under near-fault ground motions (Part 2: Forward-directivity input). Front. Built Environ. 1:13. doi: 10.3389/fbuil.2015.00013
Kojima, K., and Takewaki, I. (2015c). Critical input and response of elastic-plastic structures under long-duration earthquake ground motions. Front. Built Environ. 1:15. doi: 10.3389/fbuil.2015.00015
Kojima, K., and Takewaki, I. (2016). Closed-form critical earthquake response of elastic-plastic structures with bilinear hysteresis under near-fault ground motions. J. Struct. Construct. Eng. 726, 1209–1219 (in Japanese). doi: 10.3130/aijs.81.1209
Kojima, K., and Takewaki, I. (2017). Critical steady-state response of single-degree-of-freedom bilinear hysteretic system under multi impulse as substitute of long-duration ground motion. Front. Built Environ. 3:41. doi: 10.3389/fbuil.2017.00041
Liu, C. S. (2000). The steady loops of SDOF perfectly elastoplastic structures under sinusoidal loadings. J. Mar. Sci. Technol. 8, 50–60.
Nabeshima, K., Taniguchi, R., Kojima, K., and Takewaki, I. (2016). Closed-form overturning limit of rigid block under critical near-fault ground motions. Front. Built Environ. 2:9. doi: 10.3389/fbuil.2016.00009.
Roberts, J. B., and Spanos, P. D. (1990). Random Vibration and Statistical Linearization. New York, NY: Wiley.
Suzuki, C., Tsuji, M., Yoshitomi, S., and Takewaki, I. (2009). Reduced load and structure models via inverse formulation for time-history wind response analysis of high-rise buildings, J. Struct. Constr. Eng. 74, 1073–1081. doi: 10.3130/aijs.74.1073 (in Japanese)
Takewaki, I., Moustafa, A., and Fujita, K. (2012). Improving the Earthquake Resilience of Buildings: The Worst Case Approach. London: Springer.
Takewaki, I., Murakami, S., Fujita, K., Yoshitomi, S., and Tsuji, M. (2011). The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 31, 1511–1528. doi: 10.1016/j.soildyn.2011.06.001
Takewaki, I., Taniguchi, R., and Kojima, K. (2017). Critical response of elastic-plastic structures to near-fault ground motions and its application to base-isolated building structures, Chapter 6, “International Symposium in Earthquake Engineering and Structural Dynamics” in memory of late Professor Ragnar Sigbjörnsson, Conference in Reykjavik - June 2017, (Earthquake Engineering and Structural Dynamics in Memory of Ragnar Sigbjörnsson), 123–141.
Takewaki, I., and Tsujimoto, H. (2011). Scaling of design earthquake ground motions for tall buildings based on drift and input energy demands. Earthq. Struct. 2, 171–187. doi: 10.12989/eas.2011.2.2.171
Taniguchi, R., Kojima, K., and Takewaki, I. (2016). Critical response of 2DOF elastic-plastic buiding structures under double impulse as substitute of near-fault ground motion. Front. Built Environ. 2:2. doi: 10.3389/fbuil.2016.00002
Appendix
Proof of Maximization of Total Input Energy by Each Impulse
It is proved here that the zero restoring-force timing maximizes the total input energy by each impulse. The total input energy ΔE by each impulse is the increment of the total mechanical energy just before and after the input of each impulse and ΔE can be expressed as follows.
where denote the velocity of the first and second masses, respectively, just before the input of each impulse. When the sum of momenta is maximized, ΔE becomes maximum.
The equations of motion can then be expressed by
where f1(t), f2(t) denote the restoring forces in the first and second stories. Eqs. (A2a, b) can be transformed into the following equation.
By integrating Eq. (A3) from t = t* to , the following equation can be obtained.
where denote the timing of impulse input and the time interval of impulses. By manipulating Eq. (A4), the sum of momenta P of the first and second stories can be obtained as follows.
where it is noted that and in the steady state. By differentiating Eq. (A5) by t0, the following equation can be derived.
The timing of maximizing ΔE can therefore be characterized by
Since ΔE is stationary at the zero restoring-force timing, Eq. (A7) is a necessary condition for the critical impulse timing.
Keywords: critical excitation, 2DOF model, elastic-plastic response, long-duration ground motion, base-isolated building, resonance
Citation: Saotome Y, Kojima K and Takewaki I (2019) Critical Earthquake Response of 2DOF Elastic-Perfectly Plastic Model Under Multiple Impulse as Substitute for Long-Duration Earthquake Ground Motions. Front. Built Environ. 4:81. doi: 10.3389/fbuil.2018.00081
Received: 16 September 2018; Accepted: 13 December 2018;
Published: 09 January 2019.
Edited by:
Katsuichiro Goda, University of Western Ontario, CanadaReviewed by:
Fabio Di Trapani, Politecnico di Torino, ItalyClaudia Casapulla, University of Naples Federico II, Italy
Copyright © 2019 Saotome, Kojima and Takewaki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Izuru Takewaki, dGFrZXdha2lAYXJjaGkua3lvdG8tdS5hYy5qcA==
 Yoshito Saotome1
Yoshito Saotome1 Kotaro Kojima
Kotaro Kojima Izuru Takewaki
Izuru Takewaki