- Department of Civil and Building Engineering, and Architecture, Polytechnic University of Marche, Ancona, Italy
The subject of this work is the Sant'Agostino Sanctuary in Offida (Italy); we investigated both the dynamic behavior and the seismic vulnerability of the complex, used nowadays in its parts as school building, oratory, and church. Offida is in central Italy; the village has been severely damaged by the last seismic events of 2016. The sanctuary was heavily damaged by the earthquake of 24 August 2016. We recurred to finite elements to estimate the vulnerability of the sanctuary and its dynamic response, considering masonry's non-linear behavior by means of proper constitutive assumptions. To estimate how the monastery bears the lateral loads related to the expected demands resulting from seismic actions (N2 method) using non-linear static analysis (Pushover), we recurred to a homogenized material and smeared cracking and crushing constitutive law. As may be remarked by observing buildings that share the same features of the sanctuary and, moreover, by comparing seismic demand vs. capacity, the structure is prone to massive damage leading to collapse. The paper underlines how advanced numerical analysis grants fundamental data on how historical masonry buildings behave under seismic action, providing a method that may easily be implemented at historic monasteries in Europe.
Introduction
The intense seismic activity that affected many areas of Italy over the last decades clearly showed how much care should be taken of architectural heritage and its preservation. Assessing the seismic vulnerability of a monumental masonry building may be a difficult task to accomplish, considering how peculiar these structures usually are, requiring sophisticated and computationally heavy numerical models to have a proper estimation of their dynamical response under seismic action. Most recent Italian earthquakes (Umbria-Marche 1997–1998, Abruzzo 2009, Emilia-Romagna 2012, Central Italy 2016), caused irreparable damages to many elements of the architectural heritage, such as monumental buildings, churches and steeples (Ceci et al., 2010; Acito et al., 2014; Milani and Valente, 2015).
Protecting historical buildings from seismic activity plays a significant role on public safety, considering how European countries, moreover Italy, have such a various architectural heritage that is still in use, most of the times hosting strategic public functions (Asteris et al., 2014). However, such buildings obviously do not grant proper safety against seismic actions, since their design criteria do not take into account lateral resistance and ductility in favor of efficiently bearing gravity loads; housing significant functions in those structures, especially during emergencies of any kind, involves the attainment of the required safety levels (Clementi et al., 2015).
The features that all monumental masonry buildings share, such as being so complex, irregular, mainly designed to bear gravity loads and way more massive than modern architecture, make structural behavior uneasy to estimate, especially when it comes to evaluating it under seismic action. Despite its being challenging, proper modeling of masonry buildings is fundamental to seismic resistant design or to assess earthquake vulnerability. While contemporary structures are basically made of industrial based components, such as RC or steel, which make their structural behavior uniform and certain (Pierdicca et al., 2016b, 2018), ancient masonry structures require the acknowledgment of more parameters to be modeled, like floors' stiffness (diaphragm effect) or connections between orthogonal walls and structural and non-structural elements (Betti and Vignoli, 2008a, 2011; Bartoli et al., 2013; Clementi et al., 2018a).
Masonry macro elements are made of bricks bonded by mortar, so they can be seen as a composite system whose parts are characterized by a very different mechanical behavior, making structural modeling a challenging activity, as the wide range of designs available at the state of the art seems to prove (Asteris et al., 2015). No-Tension Material models and their mechanical characterization derive from the obvious fact that masonry does not offer a significant resistance to tensile stresses. To take into proper account how masonry is characterized by a non-linear response, starting from the lowest deformation levels, the hypothesis of unilateral mechanical behavior may be applied to the theories of limit analysis, leading to models able to estimate the collapse loads of masonry structures (Del Piero, 1998; Milani et al., 2007; Milani, 2011). Inelastic phenomena that affect masonry buildings under seismic action leading to local phenomena of softening, failure and strain localization, such as sliding, cracking, crushing at the mortar joints, tensile fracture of bricks, may be analyzed by means of micro-mechanical models, characterized by elasto-plastic laws (Lotfi and Shing, 1994; Lourenço and Rots, 1997) or damage theories (Luciano and Sacco, 1998). At the state of the art, many homogenization techniques are available to obtain continuum models, since representing bricks and joints would not be possible when modeling monumental buildings, leading to way too computationally heavy FEM (Zucchini and Lourenço, 2002; Lourenço, 2009; Addessi et al., 2010); these various approaches traced the path to the related macro-mechanical models, moving from the rigorous application of the homogenization theory for periodic media (Anthoine, 1995) to two-steps approximated strategies (Pande et al., 1989). Acary (2001) gives a complete review of the homogenization techniques described above, while (Luciano and Sacco, 1997; Zucchini and Lourenço, 2002, 2004; Addessi et al., 2010) focus on historical masonry walls.
Although simplified models may be the reference to represent the structural behavior of masonry buildings and all their peculiarities, it appears challenging to apply proper simplifications while keeping the requested level of modeling accuracy. At the state of the art, we may identify three different modeling strategies. The most recurrent modeling approach we find nowadays is the Equivalent Frame Method (Caliò et al., 2012; Lagomarsino et al., 2013; Quagliarini et al., 2017), which designs the walls as an idealized frame where the non-linear response is concentrated on deformable elements connected by rigid nodes representing not usually damage prone structural components. Starting from a careful seismic phenomena observation that leads to pointing out how cracks and failure modes mostly concentrate in recurrent elements, piers and spandrels may be seen as the two main structural components, especially when it comes to analyzing the in-plane response of complex masonry walls with openings. Another frequently used approach provides for the use of finite elements schemes to model masonry structures as they were continuous; current literatures offers recurrent examples of how this modeling strategy may be applied with ease to historical buildings, such as monasteries (Lourenço et al., 2007; Betti and Vignoli, 2008a), churches (Betti and Vignoli, 2008b; Milani and Valente, 2015; Clementi et al., 2017a; Formisano et al., 2018), bridges (Betti et al., 2008), steeples or towers (D'Ambrisi et al., 2012; Minghini et al., 2014; Carpinteri et al., 2015), ancient city centers (Formisano et al., 2015). To gain exhaustive comprehension of seismic phenomena, analysis output usually comes from combining the results given by different sets of parameters, since the models are progressively refined, especially in terms of fracture and plasticity. In the two methods described above, dynamical problems are reduced to elementary static issues (equivalent pushover schemes), since equivalent horizontal static forces make up for seismic loadings. As an alternative to the Equivalent Frame Method, masonry buildings may be modeled as distinct elements in an assembly of blocks affected by unilateral frictional contacts (Jean, 1999; Clementi et al., 2018b; Poiani et al., 2018).
After carefully analyzing masonry's peculiarities, it seems clear how turning to continuous material leads to the most representative structural models, especially when those are related to irregular complexes. Many non-linear mechanisms proper of concrete structures, such as damage deriving, friction-plasticity, crushing or cohesion, are already implemented in many structural software, yet there is a blatant lack of effective instruments when it comes to design 2D and 3D non-linear models of masonry buildings.
This work aims to clearly show how delicate yet crucial it is to properly take into account the three-dimensional behavior of the complex, underlining its structural weaknesses. To obtain a representative numerical model, a preliminary survey was performed in order to get all the required parameters, such as the geometry of the structure and the mechanical properties of masonry material, combined with a careful historical and archival research. Once all the requested data were collected, the designed 3D finite element model, endowed with an elastic plastic (with softening) constitutive damage law, was used to perform a wide number of non-linear static analysis (Clementi et al., 2017b). To make this model and its design features useful to many other historical masonry complexes, we opted for a smeared fracture energy approach.
The paper is organized as follows. In sections Historical Developments and Description of the Building in its Current Configuration, we described the historical developments, the characteristics of the material and the geometry of the case study situated in Offida (Central Italy), which are the starting point for subsequent developments. In section Damage After Seismic Sequence of 2016 the actual damage is described. In section Structural Analysis Methodology is illustrated the modeling strategy. In section Global Seismic Behavior sensitivity analyses of the case study are described to assess the global condition of the structure. In this section also the procedure defined for isolated churches in Brandonisio et al. (2013) is applied to the monastery, constituting de facto an extension of the method to more complex structures. The paper ends with some conclusions (section Conclusions).
Historical Developments
To have proper understanding of how each part composing the sanctuary developed over the centuries, a preliminary historical analysis was carried out.
The foundation of the monastery's early nucleus is dated to the XIV century, when the relics related to the Eucharistic Miracle of Lanciano arrived in Offida leading to the replacement of the original church of St. Mary Magdalene by a greater one that the Augustinians decided to name their own to St. Augustine. Its construction lasted from 1338 to 1441. The works of enlargement, from the basements, were completed during the priory of a friar Jacopo in 1441. The cloister with quadrilateral closed shape is realized during 1574 using a long line of octagonal columns, whose basements are stone capitals, and surmounted by round arches.
At the center of the abbey, we find the usual well; the cloister led to the refectory. The convent was amended several times (from 1609 to 1618) and even renewed its foundations in 1625. The façade is Baroque (1686). The interior was modified and extended in the XVIII century with a Latin cross, with a dome inside a tambour and it was decorated with late baroque stucco and valuable wooden furniture (e.g., chorus and confessionals walnut of the cabinetmaker Alessio Donati from Offida). The interiors also preserve a precious reliquary cross (the “holy cross” that protects the relic of that miracle), it operates in silver gilt made in Venice in the XIV century and another reliquary of the art of Marche region of XV century. Other significant modifications were made between 1933 and 1937.
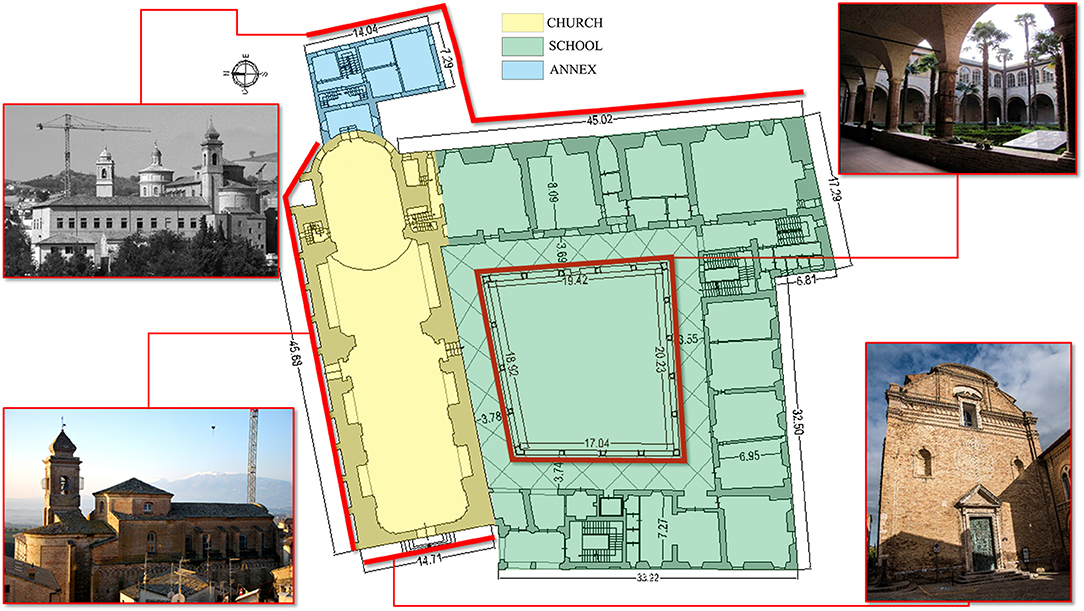
The monastery was firstly hit by L'Aquila earthquake (April 6, 2009) with a magnitude MW = 6.3. After this seismic event, the school building area was damaged, and other superficial cracks appeared in the main façade of the church. For this reason, in the 2010 a series of structural restorations was carried out on the buildings, except for the area of the church, which remained unchanged. A reconstruction/improvement on the three floors of the school building and an extensive re-roofing was done. Steel bracings or concrete slabs were inserted in some parts. The actual configuration is reported in Figure 1.
Currently, the refectory no longer exists since the rooms were turned into school classrooms, as indeed all the premises nearby the cloister. Such use began as early as 1870, after the law of confiscation of the Church's properties in 1866. The current division of the building is shown in Figure 1.
The church's walls linked, i.e., the masonry walls are connected from a structural point of view, to other parts of the oratory (annex) and school building, as proved by a few in situ tests performed on it. This means that a global analysis is appropriated for this case study.
Description of the Building in its Current Configuration
Geometrical Survey
To ensure the preliminary data required by the study, an accurate in situ survey was performed on the complex, leading to a full geometry relief, focusing on structural details, such as connections between all the macro elements, characterization of masonry texture and its irregularities. As reported in section Historical Developments, the survey is completed by a historical report on how the complex developed over the centuries.
The entire area measures ~2600 m2 for the floor where at least three elevations are present in all parts of the structure. The main dimensions of the nave are ~45.68 m of length, ~14.71 m of width and a lateral-wall height (mean value) of about ~18 m. The masonry walls' thickness is ranged between 2.55 m (nave walls) and 0.8 m (apse walls) (Figure 1). The church roof's structure is made of timber (nave). The masonry is composed of solid brick and lime mortar (Figure 2). However, the remaining parts of the monastery are also made of solid brick and lime mortar yet in a better state of preservation due to recent restorations as said in section Historical Developments. This leads to better elastic-mechanical parameters (Table 1).
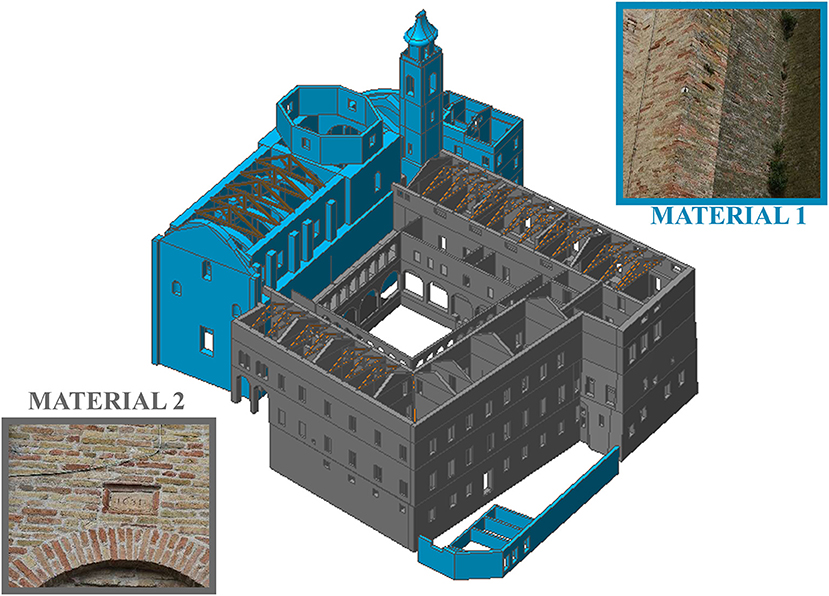
Figure 2. Technological characterizations of materials of “Sant‘Agostino's Sanctuary” in Offida (AP).
The other portions of the building are an assemblage of horizontal rectangular zones, with a length of ~45 m (East part) and a mean width of about ~32 m (South and West parts). This area has three floors with a maximum height of 11 m. In the center, there is the “Portico” with square columns on solid brick with a width of 0.45 m and cross-vault at the upper sides. All these areas contain classrooms and offices of the school.
Material Characterization
We choose not to perform a complete characterization of the materials, since the annex and the monastery do not reveal any significant damage or issue nowadays, and we were on a budget. According to the current Italian Seismic Code (Ministro dei Lavori Pubblici e dei Trasporti., 2008; Circolare Ministeriale n. 617, 2009; Ministero delle Infrastrutture e dei Trasporti., 2018) this lead to the lowest Knowledge level KL1, related to a Confidence Factor (CF) equal to 1.35, as also requested by Eurocode 8 (EN 1998-3, 2010) for concrete structures.
The Italian regulation (Ministro dei Lavori Pubblici e dei Trasporti., 2008; Circolare Ministeriale n. 617, 2009; Ministero delle Infrastrutture e dei Trasporti., 2018) and its Annex C8A.2 was the reference to define the material's compressive strength, based on Table C8A.2.1 of (Circolare Ministeriale n. 617, 2009). With a Knowledge Level KL1, the related confidence factor CF = 1.35 is applied to obtain a final design compressive strength. The tensile strength of the masonry may be estimated as the 10% of the compressive resistance as reported in Table 1, as it is generally negligible.
Damage After Seismic Sequence of 2016
After the seismic events of 2016, the church has been seriously damaged, and it is currently being made safe to prevent collapses. The existing cracks have worsted, especially on the façade and on the transept, and new cracks have appeared on the dome and the church's roof. On the façade, two long cracks pass through the wall (Figure 3). The octagonal dome has cracks on all corners due to an interaction with the pushing beams of the roof; this led to a structural failure of common rafters. The transept shows vertical and diagonal cracks on north and south sides under the windows. After the seismic sequence, many cracks also appeared inside the church, especially on the nave (Figure 3B). The square, in front of the church, has been closed owing to the possibility of façade overturn.

Figure 3. External cracks on façade, north wall of the nave and north front of the annex (A) Internal cracks of the church (B).
Structural Analysis Methodology
Seismic assessments of monumental masonry buildings may be considered challenging, taking into account the not so obvious numerical modeling of non-linear behavior of such a no tension material itself, the complex geometrical configuration and the merely experimental characterization of its components (Pierdicca et al., 2016a). In accordance with the state of the art, we find nowadays different mechanical models and their related parameters to assess the highly non-linear behavior of masonry both in tension (low tensile capacity and consequent cracking phenomena) and compression.
The macro-modeling technique described in this paper leads to an exhaustive comprehension of all the non-linear phenomena that may affect masonry buildings under seismic action, even though its computing is still difficult to apply on a complex 3D structural system because of all the requested degrees of freedom. According to the chosen modeling technique and its features, the development of the cracks modifies the stiffness of the solid elements composing the model.
The smeared crack concept, and its FE implementation, offers a variety of possibilities, ranging from fixed single to fixed multidirectional and rotating crack approaches. Here, the distinction lies in the orientation of the crack, which is either kept constant, updated in a stepwise manner, or updated continuously (Rots, 1991; Lourenço, 2009). Since smeared crack approaches do not require re-meshing of the model after the occurrence of cracks or a priori definition of possible locations of cracks, it is very convenient for FE models. Differently, the direct modeling of the crack into the mesh, with Linear and Non-linear Fracture mechanics models, is always accessible when the engineers deal with a small model, also for masonry or masonry-like materials (Clementi et al., 2008; Lenci et al., 2011, 2012).
Authors like (da Porto et al., 2010) used the isotropic rotating crack model to design panels composed by vertically perforated clay units and various types of joints, while (Manfredi et al., 2013) adopted a smeared crack model, to properly simulate how macro-models of brick masonry and adobe walls behave. Multi-directional fixed or rotating crack models also proved their great use in terms of debonding problems, e.g., (Ghiassi et al., 2013; Gattulli et al., 2014). Current practice shows how smeared crack models are versatile and require few preliminary data.
The non-linear behavior of the masonry panels that constitute the sanctuary is modeled by means of a Total Strain Crack Model based on fixed stress-strain law concepts provided by MIDAS FEA (Midas FEA, 2016), thus the cracking path is fixed to the direction of the principal strain vectors and kept constant during structure's loading; the panels were modeled with solid tetrahedron elements with 4 nodes, discretized with an optimized regular mesh (see Figure 4A).
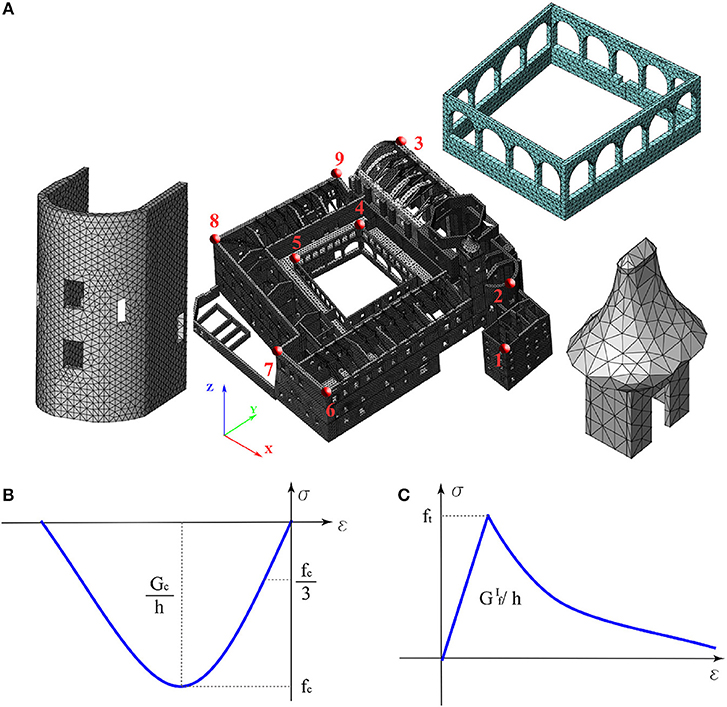
Figure 4. Finite elements model of “Sant‘Agostino's Sanctuary” in Offida (Central Italy) (A), stress–strain constitutive relations used for the simulation for masonry uniaxial compression (B), masonry uniaxial tension (C).
The selected constitutive laws take into account the complex behavior of masonry, compression behavior is modeled by means of a parabolic hardening rule and a parabolic softening branch following the peak of resistance (Figure 4B) while the tension behavior is modeled by a linear hardening branch followed by a non-linear softening branch (Figure 4C). Table 1 shows a report of fracture energies in compression (Gc) and tension (Gf), where h is the mean dimension of the mesh (Rots, 1991).
The shear retention factor (β) provides the rate of shear stiffness after cracking, which can be related to the progressive opening of the cracks or kept constant (low), in a range between 0 and 1. For the assessment described in this paper, we opted for a constant value of 0.05 as requested (Rots and de Borst, 1987; Rots, 1991).
Finite Element Model for the Global Response
The purpose of the designed numerical models was to represent all the significant features of the sanctuary, such as the geometry of the structural components with all their peculiarities and openings, the connections between all the macro elements. We also modeled the timber elements on the roofs.
One of the major focuses of the modeling phase was to choose the correct floors' in-plane stiffness, as this aspect is fundamental to comprehend structural response. According to the current Italian Standards (Ministero delle Infrastrutture e dei Trasporti., 2018), some floors which were recently restored can be considered as rigid for two coexisting reasons: solid concrete plates (i) have the minimum thickness (40 mm) and (ii) the necessary reinforcements to assure a rigid behavior (Ministero delle Infrastrutture e dei Trasporti., 2018). In other areas, differently, this assumption may not be in safe, mainly because the slabs are made of poor quality concrete or not well-connected to the peripheral walls. For this reason, two different models were analyzed, also to check the variability of the structural response due to slabs rigidity, namely:
• The model of the Current State, namely Model CS, where the slabs are modeled by the actual schemes;
• The model with totally Deformable Floor, namely Model DF, where slabs although adequately stiffened are supposed not to be connected to the peripheral walls or, the wooden slabs do not have a correct capacity design of the connector with the concrete.
After meshing, the final 3D numerical models are reported in Figure 4A with 94348 nodes, 454829 solid elements and a d.o.f. number of 372219 for Model CS and of 379062 for Model DF.
Global Seismic Behavior
According to the Italian code, the building analyzed in this paper is a “Class IV,” i.e., a strategic structure, because it is currently use as school in some parts. The recurrence period (TR, D) associated to the Limit State of Significant Damage (SLSD, or SLV in Italian) is of 1898 years, related to an expected Peak Ground Acceleration (PGA) equal to 0.283 g. The elastic response spectrum (soil type T1 and category of subsoil C are considered) is characterized by the following parameters: S = 1.272; TB = 0.175 s; TC = 0.525 s; TD = 2.733 s (Figure 5).
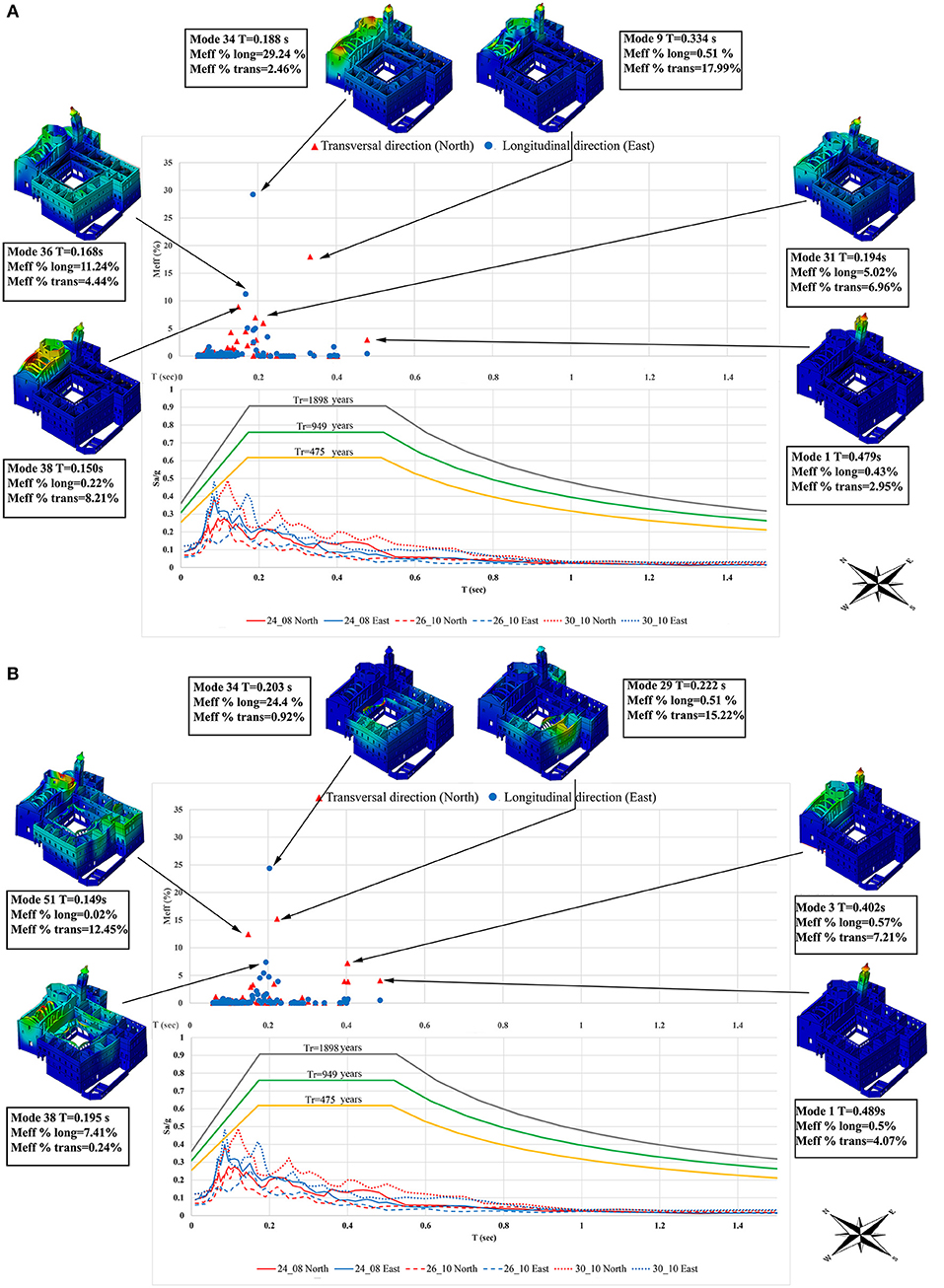
Figure 5. Distribution of modal shapes in the longitudinal and transversal directions and comparison with the pseudo-acceleration response spectra (three main shocks of Central Italy 2016–2017 seismic sequence), and the Italian code elastic response spectrum for the Model CS (A), Model DF (B).
The analyses were carried out using the horizontal components of different natural response spectra obtained from the time histories recorded near the city of Offida, with the objective of both assessing the damage caused to the sanctuary by the intense seismic activity affecting central Italy from august 2016 and evaluating the horizontal strength capacity. Unfortunately, the nearest station is the one in Ascoli Piceno [APS station in Italian Accelerometric Archive (ITACA)], as Offida has not been equipped with an accelerometric station. The two components responses spectrum (North direction coincide with X-direction, East direction coincides with Y-direction) used arise from the three main shocks recorded during the 2016 seismic events in that station: (i) 24/08/2016 with Mw = 6.0 and ML = 6.0, (ii) 26/10/2016 Mw = 5.9 and ML = 5.9, and (iii) 30/10/2016 with Mw = 6.5 and ML = 6.1. In Table 2 are reported the main characteristics of the main shocks, the time histories used, the class of the site of the station, the main distance between the ASP station and the epicenter zone where (Kadas et al., 2011):
• R_jb, is the Joyner-Boore distance, known as the smallest spacing from the site to the surface projection of the rupture surface;
• R_rup, is the shortest distance between the site and the rupture surface;
• R_epi, is the distance estimated by geometric swap.
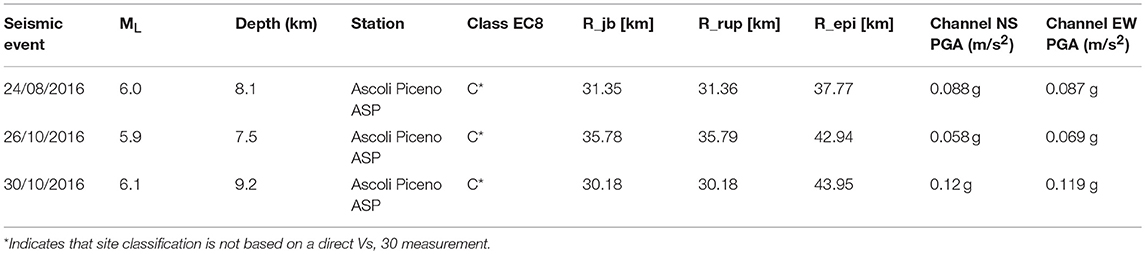
Table 2. Characteristics of main earthquakes recorded in Ascoli Piceno (ASP) station during the Central Italy seismic sequence in 2016–2017.
The comparison of the recorded spectrum and the elastic spectrum of building code previously defined is reported in Figure 5.
Linear Dynamic Analysis
Firstly, modal analysis is performed on the FEM models to identify the main frequencies, the related modal shapes and the effective modal masses (%Meff) of each mode of the Sanctuary in percentage respect to the total: at this moment the models are not calibrated with Ambient Vibration Surveys like those reported in Pierdicca et al. (2016a). We resorted to the Block Lanczos method to estimate the modal shapes, taking into proper account the quantum of d.o.f. of the numerical models. The monastery is affected by many local modes, and for this reason, 300 modes are considered to have more than 85% of excited mass.
In the upper part of Figure 5A the main modes and the associated participating masses are reported for the Model CS. Generally, for this model, the modal shapes distribution clearly shows how the monastery is affected by substantial out-of-plane deformations. The 34th mode has the highest participating mass in the longitudinal direction (Meff = 29.24%, T = 0.188 s) involving the timber, the bell tower, and the tambour. The 9th mode is characterized by a Meff = 17.99% and a period T = 0.334 s, since it affects crosswise both the aisle's lateral walls and the steeple.
To understand the influence of rigid floors modal analysis was also performed for the Model DF. In this case, 300 modes involve only the 82% of the total mass due to a higher dispersion of local modes, e.g., of the walls of the porch of school, and they are reported in the upper part of Figure 5B. The condition without rigid floors drags more the complex of the school (see upper parts of Figures 5A,B) which is further stressed with small translations in the out-of-plane directions of the walls. In fact, the participating masses involved by the principal modes of CS and DF Models, i.e., the 34th and 29th, are respectively of Meff = 24.4% longitudinally and Meff = 15.22% transversely, including both the walls of the school. Apparently, in both Models CS and DF, the 1st mode involves the bell tower in the transversal direction.
In the lower part of Figures 5A,B the elastic response spectra obtained from the ASP_station are reported to have a direct correlation with the attained accelerations. Modes with significant participating masses are characterized by periods in the range 0.18–0.38 s, where the response spectra have big values of accelerations. It is clearly remarkable that the masonry of the church's central aisle is always related to the high acceleration which to some extent may explain, albeit marginally, the presence of the damage observed on the structure at the end of the seismic sequence, considering that the spectral content of the ASP_station records would have been the same as that of the earthquake motion in Offida.
The Demand on the Macro-Elements
It is useful to provide the seismic demand on the entire building. In Figure 6, the ratio between the base shear (V) obtained in section Linear Dynamic Analysis for different response spectra [i.e., ASP_station and Italian code spectra (Ministero delle Infrastrutture e dei Trasporti., 2018)] and the total weight of the building (Wtot) are plotted for the transversal (X-direction) and longitudinal (Y-direction) directions for both Models CS and DF. The base shear V has been obtained using the Complete Quadratic Combination (CQC) method.
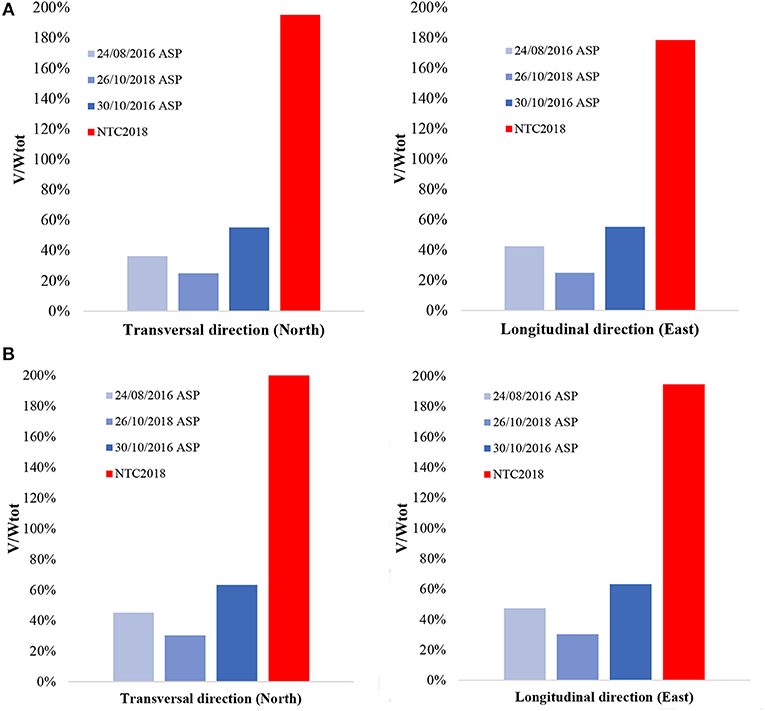
Figure 6. Base shear (V) normalized to the total weight (Wtot) for Model DF: comparison between NTC2018 and the main shocks recorded during the 24th August 2016, 26th and 30th October 2016 for the Model CS (A), Model DF (B).
Form Figure 6 is clear that the ratios V/Wtot obtained with the elastic spectrum of NTC2018 are always greater than the natural one of ASP_station, that are always in the range 22÷58%. The main observation emerging is the impossibility of being able to guarantee a high level of seismic safety, especially in comparison to the level required by the new seismic Italian law for strategic structures, for which the request of demand (and then capacity) became very high. Additionally, the school is connected to the church which, for conservation reasons, can never undergo extensive consolidation interventions. Finally, a little reduction (~10%) on the seismic demand in both directions is observable, and it is a direct consequence of the retrofitting interventions on the school zone, SC (Figure 1).
Once the seismic demand for the entire aggregate is known, to have a better perception on the real distribution of the seismic demand on the various parts of the building, we have evaluated the ratio between the base shear under each portion of the complex (Vi) and the total base shear (V), Vi/V (in percentage). The Sanctuary is divided into three main portions (see Figure 1): the church (CH), the school (SC) and the annex (AN). The main results, for both Model CS and DF, are displayed in Figure 7, showing that in longitudinal direction the shear forces are basically centered on the school building (~70%), while in the transversal direction there is an equal behavior since both the church and the school get almost the same shear force (~40%), Furthermore, Figure 7 shows that the presence of rigid floors gives a better distribution of the shear force between the church and the school both in longitudinal and transversal direction. It is also evident that, in the same case, the distribution of shear is not proportional to the acceleration and the main parts of the building with higher seismic forces are the church and the school.
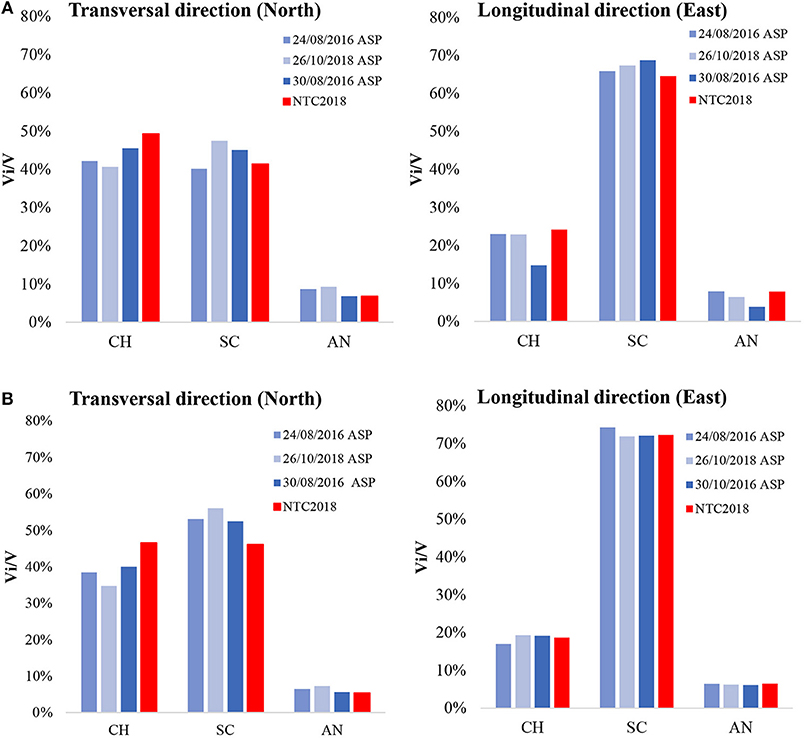
Figure 7. Seismic base shear absorbed by the church (CH), the school (SC), and the annex (AN) for the Model CS (A), Model DF (B).
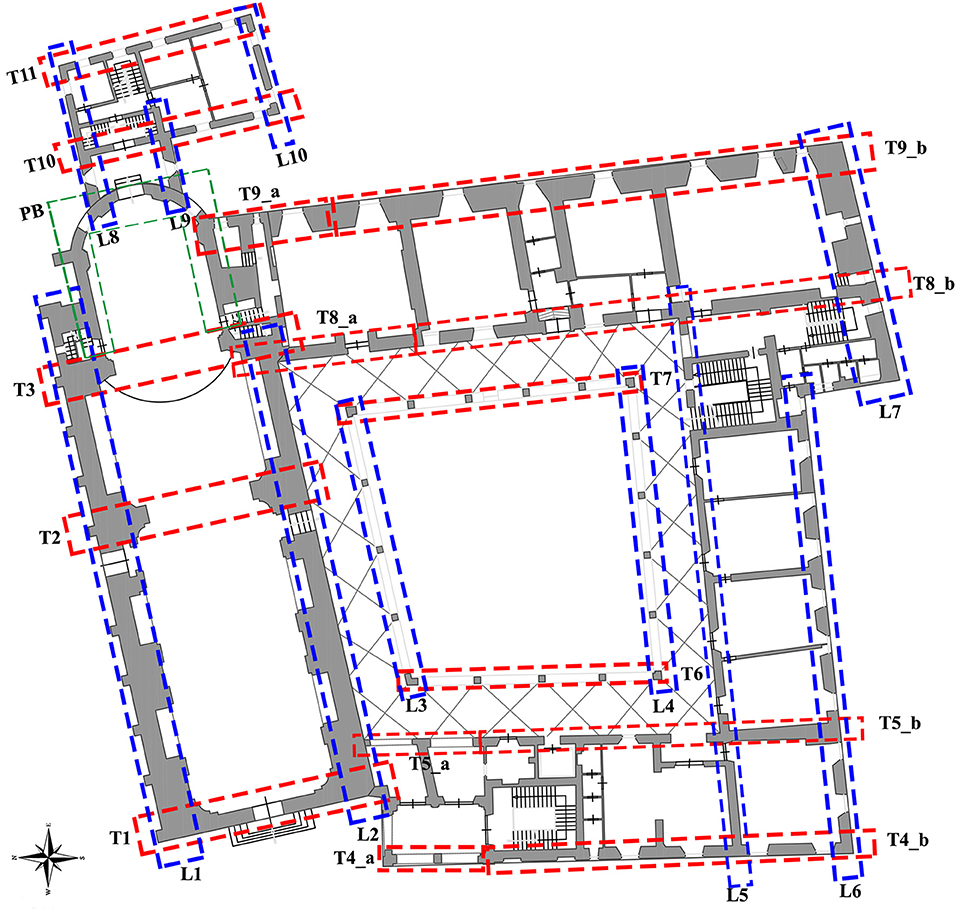
To evaluate the horizontal demand of each macro-element, the Sanctuary was divided into longitudinal and transversal elements as reported in Figure 8, with the final aim to find the most stressed wall. The ratio Vi/V (in percentage) for each macro-element in both longitudinal and transversal directions is reported in Figure 9 for Model CS and DF.
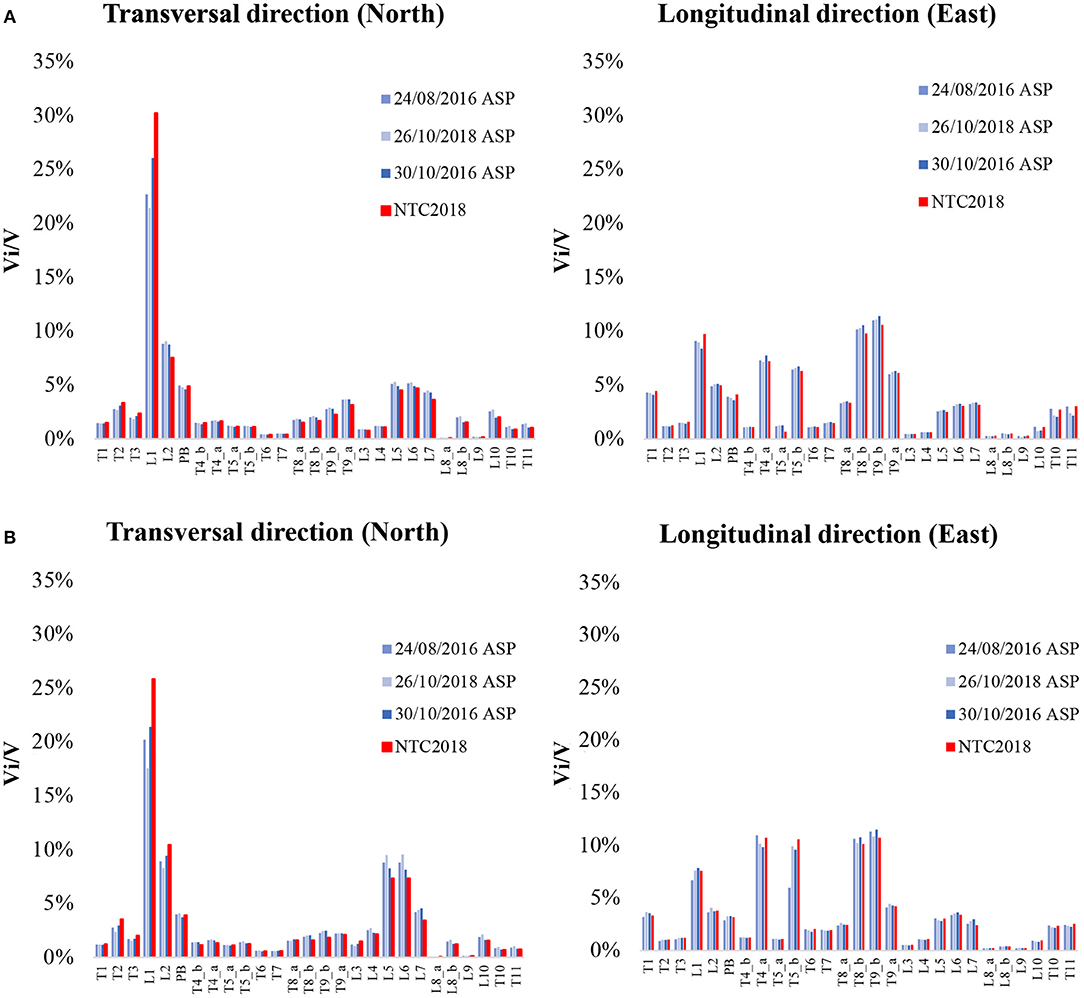
Figure 9. Distribution of base shear among macro-elements in longitudinal and transversal direction for the Model CS (A) Model DF (B).
It can be observed that, when the seismic action is applied in the transversal direction for both the models, shear forces are mainly concentrated on lateral walls of the nave, namely L1, with a Vi/V ratio between 22÷30%, the presbytery (PB) ~8÷7% and the south walls of the school with a Vi/V~5%. On the contrary, lower forces act on internal walls, e.g., L3–L4 and T6–T7, with a ratio of <3%.
When the seismic force acts in the longitudinal direction, there are fewer differences of shear forces on the macro-elements. Major Vi/V ratios are mainly concentrated in peripheral walls with a variation concerning the transverse case of the elements most stressed (actually T4–T5 and T8–T9 with a ratio in the range 5÷10%) less of L1 which is still the one with the higher demand. This result incidentally confirms what has been observed during the recent seismic sequence of Central Italy 2016–2017 that saw in the wall L1 the one with more significant damage compared to the rest of the construction (see Figure 3A), an area already lightly damaged by the L'Aquila earthquake in 2009 (see section Historical Developments).
Non-linear Static Analysis: Preliminary Considerations
The non-linear static analysis method also known as pushover has been used to properly analyze the complex's seismic behavior, by monotonically increasing horizontal loads and keeping gravity loads constant. Two systems of perpendicular horizontal forces, acting at different times, were used to take into account seismic loads. These systems lead to two load distributions that may be considered two limit states of the building capacity, one related to the masses on each floor by direct proportion (PushMass) and one equivalent to the consideration of main modes involving the 85% of participating masses in both directions (PushMode).
As can be clearly remarked by considering the load distributions described above, the pushover analysis performed is merely conventional, i.e., loads applied to the building are kept constant while the structure progressively degrades during the loading, so gradual changes in modal frequencies caused by yielding and cracking on the structure during loading are not considered. Even though the invariance of static loads may lead to an overestimation in assessing masonry buildings' seismic capacity, mostly on structures affected by a high or non-uniform impairment, a conventional pushover analysis ensures a less computationally expensive alternative to non-linear dynamic analyses. It also provides substantial data on the progressive damage occurring to buildings under seismic loads, such as the cracking.
Considering the extension of the Sanctuary, the non-linear behavior has been analyzed by varying the control point (Figure 4A). To have a proper understanding of how the seismic response develops by modifying the floors stiffness, we used the same control points.
Pushover Analysis: First Results
To ensure clarity and brevity, the capacity curves reported in this paper are those in positive X (i.e., north-direction) and Y directions (i.e., east-direction) for PushMass load distribution Figure 10.
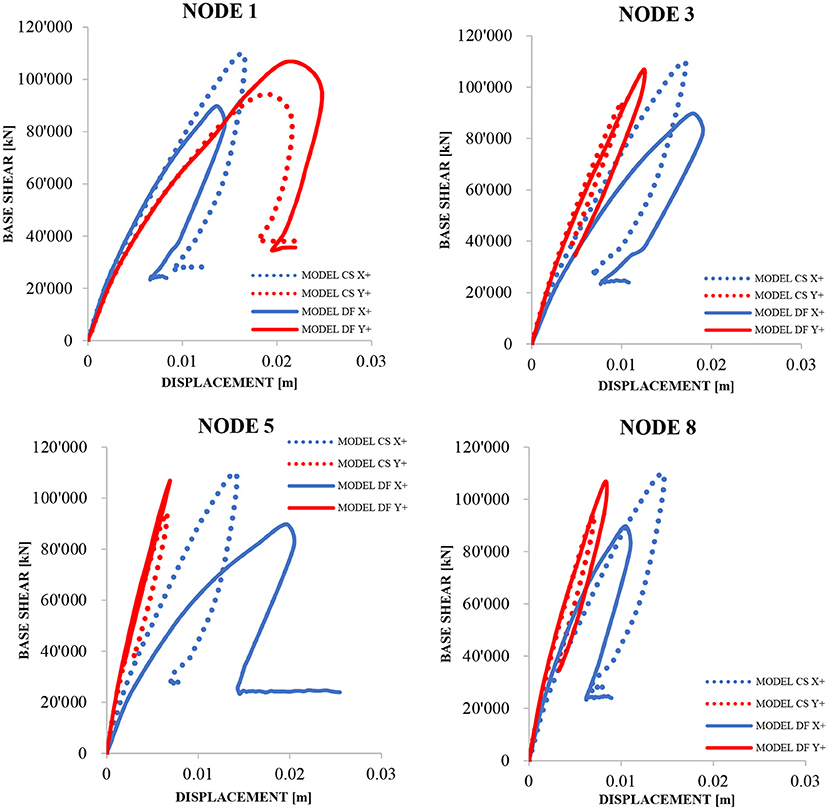
Figure 10. Capacity curves at varying of control points for Model CS and Model DF in X and Y-directions.
The critical load distribution for the complex, both for Model CS and Model DF, is in X-direction, transversal to the aisle. On that X-direction, most of the selected control points display a ductile behavior, while on Y-direction we mostly find a brittle aberrance. In X-direction, the condition of rigid floors produces an increase of resistance compared to the Model DF. In Y-direction, instead, the presence of rigid floors produces a little reduction of resistance leaving intact the stiffness and, for almost all control points, provokes a decrease of ductility. This reduction is due to an increase in the torsional effect that is going to urge the areas not affected by the 2010 intervention, such as the church and the oratory.
Figure 11 shows the development of the cracking in the Model CS and Model DF, due to horizontal loads. In both main directions, the first cracks appear on the walls of the nave and in the bell tower (top figures in each quarter). In X-Direction, the cracking distribution is more huge respect to Y-Direction (down figures in each quarter). Comparing Model DF and Model CS it is evident that the presence of rigid floors reduces the development of cracks, especially in X-direction where the Model CS shows less cracking in the upper section of the nave's walls sited next to the belfry (down figures in each quarter).
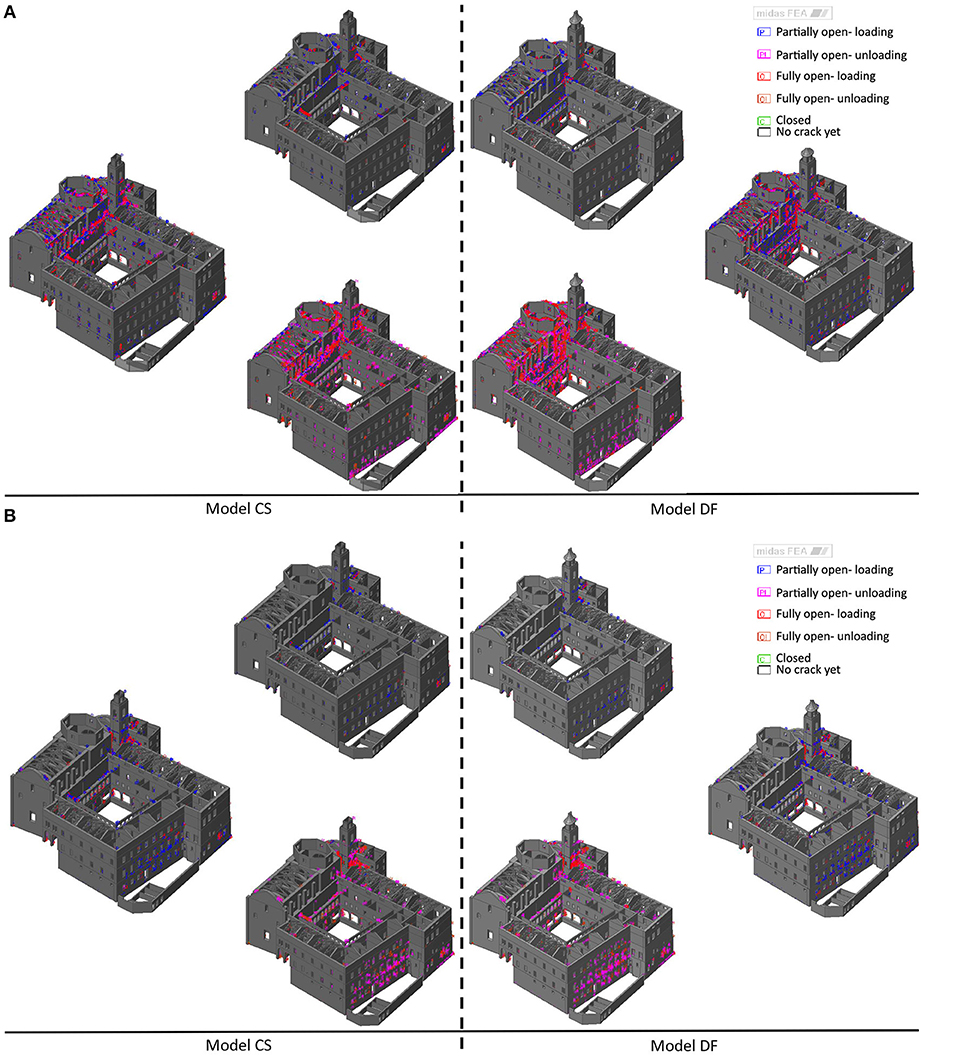
Figure 11. Crack evolution for Model CS and Model DF for uniform loads in X-direction (A) Y-direction (B).
The Capacity of the Macro-Elements
Once the seismic demand Vi, namely the strength demand, is known for different portions and macro-elements of Sant'Agostino's Sanctuary (see section Pushover Analysis: First Results), it is possible to compare the ultimate lateral strength Vu evaluated with the pushover analysis obtaining a new ratio Vi/Vu giving us the safety levels of the analyzed portion like in Brandonisio et al. (2013). For brevity issue only the results of Model CS, i.e., actual state, considering elastic spectra of the ASP_ station are described in order to have a clear assessment of the damage caused by the last seismic events that stroke Central Italy.
In Figure 12, there is a first general consideration on what part of the Sanctuary is more vulnerable, confirming that the major problems are in the transversal direction, i.e., X-direction, and the church (CH) is the most problematic part of the Sanctuary. In the same Figure 12 two horizontal lines are reported corresponding to a ratio Vi/Vu = 1, i.e., the elastic limit condition, and Vi/Vu = 2 corresponding—with a good approximation—to a given level of acceptable damage, according to the behavior factor q = 2, as defined for masonry structure in Italian Code (Ministro dei Lavori Pubblici e dei Trasporti., 2008; Circolare Ministeriale n. 617, 2009; Ministero delle Infrastrutture e dei Trasporti., 2018).
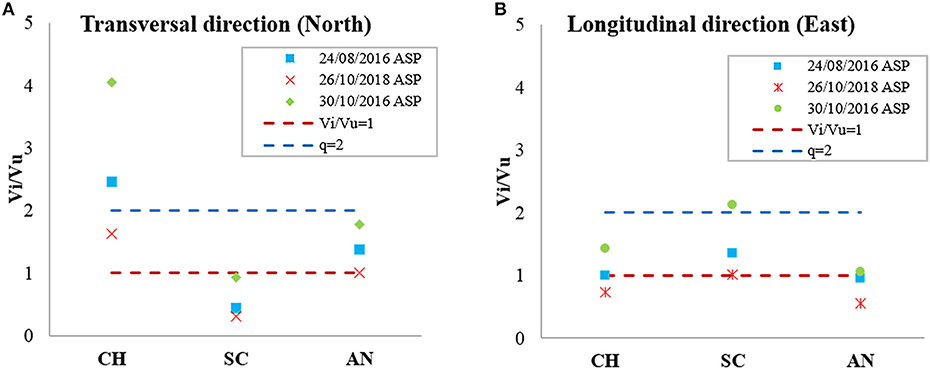
Figure 12. Horizontal seismic demand (Vi) to horizontal strength capacity (Vu) ratio of the different areas of the building for the Model CS for transversal (A), and longitudinal directions (B).
Based on these considerations, the single macro-elements of the church have been analyzed, and the primary results are reported in Figure 13. After plotting Vi/Vu, limited to the value of 10 for a better comprehension, the vulnerability of the house of worship was clearly remarkable in the transversal direction, since the North wall of the nave (L1) shows the most significant values of Vi/Vu, major than 10. L1 is characterized by small stiffness due to a height of 18 m, without internal orthogonal walls and intermediate floors, and a thickness of 2.55 m. In the longitudinal direction, the ratio of Vi/Vu shows that elements more problematic are the façade (T1) and the presbytery (PB). Again, this result agrees with the appeared damage during the Central Italy 2016–2017 seismic sequence (section Damage After Seismic Sequence of 2016).
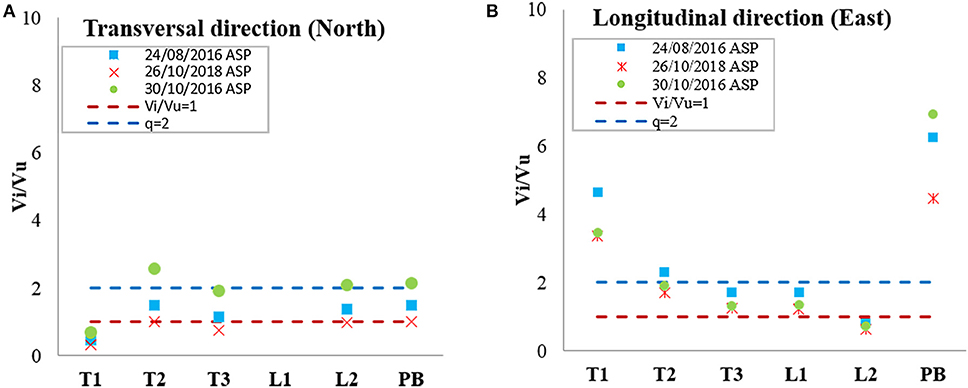
Figure 13. Horizontal seismic demand (Vi) to horizontal strength capacity (Vu) ratio for different macro-elements of the church for the Model CS for transversal (A), and longitudinal directions (B).
Further analyses will have to be conducted for higher knowledge levels (i.e., KL2 and KL3), which leads to greater resistance and a different spread of the damage, but this constitutes the topic of future works.
Conclusions
The paper approaches the seismic vulnerability of Sant'Agostino's Sanctuary in Offida (Ascoli Piceno), a small town in Central Italy. The complex is placed in a highly seismic region; the church portion has been considered unsafe after the earthquakes occurred with epicenters in Accumoli and Norcia, respectively on 24th August and 30th October 2016, and is now closed.
The 3D non-linear solid numerical model (NM) described in this paper gave the chance to investigate the seismic behavior of the complex using sensitivity analysis performed by varying control points and stiffness of the floors. First, the linear dynamic behavior is analyzed confirming the high presence of local modes slightly reduced by rigid floors introduced as a result of consolidation. To gain a proper understanding of the seismic demand, a linear dynamic analysis (obtained by natural and Italian code spectra) was performed not only on the entire complex but also on its main components and some macro-elements identified within the building.
Subsequently, the seismic demand has been compared with the seismic capacity, directly derived by pushover analyses, providing a good match with the most damaged parts and macro-elements of the complex after the seismic sequence of Central Italy in 2016–2017. This confirms that the procedure defined in Brandonisio et al. (2013) can offer an efficient tool to understand the safety of a whole complex and not only of isolated churches, also identifying the most vulnerable elements that are used as well to design local and global retrofitting interventions.
Author Contributions
AN furnished the numerical model. EG analyzed the results. FC supervised the structural analysis. SL supervised the research. All the authors contributed to the writing of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Acary, V. (2001). Contribution a la modélization mécanique et numérique des edifices maconnés (in french). Aix-en-Provence: Université de la Méditerranée - Aix-Marseille II.
Acito, M., Bocciarelli, M., Chesi, C., and Milani, G. (2014). Collapse of the clock tower in Finale Emilia after the May 2012 Emilia Romagna earthquake sequence: numerical insight. Eng. Struct. 72, 70–91. doi: 10.1016/j.engstruct.2014.04.026
Addessi, D., Sacco, E., and Paolone, A. (2010). Cosserat model for periodic masonry deduced by nonlinear homogenization. Eur. J. Mech. A Solids 29, 724–737. doi: 10.1016/j.euromechsol.2010.03.001
Anthoine, A. (1995). Derivation of the in-plane elastic characteristics of masonry through homogenization theory. Int. J. Solids Struct. 32, 137–163. doi: 10.1016/0020-7683(94)00140-R
Asteris, P. G., Chronopoulos, M. P., Chrysostomou, C. Z., Varum, H., Plevris, V., Kyriakides, N., et al. (2014). Seismic vulnerability assessment of historical masonry structural systems. Eng. Struct. 62–63, 118–134. doi: 10.1016/j.engstruct.2014.01.031
Asteris, P. G., Sarhosis, V., Mohebkhah, A., Plevris, V., Papaloizou, L., Komodromos, P., et al. (2015). “Numerical modeling of historic masonry structures,” in Handbook of Research on Seismic Assessment and Rehabilitation of Historic Structures, eds. P. Asteris, and V. Plevris (Hershey, PA: IGI Global), 213–256.
Bartoli, G., Betti, M., and Giordano, S. (2013). In situ static and dynamic investigations on the “Torre Grossa” masonry tower. Eng. Struct. 52, 718–733. doi: 10.1016/j.engstruct.2013.01.030
Betti, M., Drosopoulos, G. A., and Stavroulakis, G. E. (2008). Two non-linear finite element models developed for the assessment of failure of masonry arches. Comptes Rendus Mec. 336, 42–53. doi: 10.1016/j.crme.2007.10.014
Betti, M., and Vignoli, A. (2008a). Assessment of seismic resistance of a basilica-type church under earthquake loading: modelling and analysis. Adv. Eng. Softw. 39, 258–283. doi: 10.1016/j.advengsoft.2007.01.004
Betti, M., and Vignoli, A. (2008b). Modelling and analysis of a Romanesque church under earthquake loading: assessment of seismic resistance. Eng. Struct. 30, 352–367. doi: 10.1016/j.engstruct.2007.03.027
Betti, M., and Vignoli, A. (2011). Numerical assessment of the static and seismic behaviour of the basilica of Santa Maria all'Impruneta (Italy). Constr. Build. Mater. 25, 4308–4324. doi: 10.1016/j.conbuildmat.2010.12.028
Brandonisio, G., Lucibello, G., Mele, E., and Luca, A. De. (2013). Damage and performance evaluation of masonry churches in the 2009 L'Aquila earthquake. Eng. Fail. Anal. 34, 693–714. doi: 10.1016/j.engfailanal.2013.01.021
Caliò, I., Marletta, M., and Pantò, B. (2012). A new discrete element model for the evaluation of the seismic behaviour of unreinforced masonry buildings. Eng. Struct. 40, 327–338. doi: 10.1016/j.engstruct.2012.02.039
Carpinteri, A., Lacidogna, G., Manuello, A., and Niccolini, G. (2015). A study on the structural stability of the Asinelli Tower in Bologna. Struct. Control Heal. Monit. 23, 659–667. doi: 10.1002/stc.1804
Ceci, A. M., Contento, A., Fanale, L., Galeota, D., Gattulli, V., Lepidi, M., et al. (2010). Structural performance of the historic and modern buildings of the University of L'Aquila during the seismic events of April 2009. Eng. Struct. 32, 1899–1924. doi: 10.1016/j.engstruct.2009.12.023
Circolare Ministeriale n. 617 (2009). Cons. Sup. LL. PP., “Istruzioni per l'applicazione delle Nuove Norme Tecniche per le Costruzioni” di cui al decreto ministeriale del 14.01.2008. G.U. del 26.02.2009 n. 47, supplemento ordinario n. 27 (in Italian). Rome: Consiglio Superiore Lavori Pubblici.
Clementi, F., Gazzani, V., Poiani, M., Mezzapelle, P. A., and Lenci, S. (2018a). Seismic assessment of a monumental building through nonlinear analyses of a 3D solid model. J. Earthq. Eng. 22, 35–61. doi: 10.1080/13632469.2017.1297268
Clementi, F., Lenci, S., and Sadowski, T. (2008). Fracture characteristics of unfired earth. Int. J. Fract. 149, 193–198. doi: 10.1007/s10704-008-9239-x
Clementi, F., Milani, G., Gazzani, V., Poiani, M., Cocchi, G., and Lenci, S. (2018b). “The non-smooth contact dynamics method for the analysis of an ancient masonry tower,” in 14th International Conference of Computational Methods in Sciences And Engineering (Thessaloniki, Greece), 090004.
Clementi, F., Pierdicca, A., Formisano, A., Catinari, F., and Lenci, S. (2017a). Numerical model upgrading of a historical masonry building damaged during the 2016 Italian earthquakes: the case study of the Podestà palace in Montelupone (Italy). J. Civ. Struct. Heal. Monit. 7, 703–717. doi: 10.1007/s13349-017-0253-4
Clementi, F., Quagliarini, E., Maracchini, G., and Lenci, S. (2015). Post-World War II Italian school buildings: typical and specific seismic vulnerabilities. J. Build. Eng. 4, 152–166. doi: 10.1016/j.jobe.2015.09.008
Clementi, F., Quagliarini, E., Monni, F., Giordano, E., and Lenci, S. (2017b). Cultural heritage and earthquake: the case study of “Santa Maria della Carità” in Ascoli Piceno. Open Civ. Eng. J. 11, 1079–1105. doi: 10.2174/1874149501711011079
da Porto, F., Guidi, G., Garbin, E., and Modena, C. (2010). In-plane behavior of clay masonry walls: experimental testing and finite-element modeling. J. Struct. Eng. 136, 1379–1392. doi: 10.1061/(ASCE)ST.1943-541X.0000236
D'Ambrisi, A., Mariani, V., and Mezzi, M. (2012). Seismic assessment of a historical masonry tower with nonlinear static and dynamic analyses tuned on ambient vibration tests. Eng. Struct. 36, 210–219. doi: 10.1016/j.engstruct.2011.12.009
Del Piero, G. (1998). Limit analysis and no-tension materials. Int. J. Plast. 14, 259–271. doi: 10.1016/S0749-6419(97)00055-7
EN 1998-3 (2010). Eurocode 8: Design of Structures for Earthquake Resistance–Part 3: Assessment and Retrofitting of Buildings. City of Brussels: Eur. Comm. Stand.
Formisano, A., Florio, G., Landolfo, R., and Mazzolani, F. M. (2015). Numerical calibration of an easy method for seismic behaviour assessment on large scale of masonry building aggregates. Adv. Eng. Softw. 80, 116–138. doi: 10.1016/j.advengsoft.2014.09.013
Formisano, A., Vaiano, G., Fabbrocino, F., and Milani, G. (2018). Seismic vulnerability of Italian masonry churches: the case of the Nativity of Blessed Virgin Mary in Stellata of Bondeno. J. Build. Eng. 20, 179–200. doi: 10.1016/j.jobe.2018.07.017
Gattulli, V., Lampis, G., Marcari, G., and Paolone, A. (2014). Simulations of FRP reinforcement in masonry panels and application to a historic facade. Eng. Struct. 75, 604–618. doi: 10.1016/j.engstruct.2014.06.023
Ghiassi, B., Oliveira, D. V., Lourenço, P. B., and Marcari, G. (2013). Numerical study of the role of mortar joints in the bond behavior of FRP-strengthened masonry. Compos. Part B Eng. 46, 21–30. doi: 10.1016/j.compositesb.2012.10.017
Jean, M. (1999). The non-smooth contact dynamics method. Comput. Methods Appl. Mech. Eng. 177, 235–257. doi: 10.1016/S0045-7825(98)00383-1
Kadas, K., Yakut, A., and Kazaz, I. (2011). Spectral ground motion intensity based on capacity and period elongation. J. Struct. Eng. 137, 401–409. doi: 10.1061/(ASCE)ST.1943-541X.0000084
Lagomarsino, S., Penna, A., Galasco, A., and Cattari, S. (2013). TREMURI program: an equivalent frame model for the nonlinear seismic analysis of masonry buildings. Eng. Struct. 56, 1787–1799. doi: 10.1016/j.engstruct.2013.08.002
Lenci, S., Clementi, F., and Sadowski, T. (2012). Experimental determination of the fracture properties of unfired dry earth. Eng. Fract. Mech. 87, 62–72. doi: 10.1016/j.engfracmech.2012.03.005
Lenci, S., Piattoni, Q., Clementi, F., and Sadowski, T. (2011). An experimental study on damage evolution of unfired dry earth under compression. Int. J. Fract. 172, 193–200. doi: 10.1007/s10704-011-9651-5
Lotfi, H. R., and Shing, P. B. (1994). Interface model applied to fracture of masonry structures. J. Struct. Eng. 120, 63–80. doi: 10.1061/(ASCE)0733-9445(1994)120:1(63)
Lourenço, P. B. (2009). “Recent advances in masonry modelling: micromodelling and homogenisation,” in Multiscale Modeling in Solid Mechanics: Computational Approaches (London, UK: Imperial College Press), 251–294. Available online at: https://www.worldscientific.com/author/Galvanetto%2C+Ugo
Lourenço, P. B., Krakowiak, K. J., Fernandes, F. M., and Ramos, L. F. (2007). Failure analysis of Monastery of Jerónimos, Lisbon: how to learn from sophisticated numerical models. Eng. Fail. Anal. 14, 280–300. doi: 10.1016/j.engfailanal.2006.02.002
Lourenço, P. B., and Rots, J. G. (1997). Multisurface interface model for analysis of masonry structures. J. Eng. Mech. 123, 660–668. doi: 10.1061/(ASCE)0733-9399(1997)123:7(660)
Luciano, R., and Sacco, E. (1997). Homogenization technique and damage model for old masonry material. Int. J. Solids Struct. 34, 3191–3208. doi: 10.1016/S0020-7683(96)00167-9
Luciano, R., and Sacco, E. (1998). A damage model for masonry structures. Eur. J. Mech. A Solids 17, 285–303. doi: 10.1016/S0997-7538(98)80087-9
Manfredi, G., Lignola, G. P., and Voto, S. (2013). Military quarters in Nola, Italy—Caserma Principe Amedeo: damage assessment and reconstruction of a partially collapsed XVIII century complex. Int. J. Archit. Herit. 7, 225–246. doi: 10.1080/15583058.2011.629020
Milani, G. (2011). Simple lower bound limit analysis homogenization model for in- and out-of-plane loaded masonry walls. Constr. Build. Mater. 25, 4426–4443. doi: 10.1016/j.conbuildmat.2011.01.012
Milani, G., Lourenço, P., and Tralli, A. (2007). 3D homogenized limit analysis of masonry buildings under horizontal loads. Eng. Struct. 29, 3134–3148. doi: 10.1016/j.engstruct.2007.03.003
Milani, G., and Valente, M. (2015). Comparative pushover and limit analyses on seven masonry churches damaged by the 2012 Emilia-Romagna (Italy) seismic events: possibilities of non-linear finite elements compared with pre-assigned failure mechanisms. Eng. Fail. Anal. 47, 129–161. doi: 10.1016/j.engfailanal.2014.09.016
Minghini, F., Milani, G., and Tralli, A. (2014). Seismic risk assessment of a 50 m high masonry chimney using advanced analysis techniques. Eng. Struct. 69, 255–270. doi: 10.1016/j.engstruct.2014.03.028
Ministero delle Infrastrutture e dei Trasporti. (2018). DM 17/01/2018–Aggiornamento delle “Norme Tecniche per le Costruzioni” (in italian). Rome: Ministero delle infrastrutture e dei trasporti, 1–198.
Ministro dei Lavori Pubblici e dei Trasporti. (2008). Decreto Ministeriale 14/01/2008–Norme tecniche per le costruzioni (in Italian). Rome: Ministero delle infrastrutture e dei trasporti.
Pande, G. N., Liang, J. X., and Middleton, J. (1989). Equivalent elastic moduli for brick masonry. Comput. Geotech. 8, 243–265. doi: 10.1016/0266-352X(89)90045-1
Pierdicca, A., Clementi, F., Fortunati, A., and Lenci, S. (2018). Tracking modal parameters evolution of a school building during retrofitting works. Bull. Earthq. Eng. doi: 10.1007/s10518-018-0483-9. [Epub ahead of print].
Pierdicca, A., Clementi, F., Isidori, D., Concettoni, E., Cristalli, C., and Lenci, S. (2016a). Numerical model upgrading of a historical masonry palace monitored with a wireless sensor network. Int. J. Mason. Res. Innov. 1:74. doi: 10.1504/IJMRI.2016.074748
Pierdicca, A., Clementi, F., Maracci, D., Isidori, D., and Lenci, S. (2016b). Damage detection in a precast structure subjected to an earthquake: a numerical approach. Eng. Struct. 127, 447–458. doi: 10.1016/j.engstruct.2016.08.058
Poiani, M., Gazzani, V., Clementi, F., Milani, G., Valente, M., and Lenci, S. (2018). Iconic crumbling of the clock tower in Amatrice after 2016 central Italy seismic sequence: advanced numerical insight. Procedia Struct. Integr. 11, 314–321. doi: 10.1016/j.prostr.2018.11.041
Quagliarini, E., Maracchini, G., and Clementi, F. (2017). Uses and limits of the equivalent frame model on existing unreinforced masonry buildings for assessing their seismic risk: a review. J. Build. Eng. 10, 166–182. doi: 10.1016/j.jobe.2017.03.004
Rots, J. G. (1991). Smeared and discrete representations of localized fracture. Int. J. Fract. 51, 45–59. doi: 10.1007/BF00020852
Rots, J. G., and de Borst, R. (1987). Analysis of mixed-mode fracture in concrete. J. Eng. Mech. 113, 1739–1758. doi: 10.1061/(ASCE)0733-9399(1987)113:11(1739)
Zucchini, A., and Lourenço, P. B. (2002). A micro-mechanical model for the homogenisation of masonry. Int. J. Solids Struct. 39, 3233–3255. doi: 10.1016/S0020-7683(02)00230-5
Keywords: FE modeling, solid elements, earthquake loading, non-linear static analysis, seismic vulnerability, damage assessment
Citation: Giordano E, Clementi F, Nespeca A and Lenci S (2019) Damage Assessment by Numerical Modeling of Sant'Agostino's Sanctuary in Offida During the Central Italy 2016–2017 Seismic Sequence. Front. Built Environ. 4:87. doi: 10.3389/fbuil.2018.00087
Received: 25 August 2018; Accepted: 19 December 2018;
Published: 10 January 2019.
Edited by:
Vagelis Plevris, OsloMet–Oslo Metropolitan University, NorwayReviewed by:
Sameh Samir F. Mehanny, Cairo University, EgyptConstantinos Repapis, University of West Attica, Greece
Copyright © 2019 Giordano, Clementi, Nespeca and Lenci. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesco Clementi, ZnJhbmNlc2NvLmNsZW1lbnRpQHVuaXZwbS5pdA==
 Ersilia Giordano
Ersilia Giordano Francesco Clementi
Francesco Clementi Andrea Nespeca
Andrea Nespeca