- 1Department of Civil, Environmental and Geomatic Engineering (IBK), ETH Zurich, Zurich, Switzerland
- 2Faculty of Civil Engineering, University of Zagreb, Zagreb, Croatia
- 3Department of Materials and Laboratory of Concrete, Institut ZAG, Ljubljana, Slovenia
- 4Structural Maintenance and Safety Laboratory (MCS), EPFL, Lausanne, Switzerland
Ultra-high-performance fiber-reinforced cement-based composite (UHPFRC) has been increasingly adopted for rehabilitation projects over the past two decades, proving itself as a reliable, cost-efficient and sustainable alternative against conventional methods. High compressive strength, low permeability and high ductility are some of the characteristics that render UHPFRC an excellent material for repairing existing aged infrastructure. UHPFRC is most commonly applied as a surface layer for strengthening and rehabilitating concrete structures such as bridge decks or building slabs. However, its implementation with steel structures has so far been limited. In this work, the UHPFRC strengthening of a steel bridge is investigated both in simulation as well as in the laboratory, by exploiting a real-world case study: the Buna Bridge. This Croatian riveted steel bridge, constructed in 1893, repaired in 1953, and decommissioned since 2010, was removed from its original location and transported to laboratory facilities for testing prior to and after rehabilitation via addition of UHPFRC slab. The testing campaign includes static and dynamic experiments featuring state-of-the-art monitoring systems such as embedded fiber optics, acoustic emission sensors and digital image correlation. The information obtained prior to rehabilitation serves for characterization of the actual condition of the structure and allows the design of the rehabilitation solution. The UHPFRC slab thickness was optimized to deliver optimal fatigue and ultimate capacity improvement at reasonable cost. Once the design was implemented, a second round of experiments was conducted in order to confirm the validity of the solution, with particular attention allocated to the interface between the steel substrate and the UHPFRC overlay, as the connection between both materials may result in a weak contact point. A detailed fatigue analysis, based on updated FEM models prior to and after strengthening, combined with the results of a reliability analysis prove the benefits of adoption of such a solution via the significant extension of the structural lifespan.
1. Introduction
Management of aging infrastructure has become a significant issue for modern societies, leading to expensive repairs or, in the worst case, tragic events resulting in human loss (collapses of the I-35 Minnesota Bridge and the Morandi Bridge in Genoa). To overcome this problem, monitoring strategies have emerged for real-time tracking of condition, combined with new rehabilitation techniques, which are cost effective and minimally invasive in terms of application and operation (Chang et al., 2003).
Within this framework, the use of ultra-high-performance fiber-reinforced cement-based composite (UHPFRC) in strengthening projects provides an efficient solution in terms of durability and increase of load capacity (Denarié et al., 2005; Moreillon and Menétrey, 2013; Tayeh et al., 2013; Denarié and Brühwiler, 2015; Martín-Sanz et al., 2016). UHPFRC presents remarkable compression and tension strength as well as low permeability, rendering the material not only well suited for structural enhancement, but also beneficial for waterproofing (Habel, 2004; Fehling et al., 2014). Despite its almost exclusive use with concrete bridges, the combination of UHPFRC with steel could offer similar improvement potential. Some of the current research pertains to the rehabilitation of existing orthotropic decks, where a UHPFRC layer can ameliorate fatigue issues, especially at the weld between the deck plate and the longitudinal stiffeners. Marchand et al. (2012) quantify this reduction to lie in a range between 30 and 60%, as compared to the bare system. In the work of Dieng et al. (2013), the application of a UHPFRC layer in place of a bituminous material is studied, highlighting reductions in stresses and deflections. However, decks comprising a UHPFRC layer connected to steel girders have also been designed, as described by Fehling et al. (2011) and Yoo and Choo (2016). Other projects include the use of UHPFRC in local zones, such as corroded beam ends (Zmetra et al., 2015) or joints. An example of the latter is found in the rehabilitation of the Pulaski Skyway (McDonagh and Foden, 2016), where UHPFRC was employed to fill the connections between new precast concrete slabs and existing steel girders. Nevertheless, a common question arises relating to the bonding of UHPFRC and steel. Several studies have been carried out to check the behavior of the connection while using steel studs (Luo et al., 2015a,b; Gascon et al., 2017), demonstrating that the strength of studs embedded in UHPFRC is significantly higher than those included in other high-strength concrete matrices.
A different application for this material pertains to the strengthening of riveted bridges subjected to fatigue or extreme loads, where a slab enables a composite action and elevates the neutral axis of the section, reducing the maximum stress level. The concept, already in use with conventional concrete (Frangopol et al., 2001; Kwon et al., 2009), has been implemented for the first time using UHPFRC onto the Buna bridge case study, a decommissioned steel structure, more than 60 years old. In order to assess its performance, static testing was carried out prior to and after rehabilitation, by means of state-of-the-art sensing technologies, such as Digital Image Correlation (DIC), Acoustic Emission (AE) or embedded Fiber Optics (FO). Furthermore, vibration modal analysis was performed, including either a simulated ambient excitation via random hits by multiple hammers or an induced vibration by means of a shaker. The preliminary tests prior to rehabilitation are explained in the works of Dzajic (2014) and Martín-Sanz et al. (2018). The results of the testing allowed the calibration of a physical Finite Element (FE) model at every implementation stage, serving as a design tool for the new slab, validation method for the result and as a tool for predicting different types of failures, in addition to those tested. In this work, the FE model is exploited to carry out a fatigue analysis, for both stages (prior to and after strengthening), based on the Palmgren-Miner rule (Miner, 1945). In this analysis, the elements prone to fatigue include not only the existing structure but also the stud connection between the slab and the steel. Furthermore, in order to assess the efficiency of the composite action and the benefits of the rehabilitation solution, a reliability analysis is conducted (Ditlevsen and Madsen, 1996; Melchers and Beck, 2018), looking into buckling and capacity loads.
This paper comprises two main sections: In the first chapter, the case study will be introduced in detail, describing the experimental phases, the strengthening design, as well as the testing results. The second chapter establishes Performance Indicators (PI) for quantifying the adequacy of the rehabilitation strategy.
2. Case Study
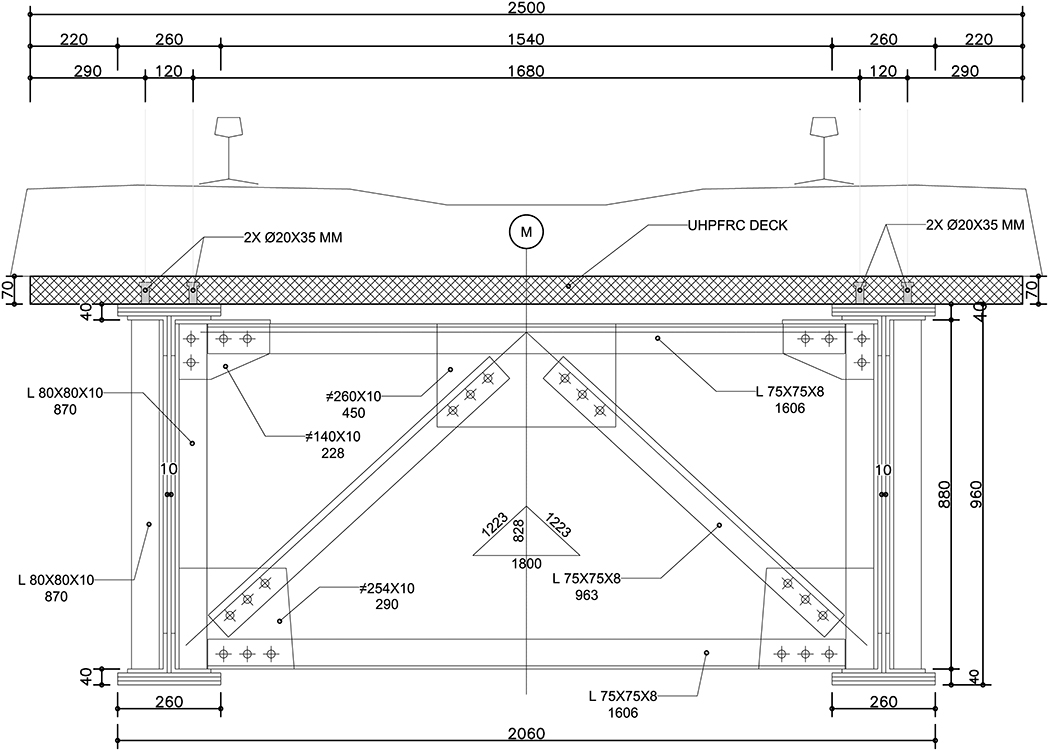
The Buna bridge formed a component of to the Croatian Railway network since 1893, when it was constructed, until its decommissioning in 2010. It stands as a good example of the steel bridge construction techniques of that period, i.e., steel plates joined by riveted connections. The structure, almost 9 m long, comprises two main girders of 0.9 m depth, tied to each other every 2.26 m by means of L shape profiles. Diagonal L beams in a zig-zag disposition close the lattice on the top, leaving a space of 1.8 m between the two girders. Wooden sleepers were directly supported over the bridge without any covering slab. Figure 1 illustrates the configuration of the structure.
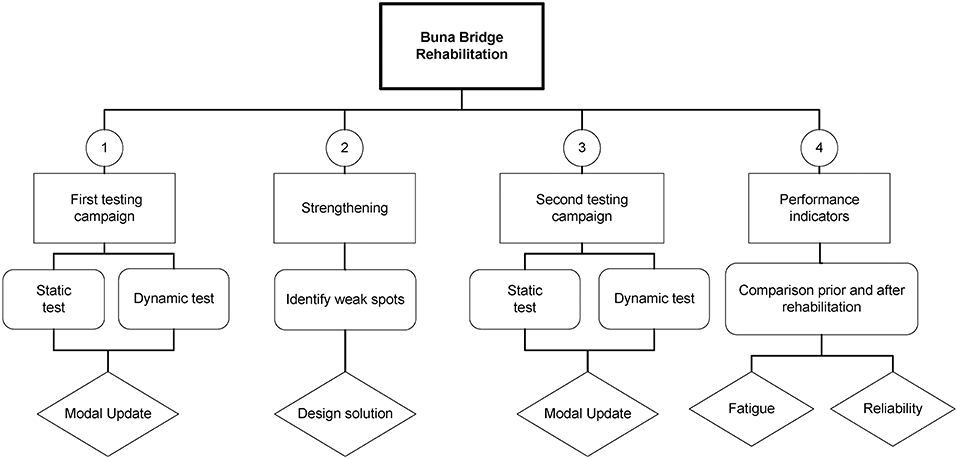
Once the bridge was decommissioned, it was transported to laboratory facilities (first, to the company IGH in Zagreb, for static testing, afterwards to the Viadukt company for dynamic testing, and finally to the ZAG institute in Ljubljana for strengthening and final testing), in order to define its behavior and to find an economical and practical strengthening solution that could prove useful in future projects. To this end, the workflow presented in Figure 2 was followed. Firstly, an initial testing campaign was planned, aiming to obtain enough data to create an accurate Finite Element (FE) Model able to reproduce the current behavior of the structure. Once the model was tuned, a strengthening solution was designed to ameliorate the existing capacity and prevent future damage. A second testing campaign followed in order to validate the results of the design. Finally, the FE models derived from the tests serve for determining Performance Indicators (PIs) for both systems, prior to and after rehabilitation. In doing so, a reference on the adequacy of the strengthening can be established.
2.1. Testing Campaign Prior to Rehabilitation
The first testing campaign dealt with the original structure prior to rehabilitation and was performed in two stages. The first one, described by Dzajic (2014), consisted of a static test up to a maximum load as per Load Model 71 specified in the Eurocode (EN 1991-2, 2003), where strain at the flanges at mid-section as well as deflections were obtained. Figure 3 illustrates the loading distribution over the bridge. In a second phase, a dynamic analysis was conducted under two different excitations: (a) ambient vibration, obtained by manually and randomly hitting the structure with two hammers, simulating conditions that are suitable for Operational Modal Analysis (OMA), and (b) swept sine vibration from a shaker mounted horizontally and vertically at mid-span with shaker also measured (Experimental Modal Analysis, EMA). To replicate the conditions of on-site testing to the extent possible, the structure was tested with the original elastomeric bearings, although rails and sleepers were removed.

Figure 3. Load application for static test. On the left, bridge prior the rehabilitation, on the right, bridge after strengthening.
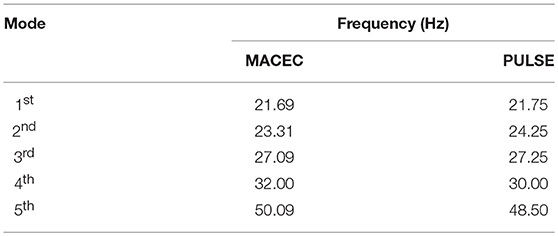
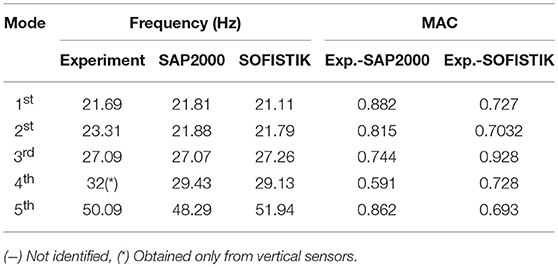
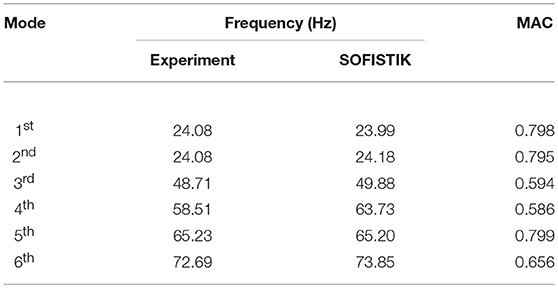
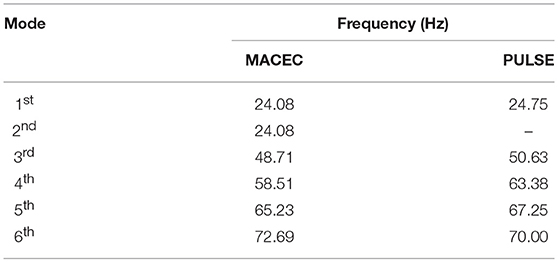
In order to obtain an accurate representation of mode shapes, 119 points along the structure were measured, both in the vertical and the transverse direction. Since such a large number of sensors was not available, a roving test was conducted, relying on the dynamic reciprocity (or Betti-Rayleigh) principle, with 5 PCB sensors in the case of OMA and 15 for EMA. Two distinct processing methods were used for each test (operational and experimental modal analysis), namely the PULSE software from Bruel & Kjær (Kjaer, 2016) and the MACEC Matlab toolkit (Reynders et al., 2011), respectively, demonstrating good agreement between the obtained results. Table 1 offers a comparison between the identified modes in the PULSE and MACEC software. Different identification methods were employed within each software, namely the Frequency Domain Decomposition (FDD) in Pulse and the Poly-reference least squares complex frequency domain estimator (pLSCF) in MACEC. In this work, frequencies and mode shapes acquired via the MACEC software analysis will be used as the reference results from the experiment.
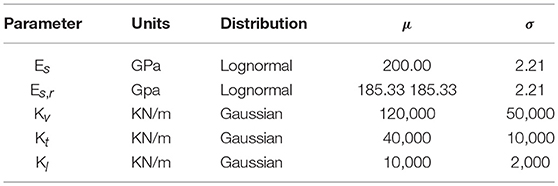
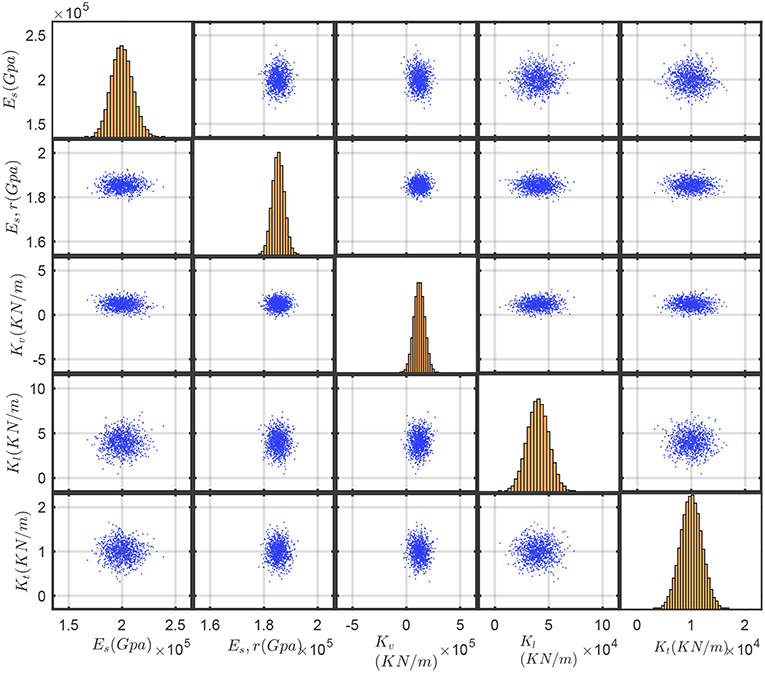
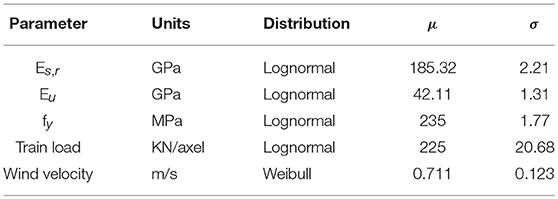
Once the modal parameters were identified, a numerical FE model was developed in SAP2000 (CSI, 2010) in order to perform model updating, so that a model that is true to the real-life system may be established. This ought to serve as the structure's digital twin for further simulations beyond those featured in the conducted experiments. To this end, a Monte Carlo (MC) simulation was carried out, considering as input the parameters driving the modal properties of the structure, namely the elastic modulus of steel (Es) and the bearing coefficients in vertical, transverse and lateral directions (Kv, Kt, and Kl, respectively). The statistical parameters for Es are obtained from Hess et al. (2002). For the case of the spring coefficients, a mean value is offered by the manufacturer, and a Gaussian distribution was herein considered. The characteristics of the distributions are offered in Table 2 and further illustrated in Figure 4. A preliminary attempt, relying on these input variables, was not able to render accurate results, therefore a thorough analysis of the connections was deemed necessary. In the Buna bridge, the flanges of the main girders comprise 10 mm thickness plates, joined together by rivets, resulting in sections ranging from 20 to 40 mm in total depth. Based on the works of Rathbun (1936) and Kulak et al. (2001), it is proven that the grip length of a rivet (the distance between head and tail) influences the connection stiffness. Consequently, a different elastic modulus (Es, r) was considered to account for each flange thickness, allowing for a more precise result for the FE model updating. A lognormal distribution was once again considered for this case. In order to find the appropriate set of parameters, a fitness function F relying on frequencies and Modal Assurance Criterion (MAC) value is implemented as per Equation 1
where fi and modei represent the frequencies and modes from the SAP model, and fe and modee indicate those identified in the experiment.
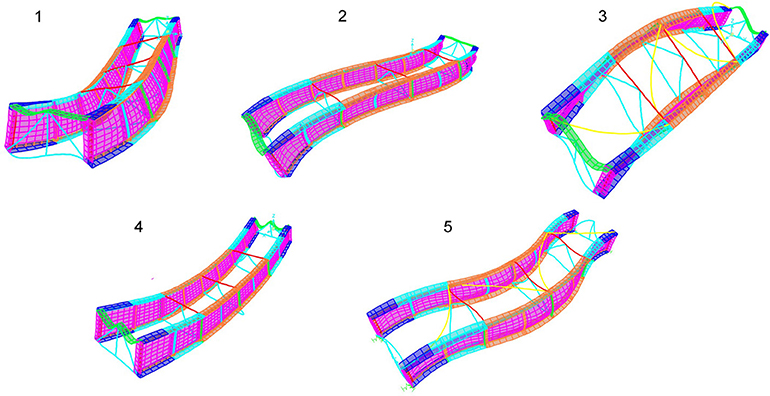
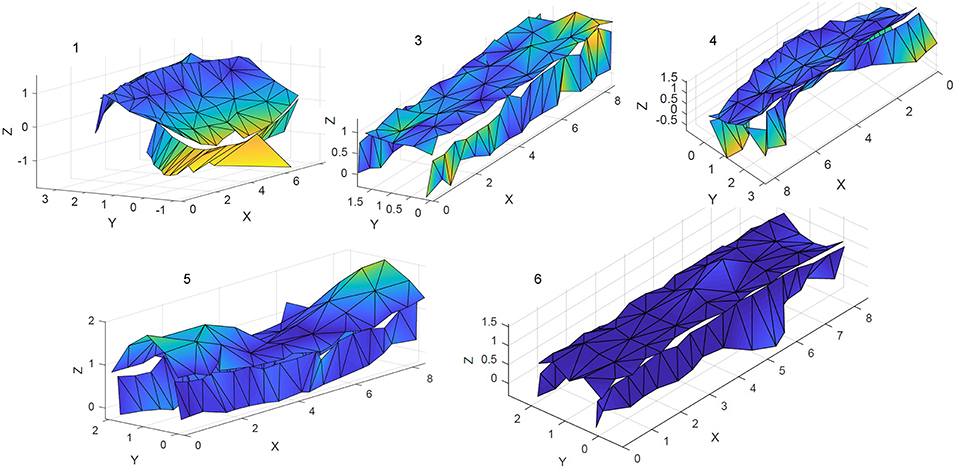
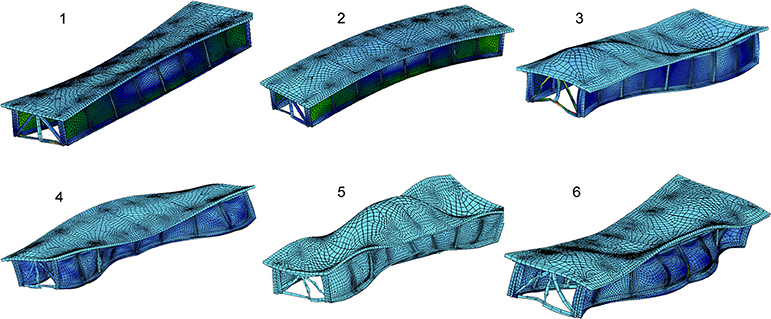
In addition to a simple structural model established in SAP2000, a SOFiSTiK model [SOFiSTiK (2016)] was further developed, since the latter allows for more refined implementation that is essential for the fatigue analysis to be conducted as part of the performance assessment of the rehabilitation solution. Material properties and geometry are kept consistent between the two numerical models. A comparison between the deflection and the strains at mid span, for the experiment and the model, is reported in Table 3. Moreover, the summary of the most relevant frequencies for the experiment and both models are presented in Table 4, including a comparison of mode shape approximation in terms of the MAC value. Furthermore, Figures 5–7 illustrate the mode shapes identified from the experiments and those computed via the SAP2000 and SOFiSTiK numerical models, respectively. The FEM analysis reports existence of a further mode in between the 27.09 and 50.9 Hz frequencies, which was only picked up in the experiment when analyzing the vertical sensors and omitting the horizontals. As can be deduced from the obtained MAC values, the poor lateral connections of the main girders and the possibly uneven support on the bearings, placed over irregular concrete blocks, hinder a perfect match of the experimental mode shapes from appearing by means of the FE model representations, although the approximation is considered adequate. The first three modes present a lateral component, intermixed with a vertical response, whereas 4 and 5th exhibit a higher vertical component. Mode 5 appears to be a coupled bending/lateral mode, which is weakly captured in the experiment.
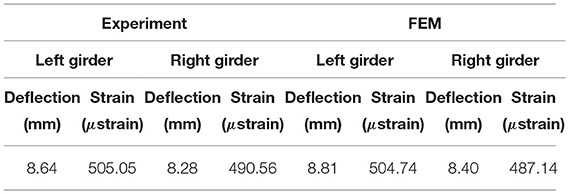
Table 3. Comparison of static test results between SOFiSTiK FE model and experiment prior rehabilitation.
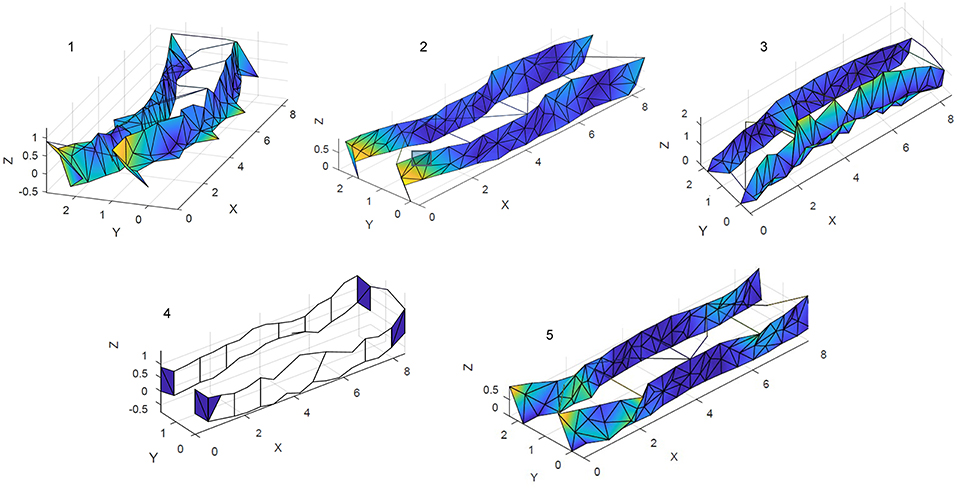
Figure 5. From left to right, from top to bottom, identified modes 1, 2, 3, 4 and 5 for the original structure.
2.2. Strengthening Solution
Based on the testing, it was possible to identify weak spots in the original structure, aiming to:
• Reduce the maximum tensile stress in the lower flange of the girders in order to avoid fatigue problems at the riveted joints. It is important to note at this point that the structure displayed sufficient capacity already in its original configuration. However, the strengthening reported herein serves as a case study for further rehabilitation projects in need of repair and to assess the improvement rendered by adoption of the UHPFRC rehabilitation solution.
• Increase the load transfer capacity in the transverse direction. In the original bridge, the only structural elements allowing this transfer are the triangular transverse lattices and top diagonals. For an unbalanced train load, an equal distribution of vertical loads between the girders is achieved by means of the sleepers and rails. However, for lateral loads such as wind, the sliding connection that sleepers ensure is not able to transmit the loads to both main elements.
• From an environmental perspective, the chosen rehabilitation option should protect the riverbed from spillage of contaminated substances such as oil or flammable materials.
For complying with all previous requirements, the chosen solution opted for a cementitious-based slab to be placed atop the girders, connected with steel studs, in pursuance of a composite section with an elevated neutral axis. In place of using conventional concrete, UHPFRC was chosen for the envisioned strengthening scheme due to its aforementioned outstanding mechanical and durability properties. Major advantageous benefits include (a) a reduction of the depth of the section in comparison to use of other cementitious materials and, consequently, a decrease in the added weight, (b) a better adjustment of the rail profile due to the reduced depth, (c) creation of a durable waterproof membrane, offering protection not only for the underlying steel but also for the studded connections, and (d) minimizing the required downtime in case of on-site repair, due to the easy and fast application of the material.
The feasibility of the implementation in a real project was also taken into account. A major concern involved the employment of the previous wooden sleepers on top of the slab, as uneven contact will result in an irregular stress distribution. For the particular case of the Buna Bridge we opted for the most economical option, namely the application of a high-strength mortar atop the slab prior to placing the sleepers. Other possibilities include the use of direct fastening or optimized fixed track systems using UHPFRC in place of concrete (Cui and Chew, 2000).
Another practical aspect pertains to drainage. Although in the experimental campaign the slab was casted flat, UHPFRC is able to provide a slope, as proven by Denarié et al. (2005). For a real application, a 2% slope may be easily realized by using fresh UHPFRC with thixotropic properties.
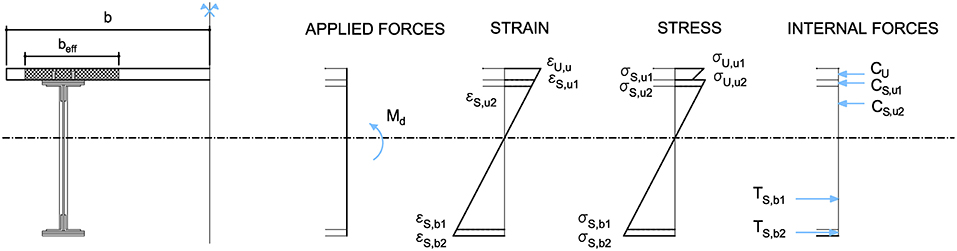
In order to design the slab, an analytical approach is firstly followed, adapting the formulation established in the Swiss code 2052 (2016) as per Figure 8. The aforementioned code overviews the behavior of composite sections made of concrete and UHPFRC, but excludes instances of UHPFRC-steel composite sections. Therefore, for the case that pertains herein, a modification is included to account for this differentiated combination of materials: the effective length of the slab beff is reduced, taking into account the ratio n between the elastic modulus of steel (Es) and concrete (Ec), as in conventional composite sections comprising concrete and steel. The design of the Buna Bridge slab aims to reduce the stresses in the lower flange by 40%, therefore this condition is imposed in the calculation. Based on these considerations, a depth of 70 mm is established as the required dimension. A numerical model of the slab has been subsequently established in the updated SOFiSTiK model, introducing reinforcement in transverse direction with rebar of ϕ12 mm spaced at 250 mm. In Figure 9 the midspan section is detailed. The connection between the slab and the existing girders was achieved by means of two lines of welded steel studs, of 19 mm diameter, spaced at 100 mm, following the conventional construction for composite structures (Johnson, 2018). Particular attention was placed on enabling the connection, since despite the broad experience in place for UHPFRC-concrete structures, where adequate bonding is ensured, limited experience is available regarding steel-UHPFRC connections. However, Gascon et al. (2017) carried out experiments over 5 specimens with different types of concrete and studs, demonstrating that using the latter in combination with UHPFRC leads to an increase on bearing capacity and provides high ductility detail. Furthermore, Yoo and Choo (2016) demonstrated that current design codes are conservative when designing a studded connection with UHPFRC and that for a certain stud spacing, the connection can be modeled as a perfect bond. For this reason, the formulation proposed in the Eurocode EN 1994-1 (2005) for composite sections was followed, which determines the shear resistance PRd of a headed stud as the minimum value given in function of either the steel resistance, which reads
or the concrete resistance, calculated as
where γv is the partial factor, equal to 1.25, d indicates the diameter of the stud, fu denotes the tensile strength of the stud material, fck is the compressive concrete strength, and α is a factor related to the dimensions of the stud as compared to the depth of the concrete section.
The bridge was modeled in SOFiSTiK using shell elements and was calculated following the Mindlin plate theory extended by a non-conforming formulation. The non-linear behavior of the UHPFRC is included by means of non-linear stress-strain laws, considering tension hardening and softening after cracking, depending on fracture energy.
The UHPFRC recipe chosen for the project was developed in the ZAG laboratory, using cement CEMI 52.5R from Anhovo, with steel fibers (length Lf= 10 mm, diameter df= 0.2 mm) and 3.9% fiber volume fraction. It is important to note that the mixing was carried out in an ordinary concrete plant and transported for 30 min by means of a conventional concrete mixer truck, handled by workers with no specific training on UHPFRC deployments. Due to the humidity conditions in the location where the cement bags were stored, the mix presented a lower workability than expected, thus the slab eventually became 79 mm thick in lieu of the 70 mm intended in the original design. Material tests were conducted following the Swiss norm for UHPFRC, SIA2052 (2016), delivering a compressive strength (f'=c) of 154.5 MPa and a tensile strength (ft) of 12 MPa at 56 days. The elastic modulus was obtained from compression tests, rendering a value of 42.1 GPa.
2.3. Testing Campaign After Rehabilitation
2.3.1. Static Test
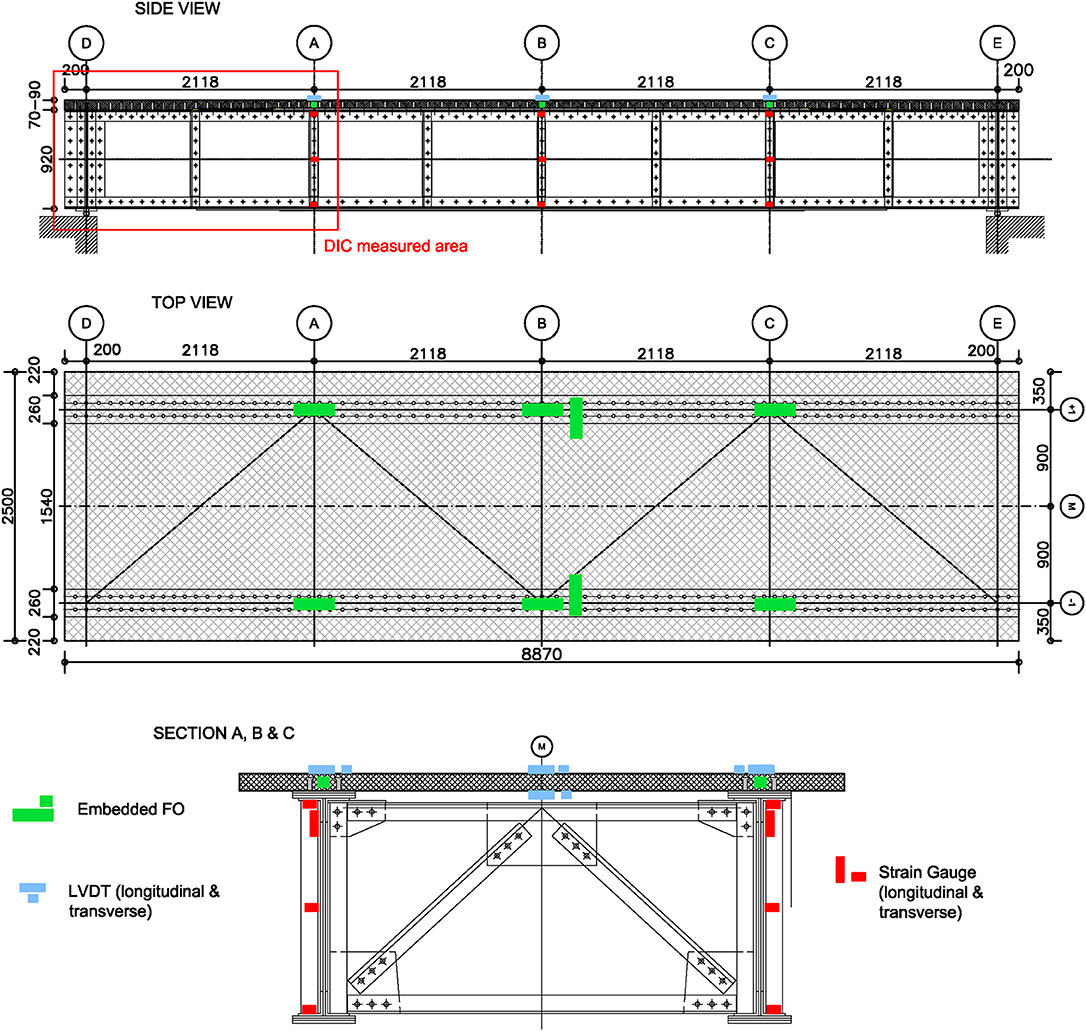
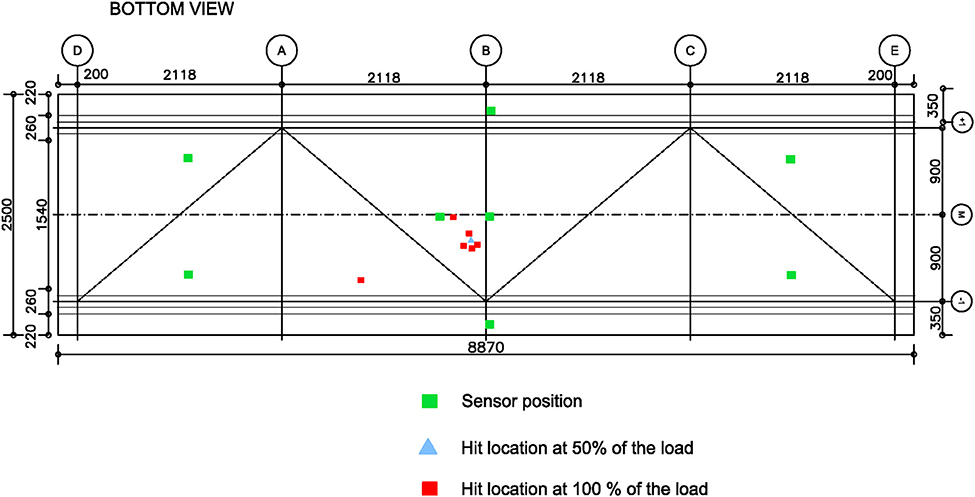
For the static test, strain gauges and LVDTs were placed on 3 sections (midspan and quarter bridge) with the configuration described in Figure 10, in order to locate the neutral axis of the section as presented by O'Connor et al. (2017) and to allow adequate calibration of the FE model as accurately as possible. Moreover, 3D Digital Image Correlation was applied on one quarter of the bridge, toward the support, where higher shear is expected and hence a slip between the UHPFRC-steel surfaces may occur. Furthermore, 8 Acoustic Emission (AE) sensors were placed on the bottom part of the UHPFRC slab. The AE technology will be further explored in a third testing phase, lying outside of the scope of this paper, where the bridge will be artificially damaged and measured. Figure 11 illustrates the sensor placement as well as the hits obtained in the 3 phases of the test, namely a load application of 20%, with no events recorded, 50% and 100%. The experiment was performed in the same fashion as the previous static test on the original structure, as described by Dzajic (2014), where the maximum load was 1530 KN, applied by means of two hydraulic jacks distributing the force over 8 points on the rails (Figure 3).
With the processed results from sensors and material properties, modal-based FE model updating was performed anew, by only varying the UHPFRC parameters as the further structural parameters are considered to be identified in the first testing phase.
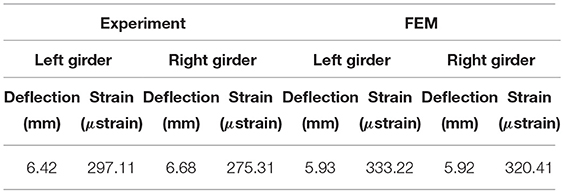
The DIC technology was exploited to investigate the bond between the UHPFRC slab and the steel. As an initial hypothesis, the connection was considered as fully restrained for the design of the slab, with this assumption subject to validation from DIC measurements. Figure 12 includes a graphical description on DIC identified points, as well as the measured vertical and lateral displacements of points P3 and P7, located in the UHPFRC slab and steel flange, respectively, demonstrating a horizontal shift of 0.06 mm. Taking into account that the points are not perfectly aligned, due to the beveled edge of the slab, and the DIC resolution error (0.008 mm), the obtained results confirm the assumption of no slip between UHPFRC slab and steel. Furthermore, the state of the connection between both materials may be used to establish a Performance Indicator. In a healthy condition, this slip should be considered minimal; however, if an extreme event occurs, ductility must be ensured by the deformation of the studs, as established in the Eurocode EN 1994-1 (2005). Luo et al. (2015b) demonstrate that studs embedded in UHPFRC are able to provide higher ductility than when embedded in concrete. Another PI may be extracted from the strain and deflection measurements. Firstly, these allow for the validation of the FE model via direct comparison of results, as illustrated in Figure 13, in terms of the neutral axis position. Based on this figure, it may be observed that the model predicts strain that is 8% higher than in the experiment, which may be attributed to a more distributed loading on the bridge due to the sleepers, which is an element not accounted for by the FE model. The differences on measured strains between the top steel flanges and the UHPFRC may be attributed to the different position of the sensors, as positioning on the exact spot is not possible. Furthermore, the FEM presents a straight strain profile, typical of steel sections in elastic regime. The deviation from a straight line in the experiment may result from the irregularity of the section where the strain gauge is placed. Moreover, maximum stresses stand for a common indicator in codes/standards concerning the structural safety, when exceeding yielding or fatigue stresses. As mentioned in previous chapters, the original bridge comprised a healthy state of adequate capacity; however, in order to confirm potential of the employed rehabilitation strategy, the design of the slab is focused on reducing the maximum stress by a level of 40%. Table 5 describes strains and deflections obtained from the experimental campaign and the FEM analysis relying on the SOFiSTiK model, indicating a reduction in stress of 41.5 and 19.3% for deflections, in comparison to the original structure. In further assessing performance, a detailed fatigue analysis follows in section Fatigue.
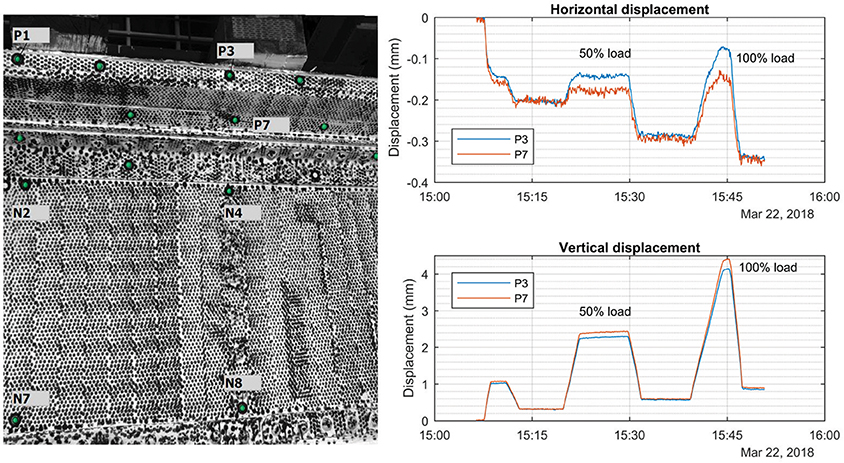
Figure 12. On the left, location of point P3 (steel) and P7 (UHPFRC). On the right, the respective displacements in vertical and lateral directions.
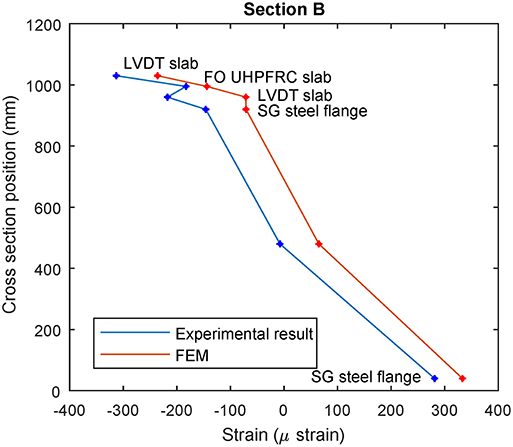
Figure 13. Strain values obtained from experiment and FEM, at the midspan of the bridge. Experimental values present average value of both girders.
2.3.2. Dynamic Testing
In terms of vibration testing, 61 extra locations were measured on the slab, rendering a total of 180 computed points. The experiment was conducted as described in the previous paragraphs, utilizing random hammer and shaker excitations, analyzed with the same software. In this case, the OMA was conducted not only with PULSE but also with MACEC. The results from EMA in MACEC offered better results and are presented in this chapter. Due to the large amount of setups needed to cover all points, the MACEC procedure was automated based on the work described by Reynders et al. (2012) and Leyder (2018), relying on a three-stage procedure: firstly, all certain spurious modes are removed from the stabilization diagram, and secondly, a hierarchical clustering is employed to group remaining similar modes and lastly, one single physical mode is chosen from the cluster. An additional step is herein included, since with the aforementioned methodology not all the setups were able to produce the same number of modes. In order to overcome this issue, the total number of modes was defined beforehand and the clustering was completed based on similarity of MAC (Modal Assurance Criterion) values.
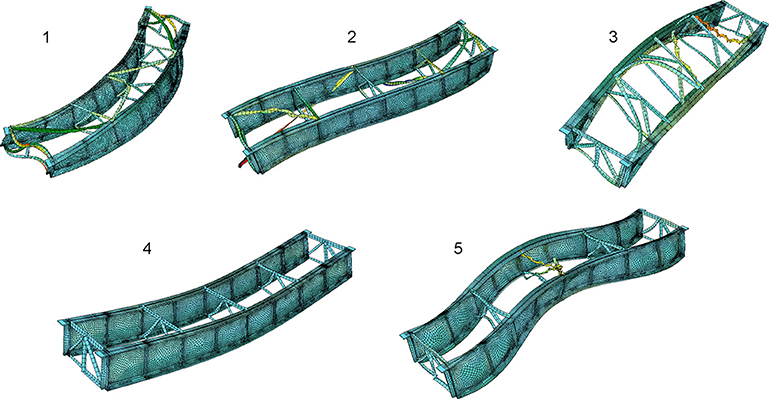
Table 6 presents the modal frequencies identified (using the MACEC toolkit) from the experiment vs. the corresponding frequencies in the model, whereas Figures 14, 15 illustrate the experimentally identified and simulated mode shapes. For reasons of completeness, we offer a comparison of the results from MACEC and Pulse deployed in Table 7, where sufficient agreement is found between the two analysis options. In this second test, the boundary conditions were reconfigured so as to assure a stable placement of the bridge on top of the bearings. It can be appreciated that, in comparison with the former test, the lateral frequencies appear at higher modes due to the increase of stiffness offered by the composite section. In the strengthened structure as well, closely spaced modes are predicted by the FE model at around 24 Hz (a pure first vertical mode and an interaction between first and second), whereas the experiments allows for the inference of only one of these two numerically predicted modes.
3. Performance Indicators
3.1. Introduction
The results hitherto explained may serve for a comparison between the bridge prior to and after rehabilitation; however, the benefits of the strengthening remain qualitatively unstated. Consequently, an important phase of the project comprises the analysis of Performance Indicators (PI), which allow a characterization of each structure, in order to demonstrate the adequacy of the proposed solution. Several studies regarding PI selection for European road bridges have been carried out in the past (Stipanovic and Klanker, 2016; Strauss et al., 2016), although many of them pertain to concrete structures subjected to non dynamic loads. For the particular case of the Buna Bridge, three PIs have been selected to demonstrate and quantify the improvement between both structures, specifically reliability based on maximum loads, buckling capacity and fatigue.
3.2. Reliability Based on Maximum Load Capacity
A classic approach to define the structural performance of a given system involves a comparison of the demand parameter S (such as the Stress produced on an element) with the capacity or Resistance, R. A refined analysis of this method includes uncertainties on the latter parameters, representing them by their known probability density functions fS and fR, respectively. The safety of a structural element is ensured if the resistance is higher than the demand, defining the following probability of failure (pf) or limit state function (G), as
where D represents the failure domain (Melchers and Beck, 2018). Subsequently, the reliability β is defined as the complement of the probability of failure. In case of normal, random distributions, the equation reads as
with ϕ() representing the normal distribution function.
As a result of the knowledge gained through the modal updating process, it is possible to identify the most influencing parameters on the analysis outcome, thus five elements are defined according to their probability distributions instead of their deterministic values. Regarding Resistance, material properties such as yielding stress of steel (fy), elastic modulus of UHPFRC (EU) and steel (Es) are chosen. Statistical parameters for steel are obtained from Hess et al. (2002), whereas those which are UHPFRC-related are acquired from the field experiment. The mean value for steel is reduced to account for the previous observation related to the difference in stiffness of riveted plates. In terms of Stress, two types of live loads are studied: trains and wind. The former is included in the model based on the results published by James (2003) and HŽ-Infrastruktura (2013), offering mean value, standard deviation and type of probabilistic distribution for freight trains. Moreover, the correction factors instructed by the Eurocode EN 1991-2 (2003) α and the dynamic factor Φ are applied, although no uncertainty is included for these. A similar procedure is observed for the wind loads, generally defined in the Eurocode 1991-1-4 (2005) as a pressure qp depending on the wind velocity vm as stated in Equations 6, 7:
where z represents the height of the structure under consideration, cr is the roughness factor, co stands for the orography factor, vb defines the basic wind velocity, lv determines the turbulence factor and ρ represents the air density. Statistical parameters of wind velocity are obtained from Bajic and Peros (2005), whereas the rest of the factors remain deterministic. Table 8 presents a summary of the selected inputs.
The limit function is chosen as the exceedance of the elastic stress limit of the steel at hot spot locations, i.e., midspan of the bridge, under the action of dead loads (weight of bridge elements, D) and the aforementioned live loads, as presented in Equation 8:
It is suggested that plastification at the flanges will eventually lead to a mechanism and therefore a collapse of the structure.
The reliability procedure is performed in four stages explained herein:
• In the first place, 1,000 sets based on the variables described above are generated using the Latin Hypercube Sampling implemented in UQLab (Marelli and Sudret, 2014), divided in two batches with 5,000 iterations each.
• Subsequently, the sets are implemented in an ABAQUS (Hibbett et al., 1998) FE model (based on the SOFISTIK updated model) and results are obtained at hot locations. This second model was developed using a diferent software for logistic reasons, as the 1,000 iterations could be run within the ETH cluster. For this case, the steel elements are modeled as shells, whereas the UHPFRC slab is conformed by solid elements with embedded rebar. The connection between both materials is still considered as rigid. UHPFRC was modeled as a non linear material. The model was compared against test results obtaining a good fit, therefore it is considered to offer the same results as the SOFISTIK method.
• Thirdly, in order to increase the number of outputs within a reasonable analysis time, a surrogate model was introduced. Polynomial Chaos Expansion (PCE) has proven to be a reliable and efficient tool for such a task and it is also available in UQLab. The reader is referred to the works of Blatman and Sudret (2010) for a more detailed introduction on this topics, as well as in the work of Spiridonakos and Sudret (2016), which discusses surrogate construction for the extended case of nonlinear dynamical systems.
• Finally, the reliability analysis is performed by means of a Monte Carlo (MC) simulation over the PCE dataset.
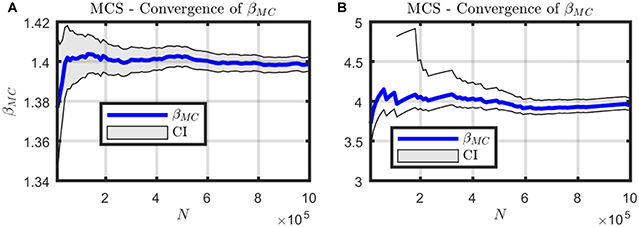
The reliability factor β for the original structure reaches a value of 3.48, indicating a probability of failure of 2.48e-4 . For the strengthened structure this value is smaller than 10−7 (equivalent to a β of 5.20), however the algorithm is not able to run beyond this point due to the smaller failure probability. According to the Eurocode, a β equal to 3.8 for a 50 year targeted life period is recommended, a value which is surely achieved when including the UHPFRC slab. It is worth noticing that the reliability index offered by the original structure indicates that it remains able to carry the actual train loads. The enhancement offered by the UHPFRC in this project serves a proof of concept for other structures in need of stresses amelioration, as well as the benefits established in section Strengthening Solution.
In considering a future network capacity, another reliability study has been carried out, assuming the same parameters previously described although considering an increase on traffic loads of 20% and maintaining the same wind loading. For this case, the reliability of the structure without strengthening is reduced to 1.39, whereas the new design reaches a reliability index β equal to 3.95. The iterations for this last approach are shown in Figure 16.
3.3. Buckling
A similar procedure was followed to study the buckling behavior of the structure. The same probabilistic distributions for materials and loads were applied although the reliability analysis was eventually not carried out, as the probability of failure of the original structure appeared negligible. For the worst-case scenario, the first buckling mode provided a load factor (value that multiplies a given load for buckling to occur) of 4.08 and concerned only local modes of the plate girders. A global effect appears for a load factor equal to 6.44. Despite these values resulting in an improvement when applying strengthening solution (4.69 and 12.10, respectively), the most efficient method to ameliorate the local buckling of the thin girder plates relies on the inclusion of stiffeners and not the UHPFRC slab, therefore this PI is not considered relevant for this case.
3.4. Fatigue
Fatigue damage constitutes an important consideration for steel bridges (Schilling, 1978; Chan et al., 2001) and may be the design driver for numerous structural details, such as connections or riveted regions. To this end, this section is focused on fatigue analysis, so as to highlight the impact of the proposed strengthening approach to the fatigue behavior of the bridge. Although such an effect may also be quantified in terms of the associated reliability (Tatsis et al., 2017), it is herein illustrated via the remaining service life of four representative structural points, which are selected on the basis of maximum stress concentrations factors.
Fatigue life prediction on steel structures is typically based on Miner's rule, also known as the linear accumulation rule, which constitutes one of the most commonly used cumulative damage models. As such, Miner's rule defines the damage on a structural point subjected to cyclic stress of a certain amplitude Δσj as the ratio of operational cycles n(Δσj) to the number of cycles to failure N(Δσj). Subsequently, the damage induced by cycles of different stress levels is calculated by linear superposition of all individual contributions. In case of measured or numerically derived stress time histories, the number of operational cycles is typically evaluated using a cycle counting method, with the rainflow-counting algorithm being the most accurate and widely adopted approach in fatigue analysis Suresh (1998). On the other hand, the number of cycles to failure is obtained with the aid of an S − N curve, yielding the final expression for damage accumulation
where M denotes the number of bands in the stress spectrum while C and m are material-dependent variables, denoting a fatigue strength constant and the slope of the S − N curve, respectively.
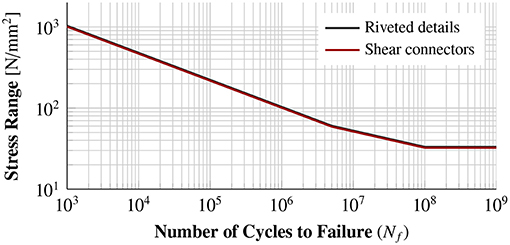
To compare the fatigue behavior of the bridge at the aforementioned hot-spot locations, which are illustrated in Figure 17, before and after strengthening, the S − N curve proposed by 269-3 (2011) for riveted construction details is utilized, which reads
where m = 5 denotes the slope while , with ΔσC indicating the detail category stress range, and , with ΔσD = 0.725 · ΔσC designating the constant amplitude fatigue limit. According to the considered details, which fall in the category of continuous riveting between flange angles and web plate in build-up flexural girders, the detail category stress ΔσC is equal to 80 MPa. In turn, the constant amplitude fatigue limit is equal to 58 MPa and the cut-off limit ΔσL amounts to 36.8 MPa, resulting in the curve depicted in Figure 18.
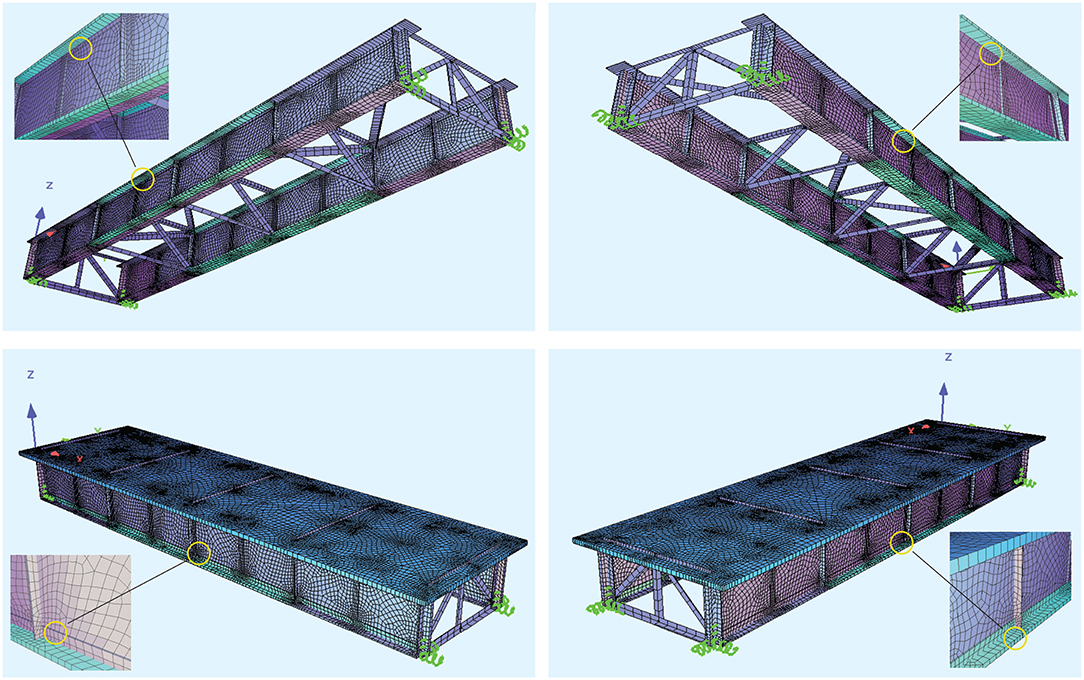
Figure 17. Structural details d1 (top left), d2 (top right), d3 (bottom left) and d4 (bottom right).
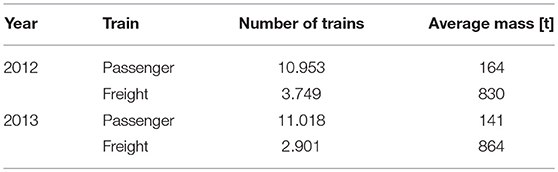
Due to the absence of actual vibration measurements, which would facilitate the evaluation of accumulated fatigue damage on the basis of real operational quantities (Papadimitriou et al., 2011; Saberi et al., 2016), the results presented herein are based on simulated data, which are generated in accordance with the traffic actions specified in EN 1991-2 (2003). Within this context, the yearly recorded traffic loads on an identical Croatian railway line between 2012 and 2013, as published by HŽ-Infrastruktura (2013) and reported in Table 9, are used to determine the traffic mix and train types running on the bridge. Considering that the maximum allowed speed in the zone is 120 km/h and the recorded traffic load is relatively small, compared to the categories proposed by the guidelines, the bridge is characterized and subsequently analyzed as one with light traffic mix and a total volume of 25.3 · 106 tons per year.
The effect of strengthening on the vibration response of the bridge, and by extension on the fatigue lifetime, is illustrated through the results of a dynamic analysis using train types 1, 2, 5, and 9 (EN 1991-2, 2003), which essentially represent the light traffic mix. To this end, the stress time histories at the structural detail d3, when both systems are excited by a Type 1 passenger traveling at 120 km/h, are compared in Figure 19. It is shown that the bridge in nominal state experiences considerably larger stress of –54.7 MPa as opposed to the strengthened system, which reaches a maximum stress of –19.1 MPa. Evidently, such a reduction is owed to the additional compressive zone provided by the UHPFRC slab, which practically assumes the bulk of compressive stresses and relieves the upper side of the steel frame. Similarly, although to a lesser extent, the lower and tensile part of the strengthened structure experiences stress cycles of smaller amplitude. The composite cross-section features an elevated neutral axis, due to the presence of the slab, as opposed to the pure steel cross-section, which offers a larger tensile zone and therefore experiences considerably reduced stresses under the same loads. This effect is clearly depicted in Figure 20, in terms of the stress time history developed in structural detail d2. It is seen that the maximum stress developed at the steel frame, initially amounts to 45.6 MPa and upon rehabilitation reduces to 34.4 MPa, when both systems are subjected to Type 2 train loads.
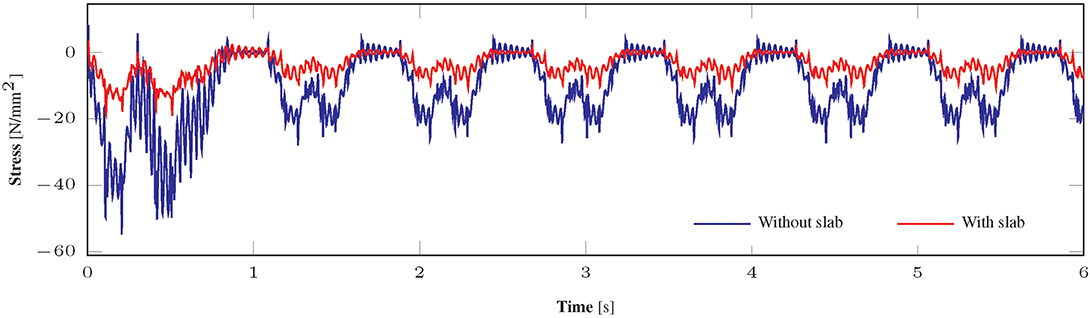
Figure 19. Stress time history at structural detail d3 upon excitation of the bridge with Type 1 train.
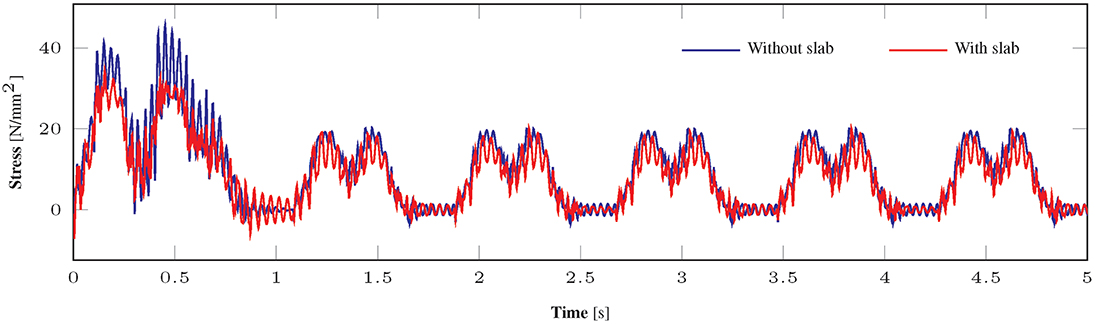
Figure 20. Stress time history at structural detail d2 upon excitation of the bridge with Type 2 train.
On top of the considerable vibration mitigation, the proposed strengthening approach provides an even more pronounced effect on the fatigue behavior, which oftentimes constitutes the design driver for steel bridges. To quantify this benefit, the fatigue life of each structural detail is calculated by means of the Palmgren-Miner rule, which is jointly used with the rainflow-counting (RFC) method. Concretely, the stress cycles of the simulated time histories are first counted using RFC and the use of Palmgren-Miner rule in conjunction with the S − N curve yields the fatigue damage accumulated on each one of the considered structural points. This damage is finally projected to a yearly basis, according to the indicated traffic volume, and the remaining fatigue lifetime is obtained as the reciprocal of the yearly accumulated damage.
The remaining service life of each structural detail is reported in Table 10, where it is shown that fatigue life of the non-strengthened structure is consumed in 21 years, with structural detail d2 resulting as the weak point. On the other hand, a significantly longer fatigue life, which is determined by a different structural detail, is ensured by rehabilitating the bridge. In this case, structural detail d4 becomes the decisive point, with a remaining service life of 119 years. It should be noted here that details d3 and d4 are located on the lower and tensile zone of the frame, while details d1 and d2 lie on the upper and compressive area, which is essentially characterized by significantly higher fatigue strength. Although, in practice, fatigue cracks may as well develop under compressive loading (Fleck et al., 1985), the service life is most probably determined by the critical locations subjected to fully or partially tensile stress conditions. In this sense, the benefit of strengthening in terms of fatigue behavior may be quantified by the additional service life of hot-spots d3 and d4, which amounts to almost 55 years.
Finally, to demonstrate that the proposed strengthening approach does not introduce any weak structural points in the system, in terms of fatigue behavior, the remaining life of the welded stud shear connectors, between the UHPFRC slab and the steel frame, as well as for the base material in the vicinity of the studs is calculated. In contrast with the previously examined hot-spots, these structural details are mainly subjected to shear stress. Therefore, upon ensuring that the steel flange always remains under compression, the fatigue assessment is carried out in terms of shear stresses alone 1994-2 (2006). The accumulated damage is calculated using the S − N curve of Equation (11), in terms of shear stresses (Figure 18), with both components falling within the detail category of 80 MPa. The results of such an analysis indicate a notably high remaining life, which, similarly to the critical locations under compression, amounts to more than 200 years of remaining life.
4. Conclusions
This work overviews implementation and performance of the so-far little exploited UHPFRC-steel composite design for strengthening of riveted bridges, which may be extended to further types of steel constructions. The proposed solution comprises the addition of a UHPFRC slab connected to steel girders by conventional means, such as steel studs, leading to a reduction of stresses of 40% and deflections of 20% in the case that pertains herein. These ameliorations may differ depending on the size of the structure (higher reduction for small girders and lower when dealing with large structures). A first estimation of the slab depth was obtained with simple analytical models, which may be implemented in practice and customized according to the needs of each particular case.
When designing the slab, four main aspects were taken into consideration: the aforementioned reduction in stress, the bonding between slab and steel, the feasibility of the implementation in a real structure and the efficiency of the solution in comparison with other possible rehabilitation methods, in economic and sustainable terms.
To address the first two topics, a series of experimental tests has been carried out for the strengthened and rehabilitated structure, including static and dynamic testing. The information obtained comprises a twofold objective: firstly, it allows for a direct comparison of Performance Indicators, such as static deflections or maximum observed stresses. Secondly, the retrieved and analyzed information serves for updating of a structural model, which allows improvement of the structure, by defining a strengthening scheme, as well as evaluation of the structure (prior to and after rehabilitation) under diverse loading conditions. Use of this updated numerical model allows for fashioning of new PIs, which in turn prove that the UHPFRC strengthening achieves the intended 40% reduction in stresses and the efficiency of the bonding solution using steel studs.
Furthermore, the experimental campaign carried out at the laboratory may be extended for use in field conditions in order to assess the "health state" of existing structures. Structural Health Monitoring techniques offer viable means to such an end, via vibration-based or non-contact deflection measurement schemes. Such sensory feedback in operating conditions may be used to extract PIs, which may support decisions on whether an existing structure could remain in use, or a strengthening/rehabilitation or even replacement is needed for ensuring the target capacity and safety.
Regarding the last two items, when adopting a strengthening solution involving a conventional concrete C40/50, a slab of 150 mm depth would have been required in order to obtain similar results in terms of stresses. UHPFRC allows for the reduction of this dimension, avoiding issues with the railway profile, and permits a faster and therefore economical implementation. Nevertheless, the benefits of the UHPFRC solution pertain not only to the reduction in stresses and deflections, but also to the intrinsic durability concerning the material itself, as well as the additional protection offered to reinforcement bars and steel owing to the UHPFRC-waterproofing capabilities. In conclusion, adoption of UHPFRC leads to a more durable and sustainable rehabilitated structure, with no additional requirements either in terms of manpower or machinery, as conventional elements were employed in all the phases of the construction (casting, welding and curing of the solution).
Author Contributions
HM-S was in charge of the experiment design as well as the rehabilitation proposal. Furthermore, she has performed the system identification modeling and studies on reliability. Finally, she has further carried out he major part of the writing and organization of the text. DD has actively contributed in the experimental design and testing processing, as well as in the result analysis. KT has participated in the fatigue analysis, reliability and writing. IS has contributed with the project organization, as well as AS. ID worked in the static and modal analysis results. UB helped in the experimental phase of the work in ZAG. EB and EC have collaborated on the experimental and methodological development, proofreading and the cross-check of the results.
Funding
The authors would like to gratefully thank the Swiss National Science Foundation (SNSF) within the context of project 154060 and the Cost Action TU1406 for their financial support.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to acknowledge the company VIADUKT in Zagreb and the ZAG institute in Ljubljana, where the first and second tests were performed, respectively, for their support during the experimental phase.
References
1991-1-4, E. (2005). Eurocode 1: Actions on Structures-Part1-4: General Actions-Wind Actions; bs en 1991-1-4: 2005. European Committee fof Standardization.
1994-2, E. (2006). Eurocode 4: Design of Composite Steel and Concrete Structures. European Committee for Standardization.
2052, S. (2016). “Sia 2052. ultra-hochleistungs-faserbeton (uhfb),” in Baustoffe, Bemessung und Ausführung, Swiss Society of Architects and Engineers, SIA Zurich.
269-3, S. (2011). Swiss Standards: SIA 269/3-2011 Existing Structures-Steel stuctures. Swiss Society of Enginners adn Architects.
Bajic, A., and Peros, B. (2005). Meteorological basis for wind loads calculation in croatia. Wind Struct. 8, 389–406. doi: 10.12989/was.2005.8.6.389
Blatman, G., and Sudret, B. (2010). An adaptive algorithm to build up sparse polynomial chaos expansions for stochastic finite element analysis. Probabil. Eng. Mech. 25, 183–197. doi: 10.1016/j.probengmech.2009.10.003
Chan, T. H., Li, Z., and Ko, J. M. (2001). Fatigue analysis and life prediction of bridges with structural health monitoring data—part ii: application. Int. J. Fatigue 23, 55–64. doi: 10.1016/S0142-1123(00)00069-4
Chang, P. C., Flatau, A., and Liu, S. (2003). Health monitoring of civil infrastructure. Struct. Health Monit. 2, 257–267. doi: 10.1177/1475921703036169
CSI, S. V. (2010). 8, 2002. Integrated Finite Element Analysis and Design of Structures Basic Analysis Reference Manual. Berkeley, CA: Computers and Structures, Inc.,.
Cui, F., and Chew, C. (2000). The effectiveness of floating slab track system—part i. receptance methods. Appl. Acoust. 61, 441–453. doi: 10.1016/S0003-682X(00)00014-1
Denarié, E., and Brühwiler, E. (2015). “Cast-on site uhpfrc for improvement of existing structures - achievements over the last 10 years in practice and research,” in 7th Workshop on High Performance Fiber Reinforced Cement Composites, 1-3, June 2015 (Stuttgart).
Denarié, E., Brühwiler, E., Znidaric, A., Houstand, Y., and Rohleder, R. (2005). “Full scale application of uhpfrc for the rehabilitation of bridges – from the lab to the field,” in SAMARIS Sustainable and Advanced MAterials for Road InfraStructure WP 14: HPFRCC for Rehabilitation. Deliverable D22. Brussels.
Dieng, L., Marchand, P., Gomes, F., Tessier, C., and Toutlemonde, F. (2013). Use of uhpfrc overlay to reduce stresses in orthotropic steel decks. J. Construct. Steel Res. 89, 30–41. doi: 10.1016/j.jcsr.2013.06.006
Ditlevsen, O., and Madsen, H. O. (1996). Structural Reliability Methods, Vol. 178. New York, NY: Wiley New York.
Dzajic, I. S. A. a. O. I. S (2014). “Rehabilitation of steel railway bridges by implementation of uhpfrc deck,” in 3rd Internationl Conference on Road and Rail Infrastructure. Split.
EN 1991-2 (2003). Eurocode 1: Actions on Structures: Part 2: Traffic Loads on Bridges. European Committee fof Standardization.
EN 1994-1 (2005). Eurocode 4: Design of Composite Steel and Concrete Structures. Part 1-1. European Committee for Standardization.
Fehling, E., Bunje, K., and Schmidt, M. (2011). “Gärtnerplatz–bridge over river fulda in kassel: Multispan hybrid uhpc-steel bridge,” in Designing and Building With UHPFRC, eds F. Toutlemonde and J. Resplendin (London; Hoboken, NJ: ISTE and Wiley).
Fehling, E., Schmidt, M., Walraven, J., Leutbecher, T., and Fröhlich, S. (2014). Ultra-High Performance Concrete UHPC: Fundamentals, Design, Examples. Germany: John Wiley & Sons.
Fleck, N. A., Shin, C. S., and Smith, R. A. (1985). Fatigue crack growth under compressive loading. Eng. Fract. Mech. 21, 173–185.
Frangopol, D. M., Kong, J. S., and Gharaibeh, E. S. (2001). Reliability-based life-cycle management of highway bridges. J. Comput. Civil Eng. 15, 27–34. doi: 10.1061/(ASCE)0887-3801(2001)15:1(27)
Gascon, B., Massicotte, F., and Lagier, A. (2017). “Behaviour of headed shear stud connectors in composite beams with uhpfrc connection,” in Conference: AFGC-ACI-fib-RILEM Int. Symposium on Ultra-High Performance Fibre-Reinforced Concrete (Montpellier).
Habel, K. (2004). “Structural behaviour of elements combining ultra-high performance fibre reinforced concretes (uhpfrc) and reinforced concrete,” in Thèse N° 3036, École Polytechnique Fédérale de Lausanne. Lausanne.
Hess, P. E., Bruchman, D., Assakkaf, I. A., and Ayyub, B. M. (2002). Uncertainties in material and geometric strength and load variables. Naval Eng. J. 114, 139–166. doi: 10.1111/j.1559-3584.2002.tb00128.x
Hibbett, Karlsson, and Sorensen (1998). ABAQUS/Standard, Vol. 1. Providence: Hibbitt; Karlsson & Sorensen.
HŽ-Infrastruktura (2013). Statistics of hŽ infrastruktura for 2013. Technical report, HŽ Infrastruktura.
Johnson, R. P. (2018). Composite Structures of Steel and Concrete: Beams, Slabs, Columns and Frames for Buildings. Hoboken, NJ: John Wiley & Sons.
Kulak, G. L., Fisher, J. W., and Struik, J. H. (2001). Guide to Design Criteria for Bolted and Riveted Joints, 2nd Edn. Chicago: Research Council on Structural Connections.
Kwon, G., Engelhardt, M. D., and Klingner, R. E. (2009). Strengthening bridges by developing composite action in existing non-composite bridge girders. Struct. Eng. Int. 19, 432–437. doi: 10.2749/101686609789847109
Leyder, C. (2018). Monitoring-Based Performance Assessment of an Innovative Timber-Hybrid Building. Ph.D. thesis, ETH Zurich.
Luo, Y., Hoki, K., Hayashi, K., and Nakashima, M. (2015a). Behavior and strength of headed stud–sfrcc shear connection. i: Experimental study. J. Struct. Eng. 142:04015112. doi: 10.1061/(ASCE)ST.1943-541X.0001363
Luo, Y., Hoki, K., Hayashi, K., and Nakashima, M. (2015b). Behavior and strength of headed stud–sfrcc shear connection. ii: Strength evaluation. J. Struct. Eng. 142:04015113. doi: 10.1061/(ASCE)ST.1943-541X.0001372
Marchand, P., Gomes, F., Dieng, L., Baby, F., Renaud, J., Massotte, C., et al. (2012). Behaviour of an orthotropic bridge deck with a uhpfrc topping layer. Siegert D., Toutlemonde F., Hipermat, 905–912.
Marelli, S., and Sudret, B. (2014). “Uqlab: a framework for uncertainty quantification in matlab,” in Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management (Liverpool), 2554–2563.
Martín-Sanz, H., Chatzi, E., and Brühwiler, E. (2016). “The use of ultra high performance fibre reinforced cement-based composites in rehabilitation projects: a review,” in Conference: 9th International Conference on Fracture Mechanics of Concrete and Concrete Structures. Berkeley.
Martín-Sanz, H., Tatsis, K., Damjanovic, D., Sanja, A., Brühwiler, E., and Chatzi, E. a. (2018). “Towards the use of uhpfrc in rehabilitation bridges: the buna bridge,” in Proceedings of Life-Cycle Analysis and Assesment in Civil Enginering: Towards an Integrated Vison. IALCCE 2018. Ghent.
McDonagh, M., and Foden, A. (2016). “Benefits of ultra-high performance concrete for the rehabilitation of the pulaski skyway,” in First International Interactive Symposium on UHPC (Des Moines), 1–10.
Melchers, R. E., and Beck, A. T. (2018). Structural Reliability Analysis and Prediction. Hoboken, NJ: John Wiley & Sons.
Moreillon, L., and Menétrey, P. (2013). “Rehabilitation and strengthening of existing rc structures with uhpfrc: various applications,” in Proceedings of International Symposium on Ultra-High Performance Fiber-Reinforced Concrete (Marseille), 127–136.
O'Connor, S. M., Zhang, Y., Lynch, J. P., Ettouney, M. M., and Jansson, P. O. (2017). Long-term performance assessment of the telegraph road bridge using a permanent wireless monitoring system and automated statistical process control analytics. Struct. Infrastruct. Eng. 13, 604–624. doi: 10.1080/15732479.2016.1171883
Papadimitriou, C., Fritzen, C. P., Kraemer, P., and Ntotsios, E. (2011). Fatigue predictions in entire body of metallic structures from a limited number of vibration sensors using Kalman filtering. Struct. Control Health Monit. 18, 554–573. doi: 10.1002/stc.395
Rathbun, J. C. (1936). Elastic properties of riveted connections. Am. Soc. Civil Eng. Trans. 101, 524–563.
Reynders, E., Houbrechts, J., and De Roeck, G. (2012). Fully automated (operational) modal analysis. Mech. Syst. Signal Proc. 29, 228–250. doi: 10.1016/j.ymssp.2012.01.007
Reynders, E., Schevenels, M., and De Roeck, G. (2011). Macec 3.2: A Matlab Toolbox for Experimental and Operational Modal Analysis. Leuven University, Belgium Google Scholar.
Saberi, M. R., Rahai, A. R., Sanayei, M., and Vogel, R. M. (2016). Bridge fatigue service-life estimation using operational strain measurements. J. Bridge Eng. 21:04016005. doi: 10.1061/(ASCE)BE.1943-5592.0000860
Schilling, C. (1978). Fatigue of Welded Steel Bridge Members Under Variable-Amplitude Loadings. NCHRP Report.
Spiridonakos, M.D., and M. C. C. E. Sudret, B. (2016). Surrogate modeling for stochastic dynamical systems by combining narx models and polynomial chaos expansions. Int. J. Uncert. Quant. 64, 313–339. Available online at: http://arxiv.org/abs/1604.07627
Stipanovic, I., and Klanker, G. (2016). “Performance goals for roadway bridges,” in 8th International Conference on Bridge Maintenance, Safety and Management 2016 (Foz do Iguaçu: CRC Press/Balkema).
Strauss, A., Vidovic, A., Zambon, I., Dengg, F., Tanasic, N., and Matos, J. C. (2016). “Performance indicators for roadway bridges,” in IABMAS Conference 2016 (Foz do Iguaçu: Taylor & Francis), 965–970.
Tatsis, K., Chatzi, E., and Lourens, E.-M. (2017). “Reliability prediction of fatigue damage accumulation on wind turbine support structures,” in Proceedings of the 2nd ECCOMAS Thematic Conference on Uncertainty Quantification inComputational Sciences and Engineering. Rhodes.
Tayeh, B. A., Bakar, B. A., Johari, M. M., and Voo, Y. L. (2013). Utilization of ultra-high performance fibre concrete (uhpfc) for rehabilitation–a review. Proc. Eng. 54, 525–538. doi: 10.1016/j.proeng.2013.03.048
Yoo, S.-W., and Choo, J. F. (2016). Evaluation of the flexural behavior of composite beam with inverted-t steel girder and steel fiber reinforced ultra high performance concrete slab. Eng. Struct. 118, 1–15. doi: 10.1016/j.engstruct.2016.03.052
Zmetra, K., Zaghi, A. E., and Wille, K. (2015). “Rehabilitation of steel bridge girders with corroded ends using ultra-high performance concrete,” in Structures Congress 2015 (Portland), 1411–1422.
Nomenclature
Keywords: UHPFRC, strengthening, modal analysis, reliability, fatigue, system identification, performance indicators
Citation: Martín-Sanz H, Tatsis K, Damjanovic D, Stipanovic I, Sajna A, Duvnjak I, Bohinc U, Brühwiler E and Chatzi E (2019) Getting More Out of Existing Structures: Steel Bridge Strengthening via UHPFRC. Front. Built Environ. 5:26. doi: 10.3389/fbuil.2019.00026
Received: 17 December 2018; Accepted: 18 February 2019;
Published: 16 April 2019.
Edited by:
Branko Glisic, Princeton University, United StatesReviewed by:
Mohammad Alhassan, Jordan University of Science and Technology, JordanPavel Ryjek, Czech Technical University, Czechia
Copyright © 2019 Martín-Sanz, Tatsis, Damjanovic, Stipanovic, Sajna, Duvnjak, Bohinc, Brühwiler and Chatzi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Henar Martín-Sanz, bWFydGluLXNhbnpAaWJrLmJhdWcuZXRoei5jaA==
 Henar Martín-Sanz
Henar Martín-Sanz Konstantinos Tatsis1
Konstantinos Tatsis1 Aljosa Sajna
Aljosa Sajna Ivan Duvnjak
Ivan Duvnjak Eugen Brühwiler
Eugen Brühwiler Eleni Chatzi
Eleni Chatzi