- 1Department of Civil and Building Engineering, and Architecture, Polytechnic University of Marche, Ancona, Italy
- 2Department of Architecture, Built Environment and Construction Engineering ABC, Polytechnic of Milano, Milan, Italy
The renaissance bell tower of San Benedetto in Ferrara (Italy) has been investigated to understand its nonlinear dynamics correctly with the Non-Smooth Contact Dynamic (NSCD) method. The masonry structure has been modeled with the Discrete Element Methods (DEM), assuming rigid blocks and frictional joints, with the aim to recreate the tower in the actual configuration with the inclination and in a fictitious perfect vertical shape in order to assess the influence of the initial slope on its dynamics. The contacts between blocks are governed by the Signorini's impenetrability condition and by dry-friction Coulomb's law. Both configurations have been analyzed inducing real seismic excitations of various types and intensities, corresponding to the six main seismic events of the last few decades in Italy. Thus, the seismic vulnerability of the examined tower is clearly expressed in the numerical results, proving the effects due to the inclination on the amplification of the vulnerability and the several possible collapse mechanisms. Moreover, the NSCD has demonstrated to be a powerful numerical technique to obtain highly accurate results in the structural analyses of masonry structures in the nonlinear range.
Introduction
A major research field in structural engineering concerns the structural safety and seismic assessment of the masonry buildings, especially historic structures, to preserve their main architectural features in the cultural heritage (Roca et al., 2013). In the last few decades, a significant number of structures was severely damaged, especially monumental buildings, churches and belfries, by the most recent Italian earthquakes such as Umbria-Marche 1997–1998, Abruzzo 2009, Emilia-Romagna 2012, Central Italy Earthquake 2016 (Lagomarsino and Podestà, 2004; Brandonisio et al., 2013; Milani, 2013; Clementi et al., 2017).
Among the buildings belonging to the heritage of Italian architecture, the masonry structures characterized by a predominantly vertical development, such as towers and belfries, are prevalent. In this context, the detailed analysis of interpretative models that can successfully define the effects of the earthquakes is an indispensable mean to know and predict the behavior of unplanned masonry buildings under seismic forces (Pellegrini et al., 2018).
The primary challenge is the mechanical behavior of the masonry structures which significantly depends on the complex nature of the masonry itself. Thus, an accurate numerical model has to take into account the discontinuity of ancient masonry structures, characterized by units, like bricks, stones, blocks, voids, and mortar. For this purpose, the constitutive laws and the material properties assume a relevant aspect in the model (Clementi et al., 2015; Terracciano et al., 2015; Valente and Milani, 2016; Formisano et al., 2017), to represent the proper quality of masonry walls, which decrease severely in case of poor material or incorrect construction techniques, and the different range of stresses that exist in masonry structures.
In general, experimental and numerical analyses of masonry are widely showed in literature, in particular with the finite element (Acito et al., 2014; Cavalagli and Gusella, 2015; Valente and Milani, 2016; Clementi et al., 2018a; Formisano et al., 2018; Giordano et al., 2019), that allows analyzing the dynamics beyond the elastic behavior, but it does not explicitly consider the interaction between the blocks. Furthermore, the non-smooth behavior near collapse, i.e., when the blocks slide and impact between them, is not introduced also in sophisticated analyses such as micro-modeling that distinguishes the elements of masonry. Hence, in this work, to study this high nonlinearity of the historic structures and to identify the typologies of collapse has been used the advance rigid-body dynamics formulation belonging to the distinct element method (DEM) (Poiani et al., 2018).
This approach can reproduce all the possible collapse mechanisms, peculiarities of historic masonry, large displacements and common contact phenomena such as the stick-slip transition, representing a sudden change in motion at the collision. Furthermore, the DEM is particularly successful since each masonry unit is individually modeled and the joints represent the natural planes of slip and crack. The number of blocks in the numerical model should be adjusted between computational cost and realistic structural behavior.
To the authors' knowledge, the non-smooth nature of the dynamic response of towers is not analyzed in depth. For this reason, in the present work, a DEM code which implements the Non-Smooth Contact Dynamics (NSCD) method (Moreau, 1988; Chetouane et al., 2005; Dubois et al., 2018) is used to analyze the dynamic behavior of an inclined existing masonry tower. The masonry is simulated using an assembly of rigid bodies approximately equal to the real geometry of bricks, but with greater dimensions to take into account the thickness of the mortar. The analyses are done with the LMGC90 code which works with a solver able to compute the nonlinear dynamics of complex masonry structures in the 3D space, and with a post-processing program allowing to plot all the quantities of interest, in order to compare the numerical predictions with the real damages.
Hence, in this work, to figure out the nonlinear dynamics of a renaissance bell tower, six different sets of ground accelerations related to most recent Italian earthquakes have been considered. The analyzed masonry bell tower belongs to the San Benedetto's complex in Ferrara (Italy) and presents an unusually high inclination, Figure 1. Therefore, for all cases, it is possible to evaluate a comparison between the inclined and vertical tower, in order to understand, in a qualitatively and quantitatively manner, the slope's influence on the dynamics and failure mechanisms.
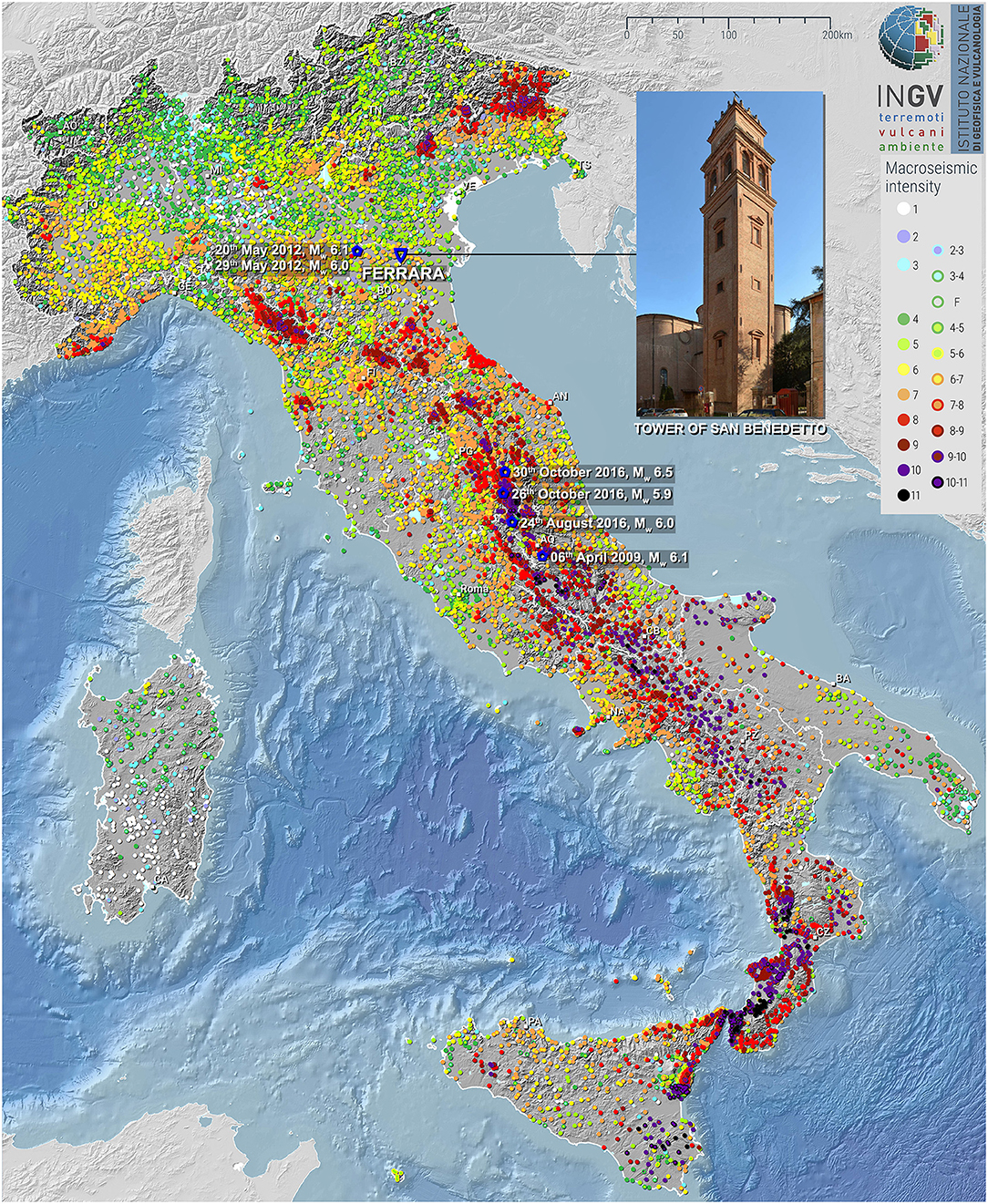
Figure 1. Maps of the geographical location of the bell tower of San Benedetto in Ferrara (Italy) and Italian Macroseismic intensity (https://emidius.mi.ingv.it/), with the position of the six main seismic events of the last few decades in Italy taken into account for analyses.
A brief description of San Benedetto's tower
The complex of San Benedetto in Ferrara goes back to the fifteenth century. The Church was built for the Benedictines of Pomposa between 1496 and 1553 and consecrated in 1563, while the bell tower was built in 1621. In 1611 Ludovico Ariosto was buried there, according to his will, where now there is the altar of the Madonna, to be then transferred to the Ariostea public library in 1801 at the behest of General de Miollis, at that time in Ferrara after the occupation of the city from the Napoleonic army. After being used as army camp and stable during the French Revolution, it was restored and reopened to worship in 1812. In 1944 the church was severely hit and destroyed in large part by the English bombing, as visible in Figure 2A. It was entirely rebuilt on the original design in 1954 (see Figure 2B).

Figure 2. Complex of San Benedetto in Ferrara (Italy) after the bombing of the World War in 1944 (A), a view of the bell tower and the complex after rebuilding (B).
On 15th June 2007, a great fire was developed in the central apse of the church, and the investigators have hypothesized it as a malicious cause. The fire was then quickly tamed without making any victims, but it damaged the whole church. Damages involve structures, installations, organ, works of art. The restoration is currently underway.
Differently, the masonry tower was built on the design of Giovan Battista Aleotti from 1621 and completed in 1646, due to the development of foundation settlements at a very early stage of the construction process. The bell tower is high about 55 m, and it has a square cross-section with a long side of 7.33 m. The structure is quite regular along the height, with the different upper part that is about 5.7 × 5.7 m, as in Figures 3D,E. There is only a floor at 32.0 m, where are located the bells, and another at 39.8 m, which consist of two cross vaults.

Figure 3. San Benedetto church and the bell tower in Ferrara (Italy) (A); inside the belfry (B) and the base of the tower(C); drawings of the cross sections (D), East-West façade of the masonry and vertical cross section (E); original drawing of the survey on the overhang of the bell tower in 1883 (Historical Archive of Ferrara) (F).
The vertical structure is characterized by massive regular brick walls, with internally visible reductions of thickness varying from 1.40 m at the base up to 0.65 m on the last floor, and a dome made by masonry bricks closing at the top. The belfry consists of large arches with measuring 1.65 × 3.91 m, and it is topped with a cell with smaller rectangular openings with dimensions 1.49 × 3.2 m. Lastly, the vertical connection is guaranteed only by steel stairs, consider as a load in the numerical model.
As consequence of a storm, in 1842 there was the collapse of the summit of the bell tower of Aleotti, that was particularly serious because it also damaged the covered church choir of San Benedetto, which then had to be repaired, as later was restored the bell cell. Subsequently, new damages were recorded due to fortuitous situations and storms, first in 1880 and then in 1933. These events, together with the nature of the ground and other static problems, meant that the high construction came out of its barycenter since the 1600s; so that the inclination was accentuated more and more in the following centuries, until the earthquake of 2012, after which the structure has suffered clearly cracks on North and South façade. Now the tower has a notable overhang in one of the geometrical directions.
The results of 2008 survey exhibit a horizontal displacement of the centroid of the top section of the structure (52.45 m from the base) equal to 0.50 m along the northward direction and almost 2.82 m along the westward direction, whereas in 1883 survey they were respectively equal to 0.40 and 2.50 m (see Figure 3F). The overhang values are gradually increasing (Pellegrinelli et al., 2014) and, recently, the equilibrium conditions have been assessed carefully in static conditions to have an insight into both the stability of the structure and the residual capacity against possible, albeit small, seismic events. Also a dynamic identification with a calibration of a first classical Finite Element Model (FEM) was also done in 2016 (Clementi et al., 2018b).
Distinct element method for historical masonry
At present, the simulation of masonry structures does not have a straightforward or unified approach. Indeed, according to the required level of accuracy and computational cost, there are several numerical approaches in the current structural engineering's knowledge. In practice is commonly used the FEM, which takes into account the numerical model as a continuous medium (Betti et al., 2014; Pierdicca et al., 2016; Valente and Milani, 2016; Sarhosis et al., 2018) whose geometry and behavior are described using pre-defined finite elements. This approach allows to represent several masonry behaviors, nevertheless for an advanced numerical modeling of ancient structures view as discontinuous units, with stiff bodies and deformational behavior at the joints, it is necessary the use of the Discrete Element Method (DEM). Concerning DEMs, the structure is characterized by an assembly of 3D separate bodies, deformable or stiff, and by points of contacts on the interfaces between the bodies, which represent the interaction at masonry's joints. The motion of the bodies is governed by contact laws (Lemos, 2007), that are different in order to estimate widespread interactions (Asteris et al., 2015).
Among the various approach, an NSCD method has been implemented in the LMGC90 software, which is an open source software, within a non-smooth dynamics framework, with an implicit time integration, and implicit contact solvers (i.e., nonlinear Gauss-Seidel (NLGS), preconditioned conjugate gradient with projection (PCGP), etc.). Furthermore, the applications with many interacting 3D bodies are reachable through parallel computing (shared or distributed memory) and during computation, it is possible to check the relevance of the analysis through some global indicators (convergence norm, quality of interaction laws computation, etc.).
As a rule, the interaction between bodies, in DEM application, is examined in the contact localized at point assumption, in which the normal and shear stress vector are functions of the relative displacement and velocity of the contacting objects. This simplification, however, still allows right accuracy if a sufficient number of contact points is used.
NSCD for Masonry Structures Modeling
The NSCD method is based on a particular formulation of the equation of motion, as firstly explained by Moreau (1988). The “non-smooth” regards to the specific laws used to model mechanical systems with unilateral contacts and friction. The second-order dynamics is characterized by velocity jumps due to the impacts, with unilateral kinematic constraints on the position, which introduce to non-smoothness in time and space.
The non-smoothness in the interaction laws are written as multi-valued mappings between contact reactions and the relative velocity, in the framework of the NSCD method (Dubois et al., 2018). Fairly large time steps are permitted by this method. In fact, the multi-contact problem resolution consists in solving two groups of unknowns which are global ones, as kinematic space unknowns related to the blocks, and local ones as contact space unknowns, related to interactions, linked together thanks to kinematic and duality relationships.
Furthermore, the action and reaction law define the contact forces between two blocks in the NSCD method. Thus, to control the contact forces is necessary to compute the interaction of the antagonist body A on the candidate body C (see Figure 4), which is the force rα acting at the contact point between these two bodies. At the contact, that is considered as punctual for simplifying, it is possible to set a local frame consisting of three vectors, in 3D model, including a normal vector nα pointing from A to C and two tangential vectors sα and tα, which define the tangential space by respecting this convention sα ∧ tα = nα. Moreover, the distance between body A and C along the normal direction is defined as the gap gα, which is positive for rigid bodies and there is not interpenetration between blocks.
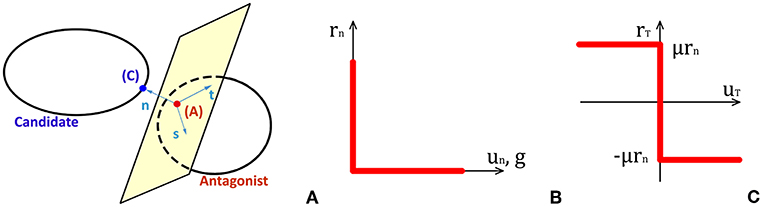
Figure 4. Relation between candidate and antagonist in 3D space (A), Signorini's impenetrability condition (B), and friction Coulomb's law (C).
Furthermore, it is required to correlate the local forces to the contribution of contact α to the resultant global force, using a linear mapping Hα, by the following equation:
where Hα(q) is a mapping which contains the local information about contactors, where q is the configuration parameter which can represent the discretized displacement or any generalized coordinates of the rigid motion. Additionally, it is possible to calculate the global resultant contact forces exerted on objects with the relation
The velocity is analyzed with the same procedure. The relative velocity uα at the contact point is defined for two bodies in contact by the following equation:
where HT is the transpose of H, v is the time derivative of q, and t is the time. The relative velocity is decomposed in a normal component represented by uα, n and a tangential component uα, T = (uα, s, uα, t). It should be noted that the derivative of the gap function g is equal to the normal component of the relative velocity:
During the evolution of the model, it is impossible to describe the acceleration as the usual second time derivative of the configuration parameter because it could be introduced shocks with multi-contact systems, which produce velocity discontinuities concerning time. Hence, the equation of motion will be written as
where dt is the Lebesgue measure on ℝ, dv is a differential measure of velocity denoting the acceleration measure and dI is a differential measure of impulse representing forces. The matrix M in the last equation is the mass matrix and the vector F(q, v, t) is the vector of internal and external discretized forces acting on the system.
To determine the value of each component of rα is important to have additional information about contact forces. These data are primordial to complete the Equation (5) and to describe the motion of the system. To simplify the writing, it is here considered the two-dimensional case, the s-components of rα is disregard, the symbol α is omitted, and it is considered only rn and rT which represent the normal and tangential components of the force in the local frame, respectively. The reaction force always has a positive normal component or at least equal to zero when the contact disappears. In fact, it is not possible to have penetration between bodies in the system, as mentioned above with the impenetrability of contact, and there is not attraction among contacting bodies. This contact behavior is the so-called Signorini's condition or the first unilateral constraint:
Regarding the cohesive contact instead, that is not the case considered here, the shifting can be applied to rn and rT and it assumes a value equal to zero if the contact is interrupted.
Concerning the case of Coulomb dry friction or the second unilateral constraint, it can be expressed by the equations below:
As in Equation (7), the main features are that the friction force lies in Coulomb's cone, with ||rT|| ≤ μrn and μ friction coefficient, and, in the slip phase, the friction resultant force is opposed to the sliding velocity with value a equal to μrn, when the sliding velocity uT is different from zero.
It is important to highlight that it is not necessary to manage explicitly the contact events in the time-stepping integration scheme, as in the case of the event-driven scheme. The time subdivision is done on intervals [ti, ti+1] of length h and it is fixed; consequently it is possible to deal with a great number of discontinuities during a one-time step, and the contact problem is solved over the range in terms of measures of this interval and not in a point-wise way. Thus, the equation is integrated on each time step, which involves to
where the variable vi + 1 denotes the approximation of the right limit of the velocity at the time ti + 1, and qi + 1 ≈ q(ti + 1). For impulse the I, it is integrated the measure dI over the time interval [ ti, ti+1]
Afterward, it is introduced the θ-method as time-integration algorithm, that is an implicit scheme and it remains between 0.5 and 1 for the stability condition of the scheme, to approximate the two integrals of the system introduced before in Equation (8), which leads to the following equation:
Furthermore, the latter scheme in Equation (10) allows obtaining the energy balance analysis in the case of non-smooth motion with impact. To have a look on the total mechanical energy of the system, it is important to highlight that the dissipated energy of this system represents the work done by the contact impulse at the time of impact ti. Note that completely inelastic impacts at contacts are assumed, leading to a loss of energy after each impact. Lastly, a detailed analysis of the energy balance for non-smooth systems can be found in Maschke et al. (2001).
Hence, it is essential to stress the fact that to investigate the ancient masonry towers it is necessary to do some observations on the NSCD method used here, which relies on modeling simplifications. The main assumption is that the blocks are stiff. Moreover, we add a perfectly plastic impact law to the contacts between blocks, in addition to the Signorini's impenetrability condition, i.e., Newton law with restitution coefficient equal to zero, which involves no bounces after collisions. According to this, there are valuable advantages regarding the contribution of impacts to the computational complexity, that is modest since they are modeled in a very basic and simple way, and about the perfectly plastic impact, which dissipates energy. Actually, regarding the integration, this dissipation improves the stability of the numeric computation and, from an engineering perspective, it is represented by the material failures and cracks of bricks after the impacts. Furthermore, another relevant aspect is the dissipation of energy that occurs using dry frictional joints and without viscous damping.
The MODELING of the tower
The main purpose of the modeling with the proposed approach is to recreate the geometrical and mechanical properties of the masonry in order to have the greatest resemblance with the complex configuration of the real structure and afterward to highlight the influence of the inclination on the dynamic response of the tower.
To achieving this objective, the models follow the revealed measures in loco of the tower and the structure properties, according to the previous survey of the past in historical archive (see Figure 3). The discretization of masonry with rigid blocks is made as much as possible neat, by including the thickness of the mortar in the dimensions of the bricks and thus giving a zero dimension to the joints, as shown in Figure 5. Therefore, the blocks assume different dimensions, but they are clearly regular and convex objects. Concerning other parameters as the mass density, it is related to the existing masonry, and it assumes the specific value of 18 kN/m3 as indicated in the (Circolare Ministeriale n., 617, 2009).
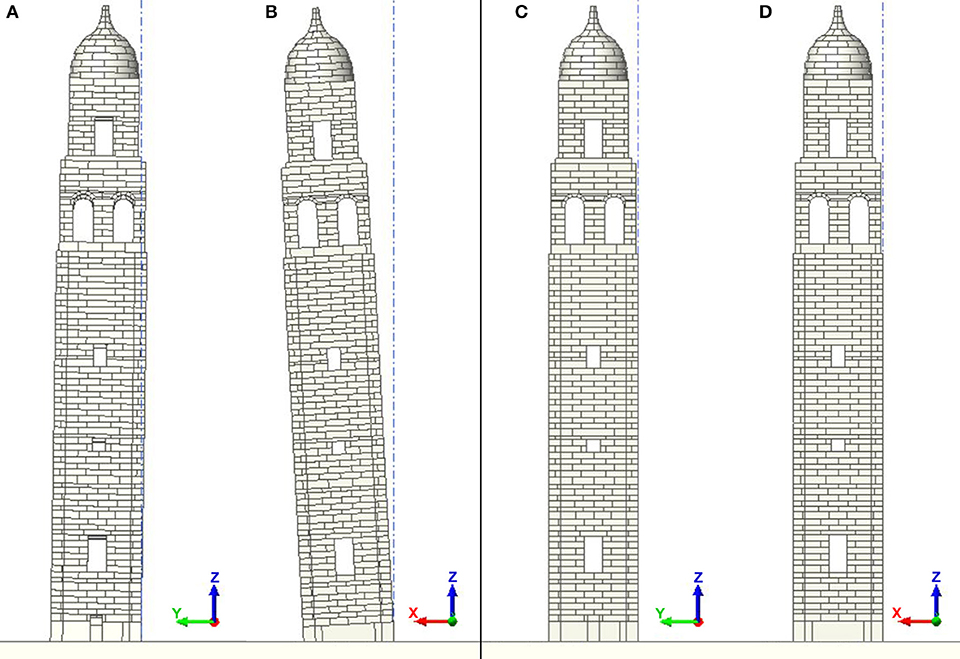
Figure 5. The numerical models of the bell tower of San Benedetto in Ferrara (Italy) with the NSCD method (A,B) in the real inclined condition (C,D) and in fictitious vertical configuration.
As a rule, in ancient structures, there are relevant phenomena of degradation, and thus the mortar loses its quality over time (Vasconcelos and Lourenço, 2009), reducing the friction coefficient until a value of 0.3 for a very poor kind. However, for a recent structure or a careful design of retrofitting, the friction can reach a value equal to 0.8. To define the frictional behavior of the structure, overlooking the interaction of the masonry with the foundation, it has been chosen a value equal to μ = 0.9, for the relationship between structure and basement, and a value of μ = 0.5, for the interaction between the blocks of the buildings.
Hence, for modeling of the tower of San Benedetto, it has been taken into account the condition of the structure with the benefits of the latest renovation and, at the same time, the degradation of material over time. This approach it has been followed for the real configuration of the tower with the actual inclination (in Figures 5A,B) and, also, for the vertical configuration (i.e., without the initial slope as reported in Figures 5C,D) in order to have an insight on the effect of the initial inclination on the seismic behavior of the tower, and on the possible activation of mechanisms.
Several analyses have been implemented applying to the system firstly the gravity loads and afterward the different ground accelerations: the dynamic behavior has been elaborate on shocks action of real events imported on the main directions of the base of the tower. The main shocks considered have various specifications; all of these are obtained by the records of seismic events occurred in the Italian territory. In particular, the recordings of velocities have been taken by the stations of the epicenters, and in this paper all three components, i.e., two on horizontal x and y and one on vertical z directions, are used. It has been considered two shocks events of a sequence of 2012 that took place in North-East of Italy, near Ferrara where is located the analyzed tower, and further four earthquakes of the highly active seismological area of the Central Italy, which belong to separate seismic sequences of 2009 and 2016:
(i) 06th April 2009 L'Aquila with ML = 5.9 and MW = 6.1 [AQV station in Italian Accelerometric Archive (ITACA)],
(ii) 20th May 2012 Mirandola with ML = 5.9 and MW = 6.1 (MRN station in ITACA),
(iii) 29th May 2012 Mirandola with ML = 5.8 and MW = 6.0 (MRN station in ITACA),
(iv) 24th August 2016 Amatrice with ML = 6.0 and MW = 6.0 (AMT station in ITACA),
(v) 26th October 2016 Campi with ML = 5.9 and MW = 5.9 (CMI station in ITACA),
(vi) 30th October 2016 Forca Canapine ML = 6.1 and MW = 6.5 (FCC in ITACA).
The location of epicenters are plotted in Figure 1, and the comparison between the characteristics of the seismic accelerations is reported in Table 1, where (Luzi et al., 2008, 2017; Pacor et al., 2011):
• Rjb, is the Joyner-Boore distance, known as the smallest spacing from the site to the surface projection of the rupture surface;
• Rrup, is the shortest distance between the site and the rupture surface;
• Repi, is the distance estimated by the geometric swap.
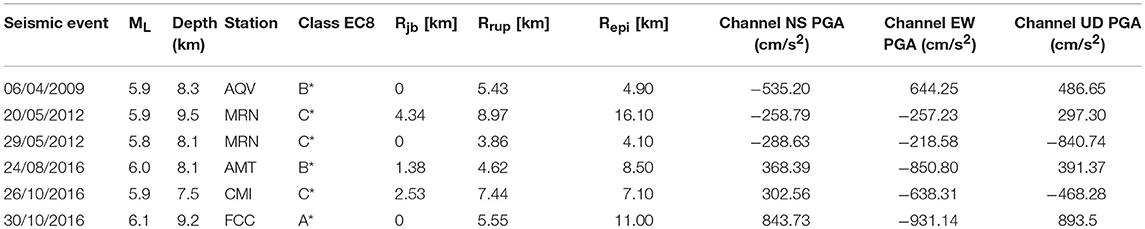
Table 1. Characteristics of main earthquakes recorded in L'Aquila (AQV), Mirandola (MRN), Amatrice (AMT), Campi (CMI), Forca Canapine (FCC) stations during the main seismic events of the last few decades in Italy, where * indicates that site classification is not based on a direct Vs,30 measurement.
Numerical results
The results of all numerical analyses performed on the bell tower of San Benedetto in Ferrara are shown in Figure 6, where are plotted the last configuration of the TH, obtained by the nonlinear dynamic simulations under shocks excitations.
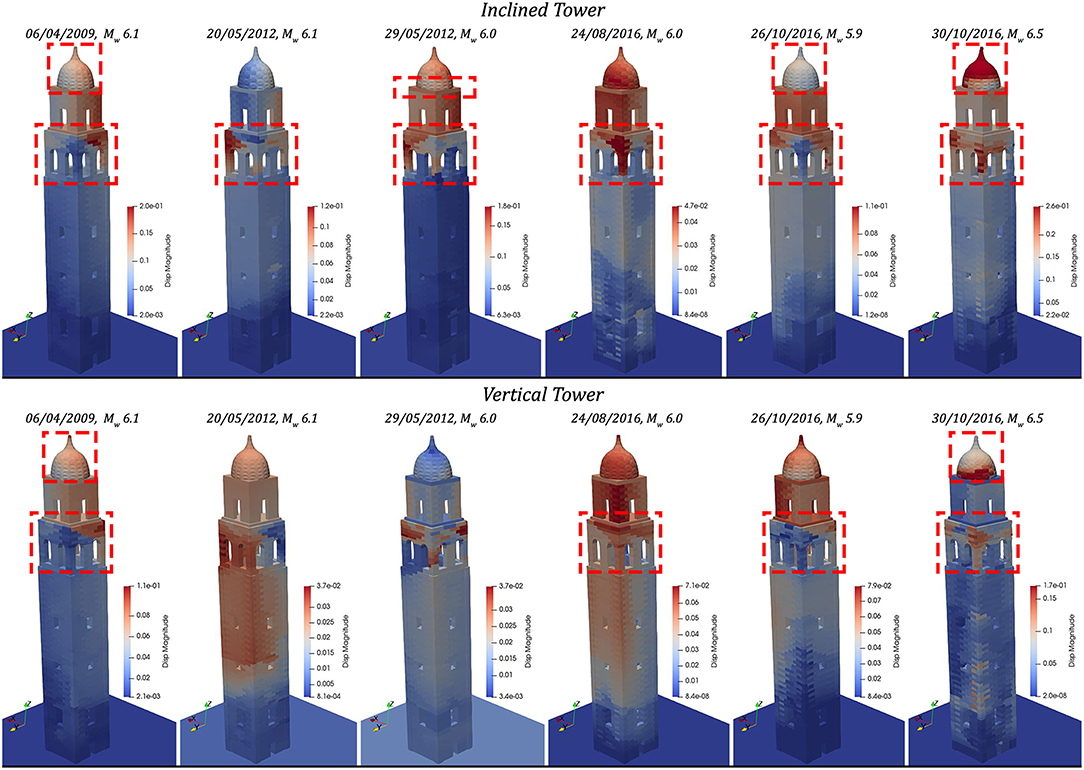
Figure 6. Final configurations of the failure mechanisms of the bell tower of San Benedetto in Ferrara (Italy) under the six main seismic events of the last few decades in Italy, for the inclined real configuration and the other one vertical fictitious.
All the events generate the activation of failure mechanisms of the upper part of the structures and cracks along the vertical dimension of the tower. Obviously, these results point out the adverse effects of the openings, distributed to different heights on the vertical walls, on the dynamic response of the considered tower. In particular, the most extensive damage -for both models of the tower- is due to the ground acceleration of the shock of 30th October 2016, which is the biggest and the most recent event in Italy. In Figure 6, it is already appreciable the increased vulnerability of the structure due to the inclination, but in order to have a clear picture of the numerical damage in Figures 7, 8 are also reported enlargements.
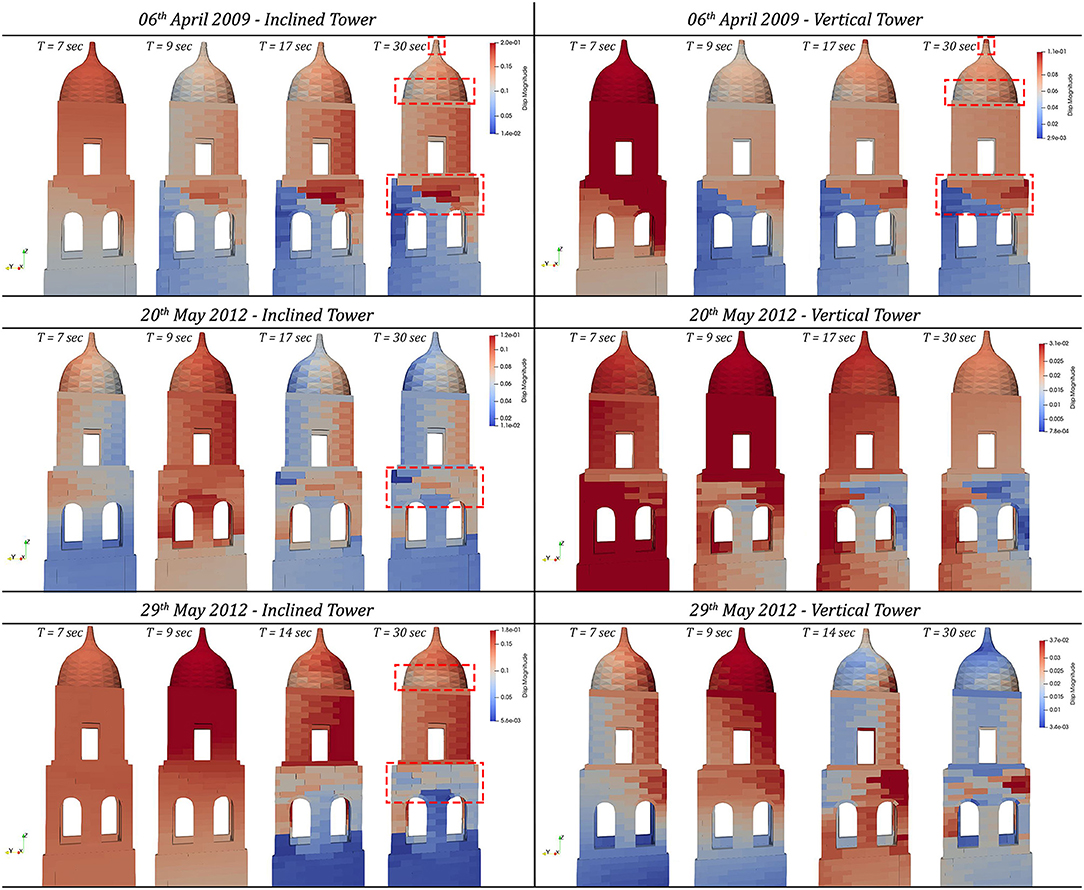
Figure 7. Failure mechanism of the bell tower of San Benedetto in Ferrara (Italy) for the inclined real configuration and the fictitious vertical one.
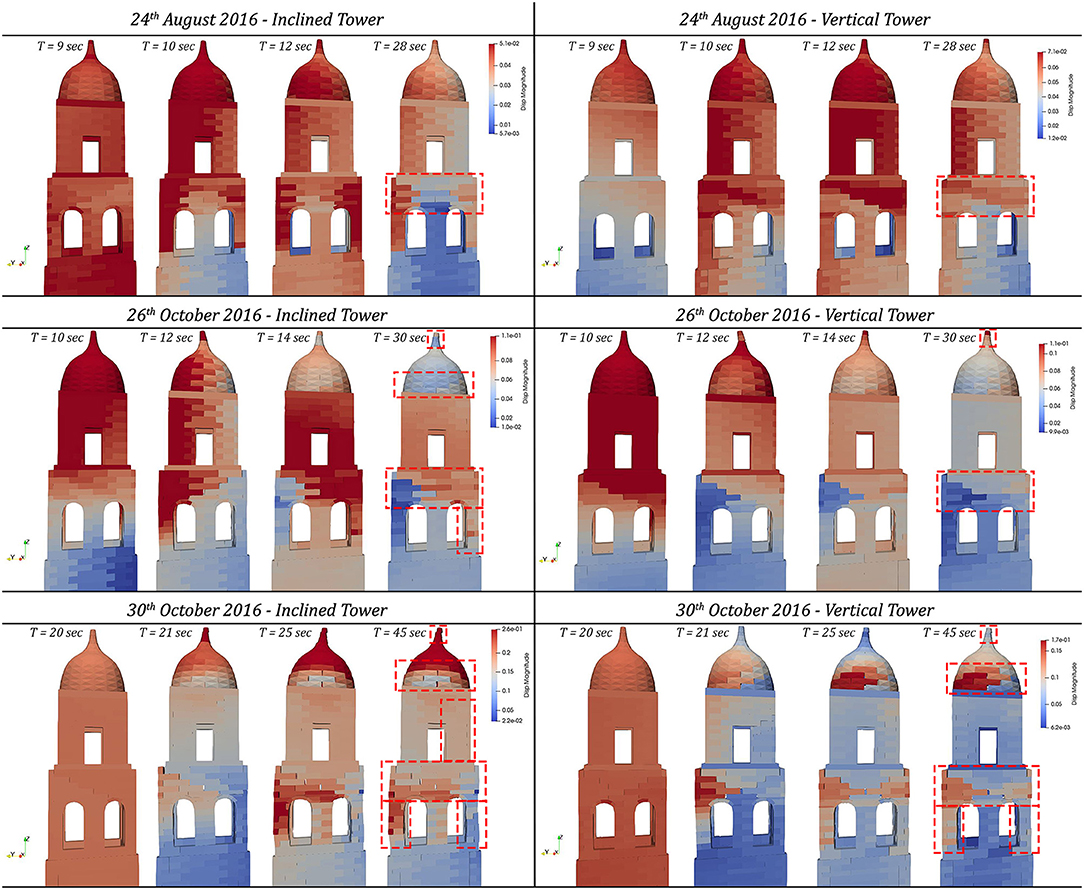
Figure 8. Failure mechanism of the bell tower of San Benedetto in Ferrara (Italy) for the inclined real configuration and the fictitious vertical one.
Firstly, it is necessary to pay attention to the damage mechanism of the upper part of the tower visible in Figures 7, 8, where it is evident the failure of the bell cell and the dome for every seismic load used in the 12 different simulations done. The main mechanism involves the mullioned windows of the belfry, which engender a vulnerability for the masonry walls with diffuse cracks on it and dislocations of blocks of the piers. These displacements are more highlighted on the results of earthquakes of 26 and 30th October 2016 (Figure 8), in particular for the inclined tower, which suffered the amplification of these movements.
Additionally, the failure of the dome arises in all results, and the activation of its mechanism is similar at varying of the different dynamic actions. Thus, it is more developed in simulations with the recorded velocities of 06th April 2009 (in Figure 7), 24th August 2016, 26th October 2016 and 30th October 2016 (in Figure 8). The damages consist of the massive displacements of the blocks at the base of the dome and the rotation of the pinnacle. Again, these motions are more significant in the cases of the inclined tower.
To explain in detail the differences of the dynamic response between inclined and vertical towers and to highlight the effects of amplification of slope on the damage mechanism and on the vulnerability of the masonry, the displacements of several control points over time of both configurations of the bell tower are analyzed.
The displacements Time Histories (THs) related to the pinnacle of the dome, namely the control point #1, are reported in Figure 9, with the use of the solid line to plot the results of the inclined tower and the dotted line to show the results of the vertical structure. In this graph, at varying of the seismic actions, it is possible to observe that the resultant displacements of both models are similar, with bigger values in the inclined case. This permits a more precise reading of the damage reported in Figures 7, 8 concerning the activation of the mechanism of the dome for this event, in particular the overturning of the pinnacle, much more noticeable for the model with the slope. Naturally, this result becomes more meaningful in the dynamic analyses with the earthquake of 30th October 2016, for which is plotted residual displacement for the point #1 of ~45 cm for the inclined and of ~10 cm for the vertical configurations. The same behavior is exhibited with the other earthquakes, with lower deviation from the values of the displacements of the two configurations considered for the tower.
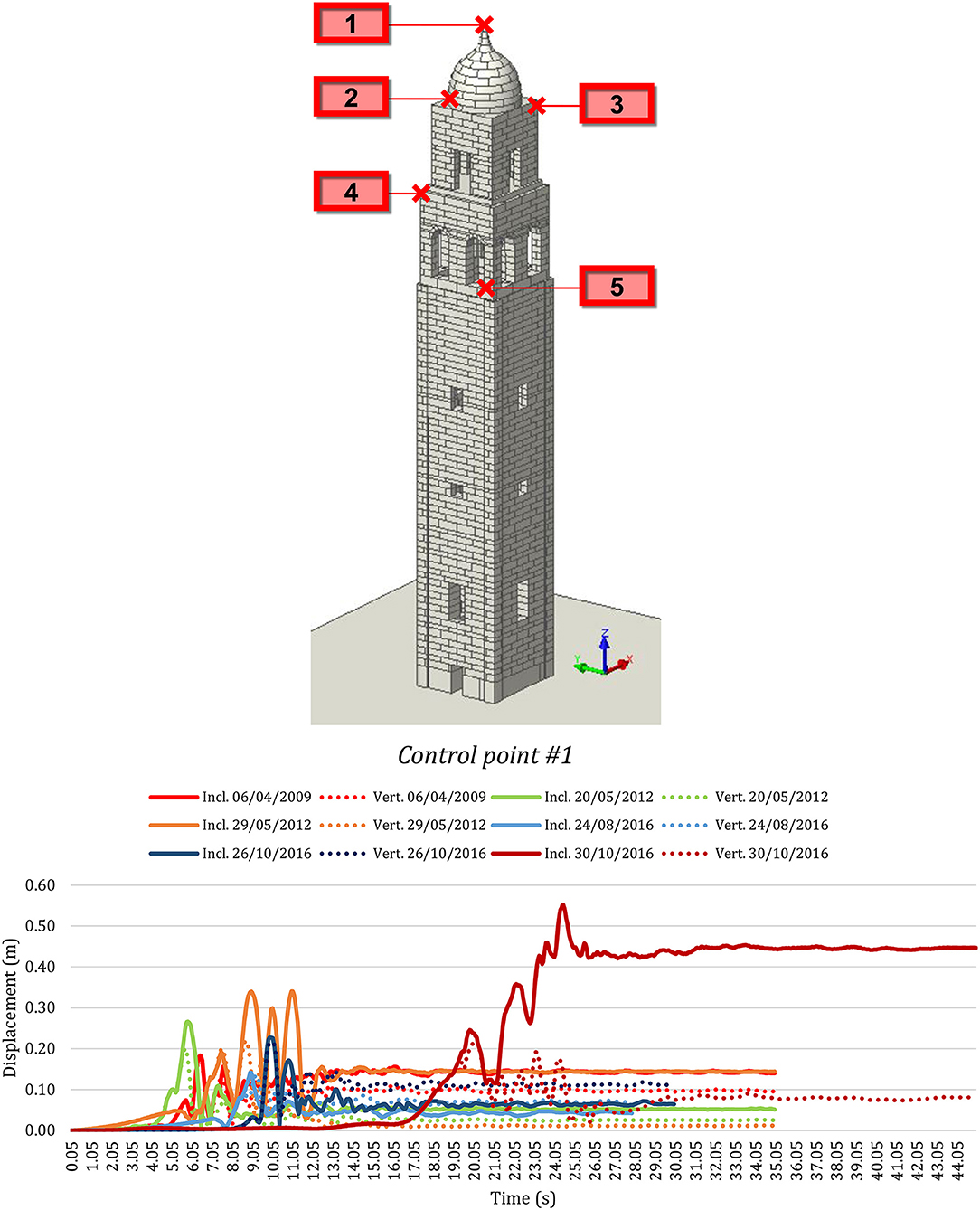
Figure 9. Displacements time histories of the control point #1 of the bell tower of San Benedetto in Ferrara (Italy) for the inclined real and the fictitious vertical configurations for the six main Italian earthquakes of the last few decades.
Similarly, for the earthquakes of 24th August 2016 and of 26th October 2016 the main results related to the peak shifts show higher values for the control points #1 of the inclined model than of the vertical one. Instead, the residual displacement is noticeably lower for the inclined configuration than the second one. Hence, for these events, the pinnacle exhibits a more vulnerability in the case of the vertical tower, which has a higher resistance in the bottom part of the masonry.
The dynamic responses of the control point #2, which is at the base of the dome, are pointed out in Figure 10 where a comparison between both configurations of the tower for the six seismic events are reported. Also in this case, the displacements THs introduce higher values of the displacement's peak for the inclined model than of the vertical one. Similarly, the residual shift has higher values for the inclined tower than the vertical tower for the shocks of 06th April 2009, 20th May 2012 and 29th May 2012, and, on the other hand, it has lower values for the inclined than the vertical configurations for the earthquakes of 24th August 2016, 26th October 2016 and 30th October 2016. These last have a smaller gap between the values than the first three. In fact, for the events of 29th May 2012, the residual displacement is ~12 cm for the inclined tower and ~2 cm for the vertical one. Hence, these results correspond to an explicit activation of the in-plane mechanism with sliding of blocks at the base of the dome for all the analyses of the inclined model, overall with greatest dislocations.
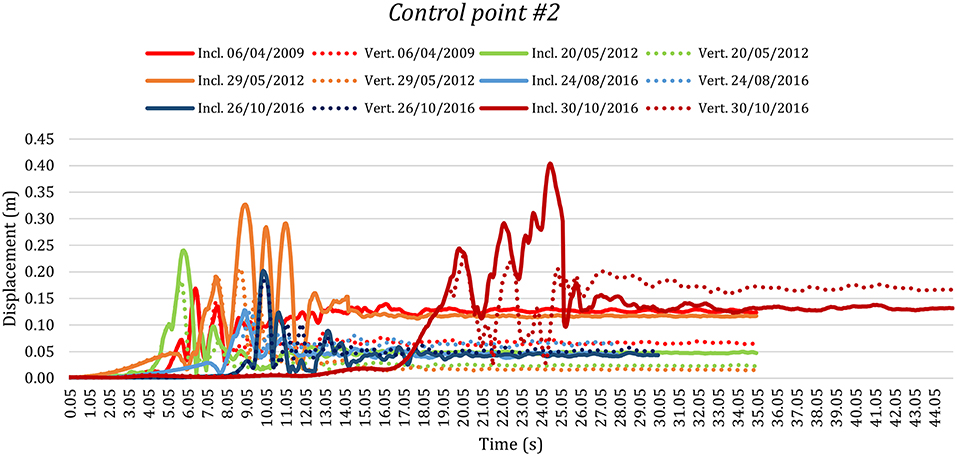
Figure 10. Displacements time histories of the control point #2 of the bell tower of San Benedetto in Ferrara (Italy) for the inclined real and the fictitious vertical configurations for the six main Italian earthquakes of the last few decades.
Regard to the displacements THs of the control point #3, belonging to the top of the tower, they present comparable values of displacement with those illustrated in Figure 11 for all the seismic events. The resultant displacements are greater for the inclined tower than the vertical, except for the earthquakes of 24th August 2016 and 26th October 2016, in which the values are almost the same for both models. The main difference of the values regards to the residual displacement of the shocks of 29th May 2012, which is near to 15 cm for the inclined tower and between 3 and 4 cm for the vertical one, and of 30th October 2016 that is equal to 18 cm for the inclined configuration and near to 4 cm for the vertical one. There are other two results which are no doubt slightly less significant but nonetheless they are still of importance, such as the residual displacement of the dynamic actions of 06th April 2009, that is equal to 15 cm for the inclined configuration and near to 6 cm for the vertical one, and 20th May 2012, which is near to 8 cm for the inclined tower and near to 3 cm for the vertical one.
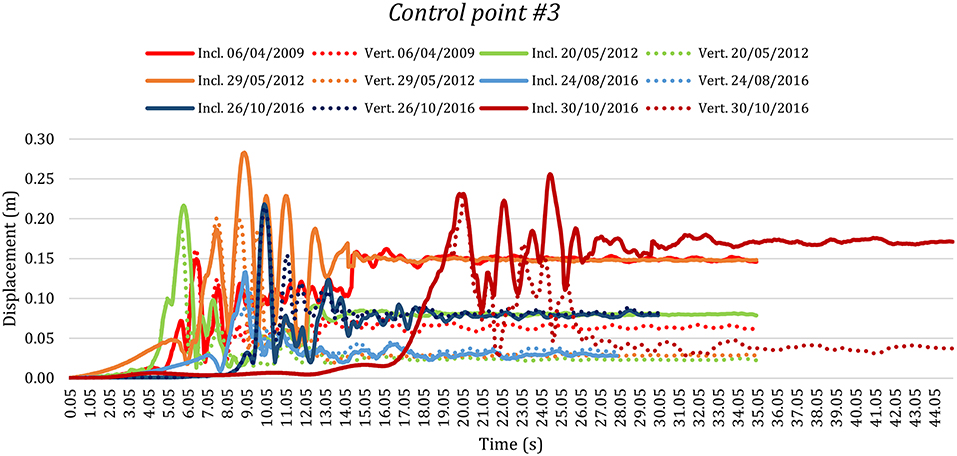
Figure 11. Displacements time histories of the control point #3 of the bell tower of San Benedetto in Ferrara (Italy) for the inclined real and the fictitious vertical configurations for the six main Italian earthquakes of the last few decades.
Looking at the displacements THs of the control point #4 plotted in Figure 12, it is noticeable that the overall behavior is similar in both cases for all dynamic actions. In particular, it is noticeable the activation of a damage mechanism for the event of 30th October 2016 for both the configurations, with the values of the residual displacement between 17 and 18 cm for the inclined tower and between 13 and 14 cm for the vertical tower. Otherwise, there is not an explicit activation of mechanism for the shocks of 20th May 2012 for both models, remaining with residual displacements between 2 and 3 cm. Other and different considerations shall be made concerning the seismic analyses with recorded ground velocity of 06th April 2009, 29th May 2012 and 26th October 2016, in which the values of the residual displacement of the control point #4 for the inclined tower are respectively more or less equal to 6, 8, and 5 cm, and instead, for the vertical tower are correspondingly equal to 2, 3, and 4. Therefore, for these analyses there is a light amplification of sliding and damages for the tower with the slope. For the seismic event of 24th August 2016 a reversed situation compared to the previous results is noticeable: the residual displacement has a bigger value (of about 7 cm) for the vertical than the inclined configurations (of about 5 cm).
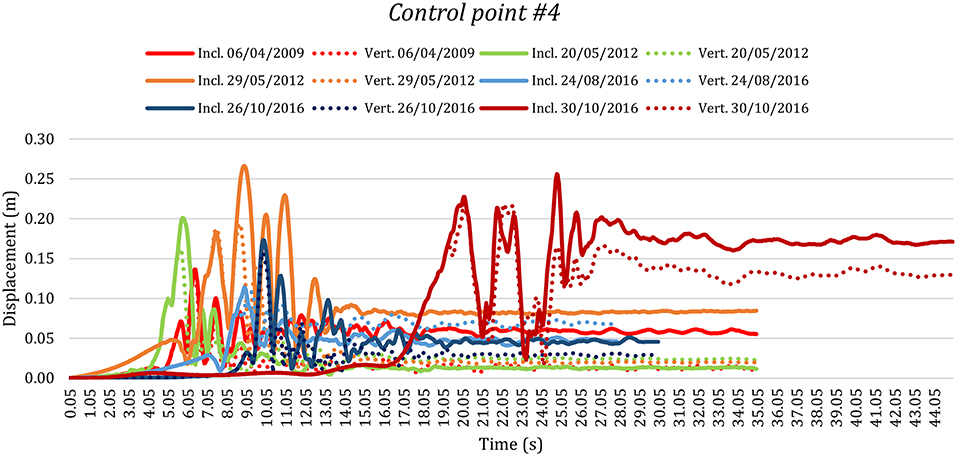
Figure 12. Displacements time histories of the control point #4 of the bell tower of San Benedetto in Ferrara (Italy) for the inclined real and the fictitious vertical configurations for the six main Italian earthquakes of the last few decades.
Similar considerations can be done with regard to the control point #5, shown in Figure 13, which is the lowest one along the height of the structure. It presents similar resultant displacements for both configurations of the tower and, again, overall lesser values for the vertical configuration. This is especially highlighted for the events of 06th April 2009 and 30th October 2016, which have values of the residual displacement for the inclined tower more or less equal to 9 and 8 cm, respectively, and for the vertical tower equal to 5 cm and between 6 and 7 cm, respectively. Otherwise, the events of 20th May 2012 and 26th October 2016 exhibit bigger values of the residual displacement for the inclined than the vertical one, but with small deviations between them. Whereas, the values of the residual displacement are higher for the vertical configuration than the inclined one for the shocks of 29th May 2012 for which are equal to 3 cm (inclined) and 2 cm (vertical), and of 24th August 2016 for which are 2÷3 (inclined) cm and 3÷4 cm (vertical).
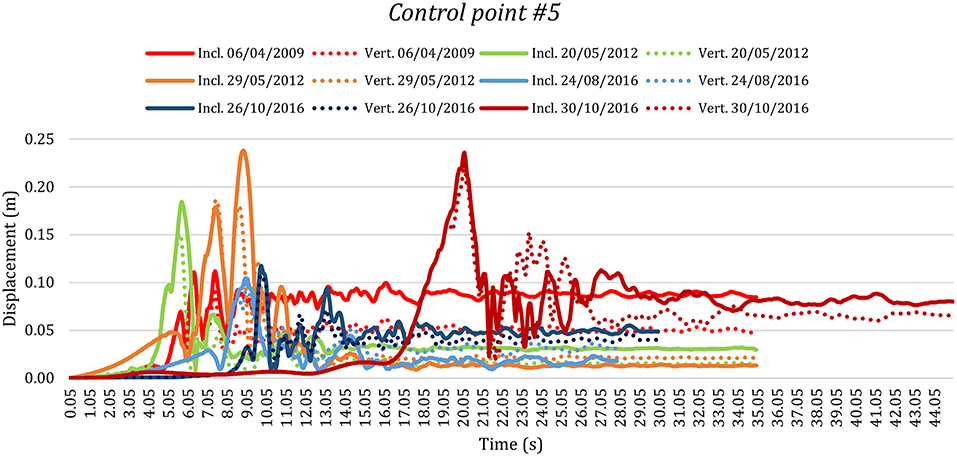
Figure 13. Displacements time histories of the control point #5 of the bell tower of San Benedetto in Ferrara (Italy) for the inclined real and the fictitious vertical configurations for the six main Italian earthquakes of the last few decades.
Finally, in Figure 14 is plotted the dissipated energy due to the friction at varying of the shocks for both the models. Hence, it is possible to observe that the dissipations of energy firstly have a high increase and then remain more or less unchanged during the velocity of the six main Italian earthquakes of the last few decades used for the dynamic analyses. Furthermore, the dissipated energy presents quite near values over the all-time for the different models, with increased values for the inclined tower (indicated with solid line) than the vertical one (indicated with dotted line), consistent with all the results of the analyses examined above.
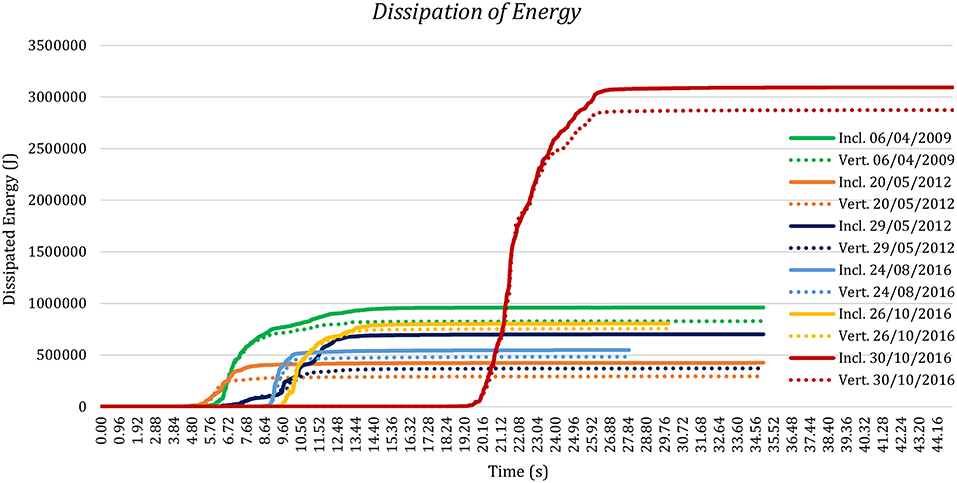
Figure 14. Evolution of the dissipated energy of the bell tower of San Benedetto in Ferrara (Italy) for the inclined real and the fictitious vertical configurations for the six main Italian earthquakes of the last few decades.
It is possible to conclude that the initial inclination of the tower leads to greater damage in the area of the belfry and along the trunk and the damage is greater with the magnitude of the considered earthquake. Also, the non-symmetry of the damage is accentuated in the presence of an initial inclination. Otherwise the perfectly vertical tower amplifies the damage in the top area, leaving the rest of the structure undisturbed, unless there are very intense earthquakes.
Conclusions
An inclined existing masonry tower has been modeled by means of the DEM and the NSCD method has been used to study its complex nonlinear behavior and the effect of an initial inclination on the seismic vulnerability.
The numerical models used do not reproduce the exact stone block shapes, but it preserves the real horizontality of the mortars joint with an average dimension of the units of the texture to have a rational compromise between the computational burden and the request of comprehensive description of the masonry of the tower. In fact, the models provided a fairly good representation of the observed displacements and near collapse modes.
The structural model of the existing tower has been carefully examined with the real inclined and a fictitious vertical configuration, under the action of the most six destructive Italian seismic events of the last 10 years.
In the case of the inclined structure, an obvious increment of the failure mechanisms has been remarked, compared to the structure without overhang. On the other hand, the dome introduces a well-known weakness to the assessment of the tower's vulnerabilities in both configuration, even if it is more damaged in the perfectly vertical configuration. Differently, the bell cell, another perfectly knows vulnerability of the masonry towers, it is more damaged in the presence of initial inclination.
As a result, the meaningful increased vulnerability of the inclined bell tower is demonstrated by the largest damages and the weakness along all height of the tower itself. At the same time, the greater values of the displacements and the dissipation of energy over time for the structure with slope under different dynamic input confirm the negative impact of the inclination on the tower, that makes it less durable respect to dynamic actions.
Finally, the DEM significantly has proving to be a powerful numerical approach to analyzed dynamics behavior of historic masonry structures in the nonlinear field, also by means of the NSCD method, that allows to point out in depth the masonry's vulnerabilities.
Author Contributions
AF created the numerical model, FC analyzed the results, GM supervised the research. All the authors contributed to the writing of the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Acito, M., Bocciarelli, M., Chesi, C., and Milani, G. (2014). Collapse of the clock tower in Finale Emilia after the May 2012 Emilia Romagna earthquake sequence: numerical insight. Eng. Struct. 72, 70–91. doi: 10.1016/j.engstruct.2014.04.026
Asteris, P. G., Sarhosis, V., Mohebkhah, A., Plevris, V., Papaloizou, L., Komodromos, P., et al. (2015). “Numerical Modeling of Historic Masonry Structures,” in Handbook of Research on Seismic Assessment and Rehabilitation of Historic Structures, eds. P. Asteris and V. Plevris (Hershey, PA: IGI Global), 213–256.
Betti, M., Galano, L., and Vignoli, A. (2014). Comparative analysis on the seismic behaviour of unreinforced masonry buildings with flexible diaphragms. Eng. Struct. 61, 195–208. doi: 10.1016/j.engstruct.2013.12.038
Brandonisio, G., Lucibello, G., Mele, E., and De Luca, A. (2013). Damage and performance evaluation of masonry churches in the 2009 L'Aquila earthquake. Eng. Fail. Anal. 34, 693–714. doi: 10.1016/j.engfailanal.2013.01.021
Cavalagli, N., and Gusella, V. (2015). Dome of the basilica of santa maria degli angeli in assisi: static and dynamic assessment. Int. J. Archit. Herit. 9, 157–175. doi: 10.1080/15583058.2014.951799
Chetouane, B., Dubois, F., Vinches, M., and Bohatier, C. (2005). NSCD discrete element method for modelling masonry structures. Int. J. Numer. Methods Eng. 64, 65–94. doi: 10.1002/nme.1358
Circolare Ministeriale n 617 (2009). Cons. Sup. LL. PP., “Istruzioni per l'applicazione delle Nuove Norme Tecniche per le Costruzioni” di cui al decreto ministeriale del 14.01.2008. G.U. del 26.02.2009 n. 47, supplemento ordinario n. 27. (in Italian).
Clementi, F., Gazzani, V., Poiani, M., Mezzapelle, P. A., and Lenci, S. (2018a). Seismic assessment of a monumental building through nonlinear analyses of a 3D solid model. J. Earthq. Eng. 22, 35–61. doi: 10.1080/13632469.2017.1297268
Clementi, F., Pierdicca, A., Milani, G., Gazzani, V., Poiani, M., and Lenci, S. (2018b). “Numerical model upgrading of ancient bell towers monitored with a wired sensors network,” in 10th International Masonry Conference (IMC_10), eds. S. Milani, G., Taliercio, A., Garrity (Milano), 1–11.
Clementi, F., Quagliarini, E., Maracchini, G., and Lenci, S. (2015). Post-world war II Italian school buildings: typical and specific seismic vulnerabilities. J. Build. Eng. 4, 152–166. doi: 10.1016/j.jobe.2015.09.008
Clementi, F., Quagliarini, E., Monni, F., Giordano, E., and Lenci, S. (2017). Cultural heritage and earthquake: the case study of “Santa Maria Della Carità” in Ascoli Piceno. Open Civic Eng. J. 11, 1079–1105. doi: 10.2174/1874149501711011079
Dubois, F., Acary, V., and Jean, M. (2018). The contact dynamics method: a nonsmooth story. Comptes Rendus Mécanique 346, 247–262. doi: 10.1016/j.crme.2017.12.009
Formisano, A., Di Lorenzo, G., Iannuzzi, I., and Landolfo, R. (2017). Seismic vulnerability and fragility of existing italian industrial steel buildings. Open Civ. Eng. J. 11, 1122–1137. doi: 10.2174/1874149501711011122
Formisano, A., Vaiano, G., Fabbrocino, F., and Milani, G. (2018). Seismic vulnerability of Italian masonry churches: the case of the Nativity of Blessed Virgin Mary in Stellata of Bondeno. J. Build. Eng. 20, 179–200. doi: 10.1016/j.jobe.2018.07.017
Giordano, E., Clementi, F., Nespeca, A., and Lenci, S. (2019). Damage assessment by numerical modeling of sant'agostino's sanctuary in offida during the central italy 2016–2017 Seismic Sequence. Front. Built Environ. 4:87. doi: 10.3389/fbuil.2018.00087
Lagomarsino, S., and Podestà, S. (2004). Damage and vulnerability assessment of churches after the 2002 Molise, Italy, Earthquake. Earthq. Spectra 20, S271–S283. doi: 10.1193/1.1767161
Lemos, J. V. (2007). Discrete Element Modeling of Masonry Structures. Int. J. Archit. Herit. 1, 190–213. doi: 10.1080/15583050601176868
Luzi, L., Hailemikael, S., Bindi, D., Pacor, F., Mele, F., and Sabetta, F. (2008). ITACA (ITalian ACcelerometric Archive): a web portal for the dissemination of italian strong-motion Data. Seismol. Res. Lett. 79, 716–722. doi: 10.1785/gssrl.79.5.716
Maschke, R., Lozano, B., Brogliato, O., and Egeland, O. (2001). Dissipative Systems Analysis and Control. London, UK: Theory and Applications.
Milani, G. (2013). Lesson learned after the Emilia-Romagna, Italy, 20–29 May 2012 earthquakes: a limit analysis insight on three masonry churches. Eng. Fail. Anal. 34, 761–778. doi: 10.1016/j.engfailanal.2013.01.001
Moreau, J. J. (1988). “Unilateral Contact and Dry Friction in Finite Freedom Dynamics,” in Nonsmooth Mechanics and Applications (Vienna: Springer Vienna), 1–82.
Pacor, F., Paolucci, R., Luzi, L., Sabetta, F., Spinelli, A., Gorini, A., et al. (2011). Overview of the Italian strong motion database ITACA 1.0. Bull. Earthq. Eng. 9, 1723–1739. doi: 10.1007/s10518-011-9327-6
Pellegrinelli, A., Furini, A., and Russo, P. (2014). Earthquakes and ancient leaning towers: geodetic monitoring of the bell tower of San Benedetto Church in Ferrara (Italy). J. Cult. Herit. 15, 687–691. doi: 10.1016/j.culher.2013.12.005
Pellegrini, D., Girardi, M., Lourenço, P. B., Masciotta, M. G., Mendes, N., Padovani, C., et al. (2018). Modal analysis of historical masonry structures: linear perturbation and software benchmarking. Constr. Build. Mater. 189, 1232–1250. doi: 10.1016/j.conbuildmat.2018.09.034
Pierdicca, A., Clementi, F., Isidori, D., Concettoni, E., Cristalli, C., and Lenci, S. (2016). Numerical model upgrading of a historical masonry palace monitored with a wireless sensor network. Int. J. Mason. Res. Innov. 1:74. doi: 10.1504/IJMRI.2016.074748
Poiani, M., Gazzani, V., Clementi, F., Milani, G., Valente, M., and Lenci, S. (2018). Iconic crumbling of the clock tower in Amatrice after 2016 central Italy seismic sequence: advanced numerical insight. Procedia Struct. Integr. 11, 314–321. doi: 10.1016/j.prostr.2018.11.041
Roca, P., Cervera, M., Pel,à, L., Clemente, R., and Chiumenti, M. (2013). Continuum FE models for the analysis of Mallorca Cathedral. Eng. Struct. 46, 653–670. doi: 10.1016/j.engstruct.2012.08.005
Sarhosis, V., Milani, G., Formisano, A., and Fabbrocino, F. (2018). Evaluation of different approaches for the estimation of the seismic vulnerability of masonry towers. Bull. Earthq. Eng. 16, 1511–1545. doi: 10.1007/s10518-017-0258-8
Terracciano, G., Di Lorenzo, G., Formisano, A., and Landolfo, R. (2015). Cold-formed thin-walled steel structures as vertical addition and energetic retrofitting systems of existing masonry buildings. Eur. J. Environ. Civ. Eng. 19, 850–866. doi: 10.1080/19648189.2014.974832
Valente, M., and Milani, G. (2016). Seismic assessment of historical masonry towers by means of simplified approaches and standard FEM. Constr. Build. Mater. 108, 74–104. doi: 10.1016/j.conbuildmat.2016.01.025
Keywords: masonry tower, inclination effect, vulnerability, nonlinear dynamic analysis, non-smooth contact dynamic (NSCD)
Citation: Ferrante A, Clementi F and Milani G (2019) Dynamic Behavior of an Inclined Existing Masonry Tower in Italy. Front. Built Environ. 5:33. doi: 10.3389/fbuil.2019.00033
Received: 08 January 2019; Accepted: 27 February 2019;
Published: 20 March 2019.
Edited by:
Antonio Formisano, University of Naples Federico II, ItalyReviewed by:
Ernesto Grande, Università degli Studi Guglielmo Marconi, ItalyAndrea Chiozzi, University of Ferrara, Italy
Copyright © 2019 Ferrante, Clementi and Milani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francesco Clementi, ZnJhbmNlc2NvLmNsZW1lbnRpQHVuaXZwbS5pdA==
 Angela Ferrante
Angela Ferrante Francesco Clementi
Francesco Clementi Gabriele Milani
Gabriele Milani