The Dynamic Effect of Downburst Winds on the Longitudinal Forces Applied to Transmission Towers

Introduction

Background

Electricity is a vital component of our contemporary way of living. The reliability of such a crucial element to socio-economical growth is heavily dependent on the sustainability and resiliency of transmission line system components facing various weather-related loading conditions. Aside from the conventional loading attributed to synoptic wind, loading cases associated with thunderstorms (i.e., tornadoes and downbursts), have recently been acknowledged for their devastating impact on transmission line systems. Fujita (1985a) first defined downbursts as “a strong downdraft that induces an outburst of damaging wind near the ground” are believed to be the major cause of transmission line failures (Miguel et al., 2018). Kanak et al. (2007) reported the failure of 19 towers in Slovakia due to a downburst event. Another event that occurred in Manitoba, Canada, has been reported by McCarthy and Melsness (1996) and resulted in the failure of 19 transmission towers. Similarly, Hydro One Ontario Company (Ontario, Canada) revealed that the failures of their two towers near Waubaushene were due to a downburst event (Hydro One Failure Report, 2006). These incidents, as well as those that occurred in Australia as reported by Li (2000), and in China as reported by Zhang (2006), have directed researchers to study the effect of downburst loading on transmission line systems.

Researchers studying the effect of downbursts on transmission line systems have followed different paths in choosing the wind field used to examine the behavior of different transmission line components corresponding to downburst loading cases. Despite the availability of different numerical approaches to generate thunderstorm outflows (Ponte and Riera, 2007; Solari et al., 2017), many researchers used wind fields developed using computational fluid dynamics (CFD). Shehata et al. (2005) scaled up the wind field resulting from the CFD simulation conducted by Kim and Hangan (2007) to study the behavior of both the conductors and the supporting towers due to the applied downburst wind field. Finite element analysis showed that downburst loading might yield higher peak values of internal forces than that resulting from straight line winds. The study also concluded that the consideration of six spans should suffice when studying a localized downburst event. Building on that study, another investigation was conducted by Shehata and El Damatty (2007) to study the spatial configuration of a downburst that would lead to the highest forces in the members of a guyed tower. The results of that study emphasize the importance of considering the spatial locality of the event, which proved to be essential when studying transmission line structures extending for great horizontal distances. To generate the wind field, the same procedures were adopted by Darwish and El Damatty (2011) and Mara and Hong (2013) who also concluded that downburst loading can lead to more severe loading conditions compared to normal wind loading cases depending on the jet velocity considered.

It is worth mentioning that all the aforementioned studies could only use the quasi-static analysis approach, given only time-varying mean velocity fields were available from the URANS simulations of Kim and Hangan (2007). This was generally justified by the fact that the studied structural components, whether the conductors or the tower structures, have distinctive natural periods, which are relatively distant from that of the loading phenomenon. Yet, further studies have considered the dynamic effect associated with downburst loading to investigate its impact on the structural elements. To do so, researchers had to produce the fluctuating component using different techniques, and then super-impose it on the mean component. In the case of Darwish et al. (2010), researchers extracted the turbulent component from field measurements that were reported by Holmes et al. (2008), and then added it to the time histories of the moving mean component produced by RANS CFD simulations. The study concluded that inclusion of the turbulent component into the dynamic analysis showed minor differences compared to the quasi-static analysis, which was attributed to the high aerodynamic damping exhibited by the conductors, attenuating the dynamic response. Another approach was used by Wang et al. (2009) who studied the dynamic response of tall transmission towers, where the turbulent component was synthetically produced using harmony superposition method combined with Fast Fourier Transform (FFT) algorithm, and the same conclusion was reached, that the dynamic effect could be neglected due to the difference in frequencies between the tower and the studied event.

Savory et al. (2001) utilized the empirical model developed by Holmes and Oliver (2000) to produce downburst wind field, and evaluate the loading on lattice towers by performing dynamic analysis on the tower structures. The analysis concluded that the tower structures were found to be safe, suggesting failure occurrence is dependent on the inclusion of conductor loading in the analysis. Dynamic performance was also evaluated by Lin et al. (2012), who used the slot jet model discussed by Lin and Savory (2006) to test an aero-elastic model of a transmission line system in a boundary layer wind tunnel, simulating downburst wind field. Results from the downburst wind field test cases were compared to those of the synoptic wind, and results showed less significance of dynamic effect, and a generally quasi-static behavior.

Furthermore, researchers studying downbursts on transmission line systems can also be categorized based on the components examined in their studies. While Aboshosha et al. (2016), Lin et al. (2012), Shehata et al. (2005), Shehata and El Damatty (2007), Darwish and El Damatty (2011), and Elawady et al. (2017) considered the combined tower-line system, Mara et al. (2010), Mara and Hong (2013), and Savory et al. (2001) have considered the effect of downburst loading on the supporting tower structures alone with no regard for the conductors. On the other hand, Aboshosha and El Damatty (2014a,b); Aboshosha and El Damatty (2015b), Darwish et al. (2010), and Elawady and El Damatty (2016) have focused on the conductors, studying their impact either on the loading process, or their aerodynamic damping. The current study is an extension of the work performed by Elawady and El Damatty (2016). It examines the limitations associated with the analysis of Elawady and El Damatty (2016), the validity of their assumptions, and finally the applicability of the wind field used.

Problem Definition

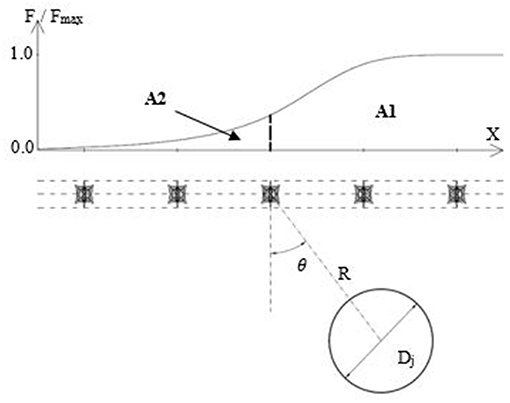
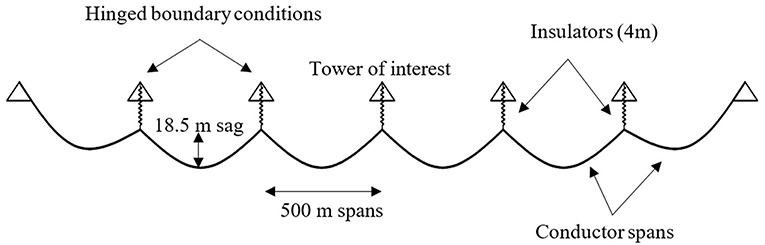
Elawady and El Damatty (2016), complimented a series of previous studies that investigated the effect of downburst loading on transmission line systems. The studies performed by Darwish and El Damatty (2011) and Shehata and El Damatty (2007) looked into the effect of the localized nature of downburst loading on transmission line systems. This special feature of downburst loading, where the loading is not constant across spans, results in different structural behavior than that resulting from straight line winds. One of their cases, which they termed oblique load case, has the downburst positioned such that the angle theta “θ” between a line perpendicular to the tower and a line joining the downburst center with the tower is >0, as shown in Figure 1.

FIGURE 1

Figure 1. Oblique load case illustration with downburst loading force distribution along spans.

Such cases result in differential loading on the consecutive conductor spans attached to the tower of interest. Figure 1 illustrates that through areas A1 and A2. Area A1 represents the total force acting on the conductors to the right of the tower of interest (closer to the downburst center), and area A2 represents the total force on the conductors to the left of the tower of interest (away from the downburst center). The loading exhibited due to this case is similar in configuration to that of the broken wire loading case considered by ASCE-74 (2010). This case is of particular importance to components like the cross-arms that can experience large moments due to the longitudinal forces. Aboshosha and El Damatty (2013) showed that these longitudinal forces can exceed the associated transverse forces by up to 60%. Yet, varying downburst parameters like the radial distance R, obliquity angle θ and jet diameter D_j, can lead to loading cases that are more severe than that of the broken wire.

As such, Elawady and El Damatty (2016) conducted an elaborate parametric study to find the configuration resulting in the highest longitudinal loading. To do so, the authors utilized the technique described by Aboshosha and El Damatty (2015b) to compute the reactions on a six-span conductor system. The loads applied to the system were those corresponding to the downburst wind field generated by Kim and Hangan (2007). However, the wind field used only contains the moving mean component of the flow and did not contain the fluctuating component. As such, the dynamic effect of the wind loading is excluded. In addition, extruding a three dimensional wind field from two dimensional CFD analysis results in the assumption of full correlation. This can result in computing values of longitudinal reactions that are not conservatives.

This study aims to quantify the influence of these limitations and judge the applicability of quasi-static analysis compared to dynamic analysis. To do so, the current study will conduct the following steps:

1. Develop a numerical structural analysis model for calculating the response of a multi-spanned conductor system to downburst wind loading.

2. Compare model results with experimental test results to ensure applicability for the problem under consideration

3. Perform the numerical analysis at full-scale using the developed model, and assess the effect of neglecting the dynamic analysis on the magnitude of the longitudinal forces.

4. Examine the sensitivity of the computed results to changing the wind field characteristics within the limits found in field measurements.

Accordingly, the following sections outline the current study. The second section (section Model-Scale Analysis) describes the analysis performed at model-scale. The full-scale analysis is presented in the third section (section Full-Scale Analysis). The technique used in generating the turbulent component is described, and the analysis results are demonstrated. Section Analysis of Result's Sensitivity to Wind Field Parameters examines the sensitivity of the computed results to the wind field characteristics used in the full-scale analysis, and compares it to the characteristics of wind fields reported by previous literature. Finally, the last section (section Conclusions) lists the conclusions drawn from the conducted work.

Model-Scale Analysis

In this section, a numerical model is proposed to dynamically resolve the longitudinal reactions of transmission lines on supporting towers due to downburst loading. The model and the wind field used are discussed in the first subsection (section Numerical Model), and the results are compared with experimental results in the second subsection (section Model Scale Results and Verification).

Numerical Model

Dynamic analysis of conductor systems under downburst loading is a complicated task due to the geometric nonlinearity of the conductors. In addition, the time varying properties of the wind field require properties such as the aerodynamic damping to be modified throughout time. Previous studies that conducted dynamic analyses on transmission line systems due to synoptic wind such as Dua et al. (2015), Keyhan et al. (2013), and McClure and Lapointe (2003) considered an equivalent viscous damping to account for the aerodynamic damping. The values used by Dua et al. (2015) and Keyhan et al. (2013) were those resulting from the fluid structure interaction model computed by the latter study. These values were then implemented through different commercial software packages to enable 3D finite element analysis. It can be argued that the constant damping values used are in line with the expression proposed by Davenport (1962) and shown in equation (1). The aerodynamic damping value per mode i is shown to depend on the air density ρ, the drag coefficient C_D, the conductor diameter D, the wind velocity V, conductor mass m, and finally the frequency of the ith mode f_i. Thus, for studies such as these that considered synoptic wind, a constant damping value is considered reasonable, as synoptic wind can be reasonably approximated as a stationary random process with a constant statistical mean.

$\begin{array}{ll}{\zeta }_{\text{a}\text{i}}=\frac{\rho C_{D}DV}{4\pi m{f}_i}& (1)\end{array}$

In contrast, researchers like Darwish et al. (2010) and Aboshosha and El Damatty (2015b) used a modified version of the aerodynamic damping expression to account for the temporal variation of wind speed and resultant aerodynamic damping. The time dependent damping is a special feature that complicates the analysis and requires special numerical tools. To overcome this, it is proposed that a single value of aerodynamic damping, representative of the entire event, be implemented. An experiment that was part of the research program presented by Elawady et al. (2017) will be used to verify the numerical model. The next sub-section (Model Scale Results and Verification) will elaborate on the experimental setup and verification of the numerical model.

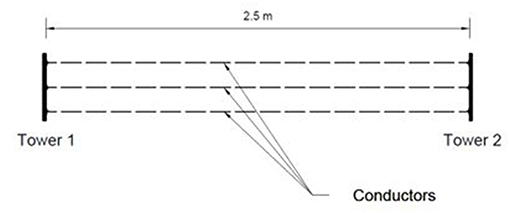
A SAP2000 model was developed to simulate a single span of cable elements with a span of 2.5 m and a sag of 0.0975 m as shown in Figure 2. The boundary conditions were set as hinged on both ends, and the simulated 2-noded cable element had the properties reported by Elawady et al. (2017). Modal analysis was first conducted to determine the natural frequencies for different modes of the system, and damping values were computed per mode using equation (1). The most challenging aspect of the procedure was the choice of a single value of velocity that could represent the whole time history in calculating a fixed aerodynamic damping value.

FIGURE 2

Figure 2. Layout of tested conductor system.

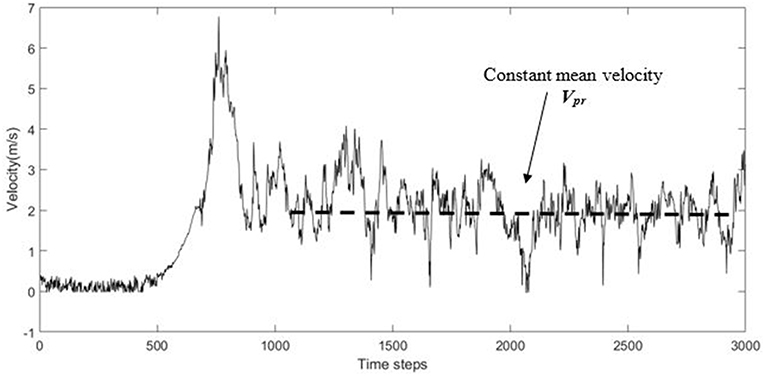
The mean wind field used in this analysis was that resulting from the CFD analysis simulating the WindEEE dome downburst as reported by Ibrahim et al. (2017). As for the turbulent component used, the wind field reported by Elawady et al. (2017) was superimposed on the mean component. This was done using an approach similar to that used by Darwish et al. (2010). Examining the resulting velocity time history shown in Figure 3, it appears that the early part of the time history, where the ramping occurs, is completely governed by the mean part of the flow. This can be concluded since the amplitudes of the higher frequencies related to the turbulent component are small during this period. Yet, the part that follows the ramping appears to have a rather constant mean, with fluctuating velocity fluctuating around that fixed value. Hence, it is suggested that the constant value of damping is to be calculated using the constant value following the ramping, which will be annotated V_pr in the sections that follow.

FIGURE 3

Figure 3. Time history of radial velocity for a probe point.

With the velocity value known, damping values were computed, and proportional damping coefficients were calculated based on the frequencies provided by the modal analysis. Loads were implemented as time histories of transverse forces acting as point loads on cable nodes. The analysis was then conducted as a transient non-linear direct integration case, considering the p-delta effect with large displacements. To test the sensitivity of the computed response to the chosen constant damping computed based on V_pr, the analysis was repeated two more times; using half the initial damping, and a quarter of it. The results presented in Figure 4, which shows the time history of the computed longitudinal reaction R_X, suggest that the assumption of concentrating on the post ramping region for evaluating the aerodynamic damping values is in fact a valid assumption. This is due to the agreement between the three plots for the ramping zone, despite the significantly varying damping values, and the differences being limited to the post ramping part of the time history. Elaborating more on that, it appears that the zone right after the ramping, denoted as Zone 1, is also insensitive to the change of damping values. Meanwhile, the time history beyond that zone, denoted as Zone 2, is the part affected by the change in damping values, implying the importance of considering damping for this zone.

FIGURE 4

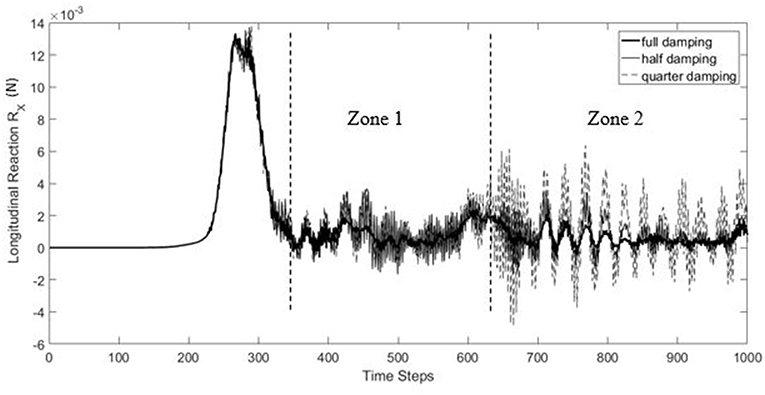
Figure 4. Comparison between time histories of longitudinal reaction R_X corresponding to different damping.

Model Scale Results and Verification

As mentioned in section Numerical Model, the experiment conducted was part of the research program presented by Elawady et al. (2017) to test aeroelastic models of transmission line systems under the action of downbursts simulated at the Wind Engineering, Energy and Environment (WindEEE) Research Institute. To simulate downbursts, an upper chamber that has six fans is pressurized until a steady pressure is reached. The flow is then released from the upper chamber through a 3.2 m opening (jet diameter) toward the hexagonal testing chamber (25 m edge-to-edge with height of 3.8 m). The flow impinges the ground, creating a downburst that radiates in every direction until it exits through the opening on the peripheral walls. Further details regarding the facility can be found in the work presented by Jubayer et al. (2016). It is worth noting that although the facility is capable of producing horizontal background flow, this study only considered the basic impinging jet model. This decision was based on the study conducted by Darwish et al. (2010) who found the basic impinging jet model with no background flow to cause the most critical loading condition on the cross-arms by producing the highest longitudinal reactions.

As for the tested structure, a single cable span, similar to the schematic shown in Figure 2 with dimensions similar to the numerical model in the previous section, was hung between two rigid frames using leaf springs to measure the resulting straining actions as presented in Figure 5.

FIGURE 5

Figure 5. Leaf spring instrumentation at cable ends.

Results from the numerical simulation were compared to the experimental data to verify the numerical model, as well as the validity of considering a constant damping value. As shown in Figure 6, the time history of the longitudinal reaction seems to be comparable. Yet, there seems to be discrepancy in the zone preceding time step number 600. This discrepancy is believed to have no effect on judging the sensitivity to dynamics due to two reasons; first, the time zone at which it happens is not expected to experience dynamic amplification as it is in the immediate vicinity of the ramping zone. This means it is in Zone 1 in Figure 4, which was found to be insensitive to change the damping values. Second, close examination of the response at that zone show clearly that the abrupt increase in the response value is a mean governed behavior due to the relatively low frequency at which the increase happens. This sudden increase is believed to be related to the vertical component of the wind speed, which is ignored in the current wind field due to its secondary effect compared to the radial component (Elawady and El Damatty, 2016). It appears that the leading vortex would cause such effect due to the downward directed vertical component of the flow at the trailing edge of the vortex. Nevertheless, considering the zone beyond time step number 600, which is where the dynamic action is expected to develop, the difference in peak dynamic amplification was found to be < 5%, which was assumed an acceptable level of agreement between the experimental and the numerical results. Hence, building on the agreement found, the current numerical model with the assumptions elaborated will be used for the full-scale analyses discussed in the following sections.

FIGURE 6

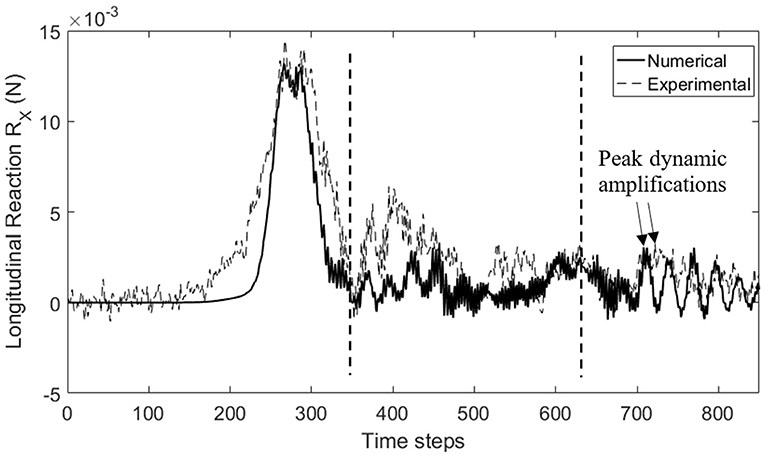
Figure 6. Comparison of longitudinal reaction time histories from numerical and experimental simulations.

Full-Scale Analysis

In this section, the wind field used in the analysis is described in the first subsection (section Wind Field). It is the result of superimposing a synthetically generated turbulent component on a scaled-up mean component resulting from the CFD analysis by Kim and Hangan (2007). The second subsection (section Numerical Model) elaborates on the modeled structure and the parameters considered. The last subsection (section Full-scale Model Results and Discussion) presents the results of the numerical simulation, and their interpretation.

Wind Field

Mean Component

As described in the section Introduction, the majority of researchers studying downbursts loading of transmission line systems used CFD-generated wind field to determine the loading on the structure system. The current study utilizes the wind field produced by Kim and Hangan (2007). An elaborate description of the numerical model and the validation with full-scale data can be found in that study. Nevertheless, the study was conducted on a model-scale, which needs to be scaled up to produce a full-scale wind field. Accordingly, the current study adopted the scaling procedure proposed by Shehata et al. (2005) which relates the length scale to the jet dimensions, and the velocity scale to the velocity of the downdraft at the jet inlet, and finally, the time scale as the ratio between the length and the velocity scales. The jet diameter used was 1,000 m, and the downdraft velocity was 70 m/s. The downburst size was chosen to be of average size (Hangan et al., 2008). Yet, the downdraft velocity, which is comparable to near-surface velocity, was chosen to be higher than common stationary downburst ground velocities in field that are usually less as reported by Holmes et al. (2008), Ponte and Riera (2010), and Zhang et al. (2017). The higher velocity was chosen since design analyses are usually conducted on critical values that would cause failures of transmission lines.

The mean velocity data were computed at the coordinates of the conductor nodes relative to the jet center. The case considered for this study was that identified by Elawady and El Damatty (2016) as the most critical case for longitudinal reactions corresponding to downburst loading. Referring to Figure 1, this is the case where the jet center is at an obliquity angle θ = 30 degrees, and R = 1.6 times the jet diameter, as well as having the span length equal to half the jet diameter.

Realizing that the study by Kim and Hangan (2007) yielded a 2D flow field, extruding the wind field circumferentially results in a perfectly correlated flow field. Moreover, the resulting wind field lacks any turbulence, since the study was conducted using RANS turbulence model. Accordingly, the remainder of this section will present the procedure adopted to generate turbulence that is to be added to the mean wind field.

Turbulent Component

The turbulent component of the wind field is essential for the current analysis and has to be generated by a technique that does two things; first, introduce the high frequency fluctuations that are to be added to the mean component of the flow, and second, ensure the generated turbulence maintains the statistical characteristics desired. This should be applicable for both types of properties; single point properties (spectra and turbulence intensities), and cross-space properties (coherencies and length scales). Different techniques can be found in the literature for synthetically generating turbulent time histories; the reader is referred to Huang et al. (2010), Kim et al. (2013), Klein et al. (2003), and Kondo et al. (1997).

The technique used to generate the turbulent component of the flow, named Consistent Discrete Random Flow Generation (CDRFG), has been proposed and thoroughly explained in Aboshosha et al. (2015b). The technique is used to generate the fluctuating component of the flow using: the mean velocity u_r, the turbulence intensity I_r, the decay coefficient in each direction C_j, the length scale in each direction, the spectral content distribution, and a characteristic length D that relates to the size of the studied problem. The study proposed discretizing the frequency content into segments, which should produce a better conforming spectral content, as well as a matching coherency with the expression proposed by Davenport (1993). For the current study, two changes were applied: (1) the frequencies were discretized using a logarithmic scale rather than a linear one to capture finer frequency scales corresponding to large vortices, and (2) the spatial discretization were changed from a Cartesian system to a polar system using the radial distance from the jet center R, the angular coordinate θ, and the height Z. To ensure consistency of the coordinates system, θ was replaced by the coordinate R. θ, representing the circumferential coordinate, where R and Z are in meters, and θ is in radians.

The steps used by the technique to generate the turbulent velocity component can be found in the original study. The technique requires the input of values characterizing the turbulent wind field. The first value required is the mean wind velocity, which in the case of synoptic wind is a single value that is easy to determine based on the point height, where a conventional vertical power profile is enough to characterize the flow for a whole plane perpendicular to the flow. In contrast, the downburst wind field is more complex due to the localized nature of the flow, which means no single plane can represent the flow. Accordingly, for each point, the value of V_pr, introduced previously, is used as u_r based on the observation that the post ramping section of the time history is the part affected by the inclusion of dynamics and thus turbulent flow into analysis. The turbulence intensity, I_r, was taken as 0.12, which reasonably agrees with the values reported by Aboshosha et al. (2015a), Holmes et al. (2008), and Orwig and Schroeder (2007). The values reported by the latter two studies are for heights much less than that of the conductor system to be studied. This will yield a wind field that is more turbulent, which means a more conservative structural response. The assumption that the turbulence intensity is height-independent is inline with the work done by Zhang et al. (2017).

The characteristic length D was chosen to be 10 times the span of the conductor system. This value was intentionally chosen to be relatively large to make sure that the coherency of large structures within the flow are maintained. On the other hand, field measurements of cross-spatial turbulence characteristics (length scales and coherency) are generally less in terms of availability in the literature. For the current study, these characteristics were deduced from the work done by Aboshosha et al. (2015a), relying on Large Eddy Simulations to find the values of length scales and coherency decay functions for the three coordinate directions, R, R.θ and Z. Length scales were related to the jet diameter, where the ratios between the length scales and the jet diameter were taken to be 0.5, 9, and 0.1 for the radial, circumferential and vertical directions, respectively. The coherency decay coefficients, C_j, were taken as 10, 0.05, and 10 for the three directions, which, along with the length scale values, imply a much higher correlation in the circumferential turbulence than the other two directions.

In addition, the bounding limitation presented by the original study of β = 6, which is a parameter used to calibrate the coherencies, is now removed as it was found to be inapplicable for this scale of application. Finally, the radial turbulence component is generated using the expression presented by the last step. For more details regarding the technique used (CDRFG), the reader is referred to Aboshosha et al. (2015b).

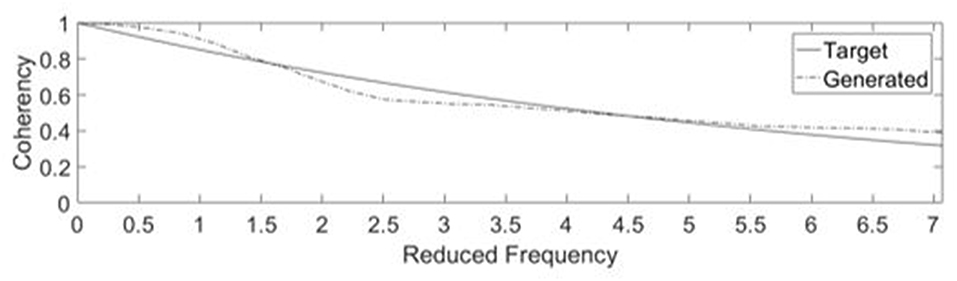
The coherency for the circumferential directions is compared with the target decay function plotted using the decay constant C_θ (0.05) in Figure 7 assuming a separation distance D_j. The agreement between both plots adds confidence in the technique used. It can also be noted that the figure is calibrated in reduced frequency using Taylor's hypothesis at which the reduced frequency is the frequency in Hz multiplied by the ratio between the span and the jet velocity as an indication of the most important length scales related to the considered problem where 1 is the scale corresponding to the span of the system considered.

$\begin{array}{ll}{V}_{modulated}(t)=\frac{V_{mean}(t)}{V_{pr}}\times V_{generated}(t)& (2)\end{array}$

The resulting time histories were then superimposed on the mean values generated from the previous section. Yet, the time histories could not be linearly added for the entire range, as the first part of the mean time history, until the end of the ramping, starts from a zero value, and experiences great fluctuations until it reaches the value of V_pr. Therefore, the turbulent time history was first calibrated using the modulation function given by equation (2), where the generated turbulence velocities were scaled based on the ratio between the mean velocity of the time instant and V_pr.

FIGURE 7

Figure 7. Comparison between target and generated coherencies for circumferential direction.

Numerical Model

The next step was to convert the velocity time history of each point into a force time history using equation (3), where the force F_(t) depends on the air density ρ, the drag coefficient C_D, and finally the velocity V_(t). The force time histories are then applied as point loads at the corresponding nodes, similar to the model-scale numerical model verified experimentally in section Model-Scale Analysis. A schematic of the modeled structure is shown in Figure 8.

$\begin{array}{ll}F(t)=\frac{1}{2}\rho C_D{V}^2& (3)\end{array}$

The current model is that proposed by Shehata et al. (2005), who showed that modeling three spans at both sides from the considered tower should suffice to model the effect of consecutive spans on the computed reactions. As illustrated by the schematic, the connection between the cable spans and the towers, modeled as hinged boundary conditions due to their relative stiffness, is also complimented by insulators at the intermediate connections, which are modeled as frame elements. Finally, the conductor spans are modeled as 2-noded cable elements that are divided into 90 segments per span to enable load application. Dimensions and properties of the considered conductor system and downburst data are shown in Table 1.

FIGURE 8

Figure 8. Schematic of analyzed structure system.

TABLE 1

Table 1. Properties of the conductor system and the downburst.

As applied in the model-scale analysis, a damping value that is independent of time will be used for the full-scale analysis. The velocity used to compute damping is the V_pr of the node corresponding to the tower of interest. Damping coefficients were then computed, and implemented into the SAP2000 model as discussed in section Model-Scale Analysis.

Full-Scale Model Results and Discussion

The resulting time history of the longitudinal reaction from the dynamic analysis is shown in Figure 9. It is obvious that the peak response is entirely governed by the ramping part, which is less sensitive to the dynamic effect as proven in section Model-Scale Analysis. For the sake of comparison, and similar to the approach Elawady and El Damatty (2016) used in their analysis, the current analysis was done quasi-statically using the technique developed by Aboshosha and El Damatty (2015a). The analysis only used the mean component of the flow which was scaled up to reach the peak value of the ramping zone. This is based on the hypothesis that the ramping zone does not experience any dynamic amplification, and thus the background value can be considered as the peak value with no reduction. The resulting time history from the quasi-static analysis is also plotted in Figure 9.

FIGURE 9

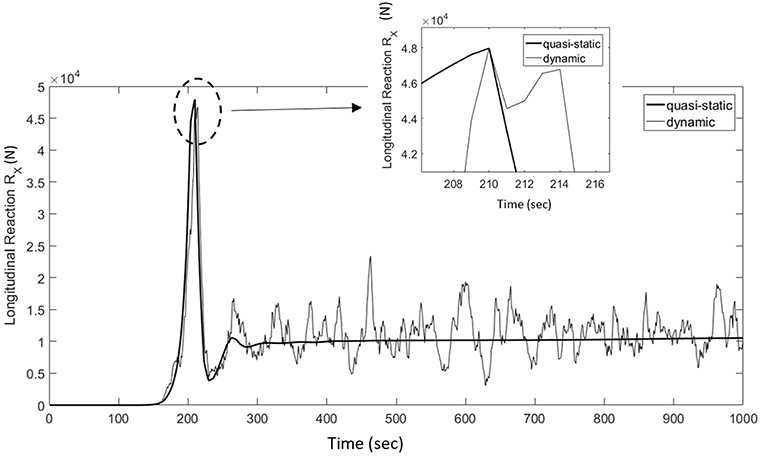
Figure 9. Time history of longitudinal reaction for quasi-static analysis compared to dynamic analysis.

To quantify the effect of the correlation between spatially separated points on the computed reactions, analysis was conducted using a fully correlated wind field. To achieve full correlation a single turbulent time history was scaled at each point based on its peak mean velocity. The resulting time history is plotted against that resulting from the turbulent (uncorrelated) wind field in Figure 10. As shown in the magnified portion of the plot, the increase in the computed reaction due to considering full correlation of turbulence is in the order of 0.5%. This was expected due to the fact that the generated turbulence had significant correlation in the circumferential direction (i.e., C in the R.θ direction = 0.05).

FIGURE 10

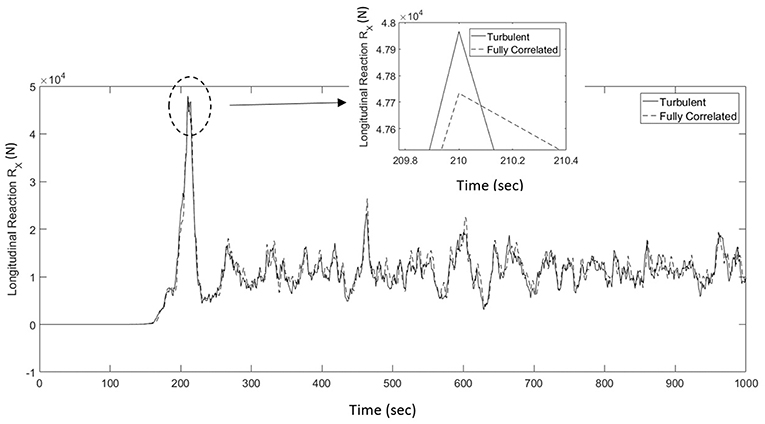
Figure 10. Time history of longitudinal reaction for turbulent wind field compared to fully correlated wind field.

Accordingly, judging based on the resulting time histories plotted in Figures 9, 10, the following conclusions can be drawn:

1. The peak value of the reaction is governed by the mean component, as no amplification was found within the ramping zone for Figure 9, at which the peak reaction occurs. This clearly means that the dynamic effect on the computed reactions is negligible.

2. Considering that the increase in the computed reaction due to accounting for spatial correlations, shown in Figure 10, reaches no more than 0.5%, current results suggest that spatial correlations can be ignored when calculating longitudinal forces during downbursts.

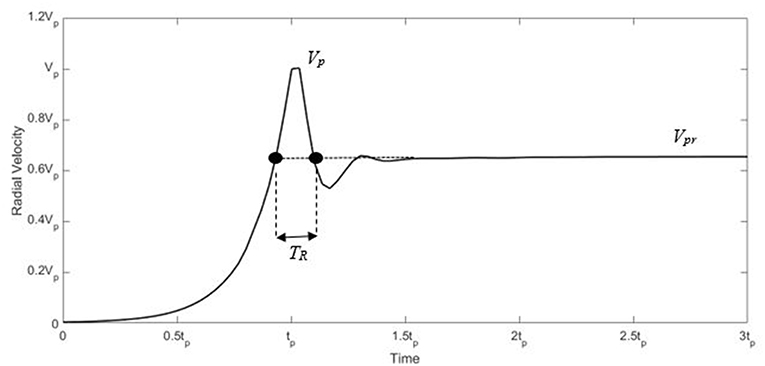
Another factor that might be of significance is that the ratio between V_pr, the post ramping velocity, and V_p, the peak velocity, where the ratio considered in the current analysis was about 0.65. This ratio is squared when considering forces, and thus would have considerable effects on the computed results within the post ramping section. Therefore, it is essential to know where this ratio stands compared to full-scale measurements in the literature, to determine whether this analysis is on the conservative side of computing the longitudinal reaction due to downburst loading or not. Another factor that can be of importance when calculating the longitudinal reaction due to downburst loading is the ramping period T_R shown in Figure 11. This is the period enclosed by the ramping zone between the value of V_pr before and after the ramping. The fact that the differential loading is the main cause of the longitudinal reaction gives a high significance to the period T_R, since the phenomenon is localized and heavily time dependent. The next section of this study will examine the effect of the ratio between V_pr and V_p, as well as the value of T_R, on the computed longitudinal reaction values for different values of jet speed.

FIGURE 11

Figure 11. Illustration of the annotations used to characterize the downburst time history.

Analysis of Result's Sensitivity to Wind Field Parameters

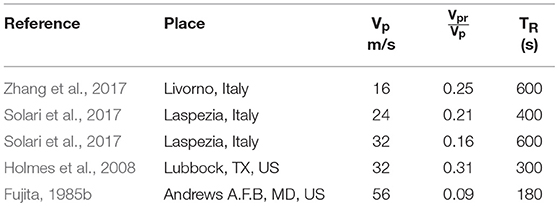
Due to the locality of the downburst wind field, as well as its time dependency, it is of utmost importance to characterize the wind field. This is suggested to be done through the factors V_pr, V_p, and T_R as illustrated in Figure 11. The current section compares the wind field used in this study to field measurements using the suggested parameters. A sample of the characteristics of downburst time histories available in the literature is shown in Table 2. It should be noted that values of V_pr in the field measurements are taken as the average of the post ramping zone in the figures reported by the referenced studies. Values of V_p vary within a wide range. It can also be noted that no relationship between the ratio $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ and the value of V_p can be deduced. This might be due to the limited number of data, which limits the deduction of a conclusive relation between the two values. Yet, the ratio $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ range between 0.1 and 0.3. Comparing these values to the value used in the current analysis, it appears that the dynamic effect of downburst loading will have even less significance if the new values are used, which further supports using the quasi-static approach. Furthermore, the value of T_R seems to lack any relation to the values of peak near-surface velocities, which contradicts the scaling method used in this analysis. As mentioned before, the time scale used in scaling up the wind field is the ratio between the length scale and the velocity scale. This would result in large time scaling ratios for lower jet speeds, and in turn, smaller scaling ratios for higher values of speed, which affects the peak duration, identified by T_R.

TABLE 2

Table 2. Comparison of downburst characteristics from different studies.

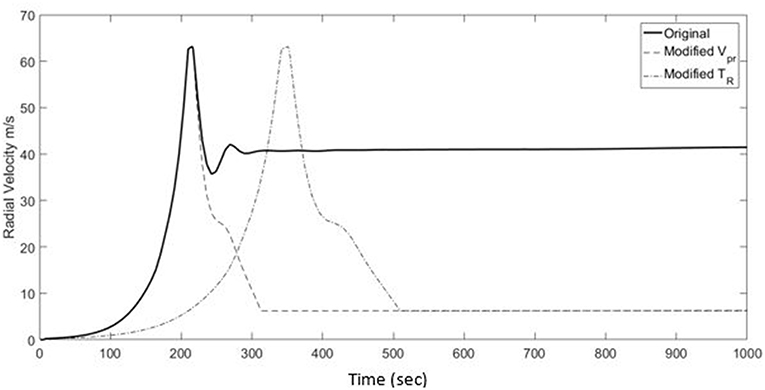
Two modifications were implemented; the first was to alter the $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ ratio varying between values of 0.1–0.6. The second modification was applied to the time histories resulting from the first modification, where the time history was time scaled to reach values of T_Rranging between 100 and 600 s. The modifications were done based on velocity scaling ratios and time scaling ratios that were taken as a ratio between the desired values, and the values of the time history corresponding to the node at the tower of interest. The time histories shown in Figure 12 show the original time history, plotted against a modified $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ ratio of 0.1, and another time history with a modified T_R of 300 s.

FIGURE 12

Figure 12. Modified time histories of radial velocity.

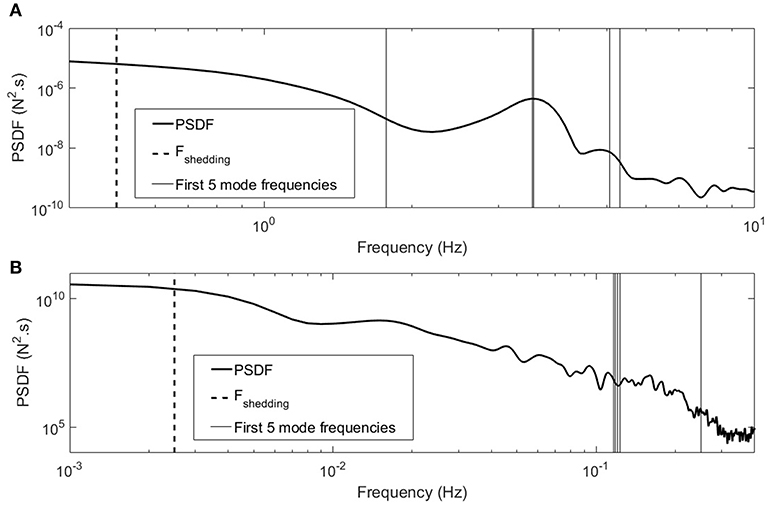
To judge the applicability of using a quasi-static approach, as well as explore how the modification of T_R would alter the conclusion reached in section Full-Scale Analysis, the comparison shown in Figure 13 has been conducted. As shown, the shedding frequency, which is considered to be a measure of the highest energy containing frequency is compared for the first 5 modes of the structure. The frequencies of the modes are plotted on top of the Power Spectral Density Function (PSDF) of the fluctuating component of the resulting longitudinal reactions for (A) the model-scale, and (B) the full-scale. It is clear that for the model-scale analysis the mode frequencies are closer in magnitude to the magnitude of the shedding frequency, which implies that the mode frequencies are likely to encounter frequencies that have relatively higher energy, being close to the shedding frequency. This is not the case for the full-scale analysis shown in figure (B), where the first mode frequency is about two orders of magnitude larger than the shedding frequency, which implies that the frequencies encountered by these modes are expected to have relatively low energy, and therefore not expected to develop dynamic magnification. Extrapolating from that hypothesis, the effect of increasing T_R is not expected to develop any more dynamic effect than the unmodified case, since the increase in T_R means the shedding frequency will decrease, and thus more distinction between it and the mode frequencies.

FIGURE 13

Figure 13. Mode frequencies compared to shedding frequency for (A) model-scale and (B) full-scale.

Accordingly, from that point forward, analyses were conducted quasi-statically, using the modified velocity time histories that reflect realistic values of $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ and T_R. This was done using two bounds of jet velocities, 25 and 70 m/s, to examine the effect of time scaling, which is inversely proportional to the velocity scale, and thus depends on the jet velocity. The results demonstrate no changes in the computed values of longitudinal reactions for different values of T_R. As for the $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ ratio, no change was observed for the lower bound of the jet velocity, and a minor dependency on the $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ ratio was evident for the upper bound of jet velocity showing a decrease of 5% for the computed reaction with the decrease in $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ from 0.6 to 0.1. Although affected by the value of $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$, the longitudinal reaction only shows a minor decrease for lesser values of $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$. This indicates that the longitudinal reaction values computed using the original time histories are conservative.

Conclusions

The current study focused on the computation of longitudinal reactions in transmission line systems due to the differential loading imposed by downburst wind fields. In the course of studying this effect, the following points summarize the methodology and findings of this study:

1- The numerical simulation has been validated using experimental results of a single span conductor provided by a previously conducted experiment (Elawady et al., 2017). Results of the comparison between the numerical and the experimental models shows the following:

a. The ramping zone was found to be independent of the damping values used, which suggests it is primarily governed by the mean and background components. Therefore, aerodynamic damping was computed using a single value for velocity, dealing with the post ramping zone as synoptic flow in a quasi-static approach.

b. The quasi approach of estimating the aerodynamic damping value has been verified, where the results of the numerical model were within range of the experimental results.

2- The wind field of the full-scale model was composed of two parts; a mean component which was taken from a previous CFD study, and a turbulent component that was synthetically generated, and superimposed on the mean component. The resulting time histories were examined to check for the spatial correlations, and good agreement has been found, especially for the lower range of frequency, which corresponds to larger spatial scales.

3- Results of dynamic analyses showed that the peak reactions were always related to the ramping zone, with no significant dynamic amplification in the zone of post ramping. The comparison of the results with quasi-static models showed the adequacy of using a quasi-static numerical model when resolving the peak reactions.

4- The downburst wind field used was examined and compared with downburst time histories from the literature, particularly observing two main parameters, $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ and T_R. Modifying the simulated time histories to match different values of the two features and re-conducting the analyses yielded the conclusion that the longitudinal reactions are independent of T_R. This was also the case for different values of $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$ examined at different jet velocities. Yet, the only case that showed a difference was that of higher velocity and least value of $\frac{{\text{V}}_{\text{p}\text{r}}}{{\text{V}}_{\text{p}}}$, which showed a minor decrease, not more than 5%.

Finally, the availability of more structured and well representative sets of meteorological data would be useful to get better validation of the work done. Furthermore, a probabilistic approach that considers the variability of downburst characteristics, along with transmission line properties, would be beneficial to compare with the current study.

Author Contributions

II is a Ph.D. student under the supervision of AED. This research is part of the Master's thesis work of II. The numerical analyses were conducted by II, under the supervision of AED. AE conducted the experimental work under the supervision of AED and helped with incorporating the experimental results, as well as revising the manuscript. The interpretation of the results, the drawn conclusions, and the drafting were done by II under the supervision of AED and approved by AE. The authors agree to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like gratefully acknowledge the financial support of Hydro One Inc., the National Research Council of Canada (NSERC) as well as the Ontario Centers of Excellence (OCE). The authors are also acknowledging the technical collaboration and advice provided by the WindEEE Research Institute knowledgeable staff.

References

Aboshosha, H., Bitsuamlak, G., and El Damatty, A. A. (2015a). Turbulence characterization of downbursts using LES. J. Wind Eng. Ind. Aerodyn. 136, 44–61. doi: 10.1016/j.jweia.2014.10.020

CrossRef Full Text | Google Scholar

Aboshosha, H., and El Damatty, A. (2015a). Engineering method for estimating the reactions of transmission line conductors under downburst winds. Eng. Struct. 99, 272–284. doi: 10.1016/j.engstruct.2015.04.010

CrossRef Full Text | Google Scholar

Aboshosha, H., and El Damatty, A. A. (2013). “Downburst induced forces on the conductors of electric transmission lines and the corresponding vulnerability of towers failure,” in Proceeding of the General Conference of the Canadian Society of Civil Engineering(CSCE 2013) (Montreal, QC).

Google Scholar

Aboshosha, H., and El Damatty, A. A. (2014a). Span reduction factor of transmission line conductors under downburst winds span reduction factor of transmission line. J. Wind Eng. 11, 13–22. doi: 10.3850/978-981-07-8012-8_P11

CrossRef Full Text | Google Scholar

Aboshosha, H., and El Damatty, A. A. (2014b). Effective technique to analyze transmission line conductors under high intensity winds. Wind Struct. An Int. J. 18, 235–252. doi: 10.12989/was.2014.18.3.235

CrossRef Full Text | Google Scholar

Aboshosha, H., and El Damatty, A. A. (2015b). Dynamic response of transmission line conductors under downburst and synoptic winds. Wind Struct. An Int. J. 21, 241–272. doi: 10.12989/was.2015.21.2.241

CrossRef Full Text | Google Scholar

Aboshosha, H., Elshaer, A., Bitsuamlak, G. T., and El Damatty, A. A. (2015b). Consistent inflow turbulence generator for LES evaluation of wind-induced responses for tall buildings. J. Wind Eng. Ind. Aerodyn. 142, 198–216. doi: 10.1016/j.jweia.2015.04.004

CrossRef Full Text | Google Scholar

Aboshosha, H., Ibrahim, A., El Damatty, A. A., and Hamada, A. (2016). “Dynamic behaviour of transmission lines structures under synoptic wind loads,” in 2016 CIGRE-IEC Colloquium.

Google Scholar

ASCE-74 (2010). American Society of Civil Engineers (ASCE). Guidelines for Electrical Transmission Line Structural Loading. ASCE Manuals and Reports on Engineering Practice, No. 74, New York, NY.

Darwish, M. M., and El Damatty, A. A. (2011). Behavior of self supported transmission line towers under stationary downburst loading. Wind Struct. An Int. J. 14, 481–498. doi: 10.12989/was.2011.14.5.481

CrossRef Full Text | Google Scholar

Darwish, M. M., El Damatty, A. A., and Hangan, H. (2010). Dynamic characteristics of transmission line conductors and behaviour under turbulent downburst loading. Wind Struct. An Int. J. 13, 327–346. doi: 10.12989/was.2010.13.4.327

CrossRef Full Text | Google Scholar

Davenport, A. G. (1962). Buffeting of a suspension bridge by storm winds. J. ASCE Struct. Div. 88, 233–264.

Google Scholar

Davenport, A. G. (1993). “How can we simplify and generalize wind loads?,” in Proceedings of the Third Asia-Pacific Symposium on Wind Engineering. Keynote Lecture (Hong Kong).

Google Scholar

Dua, A., Clobes, M., and Höbbel, T. (2015). Dynamic analysis of overhead transmission line under turbulent wind loading. Electron. J. Struct. Eng. 15, 46–54. doi: 10.4236/ojce.2015.54036

CrossRef Full Text | Google Scholar

Elawady, A., Aboshosha, H., El Damatty, A., Bitsuamlak, G., Hangan, H., and Elatar, A. (2017). Aero-elastic testing of multi-spanned transmission line subjected to downbursts. J. Wind Eng. Ind. Aerodyn. 169, 194–216. doi: 10.1016/j.jweia.2017.07.010

CrossRef Full Text | Google Scholar

Elawady, A., and El Damatty, A. A. (2016). Longitudinal force on transmission towers due to non-symmetric downburst conductor loads. Eng. Struct. 127, 206–226. doi: 10.1016/j.engstruct.2016.08.030

CrossRef Full Text | Google Scholar

Fujita, T. T. (1985a). The Downburst: Microburst and Macroburst. Satellite and Mesometeorology Research Project (SMRP), Research Paper 210, Department of Geophysical Science, University of Chicago.

Fujita, T. T. (1985b). The Downburst. Report of Projects NIMROD and JAWS, University of Chicago.

Hangan, H., Hashemi-tari, P., and Kim, J. (2008). “Modeling of high intensity winds,” in 18th Analysis and Computation Specialty Conference Modeling.

Google Scholar

Holmes, J. D., Hangan, H. M., Schroeder, J. L., Letchford, C. W., and Orwig, K. D. (2008). A forensic study of the Lubbock-Reese downdraft of 2002. Wind Struct. An Int. J. 11, 137–152. doi: 10.12989/was.2008.11.2.137

CrossRef Full Text | Google Scholar

Holmes, J. D., and Oliver, S. E. (2000). An empirical model of a downburst. Eng. Struct. 22, 1167–1172. doi: 10.1016/S0141-0296(99)00058-9

CrossRef Full Text | Google Scholar

Huang, S. H., Li, Q. S., and Wu, J. R. (2010). A general inflow turbulence generator for large eddy simulation. Jnl. Wind Eng. Ind. Aerodyn. 98, 600–617. doi: 10.1016/j.jweia.2010.06.002

CrossRef Full Text | Google Scholar

Hydro One Failure Report (2006). Failure of Towers 610 and 611, Circuit X503E - 500 kV Guyed Towers Near the Township of Waubaushene. Ontario, August 2, 2006. Failure Investigation Report, 2006.

Ibrahim, I., Aboshosha, H., and El Damatty, A. A. (2017). “Numerical simulation of WINDEEE dome downburst for open terrain using physical roughness elements,” in Proceedings of the 7th European African Conference on Wind Engineering (Liege).

Google Scholar

Jubayer, C., Elatar, A., and Hangan, H. (2016). “Pressure distributions on a low-rise building in a laboratory simulated downburst,” in 8th International Colloquium on Bluff Body Aerodynamics and Applications (Boston, MA: Northeastern University).

Google Scholar

Kanak, J., Benko, M., Simon, A., and Sokol, A. (2007). Case study of the 9 May 2003 windstorm in southwestern Slovakia. Atmos. Res. 83, 162–175. doi: 10.1016/j.atmosres.2005.09.012

CrossRef Full Text | Google Scholar

Keyhan, H., McClure, G., and Habashi, W. G. (2013). Dynamic analysis of an overhead transmission line subject to gusty wind loading predicted by wind - conductor interaction. Comput. Struct. 122, 135–144. doi: 10.1016/j.compstruc.2012.12.022

CrossRef Full Text | Google Scholar

Kim, J., and Hangan, H. (2007). Numerical simulations of impinging jets with application to downbursts. J. Wind Eng. Ind. Aerodyn. 95, 279–298. doi: 10.1016/j.jweia.2006.07.002

CrossRef Full Text | Google Scholar

Kim, Y., Castro, I. P., and Xie, Z. (2013). Divergence-free turbulence inflow conditions for large-eddy simulations with incompressible flow solvers. Comput. Fluids 84, 56–68. doi: 10.1016/j.compfluid.2013.06.001

CrossRef Full Text | Google Scholar

Klein, M., Sadiki, A., and Janicka, J. (2003). A digital filter based generation of inflow data for spatially developing direct numerical or large eddy simulations. J. Comp. Phys. 186, 652–665. doi: 10.1016/S0021-9991(03)00090-1

CrossRef Full Text | Google Scholar

Kondo, K., Murakami, S., and Mochida, A. (1997). Generation of velocity fluctuations for inflow boundary condition of LES. J. Wind Eng. Ind. Aerodyn. 67–68, 51–64. doi: 10.1016/S0167-6105(97)00062-7

CrossRef Full Text | Google Scholar

Li, C. Q. (2000). A stochastic model of severe thunderstorms for transmission line design. Prob. Eng. Mech. 15, 359–364. doi: 10.1016/S0266-8920(99)00037-5

CrossRef Full Text | Google Scholar

Lin, W. E., and Savory, E. (2006). Large-scale quasi-steady modelling of a downburst outflow using a slot jet. Wind Struct. An Int. J. 9, 419–440. doi: 10.12989/was.2006.9.6.419

CrossRef Full Text | Google Scholar

Lin, W. E., Savory, E., Mcintyre, R. P., Vandelaar, C. S., and King, J. P. C. (2012). The response of an overhead electrical power transmission line to two types of wind forcing. J. Wind Eng. Ind. Aerodyn. 100, 58–69. doi: 10.1016/j.jweia.2011.10.005

CrossRef Full Text | Google Scholar

Mara, T. G., Galsworthy, J. K., and Savory, E. (2010). Assessment of vertical wind loads on lattice framework with application to thunderstorm winds. Wind Struct. An Int. J. 13, 413–431. doi: 10.12989/was.2010.13.5.413

CrossRef Full Text | Google Scholar

Mara, T. G., and Hong, H. P. (2013). Effect of wind direction on the response and capacity surface of a transmission tower. Eng. Struct. 57, 493–501. doi: 10.1016/j.engstruct.2013.10.004

CrossRef Full Text | Google Scholar

McCarthy, P., and Melsness, M. (1996). Severe weather elements associated with September 5, 1996 hydro tower failures near Grosse Isle, Manitoba, Canada. Manitoba Environment Service Centre, Environment Canada, 21.

McClure, G., and Lapointe, M. (2003). Modeling the structural dynamic response of overhead transmission lines. Comput. Struct. 81, 825–834. doi: 10.1016/S0045-7949(02)00472-8

CrossRef Full Text | Google Scholar

Miguel, L., Riera, J., and Miguel, L. (2018). Assessment of downburst wind loading on tall structures. J. Wind Eng. Ind. Aerodyn. 174, 252–259. doi: 10.1016/j.jweia.2018.01.015

CrossRef Full Text | Google Scholar

Orwig, K. D., and Schroeder, J. L. (2007). Near-surface wind characteristics of extreme thunderstorm outflows. J. Wind Eng. Ind. Aerodyn. 95, 565–584. doi: 10.1016/j.jweia.2006.12.002

CrossRef Full Text | Google Scholar

Ponte, J., and Riera, J. (2007). Wind velocity field during thunderstorms. Wind Struct. An Int. J. 10, 287–300. doi: 10.12989/was.2007.10.3.287

CrossRef Full Text | Google Scholar

Ponte, J., and Riera, J. (2010). Simulation of extreme wind series caused by thunderstorms in temperate latitudes. Struct. Saf. 32, 231–237. doi: 10.1016/j.strusafe.2010.02.002

CrossRef Full Text | Google Scholar

Savory, E., Parke, G. A. R., Zeinoddini, M., Toy, N., and Disney, P. (2001). Modelling of tornado and microburst-induced wind loading and failure of a lattice transmission tower. Eng. Struct. 23, 365–375. doi: 10.1016/S0141-0296(00)00045-6

CrossRef Full Text | Google Scholar

Shehata, A. Y., and El Damatty, A. A. (2007). Behaviour of guyed transmission line structures under downburst wind loading. Wind Struct. 10, 249–268. doi: 10.12989/was.2007.10.3.249

CrossRef Full Text | Google Scholar

Shehata, A. Y., El Damatty, A. A., and Savory, E. (2005). Finite element modeling of transmission line under downburst wind loading. Finite Elem. Anal. Des. 42, 71–89. doi: 10.1016/j.finel.2005.05.005

CrossRef Full Text | Google Scholar

Solari, G., Rainisio, D., and De Gaetano, P. (2017). Hybrid simulation of thunderstorm outflows and wind-excited response of structures. Meccanica. doi: 10.1007/s11012-017-0718-x

CrossRef Full Text | Google Scholar

Wang, X., Lou, W., Li, H., and Chen, Y. (2009). Wind-induced dynamic response of high-rise transmission tower under downburst wind load. J. Zhejiang Univ. 43, 1520–1525. doi: 10.3785/j.issn.1008-973X.2009.08.031

CrossRef Full Text | Google Scholar

Zhang, S., Solari, G., De Gaetano, P., Burlando, M., and Repetto, M.P. (2017). A refined analysis of thunderstorm outflow characteristics relevant to the wind loading of structures. Probabilistic Eng. Mech. 54, 9–24. doi: 10.1016/j.probengmech.2017.06.003

CrossRef Full Text | Google Scholar

Zhang, Y. (2006). Status quo of wind hazard prevention for transmission lines and countermeasures. East China Electr. Power 34, 28–31.

Google Scholar