System Identification of Large-Scale Bridges Using Target-Tracking Digital Image Correlation

This paper characterizes the extensive research activities conducted in the Earthquake Engineering Laboratory of University of Nevada, Reno, in the field of dynamic monitoring and system identification of three 1/3-scale two-span bridges. The first part of the study briefly presents the verification of target-tracking Digital Image Correlation (DIC) results as compared to conventional sensors, e.g., string potentiometers and triaxial accelerometers from one of the three bridge tests. Structural system identification is presented in the second part for the other two bridges with a focus on determining structural model parameters based on the DIC measured response data. All bridges were tested under bidirectional earthquake loading using the multiple shake table array. However, the system identification used data collected from white noise runs before and after the seismic tests. A quasi-linear response of the system was assumed because of the low intensity white noise base excitations, and the modal parameters were estimated accordingly. Using the structural vibration data recorded by target-tracking DIC at various locations on the bridges, five system identification methods were applied to analyze the modal parameters of the tested bridges. The results were used to estimate the frequency, damping ratio, and mode shapes of the bridges in two states. The initial state is before seismic testing and the end state is the damaged state after the completion of the seismic tests. The results show that the applied methods provide a reasonable estimate of the natural frequency and damping ratio of the bridge systems in the original and damaged states.

Introduction

For system identification for civil engineering applications, structures such as bridges, buildings, towers, etc. are the systems and the structural or system identification mostly stands for the extraction of the modal parameters: Eigen frequencies, damping ratios, and mode shapes. In this context, stochastic input is used, which means that the structure is excited by an unknown ambient input force and only the output (e.g., acceleration) measurements are available (Peeters and De Roeck, 2000). The estimated modal parameters could be used as input for damage localization procedures. The aim of the system identification is to determine the structural modal parameters from dynamic measurements, which are very useful in the model update, damage assessment, active control and original design reevaluation (Xu et al., 2002). Typically, for ambient testing of large structures, not all outputs can be measured at once but they are divided into several setups with overlapping sensors. Candidates for the reference outputs are the sensors which are common to every setup, because they are placed at optimal locations on the structure where it is expected that all modes of vibration are present in the measured data. However, such an optimal location is not easy to determine, especially in the case of a large structure like a bridge with many components, e.g., deck, girders, piers, etc. Therefore, the application of distributed sensors is preferred to collect data from random points along structure so that the estimated location which excites all modes of vibration can be determined using the modal analysis procedure.

The target-tracking Digital Image Correlation (DIC) monitoring technology employs non-contact vision-based monitoring, which allows the application of distributed sensors and is currently emerging in the field of structural health monitoring. DIC is primarily enabled by the template matching techniques as one of the most effective techniques in tracking objects, a concept primarily introduced by Sutton et al. (2009) and followed by several other studies (e.g., Fukuda et al., 2010; Lee et al., 2012; Santos et al., 2012; Schumacher and Shariati, 2013; Cigada et al., 2014; Wu et al., 2014). Other well-known template-matching algorithms including DIC were demonstrated by Gao et al. (2015), Barhli et al. (2015), and Jiang et al. (2015), while some works on edge detection and target-free pattern matching were provided by Abdel-Qader et al. (2003) and Yoon et al. (2016). Applications of DIC were also extended to extract mode shapes and measure vibrations of small-scale structures. For example, Helfrick et al. (2011) used full-field measurement to conduct modal testing and mode shape correlation for a dryer-cabinet panel under forced vibrations from a hanging mechanical shaker.

Recently in the past decade, several studies and field applications explored the possibility of using non-contact vision-based systems for larger applications such as bridge monitoring and system identifications (e.g., Lee and Shinozuka, 2006; Yoneyama et al., 2007; Chiang et al., 2011; Peddle et al., 2011; Nonis et al., 2013; Murray et al., 2014; Ribeiro et al., 2014; Ye et al., 2015; Pan et al., 2016; Niezrecki et al., 2018). The related works of measuring 3D displacement of bridge structures could be found in Santos et al. (2012) where 3D displacements of the bridge deck were measured. Another relevant study is Nonis et al. (2013), and more recent work from the same group Niezrecki et al. (2018), where 3D-DIC was used for periodic and non-destructive inspection of concrete bridges to locate non-visible cracks in concrete, quantify spalling, and measure bridge deformation. However, most of the studies either focused on demonstrating the concept or had other limitations in the application. For example, Feng and Feng (2017) recently used video monitoring technology to identify natural frequencies and planer mode shapes with an excellent comparison to the accelerometers. However, one video camera, and in turn only 2D measurements were used. The video monitoring system was also used to monitor railroad bridges (Feng et al., 2015) in which the sensors measured the dominant frequencies of the train-bridge system subjected to freight loads. Such methods have offered effective alternatives to displacement measurement of bridges where measured targets can be a high-resolution low-power light emitting diodes (LEDs) as shown by Wahbeh et al. (2003). It is noted that regardless of the extensive previous efforts, vision-based monitoring systems still face several field challenges, such as the requirement for stable camera mounting, measurement errors caused by lighting changes, and atmospheric effects affecting light refraction, which has a significant impact in a long-term monitoring (Brownjohn et al., 2017).

In this paper, the focus is to demonstrate the validity of 3D measurements obtained from cameras and processed using DIC for system identification of bridge structures. The novelty of this study lies in the application as no previous studies used full 3D DIC or point tracking for system identification and monitoring of full bridge systems as outlined before. Even relevant studies on system identification and mode shape extraction (e.g., Helfrick et al., 2011) focused on smaller applications or mechanical systems. This study benefited from three different 1/3-scale two-span bridges that were recently tested at the multi-shake table array at the Earthquake Engineering laboratory at the University of Nevada, Reno. The goal of these shake table tests was mainly verifying evolving Accelerated Bridge Construction (ABC) connections for concrete and steel bridges. However, extensive DIC monitoring was done for all three tests, with various other objectives as presented in this paper. Our first objective is to verify the 3D DIC monitoring technique for dynamic and vibration measurement, for which results from the first bridge test were used. Another objective is to demonstrate DIC measurements for system identification when a low frame rate is used in monitoring. For this purpose, five different system identification methods are applied and compared to identify whether some methods work better for DIC measured data. The system identification used results from the second and third bridge tests, mainly ambient vibration from white noise signals applied before and after the seismic tests. The system identification methods considered and compared in this study are the classical spectrum estimation using Fast Fourier Transform (FFT) and the Autoregressive Covariance (AR) methods, as well as the Experimental Modal Analysis (EMA) using the Peak-Picking (PP), the Least Square Complex Exponential (LSCE) and the Stochastic Subspace Identification (SSI) methods.

There are a few limitations for this study that are listed here for completeness. The sought comparison of different system identification techniques on experimental modal analysis can be subjective for a few reasons. First, there is the lack of a reference sensor, which means that the methods can only be compared relative to one another. Another issue has to do with the purpose of the analysis; some are only interested in natural frequency, in damping ratio, or in obtaining mode shapes. This subjective choice depends on the actual application. Then, there is the limited duration of recorded data such as in the case of laboratory testing. For example, the FFT approach has the limitation of analyzing short data records. The most prominent limitation of FFT results from the ability of the method to distinguish the spectral responses of two or more signals (Kay and Marple, 1981; Lobos et al., 2001). It assumes that only harmonics are present in the signal with a fixed periodic interval, while in reality, the periodicity intervals are varied and very long, which limits the FFT approach to analyze short data records. Therefore, in this paper, the emphasis is to put on the assessment of the quality of the estimated modal parameters.

The monitored bridges in this paper involved distributed sensors (or targets) on bridges subjected to white noise excitation which was recorded in short duration between 11 and 27 s, with sampling rates of 30 and 40 Hz. The target's location and distribution aimed at approximating and capturing at least three modes of vibration of the two-span bridge systems. The recording duration and sampling rate imply that the considered system identification techniques are also evaluated for their validity to handle short duration records, short data length, and low sampling rates. A dedicated conventional structural health monitoring system using accelerometers for instance was not considered, i.e., no common reference system is used. However, the objective as previously mentioned is comparing the methods and discussing the strong and weak sides of the different techniques as well as the consistency in deducing modal properties from targets located in different locations in bridges. The comparison is based mainly on the estimated natural frequencies and damping ratios.

This paper is organized into several sections. Following this introduction, the background and theory behind the different identification methods are briefly reviewed in the second section. The third section presents the principal of target-tracking DIC as well as the monitoring setup. The verification of target-tracking DIC in the time (displacement) and frequency domain using the first bridge test is discussed in section four. Next, the identification of the other two bridges using selected system identification methods is discussed. The last sections present a summary of the results comparison and then the overall conclusions of the study.

System Identification Techniques and Background

In this section, a brief overview of the system identification methods that have been widely used is presented. This overview does not cover all existing methods as only a limited number of methods applicable in the EMA method were chosen. Among the frequency domain methods, which use either Frequency Response Function (FRF) or output spectra as primary data, we select the peak-picking (PP) method and LSCE method (Brown et al., 1979). Among the time domain methods, the SSI methods are applied. The latter assumes that a structure excited by white noise can be described by a stochastic space model. The modal parameters are obtained by Eigen value decomposition. The natural frequency from these methods is compared with the results from the spectral analysis, i.e., the classical FFT and Autoregressive (AR) methods. The damping ratio can be computed and compared from the LSCE and SSI techniques, while the mode shape is only computed using the SSI model.

Fast Fourier Transform (FFT) and Autoregressive (AR) Model

Fourier transform is a non-parametric power spectrum estimation method and is one of the most common methods to extract the fundamental frequency of a signal using spectrum estimation. Since the FFT method needs long duration data records for suitable frequency resolution, it is applied to windowed data sets which assume all data are equal to zero except the data in the window. On the other hand, some spectral losses occur because of the windowing process and these losses mask weak signals in the data (Dzhaparidze, 2012). The estimation of the power spectra involves sectioning the signal and computing periodograms of the signal, which are modified by applying a data window, and averaging the modified periodograms (Welch, 1967). A detailed algorithm of this method can be found in Cooley and Tukey (1965). The AR model for spectral estimation offers an alternative to the FFT periodogram (Kay, 1988; Marple and Carey, 1989). Compared with non-parametric techniques, the AR method is a parametric model which can provide superior spectral resolution. Their relative advantage over FFT-based spectral estimates increases with decreasing gate length. For signal-to-noise ratios (SNRs) >0 dB, the AR spectral estimate has better frequency resolution than that of the conventional periodogram estimate. For short data records, the AR method yields reasonable spectral estimates (Bard, 1974). The computations of AR coefficients in this study are conducted using the so-called Covariance method (Marple and Carey, 1989). A problem that may be encountered in applying AR modeling is selecting the proper model order. When the order is too high, the spurious detail in the spectra may be the result, whereas lower order yields rather smooth spectra.

Peak Picking (PP)

The most widely used method in civil engineering to determine the Eigen frequencies of a structure using the EMA method is the rather simple PP method (Bishop and Gladwell, 1963). PP is a frequency domain parameter in a single degree-of-freedom (SDOF) method to make local estimates of frequency and damping; therefore, it is only suitable for data with well-separated modes. The natural frequencies are simply taken from the observation of the peaks on the graphs of the magnitude of the response. The damping ratios are calculated from the sharpness of the peaks and the mode shapes are calculated from the ratios of the peak amplitudes at various points in the structure.

Stabilization Diagram

The key difficulty in applying system identification for EMA of large-scale structures is the selection of the model order and of the corresponding system poles. To address this problem, the concept of a stabilization diagram is introduced. It separates the true physical model from the spurious numerical ones. Experience from a large range of problems shows that in such analysis, the pole values of the physical Eigen modes always appear at a nearly identical frequency, while mathematical poles tend to scatter around the frequency range. The pole values at different orders are just being combined into one single diagram, with the horizontal axis as the pole frequency and the vertical axis as the model order. If the differences in Eigen frequencies and damping ratios are within pre-set limits, the pole under consideration is labeled as a stable one. The spurious numerical poles will not stabilize at all during this process and can be sorted out of the modal parameter data set more easily (Allemang and Brown, 1982; Heylen et al., 1995; Peeters and De Roeck, 2000). The stable pole is indicated by symbols in this diagram, and this study determines the criteria for a stable pole as a natural frequency of 1% and a damping ration of 5%.

Least Square Complex Exponential (LSCE) and Stochastic Subspace Identification (SSI)

The LSCE method (Brown et al., 1979) allows the estimation of modal frequency and damping for several modes simultaneously. Since all data are analyzed simultaneously, global estimates are obtained. The most advanced method for ambient vibration measurement is likely the SSI technique, proposed by Peeters and De Roeck (2000). The SSI method, as presented by Van Overschee and De Moor (2012), is a time-domain method which identifies a stochastic state space model from output-only measurements. The state space model is a very general model that is also suitable for our purposes: it can describe a linear vibrating structure excited by white noise. Subspace identification does not involve any non-linear computations and is therefore much faster.

Target-Tracking Digital Image Correlation (DIC) Monitoring

Principal

In the target-tracking method, an artificial target acts as an independent sensor on the structure with salient features and some known dimensions, so more than one target is mostly preferable to obtain a wide range of data in the entire structure. The targets must rigidly attach to the structure, avoiding possible rotation and translation, and also to provide a reference point or line to determine the projection transformation relating the image and the structural coordinate system (Hartley and Zisserman, 2003; Park et al., 2015). In this study, circular black and white stickers with specific dimensions that vary based on the application were used as artificial targets. Some targets were numbered, designated as coded targets, for easier identification by the software that generates the scaling factor in the calibration. The coded targets on their ends are recognized by the software due to their unique white dots configuration which also allows the recognition of length, and in turn, provides proper scaling for the calibration step. Each target is unique, making the subsequent images mutually oriented, and the 3D coordinates could be determined based on recognized target positions.

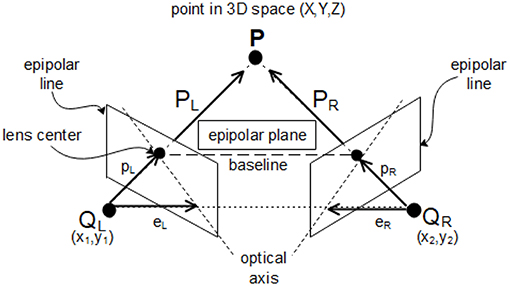
Calibrating cameras is a crucial step for generating 3D measurements and is conducted using GOM Correlate Professional [Computer Software] (2017) and TRITOP Professional [Computer Software] (2017) point tracking software. The theory of camera self-calibration as well as the technique implemented in the calibration process can be found in Maybank and Faugeras (1992), Zhang (2000), and Sutton et al. (2009). The triangulation and bundle adjustment principles (Mikhail et al., 2001) play an important role in determining the camera and target locations. The point tracking software used to calibrate the cameras has the capability of measuring objects' sizes that vary between 0.1 and 10 meters, has an accuracy of 0.01 mm and provides the result in a very short time (see Buń et al., 2015 for more details). The distance between the camera matrix and the targets is determined and calculated using an epipolar geometry and triangulation process as illustrated in Figure 1. The triangulation requires two separate images; therefore, at least two cameras are required in this process. By determination of the relations on the basis of at least two images of a measured object, the triangulation process can be performed to determine 3D coordinates of the measured points (Hartley and Sturm, 1997; Zhang, 1998).

FIGURE 1

Figure 1. Epipolar geometry and triangulation method.

Camera Calibration and Results

Before performing measurements using the TRITOP system, the camera position should be determined and the targets should be attached to the structure accordingly. The first step in setting up the system was determining the camera locations, then positioning and configuring the cameras, attaching the targets on the bridge, and calibrating the cameras. For DIC setup, a combination of coded targets (numbered targets) and seven un-coded ones (not-numbered targets) that were attached on the bridge and illuminated by lightings was used. The targets were printed on adhesive stickers in which the diameter of the white and black circular targets was 1.3 in (~3.3 cm) and 2.6 in (~6.6 cm), respectively. Given that the bridge structural response was governed by the middle pier, all the targets were distributed along the columns and the girders close to the North column only, as illustrated in Figure 2. All targets were properly attached to the structure to avoid any possible translation and rotation during the tests. Since the working volume for the calibration was too large to conduct a close-range calibration, a wide area calibration should be performed so that all targets could be captured from a remote area away from the bridge. Therefore, for the best and desirable field of view of the monitored bridges, all DIC monitoring took place from one of the rooms overlooking the shake table lab as shown in Figure 2.

FIGURE 2

Figure 2. Test setup and DIC targets for all three bridges along with the DIC cameras setup and selected targets for verification from Bridge #1 test.

After determining the monitoring location as well as placing targets on the bridge, the next step was to determine the camera position inside the monitoring room. A working distance of ~12 m was measured between the bridge and the cameras, and a maximum camera separation of 2.4 m (based on the room dimension) was selected covering and clearly showing all distributed targets on the bridge. Due to a large separation between the cameras, a rigid bar could not be used to connect them. Instead, both cameras were separated independently from each other using tripods, and a careful inspection was taken to ensure that both cameras were aligned and aimed at the same angle toward the bridge. After preparation of the object and the monitoring setting, a calibration object should be selected which should be associated with the large measurement of the bridge volume. Therefore, instead of using a large calibration panel, at least two calibration objects in the terms of calibration bars were measured from the center of two different coded targets on the monitored bridge. To analyze a given calibration bar, this bar should be visible in at least two photographs, but more photographs would improve the accuracy.

Before performing the calibration as well as before conducting a test, additional lights should be used so that all the targets were properly exposed on the cameras. Figure 2 shows the lighting location on the lab floor in which the minimum of 4 sets of lighting are used so that all the targets are illuminated adequately. The calibration was then conducted in which 18 calibration images were captured separately by the left camera and then followed by the right one in a specific sequence and order. The sequence involved a preliminary orientation for the whole structure by taking at least four pictures with all targets clearly visible. Between each of these four pictures, the camera was rotated with a 90° angle in the lens axis to account for the possible rotation of all targets during a test or vibration. Then, 13 still pictures were taken by moving the cameras back and forth from their tripods while the last picture was taken on the tripod identifying each camera position. Each calibration picture was instantly sent to the computer, and the actual calculations of the calibration were performed after all images from both cameras were taken. The calibration bars were used as input in the software. An example of the calibration result is shown in Figure 3 for Bridge#1. The calibration bars of this bridge were the distance between targets #414 to #416 and #400 to #408, which were measured as 35.7 in and 37.5 in, respectively. The orientation of the camera toward the bridge as well as the horizontal and vertical distances can be identified from the calibration result. The example of image rays shown by the left camera in Figure 3 suggests that the monitoring setup was capable of reaching all the targets, even those located on the South column. Figure 3 also clearly shows that the cameras moved back and forth during calibration, considering the target positions in different orientations, but the position of the cameras remained parallel to the structure. The coded and un-coded targets were identified by the software in which a different numbering was used for the un-coded ones as given in Figure 3. To judge or assess whether a calibration was successful, the average recognition error was calculated by the software and should be <0.03 pixels for acceptable results, which was achieved in all the tests conducted in this study.

FIGURE 3

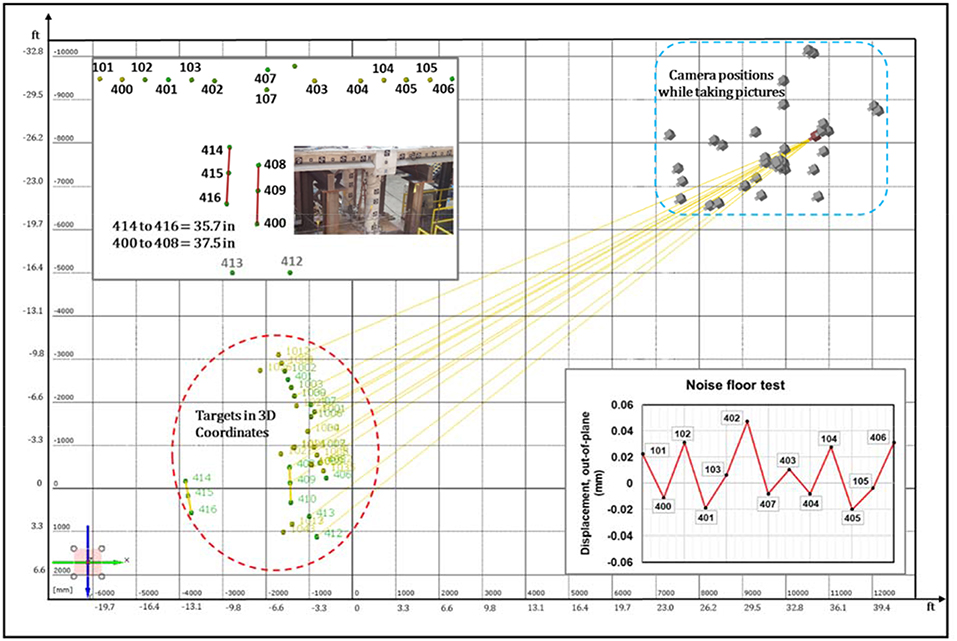
Figure 3. Calibration results of Bridge#1 showing targets in 3D coordinates, camera position while taking calibration pictures, and the image rays from left camera reaching all targets; the result of noise floor test of targets on deck.

A noise-floor test was done before conducting the test by taking a sequence of images of the bridge after the calibration was achieved successfully. In such a test, the monitoring setup was similar to the calibration setup without changing any camera settings and with all lights on. The out-of-plane direction, i.e., the direction toward the camera focus, was used to identify the noise floor since most of the structures had a measured displacement of <20 μm in this direction (Helfrick et al., 2011). The results of this test are shown in Figure 3, which illustrates that while the displacement should be very close to zero across the measured targets, some targets, e.g., #402 and #405, contain more noise than others. The possible glare off the object surface due to reflection from the glass window, overexposure to lighting, or inability of target location to be clearly seen by both cameras at once due to steep angles were the possible causes of this problem (Helfrick et al., 2011). The lighting or the camera location could be adjusted to solve this issue; however, these problems were not tackled to demonstrate the robustness of the technique even when such a noise floor existed.

DIC System Hardware and Software

In this study, the DIC target-tracking algorithm after Sutton et al. (2009), which is readily implemented in the image-processing software packages, was used on a portable computer. During the measurements, the sequence of images was captured by two high-speed cameras (IL5QM4 Fastec Imaging, USA) which were placed on tripods and powered by two AC adaptors. The cameras were controlled over LAN via FasMotion software (Version 1.9.14, Fastec Imaging, USA) so that both cameras were able to conduct measurement simultaneously and transferred data from each camera to the computer. The example of the camera setting in laboratory monitoring is shown in Figure 2. The computer obtained the 2D coordinate measurement data and converted it to 3D coordinate data using TRITOP (GOM, Inc.) software, which defined the 3D coordinates of object points at quasi-static conditions in their orientation in space. The image processing of the test results was conducted in GOM photogrammetric software (GOM, Inc.). The images captured by cameras were digitized into a full resolution of 2,560 × 2,048 pixel images in 8-bit grayscale and streamed into a USB 3.0 cable with the sampling rate which was carefully chosen. The selected sampling rate needed to avoid aliasing, i.e., it needed to be at least higher than the Nyquist frequency of the structure. By processing the digital images in a GOM software package, time histories of the displacement and acceleration of each target on the structure were obtained and used for the system identification.

Monitoring and Testing Setup

The proposed vision target-tracking technique in measuring dynamic behavior was experimentally evaluated before through several steel frames shake table tests at the Earthquake Engineering Laboratory of University of Nevada, Reno (Ngeljaratan and Moustafa, 2017, 2018). However, a standalone verification study for bridge structures is presented in the next section for completeness. For verification purposes, the first bridge model was used, which was a 1/3-scaled two-span concrete bridge with 3.4 m width in the transverse direction (North-South). The bridge had one two-column pier where the column height was 3 m and they were spaced at 1.8 m. For all the bridge tests, the middle shake table, as shown in Figure 2, was driven by either a unidirectional white noise or bidirectional earthquake loading. The white noise was typically applied in the transverse and longitudinal directions one at a time before any seismic testing to capture the dynamic properties of the bridge. The system identification was conducted on two other bridges with dimension and properties as shown in Table 1. For identification purposes, the white noise tests were repeated after each seismic test. For all three bridges, at least eight seismic tests were conducted, with increasing intensity from 20% of an equivalent Design Earthquake (DE) level up to 200% DE. The white noise between and after these seismic tests aimed at capturing the dynamic behavior as damage accumulated in the bridge, mainly in the pier columns.

TABLE 1

Table 1. Bridge dimensions and test setup.

The cameras captured thousands of images sampled at 30 and 40 frames per second (fps), which guranteed that the sampling frequency is much larger than the Nyquist frequency of such bridge models (Nyquist frequency was within 2–5 Hz). Both cameras captured the bridge motions simultaneously, and then each frame (image) was downloaded to the portable computer, which was equipped with image processing software to generate the displacement time histories of each target. The average scaling factor of the sensor obtained from each calibration is shown in Table 2. For verification purposes, a reference string potentiometer (SP) that measured displacements at a sampling frequency of 256 Hz was used. It is noted that DIC and SP measurements had different time domains, so careful synchronization was done as part of the post-processing to compare the results from the two sensors.

TABLE 2

Table 2. Monitoring setup.

Verification of Spectral Analysis Results Using Accelerometer Data of a Laboratory-Scaled Model Bridge

A two-span bridge with ABC connections scaled at about 1/3-scale, designated as Bridge #1 in Figure 2, was tested under several ground motions with increasing scale as previously mentioned, and was used as the test bed to verify the DIC measurements. For verification purposes, the displacement histories from DIC and conventional SP were compared for the seismic tests, i.e., when earthquake ground motions were applied. The acceleration data recorded from DIC and conventional accelerometers were also used from one of the white noise runs in the longitudinal direction (East-West) to do a second set of verification. This is to show the capability of the vision sensor to identify the fundamental vibration frequency of the bridge in that direction.

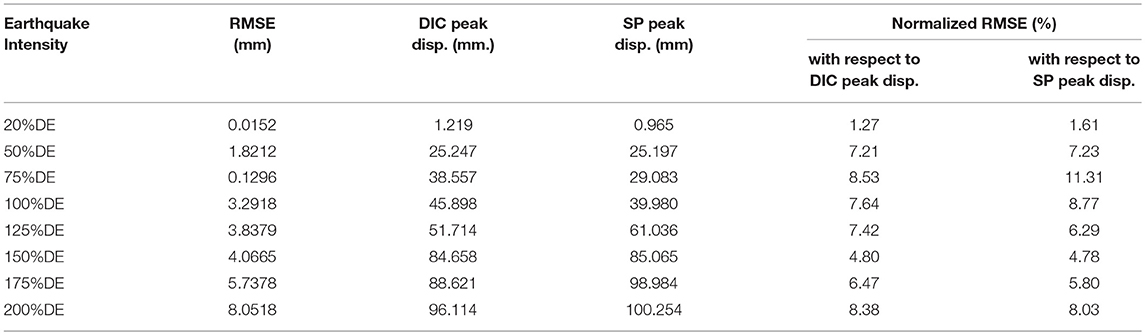
Figure 4 shows the comparison between the target-tracking displacements measured at target #407 at the bent cap level (see Figure 2 for target ID) and the SP measurements only in the transverse direction for all eight different earthquake intensity levels. It is noted that the recording of both measurement types had different time reference, and thus the response signals from the SP were adjusted to have a similar starting point in time as the DIC measurements. It is also noted that DIC used a practical 30 Hz sampling rate vs. a 256 Hz for the string potentiometer. To accurately calculate the difference in measurements at every data point, all the DIC results were re-sampled at 256 Hz within a 0.0001 tolerance in post-processing. The target-tracking DIC response shown in Figure 4 is the processed response after resampling. To quantify the accuracy and precision of the vision-based point tracking DIC technique, an error analysis was performed using the Root Mean Square Error (RMSE) given in Equation 1.

$\begin{array}{ll}RMSE=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{(x_i-y_i)}^2}& (1)\end{array}$

where n is the amount of measurement data; x_i and y_i are the ith displacement data at time t_i from the resampled DIC and string potentiometers response, respectively. The RMSE is calculated in displacement units, i.e., mm. To relate the RMSE to the corresponding displacement and earthquake intensity level, the RMSE values were normalized with respect to the peak displacement values observed from both DIC and SP for all tests. A summary of the absolute and normalized RMSE along with peak transverse displacements recorded from the tests is presented in Table 3. As shown in the table, the normalized RMSE is consistently <9% (except for one test run). The slight difference is attributed to the fact that the 1D SP measurements were not corrected for triangulation given that the tests were bidirectional. Therefore, such difference is acceptable and confirms the accuracy of DIC and validates the technique that feasibly and practically used only 30 fps for cameras recording.

FIGURE 4

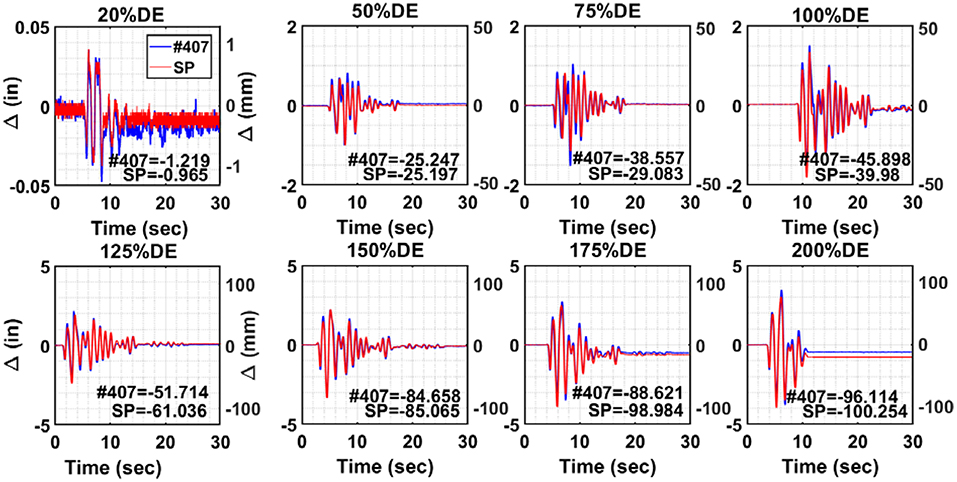
Figure 4. Displacement time histories comparison between target-tracking DIC and string potentiometer.

TABLE 3

Table 3. Measurement error between target-tracking DIC and SP.

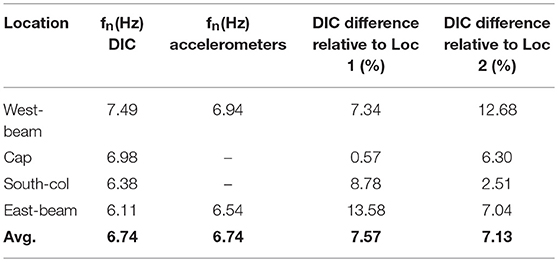
For the second verification set, the objective was to simply compare the first fundamental frequency of the bridge from spectral analysis of both DIC and accelerometers measurements. The spectra of DIC presented here only shows the first peak. The sampling rate for the accelerometer was 256 Hz while 30 Hz or fps was used for the DIC vision-sensor in order to obtain a recording length of ~30 s, which was almost half the duration of the white noise motion recorded by the accelerometers. The targets were distributed in the Region of Interest (ROI) as shown in Figure 2, in which random points located on the cap, east, and west beam as well as south column were selected for verification with the resulting acceleration time histories shown in Figure 5. Two triaxial accelerometers located on the West (Loc.1) and East (Loc.2) sides on the top of the bridge were selected for comparison with the recorded acceleration time histories as shown in Figure 5. The AR method was chosen to generate frequency resolutions of acceleration recorded by accelerometers and by the vision sensor. To obtain the power spectrum of the accelerometer signal with the AR method, the signals were divided into overlapping segments with 50% overlap, computing the modified periodogram of each segment, then averaging the PSD estimates. The results are shown in Figure 5 and Table 4 where the first determined fundamental frequency is in the range of 6.5–7 Hz for the two locations. Spectral analysis results of vision sensor signal using AR method are also shown in Figure 5. The determined frequency ranged between 6.1 and 7.5 Hz and the target location on the cap beam gives the closest result to the accelerometer, with only a 0.57% difference. In general, the results demonstrate consistent performance of the AR method showing the average fundamental frequency of the bridge measured by DIC and accelerometers as 6.74 Hz. Moreover, the difference in the determined frequency was about 7% on average between DIC and accelerometers, which is considered acceptable and provided confidence to proceed to the system identification studies.

FIGURE 5

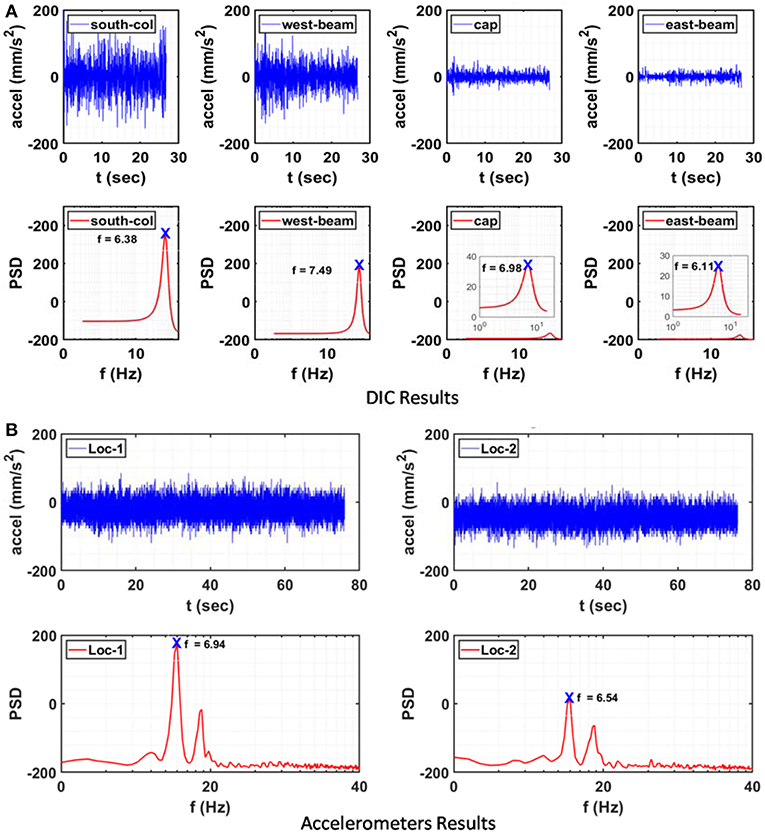
Figure 5. Recorded acceleration and PSD estimate: (A) DIC signals using AR method; (B) Accelerometers using AR method.

TABLE 4

Table 4. Difference between first fundamental frequency DIC-target tracking and accelerometers.

System Identification of Bridges

In this section, the expected modal criteria are presented using input-output relationship of targets located on the bridge as shown in Figure 6. The frequency response of the bridges in healthy state (initial, i.e., before seismic tests) and damaged state (end, i.e., after a series of eight seismic tests with increasing amplitude) is obtained by low-intensity white-noise random excitation. White noise inputs have low amplitudes, so they cause no further damage to the bridges, which is ideal for identification in a damaged state. The input white noise applied to the bridges was a 75-s random excitation. In this study, the results of simulated white noise signals from two bridges are presented, in which the signals are recorded in the transverse direction for Bridge#2 (steel bridge as shown in Figures 2, 6) and in the longitudinal direction for Bridge#3 (concrete bridge, shown in Figures 2, 6). The recording was conducted before and after eight runs of seismic tests. Thus, the frequency content of the signal was expected to shift, indicating the change of stiffness and damage on the bridges. For this analysis, MATLAB was used to extract the bridge natural frequency from the FFT and AR spectrums and to obtain the bridge modal properties using LSCE, PP, and SSI methods as explained later. For verification of the bridges using the FFT and AR methods, the acceleration data from a single target located at the cap were processed as shown in Figure 6. As for the identification using the LSCE, PP, and SSI methods, the data recorded at the bottom of the column, illustrated in Figure 6, was used as the input data, while the accelerations from the other six targets were analyzed as the output data. Results of the fundamental frequency and damping ratios of each method are represented below and compared with each other.

FIGURE 6

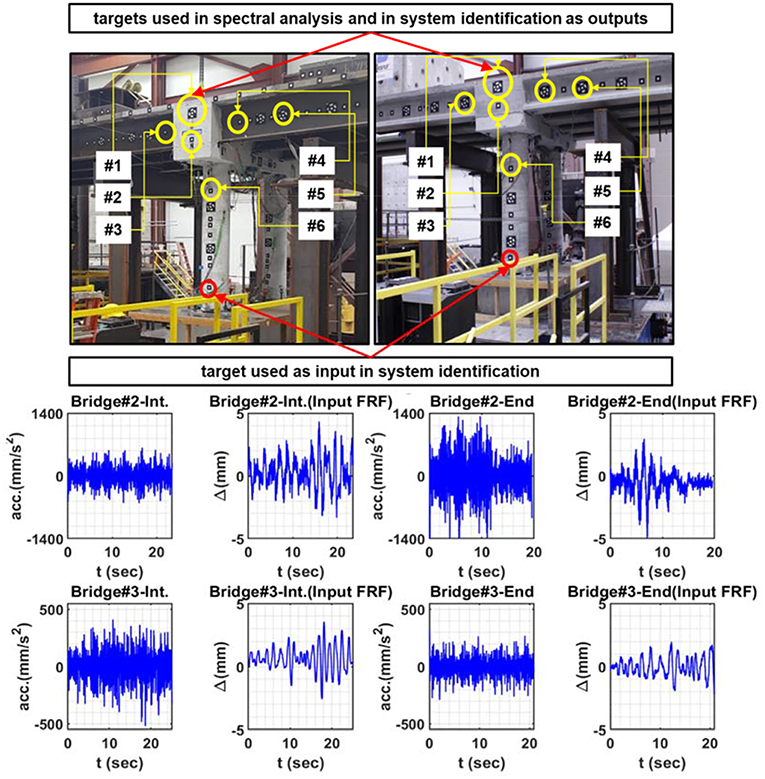
Figure 6. DIC target locations on Bridge #2 and Bridge #3 used in spectral analysis and system identification (top); sample acceleration (output, target #1) and displacement signals (input) obtained for initial and end states of the bridges (bot).

Spectral Analysis Method (FFT and AR Methods)

Figure 7 shows the transverse ambient vibration responses of Bridge#2 as well as the longitudinal response of Bridge#3, recorded at the cap beam using the acceleration record before and after the seismic tests. The total length of the initial record is 23.5 s, with 784 data points and a sampling rate of 30 Hz, while the end record has a similar number of data points with a duration of 19.6 s. Figure 7 shows the results of the spectral estimation with the obtained Eigen frequencies summarized in Table 5. If the FFT frequency spectrum of Bridge #2 is examined, it is seen that the highest peak is at 3.78 Hz with the smaller one at 11.25 Hz. The AR spectrum of the same signal is also shown in Figure 7 and the peaks are shown at 3.33 Hz, with a higher amplitude at 6.96 and 10.52 Hz. After the seismic tests, the frequency of the bridge was reduced to 1.53 and 1.25 Hz when determined using the FFT and AR methods, respectively. For the heavier concrete bridge (Bridge#3), the FFT spectrum shows a fundamental frequency of 5.34 Hz and second mode as 9.64 Hz. The fundamental frequency dropped to 3.11 Hz after seismic tests. The AR method for Bridge#3 shows only a single peak at 5.69 Hz, which shifted to 3.59 Hz after seismic tests.

FIGURE 7

Figure 7. Sample of PSD spectrum before and after the seismic tests from: (A) transverse white noise for the steel girder bridge, and (B) longitudinal white noise for concrete bridge.

TABLE 5

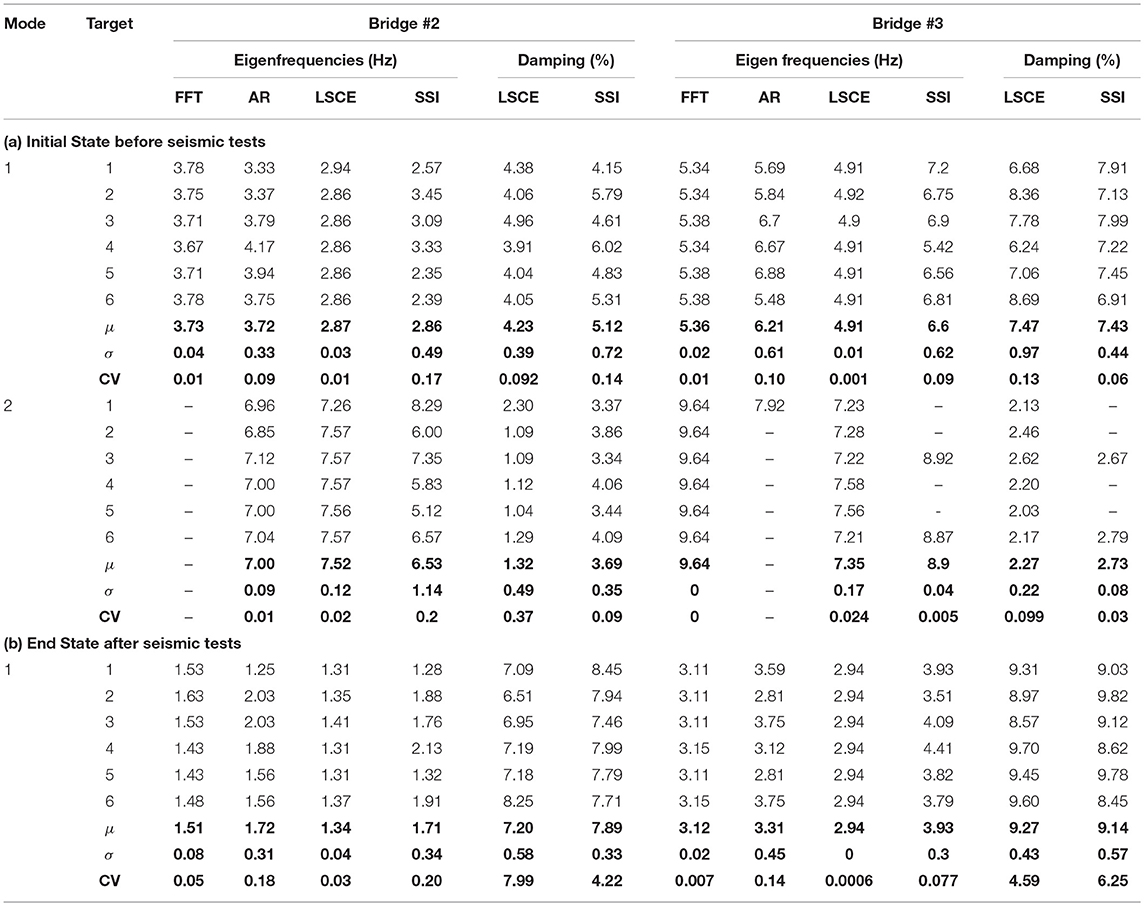
Table 5. Estimated Eigen frequencies and damping ratios of the two bridge models along with the average and standard deviations from six targets.

Frequency Domain Method (PP and LSCE Methods)

For the PP method, the data points were transformed into the frequency domain and averaged to estimate the power spectral densities. By applying the procedures previously described in section System Identification Techniques and Background, estimates of the natural frequencies and damping ratios can be obtained. The LSCE method was applied to the auto and cross-correlations of the responses. The correlation functions were used in the method to extract the natural frequencies and damping ratios. Stabilization diagrams showing the stability of the pole as a function of increasing model order were used to distinguish the spurious modes from the physical ones in which the criteria for stability were sat as 1% for natural frequency and 5% for damping. It is noted that mode shapes cannot be determined from both methods but can be defined using the SSI method as will be shown later.

The LSCE method, described previously, uses all data from the six targets located on the bridges to estimate global estimates of modal frequency and damping. A stabilization diagram can again be created to determine the optimal number of modes. The frequency response and stability diagrams from the LSCE method before and after seismic tests for Bridge#2 and Bridge#3 are shown in Figures 8, 9, respectively, for the six identified targets. The figures show the variation of the computed frequencies with the order of polynomial form considered in the model. However, the method can provide a stable pole at lower or higher modes at a specific model order. For example, in Figure 8 for Bridge#2 at the initial response, target#2 to target#6 show a stable frequency pole around 3 Hz. This pole only occurs at one model order, say at the model order of 14 for target#3. Thus, this pole is not identified as the physical pole and is ignored in the identification process, i.e., although the LSCE method produces natural frequencies and damping ratio, the results are not stable. Nevertheless, three natural frequencies can be captured, say for target#6 (located on North bent) on Bridge#2 as 2.86, 7.57, and 9.17 Hz, respectively, with these values identified as more stable than the others. Using the LSCE method, physical poles tend to “wander” in the stabilization diagram, especially at larger model order.

FIGURE 8

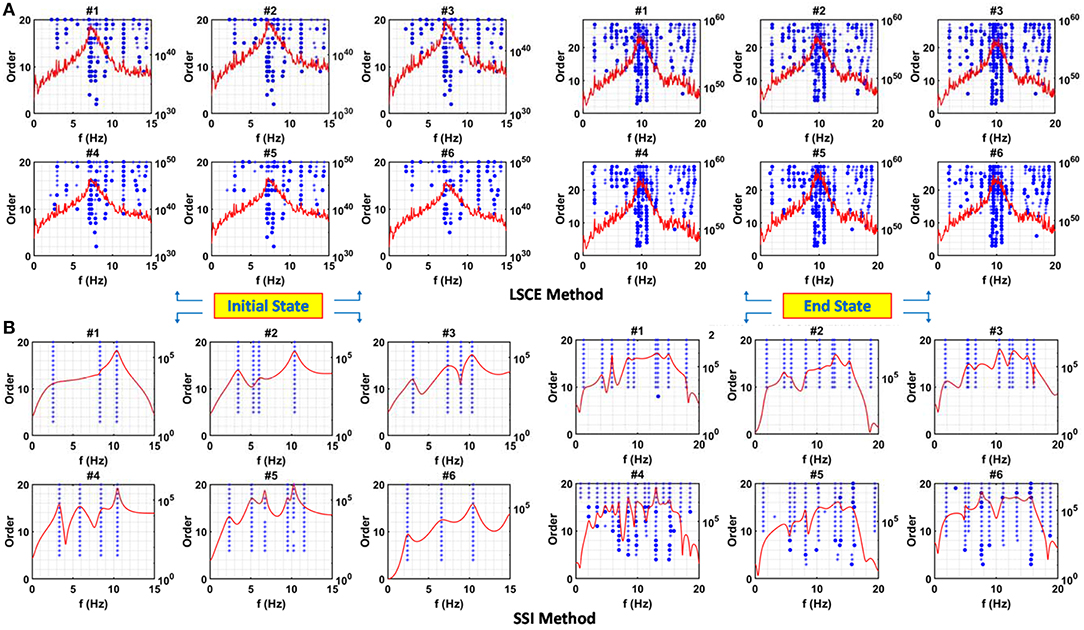
Figure 8. Frequency response and stabilization diagram of the steel girder bridge (Bridge #2) using (A) LSCE methods and (B) SSI methods before and after the seismic tests (initial and end states). The criteria are 1% for frequencies and 5% for damping ratios, symbols in stabilization diagram “*”indicates stable frequency and damping; “o” is stable frequency.

FIGURE 9

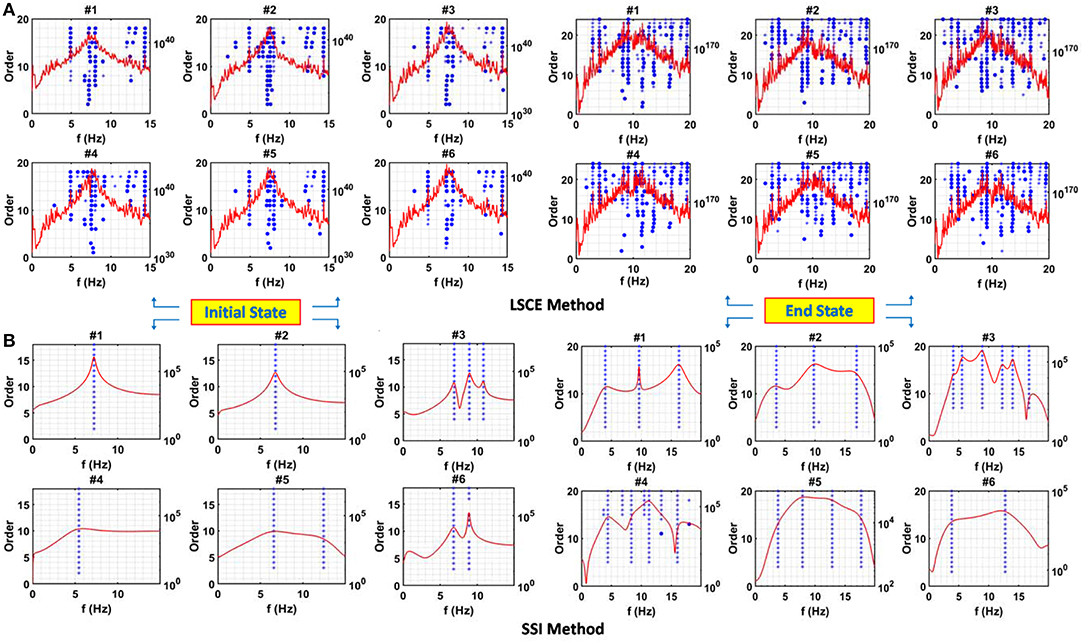
Figure 9. Frequency response and stabilization diagram of the concrete girder bridge (Bridge #3) using (A) LSCE methods and (B) SSI methods before and after the seismic tests (initial and end states). The criteria are 1% for frequencies and 5% for damping ratios, symbols in stabilization diagram “*”indicates stable frequency and damping; “o” is stable frequency.

In Table 5, the convergence of the poles is reported for the identified first, second and third Eigen frequencies when the order of the system is increased. They are identified using the stable poles with the stability criteria mentioned above. An example of the detailed result is provided here using target#1 located on cap for both type of bridges. The harmonic frequency at 7 Hz for Bridge#2 and Bridge#3 is clearly visible in the plot because of its high peak. There are also smaller peaks at a frequency below the harmonic frequency, with the lowest computed as 2.94 Hz using LSCE method and 3.94 Hz using the PP method for Bridge#2. For Bridge#3, the lower modes are computed as 4.91 Hz for both PP and LSCE methods. As shown in Table 5, these modes are stable modes, i.e., stable frequency and damping are obtained using both methods. The change in the fundamental frequency of the bridges after seismic tests can be also observed, in which LSCE computes the shifted frequency as 1.31 Hz while PP shows 1.98 Hz for damaged Bridge#2. Similarly, Bridge#3's frequency dropped to 2.94 and 3.49 Hz as determined from the LSCE and PP methods, respectively. Another observation for Bridge#3 is that the third mode could not be detected using the DIC 30 fps sampling rate for the initial response. For damping, the first, second and third Eigen frequencies for Bridge#2 are associated with estimated damping ratios of 4.38, 2.3, and 1.05%, respectively using the LSCE method. Only damping ratios for the first two modes were found from the PP method for Bridge#2 and estimated as 1.53 and 0.43%, respectively. As for Bridge#3, two damping ratios were identified: 6.68 and 2.13% for the LSCE method and 1.05 and 1.12% for the PP method. The advantages of the PP method are that it is easy to apply and provides fast estimates. However, the determined damping varied significantly from what was estimated from the LSCE method, which can be attributed to the fact that the PP method determines damping using the half bandwidth estimation approach, which is not comparable to LSCE. On the other hand, the advantage of LSCE is the ability to globally identify modal parameters, and it can be seen that it provides sound estimates of the natural frequencies and damping ratios that are comparable to the SSI method discussed next.

Time-Domain Method (SSI Method)

Similar to the LSCE and PP methods, with respect to the selection of the model order, the stability of frequencies, damping ratios, and mode shapes was investigated for increasing model order in stabilization diagrams when the SSI method is used. Figures 8, 9 show the different mode frequencies as a function of the increasing model order for both bridges. Note that the SSI method was applied to the time responses, and the stabilization diagram was obtained for both bridges. The natural frequencies, damping ratios, and unscaled mode shapes of the bridges are estimated using the SSI method. The results of natural frequencies and damping ratios are given in Table 5.

In Figures 8, 9, the diagrams for SSI Bridge#2 and Bridge#3 are also presented using the six identified targets. Physical poles show up as stable ones while numerical poles do not become stable with increasing orders. For the initial state of Bridge#2 and Bridge#3, the SSI stability diagrams indicate that stable poles are identified at a lower model order. As for the end response, the higher order is required for Bridge#2 to reach a stable pole. Different numbers of physical poles are also observed on the targets on Bridge#2 for the same model order of 20. Target#5 for example, located at West beam, shows 6 stable poles in the initial state while two targets on the cap beam show only three stable poles. As for Bridge#3, three stable poles are observed at target#3 located on East beam, while targets on cap beam show only one stable pole. Clear peaks are also observed more in the stabilization diagram of Bridge#2 as compared to Bridge#3, indicating that a model order higher than 20 is necessary for analyzing signals from Bridge#3 to obtain more clear peaks in the power spectra, particularly at the West side of the bridge. For convenience and completeness, Table 5 summarizes all identification results as obtained from the different targets, which is discussed later in section Results comparison.

In Table 5 for Bridge #2, the vibration frequency of the first three modes recorded on target #1 were identified as 2.57, 8.29, and 10.37 Hz, respectively. By reference to Figure 8, it is clear that the peak for the second mode (8.29 Hz) is not clearly visible in the frequency response function plot. However, stable poles are present at this particular frequency starting at a very low model order, and in turn, this peak reflects a stable physical mode. Using the SSI method, the fundamental frequency in the damaged state also dropped to 1.28 Hz, which shows a similar trend as the previous methods. The natural frequency for Bridge#3 using target #1 was computed as 7.2 Hz, and only one mode was excited in this case. The similar trend of decreasing frequency is also observed showing 3.93 Hz at the damaged states. The damping ratios for Bridge#2 is computed as 4.15%, while Bridge#3 shows higher damping as 7.91%. These results for damping ratios are close to the ones computed by the LSCE method, i.e., 4.38 and 6.68% for Bridge#2 and Bridge#3, respectively.

Mode Shapes

Computing mode shapes using the SSI method was done by fitting the power- and cross-spectral densities between the responses and the selected reference target in a least squares sense. The power- and cross-spectral densities were estimated on the basis of the Discrete Fourier Transform (DFT) and segment-based averaging. The segment size data points and 50% overlap was used. A Hanning window was used to reduce the leakage effects. As the excitation was different for each target, the mode shapes were separately identified for each target, then stitched together as shown in 10. For easier interpretation, the mode shapes are schematically approximated and also shown in Figure 10. The first mode of Bridge#2 is a transverse flexural/bending mode, and there is a longitudinal flexural/bending mode for Bridge#3. A real and imaginary part of the mode shape is also plotted in the figures. The real part of the Eigen vector is related to the mass and stiffness distribution of the structure, whereas the complex part can be caused by several effects such as non-proportional damping or non-linear behavior.

FIGURE 10

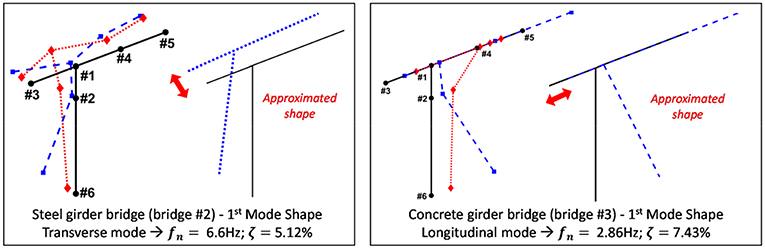
Figure 10. Mode shape of the first mode obtained with SSI. Real (blue-square) and imaginary (red-diamond) parts of analytical mode shapes. Both parts are amplified by a factor of 10.

Results Comparison

In this section, the consistency and accuracy of the system identification results of the different methods in terms of the modal parameters are compared. Table 5 comprehensively summarizes all the system identification results obtained in this study for Bridges #2 and #3 side by side. The table is also divided into two parts, (a) and (b), to present the results for the initial and end states of the bridges, respectively. The table contains identification results for the FFT, AR, LSCE, and SSI methods. For the LSCE and SSI methods, the stable poles are selected from the stabilization diagrams. There are six targets used in the identification, so there are six estimates for every Eigen frequency and damping ratio. The calculated values for mean (μ), standard deviation (σ), and coefficient of variance (CV) as obtained from all six targets are also presented. No statistical information is presented for mode shapes since only the SSI method provides the mode shape estimates.

Fundamental Frequency

The first and second mode frequencies computed using the FFT, AR, LSCE, and SSI methods from all targets on bridges are shown in Table 5 for Bridge#2 and Bridge#3. The average-initial frequency of Bridge#2 using the spectral estimation methods FFT and AR, is obtained as 3.73 Hz while the LSCE and SSI methods closely provide an estimate of 2.87 Hz for the first mode. The second mode is observed in the AR method as ~7 Hz vs. 7.5 and 6.5 Hz from LSCE and SSI, respectively. The fundamental frequency in the end state for Bridge#2 is found to be within the range 1.5–1.7 Hz using spectral estimation vs. 1.34 and 1.71 Hz from the LSCE and SSI model estimates, respectively. The range of estimates for the fundamental frequency for Bridge #3, i.e., 5.0–6.6 Hz, is consistently higher than Bridge#2, which is expected because of the lighter bridge superstructure and stiffer columns reflecting the different ABC column-to-footing connections. On the other hand, and unlike Bridge#2, the SSI model only predicts one stable mode for most of the targets on Bridge#3. Only two targets, i.e., #3 (at East-beam) and #6 (at the top of North-bent), show two physically stable modes.

According to the variation statistics shown for the first and second natural frequencies in Table 5, the lowest standard deviation for the first mode within all six targets is given by the LSCE method as 0.03 and 0.01 Hz for Bridge#2 and Bridge#3, respectively. The SSI method provides the largest standard deviation at 0.49 Hz for Bridge#2 and 0.62 Hz for Bridge#3. The large standard deviation using the SSI method is caused by the determination of model order that in this case, is determined to be similar for all targets, i.e., 20 model order. Signals from each target should be treated and analyzed differently using different model orders so that the excited mode can be seen more clearly by the increasing model order and generate more stable poles. However, from the CV values, it is shown that the SSI results distribution among the six targets is still considered having low variance and the results are reasonably acceptable.

Damping Ratio

The results of the estimated damping ratio computed using the LSCE and SSI methods for both bridges are shown in Table 5. The LSCE model of Bridge#2 estimates an average of 4.23% damping, which increases to 7.2% after the seismic test, while the SSI technique computes 5.12% damping, which also increases after the series of the seismic test to 7.89%. Higher damping is observed on Bridge#3, which is estimated as 7.47% using the LSCE method and 7.43% with the SSI method. This damping also increases to 9.27% as computed by LSCE and 9.14% as calculated by the SSI method. The damping results from these two methods are very comparable. The slightly higher damping observed for the concrete bridge (Bridge #3) is expected relative to steel girder bridges. Moreover, the inherent damping is generally expected to be larger in the damaged state of the bridge due to the increased number of cracks and other energy dissipating mechanisms.

The variation or uncertainty in the damping ratio estimates from the six targets is slightly lower as compared to the vibration frequencies. The CV for damping as computed from the six targets using the SSI method is overall lower than the LSCE method. To be specific, the overall average σ and CV from the initial state's 2 modes and end state fundamental mode for both bridges can be calculated for the SSI and LSCE methods as 0.42% and 0.07 vs. 0.5% and 0.14, respectively. Therefore, it can be concluded that the damping ratio computed using the SSI method is more precise compared to the LSCE method. In addition, it should be noted that 6 targets might not be a large enough number for statistical significance, but the standard deviation and coefficient of variation values shown in Table 5 provide confidence that the identification results are acceptable. Nevertheless, if more targets are used, closer values for the standard deviation from the different methods can be obtained and the identification process can be enhanced in general.

Summary and Conclusions

This paper presents system identification results obtained from using novel non-contact target-tracking DIC to monitor three large-scale bridge structures that were tested at a multi-shake table array under earthquake and white noise excitations. The technique was first validated then the performance of different system identification methods was compared and discussed for the DIC-generated signals. Several identification methods were used to extract the frequency, damping ratio and mode shapes of the bridges, including the spectral estimation FFT and AR methods, the peak picking EMA method, the LSCE method and the SSI method for estimation of state space systems. The following are concluding remarks from this study:

• Vision-based target-tracking using the DIC technique was validated for seismic and dynamic response monitoring in the time and frequency domains. From seismic testing of one of the bridge models, 9% or less difference was observed in the displacement time histories and peak values between the DIC and conventional string potentiometers. The AR method was used to determine the fundamental frequency, and 7.5% or less difference was found between DIC and accelerometers. The comparable results obtained from DIC and conventional sensors provided confidence to further use the DIC signals for full system identification.

• The structural health monitoring conducted in this paper involved the use of several distributed targets attached to two bridge structures to obtain response signals using DIC when the bridges were subjected to white noise excitation. The DIC settings included short duration recording between 11 and 27 s with recording rates of 30 and 40 fps. System identification was successful using these practical settings, which provided good results for the modal properties. The natural frequencies and damping ratios of both bridges could be estimated, and some targets captured up to three modes of vibration.

• The identified fundamental frequency of the initial state, i.e., before seismic damage, for the steel Bridge#2 and concrete Bridge#3 varied from 2.8 to 3.8 Hz and from 4.9 to 6.2 Hz, respectively. An average damping ratio of about 4.7 and 7.5% was identified for the two bridges in their initial state, respectively. The processed DIC signals also effectively captured the end state frequency and damping of both bridges after the seismic tests. The frequency dropped to about 1.5 and 3.2 Hz, while the damping ratio increased to about 7.5 and 9.2% for Bridge#2 and Bridge#3, respectively, due to the seismic damage.

• Variation in the modal properties, especially frequency, was observed between the methods and from the multiple targets. Less variation was observed in the estimated damping ratios, and some methods, e.g., LSCE and SSI, returned very comparable values. Thus, more targets are recommended for practical applications, especially so that a large number of DIC targets can be feasibly deployed.

• Classical FFT, AR, peak-picking and other non-parametric methods that are fast and easy to use gave reasonable estimates when used for DIC signals. Such methods can be applied to get quick estimates of the frequencies. However, more sophisticated time domain methods such as SSI are recommended for more accurate results or to obtain additional information that cannot be provided by non-parametric methods such as damping ratio or mode shapes. Thus, it is not the intention to elect a winner method but to highlight the fact that a preferable method depends mainly on the application.

• Overall, DIC signals from practical recording durations and rates can be successfully used for structural system identification as demonstrated for two bridge structures in this paper. The hardware used in this study is state-of-the-art specialized monochrome cameras. Therefore, future work can consider the use of commercial lower end, DSLR, or surveillance cameras to further validate DIC techniques for signal processing and continuous monitoring, and identify the optimum field views, lighting conditions and targets distribution for more feasible hardware.

• Continuous monitoring is important for critical infrastructure like bridges and should not be considered only for routine inspection or post-disaster assessment. Continuous monitoring should not be confused with real-time monitoring, which is not possible using DIC yet due to the required post-processing. However, the way DIC can be envisioned for continuous monitoring is that the hardware (mainly cameras) should be calibrated once and then permanently installed, e.g., as the in case of surveillance cameras, and the collected images/videos should be processed regularly using automated algorithms to inform whether any changes in the structure health took place. This vision will require more research as well but it is becoming possible with the advancements in high-speed data acquisition and communication systems, efficient operating software, and computing power for data processing.

Author Contributions

LN worked on this study as part of her doctoral research under the supervision of MM.

Funding

The DIC equipment used in this study was funded in part by the Civil and Environmental Engineering Department and the College of Engineering at the University of Nevada, Reno.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors like to thank Prof. M. (Saiid) Saiidi for providing us with the opportunity to monitor all three bridge shake table tests. The authors also thank the doctoral students who worked on these tests, Mr. Jose Benjumea, Ms. Elmira Shoushtari, and Mr. Jared Jones, for their cooperation and help.

References

Abdel-Qader, I., Abudayyeh, O., and Kelly, M. E. (2003). Analysis of edge-detection techniques for crack identification in bridges. J. Comput. Civil Eng. 17, 255–263. doi: 10.1061/(ASCE)0887-3801(2003)17:4(255)

CrossRef Full Text | Google Scholar

Allemang, R. J., and Brown, D. L. (1982). “A correlation coefficient for modal vector analysis,” in Proceedings of 1st International Modal Analysis Conference (Orlando, FL: Society for Experimental Mechanics), 110–116.

Google Scholar

Bard, Y. (1974). Nonlinear Parameter Estimation. New York, NY: Academic Press. 351.

Google Scholar

Barhli, S., Hollis, D., Wieneke, B., Mostafavi, M., and Marrow, T. (2015). “Advanced 2D and 3D digital image correlation of the full-field displacements of cracks and defects,” in Evaluation of Existing and New Sensor Technologies for Fatigue, Fracture and Mechanical Testing: ASTM International (Toronto, ON). doi: 10.1520/STP158420140052

CrossRef Full Text | Google Scholar

Bishop, R. E. D., and Gladwell, G. M. L. (1963). An investigation into the theory of resonance testing. Philos. Trans. R Soc. Lond. 255, 241–280. doi: 10.1098/rsta.1963.0004

CrossRef Full Text | Google Scholar

Brown, D. L., Allemang, R. J., Zimmerman, R., and Mergeay, M. (1979). Parameter Estimation Techniques for Modal Analysis. SAE Technical Paper Series, 790221. doi: 10.4271/790221

CrossRef Full Text | Google Scholar

Brownjohn, J. M. W., Xu, Y., and Hester, D. (2017). Vision-based bridge deformation monitoring. Front. Built Environ. 3:23. doi: 10.3389/fbuil.2017.00023

CrossRef Full Text | Google Scholar

Buń, P., Górski, F., Wichniarek, R., Kuczko, W., Hamrol, A., and Zawadzki, P. (2015). Application of low-cost tracking systems in educational training applications. Proc. Comput. Sci. 75, 398–407. doi: 10.1016/j.procs.2015.12.263

CrossRef Full Text | Google Scholar

Chiang, C.-H., Shih, M.-H., Chen, W., and Yu, C.-P. (2011). “Displacement measurements of highway bridges using digital image correlation methods.” in Paper Presented at the Seventh International Symposium on Precision Engineering Measurements and Instrumentation (Yunnan). doi: 10.1117/12.904303

CrossRef Full Text | Google Scholar

Cigada, A., Mazzoleni, P., and Zappa, E. (2014). Vibration monitoring of multiple bridge points by means of a unique vision-based measuring system. Exp. Mech. 54, 255–271. doi: 10.1007/s11340-013-9784-8

CrossRef Full Text | Google Scholar

Cooley, J. W., and Tukey, J. W. (1965). An algorithm for the machine calculation of complex Fourier series. Math. Comput. 19, 297–301. doi: 10.1090/S0025-5718-1965-0178586-1

CrossRef Full Text | Google Scholar

Dzhaparidze, K. (2012). Parameter Estimation and Hypothesis Testing in Spectral Analysis of Stationary Time Series. Berlin: Springer Science and Business Media.

Google Scholar

Feng, D., and Feng, M. Q. (2017). Experimental validation of cost-effective vision-based structural health monitoring. Mech. Syst. Signal Process. 88, 199–211. doi: 10.1016/j.ymssp.2016.11.021

CrossRef Full Text | Google Scholar

Feng, M. Q., Fukuda, Y., Feng, D., and Mizuta, M. (2015). Nontarget vision sensor for remote measurement of bridge dynamic response. J. Bridge Eng. 20, 04015023. doi: 10.1061/(ASCE)BE.1943-5592.0000747

CrossRef Full Text | Google Scholar

Fukuda, Y., Feng, M. Q., and Shinozuka, M. (2010). Cost-effective vision-based system for monitoring dynamic response of civil engineering structures. Struct. Control Health Monit. 17, 918–936. doi: 10.1002/stc.360

CrossRef Full Text | Google Scholar

Gao, Y., Cheng, T., Su, Y., Xu, X., Zhang, Y., and Zhang, Q. (2015). High-efficiency and high-accuracy digital image correlation for three-dimensional measurement. Opt. Lasers Eng. 65, 73–80. doi: 10.1016/j.optlaseng.2014.05.013

CrossRef Full Text | Google Scholar

GOM Correlate Professional [Computer Software] (2017). GOM Correlate-Evaluation Software for 3D Testing, GOM Precise Industrial 3D Metrology.

Google Scholar

Hartley, R., and Zisserman, A. (2003). Multiple View Geometry in Computer Vision. Cambridge, UK: Cambridge University Press. doi: 10.1017/CBO9780511811685

CrossRef Full Text | Google Scholar

Hartley, R. I., and Sturm, P. (1997). Triangulation. Comput. Vis. Image Understand. 68, 146–157. doi: 10.1006/cviu.1997.0547

CrossRef Full Text | Google Scholar

Helfrick, M. N., Niezrecki, C., Avitabile, P., and Schmidt, T. (2011). 3D digital image correlation methods for full-field vibration measurement. Mech. Syst. Signal Process. 25, 917–927. doi: 10.1016/j.ymssp.2010.08.013

CrossRef Full Text | Google Scholar

Heylen, W., Lammens, S., and Sas, P. (1995). Modal Analysis Theory and Testing. Leuven: Department of Mechanical Engineering, Katholieke University.

Google Scholar

Jiang, Z., Kemao, Q., Miao, H., Yang, J., and Tang, L. (2015). Path-independent digital image correlation with high accuracy, speed and robustness. Opt. Lasers Eng. 65, 93–102. doi: 10.1016/j.optlaseng.2014.06.011

CrossRef Full Text | Google Scholar

Kay, S. M. (1988). Modern Spectral Estimations: Theory and Application. Pearson Education.

Google Scholar

Kay, S. M., and Marple, S. L. (1981). Spectrum analysis—a modern perspective. Proc. IEEE 69, 1380–1419. doi: 10.1109/PROC.1981.12184

CrossRef Full Text | Google Scholar

Lee, J.-J., Ho, H.-N., and Lee, J.-H. (2012). A vision-based dynamic rotational angle measurement system for large civil structures. Sensors 12, 7326–7336. doi: 10.3390/s120607326

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, J.-J., and Shinozuka, M. (2006). Real-time displacement measurement of a flexible bridge using digital image processing techniques. Exp. Mech. 46, 105–114. doi: 10.1007/s11340-006-6124-2

CrossRef Full Text | Google Scholar

Lobos, T., Kozina, T., and Koglin, H.-J. (2001). Power system harmonics estimation using linear least squares method and SVD. IEE Proc. Generat. Transm. Distr. 148, 567–572. doi: 10.1049/ip-gtd:20010563

CrossRef Full Text | Google Scholar

Marple, S.L., and Carey, W. M. (1989). Digital Spectral Analysis: With Applications, Vol. 5. Upper Saddle River, NJ: Prentice-Hall Englewood Cliffs.

Google Scholar

Maybank, S. J., and Faugeras, O. D. (1992). A theory of self-calibration of a moving camera. Int. J. Comput. Vis. 8, 123–151. doi: 10.1007/BF00127171

CrossRef Full Text | Google Scholar

Mikhail, E. M., Bethel, J. S., and McGlone, J. C. (2001). Introduction to Modern Photogrammetry. New York, NY: John Wiley.

Google Scholar

Murray, C., Hoag, A., Hoult, N. A., and Take, W. A. (2014). Field monitoring of a bridge using digital image correlation. Proc. Instit. Civil Eng. Bridge Eng. 168, 3–12. doi: 10.1680/bren.13.00024

CrossRef Full Text | Google Scholar

Ngeljaratan, L., and Moustafa, M. A. (2017). “Digital image correlation for dynamic shake table test measurements,” in Proceeding of 7th International Conference AESE (Pavia), 741–752.

Google Scholar

Ngeljaratan, L., and Moustafa, M. A. (2018). “Novel digital image correlation instrumentation for largescale shake table test,” in Proceedings of the 11th NCEE (Los Angeles, CA).

Google Scholar

Niezrecki, C., Baqersad, J., and Sabato, A. (2018). “Digital image correlation techniques for NDE and SHM,” in Handbook of Advanced Non-Destructive Evaluation, eds N. Ida and N. Meyendorf (New York, NY: Springer International Publishing AG), 1–46. doi: 10.1007/978-3-319-30050-4_47-1

CrossRef Full Text | Google Scholar

Nonis, C., Niezrecki, C., Yu, T.-Y., Ahmed, S., Su, C.-F., and Schmidt, T. (2013). “Structural health monitoring of bridges using digital image correlation,” in Paper Presented at the Health Monitoring of Structural and Biological Systems 2013 (San Diego, CA). doi: 10.1117/12.2009647

CrossRef Full Text | Google Scholar

Pan, B., Tian, L., and Song, X. (2016). Real-time, non-contact and targetless measurement of vertical deflection of bridges using off-axis digital image correlation. Ndt E Int. 79, 73–80. doi: 10.1016/j.ndteint.2015.12.006

CrossRef Full Text | Google Scholar

Park, S., Park, H., Kim, J., and Adeli, H. (2015). 3D displacement measurement model for health monitoring of structures using a motion capture system. Measurement 59, 352–362. doi: 10.1016/j.measurement.2014.09.063

CrossRef Full Text | Google Scholar

Peddle, J., Goudreau, A., Carlson, E., and Santini-Bell, E. (2011). Bridge displacement measurement through digital image correlation. Bridge Struct. 7, 165–173. doi: 10.3233/BRS-2011-031

CrossRef Full Text | Google Scholar

Peeters, B., and De Roeck, G. (2000). Reference based stochastic subspace identification in civil engineering. Inverse Probl. Eng. 8, 47–74. doi: 10.1080/174159700088027718

CrossRef Full Text | Google Scholar

Ribeiro, D., Calçada, R., Ferreira, J., and Martins, T. (2014). Non-contact measurement of the dynamic displacement of railway bridges using an advanced video-based system. Eng. Struct. 75, 164–180. doi: 10.1016/j.engstruct.2014.04.051

CrossRef Full Text | Google Scholar

Santos, C. A., Costa, C. O., and Batista, J. P. (2012). Calibration methodology of a vision system for measuring the displacements of long-deck suspension bridges. Struct. Control Health Monit. 19, 385–404. doi: 10.1002/stc.438

CrossRef Full Text | Google Scholar

Schumacher, T., and Shariati, A. (2013). Monitoring of structures and mechanical systems using virtual visual sensors for video analysis: fundamental concept and proof of feasibility. Sensors 13, 16551–16564. doi: 10.3390/s131216551

CrossRef Full Text | Google Scholar

Sutton, M. A., Orteu, J. J., and Schreier, H. (2009). Image Correlation for Shape, Motion and Deformation Measurements: Basic Concepts, Theory and Applications. Berlin: Springer Science and Business Media.

Google Scholar

TRITOP Professional [Computer Software] (2017). TRITOP - Optical 3D Coordinate Measuring Machine, GOM Precise Industrial 3D Metrology.

Google Scholar

Van Overschee, P., and De Moor, B. (2012). “Subspace identification for linear systems,” in Theory—Implementation—Applications (Berlin: Springer Science & Business Media).

Google Scholar

Wahbeh, A. M., Caffrey, J. P., and Masri, S. F. (2003). A vision-based approach for the direct measurement of displacements in vibrating systems. Smart Mater. Struct. 12:785. doi: 10.1088/0964-1726/12/5/016

CrossRef Full Text | Google Scholar

Welch, P. (1967). The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified periodograms. IEEE Trans. Audio Electroacoust. 15, 70–73. doi: 10.1109/TAU.1967.1161901

CrossRef Full Text | Google Scholar

Wu, L.-J., Casciati, F., and Casciati, S. (2014). Dynamic testing of a laboratory model via vision-based sensing. Eng. Struct. 60, 113–125. doi: 10.1016/j.engstruct.2013.12.002

CrossRef Full Text | Google Scholar

Xu, L., Guo, J., and Jiang, J. (2002). Time–frequency analysis of a suspension bridge based on GPS. J. Sound Vib. 254, 105–116. doi: 10.1006/jsvi.2001.4087

CrossRef Full Text | Google Scholar

Ye, X., Yi, T.-H., Dong, C., Liu, T., and Bai, H. (2015). Multi-point displacement monitoring of bridges using a vision-based approach. Wind Struct. 20, 315–326. doi: 10.12989/was.2015.20.2.315

CrossRef Full Text | Google Scholar

Yoneyama, S., Kitagawa, A., Iwata, S., Tani, K., and Kikuta, H. (2007). Bridge deflection measurement using digital image correlation. Exp. Tech. 31, 34–40. doi: 10.1111/j.1747-1567.2006.00132.x

CrossRef Full Text | Google Scholar

Yoon, H., Elanwar, H., Choi, H., Golparvar-Fard, M., and Spencer, B. F. (2016). Target-free approach for vision-based structural system identification using consumer-grade cameras. Struct. Control Health Monit. 23, 1405–1416. doi: 10.1002/stc.1850

CrossRef Full Text | Google Scholar

Zhang, Z. (1998). Determining the epipolar geometry and its uncertainty: a review. Int. J. Comput. Vis. 27, 161–195. doi: 10.1023/A:1007941100561

CrossRef Full Text | Google Scholar

Zhang, Z. (2000). A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 22, 1330–1334. doi: 10.1109/34.888718

CrossRef Full Text | Google Scholar