Plastic Buckling Paradox: An Updated Review

Introduction

Buckling in most engineering applications is a physical phenomenon which occurs when the deformed configuration of a structure undergoes a relatively sudden variation in shape with a noticeable increase in displacements and strains. The most well-known example is that of a reasonably straight and slender column which suddenly deviates from its original position due to compression forces, which may result in a catastrophic collapse of the whole. However, from both a theoretical and an engineering viewpoint, the most important phase of buckling generally occurs before deformations become significantly large, that is, when the buckled structure appears to the naked eye only slightly deformed (Bushnell, 1982).

Plastic buckling is both a geometrical and material nonlinear problem. The geometrical nonlinearity stems from the nonlinearity of the kinematic relations which represent the large displacements and rotations of the structure, while the material nonlinearity, such as plasticity, is due to the nonlinearity of the material constitutive relationships.

Plastic buckling of structures has been the subject of many research studies since the end of the nineteenth century. The first study on the inelastic stability of structures was published in 1889 by Engesser for simple compressed metal struts (Hutchinson, 1974) by substituting the elastic modulus E with the tangent modulus E_t in the Euler’s formula for the buckling load.

In 1895, Engesser corrected his original simplified theory by accounting for the different tangent modulus of the tensioned side of the cross section. He thus proposed to evaluate the buckling load of a strut by replacing the elastic modulus with a reduced modulus of elasticity E in the Euler’s formula. This proposal was validated by a series of tests conducted by von Karman on mild-steel columns (Gerard, 1962).

However, for years, engineers wondered if the reduced modulus theory was actually correct because experimental buckling loads of aluminum alloy columns were closer to those predicted by the tangent-modulus theory. Shanley (1947) resolved this dilemma by carefully conducting experiments on aluminum columns in conjunction with a critical revision of the theory. He suggested that the plastic buckling load obtained by the tangent-modulus theory could be considered the lowest load at which a straight column remained stable and it should be therefore considered as the actual buckling load. During the buckling process, the mean stress on the bucked column might exceed the tangent-modulus stress but it would never go beyond the reduced-modulus stress.

In the following years, Duberg and Wilder (1952) confirmed Shanely’s hypothesis and concluded that if the initial imperfection of the column tended to vanish, the buckling load of the column was in line with tangent-modulus theory at which the lateral deflection started to take place. They pointed out that the structural behavior of the perfect column beyond the load predicted by the tangent-modulus theory depends on the stress–strain relationship of the material.

However, inelastic buckling for shells and plates is a much more complex phenomenon. In fact, the equations for shells and plates are more applicable to the approximations than those for a deflected beam (Guarracino, 2007; Guarracino and Walker, 2008) and the constitutive relationships are not limited to a simple uniaxial stress–strain law, which is obtained by means of a simple tensile test.

Several shells and plates tests were carried out in the late 1940s and early 1950s and solutions for the bifurcation load were obtained for many cases of interest. However, many studies reported that the deformation theory of plasticity, which is clearly less physically sound than the flow theory of plasticity (Hill, 1950; Mendelson, 1968), seemed to predict buckling loads in better agreement with experimental results than those obtained from the flow theory of plasticity. This fact was called the “plastic buckling paradox” and has been observed in a wide range of shell structures, such as cruciform columns, plates, tori spherical domes, and circular cylinders under different loading conditions and with different boundary conditions. As a result, intensive research studies, including numerical, analytical, and experimental investigations, have been carried out to resolve the plastic paradox since the early 40s. Some studies concluded that the possible reason for the discrepancies in the results between the plasticity theories was likely due to the assumption of small deformation or the exclusion of transverse shear deformation in buckling analysis, while other studies concluded that including imperfections in conjunction with the flow theory could reduce the discrepancies in the results between the flow and the deformation theory. Other researchers suggested that the deformation theory tended to predict lower buckling stresses than those predicted by the flow theory since it predicted a lower plastic shear modulus as the level of plasticity increased. In the early 90s Yun and Kyriakides (1990) claimed that the plastic buckling paradox had to be still considered “unresolved” and available explanations were still judged “inconclusive” (Teng, 1996). Since then, research studies have confirmed once again that the deformation theory predictions are more in-line with experimental results than those of flow theory. Several researchers accepted this fact and made reference only to the deformation theory in their analytical analysis (Mao and Lu, 2002; Zhang et al., 2015). The main aim of this paper is thus to present a critical review of the available literature and to illustrate the most recent explanations proposed by Shamass et al. (2014; 2015a; 2015b; 2017) and Guarracino and Simonelli (2017, 2018). The review is directed to a broad audience and, for this reason, many concepts are recalled and simplified as much as possible in order to be palatable to non-specialists in the field.

The Flow and Deformation Theories of Plasticity and the Plastic Buckling Paradox

Two main plasticity models are commonly in use in the strain hardening range: the “deformation theory” of plasticity and the “flow theory” of plasticity. In both of these theories, the plastic deformations do not allow volume changes as plastic yielding is governed by the second invariant J₂ of the deviatoric part of the stress tensor, and in this respect they are both called J₂ theories (Shamass et al., 2014). The main difference between these two theories is that the deformation theory of plasticity assumes that the stress is uniquely determined by the current state of strain at any time and point of a solid body, and therefore, it is in a special class of path-independent nonlinear elastic constitutive laws, while the flow theory of plasticity assumes that the stress at any point and time is a function not only of the current strain but also of the strain history at the same point. In the deformation theory of plasticity, after a strain reversal in the plastic range, the initial loading curve is followed. On the contrary, as it is found experimentally in physical tests, according to the flow theory of plasticity after a strain reversal in the plastic range the unloading takes place following the initial elastic path, and when the loading is totally removed, a permanent plastic strain is left. This makes the constitutive relationship path-dependent. In this respect, the flow theory is an incremental theory of plasticity.

For the incremental theory, the Prandtl–Reuss flow rule is

$${\stackrel{.}{\mathrm{\epsilon }}}_{ij}^p=\frac{3{\stackrel{.}{\overline{}}\mathrm{\epsilon }}^p}{2\overline{\mathrm{\sigma }}}{s}_{ij}=\frac{3\stackrel{.}{\overline{}}\mathrm{\sigma }}{2H\overline{\mathrm{\sigma }}}{s}_{ij}=\frac{3\stackrel{.}{\overline{}}\mathrm{\sigma }}{2\overline{\mathrm{\sigma }}}\left(\frac{1}{E_t}-\frac{1}{E}\right)s_{ij}(1)$$

where E and E_t are the elastic modulus and tangent modulus, respectively (see Figure 1), and $\overline{\mathrm{\sigma }}$ is the effective stress, s_ij = σ_ij -σ_kkδ_ij /3 is the stress deviator, and δ_ij is the Kronecker symbol, equal to one for i=j and zero otherwise.

FIGURE 1

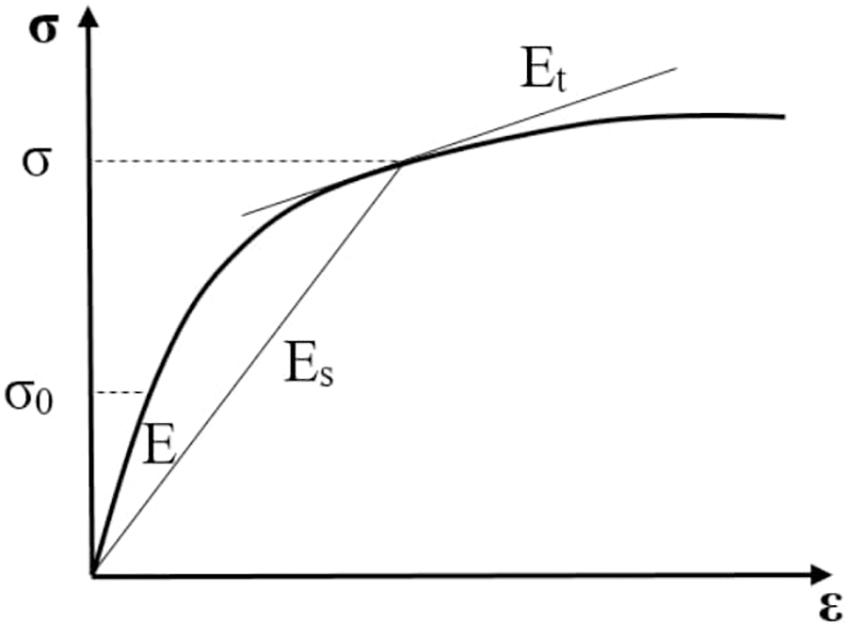
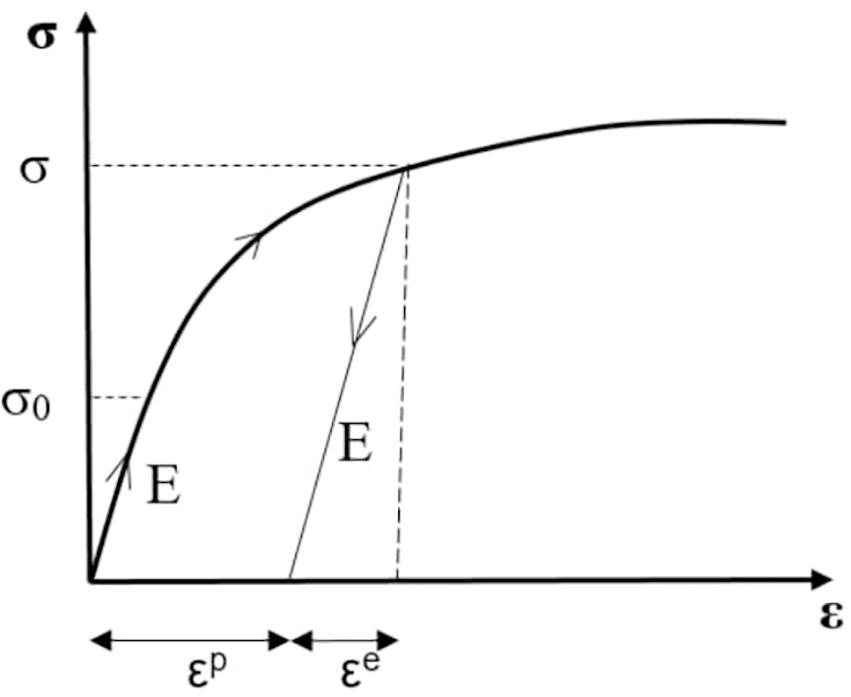
Figure 1. Elastic E, tangent E_t and secant E_s moduli in a simple tensile test. σ_o is the linear elastic limit stress.

It is assumed that the total rate of strain can be split into a sum of the elastic part and of the plastic part.

$${\stackrel{.}{\mathrm{\epsilon }}}_{ij}={\stackrel{.}{\mathrm{\epsilon }}}_{ij}^e+{\stackrel{.}{\mathrm{\epsilon }}}_{ij}^p(2)$$

The elastic strain rate according to generalized Hook’s Law is given by

$${\stackrel{.}{\mathrm{\epsilon }}}_{ij}^e=\frac{1+\mathrm{\nu }}{E}{\stackrel{.}{s}}_{ij}+\frac{1-2\mathrm{\nu }}{3E}{\mathrm{\delta }}_{ij}{\stackrel{.}{\mathrm{\sigma }}}_{kk}(3)$$

where ν is the Poisson’s ratio.

Therefore, by adding Eqs (1) and (3), the complete relationship between the rate of stresses and strains results in:

$${\stackrel{.}{\mathrm{\epsilon }}}_{ij}=\frac{1}{E}\left(\left(1+\mathrm{\nu }\right){\stackrel{.}{s}}_{ij}+\frac{1-2\mathrm{\nu }}{3}{\mathrm{\delta }}_{ij}{\stackrel{.}{\mathrm{\sigma }}}_{kk}+\frac{3\stackrel{.}{\overline{}}\mathrm{\sigma }}{2\overline{\mathrm{\sigma }}}\left(\frac{E}{E_t}-1\right)s_{ij}\right)(4)$$

With respect to the deformation theory, Hencky (1924) proposed a stress–strain relationship in which the total strain is related directly to the total actual stress status. The total plastic strain is (Mendelson, 1968)

$${\mathrm{\epsilon }}_{ij}^p=\frac{3}{2}\frac{{\overline{\mathrm{\epsilon }}}^p}{\overline{\mathrm{\sigma }}}{s}_{ij}(5)$$

where ${\overline{\mathrm{\epsilon }}}^p$ is the effective plastic strain.

As it refers to the plastic strain function of the current state of the stress only, it is independent from the loading history. This assumption significantly simplifies the plastic problem with respect to the actual physical behavior, since experimental evidence shows that the plastic strains are generally dependent on the loading path. In order to explicate Eq. (5), it is observed that, under the small strain hypothesis, the total strain can again be written in terms of an elastic and a plastic part as

$${\mathrm{\epsilon }}_{ij}={\mathrm{\epsilon }}_{ij}^e+{\mathrm{\epsilon }}_{ij}^p(6)$$

The elastic strain according to generalized Hooke’s law is given again by

$${\mathrm{\epsilon }}_{ij}^e=\frac{1+\mathrm{\nu }}{E}{s}_{ij}+\frac{1-2\mathrm{\nu }}{3E}{\mathrm{\delta }}_{ij}{\mathrm{\sigma }}_{kk}(7)$$

Replacing into Eq. (6) it is

$$E{\mathrm{\epsilon }}_{ij}=\left(1+\mathrm{\nu }\right)s_{ij}+\frac{1-2\mathrm{\nu }}{3}{\mathrm{\delta }}_{ij}{\mathrm{\sigma }}_{kk}+\frac{3}{2}E\frac{{\overline{\mathrm{\epsilon }}}^p}{\overline{\mathrm{\sigma }}}{s}_{ij}(8)$$

and the ratio between the effective plastic strain and the effective stress is

$$\frac{{\overline{\mathrm{\epsilon }}}^p}{\overline{\mathrm{\sigma }}}=\frac{1}{E_s}-\frac{1}{E}(9)$$

where E_s is the secant modulus (see Figure 1).

Eq. (8) can be re-written as:

$${\mathrm{\epsilon }}_{ij}=\frac{1}{E}\left[\left(1+\mathrm{\nu }\right)s_{ij}+\frac{1-2\mathrm{\nu }}{3}{\mathrm{\delta }}_{ij}{\mathrm{\sigma }}_{kk}+\frac{3}{2}\left(\frac{E}{E_s}-1\right)s_{ij}\right](10)$$

In the J₂ flow theory of plasticity the unloading takes place along a line parallel to the initial linear elastic path, as experimentally observed for most metals (see Figure 2), while in the J₂ deformation theory the loading and the unloading take place along the same nonlinear stress–strain path.

FIGURE 2

Figure 2. Unloading in the flow theory of plasticity.

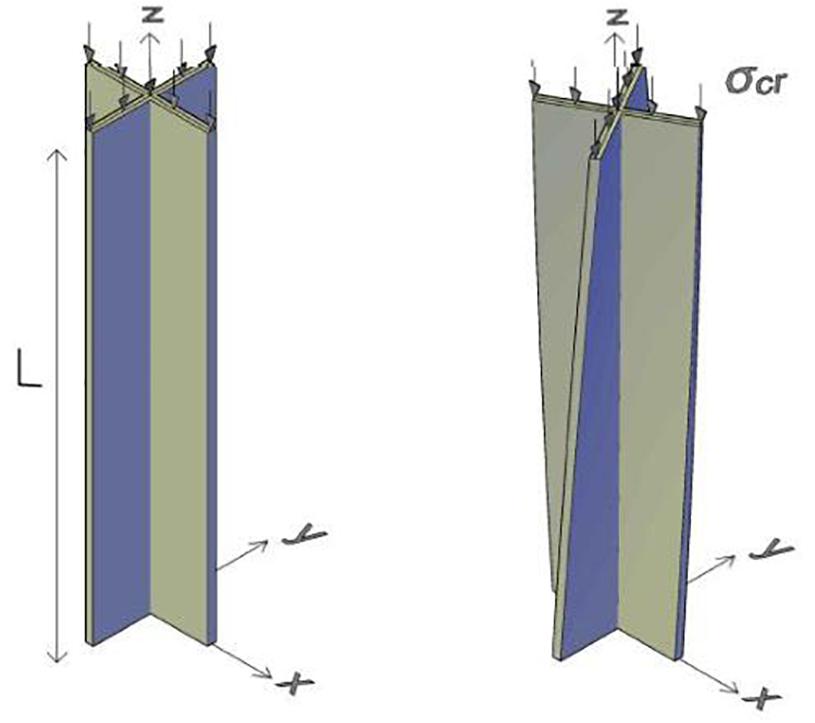
Therefore, the general agreement among engineers and researchers is that the flow theory of plasticity is more physically acceptable than the deformation theory of plasticity. However, it has been repeatedly found by many authors (e.g., Lee, 1962; Durban and Zuckerman, 1999; Mao and Lu, 1999) that the deformation theory predicts plastic buckling loads that are more in-line with experimental ones than those obtained by the flow theory of plasticity, which tends to overestimate the value of the plastic buckling load. One of the simplest examples of this paradox is found in the study of the torsional buckling of a cruciform column under axial compression, as shown in Figure 3.

FIGURE 3

Figure 3. Torsional buckling of cruciform column under axial compression.

The torsional buckling of an axially compressed cruciform column was first discussed by Stowell (1948) and Onat and Drucker (1953). If the compressed column is not too slender, it tends to buckle in a torsional mode. When the applied stress exceeds the material yield stress, the twisting structure attains a plastic state in the entire cross-section. In the pre-bifurcation, only compressive stress is present, while the torsional mode involves a combination of compression and shear stress.

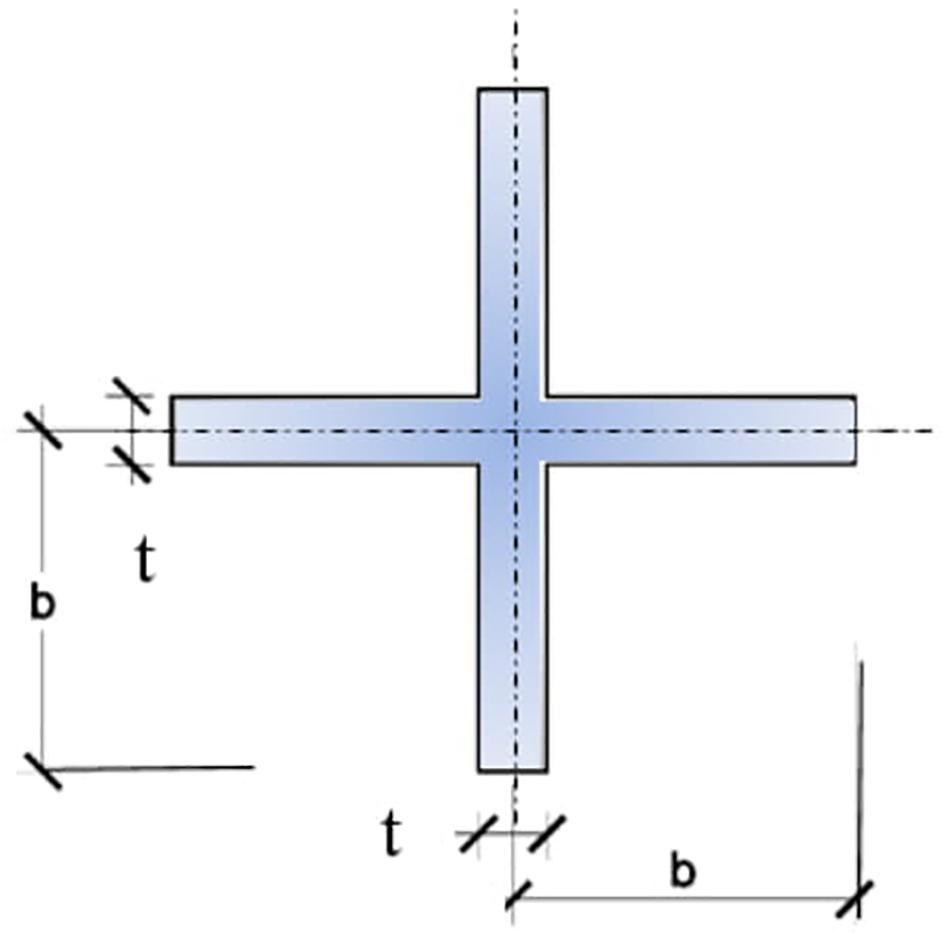
Denoting by t and b the thickness and width of the flanges of the cross-section, in the elastic range (see Figure 4), under the assumptions that the length L is not enough to trigger Euler buckling, and that b≫ t, the critical stress initiating torsional buckling is

FIGURE 4

Figure 4. Cross-section of cruciform column.

$${\mathrm{\sigma }}_{cr}=G\frac{t^2}{b^2}(11)$$

where G is the elastic shear modulus

$$G=\frac{E}{2\left(1+\mathrm{\nu }\right)}(12)$$

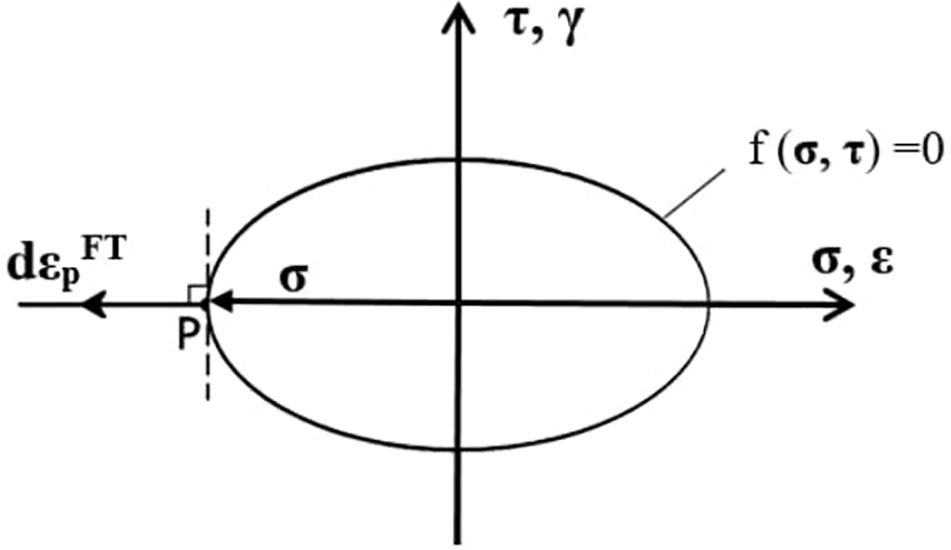
According to the J₂ flow theory of plasticity, any increment of the plastic strains in the plastic domain takes places normally at the yield surface. Since the stress status in the pre-buckling state is a simple uniaxial compression and given that the yield surface is smooth, (see Figure 5) the increments in the shear stress and strain components are related by the elastic shear modulus. Therefore, the Eq. (11) still holds true.

FIGURE 5

Figure 5. Plastic strain increment for a perfect cruciform column according to the flow theory.

However, the instantaneous shear modulus can be derived from the deformation theory of plasticity by taking into consideration a state of pure shear stress. Since ε_ij =γ /2 and σ_kk =τ, the Eq. (10) becomes

$$\frac{1}{2}\mathrm{\gamma }=\frac{1+\mathrm{\nu }}{E}\mathrm{\tau }+\frac{3}{2}\left(\frac{1}{E_s}-\frac{1}{E}\right)\mathrm{\tau }$$

Therefore, the shear modulus predicted by the deformation theory is

$$G_s=\frac{\mathrm{\tau }}{\mathrm{\gamma }}=\frac{E_s}{3+\left(2\mathrm{\nu }-1\right)\frac{E_s}{E}}(13)$$

The torsional buckling stress is thus

$${\mathrm{\sigma }}_{cr}=G_s\frac{t^2}{b^2}(14)$$

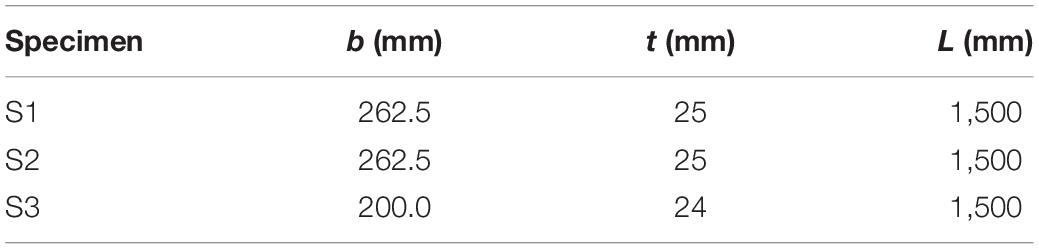
Hopperstad et al. (1999) tested three cruciform column specimens, namely S1, S2, and S3, made from aluminium alloy, as specified in Table 1. The specimens S1 and S2 were made from AA6082-T4 and AA6082-T6, respectively, while the specimen S3 was made from AA6061-T6. Figure 6 shows the experimental critical stresses for cruciform column specimens made from aluminium alloy and tested by Hopperstad et al. (1999). The critical stresses predicted by the flow theory, Eq. (11), and the deformation theory, Eq. (14), are compared with the tests results (Guarracino and Simonelli, 2017). It is clear that the flow theory overestimates the torsional buckling stresses while the deformation theory results are in good agreement with the experimental results. It has to be pointed out that the predicted torsional buckling stresses shown in Figure 6 have been calculated for a perfect column.

TABLE 1

Table 1. The dimensions and the aluminium alloy materialsof the specimens.

FIGURE 6

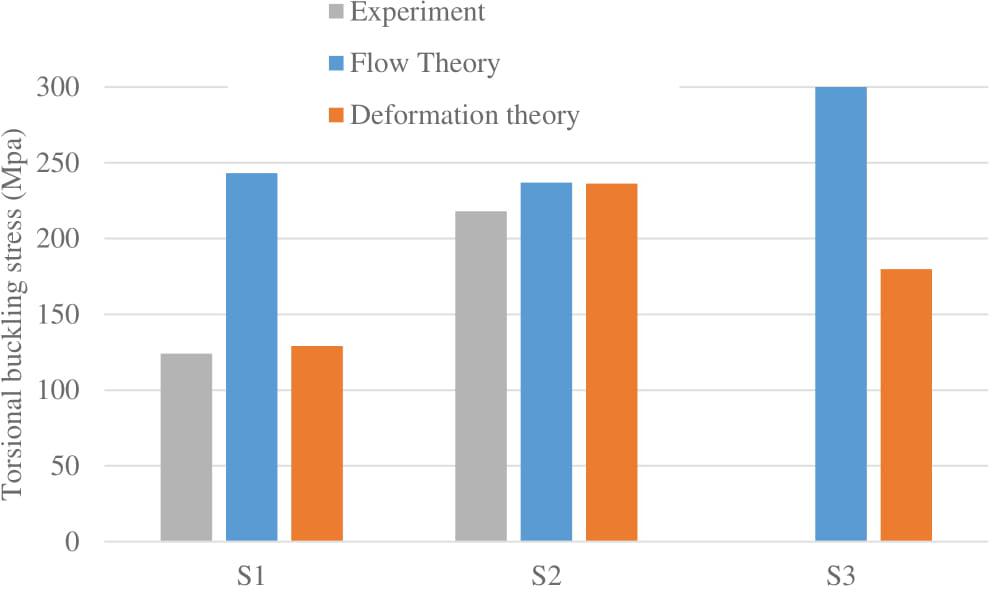
Figure 6. Torsional buckling stress for perfect crucified columns obtained using the flow and deformation theories of plasticity vs test results (Guarracino and Simonelli, 2017).

Investigations of the Plastic Buckling Paradox in the Literature

Replacement of the Effective Shear Modulus

Onat and Drucker (1953) found that collapse loads predicted by the flow theory for cruciform columns with a small initial twist were slightly higher than the bifurcation loads predicted by deformation theory. It seemed that a small amount of imperfection-related shear strains in the pre-bifurcation analysis were enough to reduce the elastic shear modulus value G predicted by the flow theory to the value closer to the effective shear modulus predicted by deformation theory (Bushnell, 1982). However, the extreme sensitivity of shear modulus to small imperfection-related shearing strains applied in the plastic range led to the proposal of a replacement of the elastic shear modulus considered by the flow theory with the effective shear modulus predicted by the deformation theory in the buckling analyses (Bushnell, 1982; Teng and Rotter, 1989). Ore and Durban (1989) studied the elastic-plastic buckling of annular plates subjected to pure shear using both the flow and deformation theories of plasticity. They again found that the discrepancies in the predictions between the flow and deformation theories of plasticity were due to the difference in the magnitude of the instantaneous moduli in the plastic range with the flow theory modulus considerably higher than the deformation theory one.

Lay (1965) also proposed that a modified shear modulus in the plastic range should be employed when using the flow theory. Drucker (1949) had pointed out that taking into account a small initial imperfection or twist in a compressed plate would greatly reduce the shear modulus predicted by the flow theory and might well provide a solution to the paradox. Tuğcu (1991a) studied analytically the effect of small amounts of in-plane shear stresses in thin rectangular plates under biaxial loading conditions on the flow and deformation theories buckling stress predictions. Tuğcu concluded that a considerable reduction in the flow theory buckling stresses could be achieved when small non-zero in-plane shear stresses were included in the analysis. In a later paper, Zhang and Wang (2011) analytically obtained the elastoplastic buckling stresses for thick rectangular plates. Similarly to the previously mentioned argument by Bushnell (1982) and Ore and Durban (1989), they observed that as the level of plasticity increased, the deformation theory predicted an in-plane shear modulus smaller than the one predicted by the flow theory, which resulted in lower buckling stress values by the deformation theory. However, Teng and Rotter (1989) revealed that the buckling pressures for an internally pressurized Tori spherical Head yielded to the flow theory, considering the effective shear modulus were almost identical to those without considering the effective shear modulus. Furthermore, Giezen (1988) found, using the BOSOR5 program (Bushnell, 1986), that the use of the effective shear modulus from the deformation theory in the flow theory led to a certain reduction in the buckling pressures for cylinders subjected to non-proportional loading, but not as much as to make them comparable with the buckling results predicted by the deformation theory. In recent papers, Shamass et al. (2017) found that employing the effective shear modulus in the flow theory can reduce the buckling loads but the results are still greater than the buckling loads predicted by the deformation theory. Additionally, they found that as the boundary of the cylinders were more restrained, the flow theory failed to predict correctly the buckling loads for cylinders subjected to high values of axial loads even with the use of the effective shear modulus.

Becque (2010) proposed a theory for the inelastic buckling of perfect plates based on a new proposal for the shear stiffness in the flow theory from second order considerations. Becque claimed that the proposed relation between the shear stress increments and the total shear strain at the onset of plastic buckling effectively overcame the plastic buckling paradox for long simply supported plates under axial thrust (Becque, 2010) or for annular plates subjected to pure shear (Becque, 2013). Shamass (2017) assessed the efficiency of Becque’s in reducing the discrepancy in the results between the flow and deformation theories for cylinders subjected to combined external pressure and axial tension with different boundary conditions. It was found that the employment of the shear modulus proposed by Becque (2010) in the flow theory led to a certain reduction in the value of the buckling pressures but not as much as to make them comparable with the predictions from the deformation theory for high values of the axial tensile stress. Moreover, by increasing the level of restraint of the cylinders, the flow theory failed to predict buckling at all. Thus, Shamass et al. (2015b), Shamass (2017) concluded: “it is so clear that the difference in buckling predictions between flow and deformation theory can be only partially attributed to the difference in the shear modulus used for the bifurcation buckling analysis.” However, Moghadam (2015) expressed some concerns about Becque’s approach and noticed that the use of Mohr’s circle to obtain the plastic shear strain variation was questionable, since it implied multiplying the plastic strain variation by small rotations, which led to zero plastic shear strain. Moghadam also added that, in his/her view, the Becque’s plastic shear modulus related the shear stress increment to the shear strain in an arbitrarily rotated reference system, given that the plastic strain increment in the original system did not possess any plastic shear strain components. Furthermore, Moghadam stated that for the derivation of the incremental stress–strain relationship, Becque did not take into account the influence of the stress increment in the short direction of the long simply supported plates on the plastic strain increment in the normal direction, given that biaxial stresses were induced from buckling. Becque (Private communication, 2020) argued that the ratio of the shear stresses and the infinitesimal shear strains during the small rotations provided the finite value of the shear modulus. Since the shear stresses or the transversal bending stresses in the plate are initially infinitesimal, they do not affect the flow rule, and this addresses Moghadam’s comment about the bi-axial stress state. Furthermore, Becque (Private communication, 2020) pointed out that the rotated co-ordinate system is not arbitrary, as claimed by Moghadam, but follows the material as it deforms: buckling problems always require consideration of the deformed state and Becque’s proposed model shows that this should also apply to the application of the flow rule in order to get realistic results. It is a fact that Becque’s model shows a very good correlation with extensive experimental data.

At the time of the present review Becque’s (2010) and Guarracino and Simonelli’s (2017) contributions appear to be the most recent attempts to get to the root of the problem through a comprehensive analysis of all the parameters involved in the constitutive laws.

Considerations on the Initial Imperfections

Following Onat and Drucker (1953); Hutchinson and Budiansky (1976) showed that more accurate predictions could be obtained from the flow theory if extremely small imperfections were taken into account for axially compressed cruciform columns. Neale (1974) estimated the plastic buckling of cylinders subjected to torsion using the flow theory of plasticity in the presence of imperfections and found that the critical torsional stress was reduced by extremely small and unavoidable imperfections, but that it was not sensitive to the magnitude of imperfections.

Cicala (1950) concluded in his approximate analysis of strips that small imperfections in the specimen would reduce the bifurcation load predicted by flow theory to the level of the deformation theory. Hutchinson (1972) investigated the imperfection sensitivity of spherical shells subjected to external pressure in the plastic range. He found that the deformation theory predictions were smaller than those of the flow theory by about 7%. However, once the imperfection amplitude became about 10% of the shell thickness, there were no differences between the flow and deformation theory buckling pressures. This indicated that the imperfection-sensitivity of spherical shells was potentially important in the plastic range. Furthermore, Tuğcu (1991a) investigated the effects of out-of-plane defects of thin rectangular plates under biaxial loading on the plastic buckling and observed that the variation of the buckling stresses was greater for the flow theory than for the deformation theory. However, the imperfection sensitivity in the plastic range is not as severe a problem as it is in the elastic range for shell structures since the plastic buckling of shell structure generally occurs at high thickness-to-radius ratios. Furthermore, Shamass et al. (2014), via an accurate geometrically non-linear finite-element analysis, showed that both the flow and deformation theories displayed low imperfection sensitivity in the case of axially compressed circular shells with high thickness-to-radius ratios, while both theories showed an increase in the imperfection sensitivity for low thickness-to-radius ratios.

On the other hand, a recent research by Guarracino and Simonelli (2017) investigated the torsional buckling of cruciform columns by means of the classical formulations of the flow and deformation theories of plasticity and concluded that “it is not only necessary to consider an imperfect column, as generally suggested in the past, but also to account correctly for the effects of the imperfection up to the point where the limit load is attained. In such manner a very good agreement between the results from the flow theory of plasticity and other analytical and experimental results can be obtained on the basis of classic formulae only.”

Guarracino and Simonelli examined the problem from its roots and derived an enhanced expression for the tangent shear module. Figure 7 illustrates the torsional buckling stresses calculated using the flow theory based on their proposed procedure and the deformation theory of plasticity, together with available experimental results conducted by Hopperstad et al. (1999). It is evident that the proposed procedure achieved results that were in very good agreement with both the deformation theory and the experimental results.

FIGURE 7

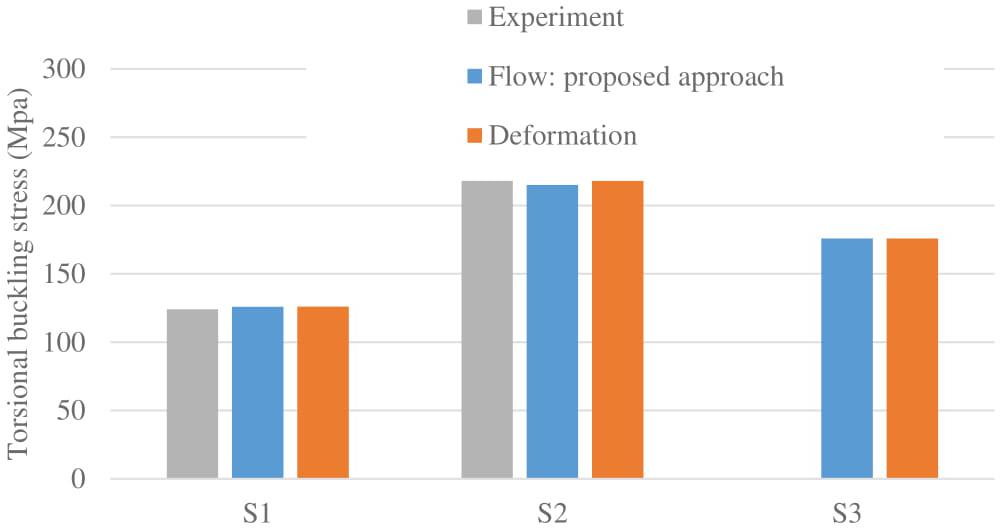
Figure 7. Comparison between the torsional buckling stresses obtained by the plasticity theories and experimental results (with imperfection size 10% of the flange thickness) (Guarracino and Simonelli, 2017).

Considerations on Different Material Constitutive Models

Some researchers attempted to address the paradox by taking into account different formulations of the material constitutive model and its associated factors. Batdorf and Budiansky (1949) stated that it was very possible that both the flow and deformation theories of plasticity were, after all, incorrect. Therefore, they proposed “a theory of plasticity based on the concept of slip for the relationship between stress and strain for initially isotropic materials in the strain hardening range.” Batdorf (1949) developed an entirely new plasticity theory that was neither flow nor deformation type and was based on the concept of slip theory. Sewell (1973) investigated the bifurcation stress using the flow theory with different yield surfaces for a simply supported plate in uniaxial compression. He concluded that the existence of a corner on the yield surface, such as Tresca yield surface, could give origin to a substantial reduction of the bifurcation stress in comparison to that obtained using a smooth yield-surface such as von Mises. The amount of the reduction was about 10–30% and depended on the values of several parameters considered for the problem. However, Hutchinson (1974) pointed out that if the Tresca yield surface was used in the analysis of cruciform columns, the effective shear modulus of the flow theory could not be reduced.

Bardi and Kyriakides (2006) tested stainless steel tubes subjected to axial compression. They reported the experimental critical stresses and strains at the onset of wrinkling, and the number and wavelength of buckling modes. Furthermore, they calculated analytically the same quantities using the flow and deformation theories of plasticity under the assumption of either isotropic or anisotropic material behavior. They concluded that the flow theory over-predicted the critical stresses, strains, and the wavelength of wrinkles while the deformation theory led to critical stresses and strains in good agreement with the test results. The influence of anisotropy on the wavelength of the wrinkles predicted by the flow theory was very significant. Additionally, they observed that when the anisotropy was modeled in flow and deformation theories, the critical stress and strain were hardly affected. On the other hand, Tuğcu (1998) stated that although the evaluation of the material anisotropy was not expected to play a vital role in reducing the flow theory predictions on account of the limited value of buckling strain, the existence of an intrinsically anisotropic material could be an important factor when the shear was involved in a critical buckling mode such as torsion buckling of cylinders or shear buckling of panels. Therefore, accurate representations of the material behavior and test conditions were essential to obtain reliable flow theory predictions.

Considerations on the Transverse Shear Deformation

Ambartsumjan (1963) investigated the inelastic buckling of plates subjected to combined bi-axial compressive and shear loading and recommended taking into account the transverse shear deformation of the plate when using the flow theory of plasticity. Wang et al. (2001) considered the effect of the transverse shear deformation by using the Mindlin thick plate theory in the analytical study of rectangular plates subjected to uniaxial or equi-biaxial loading and circular plates subjected to uniform radial load. Once more, they found that the buckling stresses obtained by the flow theory were larger than those obtained by the deformation theory, particularly for clamped plates. The differences in the buckling results between these two theories increased with the ratio E/σ_y, plate thickness, and the exponent n in the Ramberg–Osgood expression, where E and σ_y are the Elastic modulus and the yield stress of the material.

Considerations on the Deformations in the Pre-bifurcation State

Murphy and Lee (1971) investigated the inelastic buckling behavior of cylindrical shells subjected to axial compressive loads with edge constrains and using a modified flow theory of plasticity based on the material stress history. The nonlinear strain-displacement relationship, initial imperfections, and edge constrains were taken into consideration and their effects were analyzed in the pre- and post-buckling phases. Murphy and Lee (1971) concluded that when a modified flow theory of plasticity was employed with inclusion of edge radial restraints and finite deformation in the pre-buckling phase, the critical stresses were accurate for the case of cylinders subjected to axial compression.

In another paper, Wang and Huang (2009) examined the inelastic buckling of rectangular plates subjected to biaxial loading (with σ₂ = −σ and σ₁ = ξσ, tensile, or compressive load in the perpendicular direction). The authors concluded that the infinitesimal deformation assumption for the strain–displacement relationships used in the governing of differential equations for buckling might possibly be the reason for the large discrepancy in the results predicted by the flow and the deformation theory of plasticity. Therefore, such an assumption should be checked after obtaining the buckling stress results from flow and deformation theories. For the numerical examples considered in their investigation, they found that this assumption was always satisfied when the deformation theory was used, while the assumption was satisfied for the flow theory only for a small range of loading parametersξ. In other words, the critical buckling loads obtained by flow theory were not valid when they were diverted from the deformation theory predictions.

Considerations on the Actual Boundary Conditions

Bushnell (1982) performed numerical investigations using the code BOSOR5 about the end effect of cylindrical shells under axial compressive load. The numerical model included end radial constraints and was based on the flow theory of plasticity. He showed that the end radial constraints essentially erased the differences between the experimental and the theoretical buckling stresses predicted by flow theory.

Gjelsvik and Lin (1976) studied the plastic buckling of plates subjected to biaxial compressive stress together with shear stress along the edges, which represented unavoidable boundary stresses. They found that buckling compressive stresses obtained by the flow theory of plasticity were in excellent agreement with test results. In another paper, Tuğcu (1998) investigated the effect of the axial load, applied in one direction of infinitely long simply supported panels, on the critical shear stress applied in the other direction. He noticed that the buckling shear stresses predicted by the flow theory were more sensitive to axial load than those predicted by the deformation theory. Based on this observation, he suggested that the details of the experimental set-up and boundary conditions, which caused secondary stresses, should be investigated in depth before assessing the reliability of flow theory predictions. However, Damkilde (1985) showed, by means of numerical analysis of cruciform columns subjected to axial compressive stress, that the deformation theory results were considerably lower than those by the flow theory even if the frictional restrain on the loaded edges was considered.

Sensitivity of the Predictions by Different Plasticity Theories

Many studies have been focused on the sensitivity of both the flow and the deformation theory predictions to non-proportional loading, shell geometry, and material parameters. Kadkhodayan and Maarefdoust (2014) investigated the plastic buckling of thin rectangular plates subjected to either uniformly or linearly varying biaxial in-plane loading with different edge conditions. They found that the discrepancies in the buckling results between the flow and deformation theories increased by applying boundary conditions closer to fully clamped plates and increased by increasing the thickness-to-length ratio. Moreover, good agreement between the flow theory and the deformation theory results were found for plates subjected to equi-biaxial loading rather than for plates subjected to uniaxial loading. Durban and Zuckerman (1999) examined analytically the elastic-plastic buckling of rectangular plates subjected to simultaneous biaxial loads (uniform compressive load σ₂ = −σ and tensile or compressive load σ₁ = ξσ in the perpendicular direction, where ξ is the “biaxial loading ratio”). Different thickness ratios, aspect ratios, biaxial loading ratios, and boundary conditions were considered in the analysis. They observed that the compressive plastic buckling stresses predicted by the flow theory were consistently higher than those predicted by the deformation theory. However, the discrepancies in the compressive buckling loads predicted by the two theories reduced with the reduction of transverse tensile load and plate thickness ratio. They found that the flow theory was more sensitive to the stabilizing tensile load than the deformation theory. On the other hand, the deformation theory predictions were more sensitive to the plate thickness ratio than the flow theory ones.

Kosel and Bremec (2004) studied the plastic buckling of an annular circular plate with inner diametera, outer diameter b, and plate thicknesst, subjected to axial in-plane loads on the inner and outer edges. The material model assumed in the analytical analysis was elastic with plastic linear hardening. The slenderness η = b/t and its limitη_pl = (b/t)_pl, the discrepancies in the buckling results predicted by the flow and deformation theory increased by increasing the plastifications (i.e., decreasing the ratio η/η_pl) and the ratio a/b. Moreover, Ore and Durban (1992) analytically investigated the plastic buckling of axially compressed cylindrical shells and observed that the discrepancies in the buckling results by the flow and deformation theories were noticeable only at low values of the strain hardening parameter in the Ramberg–Osgood expression. Blachut et al. (1996) conducted experimental and numerical analyses on various cylinders made from mild-steel and subjected to constant axial tension and increasing external pressure. Using BOSOR5 (Bushnell, 1986), they found that the agreement between the buckling pressures predicted by the flow and the deformation theory were strongly dependent on the length-to-diameter ratio and on the value of the applied axial tension. Good agreement between plastic buckling pressures predicted by the flow theory with those predicted by the deformation theory were noticeable only when the cylinders were rather short and the tensile axial load vanished, or for certain ranges of combined loading for longer cylinders. In all other cases, the flow theory overestimated experimental buckling pressures and predicted unrealistic large plastic strains. In a similar study, Giezen et al. (1991) conducted experiments on tubes made of aluminium alloy 6061-T4 characterized by a length-to-diameter ratio equal to one and subjected to combined axial tension and external pressure. Additionally, they conducted numerical analyses on the same tubes once again using the code BOSOR5. The numerical results showed that the buckling pressures predicted by the flow theory increased with increasing applied tensile load while the test results showed a reduction in buckling pressure with increasing axial tensile load. On the other hand, the buckling pressures predicted by the deformation theory revealed the same trend of the experimental results. However, it significantly under-predicted the buckling pressures observed experimentally for some loading paths. Therefore, Giezen (1988) concluded that neither the flow theory nor the deformation theory could reliably predict the plastic buckling load. Tugcu (1991b) investigated analytically the buckling of cylinders subjected to combined axial load and torque or subjected to combined external pressure and torque. Again, he found that the flow theory was more sensitive to the interactive loading than the deformation theory, although the critical loads predicted by flow theory were smaller than those predicted by the deformation theory in some loading regions.

Effects of the Kinematic Constraints Used in Analytical Treatments

Shamass et al. (2014; 2015a; 2015b; 2017) investigated numerically the plastic buckling of cylindrical shells subjected to axial compressive load (Figure 8A) or to combined external pressure and axial tensile load (Figure 8B). The numerical results were compared with accurate physical test results conducted by Lee (1962) and Batterman (1965) for cylinders under axial compressive load and Blachut et al. (1996) and Giezen et al. (1991) for cylinders subjected to combined actions. In Lee and Batterman’s experiments, the specimens were cylinders made of aluminium alloy 3003-0 and 2024-T4. In the test carried out by Blachut et al. (1996) and Giezen et al. (1991), the specimens were made of mild steel and aluminium alloy 6061-T4. Shamass et al. noticed that the assumed harmonic buckling shapes adopted for the calculation of the plastic buckling stresses and of the corresponding buckling mode resulted in kinematically constraining the buckled shell, causing a stiffer response of the structure and, as a result, an overestimation of the buckling stresses. This assumption was reproduced numerically for axially compressed cylinders with axisymmetric shell elements (SAX1 in ABAQUS) and with imposed kinematic constraints in order to reproduce the same number of half waves predicted by the analytical solution, for both the flow and deformation theories. The dimensions of these cylinders are shown in the Table 2. Figure 9 illustrates some experimental plastic buckling results for cylinders subjected to axial compression and tested by Lee (1962), together with the numerical plastic buckling results obtained using both the flow and deformation theories with and without kinematical constraints. As seen from Figure 9, Shamass et al. (2014), by means of a geometrically non-linear finite element modeling, found that both the flow and deformation theories without kinematic constraints predicted buckling loads with an acceptable level of plastic strains. In fact, the buckling loads calculated by the flow theory were in very good agreement with the test results. On the other hand, the flow theory overestimated the plastic buckling when the kinematic constraints were imposed in the numerical models. They concluded that the reason for the “plastic buckling paradox” seemed to be due to the over-constrained kinematics assumed in many analytical treatments, when a certain harmonic buckling shape was prescribed. This resulted in an overestimation of the buckling load when the flow theory of plasticity was employed, while the deformation theory naturally counterbalanced the excessive constraining and provided results which were much lower that the flow theory ones. On the other hand, the kinematic was free in the finite element analysis.

TABLE 2

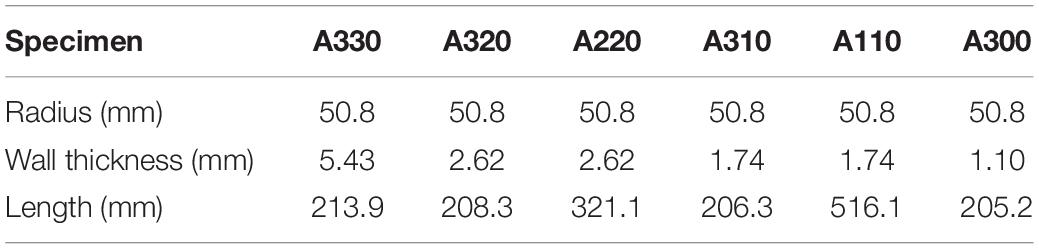
Table 2. Geometry of aluminium alloy 3003-0 cylinderstested by Lee (1962).

FIGURE 8

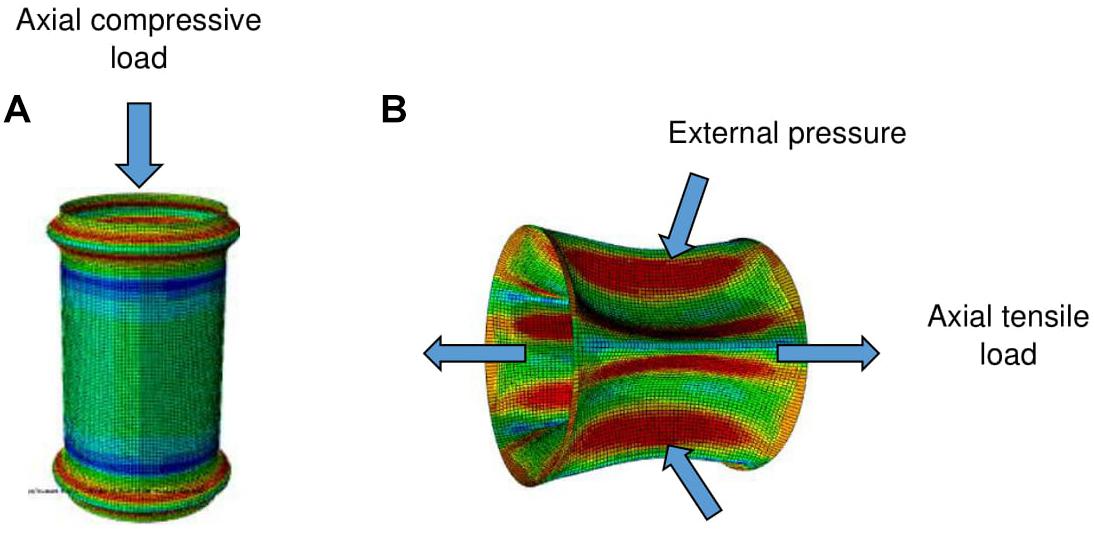
Figure 8. (A) a cylinder subjected to axial compressive load. (B) A cylinder subjected to combined axial tension and external pressure.

FIGURE 9

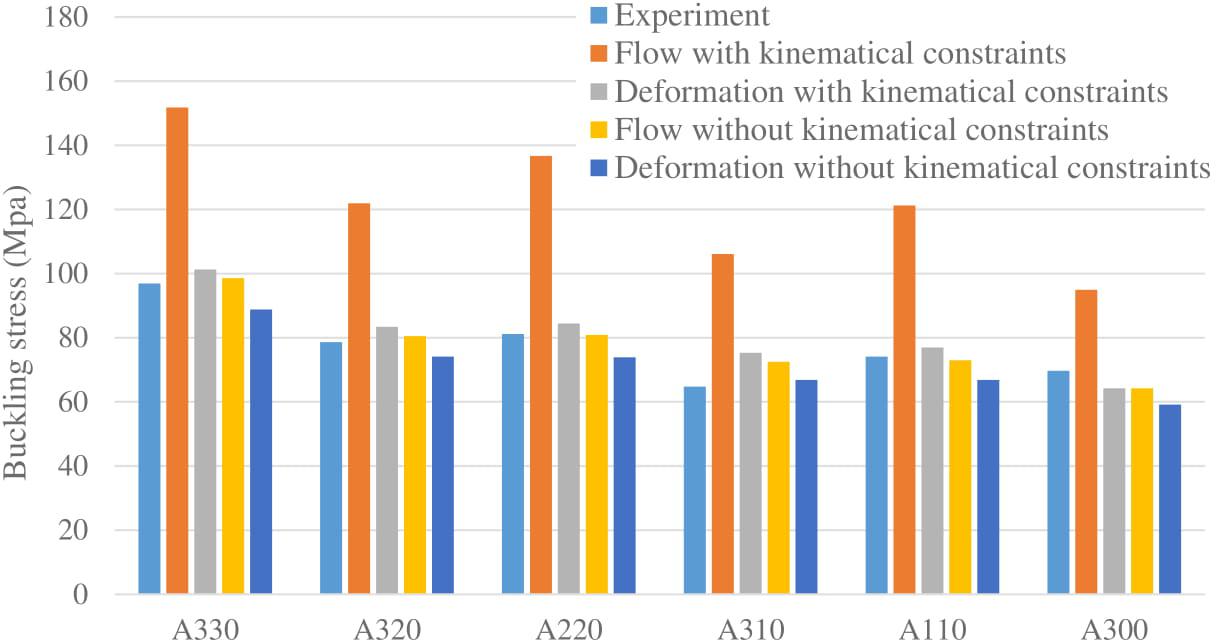
Figure 9. Comparison between the buckling stresses obtained numerically with and without kinematic constraints (Shamass et al., 2014, 2015a, 2015b, 2017).

Overall, the analytical analyses of the elastic-plastic buckling of cylinders subjected to non-proportional loading (i.e., combined external pressure and tensile load) studied by Shamass et al. (2015a) showed that the discrepancies in the analytical plastic buckling pressures predicted from both the flow and deformation theories of plasticity take place when the buckling modes predicted by the plasticity theories do not coincide. This was also noticed by Guarracino and Simonelli (2018), who pointed out that a mode switching phenomenon can also lead to critical loads predicted by the deformation theory higher than those by the flow theory. It was concluded by Guarracino (2019) that “the different approach in modeling the material behavior is capable to generate a mode jumping from the shape of the initial imperfection which may reverse the reported superior reliability of the predictions by the deformation theory of plasticity with respect to the flow theory of plasticity.”

Conclusions

Shell structures are extensively used in many engineering applications and can be found in a variety of natural structures, from geology to biology. As a consequence, the buckling of shells and plates in the elastic-plastic range has received extensive attention by a very large number of researchers over many years. The present review has attempted to comment on the results from several studies on the so called “Plastic Buckling Paradox,” i.e., that the results from the two main plasticity theories used to predict the buckling stress, namely the incremental or flow theory of plasticity and the deformation theory of plasticity, seem to provide quite different results. In fact, the flow theory has been reported to overestimate the buckling loads observed experimentally while the deformation theory provides results more in-line with test results.

Various explanations for the plastic buckling paradox have been proposed in the literature and have been here recalled.

The author’s point of view is that, contrary to the common belief, there is no “Plastic Buckling Paradox.” The flow theory can predict buckling with good accuracy if geometrical and material analyses including imperfections are conducted. The apparent paradox is not due to the limitations of the flow theory, but rather to a number of combined approximations, which have been here reviewed.

Author Contributions

RS conducted the Methodology, Investigation, Writing and analysis.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ambartsumjan, S. A. (1963). On the stability of inelastic plates with consideration of shear deformation. PMM 27, 753–757.

Google Scholar

Bardi, F. C., and Kyriakides, S. (2006). Plastic buckling of circular tubes under axial compression - Part I: experiments. Int. J. Mech. Sci. 48, 830–841.

Google Scholar

Batdorf, S. B. (1949). Theories of plastic buckling. J. Aeronaut. Sci. 16, 405–408.

Google Scholar

Batdorf, S. B., and Budiansky, B. (1949). A mathematical theory of plasticity based on the concept of slip. NACA Tech. Note 1871, 1–36.

Google Scholar

Batterman, S. C. (1965). Plastic buckling of axially compressed cylindrical shells. AIAA J. 3, 316–325.

Google Scholar

Becque, J. (2010). Inelastic plate buckling. J. Eng. Mech. 136, 1123–1130.

Google Scholar

Becque, J. (2013). “Inelastic buckling of annular plates in shear,” in Research and Applications in Structural Engineering, Mechanics and Computation, ed. A. Zingoni (London: CRC Press), 371–372.

Google Scholar

Becque, J. (2020). Private communication. February.

Google Scholar

Blachut, J., Galletly, G. D., and James, S. (1996). On the plastic buckling paradox for cylindrical shells. Proc. Inst. Mech. Eng. Part C 210, 477–488.

Google Scholar

Bushnell, D. (1982). “Plastic buckling,” in Pressure Vessels and Piping: Design Technology – 1982, A Decade of Progress, eds S. Y. Zamrik and D. Dietrich (New York, NY: American Society of Mechanical Engineers), 47–117.

Google Scholar

Bushnell, D. (1986). “BOSOR5 – program for buckling of complex, branched shells of revolution including large deflections, plasticity and creep,” in Structural Analysis Systems – 2, ed. A. Niku-Lari (New York, NY: Pergamon Press), 25–54.

Google Scholar

Cicala, P. (1950). On plastic buckling of a compressed strip. J. Aeronaut. Sci. 17, 378–379.

Google Scholar

Damkilde, L. (1985). Elastic-plastic buckling of a finite length cruciform column. Comput. Struct. 21, 521–528.

Google Scholar

Drucker, D. C. (1949). A discussion of theories of plasticity. J. Aeronaut. Sci. 16, 567–568.

Google Scholar

Duberg, L. E., and Wilder, T. W. (1952). Inelastic Column Behaviour. NACA Technical Report No. 1072. Washington, DC: NACA.

Google Scholar

Durban, D., and Zuckerman, Z. (1999). Elastoplastic buckling of rectangular plates in biaxial compression/tension. Int. J. Mech. Sci. 15, 751–765.

Google Scholar

Gerard, G. (1962). Introduction to Structural Stability Theory. New York, NY: McGraw-Hill.

Google Scholar

Giezen, J. J. (1988). Plastic Buckling of Cylinders under Biaxial Loading. Ph.D. thesis, California Institute of Technology, Pasadena, CA.

Google Scholar

Giezen, J. J., Babcock, C. D., and Singer, J. (1991). Plastic buckling of cylindrical shells under biaxial loading. Exp. Mech. J. 31, 337–343.

Google Scholar

Gjelsvik, A., and Lin, G. S. (1976). Plastic Buckling of Plates with Edge Frictional Shear Effects’ (No. TR-50). New York, NY: Columbia University.

Google Scholar

Guarracino, F. (2007). Considerations on the Numerical Analysis of Initial Post-Buckling Behaviour in Plates and Beams. Thin Walled Struct. 45, 845–848.

Google Scholar

Guarracino, F. (2019). Remarks on the stability analysis of some thin-walled structures in the elastic-plastic range. Thin Walled Struct. 138, 208–214.

Google Scholar

Guarracino, F., and Simonelli, M. G. (2017). The torsional instability of a cruciform column in the plastic range: analysis of an old conundrum. Thin Walled Struct. 113, 273–286.

Google Scholar

Guarracino, F., and Simonelli, M. G. (2018). Numerical evaluation of plastic buckling of short cylinders under combined loading. Int. J. Struct. Stab. Dyn. 18:1850081.

Google Scholar

Guarracino, F., and Walker, A. (2008). Some comments on the numerical analysis of plates and thin-walled structures. Thin Walled Struct. 46, 975–980.

Google Scholar

Hencky, H. Z. (1924). Theorie Plastischer Deformationen und der hierdurch im Material hervorgerufenen Nachspannungen. Z. Angew. Math. Mech. 4, 323–334.

Google Scholar

Hill, R. (1950). The Mathematical Theory of Plasticity. New York, NY: Oxford University Press Inc.

Google Scholar

Hopperstad, O. S., Langseth, M., and Tryland, T. (1999). Ultimate strength of aluminium alloy outstands in compression: experiments and simplified analysis. Thin Walled Struct. 34, 279–294.

Google Scholar

Hutchinson, J., and Budiansky, B. (1976). “Analytical and numerical study of the effects of initial imperfections on the inelastic buckling of a cruciform column,” in Proceedings of the IUTAM Symposium on Buckling of Structures, ed. B. Budiansky (Berlin: Springer), 98–105.

Google Scholar

Hutchinson, J. W. (1972). On the postbuckling behavior of imperfection-sensitive structures in the plastic range. J. Appl. Mec. Trans. ASME 39, 155–162.

Google Scholar

Hutchinson, J. W. (1974). Plastic buckling. Adv. Appl. Mech. 14, 67–144.

Google Scholar

Kadkhodayan, M., and Maarefdoust, M. (2014). Elastic/plastic buckling of isotropic thin plates subjected to uniform and linearly varying in-plane loading using incremental and deformation theories. Aerosp. Sci. Technol. 32, 66–83.

Google Scholar

Kosel, F., and Bremec, B. (2004). Elastoplastic buckling of circular annual plates under uniform in-plane loading. Thin Walled Struct. 2, 101–117.

Google Scholar

Lay, M. G. (1965). Flange local buckling in wide-flange shapes. J. Struct. Div. 91, 95–116.

Google Scholar

Lee, L. (1962). Inelastic buckling of initially imperfect cylindrical shells subjected to axial compression. J. Aerosp. Sci. 29, 87–95.

Google Scholar

Mao, R., and Lu, G. (1999). Plastic buckling of circular cylindrical shells under combined in-plane loads. Int. J. Solids Struct. 38, 741–757.

Google Scholar

Mao, R., and Lu, G. (2002). A study of elastic-plastic buckling of cylindrical shells under torsion. Thin Walled Struct. 40, 1051–1071.

Google Scholar

Mendelson, A. (1968). Plasticity: Theory and Application. New York, NY: Macmillan Company.

Google Scholar

Moghadam, J. S. (2015). Plastic Buckling of Columns and Plats. Ph.D. dissertation, Imperial College, London.

Google Scholar

Murphy, L. M., and Lee, L. H. N. (1971). Inelastic buckling process of axially compressed cylindrical shells subject to edge constraints. Int. J. Solids Struct. 7, 1153–1170.

Google Scholar

Neale, K. W. (1974). A method for the estimation of plastic buckling loads. Int. J. Solids Struct. 10, 217–230.

Google Scholar

Onat, E. T., and Drucker, D. C. (1953). Inelastic instability and incremental theories of plasticity. J. Aeronaut. Sci. 20, 181–186.

Google Scholar

Ore, E., and Durban, D. (1989). Elastoplastic buckling of annular plates in pure shear. J. Appl. Mech. 56, 644–651.

Google Scholar

Ore, E., and Durban, D. (1992). Elastoplastic buckling of axially compressed circular cylindrical shells. Int. J. Mech. Sci. 34, 727–742.

Google Scholar

Sewell, M. J. (1973). A yield-surface corner lowers the buckling stress of an elastic-plastic plate under compression. J. Mech. Phys. Solids 21, 19–45.

Google Scholar

Shamass, R. (2017). Numerical and Analytical Investigation into the Plastic Buckling Paradox for Metal Cylinders. Ph.D. dissertation, Brunel University London, London.

Google Scholar

Shamass, R., Alfano, G., and Guarracino, F. (2014). A numerical investigation into the plastic buckling paradox for circular cylindrical shells under axial compression. Eng. Struct. 75, 429–447.

Google Scholar

Shamass, R., Alfano, G., and Guarracino, F. (2015a). An analytical insight into the buckling paradox for circular cylindrical shells under axial and lateral loading. Math. Problems Eng. 2015:514267. doi: 10.1155/2015/514267

CrossRef Full Text | Google Scholar

Shamass, R., Alfano, G., and Guarracino, F. (2015b). An investigation into the plastic buckling paradox for circular cylindrical shells under non-proportional loading. Thin Walled Struct. 95, 347–362.

Google Scholar

Shamass, R., Alfano, G., and Guarracino, F. (2017). On elastoplastic buckling analysis of cylinders under nonproportional loading by differential quadrature method. Int. J. Struct. Stab. Dyn. 17:1750072.

Google Scholar

Shanley, F. R. (1947). Inelastic column theory. J. Aeronaut. Sci. 14, 261–267.

Google Scholar

Stowell, E. (1948). A Uni?ed Theory of Plastic Buckling of Columns and Plates. NACA Technical Report No. 1556. Washington, DC: NACA.

Google Scholar

Teng, J. G. (1996). Buckling of thin shells: recent advances and trends. Appl. Mech. Rev. 49, 263–274.

Google Scholar

Teng, J. G., and Rotter, J. M. (1989). Non-symmetric bifurcation of geometrically nonlinear elastic-plastic axisymmetric shells under combined loads including torsion. Comput. Struct. 32, 453–475.

Google Scholar

Tuğcu, P. (1991a). Plate buckling in the plastic range. Int. J. Mech. Sci. 33, 1–11. doi: 10.1016/j.diabres.2012.04.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Tugcu, P. (1991b). On plastic buckling predictions. Int. J. Mech. Sci. 33, 529–539.

Google Scholar

Tuğcu, P. (1998). Effect of axial loading on plastic buckling of long strips under pure shear. Comput. Struct. 66, 155–161.

Google Scholar

Wang, C. M., Xiang, Y., and Chakrabarty, J. (2001). Elastic/plastic buckling of thick plates. Int. J. Solids Struct. 38, 8617–8640.

Google Scholar

Wang, X., and Huang, J. (2009). Elastoplastic buckling analyses of rectangular plates under biaxial loadings by the differential quadrature method. Thin Walled Struct. 47, 14–20.

Google Scholar

Yun, H., and Kyriakides, S. (1990). On the beam and shell modes of buckling of buried pipelines. Soil Dyn. Earthq. Eng. 9, 179–193.

Google Scholar

Zhang, W., and Wang, X. (2011). Elastoplastic buckling analysis of thick rectangular plates by using the differential quadrature method. Comput. Math. Appl. 61, 44–61.

Google Scholar

Zhang, Y., Huang, H., and Han, Q. (2015). Buckling of elastoplastic functionally graded cylindrical shells under combined compression and pressure. Compos. Part B Eng. 69, 120–126.

Google Scholar