- Department of Architecture, Faculty of Engineering Science, KU Leuven, Leuven, Belgium
Whereas reticulated domes (i.e., domes composed of bars) are very material-efficient in general, the geodesic dome is claimed to be superior according to its patent holder, Richard Buckminster Fuller. Recent studies on the optimal design of reticulated domes do not allow a direct comparison between the geodesic dome and other dome types because the test cases are not subjected to the same loads. This paper aims to determine which type of reticulated dome is superior in terms of material efficiency by comparing the minimized weight of different dome types, taking into account stress and buckling constraints. The study includes hemispherical Schwedler, Kiewitt, and geodesic domes with a diameter of 16m, and a gravity load of 2kNm−2. Full enumeration is used to optimize the discrete variables (number of rings, subdivisions along each ring, …), while a gradient-based algorithm is used for the continuous variables (member sections). The results show that the claim of uniform stressing in a geodesic dome is legitimate: if all members are assigned the same size, a geodesic dome is generally more evenly stressed and up to 28% lighter than other dome types of similar size. However, if all members are sized individually, the Schwedler dome is the lightest.
1. Introduction
Reticulated domes (i.e., domes composed of bars) with various patterns (Figure 1) have been built to span large surfaces, demonstrating their material efficiency. The geodesic dome is often assumed to be superior because its patent holder, Richard Buckminster Fuller, claimed that the resulting framework will be characterized by more uniform stressing of the individual members than is possible with any construction heretofore known (US patent 2,682,235A). This -unverified- claim implies that it is a fully stressed design, which is a measure for optimal material use under certain conditions (Patnaik and Hopkins, 1998).
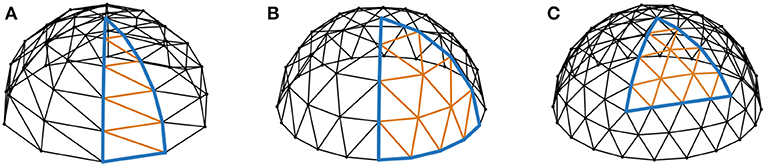
Figure 1. Three commonly built dome types are compared in this paper: (A) the Schwedler dome, (B) the Kiewitt dome, (C) the geodesic dome. Each type is described parametrically as a repetition of one subdivided module, which is highlighted in the figure.
In the past decades, several authors have studied the optimal design of reticulated domes: Liu and Ye (2014) applied a metaheuristic algorithm (GASA) to optimize the stiffness distribution of hemispherical domes subjected to a seismic load such that the domes would not collapse due to material failure without clear prior warnings. Saka (2007a,b) minimized the weight of a geodesic dome under a vertical point load, Kaveh and Talatahari addressed the optimization of Kiewitt (Kaveh and Talatahari, 2011), Schwedler and ribbed domes (Kaveh and Talatahari, 2010a), Kaveh and Razaei optimized different types of single (Kaveh and Razaei, 2016a,b) and double layer (Kaveh and Razaei, 2018) domes, both Çarbas and Saka (2012) as well as Kaveh and Talatahari (2010b) performed a comparative study of different types of reticulated domes. However, these studies are not fully conclusive because the different types of dome were not subjected to the same loads. Moreover, often unrealistic loads were applied: distributed loads were not considered in most studies, although they are the predominant load for reticulated domes.
This paper aims to determine which type of reticulated dome is superior through a comparative study of the minimized weight of Kiewitt, Schwedler and geodesic domes with a span of 16m and a gravity load of 2kNm−2. The number of rings, subdivisions along each ring, and the sections of all bars are varied to minimize the total weight of each variant, taking into account stress and buckling constraints. Full enumeration is used for the discrete variables (number of rings, subdivisions along each ring, …), while a gradient-based algorithm is used for the continuous variables (member sections).
This paper is structured as follows: in the second section, the structural models are discussed, specifying which topologies, boundary conditions and loads are considered. In the third section, the optimization problem is formulated. In the fourth section, the result are presented, followed by some concluding remarks.
2. Structural Models
The test case structures in this comparative study are all hemispherical domes with a diameter of 16m. The domes consist of hollow circular bars with a variable outer diameter de and a wall thickness equal to f × de, where f is a fixed ratio of 0.04. The material is modeled as steel with an elastic modulus E = 210GPa, a yield stress fy = 235MPa, and a density ρ = 7, 850kgm−3.
2.1. Layout
Three common dome types are compared in this paper: the Schwedler, Kiewitt and geodesic dome.
2.1.1. Schwedler Dome
The pattern of a Schwedler dome is characterized by meridional ribs and circumferential rings, which are braced by diagonal bars (Figure 1A). Consequently, the pattern is described by two subdivision frequencies: sm determines the number of subdivisions along the meridional ribs, and hence the number of horizontal rings, and sc determines the number of segments along each circumferential ring. Figure 1A shows a Schwedler dome with subdivision frequencies sm = 5 and sc = 10, highlighting one segment.
2.1.2. Kiewitt Dome
The pattern of a Kiewitt dome consists of a series of subdivided triangles along the circumferential direction, which have a common vertex at the crown of the dome (Figure 1B). The pattern is therefore also characterized by two subdivision frequencies: sc determines the number of triangles along the circumferential direction, and st determines the number of subdivisions along each edge of its triangles. Figure 1B shows a Kiewitt dome with subdivision frequencies sc = 5 and st = 4, and highlights one of the triangles that are repeated along its circumference.
2.1.3. Geodesic Dome
The pattern of a geodesic dome is generated by subdividing the faces of a regular polyhedron, and projecting the subdivided polyhedron onto the surface of its circumscribed sphere (Figure 1C). The polyhedron that was used in this study is an icosahedron (a regular polyhedron with 20 triangular faces), as was the case in the aforementioned patent of Richard Buckminster Fuller. This pattern is characterized by only one subdivision frequency st, which determines the number of subdivisions along each edge of the triangular faces. Figure 1C shows a geodesic dome with a subdivision frequency st of 4, highlighting one of its original triangular faces.
2.2. Boundary Conditions
The boundary conditions simulate common support conditions from building practice: the domes are supported by pinned supports along their perimeter. Hence, all translations at the base of the domes are restricted (Figure 2).
2.3. Loading
All loads acting on the domes are combined into a single gravity load of 2kNm−2, measured per unit area of the triangulated surface of the domes (Figure 3). To allocate this distributed load to the nodes, triangular shell elements with zero stiffness are defined along the surface of the domes. The shape functions of these shell elements are then used to determine equivalent nodal loads (Bathe, 1996).
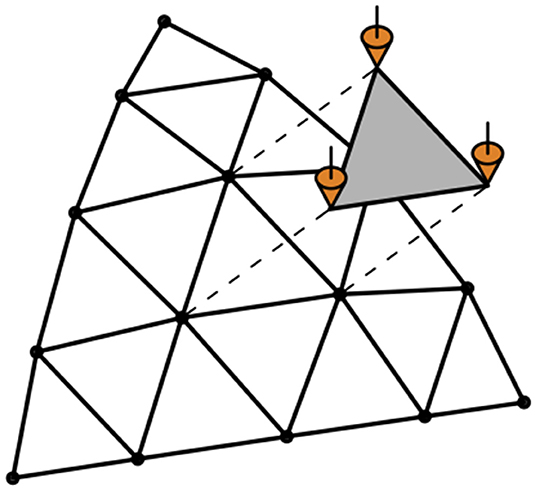
Figure 3. A gravity load of 2kNm−2 is assigned to the nodes using the shape functions of triangular shell elements.
3. Methodology
To determine which dome type is superior in terms of material efficiency, the minimized weight of each variant is compared for various subdivision frequencies. Full enumeration is used to assess all subdivision frequencies within a realistic range, whereas a gradient-based algorithm is used to identify the lightest member sections, given stress and buckling constraints. The optimization problem consists of finding the member sizes that minimize the total weight W of the structure, while satisfying stress and buckling constraints. As the domes consist of circular bars, the diameters de of the bars serve as design variables. These diameters are treated as continuous variables and can have any value within a predefined range. This range is limited by a lower bound dmin to prevent numerical instabilities (singular or ill-conditioned stiffness matrices), and an upper bound dmax to ensure that the results are realistic. The buckling constraints prescribe that the axial force Ne in each member should not exceed the critical Euler bucking load , while the stress constraints limit the stresses σe to an upper and lower limit value, σmax and σmin, respectively. The limit values considered here are equal to the yield stress (235MPa), divided by a safety coefficient of 1.15. The optimization problem is formulated as follows:
The optimization problem is implemented in MATLAB and solved using the Interior Point method (IP) for problems where all members are restricted to have the same size, and Sequential Quadratic Programming (SQP) for problems where different member sizes are considered, as clarified below. Both IP and SQP are gradient-based solvers that are available in the MATLAB toolbox Fmincon. The solvers require the sensitivities, the derivatives of the objective and constraint functions, to efficiently update the design variables at each iteration of the optimization process. Analytical expressions are obtained for all sensitivities to exclude truncation errors and other types of error commonly associated with numerical and semi-analytical methods (Barthelemy and Haftka, 1988). The sensitivities have been validated by comparing the analytical expressions to a finite difference approximation for a representative test case.
4. Results
All results were generated using the default values for the parameters of the optimization algorithm, except for the constraint tolerance and the maximum number of iterations. The latter two parameters were set to 10−10 and 50, respectively, to limit the overall computation time without affecting the results. In the initial structure, all bars have an outer diameter of 50 mm, although the exact value of this starting point has no appreciable effect on the results.
4.1. Single Bar Sections
In this subsection, the case is considered where all members of a dome are required to have the same size. The optimized designs obtained for the dome configurations from Figure 1 are shown in Figure 4, together with the normal forces acting in all their members. Due to the restriction that all bars must have the same section, all members are assigned the size of the largest element, i.e., the bar with the highest buckling or yield load, as is clearly visible in Figure 4. Consequently, domes with a uniform distribution of forces are less affected by this constraint than domes with a non-uniform force distribution.
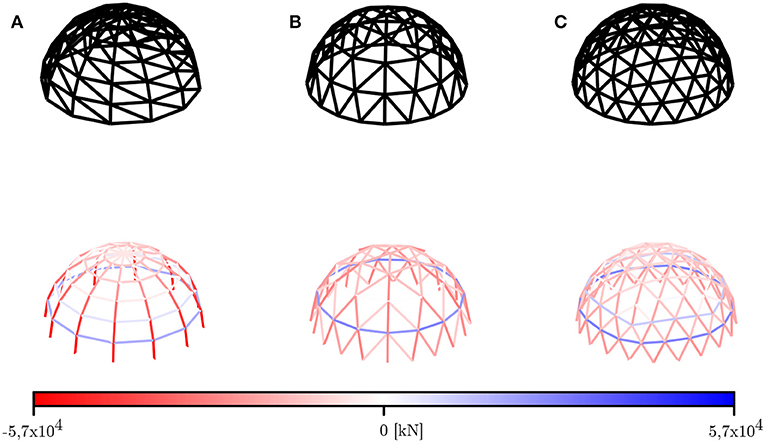
Figure 4. Optimized design (top) and member forces (bottom) of (A) the Schwedler dome, (B) the Kiewitt dome, and (C) the geodesic dome if all members are restricted to have the same size. Compressive member forces are shown in red, tensile member forces in blue.
As Figure 4 illustrates, the internal forces of the optimized structures allow for a clear distinction in two groups: structures with an orthogonal grid like the Schwedler dome, and structures with a three-way grid like the Kiewitt and geodesic dome. The orthogonal grid of meridional and circumferential bars of a Schwedler dome resembles the principal stress orientations in a continuous dome, and the forces act accordingly: the meridional ribs experience a compressive force that increases from crown to base, while the circumferential rings are under compression near the top, and in tension at the base (Figure 4A). The Kiewitt and geodesic dome have a three-way grid pattern, which results in a more complex and uniform distribution of forces. The highest compressive and tensile member forces in the Kiewitt and geodesic domes are of similar magnitude, whereas the highest compressive member forces in a Schwedler dome are up to 3 times as high as the highest tensile member forces. This supports the claim of uniform stressing stated by Richard Buckminster Fuller.
Next, a large number of domes with different subdivision frequencies is considered. Figure 5 shows the minimized weight of each dome configuration as a function of the total bar length of the domes. The total bar length of a dome is obtained by adding the lengths of all its members. The weight of all dome types generally decreases for an increasing total bar length, which corresponds to more elements and thus higher subdivision frequencies. A higher number of elements will reduce the buckling length of each member, hence the improvement in performance. For almost all subdivision frequencies, the Kiewitt and geodesic domes perform best because their internal forces are more uniform than those in a Schwedler dome (Figure 4). Moreover, under a strictly vertical load, the diagonal members of a Schwedler dome are redundant in the sense that they carry no internal forces. Hence, by assigning the same section to the whole structure, these elements contribute significantly to the overall structural weight, without providing any structural benefit. Whereas, Figure 5 only shows the minimized weight for domes with a radius of 8m, similar results have been obtained for domes with different radii.
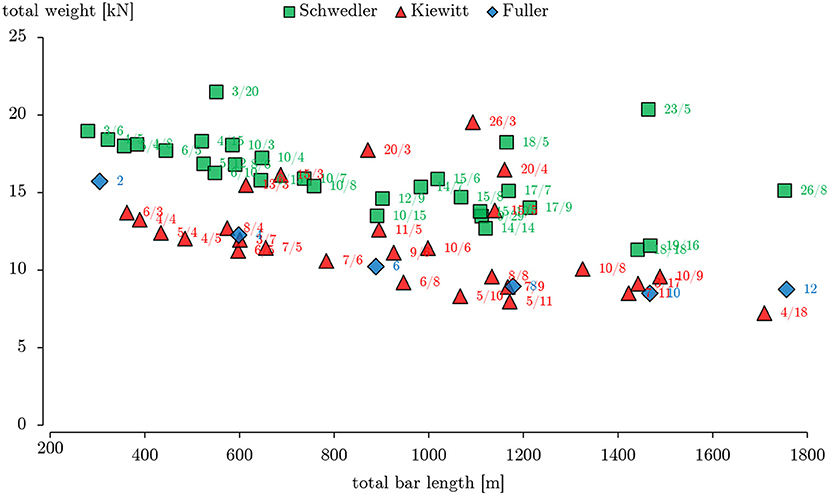
Figure 5. Minimized weight of Schwedler, Kiewitt, and geodesic domes if all their members are restricted to have the same cross-sectional size.
4.2. Variable Bar Sections
In this subsection, the case is considered where the diameter of each member is allowed to vary independently. Figure 6 shows the optimized designs for the same dome configurations that were shown in Figures 1, 4. The Schwedler dome has a very distinct pattern in which the meridional ribs increase in size from crown to base, and the circumferential bars have the largest sections near the crown and base. Elements that carry small member forces, such as the diagonal bars, have significantly smaller sizes. Contrarily, the Kiewitt and geodesic dome have a more uniform layout and distribution of forces due to their three-way grid pattern, as discussed above. A comparison of the layout and the member forces indicates that the sizing of each member is proportionate to the internal forces present in that member, as should be expected.
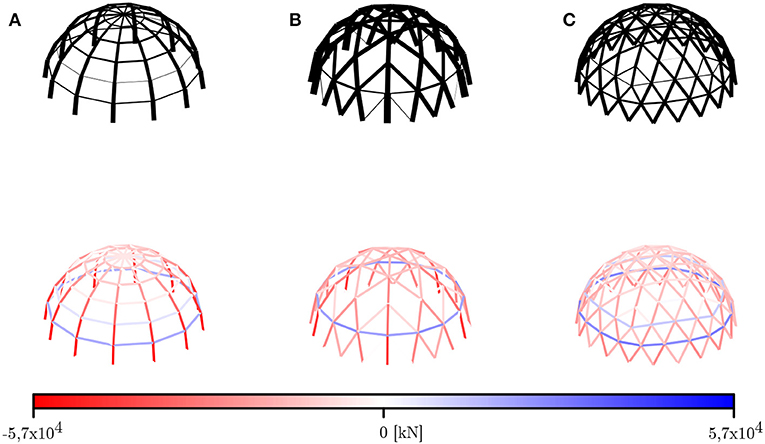
Figure 6. Optimized design (top) and member forces (bottom) of (A) the Schwedler dome, (B) the Kiewitt dome, and (C) the geodesic dome if each member is sized individually. Compressive member forces are shown in red, tensile member forces in blue.
Figure 7 shows the minimized weight of each dome configuration as a function of the total bar length of the domes. The Schwedler dome now performs significantly better than the two other dome types. However, Schwedler and Kiewitt domes with a low meridional/triangular subdivision frequency perform poorly, even if the circumferential subdivision frequency is high. Such domes have fewer circumferential rings, and thus longer meridional bars, which makes them susceptible to buckling. Similar results have been obtained for domes with different radii, as was the case for the single bar problem described above.
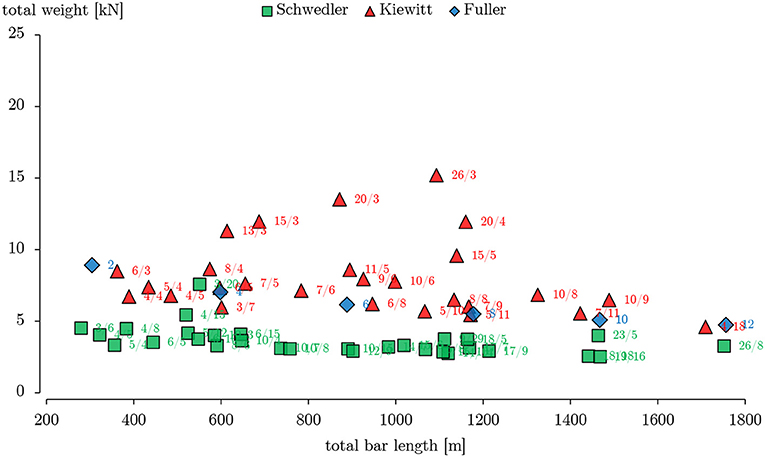
Figure 7. Minimized weight of Schwedler, Kiewitt, and geodesic domes if each member is sized individually.
5. Conclusion
In his patent, Richard Buckminster Fuller claimed that a geodesic dome will be characterized by more uniform stressing of the individual members than is possible with any construction heretofore known (US patent 2,682,235A). This claim suggests that the geodesic dome is a fully stressed design, which is a measure for optimal material-efficiency under certain conditions.
This paper verified which type of reticulated dome is the most material-efficient through a comparative study of the minimized weight of hemispherical Kiewitt, Schwedler and geodesic domes with a span of 16m and a gravity load of 2kNm−2. The number of rings, subdivisions along each ring, and the sections of all bars were varied to minimize the total weight of each variant, taking into account stress and buckling constraints. Full enumeration was used for the discrete variables (number of rings, subdivisions along each ring, …), while a gradient-based algorithm was used for the continuous variables (member sections).
The results support the claim of uniform stressing in a geodesic dome: if all members are assigned the same size, a geodesic dome is more evenly stressed and generally lighter than other dome types of similar size. However, if all members are sized individually, a Schwedler dome performs significantly better because its orthogonal grid resembles the principal stress orientations in a continuous dome, resulting in an efficient transfer of forces to the supports. While these results were shown for domes with a radius of 8m, the same conclusions are valid for any other choice of radius.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
WG and MS supervised CM and TR, who implemented the first version of the computer algorithm based on a toolbox developed by MS and coworkers. CM and TR then gathered the data and wrote a report on the data. WG reassessed the data, generated all the relevant output and wrote the manuscript. MS conceived the project, supervised its execution, and commented the written manuscript.
Funding
WG was a doctoral fellow of the Research Foundation Flanders (FWO) (grant number 11D7118N). The financial support was gratefully acknowledged.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Barthelemy, F. B., and Haftka, R. T. (1988). Accuracy analysis of the semi-analytical method for shape sensitivity calculation. Mech. Based Des. Struct. Mach. 18, 407–432. doi: 10.2514/6.1988-2284
Çarbas, S., and Saka, M. P. (2012). Optimum topology design of various geometrically nonlinear latticed domes using improved harmony search method. Struct. Multidiscipl. Optimiz. 45, 377–399. doi: 10.1007/s00158-011-0675-2
Kaveh, A., and Razaei, M. (2016a). Topology and geometry optimization of different types of domes using ECBO. Sci. Iran. Trans. Civil Eng. 1, 1–25. doi: 10.12989/acd.2016.1.1.001
Kaveh, A., and Razaei, M. (2016b). Topology and geometry optimization of single-layer domes utilizing CBO and ECBO. Sci. Iran. Trans. Civil Eng. 23, 535–547. doi: 10.24200/sci.2016.2137
Kaveh, A., and Razaei, M. (2018). Optimal design of double-layer domes considering different mechanical systems via ECBO. Iran. J. Sci. Technol. Trans. Civil Eng. 42, 333–344. doi: 10.1007/s40996-018-0123-2
Kaveh, A., and Talatahari, S. (2010a). Optimal design of Schwedler and ribbed domes via hybrid Big Bang Big Crunch algorithm. J. Construct. Steel Res. 66, 412–419. doi: 10.1016/j.jcsr.2009.10.013
Kaveh, A., and Talatahari, S. (2010b). Optimal design of single layer domes using meta-heuristic algorithms; a comparative study. Int. J. Space Struct. 25, 217–227. doi: 10.1260/0266-3511.25.4.217
Kaveh, A., and Talatahari, S. (2011). Geometry and topology optimization of geodesic domes using charged system search. Struct. Multidiscipl. Optimiz. 43, 215–229. doi: 10.1007/s00158-010-0566-y
Liu, W., and Ye, J. (2014). Collapse optimization for domes under earthquake using a genetic simulated annealing algorithm. J. Construct. Steel Res. 97, 59–68. doi: 10.1016/j.jcsr.2014.01.015
Patnaik, S. N., and Hopkins, D. A. (1998). Optimality of a fully stressed design. Comput. Methods Appl. Mech. Eng. 165, 215–221. doi: 10.1016/S0045-7825(98)00041-3
Saka, M. (2007a). Optimum geometry design of geodesic domes using harmony search algorithm. Comput. Struct. 10, 595–606. doi: 10.1260/136943307783571445
Keywords: reticulated domes, structural optimization, Schwedler dome, Kiewitt dome, geodesic dome, material efficiency
Citation: Gythiel W, Mommeyer C, Raymaekers T and Schevenels M (2020) A Comparative Study of the Structural Performance of Different Types of Reticulated Dome Subjected to Distributed Loads. Front. Built Environ. 6:56. doi: 10.3389/fbuil.2020.00056
Received: 13 December 2019; Accepted: 07 April 2020;
Published: 22 May 2020.
Edited by:
Vagelis Plevris, OsloMet-Oslo Metropolitan University, NorwayReviewed by:
Francesco Tornabene, University of Salento, ItalyMichele Betti, University of Florence, Italy
Copyright © 2020 Gythiel, Mommeyer, Raymaekers and Schevenels. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Willem Gythiel, d2lsbGVtLmd5dGhpZWxAa3VsZXV2ZW4uYmU=
 Willem Gythiel
Willem Gythiel Christiaan Mommeyer
Christiaan Mommeyer Mattias Schevenels
Mattias Schevenels