General Dynamic Collapse Criterion for Elastic–Plastic Structures Under Double Impulse as Substitute of Near-Fault Ground Motion

Introduction

The dynamic collapse of structures is of permanent interest in the field of structural and earthquake engineering and applied mechanics. Historically, many significant works have been conducted (Jennings and Husid, 1968; Sun et al., 1973; Tanabashi et al., 1973; Bertero et al., 1978; Takizawa and Jennings, 1980; Bernal, 1987, 1998; Nakajima et al., 1990; Ger et al., 1993; Challa and Hall, 1994; Hall, 1998; Hjelmstad and Williamson, 1998; Uetani and Tagawa, 1998; Araki and Hjelmstad, 2000; Sasani and Bertero, 2000; Ibarra and Krawinkler, 2005; Adam and Jager, 2012). While earthquake and structural engineering made clear its significance in the real world, e.g., safety check of structures and infrastructures, applied mechanics contributed to the theoretical advancement in this field (Herrmann, 1965; Ishida and Morisako, 1985; Maier and Perego, 1992; Araki and Hjelmstad, 2000; Williamson and Hjelmstad, 2001).

It seems that the first theoretical achievement on collapse of structures subjected to earthquake ground motions was made by Jennings and Husid (1968). They dealt with a single-degree-of-freedom (SDOF) system with an elastic–plastic spring and demonstrated that the P-delta effect makes the natural period of the structure longer. Sun et al. (1973) focused on the free vibration of the SDOF system subjected to an initial impact and made clear the stability or collapse boundary. Extension to multi-degree-of-freedom (MDOF) systems has also been attempted (Takizawa and Jennings, 1980; Nakajima et al., 1990).

The tangent stiffness has also attracted some researchers in the investigation of dynamic response of elastic–plastic structures in view of instability. If the tangent stiffness goes into the negative range, residual displacements are induced and accelerated. In addition, there were some discussions that a negative eigenvalue of the tangent stiffness matrix is strongly related to either the accumulation of deformation (Uetani and Tagawa, 1998) or the localization of deformation (Maier and Perego, 1992). Dynamic collapse behaviors and responses of actual and realistic frame models have been investigated by some researchers (Ger et al., 1993; Challa and Hall, 1994; Hall, 1998; Sivaselvan et al., 2009). Through such investigations, various effects, such as non-linear geometric effect, non-linear material behavior, and spread of the plastic zone, were incorporated in the numerical methods.

However, it does not seem that a simple dynamic collapse criterion has been proposed even for a rather simple input except the recent work (Kojima and Takewaki, 2016b). In the paper of Kojima and Takewaki (2016b), a simple closed-form dynamic collapse criterion has been proposed for the double impulse as a simplification of the near-fault ground motion by taking full advantage of the energy balance law. They focused on the non-linear resonant situation (Drenick, 1970; Takewaki, 2002; Moustafa et al., 2010) and showed that several collapse patterns exist.

The effects of near-fault ground motions on structural response have been studied extensively (Bertero et al., 1978; Hall et al., 1995; Sasani and Bertero, 2000; Alavi and Krawinkler, 2004; Makris and Black, 2004; Mavroeidis et al., 2004; Kalkan and Kunnath, 2006; Xu et al., 2007; Rupakhety and Sigbjörnsson, 2011; Yamamoto et al., 2011; Jarernprasert et al., 2013; Minami and Hayashi, 2013; Khaloo et al., 2015; Vafaei and Eskandari, 2015). These many investigations classified the input characteristics into two ones, i.e., the fling-step input and the forward-directivity input (Mavroeidis and Papageorgiou, 2003; Bray and Rodriguez-Marek, 2004; Kalkan and Kunnath, 2006; Mukhopadhyay and Gupta, 2013a,b; Zhai et al., 2013; Hayden et al., 2014; Yang and Zhou, 2015).

While the inelastic earthquake responses were analyzed for the steady-state response to a harmonic input or the non-stationary response to a simple sinusoidal input in the 1960s−1970s (Caughey, 1960a,b; Iwan, 1961, 1965a,b; Kojima and Takewaki, 2015a,c, 2016a,b) developed a completely different innovative approach to the peak elastic–plastic response using an energy balance law without solving directly the equations of motion. Furthermore, the resonant and overturning phenomena have been investigated from various viewpoints (Chatzis and Smyth, 2012; Makris and Vassiliou, 2013; Casapulla, 2015; Nabeshima et al., 2016; Casapulla and Maione, 2017).

In this paper, a dynamic collapse criterion for elastic–plastic structures under near-fault ground motions is derived analytically by approximately transforming near-fault ground motions into a double impulse and using an energy balance law. A negative post-yield stiffness is introduced to treat the P-delta effect in the single-degree-of-freedom (SDOF) model. The principal part of fling-step near-fault ground motions is modeled by a one-cycle sine wave and then a double impulse. The use of the double impulse enables the efficient use of the energy approach in the derivation of explicit expressions of a complicated elastic–plastic response of structures with negative post-yield stiffness. In contrast to the previous work (Kojima and Takewaki, 2016b) for the resonant critical case, a general collapse criterion is provided for the velocity amplitude and the frequency of the double impulse. It is significant that no iteration is needed in the derivation of the dynamic collapse criterion except the solution of transcendental equations. It is shown that discussions on several patterns of dynamic collapse behaviors introduced in the previous critical case are useful for deriving a boundary between the collapse and the non-collapse in the plane of the input velocity and the input frequency. The most important point to be remarked is that the critical state (Kojima and Takewaki, 2016b) corresponding to the non-linear resonance does not necessarily provide the minimum input velocity level with respect to arbitrary impulse timing. The validity of the proposed dynamic collapse criterion is examined by the numerical response analysis for structures under double impulses with collapse or non-collapse parameters.

There exist two major advantages of the proposed method against the method using time-history response analysis: (1) if the collapse limit figure is prepared, structural designers can judge the state of collapse or non-collapse at once without time-history response analysis and know the safety factor (both for velocity level and input frequency) for the collapse without many time-history response analyses, and (2) while time-history response analysis of the structural model with negative post-yield stiffness exhibits the response results sensitive to the time increment of the numerical integration, the proposed method does not have such drawback (transcendental equation can be solved stably). Furthermore, since the proposed collapse limit figure is drawn in a normalized form with respect to input velocity level and input frequency, it can be used for various combinations of structural models and input properties.

Double-Impulse Input

As explained in the previous papers (Kojima and Takewaki, 2015a,b; Kojima et al., 2015), two types are distinctive in near-fault ground motions. The fault-parallel fling-step input can be expressed by a one-cycle sinusoidal wave (Mavroeidis and Papageorgiou, 2003; Kalkan and Kunnath, 2006) and the fault-normal forward-directivity input can be represented by three sinusoidal wavelets (see Figure 1). The fling step results from the permanent displacement of the ground induced by the fault dislocation and the forward directivity effect can be explained by the relation of the movement of the rupture front with the site. In this paper, a double impulse is used following the references (Kojima and Takewaki, 2015a, 2016a; Kojima et al., 2015). The double impulse enables the derivation of a straightforward expression of the elastic–plastic responses based on an energy approach by taking advantage of the properties of free vibrations. Another advantage of the double impulse is the ease of the derivation of the critical resonant timing of impulses which is not possible for the sinusoidal and other inputs without a repetitive procedure. While most of the conventional methods (Caughey, 1960a,b; Iwan, 1961) use the equivalent linearization techniques for the structural model under the original unchanged input, the method using the double impulse (Kojima and Takewaki, 2015a,b) employs the transformation of the input for the unchanged structural model. This property leads to an advantageous feature that the method using the double impulse is appropriate even for large plastic deformation.

FIGURE 1

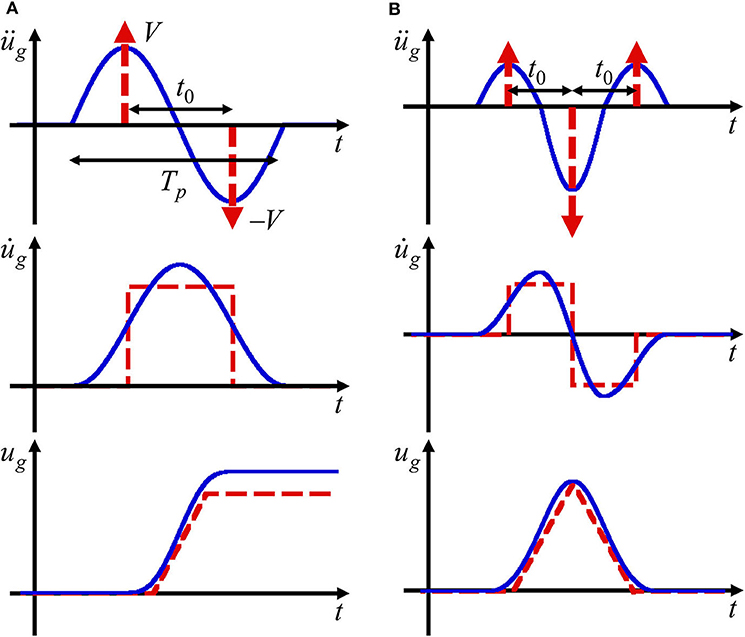
Figure 1. Transformation of acceleration wavelets into a series of impulses. (A) Fling-step input (blue) and double impulse (red). (B) Forward-directivity input (blue) and triple impulse (red) (Kojima and Takewaki, 2016b).

Consider a simplified ground acceleration ü_g(t) as shown in Figure 1A (Kojima and Takewaki, 2015a) which is expressed by

$\begin{array}{ll}{\ddot{u}}_g(t)=V\delta (t)-V\delta (t-t_0)& (1)\end{array}$

V is the velocity amplitude in both positive and negative directions, and t₀ is the time interval of two impulses. The time derivative is denoted by an over-dot. Figure 1A also illustrates the comparison with the corresponding one-cycle sinusoidal wave. For reference, the velocity and displacement of both inputs are plotted in Figures 1A,B indicates the triple impulse as a substitute of a forward-directivity input. Good agreement can be observed even in the form of velocity and displacement. However, the correspondence in the response should be discussed carefully (see Kojima and Takewaki, 2016a).

The Fourier transform of the acceleration ü_g(t) of the double impulse can be derived as,

$\begin{array}{ll}{\ddot{U}}_g(\omega )={\displaystyle {\int }_{-\infty }^{\infty }\left\{V\delta \left(t\right)-V\delta \left(t-t_0\right)\right\}{e}^{-\text{i}\omega t}}dt\text{=}V\left(1-e^{-\text{i}\omega t_0}\right)& (2)\end{array}$

Previous Work on Collapse Limit for Non-linear Resonant Input

Kojima and Takewaki (2016b) treated the case of non-linear resonant input to derive the collapse limit of a bilinear hysteretic SDOF model with negative second slope under the double impulse. The terminology “nonlinear resonant input” in this paper means the case where the non-linear response of the SDOF model attains the maximum with respect to the interval of two impulses of the double impulse. When the restoring-force in the second stiffness range becomes zero, the model collapses. This is because the model cannot sustain the external force at this stage (Kojima and Takewaki, 2016b). Let f and u denote the restoring force of the spring of stiffness k and the displacement of the mass m, respectively. In addition, let f_y and d_y denote the yielding force and the yield displacement, respectively. The natural period of this SDOF model is denoted by $T_1=2\pi /{\omega }_1({\omega }_1=\sqrt{k/m}:\text{natural circular frequency})$. The ratio of the second slope to the initial slope is expressed by α. The negative stiffness depends on the magnitude of elastic stiffness and the effect of the P–Δ effect. When the magnitude of the effect of the P–Δ effect against the elastic stiffness is large, the post-yield stiffness is apt to become negative. V_y denotes the velocity level at which the SDOF model just attains the yield level after the first impulse. In this non-linear resonant case, the second impulse acts at the point of zero restoring force in the first slope range with a positive slope. They classified the collapse pattern into five patterns, i.e., pattern 1, pattern 2, pattern 3, additional pattern 1, and additional pattern 2. Pattern 1 is the collapse pattern such that the SDOF model collapses after the second impulse without plastic deformation after the first impulse. Pattern 2 is the collapse pattern such that the SDOF model collapses after the second impulse with plastic deformation after the first impulse. Pattern 3 is the collapse pattern such that the SDOF model collapses after the second impulse with plastic deformation after the first impulse and with closed loop after the second impulse. Additional pattern 1 is the collapse pattern such that the SDOF model collapses after the first impulse. Additional pattern 2 is the collapse pattern such that the SDOF model has an elastic limit after the second impulse.

Figure 2 summarizes the collapse limit of input velocity amplitude with respect to the second slope.

FIGURE 2

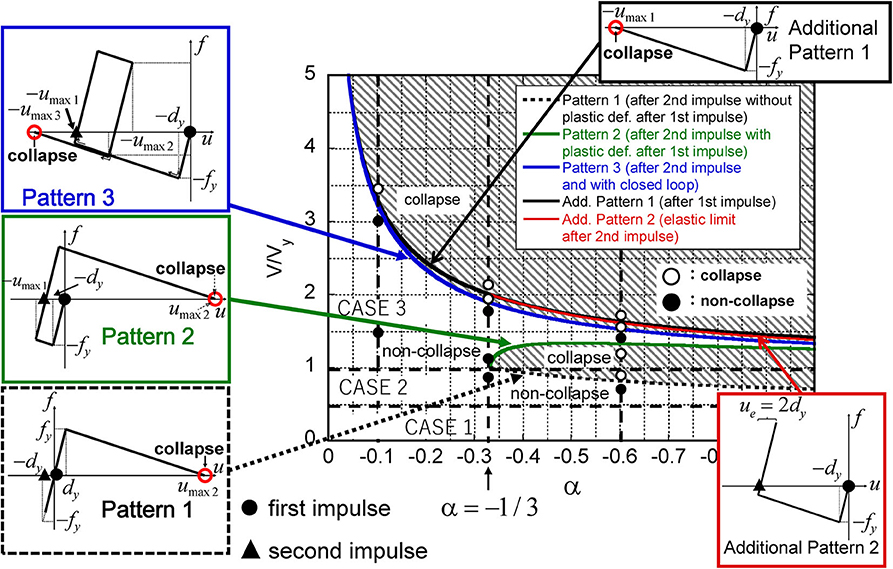
Figure 2. Regions of collapse and non-collapse and several patterns of collapse limit (patterns of collapse).

CASE 1 indicates the input velocity range such that the SDOF model remains elastic even after the second impulse. CASE 2 expresses the input velocity range such that the SDOF model remains elastic after the first impulse and goes into the plastic range after the second impulse. CASE 3 presents the input velocity range such that the SDOF model goes into the plastic range after the first impulse.

Classification Based on Input Level of Double Impulse and Timing of Second Impulse

In this section, a preparation for the next section to derive the collapse limit is made. Two classifications, one based on the input level of the double impulse and the other based on the timing of the second impulse, are introduced.

In the first classification based on the input level of the double impulse, three cases exist, i.e., CASE-A, B, C.

CASE-A: The input velocity leve satisfies 0 ≤ V/V_y ≤ 1.

CASE-B: The input velocity level satisfies $1<V/V_y<\sqrt{1-(1/\alpha )}$.

CASE-C: The input velocity level satisfies $V/V_y\ge \sqrt{1-(1/\alpha )}$.

The parameter $\sqrt{1-(1/\alpha )}$ is related to the coefficient such that the structure just attains the collapse under only the first impulse with the input velocity level $V/V_y=\sqrt{1-(1/\alpha )}$ (Kojima and Takewaki, 2016b). This classification is different from CASE-1, 2, 3 in the previous section which are defined for resonant critical input. In non-resonant cases, a different kind of classification is necessary.

In the second classification based on the timing of the second impulse, four cases exist, i.e., CASE-I, II, III, and IV.

CASE-I: The structure does not yield after the first impulse, and the second impulse acts.

CASE-II: The structure goes into the plastic range after the first impulse, and the second impulse acts before the structure attains the maximum displacement or before the structure collapses under only the first impulse.

CASE-III: The structure goes into the plastic range after the first impulse, and the second impulse acts while the structure exhibits a harmonic free vibration after the attainment of the maximum displacement.

CASE-IV: The structure collapses before the action of the second impulse.

Consider the principal points on the restoring-force characteristic, Point O: origin, Point A: initial yielding point, Point B: point of the maximum displacement after the first impulse, Point C: point of zero restoring force after the first impulse, Point D: point of collapse after the first impulse, Point E: point of zero velocity after Point C, Point F: point of zero restoring force after Point E, Point P: the maximum displacement in the negative direction (CASE-A), and Point Q: the maximum displacement in the positive direction (CASE-A). The time between two principal points (e.g., O and A) is indicated by t_OA.

(CASE-A)

In CASE-A (Figure 3A), it is evident that

$\begin{array}{ll}{t}_{OP}/T_1=t_{PC}/T_1=t_{CQ}/T_1=t_{QF}/T_1=0.25& (3)\end{array}$

This is because the vibration after the first impulse is a free vibration of an elastic SDOF model.

FIGURE 3

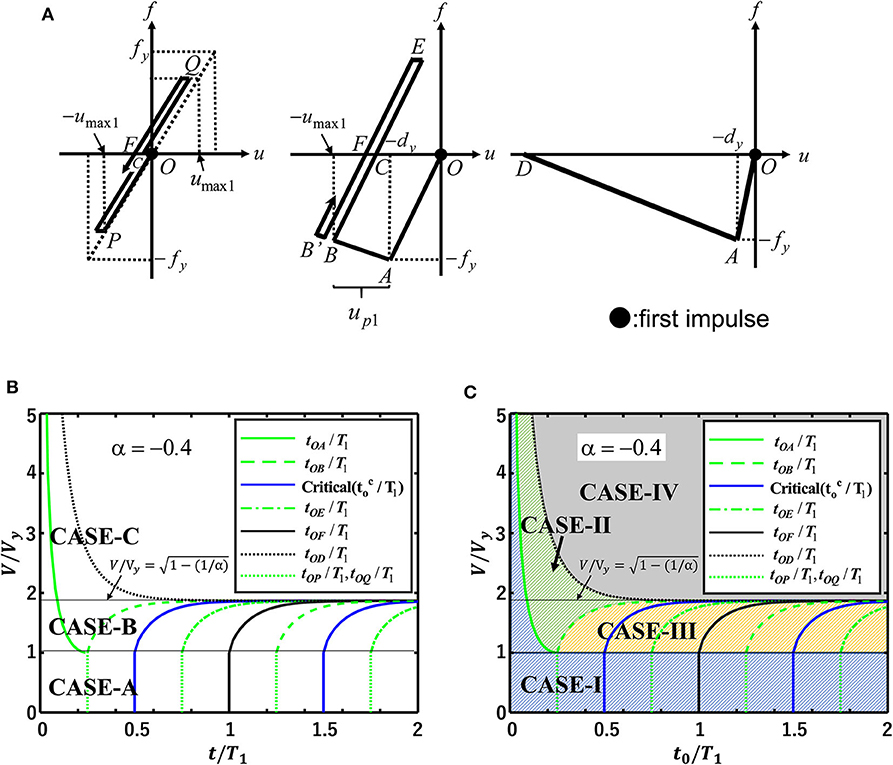
Figure 3. Classification based on input level of double impulse and timing of second impulse. (A) Force–deformation relation depending on input level of double impulse. (B) Classification based on input level of double impulse and time between origin O and principal points. (C) Classification based on timing of second impulse.

(CASE-B)

In CASE-B ($1<V/V_y<\sqrt{1-(1/\alpha )}$) (Figure 3A), the ratio of the time between Points O and A to T₁ can be expressed by

$\begin{array}{ll}{t}_{OA}/T_1=\{\text{arcsin}(V_y/V)\}/(2\pi )& (4)\end{array}$

In this case, the following condition must be satisfied.

$\begin{array}{ll}0<\text{arcsin}(V_y/V)<\pi /2& (5)\end{array}$

The plastic deformation u_p1 after the first impulse can be expressed by using the energy balance law (Kojima and Takewaki, 2015a, 2016b) between the point of the first impulse and the maximum deformation point.

$\begin{array}{ll}{u}_{p1}/d_y=(1/\alpha )[-1+\sqrt{1-\alpha \{1-{(V/V_y)}^2\}}]& (6)\end{array}$

The time history from Point A through Point B and the time t_AB between Points A and B are derived next. The equation of motion from Point A through Point B is

$\begin{array}{ll}m\ddot{u}+\alpha ku-(1-\alpha )k{d}_y=0& (7)\end{array}$

The energy balance law between Points O and A yields

$\begin{array}{ll}m{V}^2/2=(m{v_A}^2/2)+(k{d_y}^2/2)& (8)\end{array}$

Equation (8) provides the velocity v_A at Point A.

$\begin{array}{l}{v}_A=-\sqrt{V^2-{({\omega }_1{d}_y)}^2}=-\sqrt{V^2-{V_y}^2}\\ =-\{\sqrt{{(V/V_y)}^2-1}\}{V}_y& (9)\end{array}$

From Equation (7) and the initial condition (u(t = 0) = −d_y, $\stackrel{\bullet }{u}(t=0)=v_A$), the displacement and velocity between Points A and B are

$\begin{array}{l}u(t)=-(1/\alpha )d_y\text{ cosh}(\sqrt{-\alpha }{\omega }_{1}t)\\ -d_y\sqrt{\{{(V/V_y)}^2-1\}/(-\alpha )}\text{ sinh}(\sqrt{-\alpha }{\omega }_{1}t)\\ +\{(1/\alpha )-1\}{d}_y& (10)\end{array}$

$\begin{array}{l}\stackrel{\bullet }{u}(t)=(1/\sqrt{-\alpha })V_y\text{sinh}(\sqrt{-\alpha }{\omega }_{1}t)\\ -V_y\sqrt{{(V/V_y)}^2-1}\text{cosh}(\sqrt{-\alpha }{\omega }_{1}t)& (11)\end{array}$

The ratio of the time between Points A and B to T₁ can be expressed by

$\begin{array}{l}{t}_{AB}/T_1=\frac{1}{2\pi \sqrt{-\alpha }}arctanh\sqrt{-\alpha \{{(V/V_y)}^2-1\}}\\ =\frac{1}{4\pi \sqrt{-\alpha }}\text{ln }\left[\frac{1+\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}{1-\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}\right]& (12)\end{array}$

The time history after Point B and the times between two principal points are derived next. The equation of motion (free vibration) after Point B (maximum displacement point) can be described by

$\begin{array}{ll}m\ddot{u}+ku+(1-\alpha )k{u}_{p1}=0& (13)\end{array}$

The solution of Equation (13) for the initial condition $u(t=0)=-d_y-u_{p1},\stackrel{\bullet }{u}(t=0)=0$ and t = 0 at Point B leads to

$\begin{array}{ll}u(t)=-(d_y+\alpha u_{p1})\text{ cos}({\omega }_{1}t)-(1-\alpha )u_{p1}& (14)\end{array}$

$\begin{array}{ll}\stackrel{\bullet }{u}(t)=\{1+\alpha (u_{p1}/d_y)\}{V}_y\text{sin}({\omega }_{1}t)& (15)\end{array}$

The following results for the ratios of the times between the principal points to T₁ can be obtained.

$\begin{array}{ll}{t}_{BC}/T_1=0.25& (16)\end{array}$

$\begin{array}{ll}{t}_{BC}/T_1=t_{CE}/T_1=t_{EF}/T_1=0.25& (17)\end{array}$

Based on these results, the ratio of the critical interval of the double impulse to T₁ can be expressed by

$\begin{array}{l}\frac{{t_0}^c}{T_1}=\frac{t_{OA}}{T_1}+\frac{t_{AB}}{T_1}+\frac{t_{BC}}{T_1}=\frac{1}{2\pi }\text{arcsin}\left(\frac{V_y}{V}\right)\\ +\frac{1}{4\pi \sqrt{-\alpha }}\text{ln }\left[\frac{1+\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}{1-\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}\right]+\frac{1}{4}& (18)\end{array}$

(CASE-C)

Consider CASE-C (Figure 3A). As in CASE-B, the condition (5) is satisfied. The displacement and velocity after yielding (Point A) can be expressed by Equations (10), (11) as in CASE-B. Since the displacement at the collapse (Point D) is −dy{1−(1/α)} and u(t_AD) = −dy{1−(1/α)} for time t from Point A, the ratio of the time between Point A and Point D to T₁ can be obtained as

$\begin{array}{ll}{t}_{AD}/T_1=\frac{1}{4\pi \sqrt{-\alpha }}\text{ln }\left[\frac{1+\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}{-1+\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}\right]& (19)\end{array}$

Figure 3B shows the classification based on the input level of the double impulse and the time between origin O and principal points for the case α =-0.4. In this case of α =-0.4, CASE-A, B, C exist. The normalized time t_OA between two principal points (O and A) is indicated by a solid light green line. This line exists only in CASE-B and C. The normalized time t_OD between two principal points (O and D) is indicated by a dotted black line. This line exists only in CASE-C. The normalized time t_OP or t_OQ between two principal points (O and P or O and Q) is indicated by a dotted light green line. This line exists only in CASE-A (elastic response after the first impulse). The normalized times t_OB, t_OE between two principal points (O and B, O and E) are indicated by a dashed light green line and a dashed–dotted light green line. These lines exist only in CASE-B (elastic response after the first impulse). The normalized time t_OF between two principal points (O and F) is indicated by a solid black line. This line exists only in CASE-A and B. Finally, the normalized critical time interval ${t_0}^c$ between two impulses is indicated by a solid blue line. This line exists only in CASE-A and B. These boundaries of arrival times are useful for the classification of regions.

On the other hand, Figure 3C presents the classification of regions based on the timing of the second impulse for the case α =-0.4. In this case of α =-0.4, CASE-I, II, III, IV exist. CASE-I exists in CASE-A, B, C and CASE-II exists in CASE-B and C. Furthermore, CASE-III exists in CASE-B and CASE-IV exists in CASE-C. Once such classification of regions based on the timing of the second impulse is conducted, the judgment of collapse or non-collapse is made efficiently by introducing the energy balance law (Kojima and Takewaki, 2015a, 2016b).

Determination of Collapse Limit Input Velocity of Double Impulse With Arbitrary Interval

Consider here several collapse patterns, Collapse patterns 1′-4′. This naming comes from the similarity to the previous formulation for the non-linear resonant case (Kojima and Takewaki, 2016b). Collapse pattern 4′ represents a new type.

Collapse Pattern 1′

The first collapse pattern is the case where the structure remains elastic after the first impulse and attains the collapse limit after the second impulse with arbitrary timing as shown in Figure 4A.

FIGURE 4

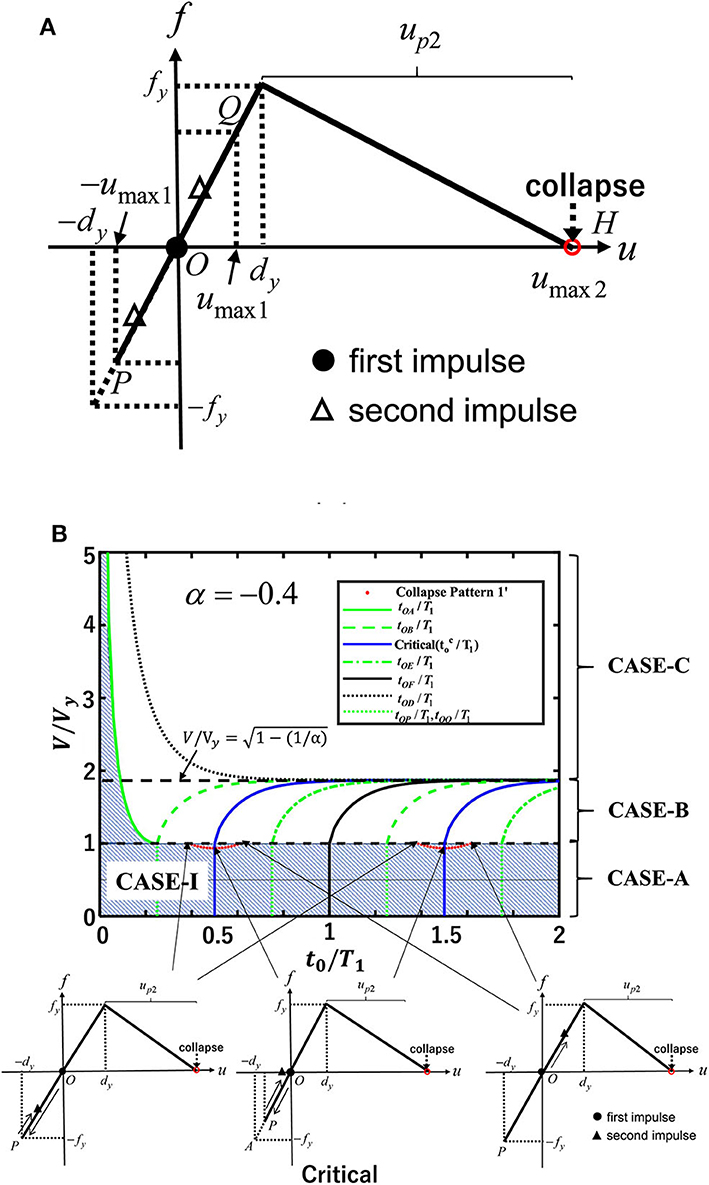
Figure 4. Collapse pattern 1′ (CASE-A): (A) Restoring-force characteristic. (B) Second impulse timing t₀/T₁-input velocity relation.

Let O and A denote the point of the first impulse (origin of the restoring force characteristic) and the point of initial yielding in the negative direction. The interval of two impulses is denoted by t₀, and the passing time between Points O and A is indicated by t_OA. Since the structure does not yield after the first impulse, the following two cases exist.

$\begin{array}{ll}\text{CASE-I}=\{\begin{array}{ll}0\le V/V_y\le 1\hfill & \left(\text{CASE-A}\right)\hfill \\ 1.0<V/V_y\hfill & (\text{CASE-B},\text{C})\text{ and }0<t_0\le t_{OA}\hfill \end{array}& (20)\end{array}$

Consider the respective cases shown in Figure 3.

[0 ≤ V/V_y ≤ 1 (CASE-A)]

Figure 4A shows the collapse pattern 1′ in CASE-A. In this figure, the timing of the second impulse is also indicated. In CASE-A (0 ≤ V/V_y ≤ 1), the structure does not collapse for the input 0 < V/V_y ≤ 0.5. Therefore, the condition 0.5 < V/V_y ≤ 1 is necessary to satisfy the collapse condition.

The displacement and velocity of the mass just before the second impulse can be expressed by

$\begin{array}{ll}{u}^{*}=-(V/{\omega }_1)\text{ sin}({\omega }_1{t}_0)=-(V/V_y)d_y\text{ sin}\{2\pi (t_0/T_1)\}& (21)\end{array}$

$\begin{array}{ll}{v}^{*}=-V\text{ cos}({\omega }_1{t}_0)=-V\text{ cos}\{2\pi (t_0/T_1)\}& (22)\end{array}$

When the structure just attains a zero restoring force after the second impulse, the plastic deformation u_p2 after the second impulse can be obtained as

$\begin{array}{ll}{u}_{p2}=-(1/\alpha )d_y& (23)\end{array}$

The energy balance law between the state just after the second impulse and the collapse Point H in Figure 4A can be expressed by

$\begin{array}{ll}m{(v^{*}+V)}^2/2+k{u}^{*2}/2=(f_y{d}_y/2)+f_y{u}_{p2}+(\alpha k{u_{p2}}^2/2)& (24)\end{array}$

Substitution of Equations (21), (22), and (23) into Equation (24) leads to the collapse limit input velocity for CASE-A in collapse pattern 1′.

$\begin{array}{ll}V/V_y=\sqrt{\frac{1-(1/\alpha )}{2-2\text{ cos}(2\pi t_0/T_1)}}& (25)\end{array}$

Since 0.5 < V/V_y ≤ 1 is necessary, the following condition for α and t₀ must be satisfied.

$\begin{array}{ll}1/\alpha \ge 2\text{ cos}(2\pi t_0/T_1)-1& (26)\end{array}$

Figure 4B shows the collapse limit input velocity for α = −0.4 for CASE-A in collapse pattern 1′. It can be observed that the critical case for t₀/T₁ = 0.5 (Kojima and Takewaki, 2016b) gives the minimum collapse limit input velocity. In Figure 4B, the timing of the second impulse is also indicated.

[1.0 < V/V_y (CASE-B, C) and 0 < t₀ ≤ t_OA]

After some manipulation, it was found that α ≤ −1 is required in this case to satisfy the collapse condition in collapse pattern 1′. Since a usual case corresponds to the model with α > −1, the detail of analysis is not shown here.

Collapse Pattern 2′

The second collapse pattern is the case where the structure exhibits plastic deformation after the first impulse and attains the collapse limit after the second impulse (see Figure 5A). Since the structure exhibits plastic deformation after the first impulse in this case, V/V_y > 1 must be satisfied.

FIGURE 5

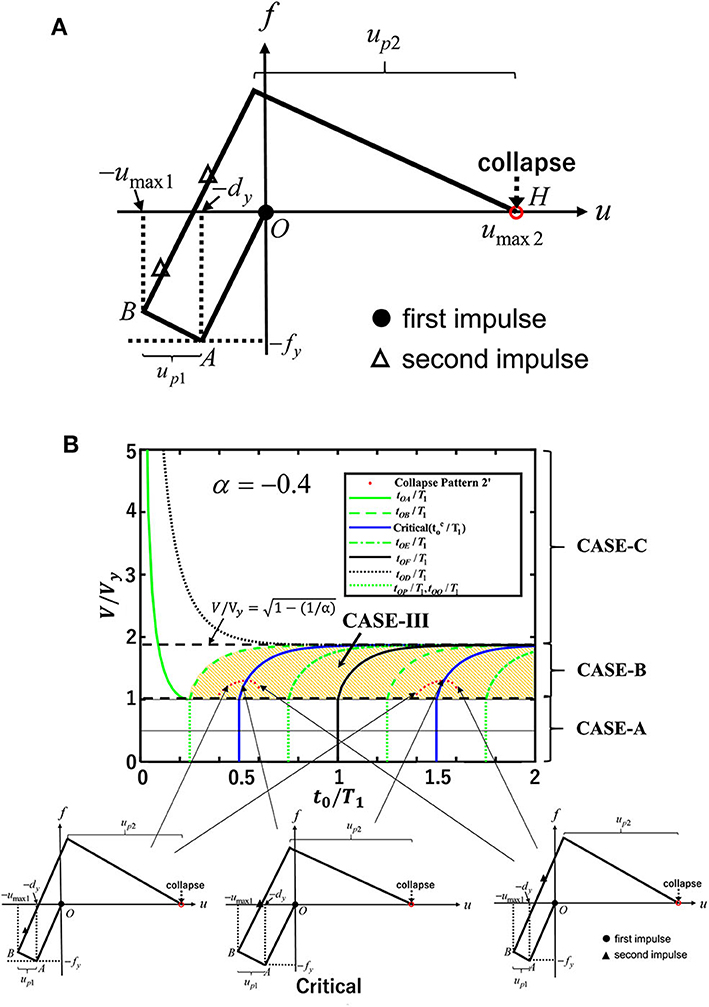
Figure 5. Collapse pattern 2′ (CASE-B), (A) Restoring-force characteristic. (B) The collapse limit input velocity for α =-0.4.

Because the second impulse acts after the structure goes into a plastic region under the first impulse, the case is divided into the following two cases, CASE-II and CASE-III.

$\begin{array}{ll}\{\begin{array}{l}\text{CASE-II}=\{\begin{array}{ll}1<V/V_y<\sqrt{1-(1/\alpha )}\hfill & (\text{CASE-B})\text{ and }{t}_{OA}<t_0\le t_{OB}\hfill \\ \sqrt{1-(1/\alpha )}\le V/V_y\hfill & (\text{CASE-C})\text{ and }{t}_{OA}<t_0\le t_{OD}\hfill \end{array}\\ \text{CASE-III}=1<V/V_y<\sqrt{1-(1/\alpha )}(\text{CASE-B})\text{ and }{t}_{OB}\le t_0\end{array}& (27)\end{array}$

[$1<V/V_y<\sqrt{1-(1/\alpha )}$ (CASE-B) and (CASE-II)]

Since the second impulse acts before the attainment of the maximum displacement (Point B) after the yielding under the first impulse, the interval of two impulses has to satisfy

$\begin{array}{l}\{\text{arcsin }(V_y/V)\}/(2\pi )\le t_0/T\le \{\text{arcsin }(V_y/V)\}/(2\pi )\\ +\frac{1}{4\pi \sqrt{-\alpha }}\text{ln }\left[\frac{1+\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}{1-\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}\right]& (28)\end{array}$

The displacement and velocity at time t^* just before the action of the second impulse can be obtained from Equations (10), (11).

$\begin{array}{l}{u}^{*}=u_{AB}(t^{*}-t_{OA})\\ =-(1/\alpha )d_y\text{ cosh}(\sqrt{-\alpha }{\omega }_1\left(t^{*}-t_{OA}\right))\\ -d_y\sqrt{\{{(V/V_y)}^2-1\}/(-\alpha )}\text{ sinh}\left(\sqrt{-\alpha }{\omega }_1\left(t^{*}-t_{OA}\right)\right)\\ +\{(1/\alpha )-1\}{d}_y& (29)\end{array}$

$\begin{array}{l}{v}^{*}={\dot{u}}_{AB}\left(t^{*}-t_{OA}\right)\\ =\sqrt{\left(-1/\alpha \right)-\left\{{\left(V/V_y\right)}^2-1\right\}}{V}_y\mathrm{ sinh}[\sqrt{-\alpha }{\omega }_1\left(t^{*}-t_{OA}\right)\\ -\text{arctanh }\sqrt{-\alpha \{{(V/V_y)}^2-1\}}]& (30)\end{array}$

t_OA in Equations (29), (30) can be obtained from Equation (4). The plastic deformation after the first impulse can be expressed by

$\begin{array}{ll}{u}_{p1}=-(u^{*}+d_y)& (31)\end{array}$

When the maximum displacement after the second impulse just attains a zero restoring force, the plastic deformation after the second impulse can be expressed by

$\begin{array}{ll}{u}_{p2}=u_{p1}-(1/\alpha )d_y& (32)\end{array}$

The energy balance law between the point just after the second impulse and the point H where the maximum displacement after the second impulse just attains a zero restoring force can be expressed by

$\begin{array}{l}m{(v^{*}+V)}^2/2+\{k{(d_y+\alpha u_{p1})}^2/2\}=\{k{(d_y-\alpha u_{p1})}^2/2\}\\ +(f_y-\alpha k{u}_{p1})u_{p2}+(\alpha k{u_{p2}}^2/2)& (33)\end{array}$

Substitution of Equations (4), (29)–(32) into Equation (33) provides the collapse input velocity level V/V_y for collapse pattern 2′.

After some manipulation, it was found that α ≤ −1 is required in this case to satisfy the collapse condition in collapse pattern 2′. Since a usual case corresponds to the model with α > −1, the detail of analysis is not shown here.

[$\sqrt{1-(1/\alpha )}\le V/V_y$ (CASE-C) and (CASE-II)]

Since the second impulse acts before the attainment of the collapse point D with a zero restoring force after the yielding under the first impulse, the following condition must be satisfied from Equations (4), (19).

$\begin{array}{l}\{\text{arcsin}(V_y/V)\}/(2\pi )\le t_0/T\le \{\text{arcsin}(V_y/V)\}/(2\pi )\\ +\frac{1}{4\pi \sqrt{-\alpha }}\text{ln }\left[\frac{1+\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}{-1+\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}\right]& (34)\end{array}$

After some manipulation, it was found that α ≤ −1 is required in this case to satisfy the collapse condition in collapse pattern 2′. Since a usual case corresponds to the model with α > −1, the detail of analysis is not shown here.

[$1.0\le V/V_y<\sqrt{1-(1/\alpha )}$ (CASE-B) and (CASE-III)]

Figure 5A shows the collapse pattern 2′ in CASE-B. In this figure, the timing of the second impulse is also indicated. In this case, the structure collapses under the second impulse after it goes into a plastic region under the first impulse. Since the second impulse acts after the structure goes into a plastic region and attains the maximum deformation (Point B), Equations (4), (12) require to satisfy the condition

$\begin{array}{l}\{\text{arcsin}(V_y/V)\}/(2\pi )\\ +\frac{1}{4\pi \sqrt{-\alpha }}\text{ln }\left[\frac{1+\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}{1-\sqrt{-\alpha \{{(V/V_y)}^2-1\}}}\right]\le t_0/T& (35)\end{array}$

In this case, the displacement and velocity of the mass just before the action of the second impulse are described from Equations (14) and (15) as

$\begin{array}{l}{u}^{*}=u(t_0-(t_{OA}+t_{AB}))\\ =-(d_y+\alpha u_{p1})\text{ cos }\left[{\omega }_1\left\{t_0-(t_{OA}+t_{AB})\right\}\right]-(1-\alpha )u_{p1}& (36)\end{array}$

$\begin{array}{l}{v}^{*}=\stackrel{\bullet }{u}(t_0-(t_{OA}+t_{AB}))\\ =\{1+\alpha (u_{p1}/d_y)\}{V}_y\text{sin }\left[{\omega }_1\{t_0-(t_{OA}+t_{AB})\}\right]& (37)\end{array}$

t_OA and t_AB in Equations (36), (37) can be obtained from Equations (4), (12). The plastic deformation u_p1 after the first impulse can be derived by using the energy balance law between the point just after the first impulse and the point of the maximum deformation (Point B). The plastic deformation u_p2 after the second impulse can be obtained as Equation (32).

The energy balance law between the point just after the second impulse and the point of the maximum deformation u_max2 = d_y − u_p1 + u_p2 after the second impulse (Point H) can be expressed as

$\begin{array}{l}m{(v^{*}+V)}^2/2+k{\{u^{*}-(\alpha -1)u_{p1}\}}^2/2=\{k{(d_y-\alpha u_{p1})}^2/2\}\\ +(f_y-\alpha k{u}_{p1})u_{p2}+(\alpha k{u_{p2}}^2/2)& (38)\end{array}$

Since substitution of Equations (4), (6), (12), (32), (36), (37) into Equation (38) provides the transcendental equation, it is difficult to derive a closed-form expression for the input velocity corresponding to the collapse. To determine the input velocity corresponding to the collapse, this transcendental equation can be computed for given α and t₀.

Figure 5B shows the collapse limit input velocity for α = −0.4 for CASE-B in collapse pattern 2′.

Collapse Pattern 3′

The third collapse pattern is the case where the structure exhibits plastic deformation after the first impulse and attains the collapse limit with a closed loop after the second impulse (Kojima and Takewaki, 2016b).

Since the structure exhibits plastic deformation after the first impulse in this case, V/V_y > 1 must be satisfied. Because the second impulse acts after the structure goes into a plastic region under the first impulse, the case is divided into two cases, CASE-II and CASE-III, as shown in Equation (27). According to the classification shown in Equation (27), the collapse limit velocity corresponding to the collapse pattern 3′ is derived.

[$1<V/V_y<\sqrt{1-(1/\alpha )}$ (CASE-B) and (CASE-II)]

Figure 6A shows the collapse pattern 3′ in CASE-B and CASE-II. In this figure, the timing of the second impulse is also indicated. In this case, the structure exhibits a closed loop and collapses under the second impulse after it goes into a plastic region under the first impulse. The second impulse acts before the structure goes into the unloading path naturally and experiences plastic deformation in the positive direction and then in the negative direction.

FIGURE 6

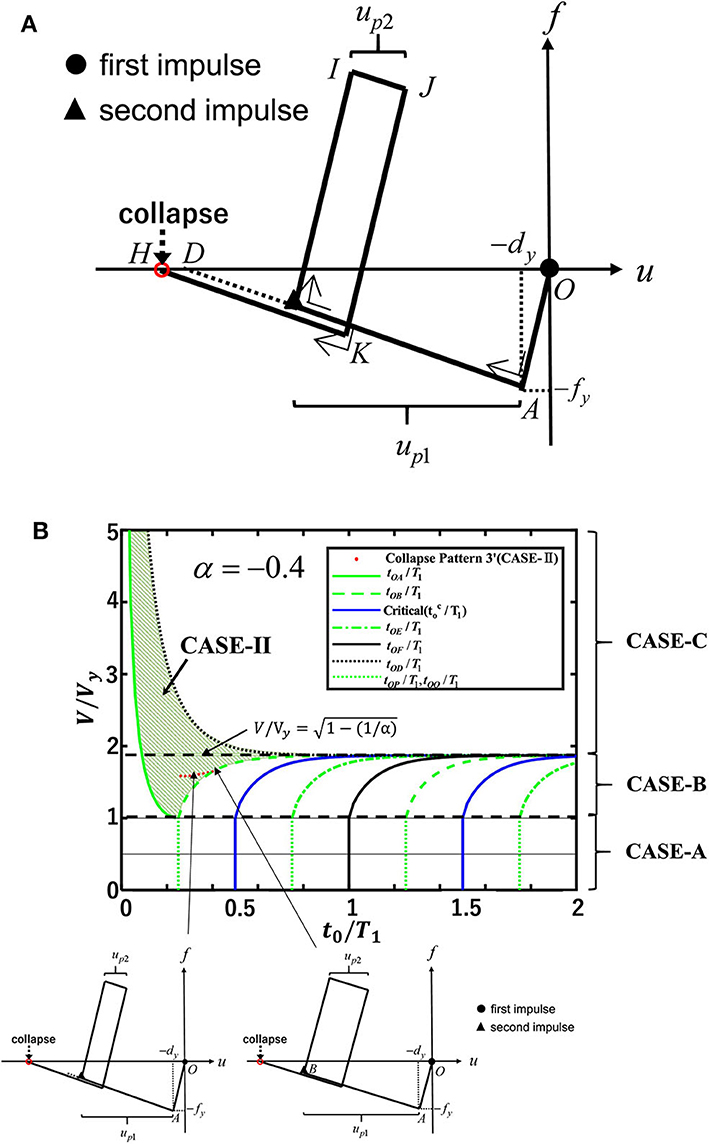
Figure 6. Collapse pattern 3′ (CASE-B and CASE-II). (A) Restoring-force characteristic. (B) Second impulse timing t₀/T₁-input velocity relation.

Since the second impulse acts before the structure goes into the unloading path naturally at Point B, the impulse interval t₀ must satisfy Equation (28).

In this case, the displacement and velocity of the mass just before the action of the second impulse are described from Equations (29) and (30). t_OA in Equations (29), (30) can be obtained from Equation (4). As shown in Figure 6A, the plastic deformation u_p1 after the first impulse can be derived as in Equation (31).

The energy balance law between the point just after the second impulse and the point J in Figure 6A can be expressed by

$\begin{array}{l}m{(v^{*}+V)}^2/2+k{(u^{*}+\alpha u_{p1})}^2/2=\{k{(d_y-\alpha u_{p1})}^2/2\}\\ +(f_y-\alpha k{u}_{p1})u_{p2}+(\alpha k{u_{p2}}^2/2)& (39)\end{array}$

The plastic deformation u_p2 after the second impulse can be obtained from Equation (39). In this case, the condition 0 < u_p2 < −(1/α)d_y must be satisfied. By solving the quadratic equation, Equation (39), under the condition 0 < u_p2 < −(1/α)d_y, u_p2 can be obtained in closed form.

$\begin{array}{l}{u}_{p2}=-\{(d_y/\alpha )-u_{p1}\}\\ -\sqrt{{\{(d_y/\alpha )-u_{p1}\}}^2+4u_{p1}{d}_y+{\{(v^{*}+V)d_y/V_y\}}^2/\alpha }& (40)\end{array}$

Another energy balance law between Point J and Point H provides

$\begin{array}{l}k{(d_y-\alpha u_{p1}+\alpha u_{p2})}^2/2=[k{\{d_y-(-\alpha u_{p1}+\alpha u_{p2})\}}^2/2]\\ -(1/\alpha )[k{\{d_y-(-\alpha u_{p1}+\alpha u_{p2})\}}^2/2]& (41)\end{array}$

The input velocity corresponding to the collapse can be obtained by solving the quartic equation transformed from Equation (41).

Figure 6B shows the collapse limit input velocity for α = −0.4 for CASE-B in collapse pattern 3′.

[$\sqrt{1-(1/\alpha )}\le V/V_y$ (CASE-C) and (CASE-II)]

Since the input velocity level in this case is too large, the solution to satisfy the collapse condition does not exist in this case.

[$1.0\le V/V_y<\sqrt{1-(1/\alpha )}$ (CASE-B) and (CASE-III)]

Figure 7A shows the collapse pattern 3′ in CASE-B and CASE-III. In this figure, the timing of the second impulse is also indicated. In this case, the structure exhibits a closed loop (BIJK) and collapses under the second impulse after it goes into a plastic region under the first impulse. The second impulse acts after the structure goes into the unloading path naturally at Point B. Since the second impulse acts after the structure goes into an unloading path naturally at Point B, the impulse interval t₀ must satisfy Equation (35).

FIGURE 7

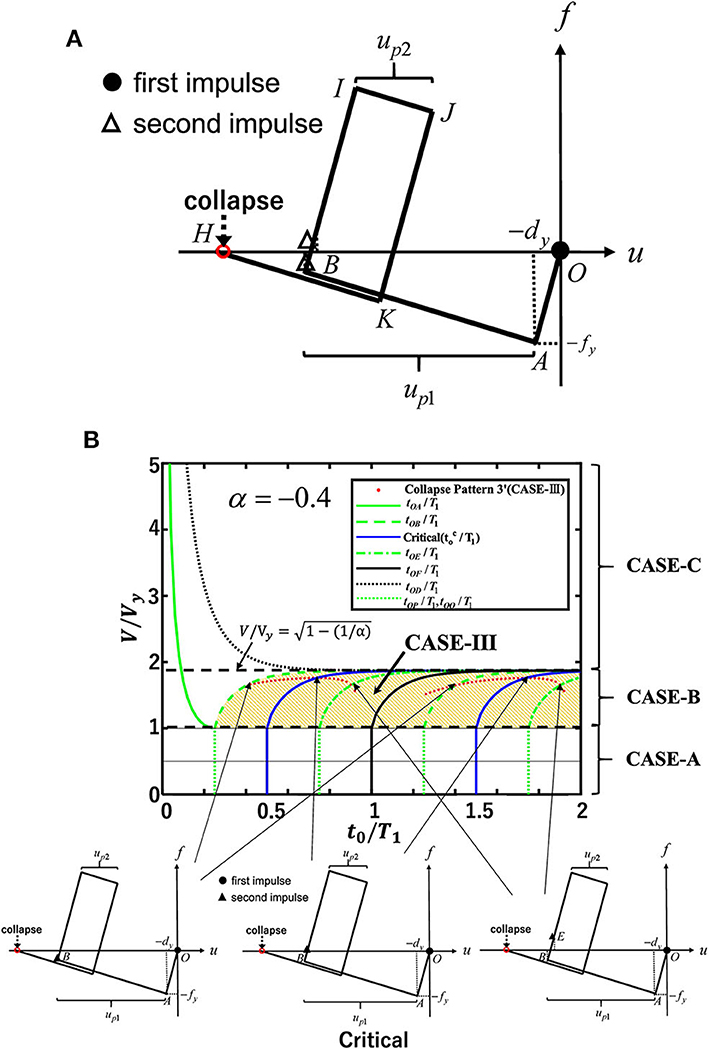
Figure 7. Collapse pattern 3′ (CASE-B and CASE-III). (A) Restoring-force characteristic. (B) Second impulse timing t₀/T₁-input velocity relation.

The displacement and velocity just before the action of the second impulse can be obtained from Equations (36), (37). t_OA and t_AB in Equations (36), (37) can be obtained from Equations (4), (12). The plastic deformation u_p1 after the first impulse can be derived as Equation (6) by using the energy balance law between the point just after the first impulse and the point of the maximum deformation (Point B) in Figure 7A.

The energy balance law between the point just after the second impulse and the point of the maximum deformation u_max2 after the second impulse (Point J in Figure 7A) can be expressed as

$\begin{array}{l}m{(v^{*}+V)}^2/2+k{\{u^{*}-(\alpha -1)u_{p1}\}}^2/2\\ =\{k{(d_y-\alpha u_{p1})}^2/2\}\\ +(f_y-\alpha k{u}_{p1})u_{p2}+(\alpha k{u_{p2}}^2/2)& (42)\end{array}$

By solving the quadratic equation, Equation (42), under the condition 0 < u_p2 < −(1/α)d_y, u_p2 can be obtained in closed form.

$\begin{array}{l}{u}_{p2}=-\{(d_y/\alpha )-u_{p1}\}\\ -\sqrt{\begin{array}{l}{\{(d_y/\alpha )-u_{p1}\}}^2-[{(d_y-\alpha u_{p1})}^2\hfill \\ -{\{(v^{*}+V)d_y/V_y\}}^2-{\{u^{*}-(\alpha -1)u_{p1}\}}^2]/\alpha \hfill \end{array}}& (43)\end{array}$

The collapse limit level in this pattern can be obtained by solving the quartic equation derived by substituting Equation (43) into Equation (41).

Figure 7B shows the collapse limit input velocity for α = −0.4 for CASE-B in collapse pattern 3′.

Collapse Pattern 4′

The fourth collapse pattern is the case where the structure exhibits plastic deformation after the first impulse and attains the collapse limit after experiencing unloading (positive direction) and reloading–reyielding (negative direction) for the second impulse.

Since the structure exhibits plastic deformation after the first impulse in this case, V/V_y > 1 must be satisfied. Because the second impulse acts after the structure goes into a plastic region under the first impulse, the case is divided into two cases, CASE-II and CASE-III, as shown in Equation (27). According to the classification shown in Equation (27), the collapse limit velocity corresponding to the collapse pattern 4′ is derived.

[$1<V/V_y<\sqrt{1-(1/\alpha )}$ (CASE-B) and (CASE-II)]

Figure 8A shows the collapse pattern 4′ for CASE-B and CASE-II. In this figure, the timing of the second impulse is also indicated. In this case, the second impulse acts before the structure goes into an unloading path naturally. The structure does not experience plastic deformation in the positive direction. Since the second impulse acts before the structure goes into an unloading path naturally at Point B, the impulse interval t₀ must satisfy Equation (28).

FIGURE 8

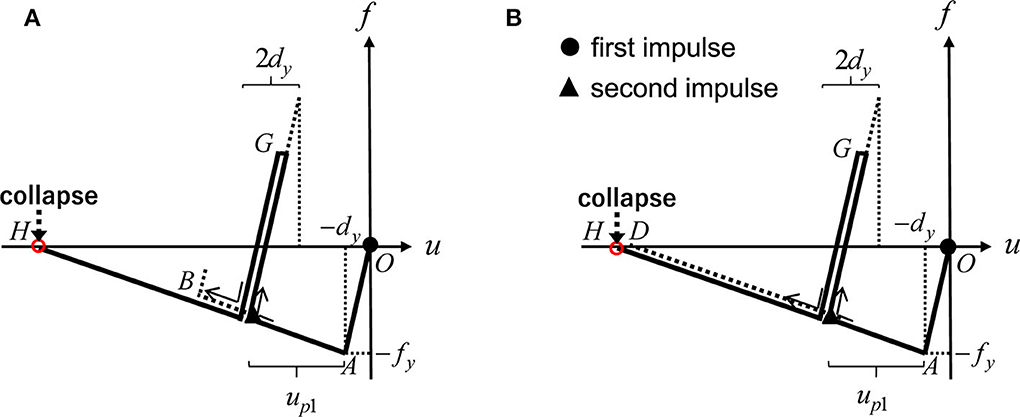
Figure 8. Restoring-force characteristic corresponding to collapse pattern 4′, (A) Case-B and CASE-II, (B) Case-C and CASE-II.

In this case, the displacement and velocity of the mass just before the action of the second impulse are expressed by Equations (29) and (30). t_OA in Equations (29), (30) can be obtained from Equation (4). As shown in Figure 8A, the plastic deformation u_p1 after the first impulse can be derived as in Equation (31). Since the structure does not go into a plastic region just after the second impulse, the following relation must hold.

$\begin{array}{ll}m{(v^{*}+V)}^2/2+k{\{u^{*}+\alpha u_{p1}\}}^2/2\le \{k{(d_y-\alpha u_{p1})}^2/2\}& (44)\end{array}$

The energy balance law between the point just after the second impulse and Point H in Figure 8A can be expressed by

$\begin{array}{l}m{(v^{*}+V)}^2/2+k{\{u^{*}+\alpha u_{p1}\}}^2/2=\{k{(d_y+\alpha u_{p1})}^2/2\}\\ -(1/\alpha )\{k{(d_y+\alpha u_{p1})}^2/2\}& (45)\end{array}$

[$\sqrt{1-(1/\alpha )}\le V/V_y$ (CASE-C) and (CASE-II)]

Figure 8B shows the collapse pattern 4′ for CASE-C and CASE-II. In this figure, the timing of the second impulse is also indicated. In this case, the second impulse acts before the structure attains the collapse state, Point D. The structure does not experience plastic deformation in the positive direction.

Since the second impulse acts before the structure attains the collapse state, Point D, the impulse interval t₀ must satisfy Equation (34).

In this case, the displacement and velocity of the mass just before the action of the second impulse are described by Equations (29) and (30). t_OA in Equations (29), (30) can be obtained from Equation (4). As shown in Figure 8B, the plastic deformation u_p1 after the first impulse can be derived as in Equation (31). Since the structure does not go into a plastic region just after the action of the second impulse, Equation (44) must be satisfied. The energy balance law between the point just after the second impulse and the point H in Figure 8A can be expressed as Equation (45).

Figure 9 shows the collapse limit input velocity for α = −0.4 for Case-B, CASE-II and CASE-C, CASE-II in collapse pattern 4′.

FIGURE 9

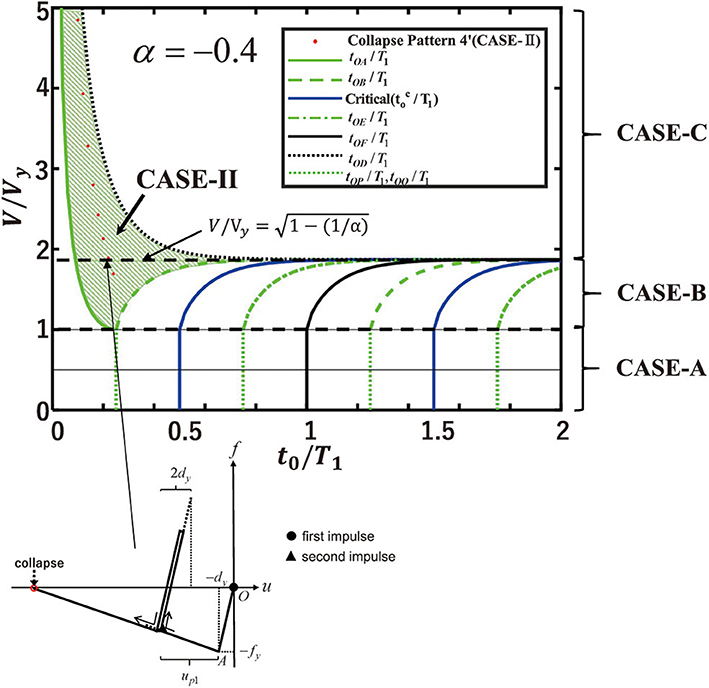
Figure 9. Second impulse timing t₀/T₁-input velocity relation for CASE-B and CASE-II, CASE-C, CASE-II in collapse pattern 4′.

[$1\le V/V_y<\sqrt{1-(1/\alpha )}$ (CASE-B) and (CASE-III)]

Figure 10A shows the collapse pattern 4′ for CASE-B and CASE-III. In this figure, the timing of the second impulse is also indicated. In this case, the second impulse acts after the structure goes into a plastic range and attains the maximum deformation, Point B. The structure does not experience plastic deformation in the positive direction. Since the second impulse acts after the structure attains the maximum deformation, Point B, the impulse interval t₀ must satisfy Equation (35).

FIGURE 10

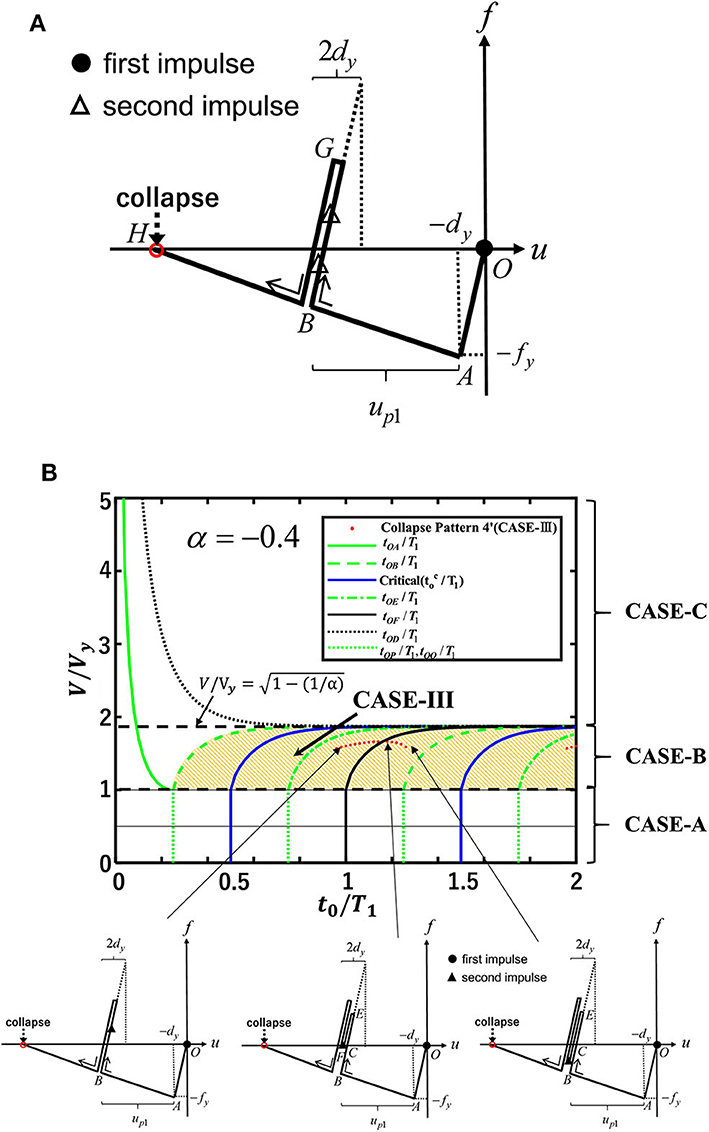
Figure 10. Collapse pattern 4′ (CASE-B and CASE-III). (A) Second impulse timing t₀/T₁-input velocity relation. (B) Second impulse timing t₀/T₁-input velocity relation.

When the structure goes into a plastic region after the first impulse and the second impulse acts after the structure attains the maximum deformation, Point B, the displacement and velocity of the mass just before the action of the second impulse are described by Equations (36) and (37). t_OA and t_AB in Equations (36), (37) can be obtained by Equations (4), (12). As shown in Figure 10A, the plastic deformation u_p1 after the first impulse can be derived as in Equation (6) by using the balance law between the point just after the first impulse and the point B of the maximum deformation.

Since the structure does not go into a plastic region just after the action of the second impulse, Equation (46) must be satisfied.

$\begin{array}{l}m{(v^{*}+V)}^2/2\\ +k{\{u^{*}-(\alpha -1)u_{p1}\}}^2/2\le \{k{(d_y-\alpha u_{p1})}^2/2\}& (46)\end{array}$

The energy balance law between the point just after the second impulse and the point H in Figure 10A can be expressed as

$\begin{array}{l}m{(v^{*}+V)}^2/2+k{\{u^{*}-(\alpha -1)u_{p1}\}}^2/2\\ =\{k{(d_y+\alpha u_{p1})}^2/2\}-(1/\alpha )\{k{(d_y+\alpha u_{p1})}^2/2\}& (47)\end{array}$

Since substitution of Equations (4), (6), (12), (32), (36), (37) into Equation (47) provides the transcendental equation, it is difficult to derive a closed-form expression for the input velocity corresponding to the collapse. To determine the input velocity corresponding to the collapse, this transcendental equation can be computed for given α and t₀.

Figure 10B shows the second impulse timing t₀/T₁-input velocity relation for Case-B and CASE-III in collapse pattern 4′.

Collapse Limit Input Velocity of Double Impulse With Arbitrary Interval for SDOF System With Various Negative Post-yield Slopes

Based on the collapse patterns explained above, a limit curve on the second impulse timing t₀/T₁-input velocity V/V_y relation for the collapse and non-collapse states can be proposed. As an example, Figure 11 shows the second impulse timing t₀/T₁-input velocity relation for the collapse and non-collapse states for α = −0.4. It should be remarked that the present SDOF model is an undamped model, and the states of t₀/T₁=0.5 and t₀/T₁=1.5 provide the same collapse limit. It can be observed that an isolated region of the collapse state exists around the level of t₀/T₁=0.5 (also 1.5) and the level of V/V_y=1. The most important point to be remarked is that the critical state (Kojima and Takewaki, 2016b) corresponding to the non-linear resonance does not necessarily provide the minimum input velocity level with respect to arbitrary impulse timing.

FIGURE 11

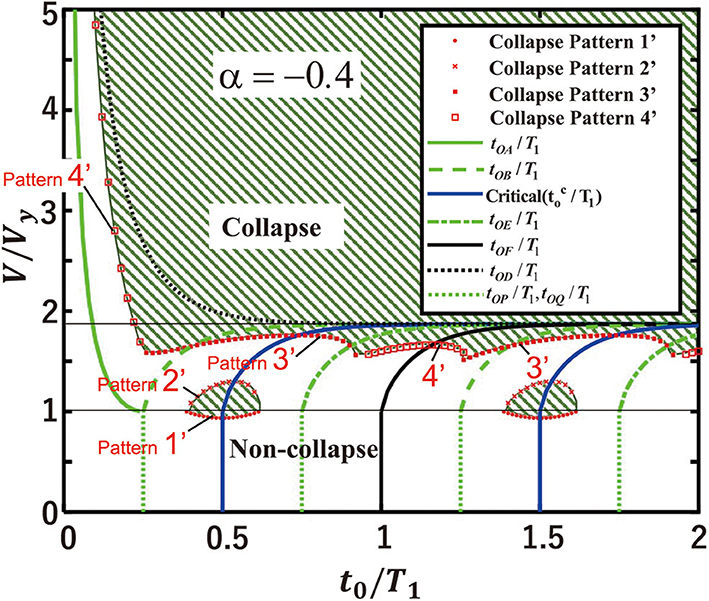
Figure 11. Second impulse timing t₀/T₁-input velocity relation for collapse and non-collapse states (α = −0.4).

Figure 12 presents the correspondence between arbitrary timing and the critical timing (Kojima and Takewaki, 2016b) of the second impulse in the collapse velocity level (α = −0.4). It can be confirmed that the states of t₀/T₁=0.5 and t₀/T₁=1.5 certainly correspond to the critical state in the reference (Kojima and Takewaki, 2016b).

FIGURE 12

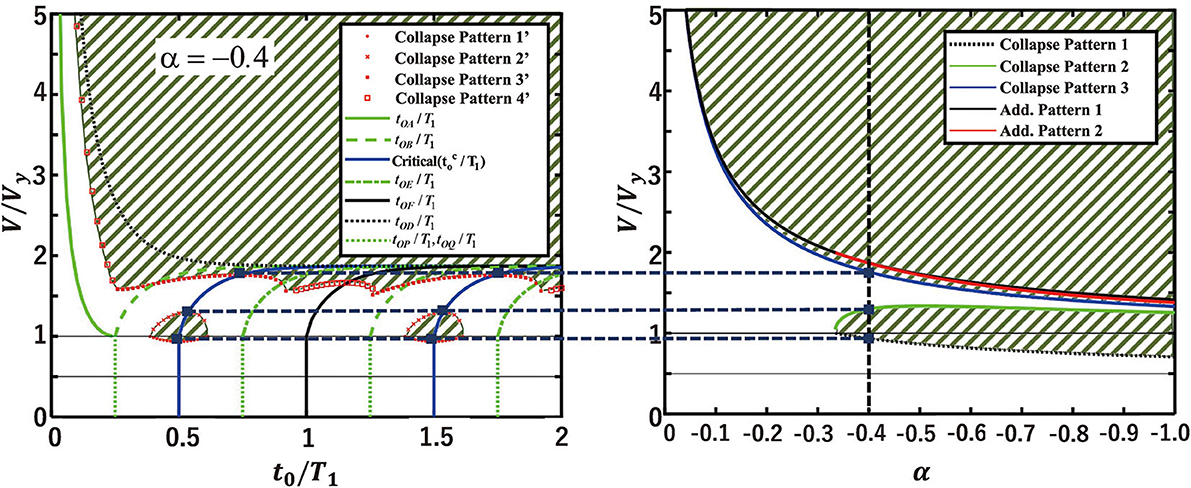
Figure 12. Correspondence between arbitrary timing and critical timing of second impulse in collapse velocity level (α = −0.4).

Figure 13 indicates the collapse limit input velocity of the double impulse with arbitrary interval for the SDOF system with various negative post-yield slopes (α = −0.2, −1/3, −0.8). The correspondence between the arbitrary timing and critical timing (Kojima and Takewaki, 2016b) of the second impulse in the collapse velocity level is also shown again. It can be found that, as the parameter α changes, different phases of the limit curve in the second impulse timing t₀/T₁-input velocity relation for collapse and non-collapse states appear and α = −1/3 gives the boundary of the change of phases. When α is larger than −1/3, the non-linear resonance does not provide the minimum input level corresponding to collapse.

FIGURE 13

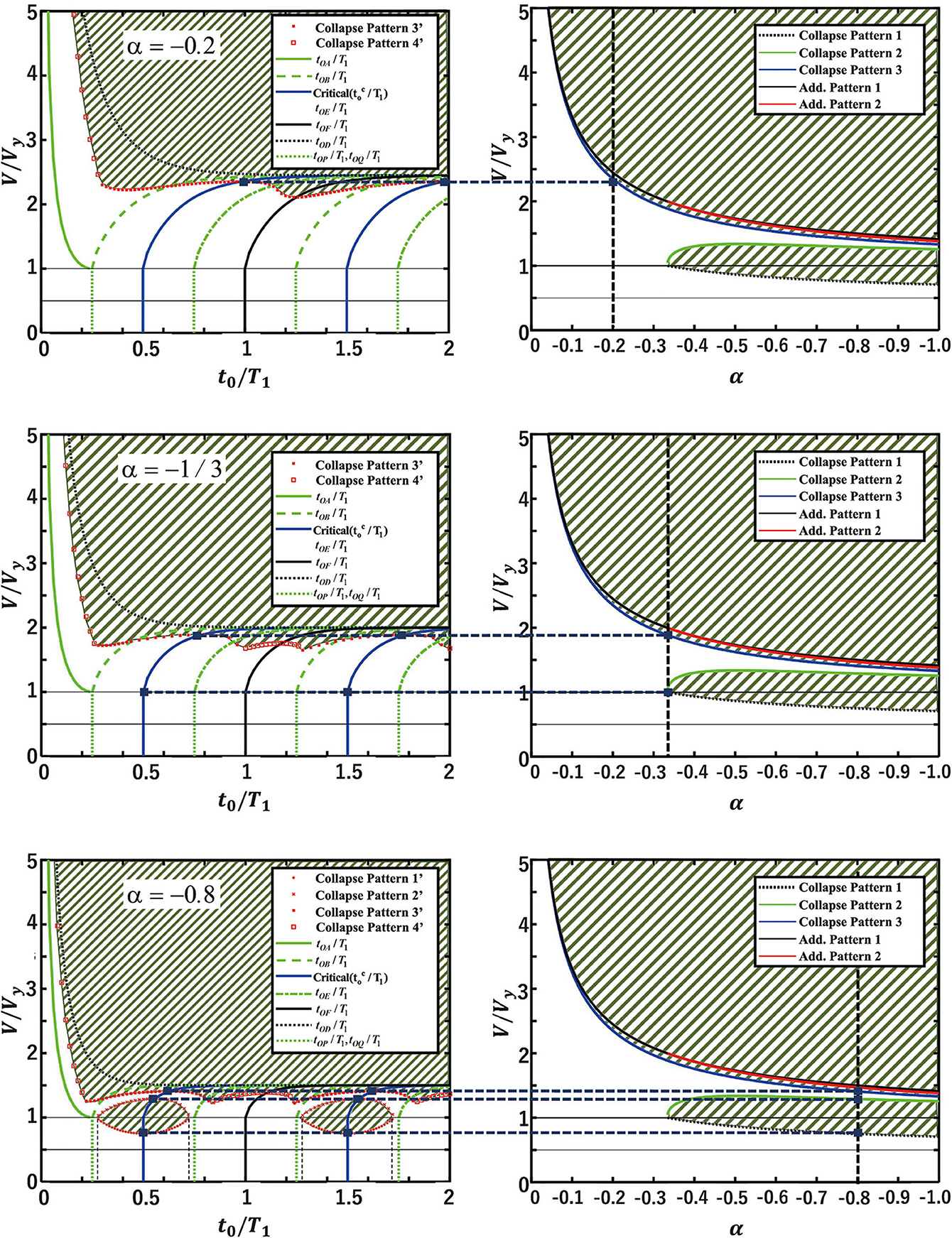
Figure 13. Collapse limit input velocity of double impulse with arbitrary interval for SDOF system with various negative post-yield slopes (α = −0.2, −1/3, −0.8).

Accuracy of Collapse Limit Input Velocity of Double Impulse With Arbitrary Interval for SDOF System With Negative Post-yield Slope

Figure 14A shows the verification of the proposed collapse limit by time-history response analysis to double impulses with various input velocities and impulse timings (α = −0.2, −0.4). Many combinations of the impulse timing and the input velocity level in the collapse and non-collapse states were selected in the case of α = −0.2, −0.4. For strict verification, many combinations of the impulse timing and the input velocity level were chosen near the boundary of the proposed limit curve. Figure 14B presents the displacement time histories of the model with α = −0.4 to five inputs (1), (2), (5), (6), (8) shown in Figure 14A. It can be observed that strict classification into the collapse state and the non-collapse state has been made with the proposed limit curve.

FIGURE 14

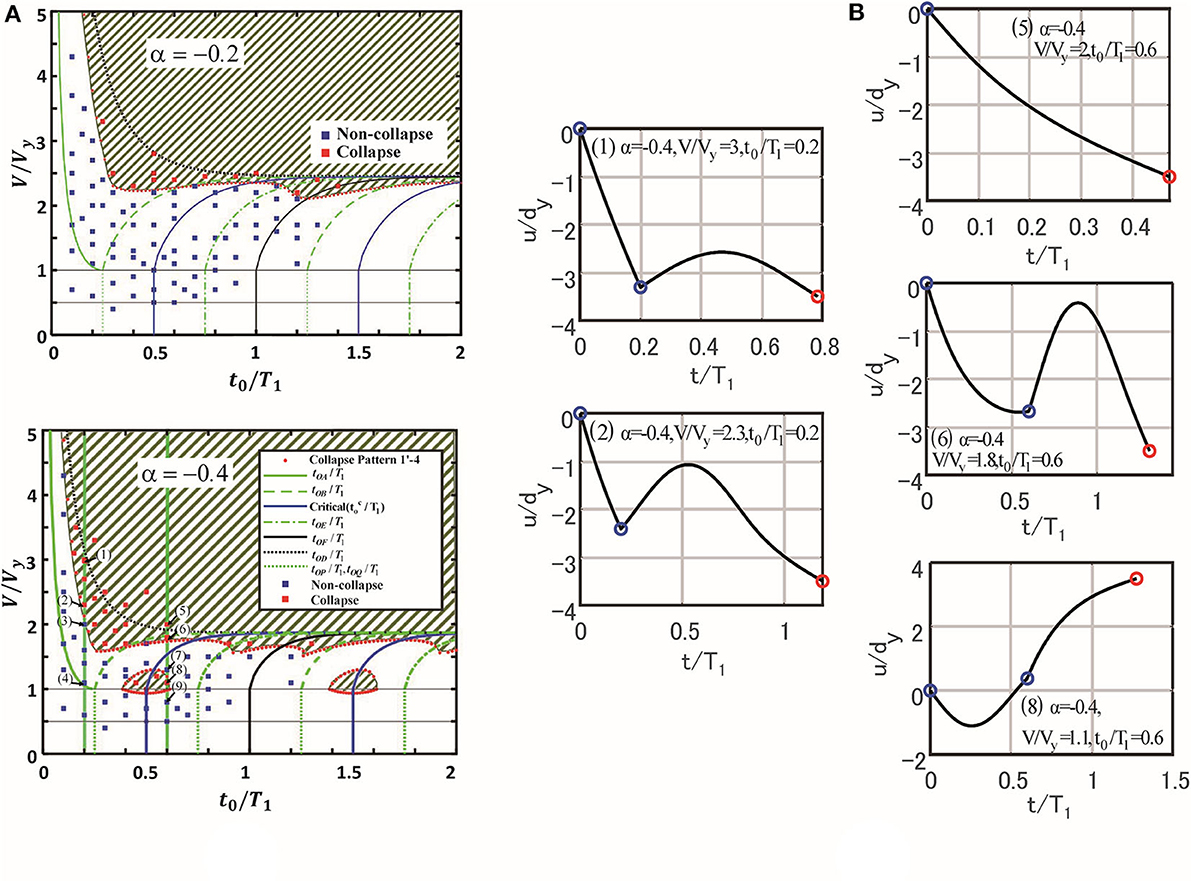
Figure 14. Verification of the proposed collapse limit by time-history response analysis to double impulses with various input velocities and impulse timings. (A) Collapse and non-collapse plot for models with α = −0.2 and −0.4. (B) Displacement time histories of model with α = −0.4 to five inputs (1), (2), (5), (6), (8) shown in (A) (blue marks indicate double impulse timings and red mark shows collapse state).

Figure 15 presents the 9 restoring-force characteristics corresponding to various combinations of the impulse timing and the input velocity level shown in Figure 14 (blue marks indicate the double impulse timings and red mark shows the collapse state). The cases (1), (2), (5), (6), (8) exhibit collapse behaviors. The response behaviors can be well-understood from these figures.

FIGURE 15

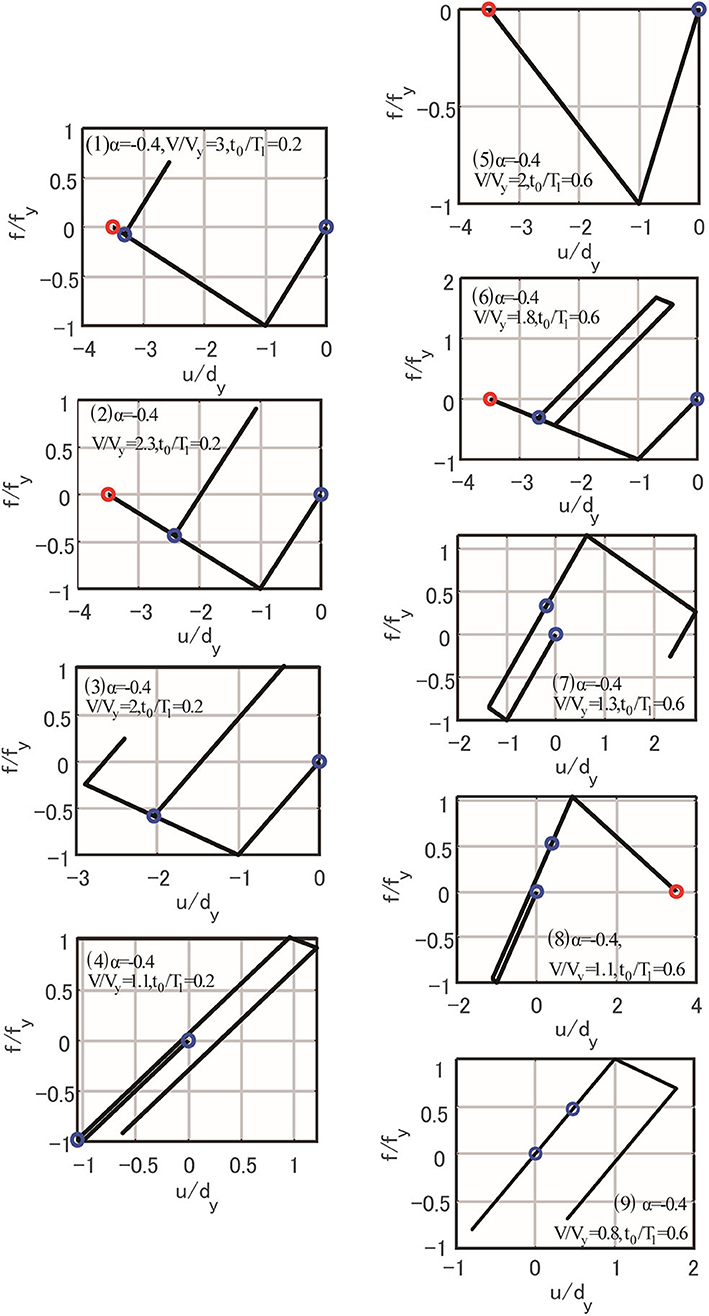
Figure 15. Restoring-force characteristics corresponding to various combinations of impulse timing and input velocity level (blue marks indicate double impulse timings and red mark shows collapse state).

Conclusions

A dynamic collapse criterion for elastic–plastic structures under double impulse as a substitute of a near-fault ground motion has been derived. The conclusions may be summarized as follows:

(1) The use of the double impulse enables the efficient use of the energy approach in the derivation of explicit expressions of a complicated elastic–plastic response of structures with the P-delta effect.

(2) In contrast to the previous work (Kojima and Takewaki, 2016b) for the resonant critical case, a general collapse criterion is provided for the velocity amplitude and the frequency of the double impulse. It is significant that no iteration is needed in the derivation of the dynamic collapse criterion.

(3) Discussions on several patterns of dynamic collapse behaviors introduced in the previous critical case are useful for deriving a boundary between the collapse and the non-collapse in the plane of the input velocity and the input frequency.

(4) The most important point to be remarked is that the critical state (Kojima and Takewaki, 2016b) corresponding to the non-linear resonance does not necessarily provide the minimum input velocity level with respect to arbitrary impulse timing.

(5) The validity of the proposed collapse criterion has been investigated by the numerical response analysis for structures under double impulses with collapse or non-collapse parameters. It has been confirmed that the proposed criterion has a reasonable accuracy.

The present paper dealt with an undamped system. This is because, if a damped system is treated, the formulation is too complicated even for the case of critical input (Saotome et al., 2019). The discussion on the damped system may be the future work.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

SH formulated the problem, conducted the computation, and wrote the paper. KK conducted the computation and discussed the results. IT supervised the research and wrote the paper. All authors contributed to the article and approved the submitted version.

Funding

Part of the present work was supported by the Grant-in-Aid for Scientific Research (KAKENHI) of Japan Society for the Promotion of Science (Nos. 17K18922, 18H01584). This support is greatly appreciated.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Adam, C., and Jager, C. (2012). “Dynamic instabilities of simple inelastic structures subjected to earthquake excitation,” in Advances Dynamics and Model-based Control of Structures and Machines, eds H. Irschik, M. Krommer, and A. K. Belyaev (Wien: Springer).

Google Scholar

Alavi, B., and Krawinkler, H. (2004). Behaviour of moment resisting frame structures subjected to near-fault ground motions. Earthquake Eng. Struct. Dyn. 33, 687–706. doi: 10.1002/eqe.369

CrossRef Full Text | Google Scholar

Araki, Y., and Hjelmstad, K. D. (2000). Criteria for assessing dynamic collapse of elastoplastic structural systems. Earthquake Engng. Struct. Dyn. 29, 1177–1198. doi: 10.1002/1096-9845(200008)29:8<1177::AID-EQE963>3.0.CO;2-E

CrossRef Full Text | Google Scholar

Bernal, D. (1987). Amplification factors for inelastic dynamic p- effects in earthquake analysis. Earthquake Engng. Struct. Dyn. 15, 635–651. doi: 10.1002/eqe.4290150508

CrossRef Full Text | Google Scholar

Bernal, D. (1998). Instability of buildings during seismic response. Eng. Struct. 20, 496–502. doi: 10.1016/S0141-0296(97)00037-0

CrossRef Full Text | Google Scholar

Bertero, V. V., Mahin, S. A., and Herrera, R. A. (1978). Aseismic design implications of near-fault San Fernando earthquake records. Earthquake Eng. Struct. Dyn. 6, 31–42. doi: 10.1002/eqe.4290060105

CrossRef Full Text | Google Scholar

Bray, J. D., and Rodriguez-Marek, A. (2004). Characterization of forward-directivity ground motions in the near-fault region. Soil Dyn. Earthquake Eng. 24, 815–828. doi: 10.1016/j.soildyn.2004.05.001

CrossRef Full Text | Google Scholar

Casapulla, C. (2015). On the resonance conditions of rigid rocking blocks. Int. J. Eng. Tech. 7, 760–771.

Google Scholar

Casapulla, C., and Maione, A. (2017). Critical response of free-standing rocking blocks to the intense phase of an earthquake. Int. Rev. Civil Eng. 8, 1–10. doi: 10.15866/irece.v8i1.11024

CrossRef Full Text | Google Scholar

Caughey, T. K. (1960a). Sinusoidal excitation of a system with bilinear hysteresis. J. Appl. Mech. 27, 640–643. doi: 10.1115/1.3644075

CrossRef Full Text | Google Scholar

Caughey, T. K. (1960b). Random excitation of a system with bilinear hysteresis. J. Appl. Mech. 27, 649–652. doi: 10.1115/1.3644077

CrossRef Full Text | Google Scholar

Challa, V. R. M., and Hall, J. F. (1994). Earthquake collapse analysis of steel frames. Earthquake Engng. Struct. Dyn. 23, 1199–1218. doi: 10.1002/eqe.4290231104

CrossRef Full Text | Google Scholar

Chatzis, M. N., and Smyth, A. W. (2012). Robust modeling of the rocking problem. J. Eng. Mech. ASCE. 138, 247–262. doi: 10.1061/(ASCE)EM.1943-7889.0000329

CrossRef Full Text | Google Scholar

Drenick, R. F. (1970). Model-free design of aseismic structures. J. Eng. Mech. Div. ASCE, 96, 483–493.

Google Scholar

Ger, J.-F., Cheng, Y., and Lu, L. W. (1993). Collapse behavior of Pino Suarez building during 1985 Mexico City earthquake. J. Struct. Eng. ASCE 119, 852–870. doi: 10.1061/(ASCE)0733-9445(1993)119:3(852)

CrossRef Full Text | Google Scholar

Hall, J. F. (1998). Seismic response of steel frame buildings to near-source ground motions. Earthquake Engng. Struct. Dyn. 27, 1445–1464. doi: 10.1002/(SICI)1096-9845(199812)27:12<1445::AID-EQE794>3.0.CO;2-C

PubMed Abstract | CrossRef Full Text | Google Scholar

Hall, J. F., Heaton, T. H., Halling, M. W., and Wald, D. J. (1995). Near-source ground motion and its effects on flexible buildings. Earthuake Spectra 11, 569–605. doi: 10.1193/1.1585828

CrossRef Full Text | Google Scholar

Hayden, C. P., Bray, J. D., and Abrahamson, N. A. (2014). Selection of near-fault pulse motions. J. Geotechn. Geoenviron. Eng. ASCE 140, 04014030. doi: 10.1061/(ASCE)GT.1943-5606.0001129

CrossRef Full Text | Google Scholar

Herrmann, G. (editor)., (1965). “Dynamic stability of structures,” in Proceedings of an International Conference Held at Northwestern University, Evanston, Illinois (Oxford, Northwestern University: Pergamon Press).

Google Scholar

Hjelmstad, K. D., and Williamson, E. B. (1998). Dynamic stability of structural systems subjected to base excitation. Eng. Struct. 20, 425–432. doi: 10.1016/S0141-0296(97)00034-5

CrossRef Full Text | Google Scholar

Ibarra, L. F., and Krawinkler, H. (2005). Global Collapse of Frame Structures Under Seismic Excitations, PEER Center Report 2005/06. Richmond.

Google Scholar

Ishida, S., and Morisako, K. (1985). Collapse of SDOF system to harmonic excitation. J. Eng. Mech. ASCE 111, 431–448. doi: 10.1061/(ASCE)0733-9399(1985)111:3(431)

CrossRef Full Text | Google Scholar

Iwan, W. D. (1961). The dynamic response of bilinear hysteretic systems (Ph.D. thesis). California Institute of Technology, Pasadena.

Google Scholar

Iwan, W. D. (1965a). “The dynamic response of the one-degree-of-freedom bilinear hysteretic system,” in Proceeding of the Third World Conference on Earthquake Engineering (Auckland and Wellington). doi: 10.1115/1.3625711

CrossRef Full Text | Google Scholar

Iwan, W. D. (1965b). The steady-state response of a two-degree-of-freedom bilinear hysteretic system. J. Appl. Mech. 32, 151–156.

Google Scholar

Jarernprasert, S., Bazan, E., and Bielak, J. (2013). Seismic soil-structure interaction response of inelastic structures. Soil Dyn. Earthquake Eng. 47, 132–143. doi: 10.1016/j.soildyn.2012.08.008

CrossRef Full Text | Google Scholar

Jennings, P. C., and Husid, R. (1968). Collapse of yielding structures during earthquakes. J. Eng. Mech. ASCE 94, 1045–1065.

Google Scholar

Kalkan, E., and Kunnath, S. K. (2006). Effects of fling step and forward directivity on seismic response of buildings. Earthquake Spectra 22, 367–390. doi: 10.1193/1.2192560

CrossRef Full Text | Google Scholar

Khaloo, A. R., Khosravi,1, H., and Hamidi Jamnani, H. (2015). Nonlinear interstory drift contours for idealized forward directivity pulses using “Modified Fish-Bone” models. Advanc. Struct. Eng. 18, 603–627. doi: 10.1260/1369-4332.18.5.603

CrossRef Full Text | Google Scholar

Kojima, K., Fujita, K., and Takewaki, I. (2015). Critical double impulse input and bound of earthquake input energy to building structure. Front. Built Environ. 1:5. doi: 10.3389/fbuil.2015.00005

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015a). Critical earthquake response of elastic-plastic structures under near-fault ground motions (part 1: Fling-step input). Front. Built Environ. 1:12. doi: 10.3389/fbuil.2015.00012

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015b). Critical earthquake response of elastic-plastic structures under near-fault ground motions (Part 2: Forward-directivity input). Front. Built Environ. 1:13. doi: 10.3389/fbuil.2015.00013

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015c). Critical input and response of elastic-plastic structures under long-duration earthquake ground motions. Front. Built Environ. 1:15. doi: 10.3389/fbuil.2015.00015

PubMed Abstract | CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2016a). Closed-form critical earthquake response of elastic-plastic structures on compliant ground under near-fault ground motions. Front. Built Environ. 2:1. doi: 10.3389/fbuil.2016.00001

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2016b). Closed-form dynamic stability criterion for elastic-plastic structures under near-fault ground motions. Front. Built Environ. 2:6. doi: 10.3389/fbuil.2016.00006

CrossRef Full Text | Google Scholar

Maier, G., and Perego, U. (1992). Effects of softening in elastic-plastic structural dynamics. Int. J. Numerical Methods Eng. 34, 319–347. doi: 10.1002/nme.1620340120

CrossRef Full Text | Google Scholar

Makris, N., and Black, C. J. (2004). Dimensional analysis of rigid-plastic and elastoplastic structures under pulse-type excitations. J. Eng. Mech. ASCE 130, 1006–1018. doi: 10.1061/(ASCE)0733-9399(2004)130:9(1006)

CrossRef Full Text | Google Scholar

Makris, N., and Vassiliou, M. F. (2013). Planar rocking response and stability analysis of an array of free-standing columns capped with a freely supported rigid beam. Earthquake Eng. Struct. Dyn. 42, 431–449. doi: 10.1002/eqe.2222

CrossRef Full Text | Google Scholar

Mavroeidis, G. P., Dong, G., and Papageorgiou, A. S. (2004). Near-fault ground motions, and the response of elastic and inelastic single-degree-freedom (SDOF) systems. Earthquake Eng. Struct. Dyn. 33, 1023–1049. doi: 10.1002/eqe.391

CrossRef Full Text | Google Scholar

Mavroeidis, G. P., and Papageorgiou, A. S. (2003). A mathematical representation of near-fault ground motions. Bull. Seism. Soc. Am. 93, 1099–1131. doi: 10.1785/0120020100

CrossRef Full Text | Google Scholar

Minami, H., and Hayashi, Y. (2013). Response characteristics evaluation of elastic shear beam for pulse waves. J. Struct. Constr. Eng. AIJ 685, 453–461. doi: 10.3130/aijs.78.453

CrossRef Full Text | Google Scholar

Moustafa, A., Ueno, K., and Takewaki, I. (2010). Critical earthquake loads for SDOF inelastic structures considering evolution of seismic waves. Earthquakes Struct. 1, 147–162. doi: 10.12989/eas.2010.1.2.147

CrossRef Full Text | Google Scholar

Mukhopadhyay, S., and Gupta, V. K. (2013a). Directivity pulses in near-fault ground motions—I: identification, extraction and modeling. Soil Dyn. Earthquake Eng. 50, 1–15. doi: 10.1016/j.soildyn.2013.02.017

CrossRef Full Text | Google Scholar

Mukhopadhyay, S., and Gupta, V. K. (2013b). Directivity pulses in near-fault ground motions—II: estimation of pulse parameters. Soil Dyn. Earthquake Eng. 50, 38–52. doi: 10.1016/j.soildyn.2013.02.019

CrossRef Full Text | Google Scholar

Nabeshima, K., Taniguchi, R., Kojima, K., and Takewaki, I. (2016). Closed-form overturning limit of rigid block under critical near-fault ground motions. Front. Built Environ. 2:9. doi: 10.3389/fbuil.2016.00009

CrossRef Full Text | Google Scholar

Nakajima, A., Abe, H., and Kuranishi, S. (1990). Effect of multiple collapse modes on dynamic failure of structures with structural instability. Struct. Eng. Earthquake Eng. JSCE 7, 1s–11s. doi: 10.2208/jscej.1990.416_13

CrossRef Full Text | Google Scholar

Rupakhety, R., and Sigbjörnsson, R. (2011). Can simple pulses adequately represent near-fault ground motions? J. Earthquake Eng. 15,1260–1272. doi: 10.1080/13632469.2011.565863

CrossRef Full Text | Google Scholar

Saotome, Y., Kojima, K., and Takewaki, I (2019). Collapse-limit input level of critical double impulse for damped bilinear hysteretic SDOF system with negative post-yield stiffness. Front. Built Environ. 5:106. doi: 10.3389/fbuil.2019.00106

CrossRef Full Text | Google Scholar

Sasani, M., and Bertero, V. V. (2000). “Importance of severe pulse-type ground motions in performance-based engineering: historical and critical review,” in Proceedings of the Twelfth World Conference on Earthquake Engineering (Auckland).

Google Scholar

Sivaselvan, M. V., Lavan, O., Dargush, G. F., Kurino, H., Hyodo, Y., Fukuda, R., et al. (2009). Numerical collapse simulation of large-scale structural systems using an optimization-based algorithm. Earthquake Engng Struct. Dyn. 38, 655–677. doi: 10.1002/eqe.895

CrossRef Full Text | Google Scholar

Sun, C.-K., Berg, G. V., and Hanson, R. D. (1973). Gravity effect on single-degree inelastic system. J. Eng. Mech. Div. ASCE 99, 183–200.

Google Scholar

Takewaki, I. (2002). Robust building stiffness design for variable critical excitations. J. Struct. Eng. ASCE 128, 1565–1574. doi: 10.1061/(ASCE)0733-9445(2002)128:12(1565)

CrossRef Full Text | Google Scholar

Takewaki, I. (2007). Critical Excitation Methods in Earthquake Engineering, Elsevier, Amsterdam, 2nd Edn in 2013 (London: Elsevier).

Google Scholar

Takizawa, H., and Jennings, P. C. (1980). Collapse of a model for ductile reinforced concrete frames under extreme earthquake motions. Earthquake Engng Struct. Dyn. 8, 117–144. doi: 10.1002/eqe.4290080204

CrossRef Full Text | Google Scholar

Tanabashi, R., Nakamura, T., and Ishida, S. (1973). “Gravity effect on the catastrophic dynamic response of strain-hardening multi-story frames,” in Proceedings of 5th World Conference. on Earthquake Engineering (Rome), 2140–2149.

Google Scholar

Uetani, K., and Tagawa, H. (1998). Criteria for suppression of deformation concentration of building frames under severe earthquakes. Eng. Struct. 20, 372–383. doi: 10.1016/S0141-0296(97)00021-7

CrossRef Full Text | Google Scholar

Vafaei, D., and Eskandari, R. (2015). Seismic response of mega buckling-restrained braces subjected to fling-step and forward-directivity near-fault ground motions. Struct. Design Tall Spec. Build. 24, 672–686. doi: 10.1002/tal.1205

CrossRef Full Text | Google Scholar

Williamson, E. B., and Hjelmstad, K. D. (2001). Nonlinear dynamics of a harmonically-excited inelastic inverted pendulum. J. Eng. Mech. ASCE 127, 52–57. doi: 10.1061/(ASCE)0733-9399(2001)127:1(52)

CrossRef Full Text | Google Scholar

Xu, Z., Agrawal, A. K., He, W.-L., and Tan, P. (2007). Performance of passive energy dissipation systems during near-field ground motion type pulses. Eng. Struct. 29, 224–236. doi: 10.1016/j.engstruct.2006.04.020

CrossRef Full Text | Google Scholar

Yamamoto, K., Fujita, K., and Takewaki, I. (2011). Instantaneous earthquake input energy and sensitivity in base-isolated building, Struct. Design Tall Spec. Build. 20, 631–648. doi: 10.1002/tal.539

CrossRef Full Text | Google Scholar

Yang, D., and Zhou, J. (2015). A stochastic model and synthesis for near-fault impulsive ground motions. Earthquake Eng. Struct. Dyn. 44, 243–264. doi: 10.1002/eqe.2468

CrossRef Full Text | Google Scholar

Zhai, C., Chang, Z., Li, S., Chen, Z.-Q., and Xie, L. (2013). Quantitative identification of near-fault pulse-like ground motions based on energy. Bull. Seism. Soc. Am. 103, 2591–2603. doi: 10.1785/0120120320

CrossRef Full Text | Google Scholar