- 1Key Laboratory of Earthquake Engineering and Engineering Vibration, Institute of Engineering Mechanics, China Earthquake Administration, Harbin, China
- 2Civil and Construction Engineering Department, Western Michigan University, Kalamazoo, MI, United States
Shaking table substructure testing (STST) takes the substructure with complex behavior physically tested, with the behavior of the rest structural system being numerically simulated. This substructure testing allows the payload of a shaking table being fully utilized in testing of the most concerned part, thus significantly increases its loading capacity. The key to achieve a successful STST is to coordinate among the substructures, specifically, to satisfy compatibility, equilibrium, and synchronization at the boundary between numerical and experimental substructures. A number of studies have focused on the essential techniques of STST, and several applications have been carried out. Nonetheless, its progress is still in the preliminary stage, because of the limited applications using multi-directional shaking tables on large-scale specimens. This paper reviews a series of STSTs and their associated implementation aspects including hybrid testing frameworks, time integration algorithms, delay compensation methods, shaking table and actuator control schemes and boundary force measurement methods. The key techniques required for a successful test are also stressed, such as the force control of actuators to coordination among the substructures. Finally, challenges for future studies and applications are identified and presented.
Introduction
Shaking table test is one of the most effective ways to reproduce earthquake excitations on engineering structures by imposing a predefined earthquake ground motion at the base of a structural model. However, the testing capacity of a shaking table is often restricted by the effective payload it can support. Localized damages within a structural system are difficult to be captured using small-scale specimens weighing tens to hundreds of tons. This is the reason why shaking tables are often used to examine the global performance of a structure, but rarely on the behavior of its components. To maximize the use of available shaking table testing capacity, several methods have been proposed and applied. Some applications employed rigid frames or foundations with larger space to extend the testing area of shaking tables (Xiong et al., 2008; Ba et al., 2017; Jia et al., 2017; He et al., 2018). Although the frames and foundations consume some effective payload, they are beneficial in testing relatively light and large space specimens, such as wooden buildings and large space structures. The testing capacity can be significantly increased by constructing shaking table array (Soroushian et al., 2016; Xie et al., 2019), where several shaking tables can be flexibly configured to test long-span bridges or large space structures. Large size shaking tables, such as the largest shaking table of the world, E-Defense in Japan, and the largest outdoor shaking table in the US, are able to test large-scale to even full-scale specimens (Kim et al., 2012; Astroza et al., 2016). Although they are featured with thousands of tons of payload capacity, they are not necessarily adequate to test the entire engineering structure at acceptable scale ratio. Therefore, there is still a need to develop testing techniques for shaking tables. For example, a substructure test using the E-Defense shaking table was realized using an offline control scheme (Ji et al., 2009). To achieve large displacement and velocity responses at the top of a high-rise building, which exceeded the shaking table capacity, a rubber-mass system was designed and inserted between the table and the specimen to amplify the table input. This method, however, relies significantly on the dynamics of the target structure and characteristics of the amplifier mechanism.
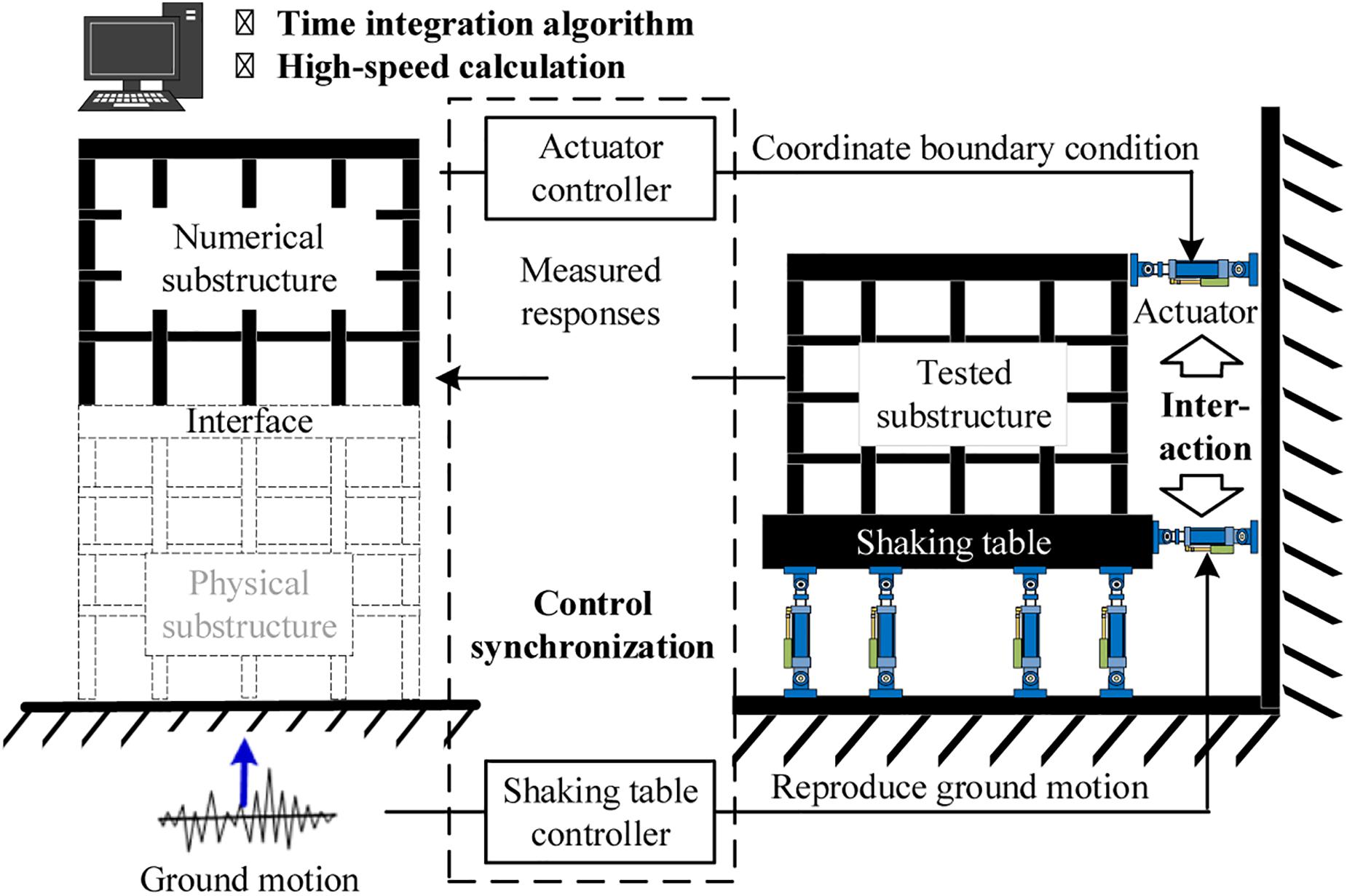
Online hybrid test (Wu et al., 2007; Gao et al., 2013; Sarebanha et al., 2019) is able to test large-scale specimens, where the dynamics of the entire structural system are solved in the computer domain with restoring forces obtained from the physical specimen. When employing the substructure technique, its testing capacity can be further extended. It is promising to combine the substructure hybrid testing technique with the shaking table testing method, namely shaking table substructure test (STST), which will provide not only a larger testing capacity, but also the flexibility in dealing with various types of specimens. In an STST as shown in Figure 1, the most concerned part is physically tested, while the rest is numerically simulated, thus significantly increasing the loading capacity through the substructure testing and becoming a potential solution to address the scale challenge faced by traditional shaking table tests. STST (Horiuchi et al., 2000; Igarashi et al., 2000; Lee et al., 2007; Wang and Tian, 2009; Wang et al., 2010; Shao et al., 2011; Nakata and Stehman, 2012; Mosalam and Günay, 2014; Xu et al., 2014; Stefanaki and Sivaselvan, 2018) was proposed at the beginning of this century and has caught more attention recently because of the large number of shaking tables and shaking table arrays constructed in China. STST, although appealing to extend the testing capacity of shaking table, is not easy to be implemented due to the difficulties in maintaining the compatibility and equilibrium at the boundaries in the space domain, while ensuring the synchronization between substructures in the time domain. Since most shaking tables are designed to reproduce a predefined acceleration time history, it is challenging to realize the boundary condition between substructures using a shaking table, which is often solved step by step during a STST. The control strategy of shaking tables, such as the tri-variable control method, is quite different from the control method of a single actuator often used in real-time hybrid test, further hindering the development of STST. The knowledge accumulated from real-time hybrid test may not be directly applicable in STST. Despite all these difficulties, STST has been developed and advanced significantly in the past two decades. It is the intention of this paper to review these progresses and identify potential challenges for future studies.
This paper firstly introduces the successful cases of STSTs applied in civil engineering, which can be categorized into two groups based on boundary implementation. The frameworks developed in these applications are reviewed next. Key techniques developed and adopted in STST are summarized, including time integration algorithms, delay compensation methods, and shaking table control schemes. The force control of actuators to coordinate substructures is specifically discussed together with boundary force measurement methods. Finally, challenges for future studies and applications are identified and presented.
State-Of-The-Art and State-Of-The-Practice of STST
Shaking table substructure testing was first proposed in Japan and then studied extensively in the United States. Because of the construction upsurge of shaking tables in China, this technology has caught a lot of attention from both Chinese academia and engineers. This section introduces several STST frameworks developed in the past two decades. The configurations and applications are summarized first. Then the procedures are compared for two types of STST which are categorized based on substructure patterns. Finally, a typical hardware integration is described for researchers who may be interested in building their own STST system.
Current Studies and Applications of STST
Early Studies Around the Year 2000
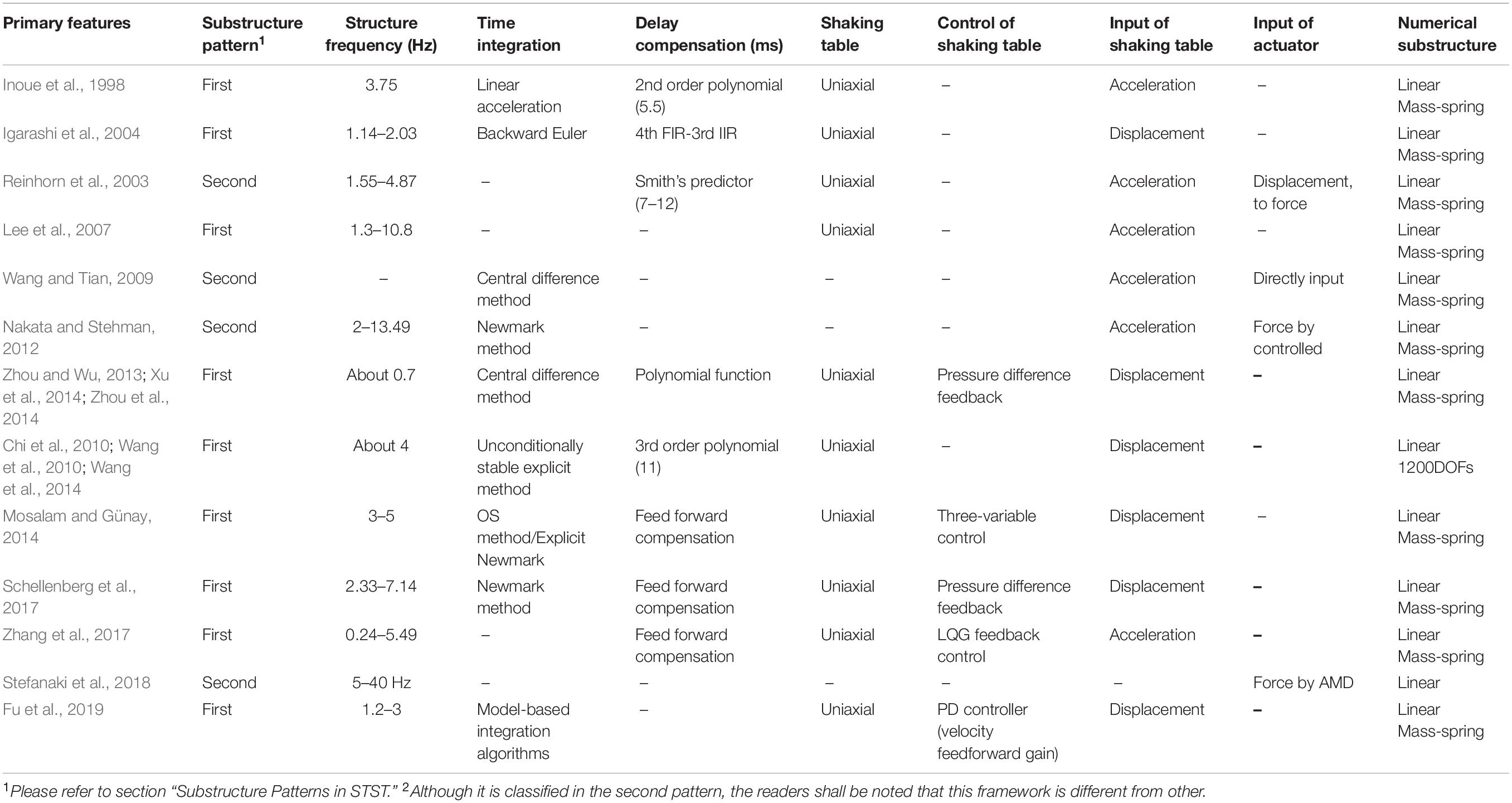
Shaking table substructure testing was first proposed in Japan to examine soil-foundation interaction effects (Konagai et al., 1998). In the same period, Inoue proposed a STST system to test mechanical systems, which was later applied to test a secondary structural system attached to a primary structural system (Inoue et al., 1998; Horiuchi et al., 2000). In this application, a uniaxial shaking table was utilized to load the secondary system, while the primary structure was numerically simulated. The fundamental frequency of the target structure was 3.75 Hz. A linear acceleration method was employed to solve the equation of motion of the structural system subject to the ground motion based on the measured reaction force from the secondary system. Because of the inherent time difference between the numerical simulation and the physical testing, the shaking table command was predicted by extrapolating following an n-th order polynomial function. It was also found out that the stability of the STST was closely related to the order of the polynomial function. If a second order function is used, the mass ratio of the secondary system over the primary system shall be less than 1/7 to maintain the stability. The total delay of the shaking table and the numerical simulation was 5.5 ms, was successfully compensated using a second-order function in the STST. Nearly identical responses were observed between the pure numerical simulation and the STST test.
Igarashi (Igarashi et al., 2000) reported a similar framework of STST. They derived the response of the entire system to the input as a transfer function considering the shaking table delay. It was found out that the mass ratio between the experimental substructure and the numerical substructure should be sufficiently small to achieve reliable testing result. For this reason, they believed that the STST system was ideal to test secondary systems in a building structure. For example, they conducted STST on the tuned mass damper (TMD) and the tuned liquid damper (TLD) which were at the top of the numerically simulated building structure (Igarashi et al., 2004). This numerical substructure was solved by the backward Euler method because of its computational efficacy. The measured base shear of the TMD or TLD was fed back and combined with the ground motion to formulate the input to the numerical simulation. The calculated roof displacement was used to drive the shaking table. To compensate the delay, a fourth-order finite-impulse-response (FIR) filter was employed to approximate the transfer function of the uniaxial shaking table, while the amplitude amplification introduced by this FIR phase-lead filter was mitigated using a third-order low-pass Butterworth infinite-impulse-response (IIR) filter as a pre-conditioner to the FIR filter. Testing was carried out on the TMD (natural frequency of 2.03 Hz) and the TLD (natural frequency of 1.14 Hz), respectively, demonstrating the feasibility of the proposed STST system.
In 2007, Lee (Lee et al., 2007) conducted a STST on a five-story building where the top two stories were selected as the experimental substructure while the rest was numerically simulated. The first five natural frequencies of the building structure ranged from 1.3 to 10.8 Hz, while the experimental substructure had two inherent frequencies of 2.5 and 8.6 Hz. The coordinated motion between the two substructures was implemented by a uniaxial shaking table with the input calculated from the numerical simulation based on the force feedback from the experimental substructure and the ground motion. To faithfully exert the absolute acceleration reference signal generated by the numerical simulation to the experimental substructure, an inverse transfer function of the measured acceleration with respect to the command signal was developed and adopted in the shaking table controller to overcome the distortion induced by the inherent dynamics of the shaking table. The test results agreed well with the numerical simulation. However, unexpected vibration of the experimental substructure was observed and passed onto the numerical simulation through force feedback. To overcome this distortion, a heavily damped experimental substructure was suggested by the authors.
Recent Studies From 2007
The above studies initiated further development of STST testing methods with more exemplary experiments. The stability of STST systems was also analyzed considering the delay due to numerical simulations and shaking tables. These studies are deemed preliminary because the substructure scheme, the shaking table controller, and the boundary coordination are relatively simple. For example, the substructure scheme of these STST tests usually took the upper stories of or secondary systems above a building structure as the experimental substructure. However, most structures suffer more seismic damages at the bottom. To extend STST application scope, more studies were performed.
Reinhorn (Reinhorn et al., 2003, 2005) proposed a unified formulation for all real-time hybrid tests using a mass-splitting coefficient and a load-splitting coefficient. This unified formulation is capable of representing various testing methods, including the traditional hybrid testing, effective force testing, real-time hybrid testing and STST, by selecting different values of the splitting coefficients. The force-based feature of this unified formulation allows easy implementation of STST. However, this leads to the challenge of actuator force control due to specimens’ resonant response and actuators’ internal friction. To address this challenge, the authors proposed to convert the closed-loop force control into a closed-loop displacement control by adding a flexible spring compliance between the specimen and the actuator. With this idea, Shao (Shao, 2007; Shao et al., 2011) built up a modularized unified real-time hybrid testing framework, including data acquisition, real-time hybrid simulator, and testing controller, which is further described in section “A Typical Hardware Configuration of STST.” A uniaxial shaking table and an actuator were employed as the loading devices in the framework to apply ground excitation and interface force at boundaries. Five testing cases of a three-story model with the natural frequencies from 1.55 to 4.87 Hz were defined based on the mass-splitting and load-splitting coefficients and examined. To compensate the time delay in the shaking table and the actuator as well as the time delay difference between the two loading devices, which ranged from 7 to 12 ms, the Smith’s predictor was adopted. The test results well demonstrated the concept of the unified formulation of dynamic hybrid testing and the effectiveness of boundary control techniques.
A similar concept was adopted by Nakata (Nakata and Stehman, 2012) to develop a STST system. To formulate the boundary conditions between experimental and numerical substructures, the boundaries were categorized into three types: (1) the experimental acceleration compatibility provides ground motion at the bottom of the experimental substructure; (2) the computational acceleration compatibility specifies absolute acceleration measured at the top of the experimental substructure to the upper numerical substructure; and (3) the interface force compatibility exerts the reaction force obtained from the numerical substructure onto the top of the experimental substructure. The computational acceleration compatibility and the interface force compatibility guaranteed the equilibrium and compatibility of the boundary between the two substructures. To bypass the difficulty of actuator force control, the authors utilized a controlled mass to apply the interface force onto the experimental substructure. A numerical study was conducted to demonstrate the feasibility of the proposed STST system where a five-story building was the prototype structure. The natural frequencies of the building ranged from 2 to 13.49 Hz. The bottom two stories were selected as the experimental substructure, while the rest was numerically simulated using the Newmark-family integration method. The results indicated a well reproduction of the target force history of the actuator through the controlled mass scheme.
Mosalam (Günay and Mosalam, 2014; Mosalam and Günay, 2014) proposed a STST system based on a uniaxial shaking table, which was employed to test electricity disconnect switches. The supporting frame of the disconnect switch was simulated numerically, while the disconnect switch on top of the supporting frame was experimentally tested on the shaking table. The natural frequencies of the numerical and the experimental substructures were about 3 and 5 Hz, respectively. The displacement at the interface between the two substructures became the input to the shaking table, while the force measured from the shaking table was fed back to the numerical substructure. To keep up the real-time loading required in the STST, the explicit Newmark integration method with a small time step of 1ms was adopted. Meanwhile, to compensate the time delay, a feed-forward error compensation scheme was developed based on a predicted error function with respect to the actuator velocity. In this study, the uniaxial shaking table is displacement-controlled, similar to those actuators used in a typical real-time hybrid testing. To achieve more accurate shaking table control, the authors developed an advanced control method based on the three-variable control (TVC) scheme (Günay and Mosalam, 2015). This STST system was later applied to substation structure, where a three-dimensional numerical substructure was efficiently solved by the operator-splitting integration method formulated for the real-time hybrid testing.
Schellenberg (Schellenberg et al., 2017) carried out a series of STST tests to examine the seismic performance of buildings with midlevel seismic isolations. The isolated superstructure, consisting of a two-story steel moment frame supported by six triple friction pendulum bearings, were physically tested on the table while the portion below was numerically modeled. The natural frequencies of the isolated superstructure in the first and second sliding stages were about 0.76 and 0.53 Hz, respectively. The first two frequencies of the fixed-base superstructure were approximately 2.33 and 7.14 Hz. The maximum frequency of the entire building was nearly 16 Hz. A lumped mass shear type building model was used. Explicit time integration algorithms, such as the explicit Newmark method, the explicit generalized alpha method and the generalized alpha-OS method, were examined in the STST tests. OpenFresco served as the middleware to coordinate the numerical substructure with the experimental superstructure through the transfer system (i.e., the shaking table). The absolute displacement at the top of the numerical substructure was used as the input to the shaking table and the corresponding story shear force was fed back to the numerical substructure. Derivative feedforward (FF) and differential pressure controls included in an MTS-493 real-time controller were used to compensate the time delay of the transfer system and to suppress the resonance around the oil column frequency. It was recommended that advanced delay compensation techniques and control strategies be adopted to improve tracking performance of the shaking table during STST, especially in the high-frequency range.
A similar study was conducted by Zhang (Zhang et al., 2017) on a 15-story midlevel isolated building. The lumped mass-spring model was used to represent the dynamics of the building structure. Frequencies of interest ranged from 0.24 to 5.49 Hz for the overall structure. In the STST test, the isolated upper six stories including the isolation layer were taken as the experimental substructure, among which the upper six stories was represented by an SDOF specimen with a natural frequency of 0.25 Hz. The lower nine stories were numerically simulated. Instead of the absolute displacement, the absolute acceleration response at the top of the numerical substructure was taken as the target command of the shaking table which served as the transfer system between the numerical and the experimental substructures. Based on a linearized model of the shake table system, a model-based control strategy was developed to accurately track the desired accelerations. The goals of this strategy were to cancel out the modeled dynamics of the shaking table through the feedforward control and to provide robustness against nonlinearities and uncertainties in the testing system through the Linear–Quadratic–Gaussian control.
Recently, Stefanaki (Stefanaki and Sivaselvan, 2018) proposed a new dynamic substructure strategy that can be used for STST. The novel aspect of this substructure strategy is to consider the numerical substructure as part of the boundary loading device so the tracking controller to reproduce the boundary compatibility (i.e., the control-structure interaction) is not required, nor the compensation of actuator delay or the time integration algorithm for the numerical substructure. Specifically, this strategy aims to replicate the behavior of the entire numerical substructure and to physically exert its influence onto the experimental substructure. To achieve this, a device conceptually similar to the one proposed by Nakata (Nakata and Stehman, 2012), called the active mass driver (AMD) was devised. This AMD adopted a simple feedforward approach and was completely decoupled from the experimental substructure. The AMD had two inputs (i.e., the control input and the feedback from the experimental substructure) and one output (i.e., the boundary condition to be imposed onto the experimental substructure). The authors derived transfer functions of the AMD system for both SDOF and two-DOF systems. They claimed that the derivation can be extended to MDOF systems. Note that a high-pass filter is needed if the damping of the system is not proportional to the stiffness. This strategy was experimentally investigated using a testing setup consisting of a shaking table and the AMD (Stefanaki and Sivaselvan, 2018). It was found out that the proposed dynamic substructure controller was effective in imitating numerical substructures with a wide range of frequencies from 5 to 40 Hz. When being applied on an experimental substructure, the interface force was generally reproduced well but with larger discrepancies at higher frequencies even with a 30 Hz low-pass filter. Nonetheless, the ability of this new dynamic substructure scheme using shaking table and the AMD was demonstrated.
Studies and Applications of STST in China
The effectiveness of STST to advance shaking table testing capability also attracted Chinese scholars’ attention. In 2009, Wang (Wang and Tian, 2009) presented the STST method and its application including the substructure coordinating procedure, the time integration method, and the boundary realization methods. In their STST system, the shaking table was used to impose the ground motion to the test specimen while simultaneously loaded by the actuator. The response measured from the specimen was sent to the numerical simulation together with the measured ground motion of the shaking table. The calculated interface force was then sent to the actuator be applied to the test specimen. The modified central difference integration was adopted and the feasibility of actuator force control was explored, but no effective solution was proposed. In the exemplary test, a three-story braced steel frame was first tested on the shaking table. Then the first story was tested as the experimental substructure loaded by the shaking table from the base and the actuator at the first floor. The force history measured from the three-story structure shaking table test was used as the input to the actuator. Although there was some time delay, the test result was relatively accurate. However, the authors claimed the delay should be eliminated in the real STST application.
In 2010, Wang (Wang et al., 2010) reported a real-time hybrid testing system using shaking table. The upper substructure was treated as the experimental substructure and the lower part was the numerical substructure. The shaking table was utilized to realize the boundary compatibility. Similar to the aforementioned STST systems, the boundary displacement or acceleration was the input to the shaking table which was numerically simulated. The measured reaction force from the experimental substructure corresponding to this boundary displacement or acceleration was fed back to the numerical substructure for the next step calculation. Wang et al. (2014) developed an explicit time integration algorithm based on the discrete control theory to efficiently solve the numerical substructure, where both displacement and velocity were explicitly formulated. When using the dual interval scheme, where the dynamics was solved using a larger time step and extrapolated using a smaller step as the command signal, the degrees of freedom of the numerical substructure model may exceed 1200 without jeopardizing the integration stability. The effect of shaking table time delay in STST was also analyzed by the root locus method using the Padé function to approximate the delay. It was found out that the stability of the system depended significantly on the mass ratio of the experimental and numerical substructures. Therefore, a third-order Lagrange polynomial function was suggested to predict the command and compensate the delay, comprehensively considering the stability and accuracy. The authors also suggested that a virtual shaking table (i.e., numerical model of the shaking table) is ideal to tune the control parameters without the risk of damaging physical specimens. Using the proposed STST framework, the authors examined several engineering problems including fluid-structure interaction (Chi et al., 2010) and soil-structure interaction (Wang et al., 2014). In the latter application, the natural frequency of the specimen was about 4.4 Hz. The maximum error in the acceleration response were about 30%. This large error maybe to attributed to the third-order extrapolation function used to compensate the time delay, that resulted in high-frequency error, while the excitation frequency being close to the oil-column resonance frequency.
A similar STST system was developed by Zhou (Zhou and Wu, 2013) which took the upper part of a building model as the experimental substructure and the lower part as the numerical substructure. In this system, the numerical substructure was solved by the central difference method (CMD), and the shaking table was controlled in displacement. To overcome the adverse effect from the oil-column resonance, the pressure difference feedback control was developed to increase the hydraulic damping ratio, so that the noises introduced by the oil-column resonance were mitigated. The effectiveness of this control scheme was demonstrated in the STST test on an SDOF structure. The STST system was applied to a storage tank considering the soil-structure interaction (Xu et al., 2014). The water sloshing frequency was 0.67 Hz. A polynomial function was employed to predict the response and compensate the inherent system delay. Only numerical simulation was conducted, and the feasibility of the proposed STST was preliminarily demonstrated. Using this STST system, an TLD controlled structure with a natural frequency of 0.77 Hz was examined (Zhou et al., 2014). The shear force of the TLD was computed based on the measured acceleration at the based of the TLD. The comparison between the measured acceleration and the command acceleration indicated a noticeable error in the frequency range of 3–25 Hz.
Fu (Fu et al., 2019) conducted comparative STST tests to study vibration control effects of particle dampers (PD) and TLD on structures. The dampers on top of the structure were tested physically, and the structure was simulated numerically by a lumped-mass spring model. Three representative model-based integration algorithms (i.e., the generalized Chen and Ricles (GCR) algorithm, the Chang algorithm and the Kolay and Ricles KR-α algorithm) were adopted to solve the equation of motion, which are all unconditionally stable and have an explicit formulation. Three substructures with frequencies of 1.2, 2, and 3 Hz were simulated by the STST tests. The boundary displacement was taken as the input to the uniaxial shaking table, which was subject to the proportional-derivative (PD) control with an added velocity feedforward gain to improve the control performance.
The primary features of the developed STST systems presented in this section and their applications are summarized in Table 1.
Substructure Patterns in STST
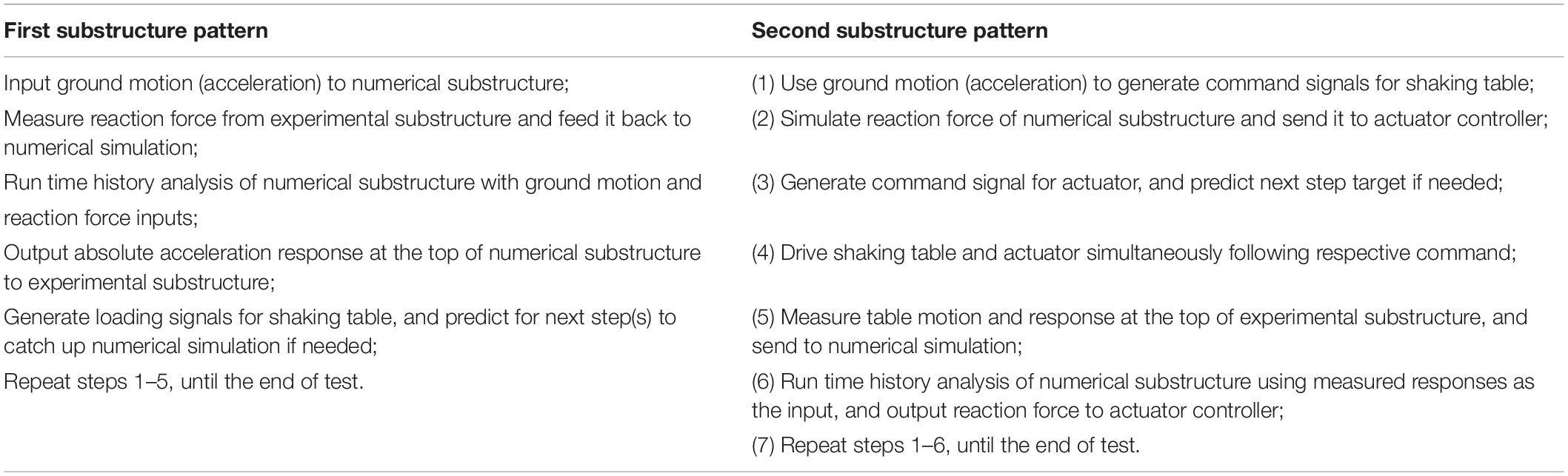
The STST applications introduced above can be classified into two categories based on substructure patterns. It can be seen that early STST tests only tested one substructure using one shaking table as the boundary coordinator, during which the upper part of a structural system was tested while the lower part was numerically simulated, as shown in Figure 2A. Compared with those early studies, recent development adopted a more general substructure pattern through which the tested substructure can be any part of a structural system. This is realized by synchronically using shaking table and actuator, as shown in Figure 2B. Although the unified formulation proposed by Reinhorn (Reinhorn et al., 2003, 2005) is able to describe both substructure patterns, this paper separately discusses these two substructure patterns so that the challenges in controlling shaking table and actuator can be explained separately.
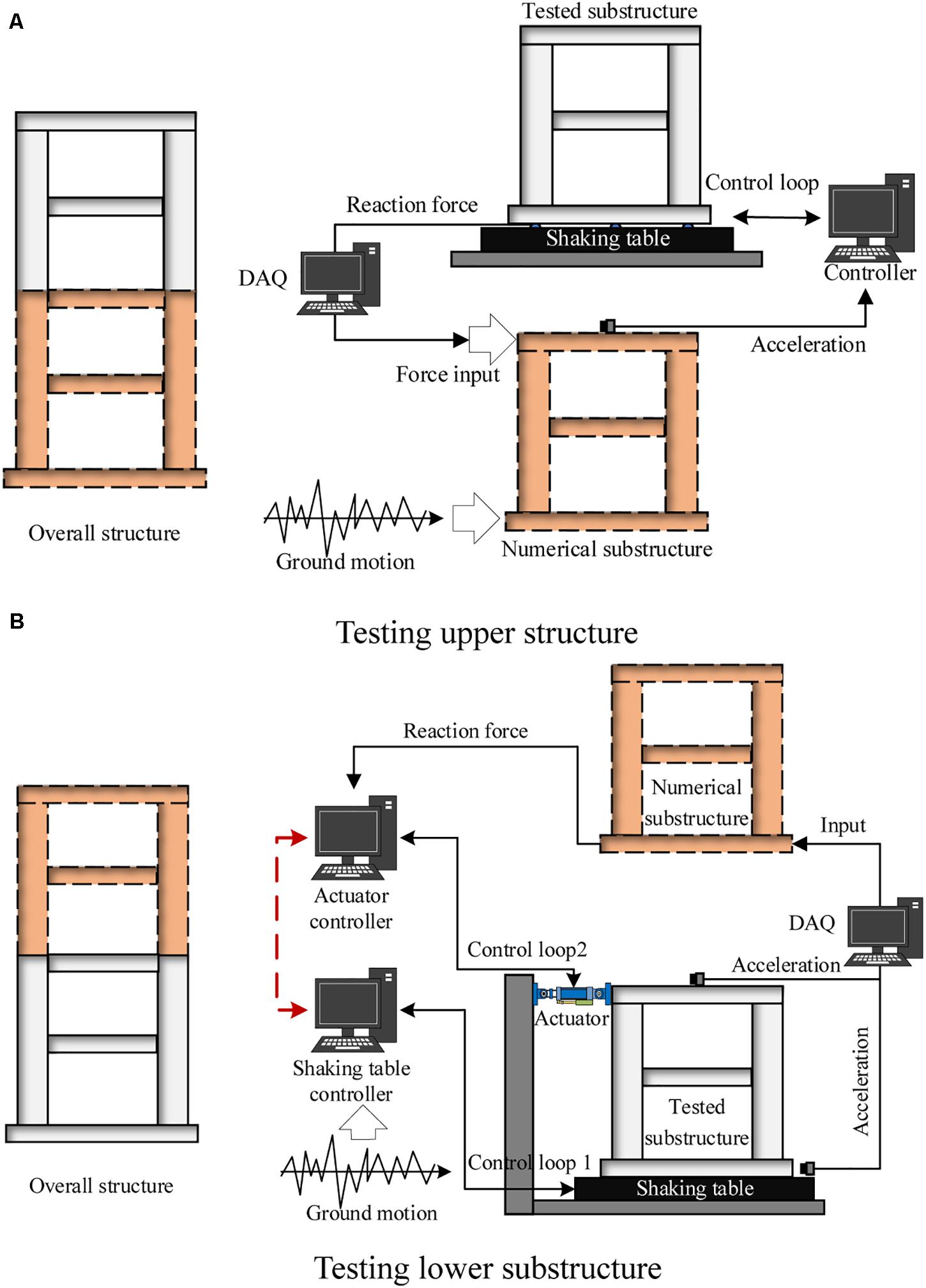
Figure 2. Substructure patterns in STST. (A) Testing upper structure. (B) Testing lower substructure.
In the first pattern, the upper structure is tested on a shaking table and the rest is numerically simulated. The response at the top of the numerical substructure, usually acceleration, is taken as the input of the shaking table to be imposed to the experimental substructure. The base shear of the experimental substructure is measured and sent to the numerical substructure as one input and earthquake ground motion is the other input. In this procedure, a closed-loop is formed from sending the acceleration response to the experimental substructure and the measured reaction force being fed back as the input. This closed-loop STST has to be conducted in real time. To achieve this, the response of the numerical substructure needs to be solved very efficiently, as is done in many real-time hybrid tests (Nakashima et al., 1992; Chen et al., 2012; Phillips and Spencer, 2013b; Ou et al., 2015). Therefore, techniques developed in these real-time hybrid tests can be directly applied herein, such as the polynomial-based prediction and the unconditionally stable explicit time integration algorithms. The difference between the STST using this substructure pattern and the real-time hybrid tests lies in the realization of the boundary condition using shaking table instead of actuator. However, the control scheme of the shaking table used in STST is significantly different from that used in the traditional shaking table tests. The input to the shaking table in STST is not pre-determined as the case in traditional tests. Thus, conventional methods to improve control accuracy, such as the offline iteration, cannot be applied in STST.
The second pattern is more complex, in which the upper part is the numerical substructure while the lower part is physically tested. The experimental substructure is excited by the shaking table from the bottom with a ground motion. The structural response, commonly the absolute acceleration measured at the top of the experimental substructure, is sent to the numerical simulation as the input for the time history analysis. The simulated reaction force of the numerical substructure is then sent to the actuator and applied to the top of the experimental substructure. Therefore, the experimental substructure is loaded by shaking table and actuator simultaneously. Because both loading devices are connected to the specimen, the controllers of the actuator and the shaking table are coupled, which shall be carefully designed typically through a de-coupling strategy to achieve a good control for both equipment. To do this, the feedbacks of both controllers would be sent to each other, as indicated by the red dashed line in Figure 2B. It shall be noted that the shaking table is usually used to reproduce a seismic acceleration history resulting in a distributed inertial force within the test specimen. Therefore, the actuator is better to be force controlled. This force-controlled dynamic STST is essentially different from the traditional real-time hybrid test methods. The ground acceleration history, usually measured from the shaking table, is used as the excitation input to the numerical substructure, to avoid the discrepancy in the ground motion excitation to the experimental and the numerical substructures. Similar to the first pattern, the simulation of the numerical substructure shall catch up with the loading speed, which implies that synchronization among shaking table, actuator and numerical simulation shall be guaranteed. Therefore, in this substructure pattern, there are two closed-control loops. One closed-loop is used to control actuator, which strongly depends on simulation results of numerical substructure. The other is used to control shaking table, may or may not depend on the numerical simulation results based on STST configuration. Please note that inherent control loop, also known as the inner controller provided by manufactories of loading devices, is still required in both substructure patterns. This inner controller may be either incorporated into the entire control strategy or operated separately.
Another substructure pattern shall be noted is the substructure strategy proposed by Stefanaki (Stefanaki and Sivaselvan, 2018). Although similar to the second substructure pattern, this pattern indeed implements the numerical substructure as a part of the boundary loading device. When designing the controller of the boundary loading device, the transfer function of numerical substructure is taken as a reference. The controlled boundary loading device shall generate the same reaction force when being given the same input. Therefore, the numerical substructure is incorporated into the inner control loop of the loading device. This way, on one hand, simplifies the entire STST system, and on the other hand, avoids the actuator-structure interaction. However, if the numerical substructure is expected to yield nonlinear response, the controller of the boundary loading device could be very complex.
Testing Procedures of STST
Testing procedures of STST with the first substructure pattern is much different from those of the second substructure pattern, as described in Table 2 and illustrated in Figure 3. The first substructure pattern starts from the numerical simulation to determine the target acceleration of the shaking table step by step. Before exciting the experimental substructure, this target acceleration is fitted using polynomial functions to predict commands of the next several steps in case numerical simulation cannot catch up with real-time loading. In the shaking table inner controller, acceleration commands are usually integrated into displacement commands to drive the actuators. Therefore, the boundary loading is essentially controlled in displacement for the experimental substructure. After loading, the boundary shear force is measured either directly by load cells or indirectly by accelerometers attached to the substructure (see section “Force Measurement at the Boundary Between Substructures in STST” for details). In the real application, a low-pass filter is usually employed to eliminate the high-frequency noise in the measurement. The procedures of the second substructure pattern are more complex, as shown in Figure 3B. The STST starts from the experimental substructure. Two control loops are required for the shaking table and the actuator, respectively. The input to the shaking table is often pre-determined (i.e., ground acceleration history), while the command to the actuator is computed step by step through numerical simulation. Both shaking table and actuator are connected to the specimen. The strong coupling between these two loading devices, therefore, needs to be addressed when designing their respective control algorithms. Moreover, the shaking table and the actuator have to be synchronized during a STST. It shall be noted that, the specimen is actually loaded by the inertial force, although the shaking table is controlled by acceleration or displacement. Therefore, a force control is preferred for the actuator.
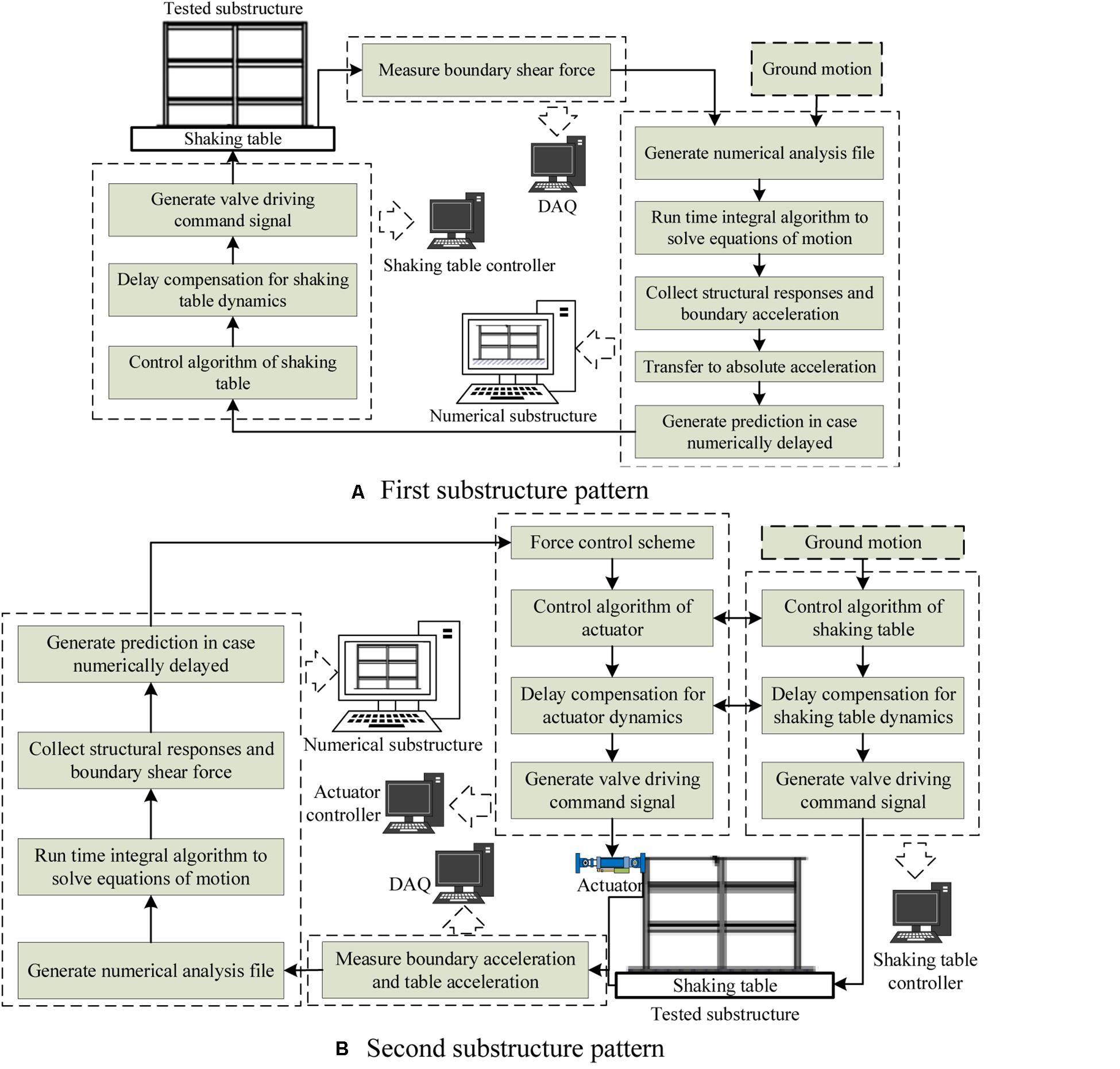
Figure 3. Detailed procedures of STST. (A) First substructure pattern. (B) Second substructure pattern.
A Typical Hardware Configuration of STST
In a typical STST system, there are three dynamic subsystems, including numerical simulation, shaking table and actuator loading systems. The three dynamic subsystems are operated simultaneously and inter-dependently by exchanging data during the test. The entire system runs in real time and in a step-by-step manner, which means any time step difference among the three dynamic subsystems shall be minimized as much as possible. To this end, devices running in real time mode shall be used and connected through high-speed data transfer cables. A typical hardware configuration of STST system consists of three modules: the data acquisition system (DAQ), the real-time hybrid simulator, and the testing controller (Shao et al., 2011). The DAQ module is composed of signal acquisition and signal conversion equipment. The collected data are transferred to the other two modules and used as inputs in algorithms running in the hybrid simulator or as reference signals in the loading devices’ controllers. The real-time hybrid simulator includes one or several real-time targets (for example, Matlab/xPC target) to simulate response of the numerical substructures from which loading commands of shaking tables and actuators are determined. In this module, the control commands are usually compensated for the time delay in loading devices and synchronization among them is ensured. The testing controller module contains shaking table controllers and actuator controllers. The nonlinearity of specimens, the interaction between loading devices and specimens, and other factors affecting control stability and precision shall be considered in this module. To achieve data exchange in a real-time pattern, these modules are equipped with the shared common random-access memory network (SCRAMNET) cards which are connected by high-speed fiber optic cables, making it possible for instant memory writing/reading of the data being exchanged among different modules. It shall be noted that, this configuration is scalable and the hybrid simulator and the testing controller at different laboratories can be connected through Internet. By this way, multiple numerical substructures and experimental substructures are combined, so that a geographically distributed STST of a large and complex structure becomes possible when the internet delay is compensated properly.
Key Technologies of STST
Numerical simulation and physical experimentation combined in a STST test are implemented in a real time environment. There are two challenges in this process, i.e., the boundary coordinating between the numerical and the experimental substructures, and the control of loading devices that impose realistic dynamic loading to the experimental substructure. To achieve a real time coordination between the two substructures, the numerical simulation has to be carried out at the real-time rate, which requires efficient time integration algorithms. The synchronization between the two substructures is also important. Particularly, the delayed command from the numerical simulation will lead to undesired loading break on the experimental substructure. On the physical experimentation part, the interaction among shaking table, actuator and experimental substructure shall be considered to design the controller for each loading device. In particular, force control of actuator is very challenging because of oil-column resonance and its internal friction. Moreover, the inherent delay of loading devices shall be minimized to avoid instable STST. Therefore, key technologies for a successful STST system include efficient numerical simulation, delay compensation schemes, accurate control of shaking tables, force control of actuators and boundary force measurement, as discussed in detail in the following sections.
Efficient Numerical Simulation
In a STST, the numerical substructure shall be solved synchronously when the experimental substructure is being loaded, which implies that boundary response shall be determined and sent to the experimental substructure before it is needed. This is not easy for a large-scale numerical model with more than 1000 DOFs. The Jacobian solution used to solve equations of motion may take a good share of memory, and the communication between the memory and the hard disk also takes time. With the fast development of computer technology, the model scale that can be implemented in memory is significantly enlarged. However, the real-time application with more than 10,000 DOFs has not been reported yet. Most STST applications adopted simplified mass-spring model according to Table 1. The study by Wang (Wang et al., 2014) is the only one that employed a larger numerical model with more than 1000 DOFs. These models, however, were elastic. If the numerical models, which are very likely, involve nonlinearity, their response simulation in real-time would be more difficult, because the iteration required to solve the nonlinearity is uncertain at each step consuming very different amount of time. High-performance computer, even super computation clusters, cannot readily solve this difficulty yet.
One method to solve this difficulty is to adopt and/or develop explicit time integration algorithms to avoid the iteration procedure. Integration algorithms, such as the CMD and the explicit Newmark method, are most suitable in hybrid tests because only the responses from the previous steps are required to determine the target displacement of the current step (Pan et al., 2015). The explicit method was also adapted to real-time hybrid testing procedure (Wu et al., 2005) and has been applied in STST [CDM method by Wang and Tian (2009); CDM method by Zhou and Wu (2013); explicit Newmark method by Mosalam and Günay (2014); explicit Runge-Kutta method by Li et al. (2011b)]. However, these explicit algorithms, although efficient, are conditionally stable, which highly depend on structural model stiffness. To overcome this difficulty, many researchers are engaged in developing unconditionally stable explicit integration algorithms. Chang (2007) developed an explicit method with unconditional stability, which is particularly suitable for online hybrid tests because of its better error propagation properties. Chen (Chen and Ricles, 2008; Chen et al., 2009) employed a discrete transfer function to study the stability of integration algorithms. By placing the poles of the discrete transfer function, a family of explicit algorithms was developed which are unconditionally stable. Similarly, Gui (Gui et al., 2014) developed a new family of explicit integration algorithms also based on discrete control theory, which are explicit for both displacement and velocity. It is worth noting that these algorithms require no factorization of damping matrix and stiffness matrix, so they are more efficient in real-time hybrid testing. Wang (Wang et al., 2018) proposed an explicit algorithm for hybrid tests based on the HHT-α algorithm. If the stiffness of a specimen is identified, the algorithm would be unconditionally stable even for specimen experiencing stiffness hardening. Different approach was adopted in the operator-splitting (OS) algorithm (Nakashima et al., 1990), during which explicit formulations are applied to the experimental substructure while implicit formulations are kept to solve the numerical substructure. This OS algorithm was later modified in a real-time hybrid test (Wu et al., 2006), and applied in a STST recently (Günay and Mosalam, 2015).
Some schemes were incorporated into time integration procedures to improve efficiency, such as the staggered integration scheme and the modal truncation scheme. The staggered integration scheme (Nakashima and Masaoka, 1999) adopted a larger time step to solve equations of motion, while using a smaller step to generate commands for actuators. An extrapolation is used to generate commands before the target value is available and it is immedicably switched to an interpolation once the target value is computed. This scheme was later applied to a STST (Wang et al., 2014). The modal truncation scheme (Gutierrez and Lopez Cela, 1998) selects lower frequency vibration modes that most influence the responses while attenuates the higher frequency modes, thus a larger step can be used to solve equations of motion.
Delay Compensation Schemes
As mentioned previously, the numerical simulation and the physical experimentation shall be synchronized in a STST test. Because loading devices require target values from the numerical simulation, whether the numerical simulation can provide such a target value in time becomes the key. This is also the reason why an efficient time integration algorithm is always desired in a real-time hybrid test. Although there are a lot of efficient time integration schemes available for STST tests, it is still possible that a numerical solution cannot find the committed state in time, especially when solving nonlinear structural models. To overcome this possible delay, a polynomial function is often used to extrapolate the target value if the calculation is not completed. Once the target is obtained from numerical simulation, interpolation of the target is triggered to drive the specimen to the correct position. This delay compensation using polynomial function is easy to be implemented and widely adopted in real-time substructure hybrid tests (Nakashima et al., 1992; Wu et al., 2005; Zhang et al., 2005; Schellenberg et al., 2009; Zhu et al., 2014a).
Another source of delay comes from the inherent dynamics of loading devices. This delay shall be minimized first prior to STST because it introduces negative damping into the dynamic system and leads to divergence. In the past decades, many delay compensation schemes have been developed and applied. They are generally classified into two groups, i.e., the polynomial function-based schemes and the model-based schemes. The former schemes are independent on dynamic systems, but rely on mathematic formulation. The latter schemes, on the contrary, are developed according to the system’s dynamic model based on modern control theories.
Horiuchi (Horiuchi et al., 1999) proposed a polynomial extrapolation method to compensate the time delay which is widely used in real-time hybrid test. He also studied the negative damping effect of time delay on the accuracy and stability of substructure testing. Since the factors affecting the delay vary during a test (e.g., due to the nonlinear stiffness of a specimen, adaptive PID controllers, etc.), it is necessary to estimate the delay accurately during the test for compensation. Most STST tests discussed above adopted polynomial functions to compensate the time delay (see Table 1). The feed-forward method (Günay and Mosalam, 2015) that uses a feed-forward gain multiplied by the command velocity and added to the servo-valve command is another math-based method. Zhu (Zhu et al., 2014b, 2015) systematically studied the delay compensation method using a 3rd order polynomial function. The stability affected by the time delay in a STST system was analyzed by the discrete-time root locus technique. It was found out that the third order polynomial function can increase the stability limitation significantly.
The model-based scheme predicts the compensated commands of the system delay by using system transfer functions, which is usually identified before a hybrid test. Then, the inverse of the identified transfer function of the combined servo-hydraulic and test specimen system is developed. In one of the early studies, the fourth order FIR filter (Igarashi et al., 2004) that approximates the system transfer function was assigned with a phase lead to cancel the phase lag. The STST developed by Shao (Shao et al., 2011) adopted the Smith Predictor to compensate the time delay, during which the predictor was designed to approach the desired plant considering both the inherent delay and the modeling errors (Sivaselvan et al., 2008). Carrion (2007) used a model-based compensation method to predict actuator’s response used as the input displacement. Later, Phillips and Spencer (2013a) developed a delay compensation method for real-time hybrid simulation based on the feedforward-feedback tracking control. Chen (Chen et al., 2009) developed a simple model for the servo-hydraulic system using a first-order discrete transfer function and applied the inverse of the model’s transfer function to compensate the actuator delay. Hayati (Hayati and Song, 2016) designed a discrete-time compensator based on an Auto-Regressive with Exogenous model (ARX model). This method provides an optimal compensation allowing actuators to track inputs with higher frequency contents up to 30 Hz. Fermandois and Spencer (2017) proposed a model-based feedforward-feedback controller to improve the robustness and compensate the time delay of the 1/5th-scale Load and Boundary Condition Box (LBCB), and this method was verified in a six-DOF loading test.
Time delay is not a constant value, which indeed significantly depends on dynamic STST systems including servo-hydraulic loading devices and test specimens. Darby (Darby et al., 2002) presented a method for estimating the delay during a test and verified this method in a twin-actuator system. Based on the fundamental concepts presented by Darby, Wallace (Wallace et al., 2005) proposed an adaptive compensation algorithm by a forward prediction to compensate the delay in the transfer system. Ahmadizadeh (Ahmadizadeh et al., 2008) used a learning gain to achieve online estimation of actuator delay. Chen (Chen and Ricles, 2010a, b; Chen et al., 2012) provided an adaptive inverse compensation procedure based on proportional and integral gains applied to a tracking indicator (TI) developed by Mercan (2007). The TI is an online indicator of phase lead or lag between actuator commands and measured displacements. To deal with inaccurate prediction and uncertain estimated delay, Wu (Wu et al., 2013) proposed a compensation scheme, in which the displacement was firstly overcompensated by an upper bound delay and the reaction force corresponding to the desired displacement was then selected by an optimal process. A robust integral actuator control method proposed by Ou (Ou et al., 2015) can be regarded as a combination of feedforward and feedback control, in which the feedback controller was based on the H∞ method. Chen (Chen and Tsai, 2012) used a dual compensation method that included an adaptive second-order phase lead compensator and an online restoring force compensator. Chae (Chae et al., 2013) developed the adaptive time series (ATS) compensator using an online real-time linear regression analysis to continuously update the coefficients of ATS compensator. Based on the principles of ATS, Palacio-Betancur and Gutierrez Soto (2019) proposed a conditional adaptive time series (CATS) compensator for a benchmark problem in which a recursive least square (RLS) algorithm is adopted for the parameter estimation of the controller to reduce computational efforts. Zhou (Zhou et al., 2019) combined a linear-quadratic gaussian controller and a polynomial-based feedforward prediction algorithm to compensate the adverse effects of time delay and uncertainties on the RTHS testing system.
Considering the numerous compensation schemes proposed for real-time hybrid tests in the past two decades, this paper only introduces some of them that can be potentially applied in STST tests.
Accurate Control of Shaking Tables
Shaking table in STST tests is employed to realize the boundary compatibility between numerical and experimental substructures. Accurate loading is of critical importance to achieve a successful STST application. During a STST test, traditional control methods of shaking table, such as offline iterative method and adaptive inverse transfer function control, cannot be directly applied, due to the step-by-step manner and the closed-loop form of STST. Moreover, shaking table often carries a large payload, leading to the shaking table-specimen interaction. Therefore, shaking table controllers shall be carefully devised for STST tests.
In the STST applications listed in Table. 1, the study on shaking table controller is very limited. The reason might be that shaking tables used in these applications were all uniaxial, and the specimen weight was relatively small compared with tables’ payload capacities. Hence, shaking tables worked essentially as a single actuator controlled in displacement or acceleration. Among these studies, Zhou (Zhou and Wu, 2013) adopted a pressure difference feedback control to overcome the adverse effect from the oil-column resonance. Günay (Günay and Mosalam, 2015) developed an advanced control method based on the TVC scheme to improve the displacement control accuracy of the shaking table. Different from the traditional TVC, a third differentiation was used to determine the jerk command to boost the frequencies above the oil-column frequency when the low-pass filter was not used to avoid distorting the displacement command. Similar control method (Li X. J. et al., 2018) was developed by incorporating jerk feedback and feed-forward signals into the control unit. The control of the frequencies higher than 50 Hz was improved. Neild (Neild et al., 2005) proposed two controllers for STST tests, i.e., a linear controller and an adaptive substructure method based on the minimal control synthesis algorithm. The adaptive controller does not require the dynamics of the shaking table and the experimental substructure, so that an accurate control of nonlinear specimens is possible.
Recent development on the control of shaking tables provides potential options for STST. Phillips (Phillips et al., 2014) proposed a model-based multi-metric control method for uniaxial shaking tables, during which the feedforward and feedback links was incorporated to accurately track an acceleration history. The robustness of this control method over the nonlinearities of the specimen and the servo-hydraulic system was demonstrated. To overcome uncertainties and nonlinearities in specimens and servo-hydraulic devices, Yang (Yang et al., 2015) proposed a hierarchical control strategy for uniaxial shaking tables. The sliding mode control technique was employed to provide robustness to compensate model nonlinearities and uncertainties experienced during tests. Experimental results demonstrated that a high control accuracy was achieved. Ryu (Ryu and Reinhorn, 2016) developed a nonlinear tracking control scheme based on the feedback linearization method to consider the nonlinear behavior of specimens. In this method, a real-time estimator using the extended Kalman filter was adopted to account for the changes and uncertainties in system models due to nonlinearities. Chen (Chen et al., 2017) proposed a control framework which incorporates a feedback controller into a weighted command shaping controller. The command shaping controller was model-based so that the control-structure interaction can be fully captured. The weights of the shaped displacement and acceleration were calculated by a linear interpolation algorithm. The robustness and accuracy of this framework was experimentally verified. Rajabi (Rajabi et al., 2018) developed a new trajectory tracking control for a ball-screw-driven shaking table. The controller was designed based on sliding mode approach with state online estimated by the extended Kalman filter or unscented Kalman filter (UKF), so it could achieve a high velocity and positioning accuracy regardless of the inherent noises, frictions, and uncertainties. In addition, other control algorithms, such as linear quadratic regulator (Kuehn et al., 1999), minimal controller synthesis algorithm (Stoten and Benchoubane, 1990; Shimizu et al., 2002), linear quadratic control with integral (Seto et al., 2002), fuzzy neural network (Chen et al., 2007), and adaptive inverse control (Dertimanis et al., 2015), have been explored to solve the difficulties in controlling shaking tables with nonlinearities and uncertainties. This paper will not discuss them all in detail due to the page limitation.
In summary, most newly developed control algorithms employ an online updated model to achieve accurate control of shaking tables, which can be applied in STST without much effort of revising.
Force Control of Experimental Substructures
In the second substructure pattern, actuator is employed to realize the boundary compatibility between numerical and experimental substructures. Simultaneously, the experimental substructure is excited by a shaking table that induces inertial force. Therefore, the actuator attached to the experimental substructure is preferred to be controlled in force. However, dynamic force control of hydraulic actuators is difficult since it requires a low impedance system rather than a high impedance as in displacement control (Nachtigal and Martin, 1990). Force control accuracy is significantly affected by the dynamic characteristics of a test specimen, especially its nonlinear behavior, and actuator’s nonlinearities, including mechanical friction, viscous damping, sealing of piston, and oil-column resonance.
Conrad and Jensen (1987) recognized that closed-loop dynamic force control was ineffective without velocity feedforward at the natural frequency of the structure due to the control-structure interaction. This finding was echoed by Dimig (Dimig et al., 1999) and Shield (Shield et al., 2001) when developing the effective force method, where an additional velocity feedback loop was incorporated to overcome the interaction. The oil column was expressed as a spring so that the force control can be achieved by displacement feedback. Inspired by the oil spring concept, Sivaselvan (Sivaselvan et al., 2008) introduced a compliance spring between actuator and structure to realize force control via a displacement-controlled actuator. The actuator has an inner closed-loop control using displacement feedback in the PID. Meanwhile, an outer control-loop takes the target force command and converts it into a displacement command of the actuator based on the Hooke’s spring law. Similarly, Chae (Chae et al., 2017) implemented compliance springs and ATS compensator to achieve accurate force tracking control of actuators. This force-control method does not require structural modeling, thus especially suitable for nonlinear structures and its satisfactory force tracking performance was experimentally demonstrated. The proposed force-control method was later applied to a real-time hybrid simulation of an RC bridge pier, during which the springs were replaced by a flexible loading frame (FLF) and its optimal control performance was further manifested (Chae et al., 2018). A different methodology developed by Nakata (Nakata and Stehman, 2012) employed a controlled mass to reproduce the boundary force between numerical and experimental substructures. The boundary force was first converted to the absolute acceleration of the controlled mass. Then the relative acceleration was obtained to calculate the relative displacement to drive the actuator. In this process, a high-pass filter was adopted to stabilize the relative displacement of the mass. The accuracy of the proposed control method was demonstrated through a numerical simulation. A similar scheme proposed by Verma (Verma et al., 2019) introduced an AMD whose impedance matches the numerical substructure so that uncertainties and nonlinearities in the dynamic system can be considered. An experiment was then conducted using an AMD at the top of the specimen during which the seismic response was well reproduced. Different from the above schemes, Nakata (Nakata et al., 2017) proposed a loop-shaping controller for the force-controlled actuator that can be applied in real-time hybrid tests. The loop-shaping controller was a model-based control method that requires a dynamic model relating the actuator valve to the force applied. The experimental results showed that the loop-shaping controller enabled accurate control of dynamic force on the specimen during the real-time hybrid simulation.
Force Measurement at the Boundary Between Substructures in STST
Accurate force control relies significantly on accurate measurement of forces. Generally, there are two methods to measure the force at the boundary between substructures in a STST: (1) the direct method that measures the force using load cells installed at the boundary and; (2) the indirect method that computes the force based on the acceleration responses of the experimental substructure measured by a network of accelerometers at the boundary (Li et al., 2011a; Li X. J. et al., 2018). The direct force measurement can be applied to both substructure patterns. In the first substructure pattern shown in Figure 2A, the shear force can be measured by a shear-type load cell (Zhou and Wu, 2013; Zhou et al., 2014), while for the second substructure pattern in Figure 2B, the dynamic force between the two substructures can be directly measured using the load cell of the actuator attached at the top of the specimen. When STST involving loading along multi-directions using a MDOF shaking table (Schellenberg et al., 2017), the direct force measurement is more complicated, and expensive triaxial loading sensors are often employed to measure the forces along multi-directions simultaneously. If the specimen is featured with concentrated masses, an indirect method could be utilized, by which the force is calculated based on the measured acceleration multiplied by the corresponding mass (Lee et al., 2007; Tian et al., 2020). It is worth noting that high-frequency noises exist in both load cells and accelerometers, which bring in challenges in direct-force control of actuators.
New Directions
STST Test Using Shaking Table Array
Multiple shaking tables (i.e., table array) constructed in the same location can be combined to perform seismic simulation of large-scale engineering structures such as large-space structures and long-span bridges. If incorporated with the STST technique, testing capacity of shaking table array can be further extended. Dorka (Dorka et al., 2006, 2007) conducted STST using distributed hydraulic shaking tables on a two-story steel frame with two TMDs on the top. Each TMD was placed on one uniaxial shaking table. The test results matched well with the shaking table test of the entire structure. Following the unified substructure scheme proposed by Reinhorn (Reinhorn et al., 2005) and the hardware framework by Shao (Shao and Reinhorn, 2012), multiple experimental substructures can be tested in one STST. The boundary coordination can be achieved in the same way as STST employing only one experimental substructure. However, physically achieving accurate boundary loading becomes more complex, and synchronizing loading devices is more critical. Several attempts have been made so far. For example, Zhu (Zhu et al., 2017) conducted a STST on two tuned liquid column dampers mounted on top of a building, during which each damper was loaded by one uniaxial shaking table, and the two shaking tables had the same input obtained from the numerical simulation. The same technique reported in a previous study (Zhu et al., 2014a) was adopted for this dual STST. Li (Li et al., 2011b) studied the effect of soil-structure interaction on a three-span bridge model installed on four shaking tables. The soil was simulated numerically and the response of each pier was input to the shaking table. The TVC controller combined with a linear controller was adopted to control the four shaking tables. Mosalam (Mosalam et al., 2016) conducted a STST test on interconnected electrical equipment using two shaking tables to quantify the influence of electrical cables on substation equipment. The supporting structure was the numerical substructure modeled by an SDOF system, and the two insulators connected by a conductor cable were tested on the two tables. These applications demonstrated the feasibility of STST using multiple shaking tables. However, there’s only one boundary shared by the substructures in these tests (i.e., the building roof in Zhu’s application, the soil-structure interface in Li’s application and the substation electrical equipment in Mosalam’s application), and the first substructure pattern was adopted for all three applications. The applications on more complex substructure pattern using multiple shaking tables and actuators have not been reported yet. It is still very challenging to realize such complex STST system.
Complete Boundary Coordination and Loading Device
The substructure patterns discussed above were generally based on multi-story building models, which means the boundaries between the substructures are either at the story level or the ground. The horizontal acceleration and the corresponding shear force can be easily imposed using shaking tables and actuators. The overturning moment and the vertical force, however, are difficult to be realized through this substructure pattern. A recent study by Stefanaki (Stefanaki and Sivaselvan, 2018; Stefanaki et al., 2018) proposed a multi-DOF loading device using multiple AMD s to realize the shear force and overturning moment from the upper numerical substructure. However, this technique is still regarded as a story-level solution. If there are multiple shear walls in a frame structure, which are very likely in reality, the story overturning may not strong, but the overturning moment on each wall shall be considered. For this kind of complex boundary condition, it requires further study.
Loading devices are utilized in STST to replicate accurate boundary condition between the two substructures or the ground motion input. Servo-hydraulic actuators have peculiarities of larger loading and power than electromagnetic ones, so that almost all large-scale civil engineering laboratories are equipped with servo-hydraulic shaking tables while electromagnetic shaking tables are mainly used in small-scale facilities for education and proof-of-concept research. However, electromagnetic shaking tables with a high frequency bandwidth, low distortion, and linear behavior have been widely adopted in qualification tests of critical equipment in aerospace and automotive industries (Wang et al., 1990) and they have the potential to apply a MDOF force loading onto the experimental substructure. For example, Verma (Verma et al., 2019) employed an electromagnetic shaking table as an AMD to verify the impedance matching method. On the other hand, it is deemed that the dynamics of electromagnetic and hydraulic shakers are remarkably similar (Carl, 2008). For examples, the natural velocity feedback in hydraulic shaking table is akin to the back electromotive force (EMF) in electromagnetic shaking table; the linearized model of hydraulic shake table has three poles, which is the same case for electromagnetic shaking table.
Application to Other Engineering Problems
At present, STST has been applied to study soil-structure interaction and seismic performance of buildings including those equipped with TMDs, and these applications are considered as traditional civil engineering problems. However, the flexible configuration enabled by STST can be easily extended to address other engineering problems. In China, the high-speed train system has been developed significantly in the last ten years. Most railways were constructed on viaducts. The train-track-bridge interaction requires extensive study before a new train system is cast into market, which is a potential application of STST. Guo (Guo et al., in review) proposed a STST system during which a multi-span bridge was numerically simulated, while the track and the car were tested on a shaking table. The shaking table served as the transfer system to reproduce the vibration introduced by the deflection of bridge girders and the random vibration of high-frequency irregularity. In this STST application, the train was stationary while the bridge was moving relatively to the train. Similar STST system can be applied to analyze vehicle’s safety on highways. The STST system is also capable of examining the fluid-structure interaction of wind turbines as explored by Tian (Tian et al., 2020), where the fluid field was numerically simulated. Underwater shaking table was recently proposed, which is deemed to be more suitable to examine fluid-structure interaction and could further expand STST application. Recent studies explored the feasibility of STST using underwater shaking table, including providing a practical similitude law (Li Z. et al., 2018) and applying to piers of a cross-sea bridge (Ding et al., 2018). All these examples show the promise of STST being applied to other engineering systems.
Summary
In a STST, the substructure with the most complex behavior is tested physically with the rest of the structure being numerically simulated. Boundary compatibility between numerical and experimental substructures is achieved by servo-hydraulic loading devices including shaking tables and actuators. This flexible testing configuration significantly extends testing capacity of shaking tables. This paper introduces frameworks and applications of existing STST and summarizes their primary features. The reported STST frameworks are classified into two categories according to their substructure patterns, i.e., testing the upper part or the lower part of a structure. A scalable hardware configuration is also introduced which can be extended for STST system involving multiple numerical and experimental substructures connected through the network. Then several key issues in developing a successful STST system are presented, including efficient algorithms of numerical simulations, delay compensation schemes, accurate control of shaking tables, force control of actuators and boundary force measurement. Finally, several future research directions identified are presented.
Shaking table substructure testing, as a new technique to examine seismic performance of engineering structures, is still in the preliminary stage. Most existing applications employed uniaxial shaking tables. The application on large multi-directional shaking table is still challenging because of the complex coupling of shaking table actuators. Therefore, accurate reproduction of boundary conditions is extremely difficult. Most delay compensation schemes were developed for a single actuator or uniaxial shaking table, without considering the coupling between them. Moreover, the experimental substructure in these applications were relatively soft, with frequencies associated with lower modes under 10 Hz. Whether these delay compensation methods are valid for high-frequency systems remains unknown. Therefore, there is a great potential to continue advancing STST technology.
The substructure patterns employed by existing STST systems are mostly at the story level of a building structure. This substructure pattern might be adequate to study structural global behavior, but cannot provide refined details to examine local behavior of a structural components because the exact boundary compatibility is not attained at the component level. Although several studies have addressed this challenge, a comprehensive study is needed to demonstrate the effectiveness of the developed techniques. One of the key issues to realize the boundary compatibility is the force control of actuators. Existing methods include adding spring compliance and employing AMD. The AMD is appealing as an integral approach to solve the force control in multiple directions. Finally, it shall be noted that one STST system might involve multiple dynamic systems, including shaking tables, actuators, and numerical simulations. It would be more complex if a shaking table array is employed. The interaction among these dynamic systems is very complex and the stability of such a system shall be well examined before a real application.
In summary, STST is appealing to be applied to seismic performance evaluation of engineering structures. But more efforts are required for more sophisticated applications. STST is also a promising technique to solve other engineering problems, during which knowledge integration of multi-disciplines is needed.
Author Contributions
All authors contributed to this review manuscript. YT wrote most part of the manuscript. XS reviewed the control of shaking tables as well as the force control of actuators. HZ gave a review on the time delay compensation program. TW suggested the structure of the manuscript.
Funding
The study received financial support from the Scientific Research Fund of Institute of Engineering Mechanics, China Earthquake Administration (2017A02), the National Science Foundation of China (51678538 and 51878630), and the Heilongjiang Provincial Natural Science Fund for Distinguished Young Scholars (Grant No. JC2018018). Any opinions, findings, conclusions, or recommendations expressed in this article are those of the authors, and do not necessarily reflect the views of the sponsors.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Ahmadizadeh, M., Mosqueda, G., and Reinhorn, A. M. (2008). Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq. Eng. Struct. Dyn. 37, 21–42. doi: 10.1002/eqe.743
Astroza, R., Ebrahimian, H., Conte, J. P., Restrepo, José, I., and Hutchinson, T. C. (2016). Influence of the construction process and nonstructural components on the modal properties of a five-story building. Earthq. Eng. Struct. Dyn. 45, 1063–1084. doi: 10.1002/eqe.2695
Ba, P. F., Zhang, Y. G., Wu, J. Z., Zhang, Z. H., and Zheng, X. J. (2017). Whole process test and dynamic failure analysis for sing-layer spherical lattice shells. J. Vibrat. Shock 36, 31–37.
Carl, J. (2008). Improved Dynamic Testing by Impedance Control. Ph.D. Thesis. Boulder, CO: University of Colorado.
Carrion, J. E. (2007). Model-Based Strategies for Real-Time Hybrid Testing. Ph.D. dissertation. Illinois, IL: University of Illinois at Champaign.
Chae, Y., Kazemibidokhti, K., and Ricles, J. M. (2013). Adaptive time series compensator for delay compensation of servo-hydraulic actuator systems for real-time hybrid simulation. Earthq. Eng. Struct. Dyn. 42, 1697–1715. doi: 10.1002/eqe.2294
Chae, Y., Lee, J., and Park, M. (2018). Real-time hybrid simulation for an RC bridge pier subjected to both horizontal and vertical ground motions. Earthq. Eng. Struct. Dyn. 47, 1673–1679. doi: 10.1002/eqe.3042
Chae, Y., Rabiee, R., Dursun, A., and Kim, C. Y. (2017). Real-time force control for servo-hydraulic actuator systems using adaptive time series compensator and compliance springs. Earthq. Eng. Struct. Dyn. 47, 854–871. doi: 10.1002/eqe.2994
Chang, S. Y. (2007). Enhanced, unconditionally stable, explicit pseudodynamic algorithm. J. Eng. Mech. ASCE 133, 541–554. doi: 10.1061/(asce)0733-9399(2007)133:5(541)
Chen, C., and Ricles, J. M. (2008). Development of direct integration algorithms for structural dynamics using discrete control theory. J. Eng. Mech. ASCE 134, 676–683. doi: 10.1061/(asce)0733-9399(2008)134:8(676)
Chen, C., and Ricles, J. M. (2010a). Improving the inverse compensation method for real-time hybrid simulation through a dual compensation scheme. Earthq. Eng. Struct. Dyn. 39, 1237–1255. doi: 10.1002/eqe.904
Chen, C., and Ricles, J. M. (2010b). Tracking error-based servohydraulic actuator adaptive compensation for real-time hybrid simulation. J. Struct. Eng. ASCE 136, 432–440. doi: 10.1061/(asce)st.1943-541x.0000124
Chen, C., Ricles, J. M., and Guo, T. (2012). Improved adaptive inverse compensation technique for real-time hybrid simulation. J. Eng. Mech. ASCE 138, 1432–1446. doi: 10.1061/(asce)em.1943-7889.0000450
Chen, C., Ricles, J. M., Marullo, T. M., and Mercan, O. (2009). Real-time hybrid testing using the unconditionally stable explicit CR integration algorithm. Earthq. Eng. Struct. Dyn. 38, 23–44. doi: 10.1002/eqe.838
Chen, J. Q., Zhang, X. Z., Tan, P., and Zhou, F. L. (2007). Application study of ILC with fuzzy neural network in shaking table control system. Int. Conf. Intell. Syst. Knowl. Eng. 580–585.
Chen, P. C., Lai, C. T., and Tsai, K. C. (2017). A control framework for uniaxial shaking tables considering tracking performance and system robustness. Struct. Control Health Monitor. 24:e2015. doi: 10.1002/stc.2015
Chen, P. C., and Tsai, K. C. (2012). Dual compensation strategy for real-time hybrid testing. Earthq. Eng. Struct. Dyn. 42, 1–23. doi: 10.1002/eqe.2189
Chi, F. D., Wang, J. T., Jin, F., and Wang, Q. (2010). Real-time dynamic hybrid testing for soil-structure-fluid interaction analysis. Rock Soil Mech. 31, 3765–3770.
Conrad, F., and Jensen, C. J. D. (1987). Design of hydraulic force control systems with state estimate feedback. IFAC Proc. Vol. 20, 307–312. doi: 10.1016/s1474-6670(17)55388-4
Darby, A. P., Williams, M. S., and Blakeborough, A. (2002). Stability and delay compensation for real-time substructure testing. J. Eng. Mech. ASCE 128, 1276–1284. doi: 10.1061/(asce)0733-9399(2002)128:12(1276)
Dertimanis, V. K., Mouzakis, H. P., and Psycharis, I. N. (2015). On the acceleration-based adaptive inverse control of shaking tables. Earthq. Eng. Struct. Dyn. 44, 1329–1350. doi: 10.1002/eqe.2518
Dimig, J., Shield, C., French, C., Bailey, F., and Clark, A. (1999). Effective force testing: a method of seismic simulation for structural testing. J. Struct. Eng. ASCE 125, 1028–1037. doi: 10.1061/(asce)0733-9445(1999)125:9(1028)
Ding, Y., Ma, R., Shi, Y., and Li, Z. (2018). Underwater shaking table tests on bridge pier under combined earthquake and wave-current action. Mar. Struct. 58, 301–320. doi: 10.1016/j.marstruc.2017.12.004
Dorka, U. E., Queval, J. C., Nguyen, V. T., and Maoult, A. L. (2006). “Real-time sub-structure testing on distributed shaking tables in CEA Saclay,” in Proceedings of 4th World Conference on Structural Control and Monitoring, San Diego, CA.
Dorka, U. E., Queval, J. C., Nguyen, V. T., and Maoult, A. L. (2007). “Substructure testing on distributed shaking tables,” in Proceeding of the 2nd International Conference on Advances in Experimental Structural Engineering (2AESE), Shanghai.
Fermandois, C. G., and Spencer, B. F. (2017). Model-based framework for multi-axial real-time hybrid simulation testing. Earthq. Eng. Eng. Vibrat. 16, 671–691. doi: 10.1007/s11803-017-0407-8
Fu, B., Jiang, H., and Wu, T. (2019). Comparative studies of vibration control effects between structures with particle dampers and tuned liquid dampers using substructure shake table testing methods. Soil Dyn. Earthq. Eng. 121, 421–435. doi: 10.1016/j.soildyn.2019.03.031
Gao, X., Castaneda, N., and Dyke, S. J. (2013). Real time hybrid simulation: from dynamic system, motion control to experimental error. Earthq. Eng. Struct. Dyn. 42, 815–832. doi: 10.1002/eqe.2246
Gui, Y., Wang, J. T., Jin, F., Chen, C., and Zhou, M. (2014). Development of a family of explicit algorithms for structural dynamics with unconditional stability. Nonlinear Dyn. 77, 1157–1170. doi: 10.1007/s11071-014-1368-3
Günay, S., and Mosalam, K. M. (2014). Seismic performance evaluation of high voltage disconnect switches using real-time hybrid simulation: II. Parametric study. Earthq. Eng. Struct. Dyn. 43, 1223–1237. doi: 10.1002/eqe.2394
Günay, S., and Mosalam, K. M. (2015). Enhancement of real-time hybrid simulation on a shaking table configuration with implementation of an advanced control method. Earthq. Eng. Struct. Dyn. 44, 657–675. doi: 10.1002/eqe.2477
Gutierrez, E., and Lopez Cela, J. J. (1998). Improving explicit time integration by modal truncation techniques. Earthq. Eng. Struct. Dyn. 27, 1541–1557. doi: 10.1002/(sici)1096-9845(199812)27:12<1541::aid-eqe799>3.0.co;2-6
Hayati, S., and Song, W. (2016). “Discrete-time compensation technique for real-time hybrid simulation,” in Proceedings of the Conference on Society for Experimental Mechanics Series, Cham, 351–358. doi: 10.1007/978-3-319-30084-9_33
He, M. J., Luo, Q., Li, Z., Dong, H. L., and Li, M. H. (2018). Seismic performance evaluation of timber-steel hybrid structure through large-scale shaking table tests. Eng. Struct. 175, 483–500. doi: 10.1016/j.engstruct.2018.08.029
Horiuchi, T., Inoue, M., and Konno, T. (2000). “Development of a real-time hybrid experimental system using a shaking table,” in Proceedings of 12th World Conference on Earthquake Engineering, Auckland.
Horiuchi, T., Inoue, M., Konno, T., and Namita, Y. (1999). Real-time hybrid experimental system with actuator delay compensation and its application to a piping system with energy absorber. Earthq. Eng. Struct. Dyn. 28, 1121–1141. doi: 10.1002/(sici)1096-9845(199910)28:10<1121::aid-eqe858>3.0.co;2-o
Igarashi, A., Iemura, H., and Suwa, T. (2000). “Development of substructured shaking table test method,” in Proceedings of 12th World Conference on Earthquake Engineering, Auckland.
Igarashi, A., Iemura, H., Tanaka, H., and Tsuruta, D. (2004). “Experimental simulation of coupled response of structural systems using the substructure hybrid shake table test method,” in Proceedings of 13th World Conference on Earthquake Engineering, Vancouver, BC.
Inoue, M., Horiuchi, T., and Momoi, Y. (1998). “Real-time hybrid experiment using a shaking table,” in Proceedings of 10th Japan Earthquake Engineering Symposium, Japanese.
Ji, X. D., Kajiwara, K., Nagae, T., Enokida, R., and Nakashima, M. (2009). A substructure shaking table test for reproduction of earthquake responses of high-rise buildings. Earthq. Eng. Struct. Dyn. 38, 1381–1399. doi: 10.1002/eqe.907
Jia, J. F., Zhao, J. Y., Guo, Y., and Ou, J. P. (2017). Shaking table tests on seismic simulation of three-dimensional isolated continuous girder bridges. China J. Highway Transport. 30, 290–298.
Kim, Y., Kabeyasawa, T., Matsumori, T., and Kabeyasawa, T. (2012). Numerical study of a full-scale six-story reinforced concrete wall-frame structure tested at E-defense. Earthq. Eng. Struct. Dyn. 41, 1217–1239. doi: 10.1002/eqe.1179
Konagai, K., Nogami, T., Katsukawa, T., Suzuki, T., and Mikami, A. (1998). Real time control of shaking table for soil-structure interaction simulation. J. Struct. Mech. Earthq. Eng. 598, 203–210. doi: 10.2208/jscej.1998.598_203
Kuehn, J., Epp, D., and Patten, N. (1999). High-fidelity control of a seismic shake table. Earthq. Eng. Struct. Dyn. 28, 1235–1254. doi: 10.1002/(sici)1096-9845(199911)28:11<1235::aid-eqe864>3.0.co;2-h
Lee, S. K., Park, E. C., Min, K. W., and Park, J. H. (2007). Real-time substructuring technique for the shaking table test of upper substructures. Eng. Struct. 29, 2219–2232. doi: 10.1016/j.engstruct.2006.11.013
Li, X. J., Li, F. F., Ji, J. B., and Wang, J. K. (2018). A new control technology of shaking based on the jerk. Adv. Eng. Sci. 50, 64–72.
Li, Z., Wu, K., Shi, Y., Li, N., and Ding, Y. (2018). Coordinative similitude law considering fluid-structure interaction for underwater shaking table tests. Earthq. Eng. Struct. Dyn. 47, 2315–2332. doi: 10.1002/eqe.3070
Li, Z. B., Li, X. L., Tang, Z. Y., and Jiang, H. G. (2011a). Research on the methods of evaluating reaction force for dynamic sub-structure experiments using shaking table. Earthq. Eng. Eng. Vibrat. 31, 65–70.
Li, Z. B., Tang, Z. Y., Ji, J. B., Li, X. L., Zhou, D. X., and Yan, W. M. (2011b). Research on the dynamic sub-structuring testing method for SSI based on shaking table array. Struct. Eng. 27, 76–81.
Mercan, O. (2007). Analytical and Experimental Studies on Large Scale Real-Time Pseudodynamic Testing. Ph. D. Dissertation. Bethlehem, PA: Lehigh University.
Mosalam, K. M., and Günay, S. (2014). Seismic performance evaluation of high voltage disconnect switches using real-time hybrid simulation: I. System development and validation. Earthq. Eng. Struct. Dyn. 43, 1205–1222. doi: 10.1002/eqe.2395
Mosalam, K. M., Günay, S., and Takhirov, S. (2016). Response evaluation of interconnected electrical substation equipment using real-time hybrid simulation on multiple shaking tables. Earthq. Eng. Struct. Dyn. 45, 2389–2404. doi: 10.1002/eqe.2767
Nachtigal, C. L., and Martin, M. D. (1990). Instrumentation and Control: Fundamentals and Applications. Hoboken, NJ: John Wiley & Sons, Inc.
Nakashima, M., Kaminosomo, T., Ishida, M., and Ando, K. (1990). “Integration techniques for substructuring pseudodynamic test,” in Proceedings of the 4th U.S. National Conference on Earthquake Engineering, Palm Springs, CA, 515–524.
Nakashima, M., Kato, H., and Takao, E. (1992). Development of real-time pseudo-dynamic testing. Earthq. Eng. Struct. Dyn. 21, 79–92. doi: 10.1002/eqe.4290210106
Nakashima, M., and Masaoka, N. (1999). Real-time on-line test for MDOF systems. Earthq. Eng. Struct. Dyn. 28, 393–420. doi: 10.1002/(sici)1096-9845(199904)28:4<393::aid-eqe823>3.0.co;2-c
Nakata, N., Erb, R., and Stehman, M. (2017). Mixed force and displacement control for testing base-isolated bearings in real-time hybrid simulation. J. Earthq. Eng. 23, 155–171.
Nakata, N., and Stehman, M. (2012). Substructure shake table test method using a controlled mass: formulation and numerical simulation. Earthq. Eng. Struct. Dyn. 41, 1977–1988. doi: 10.1002/eqe.2169
Neild, S. A., Stoten, D. P., Drury, D., and Wagg, D. J. (2005). Control issues relating to real-time substructuring experiments using a shaking table. Earthq. Eng. Struct. Dyn. 34, 1171–1192. doi: 10.1002/eqe.473
Ou, G., Ozdagli, A. I., Dyke, S. J., and Wu, B. (2015). Robust integrated actuator control: experimental verification and real-time hybrid-simulation implementation. Earthq. Eng. Struct. Dyn. 44, 441–460. doi: 10.1002/eqe.2479
Palacio-Betancur, A., and Gutierrez Soto, M. (2019). Adaptive tracking control for real-time hybrid simulation of structures subjected to seismic loading. Mech. Syst. Signal Process. 134:106345. doi: 10.1016/j.ymssp.2019.106345
Pan, P., Wang, T., and Nakashima, M. (2015). Development of Online Hybrid Testing – Theory and Applications to Structural Engineering. New York, NY: Elsevier.
Phillips, B. M., and Spencer, B. F. (2013a). Model-based feedforward-feedback actuator control for real-time hybrid simulation. J. Struct. Eng. ASCE 139, 1205–1214. doi: 10.1061/(asce)st.1943-541x.0000606
Phillips, B. M., and Spencer, B. F. (2013b). Model-based multiactuator control for real-time hybrid simulation. J. Eng. Mech. ASCE 139, 219–228. doi: 10.1061/(asce)em.1943-7889.0000493
Phillips, B. M., Wierschem, N. E., and Spencer, B. F. (2014). Model-based multi-metric control of uniaxial shake tables. Earthq. Eng. Struct. Dyn. 43, 681–699. doi: 10.1002/eqe.2366
Rajabi, N., Abolmasoumi, A. H., and Soleymani, M. (2018). Sliding mode trajectory tracking control of a ball-screw-driven shake table based on online state estimations using EKF/UKF. Struct. Control Health Monitor. 25, 1–13.
Reinhorn, A. M., Bruneau, M., Chu, S. Y., Shao, X. Y., and Pitman, M. C. (2003). “Large scale real time dynamic hybrid testing technique-Shake tables substructure testing,” in Proceedings of the 2003 Structures Congress & Exposition, Seattle.
Reinhorn, A. M., Sivaselvan, M. V., Liang, Z., Shao, X. Y., Pitman, M., and Weinreber, S. (2005). “Large scale real time dynamic hybrid testing technique-Shake tables substructure testing,” in Proceedins of the 1st International Conference on Advances in Experimental Structural Engineering, AESE, Nagoya.
Ryu, K. P., and Reinhorn, A. M. (2016). Real-time control of shake tables for nonlinear hysteretic systems. Struct. Control Health Monitor. 24, .1–.2015.
Sarebanha, A., Schellenberg, A. H., Schoettler, M. J., Mosqueda, G., and Mahin, S. A. (2019). Real-time hybrid simulation of seismically isolated structures with full-scale bearings and large computational models. Comp. Model. Eng. Sci. 120, 693–717. doi: 10.32604/cmes.2019.04846
Schellenberg, A. H., Becker, T. C., and Mahin, S. A. (2017). Hybrid shake table testing method: theory implementation and application to midlevel isolation. Struct. Control Health Monitor. 24:e1915. doi: 10.1002/stc.1915
Schellenberg, A. H., Mahin, S. A., and Fenves, G. L. (2009). Advanced Implementation of Hybrid Simulation. Report No: PEER 2009/104. Berkeley: University of California.
Seto, K., Fuji, D., Hiramathu, H., et al. (2002). “Motion and vibration control of three dimensional flexible shaking table using LQI control approach,” in Proceedings of the 2002 American Control Conference, Anchorage, AK, 3040–3045.
Shao, X., and Reinhorn, A. M. (2012). Development of a controller platform for force-based real-time hybrid simulation. J. Earthq. Eng. 16, 274–295. doi: 10.1080/13632469.2011.597487
Shao, X. Y. (2007). Unified Control Platform for Real Time Dynamic Hybrid Simulation. Ph.D. dissertation. Buffalo, NY: State University of New York.
Shao, X. Y., Reinhorn, A. M., and Sivaselvan, M. V. (2011). Real-time hybrid simulation using shake tables and dynamic actuators. J. Struct. Eng. ASCE 137, 748–760. doi: 10.1061/(asce)st.1943-541x.0000314
Shield, C. K., French, C. W., and Timm, J. (2001). Development and implementation of the effective force testing method for seismic simulation of large–scale structures. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 359, 1911–1929. doi: 10.1098/rsta.2001.0879
Shimizu, N., Shinohara, Y., and Sato, E. (2002). New development of control method of shaking table with bi- linear structures. Press. Vessels Piping Conf. 445, 75–82.
Sivaselvan, M., Reinhorn, A. M., Shao, X. Y., and Weinreber, S. (2008). Dynamic force control with hydraulic actuators using added compliance and displacement compensation. Earthq. Eng. Struct. Dyn. 37, 1785–1800. doi: 10.1002/eqe.837
Soroushian, S., Mragakis, M., Zaghi, A., Rahmanishamsi, E., Itani, A., and Pekcan, G. (2016). Response of a 2-story test-bed structure for the seismic evaluation of nonstructural systems. Earthq. Eng. Eng. Vibrat. 15, 19–29. doi: 10.1007/s11803-016-0302-8
Stefanaki, A., and Sivaselvan, M. V. (2018). A simple strategy for dynamic substructuring: I. Concept and development. Earthq. Eng. Struct. Dyn. 47, 1801–1822. doi: 10.1002/eqe.3039
Stefanaki, A., Sivaselvan, M. V., Weinreber, S., and Pitman, M. (2018). A simple strategy for dynamic substructuring: II. Experimental evaluation. Earthq. Eng. Struct. Dyn. 47, 1823–1843. doi: 10.1002/eqe.3041
Stoten, D. P., and Benchoubane, H. (1990). Robustness of a minimal controller synthesis algorithm. Int. J. Control 51, 851–861. doi: 10.1080/00207179008934101
Tian, Y. P., Wang, T., and Zhou, H. M. (2020). Reproduction of wind and earthquake coupling effect on wind turbine tower by shaking table substructure test. Int. J. Lifecycle Perform. Eng. (in press).
Verma, M., Sivaselvan, M. V., and Rajasankar, J. (2019). Impedance matching for dynamic substructuring. Struct. Control Health Monitor. 26:e2402.
Wallace, M. I., Wagg, D. J., and Neild, S. A. (2005). An adaptive polynomial based forward prediction algorithm for multi-actuator real-time dynamic substructuring. Proc. R. Soc. A Math. Phys. Eng. Sci. 461, 3807–3826. doi: 10.1098/rspa.2005.1532
Wang, J. T., Jin, F., Xu, Y. J., and Zhang, C. H. (2014). Theory and practice of real-time dynamic hybrid testing. Eng. Mech. 31, 1–14.
Wang, J. T., Wang, Q., Chi, F. D., and Jin, F. (2010). Solutions to system construction of real-time dynamic hybrid testing based on shaking -table. J. Earthq. Eng. Eng. Vibrat. 30, 16–23.
Wang, M. L., Shah, S. P., and Baker, J. P. (1990). An electromagnetic closed-loop materials testing station. Exp. Tech. 14, 52–55. doi: 10.1111/j.1747-1567.1990.tb01116.x
Wang, T., Zhou, H. M., Zhang, X. P., and Ran, T. R. (2018). Stability of an explicit time-integration algorithm for hybrid tests, considering stiffness hardening behavior. Earthq. Eng. Eng. Vibrat. 17, 595–606. doi: 10.1007/s11803-018-0465-6
Wang, X. Y., and Tian, S. Z. (2009). Principle and implementation of the hybrid testing method based on substructure techniques by using shaking table. J. Earthq. Eng. Eng. Vibrat. 29, 46–52.
Wu, B., Bao, H., Ou, J., and Tian, S. Z. (2005). Stability and accuracy analysis of the central difference method for real-time substructure testing. Earthq. Eng. Struct. Dyn. 34, 705–718. doi: 10.1002/eqe.451
Wu, B., Wang, Q., Shing, P. B., and Ou, J. (2007). Equivalent force control method for generalized real-time substructure testing with implicit integration. Earthq. Eng. Struct. Dyn. 36, 1127–1149. doi: 10.1002/eqe.674
Wu, B., Wang, Z., and Bursi, O. S. (2013). Actuator dynamics compensation based on upper bound delay for real-time hybrid simulation. Earthq. Eng. Struct. Dyn. 42, 1749–1765. doi: 10.1002/eqe.2296
Wu, B., Xu, G. S., Wang, Q. Y., and Williams, S. M. (2006). Operator-splitting method for real-time substructure testing. Earthq. Eng. Struct. Dyn. 35, 293–314. doi: 10.1002/eqe.519
Xie, W., Sun, L. M., and Lou, M. L. (2019). Shaking table test on a pile-soil-cable-stayed bridge full model under multi-support excitations. China Civil Eng. J. 52, 79–89.
Xiong, H. B., Xu, S., and Lu, W. S. (2008). Test study of fundamental periods of wood-frame houses. J. Tongji Univ. 36, 449–453.
Xu, G. S., Xu, J. F., Wang, Z., Zhou, H. M., Wu, B., Zhou, L. J., et al. (2014). Substructure testing method and numerical simulation of storage tank considering interaction between soil and structure. J. Disaster Prevent. Mitigat. Eng. 34, 347–352.
Yang, T. Y., Li, K., Lin, J. Y., Li, Y. J., and Tung, D. P. (2015). Development of high-performance shake tables using the hierarchical control strategy and nonlinear control techniques. Earthq. Eng. Struct. Dyn. 44, 1717–1728. doi: 10.1002/eqe.2551
Zhang, R. Y., Phillips, B. M., Taniguchi, S., Ikenaga, M., and Ikago, K. (2017). Shake table real-time hybrid simulation techniques for the performance evaluation of buildings with inter-story isolation. Struct. Control Health Monitor. 24:e1971. doi: 10.1002/stc.1971
Zhang, Y., Sause, R., Ricles, J. M., and Naito, C. J. (2005). Modified predictor-corrector numerical scheme for real-time pseudo dynamic tests using state-space formulation. Earthq. Eng. Struct. Dyn. 34, 271–288. doi: 10.1002/eqe.425
Zhou, H. M., and Wu, B. (2013). Validation study of shaking table hybrid test platform. J. Vibrat. Eng. 26, 500–505.
Zhou, H. M., Wu, B., Tan, X. J., and Dai, J. W. (2014). Shaking table substructure test of tuned liquid damper. China Civil Eng. J. 47, 70–75.
Zhou, H. M., Xu, D., Shao, X. Y., Ning, X. Z., and Wang, T. (2019). A robust linear-quadratic-gaussian controller for the real-time hybrid simulation on a benchmark problem. Mechan. Eng. Signal Process. 133:106260. doi: 10.1016/j.ymssp.2019.106260
Zhu, F., Wang, J. T., Jin, F., Chi, F. D., and Gui, Y. (2015). Stability analysis of MDOF real-time dynamic hybrid testing systems using the discrete-time root locus technique. Earthq. Eng. Struct. Dyn. 44, 221–241. doi: 10.1002/eqe.2467
Zhu, F., Wang, J. T., Jin, F., and Lu, L. Q. (2017). Real-time hybrid simulation of full-scale tuned liquid column dampers to control multi-order modal responses of structures. Eng. Struct. 138, 74–90. doi: 10.1016/j.engstruct.2017.02.004
Zhu, F., Wang, J. T., Jin, F., Gui, Y., and Zhou, M. X. (2014a). Analysis of delay compensation in real-time dynamic hybrid testing with large integration time-step. Smart Struct. Syst. 14, 1269–1289. doi: 10.12989/sss.2014.14.6.1269
Keywords: real-time hybrid test, shaking table substructure test, delay compensation, boundary coordination, numerical substructure
Citation: Tian Y, Shao X, Zhou H and Wang T (2020) Advances in Real-Time Hybrid Testing Technology for Shaking Table Substructure Testing. Front. Built Environ. 6:123. doi: 10.3389/fbuil.2020.00123
Received: 24 April 2020; Accepted: 07 July 2020;
Published: 07 August 2020.
Edited by:
Chia-Ming Chang, National Taiwan University, TaiwanReviewed by:
Georgios A. Drosopoulos, University of KwaZulu-Natal, South AfricaXueosng Cai, Tongji University, China
Gaston A. Fermandois, Federico Santa María Technical University, Chile
Copyright © 2020 Tian, Shao, Zhou and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tao Wang, d2FuZ3Rhb0BpZW0uYWMuY24=
 Yingpeng Tian
Yingpeng Tian Xiaoyun Shao
Xiaoyun Shao Huimeng Zhou
Huimeng Zhou Tao Wang
Tao Wang