Parametric Studies Into Creep and Shrinkage Characteristics in Railway Prestressed Concrete Sleepers

Introduction

Railway sleepers (or called “railroad ties”), which are generally manufactured using timber, concrete, steel, or other engineered materials, are one of the main safety-critical components of railway track structures (Esveld, 2001). Concrete sleepers have been initially used on rail tracks since 1884 and have recently been used almost everywhere in the world. The major roles of sleepers are (i) to transfer wheel loads from the superstructure to the substructure and (ii) to secure the gauge between rails for safe passages of trains. In reality, wheel/rail interactions over common defects in either a wheel or a rail can cause severe impact loading conditions (Remennikov and Kaewunruen, 2005; Kaewunruen, 2014; Remennikov and Kaewunruen, 2015; Kaewunruen and Remennikov, 2008a, b,c; Remenikov and Kaewunruen, 2008; Remennikov et al., 2011; Fujino and Siringoringo, 2016; Kaewunruen et al., 2016a; Yahiaoui et al., 2017). The impact loads can significantly undermine structural integrity and durability of railway sleepers over the time. Such actions can exacerbate the structural behaviors of the concrete sleepers affected by extreme or hostile environmental conditions. For example, shrinkage cracks can be further open from the dynamic actions, resulting in water and chloride penetrations, as well as carbonation and corrosion. On this ground, it is vital to understand the time-dependent behaviors of concrete sleepers in order to pre-design and risk-manage the concrete sleepers over their entire service life.

Reinforced concrete was initially used for railway sleepers over a century ago. However, poor structural performance and extensive damage have proved that traditional reinforced concrete design was not an effective solution for railway sleepers. Therefore, a prestressed concrete design concept has been developed and adopted for railway sleepers instead of traditional reinforced concrete structures. The prestressed concrete concept can result in lower maintenance costs and longer life cycles in terms of economic and technical aspects. Nowadays, the most commonly used type of sleepers around the world is the prestressed concrete type, which can provide higher serviceability, stability, and safety, especially in suburban and heavy haul rail networks (Kaewunruen and Remennikov, 2010; Parande, 2013; Taherinezhad et al., 2013; Kaewunruen, 2014; Tang et al., 2015; Padhi and Panda, 2017). Prestressed concrete sleepers must successfully perform to satisfy two key responsibilities: first, transfer the wheel loads from the rails to the ground, and later, restrain the rail gauge to ensure the dynamic and safe travels of trains. However, in some cases, creep, shrinkage, and elastic shortening stemmed from improper, unexpected material responses can foul the rail gauge by excessive time-dependent behaviors (for example, too tight rail gauge, splitting cracks at fasteners, vertical cracks along dowels, holes or web openings). Note that, in reality, concrete sleepers are often modified at construction sites to fit in other systems, such as cables, signaling devices, and drainage pipes. These modifications can further result in structural damages in concrete sleepers when excessive time-dependent behaviors are present.

Creep and shrinkage responses can largely influence the durability and long-term behaviors of prestressed concrete railway sleepers (Wakui and Okuda, 1999; Gustavson, 2002). A number of material models have been developed to predict creep and shrinkage, but those are mostly based on a generic type of concrete and on certain applications of traditional reinforced concrete structures (Wang, 1996; Warner et al., 1998; Bentz, 2000). Worldwide adoptions of prestressed concrete in long-span bridges, stadiums, silos, and confined nuclear power plants have led to various concerns by practitioners whether those predictive models could be realistically applied to prestressed concrete components (Ercolino et al., 2015; Li et al., 2015). Due to high initial prestress and elastic shortening in prestressed concrete, the creep and shrinkage effects need to be critically reevaluated. This study investigates and compares methods to evaluate creep and shrinkage effects in prestressed concrete railway sleepers. Comparison among design codes of EUROCODE2, ACI, and AS2009-3600 will provide practical insights into the long-term behavior and durability of railway concrete sleepers. The outcome of this study will help track engineers to better design, manufacture, inspect, and maintain railway infrastructures, improving asset management efficacy.

Three approaches have been adopted in order to meet the research aim. Initially, the design codes have been rigorously reviewed in order to understand how these design codes can be used to properly predict creep and shrinkage. In this stage, a calculation sheet for each code has been developed. All calculations have been carried out analytically. The, the analytical data are analyzed. The sensitivity analysis has been carried out to study the effect of creep and shrinkage. The different codes of practice are performed in order to conduct a comparative study. In practice, the concrete sleepers are manufactured within a day by accelerating the concrete strength to meet the transfer requirements. As such, more realistic losses of prestress and the resultant sleeper shortenings can be established.

This research aims at providing a principal understanding of creep and shrinkage effects for railway prestressed concrete sleepers’ design and manufacture. After introducing the design codes, the parametric analyses are presented. In this investigation, four key parameters (strength, relative humidity, age at first loading, and curing time) are considered to highlight creep and shrinkage effects. The loss of prestress as a result of deformations due to creep and shrinkage are discussed. This research will also provide a state-of-the-art review of common design criteria of prestressed concrete based on Eurocode 2, the American Concrete Institution code, and Australian Standard 2009–3600. It will then determine creep and shrinkage effects in prestressed concrete railway sleepers (Gjorv, 2013; Kaewunruen and Remennikov, 2013). The creep and shrinkage characteristics in prestressed concrete sleepers have been thoroughly investigated in the past. This study provides new findings to better understand the sensitivity of key vulnerable parameters that can significantly affect railway concrete sleepers exposed to various environmental conditions even in the same railway line in a rail network. In addition, the insights into the application of the design methods will be illustrated in order to provide a new guideline for applying those existing codes of practice.

Creep

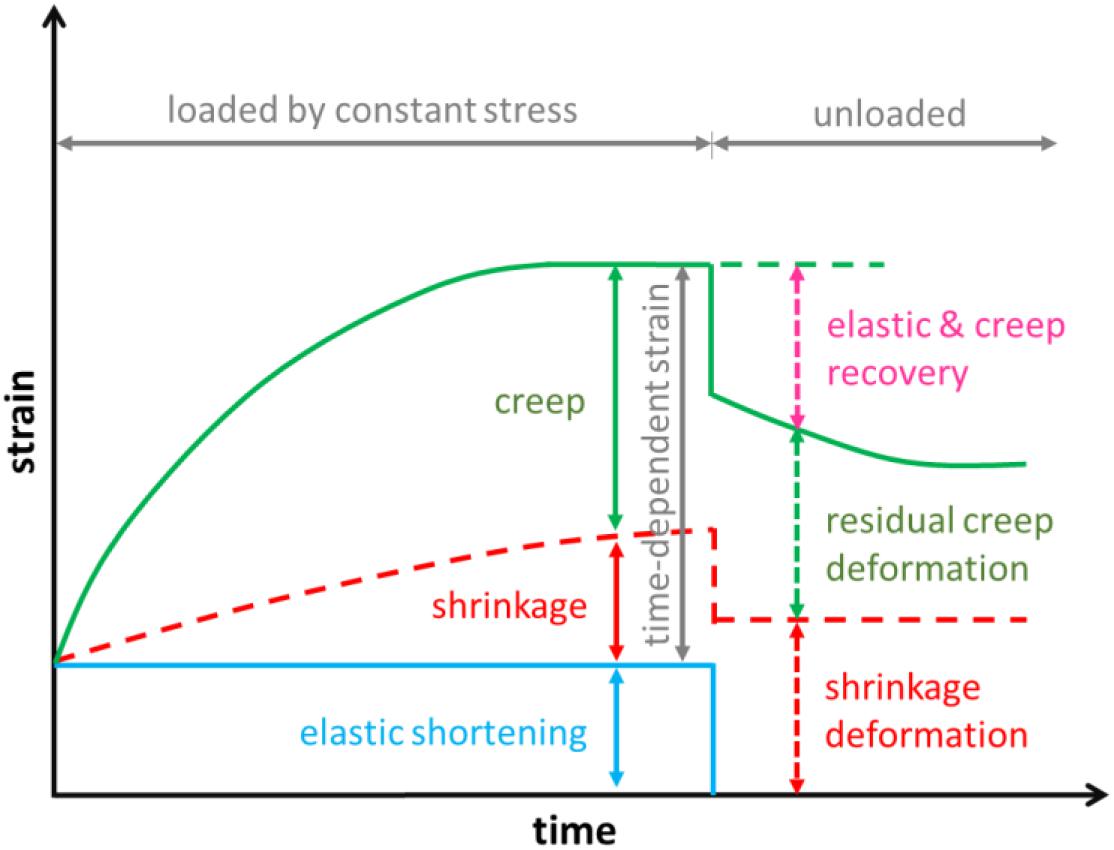
Neville (1995) stated that the strain increases with time even when the concrete is loaded constantly, due to creep effect. Therefore, creep can be defined by the increase of strain in concrete under a sustained stress. With time increments, the increased strain can be several times larger than initial strain. Generally, creep is a considerable factor in concrete structures. Bhatt (2011) stated that creep can be defined as the increase of strain with time when the stress is held constant. The displacement of concrete can gradually increase with time when the load is left in place. Such displacement can reach a value as large as three to four times of the initial or immediate elastic deformation. The inelastic deformation due to the constant load is known as creep deformation. Figure 1 shows the behavior of the creep strain over time.

FIGURE 1

Figure 1. Creep strain over time.

Creep develops in cement paste, which is made of colloidal sheets formed by calcium silicate hydrates and evaporable water. Creep can be influenced by several factors such as concrete mix and environmental and loading conditions. Creep is commonly inversely proportional to concrete strength (e.g., higher strength concrete tends to have lesser creep). In addition, aggregate content and size as well as water/cement ratio can also affect creep strain. Environmental factors like relative humidity, temperature, and exposure conditions also play a significant role on creep. Duration and magnitude of stress and the first loading age are external loading parameters in the creep predictions (Vittorio, 2011). When creep is taken into account, its influences on the design life of concrete sleepers are always evaluated under quasi-permanent combination of actions irrespective of the design situation considered, i.e., persistent, transient, or accidental. Based on such complex situation, various codes of practice simplify each critical parameter to suit its local conditions. On this ground, it is crucial to revisit each code of practice.

Eurocode 2

The total creep strain ε_cc(t,t₀) of concrete due to the constant compressive stress of σ_c applied at the concrete age of t₀ is given by

$${\mathrm{\epsilon }}_{cc}(t,t_0)=\mathrm{\phi }(t,t_0)\times \frac{{\mathrm{\sigma }}_c}{E_c}$$

where φ(t,t₀) is the final creep coefficient; E_c is the tangent modulus.

$$\mathrm{\phi }(t,t_0)={\mathrm{\phi }}_{RH}\times \frac{16.8}{\sqrt{f_{cm}}}\times \frac{1}{\left(0.1+t_0^{0.20}\right)}$$

$${\mathrm{\phi }}_{RH}=1+\frac{1-0.01\times RH}{0.1+h_0^{0.333}},f_{cm}\le 35MPa$$

$${\mathrm{\phi }}_{RH}=\left(1+\frac{1-0.01\times RH}{0.1+h_0^{0.333}}{\mathrm{\alpha }}_1\right){\mathrm{\alpha }}_2,f_{cm}>35MPa$$

$${\mathrm{\alpha }}_1={\left(\frac{35}{f_{cm}}\right)}^{0.7},{\mathrm{\alpha }}_2={\left(\frac{35}{f_{cm}}\right)}^{0.2}{f}_{cm}=f_{ck}+8\text{MPa}$$

$$t_0=t_{0,T}{\left(\frac{9}{2+t_{0,T}^{1.2}}\right)}^{\mathrm{\alpha }}\ge 0.5,\mathrm{\alpha }=\{-1\left(S\right),\mathrm{\hspace{0.33em}0}\left(N\right),\mathrm{\hspace{0.33em}1}(R)\}$$

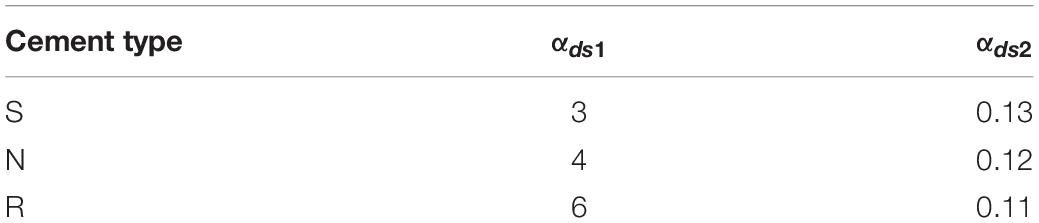
where RH is the relative humidity in percentage; h₀ is the ratio of cross-sectional area and perimeter of the member in contact with the atmosphere, h₀ = 2A_c/u; S, R, and N refer to different classes of cement.

ACI Code

According to ACI 209-92, the only predicted parameter is creep coefficient φ(t,t₀), and its empirical equation is given by

$$\mathrm{\phi }(t,t_0)=\frac{{(t-t_0)}^{\mathrm{\psi }}}{d+{(t-t_0)}^{\mathrm{\psi }}}{\mathrm{\phi }}_u$$

where φ(t,t₀) is the creep coefficient at any time t when a load is applied at age t₀; d (in days) and ψ are considered constants for a given member shape and size that define the time-ratio part. ACI-209R-92 recommends an average value of 10 and 0.60 for d and ψ, respectively; φ_u is the ultimate creep coefficient. For the ultimate coefficient φ_u, the average value is suggested using 2.35. However, the creep coefficient still needs to be modified by correction factors:

$${\mathrm{\phi }}_u=2.35{\mathrm{\gamma }}_c$$

$${\mathrm{\gamma }}_c={\mathrm{\gamma }}_{c,t0}{\mathrm{\gamma }}_{c,RH}{\mathrm{\gamma }}_{c,vs}{\mathrm{\gamma }}_{c,s}{\mathrm{\gamma }}_{c,\mathrm{\psi }}{\mathrm{\gamma }}_{sh,\mathrm{\alpha }}$$

where γ_c,t0 is the loading age factor; γ_c,RH is the ambient relative humidity; γ_c,vs is the volume-to-surface ratio of the concrete section; γ_c,s is the slump; γ_c,ψ is the amount of fine aggregate; γ_sh,α is the air content.

Australian Standard AS3600-2009

In accordance with AS3600, the creep coefficient at any time φ_cccan be determined by

$${\mathrm{\phi }}_{cc}=k_2{k}_3{k}_4{k}_5{\mathrm{\phi }}_{cc.b}$$

where k₂ is the development of creep with time; k₃ is the factor which depends on the age at first loading τ (in days); k₄ is the factor which accounts for the environment; k₅ is the factor which accounts for the reduced influence of both relative and humidity and specimen size; and φ_cc is the basic creep coefficient.

The development of creep with time k₂ can be calculated by

$$k_2=\frac{{\mathrm{\alpha }}_2{(t-\mathrm{\tau })}^{0.8}}{{(t-\mathrm{\tau })}^{0.8}+0.15t_h}$$

$${\mathrm{\alpha }}_2=1.0+1.12e^{-0.008t_h}$$

$$t_h=2A_g/u_e$$

where t is any time in days; t_h is the hypothetical thickness; A_g is the cross-sectional area of the member; and u_e is the portion of the section perimeter exposed to the atmosphere plus half the total perimeter of any voids contained within the section.

Factor k₃ which depends on the age at first loading τ can be shown as

$$k_3=\frac{2.7}{1+\log (\mathrm{\tau })}(\text{for}\mathrm{\tau }>1\text{day})$$

Factor k₄ accounts for the environment:

$$k_4=0.7\mathrm{for}\mathrm{an}\mathrm{arid}\mathrm{environment}$$

$$k_4=0.65\mathrm{for}\mathrm{an}\mathrm{interior}\mathrm{enviroment}$$

$$k_4=0.60\mathrm{for}\mathrm{a}\mathrm{temperate}\mathrm{enviroment}$$

$$k_4=0.5\mathrm{for}\mathrm{a}\mathrm{tropical}\mathrm{or}\mathrm{near}-\mathrm{coastal}\mathrm{enviroment}$$

Factor k₅ is given by

$$k_5=1.0,f_c^{\prime }\le 50\text{MPa}$$

$$k_5=\left(2.0-{\mathrm{\alpha }}_3\right)-0.02\left(1.0-{\mathrm{\alpha }}_3\right)f_c^{\prime },\mathrm{\hspace{0.33em}50}\le f_c^{\prime }\le 100\text{MPa}$$

where ${\mathrm{\alpha }}_3=0.7/(k_4\mathrm{\alpha }{}_2)$.

The basic creep coefficient φ_cc can be determined by interpolation or extrapolation from Table 1.

TABLE 1

Table 1. Basic creep coefficient in accordance with AS3600.

Shrinkage

Concrete shrinkage is the time-dependent strain in an unloaded and unrestrained specimen at a constant temperature. Shrinkage is not an entirely reversible process in comparison with creep. Both creep and shrinkage are influenced by similar factors such as relative humidity, concrete strength, and cement. Shrinkage can be divided into plastic shrinkage, chemical shrinkage, thermal shrinkage, and drying shrinkage. The shrinkage strain is usually considered to be categorized into drying shrinkage and endogenous shrinkage. Drying shrinkage is the volumetric reduction due to the loss of water during the drying process. Endogenous shrinkage is sometimes used to refer to the other part of shrinkage of the hardened concrete that is not associated with drying (i.e., this is the sum of autogenous and thermal shrinkage) (Bhatt, 2011; Gilbert et al., 2016).

Eurocode 2

The total shrinkage strain ε_cs can be given by

$${\mathrm{\epsilon }}_{cs}={\mathrm{\epsilon }}_{ds}+{\mathrm{\epsilon }}_{as}$$

where ε_ds is the drying shrinkage strain; ε_as is the autogenous shrinkage strain.

The drying shrinkage strain ε_ds can be estimated by

$${\mathrm{\epsilon }}_{ds}={\mathrm{\beta }}_{ds}(t,t_0)\times {\mathrm{\epsilon }}_{cd0}\times k_h$$

$${\epsilon }_{cd0}=0.85\left[\left(220+110{\mathrm{\alpha }}_{ds1}\right)\times \exp \left(-{\mathrm{\alpha }}_{sd2}\times 0.1f_{cm}\right)\right]\times 1.55\left[1-{(0.01RH)}^3\right]{10}^6$$

$${\mathrm{\beta }}_{ds}(t,t_0)=\frac{(t-t_s)}{\left(t-t_s\right)+0.04\sqrt{h_0^3}}$$

where k_h is a coefficient which depends on the national size h₀; RH is the relative humidity in percentage; h₀ = 2Ac/u in mm, Ac is the cross-sectional area, and u is the perimeter of the member in contact with the atmosphere. The values of parameter α_ds1 and α_ds2 as a function of the type of cement are shown in Table 2.

TABLE 2

Table 2. Cement type and coefficient.

The autogenous shrinkage strain ε_as can be calculated from

$${\mathrm{\epsilon }}_{as}={\mathrm{\beta }}_{as}(t)\times {\mathrm{\epsilon }}_{ca}(\mathrm{\infty })$$

$${\mathrm{\epsilon }}_{ca}\left(\mathrm{\infty }\right)=2.5\times (f_{ck}-10)\times {10}^{-6}$$

$${\mathrm{\beta }}_{as}\left(t\right)=1-\exp (-0.2t^{0.5})$$

ACI Code

The shrinkage strain ε_sh(t) at age of concrete t (days), predicted from the start of drying at t_c, can be calculated by

$${\mathrm{\epsilon }}_{sh}\left(t\right)=\frac{{(t-t_c)}^{\mathrm{\alpha }}}{f+{(t-t_c)}^{\mathrm{\alpha }}}{\mathrm{\epsilon }}_{shu}$$

$${\mathrm{\epsilon }}_{shu}=780\times {10}^{-6}\mathrm{mm}/\mathrm{mm}(\mathrm{in}/\mathrm{in})$$

where f (in days) and α are considered to be constant values for a given member shape and size that define the time–ratio factor, respectively. The average value for f is recommended to be 35 days of moist curing, and α is suggested to use 1.0. ε_shu is the ultimate shrinkage strain, and (t−t_c) is the time between end of curing and any time after curing.

For the ultimate shrinkage strain ε_shu, the average value is suggested to be 780×10⁻⁶mm/mm. However, the shrinkage strain still needs to be modified by correction factors:

$${\mathrm{\epsilon }}_{shu}=780{\mathrm{\gamma }}_{sh}\times {10}^{-6}\mathrm{mm}/\mathrm{mm}(\mathrm{in}/\mathrm{in})$$

$${\mathrm{\gamma }}_{sh}={\mathrm{\gamma }}_{sh,tc}{\mathrm{\gamma }}_{sh,RH}{\mathrm{\gamma }}_{sh,vs}{\mathrm{\gamma }}_{sh,s}{\mathrm{\gamma }}_{sh,\mathrm{\psi }}{\mathrm{\gamma }}_{sh,c}{\mathrm{\gamma }}_{sh,\mathrm{\alpha }}$$

where γ_sh,tc is the initial moist curing coefficient; γ_sh,RH is the ambient relative humidity coefficient; γ_sh,vs is the volume-to-surface ratio of the concrete section coefficient; γ_sh,s is the slump coefficient; γ_sh,ψ is the fine aggregate coefficient; and γ_sh,c is the cement content factor coefficient; γ_sh,α is the air content coefficient.

Australian Standard AS3600-2009

The total shrinkage strain ε_cs is shown below:

$${\mathrm{\epsilon }}_{cs}={\mathrm{\epsilon }}_{cse}+{\mathrm{\epsilon }}_{csd}$$

where ε_cse is the autogenous shrinkage strain; ε_csd is the drying shrinkage.

The autogenous shrinkage can be calculated by

$${\mathrm{\epsilon }}_{cse}=\mathrm{\epsilon }{}^{\prime }{}_{cse}(1.0-\exp \{-0.1t\})$$

$$\mathrm{\epsilon }{}^{\prime }{}_{cse}=(0.6f_c^{{}^{\prime }}-1.0)\times 50\times {10}^{-6}(f_c^{\prime }\mathrm{in}\mathrm{MPa})$$

$${\mathrm{\epsilon }}_{csd.b}=(1.0-0.008f_c^{\prime })\times \mathrm{\epsilon }_{csd.b}{}^{\prime }$$

where $\mathrm{\epsilon }_{csd.b}{}^{\prime }$ depends on the quality of the local aggregates and may be taken as 800×10⁻⁶ for concrete supplied in Sydney and Brisbane, 900×10⁻⁶ in Melbourne, and 1000×10⁻⁶ elsewhere.

The drying shrinkage strain ε_csd after the beginning of drying (t−τ_d) can be estimated as

$${\mathrm{\epsilon }}_{csd}=k_1{k}_4{\mathrm{\epsilon }}_{csd.b}$$

where k₁ is the factor, which describes the development of drying shrinkage with time; k₄ is the factor, which accounts for the environment.

The factor k₁ can be given by

$$k_1=\frac{{\mathrm{\alpha }}_1{(t-{\mathrm{\tau }}_d)}^{0.8}}{{(t-{\mathrm{\tau }}_d)}^{0.8}+0.15t_h}$$

$${\mathrm{\alpha }}_1=0.8+1.2\exp \{-0.005t_h\}$$

The factor k₄ accounts for the environment:

$$k_4=0.7\mathrm{for}\mathrm{an}\mathrm{arid}\mathrm{environment}$$

$$k_4=0.65\mathrm{for}\mathrm{an}\mathrm{interior}\mathrm{enviroment}$$

$$k_4=0.60\mathrm{for}\mathrm{a}\mathrm{temperate}\mathrm{enviroment}$$

$$k_4=0.5\mathrm{for}\mathrm{a}\mathrm{tropical}\mathrm{or}\mathrm{near}-\mathrm{coastal}\mathrm{enviroment}$$

Results and Discussion

The effects of various key parameters that have significant influences on creep, shrinkage strain, and loss of prestress are evaluated, in order to establish new practical insights for design, manufacture, and maintenance of railway concrete sleepers under uncertain settings (Kaewunruen et al., 2015, 2016b; Setsobhonkul et al., 2017; Li and Kaewunruen, 2019). The fundamental engineering properties of prestressed concrete sleepers used for calculation are based on previous investigations by Remennikov et al. (2011). The parametric results are generated for comparisons between Eurocode 2 (EC2), the American Concrete Institution’s code (ACI), and Australian Standard AS3600-2009 (AS). Figure 2 shows the cross section at rail seat of the prestressed concrete sleepers.

FIGURE 2

Figure 2. Cross section of railway sleepers (Remennikov et al., 2011).

Creep Parametric Study

Strength of Concrete

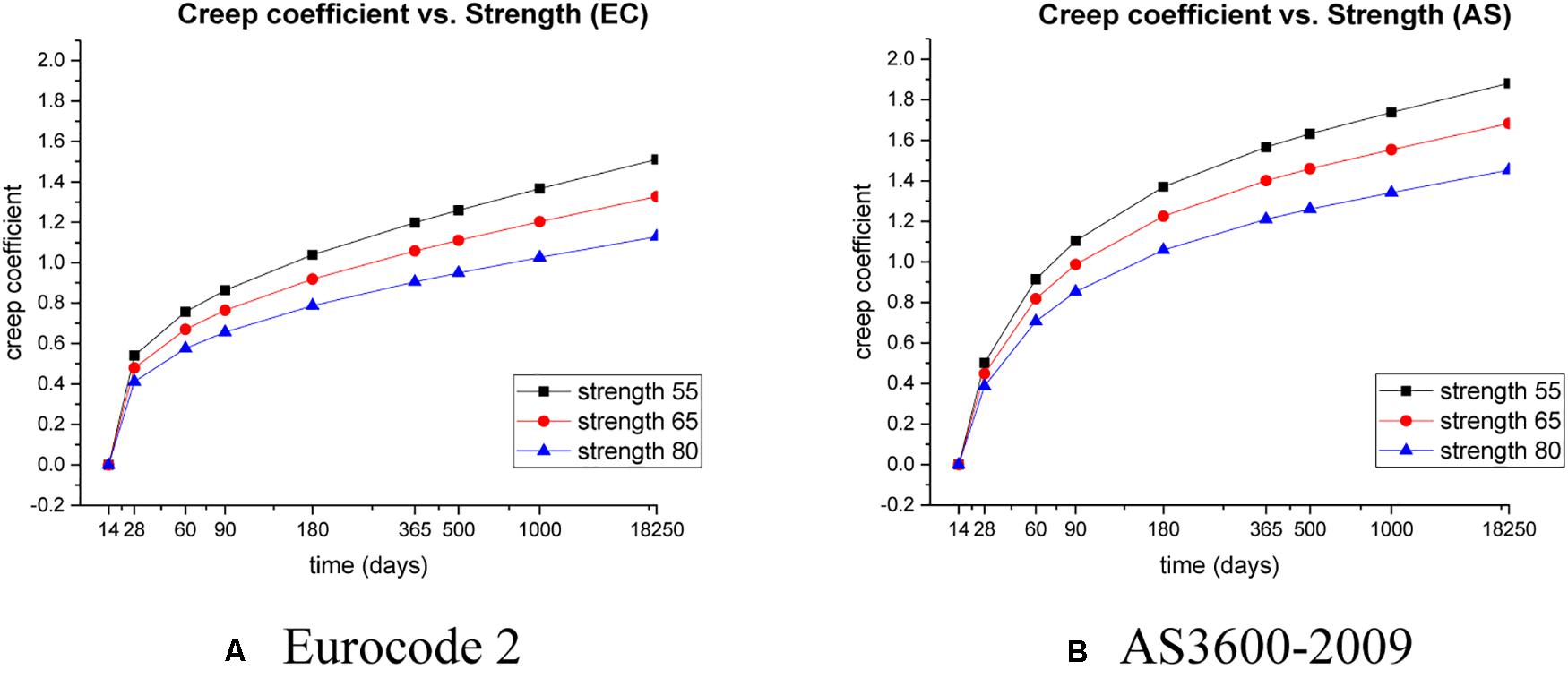
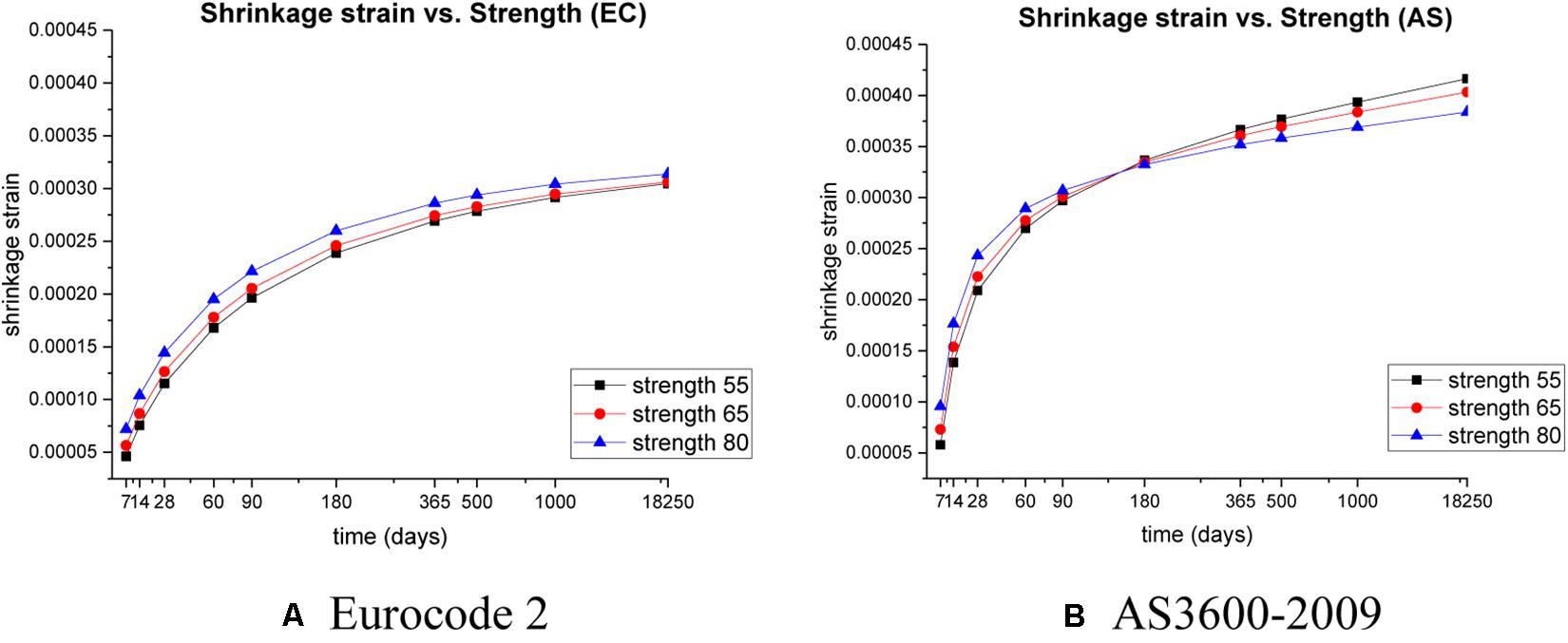
Parametric studies into the effect of concrete strength have been conducted using different characteristic strength of concrete (55, 65, and 80 MPa) in order to determine the relationships between the strength of concrete and creep curves, which are illustrated in Figure 3. It is important to note that, according to the empirical formula in ACI209R-92, the creep coefficient calculation is not directly related to concrete strength. As a result, the creep strain and creep coefficient behaviors are determined by only EC2 and AS3600, respectively. All cases are estimated from 14 days up to 18,250 days (50 years, which is a design service life of concrete sleepers) in the same conditions (e.g., uniform dimension of sleepers, 70% relative humidity, and first loading at 14 days).

FIGURE 3

Figure 3. Strength–creep relationship. (A) Euro Code 2 and (B) AS3600-2009.

Relative Humidity

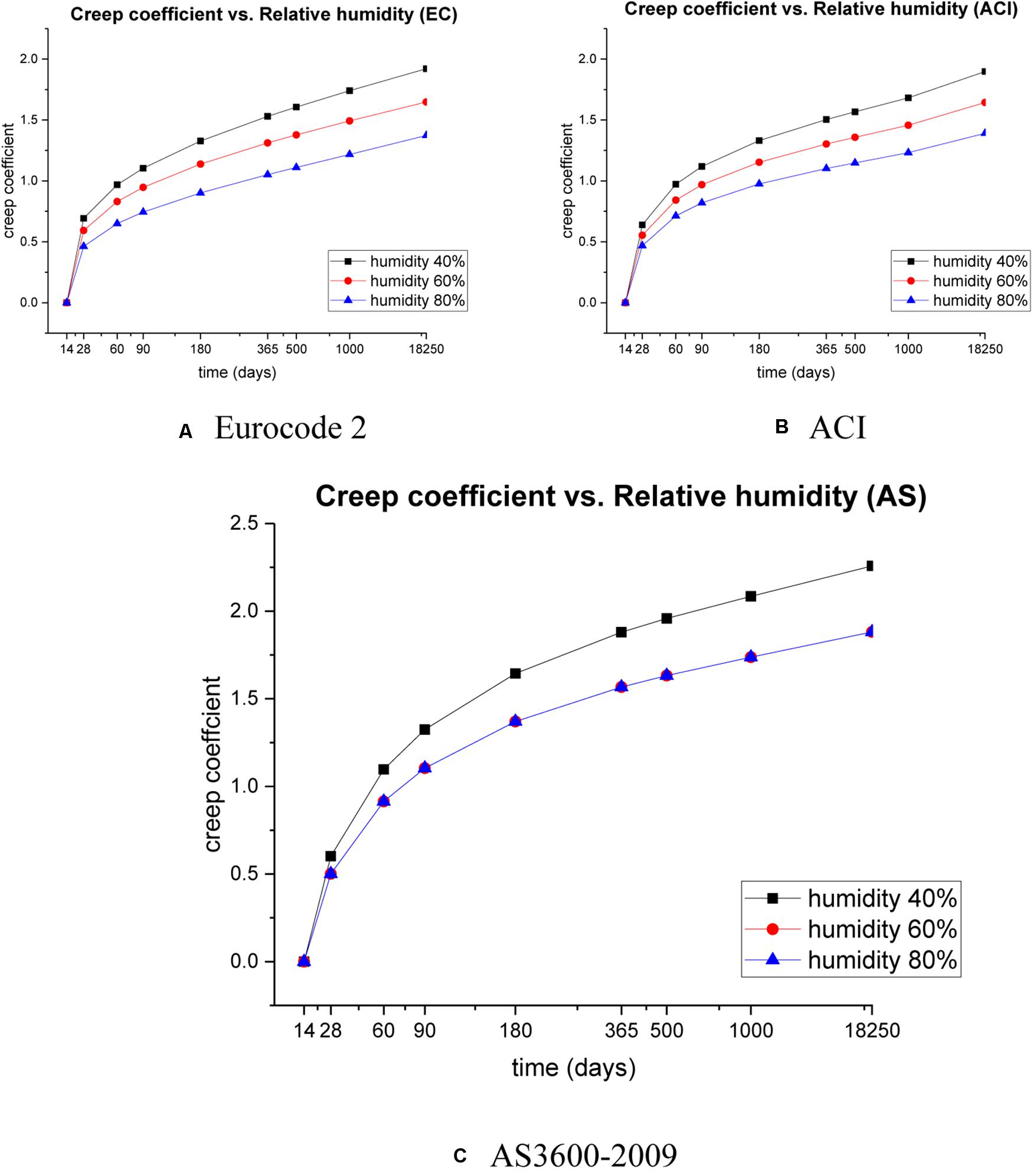
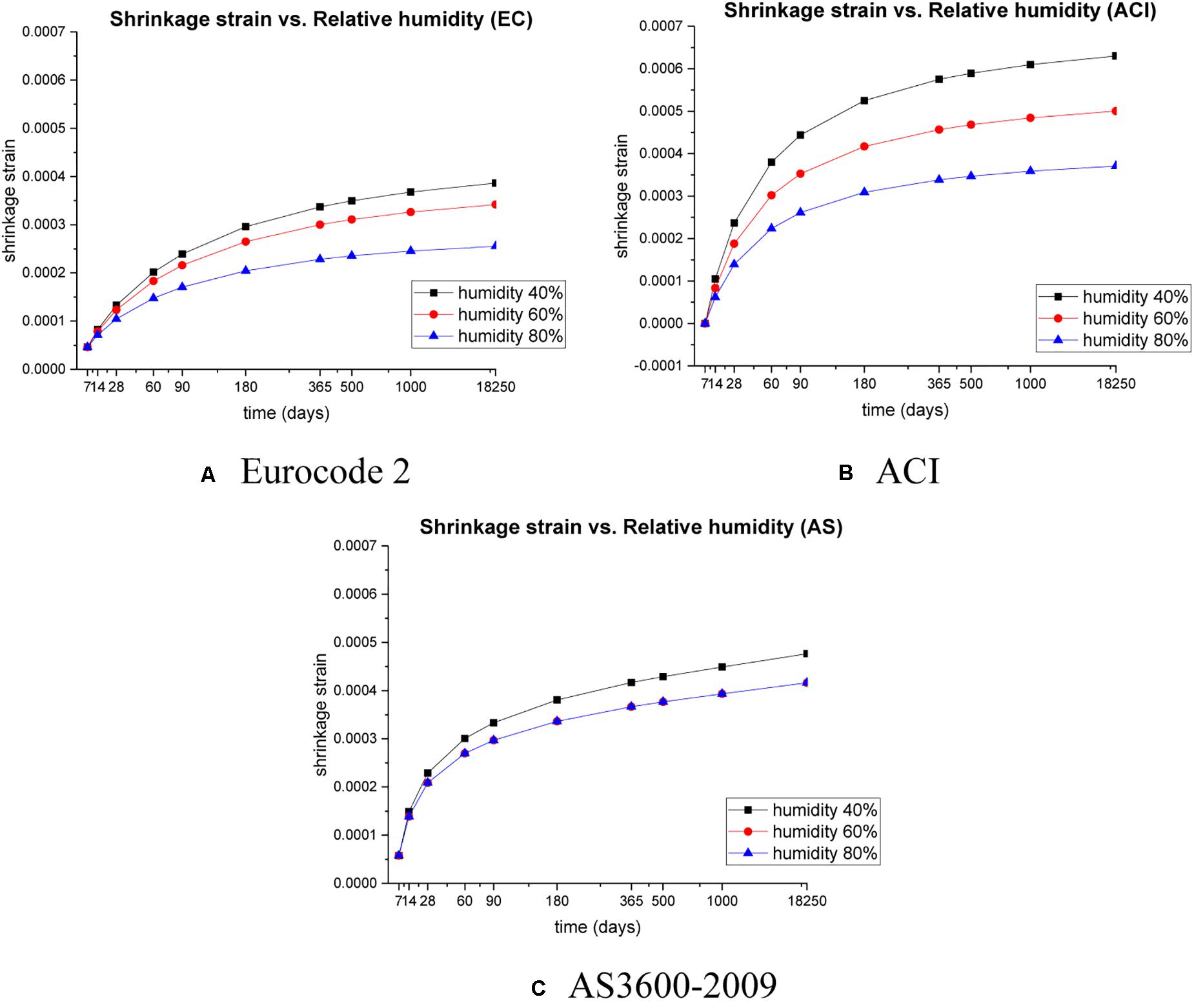
To investigate relationships between the relative humidity and creep, three cases with different relative humidity (40, 60, and 80%) are displayed from the obtained data as shown in Figure 4. The creep strain and creep coefficient are determined by using EC2, ACI, and AS3600-2009 codes, respectively. All cases are estimated from 14 days up to 18,250 days (50 years) in the same conditions (uniform dimension of sleepers, 55 MPa strength of concrete).

FIGURE 4

Figure 4. Relative humidity–creep relationship. (A) Euro Code 2, (B) ACI and (C) AS3600-2009.

Shrinkage Parametric Study

Strength

Figure 5 demonstrates the influences of different strengths on shrinkage behaviors. Note that according to the formula in ACI209R-92, the shrinkage behavior is also not directly related to concrete strength, analogously to creep. On this ground, this study focuses only on EC2 and AS3600 approaches.

FIGURE 5

Figure 5. Strength–shrinkage relationship. (A) Euro Code 2 and (B) AS3600-2009.

Relative Humidity

Figure 6 highlights the influences of different relative humidity (RH) on the shrinkage characteristics.

FIGURE 6

Figure 6. Relative humidity–shrinkage relationship. (A) Euro Code 2, (B) ACI and (C) AS3600-2009.

Curing Time

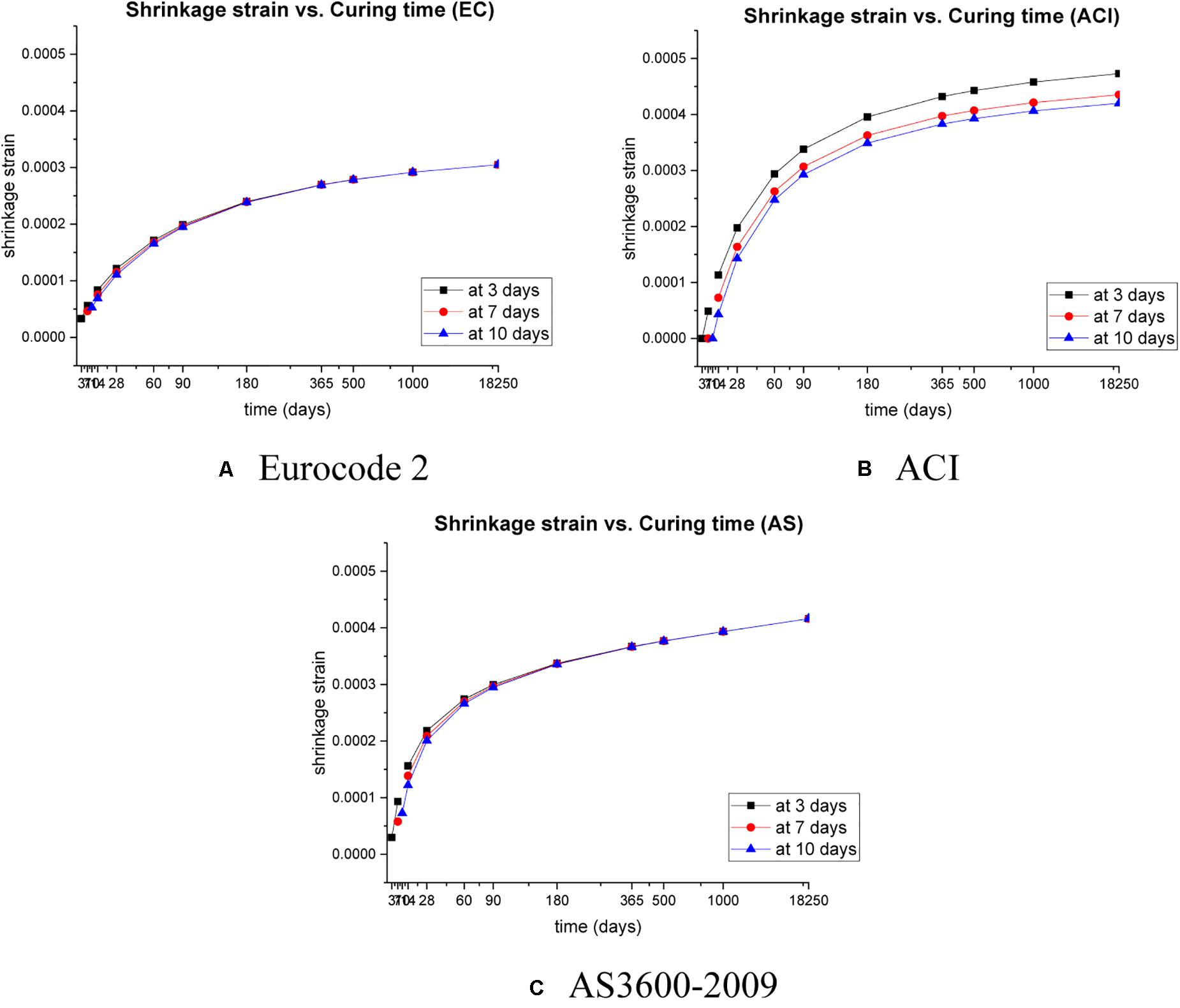
Figure 7 shows the shrinkage behaviors affected by different curing times.

FIGURE 7

Figure 7. Curing time–shrinkage relationship. (A) Euro Code 2, (B) ACI and (C) AS3600-2009.

Discussion

Based on the sensitivity analyses, the creep and shrinkage behaviors that occurred within prestressed concrete sleepers can be dependant to a variety of factors. According to the analysis results, the loss of prestress depends largely on axial strain. This implies that a large strain will result in more prestress loss in prestressed concrete sleepers.

Considering a variety of concrete strengths (i.e., 55, 65, and 80 MPa), the parametric characteristics of creep coefficient and shrinkage strain are given in Figures 3, 5. It can be observed that a higher strength of concrete exhibits lesser creep. However, the characteristics of shrinkage strain are different from creep. It is apparent that a higher-strength concrete sleeper has higher shrinkage strain at the initial stage. However, over a longer term, the total shrinkage strain of higher strength concrete becomes lesser than that of lower strength concrete. The total shrinkage strain consists of autogenous shrinkage and drying shrinkage, which is an allowance for early thermal shrinkage and is assumed to develop relatively rapidly and to increase with concrete strength.

With respect to the relative humidity, the characteristics of creep coefficient and shrinkage strain are demonstrated in Figures 4, 6. It is clear that, with the increase in the relative humidity, both creep and shrinkage in prestressed concrete sleepers decrease.

Our studies illustrate that autogenous shrinkage causes more losses of prestress for higher-strength concrete in comparison with relatively lower-strength concrete at the initial period (Australian Building Codes Board, 1994; Fryba, 1996; Stevens and Dux, 2004). In fact, our prediction results confirm the experimental investigation campaigns done in Australia (Remennikov and Kaewunruen, 2014, 2015).

By comparisons among EC2, ACI, and Australian Standard, it can be observed that the prediction results obtained from each method are not similar even exactly under the same conditions. The main reason leading to different results can be attributed to the fact that different design codes concentrate on different parameters and have been established differently. For example, the predicted strain values are largely dependent on the relative humidity and concrete strength. Higher relative humidity causes lesser creep and shrinkage, which induce lower losses of prestress. Note that the environmental factors according to Australian geographic climate are utilized in Australian Standard instead of the relative humidity. In the ACI code, the concrete strength is not directly used for time-dependent behavior predictions, but the main parameters, which are related to the concrete strength such as cement content, air content, and fine aggregate content, are heavily used in the predictions.

Conclusion

The service life of railway prestressed concrete sleepers depends largely on a variety of factors such as concrete and material characteristics, environmental conditions, dynamic loading amplitude, and external abrasions. However, time-dependent behaviors of the concrete sleepers can also influence their durability and long-term performance in the field. In real life, creep and shrinkage strains can potentially have more significant influence on the deformation of track components. In harsh environments, the railway infrastructure generally experiences highly aggressive loading conditions from increased traffics and load demands. At certain scenarios, a train derailment could happen because of track gauge change (i.e., tight gauge at such critical locations as crossing, slips, etc.). The track gauge change can be stemmed from the shortening and inelastic deflections incurred by creep and shrinkage in prestressed concrete sleepers. There are a number of existing codes of practice, enabling the predictions of creep and shrinkage. Three main design codes are examined critically in this paper. Key parameters that influence creep and shrinkage from a theoretical viewpoint for prestressed concrete sleepers are emphasized. A state-of-the-art review of research on time-dependent creep and shrinkage has been carried out in order to establish comprehensive methods for comparative analyses. This research embarks on the comparative parametric investigations into a variety of methods to determine creep and shrinkage effects in prestressed concrete railway sleepers. Comparisons among the design codes, including European Standard EUROCODE2, the American Concrete Institute ACI Code, and Australian Standard AS3600-2009, provide new practical insights into the time-dependent performance of concrete sleepers. The parametric effects of creep and shrinkage strains have been determined. Limitations of existing codes have been identified together with the recommendations and guidelines for code applications. The outcome of this study will help track engineers to better design, manufacture, inspect, and maintain railway infrastructures in order to enhance asset management efficacy and effectiveness.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

DL analyzed the data. SK contributed the materials and analysis tools. PR and AR provided technical review and advice. All authors wrote the manuscript.

Funding

This work has been further developed from an initial work published in Li et al. (2018). The authors are sincerely grateful to European Commission for the financial sponsorship of the H2020-RISE Project No. 691135 “RISEN: Rail Infrastructure Systems Engineering Network,” which enables a global research network that tackles the grand challenge in railway infrastructure resilience and advanced sensing in extreme environments (www.risen2rail.eu). In addition, this project is partially supported by European Commission’s Shift2Rail, H2020-S2R Project No. 730849 “S-Code: Switch and Crossing Optimal Design and Evaluation.” The APC is sponsored by the University of Birmingham Library’s Open Access Fund.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Australian Building Codes Board (1994). Building Code of Australia, CSIRO Division of Building, Construction and Engineering Sydney, NSW: Australian Building Codes Board.

Google Scholar

Bentz, E. C. (2000). Reinforced Concrete Sectional Analysis Using the Modified Compression Theory. Ph. D. thesis, University of Toronto, Canada.

Google Scholar

Bhatt, P. (2011). Prestressed Concrete Design to Eurocodes, 1st Edn. Abington: Spon Press.

Google Scholar

Ercolino, M., Farhidzadeh, A., Salamone, S., and Magliulo, G. (2015). Detection of onset of failure in prestressed strands by cluster analysis of acoustic emissions. Struct. Monitor. Maint. 2, 339–355. doi: 10.12989/smm.2015.2.4.339

CrossRef Full Text | Google Scholar

Esveld, C. (2001). Modern Railway Track, 2nd Edn. Netherland: The Netherlands MRT Press.

Google Scholar

Fryba, L. (1996). Dynamics of Railway Bridges. London: Thomas Telford House.

Google Scholar

Fujino, Y., and Siringoringo, D. M. (2016). Japan’s experience on long-span bridges monitoring. Struct. Monitor. Maint. 3, 233–257.

Google Scholar

Gilbert, R. I., Mickleborough, N. C., and Ranzi, G. (2016). Design of Prestressed Concrete to AS3600-2009, 2nd Edn. Boca Raton, FL: CRC Press.

Google Scholar

Gjorv, O. E. (2013). Durability design and quality assurance of major concrete infrastructure. Adv. Concrete Constr. 1, 45–63. doi: 10.12989/acc.2013.1.1.045

CrossRef Full Text | Google Scholar

Gustavson, R. (2002). Structural Behaviour of Concrete Railway Sleepers. Ph.D. thesis, Chalmers University of Technology, Sweden.

Google Scholar

Kaewunruen, S. (2014). Monitoring structural deterioration of railway turnout systems via dynamic wheel/rail interaction. Case Stud. Nondestr. Test. Eval. 19–24. doi: 10.1016/j.csndt.2014.03.004

CrossRef Full Text | Google Scholar

Kaewunruen, S., Ishida, T., and Remennikov, A. M. (2016a). Impact analyses for negative flexural responses (hogging) in railway prestressed concrete sleepers. J. Phys. 744:012101. doi: 10.1088/1742-6596/744/1/012101

CrossRef Full Text | Google Scholar

Kaewunruen, S., Sussman, J. M., and Matsumoto, A. (2016b). Grand challenges in transportation and transit systems. Front. Built. Environ. 2:4. doi: 10.3389/fbuil.2016.00004

CrossRef Full Text | Google Scholar

Kaewunruen, S., and Remennikov, A. M. (2008a). An alternative rail pad tester for measuring dynamic properties of rail pads under large preloads. Exp. Mech. 48, 55–64. doi: 10.1007/s11340-007-9059-3

CrossRef Full Text | Google Scholar

Kaewunruen, S., and Remennikov, A. M. (2008b). Effect of a large asymmetrical wheel burden on flexural response and failure of railway concrete sleepers in track systems. Eng. Fail. Anal. 15, 1065–1075. doi: 10.1016/j.engfailanal.2007.11.013

CrossRef Full Text | Google Scholar

Kaewunruen, S., and Remennikov, A. M. (2008c). Experimental simulation of the railway ballast by resilient materials and its verification by modal testing. Exp. Tech. 32, 29–35. doi: 10.1111/j.1747-1567.2007.00298.x

CrossRef Full Text | Google Scholar

Kaewunruen, S., and Remennikov, A. M. (2010). Dynamic properties of railway track and its components: recent findings and future research direction. Insight Nondestr. Test. Cond. Monitor. 52, 20–22. doi: 10.1784/insi.2010.52.1.20

CrossRef Full Text | Google Scholar

Kaewunruen, S., and Remennikov, A. M. (2013). On the residual energy toughness of prestressed concrete sleepers in railway track structures subjected to repeated impact loads. Electronic J. Struct. Eng. 13, 41–61.

Google Scholar

Kaewunruen, S., Sussman, J. M., and Einstein, H. H. (2015). Strategic framework to achieve carbon-efficient construction and maintenance of railway infrastructure systems. Front. Environ. Sci. 3:6. doi: 10.3389/fenvs.2015.00006

CrossRef Full Text | Google Scholar

Li, D., and Kaewunruen, S. (2019). Effect of extreme climate on topology of railway prestressed concrete sleepers. Climate 7:17. doi: 10.3390/cli7010017

CrossRef Full Text | Google Scholar

Li, D., Kaewunruen, S., Robery, P., and Remennikov, A. M. (2018). “Creep and shrinkage effects on railway prestressed concrete sleepers,” in ICRT 2017: Railway Development, Operations, and Maintenance, eds W. Zhai and K. C. P. Wang (Reston, VA: American Society of Civil Engineers), 394–405.

Google Scholar

Li, Z., Li, S., Lv, J., and Li, H. (2015). Condition assessment for high-speed railway bridges based on train-induced strain response. Struct. Eng. Mech. 52, 199–219. doi: 10.12989/sem.2015.54.2.199

CrossRef Full Text | Google Scholar

Neville, A. M. (1995). Properties of Concrete, 4th edn. Longman: Longman House.

Google Scholar

Padhi, S., and Panda, K. C. (2017). Fresh and hardened properties of rubberized concrete using fine rubber and silpozz. Adv. Concrete Constr. 4, 49–69. doi: 10.12989/acc.2016.4.1.049

CrossRef Full Text | Google Scholar

Parande, A. K. (2013). Role of ingredients for high strength and high performance concrete – a review. Adv. Concrete Constr. 1, 151–162. doi: 10.12989/acc.2013.01.2.151

CrossRef Full Text | Google Scholar

Remenikov, A. M., and Kaewunruen, S. (2008). A review of loading conditions for railway track structures due to train and track vertical interaction. Struct. Control Health Monitor. 15, 207–234. doi: 10.1002/stc.227

CrossRef Full Text | Google Scholar

Remennikov, A. M., and Kaewunruen, S. (2005). Determination of dynamic properties of rail pads using instrumented hammer impact technique. Acoust. Aust. 33, 63–67.

Google Scholar

Remennikov, A. M., and Kaewunruen, S. (2014). Experimental load rating of aged railway concrete sleepers. Eng. Struct. 76, 147–162. doi: 10.1016/j.engstruct.2014.06.032

CrossRef Full Text | Google Scholar

Remennikov, A. M., and Kaewunruen, S. (2015). Determination of prestressing force in railway concrete sleepers using dynamic relaxation technique. J. Perform. Constr. Facil. 29:04014134. doi: 10.1061/(asce)cf.1943-5509.0000634

PubMed Abstract | CrossRef Full Text | Google Scholar

Remennikov, A. M., Murray, M. H., and Kaewunruen, S. (2011). Reliability-based conversion of a structural design code for railway prestressed concrete sleepers. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 226, 155–173. doi: 10.1177/0954409711418754

CrossRef Full Text | Google Scholar

Setsobhonkul, S., Kaewunruen, S., and Sussman, J. M. (2017). Lifecycle assessments of railway bridge transitions exposed to extreme climate events. Front. Built Environ. 3:35. doi: 10.3389/fbuil.2017.00035

CrossRef Full Text | Google Scholar

Stevens, N. J., and Dux, P. F. (2004). A method of Designing A Concrete Railway Sleeper. International Patent No WO 2004/019772 A1, Geneva: International Bureau.

Google Scholar

Taherinezhad, J., Sofi, M., Mendis, P. A., and Ngo, T. (2013). A review of behaviour of prestressed concrete sleepers. Electronic J. Struct. Eng. 13, 1–16.

Google Scholar

Tang, K., Millard, S., and Brattie, G. (2015). Technical and economical feasibility of using GGBS in long-span concrete structures. Adv. Concrete Constr. 3, 1–14. doi: 10.12989/acc.2015.3.1.001

CrossRef Full Text | Google Scholar

Vittorio, S. (2011). Time-Dependent Behaviour of Reinforced Concrete Slabs. Advanced Design of Structures, Thesis, University of Bologna, Bologna.

Google Scholar

Wakui, H., and Okuda, H. (1999). A study on limit-state design for prestressed concrete sleepers. Concrete Lib. JSCE 33, 1–25.

Google Scholar

Wang, N. (1996). Resistance of Concrete Railroad Ties to Impact Loading. Ph.D. Thesis, University of British Columbia, Canada.

Google Scholar

Warner, R. F., Rangan, B. V., Hall, A. S., and Faulkes, K. A. (1998). Concrete Structures, Addison Wesley. Melbourne, Australia: Longman.

Google Scholar

Yahiaoui, W., Kenai, S., Menadi, B., and Kadri, E. H. (2017). Durability of self-compacted concrete containing slag in hot climate. Adv. Concrete Constr. 5, 271–288.

Google Scholar