Automated Optimal Motion Sequence of a 9-Bar Linkage

Introduction

Current optimization and energy concerns have been embedded into the design process of high-performance engineering structures and adaptive architecture to pursue optimal solutions in complex systems through usage of an increasingly available computational power. To withstand the functional requirements as well as the external conditions during their service life, energy efficient systems must follow an economic and a sustainable way of building. Lightweight shape-controlled structures benefit from the integration and replacement of the primary members with mechanical actuators. The systems may contribute to an adaptive architecture under possibly changing functional, environmental, or loading conditions. Optimization of shape-controlled structures in terms of performance, efficiency, and technical simplicity can be achieved through respective optimization processes of the control design and motion analysis. Nevertheless, adaptive structures often entail high energy amounts in their kinematics, negatively affecting their performance, and reconfigurability. From an engineering point of view, simplicity in designing and manufacturing reflects the easiness and fastness in reconfiguration and deformability. Thus, the traditional design approach can be replaced with an automated one providing a numerical procedure of an optimization-driven approach and at the same time performing an economic design by satisfying durability criteria in innovative engineering solutions (Kallioras et al., 2016).

Structural reconfigurations in adaptive architecture respond to different purposes including functional requirements or external conditions, morphological changes, manipulation, and locomotion. Our build environment can benefit from reconfigurable architecture by improving occupant comfort and increasing energy efficiency in terms of sustainability as presented in Phocas et al. (2019). A plethora of representative examples of adaptive architecture responding to external conditions can be found in several studies. Herein are some specific examples (Phocas et al., 2019): (1) Shake snow off a building’s roof; (2) Help harvest sun, wind and rain water; (3) Minimize energy losses (conduction, convection, radiation); (4) Adjust the acoustics of a building; (5) Improve lighting conditions; (6) Enhance natural ventilation; (7) Optimize the performance of a photovoltaic roof; (8) Optimize distribution of structural loading and minimize aerodynamic loads; (9) Improve space utilization/efficiency; and (10) Produce unique esthetic effects.

Over the last few years, requirements of temporary environments and aerospace structures in conjunction with the technological advancements have been pushing the boundaries of the design of reconfigurable structures, primarily in terms of deployable structures with a multifariousness in typologies and mechanisms (Pellegrino, 2001). An integrated composition of embedded active control is feasible mainly through tensegrity structures, in which their specific typology comprises autonomous and self-supported systems that are capable of effectively transferring external loading (Gantes, 2001). Dynamic models have been presented for solving the kinematics of systems with 1, 2 and 3-degree-of-freedom (DOF), in terms of minimizing energy consumption through replacement of the compression members with pneumatic actuators and the tension-only members with spring elements or cables with variable length (Hanaor, 1997; Tibert, 2002; Adam and Smith, 2008). In such cases, under external loading the stiffness of the system decreases even if the actuators are locked (Arsenault and Gosselin, 2005, 2006a,b, 2009). In addition, adequate stiffness during reconfiguration is not feasible through pneumatic actuators nor to undergo large transformations (Bel et al., 2011). For a wide range of shape adjustments, designers have to deal with the increase of the structural self-weight, the complexity of the mechanisms and the energy efficiency, whereas these topics are mostly related with the number and the characteristics of the actuators.

On the control perspective, an appropriate feedback control system and a suitable motion planning as well as control algorithms enable the performance of structural reconfigurations through the control of actuators and sensors (Fox and Kemp, 2009). The integration of active control in engineering structures in both theoretical and experimental work generally was identified by Yang and Soong (1998). In particular, mechanisms like tensegrity structures involve shape control using active struts or cables for the active structural control (Korkmaz, 2011). The “effective 4-bar” mechanism has been proposed for the reconfigurations of the 9-bar linkage in achieving flexibility and controllability, as well as minimum structural self-weight and energy consumption for the locomotion. Several different configurations, without being exclusively symmetrical, can be produced by the multi-DOF system based on the motion planning and control methodology as presented in Phocas et al. (2015). Two different actuation methods, i.e., a direct and a cable-driven actuation one, have been proposed by Phocas et al. (2015), Matheou et al. (2017, 2018). In addition, an experimental small-scale model was developed to address the integrated design process of reconfigurable structures through design, modeling, and assembly (Christoforou et al., 2019). Along these lines, a previous numerical study conducted by the authors focused on the motion sequence optimization of the 9-bar linkage (Matheou et al., 2020). This research project extends the optimization analysis by considering the self-weight and a uniform distributed vertical load of 2.5 kN/m.

In the spectrum of engineering design optimization, many numerical methods, classified in two categories, gradient-based, and derivative-free ones have been developed to meet the demands of high-performance engineering structures. State-of-the-art nature-inspired algorithms have systematically replaced the frequently used brute force design methodologies aiming to solve combinatorial problems. Search procedures like nature-inspired or bio-inspired defined by heuristic and metaheuristic algorithms are classified in derivative-free class of search algorithms. Several species in nature have developed some sophisticated techniques following specific rules basically searching for food and/or nests, as well as for survival and reproduction reasons. In general, these behaviors in nature gave rise to the design of the heuristic and metaheuristic algorithms. Along these lines, some of the well-established metaheuristic algorithms (Kallioras et al., 2018) are as follow:

– Particle swarm optimization based on the social behavior of bird flocking (PSO; Eberhart and Kennedy, 1995),

– Ant colony optimization inspired by the foraging behavior of ants (Dorigo and Stützle, 2004),

– Artificial bee colony algorithm (Karaboga and Basturk, 2008),

– Firefly algorithm, inspired by the flashing behavior of fireflies (Yang, 2008),

– Cuckoo search algorithm, mimicking the brood parasitism of cuckoo species (Yang, 2008),

– Simulated annealing, based on the process of slowly cooling heated objects to avoid defects (Van Laarhoven and Aarts, 2010),

– Harmony search, based on the improvisation procedure of jazz bands (Geem, 2010),

– Differential evolution (Storn and Price, 1997),

– Ray optimization, based on Snell’s light refraction law (Kaveh and Khayatazad, 2012),

– Genetic algorithms, inspired by natural selection (Holland, 1973),

– Krill herd, based on the simulation of the herding behavior of krill individuals (Gandomi and Alavi, 2012),

– Variants of existing methods (Sarker et al., 2014) chaotic swarming of particles, combining swarm intelligence and chaos theory (Kaveh et al., 2014), or the thermal exchange optimization, based on Newton’s law of cooling (Kaveh and Dadras, 2017).

A stochastic and population-based group of algorithms inspired by the social behavior of birds flocking and fish schooling defined the swarm optimization (Chen et al., 2013). For instance, birds or fishes, are positioned randomly representing an initial population of particles into the multidimensional search space examined (Chen et al., 2013). To find a better position or solution during the iterations of the algorithm, each particle whose position represents a solution, “travels” into the search space and adjusts its position based on its own experience, built by memorizing the best position encountered, as well as that of neighboring particles. This procedure follows a continuous loop of iterations until the termination criterion is satisfied (Li and Yao, 2012). In such a case, local search (i.e., self-experience), and global search (i.e., neighboring experience) are combined together in PSO algorithms with the purpose to balance exploration and exploitation. In the past years, PSO algorithms were of great interest for several studies (Mendes et al., 2004; Parsopoulos and Vrahatis, 2004; Van Den Bergh and Engelbrecht, 2004), while PSO algorithms proved to be efficient in handling real-world optimization problems (Poli et al., 2007).

In particular, the particle swarm optimization algorithm has been proposed to compute the optimal feasible prestress modes of a cable-strut structure by utilizing the weight coefficient (Chen et al., 2020). The multi-objective optimization problem is converted into a single-objective one by reducing the computational complexity, either with an asymmetrical or a symmetrical cable-structure (small number or multiple self-stress states, respectively). In addition, a group-theoretic approach has been utilized for the kinematic design and analysis of four symmetric deployable scissor-hinge structures aiming to trace the motion path and investigate features such as kinematic indeterminacy and minimum distance among nonadjacent components during deployment (Chen et al., 2017). Optimal synthesis techniques have been proposed, as well as for a kinematic synthesis of a 9-bar spatial mechanism, mainly to be used as a prosthetic thumb. The different configurations of the mechanism follow the kinematics and the anthropometry of the thumb (Avila-Hernández and Cuenca-Jiménez, 2018).

The advantages of the proposed Pity Beetle Algorithm (PBA) were tested in three levels by the authors in a previous study (Kallioras et al., 2018), following the testing procedure of new evolutionary and swarm type of algorithms. The assessment based on the proposed algorithmic parameters, in comparison with other state-of-the-art algorithms and in particular against the best algorithms that were identified during the CEC, 2013 competition were presented in the “Special Session and Competition on Real-Parameter Single Objective Optimization” (Liang et al., 2013b), and based on the CEC, 2014 benchmark test suite (Liang et al., 2013a). Basically, the automated optimization process for an optimal motion sequence benefits form the PBA due to its robustness and efficiency. In particular, the PBA is not influenced by the algorithmic parameters and the increase of the dimensionality and the computational effort required internally is low.

The metaheuristic search algorithm called PBA is implemented in the automated optimization-driven analysis aiming to investigate a plethora of possible sequences of a planar arch-like 9-bar linkage based on the “effective 4-bar” approach. In this case, the PBA has the ability to search large areas of possible solutions for the plethora of different sequences of the 9-bar linkage. Each reconfiguration step of the 9-bar linkage is determined by the optimization process seeking to find the optimum motion pattern for the locked and unlocked joint angles through a continuous feedback loop. The respective optimization tasks gave rise to a better performance and efficiency through a selection of the lowest maximum brake torques at the locked joints of the structure. The following sections describe the reconfiguration design approach of the proposed 9-bar linkage, while motion planning and optimization-driven analysis are presented and analyzed.

Reconfiguration Design Approach and Motion Planning

The reconfiguration approach of the 9-bar linkage presented in Figure 1 refers to the effective 4-bar concept, using a sequence of 1-DOF for each reconfiguration step by selectively releasing four joints in each step of the primary members as proposed in Christoforou et al. (2012, 2015). Among the joints of the 9-bar linkage, the two ends of the chain are connected to the ground through rotational joints, and are always unlocked to allow for the motion of the linkage in relation with the two unlocked intermediate joints. In general, the number of the actuators used in the planar n-bar mechanism is equal to the (n−3) DOF involving one geared electrical motor associated to one of the base joints as described in Christoforou et al. (2019). In such cases there is no addition to the self-weight of the moving part of the structure because the actuator directly mounts to the ground. As shown in Figure 2, the predefined initial and target position of the 9-bar linkage involve different intermediate configurations according to the selected sequence aiming to the adjustment of the systems joints to the desired values.

FIGURE 1

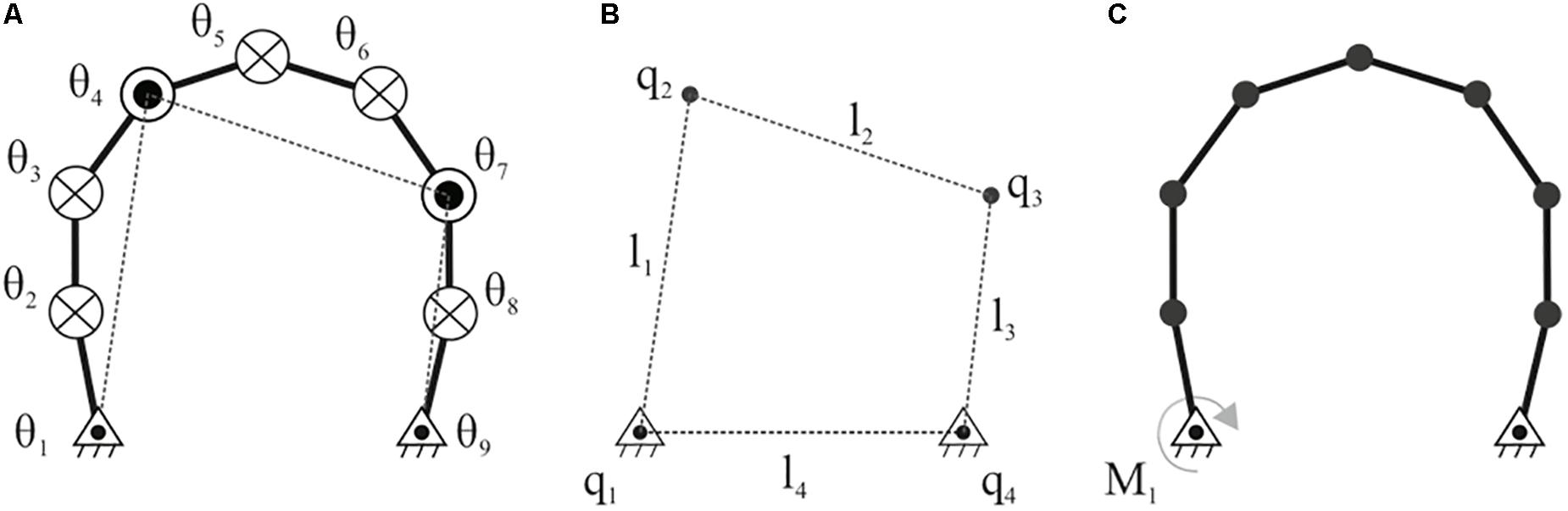
Figure 1. The effective 4-bar concept for the 9-bar linkage (⊗: locked joint, ⊙: unlocked joint, and △: pivoted–to–the-ground joint) applied at a transformation step between the initial and target positions of the systems; (A) n-bar linkage; (B) effective 4-bar; and (C) initial system configuration of base actuation.

FIGURE 2

Figure 2. The planar 9-bar linkage in its initial and target position.

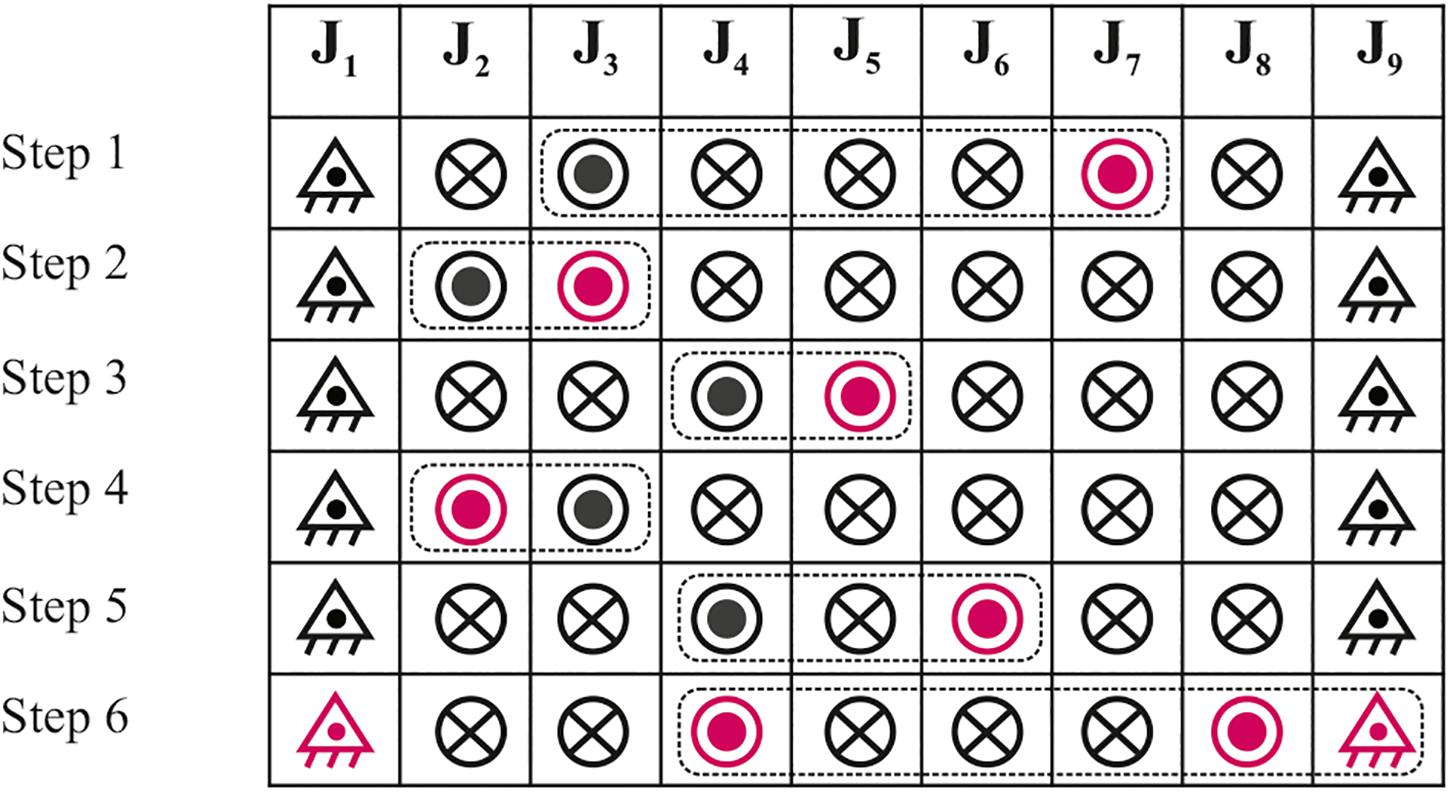
Following the “effective 4-bar” concept only one joint angle is adjusted in each intermediate step of the 9-bar linkage, while the remaining joints are controlled by electromagnetic brakes. Figures 3, 4 present an example of a control sequence with a scheduled table of the different combination of unlocked and locked joints and the reconfiguration steps, respectively. In our case study, a quasi-ellipsoid shape of 5.42 m height and 4.66 m span defines the initial configuration with the following degrees of the internal n-bar angles θ_i = [102, 168, 144, 144, 144, 144, 144, 168, 102]^T. The target configuration has a new quasi-ellipsoid shape of 4.49 m height and the same span with the respective given joint angles, such as θ_f = [124, 144, 120, 168, 144, 168, 120, 144, 124]^T. The 9-bar linkage consists of hinge-connected beam members of UPN120/100 mm and 1.75 m length assigned with aluminum of 69.9 GPa elastic modulus and 241.3 MPa yield strength.

FIGURE 3

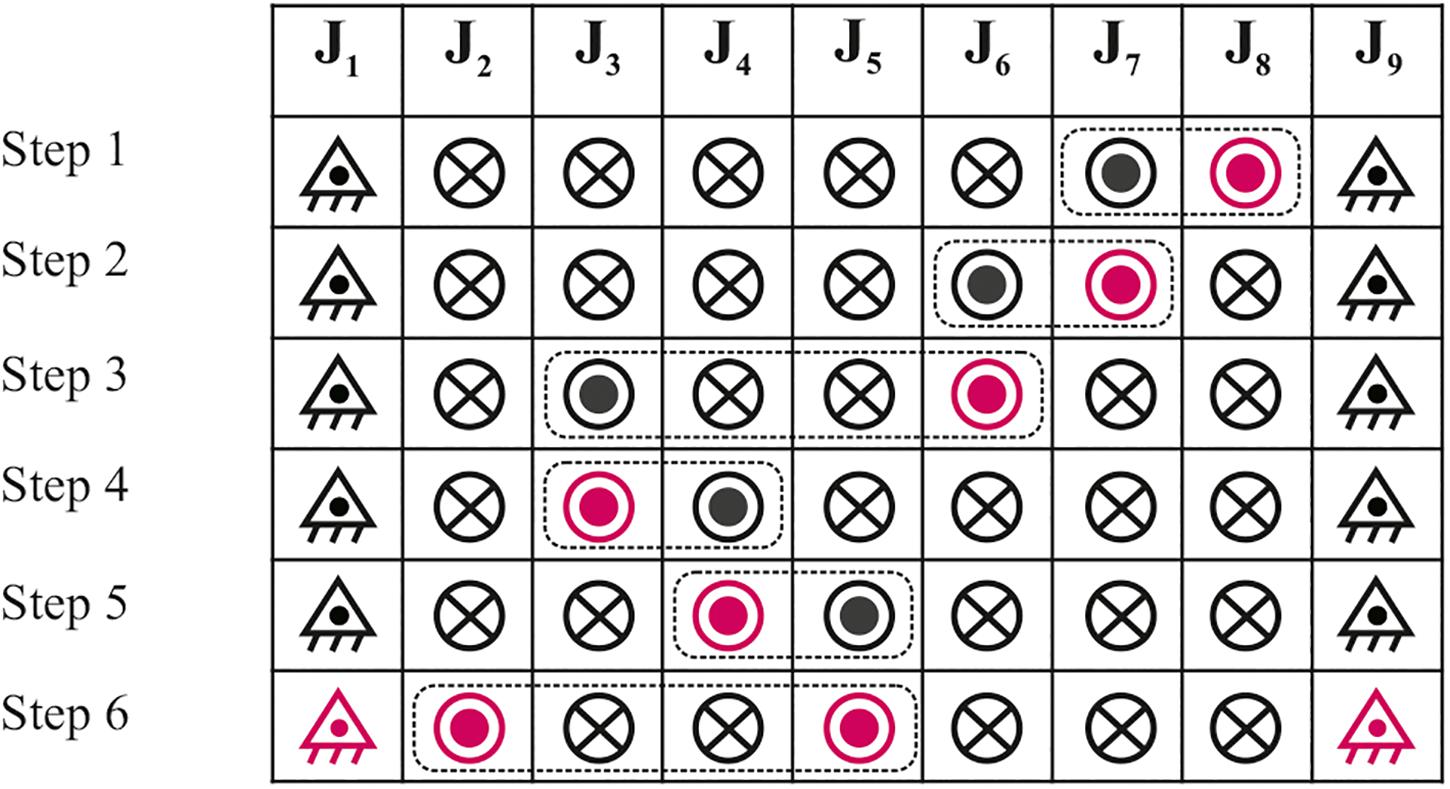
Figure 3. Scheduling table for a control sequence adopted to realize the required shape adjustment (⊗: locked joint, ⊙: unlocked joint, △: pivoted–to–the-ground joint, and shaded symbols represent the currently adjusted joints).

FIGURE 4

Figure 4. Reconfiguration steps of the 9-bar linkage.

Optimization-Driven Analysis and Simulation Study

Pity Beetle Algorithm

This paper presents the automated optimization sequence process of a predefined initial configuration of the 9-bar linkage to the target configuration involving six different intermediate steps. PBA searches for the optimum motion sequence, while the algorithm tries to find the minimum brake torques in the locked joints in each reconfiguration step concerning the self-weight and a uniform distributed vertical load of 2.5 kN/m.

In the present study, the metaheuristic search algorithm PBA is used. PBA is inspired by the aggregation behavior of a beetle species. This behavior is a sophisticated system of communication based on chemical signals (pheromones), a common feature within the subfamily of Scolytinae. One of the most common bark beetles in Europe (Liang et al., 2013a) among the different Eurasian, is the six-toothed spruce bark beetle, Pityogenes chalcographus (Coleoptera, Scolytinae), that infests mainly Norway spruce (Picea abies) together with pines (Pinus sp.), and larch (Larix decidua; Schwerdtfege, 1929; Postner, 1974; Wood and Bright, 1992; Pfeffer, 1995). P. chalcographus has been also found in Elatia (Drama, Greece; Avtzis et al., 2010), however, these species mainly occur in central and northern Europe.

Different stages compose the overall process of the P. chalcographus particles. As a first step, chemical traits that are exploited by weakened trees help pioneer male beetles to locate a suitable host (i.e., searching stage). Then, the population is significantly locally increased by the production of an aggregation pheromone, which attracts males and females (i.e., aggregation stage) when the beetles are feeding on the host. The mass infestation of the exceeded specific population can no longer be contained by the defense mechanisms. Both robust and weakened trees can be attacked at this level of the population. While there is a high density of infestation (e.g., less feeding space, higher probability of infectious diseases) with an over-crowded host tree, then an anti-aggregation pheromone is emitted by feeding beetles, so that more beetles are discouraged to attack this tree, in order to turn them to other trees (i.e., anti-aggregation stage). Therefore, the gradually expansion of the infestation into the forest is created by groups of dying or dead trees around the initially attacked tree.

The mathematical formulation of an optimization problem can be expressed in standard mathematical terms as a non-linear programming problem, which can be stated as follows:

$$\min F\left(x\right),x={[x_1,x_2,\mathrm{\dots },x_D]}^T$$

$$L_i\le x_i\le U_i,i=1,2,\mathrm{\dots },D$$

where F(x):R^D→R is a real-valued objective function to be minimized (without loss of generality) and R is the set of real numbers, x ∈ R^D is the design variables vector of dimension D, while L_i, and U_i are the lower and upper bounds of the i^th design variable.

The current position of vector $x_j^{\left(g\right)}\in R^D$ defines the j^th member of the population at the g^th search step (generation) of the algorithm in a D-dimensional search space. The main functions of the PBA refer to the implementation of the suitable host search and reproduction behavior of the bark beetles. PBA is categorized in three main steps: Initialization, New Hypervolume Selection Pattern and Update Population Position. Although the population is comprized of males and females, some male beetles act as pioneer to locate the most suitable host. Initially, the search space (i.e., first generation) generates randomly the first population (gallery/colony) position. Then, particles of the initial population aim to create new populations (i.e., second generation) by moving to other positions inside of the different hypervolumes. The size of the hypervolume that each population will cover is dependent on the quality of their birth position and the infestation factor in proximity. In every generation new populations are generated and in the third step, new populations replace the previous ones. A detailed description of the PBA framework is given by Kallioras et al. (2018).

Simulation Study

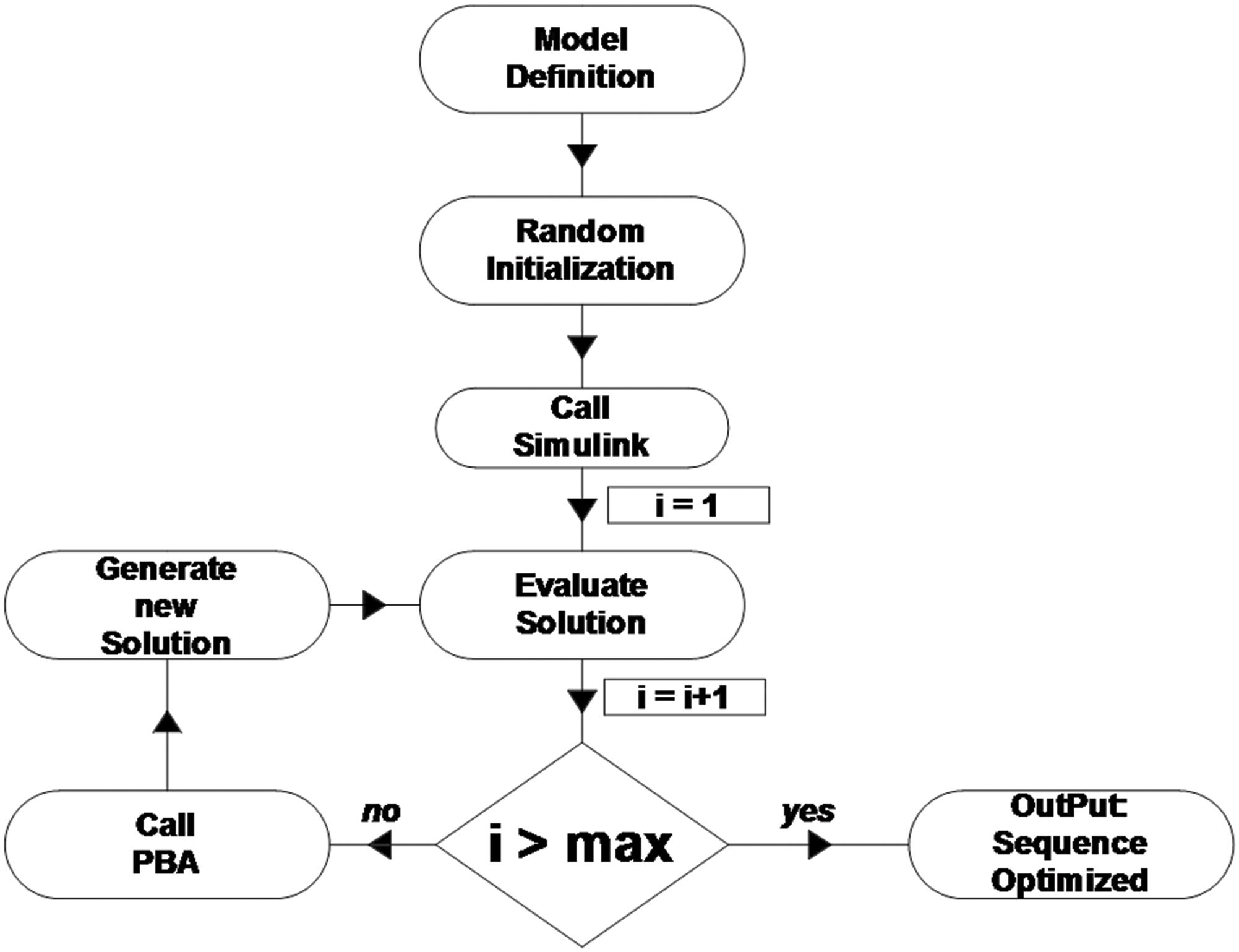
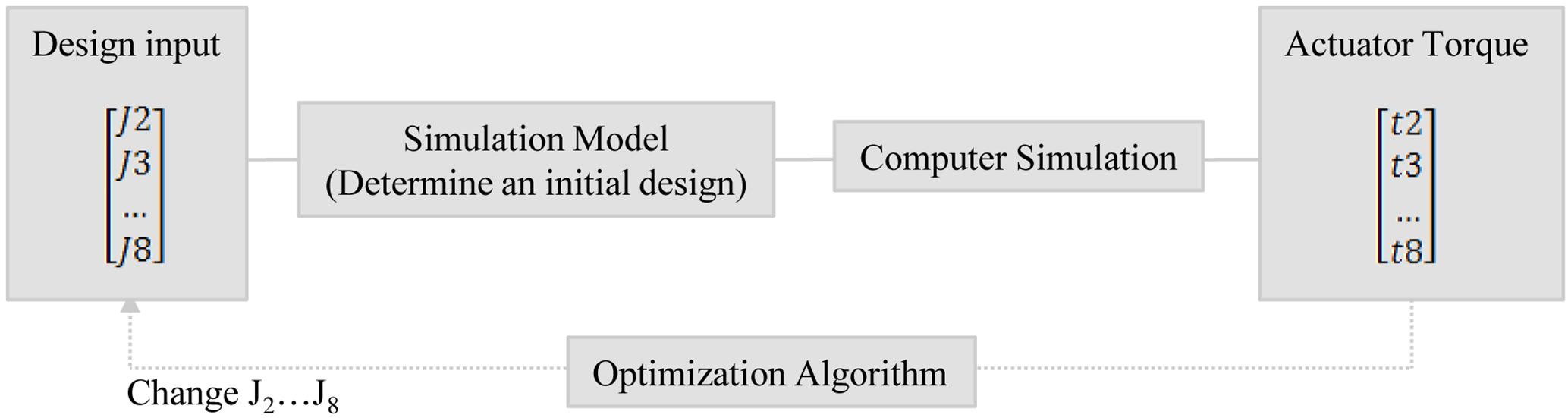
This section presents an example to demonstrate the proposed optimization-driven approach with the software MATLAB and Simulink for a Model Based-Design. Based on a 9-bar linkage modeled in Solidworks Essentials, all geometrical, mass and inertia characteristics were exported as blocks to Simulink through the Simscape Multibody Link SolidWorks plug-in. Figure 5 presents the optimization procedure and is formulated as follows: The objective function is the total torque of the system until the final position is reached. The solution vector is a vector with discrete values, which represents the nodes and the sequence of the joints’ locking and unlocking. The design constraints of the developed motion patterns are defined primarily by the selection of two unlocked joints apart from J₁ and J₉ for each reconfiguration step. The developed combination of the unlocked joints mainly refers to the two different joint angles. Therefore, one of the unlocked joint angles is adjusted to its target position, while the other one remains unlocked. Both are defined randomly by the algorithm in every reconfiguration step. If the unlocked joint is not adjusted to its target position, then it can be used again for the combinations of the next motion steps. Otherwise, when the unlocked joint is adjusted to its target position, then it remains locked and is excluded from the list of possible candidates until the end of the reconfiguration process. The discrete solutions are generated by the sampling technique described in Kallioras et al. (2018). There is no penalty for constraint violations as such solutions are avoided during the new solution generation procedure. For each position of the solution vector, a pool of possible values is generated with respect to previous position values constraints and general constraints as well. The choice for each position in the solution vector is made from its pool.

FIGURE 5

Figure 5. Indicative flowchart of the proposed procedure.

As shown in Figure 6, each step of the reconfiguration sequence follows a closed continuous feedback loop that reads all different possible motion patterns and seeks to find the optimum unlocked and locked joint angles concerning the total brake torques at the locked joints. The algorithm working in the optimization process, Simulink demonstrates dynamically the reconfiguration of the 3D model of the 9-bar linkage. In this framework, the user has the opportunity to develop a comprehensive overview of the locomotion of the different motion patterns. According to the design variables and the constraints of the algorithmic model, PBA follows a random selection of the unlocked and locked joints while it is looking for the optimal solution under the load acting on the system.

FIGURE 6

Figure 6. Automated process of the reconfiguration sequence.

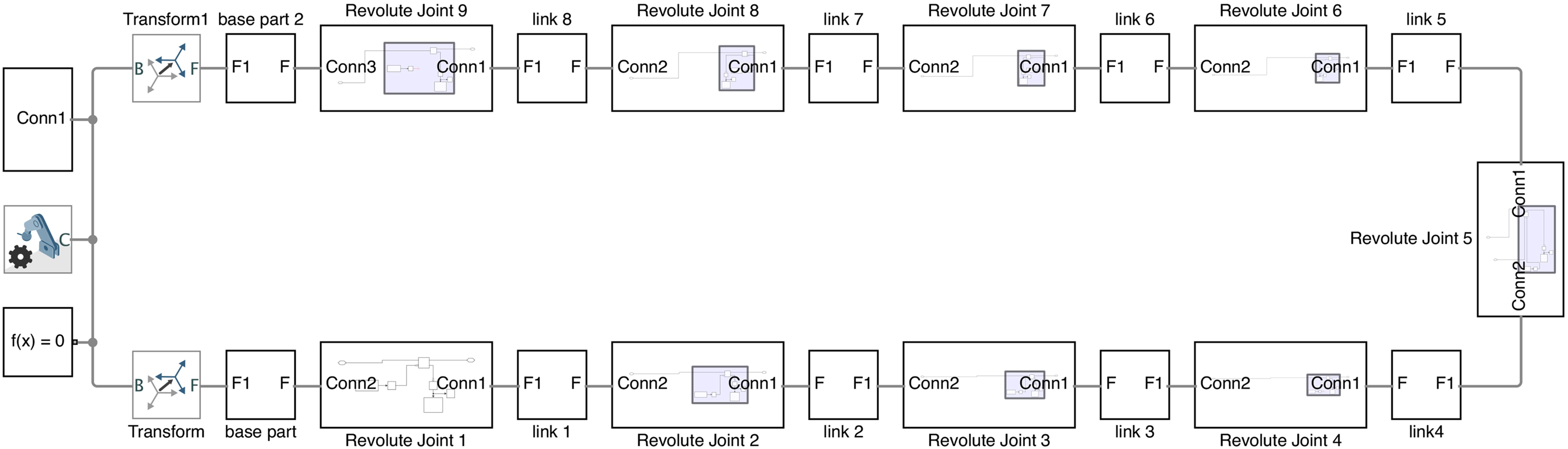
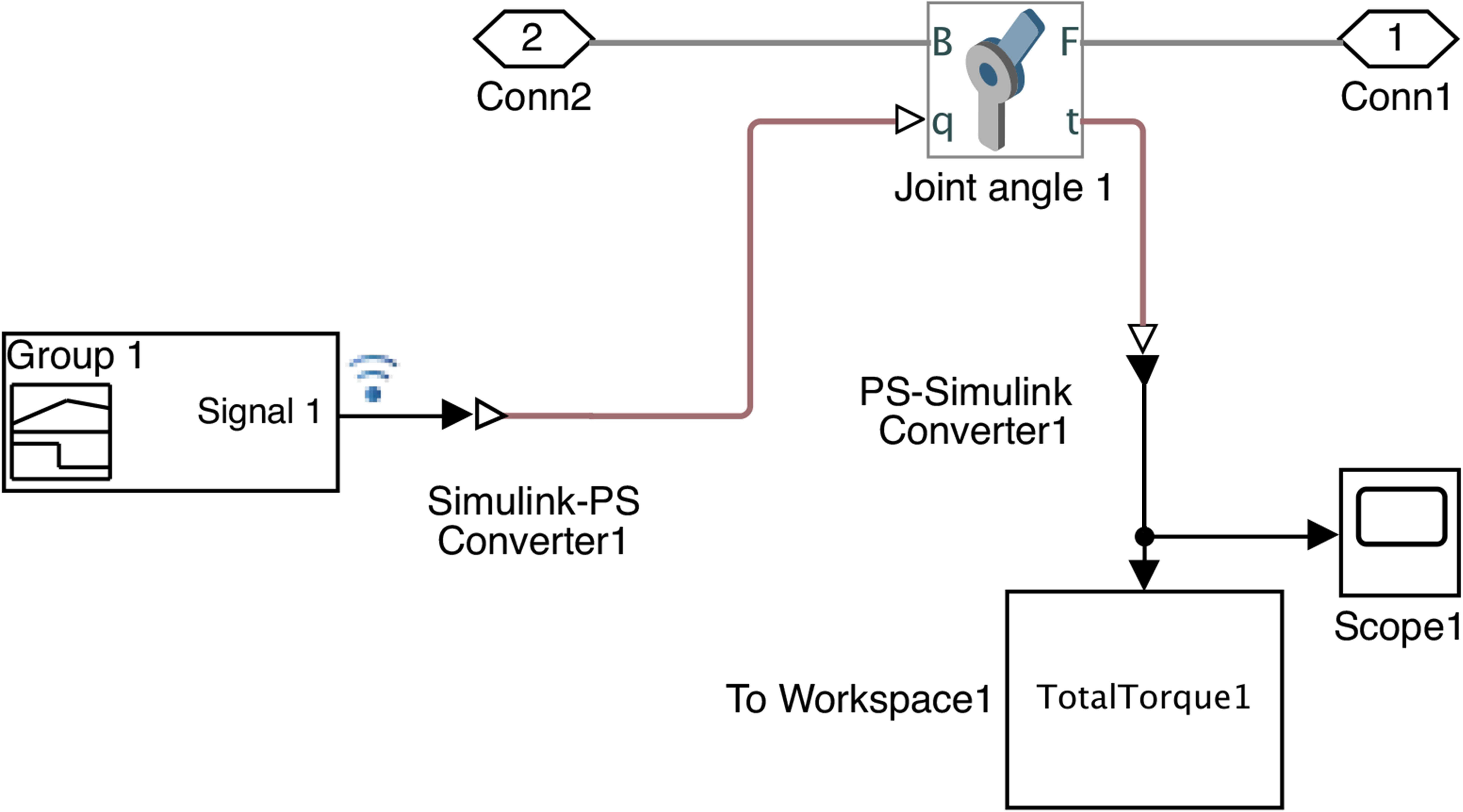
Figure 7 presents the Simulink model of the 9-bar linkage set to z axis. It consists of nine blocks of “Revolute Joints” with one rotational DOF that basically represent the hinge connections. According to the simulation time, all the new possible joint angles developed in MATLAB are identified by the “Signal Builder” block. Therefore, a “Simulink-PS Converter” block directly connected with the “Revolute Joint” block, converts the unitless Simulink input signal from MATLAB to a Physical Signal in Simulink. As shown in Figure 8, activation of sensing in the “Revolute Joint” block enables the possibility to transfer the total brake torques of each revolute joint from Simulink to the MATLAB base workspace.

FIGURE 7

Figure 7. Simulink model with all blocks and subsystems.

FIGURE 8

Figure 8. Subsystem of the “Revolute Joint 1”.

Results

Figure 9 presents the results of the optimal motion sequence solution from the predefined initial to the target configuration of the 9-bar linkage structure. The optimal motion sequence is defined through a selection of unlocked joints according to the effective 4-bar reconfiguration method, as follows Step: 1: J₇ and J₃, Step 2: J₃ and J₂, Step 3: J₅ and J₄, Step 4: J₂ and J₄, Step 5: J₆ and J₄, and Step 6: J₈ and J₄. Following the motion and pattern constraints in the algorithmic model, the selection of the motion sequence succeeds to accomplish the reconfiguration process with the lowest maximum brake torques at the locked joints in all reconfiguration steps under consideration of the structure self-weight and vertical load.

FIGURE 9

Figure 9. The optimum solution of a motion sequence.

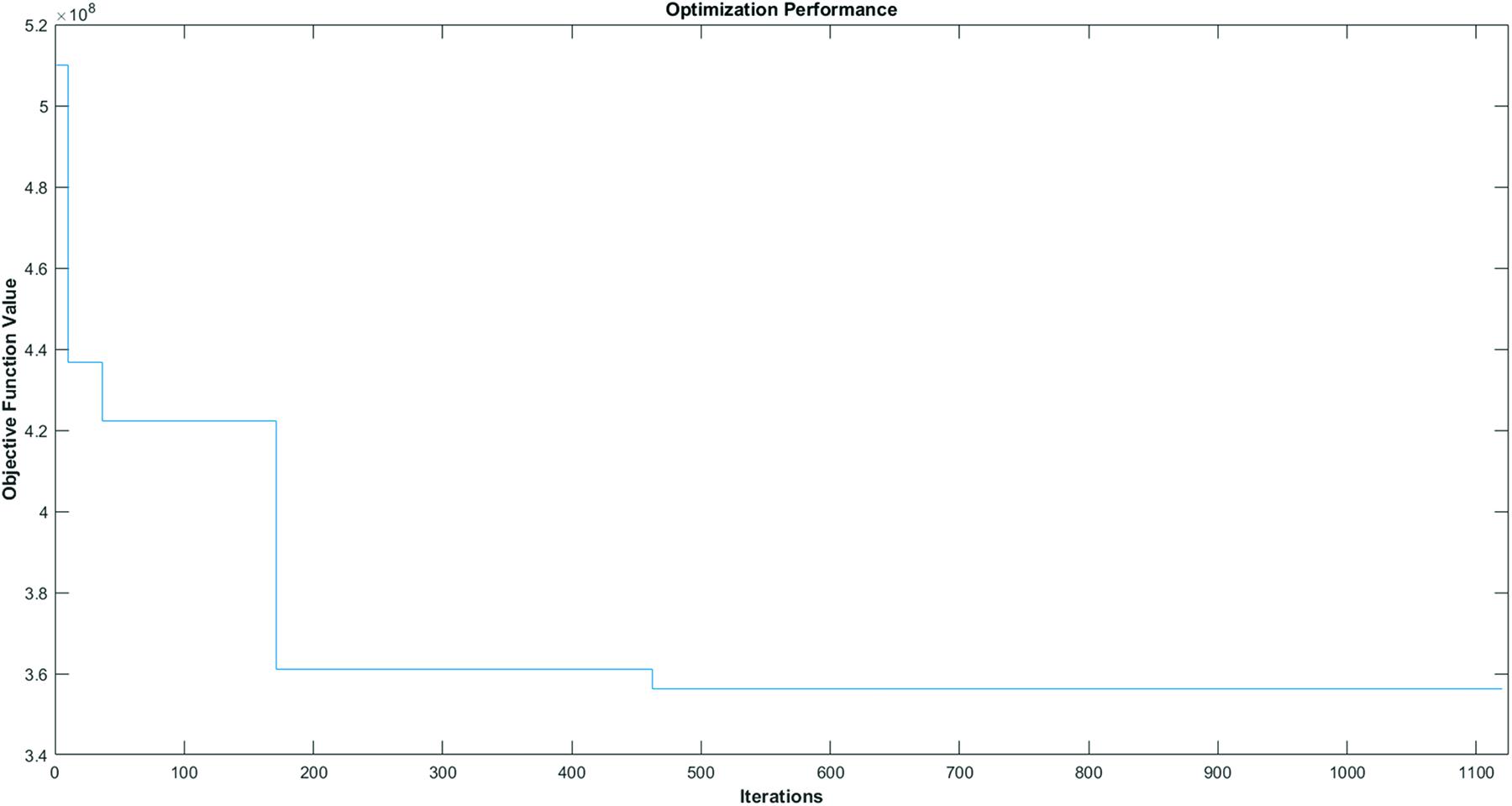
Figure 10 presents the best objective function value of the total sum of the brake torques at the locked joints for all reconfiguration steps. The above analyses show that the first solution is developed at iteration 10, and the optimal solution is given at iteration 462 amongst the plethora of the possible solutions.

FIGURE 10

Figure 10. Best objective function value.

Conclusion

An optimal motion sequence solution of a planar 9-bar linkage structure is presented among the large range of possible solutions under the structure self-weight and vertical load. Based on the robust automated optimization-driven analysis, the selection of the locked and unlocked joints throughout the reconfiguration is succeeded through the natured-inspired metaheuristic algorithm PBA. The “effective 4-bar” concept gives rise to the reconfiguration approach of the 9-bar linkage concerning the minimum structural self-weight and energy consumption by selectively releasing four joints and using one DOF in each reconfiguration step. In further improving the lightweight structure in all reconfiguration steps, from an initial to a target configuration, this project demonstrates the optimal motion sequence with the lowest maximum brake torques at the locked joints.

Besides the evaluation of the system kinematics, the work carried out reveals the integration potentialities of MATLAB and Simulink giving rise to an automated continuous feedback loop in reconfigurable engineering structures. The realization of high-performance shape-controlled structures and adaptive architecture based on principles of closed-chain robotic systems emerges a multidisciplinary topic that embraces architecture, structural engineering, kinematics and control in providing a suitable framework for the design, analysis and control. The innovative optimization-driven approach of the current project, enlightens the potential of adaptive architecture with an optimum motion path of reconfiguration, under consideration of the vertical load and the required actuator capacity. In the spectrum of reconfigurable engineering structures, the opportunities are manifold for a real-time response to external environmental stimuli (e.g., sunlight, wind conditions, etc.). The application of the proposed PBA-based optimization can be adapted, in order to be able to handle other linkage and/or reconfigurable structures. Furthermore, worth mentioning is that in case of structures with much more bars, PBA can be implemented into a cascade optimization framework proposed by Charmpis et al. (2005), Charmpis and Lagaros (2020). Further development of the project involves the application of automated optimization processes with regard to the reconfigurability of the structure in achieving better performance and efficiency, while considering both, a uniform distributed vertical and horizontal loading. Future research will be also focused on the verification of the proposed method, while aspects of the feasibility and accuracy will be included.

Discussion

On the engineering front, application of the effective 4-bar concept enables reconfigurable structures to preserve the self-weight since no actuators need to be moved about during shape adjustment, yielding thus minimum energy consumption and control complexity during actuation. By extension, the selection of an optimal system motion sequence enables the realization of the reconfigurable structures that built upon concepts of modularity and lightweight and have an optimized load-deformation behavior.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

MM, NK, NL, and MP drafted the manuscript. All authors revised and edited the manuscript.

Funding

The research study in the current article has been conducted in the frame of the Research Funding Program: Marie Skłodowska-Curie Research and Innovation Staff Exchanges (RISE) “OPTARCH – Optimization Driven Architectural Design of Structures” (No: 689983), H2020-MSCA-RISE-2015.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The content of this manuscript has been presented in part at the 1st International Conference on Optimization Driven Architectural Design, Matheou et al. (2020).

References

Adam, B., and Smith, I. F. C. (2008). Active tensegrity: a control framework for an adaptive civil-engineering structure. Comput. Struct. 86, 2215–2223. doi: 10.1016/j.compstruc.2008.05.006

CrossRef Full Text | Google Scholar

Arsenault, M., and Gosselin, C. (2005). Kinematic, static and dynamic analysis of a planar 1-DOF tensegrity mechanism. Mech. Des. 127, 1152–1160. doi: 10.1115/1.1913705

CrossRef Full Text | Google Scholar

Arsenault, M., and Gosselin, C. (2006a). Kinematic, static and dynamic analysis of a planar 2-DOF tensegrity mechanism. Mech. Mach. Theory 41, 1072–1089. doi: 10.1016/j.mechmachtheory.2005.10.014

CrossRef Full Text | Google Scholar

Arsenault, M., and Gosselin, C. (2006b). Kinematic, static and dynamic analysis of a spatial 3-DOF tensegrity mechanism. Mech. Design 128, 1061–1069. doi: 10.1115/1.2218881

CrossRef Full Text | Google Scholar

Arsenault, M., and Gosselin, C. (2009). Kinematic and static analysis of a 3-PUPS spatial tensegrity mechanism. Mech. Mach. Theory 44, 162–179. doi: 10.1016/j.mechmachtheory.2008.02.005

CrossRef Full Text | Google Scholar

Avila-Hernández, P. E., and Cuenca-Jiménez, F. (2018). Design and synthesis of a 2 DOF 9-bar spatial mechanism for a prosthetic thumb. Mech. Mach. Theory 121, 697–717. doi: 10.1016/j.mechmachtheory.2017.12.001

CrossRef Full Text | Google Scholar

Avtzis, D. N., Arthofer, W., Stauffer, C., Avtzis, N., and Wegensteiner, R. (2010). Pityogenes chalcographus (Coleoptera, Scolytinae) at the southernmost borderline of Norway spruce in Greece. Entomol. Hellenica 19, 3–13. doi: 10.12681/eh.11589

CrossRef Full Text | Google Scholar

Bel, H. N., Rhode-Barbarigos, L., and Smith, I. F. C. (2011). Analysis of clustered tensegrity structures using a modified dynamic relaxation algorithm. Solids Struct. 48, 637–647. doi: 10.1016/j.ijsolstr.2010.10.029

CrossRef Full Text | Google Scholar

Charmpis, D. C., and Lagaros, N. D. (2020). Cascade Structural Sizing Optimization With Large Numbers of Design Variables, Engineering Reports, Wiley (To appear).

Google Scholar

Charmpis, D. C., Lagaros, N. D., and Papadrakakis, M. (2005). Multi-database exploration of large design spaces in the framework of cascade evolutionary structural sizing optimization. Comput. Methods Appl. Mech. Eng. 194, 3315–3330. doi: 10.1016/j.cma.2004.12.020

CrossRef Full Text | Google Scholar

Chen, W.-N., Zhang, J., Lin, Y., Chen, N., Zhan, Z.-H., Chung, H. S.-H., et al. (2013). Particle swarm optimization with an aging leader and challengers. IEEE Transact. Evol. Comput. 17, 241–258. doi: 10.1109/TEVC.2011.2173577

CrossRef Full Text | Google Scholar

Chen, Y., Fan, L., and Feng, J. (2017). Kinematic of symmetric deployable scissor-hinge structures with integral mechanism mode. Comput. Struct. 191, 140–152. doi: 10.1016/j.compstruc.2017.06.006

CrossRef Full Text | Google Scholar

Chen, Y., Yan, J., Sareh, P., and Feng, J. (2020). Feasible prestress modes for cable-strut structures with multiple self-stress states using particle swarm optimization. J. Comput. Civil Eng. 34:882. doi: 10.1061/(ASCE)CP.1943-5487.0000882

PubMed Abstract | CrossRef Full Text | Google Scholar

Christoforou, E., Müller, A., and Phocas, M. C. (2012). “Motion planning for shape-controlled adaptable buildings resembling topologically closed-loop robotic systems,” in Proceedings of the 36th Mechanisms and Robotics Conference (MECH), ASME 2012 International Design Engineering Technical Conferences, Chicago, IL, 12–15.

Google Scholar

Christoforou, E. G., Müller, A., Phocas, M. C., Matheou, M., and Arnos, S. (2015). Design and control concept for reconfigurable architecture. Mech. Design 137, 1–8. doi: 10.1115/1.4029617

CrossRef Full Text | Google Scholar

Christoforou, E. G., Phocas, M. C., Matheou, M., and Müller, A. (2019). Experimental implementation of the effective 4-bar method on a reconfigurable articulated structure. Structures 20, 157–165. doi: 10.1016/j.istruc.2019.03.009

CrossRef Full Text | Google Scholar

Dorigo, M., and Stützle, T. (2004). Ant Colony Optimization. Massachusetts, MA: The MIT Press.

Google Scholar

Eberhart, R., and Kennedy, J. (1995). “Particle swarm optimization,” in Proceedings of the IEEE international conference on neural networks, Vol. 4, (New York, NY: Citeseer), 1942–1948.

Google Scholar

Fox, M., and Kemp, M. (2009). Interactive Architecture. New York, NY: Princeton Architectural Press.

Google Scholar

Gandomi, A. H., and Alavi, A. H. (2012). Krill herd: a new bio-inspired optimization algorithm. Commun. Nonl. Sci. Num. Simul. 17, 4831–4845. doi: 10.1016/j.cnsns.2012.05.010

CrossRef Full Text | Google Scholar

Gantes, C. J. (2001). Deployable Structures: Analysis and Design. Southampton: WIT Press.

Google Scholar

Geem, Z. W. (2010). Recent Advances in Harmony Search Algorithm. Studies in Computational Intelligence. Berlin: Springer-Verlag, doi: 10.1007/978-3-642-04317-8

CrossRef Full Text | Google Scholar

Hanaor, A. (1997). “Tensegrity: theory and application,” in Beyond the cube, ed. J. F. Gabriel (Hoboken, NJ: John Wiley & Sons), 385–408.

Google Scholar

Holland, J. H. (1973). Genetic algorithms and the optimal allocation of trials. SIAM J. Comput. 2, 88–105. doi: 10.1137/0202009

CrossRef Full Text | Google Scholar

Kallioras, N. A., Lagaros, N. D., and Avtzis, D. N. (2018). Pity beetle algorithm – A new metaheuristic inspired by the behavior of bark beetles. Adv. Eng. Softw. 121, 147–166. doi: 10.1016/j.advengsoft.2018.04.007

CrossRef Full Text | Google Scholar

Kallioras, N. Ath, Lagaros, N. D., and Avtzis, D. (2016). “A new metaheuristic inspired by bark beetles for solving engineering problems,” in Proceedings of the 11th HSTAM International Congress on Mechanics, Athens, GR, 27–30.

Google Scholar

Karaboga, D., and Basturk, B. (2008). On the performance of artificial bee colony (ABC) algorithm. Appl. Soft Comput. J. 8, 687–697. doi: 10.1016/j.asoc.2007.05.007

CrossRef Full Text | Google Scholar

Kaveh, A., and Dadras, A. (2017). A novel meta-heuristic optimization algorithm: thermal exchange optimization. Adv. Eng. Softw. 110, 69–84. doi: 10.1016/j.advengsoft.2017.03.014

CrossRef Full Text | Google Scholar

Kaveh, A., and Khayatazad, M. (2012). A new metaheuristic method: ray optimization. Comput. Struct. 112–113, 283–294. doi: 10.1016/j.compstruc.2012.09.003

CrossRef Full Text | Google Scholar

Kaveh, A., Talatahari, S., Sheikholeslami, R., and Keshvari, M. (2014). Chaotic swarming of particles: a new method for size optimization of truss structures. Adv. Eng. Softw. 67, 136–147. doi: 10.1016/j.advengsoft.2013.09.006

CrossRef Full Text | Google Scholar

Korkmaz, S. (2011). A review of active structural control: challenges for engineering informatics. Comput. Struct. 89, 2113–2132. doi: 10.1016/j.compstruc.2011.07.010

CrossRef Full Text | Google Scholar

Li, X., and Yao, X. (2012). Cooperatively coevolving particle swarms for large scale optimization. IEEE Transact. Evol. Comput. 16, 210–224. doi: 10.1109/TEVC.2011.2112662

CrossRef Full Text | Google Scholar

Liang, J. J., Qu, B.-Y., and Suganthan, P. N. (2013a). Problem Definitions and Evaluation Criteria for the CEC 2014 Special Session and Competition on Single Objective Real-Parameter Numerical Optimization. Technical Report 201311. Singapore: Nanyang Technological University.

Google Scholar

Liang, J. J., Qu, B.-Y., Suganthan, P. N., and Hernández-Díaz, A. G. (2013b). Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session and Competition on Real-Parameter Optimization. Technical Report 201212. Singapore: Nanyang Technological University.

Google Scholar

Matheou, M., Kallioras, N. A., Lagaros, N. D., and Phocas, M. C. (2020). “Motion sequence optimization of a planar structure,” in Proceedings of the 1st International Conference on Optimization Driven Architectural Design, Vol. 44, Amman, 310–317. doi: 10.1016/j.promfg.2020.02.236

CrossRef Full Text | Google Scholar

Matheou, M., Phocas, M. C., Christoforou, E. G., and Müller, A. (2017). “Comparative analysis on two actuation methods of 9-bar systems through kinematics analysis and experimental testing,” in Proceedings of the XXII Conference, The Italian Association of Theoretical and Applied Mechanics (AIMETA 2017), Salerno, 4–7.

Google Scholar

Matheou, M., Phocas, M. C., Christoforou, E. G., and Müller, A. (2018). On the kinetics of reconfigurable hybrid structures. Build. Eng. 17, 32–42. doi: 10.1016/j.jobe.2018.01.013

CrossRef Full Text | Google Scholar

Mendes, R., Kennedy, J., and Neves, J. (2004). The fully informed particle swarm: simpler, maybe better. IEEE Transact. Evol. Comput. 8, 204–210. doi: 10.1109/TEVC.2004.826074

CrossRef Full Text | Google Scholar

Parsopoulos, K. E., and Vrahatis, M. N. (2004). “UPSO: a unified particle swarm optimization scheme,” in Proceedings of the International Conference Computational Methods in Sciences and Engineering (ICCMSE 2004). Lecture Series on Computer and Computational Sciences, Vol. 1, (Zeist: VSP International Science Publishers), 868–873. doi: 10.1201/9780429081385-222

CrossRef Full Text | Google Scholar

Pellegrino, S. (2001). “Deployable structures in engineering,” in Deployable Structures. International Centre for Mechanical Sciences (Courses and Lectures), ed. S. Pellegrino (Vienna: Springer), 412.

Google Scholar

Pfeffer, A. (1995). Zentral und West Paläarktische Borken und Kern Käfer. Basel: Naturhistorisches Museum Basel.

Google Scholar

Phocas, M. C., Christoforou, E. G., and Matheou, M. (2015). Design, motion planning and control of a reconfigurable hybrid structure. Eng. Struct. 101, 376–385. doi: 10.1016/j.engstruct.2015.07.036

CrossRef Full Text | Google Scholar

Phocas, M. C., Matheou, M., Müller, A., and Christoforou, M. (2019). Reconfigurable modular bar. J. Int. Assoc. Shell Spatial Struct. 60, 78–89. doi: 10.20898/j.iass.2019.199.028

CrossRef Full Text | Google Scholar

Poli, R., Kennedy, J., and Blackwell, T. (2007). Particle swarm optimization. Swarm Intel. 1, 33–57.

Google Scholar

Postner, M. (1974). “Scolytidae, borkenkafer,” in Die forstschädlinge Europas, ed. W. Schwenke (Berlin: Paul Parey).

Google Scholar

Sarker, R. A., Elsayed, S. M., and Ray, T. (2014). Differential evolution with dynamic parameters selection for optimization problems. IEEE Transact. Evolut. Comput. 18, 689–707. doi: 10.1109/tevc.2013.2281528

CrossRef Full Text | Google Scholar

Schwerdtfege, F. (1929). Ein beitrag zur fortpflanzungsbiologie des borkenkäfers pityogenes chalcographus, L. Zeitschr. Angew. Entomol. 15, 335–427. doi: 10.1111/j.1439-0418.1929.tb00113.x

CrossRef Full Text | Google Scholar

Storn, R., and Price, K. (1997). Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Global Optimiz. 11, 341–359.

Google Scholar

Tibert, G. (2002). Deployable Tensegrity Structures for Space Applications. Ph.D. thesis, KTH Royal Institute of Technology, Stockholmm, SE.

Google Scholar

Van Den Bergh, F., and Engelbrecht, A. P. (2004). A cooperative approach to participle swam optimization. IEEE Transact. Evol. Comput. 8, 225–239.

Google Scholar

Van Laarhoven, P. J., and Aarts, E. H. (2010). Simulated Annealing: Theory and Applications (Mathematics and Its Applications). Dordrecht: Kluwer Academic Publishers.

Google Scholar

Wood, S. L., and Bright, D. E. (1992). A Catalog of scolytidae and platypodidae (Coleoptera). Great Basin Natur. Mem. 13, 1–833.

Google Scholar

Yang, J. N., and Soong, T. T. (1998). Recent advances in active control of civil engineering structures. Probab. Eng. Mech. 3, 179–188. doi: 10.1016/0266-8920(88)90010-0

CrossRef Full Text | Google Scholar

Yang, X. S. (2008). Nature-Inspired Metaheuristic Algorithms. Frome: Luniver Press.

Google Scholar