Promoting Autonomous Vehicles Using Travel Demand and Lane Management Strategies

A key challenge facing cities of today is the persistent and growing urban congestion that has significant adverse effects on economic productivity, emissions, driver frustration, and quality of life. The concept of smart cities, which can revolutionize the management of metropolitan transportation operations and infrastructure, shows great promise in mitigating this problem. Specifically, the automation and connectedness (A&C) of smart city entities such as its infrastructure, services, and vehicles, can be helpful. In this regard, this paper focuses on the potential of autonomous vehicles (AVs) and AV infrastructure, particularly during prospective transition era where there will be mixed streams of AVs and human driven vehicles (HDVs). The paper considers two aspects of this potential: connectivity-enabled travel demand management and travel infrastructure supply through lane management. To demonstrate the opportunity associated with this potential, this paper first presents an AV-enabled tradable credit scheme (TCS) to manage travel demand. Here, the transportation authority distributes travel credits to travelers directly and instantaneously using the AV's A&C features. Travelers use their A&C features to pay these credits for travel at specific locations or times-of-day according to their choices of lane types and links. With regard to supply, this paper considers that the road network consists of two lane types: AV-dedicated, and mixed traffic lanes, and develops a scheme for travel demand and lane management strategies in the AV transition era (TLMAV). Firstly, the paper models the expected travel choices based on user equilibrium concepts, at different levels of AV market penetration. Then, the existence of the optimal solution in terms of link flows and the prevailing travel credit price is demonstrated. Then the paper establishes the optimal TLMAV that minimizes total travel time subject to user equity constraints. The results demonstrate the extent to which HDV users will suffer an increase in travel cost if equity is not considered in the model. The results also show how the transportation agency can use TLMAV to keep HDV travel costs to acceptable levels, particularly during the early stages of the AV transition period. Further, the paper shows how TLMAV could be designed to gradually diminish inequity effects so that travelers, in the long term, are motivated to shift to AVs.

Introduction

Urban Congestion and the Promise of Smart Cities Concepts

The smart cities concept has received increasing interest during the last decade. In a smart city, the life quality of urban residents is improved using disruptive technologies in various areas such as energy efficiency, communication technology, and transportation mobility (USDOT, 2015, 2018; Edara et al., 2018; Ong and Hwang, 2019). The need for smart cities is accentuated by ever-increasing population growth and urbanization. The United Nations estimates that currently 55% of the world population live in urban areas and this is projected to increase to 68% by 2050 (United Nations, 2018). At several cities, the transportation, water and waste water, and energy infrastructure systems were designed decades ago to serve far smaller demand, and increasing populations have caused excess demand, and subsequently, poor levels of service (Word Bank, 2018). Unfortunately, this is unfolding at a time when urban areas are already grappling with providing the infrastructure needed to support their populations (Birkmann et al., 2016) due to funding inadequacy or lack of skilled managers. According to Grimm et al. (2008) and Alberti (2017), the confluence of structural, functional, and social evolutions have resulted in daunting challenges to city authorities as they struggle to provide critical infrastructure services for their residents.

The theme of the 2018 IEEE International Smart Cities Conference included a statement that “as sensors, data, connectivity, networks, and analytics offer opportunities to improve each of these systems independently, the common elements of the technology infrastructure offer more opportunities for interoperability across systems and to reframe how we optimize and make decisions about these systems.” The European Union (EU) defines the smart city as “a city that seeks to address issues of public interest through information and communication technology (ICT) solutions based on municipal multi-stakeholder partnerships.” The examples of stakeholders in a city include government, urban residents, and businesses. The EU considers six pillars for the smart city including smart governance, smart mobility, smart living, smart people, smart economy, and smart environment (Manville et al., 2014). In the United States, the American Society of Civil Engineers (ASCE, 2018) states that the smart cities concept is “motivated by the need for intelligent ways to provide quick and reliable information to facilitate any phase of the life cycle development of municipal infrastructure in a manner that is economic, social, and environmentally successful.” In this paper, we address the smart city elements of smart governance and smart mobility, as they pertain to the management of transportation infrastructure and operations, to address congestion. We posit that as part of smart governance, metropolitan authorities can exploit the automation and connectedness of functions, through ICT, to facilitate user charging and information sharing. In other words, the concept of smart mobility can be viewed from the perspective of implementing disruptive technologies in transportation systems application areas. The prospective use of autonomous vehicle (AV) capabilities is consistent with this quest.

Researchers have argued that AVs provide a unique opportunity for metropolitan authorities to achieve smart mobility and safety (Chang, 2019; Peeta, 2019). This disruptive technology has been well-received by business owners and the public. For example, Uber announced that it aims to achieve fully autonomous taxis by 2030 (Goddin, 2015). Since AVs are controlled by artificial intelligence, they can eliminate human errors which in turn leads to an increase in traffic safety and road capacity due to headway reduction. They are also expected to have a connectivity feature which enables them to send and receive information to/from other AVs (V2V) and intelligent roadside units (V2I). This allows the road user, particularly, trucks, to form platoons during roadway operations. This can increase the road capacity and decrease energy consumption. It is estimated that AVs are capable of increasing road capacity by up to 500 percent (Fernandes and Nunes, 2012).

The automation and connectedness (A&C) of smart city entities such as its infrastructure, services, and vehicles, can be helpful. In this regard, autonomous vehicles (AVs) and AV infrastructure have significant potential to help reduce congestion from perspectives of demand and supply, particularly during the prospective transition era which will be characterized by mixed streams of AVs and human driven vehicles (HDVs). There exist two aspects of this potential that are worthy of examination: connectivity-enabled travel demand management and travel infrastructure supply through lane management. In the subsections below, we discuss how a market-based instrument, namely, a tradable credit scheme (TCS) could be used to manage demand in the AV transition era, and how this scheme could be made more efficient using the connectivity capabilities of AVs. We also discuss different three lane types that could be established to serve demand in a targeted manner.

Lane Management for AVs

To leverage the efficacy of AVs for congestion mitigation, metropolitan authorities need to develop smart governance including transportation infrastructure planning and management strategies that can be facilitated by the automation and connectivity features of AVs. During the AV transition period, traffic flow will comprise of both AVs and human-driven vehicles (HDVs), referred to as a mixed fleet. Through connectivity and automation, AVs can help reduce headway and therefore increase capacity. However, such efficacy can be seriously jeopardized in a mixed fleet. Therefore, the establishment of AV dedicated lanes during the transition period, is increasingly gaining attention among transportation researchers (Chen et al., 2016; Ye and Yamamoto, 2018; Liu and Song, 2019). Some researchers have investigated the effectiveness of AV dedicated lanes using a bi-level framework. The concept of a bi-level framework has been applied to several problems in the context of transportation systems (Hosseininasab and Shetab-Boushehri, 2015; Gong and Fan, 2016; Hosseininasab et al., 2018; Miralinaghi et al., 2019b, 2020a). In their framework, the metropolitan authority at the upper level decides on the optimal plan for AV dedicated lanes based on the travel decisions of travelers at the lower level. Chen et al. (2016) investigated the optimal deployment plan for AV dedicated lanes during the AV transition period to minimize the social cost including the safety and total system travel costs for HDVs and AVs. They divided the transition period into small (1-year) periods and established the AV market penetration using a diffusion model (where the market penetration rates in each period depend on those in the preceding period), and compared the net benefits to AVs and HDVs in terms of safety and travel time savings. Ye and Wang (2018) proposed a simultaneous design of a traffic network, deploying AV lanes and congestion pricing to mitigate traffic congestion in the network. They showed that the integration of these planning strategies can outperform either AV lane deployment only or congestion pricing only. Wu et al. (2020) examined the system optimal design of a small network (with HDV streets and AV expressways) under congestion pricing in a bid to minimize the cost of system travel time. Using a bi-level framework, Madadi et al. (2020) investigated metropolitan agency decisions for road link retrofit, for example, installing machine-readable road signs and lane markings, to accommodate AVs. At the upper level, the total cost of link retrofit and total system travel time were minimized, and at the lower level, travelers route choice decisions were optimized using a logit-based stochastic user equilibrium model.

Although AV dedicated lanes can potentially address metropolitan traffic congestion significantly, its implementation could generate significant public opposition because the appropriation of existing HDV lanes for dedicated use by AVs, will sharply reduce available road capacity for HDVs. This, as expected, will cause a significant increase in travel time for HDV travelers. This social inequity could be further exacerbated by the relatively high purchase prices of AVs compared to HDVs at the beginning of transition period. Then, only high-income travelers will be able to afford AV purchase. In other words, the establishment of AV dedicated lanes could result in concerns of environmental justice: travel time reductions for high-income travelers and travel time increases for low-income travelers generally, even along the same corridor. Therefore, it is important to account for such inequities in the model so that its prescriptions do not impose unduly high levels of inequity on low-income travelers. On the other hand, inequity must not be pursued to the point where it fails to motivate users to shift to AVs, particularly in the long term.

AV-enabled Travel Demand Management

One of the most conventional and well-studied methods to address traffic congestion in literature is congestion pricing. First proposed by Pigou (1920), congestion pricing seeks to recover the marginal external cost that road network users impose on other users. Although it has been well-studied in literature, congestion pricing has rarely been applied in practice due to public opposition. For example, in 2007, the U.K.'s national road-use charging plan was aborted after 1.8 million opposing signatures were collected (de Palma and Lindsey, 2011). Subsequent research work on road pricing was carried out by several researchers and highway agencies including Small et al. (1989) and Bruzelius (2004). At the end of the first decade of the new millennium, a descendant of road pricing, TCS, was born. In TCS, the road authority establishes a free market for users to trade credits based on their travel needs, allocates travel credits to the users, and charges them for their use of the roads. The concept of tradable credits has long existed in the economics literature (OECD, 2001) and has been used in several contexts including emissions (Hahnt and Nolltt, 1983), energy (Berry, 2002), and recycling (Bailey et al., 2004). In transportation, the concept was first proposed by Yang and Wang (2011) and subsequently investigated by several researchers including Wang et al. (2012), Bao et al. (2014), Wang et al. (2014), Shirmohammadi and Yin (2016), and Xu and Grant-Muller (2016). Grant-Muller and Xu (2014) and Miralinaghi (2018) provided a comprehensive review of TCS literature. Miralinaghi et al. (2019a) demonstrated that a well-designed TCS can lead to the Pareto-improving scheme where all users better off compared to the case without TCS. This concept can be leveraged to address the social inequity associated with AV dedicated lanes. Researchers have stated that TCS is most successful where transactions among the transport agency, travel marketplace, and the user (vehicles) can be made quickly, seamlessly, and in real time, and where the travel credit marketplace status and information, can be viewed and interpreted quickly using automation. This could be made possible through vehicle automation and connectivity capabilities fueled by ICT infrastructure. Therefore, the coupling of automation-with-connectivity and TCS, potentially, can vastly improve the efficacy of TCS implementation.

Objectives and Scope of This Paper

Previous studies explore the impact of AV dedicated lanes on increasing the traffic mobility in the transition period toward the AV era. However, they fail to consider the social inequity impact of allocating road capacity to AVs during the transition period. In particular, AVs might not be affordable for the general public in the beginning of the transition period. Therefore, the allocation of road capacity to AVs implies a lesser travel time for high-income travelers. To the best of our knowledge, this is the first study that illustrates the social inequity due to the increase in travel time of HDVs. Further, we propose an economic instrument, namely TCS, which can help to address the social equity constraint. Specifically, this paper seeks to integrate the deployment of AV links with TCS to enable the metropolitan authority to realize the network benefits of congestion reduction and social equity. To do this, the paper develops a bi-level framework. The framework, termed travel demand and lane management in the AV transition period (TLMAV), yields the optimal amount of credit to be allocated and the travel fee, given the specified AV lane locations on the road network. We assume that AV users are also able to travel on general purpose (GP) lanes, alongside HDVs. In the upper level, the metropolitan authority seeks to minimize the cost of total system travel time subject to the constraint that HDV travelers' cost should not increase beyond pre-specified thresholds established by the metropolitan authority. These values can be established using input from the general public via survey instruments, to gauge public perceptions regarding the acceptability of the scheme. At the lower level, travelers seek to minimize their travel costs given the optimal credit allocation and charging schemes decided on at the upper level. This paper formulates this problem as a mathematical program with complementarity constraints.

The remaining sections of this paper are presented as follows; first, we introduce the preliminary thoughts and notations. Then, the bi-level model, that includes the upper-level model of the metropolitan transportation agency and the lower-level model of travelers, is formulated. Next, we use numerical experiments to investigate the impact of the TLMAV design parameters on transportation system performance, and finally discuss the results.

Preliminaries

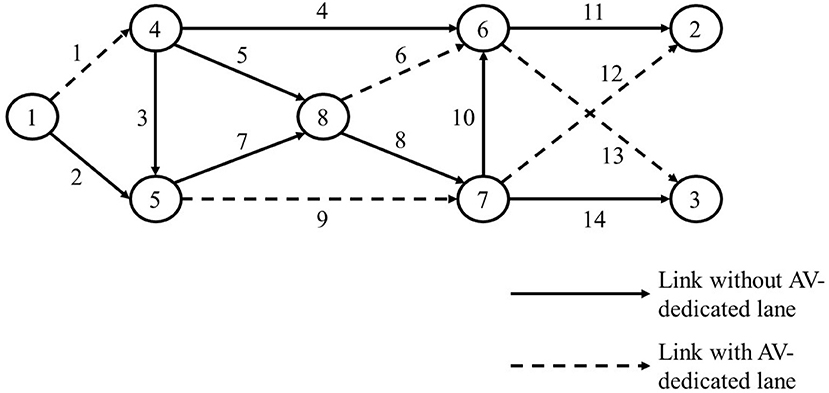
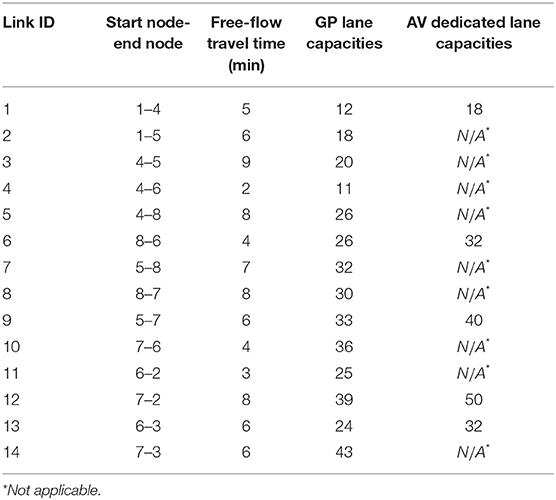
Let G(N, A) represent the directed transportation network, where A and N denote the set of links and nodes in the transportation network, respectively. Consider that the metropolitan transportation agency divides the transition horizon into T periods each with a duration of multiple years. There are two vehicle types m in transportation network: (i) HDV (type 1) and (ii) AV (type 2). Let M denote the set of these two vehicle types. To facilitate the illustration of the transportation network with AV dedicated lanes, the links with this lane type are separated into two links: AV dedicated links ($\overline{A}$) and GP links ($\overline{A}$). For example, the transportation network consists of one link (1–2) with an AV dedicated lane in Figure 1. For modeling purposes, we divide the links with AV dedicated lanes into separate AV dedicated and GP links. Link (1–2) is divided into link 1–2 as a GP lane and links (1–5 and 5–2) as AV dedicated links [including the additional node (5)]. The travel time of each link a in period t is denoted by $c_a^t$ which is the monotonically increasing function of its flow ${\nu }_a^t$. The travel time is assumed to be derived from the Bureau of Public Road (BPR) function.

FIGURE 1

Figure 1. Revision of transportation network with AV dedicated lane.

Travelers are grouped based on their socioeconomic characteristics; the set is denoted by G. The value of time of group g ∈ G using vehicle type m in period t is denoted by ${\beta }_g^{m,t}$. Travelers can enjoy a range of activities (e.g., infotainment, newspaper reading, rest, and cell phone activity) during AV trips; therefore, the travelers' value of time of group g is lower if they use AVs compared to HDVs (that is, ${\beta }_g^{1,t}\ge {\beta }_g^{2,t}$) (Tian et al., 2019). Let W denote the set of origin-destination (O-D) pairs where r(w) and s(w) denote the origin and destination of O-D pair w. The set of paths between the O-D pair w is denoted by R_w. Let ${\overline{R}}_w$ denote the subset of R_w which consists of paths with one or more of AV dedicated links. Let $q_{g,w}^{m,t}$ denote the travel demand of group g of the O-D pair w using vehicle type m in period t which is assumed to be given and independent of the TLMAV strategy. $f_{g,r,w}^{m,t}$ denotes the flow of path r of group g between the O-D pair w using vehicle type m in period t. Let ${\nu }_{g,a}^{m,t}$ denote the flow of group g using vehicle type m on link a in period t. The aggregate travel demand of the O-D pair w of group g in period t is represented by $d_{g,w}^t$. Let δ_{a, r, w} indicate a binary variable which is equal to 1 if link a belongs to path r between the O-D pair w, and equal to zero otherwise. Under TLMAV, the agency implements a specific credit allocation scheme for each vehicle type, such that n^{m, t} credits are allocated to travelers using vehicle type m in period t. Let N^{m, t} denote the total allocated credits to travelers using vehicle type m in period t (that is, $n^{m,t}\sum _{g,w}{q}_{g,w}^{m,t}=N^{m,t}$). The agency implements the lane-specific credit charging scheme under which travelers are charged $u_a^t$ credits for using link a in period t.

Methodology

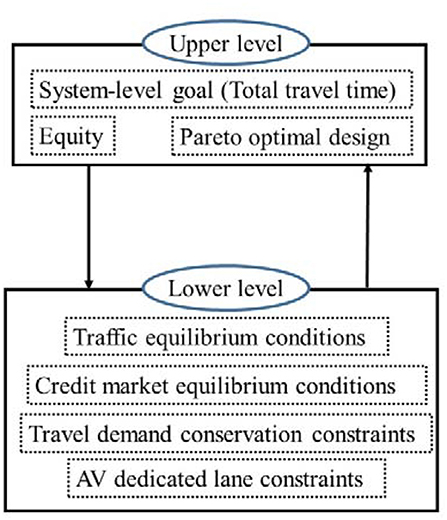
In this section, a bi-level model is developed to obtain the Pareto optimal design of TLMAV which ensures that every traveler is better off. In this bi-level model, the transportation metropolitan agency is the decision-maker at the upper level who seeks to identify the optimal credit allocation and charging schemes to minimize the total travel time. This decision is subject to constraints that include: (i) a Pareto optimal stipulation, which ensures that everyone ends up better off, and (ii) equity constraints, which ensure that HDV travelers are reimbursed for their higher travel times due to lane allocation to AVs, particularly during the early periods of the transition era. The agency (at the upper level) makes decisions with cognizance of travel choices of the travelers (who, in turn, are the decision-makers in the lower level). In other words, it is assumed that the agency can forecast travelers' route choices in response to the agency's decisions. It is further assumed that travelers seek to minimize their travel costs (which comprise of travel time cost and credit consumption cost), by choosing the optimal route and lane type. Figure 2 illustrates the structure of the bi-level model.

FIGURE 2

Figure 2. Structure of bi-level model for TLMAV design.

Upper-Level Model

In this section, we present full details of the upper-level model used to establish the credit allocation and charging schemes. The goal of the transportation agency is to minimize the total travel time during the transition horizon. The credit allocation scheme n includes the total number of allocated credits and the method of credit allocation in each period. The credit charging scheme u includes the credit fee for each link and lane in each period. In this paper, we assume that the credit allocation and charging schemes are constant within each period but may vary across the periods. The credit allocation scheme is vehicle specific which implies that credits are allocated to travelers based on their vehicle type. The credit charging scheme is link- and lane-specific which means that credits are charged based on the link and lane type used by the traveler. In the transportation network, we consider, for a pair of connected nodes, the interconnecting link with the AV dedicated lane and that with the GP lane, as two distinct links. Therefore, for a given vehicle, the number of charged credits may be different for the AV-only and the GP links that comprise of link $u_a^t$. Then, the notation for the credit charging scheme is link-specific only within each period. Based on this discussion, the upper-level model can be formulated as follows (Equations 1–6):

$\begin{array}{ll}\underset{n^{m,t},u_t^a}{\min }{\displaystyle \sum _{t\in \Gamma }{\displaystyle \sum _{a\in A}{c}_a^t({\nu }_a^t)v_a^t}}& (1)\end{array}$

$\begin{array}{ll}{B}_{g,w}^{m,t}={\mu }_{g,w}^{m,t,0}-({\mu }_{g,w}^{m,t}-p^t{n}^{m,t})\forall m,g,w,t& (2)\end{array}$

$\begin{array}{ll}{B}_{g,w}^{1,t}\ge {\varphi }^t{B}_{g,w}^{2,t}\forall g,w,t& (3)\end{array}$

$\begin{array}{ll}{n}^{m,t},u_a^t\ge 0\forall m,a,t& (4)\end{array}$

$\begin{array}{ll}{n}^{m,t}{\displaystyle \sum _{g,w}}{q}_{g,w}^{m,t}=N^{m,t}\forall m,t& (5)\end{array}$

$\begin{array}{ll}{B}_{g,w}^{m,t}\ge 0\forall m,g,w,t& (6)\end{array}$

where ${\mu }_{g,w}^{m,t}$ denotes the travel cost of group g of the O-D pair w using vehicle type m in period t. The travel cost of travelers without TLMAV (AV dedicated lane and TCS), in period t is denoted by ${\mu }_{g,w}^{m,t,0}$. The objective function (1) states that the transportation agency seeks to minimize the total system travel time. Constraint (2) derives from the benefit of travelers of group g of the O-D pair w that use vehicle type m in period t, by comparing the travel costs with and without TLMAV. Constraint (3) represents the social equity constraints where ϕ^t denotes the “equity threshold” or the lowest acceptable ratio of AV benefit to HDV benefit in period t. As it is likely that higher-income travelers will purchase AVs earlier in the transition horizon to “enjoy” AV dedicated lanes, this constraint enables the transportation agency to protect the benefit to lower-income travelers who will experience generally higher travel times due to capacity allocation (i.e., ϕ¹ = 1). However, toward the later periods of the transition era where AVs have high market penetration, the agency can gradually reduce the equity threshold so that HDV travelers are motivated to shift toward AV patronage. Constraint (4) ensures the non-negativity of allocated and charged credits. Constraint (5) determines the total number of allocated credits. Constraint (6) ensures the Pareto optimal design of TLMAV which implies that every traveler is better off with TLMAV policy intervention.

Lower-Level Model

Based on the decisions of the agency in the upper level, travelers choose routes based on their anticipated travel time and credit consumption costs. HDV travelers are restricted to the use of GP links only while AV travelers can use either GP or AV links. The lower-level model consists of travel equilibrium and credit market equilibrium conditions. The former refers to the equilibrium state under which travelers are not able to further reduce their travel costs by unilaterally changing their routes. The latter refers to the equilibrium state where credit price is positive if the credit supply in each period is consumed entirely by travelers. Given the above discussion, the lower-level problem can be formulated as the following mathematical program with equilibrium constraints (MPEC) (Equations 7–14):

$\begin{array}{l}0\le ({\displaystyle \sum _{a\in A}\left(\left({\beta }_g^{1,t}{c}_a^t\left({\nu }_a^t\right)+p^t{u}_a^t\right){\delta }_{a,r,w}\right)}+{\gamma }_{g,r,w}^{1,t}\\ -{\mu }_{g,w}^{1,t})\perp f_{g,r,w}^{1,t}\ge 0\forall g,w,t,\forall r\in R_w& (7)\end{array}$

$\begin{array}{l}0\le ({\displaystyle \sum _{a\in A}\left(\left({\beta }_g^{2,t}{c}_a^t\left({\nu }_a^t\right)+p^t{u}_a^t\right){\delta }_{a,r,w}\right)}\\ -{\mu }_{g,w}^{2,t})\perp f_{g,r,w}^{2,t}\ge 0\forall g,w,t,\forall r\in R_w& (8)\end{array}$

$\begin{array}{ll}{f}_{g,r,w}^{1,t}=0\forall g,w,t,\forall r\in {\overline{R}}_w& (9)\end{array}$

$\begin{array}{ll}0\le p^t\perp ({\displaystyle \sum _m}{N}^{m,t}-{\displaystyle \sum _{a\in A}}{u}_a^t{\nu }_a^t)\ge 0\forall t& (10)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{w,r}}{f}_{g,r,w}^{m,t}{\delta }_{a,r,w}={\nu }_{g,a}^{m,t}\forall a,t,g,m& (11)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{r\in R_w}}{f}_{g,r,w}^{m,t}=q_{g,w}^{m,t}\forall g,w,t,m& (12)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{m,g}}{\nu }_{g,a}^{m,t}={\nu }_a^t\forall a,t& (13)\end{array}$

$\begin{array}{ll}{\nu }_a^t,{\gamma }_{g,r,w}^{m,t}\ge 0\forall a,g,r,w,m,t& (14)\end{array}$

Where: ${\gamma }_{g,r,w}^{m,t}$ denotes the associated cost of travelers of group g using vehicle type m due to the AV dedicated link restriction on path r of the O-D pair w in period t. For vectors x and y, 0 ≤ x⊥y ≥ 0 denotes the following: x·y = 0, x ≥ 0 and y ≥ 0. Constraint (7) presents the user equilibrium condition, and means that AV/HDV travelers of class g use path r between the O-D pair w if its travel cost is equal to the minimum travel cost of AV/HDV travelers between the O-D pair w. It also states that the travel costs of paths between the O-D pair w are greater than or equal to the minimum travel cost of that O-D pair. Constraint (9) ensures that the HDV travelers do not use path $r\in {\overline{R}}_w$ that includes any AV dedicated link. Constraint (10) ensures that the credit price is positive in period t if and only if the credit demand of travelers is equal to the credit supply of that period. Constraints (11)–(13) derive the aggregate link flow, and link flow of travelers of different vehicle types based on the path flows. Constraint (14) denotes the non-negativity of link flows and HDV travelers cost associated with the restriction of AV dedicated lanes. The following propositions ensure the solution existence for the lower-level model.

Proposition 1. The following variational inequality (VI) problem (9), (11)–(14), (15), (16) is equivalent to MPEC (7)–(14).

$\begin{array}{ll}{\displaystyle \sum _{t\in \Gamma }}\left({\displaystyle \sum _{a\in A}}{\displaystyle \sum _{g\in G}}{\displaystyle \sum _{m\in M}}{\beta }_g^{m,t}{c}_a^t({\nu }_a^t*)({\nu }_{g,a}^{t,m}-{\nu }_{g,a}^{t,m}*)\right)\ge 0& (15)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{a\in A}}{u}_a^t{\nu }_a^t\le {\displaystyle \sum _m}{N}^{m,t}\forall t& (16)\end{array}$

(9), (11)-(14)

Proof. The VI problem (9), (11)-(14), (15), (16) is solved by (f^*, ν^*, p^*) if and only if it solves the following linear optimization problem (Equation 17 and 18):

$\begin{array}{ll}min{\displaystyle \sum _{t\in \Gamma }\left({\displaystyle \sum _{a\in A}{\displaystyle \sum _{g\in G}{\displaystyle \sum _{m\in M}{\beta }_g^{m,t}{c}_a^t({\nu }_a^t*)({\nu }_{g,a}^{t,m})}}}\right)}& (17)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{a\in A}}{u}_a^t{\nu }_a^t\le {\displaystyle \sum _m}{N}^{m,t}\forall t& (18)\end{array}$

(11)-(14), (16)

The set of Lagrangian multipliers of the credit conservation constraints (16) is denoted by σ = {σ^t, ∀t}. Let $\gamma =\left\{{\gamma }_{g,r,w}^{1,t},\forall m,g,w,t,r\in {\overline{R}}_w\right\}$ denote the set of Lagrangian multipliers associated with constraint (18). The first-order conditions of the VI problem can be formulated as a mathematical program with complementarity constraints (MPCC) as follows (Equation 19–24):

$\begin{array}{l}0\le ({\displaystyle \sum _{a\in A}\left(\left({\beta }_g^{m,t}{c}_a^t\left({\nu }_a^t\ast \right)+{\sigma }^t{u}_a^t\right){\delta }_{a,r,w}\right)}\\ -{\mu }_{g,w}^{m,t})\perp f_{g,r,w}^{m,t}\ge 0\forall m,g,w,t,\forall r\in R^w-{\overline{R}}_w& (19)\end{array}$

$\begin{array}{l}0\le ({\displaystyle \sum _{a\in A}\left(\left({\beta }_g^{m,t}{c}_a^t\left({\nu }_a^t\ast \right)+{\sigma }^t{u}_a^t\right){\delta }_{a,r,w}\right)}\\ +{\gamma }_{g,r,w}^{1,t}-{\mu }_{g,w}^{1,t})\perp f_{g,r,w}^{1,t}\ge 0\forall m,g,w,t,\forall r\in {\overline{R}}_w& (20)\end{array}$

$\begin{array}{l}0\le ({\displaystyle \sum _{a\in A}\left(\left({\beta }_g^{m,t}{c}_a^t\left({\nu }_a^t\ast \right)+{\sigma }^t{u}_a^t\right){\delta }_{a,r,w}\right)}\\ -{\mu }_{g,w}^{m,t})\perp f_{g,r,w}^{m,t}\ge 0\forall m,g,w,t,\forall r\in R^w& (21)\end{array}$

$\begin{array}{ll}{f}_{g,r,w}^{1,t}=0\forall g,w,t,\forall r\in {\overline{R}}_w& (22)\end{array}$

$\begin{array}{ll}0\le {\sigma }^t\perp ({\displaystyle \sum _m}{N}^{m,t}-{\displaystyle \sum _{a\in A}}{u}_a^t{\nu }_a^t)\ge 0\forall t& (23)\end{array}$

$\begin{array}{ll}(11)-(14)& (24)\end{array}$

where $\mu =\left\{{\mu }_{g,w}^{m,t},\forall t,g,w,m\right\}$ denotes the set of Lagrange multipliers of travel demand conservation constraint (12). The integration of constraints (19)–(21) is equivalent to constraint (7). The comparison of MPCC (11)–(13), (19)–(24) with MPEC (7)–(14) concludes that they are equivalent where σ is the set of credit price p. Hence, the solution to the VI problem (9), (11)–(16) also solves MPEC (7)–(14). This concludes the proof.

Proposition 2. The VI problem (9), (11)–(16) admits at least one solution.

Proof. The feasible solution space of the VI problem is compact and convex. Further, $c_a^t({\nu }_a^t*)$ is continuous with respect to the aggregate link flows. Then, according to Facchinei and Pang (2003), there exists at least one solution to the VI problem (9), (11)–(16).

The uniqueness of the equilibrium credit price and link flows can be proved using the approach proposed in previous studies (Wang et al., 2012; Bao et al., 2014; Miralinaghi and Peeta, 2018). The bi-level model (1)–(14) consists of equilibrium conditions and hence, it is classified as an NP¹-hard problem. There are several solution techniques such as active-set algorithm (Zhang et al., 2009; Miralinaghi et al., 2020b), and smoothing regularization (Birbil et al., 2004). In this paper, we use the relaxation method which solves the bi-level model with the direct relaxation of the equilibrium conditions, as follows (Equations 25–27):

$\begin{array}{l}({\displaystyle \sum _{a\in A}\left(\left({\beta }_g^{m,t}{c}_a^t\left({\nu }_a^t\right)+p^t{u}_a^t\right){\delta }_{a,r,w}\right)}\\ -{\mu }_{g,w}^{m,t}).f_{g,r,w}^{m,t}\le \epsilon \forall m,g,w,t,\forall r\in R_w& (25)\end{array}$

$\begin{array}{l}({\displaystyle \sum _{a\in A}\left(\left({\beta }_g^{m,t}{c}_a^t\left({\nu }_a^t\right)+p^t{u}_a^t\right){\delta }_{a,r,w}\right)}\\ -{\mu }_{g,w}^{m,t})\ge 0\forall m,g,w,t,\forall r\in R_w& (26)\end{array}$

$\begin{array}{ll}{f}_{g,r,w}^{m,t}\ge 0\forall m,g,w,t,\forall r\in R_w& (27)\end{array}$

where ε is a small positive constant.

Numerical Experiments

This section investigates the impact of travelers' heterogeneity and equity consideration on the TLMAV design. The bi-level model (1)–(14) is applied to a small network of Figure 3 that consists of eight nodes and 14 links. The characteristics of small network are presented in Table 1. The transition horizon consists of 10 periods. Travelers are divided into three groups, and it is assumed that groups 1, 2, and 3 include 20, 50, and 30% of travelers, respectively. The values of time of group 1 using HDV and AV are 15 and 5, respectively. The values of time of group 2 using HDV and AV are 20 and 10, respectively, in $/hr. The values of time of group 3 using HDV and AV are 25 and 15, respectively, in $/hr. Since the value of time can be considered as a proxy for travelers' income, groups 1 and 3 can represent the low-income and high-income classes, respectively. There are two O-D pairs where the aggregate travel demands between O-D pairs (1,2) and (1,3) are 22 and 33 in the first period, respectively. The travel demand is assumed to grow at a 10% rate during the transition horizon $(d_{g,w}^t={(1+0.1)}^{t-1}·d_{g,w}^1)$. In the first period, the demand rates consist of AVs (10%) and HDVs (90%), where the AV market penetration increases at the rate of 10% through the transition horizon.

FIGURE 3

Figure 3. Case study.

TABLE 1

Table 1. Link characteristics for the eight-node network.

First, we investigate how the TLMAV design could address the social inequity impact of AV dedicated lanes. Accordingly, four cases of traffic equilibrium conditions with different traffic management policies are investigated as follows:

Case 1. Without an AV dedicated lane, TCS, and equity consideration (referred to as no-TLMAV case).

Case 2. With an AV dedicated lane without TCS and equity consideration (referred to as the AV dedicated lane only case).

Case 3. With an AV dedicated lane and TCS without equity considerations (referred to as the No-equity case).

Case 4. With an AV dedicated lane, TCS, and equity consideration (referred to as TLMAV).

In this analysis, Case 1 is used as a benchmark to compare and understand the impact of each policy on traffic management in the transportation network. For each case, the average travel time of travelers using vehicle type m in period t can be computed as follows:

$\begin{array}{ll}{\tau }^{m,t}=\frac{{\displaystyle {\sum }_{(a,g)}}{c}_a\left({\nu }_a^t\right){\nu }_{g,a}^{m,t}}{{\displaystyle {\sum }_{(g,w)}}{q}_{g,w}^{m,t}}\forall t,m& (28)\end{array}$

Then, the average reduction of travel time cost for travelers using vehicle type m in period t under Cases 2–4 compared to Case 1 (no-TLMAV) can be calculated as follows:

$\begin{array}{ll}{\theta }^{m,t}=\frac{{\displaystyle {\sum }_{(g,w)}}{q}_{g,w}^{m,t}{\mu }_{g,w}^{m,t,0}-{\displaystyle {\sum }_{(a,g)}}{c}_a\left({\nu }_a^t\right){\nu }_{g,a}^{m,t}}{{\displaystyle {\sum }_{(g,w)}}{q}_{g,w}^{m,t}}\forall t,m& (29)\end{array}$

Finally, the average reduction of travel cost, including cost of travel time and tradable credits, for travelers using vehicle type m in period t, can be formulated as follows:

$\begin{array}{ll}{\phi }^{m,t}=\frac{{\displaystyle {\sum }_{(g,w)}}{q}_{g,w}^{m,t}·\left({\mu }_{g,w}^{m,t,0}-{\mu }_{g,w}^{m,t,0}+p^t·n^{m,t}\right)}{{\displaystyle {\sum }_{(g,w)}}{q}_{g,w}^{m,t}}\forall t,m& (30)\end{array}$

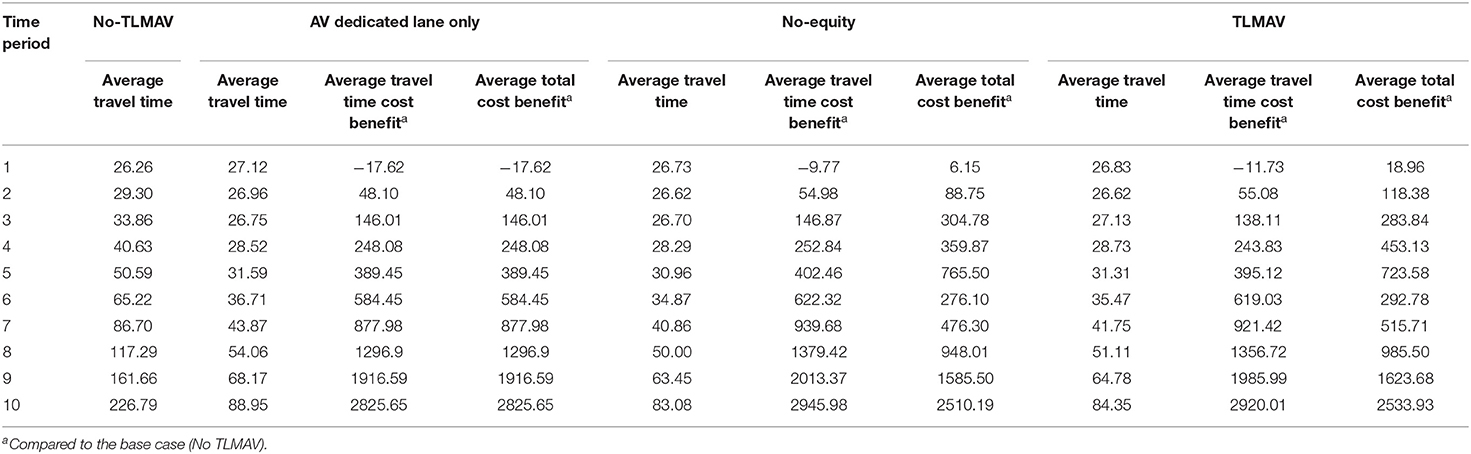
Tables 2, 3 illustrate the impact of traffic management policies under the four cases for HDV and AV users, respectively. Under Case 1, the total travel time is equal to 87,784 units. When the metropolitan transportation agency implements an AV dedicated lane (Case 2), the total travel time reduces to 42,247 units. This is mainly due to the higher capacity of the transportation network which, in turn, is due to the smaller headway associated with AV operations at AV dedicated lanes. While this leads to the drastic reduction of total or average travel time for all users in general, it leads to an increase in the average travel time of HDV users in the first period. Compared to AV users, HDV users experience higher average travel times in periods 1–5. It can be observed, however, that the average travel times of HDV and AV users are identical in periods 6–10. It is because the market penetration of AV users increases significantly toward the later periods of the transition era, and therefore AV users adjust their routes which results in identical travel time of routes with and without AV links. As explained earlier in the paper, AV users generally have a lower value of time, therefore, they have a higher travel cost reduction compared to HDV users.

TABLE 2

Table 2. Impact of traffic management policies on HDV users.

TABLE 3

Table 3. Impact of traffic management policies on AV users.

Under Case 3, the transportation agency implements TCS in addition to AV dedicated lanes without considering equity among travelers. Under the optimal TCS, the total travel time is further reduced to 41,354 units. In Case 3, although HDV users experience a smaller travel time compared to Case 1, they experience a higher credit consumption cost. This is because the optimal TCS motivates travelers to follow the system optimal behavior which causes a higher number of charged credits used by HDV users. Compared with Case 2, Case 3 leads to higher benefits in terms of total cost reduction for AV users. Clearly therefore, it is imperative to consider equity in the TLMAV design, particularly in the early years of the transition period where most travelers, mainly low-income travelers, use HDVs. The restriction on equity should be gradually relaxed over the transition horizon to provide sufficient opportunity for travelers to shift toward AVs. To implement this restriction in the model, the equity threshold in each period t is formulated as follows:

$\begin{array}{ll}{\varphi }^t=max(0,1.01-0.15t)\forall t& (31)\end{array}$

In Case 4, the TLMAV is designed. This considers AV dedicated lanes, TCS, and equity constraints. The resulting total travel time is 41,644 units. Although this exceeds the travel time associated with Case 3, it is still lower than that of case 2. Since the equity constraint aims to adjust the travel cost reduction of HDV users in the early periods of the transition era, the number of charged credits of HDV users is reduced compared to Case 3. Consequently, the system under Case 4 is not as efficient as Case 3 but it can reduce the equity gap between HDV and AV users. The effect of equity constraints diminishes toward the later periods of the transition era as the equity threshold approaches zero.

Next, we investigate the impact of the TLMAV design on the travel cost of different groups. Figure 4 illustrates the travel costs of groups 1–3 between the O-D pair 1–2 under AV dedicated only and TLMAV designs. Under the TLMAV design, the travel costs of HDV travelers of groups 1–3 are lower compared to that of the AV dedicated only lane design during periods 1–5 which reflects the importance of including the equity constraint. This equity effect is higher for group 1 in low-income class where the average reduction percentages for groups 1, 2, and 3 are equal to 42, 32, and 27%, respectively. This demonstrates another feature of this method that contributes more to the low-income travelers compared to the high-income ones. Due to the equity focus of the agency in periods 1-5, AV travelers experience higher travel costs under the TLMAV design compared to the AV dedicated lane only design. However, toward the end of the transition period, their travel costs reduce significantly. This effect is also higher for group 1 where the average travel cost percentage reduction in periods 6–10 for groups 1, 2, and 3 are 84, 40, and 28%, respectively. This ensures that the TLMAV design captures the equity across all travelers' groups irrespective of their vehicle type.

FIGURE 4

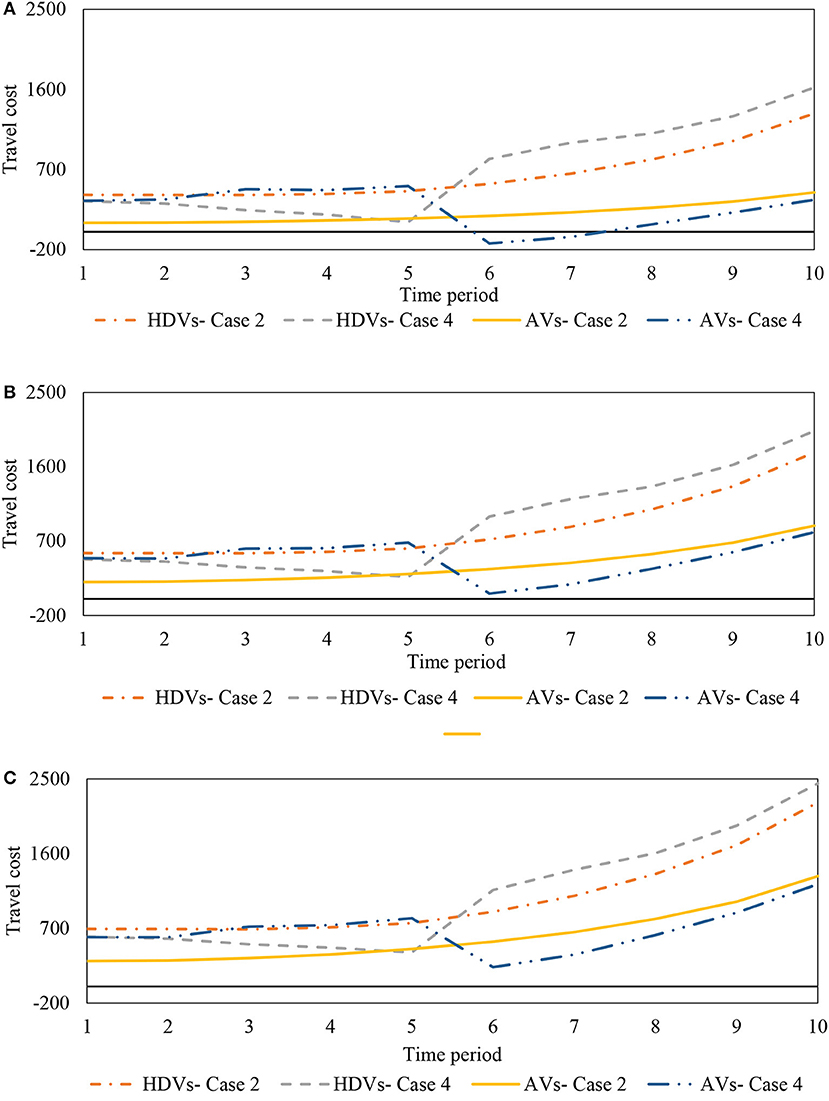
Figure 4. Travel costs of different groups under AV dedicated only and TLMAV design (Cases 2 and 4). (A) Group 1. (B) Group 2. (C) Group 3.

Finally, we investigate the impact of the equity threshold on travel cost reductions. Figure 5 illustrates the average travel cost reduction for HDV and AV users under the optimal TLMAV design with two cases of equity threshold, ϕ₁ and ϕ₂. The equity threshold ϕ₁ is derived from equation (31). The equity threshold ϕ₂ is formulated as follows:

$\begin{array}{ll}{\varphi }^t=1.01-0.15t\forall t& (32)\end{array}$

FIGURE 5

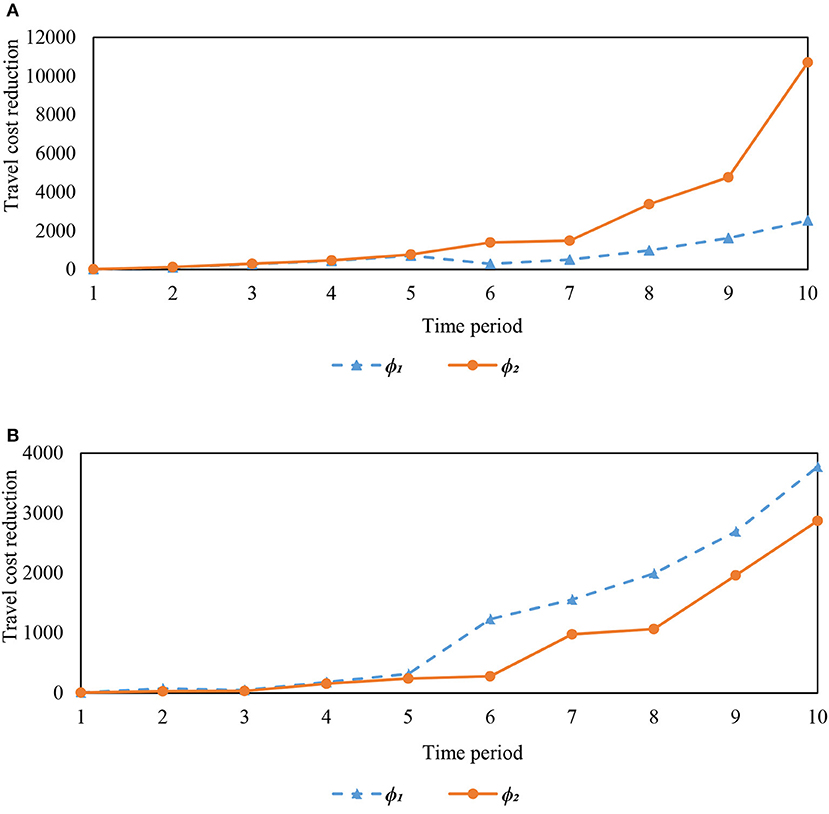
Figure 5. Average travel cost reduction for HDVs and AVs for different equity thresholds. (A) HDV. (B) AV.

Under the equity threshold ϕ₁, the optimal TLMAV design is more flexible in regulating the higher travel cost for HDV users, particularly in the later years of the transition period. As observed in Figure 5, HDV travelers experience a higher travel cost reduction under the second equity threshold compared to the first. This effect is exacerbated toward the end of transition period where unlike the first case, the equity threshold is still positive under the first case of equity threshold. Consequently, AV travelers experience a higher travel cost under the second equity threshold. However, this reduces the effectiveness of TLMAV because the total travel time increases to 41,821 units. The second case of equity threshold also leads to an inequitable scheme where the average travel cost of AV travelers, who constitute the majority of travelers, increases. This illustrates the importance of the careful design of equity thresholds which impacts TLMAV efficiency and travel cost reduction for AV and HDV users. The latter is particularly important in situations where the transport agency seeks to promote AVs.

Concluding Remarks

AV dedicated lanes on the road network can help reduce traffic congestion as AVs require a relatively smaller headway compared to HDVs. However, the appropriation of existing lanes to AV use causes reduction in the available road capacity for HDV users, resulting in an increase in their travel times and transport inequity between the two modes. To address this issue, this paper proposes a TLMAV scheme to manage travel demand during the AV transition period, while accounting for equity considerations. In this paper's bi-level framework, the upper-level model generates the Pareto optimal design of TCS by considering equity. The equity constraint ensures that the resulting reduction in travel time for AV users is not unduly excessive compared to that of HDV users. In the lower level, travelers who are grouped based on their value of time, seek to minimize their travel times. The bi-level model is formulated as MPEC and the relaxation method is used to obtain the optimal solution.

Numerical experiments are conducted to understand the performance of the proposed TLMAV design. It is demonstrated that if the transportation agency considers equity constraints in the TLMAV design, this could lead to a reduction not only in the total travel time and but also in HDV traveler cost, compared to the design with the AV dedicated lane only. This can be achieved by allocating a higher number of credits to HDVs and/or charging fewer credits for HDV use of the road. Further, it is demonstrated that the equity constraint can be formulated and included in the model, so that such a constraint is gradually relaxed through the early periods of transition era. That way, AV users receive higher benefits in terms of travel time toward the later years of the AV transition period. This capability is useful to transportation agencies that seek to promote AVs to maximize the efficiency of their transportation networks. It is also illustrated that TLMAV can promote equity across the groups by providing higher benefits for traveler groups with a lower value of time which can serve as a proxy for income. Finally, numerical experiments illustrate the importance of careful design of equity thresholds that can lead to both equity and efficiency of TLMAV.

This paper can be extended in several directions. Firstly, AVs can potentially provide several benefits in the transportation network, including safety and emissions. This paper focused only on minimizing the total travel time to mitigate traffic congestion. There are several other performance criteria that can be included in the objective function. These include:

(i) Revenue earned by the metropolitan transportation agency: in this study, it is assumed that a tradable credit scheme is revenue-neutral for the agency. However, there exist several economic instruments that can be embedded in a tradable credit scheme to recover the administrative costs of TCS implementation. For example, Nie (2012) proposed the transaction fee per credit sold in the market. In the multi-objective optimization framework, transportation agency revenue could be maximized to cover the administrative cost of the policy implementation.

(ii) Total travel time for each mode (AV vs. HDV) separately.

(iii) Emissions: the tradable credit scheme is a powerful instrument initially implemented by the European Union to address the emissions externality of the aviation industry (Ellerman and Joskow, 2008). In the context of this paper, the agency can leverage the tradable credit scheme concept to minimize vehicular emissions in metropolitan areas. For example, the vehicle emissions function is proposed by Yin and Lawphongpanich (2006) as a function of travel time, speed limit, and the length of each link. A prospective future research could use a multi-objective framework that includes a similar function.

Therefore, in future research, the problem could be formulated as a multi-objective problem where the decision factors include total system travel time, total travel time for each mode (AV vs. HDV) separately, the agency revenue, and vehicle emissions. Secondly, the current paper considers discrete sets of travelers in terms of their value of travel time. In reality, travelers have different values of time that, in future work, could be described collectively using continuous probability distributions. Thirdly, the current paper assumes that the agency has perfect information about future travel demand. In reality however, forecasts of travel demand, particularly in the long term, are characterized by significant uncertainty and this could be addressed in future work by infusing robustness into the TLMAV design. Finally, this paper identifies the optimal design of TLMAV based on the premise that the AV dedicated lane locations are known. In this respect, it will be insightful to investigate the simultaneous design of AV dedicated lane locations coupled with TLMAV. Doing this could further increase the efficiency of TLMAV outcomes in terms of the total travel time.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

SS, MT, AD, MM, and SL: study conception and design, data collection, analysis and interpretation of results, and draft manuscript preparation. All authors reviewed the results and approved the final version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This study is based on research supported by the NEXTRANS Transportation Center and the Center for Connected and Automated Transportation (CCAT), Region V University Transportation Center funded by the U.S. Department of Transportation.

Footnotes

1. ^Non-deterministic polynomial-time.

References

Alberti, M. (2017). Grand challenges in urban science. Front. Built Environ. 3:6. doi: 10.3389/fbuil.2017.00006

CrossRef Full Text | Google Scholar

ASCE (2018). Policy Statement 557 - Smart Cities.

Google Scholar

Bailey, I., Haug, B., and O'Doherty, R. (2004). Tradable permits without legislative targets: a review of the potential for a permit scheme for sterilized clinical waste in the UK. Waste Manag. Res. 22, 202–211. doi: 10.1177/0734242X04044881

PubMed Abstract | CrossRef Full Text | Google Scholar

Bao, Y., Gao, Z., Xu, M., and Yang, H. (2014). Tradable credit scheme for mobility management considering travelers' loss aversion. Transp. Res. Part E 68, 138–154. doi: 10.1016/j.tre.2014.05.007

CrossRef Full Text | Google Scholar

Berry, D. (2002). The market for tradable renewable energy credits. Ecol. Econ. 42, 369–379. doi: 10.1016/S0921-8009(02)00128-3

CrossRef Full Text | Google Scholar

Birbil, S. I., Fang, S. C., and Han, J. (2004). An entropic regularization approach for mathematical programs with equilibrium constraints. Comput. Oper. Res. 31, 2249–2262. doi: 10.1016/S0305-0548(03)00176-X

CrossRef Full Text | Google Scholar

Birkmann, J., Welle, T., Solecki, W., Lwasa, S., and Garschagen, M. (2016). Boost resilience of small and mid-sized cities. Nature 537, 605–608. doi: 10.1038/537605a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bruzelius, N. (2004). Measuring the Marginal Cost of Road Use. An International Survey. The National Academies of Sciences Engineering Medicine.

Google Scholar

Chang, C. M. (2019). “Asset management systems for a sustainable development of smart cities,” in International Conference on Smart Cities (Seoul), 16–20.

Google Scholar

Chen, Z., He, F., Zhang, L., and Yin, Y. (2016). Optimal deployment of autonomous vehicle lanes with endogenous market penetration. Transp. Res. Part C Emerg. Technol. 72, 143–156. doi: 10.1016/j.trc.2016.09.013

CrossRef Full Text | Google Scholar

de Palma, A., and Lindsey, R. (2011). Traffic congestion pricing methodologies and technologies. Transp. Res. Part C Emerg. Technol. 19, 1377–1399. doi: 10.1016/j.trc.2011.02.010

CrossRef Full Text | Google Scholar

Edara, P., Kupko, J., Lavrenz, S., Lee, S., and Puionke, C. (2018). Harnessing the “Smart Cities” Initiative to Improve Mobility for Aging and Disadvantaged Populations.

Google Scholar

Ellerman, A. D., and Joskow, P. L. (2008). The European Union's Emissions Trading System in Perspective. Arlington, VA: Pew Center on Global Climate Change.

Google Scholar

Facchinei, F., and Pang, J.-S. (2003). Finite-Dimensional Variational Inequalities and Complementarity Problems. New York, NY: Springer New York.

Google Scholar

Fernandes, P., and Nunes, U. (2012). Platooning with IVC-enabled autonomous vehicles: strategies to mitigate communication delays, improve safety and traffic flow. IEEE Trans. Intell. Transp. Syst. 13, 91–106. doi: 10.1109/TITS.2011.2179936

CrossRef Full Text | Google Scholar

Goddin, P. (2015). Uber's Plan for Self-Driving Cars Bigger than Its Taxi Disruption - Mobility Lab. Mobility Laboratory. Available online at: https://mobilitylab.org/2015/08/18/ubers-plan-for-self-driving-cars-bigger-than-its-taxi-disruption/ (accessed April 7, 2020).

Google Scholar

Gong, L., and Fan, W. (2016). Optimizing scheduling of long-term highway work zone projects. Int. J. Transp. Sci. Technol. 5, 17–27. doi: 10.1016/j.ijtst.2016.06.003

CrossRef Full Text | Google Scholar

Grant-Muller, S., and Xu, M. (2014). The role of tradable credit schemes in road traffic congestion management. Transp. Rev. 34, 128–149. doi: 10.1080/01441647.2014.880754

CrossRef Full Text | Google Scholar

Grimm, N. B., Foster, D., Groffman, P., Grove, J. M., Hopkinson, C. S., Nadelhoffer, K. J., et al. (2008). The changing landscape: ecosystem responses to urbanization and pollution across climatic and societal gradients. Front. Ecol. Environ. 6, 264–272. doi: 10.1890/070147

CrossRef Full Text | Google Scholar

Hahnt, R. W., and Nolltt, R. G. (1983). Barriers to implementing tradable air pollution permits: problems of regulatory interactions. Yale J. Regul. 1, 63–92.

Google Scholar

Hosseininasab, S.-M., and Shetab-Boushehri, S.-N. (2015). Integration of selecting and scheduling urban road construction projects as a time-dependent discrete network design problem. Eur. J. Oper. Res. 246, 762–771. doi: 10.1016/j.ejor.2015.05.039

CrossRef Full Text | Google Scholar

Hosseininasab, S.-M., Shetab-Boushehri, S.-N., Hejazi, S. R., and Karimi, H. (2018). a multi-objective integrated model for selecting, scheduling, and budgeting road construction projects. Eur. J. Oper. Res. 271, 262–277. doi: 10.1016/j.ejor.2018.04.051

CrossRef Full Text | Google Scholar

Liu, Z., and Song, Z. (2019). Strategic planning of dedicated autonomous vehicle lanes and autonomous vehicle/toll lanes in transportation networks. Transp. Res. Part C Emerg. Technol. 106, 381–403. doi: 10.1016/j.trc.2019.07.022

CrossRef Full Text | Google Scholar

Madadi, B., van Nes, R., Snelder, M., and van Arem, B. (2020). A bi-level model to optimize road networks for a mixture of manual and automated driving: an evolutionary local search algorithm. Comput. Civ. Infrastruct. Eng. 35, 80–96. doi: 10.1111/mice.12498

CrossRef Full Text | Google Scholar

Manville, C., Cochrane, G., Cave, J., Millard, J., Pederson, J. K., Thaarup, R. K., et al (2014). Mapping Smart Cities in the EU. Available online at: https://www.europarl.europa.eu/RegData/etudes/etudes/join/2014/507480/IPOL-ITRE_ET(2014)507480_EN.pdf (accessed April 7, 2020).

Google Scholar

Miralinaghi, M. (2018). Multi-Period Tradable Credit Schemes for Transportation and Environmental Applications. Available online at: https://search.proquest.com/docview/2054313993 (accessed November 21, 2018).

Google Scholar

Miralinaghi, M., and Peeta, S. (2018). A multi-period tradable credit scheme incorporating interest rate and traveler value-of-time heterogeneity to manage traffic system emissions. Front. Built Environ. 4:33. doi: 10.3389/fbuil.2018.00033

CrossRef Full Text | Google Scholar

Miralinaghi, M., Peeta, S., He, X., and Ukkusuri, S. V. (2019a). Managing morning commute congestion with a tradable credit scheme under commuter heterogeneity and market loss aversion behavior. Transp. B 7, 1780–1808. doi: 10.1080/21680566.2019.1698379

CrossRef Full Text | Google Scholar

Miralinaghi, M., Seilabi, S. E., Chen, S., Hsu, Y.-T., and Labi, S. (2019b). “Time-dependent traffic network design with multi-class projects,” in Transportation Research Board 98th Annual Meeting (Washington, DC).

Google Scholar

Miralinaghi, M., Seilabi, S. E., Chen, S., Hsu, Y. T., and Labi, S. (2020a). Optimizing the selection and scheduling of multi-class projects using a Stackelberg framework. Eur. J. Oper. Res. 286, 508–522. doi: 10.1016/j.ejor.2020.03.051

CrossRef Full Text | Google Scholar

Miralinaghi, M., Woldemariam, W., Abraham, D. M., Chen, S., Labi, S., and Chen, Z. (2020b). Network-level scheduling of road construction projects considering user and business impacts. Comput. Civ. Infrastruct. Eng. 35, 650–667. doi: 10.1111/mice.12518

CrossRef Full Text | Google Scholar

Nie, Y. (2012). Transaction costs and tradable mobility credits. Transp. Res. Part B 46, 189–203. doi: 10.1016/j.trb.2011.10.002

CrossRef Full Text | Google Scholar

OECD (2001). Extended Producer Responsibility, A Guidance Manual for Governments. Paris.

Google Scholar

Ong, G. P., and Hwang, Y. H. (2019). “A concept for a smart, cool and naturalistic active mobility infrastructure landscape for Singapore,” in 2019 International Conference on Smart Cities, 16–20.

Google Scholar

Peeta, S. (2019). “Mobility and safety in an era of automation and connectivity,” in International Conference on Transportation and Development 2019 (Alexandria, VA).

Google Scholar

Pigou, A. C. (1920). The Economics of Welfare. 1st ed. London: Macmillan and Company. Available online at: http://www.econlib.org/library/NPDBooks/Pigou/pgEWCover.html (accessed June 5, 2015).

Google Scholar

Shirmohammadi, N., and Yin, Y. (2016). Tradable credit scheme to control bottleneck queue length. Transp. Res. Rec. J. Transp. Res. Board 2561, 53–63. doi: 10.3141/2561-07

CrossRef Full Text | Google Scholar

Small, K. A., Winston, C., and Evans, C. A. (1989). Road Work : A New Highway Pricing and Investment Policy. Brookings Institution.

Google Scholar

Tian, L. J., Sheu, J. B., and Huang, H. J. (2019). The morning commute problem with endogenous shared autonomous vehicle penetration and parking space constraint. Transp. Res. Part B Methodol. 123, 258–278. doi: 10.1016/j.trb.2019.04.001

CrossRef Full Text | Google Scholar

United Nations (2018). World Urbanization Prospects The 2018 Revision. New York, NY: Available online at: https://population.un.org/wup/Publications/Files/WUP2018-Report.pdf (accessed April 7, 2020).

Google Scholar

USDOT (2015). Laying the Groundwork for Smart Connected Cities. Report published for UDOT by Volpe Center.

Google Scholar

USDOT (2018). How Does a “Smart City” Operate? Integrated Corridor Management and the Smart Cities Revolution: Leveraging Synergies.

Google Scholar

Wang, G., Gao, Z., Xu, M., and Sun, H. (2014). Models and a relaxation algorithm for continuous network design problem with a tradable credit scheme and equity constraints. Comput. Oper. Res. 41, 252–261. doi: 10.1016/j.cor.2012.11.010

CrossRef Full Text | Google Scholar

Wang, X., Yang, H., Zhu, D., and Li, C. (2012). Tradable travel credits for congestion management with heterogeneous users. Transp. Res. Part E 48, 426–437. doi: 10.1016/j.tre.2011.10.007

CrossRef Full Text | Google Scholar

Word Bank (2018). World Bank Annual Report 2018.

Google Scholar

Wu, W., Zhang, F., Liu, W., and Lodewijks, G. (2020). Modelling the traffic in a mixed network with autonomous-driving expressways and non-autonomous local streets. Transp. Res. Part E Logist. Transp. Rev. 134:101855. doi: 10.1016/j.tre.2020.101855

CrossRef Full Text | Google Scholar

Xu, M., and Grant-Muller, S. (2016). Trip mode and travel pattern impacts of a tradable credits scheme: a case study of Beijing. Transp. Policy 47, 72–83. doi: 10.1016/j.tranpol.2015.12.007

CrossRef Full Text | Google Scholar

Yang, H., and Wang, X. (2011). Managing network mobility with tradable credits. Transp. Res. Part B 45, 580–594. doi: 10.1016/j.trb.2010.10.002

CrossRef Full Text | Google Scholar

Ye, L., and Yamamoto, T. (2018). Impact of dedicated lanes for connected and autonomous vehicle on traffic flow throughput. Phys. A Stat. Mech. its Appl. 512, 588–597. doi: 10.1016/j.physa.2018.08.083

CrossRef Full Text | Google Scholar

Ye, Y., and Wang, H. (2018). Optimal design of transportation networks with automated vehicle links and congestion pricing. J. Adv. Transp. 2018:3435720. doi: 10.1155/2018/3435720

CrossRef Full Text | Google Scholar

Yin, Y., and Lawphongpanich, S. (2006). Internalizing emission externality on road networks. Transp. Res. Part D Transp. Environ. 11, 292–301. doi: 10.1016/j.trd.2006.05.003

CrossRef Full Text | Google Scholar

Zhang, L., Lawphongpanich, S., and Yin, Y. (2009). “An active-set algorithm for discrete network design problems,” in Transportation and Traffic Theory 2009: Golden Jubilee, eds H. K. L. William, S. C. Wong, and K. Lo Hong (New York, NY: Springer), 283–300.

Google Scholar

Appendix: Table of Notations