Hurricane Hazard Assessment Along the United States Northeastern Coast: Surface Wind and Rain Fields Under Changing Climate

Surface wind and rain fields are two significant elements of hurricane-induced hazards in coastal areas. Mitigation of losses due to hurricane wind and rain hazards has become an increasing urgent and challenging issue in light of changing climate and continued escalation of coastal population density, prompting the need for a more advanced risk analysis methodology to take global warming effects into consideration. In this study, the assessment of hurricane surface wind and rain hazards under changing climate is achieved by performing three simulation components, namely an enhanced hurricane track model to generate the synthesized storms (including a physics-based intensity model integrating sea surface temperature (SST), wind shear, and convective instability contributions), a newly developed thermal wind balance-based model to simulate the gradient wind profiles (explicitly considering environmental conditions of SST, temperature at the top of atmospheric boundary layer, and outflow temperature), and a height-resolving boundary-layer model to obtain the surface wind and rain fields (reducing inherent uncertainties associated with conventionally used gradient-to-surface wind speed conversion factors). A total of 10,000 years of hurricane events are generated for both observed (historical) and projected climate conditions, and a systematical comparison between these two scenarios is investigated. The simulation and comparison results highlight the important effects of a global warming scenario on hurricane surface wind and rain fields, and hence on critical civil infrastructure in hurricane-prone areas.

Introduction

Wind and rain hazards are of great significance since a substantial part of economic and life losses resulting from hurricane events are directly or indirectly related to them (e.g., wind-induced structural damage, wind-driven rain penetration, and inland flooding). Despite the significant improvements in hurricane hazard mitigation, recent events (e.g., Hurricane Irma in 2017, Harvey in 2017, and Dorian in 2019) have demonstrated that coastal areas are still highly vulnerable to landfalling hurricanes. Previous studies suggest that global warming-induced changing climate may significantly affect hurricane activities leading to more intense extreme weather events (e.g., Knutson et al., 2010; Lin et al., 2012; Emanuel, 2013; Contento et al., 2018, 2019; Marsooli et al., 2019; Snaiki et al., 2020). Several climate models were developed to assess the global warming and climate change effects on the planet, and accordingly a large climate database was generated (e.g., Lin et al., 2012). These models are essentially driven by the emission scenarios of the Intergovernmental Panel on Climate Change (IPCC). There have been efforts in the engineering community to conveniently and efficiently consider the influence of the warming climate on hurricane activities by integrating the projected environmental conditions (resulting from the climate models) into the hurricane risk assessment framework (e.g., Liu and Pang, 2013; Mudd et al., 2014, 2016; Rosowsky et al., 2016; Cui and Caracoglia, 2016; Rosowsky, 2018; Marsooli et al., 2019), generally involving a hurricane track model to generate the synthesized storms, a gradient wind model, and an approach to obtain the surface wind and rain fields. While there are several important environmental factors contributing to hurricane dynamics and thermodynamics (e.g., sea surface temperature (SST), wind shear, convective instability, temperature at the top of atmospheric boundary layer, and outflow temperature), SST is usually the only consideration in these engineering applications.

A hurricane track model is considered an effective tool in probabilistically characterizing hurricane-related hazards, where large numbers of synthetic hurricanes can be efficiently generated and derived from the statistical linear regression of a historical database (Vickery et al., 2000). The statistical-deterministic model of Emanuel et al. (2006) follows the same philosophy as the model of Vickery et al. (2000), however the former involves more computationally expensive simulations that are driven by large-scale environmental scenarios synthesized from reanalysis data and/or global climate models. To circumvent the purely empirical nature of the intensity model of Vickery et al. (2000); Snaiki and Wu (2020) developed a physics-based intensity model that is controlled by two key mechanisms, namely a growth term represented by the inward advection of the angular momentum and a decay term through the frictional forces that limits the intensity to an upper limit (i.e., the maximum potential intensity). The non-linear intensity model of Snaiki and Wu (2020) integrates not only the contribution of the SST, but also other thermodynamic and dynamic variables such as vertical wind shear and convective instability. Due to its simulation efficiency and effectiveness in the context of changing climate, the enhanced hurricane track model in Snaiki and Wu (2020) will be used here.

A gradient wind model is a key element in the hurricane wind and rain risk assessment under changing climate effects. Over the past several decades, gradient wind profiles have evolved from simple Rankine-like profiles to rectangular hyperbola-like profiles and its enhanced variants (Schloemer, 1954). For example, Holland (1980) developed an empirical shape factor (denoted as the Holland’s parameter) to adjust the rectangular hyperbola-based pressure profile shape. The gradient wind is then determined based on the prescribed pressure, by considering the gradient wind balance (i.e., among pressure-gradient, centrifugal, and Coriolis forces). Holland’s model usually fails to simultaneously represent the accurate eyewall and outer-region profiles (Ruiz-Salcines et al., 2019). Jelesnianski et al. (1992) on the other hand proposed a purely empirical wind model used for surge simulation in the Sea, Lake, and Overland Surges from Hurricanes (SLOSH) tool. Only the simulated surge, rather than wind, has been validated and compared with observational data. Emanuel (2004) also developed a gradient wind model, where the asymptotic solutions in each region within the hurricane structure are patched to obtain a unified profile. A common feature of the abovementioned gradient wind profiles is their semi-empirical nature. Comparative studies indicated that the gradient wind profiles resulting from various models introduced significant uncertainties in the hurricane hazard risk assessment (e.g., Phadke et al., 2003; Lin and Chavas, 2012). In addition, environmental conditions were usually not considered in the construction of these gradient wind models. This constraint places a limit on these models to be effectively applied to climate change scenarios. To this end, a physics-based gradient wind model resulting from thermal wind balance considerations (Riehl, 1963 and Emanuel, 2004) will be developed and utilized in this study to explicitly consider contributions from SST, temperature at the top of boundary layer, and outflow temperature to the hurricane wind structure.

The gradient-to-surface wind speed conversion factor is typically used as a conventional way to obtain the surface wind field (and rain field as it heavily depends on wind) from the gradient wind profile. This empirical conversion factor presents large spatial variability (Snaiki and Wu, 2020), and the associated surface wind adjustment may result in significant uncertainties in the hurricane hazard risk assessment (Lin and Chavas, 2012). To offer more accurate and reliable surface wind and rain field estimations, a height-resolving analytical boundary-layer wind model (Snaiki and Wu, 2017a, b) will be employed here. This wind model was essentially derived based on the scale analysis and the decomposition technique in which the wind velocity is expressed as the summation of a gradient wind component and a frictional wind component. Although the focus of this study is hurricane surface wind and rain hazards, it is noted that this height-resolving model along with the newly developed thermal wind balance-based gradient wind profile can efficiently generate the vertical profiles of both the hurricane boundary-layer wind speed and the direction between the ground-surface and gradient levels. Extensive studies have been conducted on the modeling of hurricane boundary-layer rain field, however the quantitative forecasting of rainfall remains a challenge. Several parametric models have been developed based on the dependence of rainfall on hurricane parameters (and hence on the horizontal wind speed according to the parametric wind model) (e.g., the R-CLIPER model (Tuleya et al., 2007) and PHRaM model (Lonfat et al., 2007)). However, both the R-CLIPER and PHRaM models were found to underestimate the maximum rain rate since they are based on the ensemble average of numerous hurricanes (Tuleya et al., 2007). To this end, a physics-based analytical rain rate model recently proposed by Snaiki and Wu (2018) will be used here to rapidly generate the hurricane surface rain field. Since the obtained spatial distribution of the surface rain field based on this analytical boundary-layer rain model is essentially governed by the surface wind field inside the hurricane, the consideration of climate change effects on surface rain hazards is straightforward.

In this study, the northeast United States coastline is selected to investigate the changing climate effects on hurricane surface wind and rainfall hazards. A systematical comparison of the simulation results between the historical climate condition (1991–2010) and future climate scenario (2081–2100), under the Representative Concentration Pathway 8.5 (RCP 8.5) of the IPCC fifth assessment report (Stocker, 2014), is carried out. Specifically, 10,000 years of hurricane events are generated for both climate scenarios by performing three simulation components, namely an enhanced hurricane track model to generate the synthesized storms (including a physics-based intensity model integrating SST, wind shear, and convective instability contributions) (Snaiki and Wu, 2020), a newly developed thermal wind balance-based model to simulate the gradient wind profiles (explicitly considering environmental conditions of SST, temperature at the top of the atmospheric boundary layer, and outflow temperature), and a height-resolving boundary-layer model to obtain the surface wind and rain fields (reducing inherent uncertainties associated with conventionally used gradient-to-surface wind speed conversion factors) (Snaiki and Wu, 2017a, b, 2018). The simulated results are interpreted based on the mean recurrence interval (MRI), and the corresponding return level curves of hurricane-related surface wind and rain hazards could be potentially used to serve as a fundamental building block of the changing climate risk mitigation and adaptation in hurricane-prone regions.

Gradient Wind Model Based on Thermal Wind Balance

To obtain a physics-based, analytical gradient wind model, the pioneering work of Riehl (1963) and Emanuel (1986) on relations between wind and thermal structures of hurricanes is revisited. The thermal wind balance suggests that the moist entropy s_m and the angular momentum M are related through the following relationship (Emanuel, 2004):

$-r^2\frac{\partial s_m}{\partial r}\mathrm{\Delta }T=\frac{1}{2}\frac{\partial M^2}{\partial r}(1)$

where r = radius from the storm center; ΔT = T_TBL−T₀; T_TBL = temperature at the top of the boundary layer; and T₀ = outflow temperature. The radial variation of the moist entropy first proposed by Emanuel (2012) and employed by Wang et al. (2015) is utilized in this study leading to the following expression:

$s_m(r)=\mathrm{\Delta }{s}_{m}exp\left(-r^2\mathrm{/}2{\mathrm{\lambda }}^2\right)+s_{env}(2)$

where s_env = moist entropy in the ambient air; Δs_m = moist entropy deficit; and λ = horizontal width of the moist entropy. Combining eqs (1) and (2) leads to (Wang et al., 2015):

$M(r)=\mathrm{\mu }\sqrt{2{\mathrm{\lambda }}^2\left(1-\mathrm{\epsilon }\right)-r^2\mathrm{\epsilon }}(3)$

where $\mathrm{\mu }=\sqrt{2\mathrm{\Delta }T\mathrm{\Delta }{s}_m}$; and ε = exp(−r²/2λ²). Furthermore, the moist entropy deficit can be obtained based on Emanuel’s theory in which the hurricane can be regarded as a Carnot heat engine (Emanuel, 1991):

$\Delta s_m=-\frac{R\ln \left(\raisebox{1ex}{$p_c$}\!\left/ \!\raisebox{-1ex}{$p_0$}\right.\right)}{{\epsilon }_{effi}}.(4)$

where R = ideal gas constant; p_c = hurricane central pressure; p₀ = environmental pressure; and ε_effi = thermodynamic efficiency of the Carnot cycle expressed as ${\mathrm{\epsilon }}_{effi}=\frac{SST-T_0}{SST}$. Hence, the parameter μ can be expressed as:

$\text{μ\hspace{0.17em}=\hspace{0.17em}}\sqrt{2\Delta TR\ln \left(\raisebox{1ex}{$p_0$}\!\left/ \!\raisebox{-1ex}{$p_c$}\right.\right)/{\epsilon }_{effi}}(5)$

On the other hand, the angular momentum is given by definition as M(r) = rV + 1/2fr² in which V is the tangential wind component, leading to:

$V=\frac{\mathrm{\mu }}{r}\sqrt{2{\mathrm{\lambda }}^2\left(1-\mathrm{\epsilon }\right)-r^2\mathrm{\epsilon }}-\frac{fr}{2}(6)$

where f = Coriolis parameter. As a result, combining Eqs (5) and (6) results in the following formula of the gradient wind:

$V_{gr}\text{\hspace{0.17em}=\hspace{0.17em}}\sqrt{2(2{\lambda }^2[1-\text{\hspace{0.17em}ε}]-r^2\text{ε)\hspace{0.17em}}\Delta TR\ln \left(\raisebox{1ex}{$p_0$}\!\left/ \!\raisebox{-1ex}{$p_c$}\right.\right)/(r^2{\text{ε}}_{effi})}-\frac{fr}{2}(7)$

It is noted that the horizontal width of the moist entropy λ needs to be specified to obtain the gradient wind speed. To this end, the derivative of the gradient wind with respect to the radial coordinate at the radius of maximum winds r_m is set to zero, leading to the following expression:

$\sqrt{\frac{-f}{4A}\frac{r_{\text{m}}^3}{\left(1-{\mathrm{\epsilon }}_m\right)}\sqrt{\frac{2{\mathrm{\lambda }}^2}{r_{\text{m}}^2}\left(1-{\mathrm{\epsilon }}_m\right)-{\mathrm{\epsilon }}_m}+\frac{2{\mathrm{\epsilon }}_m{r}_{\text{m}}^2}{4\left(1-{\mathrm{\epsilon }}_m\right)}+\frac{{\mathrm{\epsilon }}_m{r}_{\text{m}}^4}{4{\mathrm{\lambda }}^2\left(1-{\mathrm{\epsilon }}_m\right)}}.(8)$

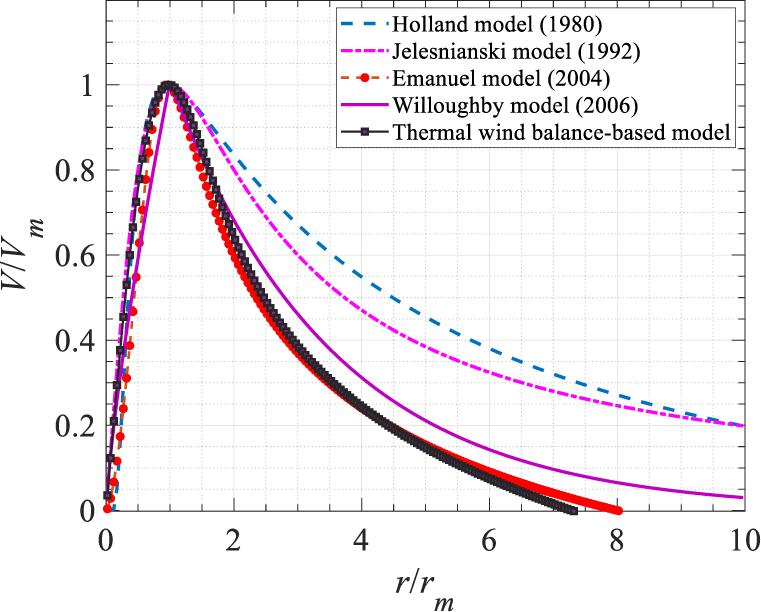
where ${\mathrm{\epsilon }}_m=\text{exp}\left[-r_{\text{m}}^2\mathrm{/}2{\mathrm{\lambda }}^2\right]$; and $A=\sqrt{2\Delta TR\ln \left(\raisebox{1ex}{$p_0$}\!\left/ \!\raisebox{-1ex}{$p_c$}\right.\right)/{\text{ε}}_{effi}.}$. Acccording to Eq (8), λ needs to be determined based on an iterative process. Usually, several iterations are sufficient to achieve the simulation convergence. It is highlighted that the developed gradient wind model based on thermal wind balance explicitly considers contributions from several environmental factors (i.e., SST, T₀, T_TBL). To assess the performance of the thermal wind balance-based gradient wind model, it is compared with four state-of-the-art gradient wind profiles. The first profile is based on the semi-empirical gradient wind model under balance of the pressure-gradient, centrifugal, and Coriolis forces (Holland, 1980):

$V(r)=\sqrt{{\left(\frac{r_m}{r}\right)}^B\frac{B\mathrm{\Delta }P\text{exp}\left[-{\left(\frac{r_m}{r}\right)}^B\right]}{\mathrm{\rho }}+\frac{r^2{f}^2}{4}}-\frac{fr}{2}(9)$

where B = Holland parameter; Δp = central pressure difference; and ρ = air density. Through the empirical B parameter, the Holland model can consider a wide spectrum of rectangular hyperbola-based pressure profiles. The second profile is based on a simple algebraic formulation proposed by Jelesnianski et al. (1992) for surge simulations:

$V(r)=V_m\frac{2r_{m}r}{r_m^2+r^2}(10)$

where V_m = maximum sustained wind speed. The Jelesnianski model is popularly utilized in the SLOSH simulation tool. The third profile is based on the asymptotic wind solutions of various regions within a hurricane (Emanuel, 2004). Emanuel (2004) patched these solutions to obtain a unified gradient wind profile for the entire hurricane structure:

$V(r)=V_m\frac{R_0-r}{R_0-r_m}{\left(\frac{r}{r_m}\right)}^m(11)$

${\left[\frac{\left(1-b\right)\left(n+m\right)}{n+m{\left(\frac{r}{r_m}\right)}^{2\left(n+m\right)}}+\frac{b\left(1+2m\right)}{1+2m{\left(\frac{r}{r_m}\right)}^{2m+1}}\right]}^{1\mathrm{/}2}$

where R₀ = radius to vanishing winds at which the difference between the hurricane and ambient winds cannot be distinguished; b, n, and m. empirical parameters governing the hurricane wind profile shape with commonly used values of b = 0.25, n = 0.9, and m = 1.6 (e.g., Emanuel et al., 2006; Lin and Chavas, 2012). The Emanuel model can consider appropriate control mechanism for each wind region of a hurricane. The fourth profile is based on two piecewise continuous functions representing the eye and outer wind regions, respectively (Willoughby et al., 2006):

$\{\begin{array}{c}\hfill V(r)=V_m{\left(\frac{r}{r_m}\right)}^{n^{\prime }}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}for\mathrm{\hspace{0.17em}\hspace{0.17em}0}\le r\le r_m\hfill \\ \hfill V(r)=V_{m}exp\left(-\frac{r-r_m}{X}\right)\mathit{\hspace{1em}}for{r}_m\le r\hfill \end{array}(12)$

where X = exponential decay length in the outer vortex; and n′ = exponent for the power law inside the hurricane eye. It is noted that the Willoughby model used here ignores the transition part that smoothly patches the two functions in Eq (12).

Figure 1 compares the four parametric wind profiles and the proposed thermal wind balance-based gradient wind model. The necessary parameters for the case study are as follows: V_m = 66m/s; r_m = 50km; R₀ = 400km;b = 0.25; m = 1.6; n = 0.9; Latitude = 28°; SST = 299K; T_TBL = 295K; T₀ = 200K; R = 287J⋅Kg⁻¹⋅K⁻¹; B = 1.24 (Powell et al., 2005); X = 127.95km; and n′ = 0.77 (Willoughby et al., 2006).

FIGURE 1

Figure 1. Comparison of the gradient wind profiles.

While all models present similar wind profiles in the inner region of the storm eyewall (inside the radius of maximum winds), the wind structure varies significantly from one model to another outside the radius of maximum winds. The wind speeds in the outer region of the Holland model and the Jelesnianski model decrease more slowly compared to those of the Emanuel model, the Willoughby model, and the thermal wind balance-based model. In general, the proposed gradient wind model agrees well with the Emanuel model in both inner and the outer regions.

Since the developed thermal wind balance-based model explicitly considers contributions of SST, T_TBL, and T₀, it provides an effective way to investigate the effects of environmental conditions on the gradient wind profile. The simulation results under the current climate (represented by thick dot-line) and changing climate (represented by thin lines corresponding to various combinations of SST, T_TBL, and T₀) are depicted in Figure 2. It should be noted that the hurricane intensity in all simulations are constant to highlight the importance of these environmental factors in the consideration of gradient winds. It can be clearly concluded from Figure 2 that the environmental factors (i.e., SST, T_TBL, and T₀) not only change the spatial distribution of the gradient wind profile, but also modify the maximum wind speed. Due to the storm translation, an additional translational component should be added to the obtained rotational component of wind field (from the thermal wind balance-based model). Specifically, a half of the hurricane translational velocity is added to the rotational component (e.g., Emanuel et al., 2006; Lin et al., 2012). Accordingly, the total gradient wind inside the hurricane is given as V_G = V_r + V_T where V_r denotes the rotational component determined by Eqs (7) and (8) and V_T = 0.5csin(β) (c and β representing translation speed and direction, respectively) is the component due to the storm translation.

FIGURE 2

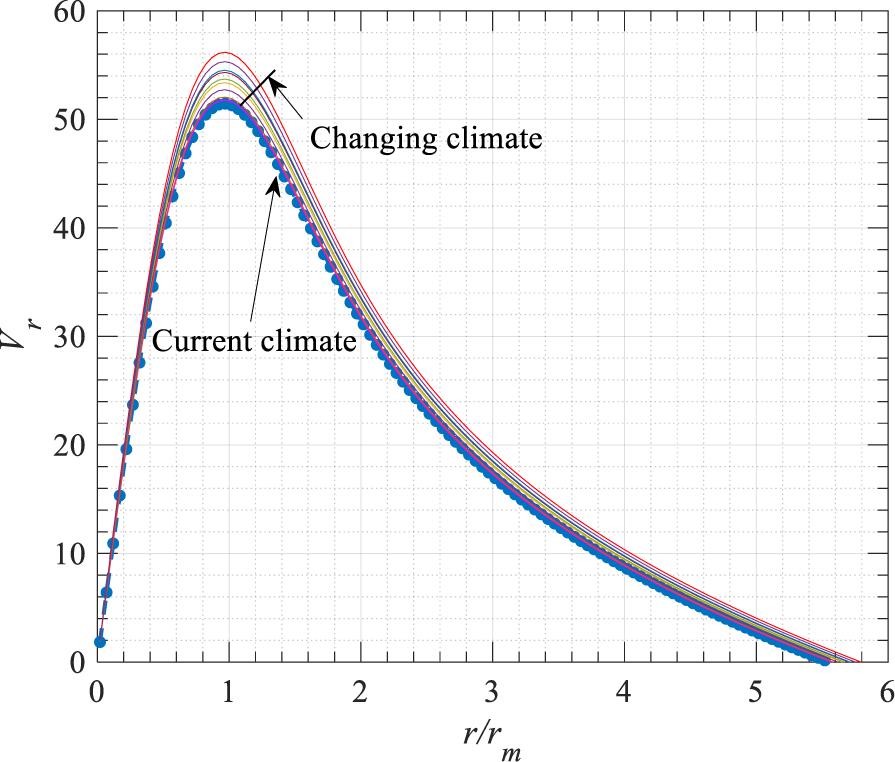
Figure 2. Comparison of the effects of current and changing climate scenarios on the gradient wind profile based on the combined effects of SST, T_TBL, and T₀.

Simulation Procedure

The simulation procedure for the hurricane surface wind and rain hazard assessment under changing climate is presented in Figure 3.

FIGURE 3

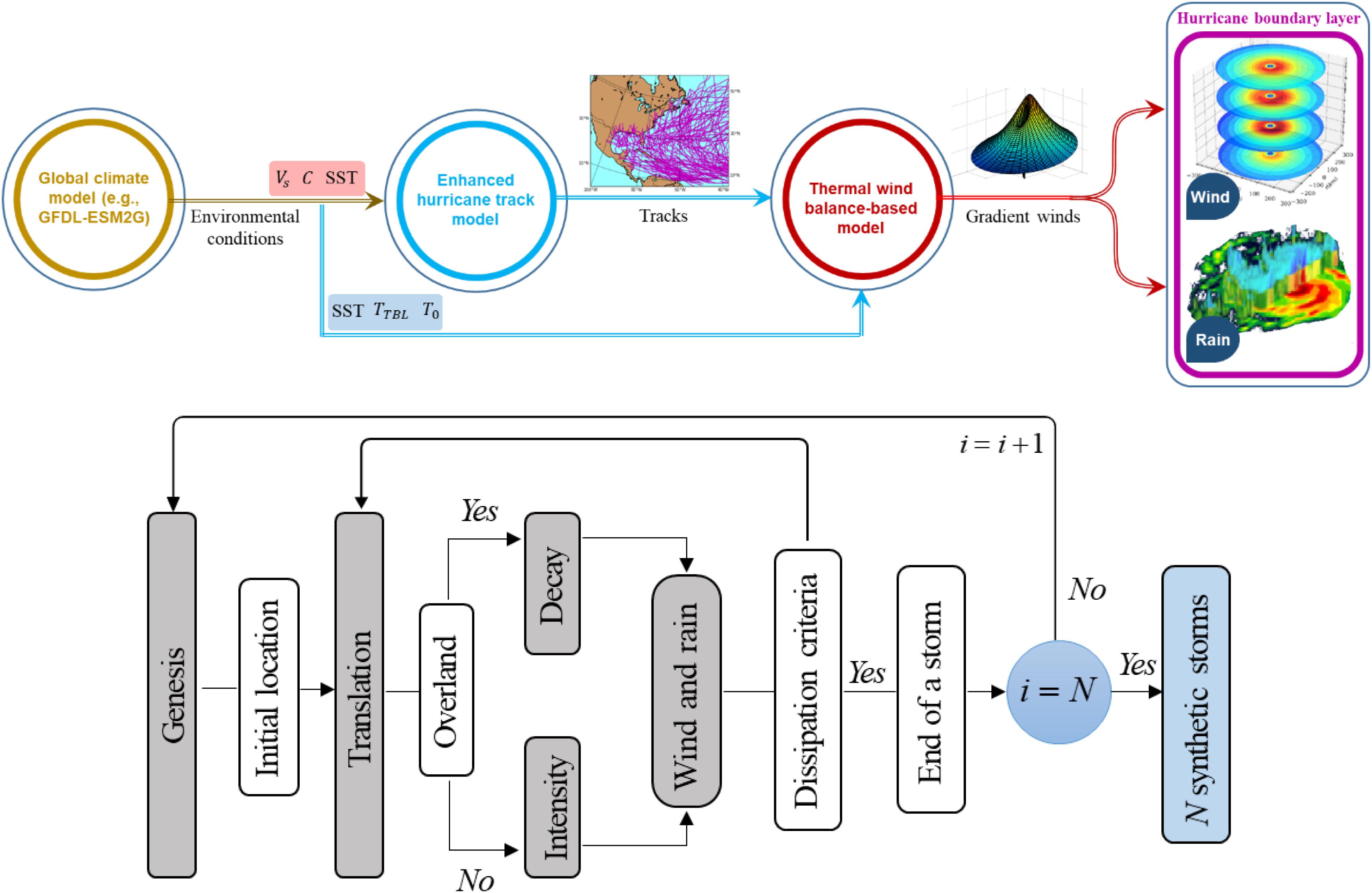
Figure 3. Simulation procedure for hurricane wind and rain: hazard assessment under changing climate (top) and track generation (bottom).

The output data from NOAA’s Geophysical Fluid Dynamics Laboratory Earth System Model Version 2G (GFDL-ESM2G) in terms of environmental conditions (i.e., wind shear V_s, convective instability C, SST, T_TBL, and T₀) is utilized to represent the future climate scenarios. Among them, SST, V_s, and C are climate inputs of the enhanced hurricane track model (Snaiki and Wu, 2020) and SST, T_TBL, and T₀ are climate inputs of the thermal wind balance-based gradient wind model (newly developed in this study). Although the employed hurricane track model includes genesis, translation, and intensity simulations, the climate change effects on the former two parts are insignificant and hence not considered here (e.g., Rosowsky et al., 2016). A total of 10,000 years of full-track synthetic hurricanes are generated for both historical and future climate scenarios. Along each track, the surface wind speed and rain rate are efficiently obtained every six hours based on the height-resolving analytical wind model (Snaiki and Wu, 2017a, b) and the physics-based analytical rainfall model (Snaiki and Wu, 2018), respectively.

Simulation Results

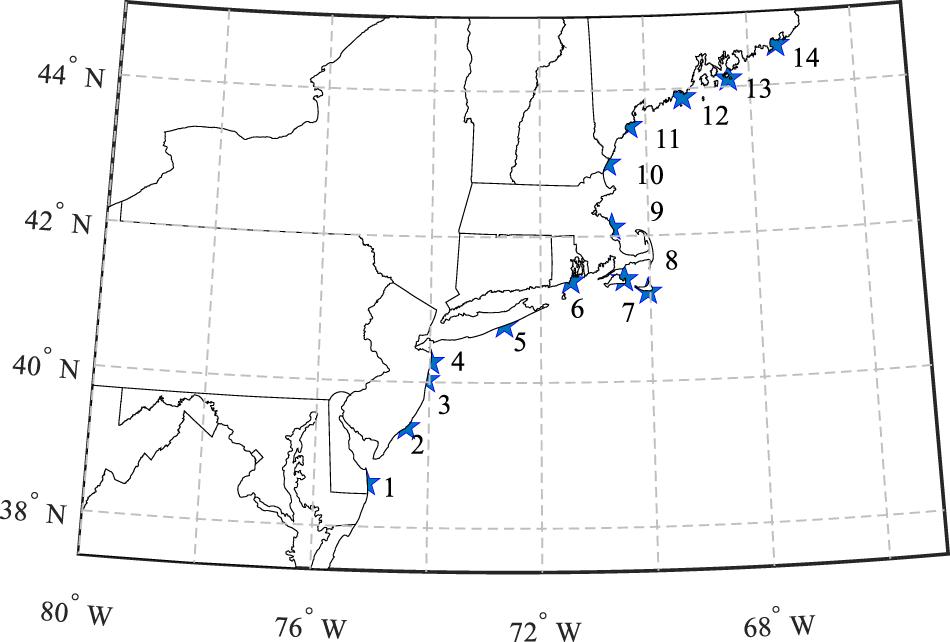
A database of synthetic hurricanes was developed in this study corresponding to 10,000-year simulations for the observed and future climate scenarios (under RCP 8.5). Fourteen mileposts along the coastline of the selected region were chosen as illustrated in Figure 4 to study the effects of the changing climate on the hurricane surface wind and rain hazards.

FIGURE 4

Figure 4. Mileposts along the coastline of the selected study region.

For hurricane hazard assessment, the wind speed and rain rate were evaluated based on the MRI expressed as:

$MRI(x_i>X)=\frac{1}{\mathrm{\gamma }P(x_i>X)}(13)$

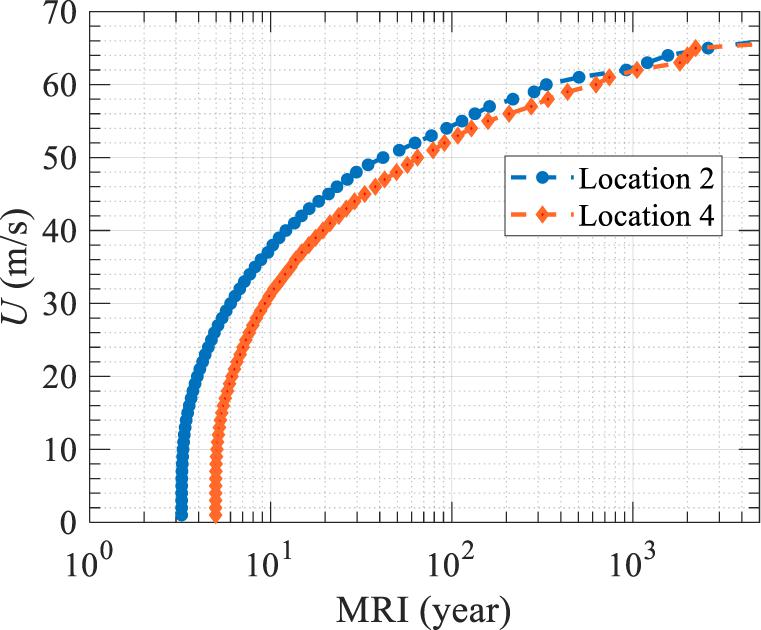
where X represents either surface wind speed or rainfall rate; P(x_i > X) = prrobability that x_i is larger than a given threshold X; and γ= mean annual occurrence rate of the hurricanes at the selected site. For illustration purposes, the MRI distribution of the surface wind speeds under RCP 8.5 climate scenario at locations 2 and 4 in Figure 4 were constructed and are depicted using a logarithmic scale in Figure 5.

FIGURE 5

Figure 5. MRI distribution of wind speeds under RCP 8.5 climate scenario.

The MRI distribution of wind speeds at locations 2 and 4 under the RCP 8.5 climate were further compared to those under the current climate for seven MRIs (i.e., 25, 50, 100, 300, 700, 1700, and 3000 years), as illustrated in Figure 6. It is noted that the simulation results of current climate were very close to the corresponding design wind speeds provided by ASCE 7-16, indicating an accurate implementation of the developed simulation procedure in Figure 3. More detailed description and validation of the used hurricane hazard assessment framework are discussed in Snaiki and Wu (2020). The low MRIs (e.g., 10 years) are not covered for this study region since the corresponding wind speed are mainly governed by the extratropical cyclones (i.e., Nor’easters). As it can be concluded from Figure 6, higher design wind speeds should be expected based on the RCP 8.5 climate scenario for both locations. For example, the current wind speed for a 50-year MRI is approximately equal to 42 m/s while it is projected to reach 50 m/s (with an increase of approximately 14%) at location 4. Furthermore, it is shown that the present 100-year wind speed may occur every 30 years or less based on the simulation results of the future climate scenario. The simulation results for all fourteen locations are presented in Figure 7, where the wind speeds for all levels of MRIs are projected to increase. It should be noted that these risk simulation findings under the RCP 8.5 climate scenario heavily depend on the global climate model used to generate the environmental parameters (Lin and Chavas, 2012).

FIGURE 6

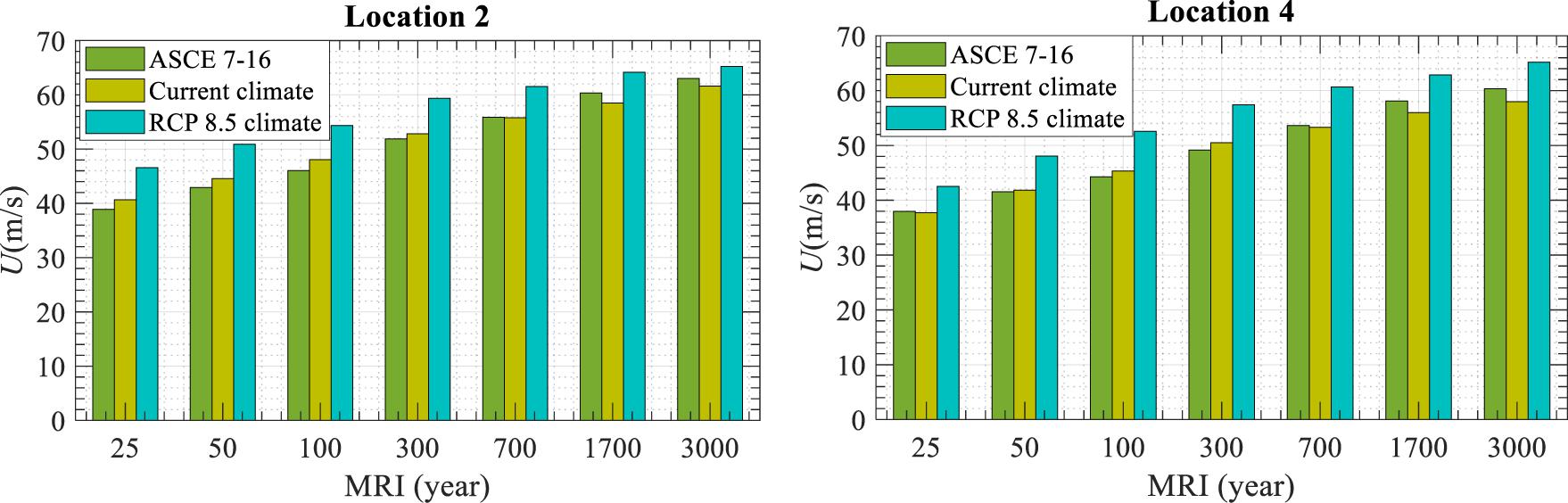
Figure 6. Comparison of the current and projected (under RCP 8.5 climate scenario) design wind speeds at two locations.

FIGURE 7

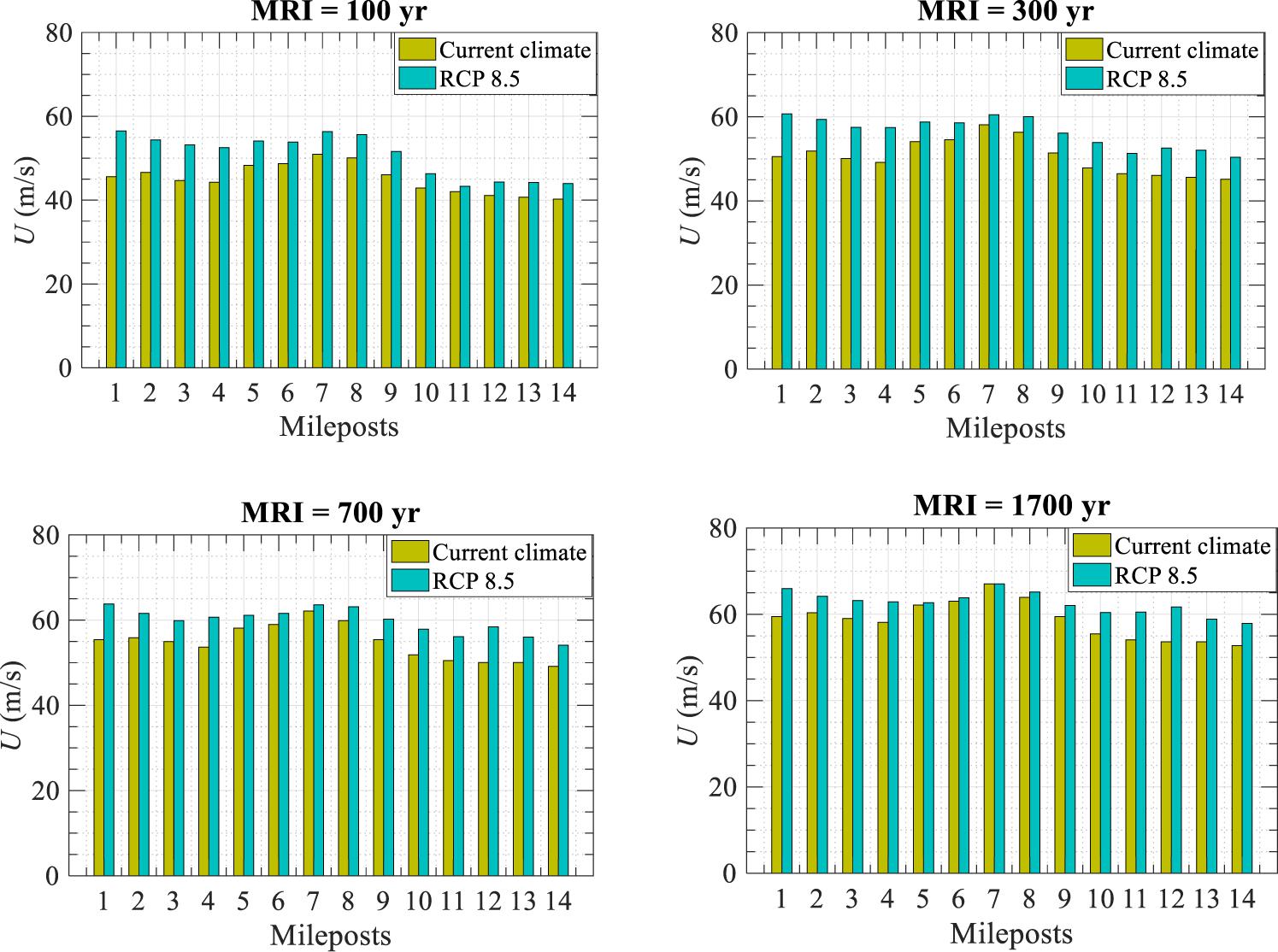
Figure 7. Comparison of the current and projected (under RCP 8.5 climate scenario) design wind speeds at various MRIs.

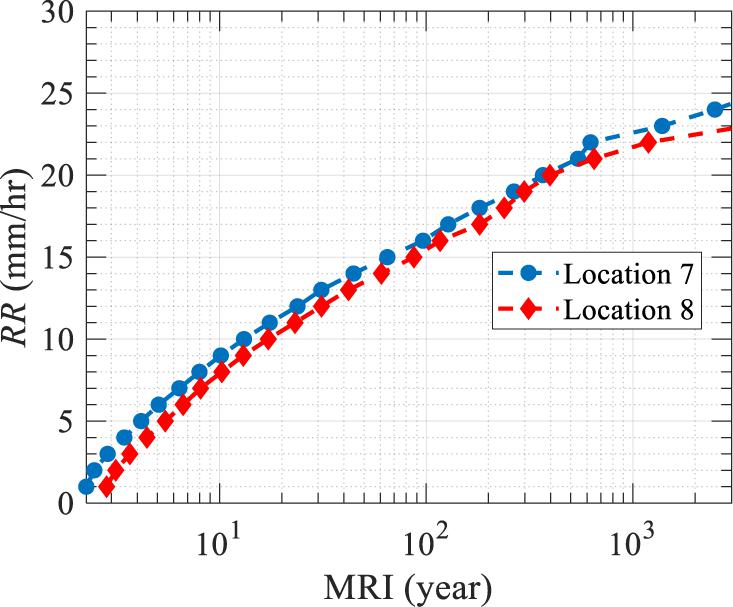
A similar approach in terms of the MRI distribution was adopted for the assessment of surface rain rates. For example, the simulation results corresponding to locations 7 and 8 are plotted in Figure 8 using a logarithmic scale. A rain rate of 16.14 mm/h is expected for the 50-year MRI at location 7, while it is approximately 15.49 mm/h at location 8 under the RCP 8.5 climate scenario. The comparison of simulated rain rate results between the current and projected climate scenarios is depicted in Figure 9. As indicated in Figure 9, the rain rates at all levels of MRIs are projected to increase following the RCP 8.5 climate scenario. For example, the current rain rate for a 100-year MRI is expected to increase by 27% from 12.63 to 16.13 mm/h at location 7. Similarly, an increase of 27% in the rain rate (from 12.15 to15.5 mm/h) for the 100-year MRI is also observed at location 8.

FIGURE 8

Figure 8. MRI distribution of rain rates at Points 7 and 8 based on the RCP 8.5 climate scenario.

FIGURE 9

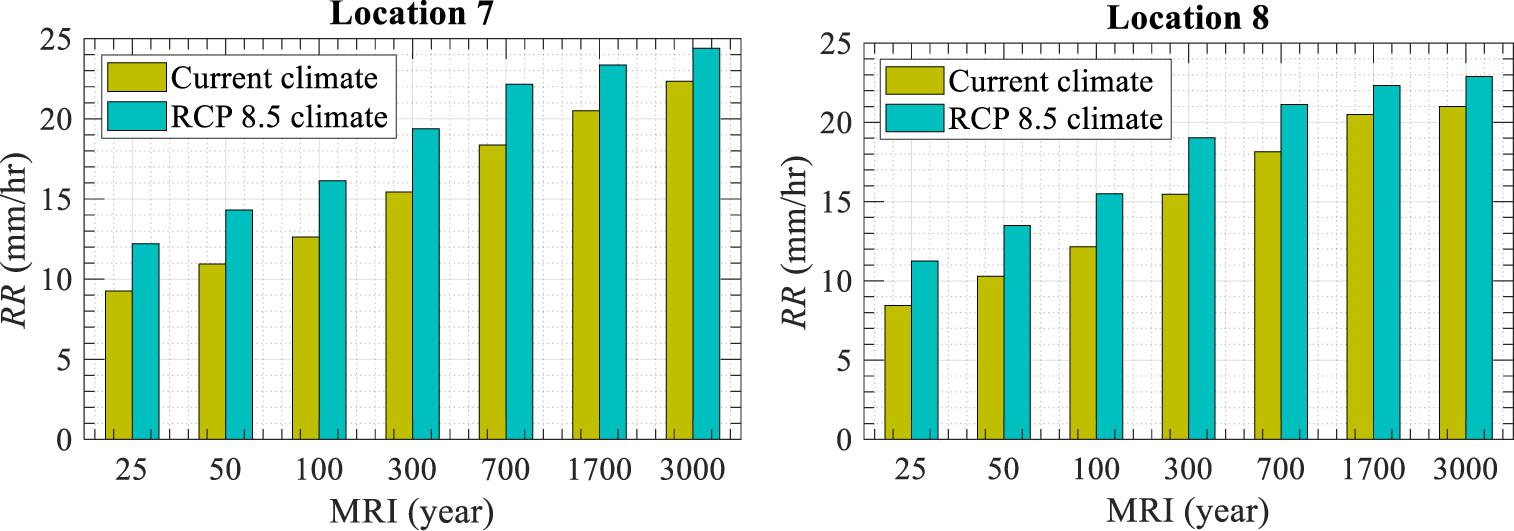
Figure 9. Comparison of the current and expected (under RCP 8.5 scenario) rain rate values at Points 7 and 8.

Concluding Remarks

In this study, an advanced hurricane hazard assessment methodology was developed to investigate the changing climate effects on hurricane surface wind and rainfall hazards. It essentially consisted of three simulation components, namely an enhanced hurricane track model to generate synthesized storms [including a physics-based intensity model integrating SST, wind shear (V_s) and convective instability (C) contributions], a newly developed thermal wind balance-based model to simulate the gradient wind profiles (explicitly considering environmental conditions of SST, temperature at the top of the atmospheric boundary layer T_TBL, and outflow temperature T₀) and a height-resolving boundary-layer model to obtain the surface wind and rain fields (reducing inherent uncertainties associated with conventionally used gradient-to-surface wind speed conversion factors). The newly developed gradient wind model based on the thermal wind balance presented good simulation results compared to the state-of-the-art gradient wind profiles. In addition, it was shown that the consideration of environmental conditions (i.e., SST, T_TBL, and T₀) in the gradient wind model not only changed the spatial distribution of the wind profiles, but also modified the maximum wind speed. A systematical comparison of the simulation results between the historical climate scenario (1991–2010) and future climate scenario (2081–2100) subjected to the RCP 8.5 was carried out for the northeast United States coastline. A total of 10,000 years of hurricane events were generated for both historical and projected climate conditions. Hurricane surface wind speed and rain rate were characterized in terms of the MRI. In general, higher hurricane surface wind speeds and rain rates were obtained for all levels of MRIs with changing climate based on the selected global climate model. For example, the wind speed corresponding to a 50-year MRI was projected under the RCP 8.5 climate scenario to increase by approximately 14% at location 4 in the studied region and an increase of 27% in the rain rate corresponding to a 100-year MRI was projected at location 8. The obtained simulation results indicate that hurricane surface wind and rain risk mitigation and adaption for civil infrastructures in coastal regions are necessary in light of a changing climate scenario.

Data Availability Statement

The historical dataset (HURDAT2) is maintained by the National Hurricane Center and available at https://oasishub.co/dataset/hurdat-2-atlantic-hurricane-database. The future climate conditions are based on the representative concentration pathways (RCP) scenarios of the IPCC fifth assessment report and the global model output data from NOAA’s Geophysical Fluid Dynamics Laboratory Earth System Model Version 2G (GFDL-ESM2G) are publically available at https://www.gfdl.noaa.gov/ipcc-ar5-models/.

Author Contributions

All authors contributed to the study conception and design, data collection, analysis and interpretation of results, drafted manuscript preparation, reviewed the results, and approved the final version of the manuscript.

Funding

This work was funded by NSF Grant # CMMI 15-37431.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors greatly acknowledge the support provided by the Institute of Bridge Engineering (IBE) at the University at Buffalo.

References

Contento, A., Xu, H., and Gardoni, P. (2018). “A physics-based transportable probabilistic model for climate change dependent storm surge,” in Routledge Handbook of Sustainable and Resilient Infrastructure, ed. P. Gardoni (Abingdon: Routledge), 662–682. doi: 10.4324/9781315142074-34

CrossRef Full Text | Google Scholar

Contento, A., Xu, H., and Gardoni, P. (2019). Risk Analysis for Hurricanes Accounting for the Effects of Climate Change. In Climate Adaptation Engineering, eds E. Bastidas-Arteaga and M. Stewart (Oxford: Butterworth-Heinemann), 39–72. doi: 10.1016/b978-0-12-816782-3.00002-4

CrossRef Full Text | Google Scholar

Cui, W., and Caracoglia, L. (2016). Exploring hurricane wind speed along US Atlantic coast in warming climate and effects on predictions of structural damage and intervention costs. Engin. Struct. 122, 209–225. doi: 10.1016/j.engstruct.2016.05.003

CrossRef Full Text | Google Scholar

Emanuel, K. (2012). Self-stratification of tropical cyclone outflow. Part II: Implications for storm intensification. J. Atmospher. Sci. 69, 988–996. doi: 10.1175/jas-d-11-0177.1

CrossRef Full Text | Google Scholar

Emanuel, K. A. (1986). An air-sea interaction theory for tropical cyclones. Part I: steady-state maintenance. J. Atmospher. Sci. 43, 585–605. doi: 10.1175/1520-0469(1986)043<0585:aasitf>2.0.co;2

CrossRef Full Text | Google Scholar

Emanuel, K. A. (1991). The theory of hurricanes. Annu. Rev. Fluid Mech. 23, 179–196. doi: 10.1146/annurev.fl.23.010191.001143

CrossRef Full Text | Google Scholar

Emanuel, K. A. (2004). Tropical cyclone energetics and structure. Atmospher. Turbul. Mesoscale Meteorol. 8, 165–191. doi: 10.1017/cbo9780511735035.010

CrossRef Full Text | Google Scholar

Emanuel, K. A. (2013). Downscaling CMIP5 climate models shows increased tropical cyclone activity over the 21st century. Proc. Natl. Acad. Sci. 110, 12219–12224. doi: 10.1073/pnas.1301293110

PubMed Abstract | CrossRef Full Text | Google Scholar

Emanuel, K., Ravela, S., Vivant, E., and Risi, C. (2006). A statistical deterministic approach to hurricane risk assessment. Bull. Am. Meteorol. Soc. 87, 299–314. doi: 10.1175/bams-87-3-299

CrossRef Full Text | Google Scholar

Holland, G. J. (1980). An analytic model of the wind and pressure profiles in hurricanes. Mon. Weather Rev. 108, 1212–1218. doi: 10.1175/1520-0493(1980)108<1212:aamotw>2.0.co;2

CrossRef Full Text | Google Scholar

Jelesnianski, C. P., Chen, J., and Shaffer, W. A. (1992). SLOSH: Sea, Lake, and Overland Surges from Hurricanes. Silver Spring: National Weather Service.

Google Scholar

Knutson, T. R., McBride, J. L., Chan, J., Emanuel, K., Holland, G., Landsea, C., et al. (2010). Tropical cyclones and climate change. Nat. Geosci. 3, 157–163.

Google Scholar

Lin, N., and Chavas, D. (2012). On hurricane parametric wind and applications in storm surge modeling. J. Geophys. Res. Atmos. 117:9120.

Google Scholar

Lin, N., Emanuel, K., Oppenheimer, M., and Vanmarcke, E. (2012). Physically based assessment of hurricane surge threat under climate change. Nat. Clim. Change 2, 462–467. doi: 10.1038/nclimate1389

CrossRef Full Text | Google Scholar

Liu, F., and Pang, W. (2013). “Influence of climate change on future hurricane wind hazards along the US eastern coast and the Gulf of Mexico,” in ATC & SEI Conference on Advances in Hurricane Engineering 2012, (Reston: ASCE), 573–584.

Google Scholar

Lonfat, M., Rogers, R., Marchok, T., and Marks, F. D.Jr. (2007). A parametric model for predicting hurricane rainfall. Mon. Weather Rev. 135, 3086–3097. doi: 10.1175/mwr3433.1

CrossRef Full Text | Google Scholar

Marsooli, R., Lin, N., Emanuel, K., and Feng, K. (2019). Climate change exacerbates hurricane flood hazards along US Atlantic and Gulf Coasts in spatially varying patterns. Nat. Commun. 10, 1–9.

Google Scholar

Mudd, L., Rosowsky, D., Letchford, C., and Lombardo, F. (2016). Joint Probabilistic Wind–Rainfall Model for Tropical Cyclone Hazard Characterization. J. Struct. Eng. 143:04016195. doi: 10.1061/(asce)st.1943-541x.0001685

CrossRef Full Text | Google Scholar

Mudd, L., Wang, Y., Letchford, C., and Rosowsky, D. (2014). Assessing climate change impact on the US East Coast hurricane hazard: temperature, frequency, and track. Nat. Hazards Rev. 15:04014001. doi: 10.1061/(asce)nh.1527-6996.0000128

CrossRef Full Text | Google Scholar

Phadke, A. C., Martino, C. D., Cheung, K. F., and Houston, S. H. (2003). Modeling of tropical cyclone winds and waves for emergency management. Ocean Eng. 30, 553–578. doi: 10.1016/s0029-8018(02)00033-1

CrossRef Full Text | Google Scholar

Powell, M., Soukup, G., Cocke, S., Gulati, S., Morisseau-Leroy, N., Hamid, S., et al. (2005). State of Florida hurricane loss projection model: Atmospheric science component. J. Wind Eng. Indust. Aerodynamics 93, 651–674. doi: 10.1016/j.jweia.2005.05.008

CrossRef Full Text | Google Scholar

Riehl, H. (1963). Some relations between wind and thermal structure of steady state hurricanes. J. Atmospher. Sci. 20, 276–287. doi: 10.1175/1520-0469(1963)020<0276:srbwat>2.0.co;2

CrossRef Full Text | Google Scholar

Rosowsky, D. V. (2018). “Assessing climate change impacts on hurricane hazards,” in Climate Change and Its Impacts, eds C. Murphy, P. Gardoni, and R. McKim (New York, NY: Springer), 93–107. doi: 10.1007/978-3-319-77544-9_6

CrossRef Full Text | Google Scholar

Rosowsky, D. V., Mudd, L., and Letchford, C. (2016). “Assessing climate change impact on the joint wind-rain hurricane hazard for the northeastern US coastline,” in Risk Analysis of Natural Hazards, eds P. Gardoni, C. Murphy, and A. Rowell (New York, NY: Springer), 113–134. doi: 10.1007/978-3-319-22126-7_8

CrossRef Full Text | Google Scholar

Ruiz-Salcines, P., Salles, P., Robles-Díaz, L., Díaz-Hernández, G., Torres-Freyermuth, A., and Appendini, C. M. (2019). On the Use of Parametric Wind Models for Wind Wave Modeling under Tropical Cyclones. Water 11:2044. doi: 10.3390/w11102044

CrossRef Full Text | Google Scholar

Schloemer, R. W. (1954). Analysis and synthesis of hurricane wind patterns over Lake Okeechobee, Florida. Washington, D.C: U.S. Weather Bureau.

Google Scholar

Snaiki, R., and Wu, T. (2017a). A linear height-resolving wind field model for tropical cyclone boundary layer. J. Wind Engin. Indust. Aerodynamics 171, 248–260. doi: 10.1016/j.jweia.2017.10.008

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2017b). Modeling tropical cyclone boundary layer: Height-resolving pressure and wind fields. J. Wind Engin. Indust. Aerodynamics 170, 18–27. doi: 10.1016/j.jweia.2017.08.005

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2018). An analytical framework for rapid estimate of rain rate during tropical cyclones. J. Wind Engin. Indust. Aerodynamics 174, 50–60. doi: 10.1016/j.jweia.2017.12.014

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2020). Revisiting Hurricane Track Model for Wind Risk Assessment. Struct. Safety 87:102003. doi: 10.1016/j.strusafe.2020.102003

CrossRef Full Text | Google Scholar

Snaiki, R., Wu, T., Whittaker, A. S., and Atkinson, J. F. (2020). Hurricane Wind and Storm Surge Effects on Coastal Bridges under a Changing Climate. Transport. Res. Rec. 2674, 23–32. doi: 10.1177/0361198120917671

CrossRef Full Text | Google Scholar

Stocker T. (ed.) (2014). Climate Change 2013: The Physical Science Basis. Cambridge: Cambridge University Press.

Google Scholar

Tuleya, R. E., DeMaria, M., and Kuligowski, R. J. (2007). Evaluation of GFDL and simple statistical model rainfall forecasts for US landfalling tropical storms. Weather Forecasting 22, 56–70. doi: 10.1175/waf972.1

CrossRef Full Text | Google Scholar

Vickery, P. J., Skerlj, P. F., and Twisdale, L. A. (2000). Simulation of hurricane risk in the US using empirical track model. J. Struct. Engin. 126, 1222–1237. doi: 10.1061/(asce)0733-9445(2000)126:10(1222)

CrossRef Full Text | Google Scholar

Wang, S., Toumi, R., Czaja, A., and Kan, A. V. (2015). An analytic model of tropical cyclone wind profiles. Quart. J. R. Meteorol. Soc. 141, 3018–3029. doi: 10.1002/qj.2586

CrossRef Full Text | Google Scholar

Willoughby, H. E., Darling, R. W. R., and Rahn, M. E. (2006). Parametric representation of the primary hurricane vortex. Part II: A new family of sectionally continuous profiles. Mon. Weather Rev. 134, 1102–1120. doi: 10.1175/mwr3106.1

CrossRef Full Text | Google Scholar